Isolated spin polarized hydrogen atoms as targets for laser-induced polarized electron acceleration

High density Spin Polarized Hydrogen (SPH) atoms, which can be prepared using UV dissociation of hydro-halide molecules, can be attractive as potential targets for laser ionization/acceleration schemes aiming to create high energy and high current polarized electron beams. However, for these SPH targets to be of practical use, they have to be spatially isolated from the halide atoms which accompany hydrogen in the parent hydro-halide molecule. We show how the UV dissociation dynamics of hydro-halides and the dissociation geometry and timing can be combined to prepare a variety of isolated SPH targets aimed to accommodate laser acceleration schemes.

1 Introduction

The preparation of high-energy and high-brightness polarized electron beams can offer advantages to various scientific fields, and in particular to high-energy and nuclear physics [1–3]. Among the various preparation methods, laser acceleration of pre-polarized targets, and in particular Spin-Polarized Hydrogen (SPH) atoms, is an attractive option. However, this method requires targets with densities in excess of $10^{16}$ ${\text{cm}}^{-3}$ to be practical.

Conventional methods for preparing gas-phase SPH atoms are the Stern-Gerlach spin separation of an H-atom beam [4], and spin-exchange optical pumping [5], however these methods are limited to SPH densities of about $10^{12}$-$10^{13}$ ${\text{cm}}^{-3}$. In contrast, the UV dissociation of various hydrohalide atoms has been shown to be able to produce SPH atoms in record densities (up to ${10}^{21}$ ${\text{cm}}^{-3}$) [6–8], and thus be the only SPH source of sufficient density for laser acceleration. Recently, various proposals have been made using this SPH source as a pre-polarized target for laser acceleration experiments [9–14].

Spin polarization in an atomic system results from the orientation of valence electrons, since any electrons participating into closed shells have zero total spin and cannot be polarized. Thus, heavy atoms, with most electrons in closed shells, are not appropriate as pre-polarized targets as the large intensities required for sufficient acceleration will inevitably lead to the ionization of most (if not all) of the unpolarized closed-shell electrons, thus reducing the overall polarization of the resulting electron beam. In contrast, SPH atoms are ideal as prepolarized targets, as SPH atoms have only one (polarized) electron.

However, the photodissociation of hydrogen halides produces SPH and halide atoms, in equal quantity, and the halide atoms provide unwanted unpolarized core electrons. Therefore, special care has to be given to spatially isolating the SPH from the halide atoms. The aim of this paper is to show that this can be achieved by choosing the timing and the geometric characteristics of two consecutive dissociation pulses. Moreover, we show how this spatial isolation can lead to further polarization selection that produces spin polarization values which are much greater than the free-space values.

We present the modeling of the SPH isolation method in Section 2, and in Section 3 we investigate the preparation of two targets. Since the overall electron polarization is controlled by the hyperfine interaction, we choose to investigating the preparation of spin polarized targets with a diameter of 4.5 $\mu$m, and 10 $\mu$m, for which the loading time corresponds to the one and two hyperfine oscillation periods.

2 Model

2.1 Dissociation fundamentals

The UV dissociation with circularly polarized light of some common hydro-halide molecules HX, such as HCl and HBr, follows the reaction:

$HX\to H\left({}^{2}S_{1/2}\right)+X\left({}^{2}P_J\right)(1)$

with $J=3/2$ corresponding to the ground and $J=1/2$ to the excited spin-orbit state of the halide atom. Despite the presence of multiple dissociation channels, which can in general produce different dissociation recoil distributions, often dissociation proceeds mainly through a perpendicular transition and results in a simple distribution of recoil velocity and spin polarization along the z-axis [6, 8, 15, 16]:

$I\left(\theta \right)=N\left(1+{\beta }_2{P}_2\left(cos\theta \right)\right)(2)$

$P\left(\theta \right)=co{s}^2\theta (3)$

with $I(\theta )$ being the SPH recoil distribution and $P(\theta )$ the spin polarization, $P_2(x)$ is the second order Legendre polynomial and ${\beta }_2$ an experimentally determined parameter, whose values lies close to 0.5 for both HCl and HBr [15], $N$ is a normalization factor, and $\theta$ = 0 is defined by the propagation direction of the circularly polarized photodissociation laser. The ns laser dissociation process results in narrow velocity distributions while the mean speed of the atomic fragments can easily be derived using energy and momentum conservation.

In Figure 1A we show the speeds and angles associated with UV dissociation and how these can be used to create isolated SPH samples. A first Dissociation Pulse (PD1) dissociates molecules in the vicinity of its focus. The velocity acquired by the fragments leads to them exiting the volume around the focus, hereby referred to as “hole”. A second Dissociation Pulse (PD2), with larger dimensions, dissociates molecules in a volume around the hole, hereby referred to as “reservoir”. The large difference between the Hydrogen and the Halogen atom speeds means that there are times in which only H atoms will have filled the hole volume. Using circularly polarized light for PD2 and well selected dimensions for the hole and reservoir allows the accumulation of highly-polarized, high density SPH atoms in the volume of the hole.

Figure 1

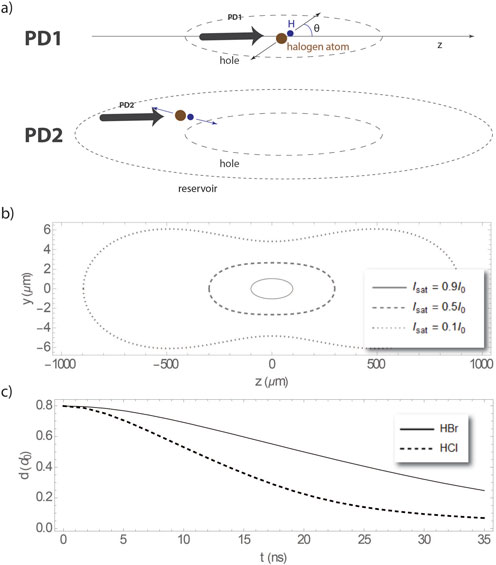
Figure 1. (A) Sequence of UV pulses PD1 (up) and PD2 (down) to create the “hole” and “reservoir”. (B) Limits of Gaussian beams when $I(y,z)=I_{\mathit{sat}}$ (C) Density inside the hole as a function of time after firing the dissociation laser pulse PD1 for $w_0$ = 4.5 $\mu$m and $I(y,z)$ = (0.55)$I_{\mathit{sat}}$.

2.2 Emptying the hole

Creating a hole devoid of atoms inside a gas-phase sample after dissociation is only viable if the (random) thermal velocities of the parent molecules are small compared to the recoil velocities of the molecular photofragments produced in the hole. In a molecular beam, the molecules can move with speeds of hundreds of meters per second, however, their thermal motion in the molecular rest frame can be cooled down to the 0.1–10 K range [17, 18]. For example, the average thermal speed of HCl molecules at 3 K (46 m/s) is much smaller than the recoil speeds of the H and Cl photofragments from photodissociation at 213 nm.

We now consider the geometry of the focused laser pulses, needed to create the hole and reservoir. The intensity distribution of a laser pulse follows Gaussian optics:

$I\left(r,z\right)=I_0\frac{w_0^2}{w{\left(z\right)}^2}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-2r^2}{w{\left(z\right)}^2}\right)(4)$

with $r^2=x^2+y^2$, and $w(z)=w_0\sqrt{1+{\left(\frac{z}{z_R}\right)}^2}$ the focus radius with $w_0$ minimum focus radius and $z_R=\frac{\pi w_0^{2}n}{\lambda }$ the Rayleigh length, $n$ the sample refraction index and $\lambda$ the laser wavelength. It is possible to engineer lasers beams with geometrical characteristics which deviate from these Gaussian beams; we will see some examples in Section 3.

When illuminating a molecular beam with UV laser light, molecular photodissociation can be initiated with a probability which depends on ${\sigma }_d$ the dissociation cross section. As a rule of thump, this probability approaches unity when $P_{cd}{\sigma }_d\approx$ 2, with $P_{cd}$ being the photon column density of the dissociating pulse. Let us denote as $I_{\mathit{sat}}$ the intensity when this condition is met. Since the laser focus is a function of z (the distance in the laser propagation direction), the condition $I(x,y,z)=I_{\mathit{sat}}$ can be satisfied for various values, as long as $I_{\mathit{sat}}<I_0$. Since the dissociation laser intensity is an experimentally controlled variable, we can choose it so that $I_{\mathit{sat}}/I_0=R$, which will result in a specific geometry for the hole: in Figure 1B, we see a two-dimensional cut of the volume which results from this condition when $R$ is chosen to be 0.1, 0.5 and 0.9. We see that for choices of $R>0.5$, the resulting shape is relatively simple and can be approximated by an ellipsoid. From now on, we will assume an ellipsoidal shape for our hole to simplify our demonstrations, however, any three-dimensional continuous shape can be easily simulated.

A realistic geometry should include gradual descending borders, since the probability for dissociation is non-zero for intensities lower, yet close to $I_{\mathit{sat}}$. We can use a generic sigmoidal function $S(r_{,}{r}_0,\mathrm{\Delta }r)=\frac{1}{1+Exp\left(\frac{r-r_0}{\mathrm{\Delta }r}\right)}$ to simulate the geometry of such a hole $H(x,y,z)$ as follows:

$H\left(\widehat{r}\right)=H\left(x,y,z\right)=S\left(\sqrt{x^2+y^2},r_{\mathit{sat}}\left(z\right),{\sigma }_{x,y}\right)(5)$

with ${\sigma }_{x,y}$ being an adjustable parameter to account for the finite width of the hole border (see Section 3). The point in space for which the condition $I=I_{\mathit{sat}}$ is met, has coordinates $x,y$ and $z$ which satisfy the condition:

$\sqrt{x^2+y^2}=r_{\mathit{sat}}\left(z\right)=\sqrt{\frac{w{\left(z\right)}^2}{2}\left(-ln\left(R\frac{w{\left(z\right)}^2}{w_0^2}\right)\right)}(6)$

If we choose a single recoil direction, characterized by $\theta$ and $\varphi$, the polar and the azimuthal angle respectively, its contribution to the time evolution of the destiny inside the hole will be (step 1: emptying the hole):

$d^{em}\left(\theta ,\varphi ,t\right)=\frac{d_0}{V_0}\int H\left(\widehat{r}\right)H\left(\widehat{r}-\vec{v}t\right)dV\left(\widehat{r}\right)(7)$

with $d_0$ being the initial density of the parent molecules, and $V_0$ the total volume of the hole, and $\vec{v}$ the velocity of the halogen atom (the H atoms move faster and leave the hole within much shorter timescales). The spatial integration is over the volume of the hole.

The total density inside the hole, as a function of time will be:

$d_{\mathit{tot}}^{em}\left(t\right)=\frac{1}{N_{\mathrm{\theta }}}{\int }_0^{\pi }{\int }_0^{2\pi }I\left(\theta \right)d^{em}\left(\theta ,\varphi ,t\right)sin\theta d\theta d\varphi (8)$

with $N_{\mathrm{\theta }}$ being the normalization factor $N_{\mathrm{\theta }}={\int }_0^{\pi }{\int }_0^{2\pi }I(\theta )sin\theta d\theta d\varphi$. In Figure 1C we see the density as a function of time for the dissociation of HBr (solid line) and HCl (dashed line) at 213 nm (hole dimensions visible in b).

2.3 Reloading isolation and polarization

The hole can be reloaded by illuminating a larger volume using a second laser pulse. We can define a “reservoir” function $R(x,y,z)$ (similar to $H(x,y,z)$), which describes the density of the molecules dissociated in the vicinity of the hole. The reservoir function $R$ can be approximated by:

$R\left(\widehat{r}\right)=R\left(x,y,z\right)=H\left(x/q,y/q,z/q\right)-H\left(x,y,z\right)(9)$

The density of the hydrogen atoms entering the hole as a function of time, for a given recoil direction is (step 2: reloading the hole):

$d^{\mathit{load}}\left(\theta ,\varphi ,t\right)=\frac{d_0}{V_0}\int H\left(\widehat{r}\right)R\left(\widehat{r}+{\vec{v}}_{H}t\right)dV\left(\widehat{r}\right)(10)$

with ${\vec{v}}_H$ being the recoil velocity of the hydrogen atoms. The total density inside the hole as a function of time will be:

$d_{\mathit{tot}}^{\mathit{load}}\left(t\right)=\frac{1}{N_{\mathrm{\theta }}}{\int }_0^{\pi }{\int }_0^{2\pi }I\left(\theta \right)d^{\mathit{load}}\left(\theta ,\varphi ,t\right)sin\theta d\theta d\varphi (11)$

The polarization of the hydrogen atoms depends on both their recoil direction and the time after dissociation. The temporal dependence results from the hyperfine interaction [7]:

$P_{HF}=\left(1-si{n}^2{\omega }_{HF}t/2\right)(12)$

with ${\omega }_{HF}=2\pi \left(1.42\right.$ × $10^9$) rad/s. We can separate these two dependencies: let’s call the total polarization as $P_{\mathit{tot}}=P_G{P}_{HF}$, the product of the hyperfine polarization and $P_G$, what we will refer to as “geometrical” polarization. The evolution of $P_G$ can be understood using a qualitative model, which makes use of the general integral:

$P_G=\frac{{\int }_{{\theta }_{\mathit{min}}}^{{\theta }_{\mathit{max}}}P\left(\theta \right)I\left(\theta \right)sin\theta d\theta }{{\int }_{{\theta }_{\mathit{min}}}^{{\theta }_{\mathit{max}}}I\left(\theta \right)sin\theta d\theta }(13)$

where ${\theta }_{\mathit{min}}$ and ${\theta }_{\mathit{max}}$ are the limiting angles for the integration $(0\le {\theta }_{\mathit{max}},{\theta }_{\mathit{min}}\le \pi )$. By setting ${\theta }_{\mathit{min}}$ = 0 and ${\theta }_{\mathit{max}}$ = $\pi$ for example, one easily obtains the free space value of 40%.

Numerically, the polarization inside the hole will be given by the similar formula:

$P_G^{\mathit{num}}=\frac{1}{N_{\mathrm{\theta }}{d}_{\mathit{tot}}^{\mathit{load}}\left(t\right)}{\int }_0^{\pi }{\int }_0^{2\pi }I\left(\theta \right)P\left(\theta \right)d^{\mathit{load}}\left(\theta ,\varphi ,t\right)d\theta d\varphi (14)$

In Figure 2A, we see the evolution of $P_G$ for three different geometries. The brown line corresponds to a hole shaped as a prolate ellipsoid, with axes a = b, c = 3a. The blue line corresponds to a spherical hole while the green line corresponds to a hole with the shape of an oblate ellipsoid (a = b, c = 0.5a). Choosing a spherical geometry for our hole (note that this is impossible to achieve experimentally using lasers), will result in $P_G$ equal to the free-space value of 40% (blue dashed line). In contrast, choosing an elliptical geometry (feasible with lasers) results in $P_G$ different from the free space value: a prolate geometry (orange dashed line) maximizes whereas an oblate geometry (green dashed line) minimizes $P_G$ as time increases.

Figure 2

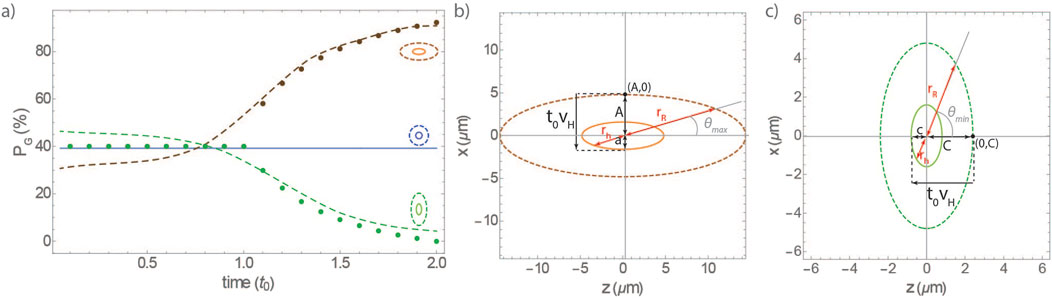
Figure 2. (A) Evolution of $P_G$ inside the hole, for three different geometries for the hole and reservoir, a prolate ellipsoid, an oblate ellipsoid and a sphere. Dashed lines: calculations using Equation 14. Points: results from Equation 13 (B) Integration angles for a given time for a prolate and (C) for an oblate ellipsoid, see text for details.

The brown and green points are values obtained for different choices for ${\theta }_{\mathit{min}}$ and ${\theta }_{\mathit{max}}$ in Equation 13. Let’s first discuss the case of a prolate ellipsoid considered in Figure 2B. The red ellipse is a slice of the hole, and the dashed brown a slice of the reservoir, in the xz plane. “a” and “A” are either of the small axes of the hole and reservoir ellipsoids. Consider the first quadrant; the complete results can be obtained by reflecting the resulting angles over the x and z-axes respectively. In the x direction, the last atoms will exit the ellipse at time $t=t_0=\frac{a+A}{v_H}$. After this time, no atoms will be present in the trap coming from this direction, thus their polarization will no longer contribute to the overall geometric polarization inside the hole. In this direction ($\theta$ = $\pi$/2), the polarization is zero (since P$(\theta )$ = ${\text{cos}}^2\theta$), thus, the overall $P_G$ inside the hole will increase (at the cost of reduced density). At a later time t, more atoms found in the outer limits of the reservoir will be exiting the hole, and in particular those for which ${\text{r}}_h+{\text{r}}_R$ = t$v_H$. Using simple geometry, one can deduce a limiting value for ${\theta }_{\mathit{max}}$ used in the integration of Equation 13 (${\theta }_{\mathit{min}}$ = 0) as a function of time, from which one can obtain the brown points in Figure 2A.

The situation is similar in the case of an oblate ellipsoidal geometry shown in Figure 2C. The light green ellipse is a slice of the hole and the dashed dark green ellipse a slice of the reservoir, in the xz plane. Here, the first atoms leaving the hole are moving in the z direction. Thus, at later times, a similar integration angle can be found as a function of time, however, now it will be the angle ${\theta }_{\mathit{min}}$ of Equation 13 (${\theta }_{\mathit{max}}$ = $\pi /2$), which results in the green points of Figure 2A.

3 Results

3.1 Isolation density and polarization

We apply this model for some characteristic geometries for the dissociation pulses. We will compare holes created using a $w_0$ = 4.5 and 10 $\mu$m spotsize lasers. In Figure 3A we plot the density inside the hole as a function of time after firing PD2 for $w_0$ = 4.5 $\mu$m spotsize (gray line) and a $w_0$ = 10 $\mu$m spotsize (black line) and R = 0.55. We see that the overall dynamics are faster for the smaller hole, which is to be expected. In Figure 3B we see the geometric polarization $P_G$ and in Figure 3C the total polarization as a function of time after firing PD2; we see that the hyperfine polarization evolution allows reaching high values for the total polarization in times that are integer multiples of the hyperfine period. This means that when a $\sim 10mu$m hole is considered, very low values of polarization can be achieved within the first hyperfine oscillation period, in contrast to the case of the smaller $\sim 4.5\mu$m hole.

Figure 3

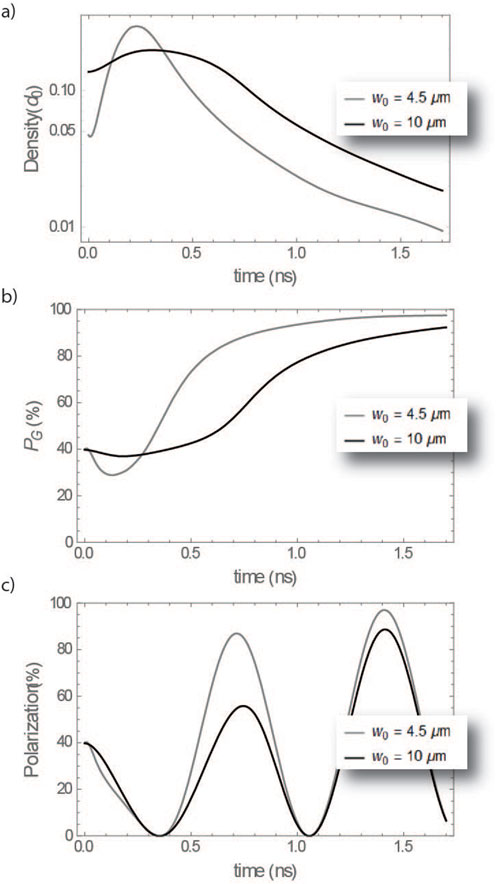
Figure 3. (A) Density inside the hole as a function of time after firing PD2 for $w_0$ = 4.5 $\mu$m spotsize (gray line) and a $w_0$ = 10 $\mu$m spotsize (black line) and R = 0.55. Geometrical polarization (B) and total polarization (C) inside the hole for the same conditions.

4 Discussion

The exact shape of the UV dissociation pulses, beyond just the spotsize, can impact these dynamics, allowing for faster loading and polarization in some circumstances. To demonstrate this, we will compare the results obtained using a Gaussian pulse with $w_0$ = 4.5 $\mu$m, with the results obtained when considering a shaped “top-hat” pulse of similar dimensions. By modulating the spatial spectrum of a Bessel beam [19], we can engineer its intensity profile, achieving a top-hat like distribution along the propagation direction, and a very narrow, Bessel-like distribution in the transverse direction. The intensity of PD1, which creates the hole, is chosen so that it surpasses a threshold intensity $I_{th}$, above which the photodissociation probability becomes one, for 2 $\mu$m in the x and y directions. This condition leads us to a pulse spatial distribution shown in Figure 4A for the x/y directions and b for the z direction.

Figure 4

Figure 4. (A) Photodissociation probability and pulse intensity along the x/y direction, for a shaped and a Gaussian pulse. (B) Photodissociation probability and pulse intensity along the z direction, for a shaped and a Gaussian pulse.

In Figure 5 we present the results obtained using a Gaussian and a top-hat pulse such as the ones shown in Figure 4. We see that the dynamics are accelerated when a top-hat pulse is used, both in density shown Figure 5A and total polarization shown in Figure 5B. However, we see that, as far as total polarization is considered, while in the first hyperfine oscillation period the improvement is important (close to 10%) it is negligible at later times.

Figure 5

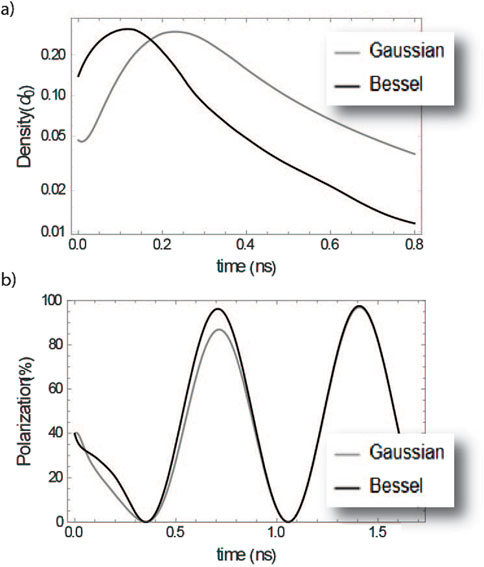
Figure 5. (A) Density inside the hole as a function of time after firing PD2, for a shaped and a Gaussian pulse and (B) total polarization.

We demonstrated here that it is possible to isolate SPH atoms, in high polarization and density, for a variety of geometries. Different sizes for the isolated sample, of course, affect the dynamics and ultimately the time on which a highly polarized sample can be prepared. On the one hand, large size targets will increase the overall charge in the polarized electron beam created after laser ionization/acceleration of such a sample. On the other hand, larger samples require longer preparation times, which might become comparable to the mean free time for collisions. It is clear that our model does not take into account collisions, and while depolarization collisions are only important in higher densities [20], close to $10^{20}$ ${\text{cm}}^{-3}$, much higher than those considered here, any collision capable of altering the trajectory of the H atom recoil (upon dissociation with PD2) will lead to deviations from the results of our model.

Let’s consider the effect of elastic non-depolarizing collisions. For example, the unpolarized H-H elastic collision cross section around 1 eV is on the order of 100 a.u. [21], whereas the triplet contribution to the cross section is somehow smaller [22], and highly spin-polarized hydrogen collisions will be dominated by triplet collisions. Such values for the total collision cross section lead to a collision mean free path of several microns and a collision free time comparable to the hyperfine period, for a density of about ${5\text{x}10}^{17}$ ${\text{cm}}^{-3}$. This means that a $w_0\approx$ 4 $\mu$m hole, practically will not be affected by collisions. Conventional wisdom would suggest that if the loading time is comparable to or exceeds the collision mean free time, then the model results will deviate from those of an actual experiment to an important extend. However, in many cases, even if the loading time exceeds the collision mean free time, the vast majority of atoms have already entered the hole much earlier. Upon entrance the hole area, the density is more than ten times smaller at all times, meaning that most SPH atoms entering the hole will not experience collisions (see Figure 6). Eventually, the maximum operating density will depend strongly on the differential elastic collision cross section, rendering its determination unfeasible without experimental investigations.

Figure 6

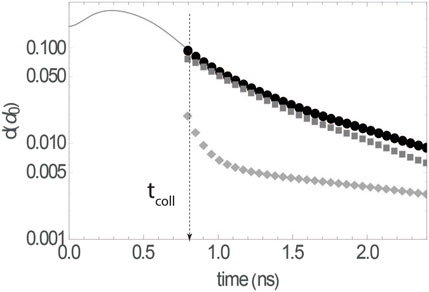
Figure 6. (A) Density inside the hole as a function of time after firing PD2, for a 10 $\mu$m Gaussian pulse (solid line). Gray squares: Density of atoms which enter the hole before $t_{\mathit{coll}}$ Gray rhombs: Density of atoms which enter the hole before $t_{\mathit{coll}}$ Black dots: Sum of the density shown with green and orange dots.

5 Conclusion

We have shown how two consecutive, UV photodissociation pulses with controlled dimensions and synchronization, can be used to create highly polarized SPH atom samples suitable for the creation of polarized high energy electron beams with laser acceleration. We have chosen to demonstrate the method in two limiting cases as far as the dimensions of the final sample are concerned, which approximates an ellipsoid with a diameter of 4.5 and 10 $\mu$m respectively. As discussed before, if the dimensions of the hole increase, so does the loading time, which eventually becomes comparable to the collision mean free time of the molecular gas in the temperature of the molecular beam and our simple model cannot be accurate.

Despite the fact that depolarizing collisions are not important in the densities and time-scales discussed here, the fact that any collision can alter the recoil direction of the colliding atoms means that their polarization in the hole has to be calculated again. Our model can be extended to account for a small number of collisions and we plan to do that in future work. If we limit the loading time to be comparable to the collision mean free time, SPH densities on the order of ${10}^{17}$ ${\text{cm}}^{-3}$ or more can be foreseen for the samples discussed here, with the SPH polarization approaching 90%, while a multitude of different geometries can be considered to facilitate various laser-acceleration schemes.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DS: Conceptualization, Investigation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. MS: Methodology, Writing–original draft. DP: Methodology, Writing–original draft. TR: Conceptualization, Investigation, Methodology, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. TR acknowledges partial financial support by the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT), grant agreement No. HFRI-FM17-3709 (project NUPOL).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sun T, Zhao Q, Xue K, Lu Z-W, Ji L-L, Wan F, et al. Reviews of modern plasma physics, 6. Springer (2022). p. 38.

Google Scholar

2. Androić D, Armstrong DS, Asaturyan A, Averett T, Balewski J, Bartlett K, et al. Nature. arXiv:1905.08283 (2018) 557:207. doi:10.48550/arXiv.1905.0828

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Schlimme BS, Achenbach P, Ayerbe Gayoso CA, Bernauer JC, Böhm R, Bosnar D, et al. Measurement of the neutron electric to magnetic form factor ratio at Q2=1.58  GeV2 using the reaction 3He[over →](e[over →],e'n)pp. Phys Rev Lett (2013) 111:132504. doi:10.1103/PhysRevLett.111.132504

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Poelker M, Coulter KP, Toporkov DK. High-density production of spin-polarized atomic hydrogen and deuterium. Phys Rev A (1994) 50:2450. doi:10.1103/PhysRevA.50.2450

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Clasie JSWXDDB, Crawford C, Gao H. Optimal visible compression rate for mixed states is determined by entanglement of purification. Phys Rev A (2006) 73:020703(R). doi:10.1103/PhysRevA.73.060301

CrossRef Full Text | Google Scholar

6. Rakitzis TP, Samartzis PC, Loomes RL, Kitsopoulos TN, Brown A, Balint-Kurti GG, et al. Spin-polarized hydrogen atoms from molecular photodissociation. Science (2003) 300:1936. doi:10.1126/science.1084809

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sofikitis D, Kannis CS, Boulogiannis GK, Rakitzis TP. Ultrahigh-density spin-polarized H and D observed via magnetization quantum beats. Phys Rev Lett (2018) 121:083001. doi:10.1103/physrevlett.121.083001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Spiliotis AK, Xygkis M, Koutrakis ME, Tazes K, Boulogiannis GK, Kannis CS, et al. Ultrahigh-density spin-polarized hydrogen isotopes from the photodissociation of hydrogen halides: new applications for laser-ion acceleration, magnetometry, and polarized nuclear fusion. Light: Sci and Appl (2021) 10:35. doi:10.1038/s41377-021-00476-y

CrossRef Full Text | Google Scholar

9. Sun T, Zhao Q, Wan F, Salamin YI, Li J-X. Generation of ultrabrilliant polarized attosecond electron bunches via dual-wake injection. Phys Rev Lett (2024) 132:045001. doi:10.1103/physrevlett.132.045001

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wen M, Tamburini M, Keitel CH. Polarized laser-WakeField-accelerated kiloampere electron beams. Phys Rev Lett (2019) 122:214801. doi:10.1103/physrevlett.122.214801

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bohlen S, Gong Z, Quin MJ, Tamburini M, Põder K. Colliding pulse injection of polarized electron bunches in a laser-plasma accelerator. Phys Rev Res (2023) 5:033205. doi:10.1103/physrevresearch.5.033205

CrossRef Full Text | Google Scholar

12. Wu Y, Ji L, Geng X, Yu Q, Wang N, Feng B, et al. Polarized electron-beam acceleration driven by vortex laser pulses. New J Phys (2019) 21:073052. doi:10.1088/1367-2630/ab2fd7

CrossRef Full Text | Google Scholar

13. Nie Z, Li F, Morales F, Patchkovskii S, Smirnova O, An W, et al. In situ generation of high-energy spin-polarized electrons in a beam-driven plasma wakefield accelerator. Phys Rev Lett (2021) 126:054801. doi:10.1103/physrevlett.126.054801

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wen M, Tamburini M, Keitel CH. Polarized laser-WakeField-accelerated kiloampere electron beams. Phys Rev Lett (2019) 122:214801. doi:10.1103/physrevlett.122.214801

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Rakitzis T, Samartzis P, Toomes R, Tsigaridas L, Coriou M, Chestakov D, et al. Photofragment alignment from the photodissociation of HCl and HBr. Chem Phys Lett (2002) 364:115–20. doi:10.1016/s0009-2614(02)01324-6

CrossRef Full Text | Google Scholar

16. Rakitzis TP, Samartzis P, Toomes R, Kitsopoulos TN. Measurement of Br photofragment orientation and alignment from HBr photodissociation: production of highly spin-polarized hydrogen atoms. J Chem Phys (2004) 121:7222–7. doi:10.1063/1.1794691

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hillenkamp SKM, Even U. The journal of chemical physics, 118 (2003). p. 8699.

CrossRef Full Text | Google Scholar

18. Even U. EPJ techniques and instrumentation, 2. Springer (2015). p. 17.

Google Scholar

19. Čižmár T, Dholakia K. Tunable Bessel light modes: engineering the axial propagation. Opt express (2009) 17:15558. doi:10.1364/oe.17.015558

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Spiliotis AK, Xygkis M, Koutrakis ME, Sofikitis D, Rakitzis TP. Depolarization of spin-polarized hydrogen via collisions with chlorine atoms at ultrahigh density. Chem Phys Impact (2021) 2:100022. doi:10.1016/j.chphi.2021.100022

CrossRef Full Text | Google Scholar

21. Krstic PS, Schultz DR. Elastic scattering and charge transfer in slow collisions: isotopes of H and H⁺colliding with isotopes of H and with He. J Phys B: At Mol Opt Phys (1999) 32:3485–509. doi:10.1088/0953-4075/32/14/317

CrossRef Full Text | Google Scholar

22. Fox GW, Gal E. Elastic cross sections of hydrogen atoms. Proc Phys Soc (1967) 90:55–61. doi:10.1088/0370-1328/90/1/308

CrossRef Full Text | Google Scholar