New method for the investigation of mode coupling in graded-index polymer photonic crystal fibers using the Langevin stochastic differential equation

The mode coupling in a graded-index polymer photonic crystal fiber (GI PPCF) with a solid core has been investigated using the Langevin equation. Based on the computer-simulated Langevin force, the Langevin equation is numerically integrated. The numerical solutions of the Langevin equation align with those of the time-independent power flow equation (TI PFE). We showed that by solving the Langevin equation, which is a stochastic differential equation, one can successfully treat a mode coupling in GI PPCFs, which is an intrinsically stochastic process. We demonstrated that, in terms of effectiveness, the Langevin equation is preferable compared to the TI PFE. The GI PPCF achieves the equilibrium mode distribution (EMD) at a coupling length that is even shorter than the conventional GI plastic optical fiber (POF). The application of multimode GI PCFs in communications and optical fiber sensor systems will benefit from these findings.

1 Introduction

In recent years, researchers have placed significant emphasis on high-speed short-range data transmission using plastic optical fiber (POF) [1,2]. POF has the advantages of a large core and an easy connection, making it a potentially best option for the home network. Various materials are used in the manufacturing of POFs, the most common being polymethyl methacrylate (PMMA) [3–16]. Because the POF material is flexible, it can be used to create POFs with different materials or specifications to suit different application requirements. PMMA has been the most widely utilized material for POF manufacture [17]. POF can typically be categorized as step-index (SI) [18] or graded-index (GI) [19], based on the distribution of the refractive index (RI), and as single-mode [20] and multimode [21], depending on the number of propagation modes. A type of POF known as GI POF has an RI distribution that steadily decreases from the core axis to the cladding. The GI distribution of RI can reduce intermodal dispersion, enhance the bandwidth, and extend the transmission range of the fiber. However, intricate doping techniques are needed to create GI POF.

The 1990s saw the successful proposal of photonic crystal fiber (PCF) [22]. The flexibility of the optical fiber is greatly increased by the microstructure of the PCFs [23–26]. The first PMMA polymer photonic crystal fiber (PPCF) was created by Argyros in 2001 [27]. As a result of its various applications, PPCF sparked research interest [28,29]. Figure 1 shows a PPCF with a core of air holes of different sizes (d), simulating a GI optical fiber. Greater control over air-hole sizes and pitch Λ is the advantage of the GI PPCF over traditional GI POF, as opposed to the latter’s requirement for complex doping procedures. Moreover, it has been found that GI PPCF outperforms conventional GI POF in terms of bandwidth and loss [30].

Figure 1

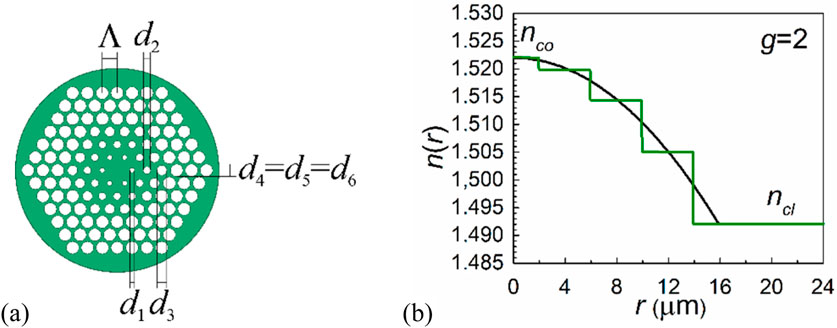
Figure 1. (A) Cross-section of the multimode GI PPCF. (B) Referent multimode GI PPCF RI performance (blue dashed line) and parabolic RI distribution (1) with g = 2 (black solid line).

The performance of the GI PPCF is significantly influenced by mode coupling. Light scattering, which occurs when random anomalies in multimode optical fibers transfer power from one mode to another, is the main cause of mode coupling. As the fiber length increases, power distribution varies until an equilibrium mode distribution (EMD) is formed at “coupling length” L_c. The fiber length at which the highest-order guiding mode altered its distribution to m = 0 is indicated by the coupling length L_c at which EMD is attained. Light is evenly dispersed, and the coupling process is practically finished beyond L_c. Since the steady-state distribution (SSD) was developed, each distribution that is released has a distinct far-field pattern. In other words, length z_s indicates the fiber length at which the output angular power distribution becomes completely independent of the launch beam. Mode coupling reduces modal dispersion and increases the transmission bandwidth [30]. It is also noteworthy that mode coupling makes it impossible to precisely characterize bandwidth and attenuation unless the SSD is fully obtained. Therefore, knowing the fiber length at which an SSD is constructed is essential.

To date, it has not been possible to examine the transmission characteristics of multimode PCFs with commercial simulation software applications. To tackle this problem, we present in this paper an efficient application of the Langevin equation to the GI PPCF mode-coupling problem. Thus, the intrinsically stochastic problem of mode coupling could be mathematically described stochastically using the Langevin equation. To the best of our knowledge, this is the first time that the Langevin equation has been used for the investigation of mode coupling in multimode GI PPCFs. For multimode GI PPCF, we found lengths for obtaining the EMD and SSD using launch beam distributions with various launch beam radial offsets. It is assumed that the air holes in the core and cladding are spaced in a regular triangular pitch (see Figure 1).

2 GI PPCF design

A GI PPCF considered in this work is shown in Figure 1. Rings 1, 2,. . . , 6 represent the six air-hole rings on the GI PPCF. A triangular lattice with a pitch of Λ is used to hold the air holes, and a polymer is considered the fiber material. The diameter of the air holes in rings 5 and 6 is the same as that of ring 4 (d₄ = d₅ = d₆).

3 TI PFE, Fokker–Planck equation, and Langevin equation

The following Equation 1 is the RI profile of the GI optical fiber [31]:

$n\left(r,\lambda \right)=\left\{\begin{array}{l}{n}_{co}\left(\lambda \right){\left[1-2\Delta \left(\lambda \right){\left(\frac{r}{a}\right)}^g\right]}^{1/2}\left(0\le r\le a\right)\\ n_{co}\left(\lambda \right){\left(1-2\Delta \left(\lambda \right)\right)}^{1/2}=n_{cl}\left(\lambda \right)\left(r>a\right)\end{array}\right..(1)$

Here, a is the core radius, g is the core index exponent, n_co(λ) is the core index measured at the fiber axis, n_cl(λ) is the cladding index, and $∆=\left(n_{co}-n_{cl}\right)/n_{co}$ is the relative index difference.

The time-independent power flow equation (TI PFE) for the GI optical fiber is [31]

$\frac{\partial P\left(m,\lambda ,z\right)}{\partial z}=\frac{D}{m}\frac{\partial P\left(m,\lambda ,z\right)}{\partial m}+D\frac{\partial P^2\left(m,\lambda ,z\right)}{\partial m^2},(2)$

where $P\left(m,\lambda ,z\right)$ is the mth principal mode power, z is the coordinate along the fiber axis, and D is a mode-coupling constant. The maximum principal mode number is given in Equation 3 [31], as follows:

$M\left(\lambda \right)=\sqrt{\frac{g\Delta \left(\lambda \right)}{g+2}}ak{n}_{co}\left(\lambda \right),(3)$

where k = 2π/λ.

The principal mode m excited at the input fiber end is given in Equation 4 [31], as follows:

$\frac{m}{M}={\left[{\left(\frac{\Delta r}{a}\right)}^g+\frac{{\theta }^2}{2\Delta }\right]}^{\left(g+2\right)/2g},(4)$

where $∆r$ is the launch beam radial offset and θ is the launch beam angle.

We first approximate Equation 2 as follows:

$\frac{\partial P\left(m,\lambda ,z\right)}{\partial z}=-V\frac{\partial P\left(m,\lambda ,z\right)}{\partial m}+D\frac{{\partial }^{2}P\left(m,\lambda ,z\right)}{\partial m^2}.(5)$

Equation 5 can be understood as a special Fokker–Planck equation [32]. One can compute the drift coefficient V using Equation 6:

$V=\frac{1}{K}{\displaystyle \sum _{i=1}^K}{V}_i,(6)$

where V_i is the drift coefficient of the ith principal mode. Later in this article, an illustration of the drift coefficient determination technique is provided.

The discretized Langevin equation can be obtained by transforming the Fokker–Planck Equation 5 [32,33], where principal mode m_n+1 at fiber length z_n+1 is given as

$m_{n+1}=m_n+Vk+\sqrt{Dk}{\omega }_n,(7)$

where k = z_f/N, z_f is the fiber length, N is the number of finite steps of length k, n = 0, 1, . ., N^-1, and ω₀, ω₁, . . ., ω_N-1 are independent Gaussian random numbers, with properties <ω_n>=0 and <ω_n ω_n’ ≥2δ_nn’. For $m_n=0$, Equation 7 reduces to Equation 8 [33]:

$m_{n+1}=\sqrt{Dk}{\omega }_n.(8)$

Thus, one obtains m_N = m(z_f). By calculating a large number of representations of ω_n and averaging in appropriate intervals Δm for $0\le m\le M$, one obtains < m(z_f)>. It should be noted that optical fiber perturbations are known to be random in nature. Examples of these perturbations include variations in diameter, stress-induced microscopic random bends, and defects in the fiber core. Thus, the stochastic process of energy redistribution in optical fiber produced by its perturbations is explicitly described and modeled using the Langevin equation because of its stochastic nature.

4 Numerical results and discussion

The following is the effective V parameter for GI PPCF:

$V=\frac{2\pi }{\lambda }{a}_{eff}\sqrt{n_0^2-n_{fsm}^2},(9)$

where a_eff = $\mathrm{\Lambda }/\sqrt{3}$ [34] and n_fsm is the effective RI of different core and cladding layers, which is obtained from Equation 9, with the effective parameter V [35]:

$V\left(\frac{\lambda }{\mathrm{\Lambda }},\frac{d}{\mathrm{\Lambda }}\right)=A_1+\frac{A_2}{1+A_3\exp \left(A_4\lambda /\mathrm{\Lambda }\right)},(10)$

where parameters A_i (i = 1 to 4) are given in Equation 11, as follows:

$A_i=a_{i0}+a_{i1}{\left(\frac{d}{\mathrm{\Lambda }}\right)}^{b_{i1}}+a_{i2}{\left(\frac{d}{\mathrm{\Lambda }}\right)}^{b_{i2}}+a_{i3}{\left(\frac{d}{\mathrm{\Lambda }}\right)}^{b_{i3}}.(11)$

The coefficients a_i0–a_i3 and b_i1–b_i3 (i = 1–4) are given in our previous work [35].

We applied our method to the GI PPCF with the following parameters: a core radius a = 4Λ = 16 μm, pitch Λ = 4 μm, fiber diameter b = 1 mm, n_co = 1.5220, and n_cl = 1.4920 [31,36]. We used M = 24 at λ = 633 nm, g = 2.0, and $∆=\left(n_{co}-n_{cl}\right)/n_{co}$ = 0.019711. The parameter D = 1482 1/m is a typical value for GI PPCF and conventional GI POFs [31,36], and V=($-1.5$ ±0.1) 1/m. We highlight that when modeling the GI PPCF, the typical values of D that characterize a standard GI POF can be utilized as the degree of mode coupling in both standard GI POFs and GI PPCFs correlates with the polymer core material. This assumption mirrors the approach taken in silica PCF modeling [37].

For Λ = 4 μm and air-hole diameters d₁ = 0.6 μm, d₂ = 0.7 μm, d₃ = 1.3 μm, and d₄ = 3.1 μm, the refractive indices n₁ = 1.5201, n₂ = 1.5145, n₃ = 1.5050, and n₄ = 1.4920, respectively, are calculated using Equations 9, 10. These parameters are chosen in order to enable the GI distribution (1) with g = 2, which then results in the best transmission properties (such as bandwidth) of the investigated PPCF. The diameter of the cladding air holes in rings 5 and 6 is d₄ = d₅ = d₆ = 3.1 μm, which corresponds to the cladding refractive index n₄ = n₅ = n₆ = n_cl = 1.4920. In Figure 2, the normalized output modal power distribution P(m,λ,z) obtained by solving the Langevin equation is compared to the numerical solutions of the TI PFE [36] at different fiber lengths. For these calculations, a Gaussian beam P(θ,z) launched with $〈\theta 〉$ = 0^o and radial offsets ∆r = 0, 4, 8, and 12 µm is used. A good agreement between the solutions of the Langevin equation and the TI PFE is shown in Figure 2. The EMD (Figure 2D) is established at a coupling length of L_c = 18 m. The SSD is observed at z≡z_s = 60 m.

Figure 2

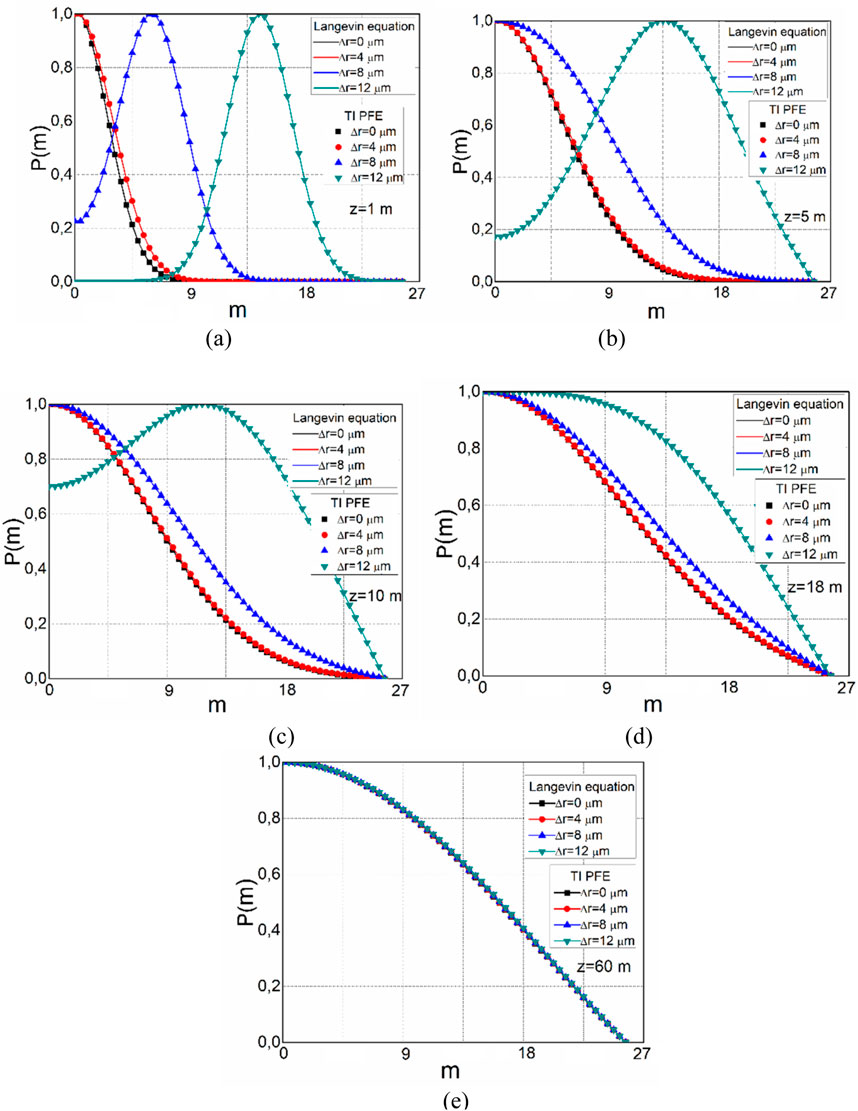
Figure 2. Modal power distribution P(m,λ,z) over a range of radial offsets $∆r$ obtained by numerically solving the Langevin Equation 7 and the TI PFE (2) [36] at lengths (A) z = 1 m, (B) z = 5 m, (C) z = 10 m, (D) z = 18 m, and (E) z = 60 m.

It should be mentioned that for standard GI POF, which we previously investigated in our study [31], a coupling length of L_c = 31 m is published. The coupling coefficient for this type of GI POF is D = 1,482 1/m. The coupling length in GI PPCF is shorter than that in traditional GI POF due to the smaller core radius and fewer propagating modes (the maximum principal mode number in conventional GI POF was M = 656). In other words, for a shorter distance, fewer propagating modes must couple together. Comparing silica PCFs to the GI PPCF, which was the focus of this investigation, showed that their mode coupling is noticeably weaker and, therefore, much longer lengths L_c ≃1.45 to 1.65 km at which an EMD is achieved and z_s≃3.30 to 3.80 km at which an SSD are established [35].

In summary, we demonstrated that mode coupling in GI POFs may be effectively treated by solving the Langevin equation (stochastic differential equation), which explicitly acknowledges a stochastic nature of energy redistribution in optical fiber produced by its perturbations. It is applicable to all GI optical fibers. This is not an issue with the Langevin equation, in contrast to the Fokker–Planck equation and TI PFE, which call for extra care in the stability of their numerical solutions. In terms of effectiveness, speed of execution, and memory usage, the Langevin equation is preferable. The Langevin equation does not have this issue, in contrast to the Fokker–Planck equation and the TI PFE, where a very fine mesh in the finite difference approach is required in order to obtain a highly accurate numerical solution (high memory consumption). The Langevin equation integration algorithm and the explicit finite difference method algorithm for the numerical solution of the TI PFE are evaluated in terms of their time efficiency (speed of execution), space efficiency (memory consumption), and complexity (solution/algorithm structure). The Langevin equation and the TI PFE take 1.5 and 2 min, respectively, to execute on an Intel(R) Core(TM) i3 CPU 540@3.07 GHz computer for the longest examined fiber length of 60 m. When expressed in terms of a 2-dim array, the memory consumption for the TI PFE and the Langevin equation is 24 × 6.0 × 10⁶ and 24 × 6.0 × 10⁵, respectively. Compared to the solution of the Langevin equation, the explicit finite difference solution of the TI PFE is more complicated. It is worth noting that the experimental setup for future experiments with the GI PPCF investigated in this work would be similar to that used in our previous work with a standard GI POF [31].

The behavior of mode coupling plays a crucial role in determining the length-dependent bandwidth of GI PCFs. Notably, the bandwidth decreases inversely proportional to lengths shorter than the coupling length L_c. Beyond this coupling length L_c, it exhibits a z−^1/2 dependency. A shorter L_c results in a quicker transition to a phase of reduced bandwidth decrease [37,38]. Compared to conventional GI POFs, GI PPCFs require shorter lengths to establish EMD and SSD, leading to a faster improvement in bandwidth enhancement [39]. This characteristic suggests that GI PPCFs are more suitable for short-range telecommunications. The findings of this research have practical implications for various communication and sensing systems utilizing multimode GI PPCFs. Understanding the modal distribution of multimode GI PPCFs at specific lengths is crucial for their integration into optical fiber sensing systems. One should also mention that, on the other hand, single-mode optical fibers are successfully used as a part of various fiber optic sensor systems [40–42]. Although single-mode and multimode optical fibers are both used in fiber optic sensor systems, they have different characteristics and are usually suited for different sensing applications. In other words, the choice between these two types of optical fibers for a particular sensing system is governed by their core diameter, distance, bandwidth, and light source.

5 Conclusion

This paper presents the numerical solution of the Langevin equation, which was used to investigate the state of mode coupling along a GI PPCF. The Langevin equation recognizes and explicitly accounts for the stochastic nature of the intrinsic perturbation effects of the GI PPCF. The results show that the length required to develop SSD and the coupling length required to obtain the EMD are both low in this fiber due to a strong mode-coupling process that is typical of POFs. One explanation for such substantial mode coupling is the large intrinsic perturbation effects in the GI PPCF. The GI PPCF under investigation in this study achieves the EMD at a length L_c that is even shorter than that in the conventional GI POF (L_c = 18 m in GI PPCFs compared to L_c = 31 m in conventional GI POFs). This is a result of the GI PPCF having fewer propagating modes due to its smaller core radius. In particular, a shorter length is required to complete the mode-coupling process when there are fewer propagating modes. Thus, a shorter L_c would result in a quicker shift to the slower bandwidth regime decrease. The fiber characterization provided in this paper is important for its use in data transmission, sensing, and power supply systems.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SS: conceptualization, funding acquisition, methodology, project administration, software, supervision, writing–original draft, and writing–review and editing. AD: conceptualization, methodology, writing–original draft, and writing–review and editing. KA: conceptualization, methodology, writing–original draft, and writing–review and editing. CC: funding acquisition, methodology, software, writing–original draft, and writing–review and editing. RM: methodology, project administration, software, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Key R&D Program of China (2022YFE0140400); by a grant from Ajman University (Grant ID: 2023-IRG-ENIT-14); by a grant from the Serbian Ministry of Science, Technological Development, and Innovations (Agreement No. 451-03–65/2024-03/200122); and by a grant from the National Natural Science Foundation of China (62003046 and 6211101138).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Leal-Junior A, Frizera A, Pontes MJ, Fasano A, Woyessa G, Bang O, et al. Dynamic mechanical characterization with respect to temperature, humidity, frequency and strain in mPOFs made of different materials. Opt Mater Express (2018) 8:804–15. doi:10.1364/ome.8.000804

CrossRef Full Text | Google Scholar

2. Min R, Ortega B, Marques C. Fabrication of tunable chirped mPOF Bragg gratings using a uniform phase mask. Opt Express (2018) 26:4411–20. doi:10.1364/oe.26.004411

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ye Y, Zhao C, Wang Z, Teng C, Marques C, Min R. Portable multi-hole plastic optical fiber sensor for liquid level and refractive index monitoring. IEEE Sens J (2023) 23:2161–8. early access. doi:10.1109/jsen.2022.3228224

CrossRef Full Text | Google Scholar

4. Teng C, Wang Y, Min R, Deng S, Deng H, Li Y, et al. Plastic optical fiber based SPR sensor for simultaneous measurement of refractive index and liquid level. IEEE Sens J (2022) 22(7):6677–84. doi:10.1109/jsen.2022.3155723

CrossRef Full Text | Google Scholar

5. Leal-Junior A, Guo J, Min R, Fernandes AJ, Frizera A, Marques C. Photonic smart bandage for wound healing assessment. Photon Res (2021) 9(3):272–80. doi:10.1364/prj.410168

CrossRef Full Text | Google Scholar

6. Leal-Junior AG, Marques C. Diaphragm-embedded optical fiber sensors: a review and tutorial. IEEE Sensors (2021) 21:12719–33. doi:10.1109/jsen.2020.3040987

CrossRef Full Text | Google Scholar

7. Fasano A, Woyessa G, Stajanca P, Markos C, Stefani A, Nielsen K, et al. Fabrication and characterization of polycarbonate microstructured polymer optical fibers for high-temperature-resistant fiber Bragg grating strain sensors. Opt Mater Express (2016) 6(2):649–59. doi:10.1364/ome.6.000649

CrossRef Full Text | Google Scholar

8. Zubel MG, Fasano A, Woyessa GT, Min R, Leal AG, Theodosiou A, et al. Bragg gratings inscribed in solid-core microstructured single-mode polymer optical fiber drawn from a 3D-printed polycarbonate preform. IEEE Sens J (2020) 20(21):12744–57. doi:10.1109/jsen.2020.3003469

CrossRef Full Text | Google Scholar

9. Akimoto Y, Asai M, Koike K, Makino K, Koike Y. Poly(styrene)-based graded-index plastic optical fiber for home networks. Opt Lett (2012) 37(11):1853–5. doi:10.1364/ol.37.001853

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Makino K, Akimoto Y, Koike K, Kondo A, Inoue A, Koike Y. Low loss and high bandwidth polystyrene-based graded index polymer optical fiber. J Light Technol (2013) 31(14):2407–12. doi:10.1109/jlt.2013.2266671

CrossRef Full Text | Google Scholar

11. Leal-Junior AG, Theodosiou A, Min R, Casas J, Díaz CR, Dos Santos WM, et al. Quasi-distributed torque and displacement sensing on a series elastic actuator’s spring using FBG arrays inscribed in CYTOP fibers. IEEE Sens J (2019) 19(11):4054–61. doi:10.1109/jsen.2019.2898722

CrossRef Full Text | Google Scholar

12. Chapalo I, Chah K, Gusarov A, Ioannou A, Pospori A, Nan Y-G, et al. Online gamma radiation monitoring using few-mode polymer CYTOP fiber bragg gratings. Opt Lett (2023) 23(1):39. doi:10.3390/s23010039

CrossRef Full Text | Google Scholar

13. Woyessa G, Rasmussen HK, Bang O. Zeonex – a route towards low loss humidity insensitive single-mode step-index polymer optical fibre. Opt Fiber Technol (2020) 57:102231–6. doi:10.1016/j.yofte.2020.102231

CrossRef Full Text | Google Scholar

14. Dash JN, Cheng X, Tam H. Low gas pressure sensor based on a polymer optical fiber grating. Opt Lett (2021) 46(5):933–6. doi:10.1364/ol.418096

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Markos C, Stefani A, Nielsen K, Rasmussen HK, Yuan W, Bang O. High-T_g TOPAS microstructured polymer optical fiber for fiber Bragg grating strain sensing at 110 degrees. Opt Express (2013) 21(4):4758–65. doi:10.1364/oe.21.004758

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Woyessa G, Fasano A, Stefani A, Markos C, Nielsen K, Rasmussen HK, et al. Single mode step-index polymer optical fiber for humidity insensitive high temperature fiber Bragg grating sensors. Opt Express (2016) 24(2):1253–60. doi:10.1364/oe.24.001253

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Broadway C, Min R, Leal-Junior AG, Marques C, Caucheteur C. Toward commercial polymer fiber bragg grating sensors: review and applications. J Light Technol (2019) 37(11):2605–15. doi:10.1109/jlt.2018.2885957

CrossRef Full Text | Google Scholar

18. Hu X, Chen Z, Cheng X, Qu H, Caucheteur C, Tam H-Y, et al. Femtosecond laser point-by-point Bragg grating inscription in BDK-doped step-index PMMA optical fibers. Opt Lett (2022) 47(2):249–52. doi:10.1364/ol.450047

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Theodosiou A, Min R, Leal-Junior AG, Ioannou A, Frizera A, Pontes MJ, et al. Long period grating in a multimode cyclic transparent optical polymer fiber inscribed using a femtosecond laser. Opt Lett (2019) 44(21):5346–9. doi:10.1364/ol.44.005346

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cheng X, Gunawardena DS, Pun CJ, Bonefacino J, Tam H. Single nanosecond-pulse production of polymeric fiber Bragg gratings for biomedical applications. Opt Express (2020) 28(22):33573–83. doi:10.1364/oe.408744

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kuang R, Ye Y, Chen Z, He R, Savović I, Djordjevich A, et al. Low-cost plastic optical fiber integrated with smartphone for human physiological monitoring. Opt Fiber Technol (2022) 71:102947. doi:10.1016/j.yofte.2022.102947

CrossRef Full Text | Google Scholar

22. Knight JC, Birks TA, Russell PSJ, Atkin DM. All-silica single-mode optical fiber with photonic crystal cladding. Opt Lett (1996) 21(19):1547. doi:10.1364/ol.21.001547

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Stefańska K, Majchrowska S, Gemza K, Soboń G, Sotor J, Mergo P, et al. Soliton trapping and orthogonal Raman scattering in a birefringent photonic crystal fiber. Opt Lett (2022) 47(16):4183–6. doi:10.1364/ol.463643

CrossRef Full Text | Google Scholar

24. Zhao S, Guo R, Zeng Y. Effects of frequency-dependent Kerr nonlinearity on higher-order soliton evolution in a photonic crystal fiber with one zero-dispersion wavelength. Phys Rev A (2022) 106(3):033516. doi:10.1103/physreva.106.033516

CrossRef Full Text | Google Scholar

25. Wang C, Lin K, Cao S, Feng G, Wang J, Abdalla AN. Polarized supercontinuum generation in CS₂-core all-normal dispersion photonic crystal fiber. IEEE Photon J (2022) 14(6):1–7. doi:10.1109/jphot.2022.3223534

CrossRef Full Text | Google Scholar

26. Heydarian K, Nosratpour A, Razaghi M. Computational study of wavelength conversion based on XGM by photonic crystal semiconductor optical amplifier. Opt Laser Technol (2022) 156(1):108531. doi:10.1016/j.optlastec.2022.108531

CrossRef Full Text | Google Scholar

27. Eijkelenborg MA, Large MCJ, Argyros A, Zagari J, Manos S, Issa NA, et al. Microstructured polymer optical fibre. Opt Express (2001) 9(7):319–27. doi:10.1364/oe.9.000319

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Woyessa G, Pedersen JKM, Fasano A, Nielsen K, Markos C, Rasmussen HK, et al. Zeonex-PMMA microstructured polymer optical FBGs for simultaneous humidity and temperature sensing. Opt Lett (2017) 42(6):1161–4. doi:10.1364/ol.42.001161

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Min R, Pereira L, Paixao T, Woyessa G, Hu X, Antunes P, et al. Chirped POF Bragg grating production utilizing UV cure adhesive coating for multiparameter sensing. Opt Fiber Technol (2021) 65:102593. doi:10.1016/j.yofte.2021.102593

CrossRef Full Text | Google Scholar

30. Lwin R, Barton G, Harvey L, Harvey J, Hirst D, Manos S, et al. Beyond the bandwidth-length product: graded index microstructured polymer optical fiber. Appl Phys Lett (2007) 91(19):191119. doi:10.1063/1.2805216

CrossRef Full Text | Google Scholar

31. Savović S, Simović A, Drljača B, Djordjevich A, Stepniak G, Bunge CA, et al. Power flow in graded index plastic optical fibers. J Lightwave Technol (2019) 37(19):4985–90. doi:10.1109/jlt.2019.2926700

CrossRef Full Text | Google Scholar

32. Risken H. The fokker-planck equation. Berlin: Springer-Verlag (1989).

Google Scholar

33. Savović S, Djordjevich A. Solution of mode coupling in step-index optical fibers by the Fokker-Planck equation and the Langevin equation. Appl Opt (2002) 41:2826–30. doi:10.1364/ao.41.002826

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Saitoh K, Koshiba M. Empirical relations for simple design of photonic crystal fibers. Opt Express (2005) 13(1):267–74. doi:10.1364/opex.13.000267

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Savović S, Kovačević MS, Simović A, Drljača B, Kuzmanović L, Djordjevich A. Method for investigation of mode coupling in multimode step-index silica photonic crystal fibers. Optik (2021) 246:167728. doi:10.1016/j.ijleo.2021.167728

CrossRef Full Text | Google Scholar

36. Savović S, Simović A, Drljača B, Kovačević MS, Kuzmanović L, Djordjevich A, et al. Power flow in multimode graded-index microstructured polymer optical fibers. Polymers (2023) 15:1474. doi:10.3390/polym15061474

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Drljača B, Savović S, Kovačević MS, Simović A, Kuzmanović L, Djordjevich A, et al. Theoretical investigation of bandwidth in multimode step-index silica photonic crystal fibers. Photonics (2022) 9(4):214. doi:10.3390/photonics9040214

CrossRef Full Text | Google Scholar

38. Simović A, Djordjevich A, Drljača B, Savović S, Min R. Investigation of bandwidth in multimode graded index plastic optical fibers. Opt Express (2021) 29(19):29587–94. doi:10.1364/oe.433481

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Savović S, Simović A, Drljača B, Kovačević MS, Kuzmanović L, Djordjevich A, et al. High bandwidth performance of multimode graded-index microstructured polymer optical fibers. Results Phys (2023) 50:106548. doi:10.1016/j.rinp.2023.106548

CrossRef Full Text | Google Scholar

40. Díaz CAR, R. A, Leitão C, Marques CA, Domingues MF, Alberto N, et al. Low-cost interrogation technique for dynamic measurements with FBG-based devices. Sensors (2017) 17:2414. doi:10.3390/s17102414

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Zhang W, Singh R, Wang Z, Li G, Xie Y, Jha R, et al. Humanoid shaped optical fiber plasmon biosensor functionalized with graphene oxide/multi-walled carbon nanotubes for histamine detection. Opt Express (2023) 31:11788–803. doi:10.1364/oe.486844

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Gomes H, Liu X, Fernandes A, Moreirinha C, Singh R, Kumar S, et al. Laser-induced graphene-based Fabry-Pérot cavity label-free immunosensors for the quantification of cortisol. Sensors Actuators Rep (2024) 7:100186. doi:10.1016/j.snr.2024.100186

CrossRef Full Text | Google Scholar