Critical droplets and replica symmetry breaking

We show that the notion of critical droplets is central to an understanding of the nature of ground states in the Edwards–Anderson–Ising model of a spin glass in arbitrary dimensions. Given a specific ground state, we suppose that the coupling value for a given edge is varied with all other couplings held fixed. Beyond some specific value of the coupling, a droplet will flip, leading to a new ground state; we refer to this as the critical droplet for that edge and ground state. We show that the distribution of sizes and energies over all edges for a specific ground state can be used to determine which of the leading scenarios for the spin glass phase is correct. In particular, the existence of low-energy interfaces between incongruent ground states, as predicted by replica symmetry breaking, is equivalent to the presence of critical droplets, whose boundaries comprise a positive fraction of edges in the infinite lattice.

1 Introduction

The nature of the low-temperature phase of the Edwards–Anderson (EA) Hamiltonian [1] in finite dimensions

${\mathcal{H}}_J=-{\displaystyle \sum _{<x,y>}}{J}_{xy}{\sigma }_x{\sigma }_y(1)$

remains unresolved. Here, ${\sigma }_x=\pm 1$ is the Ising spin at site $x$, and $⟨x,y⟩$ denotes a nearest-neighbor edge in the edge set ${\mathbb{E}}^d$ of the $d$-dimensional cubic lattice ${\mathbb{Z}}^d$. The couplings $J_{xy}$ are taken to be independent, identically distributed continuous random variables chosen from a distribution $\nu (d{J}_{xy})$, with random variable $J_{xy}$ assigned to the edge $⟨x,y⟩$. Our requirements on $\nu$ are that it be supported on the entire real line, distributed symmetrically about 0, and has finite variance; e.g., a Gaussian with mean 0 and variance 1. We denote a particular realization of the couplings by $J$.

There are, at present, four scenarios for the spin glass phase that are consistent both with numerical results and, as far as is currently known, mathematically consistent: replica symmetry breaking (RSB) [2–12], droplet-scaling [13–17], trivial–non-trivial spin overlap (TNT) [18, 19], and chaotic pairs [10, 20–22]. One of the central open questions in spin glass theory is which (if any) of these scenarios is correct and for which dimensions and temperatures.

The differences among the four scenarios at positive temperature are described elsewhere [12, 23, 24]; here, we are concerned with their different predictions at zero temperature, i.e., for the ground-state structure of the EA Hamiltonian. Of the four, two (RSB and chaotic pairs) predict the existence of many ground states, and the other two (droplet-scaling and TNT) predict the existence of only a single pair [17, 25, 26]. Although important, these differences are less fundamental than the nature of the interfaces that separate their ground states from their lowest-lying long-wavelength excitations. The presence or absence of multiplicity of ground states follows as a consequence of the nature of these excitations.

In this paper, we focus on the nature of low-energy long-wavelength excitations above the ground state and how they relate to ground state stability, with a view toward distinguishing different predictions of the four scenarios. Aside from elucidating the different (and potentially testable) predictions of these scenarios, determining the stability properties of the ground state is crucial in determining the low-temperature properties of the spin glass phase, including central questions such as multiplicity of pure states and the presence or absence of an Almeida-Thouless (AT) line [27]. We begin by defining the parameters of the study.

A finite volume ${\mathrm{\Lambda }}_L$ was chosen corresponding to a cube of side $L$ centered at the origin. A finite-volume ground state ${\sigma }_L$ is the lowest-energy spin configuration in ${\mathrm{\Lambda }}_L$, which is subject to a specified boundary condition. An infinite-volume ground state $\sigma$ is a spin configuration on all of ${\mathbb{Z}}^d$, which is defined by the condition that its energy cannot be lowered by flipping any finite subset of spins. ($\sigma$ is always defined with respect to a specific $J$, but we suppress its dependence for notational convenience.) The condition for $\sigma$ to be a ground state is then

$E_S={\displaystyle \sum _{⟨x,y⟩\in S}}{J}_{xy}{\sigma }_x{\sigma }_y>0,(2)$

where $S$ is any closed surface (or contour in two dimensions) in the dual lattice. The surface $S$ encloses a connected set of spins (a “droplet”), and $⟨x,y⟩\in S$ is the set of edges connecting spins in the interior of $S$ to spins outside $S$. The inequality in Equation 2 is strict because, by the continuity of $\nu (d{J}_{xy})$, there is zero probability of any closed surface having exactly zero energy in $\sigma$. The condition in Equation 2 must also hold for finite-volume ground states for any closed surface completely inside ${\mathrm{\Lambda }}_L$. It is then not hard to show that an alternative (and equivalent) definition, which we also use sometimes, is that an infinite-volume ground state is any convergent limit of an infinite sequence of finite-volume ground states. Given the spin-flip symmetry of the Hamiltonian, a ground state, whether of finite or infinite volume, generated by a spin-symmetric boundary condition, such as free or periodic, will appear as one part of a globally spin-reversed pair; we therefore refer generally to ground state pairs (GSPs) rather than individual ground states.

2 Interfaces and critical droplets

An interface between two infinite-volume spin configurations $\alpha$ and $\beta$ comprises the set of edges whose associated couplings are satisfied in $\alpha$ and unsatisfied in $\beta$, or vice versa; they separate regions in which the spins in $\alpha$ agree with those in $\beta$ from regions in which their spins disagree. An interface may consist of a single connected component or multiple disjoint ones, but (again using the continuity of the coupling distribution) if $\alpha$ and $\beta$ are ground states, any such connected component must be infinite in extent.

Interfaces can be characterized by their geometry and energy. They can either be “space-filling,” meaning they comprise a positive density of all edges in ${\mathbb{E}}^d$, or zero-density, in which the dimensionality of the interface is strictly less than the dimension $d$. Ground states are called incongruent if they differ by a space-filling interface [28, 29].

Interfaces can also differ by how their energies scale with volume. The energy might diverge (though not monotonically) as one examines interfaces contained within increasingly larger volumes, or it might remain $O(1)$, independent of the volume considered. We will denote the former as a “high-energy interface” and the latter as a “low-energy interface.”

An excitation above the ground state is any spin configuration obtained by overturning one or more spins in the ground state (while leaving an infinite subset of spins in the original ground state intact); therefore, an interface is the boundary of an excitation. We are primarily interested in excitations consisting of overturning droplets of large, or possibly infinite, size; because an interface is the boundary of such an excitation, the energy of the excitation is simply twice the interface energy. An excitation above a ground state may itself be a new ground state (this would require the excitation to involve overturning an infinite number of spins such that Equation 2 remains satisfied). Indeed, as proven elsewhere [9], an excitation having a space-filling interface with the original ground state may generate a new ground state entirely.

With this in mind, we present the four low-temperature spin glass scenarios in Table 1, which illustrates their various relationships (and clarifies why we consider these four scenarios together).

Table 1

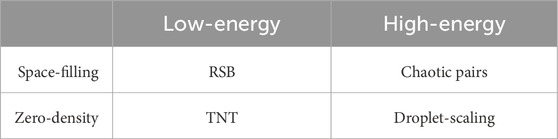
Table 1. Four scenarios described in the text for the low-temperature phase of the EA model, categorized in terms of interface geometry (rows) and energetics (columns). The column headings describe the energy scaling along the interface of the minimal long-wavelength excitations above the ground state predicted by each. Adapted from Figure 1 of [23].

As shown elsewhere [9], the existence of space-filling interfaces in the first row scenarios (RSB and chaotic pairs) implies the presence of multiple GSPs, whereas droplet-scaling and TNT both predict a single GSP [9, 25, 26, 28, 29].

Remarks on Table 1. The droplet-scaling scenario predicts a broad distribution of (free) energies for a minimal energy compact droplet of diameter $O(L)$, with a characteristic energy growing as $L^{\theta }$ with $\theta >0$ in dimensions where a low-temperature spin glass phase is present. The distribution is such that there exist droplets of $O(1)$ energy on large length scales, but these appear with a probability falling off as $L^{-\theta }$ as $L\to \infty$. In contrast, both the RSB and TNT scenarios require droplets with $O(1)$ energy to appear with positive probability bounded away from 0 on all length scales. Thus, the droplet-scaling scenario is shown in the second column of Table 1.

We now focus on the concepts of flexibility and critical droplets, which were introduced by Newman et al. [30, 31] and whose properties were described extensively in [24] (see also [26, 32]). Here, we only summarize their main features. We first provide some definitions (all with respect to some fixed coupling realization $J$):

Definition 2.1. (Newman et al. [24]) Consider the GSP ${\sigma }_L$ for the EA Hamiltonian (Equation 1) on a finite-volume ${\mathrm{\Lambda }}_L$ with boundary conditions chosen independently of $J$ (for specificity, we always use periodic boundary conditions (PBCs) in this paper). Choose an edge $b_{xy}=⟨x,y⟩$ with $x,y\in {\mathrm{\Lambda }}_L$, and consider all closed surfaces in the dual-edge lattice ${\mathbb{E}}_L^{*}$, which includes the dual edge $b_{xy}^{*}$. From Equation 2 and the continuity of the couplings, these all have distinct positive energies. There then exists a closed-surface $\partial D(b_{xy},{\sigma }_L)$, passing through $b_{xy}^{*}$, with least energy in ${\sigma }_L$. We call $\partial D(b_{xy},{\sigma }_L)$ the critical droplet boundary of $b_{xy}$ in ${\sigma }_L$ and the set of spins $D(b_{xy},{\sigma }_L)$ enclosed by $\partial D(b_{xy},{\sigma }_L)$ the critical droplet of $b_{xy}$ in ${\sigma }_L$.

Remarks. Critical droplets are defined with respect to edges rather than associated couplings to avoid confusion, given that we often vary the coupling value associated with specific edges, while the edges themselves are fixed, geometric objects.

We define the energy $E\left(D(b_{xy},{\sigma }_L)\right)$ of the critical droplet of $b_{xy}$ in ${\sigma }_L$ to be the energy of its boundary as given by Equation 2:

$E\left(D\left(b_{xy},{\sigma }_L\right)\right)={\displaystyle \sum _{<x,y>\in \partial D\left(b_{xy},{\sigma }_L\right)}}{J}_{xy}{\sigma }_x{\sigma }_y.(3)$

Definition 2.2. (Newman et al. [24]) The critical value of the coupling $J_{xy}$ associated with $b_{xy}$ in ${\sigma }_L$ is the value of $J_{xy}$, where $E\left(D(b_{xy},{\sigma }_L)\right)=0$, while all other couplings in $J$ are held fixed.

We next define the flexibility $f(J_{xy},{\sigma }_L)$:

Definition 2.3. (Newman et al. [24]) Let $J_{xy}$ be the value of the coupling assigned to the edge $b_{xy}$ in coupling realization $J$ and $J_c(b_{xy},{\sigma }_L)$ be the critical value of $b_{xy}$ in ${\sigma }_L$. We define the flexibility $f(b_{xy},{\sigma }_L)$ of $b_{xy}$ in ${\sigma }_L$ to be $f(b_{xy},{\sigma }_L)=|J_{xy}-J_c(b_{xy})|$.

Remarks. The critical value $J_c$ of an edge $b_{xy}$ with coupling value $J_{xy}$ is determined by all couplings in $J$, except $J_{xy}$. Because couplings are chosen independently from $\nu (d{J}_{xy})$, it follows that the value $J_{xy}$ is independent of $J_c$. Therefore, given the continuity of $\nu (d{J}_{xy})$, there is zero probability in a ground state that any coupling has exactly zero flexibility.

It follows from the definitions above and Equation 3 that

$f\left(b_{xy},{\sigma }_L\right)=E\left(D\left(b_{xy},{\sigma }_L\right)\right).$

Therefore, couplings which share the same critical droplet have the same (strictly positive) flexibility.

A rigorous definition of critical droplets and flexibilities within infinite-volume ground states requires use of the excitation metastate, whose definition and properties are presented in [26, 30, 31, 33]. Here, we simply note that finite-volume critical droplets and their associated flexibilities converge with their properties preserved in the infinite-volume limit, for reasons presented in [24]. This result would be trivial if all critical droplets in infinite-volume ground states were finite. However, it could also be that critical droplets can be infinite in extent in one or more directions, in which case metastates can be used to define such unbounded critical droplets which enclose an infinite subset of spins: they are the infinite-volume limits of critical droplets in finite-volume ground states.

3 Classification of critical droplets

In [24], critical droplets in infinite-volume ground states were classified according to the size of their boundary $\partial D(b_{xy},\sigma )$, which is the relevant factor in associating the presence of a given type of critical droplet with one of the scenarios in Table 1. We simplify the nomenclature used in that paper by focusing on three different kinds of critical droplets. Let $|\partial D(b_{xy},\sigma )|$ denote the number of edges in the critical droplet boundary. A finite critical droplet is one in which $|\partial D(b_{xy},\sigma )|<\infty$; in two and more dimensions, this implies that the critical droplet $D(b_{xy},\sigma )$ itself consists of a finite set of spins and thus can be completely contained within some finite volume. (A $1D$ chain is an exception: here, the critical droplet boundary of any edge consists of that edge alone, but the associated critical droplet consists of a semi-infinite chain of spins.) If these are the only type of critical droplets present, then the distribution of their sizes becomes important in answering fundamental questions involving edge disorder chaos and ground-state structure [26]. It is not hard to show that in any dimension, an EA ground state must contain at least a positive density of edges with finite critical droplets (whereas in $1D$, this is the case for all edges).

There are two kinds of critical droplets with $|\partial D(b_{xy},\sigma )|=\infty$. The first class includes those with infinite boundary $\partial D(b_{xy},\sigma )$ having a lower dimensionality than the space dimension $d$; that is, the critical droplet boundary is infinite but zero-density in ${\mathbb{E}}^d$. We refer to these as $\mathit{\text{zero}}-\text{density/}$ critical droplets (ZDCDs). (a finite critical droplet boundary also has zero density in ${\mathbb{E}}^d$, but we reserve the term “ZDCD” to apply only to critical droplets with an infinite boundary.)

Finally, there is the possibility that there exist infinite number of critical droplets whose boundary has dimension $d$, i.e., $\partial D(b_{xy},\sigma )$ comprises a positive density of edges in ${\mathbb{E}}^d$. We refer to these as space-filling critical droplets (SFCDs). These critical droplets have boundaries that pass within a distance $O(1)$ of any site in ${\mathbb{Z}}^d$; i.e., the closest distance from any site in ${\mathbb{Z}}^d$ to $\partial D(b_{xy},\sigma )$ is essentially independent of the location of the site.

Because our ground states are chosen from the zero-temperature PBC metastate (denoted ${\kappa }_J$), we can adapt a result from [25, 34, 35], which is described below:

Theorem 3.1. Let $\sigma$ denote an infinite-volume spin configuration. Then, for almost every $(J,\sigma )$ pair at zero temperature (which restricts the set of $\sigma$s to ground states corresponding to particular coupling realizations $J$), and for any type of critical droplet (finite, zero-density, or positive-density), either a positive density of edges in $\sigma$ has a critical droplet of that type or else no edges do.

The method of proof of this theorem is essentially identical to that used in [25, 35] and so will be omitted here. The conclusion is that there is zero probability that a ground state $\sigma$ chosen from ${\kappa }_J$ has a (finite or infinite) set of edges with zero density in ${\mathbb{E}}^d$ and has SFCDs (or finite critical droplets or ZDCDs).

4 Critical droplets and replica symmetry breaking

In [24], it was shown that there is a close connection between critical droplets and the four scenarios shown in Table 1. However, the results obtained were incomplete for the most prominent of the four scenarios, namely, replica symmetry breaking. In particular, it was proven there that the existence of SFCDs was a sufficient condition for some pairs of incongruent ground states to be separated by space-filling low-energy interfaces, hereafter referred to simply as “RSB interfaces” in accordance with Table 1. However, they were not shown to be necessary. This paper aimed to complete the correspondence between critical droplets and spin glass scenarios by demonstrating that the presence of SFCDs is not only sufficient but also a necessary condition for RSB interfaces to be present.

4.1 Sufficient condition

We first discuss the sufficient condition, which was derived in [24] as Theorem 8.2.

Theorem 4.1. (Newman et al. [24]). If a GSP $\sigma$ chosen from ${\kappa }_J$ has a positive fraction of edges with SFCDs, then $\sigma$ will have an RSB interface with one or more other GSPs in ${\kappa }_J$.

We reproduce the proof from reference [24] below.

Proof. In each finite-volume ${\mathrm{\Lambda }}_L$, an arbitrary edge was chosen uniformly at random within ${\mathbb{E}}_L$ (the edge set restricted to ${\mathrm{\Lambda }}_L$), and the excited-state ${\tau }_L$ generated by flipping its critical droplet was considered (with $J$ remaining fixed).

By assumption, the procedure defined above has a positive probability of generating a positive-density critical droplet, in which case the size of the interface boundary between ${\tau }_L$ and ${\sigma }_L$ scales as $L^d$. By the usual compactness arguments, the set of interfaces between the ${\tau }_L$s and ${\sigma }_L$s will converge to limiting space-filling interfaces between $\sigma$ and $\tau$, the infinite-volume spin configurations to which ${\sigma }_L$ and ${\tau }_L$ converge along one or more subsequences of ${\mathrm{\Lambda }}_L$s. By construction, the energy of the interface in any volume is twice the flexibility of the chosen edge and must decrease with $L$, so in the infinite-volume limit, the energy of the generated interface between $\tau$ and $\sigma$ remains $O(1)$ in any finite-volume subset of ${\mathbb{Z}}^d$.

Using this procedure, one such edge $b_1$ was chosen in ${\mathbb{E}}_L$, which has an SFCD in ${\sigma }_L$. By definition, the critical droplet is the lowest-energy droplet generated by changing an edge’s coupling value past its critical value. Then, Equation 2 is satisfied in ${\tau }_L$ for all closed contours or surfaces, except those passing through $b_1$. Next, a fixed cube (a “window”) centered at the origin whose edge $w$ satisfies $1\ll w\ll L$ was considered. Because $b_1$ is chosen uniformly at random within ${\mathrm{\Lambda }}_L$, it will move outside any fixed window with probability approaching one as $L\to \infty$; therefore, Equation 2 will be satisfied within any fixed window for $\tau$ itself. Consequently, $\tau$ is also an infinite-volume GSP of the Hamiltonian (Equation 1) with a positive-density low-energy interface with $\sigma$. $\diamond$

4.2 Necessary condition

In [24], it was shown that a necessary condition for the existence of RSB interfaces was the presence of at least one of two kinds of edges. The first of these consists of edges having SFCDs, and the second includes edges without SFCDs, but which lie in the critical droplet boundary of a positive density (in ${\mathbb{E}}^d$) of other edges. Next, we show that the second kind of edge is not needed and the presence of SFCDs is by itself a necessary condition. To do this, we use the concept of a metastate; an extensive introduction and review can be found in [12]. Here, we simply note that a metastate is a probability measure on the thermodynamic states of the system. Two different constructions can be found in [20, 36]. Without reference to various constructions, a metastate satisfies three properties: first, it is supported solely on the thermodynamic states of a given Hamiltonian generated through an infinite sequence of volumes with prespecified boundary conditions (such as periodic, free, or fixed). Second, it satisfies the property of coupling covariance, meaning that the set of thermodynamic states in the support of the metastate does not change when any finite set of couplings are varied. That is, correlations in the thermodynamic states may change, but every thermodynamic state in the metastate is mapped continuously to a new one as the couplings vary; no thermodynamic states flow into or out of the metastate under a finite change in couplings. Third, the metastate satisfies translation covariance, that is, a uniform lattice shift does not affect the metastate properties.

Using the properties of metastates, Arguin et al. [37] proved the following result for the EA Ising model:

Theorem 4.2. [37]. An edge correlation function $⟨{\sigma }_x{\sigma }_y⟩$, which differs with positive probability in two distinct metastates ${\kappa }_1$ and ${\kappa }_2$ was assumed. A thermodynamic state ${\mathrm{\Gamma }}_1$ with the support of ${\kappa }_1$ and similarly a thermodynamic state ${\mathrm{\Gamma }}_2$ with the support of${\kappa }_2$ was chosen. $F_L({\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2)$ denoted the free energy difference between ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ within the restricted volume ${\mathrm{\Lambda }}_L\in {\mathbb{Z}}^d$. Then, there is a constant $c>0$ such that the variance of $F_L(\mathrm{\Gamma },{\mathrm{\Gamma }}^{\prime })$ with respect to varying the couplings inside ${\mathrm{\Lambda }}_L$ satisfies

$\mathrm{V}\mathrm{a}\mathrm{r}\left(F_L\left(\mathrm{\Gamma },{\mathrm{\Gamma }}^{\prime }\right)\right)\ge c|{\mathrm{\Lambda }}_L|.(4)$

In [34, 35], the authors extended these ideas to a new kind of metastate called the restricted metastate. The idea behind restricted metastates is to start with a conventional metastate, which was constructed using an infinite sequence of volumes with PBCs (${\kappa }_J$). Next, a pure state (call it $\omega$) randomly from ${\kappa }_J$ was chosen, and then only those pure states in ${\kappa }_J$ whose edge overlap falls within a narrow prespecified range were retained. The edge overlap between two Gibbs states $\alpha$ and ${\alpha }^{\prime }$ is defined to be

$q_{\alpha {\alpha }^{\prime }}^{\left(e\right)}=\underset{L\to \infty }{\lim }\frac{1}{d|{\mathrm{\Lambda }}_L|}{\displaystyle \sum _{⟨xy⟩\in E_L}}{⟨{\sigma }_x{\sigma }_y⟩}_{\alpha }{⟨{\sigma }_x{\sigma }_y⟩}_{{\alpha }^{\prime }}.(5)$

where $E_L$ denotes the edge set within ${\mathrm{\Lambda }}_L$. This will generate a non-trivial metastate if ${\kappa }_J$ contains multiple “incongruent” pure states as predicted by RSB, i.e., pairs of pure states whose edge overlap is strictly smaller than their self-overlap. By choosing different prespecified overlaps, one can construct different restricted metastates that satisfy the conditions of Theorem 4.2, leading to the conclusion that the variance of free energy fluctuations increases linearly with the volume considered.

However, this can be done (so far) only at positive temperature because of the requirement of coupling covariance. It was shown in [35] (Lemma 4.1) that at positive temperature $q_{\alpha {\alpha }^{\prime }}^{(e)}$ was invariant with respect to a finite change in couplings. However, it is not necessarily the case that this is true for ground states because of the possibility of the existence of SFCDs. But it is also clear from Equation 5 that if SFCDs do not exist, then any finite change in couplings can affect only a zero density of edge correlations ${\sigma }_x{\sigma }_y$ (with $x$ and $y$ nearest neighbors) in either $\alpha$ or ${\alpha }^{\prime }$, now understood to refer to infinite-volume ground states. In this case, $q_{\alpha {\alpha }^{\prime }}^{(e)}$ again remains invariant under any finite change in couplings, coupling covariance is satisfied, and Theorem 4.2 can now be applied.

Now if RSB interfaces exist, then there must be ground states in the support of ${\kappa }_J$, which are mutually incongruent. Moreover, the magnitude of the energy of an interface (as measured from either $\alpha$ or ${\alpha }^{\prime }$) in ${\mathrm{\Lambda }}_L$ equals half the energy difference between $\alpha$ and ${\alpha }^{\prime }$ inside ${\mathrm{\Lambda }}_L$. But, as shown in Equation 4, the interface energy between $\alpha$ and ${\alpha }^{\prime }$—or any other pair of ground states chosen from ${\kappa }_J$—scales with $L$ (typically as $L^{d/2}$); see also Proposition 6.1 in [36]. The conclusion is that no pair of ground states in the support of ${\kappa }_J$ can differ by an RSB interface if SFCDs exist. We have therefore proved the main new result of this paper:

Theorem 4.3. If ground states in the support of the PBC metastate ${\kappa }_J$ have no edges with SFCDs, then RSB interfaces between two ground states are absent in the metastate.

Following the discussion in Section 12 of [35], we also have the following corollary:

Corollary 4.4. If ground states in the support of the two-dimensional zero-temperature PBC metastate ${\kappa }_J$ have no edges with SFCDs, then the metastate is supported on a single pair of spin-reversed ground states.

5 Discussion

Replica symmetry breaking predicts that there exist space-filling, low-energy interfaces between ground states in three and higher dimensions. We have shown that this prediction is equivalent to the presence of SFCDs for a positive density of edges in ${\mathbb{E}}^d$ in a typical ground state; that is, the presence of SFCDs is both a necessary and sufficient condition for the appearance of RSB interfaces. A stronger conclusion can be drawn in two dimensions, where ground state multiplicity relies on SFCDs: if they are absent, the zero-temperature PBC metastate ${\kappa }_J$ is supported on a single pair of spin-reversed ground states.

Where does this leave the other three scenarios appearing in Table 1? Like RSB, the chaotic pair scenario also predicts the appearance of multiple incongruent ground states separated by space-filling interfaces, but unlike RSB, the interface energy in chaotic pairs scales with $L$. To address this scenario, we require the following quantities, introduced in [24]. Let $K^{*}(b,\sigma )$ denote the number of edges in ${\mathbb{E}}^d$ whose critical droplet boundaries in ground-state $\sigma$ pass through the edge $b$. Then, for $k=\mathrm{1,2,3},\dots$, $P(k,\sigma )$ is defined to be the fraction of edges $b\in {\mathbb{E}}^d$ such that $K^{*}(b,\sigma )=k$, and let

$E_{\sigma }\left[K^{*}\right]={\displaystyle \sum _{k=1}^{\infty }}kP\left(k,\sigma \right).(6)$

That is, $E_{\sigma }[K^{*}]$ is the average number of edges whose critical droplet boundaries a typical edge belongs to in the GSP $\sigma$. Using results from this paper, Equation 6, and [24], we conclude that if SFCDs are absent and (a positive fraction of) ground states in ${\kappa }_J$ are characterized by $E_{\sigma }[K^{*}]=\infty$, then the chaotic pair scenario should hold.

It follows that neither RSB nor chaotic pairs will hold if $E_{\sigma }[K^{*}]<\infty$, which follows if $P(k,\sigma )$ falls off faster than $k^{-(2+\epsilon )}$ for any $\epsilon >0$ as $k\to \infty$. If this is the case, then ${\kappa }_J$ is supported on a single pair of spin-reversed ground states and either droplet-scaling or TNT should hold.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CN: conceptualization, formal analysis, investigation, validation, writing–original draft, and writing–review and editing. DS: conceptualization, formal analysis, investigation, validation, writing–original draft, and writing–review and editing.

Funding

The author(s) declare no that financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors thank the two reviewers for their comments on an earlier version, which helped clarify parts of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Edwards S, Anderson PW. Theory of spin glasses. J Phys F (1975) 5:965–74. doi:10.1088/0305-4608/5/5/017

CrossRef Full Text | Google Scholar

2. Parisi G. Infinite number of order parameters for spin-glasses. Phys Rev Lett (1979) 43:1754–6. doi:10.1103/physrevlett.43.1754

CrossRef Full Text | Google Scholar

3. Parisi G. Order parameter for spin-glasses. Phys Rev Lett (1983) 50:1946–8. doi:10.1103/physrevlett.50.1946

CrossRef Full Text | Google Scholar

4. Mézard M, Parisi G, Sourlas N, Toulouse G, Virasoro M. Nature of the spin-glass phase. Phys Rev Lett (1984) 52:1156–9. doi:10.1103/physrevlett.52.1156

CrossRef Full Text | Google Scholar

5. Mézard M, Parisi G, Sourlas N, Toulouse G, Virasoro M. Replica symmetry breaking and the nature of the spin glass phase. J Phys (Paris) (1984) 45:843–54. doi:10.1051/jphys:01984004505084300

CrossRef Full Text | Google Scholar

6. M Mézard, G Parisi, and MA Virasoro, editors. Spin glass theory and beyond. Singapore: World Scientific (1987).

Google Scholar

7. Marinari E, Parisi G, Ruiz-Lorenzo JJ, Ritort F. Numerical evidence for spontaneously broken replica symmetry in 3D spin glasses. Phys Rev Lett (1996) 76:843–6. doi:10.1103/physrevlett.76.843

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Marinari E, Parisi G, Ricci-Tersenghi F, Ruiz-Lorenzo JJ, Zuliani F. J Stat Phys (2000) 98:973–1074. doi:10.1023/a:1018607809852

CrossRef Full Text

9. Newman CM, Stein DL. J Stat Phys (2002) 106:213–44. doi:10.1023/a:1013128314054

CrossRef Full Text

10. Newman CM, Stein DL. Ordering and broken symmetry in short-ranged spin glasses. Cond Mat (2003) 15:R1319–64. doi:10.1088/0953-8984/15/32/202

CrossRef Full Text | Google Scholar

11. Read N. Short-range Ising spin glasses: the metastate interpretation of replica symmetry breaking. Phys Rev E (2014) 90:032142. doi:10.1103/physreve.90.032142

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Newman CM, Read N, Stein DL In: P Charbonneau, E Marinari, M Mézard, G Parisi, F Ricci-Tersenghi, G Sicuroet al. editors Spin glass theory and far beyond: replica symmetry breaking after 40 years. Singapore: World Scientific (2023). p. 697–718.

CrossRef Full Text | Google Scholar

13. McMillan WL. Scaling theory of Ising spin glasses. J Phys C (1984) 17:3179–87. doi:10.1088/0022-3719/17/18/010

CrossRef Full Text | Google Scholar

14. Bray AJ, Moore MA. Critical behavior of the three-dimensional Ising spin glass. Phys Rev B (1985) 31:631–3. doi:10.1103/physrevb.31.631

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Bray AJ, Moore MA. Chaotic nature of the spin-glass phase. Phys Rev Lett (1987) 58:57–60. doi:10.1103/physrevlett.58.57

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Fisher DS, Huse DA. Ordered phase of short-range ising spin-glasses. Phys Rev Lett (1986) 56:1601–4. doi:10.1103/physrevlett.56.1601

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Fisher DS, Huse DA. Equilibrium behavior of the spin-glass ordered phase. Phys Rev B (1988) 38:386–411. doi:10.1103/physrevb.38.386

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Marinari E, Parisi G. Effects of changing the boundary conditions on the ground state of Ising spin glasses. Phys Rev B (2000) 62:11677–85. doi:10.1103/physrevb.62.11677

CrossRef Full Text | Google Scholar

19. Palassini M, Young AP. Nature of the spin glass state. Phys Rev Lett (2000) 85:3017–20. doi:10.1103/physrevlett.85.3017

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Newman CM, Stein DL. Spatial inhomogeneity and thermodynamic chaos. Phys Rev Lett (1996) 76:4821–4. doi:10.1103/physrevlett.76.4821

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Newman CM, Stein DL. Metastate approach to thermodynamic chaos. Phys Rev E (1997) 55:5194–211. doi:10.1103/physreve.55.5194

CrossRef Full Text | Google Scholar

22. Newman CM, Stein DL. Mathematics of spin glasses and neural networks. Boston: Birkhauser (1998). p. 243–87.

CrossRef Full Text | Google Scholar

23. Newman CM, Stein DL. Ann. Henri poincaré, suppl. 1 4 (2003). p. S497.

Google Scholar

24. Newman CM, Stein DL. Ground-state stability and the nature of the spin glass phase. Phys Rev E (2022) 105:044132. doi:10.1103/physreve.105.044132

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Newman CM, Stein DL. Interfaces and the question of regional congruence in spin glasses. Phys Rev Lett (2001) 87:077201. doi:10.1103/physrevlett.87.077201

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Arguin L-P, Newman CM, Stein DL. A relation between disorder chaos and incongruent states in spin glasses on Z^d. Commun Math Phys (2019) 367:1019–43. doi:10.1007/s00220-019-03418-3

CrossRef Full Text | Google Scholar

27. de Almeida JRL, Thouless DJ. Stability of the Sherrington-Kirkpatrick solution of a spin glass model. J Phys A (1978) 11:983–90. doi:10.1088/0305-4470/11/5/028

CrossRef Full Text | Google Scholar

28. Huse DA, Fisher DS. Pure states in spin glasses. J Phys A (1987) 20:L997–L1003. doi:10.1088/0305-4470/20/15/012

CrossRef Full Text | Google Scholar

29. Fisher DS, Huse DA. Absence of many states in realistic spin glasses. J Phys A (1987) 20:L1005–10. doi:10.1088/0305-4470/20/15/013

CrossRef Full Text | Google Scholar

30. Newman CM, Stein DL. Nature of ground state incongruence in two-dimensional spin glasses. Phys Rev Lett (2000) 84:3966–9. doi:10.1103/physrevlett.84.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Newman CM, Stein DL. Commun Math Phys (2001) 224:205–18. doi:10.1007/pl00005586

CrossRef Full Text

32. Arguin L-P, Newman CM, Stein DL. In: In and out of equilibrium 3: celebrating vladas sidoravicius ME Vares, R Fernandez, LR Fontes, and CM Newman, editors. Cham: Birkhäuser (2021). p. 17–25.

CrossRef Full Text | Google Scholar

33. Arguin L-P, Damron M, Newman CM, Stein DL. Uniqueness of ground states for short-range spin glasses in the half-plane. Commun Math Phys (2010) 300:641–57. doi:10.1007/s00220-010-1130-8

CrossRef Full Text | Google Scholar

34. Newman CM, Stein DL. Overlap structure and free energy fluctuations in short-range spin glasses. J Phys A : Math Theor (2024) 57:11LT01. doi:10.1088/1751-8121/ad2b87

CrossRef Full Text | Google Scholar

35. Newman CM, Stein DL, (2024), arXiv:2407.17506.

36. Aizenman M, Wehr J. Rounding effects of quenched randomness on first-order phase transitions. Commun Math Phys (1990) 130:489–528. doi:10.1007/bf02096933

CrossRef Full Text | Google Scholar

37. Arguin L-P, Newman CM, Stein DL, Wehr J. Fluctuation bounds for interface free energies in spin glasses. J Stat Phys (2014) 156:221–38. doi:10.1007/s10955-014-1009-8

CrossRef Full Text | Google Scholar