- Physics Department, Emory University, Atlanta, GA, United States
We present a collection of simulations of the Edwards–Anderson lattice spin glass at
1 Introduction
Imagining physical systems in non-integer dimensions, such as through
To be specific, we simulate the Ising spin glass model due to Edwards and Anderson (EA) with the Hamiltonian [16].
The dynamic variables are binary (Ising) spins
To sample ground-state of the Hamiltonian in Equation 1 at high throughput and with minimal systematic errors, heuristics can only be relied on for systems with not more than

Figure 1. Phase diagram for bond-diluted spin glasses
2 Domain wall stiffness exponents
A quantity of fundamental importance for the modeling of amorphous magnetic materials through spin glasses [3, 20–23] is the domain wall or “stiffness” exponent
for the standard deviations of the domain wall energy
The importance of this exponent for small excitations in disordered spin systems has been discussed in many contexts [22, 24–28]. Spin systems with
Instead of waiting for a thermal fluctuation to spontaneously induce a domain wall, it is expedient to directly impose domains of size
As shown in Figure 2, using bond-diluted lattices for the EA system, in contrast, not only affords us a larger dynamic range in
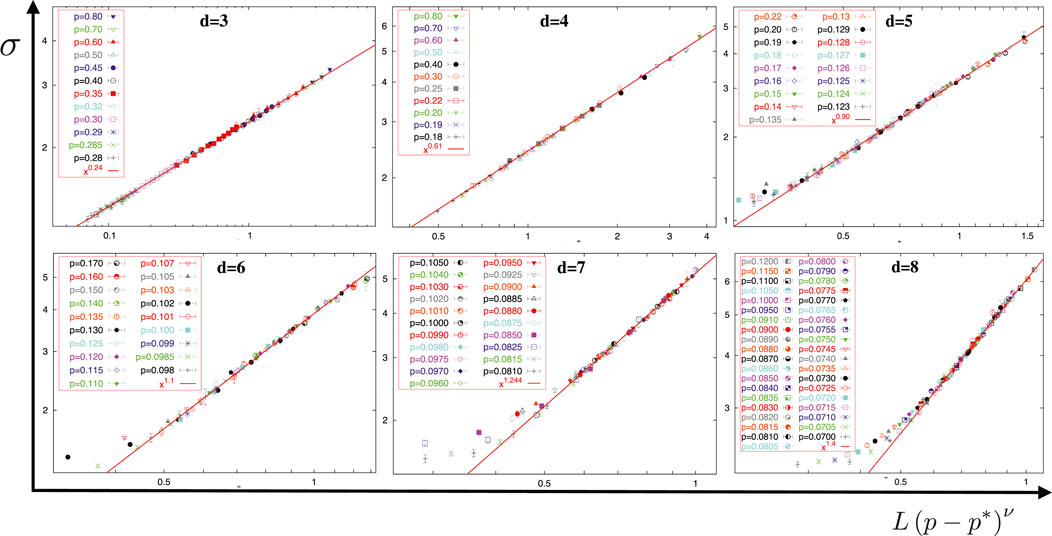
Figure 2. Data collapse for the domain wall scaling simulations of bond-diluted EA in
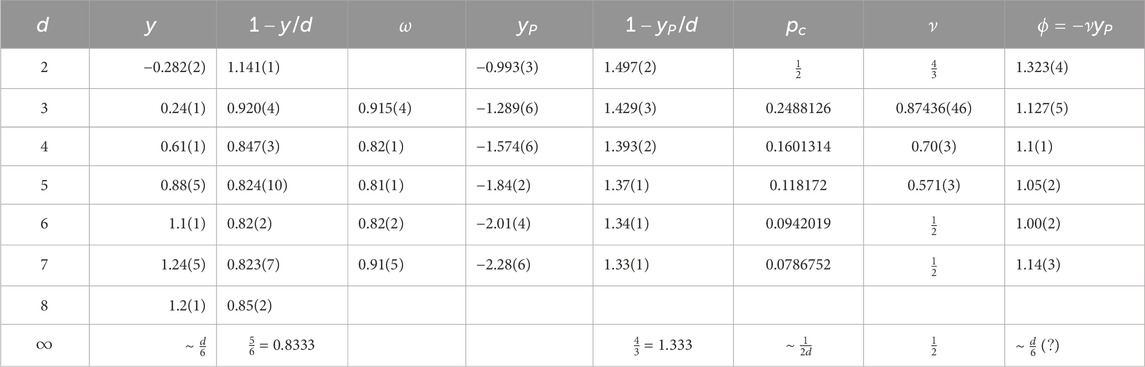
Table 1. Stiffness exponents for Edwards–Anderson spin glasses [11, 12] for dimensions
The values for
In the following section, we consider some other uses of the domain wall excitations.
3 Ground-state finite-size correction exponents
Since simulations of statistical systems are bound to be conducted at system sizes
For the ground-state energy densities in the EA system, [27] argued that such FSCs should be due to locked-in domain walls of energy
where the FSC exponent is conjectured to be
Indeed, our direct evaluation of ground-state energy densities at some fixed bond density
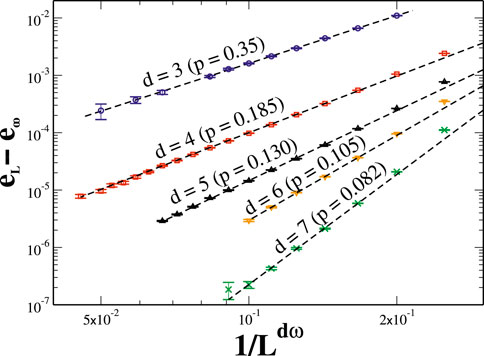
Figure 3. Plot of finite-size corrections to ground-state energies in bond-diluted lattice spin glasses (EA). For each dimension
We conducted a corresponding ground-state study at the edge of the SG regime (see Figure 1) by choosing the percolation point
4 Thermal–percolative crossover exponents
Having already determined the percolative stiffness exponents
Here, we assume that
Associating a temperature with the energy scale of the crossover in Equation 6 by
defining [51] the “thermal–percolative crossover exponent”
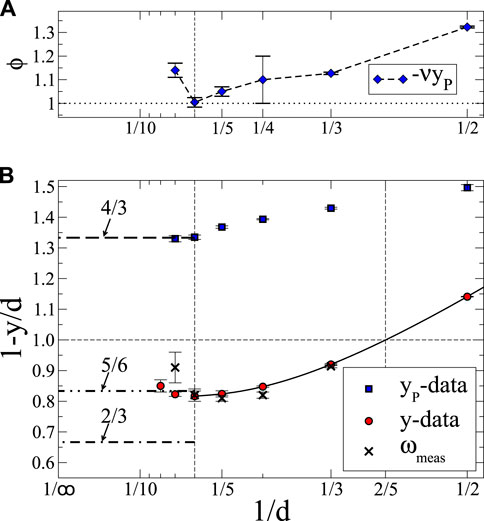
Figure 4. Plot summarizing the data for the exponents in Table 1, here plotted as a function of inverse dimension,
Of particular experimental interest is the result for
5 Conclusions
We summarized a collection of simulation data pertaining to the lattice spin glass EA over a range of dimensions, providing a comprehensive description of low-energy excitations from experimentally accessible systems to the mean-field level, where exact results can be compared with. Putting all those results side-by-side paints a self-consistent picture of domain wall excitations, their role in the stability of the ordered glass state, and their role for finite-size corrections. Extending to the very physical concept of bond density made simulations in high dimensions feasible, added accuracy, and opened up the spin-glass phase diagram, which makes new observables experimentally accessible, such as the thermal–percolative crossover exponent.
Going forward, the methods developed here could be extended to study, say, ground-state entropy and their overlaps [56] or the fractal nature of domain walls [57, 58]. Our method might also inspire new ways of using dilution as a gadget to make simulations more efficient [59].
Author contributions
SB: conceptualization, data curation, formal analysis, investigation, methodology, writing–original draft, and writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1466987/full#supplementary-material
Footnotes
1http://www.physics.emory.edu/faculty/boettcher
References
1. Wilson KG, Fisher ME. Critical exponents in 3.99 dimensions. Phys Rev Lett (1972) 28:240–3. doi:10.1103/physrevlett.28.240
2. t’Hooft G, Veltman MJG. Regularization and renormalization of gauge fields. Nucl Phys B (1972) 44:189–213. doi:10.1016/0550-3213(72)90279-9
3. Fischer KH, Hertz JA. Spin glasses, Cambridge studies in magnetism. Cambridge: Cambridge University Press (1991).
4. Mézard M, Parisi G, Virasoro MA. Spin glass theory and beyond. Singapore: World Scientific (1987).
6. Charbonneau P, Marinari E, Mezard M. Editors. Spin glass theory and far beyond. Singapore: World Scientific (2023).
7. de Dominicis C, Kondor I, Temesári T. Spin glasses and random fields. In: A Young, editor. Series on directions in condensed matter physics: volume 12. Singapore: World Scientific (1998).
8. Moore MA, Read N. Multicritical Point on the de Almeida–Thouless Line in Spin Glasses in d > 6 Dimensions. Phys Rev Lett (2018) 120:130602. doi:10.1103/physrevlett.120.130602
9. Moore MA. Droplet-scaling versus replica symmetry breaking debate in spin glasses revisited. Phys Rev E (2021) 103:062111. doi:10.1103/physreve.103.062111
10. Barahona F. On the computational complexity of Ising spin glass models. J Phys A: Math Gen (1982) 15:3241–53. doi:10.1088/0305-4470/15/10/028
11. Boettcher S. Stiffness exponents for lattice spin glasses in dimensions d = 3, . . . , 6. The Eur Phys J B - Condensed Matter (2004) 38:83–91. doi:10.1140/epjb/e2004-00102-5
12. Boettcher S. Low-temperature excitations of dilute lattice spin glasses. Europhys Lett (2004) 67:453–9. doi:10.1209/epl/i2004-10082-0
13. Boettcher S. Stiffness of the Edwards-Anderson model in all dimensions. Phys Rev Lett (2005) 95:197205. doi:10.1103/physrevlett.95.197205
14. Boettcher S, Marchetti E. Low-temperature phase boundary of dilute-lattice spin glasses. Phys Rev B (2008) 77:100405(R). doi:10.1103/physrevb.77.100405
15. Boettcher S, Falkner S. Finite-size corrections for ground states of Edwards-Anderson spin glasses. EPL (Europhysics Letters) (2012) 98:47005. doi:10.1209/0295-5075/98/47005
16. Edwards SF, Anderson PW. Theory of spin glasses. J Phys F (1975) 5:965–74. doi:10.1088/0305-4608/5/5/017
17. Boettcher S, Davidheiser J. Reduction of dilute Ising spin glasses. Phys Rev B (2008) 77:214432. doi:10.1103/physrevb.77.214432
18. Boettcher S, Percus AG. Optimization with extremal dynamics. Phys Rev Lett (2001) 86:5211–4. doi:10.1103/physrevlett.86.5211
19.In: A Hartmann, and H Rieger, editors. New optimization algorithms in physics. Berlin: Wiley VCH (2004).
20. Southern BW, Young AP. Real space rescaling study of spin glass behaviour in three dimensions. J Phys C: Solid State Phys (1977) 10:2179–95. doi:10.1088/0022-3719/10/12/023
21. McMillan WL. Scaling theory of Ising spin glasses. J Phys C: Solid State Phys (1984) 17:3179–87. doi:10.1088/0022-3719/17/18/010
22. Fisher DS, Huse DA. Ordered phase of short-range Ising spin-glasses. Phys Rev Lett (1986) 56:1601–4. doi:10.1103/physrevlett.56.1601
23. Bray AJ, Moore MA. Heidelberg colloquium on glassy dynamics and optimization In: L Van Hemmen, and I Morgenstern, editors. Proceedings of a colloquium on spin glasses, optimization and neural networks held at the University of Heidelberg. New York: Springer (1986). p. 121.
24. Krzakala F, Martin O. Spin and link overlaps in three-dimensional spin glasses. Phys Rev Lett (2000) 85:3013–6. doi:10.1103/physrevlett.85.3013
25. Palassini M, Young AP. Nature of the spin glass state. Phys Rev Lett (2000) 85:3017–20. doi:10.1103/physrevlett.85.3017
26. Palassini M, Liers F, Jünger M, Young AP. Interface energies in Ising spin glasses. Phys Rev B (2003) 68:064413. doi:10.1103/physrevb.68.064413
27. Bouchaud J-P, Krzakala F, Martin OC. Energy exponents and corrections to scaling in Ising spin glasses. Phys Rev B (2003) 68:224404. doi:10.1103/physrevb.68.224404
28. Aspelmeier T, Moore MA, Young AP. Interface energies in ising spin glasses. Phys Rev Lett (2003) 90:127202. doi:10.1103/physrevlett.90.127202
29. Bray AJ, Moore MA. Lower critical dimension of Ising spin glasses: a numerical study. J Phys C: Solid State Phys (1984) 17:L463–8. doi:10.1088/0022-3719/17/18/004
30. Franz S, Parisi G, Virasoro MA. Interfaces and lower critical dimension in a spin glass model. J Phys (France) (1994) 4:1657–67. doi:10.1051/jp1:1994213
31. Hartmann AK, Young AP. Lower critical dimension of Ising spin glasses. Phys Rev B (2001) 64:180404(R). doi:10.1103/physrevb.64.180404
32. Guchhait S, Orbach R. Direct dynamical evidence for the spin glass lower critical dimension 2 < dℓ < 3. Phys Rev Lett (2014) 112:126401. doi:10.1103/physrevlett.112.126401
33. Maiorano A, Parisi G. Support for the value 5/2 for the spin glass lower critical dimension at zero magnetic field. Proc Natl Acad Sci U S A (2018) 115:5129–34. doi:10.1073/pnas.1720832115
34. Hartmann AK. Ground-state clusters of two-three-and four-dimensional ± JIsing spin glasses. Phys Rev E (2000) 63:016106. doi:10.1103/physreve.63.016106
35. Parisi G, Rizzo T. Large deviations in the free energy of mean-field spin glasses. Phys Rev Lett (2008) 101:117205. doi:10.1103/physrevlett.101.117205
36. Lorenz CD, Ziff RM. Precise determination of the bond percolation thresholds and finite-size scaling corrections for the sc, fcc, and bcc lattices. Phys Rev E (1998) 57:230–6. doi:10.1103/physreve.57.230
37. Grassberger P. Critical percolation in high dimensions. Phys Rev E (2003) 67:036101. doi:10.1103/physreve.67.036101
38. Deng Y, Blöte HWJ. Monte Carlo study of the site-percolation model in two and three dimensions. Phys Rev E (2005) 72:016126. doi:10.1103/PhysRevE.72.016126
40. Pal KF. The ground state of the cubic spin glass with short-range interactions of Gaussian distribution. Physica A (1996) 233:60–6. doi:10.1016/s0378-4371(96)00241-5
42. Boettcher S. Analysis of the relation between quadratic unconstrained binary optimization and the spin-glass ground-state problem. Phys Rev Res (2019) 1:033142. doi:10.1103/physrevresearch.1.033142
43. Boettcher S. Deep reinforced learning heuristic tested on spin-glass ground states: the larger picture. Nat Commun (2023) 14:5658. doi:10.1038/s41467-023-41106-y
44. Boettcher S. Extremal optimization for Sherrington-Kirkpatrick spin glasses. The Eur Phys J B (2005) 46:501–5. doi:10.1140/epjb/e2005-00280-6
45. Boettcher S. Simulations of ground state fluctuations in mean-field Ising spin glasses. J Stat Mech Theor Exp (2010) 2010:P07002. doi:10.1088/1742-5468/2010/07/p07002
46. Aspelmeier T, Billoire A, Marinari E, Moore MA. Finite-size corrections in the Sherrington–Kirkpatrick model. J Phys A: Math Theor (2008) 41:324008. doi:10.1088/1751-8113/41/32/324008
48. Boettcher S. Numerical results for ground states of spin glasses on Bethe lattices. Eur Phys J B - Condensed Matter (2003) 31:29–39. doi:10.1140/epjb/e2003-00005-y
49. Zdeborová L, Boettcher S. A conjecture on the maximum cut and bisection width in random regular graphs. J Stat Mech Theor Exp (2010) 2010:P02020. doi:10.1088/1742-5468/2010/02/p02020
50. Boettcher S. Ground state properties of the diluted Sherrington-Kirkpatrick spin glass. Phys Rev Lett (2020) 124:177202. doi:10.1103/physrevlett.124.177202
51. Banavar JR, Bray AJ, Feng S. Critical behavior of random spin systems at the percolation threshold. Phys Rev Lett (1987) 58:1463–6. doi:10.1103/physrevlett.58.1463
52. Bray AJ, Feng S. Percolation of order in frustrated systems: the dilute J spin glass. Phys Rev B (1987) 36:8456–60. doi:10.1103/physrevb.36.8456
53. Poon SJ, Durand J. Magnetic-cluster description of spin glasses in amorphous La-Gd-Au alloys. Phys Rev B (1978) 18:6253–64. doi:10.1103/physrevb.18.6253
54. Beckman O, Figueroa E, Gramm K, Lundgren L, Rao KV, Chen HS. Spin wave and scaling law Analysis of amorphous (FexNix)75P16B6Al3by magnetization measurements. Phys Scr (1982) 25:726–30. doi:10.1088/0031-8949/25/6a/017
55. Vincent E. Ageing and the glass transition. In: M Henkel, M Pleimling, and R Sanctuary, editors. Ageing and the glass transition. Heidelberg: Springer (2007). 716 of Springer Lecture Notes in Physics, condmat/063583.
56. Boettcher S. Reduction of spin glasses applied to the Migdal-Kadanoff hierarchical lattice. Eur Phys J B - Condensed Matter (2003) 33:439–45. doi:10.1140/epjb/e2003-00184-5
57. Wang W, Moore MA, Katzgraber HG. Fractal dimension of interfaces in Edwards-Anderson and long-range Ising spin glasses: determining the applicability of different theoretical descriptions. Phys Rev Lett (2017) 119:100602. doi:10.1103/physrevlett.119.100602
58. Vedula B, Moore MA, Sharma A. Evidence that the AT transition disappears below six dimensions (2024). doi:10.48550/arXiv.2402.03711
Keywords: Edwards–Anderson spin glass, critical dimension, domain wall excitations, ground-state energies, percolation, heuristic algorithms
Citation: Boettcher S (2024) Physics of the Edwards–Anderson spin glass in dimensions d = 3, … ,8 from heuristic ground state optimization. Front. Phys. 12:1466987. doi: 10.3389/fphy.2024.1466987
Received: 18 July 2024; Accepted: 13 August 2024;
Published: 20 September 2024.
Edited by:
Konrad Jerzy Kapcia, Adam Mickiewicz University, PolandReviewed by:
Francisco Welington Lima, Federal University of Piauí, BrazilEkrem Aydiner, Istanbul University, Türkiye
Copyright © 2024 Boettcher. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefan Boettcher, c2JvZXR0Y0BlbW9yeS5lZHU=
 Stefan Boettcher
Stefan Boettcher