Designing electromagnetic resonators with quasinormal modes

Micro- and nanoresonators, which enable light trapping in small volumes for extended durations, play a crucial role in modern photonics. The optical response of these resonators is determined by their fundamental resonances, known as quasinormal modes (QNMs). Over the past decade, the electromagnetic theory of QNMs has undergone significant development and has now reached a level of maturity that allows its reliable application to numerous contemporary electromagnetic problems. In this review, we explore recent applications of QNM theory for designing and understanding micro and nanoresonators. We highlight why QNMs provide deep physical insights and enhance computational efficiency in scenarios involving mode hybridization and perturbation.

1 Introduction

Micro or nanoresonators play a crucial role in advancing modern photonics [1, 2]. The interaction of light with optical resonators is fundamentally governed by the excitation of intrinsic natural resonant modes. When excited by a pulse, these modes initially store energy and subsequently release it through exponential decay. Known as quasinormal modes (QNMs), they are source-free solutions, $\left[{\stackrel{\sim }{\mathbf{E}}}_m\left(\mathbf{r}\right),{\stackrel{\sim }{\mathbf{H}}}_m\left(\mathbf{r}\right)\right]\exp \left(-\mathit{i}{\stackrel{\sim }{\mathit{\omega }}}_{\mathit{m}}\mathit{t}\right)$ to Maxwell’s equations with complex frequencies ${\stackrel{\sim }{\omega }}_m$

$\nabla \times {\stackrel{\sim }{\mathbf{E}}}_m=i{\stackrel{\sim }{\omega }}_m{\mu }_0{\stackrel{\sim }{\mathbf{H}}}_m,\nabla \times {\stackrel{\sim }{\mathbf{H}}}_m=-i{\stackrel{\sim }{\omega }}_m\mathrm{\epsilon }\left(\mathbf{r},{\stackrel{\sim }{\omega }}_m\right){\stackrel{\sim }{\mathbf{E}}}_m,(1)$

and satisfy the outgoing-wave condition for $\left|\mathbf{r}\right|\to \infty$. Hereafter, ${\stackrel{\sim }{\mathbf{E}}}_m$ and ${\stackrel{\sim }{\mathbf{H}}}_m$ respectively denote the normalized electric and magnetic fields [3, 4], $\mathrm{\epsilon }$ denotes the possibly dispersive permittivity tensors. Unlike the normal modes of Hermitian systems, which have real frequencies, the imaginary part $\text{Im}\left({\stackrel{\sim }{\omega }}_m\right)$ is non-zero, accounting for absorption or radiation losses [3].

The QNMs of electromagnetic resonators are characterized by two main quantities: their mode volume (${\stackrel{\sim }{V}}_m$) and quality factor ($Q_m$) [4, 5]. The former is related to the spatial extent of the electromagnetic field and the latter is proportional to the confinement time in units of the optical period, $Q_m=-\left(1/2\right)\text{Re}\left({\stackrel{\sim }{\omega }}_m\right)/\text{Im}\left({\stackrel{\sim }{\omega }}_m\right)$ [3, 5, 6].

High-$Q$ resonators trap light for long time, whereas small mode volume resonators confine light in tiny volumes. Resonators with large $Q_m/{\stackrel{\sim }{V}}_m$ ratios strongly enhance the interaction between the trapped photons and the host materials, giving rise to significant nonlinear, quantum and optomechanical effects [1–4].

Photonic applications generally rely on two types of structures which respectively offer high $Q_m$ and small ${\stackrel{\sim }{V}}_m$. High- $Q$ resonators, typically with $Q_m$ ∼${10}^6$, are usually fabricated using lossless dielectric materials, such as the photonic crystal microcavities (Figure 1A). These structures can confine light for extended periods of time (typically $Q_m$ cycles) within volumes of about the resonant wavelength cube ${\lambda }_R^3$.

Figure 1

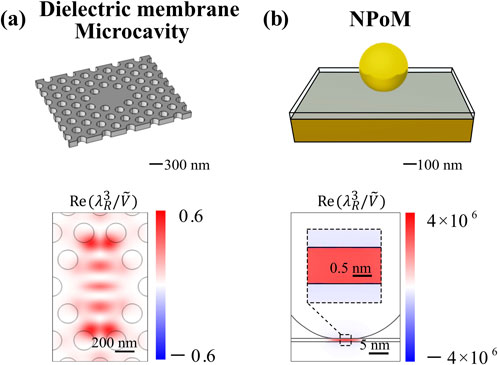
Figure 1. Examples of micro and nanocavities. (A) A photonic-crystal microcavity with a 330 nm lattice constant in a 320 nm-thick dielectric membrane has typical resonance wavelengths ${\lambda }_R$ at 1.5 µm. (B) A metal NPoM structure consists of a faceted gold nanoparticle (radius R = 20 nm) separated from a gold substrate by a 1 nm-thick dielectric film. The maps depict the real part of the inverse mode volume, $\text{Re}\left(1/{\stackrel{\sim }{V}}_m\right)$. The microcavity confines light within approximately ${\lambda }_R^3$, whereas the NPoM achieves a minimum mode volume of about ${10}^{-7}{\lambda }_R^3$. Note that the imaginary part, $\text{Im}\left(1/{\stackrel{\sim }{V}}_m\right)$, of the mode volume is not shown. Adapted from [5].

Resonators with mode volumes significantly smaller than ${\lambda }_R^3$ are engineered using metallic nanostructures that support localized plasmons [7]. One notable example is the nanoparticle-on-mirror (NPoM) construct (Figure 1B) [2, 8], which represents a current area of research interest. NPoM trap light in nanometer-sized dielectric gaps between two metal surfaces, achieving mode volumes as small as $\sim {10}^{-7}{\lambda }_R^3$. However, this exceptional spatial field confinement comes with a drawback: the inherent absorption of the materials restricts the quality factor to small values, $Q\sim 10-100$.

QNMs can be used to expand the electromagnetic field ${\mathbf{E}}^s\left(\mathbf{r},\omega \right)\exp \left(-i\omega t\right)$ scattered by resonators illuminated by monochromatic waves at frequency $\omega$ [3, 9]

${\mathbf{E}}^s\left(\mathbf{r},\omega \right)={\sum }_m{\alpha }_m\left(\omega \right){\stackrel{\sim }{\mathbf{E}}}_m\left(\mathbf{r}\right),(2)$

where the ${\alpha }_m$’s are modal excitation coefficients. The latter are known analytically and can be calculated as a spatial overlap between the normalized QNM field and the incident wave. They describe the contribution of the resonance modes to the optical response. A time-domain QNM expansion formula can also be derived from Equation 2 by performing a Fourier transformation from the frequency domain to the temporal domain

${\mathbf{E}}^s\left(\mathbf{r},t\right)=\text{Re}\left[{\sum }_m{\beta }_m\left(t\right){\stackrel{\sim }{\mathbf{E}}}_m\left(\mathbf{r}\right)\right].(3)$

In the past decade, there have been significant advancements in electromagnetic QNM theory. These include resolving the critical issue of QNM normalization [10–15], testing completeness of the QNM expansion across various systems [10, 16–23], and extending the analysis to the temporal domain [20, 24–27].

Nowadays, QNM theory is extensively utilized in designing optical resonators for various applications [28–30], including second- and higher-harmonic generation [31–33], optical parametric oscillators [34], Bell state generation [35], random lasing [36, 37], cavity QED [38–40], chiral molecule sensing [41, 42], quantum plasmonics [43–45], structural color generation [46], visual appearance generation [47], random medium [48], and ultrafast optics [24, 27]. But why are QNMs essential for nanoresonator design?

One explanation lies in the unique physical insights provided by QNM theory, which are often unattainable from brute-force numerical simulations. While the latter can be used to accurately compute the resonant spectra of resonator responses [2, 49–52], the spectrum interpretation can be indirect and sometimes incomplete. For instance, far-field incident light might not efficiently excite all modes, causing dark modes to be overshadowed by bright ones in the spectra. Additionally, spectrally overlapping resonances are difficult to distinguish, even with semi-analytical tools like the temporal-coupled mode theory [53, 54]. These resonances might merge to form a complex Fano response that appears as a single bell-like response, potentially leading to an incorrect interpretation with a single resonance [11, 55].

In contrast, QNMs are intrinsic to the system and independent of the incident field. By computing QNMs, optical dark modes can be identified unambiguously [56–60], and spectrally overlapping modes can be distinguished [11, 55, 61]. QNM expansion methods allow the reconstruction of optical scattering spectra [3, 9, 14, 20, 62, 63] with a weighted sum of QNMs. They may also provide explicit formula for the local density of electromagnetic states [11, 62, 64–67], a quantity of prime interest to interpret the optical response of resonators coupled with quantum emitters.

Another explanation is that electromagnetic QNM theory may also offer a significant improvement in computational efficiency over classical modeling tools that operate in the real-frequency or temporal domains. In frequency-domain simulations, calculations are repeated for each frequency, while in time-domain simulations, they must be repeated for different excitation fields.

The QNM expansion formula in Equation 2, which includes analytically-known ${\alpha }_m$ coefficients, allows efficient computation of the optical responses to arbitrary incident waves, once the dominant QNMs are determined [3, 68]. This efficiency is particularly useful for predicting the responses of resonant structures to various incident fields [69]. Applications include calculating the bidirectional reflectance distribution function (BRDF) of disordered metasurfaces [47], and assessing optical forces [70, 71], for instance.

Recent advancements in QNM perturbation [72, 73] and coupled QNM-theory [74–76] enable the prediction of the QNMs of altered geometries based on the QNMs of the initial geometry. They enhance computational efficiency not only for frequency sweeps but also for varying parameters such as shape or permittivity. This is particularly valuable for inverse design problems that require optical responses over plenty of parameter spaces.

This review aims to highlight recent advancements in applying QNMs to nanoresonator design, emphasizing the benefits of using QNM theory. Special focus is placed on how QNMs provide deep physical insights and enhance computational efficiency in mode hybridization and perturbation scenarios. For readers interested in the detailed physics and mathematical properties of electromagnetic QNMs, references such as [3, 5, 9, 10] are recommended. This article is structured as follows: a brief overview of key concepts on electromagnetic QNMs, followed by a discussion of their applications in resonator design.

2 QNM theory in a nutshell

2.1 Computation of electromagnetic QNMs

The computation of electromagnetic QNMs is now routinely performed using mode solvers for Maxwell’s equations [77]. The most common method involves calculating the poles of the resonator response (either a scattering-matrix element or a component of the scattered field at a specific spatial position) by driving the system with a source emitting at complex frequencies until the response diverges. Alternatively, one can directly solve the eigenvalue problem defined by Equation 1.

A few open-source software packages dedicated to QNM computation are available [77–79], including our comprehensive released freeware, MAN [68], which implements the pole-searching method or directly solves the eigenvalue problem.

2.2 The QNM divergence

QNM fields exponentially grow in space far away from the resonators, typically taking the form of a leaky spherical wave, ${\mathit{r}}^{-1}\exp \left[\mathit{i}{\stackrel{\sim }{\mathit{\omega }}}_{\mathit{m}}\left(-\mathit{t}+\mathit{r}/\mathit{c}\right)\right]$ as $r\to \infty$ in 3D open spaces. The spatial divergence has significantly slowed down the development of the electromagnetic QNM theory, just like in related areas, e.g., gravitational waves [80–84].

First, the spatial divergence raises difficulties in normalizing the QNMs fields [10]. Second, the spatial divergence also raises the question of whether the expansions of Equations 2, 3 are complete or not and when completeness is achieved, for what subspace [3, 85]. Indeed, note that the scattered field at real frequency always vanishes as $r^{-1}$ for $r\to \infty$; it seems unlikely that expansions relying on fields that all divergence for $r\to \infty$ may capture the special decay. In addition to the issue of incompleteness, the divergence appears to contradict our physical intuition, raising doubts about whether it ‘truly corresponds to any physical reality,’ as was noted long ago [86].

These issues have been addressed through extensive efforts notably over the past three decades.

Various frameworks for QNM normalization have been developed [10–15, 87, 88], and the completeness of QNM expansions (possibly augmented by numerical modes arising from QNM regularization [16, 20]) has been verified analytically and numerically in numerous examples [10, 16–23]. A recent review [10] provides advanced details and traces historical errors.

One widely adopted normalization framework is the PML-regularization method [11]. In this approach, the continuous Maxwell operator from Equation 1 is replaced by a linear operator within a finite physical domain bounded by perfectly matched layers (PMLs). The latter maps infinite open spaces into regularized Hilbert spaces, by converting the exponential growth of QNM fields in open space to an exponential decay within the PMLs. The regularized QNMs become square-integrable and are normalized with a volume integral over the physical domain $\mathrm{\Omega }$ inside the PML and the PML domain ${\mathrm{\Omega }}_{PML}$

${\iiint }_{\mathrm{\Omega }\cup {\mathrm{\Omega }}_{PML}}{\stackrel{\sim }{\mathbf{E}}}_m·\frac{\partial \omega \epsilon }{\partial \omega }{\stackrel{\sim }{\mathbf{E}}}_m-{\stackrel{\sim }{\mathbf{H}}}_m·\frac{\partial \omega \mu }{\partial \omega }{\stackrel{\sim }{\mathbf{H}}}_m{d}^3\mathbf{r}=1.(4)$

With Equation 4, analytical expressions for the modal expansion coefficients can be derived from first-principle calculations [11, 20]. Moreover, the QNM expansion augmented by numerical modes is complete for all $\mathbf{r}$ within the regularized space, including the PML domain. For non-dispersive resonators, biorthogonality warranties the uniqueness of the expansion coefficients ${\alpha }_m$. In the presence of dispersion, formulas of ${\alpha }_m$ depend on the choosing of the auxiliary field used for linearization and different methods for splitting the source term in Maxwell equation. Once these factors are defined ${\alpha }_m$ is also uniquely determined [10, 18, 20].

The PML regularization offers a framework to mimic the Hermitian system, by ensuring completeness and eliminating divergence. However, it does not offer a clear physical interpretation of the implications of the impact of QNM spatial divergence when analyzing the interaction of resonance with remote bodies positioned far away from resonators, where QNM fields largely diverge, as demonstrated in a recent study [89]. This study confirms that although QNM divergence leads to spectral instability, it does not cause any inconsistencies. The optical response of resonators disturbed by a distant body remains largely unchanged and can be accurately predicted using first-order QNM perturbation theory. It is also noteworthy that similar conclusions have been drawn in the context of gravitational waves [90–92].

3 Applications of QNMs in the design of optical resonators

The essence of resonance design involves perturbing and hybridizing resonances to achieve specific optical responses. Traditionally, this process involves performing repeated full-wave simulations at real frequencies [2, 28, 49–52]. However, as mentioned in the introduction, this conventional approach encounters significant physical and computational limitations. In this section, we explore several examples to demonstrate how QNM methods overcome these challenges and facilitate the design of modern optical resonators, focusing first on QNM hybridization and then on QNM perturbation.

3.1 QNM hybridization

The motivations for mode hybridization are twofold.

First, hybridization allows us to combine the properties of different resonant modes to create new modes with distinct multifunctional properties [56–61, 93–95], e.g., modes with both magnetic and electric responses [61, 93, 95–97], modes with both high radiative efficiency and small mode volume [2, 56, 58–60, 98]. A well-known example is the hybridization of photonic microcavities and plasmonic resonator modes [99–101]. This approach utilizes plasmonic components to achieve deep subwavelength confinement (small mode volumes), while preserving a relatively high $Q$ factor, which is inherited from the photonic cavity.

Second, hybridization induces a chemical-like “reaction” between modes, creating new modes with unique properties that go beyond a simple combination of the original modes. This serves as the second motivation for mode hybridization. For instance, when the eigenfrequencies of two QNMs cross each other as a parameter varies, the $Q$ factor of one mode can be significantly boosted reaching exceptionally high values [33, 102, 103]. Additionally, some studies have engineered interactions between modes to achieve exceptional points [104–107], where both the eigenvalues and eigenvectors of the interacting modes coalesce.

3.1.1 Mixing mode properties

A key feature of the QNM framework is its ability to compute the intrinsic properties of resonators and understand how these properties are affected by mode hybridization [56–60]. This capability allows for the design and optimization of nanoresonators, offering both computational efficiency and clear physical insights. This aspect is illustrated in Figure 2, with a structure known as a picocavity [2, 108–110]. The latter consists of a NPoM, but additionally encompasses an individual atomic-scale protuberance on one of the gap surfaces, as shown in Figure 2A. This structure, which has recently garnered significant attention [2, 56, 57, 108–110], demonstrates an impressive capability to confine light.

Figure 2

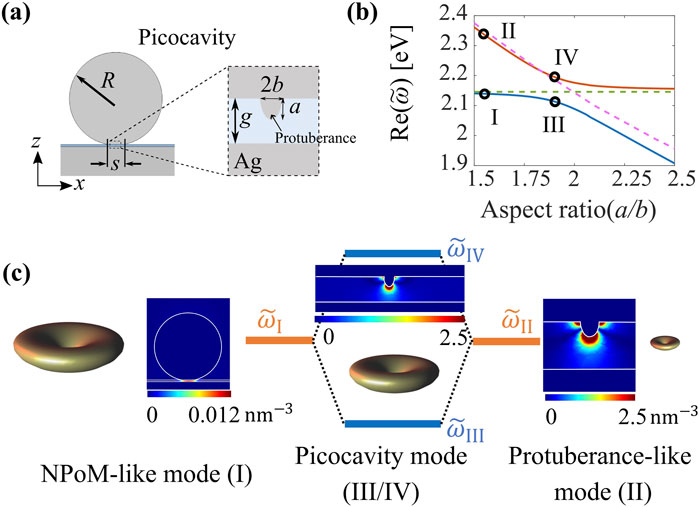
Figure 2. Mixing the properties of two QNMs by hybridization. (A) Schematic representation of a picocavity comprising an atomic-scale protuberance on a flat metal surface and a NPoM structure, each supporting a QNM. (B) Resonance frequencies as a function of the aspect ratio a/b of the protuberance. The mode of the protuberance strongly hybridizes with the mode of the NPoM for $a/b\approx 2$. (C) Energy level diagram illustrating the hybridization when the frequencies of the NPoM and protuberance modes are similar for $a/b=2$. Outside the hybridization region, the structure exhibits an NPoM-like mode (QNM I in (b)) and a protuberance-like mode (QNM II in (b)). The NPoM-like mode has a relatively large mode volume and high radiative efficiency, while the protuberance-like mode features an ultra-small mode volume and a low radiative efficiency. The near-field maps depict the real part of the inverse mode volume $1/{\stackrel{\sim }{V}}_m$, while the far-field radiation diagrams illustrate how the normalized QNMs radiate in the far field. (A) and (B) are adapted from [56].

Picocavities exhibit two types of QNMs [56, 57]. One type features an electric field that is highly localized near the protuberance, while the other exhibits electric field distributions akin to QNMs found in NPoM structures. We classify these as protuberance-like and NPoM-like QNMs, respectively. As depicted in Figure 2C, the protuberance-like QNM (mode II) provides extremely confined field characteristics, achieving a minimum mode volume below one cubic nanometer. However, due to the significant size disparity between the protuberance and the photon wavelength, this mode exhibits very low radiative efficiency. It cannot be efficiently excited by far-field sources (such as plane waves); when excited by a near-field emitter, almost all energy is converted into Ohmic losses in the metal, with minimal photon radiation in the far-field.

The mode volume of the NPoM-like mode (mode I) is much larger than that of the protuberance-like QNM. However, it offers high radiative efficiency and can be excited from the far-field. Its radiative efficiency, characterized by the intrinsic radiative diagram in Figure 2C, is approximately 20 times greater than that of the protuberance-like QNM.

A natural approach to achieve both high radiative efficiency and small mode volume involves coupling these two types of modes. The QNM framework facilitates monitoring the intrinsic properties as the modes hybridize. Figure 2B illustrates the eigenfrequencies of the hybridized QNMs as a function of the protuberance’s aspect ratio, depicted by the red and blue solid curves. As the aspect ratio increases, the protuberance-like mode undergoes a redshift, and an anticrossing of resonant frequencies occurs when its eigenfrequency approaches the energy of the NPoM mode. In this region, the QNMs are significantly hybridized. As depicted in Figure 2C, both modes achieve a mode volume of less than 1 nm³ and demonstrate high radiative efficiency, combining the advantageous characteristics of both NPoM and protuberance modes.

3.1.2 Engineering the mode interaction

Another significant application of QNM theory lies in engineering mode interactions [102, 111–113] to create new modes with properties distinct from a simple mixture of the original modes.

To illustrate our purpose, let us consider a resonator and let us deform it (Figure 3A). If we assume that two dominant QNMs are driving the resonator response, the new eigenfrequencies, ${\stackrel{\sim }{\omega }}_{hyb}$, of the deformed modes can be determined by solving a 2x2 eigenvalue problem [72]

$\left(\begin{array}{cc}{\stackrel{\sim }{\omega }}_1& 0\\ 0& {\stackrel{\sim }{\omega }}_2\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\end{array}\right)={\stackrel{\sim }{\omega }}_{hyb}\left(\begin{array}{cc}1+V_{11}& V_{12}\\ V_{21}& 1+V_{22}\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\end{array}\right)(5)$

where ${\stackrel{\sim }{\omega }}_{1\left(2\right)}$ are the QNM eigenfrequencies of the undeformed structure, ${\stackrel{\sim }{\omega }}_{hyb}$ is the unknown eigenfrequency of the deformed structure, and $a_1$ and $a_2$ are the modal excitation coefficients of the unperturbed QNMs. The terms $V_{ij}$ (with $i,j$ = 1, 2) are evaluated through an integral of the modal fields over the surface $S_r$ of the initial (undeformed) structure: $V_{ij}={\iint }_{S_r}h{\stackrel{\sim }{\mathbf{E}}}_i^{+}·\Delta \mathbf{\epsilon }\left({\stackrel{\sim }{\omega }}_j\right){\stackrel{\sim }{\mathbf{E}}}_j^{-}{d}^2\mathbf{r}$, where $h$ is the deformation perpendicular to the surface boundary (it varies with the curvilinear coordinate), and ${\stackrel{\sim }{\mathbf{E}}}_i^{+}$ and ${\stackrel{\sim }{\mathbf{E}}}_j^{-}$ the electric fields of the initial (undeformed) normalized QNMs at the outer (+) or inner ($-$) surface boundary. Outward deformations ($h>0$) and inward deformation ($h<0$) deformations (see Figure 3A) correspond to permittivity changes of $\Delta \mathbf{\epsilon }$ and $-\Delta \mathbf{\epsilon }$, respectively, where $\Delta \mathbf{\epsilon }={\mathbf{\epsilon }}_{res}-{\mathbf{\epsilon }}_b$ is the difference in permittivity between the resonator and background.

Figure 3

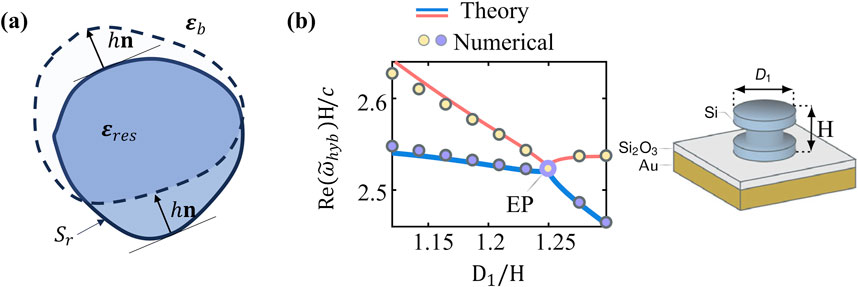
Figure 3. QNM interaction by deformation. (A) A nanoresonator is deformed with both inward and outward boundary changes. (B) Eigenfrequencies can be predicted with the analytical formula Equation 5 as we vary the shape. In (B), an exceptional point (denoted ‘EP’) is designed by deforming a nanoresonator. Full numerical calculations (circles) are compared to predictions obtained with Equation 5 (solid curves). Adapted from [72].

The $V_{ij}$ are generally complex numbers, with their imaginary parts arising from the non-Hermitian characteristics of the system. Typically, $V_{12}\ne V_{21}$, however if $\Delta \mathbf{\epsilon }\left({\stackrel{\sim }{\omega }}_2\right)\approx \Delta \mathbf{\epsilon }\left({\stackrel{\sim }{\omega }}_1\right)$, they are approximately equal.

The formula is derived using first-order approximations, ignoring contributions proportional to $h^2$ or higher-order terms for $V_{ij}$. Higher-order contributions can be included with more complex formulas. Nevertheless, except for specific cases where the first-order contribution vanishes due to symmetry, for instance, Equation 5 is accurate [72].

Using Equation 5, the new QNMs of the deformed structure are directly computed, enabling effective exploration of the parameter space to optimize the resonator shape. Figure 3B demonstrates the application of Equation 5 in designing nanoresonators that support exceptional points. This method significantly reduces the computation time needed to find the optimal design and provides insight into how geometric deformation influences mode hybridization.

3.2 Mode perturbation

QNM perturbation theory of electromagnetic resonators is particularly useful for cavity design and has been used in many applications, including evaluating optical resonator sensitivity for optical biosensing, inverse design of high-Q optical cavities [114], and understanding or engineering the interplay of classical electromagnetism with other physical phenomena or nonlinear processes, such as thermo-optics [115], Kerr [116, 117], or electron spill-out effects [43].

3.2.1 Perturbation theory for understanding refractive index changes

Traditionally, designing optical sensors involves calculating numerous resonance spectrum variations for various perturbation instances (such as position, shape, and material), which is time-consuming when using a parametric frequency scan approach. Furthermore, for very small perturbations, simulations must achieve extremely high accuracy to ensure that signal changes caused by the perturbation are not obscured by numerical noise.

Small perturbations cause a small change of the complex frequency of all the QNMs, as illustrated in Figure 4A. The small variation is conveniently predicted using cavity perturbation theory.

Figure 4

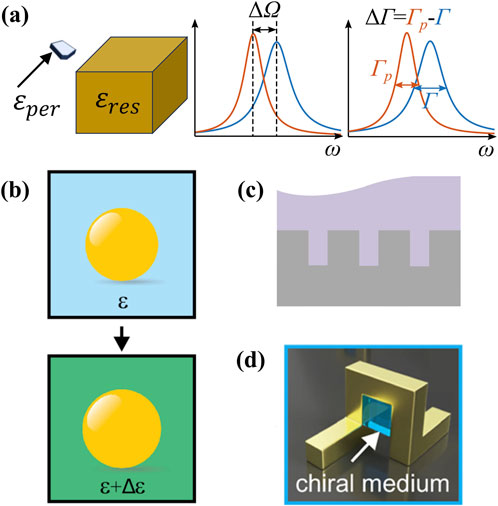
Figure 4. QNM perturbation theory for optical biosensors. (A) The introduction of a perturbation causes a resonant frequency shift $\Delta \mathrm{\Omega }$ and a linewidth change $\Delta \mathrm{\Gamma }$ in the spectral response (Equation 6) [118]. (B) The perturbation formula of Equation 6 has been extended for refractive-index changes extending over the entire open space surrounding the resonator [119]. (C) A perturbation formalism also exists for periodic structures [120]. (D) Perturbation formula has been developed for studying the index change caused by chiral mediums [41]. (B) is adapted from [119]; (C) is adapted from [120]; (D) is adapted from [41].

The correct QNM normalization allows for deriving an accurate first-order perturbation formula for non-Hermitian systems [118].

$\Delta {\stackrel{\sim }{\omega }}_m=-{\stackrel{\sim }{\omega }}_m{\iiint }_{{\mathrm{\Omega }}_{per}}\Delta \epsilon {\stackrel{\sim }{\mathbf{E}}}_m·{\stackrel{\sim }{\mathbf{E}}}_m{d}^3\mathbf{r}+O\left({\left|\Delta \epsilon \right|}^2\right),(6)$

where ${\mathrm{\Omega }}_{per}$ is the finite volume of the perturber, and $\Delta \epsilon ={\epsilon }_{per}-{\epsilon }_u$ is the difference in permittivity between the perturbed and unperturbed systems.

The predictive force of Equation 6 has been successfully validated for high-Q cavities by comparison with experimental data [121] and for low-Q plasmonic nanoresonators by comparison with full-wave computational data for various perturber shapes [118].

We may have noticed a difficulty also encountered in gravitational wave theory [80–84]: as the separation distance between the perturber and the resonator increases, the QNM field experienced by the perturber diverges. According to Equation 6, $\Delta {\stackrel{\sim }{\omega }}_m$ should also diverge, contradicting our intuitive expectations that remote perturbers should not affect resonator characteristics. This apparent contradiction has been recently studied in detail [89]. The conclusion is clear: Equation 6 remains valid regardless of how far away the perturbations are.

The issue of remote perturbations and divergent coupling requires much care as it leads to spectral instabilities. The complex frequency plane becomes increasingly populated with numerous Fabry-Perot QNMs, and the optical response of the perturbed system is dominated by these Fabry-Perot QNMs instead of the initially perturbed one. Similar QNM instability issues are encountered in the gravitational wave physics of black holes [80–84, 90–92]. The instability, also called ‘the flea in the elephant effect’, is caused by a small and remotely localized perturbation added to the black hole environment.

Equation 6 allows for the analytical evaluation of a crucial figure-of-merit (FoM) for optical resonators used in sensing applications, given by $\text{FoM}=S/\Delta \lambda$. Here $S$ represents the sensitivity, defined as the wavelength shift per unit change of the embedding medium refractive index, and Δλ is the bandwidth of the resonance. Since $1/\Delta \lambda$ is proportional to the Q factor and $S$ is proportional to $\Delta {\stackrel{\sim }{\omega }}_m$, from Equation 6, one can readily realize that $\text{FoM}\propto Q_m/{\stackrel{\sim }{V}}_m$, implying that an excellent candidate for an optical sensor should either possess a large $Q$ or a small mode volume.

The QNM perturbation toolbox for nanophotonic biosensor design has significantly expanded in recent years [41, 119, 120, 122, 123]. Equation 6 is valid for finite resonators perturbed by perturbers with finite size. This result has been extended to perturbations that cover the entire open space surrounding finite size resonators or periodic structures [119, 120, 123]. Equation 6 has also been extended to study systems that are perturbed by magnetic objects [122] or chiral molecules [41]. Refer to Figure 4 for more pictural details.

More recently, QNM perturbation theory has been further extended to predict the impact of perturbations on the optical scattering matrix [9, 41]. This extension allows for the prediction of variations in optical responses, such as changes in spectrum intensity and lineshape, beyond just frequency shifts and linewidth changes. The theory has proven crucial in the design of nanophotonic sensors for chiral molecules [124, 125]. It facilitates the rapid computation of the difference in circular dichroism spectra (ΔCD) with and without a chiral molecule. This is particularly important because, according to one of the authors [126], if the Pasteur parameter κ of the chiral molecule is extremely small, obtaining ΔCD can be computationally expensive due to the need for fine meshing to ensure the signal is above numerical noise.

3.2.2 Inverse design of optical resonators

QNM perturbation theory can be especially useful for inverse design. Equation 6 is not accurate for this critical case, as boundary variations cause abrupt field changes inside the perturbation volume ${\mathrm{\Omega }}_{per}$. This issue can be resolved using a technique known as local-field correction [127], which accounts for abrupt field changes by considering boundary conditions or the continuity of the electric field. By using local-field correction and assuming the perturbation does not cause hybridization between different QNMs, the frequency shift caused by shape deformation is given by $\Delta {\stackrel{\sim }{\omega }}_m=-{\stackrel{\sim }{\omega }}_m{\iint }_{S_r}h{\stackrel{\sim }{\mathbf{E}}}_m^{+}·\Delta \mathbf{\epsilon }\left({\stackrel{\sim }{\omega }}_m\right){\stackrel{\sim }{\mathbf{E}}}_m^{-}{d}^2\mathbf{r}$ [72, 118], where the variables are the same as those used in Equation 5. In fact, Equation 5 reduces to the present formula in the absence of mode hybridization.

One recent application of the formula can be found in [114], where QNM perturbation theory was used in combination with a gradient-based algorithm to maximize the Q-factor of cavities formed in dielectric slabs with disordered nanoholes.

3.2.3 Quantum effect

QNM perturbation theory has also been successfully applied to understand the role of quantum effects in the response of nanoresonators with ultrasmall volumes, such as NPoM structures or picocavities. In these systems, strong confinement leads to non-classical effects, such as nonlocality and electron spill-out, which cannot be predicted by Maxwell’s equations alone [128]. To accurately model these effects, numerical sampling must be significantly smaller than the Fermi wavelength, which is typically well below 1 nm [129]. This poses a significant challenge for incorporating quantum effects into classical Maxwell solvers.

QNM perturbation theory can potentially address this issue by treating non-classical effects as first-order perturbations of classical QNM fields. This approach allows for the analytical prediction of eigenfrequency changes due to non-classical corrections [43]. Recent advancements have further streamlined the computation of optical responses, such as Purcell factors and field enhancement factors [45]. They offer a quick method to evaluate how non-classical effects impact the optical properties of nanoresonators, including field confinement capability and scattering efficiency.

4 Perspectives and conclusion

Over the past decade, substantial advancements have been made in electromagnetic QNM theory, effectively addressing numerous critical challenges. The normalization of QNMs has been resolved [10–14], the completeness of QNM expansions has been confirmed for a variety of systems [10, 20, 21, 74], and the physical implications and causes of QNM divergence are beginning to be understood [89].

These developments have facilitated the creation of various analytical QNM frameworks that significantly improve the design and comprehension of micro and nanoresonators. In this review, we have highlighted recent progress, showcasing their benefits in offering greater numerical efficiency and physical insights compared to traditional design approaches. We hope this will encourage a wider adoption of QNMs and further innovation in electromagnetism and other areas of physics.

Despite these successes, research on QNMs in electromagnetism continues vigorously and several open questions remain.

One of the foremost issues is the convergence of QNM reconstruction, as described in Equations 2, 3. Achieving robust convergence is complex and influenced by numerous factors, including the material properties of the resonators [68], the choice of the formula for ${\alpha }_m$ [17, 18], and the configuration of perfectly matched layers (PML) used for regularization [19]. Currently, the community lacks a definitive guideline on optimizing these parameters to improve convergence.

Another unresolved issue is understanding the existence of various QNM decomposition formulas. As discussed in Section 2.2, in dispersive systems, the formula for ${\alpha }_m$ is sensitive to the choice of auxiliary fields and source terms. Although all formulas share a resonant pole term $1/\left({\stackrel{\sim }{\omega }}_m-\omega \right)$, they differ in a non-resonant term $f\left(\omega \right)$, which is a slow-varying function of $\omega$. Recent studies have shown that certain choice of $f\left(\omega \right)$ leads to ${\beta }_m$ in Equation 3, derived from ${\alpha }_m$, exhibiting an instantaneous response term [27, 130]. It would be important to verify that $f\left(\omega \right)$ for all the formulas offer a consistent physical interpretation.

From an application standpoint, there are numerous domains where QNM theory has yet to be fully utilized. For instance, QNM theory could potentially be applied to the analysis of spectra in photoemission electron microscopy (PEEM) [24], electron energy-loss spectroscopy (EELS), or high-order nonlinear optics [131], offering new insights and computational methods in these fields.

Finally, the recent interest in time-varying nanoresonators [132, 133], whose optical properties can be modulated on time scales comparable to the oscillation period of electromagnetic fields, has opened up new avenues for QNM research. Extending the QNM framework to model the optical response of these dynamic, non-Hermitian systems could help discover a wide range of novel effects and applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

TW: Writing–review and editing, Writing–original draft. PL: Writing–review and editing, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Agence Nationale de la Recherche (22CE24-0012-03).

Acknowledgments

PL acknowledges financial support from the WHEEL (ANR-22CE24-0012-03) Project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Vahala KJ. Optical microcavities. Nature (2003) 424:839–46. doi:10.1038/nature01939

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Baumberg JJ, Aizpurua J, Mikkelsen MH, Smith DR. Extreme nanophotonics from ultrathin metallic gaps. Nat Mater (2019) 18:668–78. doi:10.1038/s41563-019-0290-y

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lalanne P, Yan W, Vynck K, Sauvan C, Hugonin JP. Light interaction with photonic and plasmonic resonances. Laser Photon Rev (2018) 12:1700113. doi:10.1002/lpor.201700113

CrossRef Full Text | Google Scholar

4. Benisty H, Greffet JJ, Lalanne P. Introduction to nanophotonics. Oxford University Press (2022). doi:10.1093/oso/9780198786139.001.0001

CrossRef Full Text | Google Scholar

5. Wu T, Gurioli M, Lalanne P. Nanoscale light confinement: the Q’s and V’s. ACS Photon (2021) 8:1522–38. doi:10.1021/acsphotonics.1c00336

CrossRef Full Text | Google Scholar

6. Christopoulos T, Tsilipakos O, Sinatkas G, Kriezis EE. On the calculation of the quality factor in contemporary photonic resonant structures. Opt Expr (2019) 27:14505–22. doi:10.1364/OE.27.014505

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Giannini V, Fernández-Domínguez AI, Heck SC, Maier SA. Plasmonic nanoantennas: fundamentals and their use in controlling the radiative properties of nanoemitters. Chem Rev (2011) 111:3888–912. doi:10.1021/cr1002672

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Chikkaraddy R, De Nijs B, Benz F, Barrow SJ, Scherman OA, Rosta E, et al. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature (2016) 535:127–30. doi:10.1038/nature17974

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Both S, Weiss T. Resonant states and their role in nanophotonics. Semicond Sci Technol (2022) 37:013002. doi:10.1088/1361-6641/ac3290

CrossRef Full Text | Google Scholar

10. Sauvan C, Wu T, Zarouf R, Muljarov EA, Lalanne P. Normalization, orthogonality, and completeness of quasinormal modes of open systems: the case of electromagnetism [Invited]. Opt Expr (2022) 30:6846–85. doi:10.1364/OE.443656

CrossRef Full Text | Google Scholar

11. Sauvan C, Hugonin JP, Maksymov IS, Lalanne P. Theory of the spontaneous optical emission of nanosize photonic and plasmon resonators. Phys Rev Lett (2013) 110:237401. doi:10.1103/PhysRevLett.110.237401

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Muljarov EA, Langbein W, Zimmermann R. Brillouin-Wigner perturbation theory in open electromagnetic systems. Europhys Lett (2010) 92:50010. doi:10.1209/0295-5075/92/50010

CrossRef Full Text | Google Scholar

13. Muljarov EA, Langbein W. Exact mode volume and Purcell factor of open optical systems. Phys Rev B (2016) 94:235438. doi:10.1103/PhysRevB.94.235438

CrossRef Full Text | Google Scholar

14. Bai Q, Perrin M, Sauvan C, Hugonin JP, Lalanne P. Efficient and intuitive method for the analysis of light scattering by a resonant nanostructure. Opt Expr (2013) 21:27371. doi:10.1364/OE.21.027371

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Stout B, Colom R, Bonod N, McPhedran RC. Spectral expansions of open and dispersive optical systems: Gaussian regularization and convergence. New J Phys (2021) 23:083004. doi:10.1088/1367-2630/ac10a6

CrossRef Full Text | Google Scholar

16. Vial B, Nicolet A, Zolla F, Commandré M. Quasimodal expansion of electromagnetic fields in open two-dimensional structures. Phys Rev A (2014) 89:023829. doi:10.1103/PhysRevA.89.023829

CrossRef Full Text | Google Scholar

17. Truong MD, Nicolet A, Demésy G, Zolla F. Continuous family of exact Dispersive Quasi-Normal Modal (DQNM) expansions for dispersive photonic structures. Opt Expr (2020) 28:29016–32. doi:10.1364/OE.401742

CrossRef Full Text | Google Scholar

18. Gras A, Lalanne P, Duruflé M. Non-uniqueness of the quasinormal mode expansion of electromagnetic lorentz dispersive materials. J Opt Soc Am A (2020) 37:1219–28. doi:10.1364/JOSAA.394206

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Demésy G, Wu T, Brûlé Y, Zolla F, Nicolet A, Lalanne P, et al. Dispersive perfectly matched layers and high-order absorbing boundary conditions for electromagnetic quasinormal modes. J Opt Soc Am A (2023) 40:1947–58. doi:10.1364/JOSAA.499370

CrossRef Full Text | Google Scholar

20. Yan W, Faggiani R, Lalanne P. Rigorous modal analysis of plasmonic nanoresonators. Phys Rev B (2018) 97:205422. doi:10.1103/PhysRevB.97.205422

CrossRef Full Text | Google Scholar

21. Zolla F, Nicolet A, Demésy G. Photonics in highly dispersive media: the exact modal expansion. Opt Lett (2018) 43:5813–6. doi:10.1364/OL.43.005813

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Besbes M, Sauvan C. Role of static modes in quasinormal modes expansions: when and how to take them into account? Mathematics (2022) 10:3542. doi:10.3390/math10193542

CrossRef Full Text | Google Scholar

23. Sauvan C. Quasinormal modes expansions for nanoresonators made of absorbing dielectric materials: study of the role of static modes. Opt Expr (2021) 29:8268–82. doi:10.1364/OE.417909

CrossRef Full Text | Google Scholar

24. Faggiani R, Losquin A, Yang J, Marsell E, Mikkelsen A, Lalanne P. Modal analysis of the ultrafast dynamics of optical nanoresonators. ACS Photon (2017) 4:897–904. doi:10.1021/acsphotonics.6b00992

CrossRef Full Text | Google Scholar

25. Baldassari L, Millien P, Vanel AL. Modal approximation for plasmonic resonators in the time domain: the scalar case. Partial Differ Equations Appl (2021) 2:46. doi:10.1007/s42985-021-00098-4

CrossRef Full Text | Google Scholar

26. Ben Soltane I, Colom R, Stout B, Bonod N. Derivation of the transient and steady optical states from the Poles of the S-matrix. Laser Photon Rev (2023) 17:2200141. doi:10.1002/lpor.202200141

CrossRef Full Text | Google Scholar

27. Wu T, Lalanne P. Exact maxwell evolution equation of resonator dynamics: temporal coupled-mode theory revisited. Opt Expr (2024) 32:20904–14. doi:10.1364/OE.517237

CrossRef Full Text | Google Scholar

28. Huang L, Xu L, Powell DA, Padilla WJ, Miroshnichenko AE. Resonant leaky modes in all-dielectric metasystems: fundamentals and applications. Phys Rep (2023) 1008:1–66. doi:10.1016/j.physrep.2023.01.001

CrossRef Full Text | Google Scholar

29. Klimov VV. Optical nanoresonators. Phys Usp (2023) 193:263–87. doi:10.3367/UFNe.2022.02.039153

CrossRef Full Text | Google Scholar

30. Chang RK, Campillo AJ. Optical processes in microcavities. World Scientific (1996). doi:10.1142/2828

CrossRef Full Text | Google Scholar

31. Gigli C, Wu T, Marino G, Borne A, Leo G, Lalanne P. Quasinormal-mode non-hermitian modeling and design in nonlinear nano-optics. ACS Photon (2020) 7:1197–205. doi:10.1021/acsphotonics.0c00014

CrossRef Full Text | Google Scholar

32. Christopoulos T, Kriezis EE, Tsilipakos O. Multimode non-Hermitian framework for third harmonic generation in nonlinear photonic systems comprising two-dimensional materials. Phys Rev B (2023) 107:035413. doi:10.1103/PhysRevB.107.035413

CrossRef Full Text | Google Scholar

33. Koshelev K, Kruk S, Melik-Gaykazyan E, Choi J-H, Bogdanov A, Park H-G, et al. Subwavelength dielectric resonators for nonlinear nanophotonics. Science (2020) 367:288–92. doi:10.1126/science.aaz3985

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Jahani S, Roy A, Marandi A. Wavelength-scale optical parametric oscillators. Optica (2021) 8:262–8. doi:10.1364/OPTICA.411708

CrossRef Full Text | Google Scholar

35. Weissflog MA, Dezert R, Vinel V, Gigli C, Leo G, Pertsch T, et al. Nonlinear nanoresonators for Bell state generation. Appl Phys Rev (2024) 11:011403. doi:10.1063/5.0172240

CrossRef Full Text | Google Scholar

36. Türeci HE, Stone AD, Collier B. Self-consistent multimode lasing theory for complex or random lasing media. Phys Rev A (2006) 74:043822. doi:10.1103/PhysRevA.74.043822

CrossRef Full Text | Google Scholar

37. Andreasen J, Asatryan AA, Botten LC, Byrne MA, Cao H, Ge L, et al. Modes of random lasers. Adv Opt Photon (2011) 3:88–127. doi:10.1364/AOP.3.000088

CrossRef Full Text | Google Scholar

38. Lentrodt D, Evers J. Ab initio few-mode theory for quantum potential scattering problems. Phys Rev X (2020) 10:011008. doi:10.1103/PhysRevX.10.011008

CrossRef Full Text | Google Scholar

39. Lentrodt D, Diekmann O, Keitel CH, Rotter S, Evers J. Certifying multimode light-matter interaction in lossy resonators. Phys Rev Lett (2023) 130:263602. doi:10.1103/PhysRevLett.130.263602

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Medina I, García-Vidal FJ, Fernández-Domínguez AI, Feist J. Few-mode field quantization of arbitrary electromagnetic spectral densities. Phys Rev Lett (2021) 126:093601. doi:10.1103/PhysRevLett.126.093601

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Both S, Schäferling M, Sterl F, Muljarov EA, Giessen H, Weiss T. Nanophotonic chiral sensing: how does it actually work? ACS Nano (2022) 16:2822–32. doi:10.1021/acsnano.1c09796

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Almousa SF, Weiss T, Muljarov EA. Employing quasidegenerate optical modes for chiral sensing. Phys Rev B (2024) 109:L041410. doi:10.1103/PhysRevB.109.L041410

CrossRef Full Text | Google Scholar

43. Yang Y, Zhu D, Yan W, Agarwal A, Zheng M, Joannopoulos JD, et al. A general theoretical and experimental framework for nanoscale electromagnetism. Nature (2019) 576:248–52. doi:10.1038/s41586-019-1803-1

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Zhou Q, Zhang P, Chen X-W. General framework of canonical quasinormal mode analysis for extreme nano-optics. Phys Rev Lett (2021) 127:267401. doi:10.1103/PhysRevLett.127.267401

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Tao C, Zhong Y, Liu H. Quasinormal mode expansion theory for mesoscale plasmonic nanoresonators: an analytical treatment of nonclassical electromagnetic boundary condition. Phys Rev Lett (2022) 129:197401. doi:10.1103/PhysRevLett.129.197401

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Li Q, Wu T, van de Groep J, Lalanne P, Brongersma ML. Structural color from a coupled nanowire pair beyond the bonding and antibonding model. Optica (2021) 8:464–70. doi:10.1364/OPTICA.418888

CrossRef Full Text | Google Scholar

47. Agreda A, Wu T, Hereu A, Treguer-Delapierre M, Drisko GL, Vynck K, et al. Tailoring iridescent visual appearance with disordered resonant metasurfaces. ACS Nano. (2023) 17:6362–72. doi:10.1021/acsnano.2c10962

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Genack AZ, Zhang S. Wave interference and modes in random media in tutorials in complex photonic media in tutorials in complex photonic media. Bellingham, Washington, United States: SPIE Publications (2009). doi:10.1117/3.832717

CrossRef Full Text | Google Scholar

49. Kuznetsov AI, Miroshnichenko AE, Brongersma ML, Kivshar YS, Luk’yanchuk B. Optically resonant dielectric nanostructures. Science (2016) 354:aag2472. doi:10.1126/science.aag2472

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Limonov MF, Rybin MV, Poddubny AN, Kivshar YS. Fano resonances in photonics. Nat Photon (2017) 11:543–54. doi:10.1038/nphoton.2017.142

CrossRef Full Text | Google Scholar

51. Luk'Yanchuk B, Zheludev NI, Maier SA, Halas NJ, Nordlander P, Giessen H, et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat Mater (2010) 9:707–15. doi:10.1038/nmat2810

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Alaee R, Rockstuhl C, Fernandez-Corbaton I. Exact multipolar decompositions with applications in nanophotonics. Adv Opt Mater (2019) 7:1800783. doi:10.1002/adom.201800783

CrossRef Full Text | Google Scholar

53. Fan S, Suh W, Joannopoulos JD. Temporal coupled-mode theory for the Fano resonance in optical resonators. J Opt Soc Am A (2003) 20:569–72. doi:10.1364/JOSAA.20.000569

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Christopoulos T, Tsilipakos O, Kriezis EE. Temporal coupled-mode theory in nonlinear resonant photonics: from basic principles to contemporary systems with 2D materials, dispersion, loss, and gain. J Appl Phys (2024) 136:011101. doi:10.1063/5.0190631

CrossRef Full Text | Google Scholar

55. Pellegrino D, Balestri D, Granchi N, Ciardi M, Intonti F, Pagliano F, et al. Non-Lorentzian local density of states in coupled photonic crystal cavities probed by near- and far-field emission. Phys Rev Lett (2020) 124:123902. doi:10.1103/PhysRevLett.124.123902

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Wu T, Yan W, Lalanne P. Bright plasmons with cubic nanometer mode volumes through mode hybridization. ACS Photon (2021) 8:307–14. doi:10.1021/acsphotonics.0c01569

CrossRef Full Text | Google Scholar

57. Li W, Zhou Q, Zhang P, Chen XW. Bright optical eigenmode of 1 nm³ mode volume. Phys Rev Lett (2021) 126:257401. doi:10.1103/PhysRevLett.126.257401

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Zhang C, Hugonin JP, Greffet JJ, Sauvan C. Surface plasmon polaritons emission with nanopatch antennas: enhancement by means of mode hybridization. ACS Photon (2019) 6:2788–96. doi:10.1021/acsphotonics.9b00797

CrossRef Full Text | Google Scholar

59. Kongsuwan N, Demetriadou A, Horton M, Chikkaraddy R, Baumberg JJ, Hess O. Plasmonic nanocavity modes: from near-field to far-field radiation. ACS Photon (2020) 7:463–71. doi:10.1021/acsphotonics.9b01445

CrossRef Full Text | Google Scholar

60. Elliott E, Bedingfield K, Huang J, Hu S, De Nijs B, Demetriadou A, et al. Fingerprinting the hidden facets of plasmonic nanocavities. ACS Photon (2022) 9:2643–51. doi:10.1021/acsphotonics.2c00116

CrossRef Full Text | Google Scholar

61. Wu T, Baron A, Lalanne P, Vynck K. Intrinsic multipolar contents of nanoresonators for tailored scattering. Phys Rev A (2020) 101:011803. doi:10.1103/PhysRevA.101.011803

CrossRef Full Text | Google Scholar

62. Zschiedrich L, Binkowski F, Nikolay N, Benson O, Kewes G, Burger S. Riesz-projection-based theory of light-matter interaction in dispersive nanoresonators. Phys Rev A (2018) 98:043806. doi:10.1103/PhysRevA.98.043806

CrossRef Full Text | Google Scholar

63. Ming X. Quasinormal mode expansion method for resonators with partial-fraction material dispersion. arXiv preprint arXiv:2312.11048 (2023). doi:10.48550/arXiv.2312.11048

CrossRef Full Text | Google Scholar

64. Tang XT, Ma L, You Y, Du XJ, Qiu H, Guan XH, et al. Relations between near-field enhancements and Purcell factors in hybrid nanostructures of plasmonic antennas and dielectric cavities. Opt Expr (2024) 32:16746–60. doi:10.1364/OE.521090

CrossRef Full Text | Google Scholar

65. Miller OD. Fundamental limits to near-field optical response. In: Advances in near-field optics. Springer (2023). doi:10.1007/978-3-031-34742-9_2

CrossRef Full Text | Google Scholar

66. Netherwood KS, Riley H, Muljarov EA. Exceptional points in optical systems: a resonant-state expansion study. arXiv preprint arXiv:2309.12536 (2023). doi:10.48550/arXiv.2309.12536

CrossRef Full Text | Google Scholar

67. Pick A, Zhen B, Miller OD, Hsu CW, Hernandez F, Rodriguez AW, et al. General theory of spontaneous emission near exceptional points. Opt Expr (2017) 25:12325–48. doi:10.1364/OE.25.012325

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Wu T, Arrivault D, Yan W, Lalanne P. Modal analysis of electromagnetic resonators: user guide for the MAN program. Comput Phys Commun (2023) 284:108627. doi:10.1016/j.cpc.2022.108627

CrossRef Full Text | Google Scholar

69. Wu T, Arrivault D, Duruflé M, Gras A, Binkowski F, Burger S, et al. Efficient hybrid method for the modal analysis of optical microcavities and nanoresonators. J Opt Soc Am A (2021) 38:1224–31. doi:10.1364/JOSAA.428224

CrossRef Full Text | Google Scholar

70. Qi Z, Tao C, Rong S, Zhong Y, Liu H. Efficient method for the calculation of the optical force of a single nanoparticle based on the quasinormal mode expansion. Opt Lett (2021) 46:2658–61. doi:10.1364/OL.426423

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Lu X, Tao Q, Zhong Y, Liu H. Efficient method for the electrodynamics Langevin-dynamics simulation of multiple nanoparticles based on the coupling theory of quasinormal mode. ACS Photon (2024). doi:10.1021/acsphotonics.3c01904

CrossRef Full Text | Google Scholar

72. Yan W, Lalanne P, Qiu M. Shape deformation of nanoresonator: a quasinormal-mode perturbation theory. Phys Rev Lett (2020) 125:013901. doi:10.1103/PhysRevLett.125.013901

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Sztranyovszky Z, Langbein W, Muljarov EA. First-order perturbation theory of eigenmodes for systems with interfaces. Phys Rev Res (2023) 5:013209. doi:10.1103/PhysRevResearch.5.013209

CrossRef Full Text | Google Scholar

74. Muljarov EA, Langbein W. Resonant-state expansion of dispersive open optical systems: creating gold from sand. Phys Rev B (2016) 93:075417. doi:10.1103/PhysRevB.93.075417

CrossRef Full Text | Google Scholar

75. Tao C, Zhu J, Zhong Y, Liu H. Coupling theory of quasinormal modes for lossy and dispersive plasmonic nanoresonators. Phys Rev B (2020) 102:045430. doi:10.1103/PhysRevB.102.045430

CrossRef Full Text | Google Scholar

76. Tao Q, Su Y, Tao C, Zhong Y, Liu H. Efficient method for modeling large-scale arrays of optical nanoresonators based on the coupling theory of quasinormal mode. Opt Expr (2024) 32:7171–84. doi:10.1364/OE.515087

CrossRef Full Text | Google Scholar

77. Lalanne P, Yan W, Gras A, Sauvan C, Hugonin JP, Besbes M, et al. Quasinormal mode solvers for resonators with dispersive materials. J Opt Soc Am A (2019) 36:686–704. doi:10.1364/JOSAA.36.000686

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Demésy G, Nicolet A, Gralak B, Geuzaine C, Campos C, Roman JE. Non-linear eigenvalue problems with GetDP and SLEPc: eigenmode computations of frequencydispersive photonic open structures. Comput Phys Commun (2020) 257:107509. doi:10.1016/j.cpc.2020.107509

CrossRef Full Text | Google Scholar

79. Betz F, Binkowski F, Burger S. RPExpand: software for Riesz projection expansion of resonance phenomena. SoftwareX (2021) 15:100763. doi:10.1016/j.softx.2021.100763

CrossRef Full Text | Google Scholar

80. Nollert HP. Quasinormal modes: the characteristic `sound' of black holes and neutron stars. Class Quan Grav (1999) 16:R159–216. doi:10.1088/0264-9381/16/12/201

CrossRef Full Text | Google Scholar

81. Barausse E, Cardoso V, Pani P. Can environmental effects spoil precision gravitational-wave astrophysics? Phys Rev D (2014) 89:104059. doi:10.1103/PhysRevD.89.104059

CrossRef Full Text | Google Scholar

82. Jaramillo JL, Macedo RP, Al Sheikh L. Pseudospectrum and black hole quasinormal mode instability. Phys Rev X (2021) 11:031003. doi:10.1103/PhysRevX.11.031003

CrossRef Full Text | Google Scholar

83. Cheung M, Destounis K, Macedo RP, Berti E, Cardoso V. Destabilizing the fundamental mode of black holes: the elephant and the flea. Phys Rev Lett (2022) 128:111103. doi:10.1103/PhysRevLett.128.111103

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Jaramillo JL, Macedo RP, Al Sheikh L. Gravitational wave signatures of black hole quasinormal mode instability. Phys Rev Lett (2022) 128:211102. doi:10.1103/PhysRevLett.128.211102

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Ching ESC, Leung PT, Van Den Brink AM, Suen WM, Tong SS, Young K. Quasinormal-mode expansion for waves in open systems. Rev Mod Phys (1998) 70:1545–54. doi:10.1103/RevModPhys.70.1545

CrossRef Full Text | Google Scholar

86. Lamb H. On a peculiarity of the wave-system due to the free vibrations of a nucleus in an extended medium. Proc Lond Math. Soc. (1900) XXXII:208–13. doi:10.1112/plms/s1-32.1.208

CrossRef Full Text | Google Scholar

87. Leung PT, Pang KM. Completeness and time-independent perturbation of morphology-dependent resonances in dielectric spheres. J Opt Soc Am B (1996) 13:805–17. doi:10.1364/JOSAB.13.000805

CrossRef Full Text | Google Scholar

88. Lalanne P. Mode volume of electromagnetic resonators: let us try giving credit where it is due. In: arXiv preprint arXiv:2011.00218 (2020). doi:10.48550/arXiv.2011.00218

CrossRef Full Text | Google Scholar

89. Wu T, Jaramillo JL, Lalanne P. Understanding the physics related to the spatial exponential growth of electromagnetic quasinormal modes. arXiv preprint arXiv:2401 (2024):15112. doi:10.48550/arXiv.2401.15112

CrossRef Full Text | Google Scholar

90. Berti E, Cardoso V, Cheung Y, Di Filippo F, Duque F, Martens P, et al. Stability of the fundamental quasinormal mode in time-domain observations against small perturbations. Phys Rev D (2022) 106:084011. doi:10.1103/PhysRevD.106.084011

CrossRef Full Text | Google Scholar

91. Rosato RF, Destounis K, Pani P. Ringdown stability: greybody factors as stable gravitational-wave observables. arXiv preprint arXiv:2406.01692. (2024)

Google Scholar

92. Torres T. From black hole spectral instability to stable observables. Phys Rev Lett (2023) 131:111401. doi:10.1103/PhysRevLett.131.111401

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Chen W, Chen Y, Liu W. Multipolar conversion induced subwavelength high-Q Kerker supermodes with unidirectional radiations. Laser Photon Rev (2019) 13:1900067. doi:10.1002/lpor.201900067

CrossRef Full Text | Google Scholar

94. Halas NJ, Lal S, Chang WS, Link S, Nordlander P. Plasmons in strongly coupled metallic nanostructures. Chem Rev (2011) 111:3913–61. doi:10.1021/cr200061k

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Sheikholeslami SN, García-Etxarri A, Dionne JA. Controlling the interplay of electric and magnetic modes via Fano-like plasmon resonances. Nano Lett (2011) 11:3927–34. doi:10.1021/nl202143j

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Cheng Y, Oyesina KA, Xue B, Lei D, Wong AM, Wang S. Directional dipole dice enabled by anisotropic chirality. Proc Natl Acad Sci (2023) 120:e2301620120. doi:10.1073/pnas.2301620120

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Alaee R, Albooyeh M, Rahimzadegan A, Mirmoosa MS, Kivshar YS, Rockstuhl C. All-dielectric reciprocal bianisotropic nanoparticles. Phys Rev B (2015) 92:245130. doi:10.1103/PhysRevB.92.245130

CrossRef Full Text | Google Scholar

98. Tserkezis C, Esteban R, Sigle DO, Mertens J, Herrmann LO, Baumberg JJ, et al. Hybridization of plasmonic antenna and cavity modes: extreme optics of nanoparticle-on-mirror nanogaps. Phys Rev A (2015) 92:053811. doi:10.1103/PhysRevA.92.053811

CrossRef Full Text | Google Scholar

99. Cognée KG, Doeleman HM, Lalanne P, Koenderink AF. Cooperative interactions between nano-antennas in a high-Q cavity for unidirectional light sources. Light Sci Appl (2019) 8:115. doi:10.1038/s41377-019-0227-x

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Baaske M, Foreman M, Vollmer F. Single-molecule nucleic acid interactions monitored on a label-free microcavity biosensor platform. Nat Nanotechnol (2014) 9:933–9. doi:10.1038/nnano.2014.180

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Fu Y, Qing YM, Li Z, Zayats AV, Lei D. Tale of two resonances: waveguide–plasmon coupling and high Q-factor engineering on the nanoscale. ACS Photon (2022) 10:2–12. doi:10.1021/acsphotonics.2c01271

CrossRef Full Text | Google Scholar

102. Rybin MV, Koshelev KL, Sadrieva ZF, Samusev KB, Bogdanov AA, Limonov MF, et al. High-Q supercavity modes in subwavelength dielectric resonators. Phys Rev Lett (2017) 119:243901. doi:10.1103/PhysRevLett.119.243901

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Mikhailovskii MS, Poleva MA, Solodovchenko NS, Sidorenko MS, Sadrieva ZF, Petrov MI, et al. Engineering of high-Q states via collective mode coupling in chains of Mie resonators. ACS Photon (2024) 11:1657–63. doi:10.1021/acsphotonics.3c01874

CrossRef Full Text | Google Scholar

104. Miri MA, Alu A. Exceptional points in optics and photonics. Science (2019) 363:eaar7709. doi:10.1126/science.aar7709

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Li A, Wei H, Cotrufo M, Chen W, Mann S, Ni X, et al. Exceptional points and non-Hermitian photonics at the nanoscale. Nat Nanotechnol (2023) 18:706–20. doi:10.1038/s41565-023-01408-0

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Özdemir ŞK, Rotter S, Nori F, Yang L. Parity–time symmetry and exceptional points in photonics. Nat Mater (2019) 18:783–98. doi:10.1038/s41563-019-0304-9

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Solodovchenko NS, Samusev KB, Limonov MF. Quadruplets of exceptional points and bound states in the continuum in dielectric rings. Phys Rev B (2024) 109:075131. doi:10.1103/PhysRevB.109.075131

CrossRef Full Text | Google Scholar

108. Benz F, Schmidt MK, Dreismann A, Chikkaraddy R, Zhang Y, Demetriadou A, et al. Single-molecule optomechanics in picocavities. Science (2016) 354:726–9. doi:10.1126/science.aah5243

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Baumberg JJ. Picocavities: a primer. Nano Lett (2022) 22:5859–65. doi:10.1021/acs.nanolett.2c01695

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Griffiths J, De Nijs B, Chikkaraddy R, Baumberg JJ. Locating single-atom optical picocavities using wavelength-multiplexed Raman scattering. ACS Photon (2021) 8:2868–75. doi:10.1021/acsphotonics.1c01100

CrossRef Full Text | Google Scholar

111. Canós VA, Bobrovs V, Weiss T, Gao L, Shalin AS, Kivshar Y. Bianisotropic exceptional points in an isolated dielectric nanoparticle. Phys Rev Res (2024) 6:013053. doi:10.1103/PhysRevResearch.6.013053

CrossRef Full Text | Google Scholar

112. Canós Valero A, Shamkhi HK, Kupriianov AS, Weiss T, Pavlov AA, Redka D, et al. Superscattering emerging from the physics of bound states in the continuum. Nat Commun (2023) 14:4689. doi:10.1038/s41467-023-40382-y

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Colom R, Binkowski F, Betz F, Kivshar Y, Burger S. Enhanced Purcell factor for nanoantennas supporting interfering resonances. Phys Rev Res (2022) 4:023189. doi:10.1103/PhysRevResearch.4.023189

CrossRef Full Text | Google Scholar

114. Granchi N, Intonti F, Florescu M, García PD, Gurioli M, Arregui G. Q-factor optimization of modes in ordered and disordered photonic systems using non-Hermitian perturbation theory. ACS Photon (2023) 10:2808–15. doi:10.1021/acsphotonics.3c00510

CrossRef Full Text | Google Scholar

115. Lewi T, Evans HA, Butakov NA, Schuller JA. Ultrawide thermo-optic tuning of PbTe meta-atoms. Nano Lett (2017) 17:3940–5. doi:10.1021/acs.nanolett.7b01529

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Shcherbakov MR, Vabishchevich PP, Shorokhov AS, Chong KE, Choi DY, Staude I, et al. Ultrafast all-optical switching with magnetic resonances in nonlinear dielectric nanostructures. Nano Lett (2015) 15:6985–90. doi:10.1021/acs.nanolett.5b02989

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Christopoulos T, Tsilipakos O, Kriezis EE. Perturbation theory for Kerr nonlinear leaky cavities. Opt Lett (2020) 45:6442–5. doi:10.1364/OL.408336

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Yang J, Giessen H, Lalanne P. Simple analytical expression for the peak-frequency shifts of plasmonic resonances for sensing. Nano Lett (2015) 15:3439–44. doi:10.1021/acs.nanolett.5b00771

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Both S, Weiss T. First-order perturbation theory for changes in the surrounding of open optical resonators. Opt Lett (2019) 44:5917–20. doi:10.1364/OL.44.005917

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Gras A, Yan W, Lalanne P. Quasinormal-mode analysis of grating spectra at fixed incidence angles. Opt Lett (2019) 44:3494–7. doi:10.1364/OL.44.003494

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Cognée KG, Yan W, La China F, Balestri D, Intonti F, Gurioli M, et al. Mapping complex mode volumes with cavity perturbation theory. Optica (2019) 6:269–73. doi:10.1364/OPTICA.6.000269

CrossRef Full Text | Google Scholar

122. Caselli N, Wu T, Arregui G, Granchi N, Intonti F, Lalanne P, et al. Near-field imaging of magnetic complex mode volume. ACS Photon (2021) 8(8):1258–63. doi:10.1021/acsphotonics.0c01943

CrossRef Full Text | Google Scholar

123. Almousa SF, Muljarov EA. Exact theory and approximations for optical resonators in a changing external medium. Phys Rev B (2023) 107:L081401. doi:10.1103/PhysRevB.107.L081401

CrossRef Full Text | Google Scholar

124. Tang Y, Cohen AE. Optical chirality and its interaction with matter. Phys Rev Lett (2010) 104:163901. doi:10.1103/PhysRevLett.104.163901

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Warning LA, Miandashti AR, McCarthy LA, Zhang Q, Landes CF, Link S. Nanophotonic approaches for chirality sensing. ACS Nano (2021) 15:15538–66. doi:10.1021/acsnano.1c04992

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Zhang W, Wu T, Wang R, Zhang X. Surface-enhanced circular dichroism of oriented chiral molecules by plasmonic nanostructures. J Phys Chem C (2017) 121:666–75. doi:10.1021/acs.jpcc.6b09435

CrossRef Full Text | Google Scholar

127. Harrington RF. Time harmonic electromagnetic fields. McGraw-Hill (1961).

Google Scholar

128. Zhu W, Esteban R, Borisov AG, Baumberg JJ, Nordlander P, Lezec HJ, et al. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Nat Commun (2016) 7:11495. doi:10.1038/ncomms11495

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Gallinet B, Butet J, Martin OJ. Numerical methods for nanophotonics: standard problems and future challenges. Laser Photon Rev (2015) 9(9):577–603. doi:10.1002/lpor.201500122

CrossRef Full Text | Google Scholar

130. Zarouf R, Wu T, Lalanne P. The Maxwell evolution equation of electromagnetic resonators: a mathematical proof with explicit derivation. arXiv preprint arXiv:2405.00455 (2024). doi:10.48550/arXiv.2405.00455

CrossRef Full Text | Google Scholar

131. Zhu B, Cai Q, Liu Y, Zhang S, Liu W, He Q, et al. Super-resolution 3D tomography of vector near-fields in dielectric resonators. arXiv preprint arXiv:2406.13171 (2024). doi:10.48550/arXiv.2406.13171

CrossRef Full Text | Google Scholar

132. Fomra D, Ball A, Saha S, Wu J, Sojib M, Agrawal A, et al. Nonlinear optics at epsilon near zero: from origins to new materials. Appl Phys Rev (2024) 11:011317. doi:10.1063/5.0186961

CrossRef Full Text | Google Scholar

133. Maiuri M, Schirato A, Cerullo G, Della VG. Ultrafast all-optical metasurfaces: challenges and new frontiers. ACS Photon (2024). doi:10.1021/acsphotonics.4c00776

CrossRef Full Text | Google Scholar