Spectral shapes of second-forbidden single-transition nonunique β decays assessed using the nuclear shell model

Experimental and theoretical studies of $\beta$ electrons (electrons emitted in ${\beta }^{-}$-decay transitions) and their $\beta$-electron spectra have recently experienced a rapid expansion. These $\beta$ spectral shapes have been used to study total $\beta$ spectra of fission-product nuclei in the quest for explanation of the reactor-flux anomalies, and individual $\beta$ transitions in search for $\beta$ spectral shapes sensitive to the effective value of the weak axial coupling $g_{\text{A}}$. In the former case the TAGS (total absorption gamma-ray spectroscopy) can be efficiently used to measure the total $\beta$ spectral shapes and in the latter case dedicated measurements of the involved forbidden nonunique $\beta$ transitions have been deployed. The fourth-forbidden nonunique decay transitions ¹¹³$\mathrm{C}\mathrm{d}(1/2_{\text{g.s.}}^{+}){\to }^{113}\mathrm{I}\mathrm{n}(9/2_{\text{g.s.}}^{+})$ and ¹¹⁵$\mathrm{I}\mathrm{n}(9/2_{\text{g.s.}}^{+}){\to }^{115}\mathrm{S}\mathrm{n}(1/2_{\text{g.s.}}^{+})$ represent theoretically and experimentally much-studied cases where the total $\beta$ spectra consist of these single transitions. In these particular cases the TAGS method could be used to assess the effective value of $g_{\text{A}}$. In the present work we have identified five more interesting cases where a total $\beta$ spectrum consists of a single transition. These spectra correspond to second-forbidden nonunique transitions and are $g_{\text{A}}$ and/or sNME dependent, where sNME denotes the so-called small relativistic vector nuclear matrix element. These studies have been performed using the nuclear shell model with well established effective Hamiltonians. With this we target to $\beta$ transitions that would potentially be of high interest for the TAGS and present and future dedicated $\beta$-spectrum experiments.

1 Introduction

Search for beyond-the-standard-model (BSM) physics involves typically rare-events experiments measuring single and double beta decays [2, 9, 14, 15]. In particular, the neutrinoless double beta $(0\nu \beta \beta )$ decay has attracted a lot of theoretical and experimental attention due to the impact of its potential discovery on neutrino masses, lepton-number conservation and fundamental nature of the neutrino. Experimental and theoretical studies of single $\beta$ decays are important in the context of resolving the anomalies related to the antineutrino flux from nuclear reactors [24, 49, 52, 65] and in assessing the common backgrounds in the rare-events experiments themselves [48]. Measurements of $\beta$ decays of very low decay energies ($Q$ values) are also important for direct determination of the (anti)neutrino mass [3, 12, 16–18, 28, 46, 50].

It is important to note that the $0\nu \beta \beta$ half-life is proportional to the inverse 4$th$ power of the weak axial coupling $g_{\text{A}}$ [60]. The calculations of the nuclear matrix elements (NME) of the $0\nu \beta \beta$ decay rate are typically done in nuclear many-body approaches which neglect the meson-exchange two-body currents [39] and have deficiences in the many-nucleon description of the nuclear structure, like too small single-particle valence spaces, incomplete many-nucleon configurations, neglect of three-nucleon forces, etc. It has been shown that these deficiencies lead to the necessity of forcing the concept of effective axial coupling in the form of “quenching” relative to the bare-nucleon value $g_{\text{A}}=1.27$, as discussed in [59, 61, 62]. Hence, this quenching of $g_{\text{A}}$ should be interpreted as effective renormalization of the spin-isospin operator in nuclear many-body calculations. If these deficiencies are corrected, it has been shown for light nuclei that essentially no quenching is needed to properly reproduce the measured $\beta$-decay rates [21]. Since for the heavier nuclei, relevant for the $0\nu \beta \beta$ decays, the flawed models are still needed in the calculations, the pinning down of the effective value of $g_{\text{A}}$ is crucial and a great incentive for present and future $\beta$-decay experiments able to tackle this problem.

The quenching of $g_{\text{A}}$ can be accessed by measuring $\beta$-decay (partial) half-lives and energy distributions of $\beta$ electrons (electrons emitted in ${\beta }^{-}$ transitions), the so-called $\beta$(-electron) spectra. The $\beta$ spectra of forbidden $\beta$ transitions [8], in particular the nonunique ones, are of special interest for the latter experiments since the nonunique decays involve numerous NME and phase-space factors allowing $g_{\text{A}}$ dependence of the spectral shape [14], unlike in the cases of the allowed and unique forbidden ones [58]. Only in very special cases the value of $g_{\text{A}}$ is enhanced [32]. Combined with theoretical calculations the effective value of $g_{\text{A}}$ can be assessed, as done using the spectrum-shape method (SSM) [22, 23] or an enhanced version of it (enhanced SSM) [34, 35]. Recently the spectral moments method (SMM) was introduced in [31]. In the SSM the effective value of $g_{\text{A}}$ can be gained by trying to find a match between the computed template $\beta$ spectra, for different values of $g_{\text{A}}$, and the measured one.

The enhanced SSM and the SMM exploit yet an extra degree of freedom, the so-called small relativistic NME (sNME) in order to fit simultaneously the measured (partial) half-life and the $\beta$ spectral shape. Despite its smallness, the sNME can influence the (partial) half-lives and shapes of $\beta$-electron spectra quite strongly [31, 33, 47]. The sNME is particularly hard to calculate in the nuclear shell model (NSM), used in this work, leading usually to a zero value of it. However, the sNME can be related to the so-called large vector NME, l-NME, by using the CVC (conserved vector current) hypothesis [8]. Contrary to the sNME, the l-NME can be reliably calculated in the framework of the NSM. Although the CVC value of the sNME is an idealization, strictly applicable to an ideal nuclear many-body calculation [8], it still serves as a good reference in searches for realistic values of the sNME. In the present study we fit the measured half-life of a given $\beta$ transition by varying the value of the sNME.

As mentioned earlier, the reactor antineutrino spectra need to be addressed both theoretically and experimentally. This needs measurements of the total $\beta$ spectra of numerous fission-product nuclei. This has been recently accomplished by the TAGS (total absorption gamma-ray spectroscopy) measurements [4, 5, 13, 20, 51, 63]. Such kind of measurements would also be highly important in the context of the rare-events experiments in order to verify the validity of the computed total spectra in, e.g., [48]. There is also an interesting prospect for these experiments in the case the total $\beta$ spectrum consists of a single transition. In these particular cases the TAGS method could be sensitive to the effective value of $g_{\text{A}}$. There are already identified cases where the considered single $\beta$ transition exhausts 100% of the decay $Q$ window. Recently combined theory-experiment analyses of such $\beta$ decays have already been performed for the decay transitions ¹¹³$\mathrm{C}\mathrm{d}(1/2_{\text{g.s.}}^{+}){\to }^{113}\mathrm{I}\mathrm{n}(9/2_{\text{g.s.}}^{+})$ [10, 33] and ¹¹⁵$\mathrm{I}\mathrm{n}(9/2_{\text{g.s.}}^{+}){\to }^{115}\mathrm{S}\mathrm{n}(1/2_{\text{g.s.}}^{+})$ [36, 42], which are fourth-forbidden nonunique, and for the decay ⁹⁹$\mathrm{T}\mathrm{c}(9/2_{\text{g.s.}}^{+}){\to }^{99}\mathrm{R}\mathrm{u}(5/2_{\text{g.s.}}^{+})$ [44], which is second-forbidden nonunique. Very recently this decay was discussed using the sNME to fit the half-life of ⁹⁹Tc in [48]. A similar interesting spectral shape candidate, exhausting 100% of the total $\beta$-decay $Q$ window is the transition ²¹⁰$\mathrm{B}\mathrm{i}(1_{\text{g.s.}}^{-}){\to }^{210}\mathrm{P}\mathrm{o}(0_{\text{g.s.}}^{+})$ [14], which is first-forbidden nonunique. Measurements of similar $\beta$ spectra are being extended also to other potentially sensitive candidates, like in the case of the ACCESS Collaboration [43]. Additionally, an interesting new method for measuring $\beta$ spectral shapes is offered by the one recently developed at the Ion Guide Isotope Separator On-Line facility at the Accelerator Laboratory of Jyväskylä [19].

In our present work we investigate five more interesting cases where the total $\beta$ spectrum consists of a single transition, leading to a 100% branching. These spectra correspond to second-forbidden nonunique transitions and are $g_{\text{A}}$ and/or sNME dependent. We determine the values of the sNME by fitting the experimental half-lives, and the dependence of the $\beta$ spectral shape on the sNME comes from the fact that there are always two values (or none at all) of the sNME that reproduce the measured branching of a $\beta$ transition. These studies have been performed using the nuclear shell model with established effective Hamiltonians. In these investigations we have discovered $\beta$ transitions that would potentially be of high interest for the TAGS, as also for the present and future dedicated rare-events experiments.

2 Outline of the theoretical aspects

The half-life of a ${\beta }^{-}$ transition can be written as

$t_{1/2}=\frac{\kappa }{\tilde{C}},(1)$

where $\kappa$ is a constant [34, 35] and $\tilde{C}$ is the integral of the shape function $C$ over the electron energy:

$\tilde{C}={\int }_1^{w_0}C\left(w_e\right)p{w}_e{\left(w_0-w_e\right)}^2{F}_0\left(Z,w_e\right)K\left(Z,w_e\right)d{w}_e,(2)$

where the lowercase $w_e$ and $w_0$ are the electron and end-point energies $W_e$ and $W_0$ respectively, scaled by $m_e{c}^2$. $F_0(Z,w_e)$ is the Fermi function, accounting for the Coulomb interaction between the emitted electron and the daughter nucleus, and $K(Z,w_e)$ contains radiative, screening, and atomic exchange corrections. $C(w_e)$ includes phase-space factors and NMEs in a next-to-leading-order expansion of the leptonic and hadronic weak currents, as discussed in detail in [22, 23]. The simplest shape function concerns the allowed transitions, namely, the Fermi and Gamow-Teller ones for which the electron spectral shape is universal and independent of the value of the axial coupling. For the allowed transitions the total orbital angular momentum of the emitted leptons (in the case of ${\beta }^{-}$ transition, the electron and its antineutrino) is $\ell =0$, whereas for the $n$-fold forbidden ${\beta }^{-}$ transitions the leptons carry a total orbital angular momentum of $\ell =n$. Due to the increase in the orbital angular momentum, each unit of increase in the forbiddenness $n$ increases the $\beta$-decay half-life by roughly 4 orders of magnitude. Hence the forbidden transitions are not completely forbidden, but much suppressed relative to the allowed transitions. There are two categories for the forbidden transitions, namely, the unique and nonunique ones. The unique transitions have only one involved nuclear matrix element and hence the related electron spectral shape is universal. The nonunique transitions are characterized by the full complexity of the shape function and no universal electron spectral shape can be identified, but rather spectral shapes which depend on the nuclear wave functions through the many involved NMEs. For these $\beta$ transitions there also opens up the possibility that the related electron spectral shape could be $g_{\text{A}}$ dependent.

Fortunately, the highly complex shape function $C$ for the forbidden nonunique ${\beta }^{-}$ transitions can be cast in a very simple form

$C\left(w_e\right)=g_{\text{V}}^2{C}_{\text{V}}\left(w_e\right)+g_{\text{A}}^2{C}_{\text{A}}\left(w_e\right)+g_{\text{V}}{g}_{\text{A}}{C}_{\text{VA}}\left(w_e\right),(3)$

where $w_e$ is the total (rest-mass plus kinetic) energy of the emitted electron. For the weak vector coupling constant we adopt the CVC-protected value $g_{\text{V}}=1.0$. The sensitivity of the shape of the $\beta$-electron spectrum to the value of $g_{\text{A}}$ stems from the subtle interference of the combined vector $C_{\text{V}}(w_e)$ and axial $C_{\text{A}}(w_e)$ parts with the mixed vector-axial part $C_{\text{VA}}(w_e)$ of Equation (3) [23]. For some nuclei, as charted up to present days in [14, 48], this causes measurable changes in the $\beta$ electron spectra.

2.1 β- spectral shapes and their dependency on the small relativistic NMEs

The small relativistic NME (sNME) plays a crucial role in the combined analysis of beta spectral shapes and partial half-lives (branching ratios) [31, 33, 35, 48]. In these studies, the sNME is used as a fitting parameter alongside $g_{\text{A}}$ to simultaneously fit the experimental $\beta$ spectral shapes and branching ratios. In nuclear-structure calculations, the sNME accounts for contributions outside the major nucleon shells where the proton and neutron Fermi surfaces lie. Due to the limitations of the NSM valence space, which is confined to these shells, the sNME value becomes unrealistic (essentially zero) in NSM calculations.

Ideally, with infinite valence spaces and a perfect nuclear many-body theory, the sNME value is linked to the large vector NME (l-NME) by the Conserved Vector Current (CVC) hypothesis [8]. This relationship is expressed as:

${}^V\mathcal{M}_{KK-11}^{\left(0\right)}=\left(\frac{\frac{\left(-M_n{c}^2+M_p{c}^2+W_0\right)\times R}{\hslash c}+\frac{6}{5}\alpha Z}{\sqrt{K\left(2K+1\right)}\times R}\right)\times {}^V\mathcal{M}_{\mathit{KK}0}^{\left(0\right)},(4)$

where the left side represents the sNME, and the right side involves the l-NME, with $K$ denoting the order of forbiddenness ($K=1$ for first-forbidden decays and $K=2$ for second-forbidden decays). The symbols $M_n$ and $M_p$ refer to neutron and proton masses, respectively; $W_0$ is the available endpoint energy for the decay, $\hslash$ is the reduced Planck constant, $\alpha$ is the fine-structure constant, $c$ is the speed of light, $Z$ is the atomic number of the daughter nucleus, and $R=1.2A^{1/3}$ is the nuclear radius in femtometers and $A$, the nuclear mass number. Contrary to the case of sNME, the value of the l-NME can be reliably computed by the NSM as its main contributions come from the major shells housing the nucleon Fermi surfaces. Hence, the CVC value of the sNME serves as a reliable reference for its proper value.

In our ${\beta }^{-}$ decay calculations, we fit the sNME to match each individual ${\beta }^{-}$ decay half-life, incorporating screening, radiative, and atomic exchange corrections. The atomic exchange correction [41], particularly noticeable at low electron energies, was originally derived for allowed $\beta$ decays and accounts for the upward tilt seen in all curves at the very low electron kinetic energies. In the sNME fitting, the experimental half-lives are sourced from the ENSDF [1] database.

The quadratic dependence of the computed half-lives on the sNME value results in two sNME values for each decay transition that reproduce the experimental half-life. In some cases, only complex-conjugate pairs of solutions exist, indicating that the experimental data cannot be reproduced with the adopted NSM Hamiltonian. One of these two sNMEs is closer to the CVC value, often defining the “optimal” beta spectral shape. By choosing the sNME value closest to its CVC value, we obtain the most probable spectral shape for a given $\beta$-decay transition.

Therefore, while the “optimal” choice of sNMEs can be theoretically justified, its true validation depends on experimental data. Future experimental efforts are necessary to confirm whether this theoretical choice accurately represents the physical processes occurring during $\beta$ decay. However, in our current study, we shall always plot both options of values. This approach allows for a comprehensive analysis and comparison with future experiments, providing a clearer understanding of the potential variations in the beta-electron spectra and the impacts of different sNME values.

2.2 Nuclear shell-model computations

The NSM calculations were performed using the software KSHELL [54] with the following Hamiltonians: ca48mh1, used in [53]; fpg9tb [56], obtained by modifying the two-body matrix elements in the fpg interaction [55] to fit Nickel isotopes; gxpf1a [25] and gxpf1b [26], derived from the Bonn-C potential and fitting the single-particle energies and two-body matrix elements to nuclei in the fp-region; the semi-bare G-Matrix effective interaction glekpn [38]; jj45pnb, a two-nucleon potential with a perturbative G-matrix approach, with the Coulomb single-particle energies adjusted to reproduce recent results in [37]; and SVD, a CD-Bonn nucleon-nucleon potential with the single-particle energies fitted to the region ${\text{of}}^{102-132}$Sn [45].

For the $A=60$ computations, the model space for ca48mh1 includes the proton orbitals $\pi (1f_{7/2})$, $\pi (1f_{5/2})$, $\pi (2p_{3/2})$, and $\pi (2p_{1/2})$, along with the neutron orbitals $\nu (1f_{5/2})$, $\nu (2p_{3/2})$, $\nu (2p_{1/2})$, and $\nu (1g_{9/2})$. In contrast, the proton model spaces for fpg9tb, gxpf1a, and gxpf1b are identical to that of ca48mh1 but with the neutron orbitals $\nu (1f_{7/2})$, $\nu (2p_{3/2})$, $\nu (1f_{5/2})$, and $\nu (2p_{1/2})$.

For the $A=94$ and $A=98$ studies, the glekpn model space includes the proton orbitals $\pi (1f_{7/2})$, $\pi (1f_{5/2})$, $\pi (2p_{3/2})$, $\pi (2p_{1/2})$, and $\pi (1g_{9/2})$, along with the neutron orbitals $\nu (1g_{9/2})$, $\nu (1g_{7/2})$, $\nu (2d_{5/2})$, $\nu (2d_{3/2})$, and $\nu (3s_{1/2})$. In the present calculations, this model space was truncated to treat the $\pi (1f_{7/2})$ and $\nu (1g_{9/2})$ orbitals as part of the closed core, and to ensure at least four protons occupy the $\pi (1f_{5/2})$ orbital. These truncations are justified by the magic numbers 28 and 50, while the $\pi (1f_{5/2})$ adjustment is due to computational constraints and is not expected to affect the results, as only ground states and low excited states are of interest in this study. The jj45pnb model space comprises the proton orbitals $\pi (2p_{1/2})$, $\pi (2p_{3/2})$, $\pi (2f_{5/2})$, and $\pi (1g_{9/2})$, along with the neutron orbitals $\nu (1g_{7/2})$, $\nu (2d_{5/2})$, $\nu (2d_{3/2})$, $\nu (3s_{1/2})$, and $\nu (1h_{11/2})$, and no truncations were used in our computations.

Finally, the SVD model space, used for $A=126$ and $A=129$ studies, includes the proton orbitals $\pi (1g_{7/2})$, $\pi (2d_{5/2})$, $\pi (2d_{3/2})$, $\pi (3s_{1/2})$, and $\pi (1h_{11/2})$, along with the neutron orbitals $\nu (1g_{7/2})$, $\nu (2d_{5/2})$, $\nu (2d_{3/2})$, $\nu (3s_{1/2})$, and $\nu (1h_{11/2})$, again without any truncations made.

3 Results and analyses

3.1 Nuclear observables

To assess the reliability of our adopted nuclear wave functions, we first calculate their electromagnetic properties, specifically the electric quadrupole moments $(Q)$ in units of $e$barn and the magnetic dipole moments $(\mu )$ in units of the nuclear magneton $({\mu }_N)$. These computed values, along with the computed energies, are compared with the available experimental data, as shown in Figure 1; Table 1. There the properties of the involved initial and final states are analyzed both from the electromagnetic and energy points of view through comparison of our computed values, using the various shell-model Hamiltonians, with the available data. In Table 1, we present the predicted energies for the ground states of the parent isotopes and the daughter states involved in the second-forbidden non-unique beta decays. This comparison provides a measure of the reliability of the applied Hamiltonians, as also the one of Figure 1, which illustrates the comparison of the predicted and evaluated nuclear moments.

Figure 1

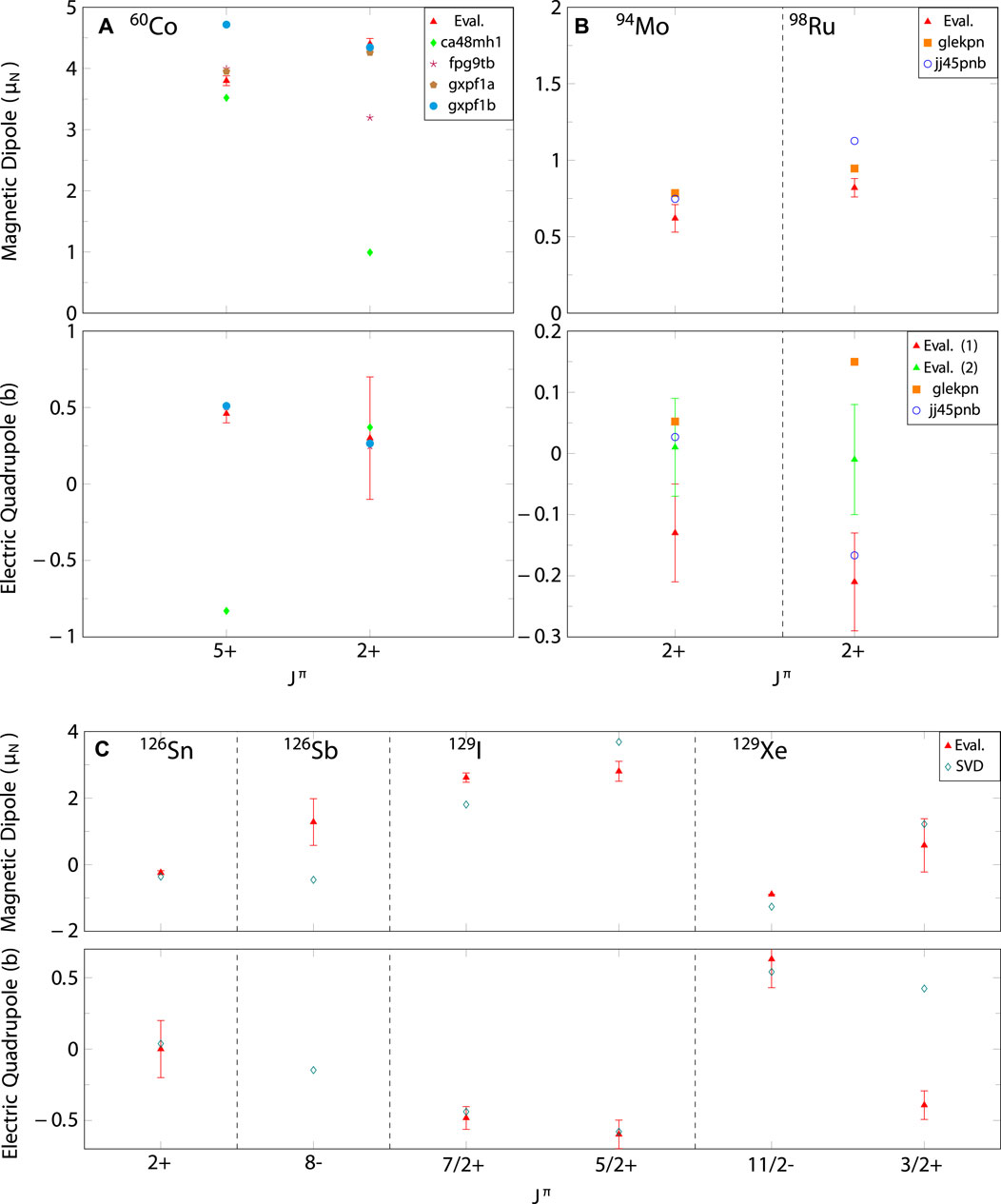
Figure 1. Comparison of the experimental and NSM-computed electric quadrupole moments $Q$ (in units of $e$barn), and magnetic dipole moments $\mu$ (in units of the nuclear magneton ${\mu }_N$) for (A) the isotopes ⁶⁰Co, (B) ⁹⁴Mo, ⁹⁸Ru, and (C) ¹²⁶Sn, ¹²⁹I, and ¹²⁹Xe. The experimental values are taken from the evaluation [1]. Evaluated data are displayed twice when two ranges of experimental values are available and are described as Eval (1) and Eval (2). The adopted effective charges are $e_{\text{eff}}^p$ = 1.5$e$ and $e_{\text{eff}}^n$ = 0.5$e$ and the bare $g$ factors $g_l(p)$ = 1, $g_l(n)$ = 0, $g_s(p)$ = 5.585, and $g_s(n)$ = $-3.826$ were used for the magnetic moments.

Table 1

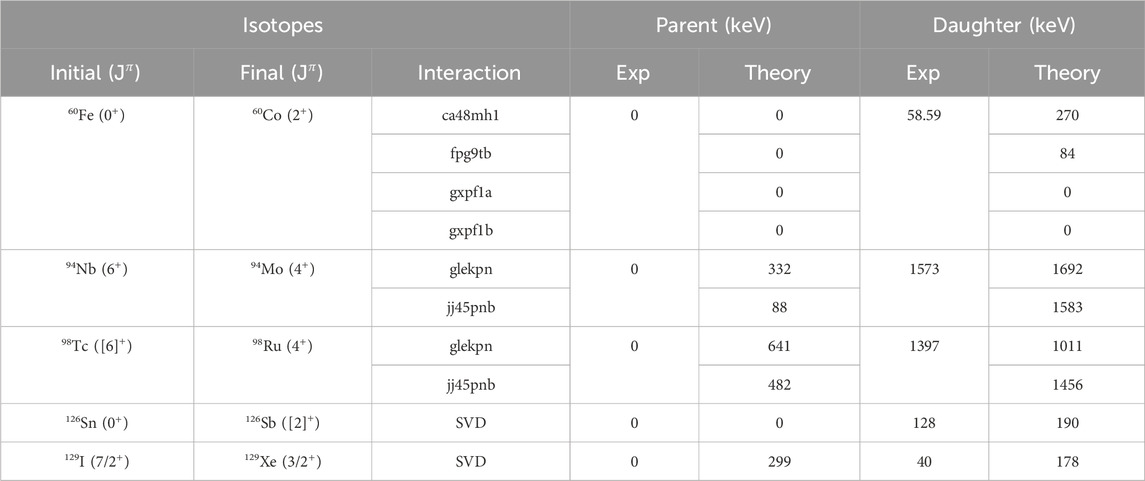
Table 1. Assessment of experimental and theoretical energy values for parent and daughter isotopes involved in non-unique second-forbidden beta decays. This table presents initial and final nuclear states with their corresponding $J^{\pi }$ values, alongside both measured (Exp.) and predicted (Theory) excitation energies in keV. Theoretical computations are based on nuclear shell-model Hamiltonians, see Section 2.2. Note: Square brackets indicate experimental uncertainties in angular-momentum assignments.

For the decay of ⁶⁰Fe to ⁶⁰Co, the interaction ca48mh1 shows significant discrepancies compared to the experimental data, failing to accurately predict both the energy levels and the nuclear moments. The fpg9tb interaction works much better, and shows good agreement with the data. In contrast, the gxpf1a and gxpf1b interactions reproduce the data less well, suggesting that these Hamiltonians should be regarded with caution, like also the ca48mh1 Hamiltonian.

For the isotopes ⁹⁴Nb, ⁹⁴Mo, ⁹⁸Tc, and ⁹⁸Ru, the interactions glekpn and jj45pnb have been applied. It is not immediately clear which of the two interactions is more reliable, as they each agree with the experimental results in different aspects. In particular, the glekpn Hamiltonian struggles to systematically predict the level schemes, despite maintaining nuclear-moment observables within acceptable limits. The jj45pnb interaction, however, consistently provides better predictions for the level schemes of the studied isotopes and shows a strong agreement with the nuclear observables of the daughter states. Overall, jj45pnb appears to be more reliable of the two, as also supported by previous studies in this mass region [48].

Lastly, the isotopes ¹²⁶Sn, ¹²⁶Sb, ¹²⁹I, and ¹²⁹Xe have been studied using the SVD Hamiltonian. This Hamiltonian shows promising results in terms of the level-scheme predictions. However, for the odd-mass nuclei ¹²⁹I and ¹²⁹Xe, there is a bit larger disparity in the predicted energies. This is expected, as odd-mass nuclei typically have a higher density of states, making it more challenging to accurately reproduce their experimental level schemes. The predicted electric quadrupole moments generally agree with the experimental data, except for the ¹²⁹Xe $(3/2^{+})$ state, which is the daughter of the ¹²⁹I $\to$ ¹²⁹Xe second-forbidden non-unique decay. In contrast, the computed magnetic dipole moments show more deviations from the data, but still mostly within acceptable limits. Despite some small deviations from the data, the SVD interaction seems a valuable tool for nuclear-structure computations in this mass region, and in particular a reliable starting point for our spectral-shape analyses.

3.2 β-spectral dependency on the weak axial coupling and the small NME

As previously mentioned, we use the sNME as a fitting parameter to match, for each selected value of the axial coupling $g_{\text{A}}$, the computed and measured half-lives of the $\beta$ decays of interest. For each value of $g_{\text{A}}$, we obtain two solutions for the value of sNME, giving two ranges of sNME values corresponding to our adopted range $g_{\text{A}}=0.8-1.2$. These sNMEs are then compared with the CVC-value of the sNME computed with Equation (4).

Figures 2–4 depict the two sets of sNMEs and indicate which of the two sets is the so-called “optimal” or closest to the CVC predicted value, denoted with the * symbols. The solid lines denote sNME solution one and the dashed lines, solution 2. Only in the case of the ¹²⁶Sn decay, see Figure 4A, does the closest-to-CVC-solution fall within two different solution sets. This, however, is a matter of definition of the two sets and only the experimental data on the $\beta$ spectral shapes, when compared with the corresponding computed shapes, will decide which set of the sNME values is the realistic one.

Figure 2

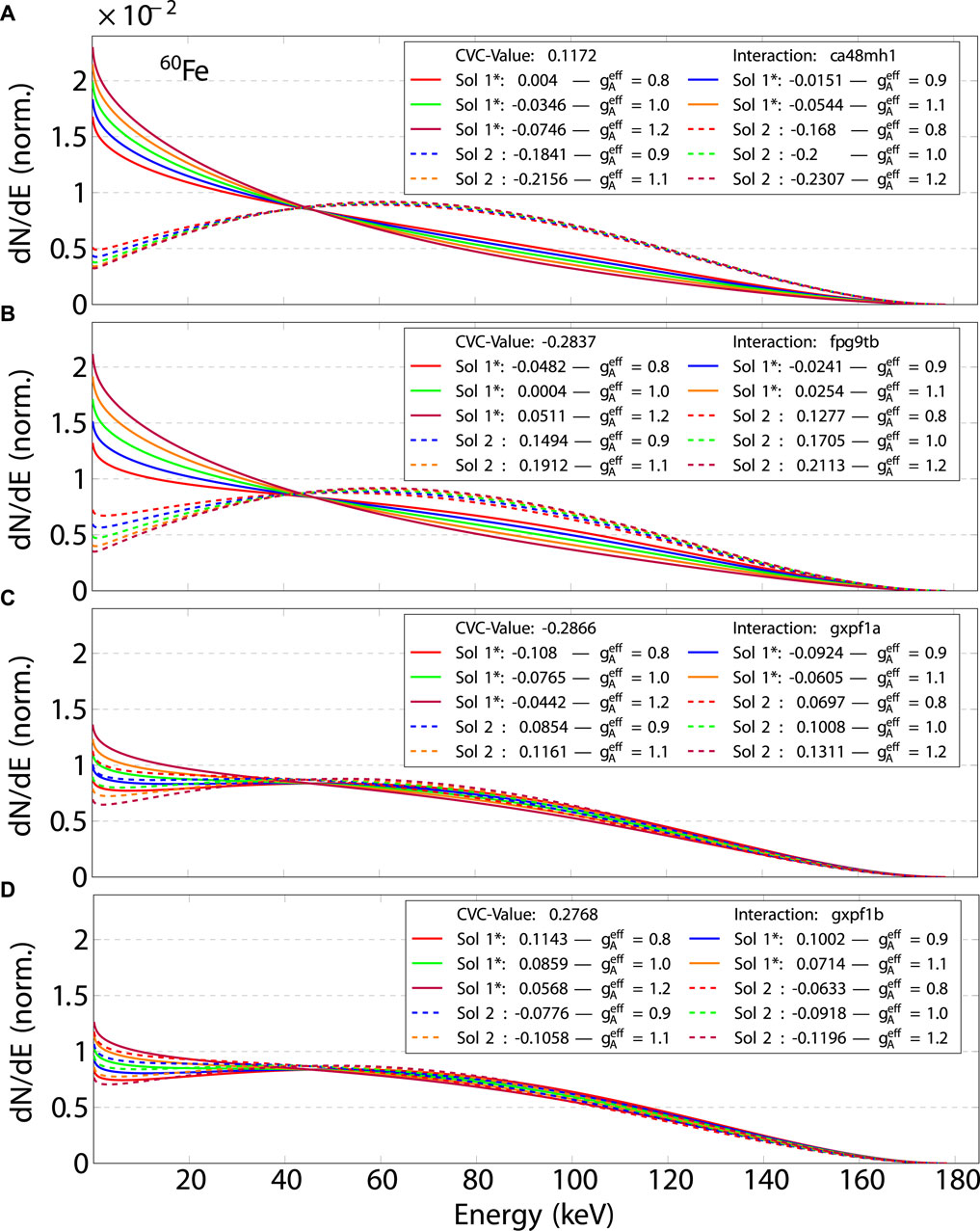
Figure 2. Computed $\beta$ spectral shapes of the second-forbidden non-unique ⁶⁰Fe$(0^{+}){\to }^{60}$Co$(2^{+})$ decay for various interactions: ca48mh1 (A), fpg9tb (B), gxpf1a (C), and gxpf1b (D). The $\beta$ spectral plots are shown with the weak axial coupling within the range of $g_{\text{A}}^{\text{eff}}=0.8-1.2$ and the corresponding sNME solutions that reproduce the experimental half-life. Solid lines represent Solution 1, and dashed lines represent Solution 2, with asterisks denoting the solution closest to the shown CVC-Value. All areas under the curves have been normalized to unity. Experimental half-life data is taken from [1].

3.3 Spectral analysis

Analyzing Figure 2, which depicts the second-forbidden non-unique decay of ⁶⁰Fe$(0^{+}){\to }^{60}$Co$(2^{+})$, we observe that the four interactions consistently demonstrate a dependency of the spectral shape on the effective $g_{\text{A}}$. Notably, there is a clear separation in the electron energy spectra below 20 keV. This suggests that if the experimental method used to measure the beta electron spectra has sufficient resolution within this range, it would be feasible to determine the weak axial coupling for this isotope. On the other hand, the experiment would also be sensitive to the shell-model Hamiltonian, which is an interesting by-product of the present analysis.

In contrast, there is a discrepancy regarding the effect of the sNME on the spectral shape between plots (a, b) and (c, d). While plots (a) and (b) exhibit distinct differences between solution sets 1 and 2, plots (c) and (d) show nearly identical shapes for both sets, indicating very weak sNME dependence. Previous analyses, based on the predicted electric and magnetic moments, demonstrated that the Hamiltonian of plot (c) had the best agreement with the data, the Hamiltonians of plots (b) and (d) a satisfactory agreement and the Hamiltonian of plot (a) did not produce consistent results for the moments. Based on this, we could expect that this decay exhibits a rather strong dependency on $g_{\text{A}}$, and possibly a rather weak dependency on the sNME.

Figure 3 depicts the decays of ⁹⁴Nb$(6^{+}){\to }^{94}$Mo$(4^{+})$ and ⁹⁸Tc$(6^{+}){\to }^{98}$Ru$(4^{+})$. For the ⁹⁴Nb decay, there is a disagreement between the Hamiltonians producing the spectral shapes in plots (a) and (b). Specifically, plot (a) shows no dependency on the effective $g_{\text{A}}$ and very weak sNME dependency, whereas plot (b) demonstrates a strong dependency on the effective $g_{\text{A}}$ and a weak sNME dependency. Given the better agreement with nuclear observables, the Hamiltonian jj45pnb of plot (b) can be considered more reliable. This conclusion is in line with previous studies in this mass region, such as [48], which have shown similar disagreements between these two interactions for ⁹⁹Tc, favoring the jj45pnb interaction. Taking the proximity of ⁹⁴Nb to ⁹⁹Tc into account as an additional factor, we expect that the ⁹⁴Nb$(6^{+}){\to }^{94}$Mo$(4^{+})$ decay is likely dependent on $g_{\text{A}}$ and only weakly dependent on sNME.

Figure 3

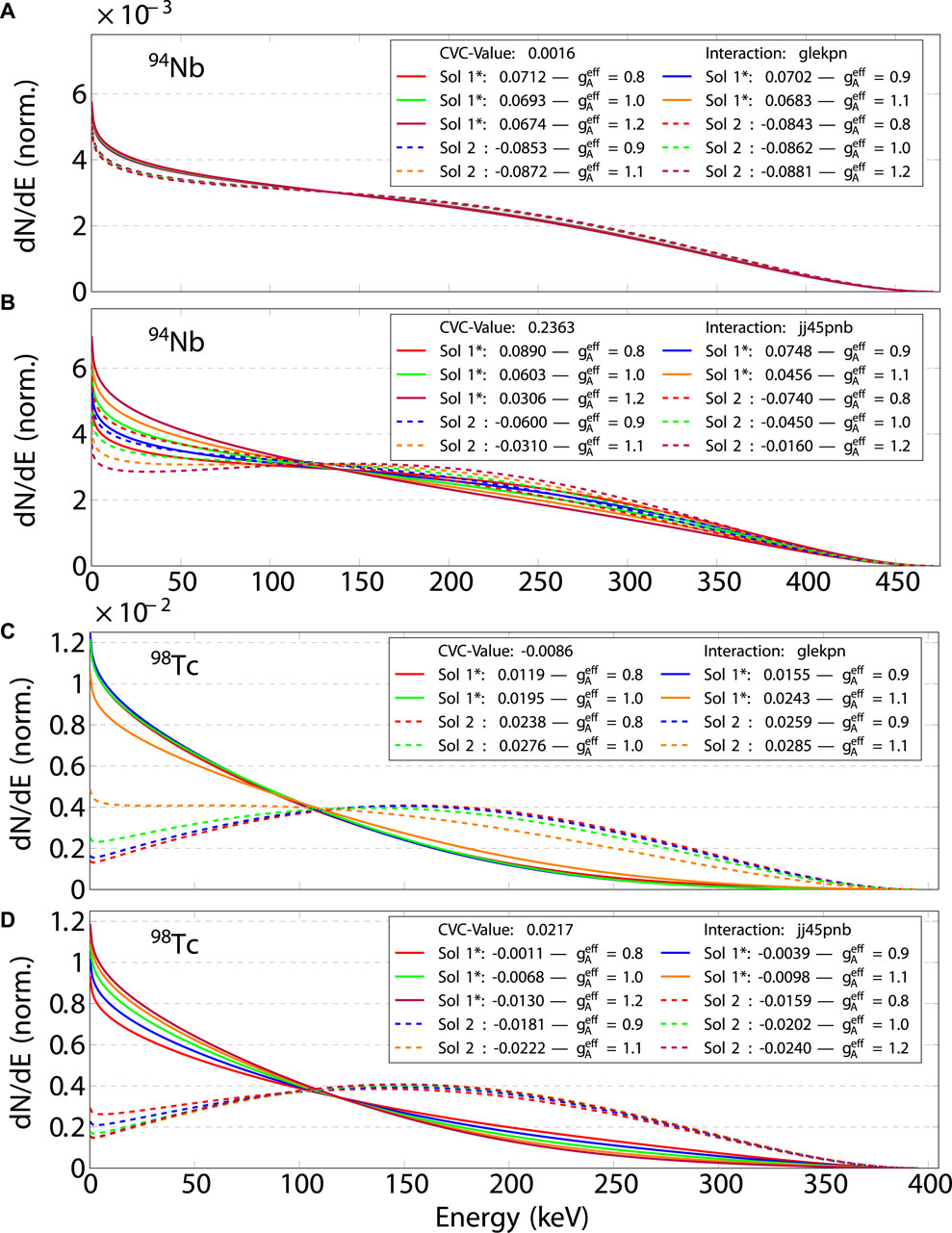
Figure 3. Similar plot as Figure 2 for the second-forbidden non-unique decays of ⁹⁴Nb$(6^{+}){\to }^{94}$Mo$(4^{+})$ with interactions glekpn (A), jj45pnb (B) and ⁹⁸Tc$(6^{+}){\to }^{98}$Ru$(4^{+})$ for interactions glekpn (C), and jj45pnb (D). The normalized to unity plots reproduce the experimental half-life for the same previous $g_{\text{A}}^{\text{eff}}$ range, except for (C), as glekpn could not reproduce the experimental half-life with $g_{\text{A}}^{\text{eff}}=1.2$. Experimental half-life data is taken from [1].

For the ⁹⁸Tc$(6^{+}){\to }^{98}$Ru$(4^{+})$ decay, plots (c) and (d) both indicate consistently a strong dependency on the effective $g_{\text{A}}$ and sNME below some 100 keV of electron kinetic energy. Based on the arguments of the above $A=94$ case, plot (d) would be the favored one.

Lastly, Figure 4 presents the decays of ¹²⁶Sn$(0^{+}){\to }^{126}$Sb$(2^{+})$ and ¹²⁹I$(7/2^{+}){\to }^{129}$Xe$(3/2^{+})$ using the SVD interaction. Although the isotopes differ, their spectral shapes appear similar due to the normalization on the $dN/dE$ axis and the energy scaling of the plots. Both decays exhibit a strong dependency on the sNME and a weak to almost negligible dependency on the effective $g_{\text{A}}$. These characteristics make them particularly useful for studies focused on the sNME.

Figure 4

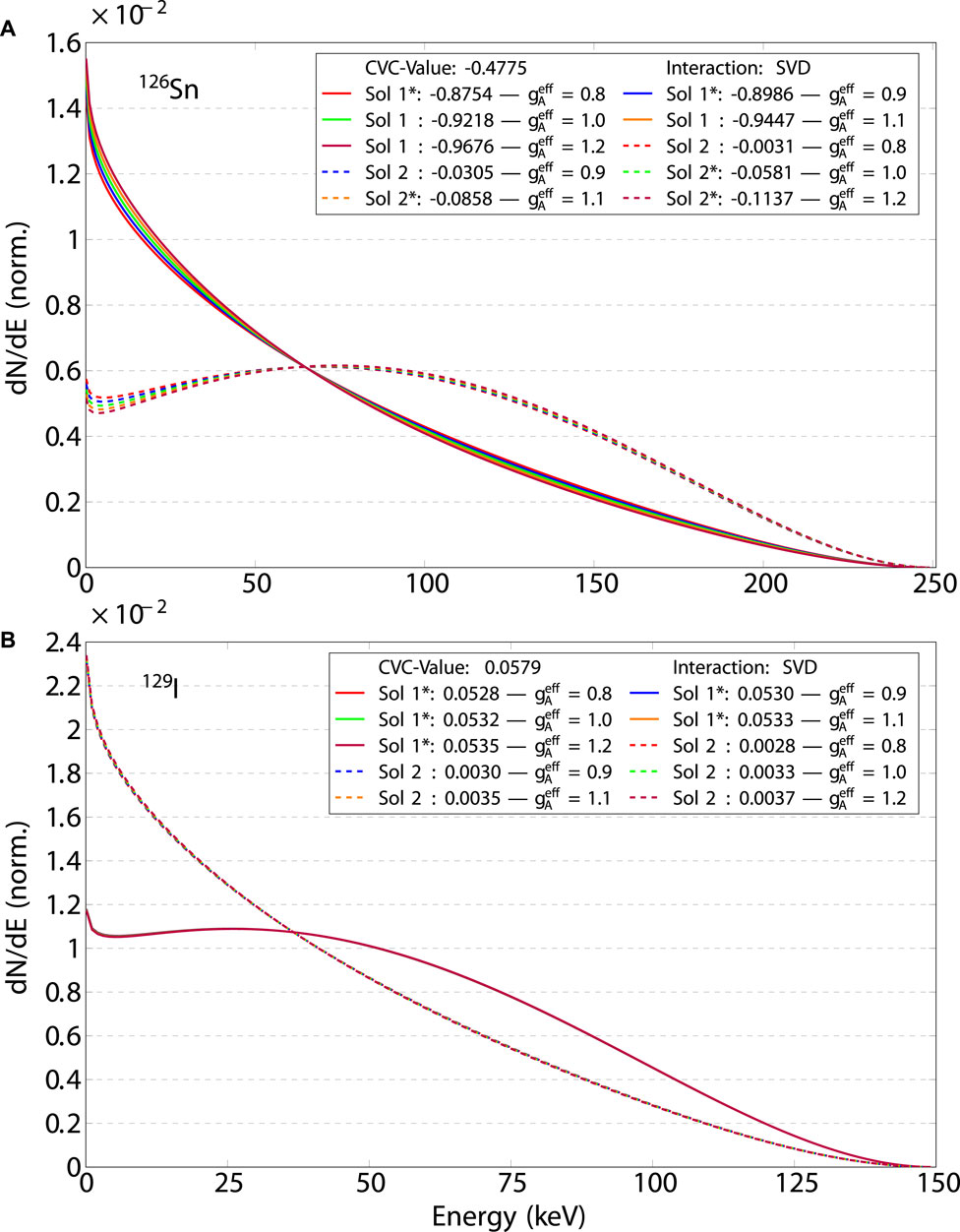
Figure 4. Similar plot as Figures 2, 3 for the second-forbidden non-unique decays of ¹²⁶Sn$(0^{+}){\to }^{126}$Sb$(2^{+})$ (A) and ¹²⁹I$(7/2^{+}){\to }^{129}$Xe$(3/2^{+})$ (B) with the interaction SVD. The normalized plots reproduce the experimental half-life for the same previous $g_{\text{A}}^{\text{eff}}$ ranges. Plot (A) is a special case where the closest to the CVC-Value sNME changes between solution sets due to the CVC-value being roughly equidistant to both solutions. Experimental half-life data is taken from [1].

There is yet another way to characterize the sensitivity of the $\beta$ spectral shape to $g_{\text{A}}$, namely, the mean $\beta$ energy ${⟨E⟩}_{\beta }$. This mean energy is shown in Table 2 for the $g_{\text{A}}$ range and decays of interest to this work. The table is indicative of the speed of change of the mean $\beta$ energy as a function of the value of the axial coupling. It also clearly indicates the differences between the two sets of sNME values when the ${⟨E⟩}_{\beta }$ ranges are very different, the decay of ⁹⁸Tc being a good example. Also, overwhelmingly, the mean energy of the Solutions 1 decreases with increasing $g_{\text{A}}$ and vice versa for the Solutions 2. It is clear that the computed mean energy helps in identifying the proper values of both $g_{\text{A}}$ and sNME when compared with the measured one. The same trick can be used even when the measured spectral shape has a low-energy threshold since the integration can be started from this threshold upwards as done in the SMM, see [31].

Table 2

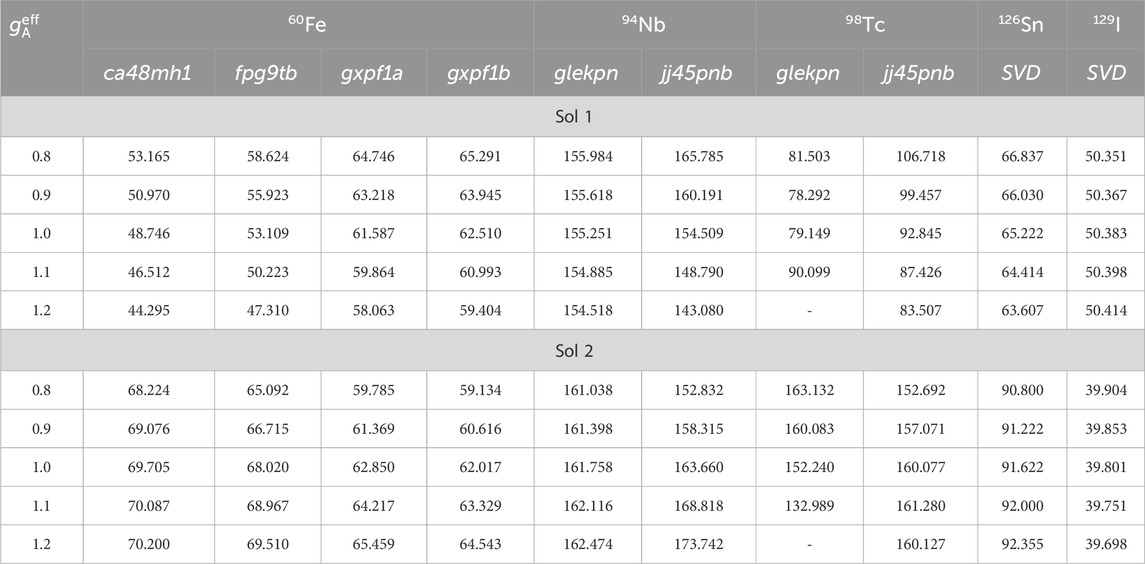
Table 2. Computed ${⟨E⟩}_{\beta }$ (mean $\beta$-energy in keV) for second-forbidden non-unique decays, associated with the interactions shown in Figures 2–4, categorized into two solution sets, Sol 1 and Sol 2, as described in the figures. The isotopes listed represent the parent nuclei involved in the decay processes.

4 Why should one measure more $\beta$ spectral shapes?

A natural question arises why should one measure the presently discussed $\beta$ spectral shapes and other ones already identified or potentially discovered in the future. Firstly, measured decay half-lives of ${\beta }^{-}$ transitions and the corresponding electron spectral shapes are together stringent tests of nuclear many-body frameworks. In particular, those nuclear models dedicated to description of the $0\nu \beta \beta$ decay, reactor antineutrinos and backgrounds in dark-matter and rare-events experiments will profit from these two constraints to their Hamiltonians and their parametrizations. In particular, the capability to properly compute the value of the sNME is a crucial probe for the adequacy of the nuclear model’s valence and configuration spaces.

Secondly, some theory frameworks can access the $0\nu \beta \beta$ NMEs without resorting to the use of the closure approximation by computing the virtual transitions through all the multipole states $J^{\pi }$ of the intermediate nucleus. These models include the pnQRPA (proton-neutron quasiparticle random-phase approximation), NSM and IBFFM-2 (microscopic interacting boson-fermion-fermion model), see the references in [14]. In these models the quenching of $g_{\text{A}}$ can be accessed multipole by multipole, for each $J^{\pi }$ separately. A lot of information for the $1^{+}$ multipole exists through the Gamow-Teller and $2\nu \beta \beta$ studies [62] but quite scarsely for the other multipoles, in particular for the first- and higher-forbidden intermediate transitions. The presently studied cases help in accessing the second-forbidden contributions to the $0\nu \beta \beta$ NMEs in the NSM calculations, and in other calculations when performed sometime in the future: The pnQRPA-based calculations of the $0\nu \beta \beta$ NMEs profit from the cases of ⁶⁰Fe$(0^{+}){\to }^{60}$Co$(2^{+})$ and ¹²⁶Sn$(0^{+}){\to }^{126}$Sb$(2^{+})$ since these transitions are directly calculable using the pnQRPA. The cases ⁹⁴Nb$(6^{+}){\to }^{94}$Mo$(4^{+})$ and ⁹⁸Tc$(6^{+}){\to }^{98}$Ru$(4^{+})$ are calculable by using the MCM (multiple-commutator model) [11, 57], being a higher-QRPA approach related to the pnQRPA. The transition ¹²⁹I$(7/2^{+}){\to }^{129}$Xe$(3/2^{+})$ is calculable using the MQPM (microscopic quasiparticle-phonon model) and IBFM-2 (microscopic interacting boson-fermion model), both used in previous spectral analyses [10, 33, 36, 42] and related to nuclear models used in double-beta calculations, as well.

Thirdly, the presently discussed ${\beta }^{-}$ decays are relevant for the $0\nu {\beta }^{-}{\beta }^{-}$ decays of ⁷⁰Zn${\to }^{70}$Ge, ^94,96Zr${\to }^{\mathrm{94,96}}$Mo, ^98,100Mo ${\to }^{\mathrm{98,100}}$Ru, ^122,124Sn ${\to }^{\mathrm{122,124}}$Te, ^128,130Te ${\to }^{\mathrm{128,130}}$Xe, and ^134,136Xe ${\to }^{\mathrm{134,136}}$Ba, allowing to estimate the effective value of $g_{\text{A}}$ for forbidden transitions in these $0\nu \beta \beta$ decays.

A further incentive for studies of the presently discussed decay transitions, and potentially others in the future, arises from needs in nuclear astrophysics [64]. First-forbidden $\beta$ decays play an important role in astrophysical scenarios, like in the context of r-process waiting-point nuclei [66]. In [66] a strong quenching of both $g_{\text{A}}$ and $g_{\text{V}}$ was obtained for the first-forbidden $\beta$ decays. This discrepancy, in particular for $g_{\text{V}}$, could likely be resolved by a proper account of the value of the sNME, guided by the spectral-shape studies in the regions of magic neutron numbers $N=\mathrm{50,82,126}$, $N=50$ being relevant for the present study. Also second-forbidden nonunique decays can be astrophysically relevant, containing the sNME aspect as shown in [29, 30].

In the case of reactor-antineutrino spectra some of the first-forbidden ${\beta }^{-}$-decay transitions of the fission residues show dependence on the value of $g_{\text{A}}$ [24]. This was noticed also in the calculation of the total $\beta$ spectrum of ⁹²Rb in [49]. In [24, 49] the extra dimension brought in by the sNME was not yet exploited but should have been in order to enable correct reproduction of the measured branching ratios of the $\beta$ transitions in the calculations. Many of the $\beta$ emitters relevant to the reactor flux anomalies are situated in the mass regions of the presently discussed nuclei and thus the calculated decay half-lives and $\beta$ spectral shapes help in pinning down the proper values of the sNME in nuclei relevant for the reactor-antineutrino flux. Furthermore, reactor-antineutrino spectra can be used for remote monitoring and diagnostic purposes in fission reactors [27] or as delineated in nonproliferation projects such as WATCHMAN [6].

Lastly, even the more modern databases for $\beta$ spectra, such as the BNBSL [7], rely on approximations for forbidden unique and non-unique decays using the code BetaShape [40] due to the impracticality of treating the entire nuclear database with detailed nuclear-structure calculations like those presented here. In this same study [7], uncertainties related to forbidden non-unique decays are noted for the case of ⁹⁸Tc, which is also examined in our work. These approximations can accumulate uncertainties, exacerbating the issues highlighted in the reactor antineutrino anomaly. Therefore, our work represents a step forward in addressing the complexities involved in forbidden non-unique cases and their nuclear-structure sensitivities, such as the sNME or the $g_{\text{A}}$ shape dependencies.

5 Summary and conclusion

In this article, we conduct a comprehensive survey of potential second-forbidden non-unique $\beta$-decay transitions that are sensitive to the effective value of the weak axial-vector coupling, $g_{\text{A}}$. This sensitivity facilitates the determination of $g_{\text{A}}$ through a comparison of computed and experimentally measured electron spectral shapes, utilizing an enhanced spectrum-shape method (SSM) introduced in this study. This enhanced method exploits the additional dimension of fitting the measured branching ratio of a $\beta$ transition by using the small relativistic vector NME, sNME, as a fitting parameter.

We focus on the decays of ⁶⁰Fe$(0^{+}){\to }^{60}$Co$(2^{+})$, ⁹⁴Nb$(6^{+}){\to }^{94}$Mo$(4^{+})$, ⁹⁸Tc$(6^{+}){\to }^{98}$Ru$(4^{+})$, ¹²⁶Sn$(0^{+}){\to }^{126}$Sb$(2^{+})$, and ¹²⁹I$(7/2^{+}){\to }^{129}$Xe$(3/2^{+})$, selected for their 100% branching ratios which are conducive to the realistic implementation of $\beta$ spectral-shape measurements. Additionally, for the first three of these transitions, multiple well-established Hamiltonians of the nuclear shell model (NSM) are available, providing a basis for a rough estimation of the uncertainties in our NSM calculations.

Our investigation has identified five $\beta$-decay transitions of significant interest for spectral-shape measurement studies. These transitions can be categorized into four distinct categories as previously defined in [48].

$•$ Category I: Includes those transitions that are sensitive to the values of both $g_{\text{A}}$ and sNME.

$•$ Category II: Contains all $\beta$ transitions that have a strong $g_{\text{A}}$ dependence but a weak sNME dependence.

$•$ Category III: Includes the $\beta$ transitions that are rather weakly sensitive to $g_{\text{A}}$ but strongly sensitive to sNME.

$•$ Category IV: Comprises those $\beta$ transitions that are rather weakly sensitive to both $g_{\text{A}}$ and sNME.

Building on the shape decomposition in Equation 3, we can map the four categories to specific components within this equation: vector $(C_{\text{V}})$, axial $(C_{\text{A}})$, and vector-axial $(C_{\text{VA}})$ terms. Category I arises under two scenarios: initially, when the vector-axial component with a significant sNME dependency, is dominant, leading to a shape influenced by both $g_{\text{A}}$ and sNME. Alternatively, it emerges when all three components exhibit comparable magnitudes, and the sensitivity to the sNME in either the vector or vector-axial components fosters a similar dependence.

Category II is characterized by the dominance of the axial component or a dominant vector-axial component with weak sNME sensitivity. Both scenarios result in shapes primarily influenced by $g_{\text{A}}$, albeit with slight to no sNME sensitivity. Conversely, Category III is defined by a dominant vector component sensitive to sNME variations, which makes the decay shape predominantly dependent on sNME with minimal influence from $g_{\text{A}}$.

Lastly, Category IV describes situations where a dominant vector component, insensitive to sNME variations, leads to a decay shape unaffected by both $g_{\text{A}}$ and sNME. This categorization provides a comprehensive framework for analyzing $\beta$-decay transitions in terms of their component sensitivities and the dominant influences affecting their spectral shapes.

Based on the $\beta$ spectral shapes and mean energies, we can then describe the computed decays as follows.

$•$ ⁶⁰Fe$(0^{+}){\to }^{60}$Co$(2^{+})$:

 $•$ For ca48mh1 and fpg9tb, it falls under Category I due to its sensitivity to both $g_{\text{A}}$ and sNME.

 $•$ For gxpf1a and gxpf1b, it is classified as Category II because of its strong dependence on $g_{\text{A}}$ and weak sensitivity to sNME. Overall, the consensus between the interactions places this transition in Category II.

$•$ ⁹⁴Nb$(6^{+}){\to }^{94}$Mo$(4^{+})$:

 $•$ glekpn shows characteristics of Category IV, indicating weak sensitivity to both $g_{\text{A}}$ and sNME.

 $•$ jj45pnb aligns with Category II whilst showing a better match with experimental observables.

$•$ ⁹⁸Tc$(6^{+}){\to }^{98}$Ru$(4^{+})$: Both interactions fall into Category I, highlighting their sensitivity to both $g_{\text{A}}$ and sNME.

$•$ ¹²⁶Sn$(0^{+}){\to }^{126}$Sb$(2^{+})$ and ¹²⁹I$(7/2^{+}){\to }^{129}$Xe$(3/2^{+})$: These transitions are best described by Category III, indicating strong sensitivity to sNME and weaker dependence on $g_{\text{A}}$.

Transitions from Category III play a crucial role in determining the appropriate value of the small relativistic vector nuclear matrix element (sNME). Specifically, they help establish whether the fitted value, ideally close to the Conserved Vector Current (CVC) value of sNME—termed the ‘optimal’—represents the correct physical choice. These transitions also aid in predicting which of the potential solutions is most likely to be real. This strategy is equally applicable to the $\beta$-decay transitions in Category I.

Furthermore, the transitions within Category I and Category II provide avenues to assess the effective value of the axial coupling. The transitions in Category II offer a more direct approach, enabling straightforward evaluations through direct measurements and comparisons with the predicted spectra.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MR: Formal Analysis, Investigation, Software, Visualization, Writing–original draft. JS: Conceptualization, Funding acquisition, Methodology, Supervision, Writing–review and editing. AN: Methodology, Writing–review and editing. SS: Funding acquisition, Project administration, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. JS, AN, and SS acknowledge support from project PNRR-I8/C9-CF264, Contract No. 760100/23.05.2023 of the Romanian Ministry of Research, Innovation and Digitization (The NEPTUN project).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. [Dataset]. ENSDF database (2024). Available from: http://www.nndc.bnl.gov/ensarchivals/ (Accessed April 2024).

Google Scholar

2. Agostini M, Benato G, Detwiler JA, Menéndez J, Vissani F. Toward the discovery of matter creation with neutrinoless ββ decay. Rev Mod Phys (2023) 95:025002. doi:10.1103/revmodphys.95.025002

CrossRef Full Text | Google Scholar

3. Aker M, Beglarian A, Behrens J, Berlev A, Besserer U, Bieringer B, et al. Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat Phys (2022) 18:160–6. doi:10.1038/s41567-021-01463-1

CrossRef Full Text | Google Scholar

4. Alcalá GA, Monserrat S, Mendoza L, Lozano AS, Coello EA, Benites MN, et al. Measurement of the ²³⁸U(n) cross section at the n_TOF facility of CERN. EPJ Web of Conferences (2023) 284:08001. doi:10.1051/epjconf/202328408001

CrossRef Full Text | Google Scholar

5. Algora A, Tain JL, Montaner-Pizá A, Morales AI, Rubio B, Durell JL, et al. Total absorption spectroscopy study of the decay of ¹⁰⁰Tc and the impact on reactor decay heat summation calculations. Eur Phys J A (2021) 57:85. doi:10.1140/epja/s10050-020-00316-4

CrossRef Full Text | Google Scholar

6. [Dataset] Askins M, Bergevin M, Bernstein A, Dazeley S, Dye ST, Handler T, et al. The physics and nuclear nonproliferation goals of watchman: a water cherenkov monitor for antineutrinos (2015). doi:10.48550/ARXIV.1502.01132

CrossRef Full Text | Google Scholar

7. Bailey G, Dronne C, Foster D, Gilbert M. Development of BNBSL: a β-ν spectra library for spectrometry applications. Appl Radiat Isot (2023) 198:110841. doi:10.1016/j.apradiso.2023.110841

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Behrens H, Buhring W. Electron radial wave functions and nuclear beta-decay (international series of monographs on physics). Oxford: Clarendon Press (1982).

Google Scholar

9. Blaum K, Eliseev S, Danevich FA, Tretyak VI, Kovalenko S, Krivoruchenko MI, et al. Neutrinoless double-electron capture. Rev Mod Phys (2020) 92:045007. doi:10.1103/revmodphys.92.045007

CrossRef Full Text | Google Scholar

10. Bodenstein-Dresler L, Chu Y, Gehre D, Gössling C, Heimbold A, Herrmann C, et al. Quenching of g_A deduced from the β-spectrum shape of ¹¹³Cd measured with the COBRA experiment. Phys Lett B (2020) 800:135092. doi:10.1016/j.physletb.2019.135092

CrossRef Full Text | Google Scholar

11. Civitarese O, Suhonen J. Two-neutrino double beta decay to excited one- and two-phonon states. Nucl Phys A (1994) 575:251–68. doi:10.1016/0375-9474(94)90188-0

CrossRef Full Text | Google Scholar

12. de Roubin A, Kostensalo J, Eronen T, Canete L, de Groote R, Jokinen A, et al. High-precision Q-value measurement confirms the potential of ¹³⁵Cs for absolute antineutrino mass scale determination. Phys Rev Lett (2020) 124:222503. doi:10.1103/physrevlett.124.222503

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Dombos AC, Guadilla V, Tain JL, Algora A, Agramunt J, Rubio B, et al. The β-decay of ⁶¹Fe: identification and study of a new pathway for element formation in neutron-rich environments. Phys Rev C (2021) 103:025810. doi:10.1103/PhysRevC.103.025810

CrossRef Full Text | Google Scholar

14. Ejiri H, Suhonen J, Zuber K. Neutrino–nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys Rep (2019) 797:1–102. doi:10.1016/j.physrep.2018.12.001

CrossRef Full Text | Google Scholar

15. Engel J, Menéndez J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rep Prog Phys (2017) 80:046301. doi:10.1088/1361-6633/aa5bc5

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Gastaldo L, Blaum K, Chrysalidis K, Day Goodacre T, Domula A, Door M, et al. The electron capture in ¹⁶³Ho experiment – ECHo. Eur Phys J Spec Top (2017) 226:1623–94. doi:10.1140/epjst/e2017-70071-y

CrossRef Full Text | Google Scholar

17. Ge Z, Eronen T, de Roubin A, Tyrin K, Canete L, Geldhof S, et al. High-precision electron-capture Q value measurement of ¹¹¹In for electron-neutrino mass determination. Phys Lett B (2022) 832:137226. doi:10.1016/j.physletb.2022.137226

CrossRef Full Text | Google Scholar

18. Ge Z, Eronen T, Tyrin K, Kotila J, Kostensalo J, Nesterenko D, et al. ¹⁵⁹Dy electron-capture: a new candidate for neutrino mass determination. Phys Rev Lett (2021) 127:272301. doi:10.1103/physrevlett.127.272301

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Guadilla V, Pérez FM, Nácher E, Orrigo SEA, Algora A, Rubio B, et al. First measurements with a new β-electron detector for spectral shape studies. J Instrumentation (2024) 19:P02027. ArXiv preprint arXiv:2305.13832 [physics.ins-det]. doi:10.1088/1748-0221/19/02/P02027

CrossRef Full Text | Google Scholar

20. Guadilla V, Valencia E, Tain JL, Algora A, Agramunt J, Rubio B, et al. High-precision β-decay half-lives of ⁶⁶Mn, ⁶⁸Co, and ⁷⁰Ni: probing Gamow-Teller strengths in Ni isotopes toward the N=40 island of inversion. Phys Rev Lett (2019) 122:042502. doi:10.1103/PhysRevLett.122.042502

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gysbers P, Hagen G, Holt JD, Jansen GR, Morris TD, Navrátil P, et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat Phys (2019) 15:428–431. doi:10.1038/s41567-019-0450-7

CrossRef Full Text | Google Scholar

22. Haaranen M, Kotila J, Suhonen J. Spectrum-shape method and the next-to-leading-order terms of the β-decay shape factor. Phys Rev C (2017) 95:024327. doi:10.1103/physrevc.95.024327

CrossRef Full Text | Google Scholar

23. Haaranen M, Srivastava PC, Suhonen J. Forbidden nonunique β-decays and effective values of weak coupling constants. Phys Rev C (2016) 93:034308. doi:10.1103/physrevc.93.034308

CrossRef Full Text | Google Scholar

24. Hayen L, Kostensalo J, Severijns N, Suhonen J. First-forbidden transitions in reactor antineutrino spectra. Phys Rev C (2019) 99:031301. doi:10.1103/physrevc.99.031301

CrossRef Full Text | Google Scholar

25. Honma M, Otsuka T, Brown BA, Mizusaki T. Shell-model description of neutron-rich pf-shell nuclei with a new effective interaction gxpf 1. The Eur Phys J A (2005) 25:499–502. doi:10.1140/epjad/i2005-06-032-2

CrossRef Full Text | Google Scholar

26. Honma M, Otsuka T, Mizusaki T, Hjorth-Jensen M, Brown BA. New effective interaction for f5pg9-shell. RIKEN Accelerator Prog Rep (2008) 41:32.

Google Scholar

27. Huber P. Reactor antineutrino fluxes – status and challenges. Nucl Phys B (2016) 908:268–78. doi:10.1016/j.nuclphysb.2016.04.012

CrossRef Full Text | Google Scholar

28. Keblbeck DK, Bhandari R, Gamage ND, Horana Gamage M, Leach KG, Mougeot X, et al. Updated evaluation of potential ultralow Q-value β-decay candidates. Phys Rev C (2023) 107:015504. doi:10.1103/physrevc.107.015504

CrossRef Full Text | Google Scholar

29. Kirsebom OS, Hukkanen M, Kankainen A, Trzaska WH, Strömberg DF, Martínez-Pinedo G, et al. Measurement of the 2⁺→0⁺ground-state transition in the β decay of ²⁰F. Phys Rev C (2019) 100:065805. doi:10.1103/PhysRevC.100.065805

CrossRef Full Text | Google Scholar

30. Kirsebom OS, Jones S, Strömberg DF, Martínez-Pinedo G, Langanke K, Röpke FK, et al. Discovery of an exceptionally strong β-decay transition of ²⁰F and implications for the fate of intermediate-mass stars. Phys Rev Lett (2019) 123:262701. doi:10.1103/PhysRevLett.123.262701

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kostensalo J, Lisi E, Marrone A, Suhonen J. ¹¹³Cd β-decay spectrum and g_A quenching using spectral moments. Phys Rev C (2023) 107:055502. doi:10.1103/physrevc.107.055502

CrossRef Full Text | Google Scholar

32. Kostensalo J, Suhonen J. Mesonic enhancement of the weak axial charge and its effect on the half-lives and spectral shapes of first-forbidden J⁺↔J⁻ decays. Phys Lett B (2018) 781:480–484. doi:10.1016/j.physletb.2018.02.053

CrossRef Full Text | Google Scholar

33. Kostensalo J, Suhonen J, Volkmer J, Zatschler S, Zuber K. Confirmation of g_A quenching using the revised spectrum-shape method for the analysis of the ¹¹³Cd β-decay as measured with the COBRA demonstrator. Phys Lett B (2021) 822:136652. doi:10.1016/j.physletb.2021.136652

CrossRef Full Text | Google Scholar

34. Kumar A, Srivastava PC, Kostensalo J, Suhonen J. Second-forbidden nonunique β^-decays of ²⁴Na and ³⁶Cl assessed by the nuclear shell model. Phys Rev C (2020) 101:064304. doi:10.1103/physrevc.101.064304

CrossRef Full Text | Google Scholar

35. Kumar A, Srivastava PC, Suhonen J. Second-forbidden nonunique β^- decays of ^59,60Fe: possible candidates for g_A sensitive electron spectral-shape measurements. Eur Phys J A (2021) 57:225. doi:10.1140/epja/s10050-021-00540-6

CrossRef Full Text | Google Scholar

36. Leder AF, Mayer D, Ouellet JL, Danevich FA, Dumoulin L, Giuliani A, et al. Determining g_A/g_V with high-resolution spectral measurements using a LiInSe₂ bolometer. Phys Rev Lett (2022) 129:232502. doi:10.1103/PhysRevLett.129.232502

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Lisetskiy AF, Brown BA, Horoi M, Grawe H. New T=1 effective interactions for the f5/2,p3/2, p1/2, g9/2 model space: implications for valence-mirror symmetry and seniority isomers. Phys Rev C Nucl Phys (2004) 70:044314. doi:10.1103/PhysRevC.70.044314

CrossRef Full Text | Google Scholar

38. Mach H, Warburton EK, Gill RL, Casten RF, Becker JA, Brown BA, et al. Meson-exchange enhancement of the first-forbidden β decay of the low-spin isomer of ⁹⁶Y(0⁻)→⁹⁶Zr (0⁺) β transition. Phys Rev C (1990) 41:226–242. doi:10.1103/physrevc.41.226

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Menéndez J, Gazit D, Schwenk A. Chiral two-body currents in nuclei: Gamow-Teller transitions and neutrinoless double-beta decay. Phys Rev Lett (2011) 107:062501. doi:10.1103/physrevlett.107.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Mougeot X. Betashape: a new code for improved analytical calculations of beta spectra. EPJ Web of Conferences (2017) 146:12015. doi:10.1051/epjconf/201714612015

CrossRef Full Text | Google Scholar

41. Niţescu O, Stoica S, Šimkovic F. Exchange correction for allowed β decay. Phys Rev C (2023) 107:025501. doi:10.1103/physrevc.107.025501

CrossRef Full Text | Google Scholar

42. Pagnanini L, Benato G, Carniti P, Celi E, Chiesa D, Corbett J, et al. Simultaneus measurement of half-life and spectral shape of ¹¹⁵In β-decay with a indium iodide cryogenic calorimeter. Phys Rev Lett (Forthcoming 2024) arXiv:2401.16059 [nucl-ex].

Google Scholar

43. Pagnanini L, Benato G, Carniti P, Celi E, Chiesa D, Corbett J, et al. Array of cryogenic calorimeters to evaluate the spectral shape of forbidden β-decays: the ACCESS project. Eur Phys J Plus (2023) 138:445. doi:10.1140/epjp/s13360-023-03500-1

CrossRef Full Text | Google Scholar

44. Paulsen M, Qian H, Liu L, Zeldes M, Zhu Y, Krane KS, et al. High precision measurement of the ⁹⁹Tc β spectrum (2023). arXiv preprint arXiv:2309.14014 [nucl-ex].

45. Qi C, Xu ZX. Monopole-optimized effective interaction for tin isotopes. Phys Rev C (2012) 86:044323. doi:10.1103/physrevc.86.044323

CrossRef Full Text | Google Scholar

46. Ramalho M, Ge Z, Eronen T, Nesterenko DA, Jaatinen J, Jokinen A, et al. Observation of an ultralow Q-value electron-capture channel decaying to ⁷⁵As via a high-precision mass measurement. Phys Rev C (2022) 106:015501. doi:10.1103/physrevc.106.015501

CrossRef Full Text | Google Scholar

47. Ramalho M, Suhonen J. Computed total β-electron spectra for decays of Pb and Bi in the ^220,222Rn radioactive chains. Phys Rev C (2024) 109:014326. doi:10.1103/physrevc.109.014326

CrossRef Full Text | Google Scholar

48. Ramalho M, Suhonen J. g_A-sensitive β spectral shapes in the mass A=86–99 region assessed by the nuclear shell model. Phys Rev C (2024) 109:034321. doi:10.1103/physrevc.109.034321

CrossRef Full Text | Google Scholar

49. Ramalho M, Suhonen J, Kostensalo J, Alcalá GA, Algora A, Fallot M, et al. Analysis of the total β-electron spectrum of ⁹²Rb: implications for the reactor flux anomalies. Phys Rev C (2022) 106:024315. doi:10.1103/physrevc.106.024315

CrossRef Full Text | Google Scholar

50. Redshaw M. Precise Q value determinations for forbidden and low energy β-decays using Penning trap mass spectrometry. Eur Phys J A (2023) 59:18. doi:10.1140/epja/s10050-023-00925-9

CrossRef Full Text | Google Scholar

51. Rice S, Algora A, Tain JL, Agramunt J, Guadilla V, Rubio B, et al. Total absorption spectroscopy study of the beta decay of ⁸⁶Br and ⁹¹Rb. Phys Rev C (2017) 96:014320. doi:10.1103/PhysRevC.96.014320

CrossRef Full Text | Google Scholar

52. Schoppmann S. Status of anomalies and sterile neutrino searches at nuclear reactors. Universe (2021) 7:360. doi:10.3390/universe7100360

CrossRef Full Text | Google Scholar

53. Schwengner R, Frauendorf S, Brown B. Low-energy magnetic dipole radiation in open-shell nuclei. Phys Rev Lett (2017) 118:092502. doi:10.1103/physrevlett.118.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Shimizu N, Mizusaki T, Utsuno Y, Tsunoda Y. Thick-restart block lanczos method for large-scale shell-model calculations. Computer Phys Commun (2019) 244:372–84. doi:10.1016/j.cpc.2019.06.011

CrossRef Full Text | Google Scholar

55. Sorlin O, Leenhardt S, Donzaud C, Duprat J, Azaiez F, Nowacki F, et al. Magicity versus superfluidity. Phys Rev Lett (2002) 88:092501. doi:10.1103/physrevlett.88.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Srivastava PC. Nuclear structure study with core excitations in Ni region: for fpg9/2 space. Mod Phys Lett A (2012) 27:1250061. doi:10.1142/s0217732312500617

CrossRef Full Text | Google Scholar

57. Suhonen J. Calculation of allowed and first-forbidden beta-decay transitions of odd-odd nuclei. Nucl Phys A (1993) 563:205–24. doi:10.1016/0375-9474(93)90602-t

CrossRef Full Text | Google Scholar

58. Suhonen J. From nucleons to nucleus: concepts of microscopic nuclear theory. Berlin: Springer (2007).

Google Scholar

59. Suhonen J. Impact of the quenching of g_A on the sensitivity of 0νββ experiments. Phys Rev C (2017) 96:055501. doi:10.1103/physrevc.96.055501

CrossRef Full Text | Google Scholar

60. Suhonen J, Civitarese O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys Rep (1998) 300:123–214. doi:10.1016/s0370-1573(97)00087-2

CrossRef Full Text | Google Scholar

61. Suhonen J, Kostensalo J. Double β decay and the axial strength. Front Phys (2019) 7. doi:10.3389/fphy.2019.00029

CrossRef Full Text | Google Scholar

62. Suhonen JT. Value of the axial-vector coupling strength in β and ββ decays: a review. Front Phys (2017) 5. doi:10.3389/fphy.2017.00055

CrossRef Full Text | Google Scholar

63. Valencia E, Tain JL, Algora A, Agramunt J, Estevez E, Jordan MD, et al. Total absorption γ-ray spectroscopy of the β-delayed neutron emitters ⁸⁷Br, ⁸⁸Br, and ⁹⁴Rb. Phys Rev C (2017) 95:024320. doi:10.1103/physrevc.95.024320

CrossRef Full Text | Google Scholar

64. Wang B.-L, Wang L.-J. First-forbidden transition of nuclear β decay by projected shell model. Phys Lett B (2024) 850:138515. doi:10.1016/j.physletb.2024.138515

CrossRef Full Text | Google Scholar

65. Zhang C, Qian X, Fallot M. Reactor antineutrino flux and anomaly. Prog Part Nucl Phys (2024) 136:104106. doi:10.1016/j.ppnp.2024.104106

CrossRef Full Text | Google Scholar

66. Zhi Q, Caurier E, Cuenca-García JJ, Langanke K, Martínez-Pinedo G, Sieja K. Shell-model half-lives including first-forbidden contributions for r-process waiting-point nuclei. Phys Rev C (2013) 87:025803. doi:10.1103/PhysRevC.87.025803

CrossRef Full Text | Google Scholar