A simple two-stage carrier-phase estimation algorithm for 32-QAM coherent optical communication systems

The combination of high-order modulation formats and linewidth-tolerant carrier phase estimation (CPE) can effectively improve spectrum efficiency and relax the limitation of laser linewidth. This paper presents a simple two-stage CPE algorithm for polarization-multiplexed (PM) 32-quadrature amplitude modulation (32-QAM) coherent optical communication systems. The algorithm uses an enhanced QPSK partitioning algorithm combined with a simplified 4th power CPE method for coarse estimation in the initial stage and maximum likelihood (ML) detection in the subsequent fine stage. The CPE algorithm significantly increases the number of symbols used in the first stage of coarse estimation. This results in a significant increase in the stability and reliability of the phase estimation, and the CPE algorithm significantly reduces the computational complexity. The optimal parameters, phase estimation performance, and system performance of the algorithm were investigated by building a 22 Gbaud PM 32-QAM coherent system simulation platform and a 5 Gbaud PM 32-QAM coherent system experimental platform. The results show that the proposed two-stage CPE algorithm has a stronger linewidth tolerance difference than the conventional QPSK, and the two-stage CPE algorithm with an optimal block length of 105 performs comparable to blind phase search (BPS). The optical signal noise Ratio (OSNR) value is 21.2 dB and the bit error rate (BER) is 1.8 × 10⁻³ for the optimal block length of 105. The receiving-end DSP unit with a flexible scheme and good communication performance will have potential applications in adaptive elastic optical networks.

1 Introduction

Coherent optical transmission systems using high-order quadrature amplitude modulation (QAM) formats joined by digital signal processing (DSP) have been paid more attention, due to their high spectral efficiency (SE) and low cost [1, 2]. Polarization-multiplexed quadrature phase-shift keying (PM-QPSK), with a data rate of 100 Gb/s, is available for commercial systems at present. Higher spectral efficiency modulation formats, such as 32-QAM, mean higher spectral resource utilization and greater per-channel transmission capacity, with reduced symbol rates and channel bandwidth [3–5].

QAM coherent optical communication can effectively improve spectral efficiency [6]. At the same time, to obtain higher data rate transmission capacity requirements, the spectral efficiency of long-distance communication can be improved by using advanced DSP schemes, which adopt higher-order data modulation formats such as 64-QAM and 128-QAM [7, 8]. For high-capacity, high-spectral efficiency optical transmission systems, the receiver-side efficient DSP algorithm is crucial in eliminating the need for expensive optical compensation devices, as it can make up for transmission impairments in the electrical digital field [9–12].

In 2024, Kumari et al. explored an optical wireless communication (OWC) system from a high-altitude platform (HAP) to a satellite, using orbital angular momentum (OAM) multiplexing orthogonal frequency division multiplexing (OFDM) technology [13]. The scheme can achieve a transmission rate of 200 Gbps per channel, maintaining a total data rate of 800 Gbps at a maximum distance of 5,000 km. It demonstrates high performance and scalability in extreme environments, especially when dealing with communications over long distances and high data rates. Reference [14] proposed a performance analysis of a symmetrical bidirectional 40 Gbps m-QAM-OFDM modulated TWDM-PON system based on multi-color LD. By combining multi-color laser diodes (LDs) for visible light communication (VLC), high-speed data transmission on a composite optical fiber/VLC network is achieved. The system can maintain a low BER under various link conditions and successfully transmit data rates up to 120 Gbps, demonstrating its effectiveness in improving transmission performance and network efficiency.

Saw et al. analyzed the FSO system based on Co-OFDM technology and analyzed the impact of atmospheric turbulence and pointing errors. An effective phase estimation algorithm can significantly reduce communication interruptions and BER caused by environmental changes, especially in higher-order QAM systems [15]. Sharma and Chaudhary proposed an OFDM-FSO integrated system to extend the FSO link at high transmission rates under clear weather conditions and evaluated the performance of the hybrid system using ODSB, OSSB, and OTSB schemes. Through accurate carrier phase control, the performance of the FSO system can be improved, especially in OFDM systems, where accurate phase estimation is crucial to signal quality [16]. In the hybrid system of wireless and wired, literature [17] studies the wired and wireless OFDM-OSSB-RoF transmission system under the high transmission rate of a 4 QAM sequence generator. It also plays a crucial role in reducing the degradation introduced by fiber dispersion under different laser spectral widths. Within a range of 10–100 km, this hybrid RoF system effectively improves the laser spectrum width by reducing it from 10 MHz to 100 kHz at a transmission rate of 10/20 Gbps.

The phase noise produced by the linewidth of the transmitter laser and the local oscillator (LO) is one of the factors conditioning the performance of the high-order QAM system, and an efficient DSP algorithm is needed for compensation and estimation. To compensate for phase noise and increase line tolerance, carrier phase estimation algorithms have attracted the attention of many scholars. They are considered key DSP algorithms for high-spectral efficiency QAM coherent optical systems [18]. Many have already researched different carrier-phase estimation methods. The extant CPE algorithms for high-order QAM systems can be divided into data-aided (DA) [19] and non-DA (NDA) methods [20, 21]. NDA CPE schemes have higher spectral efficiency because they do not cause overhead; hence, NDA CPE schemes have attracted much attention. The most popular NDA CPE schemes are the optimal-performance blind phase search (BPS) [22] or the quadrature phase-shift keying partitioning (QPSK partitioning) [23–25]. The BPS has excellent performance but high computational complexity. After constellation partition in CPE, the QPSK partitioning algorithm using a feedforward structure with low computational complexity can use conventional Viterbi–Viterbi phase estimation (VVPE) methods [26]. Moreover, multi-phase CPE algorithms exist, such as the two-stage BPS algorithms [27], the QPSK partitioning + maximum likelihood (ML) algorithm [28], and the BPS + ML algorithm [29]. However, while QPSK partitioning has relatively low computational complexity, the shortage of sufficient QPSK-like symbols and stringent linewidth requirements make it unsuitable for use as a first-stage phase estimation method for higher-order m-QAM signals, especially when the 32-QAM constellation is non-square and only a small number of QPSK symbols are available for CPE. The main innovations of this article are as follows:

(1) Innovative algorithm design: This paper uses the enhanced QPSK segmentation algorithm combined with the simplified fourth power CPE method for rough estimation, and uses ML detection for fine estimation in the subsequent stage. This two-stage design effectively increases the number of symbols available for primary estimation, thereby improving the stability and reliability of phase estimation.

(2) Excellent phase estimation: The algorithm in this article demonstrates excellent phase estimation performance and can support higher linewidth-symbol duration ($∆v\cdot T_s$) under the same OSNR conditions. The scheme can achieve lower BER at lower OSNR values, proving its robustness in noisy environments.

(3) Reduction of computational complexity: The method in this paper significantly reduces the computational complexity by combining the simplified fourth power method and ML detection. Compared with the BPS method in literature (15, 24), this scheme does not require a large number of test phases, thereby reducing the resource requirements and power consumption of hardware implementation. The computational complexity is significantly reduced by simplifying the calculation steps, which is extremely beneficial for hardware implementation. This method has lower complexity in practical applications, especially in achieving computational simplification while maintaining performance.

At present, coherent 100G long-distance transmission mainly uses QPSK, while that for 400G long-distance transmission is mainly 16QAM. In the pursuit of larger capacity and faster rates, high-order 32-QAM is a promising solution. Aiming at the difficulty of accurately estimating the phase of 32-QAM constellation diagrams, this paper proposes a simple two-stage CPE algorithm for 32-QAM coherent optical communication systems. This algorithm combines an improved QPSK partitioning technique with a simplified fourth-power CPE method for coarse estimation and uses ML detection for fine estimation in the subsequent stage. The results show that the two-order estimation method used by the CPE algorithm can track phase noise variations using shorter estimation block lengths with low complexity, compared to conventional algorithms based on QPSK partitioning and optimal BPS. The two-stage CPE algorithm proposed in this paper significantly increases the number of symbols available in the primary estimation stage, thereby enhancing the stability and reliability of phase estimation while reducing computational complexity. In addition, the computational complexity is significantly reduced through simplified calculation steps, allowing the scheme to maintain lower BER in noisy environments, showing stronger line width tolerance and better system performance than traditional methods.

2 Principle of the two-stage CPE algorithm

For QPSK signals, the VVPE algorithm can achieve carrier phase recovery very well. To apply this algorithm to QAM systems, one possible way is to extract data points from the input QAM signal sequence that have the phase characteristics of the QPSK signal and use the VVPE algorithm on such data points to remove the modulation phase information, which is called the QPSK partitioning algorithm.

Figure 1 shows that the 32-QAM symbols exist on five different rings. Based on the received sample’s different amplitudes, the traditional QPSK partitioning approach raises only the symbols highlighted using red points—that is, the symbols with modulation angles of π/4 + k·π/2 (k = 0 … 3) in Figure 1A—to the 4th power to dismiss the modulation phase data. Nevertheless, only 8/32 of the 32-QAM symbols are adopted in statistics for the traditional QPSK partitioning approach, which results in poor linewidth tolerance performance and failure to detect slips in the cycle [24].

Figure 1

Figure 1. (A) Constellation diagram for 32-QAM. (B) The enhanced QPSK partitioning scheme for 32-QAM.

In [18], an extended QPSK partitioning scheme was detailed, in which the symbols employed in QPSK partitioning are emphasized by the red, purple, and blue points in Figure 1B. The primary purpose is to increase the available symbols in QPSK partitioning of 32-QAM. In Figure 1B, the symbols in purple are rotated by 45° to minimize the phase offsets to ±11.3° to the nearest 45° diagonal, enabling those symbols to be used for CPE. Similarly, the blue constellation point on the outermost circle can also participate in carrier-phase estimation because it has a phase offset of 14° from the nearest 45° diagonal.

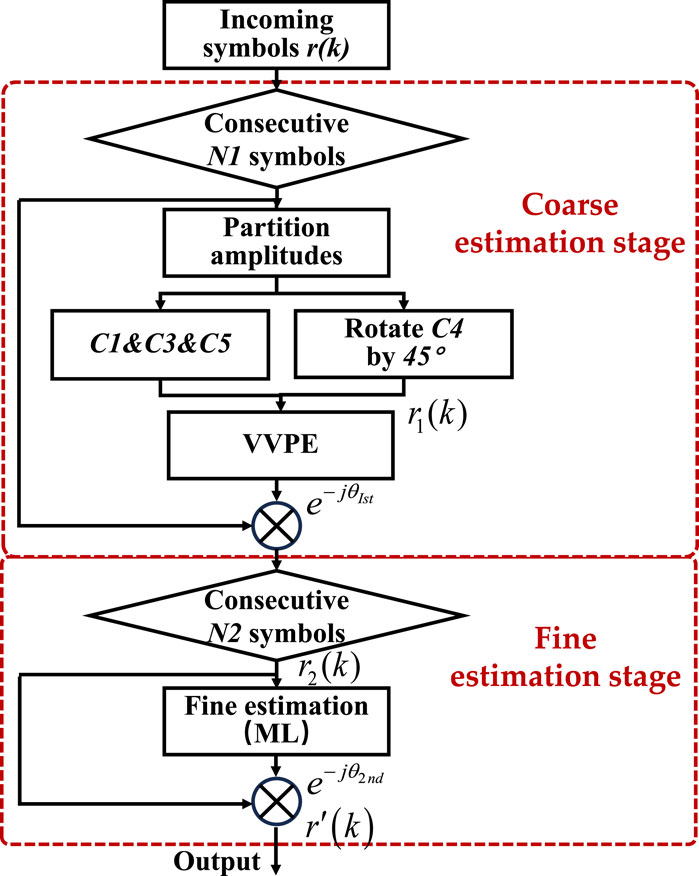
To make the CPE less computationally complex, the simplified Mth-power method [30] is applied instead of the conventional Mth-power operation, where an absolute operation is approximated and the VandV algorithm is made free of a multiplier CPE. Furthermore, maximum likelihood (ML) detection is also introduced as the second fine stage to estimate the phase more accurately. The block diagram of the simple two-stage CPE algorithm for 32-QAM is shown in Figure 2, where the enhanced QPSK division combined with the simplified 4th power CPE method is used as the initial coarse phase and the ML detection is used as the subsequent fine phase, with the following steps:

Figure 2

Figure 2. Block diagram of the two-stage CPE algorithm for 32-QAM coherent optical communication systems.

Coarse estimation stage: the input symbol $r\left(k\right)$ is taken every N1 length, C4 is rotated by 45°, then C1, C3, C5, and the rotated C4 are combined, and finally the signal $r_1\left(k\right)$ is obtained for QPSK estimation.

Fine estimation stage: the input is the output signal of the coarse estimation stage, and the output signal $r^{\prime }\left(k\right)$ is finally obtained using maximum likelihood estimation.

Figure 2 shows that, according to the enhanced QPSK partitioning algorithm, the initial stage phase estimation ${\theta }_{1st}$ can be expressed as follows:

${\theta }_{1st}=\frac{1}{4}\arg \left({\displaystyle \sum _{k=1}^{N_1}}{r_1}^4\left(k\right)\right)(1)$

The initial block of N1 symbols is selected from the input symbols $r\left(k\right)$ and the $r_1\left(k\right)$ symbols are estimated by the QPSK partitioning algorithm. $\arg \left(\cdot \right)$ represents the phase angle calculation for the estimated symbol. In the case of a received symbol not being from the usable constellations, it will be substituted with a “zero” in the vector of samples used for CPE in Equation 1.

After the first-stage estimation result is obtained and the carrier-phase coarse compensation of the N₁ consecutive symbols is completed, the shorter block length N₂ is used as the block length of the second-stage ML algorithm to better track the phase transformation. The phase estimation in the second ML stage is expressed as follows:

${\mathrm{h}}_{2nd}={\displaystyle \sum _{k=1}^{N_2}}{r}_2\left(k\right)\times {〈{\widehat{r}}_2\left(k\right)〉}^{*}(2)$

${\theta }_{2nd}={\tan }^{-1}\left[\text{Im}\left(h_{2nd}\right)/\text{Re}\left(h_{2nd}\right)\right](3)$

$r_2\left(k\right)$ indicates the signal obtained by the first stage of coarse estimation. Where ${\widehat{r}}_2\left(k\right)$ denotes the decision of $r_2\left(k\right)$, $h_{2nd}$ denotes the product of $r_2\left(k\right)$ and ${〈{\widehat{r}}_2\left(k\right)〉}^{*}$, * denotes the conjugate operation. Im(${\mathrm{h}}_{2nd}$) represents the real part of the vector $h_{2nd}$ and Re(${\mathrm{h}}_{2nd}$) represents the imaging part of $h_{2nd}$.The angle ${\theta }_{2nd}$ represents the optimal phase correction value.

Finally, as shown in Equation 4, the carrier phase estimation value ${\theta }_{2nd}$ obtained in the second stage is used to perform carrier-phase compensation on the samples $r_2\left(k\right)$ using the sliding window, $r^{\prime }\left(k\right)$ is the output signal.

$r^{\prime }\left(k\right)=r_2\left(k\right)\times \exp \left(-j{\theta }_{2nd}\right)(4)$

The main contribution of this article is to propose a simplified two-stage carrier phase estimation algorithm for 32-QAM coherent optical communication systems. This algorithm combines for the first time an improved QPSK segmentation and a simplified fourth power method for coarse estimation, and applies maximum likelihood (ML) detection in the subsequent fine estimation stage. With this innovative approach, the number of symbols available for phase estimation in the first stage is significantly increased, thereby enhancing the stability and reliability of phase estimation and significantly reducing computational complexity.

The flow chart of the CPE algorithm for QPSK partitioning is shown in Figure 3. The proposed quasi-QPSK segmentation is deployed in the first coarse estimation stage. The second stage is the fine estimation ML.

Figure 3

Figure 3. Flow chart of the CPE algorithm for QPSK partitioning.

The proposed two-stage CPE algorithm is designed for 32-QAM coherent optical communication systems to improve the accuracy of phase estimation and reduce computational complexity. The following is a detailed step-by-step explanation of the algorithm, combined with theoretical foundations and parameter settings:

2.1 Received signal processing

The received signal $r\left(k\right)$ is collected and prepared for subsequent phase estimation processing. Here $r\left(k\right)$ represents the k received symbol, i.e., $r\left(k\right)=I_k+j{Q}_k$, where $I_k$ and $Q_k$ represent the in-phase and quadrature components of the symbol, respectively. These points are located on different rings of the 32-QAM constellation diagram (e.g., C1, C3, C4, C5).

2.2 Constellation point classification and quartic processing

The constellation points are classified into different rings according to their amplitude:

C1 and C3 rings usually contain points with lower amplitudes. C4 and C5 rings contain points with higher amplitudes.

The points on each ring have different phase and amplitude characteristics. For preliminary processing, the constellation points of all received signals are first transformed to the fourth power to simplify the phase complexity. Equation 5 describes the operation of raising the complex symbol $r\left(k\right)$ of each received constellation point to the fourth power.

$r_k^4={\left(I_k+j{Q}_k\right)}^4(5)$

2.3 Rough phase estimation

Use the simplified signal $r\left(k\right)$ to make a rough phase estimation. Mainly calculate the average phase angle of all processed symbols, which is used to roughly correct the phase as shown in Equation 1.

According to the phase obtained by the rough estimation ${\theta }_{1st}$, the specific constellation point is rotated. The constellation points on the C1, C3, and C5 rings are not rotated. Because of their positional relationship, the constellation points on the C4 ring need to be rotated 45° to compensate for the phase error, as shown in Equation 6.

$r_2\left(k\right)=r\left(k\right)e^{-j\left({\theta }_{1st}+45°\right)}(6)$

2.4 Refine phase estimation

The maximum likelihood estimation (ML) method is applied to the constellation points that have been selectively rotated to further refine the phase. This step uses a more detailed algorithm to optimize the phase estimation, as shown in Equations 2, 3.

$r_2\left(k\right)$ is the signal after the rough estimation in the first stage. ${\mathrm{h}}_{2nd}$ represents an intermediate variable used for phase estimation in the fine estimation process in the second stage. ${\mathrm{h}}_{2nd}$ is used to calculate the final phase adjustment angle ${\theta }_{2nd}$ in the second stage. This angle reflects the phase deviation between the output of the first stage and the actual signal, and is a fine adjustment of the initial estimate.

2.5 Refine phase estimation

Using the carrier phase estimation value obtained in the second stage, the carrier phase compensation is performed on the sampling point through the sliding window, which is the output signal. Use the refined phase ${\theta }_{2nd}$ to perform final phase compensation on all data to ensure that the phase of the signal is completely corrected. As shown in Equation 4, $r^{\prime }\left(k\right)$ is the final compensated output signal.

3 Simulation results and discussions

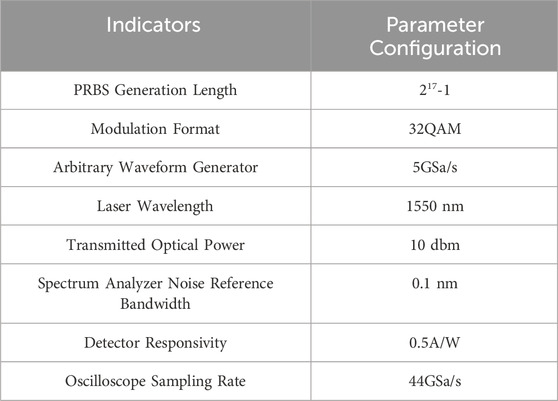
To explore the performance of the suggested two-stage CPE algorithm for 32-QAM coherent optical communication systems, a 22 Gbaud polarization-multiplexing (PM) 32-QAM simulation platform was constructed, with the phase noise simulated as a Wiener process, as shown in Figure 3. After the signals were sampled at 44 GSa/s (two samples per symbol), digital signal processing was performed. This consisted of chromatic dispersion compensation, channel adaptive equalization, polarization demultiplexing, frequency offset estimation, and finally, the target CPE algorithm. We assumed that the transition impairments had been fully compensated before CPE. As shown in Table 1, the simulation parameter diagram.

Table 1

Table 1. Simulation parameters.

Figure 4 uses a coherent system, at the transmitter side, the source data is 22Gbaud PM 32-QAM, after two IQ modulation into the fiber optic link, we use VOA to adjust the signal strength. The signal is amplified by EDFA to compensate for the transmission loss. At the receiving end, the signal is decomposed into two polarized components by PBS, which go through a 90-degree Hybrid and enter into BPDs, and the I and Q components of each polarization direction each go through a pair of BPDs, thus generating four electrical signals, Ix, Qx, Iy, Qy, which are then fed into the ADC. the signals finally enter into the DSP module for data processing and parsing.

Figure 4

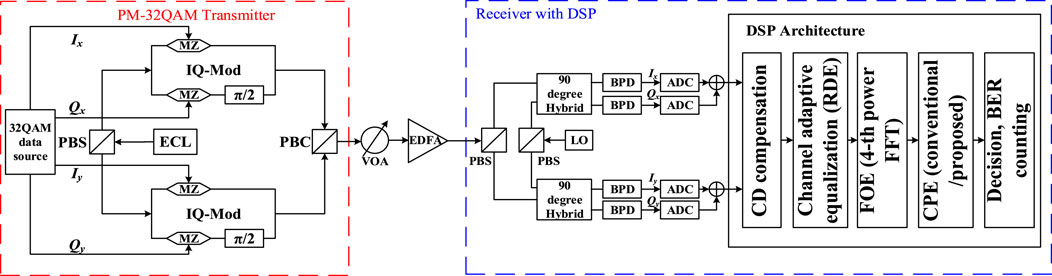
Figure 4. Block diagram of the simulation setup for 22Gbaud PM 32-QAM coherent system. IQ-Mod: in-phase-quadrature modulator. MZ: Mach-Zehnder modulator. ECL: external cavity laser. PBS: polarization beam splitter. PBC: polarization beam combiner. VOA: variable Optical Attenuator. EDFA: erbium-doped fiber amplifier. LO: local oscillator. BPD: balanced photodiode. ADC: Analog-to-digital.

As is well known, the block length has a great impact upon the BER performance for 32-QAM coherent optical systems, so the optimal length is crucial to a CPE algorithm. Usually, ASE noise coordinates with phase noise suppression are used to determine the optimal block length, because that larger block length is useful to mitigate the additive noise, while shorter block length is also expected to help maintain the phase-tracking speed. Figure 5 displays the joined linewidth–symbol duration product $∆v\cdot T_s$ vs. block length for the proposed initial-stage CPE, BPS, and QPSK partitioning with an OSNR of 24 dB at a BER of 3.8 × 10⁻³ in 32-QAM systems. The figure shows that the optimal block length for the suggested initial-stage CPE reaches 105, whereas it is 60 and 205 for the BPS and the traditional QPSK partitioning, respectively. Because the proposed enhancement of the first stage, CPE introduces more available symbols, its optimal block length is significantly lower than that of the conventional QPSK partitioning algorithm.

Figure 5

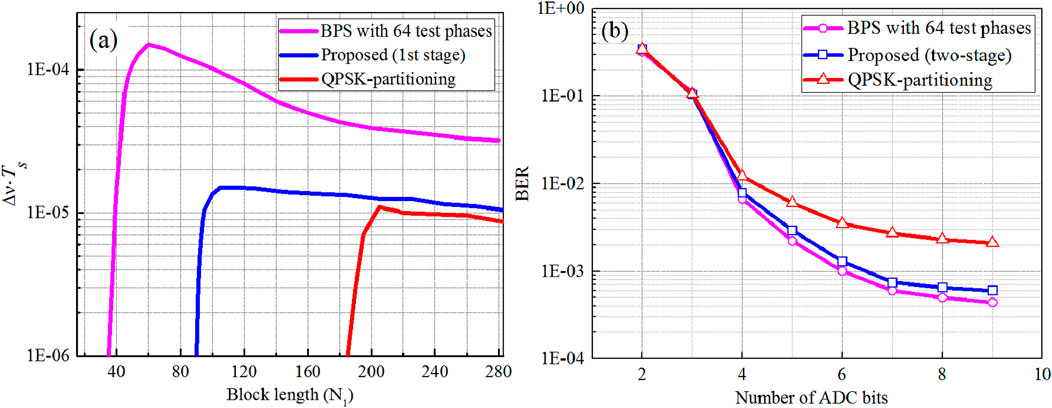
Figure 5. (A) Joined linewidth–symbol duration product $∆v\cdot T_s$ vs. block length for the suggested initial-stage CPE, BPS, and QPSK partitioning with an OSNR of 24 dB at a BER of 3.8 × 10⁻³; (B) the effect of ADC resolution on BER performance for the suggetsed phase-stage CPE and the other two algorithms at an OSNR of 24 dB with $∆v\cdot T_s$ = 5 × 10⁻⁵.

Figure 5B shows the effect of ADC resolution on BER performance for the suggested two-stage CPE and the other two algorithms at an OSNR of 24 dB with $∆v\cdot T_s$ = 5 × 10⁻⁵. Here, the influence on the suggested CPE algorithm from the ADC quantization error in the analog-to-digital converter (ADC) is investigated. The joined linewidth–symbol duration product $∆v\cdot T_s$ (for the transmitting lasers and LO) was set to 5 × 10⁻⁵. Figure 5B shows that the influence of bit resolution on the suggested two-stage CPE algorithm is slightly worse than that on the BPS algorithm but represents a significant improvement over the conventional QPSK partitioning algorithm. As shown in Figure 5, when the OSNR is 24 dB, the BER performance of the BPS algorithm under different block lengths is always better than that of the two-stage CPE and QPSK splitting algorithms. The two-stage CPE algorithm achieves the best performance when the block length is 105, while the QPSK splitting performs poorly at longer block lengths.

Figure 6 demonstrates the constellation after compensation in each period at an OSNR of 24 dB with $∆v\cdot T_s$ = 5 × 10⁻⁵. It can be seen from Figure 6A that the 32-QAM constellation strictly spins as a result of the laser-linewidth-induced phase noises. After the compensation of the suggested two-stage CPE, the 32-QAM constellation is displayed in Figure 6B, where the constellation points are generally visible but the effects of residual phase noise still exist. The aforementioned first-stage CPE proposed in Section 2 was employed to roughly compensate the phase noises using a part of the constellations. Figure 6C shows the 32-QAM constellations after the subsequent ML-stage compensation. We can conclude that the constellation diagram after the ML stage is clear and convergent.

Figure 6

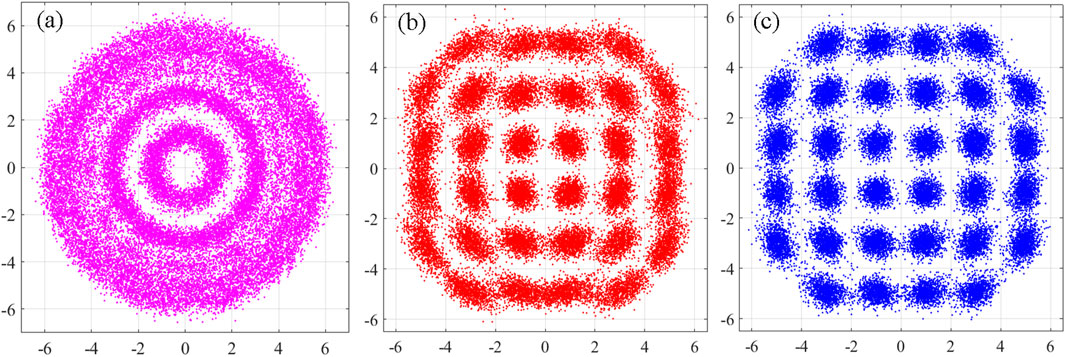
Figure 6. Constellations of 32-QAM after each stage of compensation: (A) after the frequency offset compensation; (B) after the first enhanced QPSK partitioning stage; (C) after the second ML stage. All at an OSNR of 24 dB with $∆v\cdot T_s$ = 5 × 10⁻⁵.

As can be seen from Figure 7, under different line width-symbol duration product ($∆v\cdot T_s$) conditions, the required OSNR increases with the increase of $∆v\cdot T_s$. The two-stage CPE algorithm and BPS perform better under low OSNR conditions, while QPSK splitting requires a higher OSNR to achieve the same BER performance. The required OSNR (in 0.1 nm) for each algorithm at a bit error rate (BER) of 3.8 × 10⁻³ is shown in Figure 7A, in which the linewidth–symbol duration products of the three algorithms are evaluated. The BPS has 64 test phases, and for all algorithms, the corresponding block lengths are optimal based on the results of Figure 5A. It should be noted that differential encoding is not applied here. From the figure, we can see that for the OSNR of 22 dB, a linewidth–symbol duration product $∆v\cdot T_s$ of 3 × 10⁻⁵ could be endured by the traditional QPSK partitioning, while the values were 7 × 10⁻⁵ and 1 × 10⁻⁴ for the proposed two-stage CPE and BPS, respectively. It should also be noted that although the suggested two-stage CPE algorithm has a slightly worse linewidth tolerance performance than BPS, the two-stage algorithm is approximately one-tenth more complex than BPS, and such a significant reduction in complexity is very beneficial to the hardware implementation of the algorithm.

Figure 7

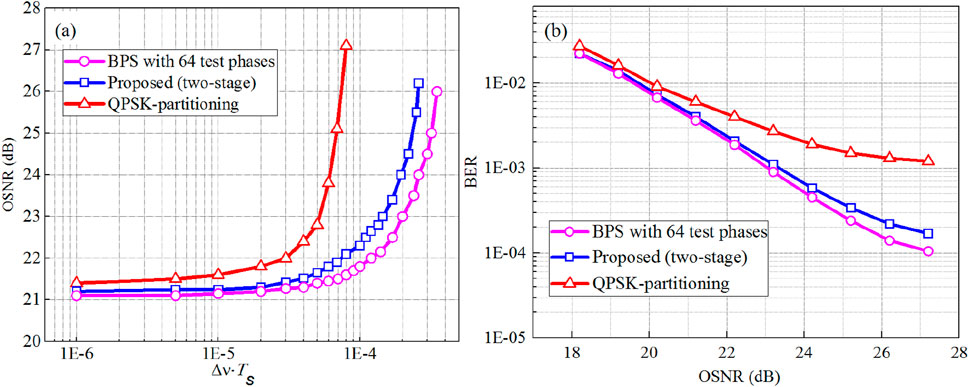
Figure 7. (A) Required OSNR versus the combined linewidth–symbol duration product $∆v\cdot T_s$ at a target BER of 3.8 × 10⁻³; (B) BER as a function of OSNR at $∆v\cdot T_s$ of 5 × 10⁻⁵.

In a 32-QAM optical coherent system with $∆v\cdot T_s$ of 5 × 10⁻⁵, the relationship between BER and OSNR is displayed in Figure 7B, showing that the suggested two-stage CPE obtains similar BER performance to the BPS algorithm with 64 test phases, while the conventional QPSK partitioning showed the worst BER performance in the simulations. As mentioned in Section 2, since the conventional QPSK partitioning algorithm can only use a small number of constellation points for carrier-phase estimation in the 32-QAM system, its phase estimation performance is significantly degraded. However, for the proposed two-stage algorithm in which enhanced QPSK partitioning combined with a simplified 4th-power method is used for the initial coarse stage while ML detection is utilized for the subsequent fine stage, it remarkably makes the CPE less computationally complex, and the performance is also desirable. We analyzed the complexity of the three schemes, as shown in Table 2, where N, N1, and N2 denote the block lengths and B denotes the number of phases. Table 3 shows the performance comparison of BPS and QPSK partitioning with the proposed CPE algorithm.

Table 2

Table 2. Complexity analysis table.

Table 3

Table 3. Algorithm performance comparison.

4 Experiment design and results

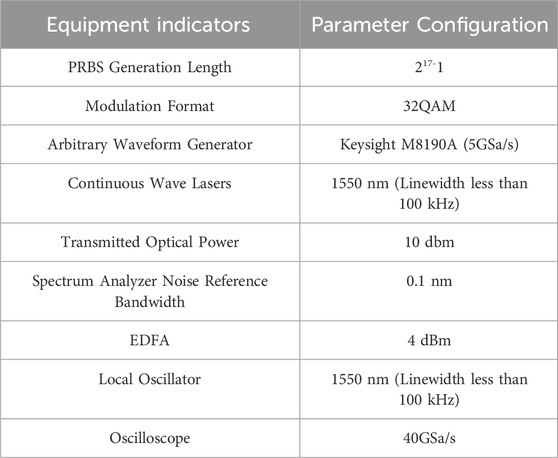
The experimental design for a 5 Gbaud PM 32-QAM back-to-back transmission system with a commercial transmitter and LO lasers is depicted in Figure 8. On the transmitter side, a pseudo-random binary sequence (PRBS) with a length of 2¹⁷-1 was mapped into 32-QAM format. Then, the digital32-QAM signals were uploaded into an arbitrary waveform generator (AWG) (Keysight M8190A) operated at 5 GSa/s for digital-to-analog (D/A) conversion. A continuous-wave laser with a linewidth of <100 kHz acted as an optical carrier for the transmitter, and the carrier’s center wavelength was 1,550 nm. The two polarizations modulated using the dual-polarization IQ modulator were combined with PBC and amplified through the EDFA, which was used for the generation of certain amount of ASE noise in the process of adjusting the OSNR. Then, the back-to-back optical signal transmitted was sent into a tunable optical filter to remove the out-of-band noise. An optical spectrum analyzer (OSA) with a noise reference bandwidth of 0.1 nm was used to gauge the OSNR. The local oscillator (LO) laser was identical to the transmitter laser, with linewidth <100 kHz at 1,550 nm. With the optical signal and LO carrier transmitted to a commercial coherent receiver to achieve photoelectric conversion, the four electrical signals were digitized using an oscilloscope working at 40 GSa/s. The offline DSP was composed of the resampling signal, I/Q imbalance compensation, chromatic dispersion (CD) compensation, polarization demultiplexing, frequency offset estimation, carrier-phase estimation, and BER counting. The experimental parameters are shown in Table 4.

Figure 8

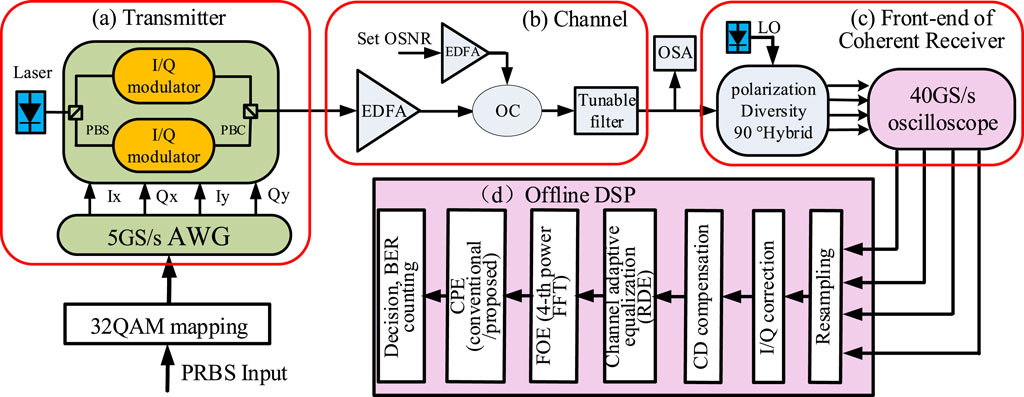
Figure 8. Block diagram of the experimental setup for the 5 Gbaud PM 32-QAM coherent system. AWG: arbitrary waveform generator. PBS: polarization beam splitter. PBC: polarization beam combiner. OC: optical coupler. EDFA: erbium-doped fiber amplifier. LO: local oscillator.

Table 4

Table 4. Experimental parameters.

The relationship between BER and OSNR for 5 Gbaud double-polarization 32-QAM coherent optical systems using commercial lasers with a linewidth of <100 kHz is displayed in Figure 9, showing that the BER performance for the traditional QPSK partitioning was the worst in the experiment. The best BER of the conventional QPSK partitioning was still larger than 1 × 10⁻³, while the proposed two-stage CPE achieved a slightly worse BER performance than the BPS algorithms with 64 test phases. Similar to the simulation results, since the conventional QPSK partitioning algorithm uses only a few constellation points for carrier-phase estimation in the 32-QAM system, its phase estimation performance was significantly degraded. Figure 9 is an experimental data graph, and the BER of all algorithms gradually decreases with the increase of OSNR. The two-stage CPE and BPS perform similarly, while the QPSK splitting algorithm performs the worst. On the other hand, the proposed two-stage algorithm with remarkably reduced total computational complexity—in which enhanced QPSK partitioning combined with a simplified 4th-power method was used for the initial coarse stage, and ML detection was utilized for the subsequent fine stage—maintained a comparable performance to the BPS. This proves that the suggested low-complexity CPE algorithm is a potential candidate for the 32-QAM coherent optical system.

Figure 9

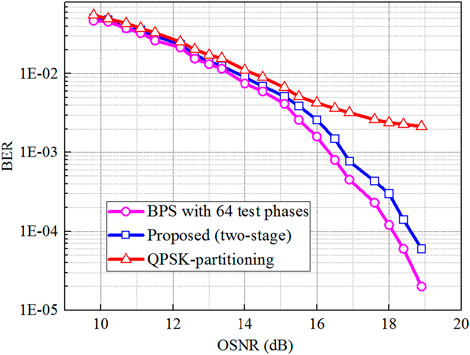
Figure 9. The relationship between BER and OSNR for the back-to-back 5 Gbaud double-polarization 32-QAM coherent optical systems.

This article builds an algorithm test platform. When the optimal block length is 105, compared with the traditional BPS, the OSNR of the proposed algorithm is 21.2 dB and the BER is 1.8 × 10⁻³, which shows that the proposed algorithm has good line width tolerance. Obvious advantage. At the same time, this solution demonstrates excellent phase estimation performance and can support higher linewidth-symbol duration $∆v\cdot T_s$ under the same OSNR conditions. Experimental data results show that it exhibits comparable performance to BPS under the same test conditions, thus proving the practicability and effectiveness of the algorithm.

Although the BPS algorithm has a high computational complexity, it shows good performance in both experimental and simulation data, especially it can maintain a low bit error rate at low OSNR values, which is suitable for applications requiring high-precision phase estimation. The two-stage CPE algorithm shows comparable bit error rate performance to BPS in both experiments and simulations, especially at medium to high OSNR values. The advantage of this algorithm is that it can significantly reduce the computational complexity while maintaining performance, making it suitable for practical deployment. QPSK segmentation has the weakest performance under all conditions, especially under low OSNR conditions, where its bit error rate is significantly higher than the other two algorithms. This may be because the algorithm only uses some symbol points for phase estimation, resulting in lower flexibility and reliability in practical applications. In summary, the two-stage CPE algorithm shows excellent performance in both experiments and simulations, especially achieving a good balance between computational complexity and bit error rate performance, making it a potential application in practice. This paper significantly reduces the computational complexity by combining the simplified fourth power method and ML detection. Literature [18, 24] can also perform phase estimation well, but the algorithm complexity is high. Compared with the traditional BPS method, this method does not require a large number of test phases, thereby reducing the resource requirements and power consumption of hardware implementation, which is extremely beneficial to hardware implementation, especially achieving computational simplification while maintaining performance.

5 Conclusion

In this study, we suggested a simple two-stage CPE algorithm for 32-QAM coherent optical communication systems. In contrast to the traditional QPSK partitioning algorithms, the proposed algorithm uses QPSK-like constellation points to perform estimation, where a simplified 4th-power method is applied for removing the complex 4th-power operation in the initial stage, and ML detection is utilized for the subsequent fine stage. Optical back-to-back numerical simulations and experiments were conducted to explore the performance of the suggested algorithm. Our findings revealed that, compared with the conventional QPSK partitioning, the proposed two-stage CPE with shorter estimation blocks has a greater linewidth tolerance. The scheme reduces the computational complexity by simplifying the calculation steps and does not require a large number of test phases, thereby reducing the need for hardware resources and power consumption. Additionally, the proposed algorithm is not only less complex, but also has comparable performance to that of the standard BPS. This algorithm provides a more efficient and economical solution when dealing with high-speed, high-order modulation formats in optical communication systems. There are still some challenges in this study. The current research is mainly limited to low baud rates and short-distance SSMF transmission scenarios. Future research can be extended to higher baud rates and longer distance transmission tests to fully evaluate the practical application potential of this solution. Secondly, in actual deployment, it may be necessary to further optimize the algorithm to adapt to different transmission conditions and dynamic network environments, such as using artificial intelligence algorithms to further improve system performance and adaptability.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MP: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Writing–original draft. XW: Funding acquisition, Writing–review and editing. XY: Investigation, Validation, Visualization, Writing–review and editing. DW: Project administration, Resources, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article. This research work was supported in part by Anhui Digital Intelligent Engineering Research Center for Agricultural Products Quality Safety (APDI202302). Anhui Education Department, and University Natural Science Research Project of Anhui Province (Grant No. 2022AH051338). This work is supported by Henan Key Laboratory of Visible Light Communications (No. HKLVLC2023-B10), Jiangxi Provincial Natural Science Foundation (20232BAB212006) and Open Fund of Advanced Cryptography and System Security Key Laboratory of Sichuan Province (Grant No. SKLACSS-202306) and (Grant No. SKLACSS-202303). This work is supported by R&D Program of Beijing Municipal Education Commission (KM202310015002), and Hubei Provincial Natural Science Foundation of China (Grant No: 2023AFB474, Grant No: 2024AFB881). This research work was supported by the Special Fund of Advantageous and Characteristic disciplines (Group) of Hubei Province.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Faruk MS, Savory SJ. Digital signal processing for coherent transceivers employing multilevel formats. J Lightw Technol (2017) 35(5):1125–41. doi:10.1109/jlt.2017.2662319

CrossRef Full Text | Google Scholar

2. Winzer PJ. Beyond 100 G ethernet. IEEE Commun Mag (2010) 48(7):26–30. doi:10.1109/mcom.2010.5496875

CrossRef Full Text | Google Scholar

3. Winzer P. High-spectral-efficiency optical modulation formats. J Lightwave Technol (2012) 30(8):3824–35. doi:10.1109/jlt.2012.2212180

CrossRef Full Text | Google Scholar

4. Zhou X, Nelson LE, Magill P, Isaac R, Zhu B, Peckham DW, et al. PDM-Nyquist-32QAM for 450-Gb/s per-channel WDM transmission on the 50 GHz ITU-T grid. J Lightw Technol (2012) 30(4):553–9. doi:10.1109/jlt.2011.2177243

CrossRef Full Text | Google Scholar

5. Otuya DO, Kasai K, Hirooka T, Yoshida M, Nakazawa M, Hara T, et al. A single-channel, 1.6 Tbit/s 32 QAM coherent pulse transmission over 150 km with RZ-CW conversion and FDE techniques. Proc Ofc/nfoec (2013) 1–3. doi:10.1364/OFC.2013.OTH4E.4

CrossRef Full Text | Google Scholar

6. Nakazawa M, Yoshida M, Kasai K, Hongou J. 20 Msymbol∕s, 64 and 128 QAM coherent optical transmission over 525 km using heterodyne detection with frequency-stabilised laser. Electron Lett (2006) 42:710–2. doi:10.1049/el:20060646

CrossRef Full Text | Google Scholar

7. Khanna G, Rahman T, Riccardi E, Pagano A, Piat AC, Calabro S, et al. Single-carrier 400G 64QAM and 128QAM DWDM field trial transmission over metro legacy links. IEEE Photon Technology Lett (2017) 29(2):189–92. doi:10.1109/lpt.2016.2632165

CrossRef Full Text | Google Scholar

8. Qian D, Huang M, Ip E, Huang Y, Shao Y, Hu J, et al. High capacity/spectral efficiency 101.7-Tb/s WDM transmission using PDM-128qam-OFDM over 165-km SSMF within C- and L-bands. J Lightwave Technology (2012) 30(10):1540–8. doi:10.1109/jlt.2012.2189096

CrossRef Full Text | Google Scholar

9. Lau APT, Gao Y, Sui Q, Wang D, Zhuge Q, Morsy-Osman MH, et al. Advanced DSP techniques enabling high spectral efficiency and flexible transmissions: toward elastic optical networks. IEEE Sig Proc Mag (2014) 31(2):82–92. doi:10.1109/msp.2013.2287021

CrossRef Full Text | Google Scholar

10. Zhou X, Nelson L. Advanced DSP for 400 Gb/s and beyond optical networks. J Lightwave Technol (2014) 32(16):2716–25. doi:10.1109/jlt.2014.2321135

CrossRef Full Text | Google Scholar

11. Winzer PJ, Neilson DT, Chraplyvy AR. Fiber-optic transmission and networking: the previous 20 and the next 20 years [Invited]. Opt Express (2018) 26(8):24190–239. doi:10.1364/oe.26.024190

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lau A, Gao Y, Sui Q, Wang D, Zhuge Q, Morsy-Osman M, et al. Advanced DSP techniques enabling high spectral efficiency and flexible transmissions: toward elastic optical networks. IEEE Signal Process Mag (2014) 31(2):82–92. doi:10.1109/msp.2013.2287021

CrossRef Full Text | Google Scholar

13. Kumari M, Mishra SK. Realization of 4 × 200 Gbps 4-QAM OFDM-OWC system using higher order OAM modes for HAP-to-satellites scenario. Photonics (2024) 11(4):294. doi:10.3390/photonics11040294

CrossRef Full Text | Google Scholar

14. Kumari M, Sheetal A, Sharma R. Performance analysis of symmetrical and bidirectional 40 Gbps TWDM-PON employing m-QAM-OFDM modulation with multi-color LDs based VLC system. Opt Quan Electron (2021) 53:455–29. doi:10.1007/s11082-021-03108-2

CrossRef Full Text | Google Scholar

15. Saw BK, Janyani V, Singh G. Analysis of coherent-OFDM modulation for FSO communication over distribution with pointing errors. Opt Commun (2023) 545:129677. doi:10.1016/j.optcom.2023.129677

CrossRef Full Text | Google Scholar

16. Sharma V, Chaudhary S. Implementation of hybrid OFDM-FSO transmission system. Int J Comput Appl (2012) 58(8):37–40. doi:10.5120/9305-3531

CrossRef Full Text | Google Scholar

17. Sharma V, Kumar S. Empirical evaluation of wired-and wireless-hybrid OFDM–OSSB–RoF transmission system. Optik (2013) 124(20):4529–32. doi:10.1016/j.ijleo.2013.01.045

CrossRef Full Text | Google Scholar

18. Yang T, Shi C, Chen X, Zhang M, Ji Y, Hua F, et al. Linewidth-tolerant and multi-format carrier phase estimation schemes for coherent optical m-QAM flexible transmission systems. Opt Exp (2018) 26(8):10599–10615. doi:10.1364/oe.26.010599

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mori Y, Zhang C, Kikuchi K. Novel configuration of finite-impulse-response filters tolerant to carrier-phase fluctuations in digital coherent optical receivers for higher-order quadrature amplitude modulation signals. Opt Express (2012) 20(24):26 236–26 251. doi:10.1364/oe.20.026236

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Gao Y, Lau APT, Yan S, Lu C. Low-complexity and phase noise tolerant carrier phase estimation for dual-polarization 16-QAM systems. Opt Exp (2011) 19(22):21717–21729. doi:10.1364/oe.19.021717

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xiang M, Fu S, Deng L, Tang M, Shum P, Liu D. Low-complexity feed-forward carrier phase estimation for M-ary QAM based on phase search acceleration by quadratic approximation. Opt Express (2015) 23(15):19 142–19 153. doi:10.1364/oe.23.019142

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Pfau T, Hoffmann S, Noe R, Lightw J. Hardware-efficient coherent digital receiver concept with feedforward carrier recovery for M-QAM constellations. Technol (2009) 27(8):989–999. doi:10.1109/JLT.2008.2010511

CrossRef Full Text | Google Scholar

23. Fatadin I, Ives D, Savory SJ. Laser linewidth tolerance for 16-QAM coherent optical systems using QPSK partitioning. IEEE Photon Technol Lett (2010) 22(9):631–3. doi:10.1109/lpt.2010.2043524

CrossRef Full Text | Google Scholar

24. Feng J, Li W, Xiao J, Han J, Li H, Huang L, et al. Carrier phase estimation for 32-QAM optical systems using quasi-QPSK-partitioning algorithm. IEEE Photon Technol Lett (2015) 28(1):75–8. doi:10.1109/lpt.2015.2483619

CrossRef Full Text | Google Scholar

25. Chen Y, Huang X. A linewidth-tolerant two-stage CPE using a new QPSK-partitioning approach and an enhanced maximum likelihood detection for 64-QAM coherent optical systems. J Lightwave Technol (2015) 33(18):3883–9. doi:10.1109/jlt.2015.2448113

CrossRef Full Text | Google Scholar

26. Viterbi AJ, Viterbi AM. Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmission. IEEE Trans Inf Theor (1983) 29(4):543–51. doi:10.1109/tit.1983.1056713

CrossRef Full Text | Google Scholar

27. Yang T, Chen X, Shi S, Sun E, Shi C. Low-complexity and modulation-format-independent carrier phase estimation scheme using linear approximation for elastic optical networks. Opt Commun (2018) 410:376–84. doi:10.1016/j.optcom.2017.10.052

CrossRef Full Text | Google Scholar

28. Bilal SM, Gabriella B. Dual stage carrier phase estimation for 16-QAM systems based on a modified QPSK-partitioning algorithm. In: Proceedings of the IEEE 15th international conference on transparent optical networks (ICTON); 2013 June 23–June 27; Cartagena, Spain: IEEE (2013).

CrossRef Full Text | Google Scholar

29. Li J, Li L, Tao Z, Hoshida T, Rasmussen JC. Laser-linewidth-tolerant feed-forward carrier phase estimator with reduced complexity for QAM. J Lightwave Technol (2011) 29(16):2358–64. doi:10.1109/jlt.2011.2159580

CrossRef Full Text | Google Scholar

30. Han J, Li W, He Z, Hu Q, Yu S. Multiplier-free carrier phase estimation for optical coherent systems. IEEE Photon Technology Lett (2016) 28(20):2168–71. doi:10.1109/lpt.2016.2586076

CrossRef Full Text | Google Scholar