A brief review of spin glass magnetometry techniques

Spin glasses are inherently dynamical. Taken properly, measurements of these materials can capture their dynamics and provide a wealth of insight into the physics of the spin glass state. In this methods review, two magnetometry methods are directly compared–ac and dc. Because these measurements are taken differently, the resulting data of each method will contain different information about spin glass behavior. This review will specifically focus on how the out-of-equilibrium effects of aging, rejuvenation, and memory manifest in each of these techniques, and how to construct protocols to measure these effects. We then describe the physical significance of each type of measurement and how to interpret their results. Finally, we explicitly detail which applications are most appropriate for which method. This will help the reader select the most helpful technique to carry out their own future experiments.

1 Introduction

Broadly speaking, spin glass magnetometry measurements come in two “flavors,” ac susceptibility, and dc magnetization. Due to the fact that spin glasses are out-of-equilibrium, it is crucial to understand how a prototypical ac and dc measurement differ from each other so that the dynamical behavior measured can be better understood. The purpose of this review is to provide insight for both types of measurements and when they are most appropriately used. This will be accomplished by introducing an ac protocol which exhibits the phenomena of aging, rejuvenation, and memory, and then briefly describing them. Analogous dc protocols will then be discussed.

Since the typical ac susceptibility measurement more easily lends itself to temperature sweeps than the typical dc measurement, this discussion will be framed from an ac perspective. The purpose of this review is to discuss spin glass magnetometry techniques, and so the focus will be on exemplifying the out-of-equilibrium dynamics seen in dc and ac experiments. Then, where it is necessary, we will point out how various pictures of spin glass behavior can be used to explain these observations.

Before introducing protocols with out-of-equilibrium effects, however, it is instructive to first show spin glass measurements without dynamics in both dc and ac settings. In a dc experiment, one can find the dynamical freezing temperature, $T_f$ by measuring the so-called “onset of irreversibility,” shown in Figure 1. This is the point where a field cooled (FC) and a zero field cooled ZFC curve begin to differ. This difference was experimentally measured for the first time in [1] and reproduced in Figure 1.

Figure 1

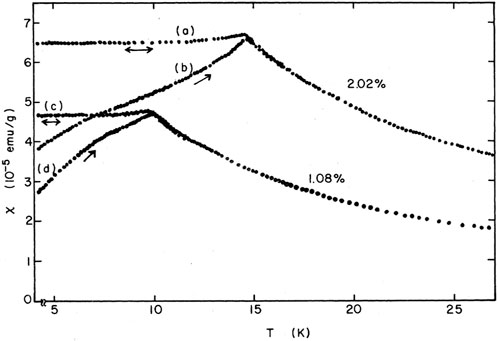
Figure 1. Field-cooled [(a) and (c)]/zero-field-cooled curves [(b) and (d)] as a function of temperature for 1.08 and 2.02 at% Mn. All measurements used an applied field of 5.90 Oe. This figure was reprinted with permission from [1].

In a FC protocol, the spin glass is always in the presence of a field. We now consider a temperature sweep from above to below the glass transition temperature, $T_g$. Above $T_g$, the system is paramagnetic, and thus the magnetization will first increase until $T=T_g$. At this temperature, the spins will begin to freeze and stay roughly constant to the lowest temperatures measured. This FC magnetization is usually thought of as static, though in reality, it varies slightly as illustrated in [2,3]. It is then compared to a ZFC curve, which is brought to the (experimentally selected) base temperature in zero field, and then raised above $T_g$ in an applied field. This magnetization increases with temperature until $T_g$, where the spins then unfreeze. At this point, since there is no longer any frozen-in order, the system will behave exactly the same way as the FC curve.

A typical ac susceptibility measurement is shown in Figure 2. As the temperature is swept (typically from above to below the transition), the real part of the magnetic susceptibility, ${\chi }^{\prime }$ has a cusp and the imaginary part, ${\chi }^{\prime \prime }$ has an inflection point. Above $T_g$, the system is a paramagnet, so there is no dissipation $({\chi }^{\prime \prime }=0)$ and the real part of the susceptibility behaves like a Curie-Weiss law. At the transition, the dissipation increases sharply as the spin glass freezes, and the in-phase response begins to decrease as spin glass order sets in. Despite the fact that ${\chi }^{\prime \prime }$ is typically a few orders of magnitude smaller than ${\chi }^{\prime }$, most experimentalists studying ac susceptibility analyze ${\chi }^{\prime \prime }$ because the size of the out-of-equlibrium effects observed are relatively larger than in ${\chi }^{\prime }$.

Figure 2

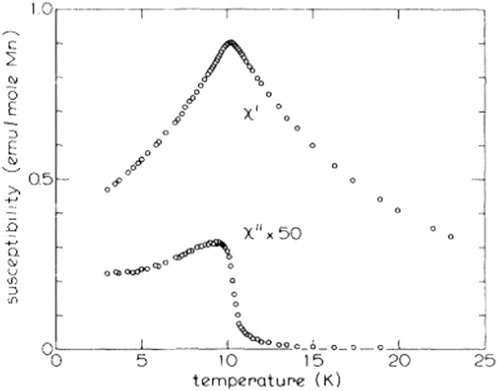
Figure 2. Real part of the ac susceptibility (top) and imaginary part of the ac susceptibility (bottom) as a function of temperature. The magnitude of the ac field is $0.1\mathrm{O}\mathrm{e}$ and the measuring frequency is $234\mathrm{H}\mathrm{z}$. These measurements were carried out on a sample of $\mathrm{A}\mathrm{g}\mathrm{M}\mathrm{n}2.98\mathrm{a}\mathrm{t}.\%$. This figure was reprinted with permission from [4].

Under the application of any magnetic field, spin glasses exhibit crossover behavior, known in theory as the de Almeida-Thouless line [5]. Experimentally, the effect of an applied magnetic field is clearly demonstrated by the experiments in [6, 7]. This means that any measured transition temperature will always be a freezing temperature and not the true glass temperature, $T_g$. However, this effect can be reduced if the experimentalist selects the lowest field possible for their sample to still obtain conclusive results. For example, the applied field in Figure 1 is $5.90\mathrm{O}\mathrm{e}$ and the amplitude of the ac field in Figure 2 is $0.1\mathrm{O}\mathrm{e}$. However, it is important to emphasize that experimental parameters such as applied field and cooling rate are known to change the dynamical freezing temperature [4, 8]. To properly determine the glass temperature $T_g$ as opposed to the dynamical freezing temperature $T_f$, one must conduct a scaling analysis as discussed in [4, 8].

Now, we return to measuring the dynamical effects observed in spin glasses. Due to the fact spin glass measurements are very protocol-dependent, it is imperative to have a control protocol for comparison. In a prototypical ac measurement, the sample starts above $T_g$ and is then lowered at a finite rate until some chosen base temperature is reached, for example, as shown in Figure 2. When comparing directly to protocols with aging, rejuvenation, and memory, this is called the “reference curve”. To demonstrate the differences between these protocols, the temperature profile as a function of time is displayed on the left panel of Figure 3, and the resulting susceptibility is displayed on the right panel of Figure 3. In this figure, the reference curve is denoted by the teal dashed line. In a dc experiment which has multiple waiting temperatures, the measurement is compared to individual protocols which only wait at one temperature. In this case, the reference protocol is called either the “isothermal” or “native” aging curve, as can be seen in [9, 10], respectively.

Figure 3

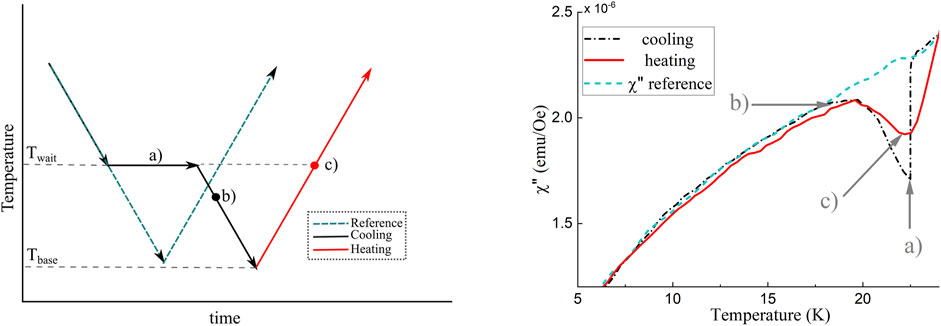
Figure 3. A simple waiting time protocol which exhibits aging, rejuvenation, and memory shown on the left and the resulting susceptibility shown on the right. The reference curve is shown as the dotted teal line in both cases. On both sides, the label a) corresponds to the aging, b) to rejuvenation, and c) to memory, which will be discussed later in this Review. This figure is adapted from [12].

2 Aging

A spin glass has a rugged energy landscape, meaning it possesses a large range of barrier heights corresponding to a wide range of relaxational timescales. Because the spin glass is seen to be dynamical on laboratory timescales, the barriers are expected to have a height that gives rise to experimentally confirmed timescales of at least up to weeks¹.

The process of hopping over barriers will induce relaxation as the system reduces its energy in a process known as “aging”. If measured in a lab, this exploration manifests as a decrease in the magnetic susceptibility, which is then attributed to the growth of the spin glass order [13, 14]. Regardless of the mechanism used to describe this growth, the community generally agrees that it grows with time spent in the spin glass state, and that this growth is very slow [13, 15, 16].

Within both the Droplet [17] and Hierarchical [18] models, aging is associated with thermal activation processes whose energy barriers are determined by the spatial size of emerging spin glass order. The larger this length scale, the higher the energy barrier. The spin glass order grows from flipping spins, which thereby induces changes to the overall magnetization [15, 19–21].

2.1 Measurements

Aging is the most easily measurable quantity in both ac and dc experiments. In this subsection, these methods will be juxtaposed to highlight the uses of each technique. While the measurements themselves differ based on whether or not ac or dc methods are used, there is some overarching commonality. During aging protocols, the system is brought to a waiting temperature $T_w$ and allowed to sit at this temperature for some waiting time $t_w$. As discussed above, this will give the spin glass time to explore the energy landscape.

2.1.1 Ac protocols

Once the reference measurement has been taken, we proceed to investigate the out-of-equilibrium effects. We begin the experiment in the same way, except instead of cooling at a continuous rate to the base temperature, cooling is stopped at an intermediate temperature, as shown by the label $\mathrm{a}$) in Figure 3.

In this part of the protocol, the ac susceptibility, defined as $\chi \equiv {\chi }^{\prime }-\text{i}{\chi }^{\prime \prime }$, relaxes over time in both the in-phase, ${\chi }^{\prime }$, and out-of-phase, ${\chi }^{\prime \prime }$, components. This relaxation marks a departure from the reference curve, and thereby establishes the spin glass as an out-of-equilibrium system. This is the most standard type of aging experiment in ac susceptibility measurements and is depicted by the vertical drop on the right side and the flat line on the left side of Figure 3. This relaxation as a function of time is shown in Figure 4.

Figure 4

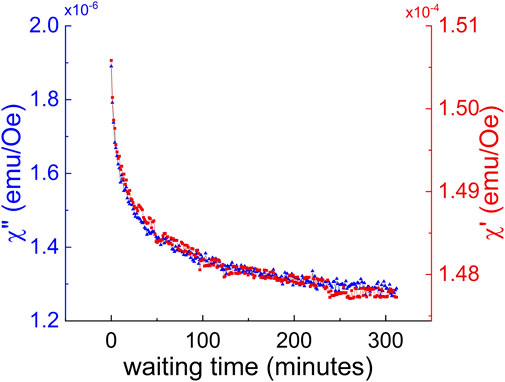
Figure 4. Aging as a function of time for both ${\chi }^{\prime \prime }$ (left) and ${\chi }^{\prime }$ (right) in a single crystal of CuMn 7.92 at.%. The two curves are overlaid on each other and plotted on linear axes to highlight that the relaxations in either susceptibility have nearly identical form. However, by looking at the axis scale, it becomes clear that the relative change in ${\chi }^{\prime \prime }$ is larger than that in ${\chi }^{\prime }$. Thus, almost all ac studies only report on ${\chi }^{\prime \prime }$, since the effects are stronger. The measuring field is 10 Oe with a frequency of 1 Hz. The sample is quenched to the waiting temperature $T/T_g=0.72$, or $T=30$ K and then aged for 200 min.

By definition, ac susceptibility measurements are sensitive to the dynamic magnetic response of the system–that is, the measured signal is related to the number of spins responding to the ac field. In a spin glass, as the spin-glass-order grows (and more spins become frozen), the system becomes less responsive to the applied field. Thus, during an aging experiment, we measure the growth of the spin glass order through the decay of the magnetic fluctuations.

2.1.2 dc protocols

Measurements which utilize dc magnetometry, compared to the protocol shown in Figure 3, are most frequently taken only at a fixed temperature. A typical dc protocol has two parts–an aging portion and a measurement portion. The field can either start off, as is the case in zero -field-cooled (ZFC) measurements, or on, as is the case in thermoremanent magnetization (TRM). A schematic of these protocols is shown in Figure 5. The main difference between the two is when the field is applied: for a ZFC measurement, the applied magnetic field is held at $0\mathrm{O}\mathrm{e}$ from above the glass temperature to the target temperature and then aged at that temperature. When the aging is completed, the field is applied. For the TRM measurement, the applied magnetic field is kept at some selected finite value from above the glass temperature and then maintained until the aging portion is complete, and then the applied field is removed.

Figure 5

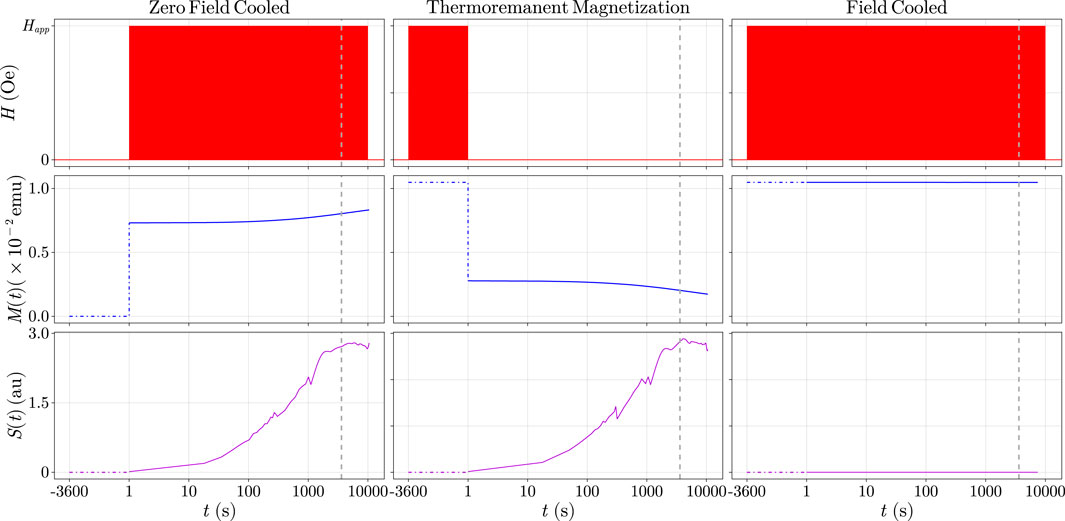
Figure 5. The three most common dc magnetization measurements are shown. In each protocol, an example set of data is plotted. From left to right columns, zero field cooled (ZFC), thermoremanent magnetization (TRM), and field cooled (FC). The top row indicates the external magnetic field applied as a function of time, the middle row is the magnetization as a function of time, and the bottom row is the resulting $S(t)\equiv \frac{\partial M}{\partial (\log t)}$ curve as a function of time. The positive $x-$axis is plotted on a log scale, with the time before the measurement starts (the waiting time) is plotted on a linear scale. The measurements during the waiting time are displayed to illustrate what the magnetization or $S(t)$ curves are expected to look like during this time and are denoted by the dot-dash lines. The key feature of the $S(t)$ curves is the presence of the peak $\sim t_w$. The waiting time is denoted by the vertical grey dashed lines in all nine panels of the figure. As can be seen, in both the left and center columns, the peak in $S(t)$ curves falls roughly on this dotted line. Note that in the center column, the $S(t)\to S(t)\times -1$ for visual clarity. In the rightmost column, the field cooled magnetization is shown. This figure can be found in [12]. This figure was made in the Julia programming [41] language using the Makie package for plotting [42].

There are other, more nuanced protocols, detailed in [22] which explore the effect on the spin glass order when a magnetic field is turned on in a variant of a TRM protocol (i.e., before or after settling at the waiting temperature). For readers who are interested in learning about the history of TRM measurements in the development of the field, [23] in this collection has a comprehensive overview. However, for brevity, these will not be discussed here.

To emphasize–dc measurements have two parts, and only the first is traditionally called “aging.” In Figure 5, this is denoted by the dot-dashed lines at negative times. However, when people discuss ac experiments, typically any time in the spin glass state is called aging. This is a subtle difference in naming conventions between the two sets of experiments which is not typically discussed.

To process dc magnetization data, the logarithmic derivative of the resulting magnetization is plotted as a function of time (traditionally on a log scale). This curve is known as $S(t)\equiv \mathrm{d}M/\mathrm{d}\log (t)$, first measured by Lundgren, Svedlindh, and Beckman [24]. It is observed that the relaxation of the magnetization displays an inflection point at approximately the waiting time $(t_w)$, so $S(t)$ will be peaked at this value. The value of the peak, $t_w^{\mathit{eff}}$, and the width of the $S(t)$ curve are determined by many factors, such as waiting time, external magnetic field, and temperature. As a rule, $t_w^{\mathit{eff}}$ is interpreted as containing information about the barrier distribution. Below, we investigate why this is.

To illustrate this, we consider a TRM (ZFC) protocol. In the aging stage of the experiment, the waiting time determines the average barrier surmounted and thus the average size of a spin glass order. After aging, once the magnetic field is removed (applied), the spin glass begins to relax to zero (the FC value for the) magnetization. If the spin glass energy landscape is made up of a distribution of Arrhenius-like barriers, then the change in magnetization as a function of time will contain information about the distribution of energy barriers of the system. If this function is peaked, the peak position will be related to the most probable barrier in the distribution [24, 25].

We then can ask why the aging portion of the experiment causes a peak in the $S(t)$. As discussed above, during aging, the spin glass order grows to some typical size. Thus, the peak in $S(t)$, a function which is a measure of the relaxation rate, will occur on the order of the typical size of spin glass order [25].

3 Rejuvenation

Aging occurs when the sample stays below the transition temperature for some fixed amount of time, as shown in Figures 4, 5. Of all the spin glass phenomena, it is the best understood. Rejuvenation occurs as the temperature is changed (traditionally decreased) after an aging protocol. Remarkably, as is observed in both ac and dc experiments, after some sufficient temperature difference, $\delta T$, the spin glass loses any knowledge of its aging history, and behaves afterwards as though it had never aged in the first place (see Figure 3).

Rejuvenation can occur with either positive or negative temperature shifts, and has been studied, for example, in Refs. [4, 9]. While there are differences in how rejuvenation manifests, the re-initialization of the aging process is common to both positive and negative temperature shifts. However, this Review will focus on the overall protocol, rather than the specific results obtained in each case.

In the following subsections, we investigate how rejuvenation appears in experiments, and their implications. Additionally, we briefly mention one possible mechanism for rejuvenation and reference experiments and simulations which test this model.

3.1 Measurements

3.1.1 Ac protocols

After an aging process is completed at $T_{w1}$ for $t_{w1}$, the temperature is then changed again. In Figure 3, the temperature is then decreased from $T_{w1}$. In this case, naïvely, we might expect the susceptibility to decrease with decreasing temperature, since the thermal energy (and therefore thermal fluctuations allowing us to explore the energy landscape) decreases with decreasing temperature. Indeed, this is seen in the reference curve. However, for procedures where the temperature is lowered following aging, the susceptibility rises back to the reference curve as if no aging occurred at all. This is known as rejuvenation. After some change in temperature, $\delta T$, the reference curve and the curve with aging and rejuvenation become the same. This effect is shown in Figure 3 in the range where ${\chi }^{\prime \prime }$ is increasing back to the reference curve upon cooling after aging.

In the case of a positive temperature shift (e.g., the temperature is raised following aging), it is traditionally more common to quench rather than heat continuously, as done in [9].

3.1.2 Dc protocols

From the description of aging using dc methods, it should be clear that it is difficult to develop dc protocols which study multi-temperature effects. Due to the fact that temperature sweeps in TRM or ZFC dc protocols face this challenge, there are generally two paths utilized².

The first way to observe rejuvenation in dc measurements is using the FC magnetization and observing differences in decays over time, as done in [2,3]. This technique is similar to ac protocols, since for this type of experiment, there is no aging time before the measurement starts. In this case, the system is quenched to the first waiting temperature $T_{w1}$ for time $t_{w1}$, then changed to the second waiting temperature $T_{w2}$ for $t_{w2}$. If, upon shifting the temperature, he aging process “restarts,” rejuvenation is said to occur. Otherwise, the aging is said to be “cumulative,” or “accumulative” [2, 3].

The second way to observe rejuvenation in a dc protocol is to measure $M(t,T_{w1},T_{w2})$ from ZFC or TRM protocols and construct an $S(t)$ curve using a temperature-step protocol, as described in [3, 9, 27]. In this case, the system is quenched to the first waiting temperature $T_{w1}$ for time $t_{w1}$, then brought to a second measuring temperature $T_{w2}$ and immediately applying (or turning off) the field and measuring the ZFC (TRM) curve.

If rejuvenation has occurred, the character of the resulting $S(t)$ curve will be different than the isothermal $S(t)$ curves at the measuring temperature. The specific details of how exactly the $S(t)$ curve evolve are complicated, but very well characterized in [4, 9]. To summarize their findings briefly: if aging is cumulative, then the peak in $S(t)$ will occur at slightly larger $t_{w_{\mathit{eff}}}$ than that of the isothermal aging curve, corresponding to the fact that the aging at $t_{w1}$ corresponded to the growth of spin glass order at the measuring temperature. If the aging is not cumulative, then the peak in $S(t)$ will occur at smaller values of $t_{w_{\mathit{eff}}}$.

Note that even if the aging is not cumulative, there tend to be long “tails” in the $S(t)$ curve, meaning that, despite the fact the sample has rejuvenated, the system still contains some knowledge of its aging at $T_{w1}$. This hints at the last dynamical effect which will be discussed in this Review: memory.

It is important to note here that there is a major discrepancy seen between rejuvenation in ac and dc measurements. In ac measurements, rejuvenation appears in the susceptibility, whereas in dc measurements, rejuvenation appears in the character of $S(t)$. Both have been associated with temperature chaos [2, 10, 28, 29]. However, in ac experiments, rejuvenation tends to takes place over a few kelvin (as in Figure 3, and [9, 29]), while dc experiments measure ranges of $\sim 0.5$K, as seen in [2,3]. The reason behind this discrepancy is not well-understood.

4 Memory

The final step in the experiment shown in Figure 3 is to raise the temperature from the base temperature back to its starting point (both chosen by the experimentalist). In the past, it was often the case that the heating rate differed from the cooling rate such as in [30]. While commonplace, it has been recently found that the relaxational dynamics markedly changes as a function of cooling rate [31], and therefore the most controlled experiments would be where all temperature changes occur at the same rate.

Like the protocols outlined for rejuvenation, $T_{w2}$ need not be lower than $T_{w1}$. Examples of both cases are shown in [4, 9]. However, the following discussion will not focus on the specific results obtained in each case. Instead, in the following subsection, we detail how memory manifests in both ac and dc experiments, and what the signatures of these measurements tells us about the spin glass state.

4.1 Measurements

4.1.1 Ac protocols

Following the canonical protocols described in Figures 2, 6, the temperature is increased from the base temperature at a constant rate. After the temperature rises beyond the aging temperature, the spin glass has an apparent memory of its previous cooling history. Since the ac susceptibility is related to the magnitude of magnetic fluctuations, a decrease in the susceptibility relative to the reference curve indicates that the spin glass is becoming more frozen relative to the reference curve as it approaches and surpasses the waiting temperature upon heating.

Figure 6

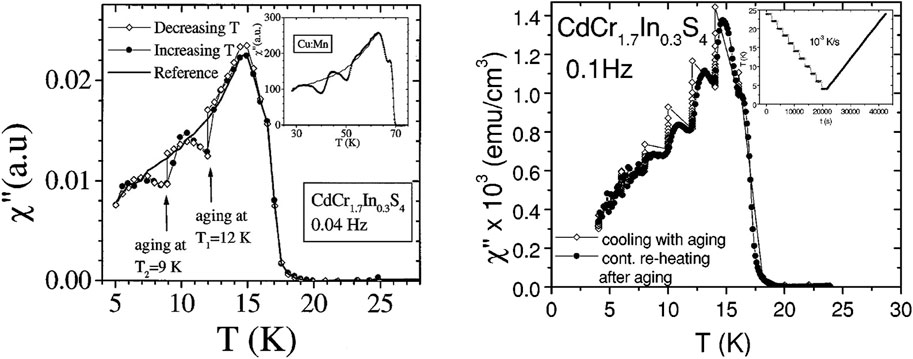
Figure 6. Left: the original memory experiment with two waiting temperatures (12 K and 9 K). Despite waiting at the low temperature for 40 h, the memory is still apparently perfect. The inset shows the reference (line) and heating (scatter) curves in the canonical spin glass, copper manganese. Right: A series of multiple aging steps upon cooling, leading to perfect memory upon continuous heating. The inset shows the temperature profile as a function of time. Both figures use the same insulating spin glass (although the ac frequencies are slightly different). The left figure is taken from [29] and the right figure is taken from [30].

A few remarkable examples of the memory effect is in Figure 6, where despite either the many temperature steps or an extremely long waiting time, memory is clearly retained upon heating. This is in contrast to the data shown in Figure 3 where, despite only aging for an hour, significant memory loss is seen. Across the literature, it can be seen that memory is often incomplete in metallic spin glasses [11, 32], but is often almost perfect in insulating spin glasses [29, 30].

4.1.2 Dc protocols

In a dc protocol investigating the memory effect, one completes a temperature cycling protocol. The first part of the experiment is the same as described in Section. 3.1.2. Now however, instead of simply turning on (or off) the field at the second temperature, the sample is aged again for $t_{w2}$ at $T_{w2}$. In the final step of the experiment, the sample is heated back to $T_{w1}$ and the field is applied (or removed). Because of the aging at $T_{w2}$, the $S(t)$ curve will now have two peaks. The location of these peaks can yield important information about the glassy dynamics.

In this case, it becomes clear why dc experiments need a control protocol. The control measurement is just an isothermal aging experiment for $t_{w1}$ at $T_{w1}$ or for $t_{w2}$ at $T_{w2}$, and so the $S(t)$ curves obtained from these two sets of measurements can be directly compared. One can see that if $t_{weff}$ from temperature cycling is smaller than the isothermal $t_{weff}$ for $T_{w1}$, then memory is reduced, as seen in metallic spin glasses in [9].

The double peak in the $S(t)$ curve is interesting in its own right as well. It indicates that there are two different typical length scales present in dc experiments where $T_{w1}$ and $T_{w2}$ are sufficiently separated. This has been interpreted to mean that the growth of spin glass order between the two temperatures are independent of each other. One of the proposed mechanisms to explain this is called “temperature chaos.” In their 1978 paper, Bray and Moore find that a sufficiently large change in temperature will destabilize the energy landscape and cause the breakup of spin glass order [33]. While this explanation has evolved since its inception, the core idea–that the metastable state at one temperature need not be metastable at a different temperature–remains the same. Recent experiments and simulations have sought to characterize the exact nature of temperature chaos to see if this explanation can account for rejuvenation, including [2, 3, 9, 10, 30, 32, 34, 35].

The results of the ac and dc experiments, taken together, indicate that the spin glass order developed at the first waiting time somehow is preserved, despite rejuvenation. Since its discovery [29], there have been many studies which have investigated this effect such as Refs. [9, 11, 30, 32, 35–38] to name just a few. While the details differ, a common explanation centers around the following description: as the temperature increases again, the larger regions of spin glass order which were previously frozen-in at the lower temperatures “unfreeze” and become active once more [9, 11, 30, 36, 38].

5 Pros and cons of each technique

The essence of spin-glass magnetometry is that the out-of-equilibrium dynamics are characterized by a dependence on two timescales. In ac experiments, these timescales are the ac frequency and the waiting time as shown in Figure 3. In dc experiments, meanwhile, the two times are the waiting time and the measuring time. Their impacts are measured using a protocol that constructs an $S(t)$ curve as shown in Figure 5. Because of the differences in how the measurements are taken, some applications are best suited for an ac measurement, while others are better suited for a dc measurement.

In spin glass research, ac susceptibility is a better tool to measure the effect of changing temperatures. In dc measurements which produce $S(t)$ curves, one cannot construct a protocol undergoing a continuous temperature sweep, because recording the magnetization is always the second step in the measurement. In either case, while temperature cycling protocols can be constructed which provide meaningful insight about the spin glass state, it is inherently more challenging in dc measurements than in ac measurements. Because of this, it is much easier to study rejuvenation and memory using ac susceptibility. Additionally, it is virtually impossible to determine the effect the cooling rate has on the evolution of the spin glass state in dc magnetometry, while this measurement is very straightforward using ac susceptibility.

On the other hand, dc magnetometry is better suited to study aging than ac susceptibility. This is because much of the dynamics in dc measurements can be wrapped up in a single physically significant number – $t_w^{\mathit{eff}}$. It is thus relatively simpler to characterize the many factors which affect the value of $t_w^{\mathit{eff}}$ such as waiting temperature, waiting time, and magnetic field. Additionally, the value of $t_w^{\mathit{eff}}$ is robust against experimental realities such as the change in signal which comes from simply needing to reload a sample. As such, characterizing the behavior $t_w^{\mathit{eff}}$ more straightforwardly allows for comparisons between quantities which are accessible in theory and simulations. This is to be contrasted with ac susceptibility measurements, where it is not as clear if a single parameter exists which captures the behavior of an aging system. Because of this, it is more difficult to quantitatively compare between ac aging curves via simulations or theory, especially since the absolute magnitude of the susceptibility depends on experimental conditions.

5.1 Experimental considerations

There are a few experimental parameters which are important to discuss. In ac experiments, the ac frequency must be sufficiently low to ensure that the dynamical relaxational effects are still visible. However, because the time it takes to acquire a single data point increases as frequency decreases, the experimentalist must determine the lowest reasonable frequency within their own logistical constraints. The effect of ac frequency on resulting spin glass measurements is examined in another submission to this collection [39].

The results in [7, 22], and [40] show that the time it takes to turn the magnetic field on or off affect the $S(t)$ curve like a waiting time effect would. If the time it takes to turn on the field is slow, this would introduce, in effect, a second waiting time in the experiment. Indeed, differences in the resulting character of the $S(t)$ measurements persist, even at very long waiting times. On the other hand, dc measurements taken in a constant field (FC) will not have these artifacts and thus can be performed in a standard magnetometer.

Likewise, both ac and dc experiments are affected by the fact that temperatures cannot change instantaneously, even when cooling at the fastest rate the instrument can. This also can act like another waiting time, as seen in [7, 22], and [31].

One final note: while the spin glass community at large treats ac and dc measurements as equivalent in the limit of zero frequency, this is hard to verify in practice because the types of experiments are typically conducted very differently from each other. As discussed in [31], there are large discrepancies between certain dc and ac results which indicate that the physics relating the two is not as straightforward as is typically assumed.

Author contributions

JF: Writing–original draft, Writing–review and editing. ED: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering, under Award No. DE-SC0013599.

Acknowledgments

The authors thank the Editors for this collection, and especially to Greg Kenning for many helpful discussions. In addition, the authors appreciate discussions with Samaresh Guchait and Ray Orbach. Finally, the authors would like to thank W. Joe Meese for his help, especially during the writing of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The longest experiment we are aware of was an unpublished result from our group at the beginning of COVID-19 lockdown taken by David C. Harrison. Even after a month of continuous measurement, aging was still seen.

²It is possible to design a protocol in other ways, such as described by the simulations in [26], but this Review will focus on the most commonly utilized protocols.

References

1. Nagata S, Keesom PH, Harrison HR. Low-dc-field susceptibility of CuMn spin glass. Phys Rev B (1979) 19:1633–8. doi:10.1103/physrevb.19.1633

CrossRef Full Text | Google Scholar

2. Zhai Q, Orbach RL, Schlagel DL. Evidence for temperature chaos in spin glasses. Phys Rev B (2022) 105:014434. doi:10.1103/physrevb.105.014434

CrossRef Full Text | Google Scholar

3. Djurberg C, Jonason K, Nordblad P. Magnetic relaxation phenomena in a cumn spin glass. Eur Phys J B-Condensed Matter Complex Syst (1999) 10:15–21. doi:10.1007/s100510050824

CrossRef Full Text | Google Scholar

4. Mulder CAM, van Duyneveldt AJ, Mydosh JA. Frequency and field dependence of the ac susceptibility of the AuMn spin-glass. Phys Rev B (1982) 25:515–8. doi:10.1103/physrevb.25.515

CrossRef Full Text | Google Scholar

5. de Almeida JRL, Thouless DJ. Stability of the sherrington-kirkpatrick solution of a spin glass model. J Phys A: Math Gen (1978) 11(5):983–90. doi:10.1088/0305-4470/11/5/028

CrossRef Full Text | Google Scholar

6. Mattsson J, Jonsson T, Nordblad P, Aruga Katori H, Ito A. No phase transition in a magnetic field in the ising spin glass fe_0.5 mn_0.5 tio₃. Phys Rev Lett (1995) 74:4305–8. doi:10.1103/physrevlett.74.4305

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lefloch F, Hammann J, Ocio M, Vincent E. Spin glasses in a magnetic field: phase diagram and dynamics. Physica B: Condensed Matter (1994) 203(1):63–74. doi:10.1016/0921-4526(94)90278-x

CrossRef Full Text | Google Scholar

8. Mulder CAM, van Duyneveldt AJ, Mydosh JA. Susceptibility of the CuMn spin-glass: frequency and field dependences. Phys Rev B (1981) 23:1384–96. doi:10.1103/physrevb.23.1384

CrossRef Full Text | Google Scholar

9. Jönsson PE, Mathieu R, Nordblad P, Yoshino H, Aruga Katori H, Ito A. Nonequilibrium dynamics of spin glasses: examination of the ghost domain scenario. Phys Rev B (2004) 70:174402. doi:10.1103/physrevb.70.174402

CrossRef Full Text | Google Scholar

10. Baity-Jesi M, Calore E, Cruz A, Fernandez LA, Gil-Narvion JM, Gonzalez-Adalid Pemartin I, et al. Temperature chaos is present in off-equilibrium spin-glass dynamics. Nat Commun Phys (2021) 4(1):74. doi:10.1038/s42005-021-00565-9

CrossRef Full Text | Google Scholar

11. Freedberg J, Joe Meese W, He J, Schlagel DL, Dan Dahlberg E, Orbach RL. On the nature of memory and rejuvenation in glassy systems, 2023.

Google Scholar

12. Freedberg J. Protocol dependence of spatially inhomogeneous magnetic systems. Conservancy University of Minnesota (2024).

Google Scholar

13. Kisker J, Santen L, Schreckenberg M, Rieger H. Off-equilibrium dynamics in finite-dimensional spin-glass models. Phys Rev B (1996) 53:6418–28. doi:10.1103/physrevb.53.6418

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Baity-Jesi M, Calore E, Cruz A, Fernandez LA, Gil-Narvion JM, Gordillo-Guerrero A, et al. Aging rate of spin glasses from simulations matches experiments. Phys Rev Lett (2018) 120:267203. doi:10.1103/physrevlett.120.267203

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Lundgren L, Svedlindh P, Beckman O. Anomalous time dependence of the susceptibility in a Cu(Mn) spin glass. J Magn Magn Mater (1983) 31–34:1349–50. doi:10.1016/0304-8853(83)90922-8

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Vincent E. Ageing, rejuvenation and memory: the example of spin glasses. In: M Henkel, M Pleimling, and R Sanctuary, editors. Ageing and the glass transition, number 716 in lecture notes in physics. Springer (2007).

Google Scholar

17. Fisher DS, Huse DA. Nonequilibrium dynamics of spin glasses. Phys Rev B (1988) 38:373–85. doi:10.1103/physrevb.38.373

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Mézard M, Parisi G, Sourlas N, Toulouse G, Virasoro M. Replica symmetry breaking and the nature of the spin glass phase. J de Physique (1984) 45(5):843–54. doi:10.1051/jphys:01984004505084300

CrossRef Full Text | Google Scholar

19. Ocio M, Alba M, Hammann J. Time scaling of the ageing process in spin-glasses: a study in csnifef 6. J de Physique Lettres (1985) 46(23):1101–7. doi:10.1051/jphyslet:0198500460230110100

CrossRef Full Text | Google Scholar

20. Chamberlin RV. Time decay of the thermoremanent magnetization in spin-glasses as a function of the time spent in the field-cooled state. Phys Rev B (1984) 30:5393–5. doi:10.1103/physrevb.30.5393

CrossRef Full Text | Google Scholar

21. Weissman MB, Israeloff NE, Alers GB. Spin-glass fluctuation statistics: mesoscopic experiments in Mn. J magnetism Magn Mater (1992) 114(1-2):87–130. doi:10.1016/0304-8853(92)90336-m

CrossRef Full Text | Google Scholar

22. Zotev VS, Rodriguez GF, Kenning GG, Orbach R, Vincent E, Hammann J. Role of initial conditions in spin-glass aging experiments. Phys Rev B (2003) 67:184422. doi:10.1103/physrevb.67.184422

CrossRef Full Text | Google Scholar

23. Kenning GG, Brandt M, Brake R, Hepler M, Tennant D. Observation of critical scaling in spin glasses below t_c using the thermoremanent magnetization. Front Phys (2024) 12. This reference will be furnished when the manuscript has been posted. doi:10.3389/fphy.2024.1443298

CrossRef Full Text | Google Scholar

24. Lundgren L, Svedlindh P, Beckman O. Experimental indications for a critical relaxation time in spin-glasses. Phys Rev B (1982) 26:3990–3. doi:10.1103/physrevb.26.3990

CrossRef Full Text | Google Scholar

25. Joh YG, Orbach R, Wood GG, Hammann J, Vincent E. Extraction of the spin glass correlation length. Phys Rev Lett (1999) 82:438–41. doi:10.1103/physrevlett.82.438

CrossRef Full Text | Google Scholar

26. Baity-Jesi M, Calore E, Cruz A, Fernandez LA, Gil-Narvion JM, Gonzalez-Adalid Pemartin I, et al. Memory and rejuvenation effects in spin glasses are governed by more than one length scale. Nat Phys (2023) 19:978–85. doi:10.1038/s41567-023-02014-6

CrossRef Full Text | Google Scholar

27. Leif Ec Lundgren . Non-equilibrium dynamics in spin glasses. In: AIP conference proceedings, 256. American Institute of Physics (1992). p. 407–16.

CrossRef Full Text | Google Scholar

28. Miyashita S, Vincent E. A microscopic mechanism for rejuvenation and memory effects in spin glasses. Eur Phys J B (2001) 22:203–11. doi:10.1007/s100510170128

CrossRef Full Text | Google Scholar

29. Jonason K, Vincent E, Hammann J, Bouchaud JP, Nordblad P. Memory and chaos effects in spin glasses. Phys Rev Lett (1998) 81:3243–6. doi:10.1103/physrevlett.81.3243

CrossRef Full Text | Google Scholar

30. Jean-Philippe B, Vincent D, Hammann J, Vincent E. Separation of time and length scales in spin glasses: temperature as a microscope. Phys Rev B (2001) 65:024439. doi:10.1103/physrevb.65.024439

CrossRef Full Text | Google Scholar

31. Freedberg J, Schlagel DL, Orbach RL, Dan Dahlberg E. Investigating the interplay between aging and rejuvenation in spin glasses. (2024).

Google Scholar

32. Jönsson PE, Yoshino H, Nordblad P. Symmetrical temperature-chaos effect with positive and negative temperature shifts in a spin glass. Phys Rev Lett (2002) 89:097201. doi:10.1103/physrevlett.89.097201

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bray AJ, Moore MA. Replica-symmetry breaking in spin-glass theories. Phys Rev Lett (1978) 41:1068–72. doi:10.1103/physrevlett.41.1068

CrossRef Full Text | Google Scholar

34. Berthier L, Young AP. Temperature cycles in the heisenberg spin glass. Phys Rev B (2005) 71:214429. doi:10.1103/physrevb.71.214429

CrossRef Full Text | Google Scholar

35. Sasaki M, Dupuis V, Bouchaud J-P, Vincent E. Deviations from perfect memory in spin glass temperature cycling experiments. Eur Phys J B (2002) 29:469–79. doi:10.1140/epjb/e2002-00327-2

CrossRef Full Text | Google Scholar

36. Paga I, He J, Baity-Jesi M, Calore E, Cruz A, Fernandez LA, et al. Quantifying memory in spin glass. Unpublished, reference be added by Publ, 2023. doi:10.48550/arXiv.2307.02224

CrossRef Full Text | Google Scholar

37. Dupuis V, Bert F, Bouchaud J-P, Hammann J, Ladieu F, Parker D, et al. Aging, rejuvenation and memory phenomena in spin glasses. Pramana J Phys (2005) 64:1109–19. doi:10.1007/bf02704172

CrossRef Full Text | Google Scholar

38. Jonason K, Nordblad P, Vincent E, Hammann J, Bouchaud J-P. Memory interference effects in spin glasses. Eur Phys J B (2000) 13(99):99–105. doi:10.1007/s100510050014

CrossRef Full Text | Google Scholar

39. Pradhan S, Harrison D, Kenning G, Schlagel DL, Guchait S. Investigation of experimental signatures of spin glass transition temperature. Front Phys (2024) Remaining information will be furnished once this manuscript is published. doi:10.3389/fphy.2024.1482907

CrossRef Full Text | Google Scholar

40. Jean-Philippe Bouchaud. Weak ergodicity breaking and aging in disordered systems. J de Physique (1992) 2(9):1705–13. doi:10.1051/jp1:1992238

CrossRef Full Text | Google Scholar

41. Bezanson J, Edelman A. Julia: A fresh approach to numerical computing. SIAM Review (2017) 59 (1), 65–98. doi:10.1137/141000671

CrossRef Full Text | Google Scholar

42. Simon D, Julius K. Flexible high-performance data visualization for Juli. J Open Source Software (2021) 6 (65), 3349. doi:10.21105/joss.03349

CrossRef Full Text | Google Scholar