Adaptive strategy for achieving fast synchronization between two memristor chaotic circuits without and with noisy perturbation

This paper presents an innovative approach for achieving rapid synchronization between two memristor chaotic circuits (MCCs), both with and without noise perturbations. The proposed adaptive control strategy effectively handles the uncertainty in control gains by adhering to predesigned update law. Additionally, this protocol is non-chattering and differentiable, avoiding the use of conventional discontinuous functions such as signum and absolute value functions. This method successfully mitigates the tremors caused by discontinuous functions. We derive two sufficient criteria using finite-time Lyapunov and stochastic finite-time Lyapunov stability methods. Numerical results validate the theoretical analysis and demonstrate the influence of noise intensity on convergence speed. Furthermore, the results have an application in image encryption transmission.

1 Introduction

In 1971, Chua introduced the concept of memristors [1]. HP Labs later confirmed their physical feasibility in 2008 [2]. Memristors, with their unique memory and nonlinear characteristics, have applications in various fields, including chaotic secure communication [3], image encryption [4, 5], non-volatile memory [6], and neural networks [7]. Following the establishment and analysis of memristive models, researchers applied them to nonlinear circuits [8]. Muthuswamy proposed a third-order nonlinear magnetic-controlled memristor model, replacing the diode in the classical Chua chaotic circuit to generate classical double vortices [9]. Bao et al. designed a simple memristive chaotic circuit and found that system stability depends on the initial state of the memristor, resulting in a unique equilibrium point [10]. Li et al. introduced a memristor into a three-dimensional system, resulting in a four-dimensional hyperchaotic system with infinite stable and unstable equilibrium points [11, 12]. They were the first to propose a line equilibrium point in a four-dimensional hyperchaotic system.

With advancements in dynamical analysis and physical implementation, research on the synchronization control of memristive chaotic systems has gained international attention [13–18]. Various novel control strategies have been designed to explore the synchronization of these systems. Yang et al. employed impulsive control methods to design a coupled synchronization controller for Chua’s chaotic system based on a cubic smooth magnetic-controlled dual memristor model [19, 20]. Wang et al. developed a nonlinear active controller using Lyapunov stability theory to achieve improved projection synchronization of a memristive chaotic system [21]. The classical sliding mode control technique has also been applied to memristive chaotic systems to achieve synchronization [5, 22]. To reduce control costs, Wu et al. adopted sampled-data control for synchronizing a class of memristive neural networks with time delays [23]. Rakkiyappan et al. proposed an active backstepping control technique for two heterogeneous memristive chaotic systems, achieving various synchronizations [24]. For heterogeneous neural networks, the synchronous and asynchronous behaviors have been revealed [25], and the effectiveness has been validated by the field-programmable gate array circuit. Li and Min have first proposed the large-scale discrete memristive Rulkov ring-star neural network model [26], which manifests rich network behaviors, including synchronization. Apart from the integer-order models, fractional-order memristive systems and their synchronization have also attracted significant attention [27–29]. But the convergence time in these works usually tends to infinity [13–29].

To acquire fast convergence rates, the finite-time control techniques have been widely applied to memristive chaotic systems. Wang et al. investigated finite-time synchronization between two memristive chaotic systems and applied this technique to image encryption [30]. Ahmad et al. discussed finite-time synchronization of memristor-based chaotic oscillators with applications insecure communication [31]. The finite-time synchronization of chaotic memristor systems has been applied to inertial neural networks, considering the effect of time-varying delays [32]. However, the estimation of the upper-bound of convergence time (UBCT) is typically restricted by the initial states of the memristive chaotic systems. To overcome this issue, Wang et al. further investigated the fixed-time synchronization problem of memristive chaotic systems [33]. Mirzaei et al. used sliding mode control to achieve fixed-time synchronization of chaotic memristor-based oscillators [34]. Despite these advancements, the UBCT in these studies is complex and often related to control parameters and system dimensions. This issue has been addressed by studying the predefined-time synchronization of memristive chaotic systems [35]. in which the UBCT is a constant. Additionally, environmental noise is a common factor affecting the synchronization of memristive chaotic systems. Ma et al. have considered the impact of stochastic noise on the fixed-time stabilization for single and synchronization for two memristor chaotic circuits [36], respectively.

One of the most important applications of chaotic systems is image encryption, and recent years have witnessed significant progress [30, 37–39]. A new 3-D chaotic dynamical system has been described in [37], and the chaotic sequences have been utilized for building a new colour image encryption algorithm, which has confirmed that the encryption mechanism has high security with high efficiency in encryption time. Then, a novel three-dimensional chaotic system with line equilibrium was proposed [38], and the obtained results were further applied into image encryption, which can effectively resist various attacks. After that, a hyperjerk system with a half line equilibrium was developed [39], and its efficiency and security have been also proved in image encryption.

However, existing control methods often use non-differentiable functions, leading to undesired chattering phenomena. Furthermore, traditional research requires pre-selected, unchanging control gains, resulting in inefficiencies and synchronization issues. This paper proposes an adaptive, non-chattering control strategy so as to achieve the finite-time synchronization of memristor chaotic circuits, and the main novelties are listed as follows:

1) The control scheme is adaptive, allowing the gains of the nonlinear control terms to be updated by the system state, automatically converging to zero upon achieving synchronization.

2) The control protocol is smooth and differentiable, eliminating the need for conventional discontinuous functions, thereby resolving the chattering issue.

3) Sufficient criteria are derived to ensure finite-time synchronization of memristor chaotic circuits, both with and without noisy perturbations.

4) The proposed adaptive fast synchronization scheme is successfully applied to image encryption.

The structure of this paper is as follows: Section 2 presents the model description and preliminaries. Section 3 derives two sufficient conditions for guaranteeing the finite-time synchronization of memristor chaotic circuits with and without noisy perturbations, respectively. Section 4 provides numerical experiments to verify the theoretical results. Section 5 concludes the paper.

2 Preliminaries and model description

2.1 Preliminaries

The ordinary differential equation (ODE) is generally represented as:

$\mathrm{d}x\left(t\right)=f\left(x\left(t\right)\right)\mathrm{d}t,(1)$

where $x\left(t\right)\in R^n$ is the state vector, and $f:R^n\to R^n$ is a nonlinear vector function. Assume the initial state $x\left(0\right)=x_0$ and $f\left(0\right)=0.$ For the deterministic system, assume the origin is one of the equilibrium points.

The stochastic differential equation (SDE) is described as:

$\mathrm{d}x\left(t\right)=f\left(x\left(t\right)\right)\mathrm{d}t+g\left(x\left(t\right)\right)\mathrm{d}W\left(t\right),t\ge t_0,(2)$

where $x\left(t_0\right)=x_0\in R^n,f:R^n\to R^n$ and $g:R^n\to R^{n\times m}$ are continuous functions with $f\left(0\right)=0$, $g\left(0\right)=0,\forall t\ge t_0.W\left(t\right)={\left[w_1\left(t\right),\dots ,w_m\left(t\right)\right]}^T$ is an $m$-dimensional Brownian motion on a complete probability space. Assume the SDE (Equation 2) has a trivial zero solution.

Definition 1. [40] For the SDE (Equation 2), define the diffusion operator $\mathcal{L}$ as:

$\mathcal{L}=\frac{\mathit{\partial }}{\mathit{\partial }t}+{\displaystyle \sum _{i=1}^n}{f}_i\left(x,t\right)\frac{\mathit{\partial }}{\mathit{\partial }{x}_i}+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\left[g\left(x,t\right)g^T\left(x,t\right)\right]}_{ij}\frac{{\mathit{\partial }}^2}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}.(3)$

If $\mathcal{L}$ acts on $V\in C^{2,1}\left(R^n\times R_{+};R_{+}\right)$, then

$\mathcal{L}V\left(x,t\right)=\frac{\mathit{\partial }V}{\mathit{\partial }t}+\frac{\mathit{\partial }V}{\mathit{\partial }x}\cdot f\left(x,t\right)+\frac{1}{2}\text{trace}\left[g^T\left(x,t\right)\frac{{\mathit{\partial }}^{2}V}{\mathit{\partial }{x}^2}\cdot g\left(x,t\right)\right],(4)$

in which $V\left(x,t\right)$ is continuously once differentiable in $t$ and twice in $x$, $C^{2,1}\left(R^n\times R_{+};R_{+}\right)$ is the family of $V\left(x,t\right)\ge 0$, $\left(x,t\right)\in R^n\times R_{+}$, $\partial V/\partial x=\left(\mathit{\partial }V/\mathit{\partial }{x}_1,\dots ,\mathit{\partial }V/\mathit{\partial }{x}_n\right)$, ${\mathit{\partial }}^{2}V/\mathit{\partial }{x}^2={\left({\mathit{\partial }}^{2}V/\mathit{\partial }{x}_i\mathit{\partial }{x}_j\right)}_{n\times n}$.

Lemma 1. [41] If there exists a continuous, positive definite function $V\left(x,t\right):R^n\times R^{+}\to R^{+},$ such that

$\dot{V}\left(x\right)\le -c{V}^{\rho }\left(x\right),\forall x\in R^n,$

then the origin is globally finite-time stable and the settling-time function is

$T_s\le \frac{V^{1-\rho }\left(x\left(0\right)\right)}{c\left(1-\rho \right)},$

where $c>0$, $0<\rho <1$.

Lemma 2. [42] If there exists a twice continuously differentiable, radially unbounded, and positive definite Lyapunov function $V\left(x,t\right):R^n\times R^{+}\to R^{+}$, real numbers $0<\gamma <1$ and $c>0$, such that

$\mathcal{L}V\left(x\right)\le -c\cdot {\left(V\left(x\right)\right)}^{\gamma },\forall x\in R^n,$

the trivial solution of the SDE is stochastically finite-time stable, and meanwhile the settling-time function

$E\left[T_s\right]\le \frac{{\left(V\left(x_0\right)\right)}^{1-\gamma }}{c\left(1-\gamma \right)},$

in which $E\left[\cdot \right]$ signifies the expectation function.

Lemma 3. [43] If $a_1,a_2,\dots ,a_n\ge 0$, then

${\displaystyle \sum _{i=1}^n}{a}_i^{\vartheta }\ge {\left({\displaystyle \sum _{i=1}^n}{a}_i\right)}^{\vartheta },0<\vartheta \le 1.$

2.2 Model description

This paper explores a 4-dimensional (4D) memristor chaotic circuit (MCC), as shown in Figure 1, described by a specific dynamic model [30]:

$\left\{\begin{array}{l}\mathrm{d}{v}_1=\frac{1}{R{C}_1}\left[v_2-v_1+GR{v}_1-RW\left(\phi \right)v_1\right]\mathrm{d}t,\\ \mathrm{d}{v}_2=\frac{1}{R{C}_2}\left(v_1-v_2+R{i}_L\right)\mathrm{d}t,\\ \mathrm{d}{i}_L=\left(-\frac{1}{L}{v}_2-\frac{r}{L}{i}_L\right)\mathrm{d}t,\\ \mathrm{d}\phi =v_1\mathrm{d}t,\end{array}\right.(5)$

in which the voltage $v_1$ ($v_2$) is across the capacitor $C_1$ ($C_2$); $Rr$ and $r$ signify two unrelated resistors; the conductance $G$ represents an active flux-controlled memristor; $\phi$ is the flux and $W\left(\phi \right)=a+3b{\phi }^2$ is the memductance of flux-controlled memristor ($a>0,b>0$); the current $i_L$ flows through the inductor $L$.

Figure 1

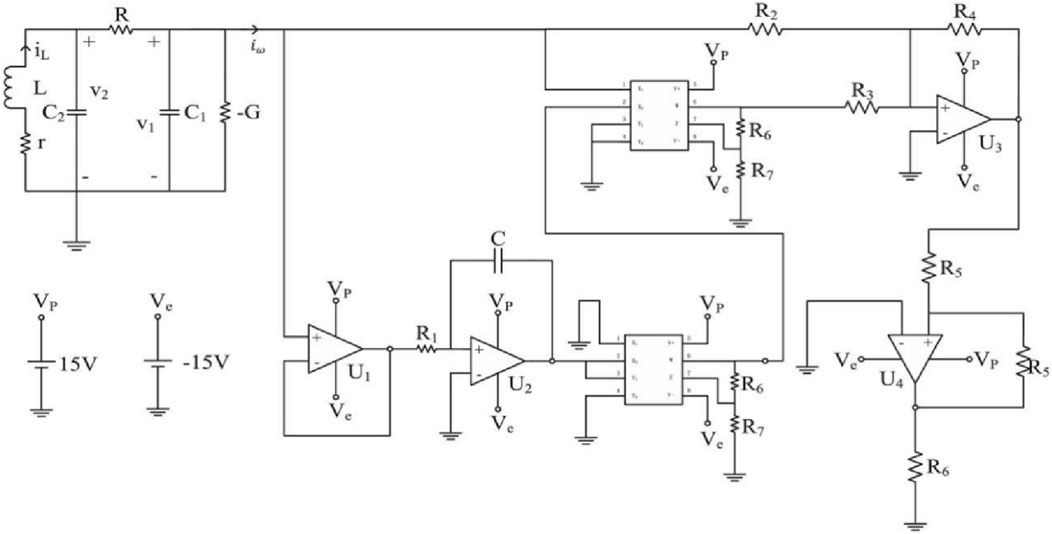
Figure 1. Complete circuit of memristor chaotic circuit [30].

By simplifying the model and introducing variables $x_1=v_1,x_2=v_2,x_3=i_L,x_4=\phi ,$ ${\alpha }_1=\frac{1}{C_1},{\alpha }_2=\frac{G-2}{C_1},{\alpha }_3=-\frac{1}{L},{\alpha }_4=\frac{r}{L},\frac{1}{C_2}=1$ and $R=1$, the dynamics of the MCC system (Equation 5) can be characterized as follows:

$\left\{\begin{array}{l}\mathrm{d}{x}_1=\left({\alpha }_1{x}_2+{\alpha }_2{x}_1-3{\alpha }_1{x}_1{x}_4^2\right)\mathrm{d}t,\\ \mathrm{d}{x}_2=\left(x_1-x_2+x_3\right)\mathrm{d}t,\\ \mathrm{d}{x}_3=\left({\alpha }_3{x}_2-{\alpha }_4{x}_3\right)\mathrm{d}t.\\ \mathrm{d}{x}_4=x_1\mathrm{d}t.\end{array}\right.(6)$

In this article, we take the parameters ${\left[{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4\right]}^T={\left[9,1.9,-10,0.3\right]}^T$ and the initial values ${\left[x_1\left(0\right),x_2\left(0\right),x_3\left(0\right),x_4\left(0\right)\right]}^T={\left[0.1,0.5,0.3,0.4\right]}^T$, and the 3D portraits of MCC (Equation 6) or (Equation 5) are displayed in Figure 2.

Figure 2

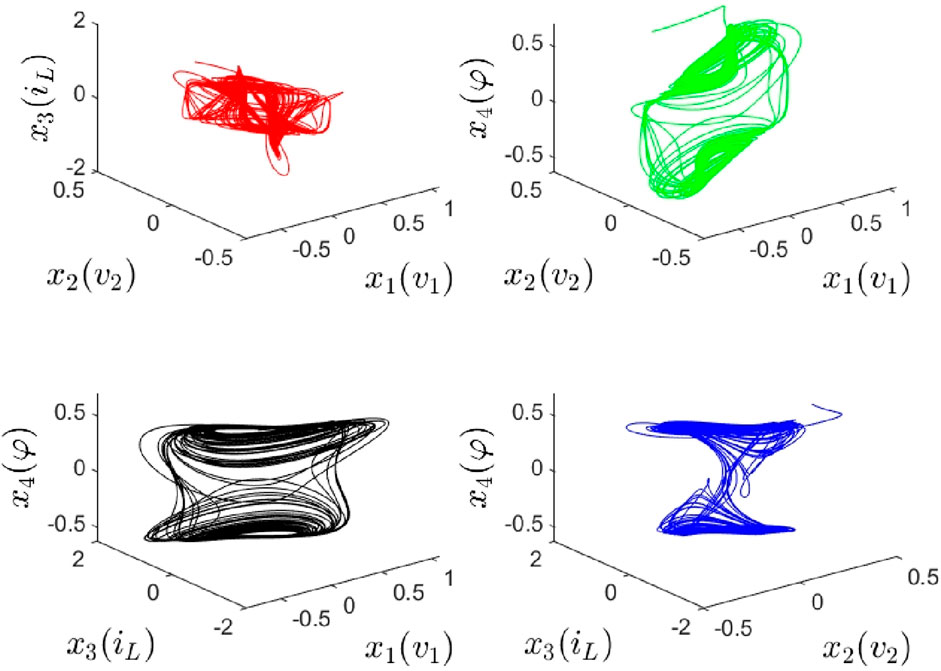
Figure 2. 3D portraits of MCC (Equation 6) or (Equation 5).

3 Main results

3.1 Adaptive fast synchronization without noisy perturbations

Take the aforementioned MCC model (Equation 6) as the drive system, and the related response MCC system containing four controllers, $u_i,i=1,2,3,4$, is ruled by

$\left\{\begin{array}{l}\mathrm{d}{y}_1=\left({\alpha }_1{y}_2+{\alpha }_2{y}_1-3{\alpha }_1{y}_1{y}_4^2+u_1\right)\mathrm{d}t,\\ \mathrm{d}{y}_2=\left(y_1-y_2+y_3+u_2\right)\mathrm{d}t,\\ \mathrm{d}{y}_3=\left({\alpha }_3{y}_2-{\alpha }_4{y}_3+u_3\right)\mathrm{d}t,\\ \mathrm{d}{y}_4=\left(y_1+u_4\right)\mathrm{d}t,\end{array}\right.(7)$

where $y_i,i=1,2,3,4,$ are the state variables. For the drive-response MCC systems (Equations 6, 7), we define the synchronization error $e_i=y_i-x_i,i=1,\dots ,4$. In this case, we can get the synchronization error system

$\left\{\begin{array}{l}\mathrm{d}{e}_1=\left({\alpha }_1{e}_2+{\alpha }_2{e}_1-3{\alpha }_1\left(y_1{y}_4^2-x_1{x}_4^2\right)+u_1\right)\mathrm{d}t,\\ \mathrm{d}{e}_2=\left(e_1-e_2+e_3+u_2\right)\mathrm{d}t,\\ \mathrm{d}{e}_3=\left({\alpha }_3{e}_2-{\alpha }_4{e}_3+u_3\right)\mathrm{d}t,\\ \mathrm{d}{e}_4=\left(e_1+u_4\right)\mathrm{d}t.\end{array}\right.(8)$

Definition 2. The finite-time synchronization between the drive-response MCC systems (Equations 6, 7) is achieved, if there exists settling-time function $T_s>0$, such that

$\underset{t\to T_s}{\lim }\left|e_i\left(t\right)\right|=0,$

and $e_i\left(t\right)\equiv 0,\forall t\ge T_s$, $i=1,2,3,4$.

In order to realize fast synchronization between MCCs (Equations 6, 7), the control protocol can be designed as follows:

$\left\{\begin{array}{l}{u}_1=3{\alpha }_1\left(y_1{y}_4^2-x_1{x}_4^2\right)-g{e}_1-g_1{e}_1^{\eta },\\ u_2=-\left({\alpha }_1+1\right)e_1-g_2{e}_2^{\eta },\\ u_3=-\left({\alpha }_3+1\right)e_2-g_3{e}_3^{\eta },\\ u_4=-e_1-c{e}_4-g_4{e}_4^{\eta },\end{array}\right.(9)$

and two gains $g$ and $c$ in the linear control terms are non-negative constants, each control gain $g_i$ in the last nonlinear term is adaptively updated complying with the law

${\dot{g}}_i=\left(1-g_i^{-1}\right)e_i^{1+\eta }-g_i^{\eta },i=1,\dots ,4,(10)$

in which the index $\eta =\frac{l}{m}$, and $l,m$ are two positive odd integers satisfying $l<m$.

Remark 1. From the designed control scheme (Equations 9, 10), one can observe that there is no any discontinuous function in it, whereas the traditional finite-time control usually contains the signum and absolute value functions [30]. Thus, the tremor issue has been successfully overcome by this investigation. In addition, the proposed control protocol is adaptive, in which the control gains $g_i,i=1,2,3,4,$ for the nonlinear term is updated following the adaptive law (Equation 10). That is, the related control gains of nonlinear terms do not need to be selected beforehand.

Theorem 1. The finite-time synchronization for the MCC systems (Equations 6, 7) will be realized by utilizing adaptive non-chattering control strategy (Equations 9, 10), if $g\ge {\alpha }_2,{\alpha }_4\ge 0,c\ge 0.$

Proof of Theorem 1. Selecting the following Lyapunov function candidate.

$V=\frac{1}{2}{\displaystyle \sum _{i=1}^4}{e}_i^2\left(t\right)+\frac{1}{2}{\displaystyle \sum _{i=1}^4}{g}_i^2\left(t\right),(11)$

differentiating it, and combining with (Equations 8, 10), we obtain

$\begin{array}{l}\dot{V}=e_1\left({\alpha }_1{e}_2+{\alpha }_2{e}_1-g{e}_1-g_1{e}_1^{\eta }\right)+e_2\left[e_1-e_2+e_3-g_2{e}_2^{\eta }-\left({\alpha }_1+1\right)e_1\right]\\ +e_3\left[{\alpha }_3{e}_2-{\alpha }_4{e}_3-g_3{e}_3^{\eta }-\left({\alpha }_3+1\right)e_2\right]+e_4\left(-c{e}_4-g_4{e}_4^{\eta }\right)\\ +{\displaystyle \sum _{i=1}^4}{g}_i\left[\left(1-g_i^{-1}\right)r_i^{1+\eta }-g_i^{\eta }\right]\\ =-\left(g-{\alpha }_2\right)e_1^2-e_2^2-{\alpha }_4{e}_3^2-c{e}_4^2-{\displaystyle \sum _{i=1}^4}{e}_i^{1+\eta }-{\displaystyle \sum _{i=1}^4}{g}_i^{1+\eta }.\end{array}$

If $g\ge {\alpha }_2,{\alpha }_4\ge 0,c\ge 0$, then

$\begin{array}{l}\dot{V}\le -{\displaystyle \sum _{i=1}^4}{e}_i^{1+\eta }-{\displaystyle \sum _{i=1}^4}{g}_i^{1+\eta }\\ =-{\displaystyle \sum _{i=1}^4}{\left(e_i^2\right)}^{\frac{1+\eta }{2}}-{\displaystyle \sum _{i=1}^4}{\left(g_i^2\right)}^{\frac{1+\eta }{2}}.\end{array}$

According to Lemma 3, we get

$\begin{array}{l}\dot{V}\le -{\left({\displaystyle \sum _{i=1}^4}{e}_i^2\right)}^{\frac{1+\eta }{2}}-{\left({\displaystyle \sum _{i=1}^4}{g}_i^2\right)}^{\frac{1+\eta }{2}}\\ =-{\left(\sqrt{2}\right)}^{1+\eta }{V}^{\frac{1+\eta }{2}}.\end{array}$

In the light of Lemma 1, the finite-time synchronization between the MCC systems (Equations 6, 7) has been achieved, and the settling-time

$T_s\le \frac{{\left(\sqrt{2V\left(e_i\left(0\right)\right)}\right)}^{1-\eta }}{1-\eta }.(12)$

Remark 2. From (Equation 12), one can find that the upper-bound of $T$ is restricted by the initial error $e_i\left(0\right)$ and the parameter $\eta$. This issue can be effectively addressed by exploring the fixed-time or predefined-time synchronization and combining with the proposed adaptive non-chattering control method.

3.2 Adaptive fast synchronization with noisy perturbations

Because the stochastic noise is ubiquitous in man-made and natural systems, this subsection further discusses the problem of finite-time synchronization between MCCs in noisy environments. In contrast to the deterministic model (Equation 6), the dynamics of drive MCC system disturbed by noise is ruled as

$\left\{\begin{array}{l}\mathrm{d}{x}_1=\left({\alpha }_1{x}_2+{\alpha }_2{x}_1-3{\alpha }_1{x}_1{x}_4^2\right)\mathrm{d}t+{\rho }_1{\sigma }_1\left(x_1\right)\mathrm{d}{\omega }_1,\\ \mathrm{d}{x}_2=\left(x_1-x_2+x_3\right)\mathrm{d}t+{\rho }_2{\sigma }_2\left(x_2\right)\mathrm{d}{\omega }_2,\\ \mathrm{d}{x}_3=\left({\alpha }_3{x}_2-{\alpha }_4{x}_3\right)\mathrm{d}t+{\rho }_3{\sigma }_3\left(x_3\right)\mathrm{d}{\omega }_3,\\ \mathrm{d}{x}_4=x_1\mathrm{d}t+{\rho }_4{\sigma }_4\left(x_4\right)\mathrm{d}{\omega }_4,\end{array}\right.(13)$

and now the response MCC system containing four controllers $u_i,i=1,2,3,4,$ in noisy environment is ruled by

$\left\{\begin{array}{l}\mathrm{d}{y}_1=\left({\alpha }_1{y}_2+{\alpha }_2{y}_1-3{\alpha }_1{y}_1{y}_4^2+u_1\right)\mathrm{d}t+{\rho }_1{\sigma }_1\left(y_1\right)\mathrm{d}{\omega }_1,\\ \mathrm{d}{y}_2=\left(y_1-y_2+y_3+u_2\right)\mathrm{d}t+{\rho }_2{\sigma }_2\left(y_2\right)\mathrm{d}{\omega }_2,\\ \mathrm{d}{y}_3=\left({\alpha }_3{y}_2-{\alpha }_4{y}_3+u_3\right)\mathrm{d}t+{\rho }_3{\sigma }_3\left(y_3\right)\mathrm{d}{\omega }_3,\\ \mathrm{d}{y}_4=\left(y_1+u_4\right)\mathrm{d}t+{\rho }_4{\sigma }_4\left(y_4\right)\mathrm{d}{\omega }_4,\end{array}\right.(14)$

where the noise intensity ${\rho }_i\ge 0$, ${\sigma }_i\left(\cdot \right)$ signifies the noise function, ${\omega }_i$ represents the one-dimensional Brownian motion. Similarly, denote the synchronization error $e_i=y_i-x_i,i=1,\dots ,4$, and the error system is ruled by

$\left\{\begin{array}{l}\mathrm{d}{e}_1=\left({\alpha }_1{e}_2+{\alpha }_2{e}_1-3{\alpha }_1\left(y_1{y}_4^2-x_1{x}_4^2\right)+u_1\right)\mathrm{d}t+{\rho }_1\left[{\sigma }_1\left(y_1\right)-{\sigma }_1\left(x_1\right)\right]\mathrm{d}{\omega }_1,\\ \mathrm{d}{e}_2=\left(e_1-e_2+e_3+u_2\right)\mathrm{d}t+{\rho }_2{\sigma }_2\left[{\sigma }_2\left(y_2\right)-{\sigma }_2\left(x_2\right)\right]\mathrm{d}{\omega }_2,\\ \mathrm{d}{e}_3=\left({\alpha }_3{e}_2-{\alpha }_4{e}_3+u_3\right)\mathrm{d}t+{\rho }_3{\sigma }_3\left[{\sigma }_3\left(y_3\right)-{\sigma }_3\left(x_3\right)\right]\mathrm{d}{\omega }_3,\\ \mathrm{d}{e}_4=\left(e_1+u_4\right)\mathrm{d}t+{\rho }_4{\sigma }_4\left[{\sigma }_4\left(y_4\right)-{\sigma }_4\left(x_4\right)\right]\mathrm{d}{\omega }_4.\end{array}\right.(15)$

Definition 3. The stochastic finite-time synchronization for the drive-response MCC systems (Equations 13, 14) is achieved in probability, if there exists settling-time function $T_s>0$, such that

$P\{\underset{t\to T_s}{\lim }\left|e_i\left(t\right)\right|=0\}=1,i=1,2,3,4,$

and $P\left\{e_i\left(t\right)=0\right\}\equiv 1,\forall t\ge T_s$, $P$ signifies the probability measure.

In particular, for the noise function, we must make the following assumption for achieving fast synchronization analytically.

Assumption 1. The noise function ${\sigma }_i\left(x_i\left(t\right)\right)$ satisfies the Lipschitz condition, and there exists a constant $q>0$, such that

$\text{trace}\left({\sigma }_i^T\left(x_i\left(t\right)\right){\sigma }_i\left(x_i\left(t\right)\right)\right)\le 2q{x}_i^T\left(t\right)x_i\left(t\right),i=1,2,3,4,$

and ${\sigma }_i\left(0\right)\equiv 0$.

Theorem 2. The stochastic finite-time synchronization for drive-response MCC systems (Equations 13, 14) will be realized by implementing the same adaptive non-chattering control scheme (Equations 9, 10), if $g\ge {\alpha }_2+q{l}_1{\rho }_1^2,q{l}_2{\rho }_2^2\le 1,q{l}_3{\rho }_3^2\le {\alpha }_4,$ and $c\ge l_4{\rho }_4^2.$

Proof of Theorem 2. Consider the same Lyapunov function candidate.

$V=\frac{1}{2}{\displaystyle \sum _{i=1}^4}{e}_i^2\left(t\right)+\frac{1}{2}{\displaystyle \sum _{i=1}^4}{g}_i^2\left(t\right).$

Let the operator $\mathcal{L}$ act on the above Lyapunov function, we can obtain

$\begin{array}{l}\mathcal{L}V=e_1\left[{\alpha }_1{e}_2+{\alpha }_2{e}_1-g{e}_1-g_1{e}_1^{\eta }\right]+e_2\left[e_1-e_2+e_3-g_2{e}_2^{\eta }-\left({\alpha }_1+1\right)e_1\right]\\ +e_3\left[{\alpha }_3{e}_2-{\alpha }_4{e}_3-g_3{e}_3^{\eta }-\left({\alpha }_3+1\right)e_2\right]+e_4\left(-c{e}_4-g_4{e}_4^{\eta }\right)\\ +\frac{1}{2}{\displaystyle \sum _{i=1}^4}{\rho }_i^2\text{trace}\left\{{\left[{\sigma }_i\left(y_i\right)-{\sigma }_i\left(x_i\right)\right]}^T\left[{\sigma }_i\left(y_i\right)-{\sigma }_i\left(x_i\right)\right]\right\}\\ +{\displaystyle \sum _{i=1}^4}{g}_i\left[\left(1-g_i^{-1}\right)e_i^{1+\eta }-g_i^{\eta }\right]\end{array}$

$\begin{array}{l}=-\left(g-{\alpha }_2\right)e_1^2-e_2^2-{\alpha }_4{e}_3^2-c{e}_4^2-{\displaystyle \sum _{i=1}^4}{e}_i^{1+\eta }-{\displaystyle \sum _{i=1}^4}{g}_i^{1+\eta }\\ +\frac{1}{2}{\displaystyle \sum _{i=1}^4}{\rho }_i^2\text{trace}\left\{{\left[{\sigma }_i\left(y_i\right)-{\sigma }_i\left(x_i\right)\right]}^T\left[{\sigma }_i\left(y_i\right)-{\sigma }_i\left(x_i\right)\right]\right\}.\end{array}$

According to Assumption 1, we obtain

$\begin{array}{l}\mathcal{L}V\le -\left(g-{\alpha }_2-q{l}_1{\rho }_1^2\right)e_1^2-\left(1-q{l}_2{\rho }_2^2\right)e_2^2-\left({\alpha }_4-q{l}_3{\rho }_3^2\right)e_3^2-\left(c-q{l}_4{\rho }_4^2\right)e_4^2\\ -{\displaystyle \sum _{i=1}^4}{e}_i^{1+\eta }-{\displaystyle \sum _{i=1}^4}{g}_i^{1+\eta }.\end{array}$

If g ≥ α₂ + ql₁ ρ₁², ql₂ ρ₂² ≤ 1, ql₃ ρ₃² ≤ α₄, c ≥ l₄ ρ₄² , then

$\begin{array}{l}\mathcal{L}V\le -{\displaystyle \sum _{i=1}^4}{e}_i^{1+\eta }-{\displaystyle \sum _{i=1}^4}{g}_i^{1+\eta }\\ =-{\displaystyle \sum _{i=1}^4}{\left(e_i^2\right)}^{\frac{1+\eta }{2}}-{\displaystyle \sum _{i=1}^4}{\left(g_i^2\right)}^{\frac{1+\eta }{2}}.\end{array}$

By Lemma 3, we get

$\begin{array}{l}\mathcal{L}V\le -{\left({\displaystyle \sum _{i=1}^4}{e}_i^2\right)}^{\frac{1+\eta }{2}}-{\left({\displaystyle \sum _{i=1}^4}{g}_i^2\right)}^{\frac{1+\eta }{2}}\\ =-{\left(\sqrt{2}\right)}^{1+\eta }{V}^{\frac{1+\eta }{2}}.\end{array}$

By Lemma 2, the stochastic finite-time synchronization between the drive-response MCC systems (Equations 13, 14) can be achieved, and the settling-time function

$E\left[T_s\right]\le \frac{{\left(\sqrt{2V\left(e_i\left(0\right)\right)}\right)}^{1-\eta }}{1-\eta }.(16)$

Remark 3. From (Equation 16), one can find that the time expectation $E\left[T_s\right]$ is also related with $e_i\left(0\right),$ i.e., the initial values of $x_i\left(0\right),y_i\left(0\right)$, and parameter $\eta$. This issue can be addressed by investigating the s-tochastic fixed-time or predefined-time synchronization with applying adaptive non-chattering control technique in the future.

Remark 4. In the drive-response MCC systems (Equations 13, 14), ${\omega }_i,i=1,2,3,4,$ represents the one-di-mensional Brownian motion. Thus, $\stackrel{.}{{\omega }_i}$ is the white noise, in which the mean value is zero. And in th-is investigation, the variance is set to be finite and the noise function is also bounded as clarified in Assumption 1. Thus, the expectation value of Equation 16) is finite and convergent in finite time.

4 Numerical experiments

To verify the theoretical results, numerical simulations are conducted. Various scenarios with different noise intensities are tested, demonstrating the effectiveness of the proposed adaptive control strategy in achieving rapid synchronization of memristor chaotic circuits.

4.1 Adaptive fast synchronization of MCCs

The initial values and parameters contained in the drive MCC system (Equation 5) or (Equation 6) have been given between Equation 6; Figure 2. For the response MCC system (Equation 7), we set the initial condition ${\left[y_1\left(0\right),y_2\left(0\right),y_3\left(0\right),y_4\left(0\right)\right]}^T={\left[0.1,0.05,0.01,0.1\right]}^T$ with the same parameter values as those in drive MCC system, and take simulation time $t=200$. For this case that there is no any control implemented, the drive MCC system (Equation 6) and response MCC system (Equation 7) exhibit chaotic behaviors as illustrated in Figure 3 (left). And the state trajectories of variables $x_i\left(y_i\right),i=1,2,3,4,$ are displayed in Figure 3 (right). From these two figures, one can observe that every pair of traces cannot overlap by themselves. That is to say, the synchronization of drive MCC system (Equation 6) and response MCC system (Equation 7) cannot be realized without any control.

Figure 3

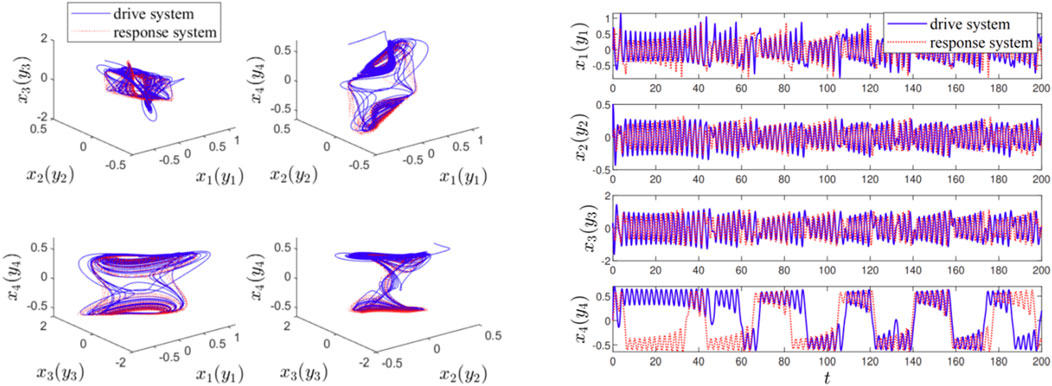
Figure 3. (left) The 3-dimensional attractor phase diagrams and (right) the state trajectories of variables $x_i\left(y_i\right),i=1,2,3,4,$ between drive-response MCC systems (Equations 6, 7) without any control, in which the initial conditions are given as ${\left[x_1\left(0\right),x_2\left(0\right),x_3\left(0\right),x_4\left(0\right)\right]}^T$$={\left[0.1,0.5,0.3,0.4\right]}^T$ and ${\left[y_1\left(0\right),y_2\left(0\right),y_3\left(0\right),y_4\left(0\right)\right]}^T$$={\left[0.1,0.05,0.01,0.1\right]}^T$.

Now, we implement the designed adaptive finite-time control scheme (Equations 9, 10) for the response MCC system (Equation 7), in which the linear control gains $g=5,c=3$, index $\eta =3/5$, and the initial nonlinear control gains $g_i\left(0\right)=0.0001,i=1,2,3,4.$ In this case, the drive-response MCC systems (Equations 6, 7) can be synchronized within time $t=5$, where the trajectories of each variable are depicted in Figure 4 (left) and the synchronization errors $e_i,i=1,2,3,4,$ will converge to zero eventually as given in Figure 4 (right). Meanwhile, the signals $u_i,i=1,2,3,4,$ of control scheme (Equation 9) are illustrated in Figure 5 (left) as well as the nonlinear gains $g_i,i=1,2,3,4,$ of (Equation 10) adaptively converge to zero finally as displayed in Figure 5 (right).

Figure 4

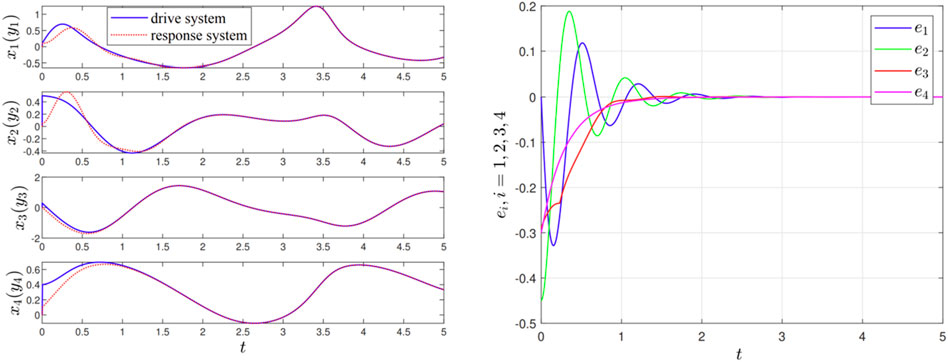
Figure 4. (left) Synchronizing state and (right) synchronization error between drive-response MCC systems (Equations 6, 7) with employing control scheme (Equations 9, 10).

Figure 5

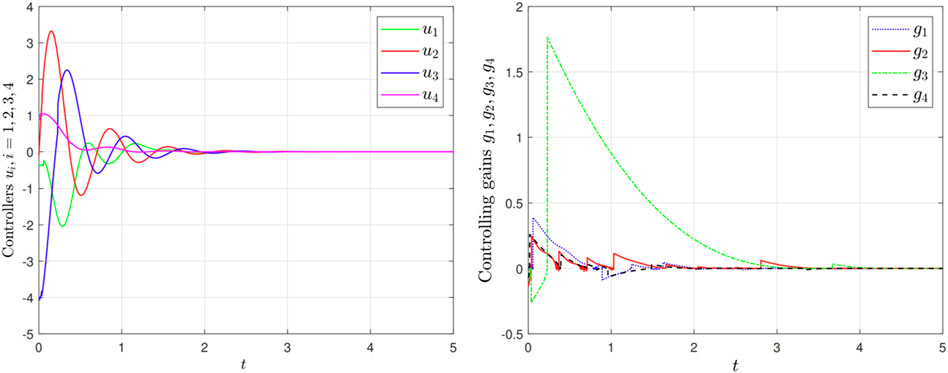
Figure 5. (left) Control signals $u_i,i=1,2,3,4,$ and (right) adaptive gains $g_i,i=1,2,3,4,$ of the nonlinear control term in (Equations 9, 10).

Furthermore, we know that the proposed adaptive finite-time control protocol (Equation 9) is non-chattering which has been reflected by the Figure 5 (left), whereas the traditional control scheme is usually designed as follows:

$\left\{\begin{array}{l}{u}_1=3{\alpha }_1\left(y_1{y}_4^2-x_1{x}_4^2\right)-g{e}_1-g_1\text{sign}\left(e_1\right){\left|e_1\right|}^{\eta },\\ u_2=-\left({\alpha }_1+1\right)e_1-g_2\text{sign}\left(e_2\right){\left|e_2\right|}^{\eta },\\ u_3=-\left({\alpha }_3+1\right)e_2-g_3\text{sign}\left(e_3\right){\left|e_3\right|}^{\eta },\\ u_4=-e_1-c{e}_4-g_4\text{sign}\left(e_4\right){\left|e_4\right|}^{\eta },\end{array}\right.(17)$

in which the parameters and control gains, including linear and nonlinear term, can be the same as those in (Equations 9, 10) except for the index $\eta =0.7.$ And the signals $u_i,1,2,3,4,$ of (Equation 17) are illustrated in Figure 6, in which there exist obvious chattering phenomena in the convergent process. In a word, this chattering matter has been overcome successfully by this investigation.

Figure 6

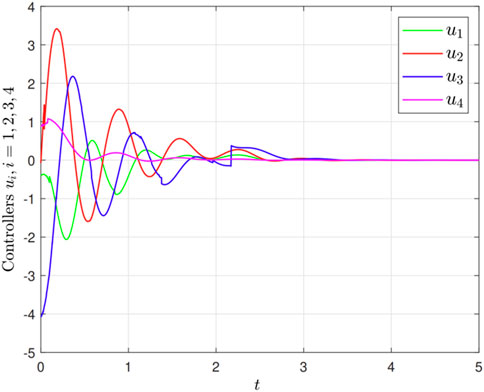
Figure 6. The traditional chattering control scheme (Equation 17).

4.2 Stochastic fast synchronization of MCCs in noisy environments

This subsection further considers the influence of environmental noise on the MCC systems. In the drive-response MCC systems (Equations 13, 14), we take the noisy intensity ${\rho }_i=0.5,$ noisy function ${\sigma }_i\left(x_i\right)=x_i,i=1,2,3,4,$ for simplicity, and the simulation time $t=200$, other parameters and initial values are the same as those in (Equations 6, 7) tested in previous subsection. For this case that there is no any control implemented, the drive MCC system (Equation 13) and response MCC system (Equation 14) exhibit stochastic chaos behaviors as illustrated in Figure 7 (left). And the state trajectories of variables $x_i\left(y_i\right),i=1,2,3,4,$ are displayed in Figure 7 (right). From these two figures, we can conclude that every pair of traces cannot overlap by themselves. In other word, the synchronization between the stochastic drive MCC system (Equation 13) and response MCC system (Equation 14) cannot be achieved without any control, in which there is a violent tremor phenomenon among them.

Figure 7

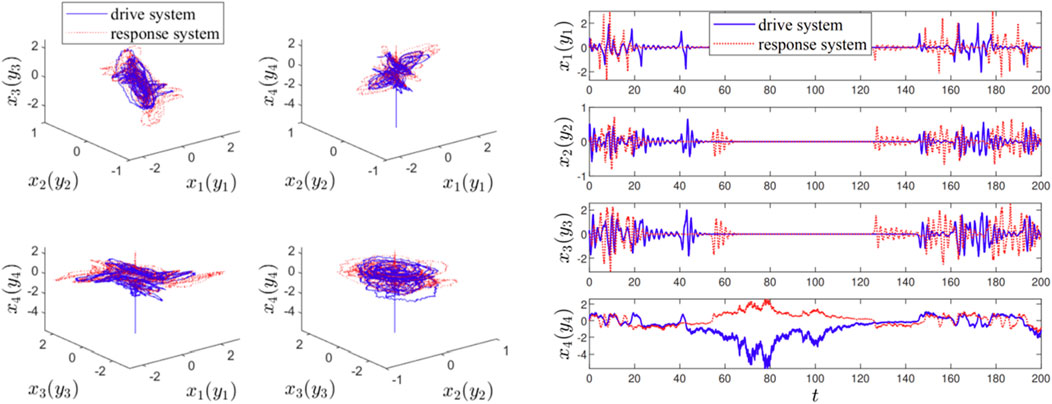
Figure 7. In noisy environments, (left) the 3-dimensional attractor phase diagrams and (right) the state trajectories of variables between drive-response MCC systems (Equations 13, 14) without any control.

In the noisy environments, we also employ the previous proposed adaptive finite-time control protocol (Equations 9, 10) for the response system (Equation 14). In this case, the stochastic drive-response MCC systems (Equations 13, 14) can also be synchronized within time $t=5$, where the trajectories of each variable are depicted in Figure 8 (left) and the synchronization errors $e_i,i=1,2,3,4,$ will converge to zero eventually in probability as given in Figure 8 (right). Meanwhile, the signals $u_i,i=1,2,3,4,$ of control scheme (Equation 9) are illustrated in Figure 9 (left) as well as the nonlinear gains $g_i,i=1,2,3,4,$ of (Equation 10) adaptively converge to zero finally as displayed in Figure 9 (right).

Figure 8

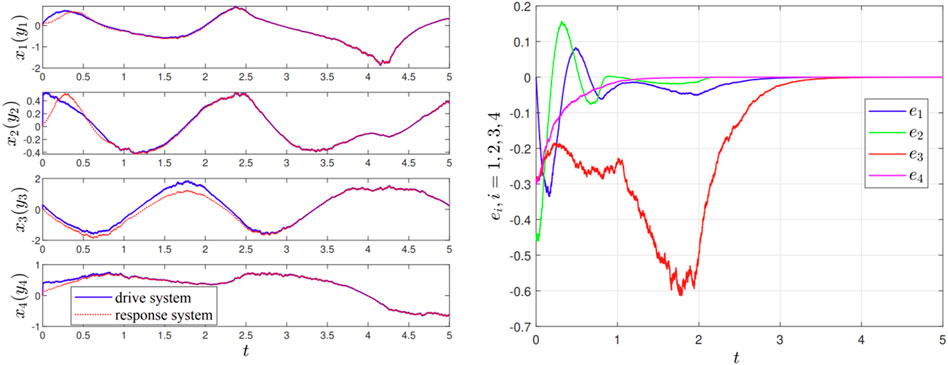
Figure 8. In noisy environments, (left) stochastic synchronizing state and (right) synchronization error between drive-response MCC systems (Equations 13, 14) with employing control scheme (Equations 9, 10).

Figure 9

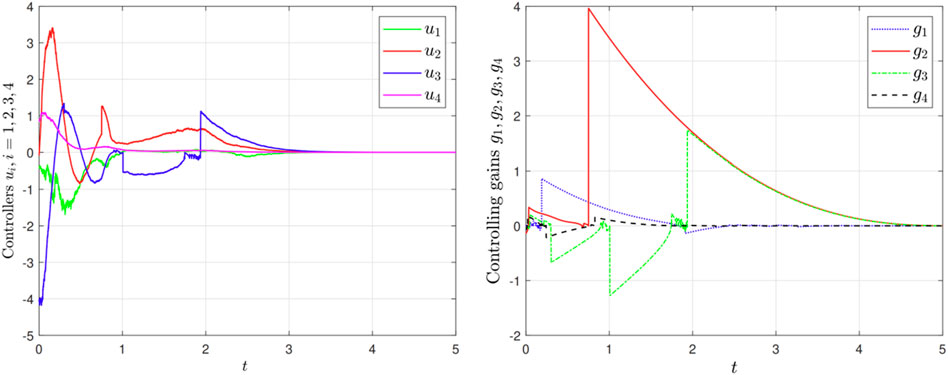
Figure 9. (left) Control signals $u_i,i=1,2,3,4,$ and (right) adaptive gains $g_i,i=1,2,3,4,$ of the nonlinear control term in (Equations 9, 10).

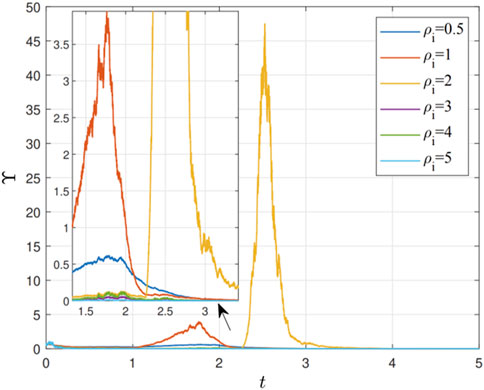
Next, we test the effect of different noisy intensities, ${\rho }_i=0.5,1,2,3,4,5,$ respectively. Finally, we define the total error $\mathrm{\Upsilon }=‖\left[e_1,e_2,e_3,e_4\right]‖,$ and the evolutions are illustrated in Figure 10, all of them will converge to zero within time $t=5,$ which reflects that the proposed control technique has anti-interference ability against different noise intensities. Looking back to the Figures 7–10, there is always vibration phenomenon in these trajectories, despite the use of smooth control protocols. Therefore, how to completely eliminate the impact of tremors is a challenging and meaningful issue.

Figure 10

Figure 10. The total error $\mathrm{\Upsilon }=‖\left[e_1,e_2,e_3,e_4\right]‖$ with different noise intensities ${\rho }_i=0.5,1,2,3,4,5,$ respectively.

4.3 Application into image encryption transmission

Algorithm 1.Pseudocode for the Encryption Algorithm.

Step 1. Read the original image and generate the plaintext matrix.

Step 2. Reorganize plaintext matrix into the sequence $h_j$ and then convert the sequence $h_j$ to the DNA sequence $h_j^{\prime }$.

Step 3. Utilize the ode45 method to solve state equations of the MCCs with the sampling interval $T$, the number of pixels $a\times b$, and the time interval $\left[t_0,t_n\right]$.

Step 4. Code discrete chaotic sequences as follows: $\left\{\begin{array}{l}w\left(4i\right)=1000\left[x_1\left(i\right)+a\right],\\ w\left(4i+1\right)=1000\left[x_2\left(i\right)+b\right],\\ w\left(4i+2\right)=1000\left[x_3\left(i\right)+c\right],\\ w\left(4i+3\right)=1000\left[x_4\left(i\right)+d\right],\end{array}\right.$In which $i=1,2,\dots ,n,a,b,c$ and $d$ are random integers from interval $\left[0,256\right]$. Thus, $p_j=w\left(j\right)\mathrm{mod}256$.

Step 5. Convert the binary sequence $p_j$ to DNA sequence $p_j^{\prime }$ composed of “A, T, C, G” by DNA coding rules.

Step 6. Encryption function executes an XOR operation: $r_j^{\prime }\left(t\right)=E\left(h_j^{\prime },p_j^{\prime }\right)=h_j^{\prime }\oplus p_j^{\prime },$

In which $E\left(x,y\right)$ is bitwise XOR operation and $r_j^{\prime }$ is ciphertext sequence.

Step 7. Convert the DNA ciphertext sequence $r_j^{\prime }$ into binary ciphertext sequence $r_j$, and then the sequence $r_j$ is reassembled into a ciphertext matrix by the previous Step 2.

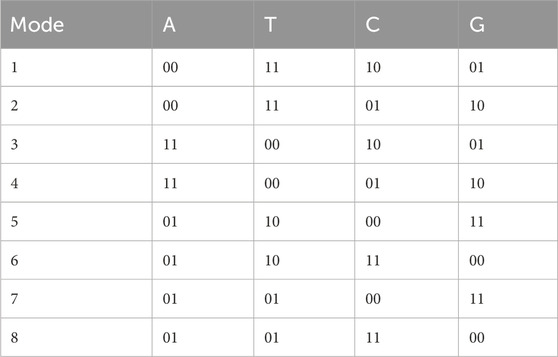
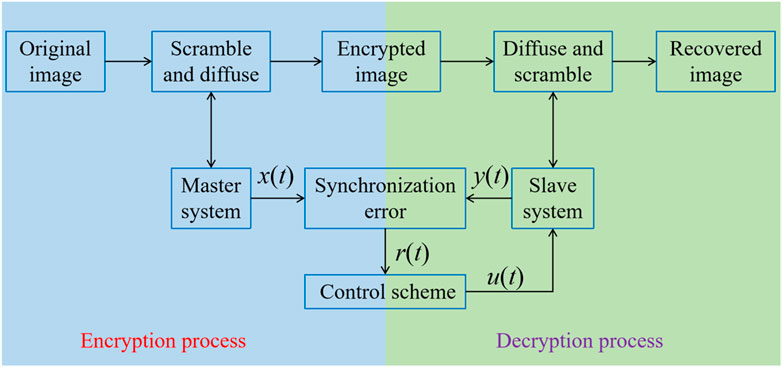
Finally and importantly, we apply the proposed adaptive fast control strategy (Equations 9, 10) into image encryption transmission. Let’s begin by introducing the DNA algorithm briefly. It is widely recognized that DNA sequences consist of four types of deoxyribonucleotides: adenine (A), guanine (G), cytosine (C), and thymine (T). In a similar manner, binary coding also has a complementary nature between the digits 0 and 1. As per the base pairing principle, binary data can be represented in eight different DNA encodings, as illustrated in Table 1. By converting binary data into a DNA sequence, we can select any one of these eight encoding methods. Building on this straightforward DNA sequence algorithm, we propose an image encryption method, with the encryption and decryption processes depicted in Figure 11. The drive system (Equation 13) and response system (Equation 14) are employed to produce chaotic sequences in the encrypter and decrypter, respectively, incorporating the DNA method as given in Algorithm 1. Using the proposed adaptive fast method for the image `Baboon', the simulation outcomes are depicted in Figure 12, where subfigure (a) represents the original image to be encrypted, subfigure (b) shows the scrambled encrypted image which appears disordered, and subfigure (c) displays the recovered image almost identical to (a). Therefore, the practicality of Theorem 1 or Theorem 2 and the effectiveness of finite-time fast synchronization between drive-response MCCs have been confirmed.

Table 1

Table 1. Method of DNA encoding.

Figure 11

Figure 11. The image transmission process.

Figure 12

Figure 12. (A) Original image. (B) Encrypted image. (C) Recovered image.

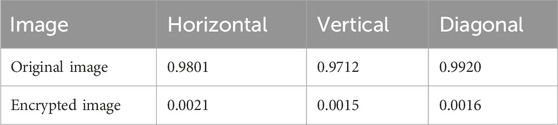
Correlation analysis. We test the correlation of 10,000 pairs of neighboring pixels in the horizontal, vertical, and diagonal directions, respectively. The calculation of correlation coefficient (CC) can be expressed as

$CC=\frac{E\left[\left(X-E\left(X\right)\right)\left(Y-E\left(Y\right)\right)\right]}{\sqrt{V\left(X\right)V\left(Y\right)}},$

in which $X$ and $Y$ are the intensity values of two adjacent pixels, $E\left(\cdot \right)$ and $V\left(\cdot \right)$ signify the mean value and variance. CC results between the adjacent positions of the original image and the encrypted image of Baboon are displayed in Table 2, which indicates that the CCs of original images are highly correlated, whereas CCs of encrypted images are basically not connected as illustrated in Figures 13, 14, respectively.

Table 2

Table 2. Correlation coefficients of adjacent pixels in Baboon’s image.

Figure 13

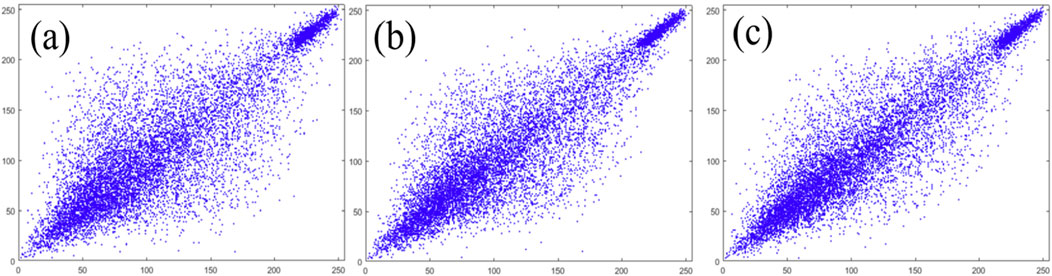
Figure 13. Correlation distributions in (A) horizontal, (B) vertical, and (C) diagonal directions of original image.

Figure 14

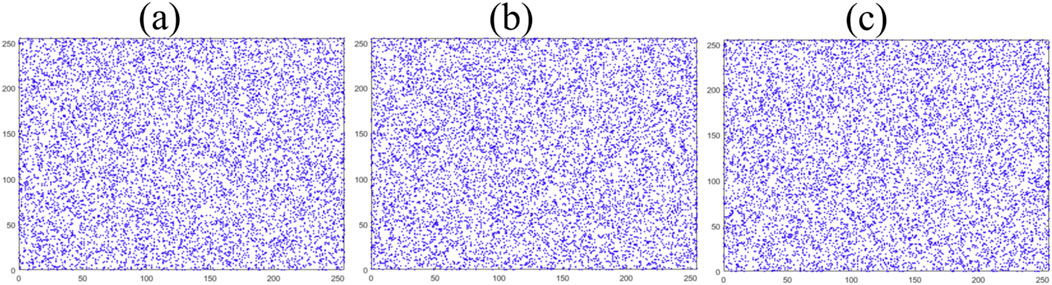
Figure 14. Correlation distributions in (A) horizontal, (B) vertical, and (C) diagonal directions of encrypted image.

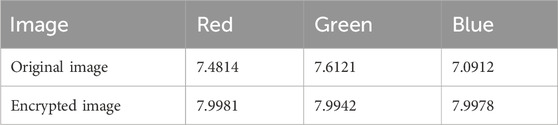
Entropy analysis. The information entropy is often used to measure the bit distribution per level of the image’s pixel values, which is defined as

$H\left(w\right)=-{\displaystyle \sum _{i=0}^{255}}p\left(w_i\right){\log }_{2}p\left(w_i\right),$

in which $p\left(w_i\right)$ is the proportion of the image grey value. $H\left(w\right)$ is the maximum information entropy for the fact that the colors are coded in $256=2^8$ symbols, i.e., all 256 symbols are equiprobable $p=1/256$, so that $H={\log }_{2}256=8$ bits. But the practical value is usually little smaller than this. For an effective algorithm, the information entropy should be very close to 8. The experimental data is given in Table 3, in which all are near 8 bits. That is, the proposed method is indeed effective.

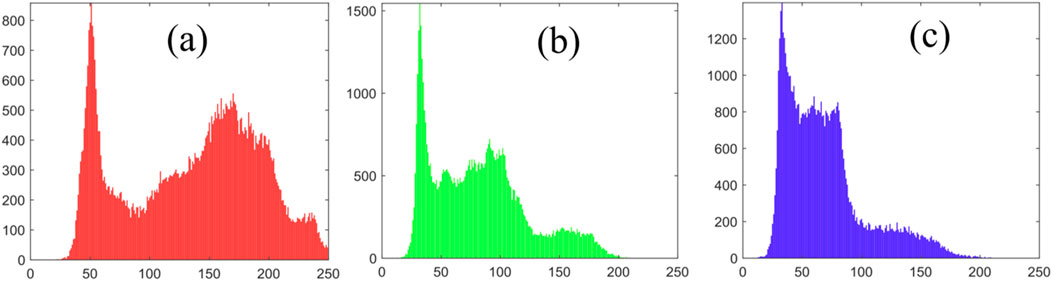
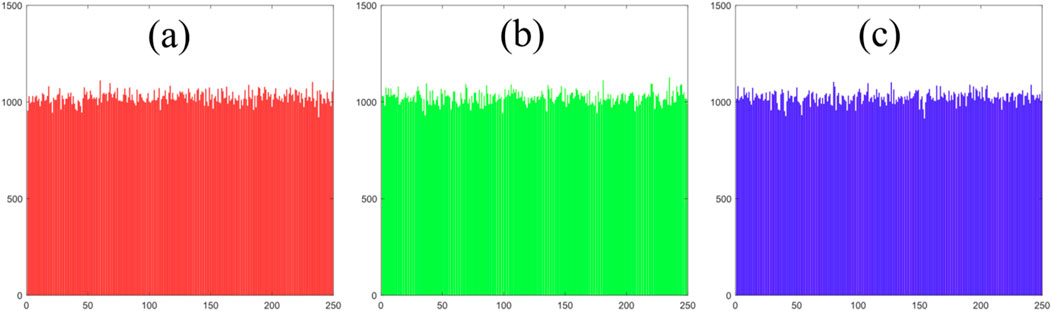
Histogram analysis. In this subsection, the histograms of the original image are compared to those of the encrypted image. Each image possesses unique histograms that reveal the effects of the image encryption algorithm’s scrambling. Histograms can directly show the statistical differences in the image before and after encryption. To thwart attackers from deciphering the image data through gray value distribution analysis, the histogram of the encrypted image should be smooth and uniform. Figure 15 displays the histograms of Figure 12A in the red, green, and blue channels, showing steep and fluctuating shapes. Conversely, Figure 16 presents the histograms of the encrypted image across the red, green, and blue channels, demonstrating uniform distributions. This uniformity indicates that statistical attacks will not allow an attacker to extract accurate information from Figure 12A using Figure 12B.

Table 3

Table 3. Information entropy of Baboon’s image.

Figure 15

Figure 15. (A) Red, (B) green, and (C) blue histograms of original image.

Figure 16

Figure 16. (A) Red, (B) green, and (C) blue histograms of encrypted image.

5 Conclusion

This study presents an innovative adaptive control strategy for fast synchronization of memristor chaotic circuits, both with and without noisy perturbations. The developed control strategy is adaptive, addressing the issue of uncertain selection of the associated controlling gains as they can adapt according to the predesigned adaptive laws. Specifically, the associated controlling gains eventually reduce to zero upon achieving synchronization, thereby minimizing the control cost. Furthermore, using the second Lyapunov method, sufficient criteria have been progressively established to achieve finite-time and stochastic finite-time synchronization of MCCs. Numerical experiments validate the theoretical conclusions and emphasize potential applications in areas like image encryption transmission. Given that the time estimation for finite-time convergence is linked to the initial conditions of MCCs, future research can utilize the proposed adaptive non-chattering control to investigate fixed-time or predefined-time synchronization.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BY: Writing–original draft, Validation, Project administration, Methodology, Funding acquisition, Conceptualization. HX: Writing–original draft, Conceptualization. LH: Writing–original draft, Software, Methodology. JW: Writing–review & editing, Software, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Science and Technology Foundation of Qingyang, China (QY-STK-2022A-017) and the National Natural Science Foundation of China (grant No. 62103166).

Acknowledgments

The authors are grateful to the Longdong University, Henan Technical College of Construction, China University of Mining and Technology, and Jiangnan University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chua L. Memristor-the missing circuit element. IEEE Trans Circuit Theor (1971) 18(5):507–19. doi:10.1109/TCT.1971.1083337

CrossRef Full Text | Google Scholar

2. Strukov DB, Snider GS, Stewart DR, Williams RS. The missing memristor found. Nature (2008) 453(7191):80–3. doi:10.1038/nature06932

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Sun J, Shen Y, Yin Q, Xu C. Compound synchronization of four memristor chaotic oscillator systems and secure communication. Chaos (2013) 23(1):013140. doi:10.1063/1.4794794

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lin Z, Wang H. Efficient image encryption using a chaos-based PWL memristor. IETE Tech Rev (2010) 27(4):318–25. doi:10.4103/0256-4602.64605

CrossRef Full Text | Google Scholar

5. Yao X, Chen X, Liu H, Sun L, He L. Adaptive sliding-mode synchronization of the memristor based sixth-order uncertain chaotic system and its application in image encryption. Front Phys (2022) 14(10):863668. doi:10.3389/fphy.2022.863668

CrossRef Full Text | Google Scholar

6. Berdan R, Lim C, Khiat A, Papavassiliou C, Prodromakis T. A memristor SPICE model accounting for volatile characteristics of practical ReRAM. IEEE Elec Dev Lett (2013) 35(1):135–7. doi:10.1109/LED.2013.2291158

CrossRef Full Text | Google Scholar

7. Pershin YV, Di Ventra M. Experimental demonstration of associative memory with memristive neural networks. Neural Netw (2010) 23(7):881–6. doi:10.1016/j.neunet.2010.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Liu X, Wang J. The simplest memristor circuit with hyperchaos. Front Phys (2022) 15(10):904200. doi:10.3389/fphy.2022.904200

CrossRef Full Text | Google Scholar

9. Muthuswamy B. Implementing memristor based chaotic circuits. Int J Bifur Chaos (2010) 20(05):1335–50. doi:10.1142/S0218127410026514

CrossRef Full Text | Google Scholar

10. Bao B, Ma Z, Xu J, Liu Z, Xu Q. A simple memristor chaotic circuit with complex dynamics. Int J Bifur Chaos (2011) 21(09):2629–45. doi:10.1142/S0218127411029999

CrossRef Full Text | Google Scholar

11. Li Q, Hu S, Tang S, Zeng G. Hyperchaos and horseshoe in a 4D memristive system with aline of equilibria and its implementation. Int J Circuit Theor Appl. (2014) 42(11):1172–88. doi:10.1002/cta.1912

CrossRef Full Text | Google Scholar

12. Li Q, Zeng H, Li J. Hyperchaos in a 4D memristive circuit with infinitely many stable equilibria. Nonlinear Dynam (2015) 79:2295–308. doi:10.1007/s11071-014-1812-4

CrossRef Full Text | Google Scholar

13. Kountchou M, Louodop P, Bowong S, Fotsin H, Kurths J. Optimal synchronization of a memristive chaotic circuit. Int J Bifur Chaos (2016) 26(06):1650093. doi:10.1142/S0218127416500930

CrossRef Full Text | Google Scholar

14. Tian A, Fu C, Su XY, Yau HT, Xiong H. Classifying and predicting salinization level in arid area soil using a combination of Chua’s circuit and fractional order sprott chaotic system. Sensors (2019) 19(20):4517. doi:10.3390/s19204517

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Yan S, Wang E, Wang Q, Sun X, Ren Y. Analysis, circuit implementation and synchronization control of a hyperchaotic system. Phys Scr (2021) 96(12):125257. doi:10.1088/1402-4896/ac379b

CrossRef Full Text | Google Scholar

16. Khan N, Muthukumar P. Transient chaos, synchronization and digital image enhancement technique based on a novel 5D fractional-order hyperchaotic memristive system. Circuits Syst Signal Proc (2022) 41(4):2266–89. doi:10.1007/s00034-021-01892-6

CrossRef Full Text | Google Scholar

17. Liu J, Wang Z, Chen M, Zhang P, Yang R, Yang B. Chaotic system dynamics analysis and synchronization circuit realization of fractional-order memristor. Euro Phys J Spec Top (2022) 231(16):3095–107. doi:10.1140/epjs/s11734-022-00640-4

CrossRef Full Text | Google Scholar

18. Cao S, Zhao T, Wang G, Zhang T, Liu C, Liu Q, et al. A mechanical defect localization and identification method for high-voltage circuit breakers based on the segmentation of vibration signals and extraction of chaotic features. Sensors (2023) 23(16):7201. doi:10.3390/s23167201

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Yang S, Li C, Huang T. Synchronization of coupled memristive chaotic circuits via state dependent impulsive control. Nonlinear Dynam (2017) 88(1):115–29. doi:10.1007/s11071-016-3233-z

CrossRef Full Text | Google Scholar

20. Zou L, Peng Y, Feng Y, Tu Z. Stabilization and synchronization of memristive chaotic circuits by impulsive control. Complexity (2017) 317:1–10. doi:10.1155/2017/5186714

CrossRef Full Text | Google Scholar

21. Wang S, Wang X, Zhou Y. A memristor-based complex Lorenz system and its modified projective synchronization. Entropy (2017) 17(11):7628–44. doi:10.3390/e17117628

CrossRef Full Text | Google Scholar

22. Wang S. A novel memristive chaotic system and its adaptive sliding mode synchronization. Chaos Solitons Fractals (2023) 172:113533. doi:10.1016/j.chaos.2023.113533

CrossRef Full Text | Google Scholar

23. Wu H, Li R, Wei H, Zhang X, Yao R. Synchronization of a class of memristive neural networks with time delays via sampled-data control. Int J Mach Learn Cyber (2015) 6:365–73. doi:10.1007/s13042-014-0271-z

CrossRef Full Text | Google Scholar

24. Rakkiyappan R, Sivasamy R, Li X. Synchronization of identical and nonidentical memristor-based chaotic systems via active backstepping control technique. Circuits Syst Signal Proc (2015) 34:763–78. doi:10.1007/s00034-014-9883-5

CrossRef Full Text | Google Scholar

25. Xiao W, Min F, Li H, Shi W. Complex motion behavior and synchronization analysis of heterogeneous neural network. IEEE Trans Circuits Syst Reg Pap (2024) 1–10. early access. doi:10.1109/TCSI.2024.3387560

CrossRef Full Text | Google Scholar

26. Li H, Min F. Large-scale memrisitive rulkov ring-star neural network with complex spatio-temporal dynamics. IEEE Trans Ind Inf (2024) 20:10259–68. early access. doi:10.1109/TII.2024.3393563

CrossRef Full Text | Google Scholar

27. Cang S, Chen Z, Wang Z, Jia H. Projective synchronisation of fractional–order memristive systems with different structures based on active control method. Int J Sensor Netw (2013) 14(2):102–8. doi:10.1504/IJSNET.2013.056609

CrossRef Full Text | Google Scholar

28. Akgul A, Rajagopal K, Durdu A, Pala MA, Boyraz OF, Yildiz MZ. A simple fractional-order chaotic system based on memristor and memcapacitor and its synchronization application. Chaos Solitons Fractals (2021) 152:111306. doi:10.1016/j.chaos.2021.111306

CrossRef Full Text | Google Scholar

29. Jiang H, Zhuang L, Chen C, Wang Z. Hidden dynamics and hybrid synchronization of fractional-order memristive systems. Axioms (2022) 11(11):645. doi:10.3390/axioms11110645

CrossRef Full Text | Google Scholar

30. Wang L, Dong T, Ge MF. Finite-time synchronization of memristor chaotic systems and its application in image encryption. Appl Math Comput (2019) 347:293–305. doi:10.1016/j.amc.2018.11.017

CrossRef Full Text | Google Scholar

31. Ahmad I, Shafiq M, Naderi B. Finite-time synchronization of four-dimensional memristor-based chaotic oscillator and applied to secure communication systems. Franklin Open (2023) 3:100015. doi:10.1016/j.fraope.2023.100015

CrossRef Full Text | Google Scholar

32. Wang J, Tian Y, Hua L, Shi K, Zhong S, Wen S. New results on finite-time synchronization control of chaotic memristor-based inertial neural networks with time-varying delays. Mathematics (2023) 11(3):684. doi:10.3390/math11030684

CrossRef Full Text | Google Scholar

33. Wang L, Jiang S, Ge MF, Hu C, Hu J. Finite-/fixed-time synchronization of memristor chaotic systems and image encryption application. IEEE Trans Circuits Syst Reg Pap (2021) 68(12):4957–69. doi:10.1109/TCSI.2021.3121555

CrossRef Full Text | Google Scholar

34. Mirzaei MJ, Aslmostafa E, Asadollahi M, Padar N. Fast fixed-time sliding mode control for synchronization of chaotic systems with unmodeled dynamics and disturbance; applied to memristor-based oscillator. J Vibr Control (2023) 29(9-10):2129–43. doi:10.1177/10775463221075116

CrossRef Full Text | Google Scholar

35. Wang Y, Li H, Guan Y, Chen M. Predefined-time chaos synchronization of memristor chaotic systems by using simplified control inputs. Solitons Fractals (2022) 161:112282. doi:10.1016/j.chaos.2022.112282

CrossRef Full Text | Google Scholar

36. Ma R, Huang Z, Xu H. Fixed-time chaotic stabilization and synchronization of memristor chaotic circuits in noisy environments. J Korean Phys Soc (2024) 84(2):90–101. doi:10.1007/s40042-023-00942-3

CrossRef Full Text | Google Scholar

37. Sambas A, Vaidyanathan S, Tlelo-Cuautle E, Abd-El-Atty B, Abd El-Latif AA, Guillen-Fernandez O, et al. A 3-D multi-stable system with a peanut-shaped equilibrium curve: circuit design, FPGA realization, and an application to image encryption. IEEE Access (2020) 24(8):137116–32. doi:10.1109/ACCESS.2020.3011724

CrossRef Full Text | Google Scholar

38. Sambas A, Vaidyanathan S, Zhang X, Koyuncu I, Bonny T, Tuna M, et al. A novel 3D chaotic system with line equilibrium: multistability, integral sliding mode control, electronic circuit, FPGA implementation and its image encryption. IEEE Access (2022) 8(10):68057–74. doi:10.1109/ACCESS.2022.3181424

CrossRef Full Text | Google Scholar

39. Sambas A, Miroslav M, Vaidyanathan S, Ovilla-Martínez B, Tlelo-Cuautle E, Abd El-Latif AA, et al. A New Hyperjerk system with a half line equilibrium: multistability, Period doubling reversals, antimonotonocity, electronic circuit, FPGA design and an application to image encryption. IEEE Access (2024) 12:9177–94. doi:10.1109/ACCESS.2024.3351693

CrossRef Full Text | Google Scholar

40. Mao X. Stochastic differential equations and applications. England: Horwood (1997).

Google Scholar

41. Bhat SP, Bernstein DS. Finite-time stability of continuous autonomous systems. SIAM J Control Optim (2000) 38(3):751–66. doi:10.1137/S0363012997321358

CrossRef Full Text | Google Scholar

42. Yin J, Khoo S, Man Z, Yu X. Finite-time stability and instability of stochastic nonlinear systems. Automatica (2011) 47(12):2671–7. doi:10.1016/j.automatica.2011.08.050

CrossRef Full Text | Google Scholar

43. Khalil HK, Grizzle JW. Nonlinear systems. Upper Saddle River: Prentice Hall (2002).

Google Scholar