On the analytical soliton-like solutions to (2+1)-dimensional fractional asymmetric Nizhnik-Novikov-Veselov system arising in incompressible fluids

Due to the numerous applications of the Nizhnik-Novikov-Veselov system (NNVS) in fluid mechanics, thus, the current investigation is focused on studying the fractional form of this model to reveal the ambiguity around many nonlinear phenomena that arise in different fluid medias. Accordingly, we aim to derive several families of symmetric solitons and traveling wave solutions to the (2 + 1)-dimensional fractional asymmetric NNVS (FANNVS), defined in conformable fractional derivatives’ sense. For this purpose, a groundbreaking analytical technique known as the modified extended direct algebraic method (mEDAM) is utilized to solve and analyze the FANNVS. According to this method, four cases with several families of soliton-like solutions are derived. Our research uncovers various soliton solutions, including solitary waves, periodic waves, shocks, dual shock waves (lump waves), and anti-shock waves. These solutions are graphically discussed to understand their dynamical proprieties against the fractional parameters. This broad range of soliton-like solutions supports the relevance of our findings and demonstrates the effectiveness of our methodology. These findings significantly advance the field by deepening our understanding of solitonic behavior in FANNVS and demonstrating the effectiveness of the medium approach in solving challenging nonlinear systems.

1 Introduction

The Fractional partial differential equations (PDEs) are very significant mathematical tools for modeling and describing complex phenomena joined with the memory effect, and we may hope that even more general results are necessary to be obtained in the future. Therefore, the contribution is to review various works on fractional differential equations or to discuss properties and fundamental solutions from the point of view of essential mathematical tools. Thus, these types of differential equations are discussed in describing several natural phenomena, such as anomalous diffusion, wave propagation in different physical mediums (e.g., plasma physics, optical communications, and fluid), and multi-scale dynamics [1–5], and others [6–11]. Therefore, fractional PDEs (FPDEs) are the optimal and most suitable option for representing various physical phenomena, engineering, and technical challenges, allowing for a more profound comprehension of the intricacy of natural events.

The exact solutions of FPDEs play a significant role in the study of nonlinear science because they give precise and clear mathematical expressions, provide deeper insights, and do away with the approximation mistakes that come with numerical approaches. Therefore, when feasible, explicit solutions are favored over numerical ones. Several effective analytical techniques have been created to solve different types of nonlinear FPDEs (NFPDEs), such as Backlund transformation [12], Darboux transformation [13], inverse scattering transform [14], unified method [15], (G’/G)-expansion method [16, 17], tanh and tanh-coth methods [18–20], modified extended direct algebraic method (mEDAM) [20–22], and numerous others [23–27]. The mEDAM stands out among these methods as a straightforward and helpful approach for locating exact soliton solutions for NFPDEs.

Soliton solutions have recently garnered considerable attention due to their presence in several environments, including nonlinear optics, plasma, shallow-water waves, and Bose-Einstein condensates [28–33]. Solitons are self-sustaining wave solutions that retain their shape and velocity while propagating [34–40]. The main objective of this study is to extensively explore soliton phenomena within the context of the (2 + 1)-dimensional fractional asymmetric Nizhnik-Novikov-Veselov system (FANNVS), which is a fractional generalization of ANNVS [41], using the unique analytical technique mEDAM. The mathematical representation of this model is introduced in the following manner:

$\begin{array}{cc}\hfill & D_t^{\alpha }p+D_x^{\beta }\left(D_x^{\beta }\left(D_x^{\beta }p\right)\right)+3D_x^{\beta }\left(pq\right)=0,\hfill \\ \hfill & D_x^{\beta }p-D_y^{\delta }q=0,0<\alpha ,\beta ,\delta \le 1,\hfill \end{array}(1)$

where $p\equiv p(x,y,t)$ & $q\equiv p(x,y,t)$ are the components of the (dimensionless) velocity. Equation 1 is the solely known isotropic Lax extension of the Korteweg-de Vries (KdV) equation. The derivative operators $D_t^{\alpha }$, $D_x^{\beta }$, and $D_y^{\delta }$ are conformable fractional derivative operators. The FANNVS plays an important role for nonlinear phenomena including shallow-water waves, long internal waves, and acoustic waves that occur in incompressible fluids and in physics of plasmas. The physics of plasma is one of the most critical physical disciplines, rich in many nonlinear phenomena that arise and propagate in different plasma systems. Plasma physics is also a crucial specialty widely used in many different applications, whether in industrial, medical, agricultural, engineering, and many others. There are many different evolution/wave equations, such as KdV-type equations [42–45], damped KdV-type equations [40, 46, 47], Kawahara-type equations [48–53], and nonlinear Schrödinger-type equations [42, 54–57], which are derived from different plasma systems and are used to describe nonlinear waves, such as solitary waves, shock waves, rogue waves, cnoidal waves, etc. Therefore, The FANNVS can be essential in analyzing and solving these wave equations in their fractional forms to study the fractional effect on these phenomena.

Many academics have used various methods to investigate the NNVM. For instance, to obtain multi-wave solutions of the time-FANNVS in a modified Riemann–Liouville context, Osman [58] used a generalized unified technique. Researchers have investigated the FANNVS utilizing a variety of methods. Similarly, Sagar and Ray [59] used the Kansa approach and multi-quadrics as their radial basis functions to examine numerical solitons for time-FANNVS. Liu [60] established the generalized fractional subequation approach and used it to find several accurate solutions to the FANNVS. Our main goal in this study, which builds on the literature, is to propose the simple approach known as mEDAM for producing novel soliton solutions for FANNVS, emphasizing kink wave and shock wave. Kink and shock solitons are two different forms of solitons in the FANNVS. When moving from one equilibrium state to another, kink solitons show a smooth transition, but shock solitons show abrupt discontinuities that resemble shock waves. The derived soliton solutions for the FANNVS possess a variety of soliton behaviors, including singular and periodic kinks, shock and anti-shock wave solutions, and dual shock waves (lump waves). We anticipate using this approach to comprehend the complex solitonic behavior inside the FANNVS thoroughly, hence advancing our understanding of nonlinear wave phenomena.

2 Methods and materials

2.1 Conformable fractional derivative

The fractional derivatives presented in Equation 1 are conformable fractional derivatives. This derivative operator of order $\beta$ is described as [61]:

$D_{\psi }^{\delta }p\left(\psi \right)=\underset{\tau \to 0}{\lim }\frac{p\left(\tau {\psi }^{1-\delta }+\psi \right)-p\left(\psi \right)}{\tau },\delta \in \left(\mathrm{0,1}\right].(2)$

The following properties of this derivative are used in transformation of FPDE in Equation 1 into a nonlinear ordinary differential equation (NODE):

$D_{\psi }^{\tau }{\psi }^r=r{\psi }^{r-\tau },(3)$

$D_{\psi }^{\tau }\left(r_1\rho \left(\psi \right)\pm r_2\eta \left(\psi \right)\right)=r_1{D}_{\psi }^{\tau }\left(\rho \left(\psi \right)\right)\pm r_2{D}_{\psi }^{\tau }\left(\eta \left(\psi \right)\right)(4)$

$D_{\psi }^{\tau }\zeta \left[\varphi \left(\psi \right)\right]={\zeta }_{\varphi }^{\prime }\left(\varphi \left(\psi \right)\right)D_{\psi }^{\tau }\varphi \left(\psi \right)=D_{\varphi }^{\tau }\zeta \left(\varphi \left(\psi \right)\right)\left[{\varphi }^{\prime \tau }\right],(5)$

where $\zeta (\psi )$ & $\varphi (\psi )$ are arbitrary differentiable functions, whereas $k$, $r_1$, & $r_2$ signify real constants in the current context.

2.2 Methodology of mEDAM

This section outlines EDAM’s operational procedures. Think about the generic FPDE [20, 22] that follows:

$Q\left(q,{\partial }_t^{\alpha }q,{\partial }_x^{\beta }q,{\partial }_y^{\delta }q,q{\partial }_x^{\beta }q,\dots \right)=0,0<\alpha ,\beta ,\delta \le 1,(6)$

where $q=f(t,x,y)$.

We follow these procedures for addressing Equation 6:

1. Firstly, a variable transformation of the form $q(t,x,y)=Q(\psi )$ where:

$\psi =\lambda \left(-k\frac{t^{\alpha }}{\alpha }+\frac{x^{\beta }}{\beta }+\frac{y^{\delta }}{\delta }\right),(7)$

is carried out.

Equation 6 is converted into a NODE of the following form:

$T\left(Q,Q^{\prime },Q^{\prime }Q,\dots \right)=0,(8)$

where $Q$ in Equation 8 has derivatives with respect to $\psi$. To get the integration’s constant, Equation 8 may occasionally be integrated once or more.

2. The solution for Equation 8 is thus assumed to be as follows:

$Q\left(\psi \right)={\displaystyle \sum _{l=-n}^n}{m}_l{\left(V\right)}^l,(9)$

where $V\equiv V(\psi )$ is the general solution of the following ODE, and $m_l(l=-n,\dots ,0,\dots ,n)$ are unknown constants that will be obtained later:

$V^{\prime }=A+BV+C{V}^2.(10)$

where $\left(A,B,C\right)$ are constants.

3. The positive integer $n$ appearing in Equation 9 is obtained by taking the homogeneous balance between the highest order derivative and the largest nonlinear component in Equation 8.

4. Then, we insert Equation 9 into Equation 8 or the equation created by integrating Equation 8, and last, we compile all the terms of $V(\psi )$ that are in the same order and produce an expression in $V(\psi )$. A system of algebraic equations in $m_l(l=-n,\dots 0,\dots ,n)$ and additional parameters is produced by equating all the coefficients in an expression to zero using the concept of comparison of coefficients.

5. This set of algebraic equations is resolved using Maple software.

6. Then, using the $V(\psi )$(general solution of (10) and the calculated unknown coefficients and other parameters, the soliton solutions to Equation 6 are examined. The following families of soliton solutions can be produced by the general solution of (Equation 10);

Family 1: When $F<0\&C\ne 0$, we get

$\begin{array}{c}{V}_1\left(\psi \right)=-\frac{B}{2C}+\frac{\sqrt{-F}\tan \left(\frac{1}{2}\sqrt{-F}\psi \right)}{2C},\hfill \\ V_2\left(\psi \right)=-\frac{B}{2C}-\frac{\sqrt{-F}\cot \left(\frac{1}{2}\sqrt{-F}\psi \right)}{2C},\hfill \\ V_3\left(\psi \right)=-\frac{B}{2C}+\frac{\sqrt{-F}\left(\tan \left(\sqrt{-F}\psi \right)\pm \left(\sqrt{jl}\sec \left(\sqrt{-F}\psi \right)\right)\right)}{2C},\hfill \\ V_4\left(\psi \right)=-\frac{B}{2C}-\frac{\sqrt{-F}\left(\cot \left(\sqrt{-F}\psi \right)\pm \left(\sqrt{jl}\csc \left(\sqrt{-F}\psi \right)\right)\right)}{2C},\hfill \\ V_5\left(\psi \right)=-\frac{B}{2C}+\frac{\sqrt{-F}\left(\tan \left(\frac{1}{4}\sqrt{-F}\psi \right)-\cot \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}{4C}.\hfill \end{array}$

Family 2: When $F>0\&C\ne 0$, we get

$\begin{array}{c}{V}_6\left(\psi \right)=-\frac{B}{2C}-\frac{\sqrt{R}\tanh \left(\frac{1}{2}\sqrt{R}\psi \right)}{2C},\hfill \\ V_7\left(\psi \right)=-\frac{B}{2C}-\frac{\sqrt{R}\coth \left(\frac{1}{2}\sqrt{R}\psi \right)}{2C},\hfill \\ V_8\left(\psi \right)=-\frac{B}{2C}-\frac{\sqrt{R}\left(\tanh \left(\sqrt{R}\psi \right)\pm \left(\sqrt{jl}sech\left(\sqrt{R}\psi \right)\right)\right)}{2C},\hfill \\ V_9\left(\psi \right)=-\frac{B}{2C}-\frac{\sqrt{R}\left(\coth \left(\sqrt{R}\psi \right)\pm \left(\sqrt{jl}csch\left(\sqrt{R}\psi \right)\right)\right)}{2C},\hfill \\ V_{10}\left(\psi \right)=-\frac{B}{2C}-\frac{\sqrt{R}\left(\tanh \left(\frac{1}{4}\sqrt{R}\psi \right)-\coth \left(\frac{1}{4}\sqrt{R}\psi \right)\right)}{4C}.\hfill \end{array}$

Family 3: When $AC>0$ & $B=0$, we get

$\begin{array}{c}{V}_{11}\left(\psi \right)=\sqrt{\frac{A}{C}}\tan \left(\sqrt{AC}\psi \right),\hfill \\ V_{12}\left(\psi \right)=-\sqrt{\frac{A}{C}}\cot \left(\sqrt{AC}\psi \right),\hfill \\ V_{13}\left(\psi \right)=\sqrt{\frac{A}{C}}\left(\tan \left(2\sqrt{AC}\psi \right)\pm \left(\sqrt{jl}\sec \left(2\sqrt{AC}\psi \right)\right)\right),\hfill \\ V_{14}\left(\psi \right)=-\sqrt{\frac{A}{C}}\left(\cot \left(2\sqrt{AC}\psi \right)\pm \left(\sqrt{jl}\csc \left(2\sqrt{AC}\psi \right)\right)\right),\hfill \\ V_{15}\left(\psi \right)=\frac{1}{2}\sqrt{\frac{A}{C}}\left(\tan \left(\frac{1}{2}\sqrt{AC}\psi \right)-\cot \left(\frac{1}{2}\sqrt{AC}\psi \right)\right).\hfill \end{array}$

Family 4: When $AC>0$ & $B=0$, we get

$\begin{array}{c}{V}_{16}\left(\psi \right)=-\sqrt{-\frac{A}{C}}\tanh \left(\sqrt{-AC}\psi \right),\hfill \\ V_{17}\left(\psi \right)=-\sqrt{-\frac{A}{C}}\coth \left(\sqrt{-AC}\psi \right),\hfill \\ V_{18}\left(\mathrm{\Phi }\right)=-\sqrt{-\frac{A}{C}}\left[\tanh \left(2\sqrt{-AC}\psi \right)\pm \left(i\sqrt{jl}{sech}_A\left(2\sqrt{-AC}\psi \right)\right)\right],\hfill \\ V_{19}\left(\psi \right)=-\sqrt{-\frac{A}{C}}\left[\coth \left(2\sqrt{-AC}\psi \right)\pm \left(\sqrt{jl}csch\left(2\sqrt{-AC}\psi \right)\right)\right],\hfill \\ V_{20}\left(\psi \right)=-\frac{1}{2}\sqrt{-\frac{A}{C}}\left[\tanh \left(\frac{1}{2}\sqrt{-AC}\psi \right)+\coth \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right].\hfill \end{array}$

Family 5: When $C=A$ & $B=0$, we get

$\begin{array}{c}{V}_{21}\left(\psi \right)=\tan \left(A\psi \right),\hfill \\ V_{22}\left(\psi \right)=-\cot \left(A\psi \right),\hfill \\ V_{23}\left(\psi \right)=\tan \left(2A\psi \right)\pm \left(\sqrt{jl}\sec \left(2A\psi \right)\right),\hfill \\ V_{24}\left(\psi \right)=-\cot \left(2A\psi \right)\pm \left(\sqrt{jl}\csc \left(2A\psi \right)\right),\hfill \\ V_{25}\left(\psi \right)=\frac{1}{2}\tan \left(\frac{1}{2}A\psi \right)-\frac{1}{2}\cot \left(\frac{1}{2}A\psi \right).\hfill \end{array}$

Family 6: When $C=-A$ & $B=0$, we get

$\begin{array}{c}{V}_{26}\left(\psi \right)=-\tanh \left(A\psi \right),\hfill \\ V_{27}\left(\psi \right)=-\coth \left(A\psi \right),\hfill \\ V_{28}\left(\psi \right)=-\tanh \left(2A\psi \right)\pm \left(i\sqrt{jl}sech\left(2A\psi \right)\right),\hfill \\ V_{29}\left(\psi \right)=-\coth \left(2A\psi \right)\pm \left(\sqrt{jl}csch\left(2A\psi \right)\right),\hfill \\ V_{30}\left(\psi \right)=-\frac{1}{2}\tanh \left(\frac{1}{2}A\psi \right)-\frac{1}{2}\coth \left(\frac{1}{2}A\psi \right).\hfill \end{array}$

Family 7: When $F=0$, we get

$V_{31}\left(\psi \right)=-2\frac{A\left(B\psi +2\right)}{B^2\psi }.$

Family 8: When $B=\mu$, $A=z\mu (z\ne 0)$ and $C=0$, we get

$V_{32}\left(\psi \right)=e^{\mu \psi }-z.$

Family 9: When $B=C=0$, we get

$V_{33}\left(\psi \right)=A\psi .$

Family 10: When $B=A=0$, we get

$V_{34}\left(\psi \right)=-\frac{1}{C\psi }.$

Family 11: When $A=0$, $B\ne 0$ and $C\ne 0$, we get

$\begin{array}{ccc}{V}_{35}\left(\psi \right)\hfill & =\hfill & -\frac{jB}{C\left(\cosh \left(B\psi \right)-\sinh \left(B\psi \right)+j\right)},\hfill \\ V_{36}\left(\psi \right)\hfill & =\hfill & -\frac{B\left(\cosh \left(B\psi \right)+\sinh \left(B\psi \right)\right)}{C\left(\cosh \left(B\psi \right)+\sinh \left(B\psi \right)+l\right)}.\hfill \end{array}$

Family 12: When $B=\mu$, $C=z\mu (z\ne 0)$ and $A=0$, we get

$V_{37}\left(\psi \right)=\frac{j{e}^{\mu \psi }}{j-zl{e}^{\mu \psi }}.$

Here, $F=\left(B^2-4AC\right)$ and $j,l>0$ are referred to as deformation parameters.

3 Execution of mEDAM

In this section, we proceed to use the mEDAM for addressing FANNVS. Now, to get the soliton solution for system (1), we start through transforming the variables as stated in Equation 7, by transforming Equation 1, the system of NODEs listed below is produced:

$\begin{array}{c}-k{P}^{\prime 2}{P}^{\prime \prime \prime }-3{\left(PQ\right)}^{\prime }=0\hfill \\ \lambda P^{\prime }=\lambda Q^{\prime },\hfill \end{array}(11)$

By integrating system (11) relative to $\psi$ for zero constant, the following result is obtained:

$\begin{array}{c}-kP+{\lambda }^2{P}^{\prime \prime }-3PQ=0,\hfill \\ P=Q.\hfill \end{array}(12)$

The following single NODE results is obtained by putting the second component of system (12) into the first part:

$-kP+{\lambda }^2{P}^{\prime \prime 2}=0.(13)$

The value of $n$ can be obtained by balancing the highest order derivative $P^{\prime \prime }$ and the nonlinear term $P^2$ which leads to $n+2=2n$, i.e., $n=2$. By substituting $n=2$ into Equation 9, we obtain the following series form solution for Equation 13.

$P\left(\psi \right)={\displaystyle \sum _{i=-2}^2}{s}_i{\left(V\right)}^i=s_{-2}{\left(V\right)}^{-2}+s_{-1}{\left(V\right)}^{-1}+s_0+s_1{\left(V\right)}^1+s_2{\left(V\right)}^2.(14)$

We generate an expression in $V\equiv V(\psi )$ by putting Equation 14 in Equation 13 and collecting every term with the same powers of $V$. A system of nonlinear algebraic equations is formed by equating all coefficients to zero. Using Maple to solve the system yields the following four sets of symmetric solutions:

Case 1

$\begin{array}{l}{m}_{-2}=0,m_{-1}=0,m_0=m_0,m_1=\frac{m_{0}B}{A},m_2=\frac{m_{0}C}{A},k=\frac{1}{2}\frac{-m_{0}F}{AC},\hfill \\ \lambda =\frac{1}{2}\sqrt{-2\frac{m_0}{AC}}.\hfill \end{array}(15)$

Case 2

$\begin{array}{l}\hfill m_{-2}=0,m_{-1}=0,m_0=m_0,m_1=\frac{6m_{0}BC}{2AC+B^2},m_2=\frac{6m_0{C}^2}{2AC+B^2},\\ k=\frac{3m_{0}F}{2AC+B^2},\lambda =\sqrt{-3\frac{m_0}{2AC+B^2}}.\hfill \end{array}(16)$

Case 3

$\begin{array}{l}\hfill m_{-2}=\frac{m_{0}A}{C},m_{-1}=\frac{m_{0}B}{C},m_0=m_0,m_1=0,m_2=0,k=\frac{1}{2}\frac{-m_{0}F}{AC},\\ \lambda =\frac{1}{2}\sqrt{-2\frac{m_0}{AC}}\hfill \end{array}(17)$

Case 4

$\begin{array}{l}\hfill m_{-2}=\frac{6m_0{A}^2}{2AC+B^2},m_{-1}=\frac{6m_{0}AB}{2AC+B^2},m_0=m_0,m_1=0,m_2=0,\\ k=\frac{3m_{0}F}{2AC+B^2},\lambda =\sqrt{-3\frac{m_0}{2AC+B^2}}\hfill \end{array}(18)$

Considering case 1 and using system (14) and corresponding general solutions of Equation 10, suggest the following families of soliton solutions for system (1).

Family 1.1: When $F<0\&C\ne 0$, we get

$u_{\mathrm{1,1}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(4CA-B^2-F{\left(\tan \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2\right)}{CA},(19)$

$u_{\mathrm{1,2}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(4CA-B^2-F{\left(\cot \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2\right)}{CA},(20)$

$u_{\mathrm{1,3}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(-F-2F\sin \left(\sqrt{-F}\psi \right)\sqrt{jl}-Fjl\right)}{CA{\left(\cos \left(\sqrt{-F}\psi \right)\right)}^2},(21)$

$u_{\mathrm{1,4}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(F+2F\cos \left(\sqrt{-F}\psi \right)\sqrt{jl}+Fjl\right)}{CA\left(-1+{\left(\cos \left(\sqrt{-F}\psi \right)\right)}^2\right)},(22)$

$u_{\mathrm{1,5}}\left(x,y,t\right)=\frac{1}{16}\frac{F}{CA{\left(\cos \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}^2\left(-1+{\left(\cos \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}^2\right)},(23)$

Family 1.2: When $F>0\&C\ne 0$, we get

$u_{\mathrm{1,6}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(4CA-B^2+F{\left(\tanh \left(\frac{1}{2}\sqrt{F}\psi \right)\right)}^2\right)}{CA},(24)$

$u_{\mathrm{1,7}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(4CA-B^2+F{\left(\coth \left(\frac{1}{2}\sqrt{F}\psi \right)\right)}^2\right)}{CA},(25)$

$u_{\mathrm{1,8}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(-F+2F\sinh \left(\sqrt{F}\psi \right)\sqrt{jl}+Fjl\right)}{CA{\left(\cosh \left(\sqrt{F}\psi \right)\right)}^2},(26)$

$u_{\mathrm{1,9}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(F+2F\cosh \left(\sqrt{F}\psi \right)\sqrt{jl}+Fjl\right)}{CA\left({\left(\cosh \left(\sqrt{F}\psi \right)\right)}^2-1\right)},(27)$

and

$u_{\mathrm{1,10}}\left(x,y,t\right)=\frac{1}{16}\frac{m_{0}F}{CA{\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2\left({\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2-1\right)},(28)$

Family 1.3: When $AC>0$ & $B=0$, we get

$u_{\mathrm{1,11}}\left(x,y,t\right)=\frac{m_0}{{\left(\cos \left(\sqrt{CA}\psi \right)\right)}^2},(29)$

$u_{\mathrm{1,12}}\left(x,y,t\right)=-\frac{m_0}{-1+{\left(\cos \left(\sqrt{CA}\psi \right)\right)}^2},(30)$

$u_{\mathrm{1,13}}\left(x,y,t\right)=\frac{m_0\left(1+2\sin \left(2\sqrt{CA}\psi \right)\sqrt{jl}+jl\right)}{{\left(\cos \left(2\sqrt{CA}\psi \right)\right)}^2},(31)$

$u_{\mathrm{1,14}}\left(x,y,t\right)=-\frac{m_0\left(1+2\cos \left(2\sqrt{CA}\psi \right)\sqrt{jl}+jl\right)}{-1+{\left(\cos \left(2\sqrt{CA}\psi \right)\right)}^2},(32)$

and

$u_{\mathrm{1,15}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0}{{\left(\cos \left(\frac{1}{2}\sqrt{CA}\psi \right)\right)}^2\left(-1+{\left(\cos \left(\frac{1}{2}\sqrt{CA}\psi \right)\right)}^2\right)},(33)$

Family 1.4: When $AC<0$ & $B=0$, we get

$u_{\mathrm{1,16}}\left(x,y,t\right)=\frac{m_0}{{\left(\cosh \left(\sqrt{-CA}\psi \right)\right)}^2},(34)$

$u_{\mathrm{1,17}}\left(x,y,t\right)=-\frac{m_0}{{\left(\cosh \left(\sqrt{-CA}\psi \right)\right)}^2-1},(35)$

$u_{\mathrm{1,18}}\left(x,y,t\right)=-\frac{m_0\left(-1+36\sinh \left(2\sqrt{-CA}\psi \right)\sqrt{jl}+324jl\right)}{{\left(\cosh \left(2\sqrt{-CA}\psi \right)\right)}^2},(36)$

$u_{\mathrm{1,19}}\left(x,y,t\right)=-\frac{m_0\left(1+2\cosh \left(2\sqrt{-CA}\psi \right)\sqrt{jl}+jl\right)}{{\left(\cosh \left(2\sqrt{-CA}\psi \right)\right)}^2-1},(37)$

and

$u_{\mathrm{1,20}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0}{{\left(\cosh \left(\frac{1}{2}\sqrt{-CA}\psi \right)\right)}^2\left({\left(\cosh \left(\frac{1}{2}\sqrt{-CA}\psi \right)\right)}^2-1\right)},(38)$

Family 1.5: When $C=A\&B=0$, we get

$u_{\mathrm{1,21}}\left(x,y,t\right)=\frac{m_0}{{\left(\cos \left(A\psi \right)\right)}^2},(39)$

$u_{\mathrm{1,22}}\left(x,y,t\right)=-\frac{m_0}{-1+{\left(\cos \left(A\psi \right)\right)}^2},(40)$

$u_{\mathrm{1,23}}\left(x,y,t\right)=\frac{m_0\left(1+2\sin \left(2A\psi \right)\sqrt{jl}+jl\right)}{{\left(\cos \left(2A\psi \right)\right)}^2},(41)$

$u_{\mathrm{1,24}}\left(x,y,t\right)=\frac{m_0\left(-1+2\cos \left(2A\psi \right)\sqrt{jl}-jl\right)}{-1+{\left(\cos \left(2A\psi \right)\right)}^2},(42)$

and

$u_{\mathrm{1,25}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0}{{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2\left(-1+{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2\right)},(43)$

Family 1.6: When $C=-A$ & $B=0$, we get

$u_{\mathrm{1,26}}\left(x,y,t\right)=\frac{m_0}{{\left(\cosh \left(A\psi \right)\right)}^2},(44)$

$u_{\mathrm{1,27}}\left(x,y,t\right)=-\frac{m_0}{{\left(\cosh \left(A\psi \right)\right)}^2-1},(45)$

$u_{\mathrm{1,28}}\left(x,y,t\right)=\frac{m_0\left(1+56\sinh \left(2A\psi \right)\sqrt{jl}-784jl\right)}{{\left(\cosh \left(2A\psi \right)\right)}^2},(46)$

$u_{\mathrm{1,29}}\left(x,y,t\right)=\frac{m_0\left(-1+2\cosh \left(2A\psi \right)\sqrt{jl}-jl\right)}{{\left(\cosh \left(2A\psi \right)\right)}^2-1},(47)$

and

$u_{\mathrm{1,30}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0}{{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2\left({\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2-1\right)},(48)$

Family 1.7: When $F=0$, we get

$u_{\mathrm{1,31}}\left(x,y,t\right)=\frac{m_0\left(A{B}^4{\psi }^2-2A\left(B\psi +2\right)B^3\psi +4C{\left(A\left(B\psi +2\right)\right)}^2\right)}{A{B}^4{\psi }^2},(49)$

Family 1.8: When $B=\mu$, $a=z\mu (z\ne 0)$ and $C=0$, we get

$u_{\mathrm{1,32}}\left(x,y,t\right)=\frac{m_0\left(A{B}^4{\psi }^2-2A\left(B\psi +2\right)B^3\psi +4C{\left(A\left(B\psi +2\right)\right)}^2\right)}{A{B}^4{\psi }^2},(50)$

with

$\psi =\frac{1}{2}\sqrt{-2\frac{m_0}{AC}}\left[-\left(\frac{1}{2}\frac{-m_{0}F}{AC}\right)\frac{t^{\alpha }}{\alpha }+\frac{x^{\beta }}{\beta }+\frac{y^{\delta }}{\delta }\right].$

This section examines several soliton solutions that arise from our investigation of the (2 + 1)-dimensional FANNVS. Our investigation focuses on the unique classification of solitons into kink and shock solitons within this system. By utilizing the innovative mEDAM to obtain these soliton solutions, one can understand the intricate dynamics of the FANNVS system. Graphical depictions clearly show the range of soliton behaviors, such as solitary kinks, periodic kinks, shock waves, dual shock waves (lump waves), and anti-shock waves. The connection between different soliton types, propagation patterns, and interactions is graphically illustrated. This graphical investigation emphasizes the importance of our findings and supports the mEDAM’s effectiveness in resolving challenging nonlinear systems. In the end, these graphical presentations highlight the revolutionary contributions of the mEDAM approach in solving complicated nonlinear phenomena while advancing our understanding of solitonic behavior in the (2 + 1)-dimensional FANNVS.

Given this study’s abundance of derived solutions, we will focus on evaluating a select few to comprehend the mechanics of the resultant waves. Similarly, we may analyze the remaining solutions using the same approach. The soliton solution (Equation 19) is discussed graphically, as shown in Figure 1 at various values for fractional parameters $\alpha$ and $\delta$. The analysis indicates that the fractional parameter $\alpha$ causes a positive shift of the wave along the $x$-axis, while the fractional parameter $\delta$ causes a negative shift of the wave along the $x$-axis as illustrated in Figures 1A,B, respectively. Similarly, the soliton solutions (Equation 24), (Equation 29), (Equation 34), (Equation 39), (Equation 44), and (Equation 46) for case 1 are graphed using identical values of the pertinent parameters that have been used in Figure 1. Additionally, it is observed that the fractional parameter $\alpha$ causes a displacement of the wave towards the positive side of the $x$-axis while the fractional parameter $\delta$ causes a displacement of the wave towards the negative side of the $x$-axis for both positive and negative solitons, as illustrated in Figures 2–7.

Figure 1

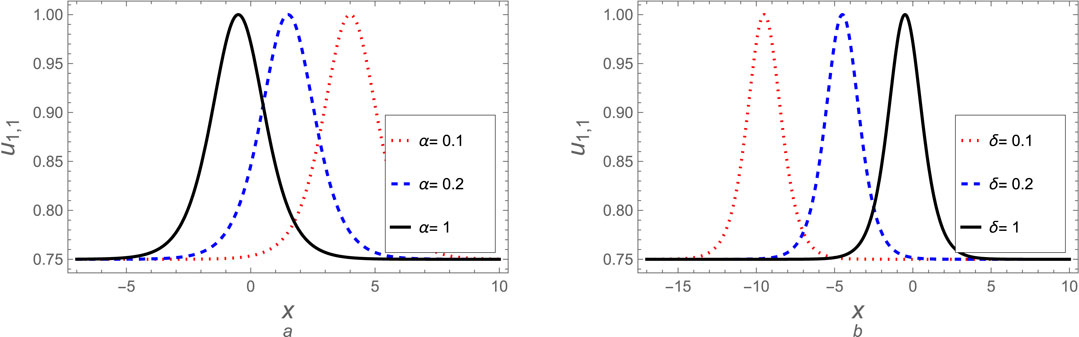
Figure 1. The soliton solution (Equation 19) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 2

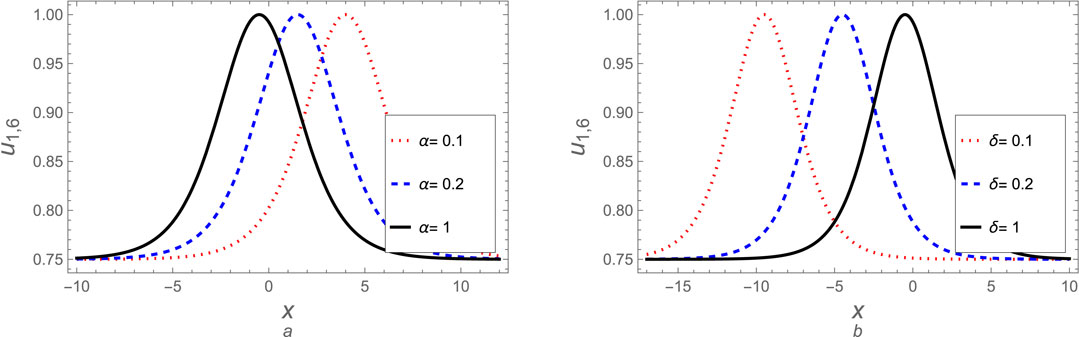
Figure 2. The soliton solution (Equation 24) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=-1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 3

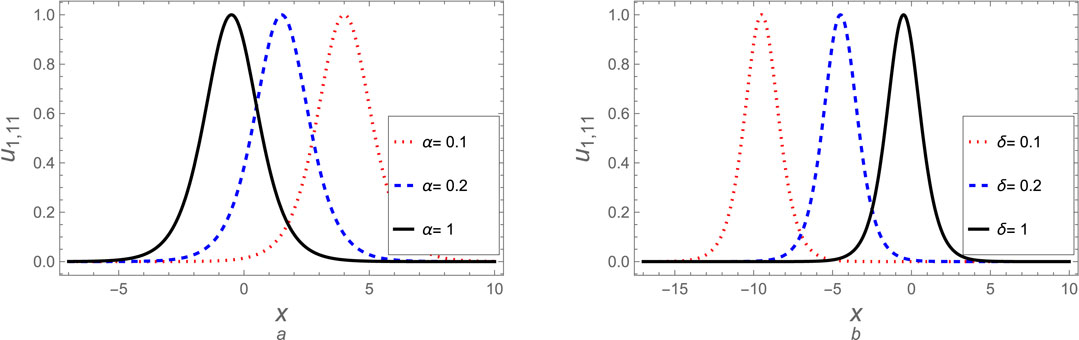
Figure 3. The soliton solution (Equation 29) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 4

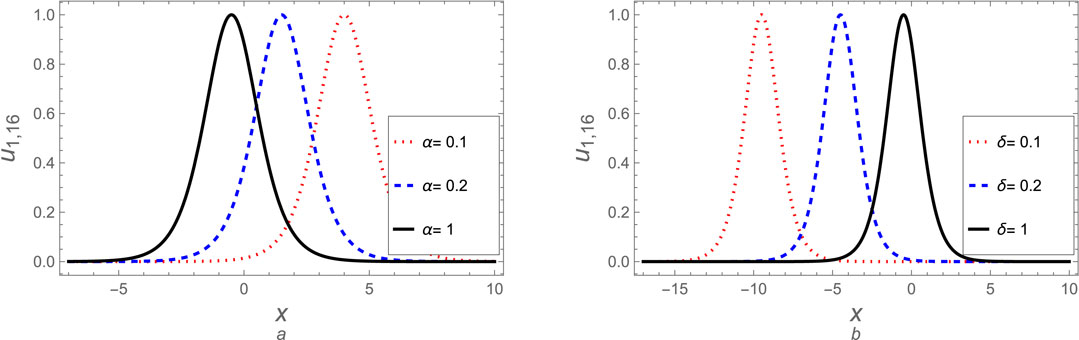
Figure 4. The soliton solution (Equation 34) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=-1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 5

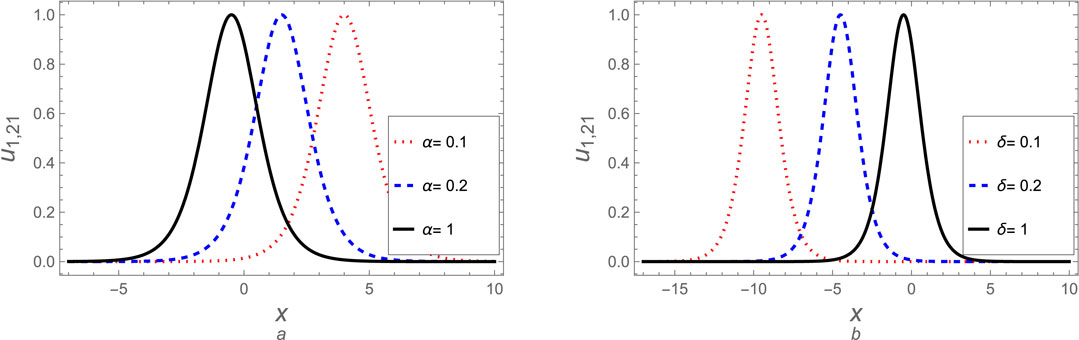
Figure 5. The soliton solution (Equation 39) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 6

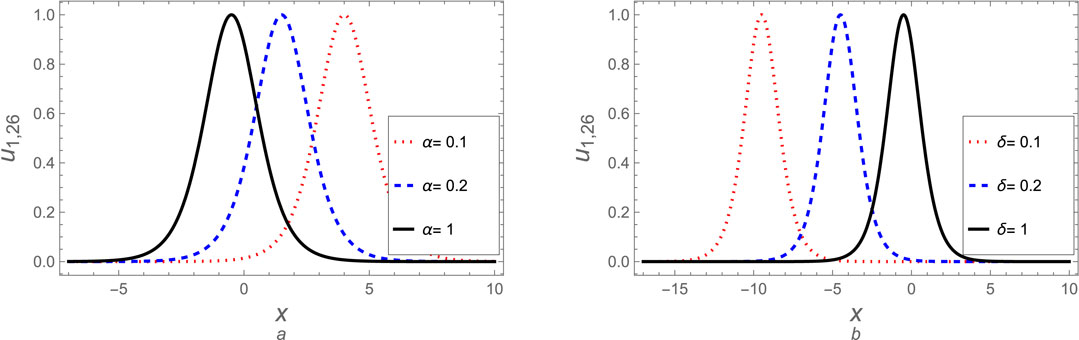
Figure 6. The soliton solution (Equation 44) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=-1,m_0=1$, and $y=1$.

Figure 7

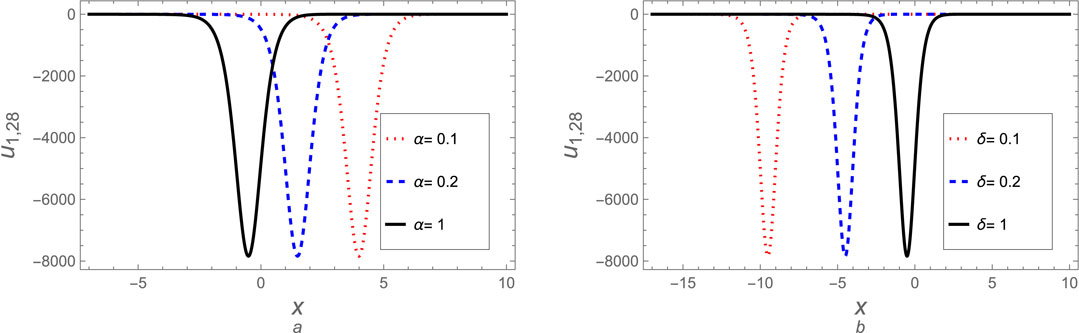
Figure 7. The soliton solution (Equation 46) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=-1,m_0=1$, and $y=1$.

Considering case 2 and using system (14) and corresponding general solutions of Equation 10, suggest the following families of soliton solutions for system (1):

Family 2.1: When $F<0C\ne 0$, we get

$u_{\mathrm{2,1}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(4AC-B^2-3F{\left(\tan \left(1/2\sqrt{-F}\psi \right)\right)}^2\right)}{2AC+B^2},(51)$

$u_{\mathrm{2,2}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(4AC-B^2-3F{\left(\cot \left(1/2\sqrt{-F}\psi \right)\right)}^2\right)}{2AC+B^2},(52)$

$u_{\mathrm{2,3}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(-3F+2F{\left(\cos \left(\sqrt{-F}\psi \right)\right)}^2-6F\sin \left(\sqrt{-F}\psi \right)\sqrt{jl}-3Fjl\right)}{{\left(\cos \left(\sqrt{-F}\psi \right)\right)}^2\left(2AC+B^2\right)},(53)$

$u_{\mathrm{2,4}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(F+2F{\left(\cos \left(\sqrt{-F}\psi \right)\right)}^2+6F\cos \left(\sqrt{-F}\psi \right)\sqrt{jl}+3Fjl\right)}{\left(-1+{\left(\cos \left(\sqrt{-F}\psi \right)\right)}^2\right)\left(2AC+B^2\right)},(54)$

and

$u_{\mathrm{2,5}}\left(x,y,t\right)=\frac{1}{8}\frac{m_0\left(+3F-8F{\left(\cos \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}^2+8F{\left(\cos \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}^4\right)}{{\left(\cos \left(1/4\sqrt{-F}\psi \right)\right)}^2\left(-1+{\left(\cos \left(1/4\sqrt{-F}\psi \right)\right)}^2\right)\left(2AC+B^2\right)},(55)$

Family 2.2: When $F>0C\ne 0$, we get

$u_{\mathrm{2,6}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(4AC-B^2+3F{\left(\tanh \left(1/2\sqrt{F}\psi \right)\right)}^2\right)}{2AC+B^2},(56)$

$u_{\mathrm{2,7}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(4AC-B^2+3F{\left(\coth \left(1/2\sqrt{F}\psi \right)\right)}^2\right)}{2AC+B^2},(57)$

$u_{\mathrm{2,8}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(2F{\left(\cosh \left(\sqrt{F}\psi \right)\right)}^2-3F+6F\sinh \left(\sqrt{F}\psi \right)\sqrt{jl}+3Fjl\right)}{{\left(\cosh \left(\sqrt{F}\psi \right)\right)}^2\left(2AC+B^2\right)},(58)$

$u_{\mathrm{2,9}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left(F+2F{\left(\cosh \left(\sqrt{F}\psi \right)\right)}^2+6F\cosh \left(\sqrt{F}\psi \right)\sqrt{jl}+3Fjl\right)}{\left({\left(\cosh \left(\sqrt{F}\psi \right)\right)}^2-1\right)\left(2AC+B^2\right)},(59)$

and

$u_{\mathrm{2,10}}\left(x,y,t\right)=\frac{1}{8}\frac{m_0\left(4F{\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2-4F{\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^4+3F\right)}{{\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2\left({\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2-1\right)\left(2AC+B^2\right)},(60)$

Family 2.3: When $AC>0$ and $B=0$, we get

$u_{\mathrm{2,11}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cos \left(\sqrt{AC}\psi \right)\right)}^2-3\right)}{{\left(\cos \left(\sqrt{AC}\psi \right)\right)}^2},(61)$

$u_{\mathrm{2,12}}\left(x,y,t\right)=-\frac{m_0\left(1+2{\left(\cos \left(\sqrt{AC}\psi \right)\right)}^2\right)}{-1+{\left(\cos \left(\sqrt{AC}\psi \right)\right)}^2},(62)$

$u_{\mathrm{2,13}}\left(x,y,t\right)=\frac{m_0\left(-2{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2+3+6\sin \left(2\sqrt{AC}\psi \right)\sqrt{jl}+3jl\right)}{{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2},(63)$

$u_{\mathrm{2,14}}\left(x,y,t\right)=-\frac{m_0\left(1+2{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2+6\cos \left(2\sqrt{AC}\psi \right)\sqrt{jl}+3jl\right)}{-1+{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2},(64)$

and

$u_{\mathrm{2,15}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0\left(-8{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^2+8{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^4+3\right)}{{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^2\left(-1+{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^2\right)},(65)$

Family 2.4: When $AC<0$ and $B=0$, we get

$u_{\mathrm{2,16}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(\sqrt{-AC}\psi \right)\right)}^2-3\right)}{{\left(\cosh \left(\sqrt{-AC}\psi \right)\right)}^2},(66)$

$u_{\mathrm{2,17}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(\sqrt{-AC}\psi \right)\right)}^2+1\right)}{{\left(\cosh \left(\sqrt{-AC}\psi \right)\right)}^2-1},(67)$

$u_{\mathrm{2,18}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(2\sqrt{-AC}\psi \right)\right)}^2-3+108\sinh \left(2\sqrt{-AC}\psi \right)\sqrt{jl}+972jl\right)}{{\left(\cosh \left(2\sqrt{-AC}\psi \right)\right)}^2},(68)$

$u_{\mathrm{2,19}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(2\sqrt{-AC}\psi \right)\right)}^2+1+6\cosh \left(2\sqrt{-AC}\psi \right)\sqrt{jl}+3jl\right)}{{\left(\cosh \left(2\sqrt{-AC}\psi \right)\right)}^2-1},(69)$

and

$u_{\mathrm{2,20}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0\left(8{\left(\cosh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^4-8{\left(\cosh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^2+3\right)}{{\left(\cosh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^2\left({\left(\cosh \left(1/2\sqrt{-AC}\psi \right)\right)}^2-1\right)},(70)$

Family 2.5: When $C=A$ and $B=0$, we get

$u_{\mathrm{2,21}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cos \left(A\psi \right)\right)}^2-3\right)}{{\left(\cos \left(A\psi \right)\right)}^2},(71)$

$u_{\mathrm{2,22}}\left(x,y,t\right)=-\frac{m_0\left(1+2{\left(\cos \left(A\psi \right)\right)}^2\right)}{-1+{\left(\cos \left(A\psi \right)\right)}^2},(72)$

$u_{\mathrm{2,23}}\left(x,y,t\right)=\frac{m_0\left(-2{\left(\cos \left(2A\psi \right)\right)}^2+3+6\sin \left(2A\psi \right)\sqrt{jl}+3jl\right)}{{\left(\cos \left(2A\psi \right)\right)}^2},(73)$

$u_{\mathrm{2,24}}\left(x,y,t\right)=-\frac{m_0\left(1+2{\left(\cos \left(2A\psi \right)\right)}^2+6\cos \left(2A\psi \right)\sqrt{jl}+3jl\right)}{-1+{\left(\cos \left(2A\psi \right)\right)}^2},(74)$

and

$u_{\mathrm{2,25}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0\left(-8{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2+8{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^4+3\right)}{{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2\left(-1+{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2\right)},(75)$

Family 2.6: When $C=-A$ and $B=0$, we get

$u_{\mathrm{2,26}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(A\psi \right)\right)}^2-3\right)}{{\left(\cosh \left(A\psi \right)\right)}^2},(76)$

$u_{\mathrm{2,27}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(A\psi \right)\right)}^2+1\right)}{{\left(\cosh \left(A\psi \right)\right)}^2-1},(77)$

$u_{\mathrm{2,28}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(2A\psi \right)\right)}^2-3+168\sinh \left(2A\psi \right)\sqrt{jl}+2352jl\right)}{{\left(\cosh \left(2A\psi \right)\right)}^2},(78)$

$u_{\mathrm{2,29}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cosh \left(2A\psi \right)\right)}^2+1+6\cosh \left(2A\psi \right)\sqrt{jl}+3jl\right)}{{\left(\cosh \left(2A\psi \right)\right)}^2-1},(79)$

and

$u_{\mathrm{2,30}}\left(x,y,t\right)=-\frac{1}{4}\frac{m_0\left(8{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^4-8{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2+3\right)}{{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2\left({\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2-1\right)},(80)$

Family 2.7: When $F=0$, we get

$\begin{array}{l}\hfill u_{\mathrm{2,31}}\left(x,y,t\right)\\ \hfill & =\frac{m_0\left(2B^4{\psi }^{2}AC+B^6{\psi }^2-12CA\left(B\psi +2\right)B^3\psi +24C^2{\left(A\left(B\psi +2\right)\right)}^2\right)}{\left(2AC+B^2\right)B^4{\psi }^2},\hfill \end{array}(81)$

Family 2.8: When $A=0$, $B\ne 0$ and $C\ne 0$, we get

$u_{\mathrm{2,32}}\left(x,y,t\right)=m_0-6\frac{m_{0}j}{\cosh \left(B\psi \right)-\sinh \left(B\psi \right)+l}+6\frac{m_0{j}^2}{{\left(\cosh \left(B\psi \right)-\sinh \left(B\psi \right)+l\right)}^2},(82)$

and

$u_{\mathrm{2,33}}\left(x,y,t\right)=m_0-6\frac{m_0\left(\cosh \left(B\psi \right)+\sinh \left(B\psi \right)\right)}{\cosh \left(B\psi \right)+\sinh \left(B\psi \right)+l}+6\frac{m_0{\left(\cosh \left(B\psi \right)+\sinh \left(B\psi \right)\right)}^2}{{\left(\cosh \left(B\psi \right)+\sinh \left(B\psi \right)+l\right)}^2},(83)$

Family 2.9: When $B=\mu$, $c=z\mu (z\ne 0)$ and $A=0$, we get

$\begin{array}{l}\hfill u_{\mathrm{2,34}}\left(x,y,t\right)\\ \hfill & =\frac{m_0\left(p^2-2pzl{\mathrm{e}}^{\mu \psi }+z^2{l}^2{\mathrm{e}}^{2\mu \psi }+6zj{\mathrm{e}}^{\mu \psi }p-6z^{2}j{\mathrm{e}}^{2\mu \psi }l+6z^2{j}^2{\mathrm{e}}^{2\mu \psi }\right)}{{\left(-p+zl{\mathrm{e}}^{\mu \psi }\right)}^2},\hfill \end{array}(84)$

with

$\psi =\sqrt{-3\frac{m_0}{2AC+B^2}}\left[-\left(\frac{3m_{0}F}{2AC+B^2}\right)\frac{t^{\alpha }}{\alpha }+\frac{x^{\beta }}{\beta }+\frac{y^{\delta }}{\delta }\right].$

Here, we can discuss some derived solutions for case 2. The soliton solutions (Equation 51), (Equation 56), (Equation 66), (Equation 71), and (Equation 76) are discussed graphically at different values for fractional parameters $\alpha$ and $\delta$ as evident in Figures 8–12, respectively. The analysis shows that the fractional parameter $\alpha$ results in a rightward wave shift along the $x$-axis. In contrast, the fractional parameter $\delta$ leads to a leftward wave shift along the $x$-axis, as depicted in Figures 8–12.

Figure 8

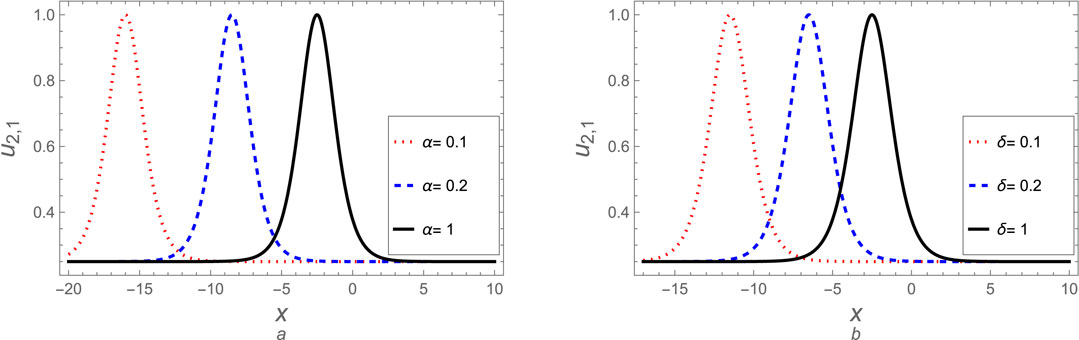
Figure 8. The soliton solution (Equation 51) for case (2) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 9

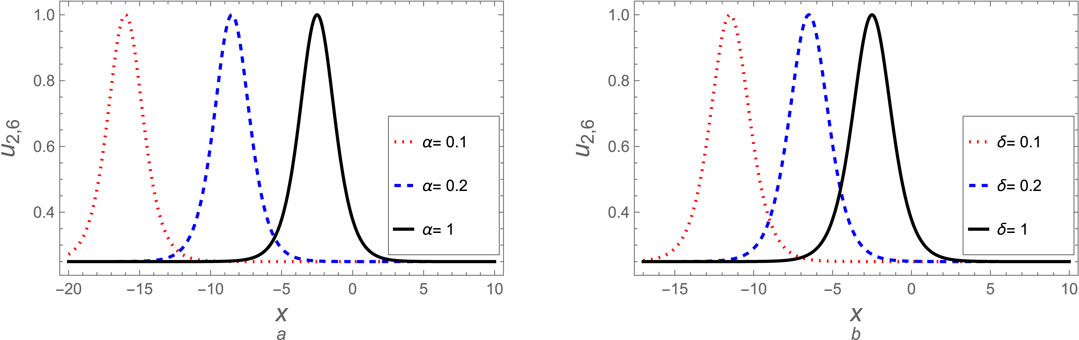
Figure 9. The soliton solution (Equation 56) for case (2) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=-1,m_0=1$, and $y=1$.

Figure 10

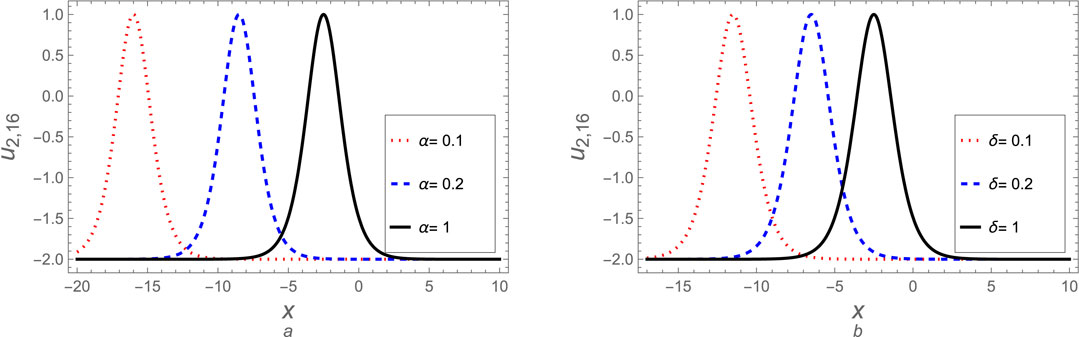
Figure 10. The soliton solution (Equation 66) for case (2) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=-1,m_0=1$, and $y=1$.

Figure 11

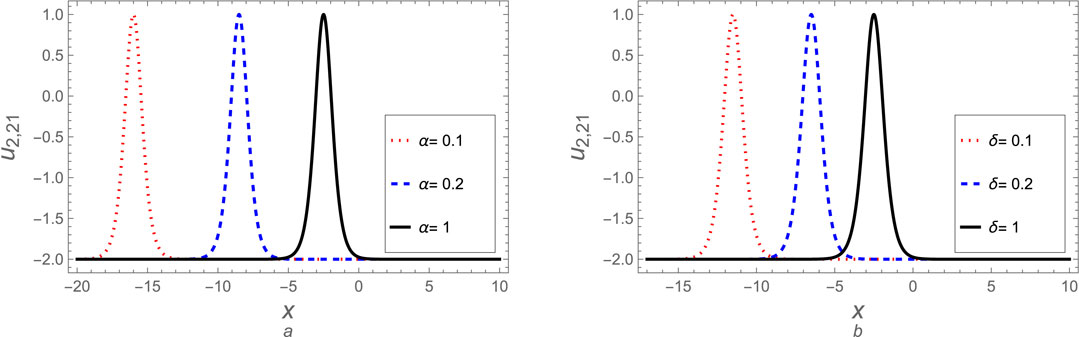
Figure 11. The soliton solution (Equation 71) for case (2) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 12

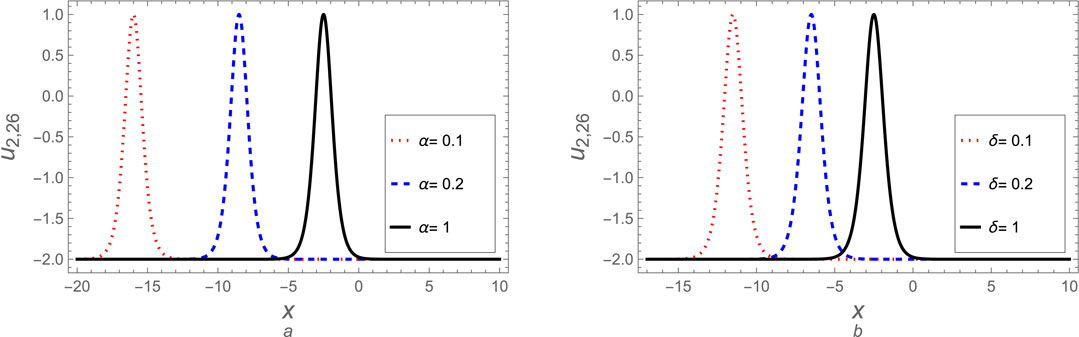
Figure 12. The soliton solution (Equation 76) for case (2) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=-1,m_0=1$, and $y=1$.

Considering case 3 and using system (14) and corresponding general solutions of Equation 10, suggest the following families of soliton solutions for system (1):

Family 3.1: When $F<0$ & $C\ne 0$, we get

$u_{\mathrm{3,1}}\left(x,y,t\right)=\frac{m_0\left[4AC-B^2-F{\left(\tan \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2\right]}{{\left(B-\sqrt{-F}\tan \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2},(85)$

$u_{\mathrm{3,2}}\left(x,y,t\right)=\frac{m_0\left[4AC-B^2-F{\left(\cot \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2\right]}{{\left(B+\sqrt{-F}\cot \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2},(86)$

$\begin{array}{cc}\hfill & u_{\mathrm{3,3}}\left(x,y,t\right)=\frac{A{m}_0}{C{\left[-\frac{1}{2}\frac{B}{C}+\frac{1}{2}\frac{\sqrt{-F}\left(\tan \left(\sqrt{-F}\psi \right)+\sqrt{jl}\sec \left(\sqrt{-F}\psi \right)\right)}{C}\right]}^2}\hfill \\ \hfill & +\frac{B{m}_0}{C\left(-\frac{1}{2}\frac{B}{C}+\frac{1}{2}\frac{\sqrt{-F}\left(\tan \left(\sqrt{-F}\psi \right)+\sqrt{jl}\sec \left(\sqrt{-F}\psi \right)\right)}{C}\right)}+m_0,\hfill \end{array}(87)$

$\begin{array}{cc}\hfill & u_{\mathrm{3,4}}\left(x,y,t\right)=\frac{A{m}_0}{C{\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{-F}\left(\cot \left(\sqrt{-F}\psi \right)+\sqrt{jl}\csc \left(\sqrt{-F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{B{m}_0}{C\left[-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{-F}\left(\cot \left(\sqrt{-F}\psi \right)+\sqrt{jl}\csc \left(\sqrt{-F}\psi \right)\right)}{C}\right]}+m_0,\hfill \end{array}(88)$

and

$\begin{array}{cc}\hfill & u_{\mathrm{3,5}}\left(x,y,t\right)=\frac{A{m}_0}{C{\left(-\frac{1}{2}\frac{B}{C}+\frac{1}{4}\frac{\sqrt{-F}\left(\tan \left(\frac{1}{4}\sqrt{-F}\psi \right)-\cot \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{B{m}_0}{C\left(-\frac{1}{2}\frac{B}{C}+\frac{1}{4}\frac{\sqrt{-F}\left(\tan \left(\frac{1}{4}\sqrt{-F}\psi \right)-\cot \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}{C}\right)}+m_0,\hfill \end{array}(89)$

Family 3.2: When $F>0$ & $C\ne 0$, we get

$u_{\mathrm{3,6}}\left(x,y,t\right)=\frac{m_0\left(4AC-B^2+F{\left(\tanh \left(\frac{1}{2}\sqrt{F}\psi \right)\right)}^2\right)}{{\left(B+\sqrt{F}\tanh \left(\frac{1}{2}\sqrt{F}\psi \right)\right)}^2},(90)$

$u_{\mathrm{3,7}}\left(x,y,t\right)=\frac{m_0\left(4AC-B^2+F{\left(\coth \left(\frac{1}{2}\sqrt{F}\psi \right)\right)}^2\right)}{{\left(B+\sqrt{F}\coth \left(\frac{1}{2}\sqrt{F}\psi \right)\right)}^2},(91)$

$u_{\mathrm{3,8}}\left(x,y,t\right)=\frac{m_0\left(-F+2F\sinh \left(\sqrt{F}\psi \right)\sqrt{jl}+Fjl\right)}{{\left(B\cosh \left(\sqrt{F}\psi \right)+\sqrt{F}\sinh \left(\sqrt{F}\psi \right)+\sqrt{F}\sqrt{jl}\right)}^2},(92)$

$u_{\mathrm{3,9}}\left(x,y,t\right)=\frac{m_0\left(F+2F\cosh \left(\sqrt{F}\psi \right)\sqrt{jl}+Fjl\right)}{{\left(B\sinh \left(\sqrt{F}\psi \right)+\sqrt{F}\cosh \left(\sqrt{F}\psi \right)+\sqrt{F}\sqrt{jl}\right)}^2},(93)$

and

$u_{\mathrm{3,10}}\left(x,y,t\right)=\frac{m_0\left(-4F{\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^4+4F{\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2+F\right)}{{\left[\begin{array}{c}\hfill 2B\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\sinh \left(\frac{1}{4}\sqrt{F}\psi \right)\hfill \\ \hfill +\sqrt{F}{\left(\sinh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2-\sqrt{F}{\left(\cosh \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}^2\hfill \end{array}\right]}^2},(94)$

Family 3.3: When $AC>0$ and $B=0$, we get

$u_{\mathrm{3,11}}\left(x,y,t\right)=\frac{m_0\left(1+{\left(\tan \left(\sqrt{AC}\psi \right)\right)}^2\right)}{{\left(\tan \left(\sqrt{AC}\psi \right)\right)}^2},(95)$

$u_{\mathrm{3,12}}\left(x,y,t\right)=\frac{m_0\left(1+{\left(\cot \left(\sqrt{AC}\psi \right)\right)}^2\right)}{{\left(\cot \left(\sqrt{AC}\psi \right)\right)}^2},(96)$

$u_{\mathrm{3,13}}\left(x,y,t\right)=\frac{m_0\left(1+2\sin \left(2\sqrt{AC}\psi \right)\sqrt{jl}+jl\right)}{1-{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2+2\sin \left(2\sqrt{AC}\psi \right)\sqrt{jl}+jl},(97)$

$u_{\mathrm{3,14}}\left(x,y,t\right)=\frac{m_0\left(1+2\cos \left(2\sqrt{AC}\psi \right)\sqrt{jl}+jl\right)}{{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2+2\cos \left(2\sqrt{AC}\psi \right)\sqrt{jl}+jl},(98)$

and

$u_{\mathrm{3,15}}\left(x,y,t\right)=\frac{m_0}{1-4{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^2+4{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^4},(99)$

Family 3.4: When $AC<0$ and $B=0$, we get

$u_{\mathrm{3,16}}\left(x,y,t\right)=\frac{m_0\left(-1+{\left(\tanh \left(\sqrt{-AC}\psi \right)\right)}^2\right)}{{\left(\tanh \left(\sqrt{-AC}\psi \right)\right)}^2},(100)$

$u_{\mathrm{3,17}}\left(x,y,t\right)=\frac{m_0\left(-1+{\left(\coth \left(\sqrt{-AC}\psi \right)\right)}^2\right)}{{\left(\coth \left(\sqrt{-AC}\psi \right)\right)}^2},(101)$

$u_{\mathrm{3,18}}\left(x,y,t\right)=\frac{m_0\left(-1+36\sinh \left(2\sqrt{-AC}\psi \right)\sqrt{jl}+324jl\right)}{{\left(\sinh \left(2\sqrt{-AC}\psi \right)+18\sqrt{jl}\right)}^2},(102)$

$u_{\mathrm{3,19}}\left(x,y,t\right)=\frac{m_0\left(1+2\cosh \left(2\sqrt{-AC}\psi \right)\sqrt{jl}+jl\right)}{{\left(\cosh \left(2\sqrt{-AC}\psi \right)+\sqrt{jl}\right)}^2},(103)$

and

$u_{\mathrm{3,20}}\left(x,y,t\right)=\frac{m_0}{{\left({\left(\sinh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^2+{\left(\cosh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^2\right)}^2},(104)$

Family 3.5: When $C=A$ and $B=0$, we get

$u_{\mathrm{3,21}}\left(x,y,t\right)=-\frac{m_0}{-1+{\left(\cos \left(A\psi \right)\right)}^2},(105)$

$u_{\mathrm{3,22}}\left(x,y,t\right)=\frac{m_0}{{\left(\cos \left(A\psi \right)\right)}^2},(106)$

$u_{\mathrm{3,23}}\left(x,y,t\right)=\frac{m_0\left(1+2\sin \left(2A\psi \right)\sqrt{jl}+jl\right)}{1-{\left(\cos \left(2A\psi \right)\right)}^2+2\sin \left(2A\psi \right)\sqrt{jl}+jl},(107)$

$u_{\mathrm{3,24}}\left(x,y,t\right)=\frac{m_0\left(-1+2\cos \left(2A\psi \right)\sqrt{jl}-jl\right)}{-{\left(\cos \left(2A\psi \right)\right)}^2+2\cos \left(2A\psi \right)\sqrt{jl}-jl},(108)$

and

$u_{\mathrm{3,25}}\left(x,y,t\right)=\frac{m_0}{1-4{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2+4{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^4},(109)$

Family 3.6: When $C=-A$ and $B=0$, we get

$u_{\mathrm{3,26}}\left(x,y,t\right)=-\frac{m_0}{{\left(\cosh \left(A\psi \right)\right)}^2-1},(110)$

$u_{\mathrm{3,27}}\left(x,y,t\right)=\frac{m_0}{{\left(\cosh \left(A\psi \right)\right)}^2},(111)$

$u_{\mathrm{3,28}}\left(x,y,t\right)=-\frac{m_0\left(1+56\sinh \left(2A\psi \right)\sqrt{jl}-784jl\right)}{{\left(-\sinh \left(2A\psi \right)+28\sqrt{jl}\right)}^2},(112)$

$u_{\mathrm{3,29}}\left(x,y,t\right)=-\frac{m_0\left(-1+2\cosh \left(2A\psi \right)\sqrt{jl}-jl\right)}{{\left(-\cosh \left(2A\psi \right)+\sqrt{jl}\right)}^2},(113)$

and

$u_{\mathrm{3,30}}\left(x,y,t\right)=\frac{m_0}{{\left({\left(\sinh \left(\frac{1}{2}A\psi \right)\right)}^2+{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2\right)}^2},(114)$

Family 3.7: When $F=0$, we get

$u_{\mathrm{3,31}}\left(x,y,t\right)=\frac{1}{4}\frac{m_0\left(A{B}^4{\psi }^2-2B^3\psi A\left(B\psi +2\right)+4C{\left(A\left(B\psi +2\right)\right)}^2\right)}{C{\left(A\left(B\psi +2\right)\right)}^2},(115)$

Family 3.8: When $A=0$, $B\ne 0$ and $C\ne 0$, we get

$u_{\mathrm{3,32}}\left(x,y,t\right)=-\frac{m_0\left(\cosh \left(B\psi \right)-\sinh \left(B\psi \right)+l-j\right)}{j},(116)$

and

$u_{\mathrm{3,33}}\left(x,y,t\right)=-m_{0}l\left(\cosh \left(B\psi \right)-\sinh \left(B\psi \right)\right),(117)$

Family 3.9: When $B=\mu$, $C=z\mu (z\ne 0)$ and $A=0$, we get

$u_{\mathrm{3,34}}\left(x,y,t\right)=\frac{m_0\left({\mathrm{e}}^{-\mu \psi }j-zl+zj\right)}{zj},(118)$

with

$\psi =\frac{1}{2}\sqrt{-2\frac{m_0}{AC}}\left(-\left(\frac{1}{2}\frac{-m_{0}F}{AC}\right)\frac{t^{\alpha }}{\alpha }+\frac{x^{\beta }}{\beta }+\frac{y^{\delta }}{\delta }\right).$

Here, we can explore many derived soliton solutions for case 3. The soliton solutions (Equation 86), (Equation 96), (Equation 101), (Equation 105), and (Equation 111) are visually analyzed for various values to the fractional parameter $\left(\alpha ,\delta \right)$, as depicted in Figures 13–17, respectively. The study indicates that the fractional parameter $\alpha$ causes a displacement of the wave towards the right along the $x$-axis. Conversely, the fractional parameter $\delta$ causes a wave shift towards the left along the $x$-axis.

Figure 13

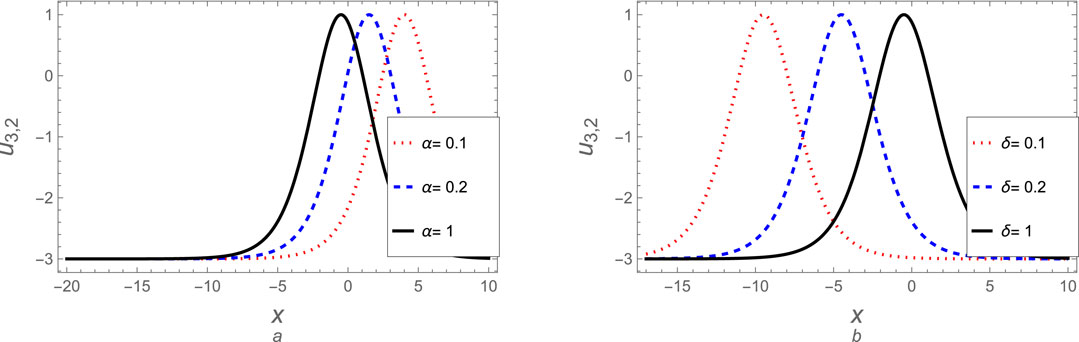
Figure 13. The soliton solution (Equation 86) for case (3) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 14

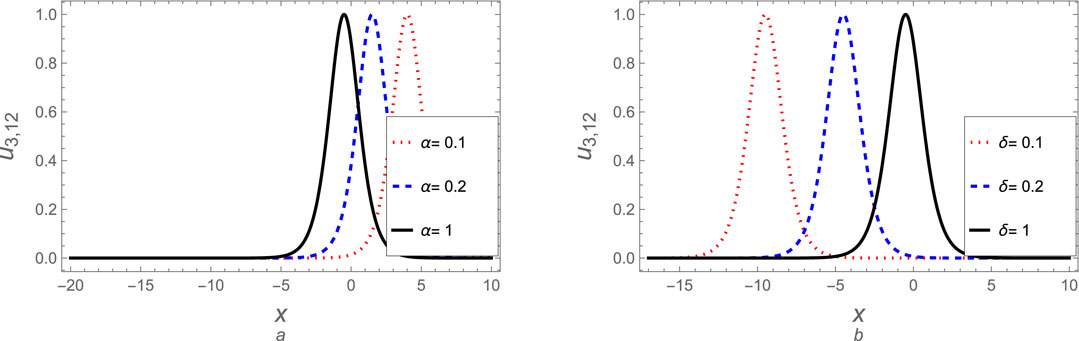
Figure 14. The soliton solution (Equation 96) for case (3) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 15

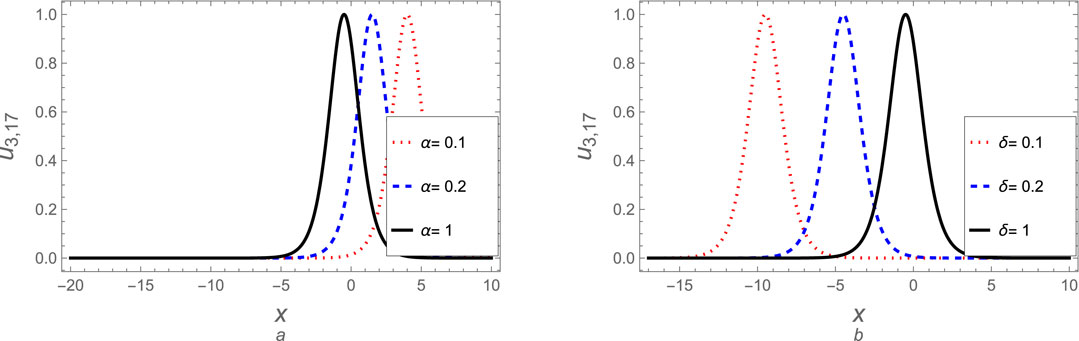
Figure 15. The soliton solution (Equation 101) for case (3) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=-1,m_0=1$, and $y=1$.

Figure 16

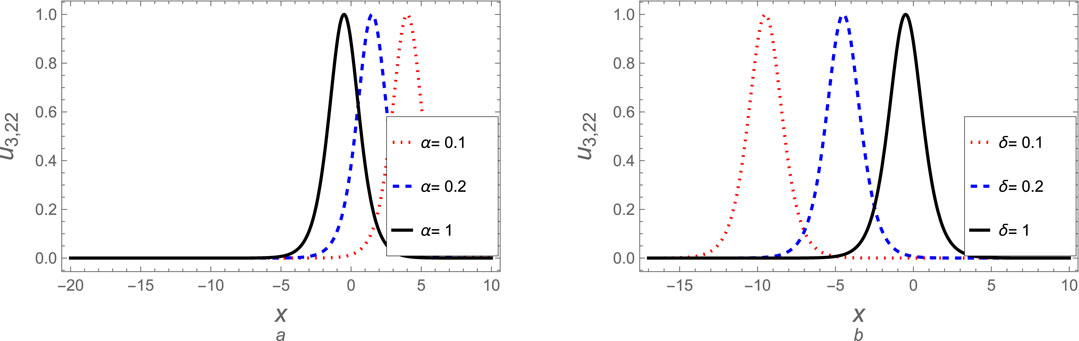
Figure 16. The soliton solution (Equation 105) for case (3) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=1,m_0=1$, and $y=1$.

Figure 17

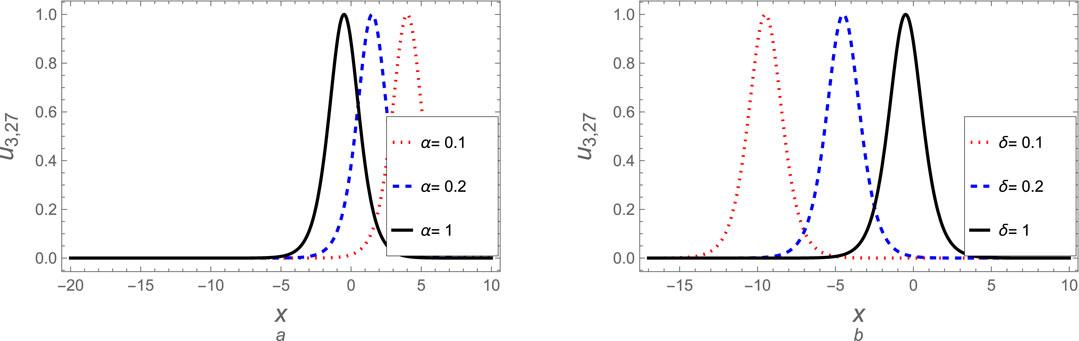
Figure 17. The soliton solution (Equation 111) for case (3) is plotted against (A) the fractional parameter $\alpha$ for $\left(\beta ,\delta \right)=\left(\mathrm{1,1}\right)$ and (B) the fractional parameter $\delta$ for $\left(\alpha ,\beta \right)=\left(\mathrm{1,1}\right)$. Here, $A=1$, $B=0,C=-1,m_0=1$, and $y=1$.

Considering case 4, and using system (14) and corresponding general solutions of Equation 10, suggest the following families of soliton solutions for system (1):

Family 4.1: When $F<0$ & $C\ne 0$, we get

$u_{\mathrm{4,1}}\left(x,y,t\right)=\frac{m_0\left[\begin{array}{c}\hfill 24A^2{C}^2-10A{B}^{2}C-2BF\sqrt{-F}\tan \left(\frac{1}{2}\sqrt{-F}\psi \right)\hfill \\ \hfill -\left(B^2-2ACF\right){\left(\tan \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2+B^4\hfill \end{array}\right]}{\left(2AC+B^2\right){\left(B-\sqrt{-F}\tan \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2},(119)$

$u_{\mathrm{4,2}}\left(x,y,t\right)=\frac{m_0\left[\begin{array}{c}\hfill 24A^2{C}^2-10A{B}^{2}C+B^4+2BF\sqrt{-F}\cot \left(\frac{1}{2}\sqrt{-F}\psi \right)\hfill \\ \hfill -\left(2AC+B^2\right)F{\left(\cot \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2\hfill \end{array}\right]}{\left(2AC+B^2\right){\left(B+\sqrt{-F}\cot \left(\frac{1}{2}\sqrt{-F}\psi \right)\right)}^2},(120)$

$\begin{array}{cc}\hfill & u_{\mathrm{4,3}}\left(x,y,t\right)=\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}+\frac{1}{2}\frac{\sqrt{-F}\left(\tan \left(\sqrt{-F}\psi \right)+\sqrt{jl}\sec \left(\sqrt{-F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{\left(2AC+B^2\right)\left(-\frac{1}{2}\frac{B}{C}+\frac{1}{2}\frac{\sqrt{-F}\left(\tan \left(\sqrt{-F}\psi \right)+\sqrt{jl}\sec \left(\sqrt{-F}\psi \right)\right)}{C}\right)},\hfill \end{array}(121)$

$\begin{array}{cc}\hfill & u_{\mathrm{4,4}}\left(x,y,t\right)=\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{-F}\left(\cot \left(\sqrt{-F}\psi \right)+\sqrt{jl}\csc \left(\sqrt{-F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{\left(2AC+B^2\right)\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{-F}\left(\cot \left(\sqrt{-F}\psi \right)+\sqrt{jl}\csc \left(\sqrt{-F}\psi \right)\right)}{C}\right)}+m_0,\hfill \end{array}(122)$

and

$\begin{array}{cc}\hfill & u_{\mathrm{4,5}}\left(x,y,t\right)=\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}+\frac{1}{4}\frac{\sqrt{-F}\left(\tan \left(\frac{1}{4}\sqrt{-F}\psi \right)-\cot \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{\left(2AC+B^2\right)\left(-\frac{1}{2}\frac{B}{C}+\frac{1}{4}\frac{\sqrt{-F}\left(\tan \left(\frac{1}{4}\sqrt{-F}\psi \right)-\cot \left(\frac{1}{4}\sqrt{-F}\psi \right)\right)}{C}\right)}+m_0,\hfill \end{array}(123)$

Family 4.2: When $F>0\&C\ne 0$, we get

$\begin{array}{ll}\hfill u_{\mathrm{4,6}}\left(x,y,t\right)& =\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\tanh \left(\frac{1}{2}\sqrt{F}\psi \right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{\left(2AC+B^2\right)\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\tanh \left(\frac{1}{2}\sqrt{F}\psi \right)}{C}\right)}+m_0,\hfill \end{array}(124)$

$\begin{array}{ll}\hfill u_{\mathrm{4,7}}\left(x,y,t\right)& =\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\coth \left(\frac{1}{2}\sqrt{F}\psi \right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{\left(2AC+B^2\right)\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\coth \left(\frac{1}{2}\sqrt{F}\psi \right)}{C}\right)}+m_0,\hfill \end{array}(125)$

$\begin{array}{cc}\hfill & u_{\mathrm{4,8}}\left(x,y,t\right)=\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\left(\tanh \left(\sqrt{F}\psi \right)+\sqrt{jl}sech\left(\sqrt{F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{\left(2AC+B^2\right)\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\left(\tanh \left(\sqrt{F}\psi \right)+\sqrt{jl}sech\left(\sqrt{F}\psi \right)\right)}{C}\right)}+m_0,\hfill \end{array}(126)$

$\begin{array}{cc}\hfill & u_{\mathrm{4,9}}\left(x,y,t\right)=\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\left(\coth \left(\sqrt{F}\psi \right)+\sqrt{jl}csch\left(\sqrt{F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{\left(2AC+B^2\right)\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{2}\frac{\sqrt{F}\left(\coth \left(\sqrt{F}\psi \right)+\sqrt{jl}csch\left(\sqrt{F}\psi \right)\right)}{C}\right)}+m_0,\hfill \end{array}(127)$

and

$\begin{array}{cc}\hfill & u_{\mathrm{4,10}}\left(x,y,t\right)=\frac{6m_0{A}^2}{\left(2AC+B^2\right){\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{4}\frac{\sqrt{F}\left(\tanh \left(\frac{1}{4}\sqrt{F}\psi \right)-\coth \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}{C}\right)}^2}\hfill \\ \hfill & +\frac{6m_{0}AB}{{\left(2AC+B^2\right)}^{-1}\left(-\frac{1}{2}\frac{B}{C}-\frac{1}{4}\frac{\sqrt{F}\left(\tanh \left(\frac{1}{4}\sqrt{F}\psi \right)-\coth \left(\frac{1}{4}\sqrt{F}\psi \right)\right)}{C}\right)},\hfill \end{array}(128)$

Family 4.3: When $AC>0$ and $B=0$, we get

$u_{\mathrm{4,11}}\left(x,y,t\right)=\frac{m_0\left(3+{\left(\tan \left(\sqrt{AC}\psi \right)\right)}^2\right)}{{\left(\tan \left(\sqrt{AC}\psi \right)\right)}^2},(129)$

$u_{\mathrm{4,12}}\left(x,y,t\right)=\frac{m_0\left(3+{\left(\cot \left(\sqrt{AC}\psi \right)\right)}^2\right)}{{\left(\cot \left(\sqrt{AC}\psi \right)\right)}^2},(130)$

$u_{\mathrm{4,13}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2+1+2\sin \left(2\sqrt{AC}\psi \right)\sqrt{jl}+jl\right)}{-1+{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2-2\sin \left(2\sqrt{AC}\psi \right)\sqrt{jl}-jl},(131)$

$u_{\mathrm{4,14}}\left(x,y,t\right)=-\frac{m_0\left(-3+2{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2-2\cos \left(2\sqrt{AC}\psi \right)\sqrt{jl}-jl\right)}{{\left(\cos \left(2\sqrt{AC}\psi \right)\right)}^2+2\cos \left(2\sqrt{AC}\psi \right)\sqrt{jl}+jl},(132)$

and

$u_{\mathrm{4,15}}\left(x,y,t\right)=-\frac{m_0\left(-8{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^2+8{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^4-1\right)}{1-4{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^2+4{\left(\cos \left(\frac{1}{2}\sqrt{AC}\psi \right)\right)}^4},(133)$

Family 4.4: When $AC<0$ & $B=0$, we get

$u_{\mathrm{4,16}}\left(x,y,t\right)=\frac{m_0\left(-3+{\left(\tanh \left(\sqrt{-AC}\psi \right)\right)}^2\right)}{{\left(\tanh \left(\sqrt{-AC}\psi \right)\right)}^2},(134)$

$u_{\mathrm{4,17}}\left(x,y,t\right)=\frac{m_0\left(-3+{\left(\coth \left(\sqrt{-AC}\psi \right)\right)}^2\right)}{{\left(\coth \left(\sqrt{-AC}\psi \right)\right)}^2},(135)$

$u_{\mathrm{4,18}}\left(x,y,t\right)=\frac{m_0\left(-2{\left(\cosh \left(2\sqrt{-AC}\psi \right)\right)}^2-1+36\sinh \left(2\sqrt{-AC}\psi \right)\sqrt{jl}+324jl\right)}{{\left(\sinh \left(2\sqrt{-AC}\psi \right)+18\sqrt{jl}\right)}^2},(136)$

$u_{\mathrm{4,19}}\left(x,y,t\right)=\frac{m_0\left(-2{\left(\cosh \left(2\sqrt{-AC}\psi \right)\right)}^2+3+2\cosh \left(2\sqrt{-AC}\psi \right)\sqrt{jl}+jl\right)}{{\left(\cosh \left(2\sqrt{-AC}\psi \right)+\sqrt{jl}\right)}^2},(137)$

and

$u_{\mathrm{4,20}}\left(x,y,t\right)=-\frac{m_0\left(8{\left(\cosh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^4-8{\left(\cosh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^2-1\right)}{{\left({\left(\sinh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^2+{\left(\cosh \left(\frac{1}{2}\sqrt{-AC}\psi \right)\right)}^2\right)}^2},(138)$

Family 4.5: When $C=A$ & $B=0$, we get

$u_{\mathrm{4,21}}\left(x,y,t\right)=-\frac{m_0\left(2{\left(\cos \left(A\psi \right)\right)}^2+1\right)}{-1+{\left(\cos \left(A\psi \right)\right)}^2},(139)$

$u_{\mathrm{4,22}}\left(x,y,t\right)=-\frac{m_0\left(-3+2{\left(\cos \left(A\psi \right)\right)}^2\right)}{{\left(\cos \left(A\psi \right)\right)}^2},(140)$

$u_{\mathrm{4,23}}\left(x,y,t\right)=\frac{m_0\left(2{\left(\cos \left(2A\psi \right)\right)}^2+1+2\sin \left(2A\psi \right)\sqrt{jl}+jl\right)}{1-{\left(\cos \left(2A\psi \right)\right)}^2+2\sin \left(2A\psi \right)\sqrt{jl}+jl},(141)$

$u_{\mathrm{4,24}}\left(x,y,t\right)=\frac{m_0\left(-3+2{\left(\cos \left(2A\psi \right)\right)}^2+2\cos \left(2A\psi \right)\sqrt{jl}-jl\right)}{-{\left(\cos \left(2A\psi \right)\right)}^2+2\cos \left(2A\psi \right)\sqrt{jl}-jl},(142)$

and

$u_{\mathrm{4,25}}\left(x,y,t\right)=-\frac{m_0\left[-8{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2+8{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^4-1\right]}{1-4{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^2+4{\left(\cos \left(\frac{1}{2}A\psi \right)\right)}^4},(143)$

Family 4.6: When $C=-A$ & $B=0$, we get

$u_{\mathrm{4,26}}\left(x,y,t\right)=-\frac{m_0\left[2{\left(\cosh \left(A\psi \right)\right)}^2+1\right]}{{\left(\cosh \left(A\psi \right)\right)}^2-1},(144)$

$u_{\mathrm{4,27}}\left(x,y,t\right)=-\frac{m_0\left[2{\left(\cosh \left(A\psi \right)\right)}^2-3\right]}{{\left(\cosh \left(A\psi \right)\right)}^2},(145)$

$u_{\mathrm{4,28}}\left(x,y,t\right)=-\frac{m_0\left[2{\left(\cosh \left(2A\psi \right)\right)}^2+1+56\sinh \left(2A\psi \right)\sqrt{jl}-784jl\right]}{{\left(\sinh \left(2A\psi \right)-28\sqrt{jl}\right)}^2},(146)$

$u_{\mathrm{4,29}}\left(x,y,t\right)=-\frac{m_0\left[2{\left(\cosh \left(2A\psi \right)\right)}^2-3+2\cosh \left(2A\psi \right)\sqrt{jl}-jl\right]}{{\left(\cosh \left(2A\psi \right)-\sqrt{jl}\right)}^2},(147)$

and

$u_{\mathrm{4,30}}\left(x,y,t\right)=-\frac{m_0\left[8{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^4-8{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2-1\right]}{{\left[{\left(\sinh \left(\frac{1}{2}A\psi \right)\right)}^2+{\left(\cosh \left(\frac{1}{2}A\psi \right)\right)}^2\right]}^2},(148)$

Family 4.7: When $F=0$, we get

$u_{\mathrm{4,31}}\left(x,y,t\right)=\frac{1}{2}\frac{m_0\left[\begin{array}{c}\hfill 3A^2{B}^4{\psi }^2-6A{B}^3\psi A\left(B\psi +2\right)\hfill \\ \hfill +4{\left(A\left(B\psi +2\right)\right)}^{2}AC+2{\left(A\left(B\psi +2\right)\right)}^2{B}^2\hfill \end{array}\right]}{\left(2AC+B^2\right){\left(A\left(B\psi +2\right)\right)}^2},(149)$

Family 4.8: When $B=\mu$, $A=z\mu (z\ne 0)$ and $C=0$,

$u_{\mathrm{4,32}}\left(x,y,t\right)=\frac{m_0\left(z^2+4z{\mathrm{e}}^{\mu \psi }+{\mathrm{e}}^{2\mu \psi }\right)}{{\left({\mathrm{e}}^{\mu \psi }-z\right)}^2},(150)$

with

$\psi =\sqrt{-3\frac{m_0}{2AC+B^2}}\left[-\left(\frac{3m_{0}F}{2AC+B^2}\right)\frac{t^{\alpha }}{\alpha }+\frac{x^{\beta }}{\beta }+\frac{y^{\delta }}{\delta }\right].$

4 Conclusion

In this work, the ground-breaking modified extended direct algebraic method (mEDAM) has been used to thoroughly analyze the (2 + 1)-dimensional fractional asymmetric Nizhnik-Novikov-Veselov system (FANNVS). Based on the proposed method, four different cases/criteria for the parameters related to solutions of FANNVS have been obtained. Several families of soliton-type solutions and other physical solutions have been derived according to each mentioned case. The graphical analysis of the derived solitons was conducted to comprehend their propagation methods and attributes, focusing on the changes in the soliton profiles against the fractional parameters. Also, graphical representations demonstrated the dynamic character of these solitons. Our study has shown various soliton solutions that may contribute to understanding some of the mysterious phenomena that arise in various fluid mediums. Our research clarifies the behavior of FANNVS solitons and highlights the mEDAM method’s effectiveness in resolving complex nonlinear systems. Our study broadens the applicability of the mEDAM technique to nonlinear systems. It considerably advances our understanding of soliton processes in the (2 + 1)-dimensional FANNVS, opening up new opportunities for scientific and engineering fields and understanding the behavior of many nonlinear waves propagating in fluid mediums.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

HY: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Writing–original draft. AA: Investigation, Methodology, Project administration, Resources, Writing–review and editing. MA: Project administration, Software, Supervision, Visualization, Writing–review and editing. RS: Writing–original draft, Writing–review and editing. SE-T: Conceptualization, Data curation, Formal Analysis, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R378), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU242283).

Acknowledgments

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R378), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU242283).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tarasov VE, Zaslavsky GM. Fractional dynamics of systems with long-range interaction. Commun Nonlinear Sci Numer Simulation (2006) 11(8):885–98. doi:10.1016/j.cnsns.2006.03.005

CrossRef Full Text | Google Scholar

2. Mendes EM, Salgado GH, Aguirre LA. Numerical solution of Caputo fractional differential equations with infinity memory effect at initial condition. Commun Nonlinear Sci Numer Simulation (2019) 69:237–47. doi:10.1016/j.cnsns.2018.09.022

CrossRef Full Text | Google Scholar

3. F Brambila, editor. Fractal analysis: applications in physics, engineering and technology. InTech: BoD–Books on Demand (2017). doi:10.5772/65531

CrossRef Full Text | Google Scholar

4. Owolabi KM, Atangana A, Akgul A. Modelling and analysis of fractal-fractional partial differential equations: application to reaction-diffusion model. Alexandria Eng J (2020) 59(4):2477–90. doi:10.1016/j.aej.2020.03.022

CrossRef Full Text | Google Scholar

5. Magin RL, Ingo C, Colon-Perez L, Triplett W, Mareci TH. Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy. Microporous Mesoporous Mater (2013) 178:39–43. doi:10.1016/j.micromeso.2013.02.054

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Adel M, Baleanu D, Sadiya U, Arefin MA, Uddin MH, Elamin MA, et al. Inelastic soliton wave solutions with different geometrical structures to fractional order nonlinear evolution equations. Results Phys (2022) 38:105661. doi:10.1016/j.rinp.2022.105661

CrossRef Full Text | Google Scholar

7. Xu M, Tan W. Intermediate processes and critical phenomena: theory, method and progress of fractional operators and their applications to modern mechanics. Sci China Ser G (2006) 49:257–72. doi:10.1007/s11433-006-0257-2

CrossRef Full Text | Google Scholar

8. Obalalu AM. Chemical entropy generation and second-order slip condition on hydrodynamic Casson nanofluid flow embedded in a porous medium: a fast convergent method. J Egypt Math Soc (2022) 30(1):6. doi:10.1186/s42787-022-00140-3

CrossRef Full Text | Google Scholar

9. Kumar D, Singh J, Al Qurashi M, Baleanu D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv Difference Equations (2019) 2019(1):278–19. doi:10.1186/s13662-019-2199-9

CrossRef Full Text | Google Scholar

10. Alam LMB, Xingfang J, Ananna SN. Investigation of lump, soliton, periodic, kink, and rogue waves to the time-fractional phi-four and (2+ 1) dimensional CBS equations in mathematical physics. Partial Differential Equations Appl Mathematics (2021) 4:100122. doi:10.1016/j.padiff.2021.100122

CrossRef Full Text | Google Scholar

11. Arqub OA, El-Ajou A, Momani S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J Comput Phys (2015) 293:385–99. doi:10.1016/j.jcp.2014.09.034

CrossRef Full Text | Google Scholar

12. Yu GF, Tam HW. A vector asymmetrical NNV equation: soliton solutions, bilinear Bäcklund transformation and Lax pair. J Math Anal Appl (2008) 344(2):593–600. doi:10.1016/j.jmaa.2008.02.057

CrossRef Full Text | Google Scholar

13. Matveev VB, Salle MA Darboux transformations and solitons, 17. Berlin: Springer (1991).

Google Scholar

14. Ablowitz MJ, Clarkson PA Solitons, nonlinear evolution equations and inverse scattering, 149. Cambridge University Press (1991). doi:10.1017/CBO9780511623998

CrossRef Full Text | Google Scholar

15. Osman MS. Nonlinear interaction of solitary waves described by multi-rational wave solutions of the (2+ 1)-dimensional Kadomtsev–Petviashvili equation with variable coefficients. Nonlinear Dyn (2017) 87(2):1209–16. doi:10.1007/s11071-016-3110-9

CrossRef Full Text | Google Scholar

16. Khan H, Barak S, Kumam P, Arif M. Analytical solutions of fractional Klein-Gordon and gas dynamics equations, via the (G/G)-expansion method. Symmetry (2019) 11(4):566. doi:10.3390/sym11040566

CrossRef Full Text | Google Scholar

17. Khan H, Baleanu D, Kumam P, Al-Zaidy JF. Families of travelling waves solutions for fractional-order extended shallow water wave equations, using an innovative analytical method. IEEE Access (2019) 7:107523–32. doi:10.1109/ACCESS.2019.2933188

CrossRef Full Text | Google Scholar

18. Wazwaz A-M. The extended tanh method for the zakharov-kuznetsov (ZK) equation, the modified ZK equation, and its generalized forms. Commun Nonlinear Sci Numer Simul (2008) 13(6):1039–47. doi:10.1016/j.cnsns.2006.10.007

CrossRef Full Text | Google Scholar

19. Wazwaz A-M. The tanh method for traveling wave solutions of nonlinear equations. Appl Mathematics Comput (2004) 154(3):713–23. doi:10.1016/s0096-3003(03)00745-8

CrossRef Full Text | Google Scholar

20. Wazwaz A-M. Partial differential equations and solitary waves theory. Berlin: Springer (2009).

Google Scholar

21. Yasmin H, Aljahdaly NH, Saeed AM, Shah R. Investigating families of soliton solutions for the complex structured coupled fractional biswas–arshed model in birefringent fibers using a novel analytical technique. Fractal and Fractional (2023) 7(7):491. doi:10.3390/fractalfract7070491

CrossRef Full Text | Google Scholar

22. Yasmin H, Aljahdaly NH, Saeed AM, Shah R. Probing families of optical soliton solutions in fractional perturbed radhakrishnan–kundu–lakshmanan model with improved versions of extended direct algebraic method. Fractal and Fractional (2023) 7(7):512. doi:10.3390/fractalfract7070512

CrossRef Full Text | Google Scholar

23. Naeem M, Yasmin H, Shah R, Shah NA, Chung JD. A comparative study of fractional partial differential equations with the help of yang transform. Symmetry (2023) 15(1):146. doi:10.3390/sym15010146

CrossRef Full Text | Google Scholar

24. Naeem M, Yasmin H, Shah R, Shah NA, Nonlaopon K. Investigation of fractional nonlinear regularized long-wave models via novel techniques. Symmetry (2023) 15(1):220. doi:10.3390/sym15010220

CrossRef Full Text | Google Scholar

25. Yasmin H, Abu Hammad MM, Shah R, Alotaibi BM, Ismaeel SM, El-Tantawy SA. On the solutions of the fractional-order sawada–kotera–ito equation and modeling nonlinear structures in fluid mediums. Symmetry (2023) 15(3):605. doi:10.3390/sym15030605

CrossRef Full Text | Google Scholar

26. Yasmin H, Alshehry AS, Saeed AM, Shah R, Nonlaopon K. Application of the q-homotopy analysis transform method to fractional-order Kolmogorov and rosenau–hyman models within the atangana–baleanu operator. Symmetry (2023) 15(3):671. doi:10.3390/sym15030671

CrossRef Full Text | Google Scholar

27. Alshehry AS, Yasmin H, Ghani F, Shah R, Nonlaopon K. Comparative analysis of advection–dispersion equations with atangana–baleanu fractional derivative. Symmetry (2023) 15(4):819. doi:10.3390/sym15040819

CrossRef Full Text | Google Scholar

28. Alber MS, Camassa R, Holm DD, Marsden JE. On the link between umbilic geodesics and soliton solutions of nonlinear PDEs. Proc R Soc Lond Ser A: Math Phys Sci (1995) 450(1940):677–92. doi:10.1098/rspa.1995.0107

CrossRef Full Text | Google Scholar

29. Iqbal MS, Seadawy AR, Baber MZ. Demonstration of unique problems from Soliton solutions to nonlinear Selkov–Schnakenberg system. Chaos, Solitons and Fractals (2022) 162:112485. doi:10.1016/j.chaos.2022.112485

CrossRef Full Text | Google Scholar

30. Hereman W, Nuseir A. Symbolic methods to construct exact solutions of nonlinear partial differential equations. Mathematics Comput Simulation (1997) 43(1):13–27. doi:10.1016/s0378-4754(96)00053-5

CrossRef Full Text | Google Scholar

31. Ma WX. Lump solutions to the kadomtsev–petviashvili equation. Phys Lett A (2015) 379(36):1975–8. doi:10.1016/j.physleta.2015.06.061

CrossRef Full Text | Google Scholar

32. Zhao Z, Chen Y, Han B. Lump soliton, mixed lump stripe and periodic lump solutions of a (2+ 1)-dimensional asymmetrical Nizhnik–Novikov–Veselov equation. Mod Phys Lett B (2017) 31(14):1750157. doi:10.1142/s0217984917501573

CrossRef Full Text | Google Scholar

33. Yang JY, Ma WX. Lump solutions to the BKP equation by symbolic computation. Int J Mod Phys B (2016) 30(28n29):1640028. doi:10.1142/s0217979216400282

CrossRef Full Text | Google Scholar

34. Wazwaz A-M. Compacton solutions of the Kawahara-type nonlinear dispersive equation. Appl Math Comput (2003) 145:133–50. doi:10.1016/s0096-3003(02)00474-5

CrossRef Full Text | Google Scholar

35. Wazwaz A-M. New solitary wave solutions to the Kuramoto-Sivashinsky and the Kawahara equations. Appl Math Comput (2006) 182:1642–50. doi:10.1016/j.amc.2006.06.002

CrossRef Full Text | Google Scholar

36. Kashkari BS, El-Tantawy SA. Homotopy perturbation method for modeling electrostatic structures in collisional plasmas. Eur Phys J Plus (2021) 136:121. doi:10.1140/epjp/s13360-021-01120-9

CrossRef Full Text | Google Scholar

37. El-Tantawy SA. Nonlinear dynamics of soliton collisions in electronegative plasmas: the phase shifts of the planar KdV-and mkdV-soliton collisions. Chaos, Solitons and Fractals (2016) 93:162–8. doi:10.1016/j.chaos.2016.10.011

CrossRef Full Text | Google Scholar

38. Wazwaz A-M. Partial differential equations and solitary waves theory. Beijing, USA: Higher Education Press (2009).

Google Scholar

39. Wazwaz A-M. Partial differential equations: methods and applications. Lisse: Balkema (2002). cop.

Google Scholar

40. Kashkari BS, El-Tantawy SA, Salas AH, El-Sherif LS. Homotopy perturbation method for studying dissipative nonplanar solitons in an electronegative complex plasma. Chaos, Solitons and Fractals (2020) 130:109457. doi:10.1016/j.chaos.2019.109457

CrossRef Full Text | Google Scholar

41. Hossen MB, Roshid HO, Ali MZ. Multi-soliton, breathers, lumps and interaction solution to the (2+ 1)-dimensional asymmetric Nizhnik-Novikov-Veselov equation. Heliyon (2019) 5(10):e02548. doi:10.1016/j.heliyon.2019.e02548

PubMed Abstract | CrossRef Full Text | Google Scholar

42. El-Tantawy SA, Wazwaz A-M, Schlickeiser R. Solitons collision and freak waves in a plasma with Cairns-Tsallis particle distributions. Plasma Phys Control Fusion (2015) 57:125012. doi:10.1088/0741-3335/57/12/125012

CrossRef Full Text | Google Scholar

43. Albalawi W, El-Tantawy SA, Salas AH. On the rogue wave solution in the framework of a Korteweg–de Vries equation. Results Phys (2021) 30:104847. doi:10.1016/j.rinp.2021.104847

CrossRef Full Text | Google Scholar

44. Shan Tariq M, Masood W, Siddiq M, Asghar S, Alotaibi BM, Sherif ME, et al. Bäcklund transformation for analyzing a cylindrical Korteweg–de Vries equation and investigating multiple soliton solutions in a plasma. Phys Fluids (2023) 35:103105. doi:10.1063/5.0166075

CrossRef Full Text | Google Scholar

45. Wazwaz A-M, Alhejaili W, El-Tantawy SA. Study on extensions of (modified) Korteweg–de Vries equations: painlevé integrability and multiple soliton solutions in fluid mediums. Phys Fluids (2023) 35:093110. doi:10.1063/5.0169733

CrossRef Full Text | Google Scholar

46. Aljahdaly NH, El-Tantawy SA. Simulation study on nonlinear structures in nonlinear dispersive media. Chaos (2020) 30:053117. doi:10.1063/1.5132557

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Kashkari BS, El-Tantawy SA. Homotopy perturbation method for modeling electrostatic structures in collisional plasmas. Eur Phys J Plus (2021) 136:121. doi:10.1140/epjp/s13360-021-01120-9

CrossRef Full Text | Google Scholar

48. El-Tantawy SA, Salas AH, Alharthi MR. Novel analytical cnoidal and solitary wave solutions of the Extended Kawahara equation. Chaos Solitons Fractals (2021) 147:110965. doi:10.1016/j.chaos.2021.110965

CrossRef Full Text | Google Scholar

49. Alyousef HA, Salas AH, Alharthi MR, El-tantawy SA. New periodic and localized traveling wave solutions to a kawahara-type equation: applications to plasma physics. Complexity (2022) 2022:9942267. doi:10.1155/2022/9942267

CrossRef Full Text | Google Scholar

50. Alharthi MR, Alharbey RA, El-Tantawy SA. Novel analytical approximations to the nonplanar Kawahara equation and its plasma applications. Eur Phys J Plus (2022) 137:1172. doi:10.1140/epjp/s13360-022-03355-6

CrossRef Full Text | Google Scholar

51. El-Tantawy SA, El-Sherif LS, Bakry AM, Alhejaili W, Wazwaz A-M. On the analytical approximations to the nonplanar damped Kawahara equation: cnoidal and solitary waves and their energy. Phys Fluids (2022) 34:113103. doi:10.1063/5.0119630

CrossRef Full Text | Google Scholar

52. El-Tantawy SA, Salas AH, Alyouse HA, Alharthi MR. Novel exact and approximate solutions to the family of the forced damped Kawahara equation and modeling strong nonlinear waves in a plasma. Chin J Phys (2022) 77:2454–71. doi:10.1016/j.cjph.2022.04.009

CrossRef Full Text | Google Scholar

53. Alyousef HA, Salas AH, Matoog RT, El-Tantawy SA. On the analytical and numerical approximations to the forced damped Gardner Kawahara equation and modeling the nonlinear structures in a collisional plasma. Phys Fluids (2022) 34:103105. doi:10.1063/5.0109427

CrossRef Full Text | Google Scholar

54. Irshad M, Ur-Rahman A, Khalid M, Khan S, Alotaibi BM, El-Sherif LS, et al. Effect of-deformed Kaniadakis distribution on the modulational instability of electron-acoustic waves in a non-Maxwellian plasma. Phys Fluids (2023) 35:105116. doi:10.1063/5.0171327

CrossRef Full Text | Google Scholar

55. Ali Shan S, El-Tantawy SA. The impact of positrons beam on the propagation of super freak waves in electron-positron-ion plasmas. Phys Plasmas (2016) 23:072112. doi:10.1063/1.4958315

CrossRef Full Text | Google Scholar

56. El-Tantawy SA, Aboelenen T. Simulation study of planar and nonplanar super rogue waves in an electronegative plasma: local discontinuous Galerkin method. Phys Plasmas (2017) 24:052118. doi:10.1063/1.4983327

CrossRef Full Text | Google Scholar

57. El-Tantawy SA, Salas AH, Alharthi MR. On the analytical and numerical solutions of the linear damped NLSE for modeling dissipative freak waves and breathers in nonlinear and dispersive mediums: an application to a pair-ion plasma. Front Phys (2021) 9:580224. doi:10.3389/fphy.2021.580224

CrossRef Full Text | Google Scholar

58. Osman MS. Multiwave solutions of time-fractional (2 + 1)-dimensional nizhnik–novikov–veselov equations. Pramana (2017) 88(4):67. doi:10.1007/s12043-017-1374-3

CrossRef Full Text | Google Scholar

59. Sagar B, Saha Ray S. Numerical soliton solutions of fractional (2+ 1)-dimensional Nizhnik–Novikov–Veselov equations in nonlinear optics. Int J Mod Phys B (2021) 35(06):2150090. doi:10.1142/s0217979221500909

CrossRef Full Text | Google Scholar

60. Liu Y, Yan L. Solutions of fractional Konopelchenko-Dubrovsky and Nizhnik-Novikov-Veselov equations using a generalized fractional subequation method. (2013). p. 1–7. Abstract Appl Anal, doi:10.1155/2013/839613

CrossRef Full Text | Google Scholar

61. Sarikaya MZ, Budak H, Usta H. On generalized the conformable fractional calculus. TWMS J Appl Eng Mathematics (2019) 9(4):792–9.

Google Scholar