On scaling of proton- boron fusion power in a nanosecond vacuum discharge

In this paper, we present the results of further PiC simulations in the full electromagnetic code of the processes leading to the proton-boron reactions in a single device for plasma confinement, based on miniature nanosecond vacuum discharge (NVD) in a cylindrical geometry. In particular, we present and discuss in more detail the α particle output for the real electrodes geometry used in the first aneutronic proton–boron fusion experiments with NVD. It follows from them that the total yield of α particles was accumulated in the initial experiments due to only single head-on converging of protons and boron ions accelerated in a very narrow potential well to the discharge axis. Further, in search of the ways for optimizing of proton–boron fusion in NVD, we study the scaling of fusion power depending on the size of the virtual cathode (or the inner radius of the anode space). The results of the PiC simulations by KARAT code show that the number of the proton-boron reactions at anode space of NVD increases with the anode volume grow, and the α particles output turns out to be proportional to the value of anode radius in the range R_A ≈ 0.1–0.5 cm. However, the number of proton-boron reactions reaches some saturation under R_A growing at the fixed time of high voltage applied and value of the energy input. In general, the formation of a more voluminous potential well (wider in radius and extended along the discharge axis), with well–defined oscillations of protons and boron ions in it, provides a noticeable increase in the output of α particles.

1 Introduction

Discovered back in the 30s of the last century [1, 2], the aneutronic proton–boron (pB) nuclear reaction p + ¹¹B → α + ⁸Be* → 3α + 8.7 MeV with the yield of almost only α particles attracts increasing both fundamental and applied interest in our time. The reason for this is not only the very exorbitant options for producing “clean” energy based on it, which could really be facilitated by the almost absence of neutrons, the possibility of direct conversion of the energy of α particles into electricity (bypassing the thermal cycle), the technological simplicity of a possible pB fusion reactor [3]. There is also a growing modern practical need for simple and reliable sources of α particles for nuclear medicine, materials science and electronics: the development of rare isotopes and medically important radionuclides, the development of alpha-voltaic converters, the study of radiation resistance of nanoscale semiconductor devices of a new generation, and other interdisciplinary applications, including aerospace [4–8]. However, the yield of the pB reaction can become noticeable only at significantly higher particle energies than is necessary for known DT or DD synthesis reactions [9]. Starting with the pioneering work of V. S. Belyaev and his colleagues in 2005 [10], the pB reaction was observed further only in experiments where laser action on boron-containing targets was somehow presented. It should be noted that great progress has been made in recent years in the study of laser–driven aneutronic pB fusion, and in increasing the yield of α particles was registered in experiments (see [11–17] and references herein).

In addition to the existing and actively developing various laser schemes, the implementation of the pB reaction in a single plasma confinement device, without external action of laser or proton beams on a boron target, is also of undoubted interest. In particular, after many years of work, pB fusion under magnetic plasma confinement, including injection of boron powder and high-energy hydrogen beams, was only recently obtained for the first time [18]. Somewhat earlier, we demonstrated pB fusion with electrodynamic plasma confinement by the field of a virtual cathode in a nanosecond vacuum discharge (NVD) [19]. In a miniature NVD of cylindrical geometry with a hollow cathode, a well-known inertial electrostatic confinement (IEC) scheme was implemented [20, 21], but with reverse polarity [22]. In this scheme, PiC modeling in the KARAT electromagnetic code [23] revealed the formation of a virtual cathode (VC) and a corresponding potential well (PW) with a depth of about 100 kV in the anode space of the NVD. It is formed when a high voltage pulse is applied to the discharge and an automatic radial injection of electrons into the anode space takes place. As a result, a quasi-stationary potential well with a size of several millimeters arising there plays the role of a micro-accelerator of protons and boron ions to energies of hundreds of keV, when the output of the pB reaction in the range of particle energies near the secondary resonance (≈150 keV) becomes already noticeable [9]. In the process of ion oscillations in potential well, head-on collisions of a part of protons and boron ions with energies of ∼100–500 keV lead to the proton–boron reactions and the appearance of α particles [19].

Previously, for a similar confinement scheme, nuclear DD synthesis with a yield of 2.45 MeV neutrons as a result of head-on collisions of deuterons with energies of 50–100 keV at the “bottom” of the PW near the discharge axis was studied numerically and experimentally in detail [24–27]. Periodic oscillations of deuterons in a potential well were accompanied in the experiment by a pulsating output of DD neutrons [27]. A favorable scaling of the DD fusion power was also confirmed [28], which increased with a decrease in the size of the VC, similar to predicted earlier for fusion scaling in the scheme of periodically oscillating plasma spheres [29, 30]. In the paper [19], the results of the first experiments on registering the output of α particles from the proton–boron reaction in the NVD plasma were presented. The experiments were preceded by detailed PiC modeling in the electromagnetic code [23] of all the processes accompanying the pB reactions, which, in particular, revealed the oscillatory nature of ions confinement in the potential well of the NVD.

In the present work, we would like to detail the previous results of PiC simulations of the pB fusion, and pay attention to specifics of the generation of α particles in demonstration experiments on aneutronic proton-boron fusion in one miniature device [19] without any external influence from a laser or a proton beam. Further, in search of an algorithm for optimizing of pB fusion in NVD, we considering a more general problem. In particular, by analogy with DD fusion in oscillating plasmas, we turn to the study of the scaling for pB fusion power by the size of the virtual cathode. Based on simulation data for the numbers of pB reactions under different values of the anode radius and other discharge parameters in a cylindrical NVD, we are coming to certain conclusions on the scaling of the pB fusion power. The results obtained are discussed in detail and compared with the scaling of DD fusion in oscillating plasmas.

2 PiC simulation of proton–boron fusion for anode-cathode geometry in a real experiment

Earlier, PiC modeling revealed the optimal geometry of the electrodes for the maximum yield of α particles from the proton-boron reaction during oscillatory plasma confinement in the NVD [19]. The corresponding PiC simulation results for the energy of oscillating ions, the emerging potential well and the yield of α particles (in arbitrary units,a.u.) are shown in Figure 1 in [19]. It was also specifically noted there that the first experiment on pB fusion at low energy vacuum discharge was conducted far from optimal calculated anode–cathode (A–C) geometries. Below at this Section, we present and discuss the results of PiC simulations in the KARAT code of the main electrodynamic processes leading to pB synthesis for the real A–C geometry used in the experiment [19]. Looking forward, this geometry was far from optimal for the good output of α particles in NVD, but it turned out to be convenient for filling with boron at that stage of the experiment development.

Figure 1

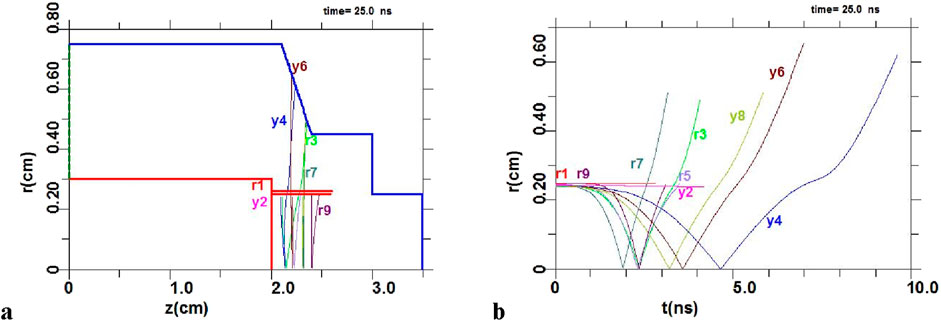
Figure 1. (A) Real geometry of the anode (red)– cathode (blue) used in the experiment on pB fusion at nanosecond vacuum discharge (NVD) [19]. The anode Pd “tube,” perpendicular to the base of the anode, is “filled” with hydrogen and boron under 2D PiC simulations [23, 28]. The trajectories of the selected groups of protons (index r) and boron ions (y) in the interelectrode space are shown; (B) The dynamics of the selected groups of protons and boron ions (with charge Z_B = +3) along the radius in the anode space in time is shown.

Indeed, during the transition from the study of DD synthesis [24–27] to the first experiments on aneutronic pB fusion in NVD, the task of delivering protons and boron ions into the anode space arose. Protons (hydrogen) could enter the anode Pd tubes, as previously deuterium [24, 25], during electrolysis in ordinary water. A new task was the delivery of boron ions into the anode space. In this regard, we used in the work [19] an old anode consisting of three short Pd tubes attached to the end of the copper base (Figure 2A in [19]). Due to the repeated use of this anode earlier in the study of DD synthesis [26], its surface contained a huge number of microcraters and a very developed microrelief as a whole [19]. This turned out to be extremely convenient for filling the surface of the old Pd anode with boron nanoparticles (∼20 nm) during cataphoresis. When irradiating such an anode with energetic autoelectrons, both protons and boron ions could appear in the erosive plasma near its surface, coinciding with the upper edge of the PW (Figure 1C in [19]). However, the anode–cathode (A–C) geometry with the old anode used in experiment differs from the PiC modeling for the optimal geometry found earlier [19], in which the oscillations of protons and boron ions in the field of the virtual cathode are well expressed.

Figure 2

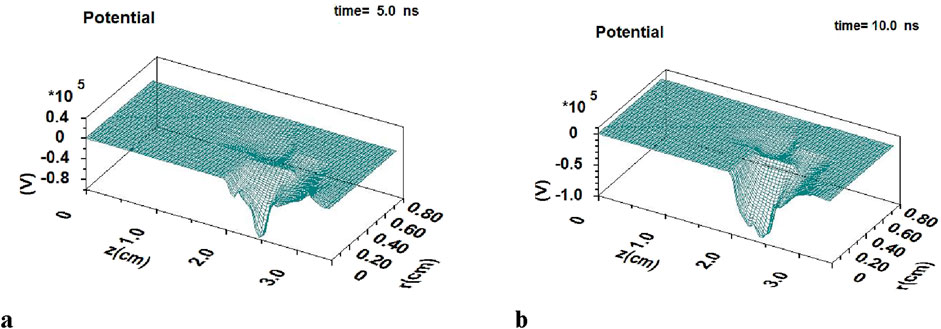
Figure 2. A potential well formed under PiC simulation by a virtual cathode in the anode space of a nanosecond vacuum discharge in experiment [19] for two moments of time: (A) t = 5 ns, The depth of PW is up to 80 kV, and (B) t = 10 ns, PW is up to 100 kV deep, approximately.

The actual A–C geometry used in the first experiments on the aneutronic pB fusion in NVD [19] is shown in Figure 1A. When modeling in the KARAT code, a TEM wave from a high-voltage generator is fed into the coaxial along the z axis on the left side, which forms an electric field between the electrodes, causing electron emission from the cathode [23, 28]. In this section, under 2D PiC simulations the experimental VA characteristics (see Figure 2B in [19]) of the voltage pulse-periodical generator were used.

In comparison with the optimal A–C geometry for ion oscillations at potential well [19], in the first experiment we had a very short anode “tube” (Figure 1A). The length of the potential well in the NVD turns out to be approximately proportional to the length of the anode tube, and for a real anode Pd tube, as we see (Figure 2A), the PW turns out to be quite small in length by z. As will be shown below (Section 3), the yield of α particles from the pB reaction have to be proportional approximately to the volume in which the synthesis takes place, i.e., the length and width of the potential well. Therefore, the shorter the anode tube in the NVD, the lower the expected reaction yield will be. In addition, the real anode Pd tubes (Figure 1A) are shifted to the discharge axis compared to their position in Figure 1A in [19]. As a result, in the experiment [19], the potential well (Figure 2) turns out to be not only narrow by z, but also small in radius r. This is also why PiC modeling of the positions of selected groups of protons and boron ions along the radius in time, as we see in Figure 1B, does not detect any oscillations of protons and boron ions at PW for a real anode. The time dependence of the energies of various groups of protons and boron ions for the experimental anode also does not contain strong periodic fluctuations in time, unlike the case of well-defined ion oscillations in a potential well [33].

Thus, it seems that in the experiment [19] we had a small and rather narrow potential wells (Figure 2) and, apart from the primary convergence of ions to the discharge axis and subsequent expansion in the time interval t ≈ 0–10 ns (Figure 1B), in fact, the absence of any oscillations of protons and boron ions (in contrast to the more optimal A - C geometry, Figure 1A in [19]). Thus, as present PiC simulation shows, the total yield of α particles accumulated from shot to shot in the experiment [19] apparently took place mainly due to a single convergence of protons and boron ions to the discharge axis (Figure 1B), and is observed only in the first 10 ns [19]. The number of pB reactions obtained from PiC simulations for experimental geometry A–C presented in Figure 1A is N_r^pB = 1.07 × 10⁹ (a.u.). The calculated values of N_r^pB in arbitrary units (a.u.) in the code KARAT [23] allow comparisons between calculations with different initial parameters of the PiC modeling, and to trace trends when they vary. Below, the results of PiC simulations of the values of N_r^pB for different volumes of NVD anode space in planned experiments are presented and discussed.

3 The proton–boron fusion power for various volumes of potential wells in the NVD anode space

Earlier, an oscillating plasma was proposed as a possible thermonuclear fusion scheme on the basis of IEC [29, 30]. The confinement and acceleration of ions in the IEC scheme takes place in the field of virtual cathode, i.e., in a deep electrostatic potential well [21]. In this scheme, the head-on ion collisions in a usual IEC device are replaced by the periodically oscillating plasma spheres (POPS) in the harmonic oscillator potential arranged due to a homogeneous electronic background. At the moment of compression, the high plasma densities and temperatures necessary for nuclear fusion could be achieved [29, 30]. An advantage of the POPS-based device is the favorable scaling obtained for the fusion power, which increases with the inverse of VC radius [30]. This feature could reduce in size and cost of each subsequent device of this type [29]. Unfortunately, in further work it was not possible to implement the original POPS ideas under nuclear fusion experiments [31]. In particular, it was shown that high compressions needed for fusion are not realizing for POPS [31].

Indeed, if the previously obtained for POPS fusion power of DD in spherical geometry P ∼ φ²_PW/r_VC [29, 30], then for the NVD of cylindrical geometry we can get by similar manner P ∼ φ²_PW L/r²_VC (φ_PW is the depth of PW, r_VC is the radius of VC, L is the length of the fusion area on the discharge axis) [28]. Scaling of DD fusion power in NVD by VC size was studied in detail in [32], where the measured values of neutron yield at the initial and subsequent stages of discharge were compared. It has been shown experimentally that when the NVD interior anode space (limited by Pd tubes) with DD fusion is reducing to the internal volume just of the single anode Pd tube with diameter Ø_A = 2 R_A = 0.08 cm ≥ 2 r_VC at the very initial stage of discharge, we are registering almost the similar values of the DD neutron output (R_A is the radius of NVD anode space, but in this case it is the internal radius of the anode Pd tube). Apparently, it is going due to reduction approximately by five times for both φ_PW and r_VC values under DD fusion at the single Pd tube interior volume in comparison with the same values in the case of DD fusion in the total anode interior restricted by the set of Pd tubes in NVD. In fact, for PW depth φ_PW ≈ 10 kV inside Pd tube the head-on collisions of deuterons with energies ≈10 keV may accompanied by DD reactions. Note, the type of similar scaling for pB fusion is not quite obvious. Remind that for noticeable proton - boron fusion the values of the threshold energies of colliding particles should be at least ten times higher [9].

Meanwhile, the question of the scaling for the release of the aneutronic pB reaction with a decrease or any changing in the virtual cathode size at NVD is of great interest. The picture here may be more complicated than for DD synthesis. In particular, for example, the protons and boron ions differ in mass and charge, and their oscillation frequencies in the anode space will be different. Note, the frequency of ions oscillations f_OSC ≈ (Ze φ_PW/2m_i)^1/2//r_VC at potential well can be estimated from the inverse time of the ion flight along the radius of the anode space to the discharge axis (Figure 1A; f_OSC ∼ u_i/r_VC, where u_i ≈ (Ze φ_PW/2m_i)^1/2 is the average velocity of an ion with a charge Z and mass m_i). This means that the maximum energies for protons and boron ions accelerating by the field of the virtual cathode will be reached the discharge axis z (the “bottom” of PW) under the different moments of time, and, obviously, that cannot be favorable for the efficiency of pB fusion in NVD.

The number of pB reactions N_r^pB = 1.07 × 10⁹ (a.u.), presented in Section 1, can be considered as a starting point for analyzing the scaling of pB fusion power in NVD. In contrast to DD synthesis in NVD, when head-on collisions of deuterons of the same mass and charge take place near the z axis of discharge, the difference in the oscillation frequencies of colliding protons and boron ions makes the processes of pB synthesis essential not only near the discharge axis, but also throughout the entire volume with a certain probability. The volume occupied by the virtual cathode, i.e., the potential well, is determined by the radius of the VC and its extent (length) along z axis in the cylindrical geometry of the NVD. To determine how the yield of α particles changes with a change in the size of the virtual cathode r_VC < R_A, we performed 2D PiC modeling in the KARAT code [23] for different volumes of NVD anode space. The results on the number of pB reactions for three values of anode radius R_A = 0.1, 0.3, and 0.5 cm are presented and discussed below. Discharge modes are selected to show here, where current I = 3 kA and voltage U = 100 kV, at which, as a rule, rather well-defined oscillations of protons and boron ions take place in the anode space (see also [23, 28] for some details of simulations for proton–boron fusion in NVD).

Figure 3 shows the geometry A–C for the single anode tube with a radius of R_A = 0.1 cm, the energies of the selected oscillating groups of protons and boron ions in time, the potential well created by the virtual cathode and the number of pB reactions depending on time. (In a real experiment, the anode in this case may be as “translucent” single hollow Pd tube filled with hydrogen and boron). The data in Figures 3A, B actually reflect the oscillatory nature of ion confinement in the potential well [19]. The PW well is narrower than in Figure 2, but significantly longer at the present mode. It can be seen from Figures 3A, C that the main pB fusion takes place in the range z = 0.5–1 cm of axis. Figure 3B shows the energies of the chosen isolated groups of protons and boron ions over time. The number of pB reactions in time is given in Figure 3D. Note that the maximum values of N_r^pB in time correlate with the moments, when the energies of boron ions are maximal. The total number of pB reactions is N_r^pB = 1.9 × 10¹⁰ in arbitrary units (Here and below the simulations were going for I = 3 kA, U = 100 kV, (with a front of voltage δt = 2 ns and δt = 5 ns for current, under duration of high voltage applied t_input ≈ 20 ns). This value N_r^pB turns out to be the maximum for various current values in the range I = 1–5 kA at a fixed value U = 100 kV, and also the maximum at a fixed value I = 3 kA for voltages in the range 60–150 kV [23]. Only for I = 4–5 kA and U = 120–150 kV, the yield of α particles will be slightly higher, but not more than twice. The complete set of pB reaction numbers for the intervals I = 1–5 kA and U = 60–150 kV for a given R_A = 0.1 cm is given in Table 1 in [23].

Figure 3

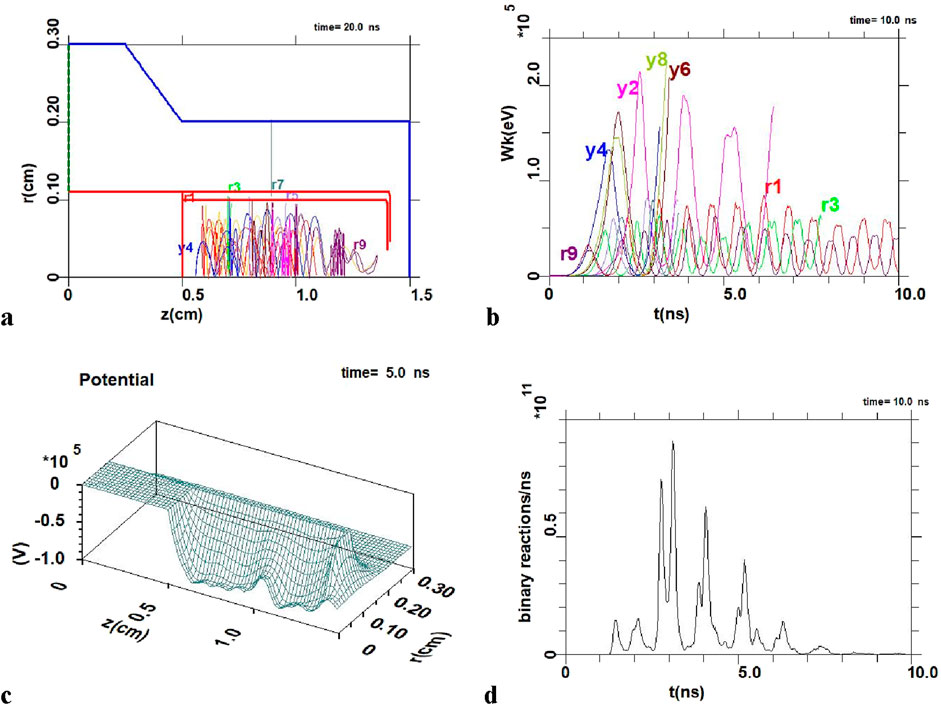
Figure 3. Mode with anode radius of R_A = 0.1 cm: (A) Geometry A–C and oscillating trajectories of selected groups of protons (index r) and boron ions (index y) in the anode space along the radius during the time t = 20 ns; (B) Energy change of selected groups of protons and boron ions over time during oscillations; (C) Narrow in radius, but long potential well with a depth of up to 100 kV; (D) The number of pB reactions from PiC simulations over time in arbitrary units (a.u.).

Table 1

Table 1. The number of pB reactions (a.u.) obtained by PiC simulations for different radii of the anodes during 20 ns under the length L ≈ 1–1.5 cm of potential well with fusing ions.

Next, Figure 4A shows the following geometry A–C for the anode space with well-defined oscillating ions, where the anode radius R_A = 0.3 cm is three times larger, compared with the first mode (Figure 3). The distance between A–C is δ_A-C = 0.2 cm here (Figure 4A). As in the previous case, well-pronounced oscillations of protons and boron ions can be noted. Figure 4B shows the energies of the isolated groups of protons and boron ions over time. The number of pB reactions in time is given in Figure 4D. Again, as for R_A = 0.1 cm (Figure 3), the maximum values of N_r^pB in time correspond to the moments, when the energies of boron ions are maximal. The corresponding potential well of the virtual cathode is presented in Figure 4C. The PW is wider than in Figure 3 for R_A = 0.1 cm, and essentially longer than for the first experiments on pB fusion in vacuum discharge [19] (Figure 2 above). We see from Figures 4A, C that the main pB fusion takes place in the range z ≈ 2–3 cm of axis. For this mode, where PW is significantly wider than in the first case, the total number of pB reactions is N_r^pB = 5,8 × 10¹⁰ (a.u.). When the current decreases to I = 2 kA, the output of α particles decreases in this case to 3.6 × 10¹⁰ (a.u.).

Figure 4

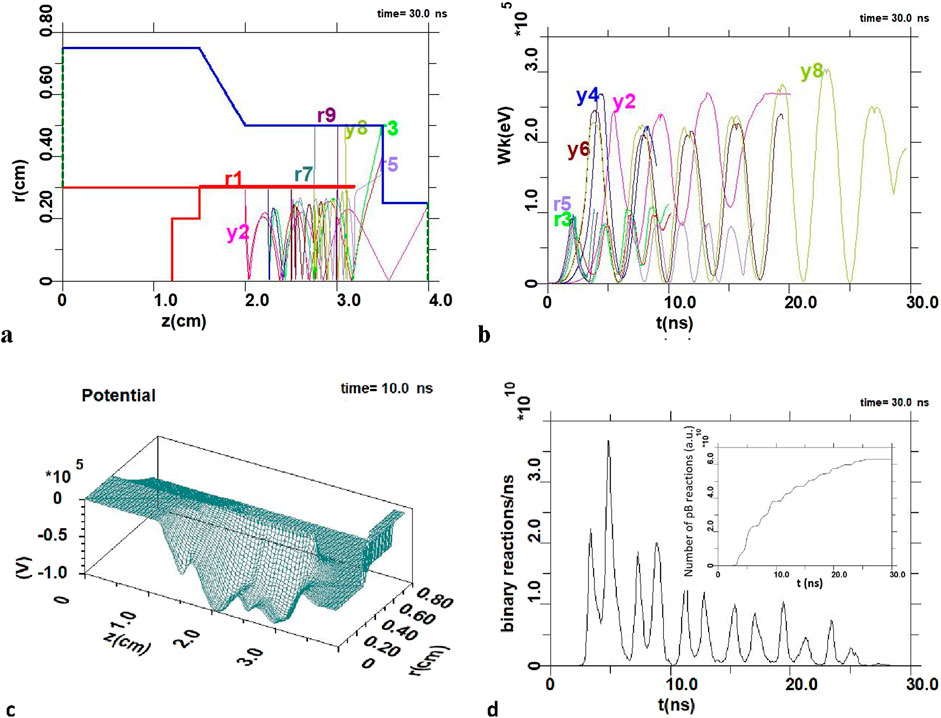
Figure 4. Mode with anode radius R_A = 0.3 cm: (A) Geometry A–C and oscillating trajectories of selected groups of protons (index r) and boron ions (y) in the anode space during t = 30 ns; (B) Energy change of selected groups of protons and boron ions over time during ions oscillations (C) Potential well of the virtual cathode at the moment of time t = 10 ns; (D) The number of pB reactions from PiC simulations over time (a.u.). The icon insert shows the change in the total number of pB reactions over time.

Further, in more detail we present the PiC simulation results for the following NVD mode with the anode radius R_A = 0.5 cm (Figure 5). As earlier, Figures 5A, B show A–C geometry for the anode space of the NVD with oscillating ions, and the potential well, correspondingly. Energy changeing of selected groups of ions over time during their oscillations in PW is shown in Figure 5C.

Figure 5

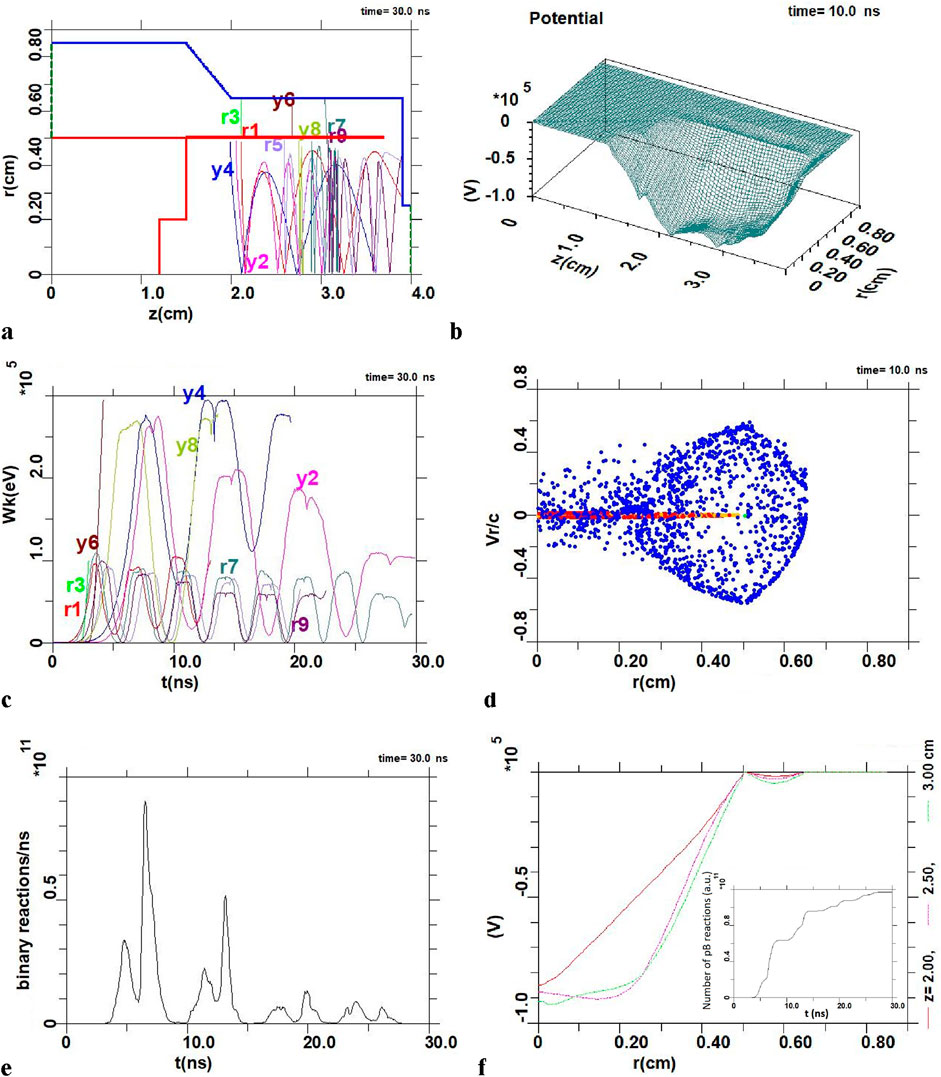
Figure 5. Mode with anode radius R_A = 0.5 cm: (A) Geometry A–C and trajectories of selected groups of protons (index r) and boron ions (y) in the anode space during t = 30 ns; (B) Potential well of the virtual cathode at t = 10 ns; (C) Energy change of selected groups of protons and boron ions over time during their oscillations; (D) Velocity all particles, including pB reaction producs [19], depending on their position along the radius. The virtual cathode is forming in the region r ≤ 0.25 cm as a result of the deceleration and acceleration of electrons in the anode space; (E) The number of pB reactions over time from PiC simulations (a.u.); (F) The potential change along the radius for three fixed values z = 2.0, 2.5, and 3.0 cm on the discharge axis at t = 10 ns. The insert shows the change in the total number of pB reactions over time.

The velocities of all particles, including some products of the pB reaction, depending on their position along the radius are shown in Figure 5D (“phase portrait”). Here the dynamics of electrons along the radius and the formation of a virtual cathode are clearly presented. The emission of electrons from the inner surface of the cathode (at r = 0.65 cm) under the action of an applied field is accompanied by their acceleration into the A-C spaces, where their energy reaches ∼100 keV when approaching the anode. Flying through a “translucent” anode (or a “grid” of thin Pd tubes attached perpendicular to the end of the anode around its circumference in a real experiment) at r = 0.5 cm, the electrons are inhibited during further movement along the radius to the z axis of discharge up to a complete stop at r ≈ 0.2 cm and further reversal in the opposite direction, Vr/c > 0. Note, the phase portrait presented in Figure 5D is the typical one for the regimes of well-defined oscillations of proton and boron ions at PW [28]. Comparing the size of the region of almost complete electron deceleration (Figure 5D), and the region of potential equalization to values where the electric field accelerating ions becomes close to zero (at the “bottom” of the potential well, Figure 5F), it can be concluded that the value r_VC ≈ R_A/2.

Well-defined radial ion oscillations (Figure 5A) in a deep and rather wide potential well (Figure 5B) of VC, during which the energy of protons and boron ions changes significantly (Figure 5C), are accompanied by a periodic proton - boron reactions (Figure 5E) under head-on collisions of ions and the appearance of α particles. Comparing Figures 5C, E, we see that the maximum number of pB reactions in time correlate with the moments of maximum energies of boron ions. The same is observed for the mode with R_A = 0.1 cm and R_A = 0.3 cm (Figures 3, 4). Recall that the frequency of ion oscillations in the potential well is f_OSC ∼ 1/r_VC. Then, since the dimensions of the virtual cathode differ about five times in the first and third modes, we see significantly different values of ion oscillation frequencies there (compare Figures 3B, 5C), and, correspondingly, a more frequent output of α particles for the case of R_A = 0.1 cm (compare Figures 3D, 5E also).

The number of pB reactions for the mode with R_A = 0.5 cm is N_r^pB ≈ 1.05 × 10¹¹. A further increase in the size of the anode to R_A = 0.7 cm at the same current and voltage is accompanied by a deterioration in oscillations, and the saturation value of N_r^pB will be ≈1.15 × 10¹¹. In general, it should be noted also that the presence of well-defined ion oscillations gives the same yield of α particles for noticeably smaller volumes of the anode space. So, for example, for the mode with I = 2 kA and U = 150 kV, where there are practically no oscillations, we have in the range R_A = 0.1–0.7 cm the number of pB reactions N_r^pB ≈ 2.1× 10⁹–3.2 ×10¹⁰.

Thus, the difference in the oscillation frequencies of protons and boron ions makes an important contribution from reactions not only on the discharge axis, but also in the entire volume of the NVD anode space. With an increase in the radius of the anode, the number of pB reactions for a fixed time t_input ≈ 20 ns of the energy input increases. But with a further increase in the R_A (and VC radius also, Figure 5F), the frequency of ion oscillations will further decrease also, and the number of oscillations during the time of voltage applied t_input will be less and less. That is, in general, protons and boron ions will collide less often even in the entire anode volume, especially at the periphery, and as a result, the total number of reactions reaches some saturation at R_A ≥ 0.7 cm. The number of pB reactions for the selected values of R_A is shown in Table 1, where the saturation trend noted above for N_r^pB is traced.

4 Concluding remarks

Thus, even in an extremely suboptimal anode configuration, in the first experiments on the aneutronic pB fusion in one miniature device it was still possible to register a certain yield of α particles [19]. PiC simulations for the real A–C geometry showed that the total observed yield of α particles was accumulated, apparently, due to single convergence of protons and boron ions to the discharge axis with each shot, and their oscillations for the anode-cathode geometry used in the experiment [19] are practically absent (see also [33] for some details).

Qualitatively, PiC simulations show that the number of the pB reactions at anode space of nanosecond vacuum discharge increases with the anode volume grow, and in the range R_A ≈ 0.1–0.5 cm the α particles output is proportional to VC radius or the value of anode radius (Table 1). However, with a fixed time of high voltage applied and magnitude of the energy input, the number of pB reactions can start to reach some saturation due to increasingly rare collisions with an increase in the anode volume along the radius. However, in this case a further definite increase in N_r^pB may be due to an increase in the length L of the potential well with pB fusion along the discharge axis.

Thus, we may conclude that scaling of pB synthesis when changing the size of the virtual cathode differs significantly from the same scaling of DD synthesis in NVD. Nevertheless, in the planned continuation of experiments on pB fusion in NVD, it is possible to hope to obtain two to three orders of magnitude higher yield of α particles than in the first experiments [19] for the discharge regimes like presented in Figure 5. Also, if the high voltage applied in the NVD is increasing, for example, to U ≈ 150 kV, we can somewhat approach the energies of proton and boron ions to the first resonant peak of pB reaction as well as to the main resonant peak of the pB reaction at 675 keV also, that will increase slightly the output of α particles.

We emphasize that for each selected diameter of the anode in the NVD, the maximum values of α particle output, when well-defined ion oscillations in the PW are realized, can be obtained for specific and different values of current and voltage, which means that the discharge energy will change. Therefore, comparing the values of N_r^pB for different NVD modes and electrode geometries, it is necessary remember that the “price” of the resulting α particles in Joules may be different.

We add that a further increase in R_A may lead to a weakening of the role of VC, a decrease in the depth of the potential well and an increasing influence of the real cathode (more precisely, an increase in the role of vertical cathode wall, at z ≈ 3.9 cm, with an increase in R_A, Figure 5A). Nevertheless, in such a hybrid mode, as shown by the preliminary simulation for anode radius R_A = 1.5 cm, a fairly noticeable number of pB reactions will also take place, but the features of ion acceleration and ion dynamics will generally change greatly. The surprising specifics of the hybrid mode will require a separate study and discussion.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YK: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft. SA: Data curation, Formal Analysis, Investigation, Software, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Ministry of Science and Higher Education of the Russian Federation (State Assignment No. 075-00270-24-00). Under the present study the work of S.N.Andreev was supported within the scientific program of the National Center for Physics and Mathematics, section No 1 “National Center for Supercomputer Architecture Research, Stage 2023-2025”.

Acknowledgments

We would like to thank Sergey Yu. Gus’kov and Alexander V. Oginov for stimulating discussions, valuable support of the work and incorporation of the PiC simulation data obtained for further developing of experiment on proton - boron fusion in vacuum discharge.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Oliphant M, Rutheford L. Experiments on the transmutation of elements by protons. Proc R Soc Lond (1933) V. A141:259.

Google Scholar

2. Dee PI, Gilbert CW. The disintegration of Boron into three α-particles. Proc R Soc Lond (1936) V. A154:279.

Google Scholar

3. McKenzie W, Batani D, Mehlhorn TA, Margarone D, Belloni F, Campbe EM, et al. HB11—understanding hydrogen-boron fusion as a new clean energy source. J. Fusion Energy (2023) 42:17. doi:10.1007/s10894-023-00349-9

CrossRef Full Text | Google Scholar

4. Cirrone GAP, Manti L, Margarone D, Petringa G, Giuffrida L, Minopoli A, et al. First experimental proof of Proton Boron Capture Therapy (PBCT) to enhance protontherapy effectiveness. Scientic Rep (2018) 8(1):1141. doi:10.1038/s41598-018-19258-5

CrossRef Full Text | Google Scholar

5. Hong E, Jungmin A, Lee J, Ham J, Park K, Jeon J. Alpha particle effect on multi-nanosheet tunneling field-effect transistor at 3-nm technology node. Micromachines (2019) 10:847. doi:10.3390/mi10120847

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Takacs S, Hermanne A, Tárkányi F, Ignatyuk A. Cross-sections for alpha particle produced radionuclides on natural silver. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2010) 268:2–12. doi:10.1016/j.nimb.2009.09.035

CrossRef Full Text | Google Scholar

7. Rebeles R, Adam A, Van den Winkel P, Tárkányi F, Takács S, Daraban L. Alpha induced reactions on 114Cd and 116Cd: an experimental study of excitation functions. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2008) 266:4731–7. doi:10.1016/j.nimb.2008.07.013

CrossRef Full Text | Google Scholar

8. Raffaelle RP, Jenkins P, Wilt D, Scheiman D, Chubb D, Castro S. Alpha voltaic batteries and methods thereof. Patent US (2011) 7:867–639.

Google Scholar

9. Atzeni S, Meyer-ter Vehn J. The physics of inertial fusion: BeamPlasma interaction, hydrodynamics, hot dense matter, 125. Oxford: Oxford University Press (2004).

Google Scholar

10. Belyaev VS, Matafonov AP, Vinogradov VI, Krainov V, Lisitsa V, Rusetski AS, et al. ObsepBation of neutronless fusion reactions in picosecond laser plasmas. Phys Rev E (2005) 72(2):026406. doi:10.1103/PhysRevE.72.026406

CrossRef Full Text | Google Scholar

11. Labaune C, Baccou C, Depierreux S, Goyon C, Loisel G, Yahia V, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun (2013) 4:2506. doi:10.1038/ncomms3506

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Picciotto A, Margarone D, Velyhan A, Bellutti P, Krasa J, Szydlowsky A, et al. Boron proton nuclear fusion enhancement induced in boron doped silicon targets by low-contrast pulsed laser. Phys Rev (2014) 4(3):031030. doi:10.1103/physrevx.4.031030

CrossRef Full Text | Google Scholar

13. Baccou C, Depierreux S, Yahia V, Neuville C, Goyon C, De Angelis R, et al. New scheme to produce aneutronic fusion reactions by laser-accelerated ions. Laser Part Beams (2015) 33(1):117–22. doi:10.1017/s0263034615000178

CrossRef Full Text | Google Scholar

14. Giufrida L, Belloni F, Margarone D, Petringa G, Milluzzo G, Scuderi V, et al. High-current stream of energetic α particles from laser-driven proton-boron fusion. Phys Rev E (2020) 101(1):013204. doi:10.1103/PhysRevE.101.013204

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Belyaev VS, Matafonov AP, Krainov VP, Kedrov AY, Zagreev BV, Rusetsky AS, et al. Simultaneous investigation of the nuclear reactions B and BC as a new tool for determining the absolute yield of alpha particles in picosecond plasmas. Phys At Nuclei (2020) 83(5):641–50. doi:10.1134/s1063778820050063

CrossRef Full Text | Google Scholar

16. Bonvalet J, Nicolai P, Rafestin D, D'humieres E, Batani D, Tikhonchuk V, et al. Energetic α-particle sources produced through proton-boron reactions by high-energy high-intensity laser beams. Phys Rev E (2021) 103(5):053202. doi:10.1103/physreve.103.053202

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Margarone D, Bonvalet JGL, Giuffrida L, Morace A, Kantarelou V, Tosca M, et al. In-target proton– boron nuclear fusion using a PW-class laser. Appl Sci V (2022) 12:1444. doi:10.3390/app12031444

CrossRef Full Text | Google Scholar

18. Magee RM, Ogawa K, Tajima T, Allfrey I, Gota H, McCarroll P, et al. First measurements of p11B fusion in a magnetically confined plasma. Nat Commun (2023) 14:955. doi:10.1038/s41467-023-36655-1

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Kurilenkov YK, Oginov AV, Tarakanov VP, Gus'kov SY, Samoylov IS. Proton-boron fusion in a compact scheme of plasma oscillatory confinement. Phys Rev E (2021) 103:043208. doi:10.1103/physreve.103.043208

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Miley GH, Murali SK. Inertial electrostatic confinement (IEC) fusion fundamentals and applications. NY: Springer (2014).

Google Scholar

21. Lavrent’ev OA. Electrostatic and electromagnetic high-temperature plasma traps. Ann N Y Acad Sci (1975) 251:152–78. doi:10.1111/j.1749-6632.1975.tb00089.x

CrossRef Full Text | Google Scholar

22. Elmore WC, Tuck JL, Watson KM. On the inertial-electrostatic confinement of a plasma. Phys Fluids (1959) 2:239–46. doi:10.1063/1.1705917

CrossRef Full Text | Google Scholar

23. Andreev SN, Kurilenkov YK, Oginov AV. Fully electromagnetic code KARAT applied to the problem of aneutronic proton–boron fusion. Mathematics (2023) 11:4009. doi:10.3390/math11184009

CrossRef Full Text | Google Scholar

24. Kurilenkov YK, Skowronek M, Dufty J. Multiple DD fusion events at interelectrode media of nanosecond vacuum discharge. J.Phys.A: Math Gen V (2006) 39:4375–86. doi:10.1088/0305-4470/39/17/s11

CrossRef Full Text | Google Scholar

25. Kurilenkov YK, Tarakanov VP, Skowronek M, Guskov SY, Dufty J. Inertial electrostatic confinement and DD fusion at interelectrode media of nanosecond vacuum discharge. PIC simulations and experiment. J Phys A: Math Theor (2009) 42:214041. doi:10.1088/1751-8113/42/21/214041

CrossRef Full Text | Google Scholar

26. Kurilenkov YK, Tarakanov VP, Gus’kov SY, Karpukhin VT, Valyano VE. Warm dense matter generation and DD synthesis at vacuum discharge with deuterium-loaded Pd anode. Contrib Plasma Phys (2011) 51:427–43. doi:10.1002/ctpp.201110014

CrossRef Full Text | Google Scholar

27. Kurilenkov YK, Tarakanov VP, Gus’kov SY, Oginov A, Karpukhin V. Oscillating ions under Inertial Electrostatic Confinement (IEC) based on nanosecond vacuum discharge. Contrib Plasma Phys (2018) 58:952–60. doi:10.1002/ctpp.201700188

CrossRef Full Text | Google Scholar

28. Kurilenkov YK, Tarakanov VP, Oginov AV, Gus’kov SY, Samoylov IS, Batani D. Oscillating plasmas for proton- boron fusion in miniature vacuum discharge. Laser and Part Beams (2023) 2023:e9. doi:10.1155/2023/9563197

CrossRef Full Text | Google Scholar

29. Park J, Nebel R, Stange S, Murali SK. Periodically oscillating plasma sphere. Phys Plasmas (2005) 12:056315. doi:10.1063/1.1888822

CrossRef Full Text | Google Scholar

30. Nebel R, Barnes DC. The periodically oscillating plasma sphere. Fusion Technology (1998) 34:28–45. doi:10.13182/fst98-a51

CrossRef Full Text | Google Scholar

31. Evstatiev E, Nebel R, Chacon L, Park J, Lapenta G. Space charge neutralization in inertial electrostatic confinement plasmas. Phys Plasmas (2007) 14:042701. doi:10.1063/1.2711173

CrossRef Full Text | Google Scholar

32. Kurilenkov YK, Tarakanov VP, Oginov AV. On scaling of DD fusion power in a nanosecond vacuum discharge. Plasma Phys Rep (2022) 48(4):443–8. doi:10.1134/s1063780x22040080

CrossRef Full Text | Google Scholar

33. Kurilenkov YK, Oginov AV, Samoylov IS. On the acceleration and confinement of ions by the field of a virtual cathode in the plasma of nanosecond vacuum discharge. High Temperatures (2024) 62(5) in press.

Google Scholar