Analytical solution of steady reconnection outflows in a time-varying three-dimensional reconnection model with generalized spatiotemporal distributions

Magnetic reconnection is a fundamental mechanism for energy conversion in the realms of space physics, astrophysics, and plasma physics. Over the past few decades, obtaining analytical solutions for three-dimensional (3D) magnetic reconnection has remained a challenging endeavor. Due to the complexity and nonlinearity of the equations, analytical solutions can only be obtained when specific spatiotemporal distributions of magnetic fields or plasma flows are provided. Particularly, the evolution of reconnection flows in time-dependent 3D reconnection has not been analytically discussed. Additionally, quasi-steady magnetic reconnection persisting for several hours can be observed in the turbulent solar wind, which raises an important question: can steady reconnection flows theoretically exist in a time-dependent 3D magnetic reconnection model? In this study, a generalized analytical model for time-dependent kinematic 3D magnetic reconnection has been constructed. In the framework of pure analytical approach, it is firstly demonstrated that steady reconnection outflows can theoretically exist within a time-varying magnetic field. We have also analytically discussed the possibility of the existence of quasi-steady reconnection flows in 3D magnetic reconnection for turbulent magnetic fields in the solar wind. These findings broaden our understanding of the stability and necessary conditions for time-dependent 3D magnetic reconnection, offering new insights into quasi-steady reconnection phenomena in real cosmic environments.

1 Introduction

Magnetic reconnection, recognized as a topological or geometrical rearrangement process of magnetic field [1], plays a significant role in the dynamics of diverse plasma environments [2–5]. Historically, the concept of magnetic reconnection advanced significantly through the exploration of two-dimensional (2D) steady-state models rooted in magnetohydrodynamic (MHD) theory [6–9]. In recent decades, significant achievements have been made in the study of magnetic reconnection, primarily through observation [10–13], numerical simulation [14–17], and experimental research [18–21]. These advancements have enriched our understanding of this fundamental phenomenon, uncovering and validating its intricate evolutionary characteristics across a wide range of astrophysical and laboratory environments. However, the theoretical analysis on magnetic reconnection, especially in seeking the analytical solutions for 3D magnetic reconnection, has faced numerous challenges due to the complexity and nonlinearity of the equations involved [22–25].

Magnetic reconnection and plasma dynamics are intricate processes governed by nonlinear coupling between magnetic fields and plasma flows. Obtaining analytical solutions within the MHD framework faces considerable challenges due to this nonlinearity. Even when equations such as the momentum and energy equations are simplified, deriving direct analytical solutions remains daunting. Consequently, previous analytical approaches have predominantly relied on simplifying theoretical equations and imposing specific constraints. A practical method involves combining Ohm’s law and simplified Maxwell equations with a particular magnetic field configuration to deduce analytical solutions [26–28].

In order to simplify the analytical process, many authors have disregarded the time variable and concentrated exclusively on static magnetic reconnection analysis. By constructing different spatial distribution of magnetic fields, they have derived diverse analytical solutions that could address different types of magnetic reconnection scenarios to some extent [29–31]. Under the assumption of stagnation point flow driving [32–34] and based on the linear X-point theory [35], Craig et al. [36–38] developed a set of hybrid analytic solutions describing reconnection processes with X-type topology magnetic field lines and intricate current structures. In addition, a notable instance is the derivation of self-similar solutions [39], which simplify the intricate problem by linearly expanding a magnetized plasma under self-similar evolution conditions. Moreover, along with the localized resistivity assumption, pioneering works on the slippage reconnection process within a finite diffusion region [40, 41] resulted in the identification of kinematic solutions of the null or non-null magnetic reconnection [42–45] featuring a reverse rotational flow in a hyperbolic magnetic field.

Sporadic studies have addressed the scenarios involving temporal changes in analytical solutions for 3D magnetic reconnection [46–50]. While the inclusion of time variable makes the solution of the equation set more complex, often requiring the imposition of additional restrictions. By utilizing various initial conditions, Anderson and Priest [51] investigated the time-dependent solution of the MHD equations for magnetic annihilation in a time-varying stagnation point flow. Wilmot-smith et al. [52] examined a series of magnetic diffusion with assumed magnetic diffusivity under the effect of a defined magnetic flux velocity. Additionally, Hornig and Priest [26] attempted to incorporate a time-dependent factor in the expression of electric potential within the framework of the time-independent equation set. Most notably, all of these efforts cannot address how reconnection flows evolve over time. Recently, based on the method employed by Hornig et al. [26], we have constructed a time-dependent 3D model by directly introducing time variables into the equation set [53]. It has been found that spiral plasma flows can be generated if the magnetic field changes exponentially with time.

As mentioned above, the inherent complexity and nonlinearity of the governing equations in magnetic reconnection and plasma dynamics present formidable obstacles to deriving analytical solutions without imposing specific spatiotemporal distributions of magnetic fields and plasma flows. However, such distributions, tailored for analytical tractability, are seldom representative of real cosmic environments, thus constraining the practical utility of these solutions. Significantly, both magnetic fields and plasma flows exhibit intrinsic temporal variability, making stationary analytical solutions unsuitable for accurate predictions and empirical validation. The absence of temporal dynamics in these static solutions leads to significant discrepancies between theoretical predictions and empirical observations. Furthermore, in time-dependent 3D models, if the magnetic field varies with time, the deduced plasma flows will also exhibit temporal variations [53]. So, even if the time-dependent analytical solutions offer advancements by integrating temporal variations, they will still encounter challenges in elucidating quasi-steady reconnection phenomena.

The prolonged magnetic reconnection phenomena in the solar wind, characterized by the presence of a pair of Alfvenic reconnection jets, have been reported for years [54–56]. These reconnection jets, which are signatures of ongoing magnetic reconnection, have been observed to persist over extended periods, indicating the long-lasting nature of the reconnection process in the solar wind environment [57]. Observations reveal that such phenomena are very common, occurring approximately 1.5 times per day, with a typical reconnection rate of ∼0.05, and can persist for at least 5 h [58]. Remarkably, the reconnection exhausts measured between 1 and 5.4 AU do not appear significantly broader than those measured between 0.3 AU and 1.0 AU, maintaining good planarity in their structure [59–61]. Intriguingly, given the turbulent nature of the solar wind, where magnetic fields and plasma flows vary continuously over time, it seems counterintuitive for such quasi-steady reconnection exhausts to exist from the perspective of time-dependent 3D analytical solutions [62]. Nevertheless, the inherent characteristic of turbulence is its unpredictability, which cannot be fully expressed analytically in four-dimensional spacetime. Consequently, researchers have mainly focused on providing theoretical analysis [63] and numerical simulations [64, 65] to incorporate the effect of turbulence on magnetic reconnection in earlier studies. Notably, the turbulence generated during magnetic reconnection is self-consistently simulated, appearing after 32–64 Alfven time and being caused by two beam instabilities with 3D Particle in cell simulations [66, 67]. Moreover, MHD simulations [68] demonstrate a fast growth of turbulent energy by 3 orders of magnitude over one Alfven time, indicating a considerably shorter timescale for turbulence self-generation during reconnection. To date, however, quasi-steady reconnection flows in 3D magnetic reconnection for turbulent magnetic fields have never been proven through a purely theoretical analytical approach.

Therefore, the question arises: can steady reconnection theoretically persist within a time-varying magnetic field scenario? If generalized spatiotemporal distribution forms of the magnetic field and magnetic diffusivity are given, can we analytically obtain steady reconnection outflows from the time-dependent 3D magnetic reconnection model? Furthermore, if such steady reconnection outflows can occur in a time-varying magnetic field, what conditions must the spatiotemporal distributions of the magnetic field and magnetic diffusivity fulfill? In this letter, we analytically solve the time-dependent kinematic 3D magnetic reconnection with generalized spatiotemporal distribution forms of the magnetic field and magnetic diffusivity. The existence and the conditions of steady reconnection outflows are discussed.

2 Time-dependent magnetic reconnection model with generalized forms

Based on the method introduced by Hornig and Priest [26] and following a similar approach used in our previous studies [53], we construct a time-dependent model by integrating temporal variables directly into the Maxwell-Faraday equations. Consequently, the governing equations of the system can be succinctly expressed as follows:

$\mathit{E}+\mathit{u}\times \mathit{B}=\eta \mathit{J},(1)$

$\nabla \times \mathit{E}=-\partial \mathit{B}/\partial t,(2)$

$\nabla \cdot \mathit{B}=0,(3)$

$\nabla \times \mathit{B}={\mu }_0\mathit{J}.(4)$

Here the first equation is Ohm’s law, while the others are Maxwell’s equations. Here, u denotes the velocity of the plasma, while E, B and J refer to the electric field, magnetic field and current density respectively. η and μ₀ represent the magnetic diffusion coefficient and the permeability of the vacuum, respectively.

Previous studies have always facilitated analytical derivation and resolved the flow field by providing specific spatiotemporal distributions of B and η. However, as discussed in the introduction, quasi-steady reconnection exhausts could persist in turbulent solar wind, where the magnetic fields and magnetic diffusion coefficients cannot be given in any specific form. Therefore, in this work, we deviate from past practices by refraining from specifying particular spatiotemporal distributions of B and η. Instead, we adopt a more general approach and assume that the temporal and spatial variables can be expressed in a separable form. By following the similar derivation method [26, 53], the B can be expressed as follows:

$\mathit{B}\left(x,y,z,t\right)=\mathit{B}\left(\mathit{r}\right)B\left(t\right)(5)$

here r represents the three components of the Cartesian coordinate system. The analytical expressions of field lines can be found by solving:

$\partial \mathit{X}\left(s,t\right)/\partial s=\mathit{B}\left(\mathit{X}\left(s,t\right)\right)(6)$

where s is the parameter satisfying $ds=d\lambda /\left|\mathit{B}\right|$, and λ represents the distance along the magnetic field lines. Here we mainly discuss the variable separated case $\mathit{X}\left(s,t\right)=\mathit{X}\left(s\right)\mathit{X}\left(t\right)$.

Then we can obtain the equations of the magnetic field lines $\mathit{X}\left({\mathit{r}}_0,s\right)$ and the corresponding inverse mapping ${\mathit{X}}_0\left(\mathit{r},s\right)$ in term of an initial point ${\mathit{r}}_0$:

$\mathit{X}=f\left({\mathit{r}}_0,s\right)(7)$

${\mathit{X}}_0=F\left(\mathit{r},s\right)(8)$

Furthermore, incorporating a time-dependent magnetic field allows us to express the electric field as follows:

$\mathit{E}=-\nabla \varphi -\partial \mathit{A}/\partial t(9)$

where A is the magnetic vector potential, and $\mathit{B}=\nabla \times \mathit{A}$. Substituting Equation 9 in Equation 1 yields

$-\nabla \varphi -\partial \mathit{A}/\partial t+\mathit{u}\times \mathit{B}=\eta \mathit{J}(10)$

Based on the analysis method of Hornig and Priest [26] and the boundary conditions of Chen et al. [53], the electric potential can be derived as:

$\varphi =-\int \left(\eta \mathit{J}\cdot \mathit{B}+\partial \mathit{A}/\partial t\cdot \mathit{B}\right)ds+{\varphi }_0(11)$

Here, we still set ${\varphi }_0=0$. Similarly, a general form of the local resistivity is given as $\eta =\eta \left(\mathit{r}\right)\eta \left(t\right)$, and substituting Equation 7 into Equation 11, we can obtain $\varphi \left({\mathit{X}}_0,s\right)$. After which we get $\varphi \left(\mathit{X}\right)$ by using Equation 8.

By taking the scalar product of both sides of Equation 10 with B and combining Equations 5, 6, the analytical expression for the velocity perpendicular to the magnetic field can be derived as:

$\begin{array}{l}{\mathit{u}}_{\perp }=\left(\mathit{E}-\eta \mathit{J}\right)\times \mathit{B}/{\left|\mathit{B}\right|}^2\\ =\{\nabla F\left[\eta \left(t\right)B^2\left(t\right)\int \eta \left(\mathit{r}\right)\mathit{J}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds+B^{\prime }\left(t\right)B\left(t\right)\int \mathit{A}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]\\ -B^{\prime }\left(t\right)\mathit{A}\left(\mathit{r}\right)-\eta \left(t\right)B\left(t\right)F\left[\eta \left(\mathit{r}\right)\mathit{J}\left(\mathit{r}\right)\right]\}\times \mathit{B}\left(\mathit{r}\right)/\left({\left|\mathit{B}\left(\mathit{r}\right)\right|}^{2}B\left(t\right)\right)\end{array}(12)$

where F denotes the transformation mapping a function from vector s to one of x. Note that the implicit form of the reconnection flow is intricate. To investigate the existence of steady reconnection plasma flows, the condition $\partial {\mathit{u}}_{\perp }/\partial t=0$ in the generalized time-dependent system will be analyzed. To ensure meaningful results, we will discuss the case where both the magnetic field and the magnetic diffusivity vary with time ($\partial \eta /\partial t\ne 0$ and $\partial B/\partial t\ne 0$). Additionally, the dimensionless approach is employed for the sake of simplicity.

3 The existence of stationary plasma flow with generalized forms

The presence of a stationary plasma flow requires that the partial derivative of velocity with respect to time equals zero, $\partial {\mathit{u}}_{\perp }/\partial t=0$. By performing a temporal partial differentiation on Equation 12, we have derived the conditions that guarantee the existence of a stationary plasma flow within the system:

$k_1\left[\eta \prime \left(t\right)B\left(t\right)+\eta \left(t\right)B\prime \left(t\right)\right]+k_2{B}^{″}\left(t\right)-k_3\left(B^{″}\left(t\right)B\left(t\right)-B^{\prime }{\left(t\right)}^2/B^2\left(t\right)\right)-k_4{\eta }^{\prime }\left(t\right)=0(13)$

Where k_i are introduced as specific expressions for the sake of simplicity:

$\left\{\begin{array}{l}{k}_1=\nabla F\left[\int \eta \left(\mathit{r}\right)\mathit{J}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]\times \mathit{B}\left(\mathit{r}\right)/{\mathit{B}}^2\left(\mathit{r}\right)\\ k_2=\nabla F\left[\int \mathit{A}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]\times \mathit{B}\left(\mathit{r}\right)/{\mathit{B}}^2\left(\mathit{r}\right)\\ k_3=\mathit{A}\left(\mathit{r}\right)\times \mathit{B}\left(\mathit{r}\right)/{\mathit{B}}^2\left(\mathit{r}\right)\\ k_4=F\left[\eta \left(\mathit{r}\right)\mathit{J}\left(\mathit{r}\right)\right]\times \mathit{B}\left(\mathit{r}\right)/{\mathit{B}}^2\left(\mathit{r}\right)\end{array}\right.(14)$

Neglecting the trivial solutions and assuming $B\prime \left(t\right)\ne 0,\eta \prime \left(t\right)\ne 0$, we infer three distinct categories of constraints on the stationary plasma flow from Equation 13: scenarios where each term is zero, situations where some terms are nonzero, and cases where every term is nonzero. Specifically, we systematically discussed the following six situations:

Case Ⅰ, $k_i$ in Equation 13 are all zero:

$\left\{\begin{array}{l}{k}_1=0,\\ k_2=0,\\ k_3=0,\\ k_4=0.\end{array}\right.(15)$

From Equation 14 We deduce that:

$\left\{\begin{array}{l}\nabla F\left[\int \eta \left(\mathit{r}\right)\mathit{J}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]=a_1\mathit{B}\left(\mathit{r}\right),\\ \nabla F\left[\mathit{A}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]=a_2\mathit{B}\left(\mathit{r}\right),\\ \mathit{A}\left(\mathit{r}\right)=a_3\mathit{B}\left(\mathit{r}\right),\\ \mathit{J}\left(\mathit{r}\right)=a_4\mathit{B}\left(\mathit{r}\right).\end{array}\right.(16)$

Here a₁, a₂, a₃ and a₄ are all nonzero constants. It is worth noting that in such a scenario, the system does not impose any requirements on the temporal variations of the magnetic field and magnetic diffusion coefficient. As long as the spatial distribution of the magnetic field and magnetic diffusion coefficient satisfies the equations mentioned above, it is sufficient to generate stationary plasma flow. However, the third equation in equation set (16) imply that the magnetic field should be at least irrotational, and the forth equation requires the magnetic field to be force-free.

Case Ⅱ, $k_1\ne 0$ and the first term in Equation 13 is zero:

$\left\{\begin{array}{l}\eta \prime \left(t\right)B\left(t\right)+\eta \left(t\right)B\prime \left(t\right)=0,\\ k_2=0,\\ k_3=0,\\ k_4=0.\end{array}\right.(17)$

We derive that:

$\left\{\begin{array}{l}{\left[\eta \left(t\right)B\left(t\right)\right]}^{\prime }=0,\\ \nabla F\left[\int \mathit{A}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]=a_1\mathit{B}\left(\mathit{r}\right),\\ \mathit{A}\left(\mathit{r}\right)=a_2\mathit{B}\left(\mathit{r}\right),\\ \mathit{J}\left(\mathit{r}\right)=a_3\mathit{B}\left(\mathit{r}\right).\end{array}\right.(18)$

Where a₁, a₂, a₃ are all nonzero constants. This case additionally requires that the partial derivative of the product of the magnetic diffusion coefficient and the magnetic field with respect to time is zero. Other requirements are similar to those in Case I.

Case Ⅲ, $k_2\ne 0$ and the second term in Equation 13 is zero:

$\left\{\begin{array}{l}{k}_1=0,\\ B^{″}\left(t\right)=0,\\ k_3=0,\\ k_4=0.\end{array}\right.(19)$

We can get:

$\left\{\begin{array}{l}\nabla F\left[\int \eta \left(\mathit{r}\right)\mathit{J}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]=a_1\mathit{B}\left(\mathit{r}\right),\\ B\left(t\right)=a_{2}t+a_3,\\ \mathit{A}\left(\mathit{r}\right)=a_4\mathit{B}\left(\mathit{r}\right),\\ \mathit{J}\left(\mathit{r}\right)=a_5\mathit{B}\left(\mathit{r}\right).\end{array}\right.(20)$

Where a₁, a₂, a₄, a₅ are all nonzero constants, and a₃ is constant. This case additionally requires that the magnetic field must change linearly with time. Other requirements are similar to those in Case I.

Case Ⅳ, $k_3\ne 0$ and the third term in Equation 13 is zero:

$\left\{\begin{array}{l}{k}_1=0,\\ k_2=0,\\ B^{″}\left(t\right)B\left(t\right)-B^{\prime }{\left(t\right)}^2=0,\\ k_4=0.\end{array}\right.(21)$

It can be obtained that:

$\left\{\begin{array}{l}\nabla F\left[\int \eta \left(\mathit{r}\right)\mathit{J}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]=a_1\mathit{B}\left(\mathit{r}\right),\\ \nabla F\left[\int \mathit{A}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]=a_2\mathit{B}\left(\mathit{r}\right),\\ B\left(t\right)=a_3{e}^{a_{4}t},\\ \mathit{J}\left(\mathit{r}\right)=a_5\mathit{B}\left(\mathit{r}\right).\end{array}\right.(22)$

Where a₁, a₂, a₃, a₅ are all nonzero constants, and a₄ is constant. This case additionally requires that the magnetic field must change exponentially with time. Other requirements are similar to those in Case I.

Besides, there are situations that bind the system even further:

Case Ⅴ, both the first and third term in Equation 13 are zero:

$\left\{\begin{array}{l}\eta \prime \left(t\right)B\left(t\right)+\eta \left(t\right)B\prime \left(t\right)=0,\\ k_2=0,\\ B^{″}\left(t\right)B\left(t\right)-B^{\prime }{\left(t\right)}^2=0,\\ k_4=0.\end{array}\right.(23)$

It suggests that:

$\left\{\begin{array}{l}\eta \left(t\right)=a_2{e}^{-a_{1}t},\\ \nabla F\left[\int \mathit{A}\left(\mathit{r}\right)\cdot \mathit{B}\left(\mathit{r}\right)ds\right]=a_3\mathit{B}\left(\mathit{r}\right),\\ B\left(t\right)=a_4{e}^{a_{1}t},\\ \mathit{J}\left(\mathit{r}\right)=a_5\mathit{B}\left(\mathit{r}\right).\end{array}\right.(24)$

Where a₁, a₂, a₃, a₄, a₅ are all nonzero constants. Based on the above conditions, the steady flow can exist when the temporal variation of the magnetic field and the magnetic diffusion coefficient can be expressed as an exponential relationship. Other requirements are similar to those in Case I.

Case Ⅵ, both the first and second term in Equation 13 are zero:

$\left\{\begin{array}{l}\eta \prime \left(t\right)B\left(t\right)+\eta \left(t\right)B\prime \left(t\right)=0,\\ B^{″}\left(t\right)=0,\\ k_3=0,\\ k_4=0.\end{array}\right.(25)$

It can be parsed that:

$\left\{\begin{array}{l}\eta \left(t\right)=a_1/\left(a_{2}t+a_3\right),\\ B\left(t\right)=a_{2}t+a_3,\\ \mathit{A}\left(\mathit{r}\right)=a_4\mathit{B}\left(\mathit{r}\right),\\ \mathit{J}\left(\mathit{r}\right)=a_5\mathit{B}\left(\mathit{r}\right).\end{array}\right.(26)$

Here a₁, a₂, a_4, a₅ are all nonzero constants, and a₃ is constant. This situation requires that the magnetic diffusivity is inversely proportional to time, while the magnetic field varies linearly with time. Other requirements are similar to those in Case I.

It should be noted that the condition where both the second and third non-parametric terms are zero in Equation 13 does not hold since ${\eta }^{\prime }\left(t\right)\ne 0$. Additionally, in other cases where Equation 13 contains non-zero terms, the presence of complex expressions makes it impractical to explicitly express their physical meaning. To maintain completeness, these cases are provided in the Supplementary Appendix SA1. Furthermore, unlike 2D magnetic reconnection, where reconnection occurs only at X-type null points, 3D magnetic reconnection can occur at locations where the magnetic field does not vanish. Consequently, the conditions required for steady reconnection flows in 3D magnetic reconnection discussed here from Equations 15–26 are distinct from those in classical reconnection models [6–8] and cannot be directly compared.

4 Discussion and conclusion

From the analysis of the above results, it can be observed that the existence conditions for steady reconnection flows impose very strict requirements on the spatial distribution of the magnetic field. However, in terms of the time variable, common variations such as linear or exponential changes can meet the requirements. Although very few regions simultaneously satisfy these conditions in actual cosmic space, it is proven that steady reconnection flows can be analytically obtained from the time-dependent 3D magnetic reconnection model. Specifically, if the spatiotemporal distributions of the magnetic field and magnetic diffusivity follow the constraints referred to above, steady reconnection can theoretically persist within a time-varying magnetic field scenario.

As introduced above, the solar wind is full of turbulence where the distribution of the magnetic field and the magnetic diffusion coefficient cannot meet any form of the above theoretical analysis, but we can still observe quasi-steady magnetic reconnection exhausts persisting for hours. Our work may shed some light on this phenomenon. According to Fourier’s theorem, any periodic or non-periodic signal can be decomposed into a combination of harmonically related sinusoidal signals. Therefore, the turbulent magnetic field in the solar wind can be decomposed into a series of sinusoidal signals. If we can prove that there exists a quasi-steady flow field corresponding to a time-varying magnetic field such as a sinusoidal signal in 3D magnetic reconnection, then the turbulent solar wind might have the possibility to produce quasi-steady magnetic reconnection. Following the method adopted before, we assume a classical X-type magnetic field along with a sinusoidal time-dependent perturbation:

$\mathit{B}\left(\mathit{r},t\right)=\left(y/L,k^{2}x/L,B_{\mathrm{z}}\right)\left(B_1+B_2\sin \left(\omega t\right)\right)(27)$

Here the reconnecting field component, $B_{xy}=\left(y/L,k^{2}x/L\right)$ and the guide field component B_z are specifically addressed to analyze the effect of the guide field on the stability of the reconnection outflows. To make Equations 1–4 analytically solvable, and by following the similar derivation method [26, 53], we construct the following magnetic vector potential:

$\mathit{A}\left(\mathit{r},t\right)=\left(k^{2}xz/L,B_{\mathrm{z}}x,y^2/\left(2L\right)\right)\left(B_1+B_2\sin \left(\omega t\right)\right)(28)$

Assuming $\mathit{X}\left(s,t\right)=\mathit{X}\left(s\right)X\left(t\right)$, the corresponding inverse mapping of $\mathit{X}\left(x_0,s\right)$ can be written as:

$X_0=\mathit{x}\cosh \left(\mathit{k}\mathit{s}/\mathit{L}\right)-\mathit{y}\sinh \left(\mathit{k}\mathit{s}/\mathit{L}\right)/\mathit{k}(29)$

$Y_0=y\cosh \left(ks/L\right)-kx\sinh \left(ks/L\right),(30)$

$Z_0=-s+z.(31)$

Adopting the same boundary conditions [53], the magnetic diffusion coefficient is also set as:

$\eta \left(x_0,y_0,s\right)={\eta }_0\exp \left(-\left(s^2+x_0^2+y_0^2\right)/l^2\right)(32)$

where l is a constant that governs the scale of a non-ideal region. Here, the electric field can be deduced from Equations 9, 11 and Equations 27–32. Then, the flow can be determined as follows:

${\mathit{u}}_{\perp }=\frac{\left(\mathit{E}-\eta \mathit{J}\right)\times \mathit{B}}{{\mathit{B}}^2}(33)$

The solid lines in Figure 1 represent the magnetic field variations, while the dashed lines represent the outflows deduced from Equation 33. It is evident that the outflows exhibit corresponding periodic oscillations in response to the periodic variations of the magnetic field. In scenarios with lower guide field conditions, the system tends to amplify the fluctuations in the magnetic field, leading to increases in the amplitude of velocity disturbances. As the guide field increases, these disturbances are suppressed, and the oscillation amplitude of the outflows gradually decreases. Notably, when B_z/B_xy > 0.2, the outflow exhibits obvious stability. Hence, the presence of the guide field significantly enhances the stability of the reconnection outflow. Figure 1 also reveals that for a sinusoidally varying magnetic field, 3D magnetic reconnection can generate a quasi-steady flow that corresponds to these magnetic field variations if a suitable range of angular frequencies, disturbance amplitudes and guide field are satisfied.

Figure 1

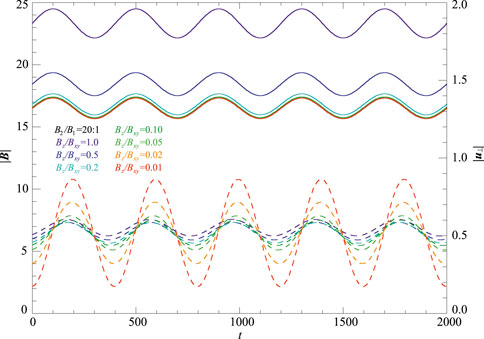
Figure 1. Schematic representation of the temporal variations in magnetic field (solid lines) and outflow (dashed lines) in a 3D magnetic reconnection for parameters: k = 2, L = 10, l = 1, B₁ = 20, B₂ = 1, ω = π/200, x = 2, y = 2, z = 2. Different colors denote different B_z/B._xy.

It should be noted that the single X-type topology for solar wind reconnection exhausts has never been completely observed. There are only fragmentary observational evidences from multi-spacecraft measurements suggesting that the most likely geometric structure of the reconnection exhaust is a large-scale X-line shape [54–56, 61]. Since a single spacecraft can only observe the solar wind passing by it, providing essentially one-dimensional observations without three-dimensional information, the actual reconnection topology for solar wind could be more complex. However, our intention here was not to argue whether the reconnection exhaust should conform to such a classical X-type structure, but rather to discuss the possibility of quasi-steady reconnection flow. In addition, the above analysis does not essentially incorporate any turbulent components in the classical sense, whereas turbulence has been demonstrated in the literature to significantly affect magnetic field diffusivity, i.e., reconnection diffusion and reconnection rate [63, 65]. From this point of view, the analysis primarily represents a laminar flow perspective. Nevertheless, this approach could also serve as a purely theoretical framework for analytically validating the potential existence of quasi-steady flows in 3D magnetic reconnection within disturbed magnetic field configurations. By adopting Fourier’s signal decomposition approach, the above efforts might still enhance our ability to interpret reconnection phenomena in turbulent solar wind.

In summary, due to the complexity and difficulty of analytical work, many previous studies have disregarded the time variable and focused exclusively on static magnetic reconnection analysis to deduce solutions. Consequently, most of these works cannot address how reconnection flows evolve over time. In this paper, we analytically solve the time-dependent kinematic 3D magnetic reconnection with generalized spatiotemporal distribution forms of the magnetic field and magnetic diffusivity. Although the required spatiotemporal distributions are too strict to be found in actual cosmic space, through a purely theoretical analytical approach, we have demonstrated for the first time that steady reconnection flow can exist. These results could contribute to a deeper understanding of the stability and conditions required for the existence of 3D magnetic reconnection, offering new insights into quasi-steady reconnection in various cosmic environment.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YLC: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. YW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. FSW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. XSF: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. ZLZ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. BYW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. PBZ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. CWJ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. YXG: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. LDW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. XJS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing. XJX: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is jointly supported by the National Natural Science Foundation of China 42174199, Guangdong Basic and Applied Basic Research Foundation 2023B1515040021, Shenzhen Technology Project JCYJ20210324121210027 and RCJC20210609104422048, and Shenzhen Key Laboratory Launching Project No. ZDSYS20210702140800001.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1439949/full#supplementary-material

References

1. Titov VS. Generalized squashing factors for covariant description of magnetic connectivity in the solar corona. Astrophys J (2007) 660:863–73. doi:10.1086/512671

CrossRef Full Text | Google Scholar

2. Vytenis V. Theoretical models of magnetic field line merging. Rev Geophys And Space Phys (1975) 13:303–36. doi:10.1029/RG013i001p00303

CrossRef Full Text | Google Scholar

3. Giovanelli RG. A theory of chromospheric flares. Nature (1946) 158:81–2. doi:10.1038/158081a0

CrossRef Full Text | Google Scholar

4. Russell CT, Elphic RC. ISEE observations of flux-transfer events at the dayside magnetopause. Geophys Res Lett (1979) 6(1):33–6. doi:10.1029/GL006i001p00033

CrossRef Full Text | Google Scholar

5. Lee LC, Fu ZF. A theory of magnetic-flux transfer at the earths magnetopause. Geophys Res Lett (1985) 12(2):105–8. doi:10.1029/GL012i002p00105

CrossRef Full Text | Google Scholar

6. Parker EN. Sweet's mechanism for merging magnetic fields in conducting fluids. J Geophys Res (1957) 62:509–20. doi:10.1029/JZ062i004p00509

CrossRef Full Text | Google Scholar

7. Sweet PA. The neutral point theory of solar flares. In: Symposium - international astronomical Union (1958). England: University of London Observatory, 123–34.

CrossRef Full Text | Google Scholar

8. Petschek HE. Magnetic field Annihilation. In: The Physics of Solar Flares, Proceedings of the AAS-NASA Symposium; 28-30 October, 1963; Greenbelt, MD: Goddard Space Flight Center. Editor NH Wilmot Washington, DC, 425 (1964).

Google Scholar

9. Birn J, Priest ER. Reconnection of magnetic fields: magnetohydrodynamics and collisionless theory and observations. Cambridge: Cambridge University Press (2007).

Google Scholar

10. Burch JL, Torbert RB, Phan TD, Chen L-J, Moore TE, Ergun RE, et al. Electron-scale measurements of magnetic reconnection in space. Science. 2016;352(6290):aaf2939. doi:10.1126/science.aaf2939

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Vilmer N, Mackinnon AL, Hurford GJ. Properties of energetic ions in the solar atmosphere from γ-ray and neutron observations. Space Sci Rev (2011) 159(1-4):167–224. doi:10.1007/s11214-010-9728-x

CrossRef Full Text | Google Scholar

12. Benz AO. Flare observations. Living Rev Solar Phys (2017) 14(1):2. doi:10.1007/s41116-016-0004-3

CrossRef Full Text | Google Scholar

13. Phan TD, Bale SD, Eastwood JP, Lavraud B, Drake JF, Oieroset M, et al. Parker solar probe in situ observations of magnetic reconnection exhausts during encounter 1. The Astrophysical J Suppl Ser (2020) 246(2):34. doi:10.3847/1538-4365/ab55ee

CrossRef Full Text | Google Scholar

14. Fujimoto K. Multi-scale kinetic simulation of magnetic reconnection with dynamically adaptive meshes. Front Phys (2018) 6. doi:10.3389/fphy.2018.00119

CrossRef Full Text | Google Scholar

15. Sisti M, Faganello M, Califano F, Lavraud B. Satellite data based 3D simulation of kelvin helmholtz instability and induced magnetic reconnection at the earth's magnetopause. Geophys Res Lett (2019) 46(21):11597–605. doi:10.1029/2019gl083282

CrossRef Full Text | Google Scholar

16. Lapenta G, Markidis S, Goldman MV, Newman DL. Secondary reconnection sites in reconnection-generated flux ropes and reconnection fronts. Nat Phys (2015) 11(8):690–5. doi:10.1038/nphys3406

CrossRef Full Text | Google Scholar

17. Pezzi O, Liang H, Juno JL, Cassak PA, Vásconez CL, Sorriso-Valvo L, et al. Dissipation measures in weakly collisional plasmas. Monthly Notices R Astronomical Soc (2021) 505(4):4857–73. doi:10.1093/mnras/stab1516

CrossRef Full Text | Google Scholar

18. Rosenberg MJ, Li CK, Fox W, Igumenshchev I, Seguin FH, Town RP, et al. A laboratory study of asymmetric magnetic reconnection in strongly driven plasmas. Nat Commun (2015) 6:6190. doi:10.1038/ncomms7190

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bolaños S, Sladkov A, Smets R, Chen SN, Grisollet A, Filippov E, et al. Laboratory evidence of magnetic reconnection hampered in obliquely interacting flux tubes. Nat Commun (2022) 13(1):6426. doi:10.1038/s41467-022-33813-9

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Yamada M, Chen LJ, Yoo J, Wang S, Fox W, Jara-Almonte J, et al. The two-fluid dynamics and energetics of the asymmetric magnetic reconnection in laboratory and space plasmas. Nat Commun (2018) 9(1):5223. doi:10.1038/s41467-018-07680-2

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Angus JR, Link AJ, Schmidt AE. 1D kinetic study of pinch formation in a dense plasma focus: transition from collisional to collisionless regimes. Phys Plasmas (2021) 28(1):1–5. doi:10.1063/5.0028988

CrossRef Full Text | Google Scholar

22. Hesse M, Schindler K. A theoretical foundation of general magnetic reconnection. J Geophys Res (1988) 93(A6):5559–67. doi:10.1029/JA093iA06p05559

CrossRef Full Text | Google Scholar

23. Schindler K, Hesse M, Birn J. General magnetic reconnection, parallel electric fields, and helicity. J Geophys Res (1988) 93(A6):5547–57. doi:10.1029/JA093iA06p05547

CrossRef Full Text | Google Scholar

24. Hantao J. Major scientific challenges and opportunities in understanding magnetic reconnection and related explosive phenomena in magnetized plasmas. White Paper Plasma 2020 Decadal Surv (2019) 1–4. doi:10.48550/arXiv.2004.00079

CrossRef Full Text | Google Scholar

25. Pontin DI, Priest ER. Magnetic reconnection: MHD theory and modelling. Living Rev Solar Phys (2022) 19(1):1. doi:10.1007/s41116-022-00032-9

CrossRef Full Text | Google Scholar

26. Hornig G, Priest E. Evolution of magnetic flux in an isolated reconnection process. Phys Plasmas (2003) 10:2712–21. doi:10.1063/1.1580120

CrossRef Full Text | Google Scholar

27. Pontin DI, Hornig G, Priest ER. Kinematic reconnection at a magnetic null point: spine-aligned current. Geophys and Astrophysical Fluid Dyn (2004) 98(5):407–28. doi:10.1080/0309192042000272324

CrossRef Full Text | Google Scholar

28. Pontin DI. Three-dimensional magnetic reconnection regimes: a review. Adv Space Res (2011) 47(9):1508–22. doi:10.1016/j.asr.2010.12.022

CrossRef Full Text | Google Scholar

29. Titov VS, Tassi E, Hornig G. Exact solutions for steady reconnective annihilation revisited. Phys Plasmas (2004) 11(10):4662–71. doi:10.1063/1.1789159

CrossRef Full Text | Google Scholar

30. Tassi E. Analytical solutions for reconnective magnetic annihilation. In: AIP Conference Proceedings2004. 76–9.

Google Scholar

31. Mellor C, Priest ER, Titov VS. Exact solutions for spine reconnective magnetic annihilation. Geophys Astrophysical Fluid Dyn (2002) 96(2):153–71. doi:10.1080/03091920290004470

CrossRef Full Text | Google Scholar

32. Priest ER, Sonnerup BUO. Theories of magnetic field annihilation. Geophys J R Astronomical Soc (1975) 41:405–13. doi:10.1111/j.1365-246X.1975.tb01623.x

CrossRef Full Text | Google Scholar

33. Parker EN. Comments on the reconnexion rate of magnetic fields. J Plasma Phys (1973) 9(1):49–63. doi:10.1017/s0022377800007327

CrossRef Full Text | Google Scholar

34. Sonnerup BUO, Priest ER. Resistive MHD stagnation-point flows at a current sheet. J Plasma Phys (1975) 14:283–94. doi:10.1017/S0022377800009570

CrossRef Full Text | Google Scholar

35. Craig IJD, McClymont AN. Dynamic magnetic reconnection at an x-type neutral point. Astrophys J (1991) 371(1):L41–L4. doi:10.1086/185997

CrossRef Full Text | Google Scholar

36. Craig IJD, Fabling RB, Henton SM, Rickard GJ. An exact solution for steady state magnetic reconnection in three dimensions. Astrophysical J Lett (1995) 455(2):L197–9. doi:10.1086/309822

CrossRef Full Text | Google Scholar

37. Craig IJD, Henton SM. Exact solutions for steady-state incompressible magnetic reconnection. Astrophys J (1995) 450:280–8. doi:10.1086/176139

CrossRef Full Text | Google Scholar

38. Craig IJD, Fabling RB. Exact solutions for steady-state, spine, and fan magnetic reconnection. Astrophys J (1996) 462:969–76. doi:10.1086/177210

CrossRef Full Text | Google Scholar

39. Yang WH. Self-similar evolution of magnetized plasmas .2. nonequilibrium solutions and hubbles expansion. Astrophys J (1994) 425(2):439–41. doi:10.1086/173998

CrossRef Full Text | Google Scholar

40. Priest ER, Hornig G, Pontin DI. On the nature of three-dimensional magnetic reconnection. J Geophys Res (2003) 108(A7). doi:10.1029/2002ja009812

CrossRef Full Text | Google Scholar

41. Hornig G, Schindler K. Magnetic topology and the problem of its invariant definition. Phys Plasmas (1996) 3(3):781–91. doi:10.1063/1.871778

CrossRef Full Text | Google Scholar

42. Pontin DI, Hornig G, Priest ER. Kinematic reconnection at a magnetic null point: fan-aligned current. Geophys and Astrophysical Fluid Dyn (2005) 99(1):77–93. doi:10.1080/03091920512331328071

CrossRef Full Text | Google Scholar

43. Wilmot-Smith A, Hornig G, Priest E. Dynamic non-null magnetic reconnection in three dimensions. I. Particular solutions. Proc R Soc A: Math Phys Eng Sci (2006) 462(2074):2877–95. doi:10.1098/rspa.2006.1697

CrossRef Full Text | Google Scholar

44. Wilmot-Smith AL, Priest ER. Flux tube disconnection: an example of three-dimensional reconnection. Phys Plasmas (2007) 14(102903):1–9. doi:10.1063/1.2783257

CrossRef Full Text | Google Scholar

45. Wilmot-Smith AL, Hornig G, Priest ER. Dynamic non-null magnetic reconnection in three dimensions–II: composite solutions. Geophys and Astrophysical Fluid Dyn (2009) 103(6):515–34. doi:10.1080/03091920903164294

CrossRef Full Text | Google Scholar

46. Wilmot-Smith AL, Hornig G. A time-dependent model for magnetic reconnection in the presence of a separator. The Astrophysical J (2011) 740(2):89. doi:10.1088/0004-637x/740/2/89

CrossRef Full Text | Google Scholar

47. McMahon LC. Visco-resistive length scale in flux pile-up and series solutions for magnetic reconnection. Phys Plasmas (2017) 24(5). doi:10.1063/1.4982663

CrossRef Full Text | Google Scholar

48. Priest ER, Titov VS, Grundy RE, Hood AW. Exact solutions for reconnective magnetic annihilation. Proc Math Phys Eng Sci (2000) 456:1821–49. doi:10.1098/rspa.2000.0588

CrossRef Full Text | Google Scholar

49. Pritchett PL. The onset of magnetic reconnection in three dimensions. Phys Plasmas (2013) 20(8). doi:10.1063/1.4817961

CrossRef Full Text | Google Scholar

50. Luo L, Xu X, Song L, Zhou M, Zhou Z, Man H, et al. The current tension electric field in the generalized Ohm's law. Geophys Res Lett (2024) 51(4). doi:10.1029/2023gl107191

CrossRef Full Text | Google Scholar

51. Anderson C, Priest ER. Time-dependent magnetic annihilation at a stagnation point. J Geophys Res Space Phys (1993) 98(A11):19395–407. doi:10.1029/92ja02723

CrossRef Full Text | Google Scholar

52. Wilmot-Smith AL, Priest ER, Hornig G. Magnetic diffusion and the motion of field lines. Geophys and Astrophysical Fluid Dyn (2005) 99(2):177–97. doi:10.1080/03091920500044808

CrossRef Full Text | Google Scholar

53. Chen Y, Wang Y, Wei F, Feng X, Zhou Z, Wang B, et al. Analytical solutions for time-dependent kinematic three-dimensional magnetic reconnection. PLOS ONE (2023) 18(5):e0286138. doi:10.1371/journal.pone.0286138

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Davis MS, Phan TD, Gosling JT, Skoug RM. Detection of oppositely directed reconnection jets in a solar wind current sheet. Geophys Res Lett (2006) 33(19):L19102. doi:10.1029/2006gl026735

CrossRef Full Text | Google Scholar

55. Phan TD, Gosling JT, Davis MS, Skoug RM, Oieroset M, Lin RP, et al. A magnetic reconnection X-line extending more than 390 Earth radii in the solar wind. Nature (2006) 439(7073):175–8. doi:10.1038/nature04393

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Wang Y, Wei FS, Feng XS, Zhang SH, Zuo PB, Sun TR. Energetic electrons associated with magnetic reconnection in the magnetic cloud boundary layer. Phys Rev Lett (2010) 105(19):195007. doi:10.1103/PhysRevLett.105.195007

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Gosling JT. Magnetic reconnection in the solar wind. Space Sci Rev (2012) 172(1-4):187–200. doi:10.1007/s11214-011-9747-2

CrossRef Full Text | Google Scholar

58. Gosling JT, Eriksson S, Blush LM, Phan TD, Luhmann JG, McComas DJ, et al. Five spacecraft observations of oppositely directed exhaust jets from a magnetic reconnection X-line extending >4.26 × 10⁶ km in the solar wind at 1 AU. Geophys Res Lett (2007) 34(20):L20108. doi:10.1029/2007gl031492

CrossRef Full Text | Google Scholar

59. Gosling JT, Eriksson S, Schwenn R. Petschek-type magnetic reconnection exhausts in the solar wind well inside 1 AU: helios. J Geophys Res Space Phys (2006) 111(A10). doi:10.1029/2006JA011863

CrossRef Full Text | Google Scholar

60. Gosling JT, Eriksson S, Skoug RM, McComas DJ, Forsyth RJ. Petschek-type reconnection exhausts in the solar wind well beyond 1 AU: ulysses. The Astrophysical J (2006) 644(1):613–21. doi:10.1086/503544

CrossRef Full Text | Google Scholar

61. Gosling JT, Phan TD, Lin RP, Szabo A. Prevalence of magnetic reconnection at small field shear angles in the solar wind. Geophys Res Lett (2007) 34(15). doi:10.1029/2007gl030706

CrossRef Full Text | Google Scholar

62. Li T, Priest E, Guo R. Three-dimensional magnetic reconnection in astrophysical plasmas. Proc R Soc A: Math Phys Eng Sci (2021) 477(2249). doi:10.1098/rspa.2020.0949

CrossRef Full Text | Google Scholar

63. Lazarian A, Vishniac ET. Reconnection in a weakly stochastic field. The Astrophysical J (1999) 517:700–18. doi:10.1086/307233

CrossRef Full Text | Google Scholar

64. Eyink G, Vishniac E, Lalescu C, Aluie H, Kanov K, Bürger K, et al. Flux-freezing breakdown in high-conductivity magnetohydrodynamic turbulence. Nature (2013) 497(7450):466–9. doi:10.1038/nature12128

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Kowal G, Lazarian A, Vishniac ET, Otmianowska-Mazur K. Numerical tests of fast reconnection in weakly stochastic magnetic fields. The Astrophysical J (2009) 700(1):63–85. doi:10.1088/0004-637x/700/1/63

CrossRef Full Text | Google Scholar

66. Muñoz PA, Büchner J. Kinetic turbulence in fast three-dimensional collisionless guide-field magnetic reconnection. Phys Rev E (2018) 98(4):043205. doi:10.1103/physreve.98.043205

CrossRef Full Text | Google Scholar

67. Zharkova V, Xia Q. Kinetic plasma turbulence generated in a 3D current sheet with magnetic islands. Front Astron Space Sci (2021) 8. doi:10.3389/fspas.2021.665998

CrossRef Full Text | Google Scholar

68. Kowal G, Falceta-Gonçalves DA, Lazarian A, Vishniac ET. Statistics of reconnection-driven turbulence. The Astrophysical J (2017) 838(2):91. doi:10.3847/1538-4357/aa6001

CrossRef Full Text | Google Scholar