Preparations for pB11 tests in the FF-2B dense plasma focus

The dense plasma focus (DPF) device has great potential as a fusion energy generator using hydrogen-boron (pB11) fuel¹. Experiments using deuterium have already demonstrated mean ion energies >200 keV, in the range needed for burning pB11². To test that potential, we are preparing for experiments with hydrogen-boron fuel in the megampere DPF device, FF-2B. We plan to use isotopically-pure decaborane (B₁₀H₁₄) as the fuel source and have installed equipment for the safe handling and disposal of the toxic vapors from this material. High isotopic purity of the boron-11 is required to avoid generation of radioactive Be-7. While the main pB11 fusion reaction produces no neutrons, two side reactions do produce both neutrons and radioactive C-11. We show how these reaction products can be used with suitable detectors to provide accurate data on fusion yield, and the density and ion energy of the confined fusion-producing plasma.

1 Introduction

For pB11 fusion the DPF has several large advantages, which have been discussed in the literature [1]. First, pB11 requires mean ion energies well above 100 keV for adequate reaction rates and only the DPF, the z-pinch and laser have demonstrated the ability to reach such ion energy [3]. LPPFusion’s FF-1 device achieved in 2016 a record mean ion energy >200keV, enough to initiate significant pB11 burn [2]. The ten-shot mean ion-energy of 125 keV was also high in the same experimental series. Similarly, these same three devices are the only ones that have demonstrated the capability of achieving high ion densities >10¹⁵/cm³. In the DPF, densities as high as 10²¹/cm³ have been demonstrated, although not yet simultaneously with high ion energy [4]. Such high densities have great advantages in any future fusion generators. Among these are relatively compact, low-cost devices, and the DPF is certainly among the lowest cost fusion devices today, with large megampere devices costing less than $ 1 million to construct [3].

In addition, the high magnetic fields associated with such high densities make possible the use of the quantum magnetic field effect to reduce bremsstrahlung radiation [5]. This is particularly important with pB11 fuel, where the relatively higher Z of boron nuclei tends to increase bremsstrahlung. Finally, DPF device allow high efficiency of energy transfer from the capacitor bank into the fusion-producing plasmoids. Efficiencies >10% have been achieved [6] in converting capacitor bank energy into x-ray emission, and considerably higher efficiency of energy transfer into the plasmoid is clearly possible, since total energy in the plasmoid must significantly exceed x-ray emission.

Based on these advantages, researchers have for decades considered using DPF device to burn pB11 fuel [7–10]. However, the significant challenges of switching from the inexpensive and convenient deuterium fuel to boron fuels have prevented successful tests so far. It is in this context that LPPFusion is preparing new experiments that we expect will for the first time achieve observable amounts of pB11 fusion in a DPF device, a combination we have termed “Focus Fusion”.

2 Decaborane fuel

To introduce hydrogen and boron into the DPF vacuum chamber, we’ve chosen to use the vapor state of the compound decaborane (B₁₀H₁₄). There are a number of advantages to this compound. First is simplicity. While decaborane is a solid powder at room temperature, modest heating generates sufficient vapor pressure for DPF functioning [11]. This means that, with suitable handling, the fuel can be fed into the chamber in the same way as deuterium or other commonly-used fill gases.

Other methods of introducing boron have been proposed, but they are all more complex. Solid boron can be introduced into the pinch region either by emplacing a solid boron target at the center of the anode or by dropping small pellets of boron through the anode, timed to arrive at the same time as the pinch currents. The solid boron can then by vaporized and ionized either by a laser pulse or, if the pellet is small enough, by the hot plasma in the current sheath [9, 12].

In addition, a boron-containing gas can be introduced only at the anode through a gas-puff, in which a fast valve shoots the gas into the hole in the anode, again timed to arrive right before the pinch time of the DPF.

These methods have the advantage that hydrogen can be used as the fill gas and that therefore any problems arising from the breakdown of decaborane or during the rundown of the current sheath as it moves to the end of the anode are avoided. The significant disadvantage of all of them is their inherent additional layers of complexity. It is well-known that the performance of the DPF depends greatly on the symmetry of the compression phases. The introduction of the laser or pellet vaporization or gas puff means that there is a second independent process that must be made highly symmetrical and also highly synchronous with the current sheath. If insurmountable problems are encountered with decaborane, these methods are certainly possible alternative paths, but they inevitably require a higher level of effort and time than the fill-gas approach.

Decaborane is only one of a class of boranes—hydrogen-boron compounds. We selected decaborane for two reasons. First, it is the borane with the largest ratio of boron to hydrogen, 0.71. This means that we can easily achieve any boron mix below this level by adding or removing hydrogen gas. For the other boranes, ratios above 0.56 are not accessible. Second, decaborane is a solid at room temperature and acquires a vapor pressure of only 20 torr at 100°C. This means that in the event of a vacuum system failure, the gas will always be at negative pressure relative to the exterior, a safety feature. In contrast, pentaborane, diborane and borane are all gases at room temperature, and are all, like decaborane, toxic, so can escape into the laboratory or the environment if a gas line leaks.

The solid decaborane powder itself poses little hazard. At 40°C, about as hot as it gets in the environment, the vapor pressure of decaborane amounts to 1.6 mg per cubic meter of air. The NIOSH immediate danger to life and health (IDLH) level for decaborane is 15 mg per cubic meter of air, almost ten times higher. By comparison, iodine, which is just about as toxic in gaseous form, has a vapor pressure at 40°C that is about 300 times higher than decaborane.

When decaborane is vented to the atmosphere, it can be destroyed simply by bubbling through water, which converts it and other boranes to harmless boric acid and hydrogen. We have already installed a bubbler in our exhaust line in preparation for decaborane tests.

One valid safety concern that does arise not only for decaborane but for all boron fuels is the production of Be-7 by fusion reactions with B-10. For natural boron, with 20% B-10, the reaction of protons with B-10 has a significant yield which rises with mean ion energy somewhat faster than does the fusion yield for B-11. For a typical ion energy of 600 keV, B-10 reactions are about 4% of B-11 reactions. Given the 53-day half-life of Be-7, considerable amounts could accumulate if high fusion yield was achieved. The decay of Be-7 results in the emission of 0.477 MeV gamma rays, which require significant shielding.

For example, for 25 shots per week and 50 kJ fusion yield per shot, a level which would be required to demonstrate net energy from the device, Be-7 radiation at 1 m from the vacuum chamber would be 250 mR/h, 12,000 times the standard background level. In other words, at this modest rate of firing, even 4J of fusion energy per shot would exceed the background radiation level without shielding. By comparison, deuterium’s 2.45 MeV neutrons do not produce detectable amounts of activation even compared with the low background level of 4 μR/h in our laboratory.

To address this safety concern, we procured isotopically pure decaborane with 0.07% B-10.This represents a 350-fold reduction in B-10 abundance and thus Be-7 production. So, even with the optimistic fusion yields above, radiation would be only 35 times background or 0.7 mR/h. Safety limits will not be exceeded in this case if work in the immediate vicinity of the vacuum chamber is limited to 3 h/week per person. This is certainly adequate for experimental purposes.

In the case of a future working fusion generator (not, like FF-2B, an experimental device) with 10⁸ shots per week, some combination of higher purity and engineering measures to prevent the Be-7 from depositing on the Be-8 electrodes can reduce radiation to safe levels for maintenance personnel. If Be-7 particles are continually filtered from the DPF exhaust to a shielded container, for a maintenance shutdown, a chamber should contain only one chamber-fill worth of Be-7 or only 25 min production. Reducing B-10 to a ppm level, not technically challenging with mass-production, should eliminate excess radiation in this case as well.

Another safety consideration arises from the side reaction p+¹¹B → ¹¹C+n. While only occurring at high energies and producing far fewer reactions than the main aneutronic reaction, this reaction can cause a potential safety hazard if the C-11 reacts chemically with the H in the chamber to form radioactive methane. At this time, we have no way to estimate how much of the C-11 will react this way and how much will be deposited by the ion beam in the drift tube. To deal with this potential hazard, we have made the functioning of the experimental chamber entirely remote and will hold exhaust gases in a dump chamber overnight to allow for complete decay.

In the DPF, approximate fill pressures can be calculated on the basis of known vapor-pressure temperature relations for decaborane and the expected operating conditions. The vapor pressure of decaborane can be closely approximated by log(p) = −4884/T −7.06 log(T)+29.676, where p is in bars and T is K. We expect peak Alfven velocities during the run-down phases of about 6.6 cm/μs. With our FF-2B anode radius of 2.8 cm and an expected maximum current of FF-2B of 2.7 MA, we would expect a maximum ion density of 7.3 × 10¹⁸/cm³ with pure decaborane, equivalent to a pressure of 10 torr. This can be obtained with a heating temperature of only 90°C.

3 Diagnostic techniques

The great advantage of pB11 fusion—that the main reaction produces no neutrons—poses a problem for plasma diagnostics, since the reaction product—alpha particles--can’t exit the vacuum chamber as the neutrons easily can. While the alphas can be measured with instruments inside the chamber, the high energy densities typical of the DPF make the design of survivable instruments difficult. Instead, we have taken the approach to diagnosing the plasma using neutrons and gamma rays that result from secondary reactions both of the initial fuel and with the product alphas.

There are two secondary reactions that are of importance in pB11 fusion. As already noted, in the high energy tail of the ion energy distribution the reaction p+¹¹B → ¹¹C+n occurs with a threshold energy of 3 MeV and a net energy of −2.8 MeV (endothermic). Second, once alpha particles are produced, they can react with B-11 nuclei via α+¹¹B → ¹⁴N+n. This reaction has a threshold of 0.3 MeV and energy release of 157 keV, but the main cross section peaks at 0.24 b at 5 MeV. This means that the main contribution to the reaction comes from alpha particles slowing down from the energy that they have from the initial reaction. The alpha particle energy spectrum extends to 6 MeV with a peak at 4.2 MeV. In turn, this makes the neutron production mainly dependent on the number of alpha particles produced, since the alphas encounter a similar number of nuclei during slow-down regardless of the plasma density. That is, a higher density means a faster slow-down but the surface density of particles traversed during slow down, and thus the probability of fusion reactions, is unchanged. Approximately one N-14 reaction occurs for every 70 pB11 reactions.

This is the case for plasma with nτ >2 × 10¹³ s/cm³. For shorter-lived plasmas, slowing down is not complete during the plasma lifetime. By comparison, the highest nτ obtained with our experiments is 2.4 × 10¹² s/cm³. However, we expect to achieve nτ >2 × 10¹³ s/cm³ prior to initiating pB11 experiments, by improving the symmetry of the DPF breakdown and thus of the current sheath. This will in turn improve the symmetry of the compression phase and thus the density of the plasmoid.

In both secondary reactions, emitted neutrons can be recorded with time-of-flight (ToF) PMTs (scintillators coupled to photomultiplier tubes) to obtain a neutron energy spectrum. Due to the very different energetics of the reactions, the contributions of the two sources can be easily distinguished. Since the reaction producing C-11 is sensitive to the ion temperature and the N-14 reaction is not, modeling the resulting neutron spectrum can yield a measurement of T_i. In turn, this value can be used to derive the product n²Vτ where V is plasmoid volume. The combined signals of the two ToF (plus additional PMTs we have located closer to the device) can provide τ.

In our experiments we use PMTs located perpendicular to the axis of the device at 11.5 m (NTF or near time of flight) and 17.5 m (FTF or far time of flight). In experiments with deuterium, we’ve obtained good-quality neutron energy spectra from hundreds of shots [2]. Figure 1 shows simulated arrival times and amplitudes of neutron signals at the FTF for a Maxwellian plasma with mean T_i = 1 MeV. The signal for the N-14 reaction is calculated simply from the reaction cross section and slowing-down rate. The signal for the C-11 reaction is calculated from the reaction rate for a Maxwellian distribution. For this example, a high T_i is chosen to make the C-11 signal comparable in amplitude to the N-14 signal. For lower T_i it will be smaller. Since the early peak due to the slowing-down alphas around 500 ns and the late peak due to the C-11 reaction from 1,100–1,220 ns practically do not overlap, the two sources can be modeled almost independently.

Figure 1

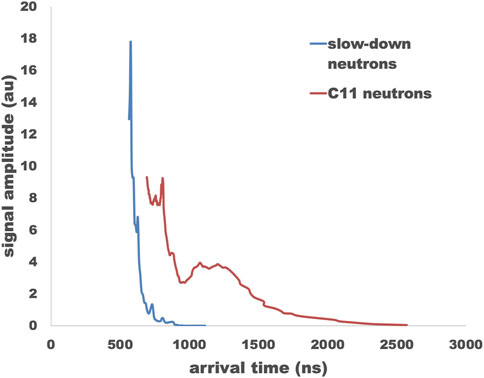
Figure 1. Simulated neutron PMT signals from 1 MeV plasma showing difference between neutrons emitted by pB11reactions producing C11 (red line) and those emitted from He-B11 reactions during alpha particle slow-down.

The PMTs can produce useful time-of-flight signals with as few as 2 × 10⁹ neutrons emitted, which can be produced from the N-14 reaction in plasmas that produce a minimum of 1.4 × 10¹¹ pB11 reactions. However, we also detect neutrons with a silver activation detector at only 1.3 m from the source. This has about 4 times better sensitivity, allowing the detection of neutrons indicating as few as 3.5 × 10¹⁰ pB11 reactions. By comparison, our best results so far with deuterium, which is far less reactive, is 2.5 × 10¹¹ reactions.

Since the C-11 PMT signal is strongly dependent on T_i, with the ratio of C11/pB11 reactions going from 2 × 10⁻⁷ to 2 × 10⁻² as T_i goes from 200 keV to 1 MeV, the C-11 data is not significant until T_i >600 keV. However, the total number of C-11 reaction can be measured more sensitively by measuring the γ-rays emitted in the decay of C-11. With a half-life of only 20 min, C-11 is easily detectable.

With a Geiger counter as few as 6 × 10⁶ C-11 nuclei can be detected at a distance of 10 cm. A γ-ray spectrometer can detect the line radiation from as few as 5 × 10⁵ nuclei at the same distance. While laboratory γ-ray spectrometers are costly, consumer products are now available for as little as $300 which produce excellent results [13]. This performance means that C-11 reactions can be detected even at T = 200 keV for 2.5 × 10¹² pB11 reactions.

At higher levels of fusion burn, the γ-ray spectrometers can measure the ratio of alpha particles to p and B-11 nuclei directly the ion beam emitted from the plasmoid. When the ions in the ion beam strike the sides and bottom of the drift tube that extends from the vacuum chamber, they produce a γ-ray spectrum that allows the characterization of the energy spectra of the ions. The acceleration process in the plasmoid generates a high electric field that gives the ions a spectrum of energies proportional to their atomic charges. This in turn produces peaks in the γ-ray spectrum that are proportional to the abundance of the three nuclear species—protons, alphas and borons—in the beam.

Using deuterium fuel, we’ve obtained typical spectra from the beams in tests of the γ-ray spectrometers (Figure 2). With standard formula for scaling of γ-ray emission with different nuclei, we have produced simulated γ-ray spectra for beams with 0%, 10% and 50% burn-up of pB11 fuel. The energy of the ions is proportional to Z, while the amplitude of the γ-ray emission is proportional to Z². As can be seen (Figure 3) these high-burn conditions can easily be distinguished in the γ-ray spectra. Total charge transferred can be measured by a Rogowski coil, so changes in total beam intensity can be distinguished from changes in burn-up.

Figure 2

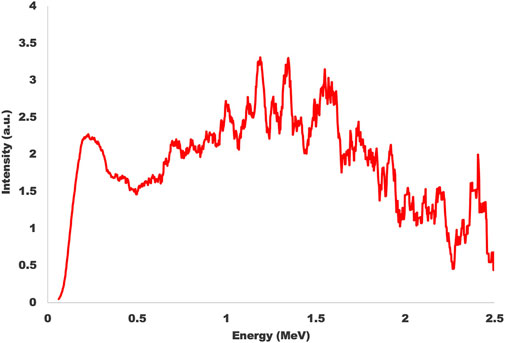
Figure 2. Gamma-ray spectrum from typical ion beam. Intensity is plotted as gamma ray intensity per logarithmic unit of gamma ray energy. Background has not been removed in this plot and is the cause of the peak at 0.3 MeV.

Figure 3

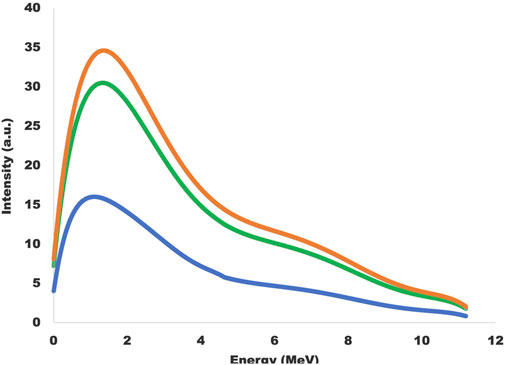
Figure 3. Simulated ion beam gamma ray spectra for 0% (orange line) 10% (green line) and 50% (blue line) burn up of pB11 fuel. In all cases the total charge of the beam is the same. The gamma ray intensity declines because single boron nuclei produce more radiation than three alpha particles.

4 Experimental plans

At present we are still completing the final tests to optimize the functioning of FF-2B with deuterium fuel. Once this is done, in the near future, we intend to start mixing increasing amount of hydrogen with the deuterium in preparation for using hydrogen-decaborane mixes. We need to eliminate deuterium from the mix before introducing decaborane, since the neutrons from deuterium reactions will interfere with the measurements described in section 3. This will involve further optimization, as the run-down times for the device require maintaining an approximately constant mass density in the plasma. However, increasing mixes of hydrogen with deuterium will require higher pressures to maintain the mass density and that may in turn make breakdown in the initial phases of the pulses more difficult and asymmetrical. We are currently developing methods of overcoming this breakdown asymmetry.

Once optimal conditions are reached with no deuterium present, we will begin introducing small amounts of decaborane with the initial goal of observing measurable amounts of pB11 fusion. Only once we have achieved optimal function with hydrogen-heavy mixes will we move toward more boron-heavy mixes. Since the breakdown characteristics of decaborane have not been well-studied, we expect that conditions will have to be adjusted as a pure decaborane operation is approached.

5 Conclusion

Preparations for experiments with hydrogen boron fuel using a dense plasma focus device are nearly complete at LPPFusion facilities. We expect that we will be able with these initial experiments to measure the number of fusion reactions taking place as well as the mean ion energy density and confinement time of the plasma. Initial experiments with dilute decaborane mixes with hydrogen will pave the way for later experiments with pure decaborane.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

EL: Conceptualization, Writing–original draft, Writing–review and editing. SH: Investigation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Funded by LPPFusion. We thank our investors and donors.

Conflict of interest

Authors EL and SH were employed by LPPFusion, Inc.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lerner EJ, Hassan SM, Karamitsos-Zivkovic I, Fritsch R. Focus fusion: overview of progress towards p-B¹¹ fusion with the dense plasma focus. J Fusion Energ (2023) 42:7. doi:10.1007/s10894-023-00345-z

CrossRef Full Text | Google Scholar

2. Lerner EJ, Hassan SM, Karamitsos I, Von Roessel F. Confined ion energy >200 keV and increased fusion yield in a DPF with monolithic tungsten electrodes and pre-ionization. Phys Plasmas (2017) 24(10):102708. doi:10.1063/1.4989859

CrossRef Full Text | Google Scholar

3. Lerner EJ, Hassan SM, Karamitsos-Zivkovic I, Fritsch R. What are the fastest routes to fusion energy? Phys Plasmas (2023) 30(12):120602. doi:10.1063/5.0170216

CrossRef Full Text | Google Scholar

4. Sakurai A, Shimoda K, Hirano K. Production of a solid density plasma by a plasma focus discharge. Jpn J Appl Phys (1978) 17:1687–8. doi:10.1143/jjap.17.1687

CrossRef Full Text | Google Scholar

5. Lerner EJ. In: E Panarella, editor. Current trends in international fusion research—proceedings of the fifth symposium. Ottawa, ON: National Research Council of Canada (2007).

Google Scholar

6. Filippov NV, Filippova TI, Khutoretskaia IV, Mialton VV, Vinogradov VP Megajoule scale plasma focus as efficient X-ray sourcePhysics Letters A, 211 (1996). p. 168.

CrossRef Full Text | Google Scholar

7. Witalis EA. Magnetically induced plasma rotation and the dense plasma focus. Z für Naturforschung A (1983) 38(9):949–58. doi:10.1515/zna-1983-0901

CrossRef Full Text | Google Scholar

8. Abolhasani S, Habibi M, Amrollahi R. Analytical study of quantum magnetic and ion viscous effects on p11B fusion in plasma focus devices. J Fusion Energ (2013) 32:189–95. doi:10.1007/s10894-012-9547-z

CrossRef Full Text | Google Scholar

9. Scholz M, Król K, Kulińska A, Karpiński L, Wójcik-Gargula A, Fitta M. On the possibility of initiating the proton–boron nuclear fusion reaction in the plasma-focus device. J Fusion Energ (2019) 38:522–30. doi:10.1007/s10894-019-00225-5

CrossRef Full Text | Google Scholar

10. Yousefi HR, Haruki T, Sakai JI, Lumanta A, Masugata K. Simulations of effective heating in heavy-ion beam-fusion: high density plasmas in plasma focus devices. Phys Lett A (2009) 373:2360–3. doi:10.1016/j.physleta.2009.04.069

CrossRef Full Text | Google Scholar

11. Miller GA. The vapor pressure of solid decaborane. J Phys Chem (1963) 67(6):1363–4. doi:10.1021/j100800a507

CrossRef Full Text | Google Scholar

12. Sadowski M.J, Paduch M, Kubes P, Krauz V, Gribkov V. A. Recent Achievements of Plasma Studies within PF-1000U Facility. Acta Physica Polonica A. (2020) 138:613–621. doi:10.12693/APhysPolA.138.613

CrossRef Full Text | Google Scholar

13. Radiacode. Available from: https://www.radiacode.com/products#!/Detector-of-nuclear-radiation-and-spectrometer-Radiacode-103/p/602724693/category=0.