- 1Department of Community Health Sciences, University of Manitoba, Winnipeg, MB, Canada
- 2Center for Healthcare Innovation, University of Manitoba, Winnipeg, MB, Canada
Compartmental models of disease spread have been well studied on networks built according to the Configuration Model, i.e., where the degree distribution of individual nodes is specified, but where connections are made randomly. Dynamics of spread on such “first order” networks were shown to be profoundly different compared to epidemics under the traditional mass action assumption. Assortativity, i.e., the preferential mixing of nodes according to degree, is a second order property that is thought to impact epidemic trajectory. We first show how assortative mixing can come about from individual preferences to connect with others of lower or higher degree, and propose an algorithm for constructing such a network. We then investigate via simulation how this network structure favors or inhibits diffusion processes, such as the spread of an infectious disease.
1 Introduction
Network architecture plays an essential role in the dynamics of diffusion processes. Heterogeneity in degree distribution was shown to induce radically different behaviors of processes compared to homogeneous networks, which are often assumed when modeling epidemic spread (e.g., a fully connected network). For example, when the degree distribution is power law with exponent less than 3, the epidemic threshold can be as low as zero [1, 2] and references therein. While diffusion dynamics on first order networks–by which we mean networks defined by degree distribution without higher order structure–are well understood [3–5], less is known about the behavior of such processes on second order networks. These are networks where both the degree (
While the discoveries in the physics literature on networks represent conceptual advances compared to the original 1927 paper of Kermack and McKendrick [10], which relied on the homogeneity assumption, and on which much of the later epidemiologic modeling is based, there are some important shortcomings related to modeling a realistic SIR epidemic. The literature has largely overlooked network construction aimed at building realistic human populations, in which epidemics spread. Classical network building algorithms, such as the configuration model (CM), the Barabási and Albert, and Erdős-Rényi graphs [11–13], are too limited as they cannot account for second order properties. The network construction algorithm in [14] is based on rewiring edges and can exactly replicate the edge matrix of a graph (
The literature on mechanistic network construction algorithms often comes from the fields of ecology and economic game theory. To study animal mating behavior, [17] introduces an algorithm where encounters based on selectivity have the potential to lead to permanent bonds (or edges) in a bipartite graph. Sophisticated network formation processes arise out of assumptions in game theory, where players (vertices) are assumed to have a utility function; based on other players’ decisions, each player forms connections seeking to maximize his or her utility, possibly over a number of time steps. For instance, [18] builds a bipartite network where each node attaches to an existing node with probability based on individual characteristics. They apply this to a network of mentors and students from academia to show the existence of a glass ceiling effect. [19] Investigate how a network of friendships is made, based on agents making optimal decisions who to befriend, subject to capacity constraints. In these situations, assortative mixing arises as a byproduct of network construction. While the mechanistic approaches described so far have a claim to realism, they may be unnecessarily complex for studying SIR epidemics. We do not need to know all the details and stages of network formation, and thus, in this paper, we introduce a simplified network construction algorithm, based on preference to connect. We take the view that there are latent preferences that determine how individuals form connections, which echoes existing literature in both ecology and economics. To circumvent subject-specific mechanisms, we do not seek to explain individual behavior or preferences, instead assuming random sampling without replacement, where the probability of selection is based on strength of the preference. Our goal in the first part of this paper is to create a rich family of graphs via a preference function which is flexible enough to lead to a large variety of edge matrices in the constructed networks.
Once we have a process for generating networks with different assortativity profiles, in the second part of the paper we investigate epidemic spread over the constructed networks. As benchmark, we compare the epidemic curves against spread over configuration model (CM) network [11], which has been studied extensively and is neutral in terms of assortativity. One particular point we will be paying attention to is whether the epidemic spread is predictable in terms of quantities one might hope to observe in reality. For infectious diseases, it is unlikely that one would be able to measure either individual degrees or the matrix E in a human population. However, the cumulative fraction of infected individuals through time is much more easily available, for instance, via a serological survey administered to the general population (see, e.g., [20]). In first order networks, it was shown that the SIR dynamics of spread are predictable in terms of the fraction of remaining susceptibles
Our main contributions are:
• Proposing a stochastic algorithm to construct networks based on preference to connect. And creating a rich family of networks based on a flexible preference formulation.
• Showing how to derive the marginal degree preference based on a general preference function that can be based on any number of exogenous features.
• We investigate the shapes of the epidemic curves, and total epidemic sizes by transmissibility. In particular, our epidemic simulation results support the hypothesis that the effective reproductive number is predictable as a univariate function of the susceptible fraction
2 Materials and methods
2.1 Setup and notation
Assume we have an undirected graph
where
We further introduce a preference metric that determines the likelihood that two vertices (individuals) will form an edge, if given the option to connect. Define a preference function
In the simplest case, preference to connect depends on the individuals’ degrees, referred to as degree correlation [2]. We propose the following form of the preference function
Note that function
If we store this pmf in a matrix
The form Eq. 2 entertains a few special cases that may be realistic in various situations:
• Case 1. Similarity. Setting
• Case 2. Dissimilarity. Same setting
• Case 3. Co-operation. When setting
In a broader context, individuals’ preference to form connections depends on other characteristics besides (or in addition to) their number of edges (degree). In human populations, demographic covariates such as income, age, and gender, may all be relevant. Suppose that individuals
where
2.2 Network building algorithm 1: preference determined by degree
Starting from a preference function
Step 1. Create a list of N vertex IDs (e.g., number each vertex with a label in
Step 2. Create another list L containing all vertices from Step 1, and add duplicates such that each ID appears the same number of times as their assigned degree.
LOOP While there are still unpaired ID copies:
Step 3. Select a pair of degrees with probabilities given in matrix
Step 4. Randomly pick a vertex with degree
Step 5. If all vertices with initial degrees
END LOOP
Step 6. Return the linked list of paired IDs determined in Step 4. Optionally, compute the edge matrix
This algorithm can be viewed as a second-order extension to the configuration model algorithm, where nodes are now matched randomly from list L according to matrix
While this building procedure assumes a preference function
2.3 Obtaining the marginal degree preference function from a multivariate distribution
Using a preference function
If we call this marginal preference function
This says what we would expect intuitively, i.e., that
2.4 Network building algorithm 2: via copulas
As the margins of matrix
is a valid bivariate distribution function having marginal
The algorithm to build the network has the same steps outside the loop as before. The steps inside the loop change as follows.
LOOP While there are still unpaired ID copies:
Step 3. Generate a pair of uniform variates
Step 4. Randomly pick a vertex with degree
Step 5. If any of degree classes
END LOOP
The advantage inherent in the copula construction algorithm is that there is no mismatch between the fraction of edges of a certain degree pair in the theoretical model, and the fraction of edges in the same pair present in the final network. The two can be matched exactly–up to randomness in the algorithm. This is due to the fact that a copula is consistent with any marginal distribution, unlike construction via a preference function, which is, in general, inconsistent with the marginal degree distribution of vertices. A (relatively small) price to pay is that only a subset of the nominal copula is used, i.e., roughly speaking we are using only points
2.5 Algorithm extensions
The current algorithm can be expanded in a few directions for increased realism. One fairly obvious extension is to allow for asymmetric preferences, i.e.,
One potential mechanism for determining priority in matching is how desirable, or sought-after, a vertex, or a class of vertices, is. Assuming homogeneity of vertices in each degree class, we use the following process to rank desirability. Before any connection is established, we allow each individual (vertex) to send messages to other individuals, such that the expected number of messages received by an individual with degree i from one with degree j is proportional to
Notice that desirability is heavily influenced by rarity of certain degrees: if
Step 3. Select a pair of degrees
The other steps remain the same as before. This version of the algorithm effectively blocks classes with low priority from choosing, and they will end up pairing with whoever is left, after the higher priority classes are all connected. This will produce a different network and edge matrix compared to the implementation in Section 2.2, although a full investigation of this difference is beyond the scope of the present paper.
2.6 Metrics
For our networks we compute the assortativity coefficient, defined by [14] to be the Pearson correlation coefficient between the excess degree of two nodes connected by an edge. This is given by
where
We further introduce a metric to determine the distance between individual preferences and where the network ends up. Define the normalized preference matrix
where
2.7 Epidemic spread
Assume that infection lasts for one time unit, after which the infected individual is removed, as in the standard SIR compartmental framework. We initially infect a small number of random vertices in the network. At each time point, infection may pass with probability
3 Numerical experiments
3.1 Network generation
(a) Preference function based on degree alone. We simulate networks with
(b) Covariate–induced preferences. As an application to illustrate the use of Eq. 6, we build a network for a case when preference to connect is based on income (
(c) Construction via copula algorithm. We construct a network using the Gumbel copula with parameter
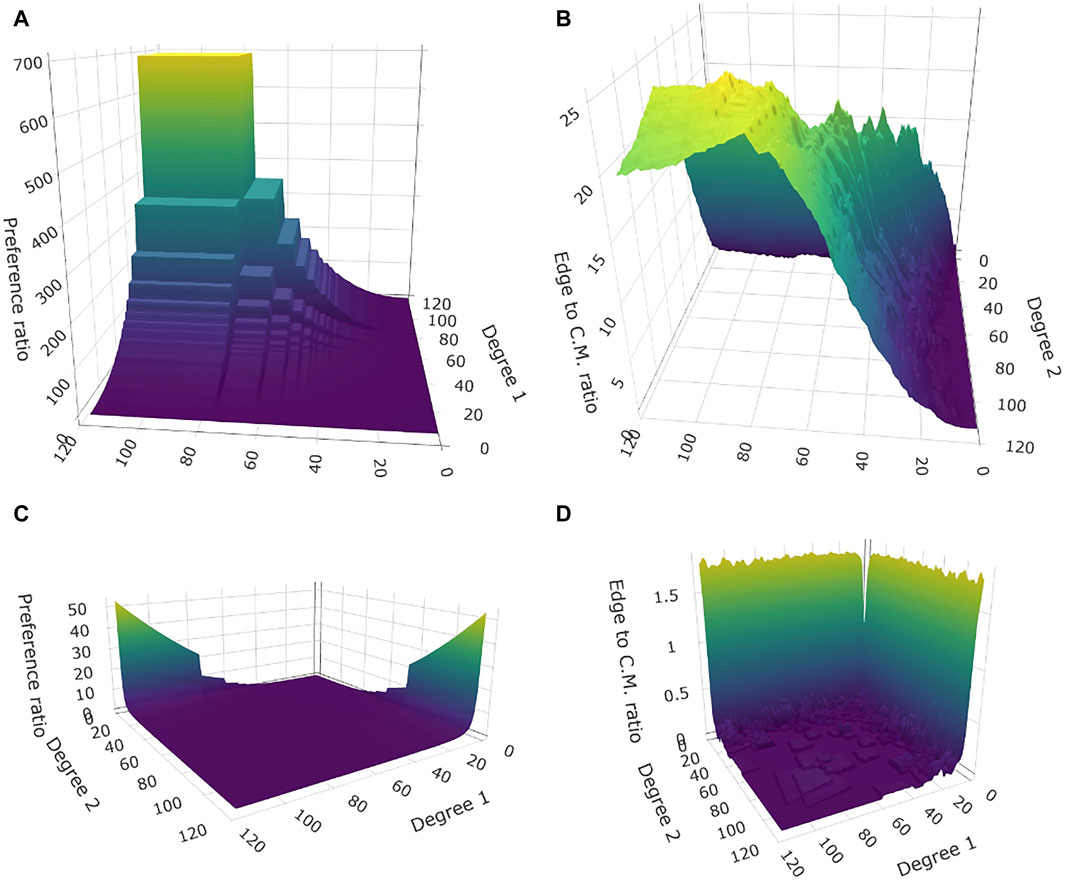
Figure 1. Networks built according to a preference function. Assortative network with
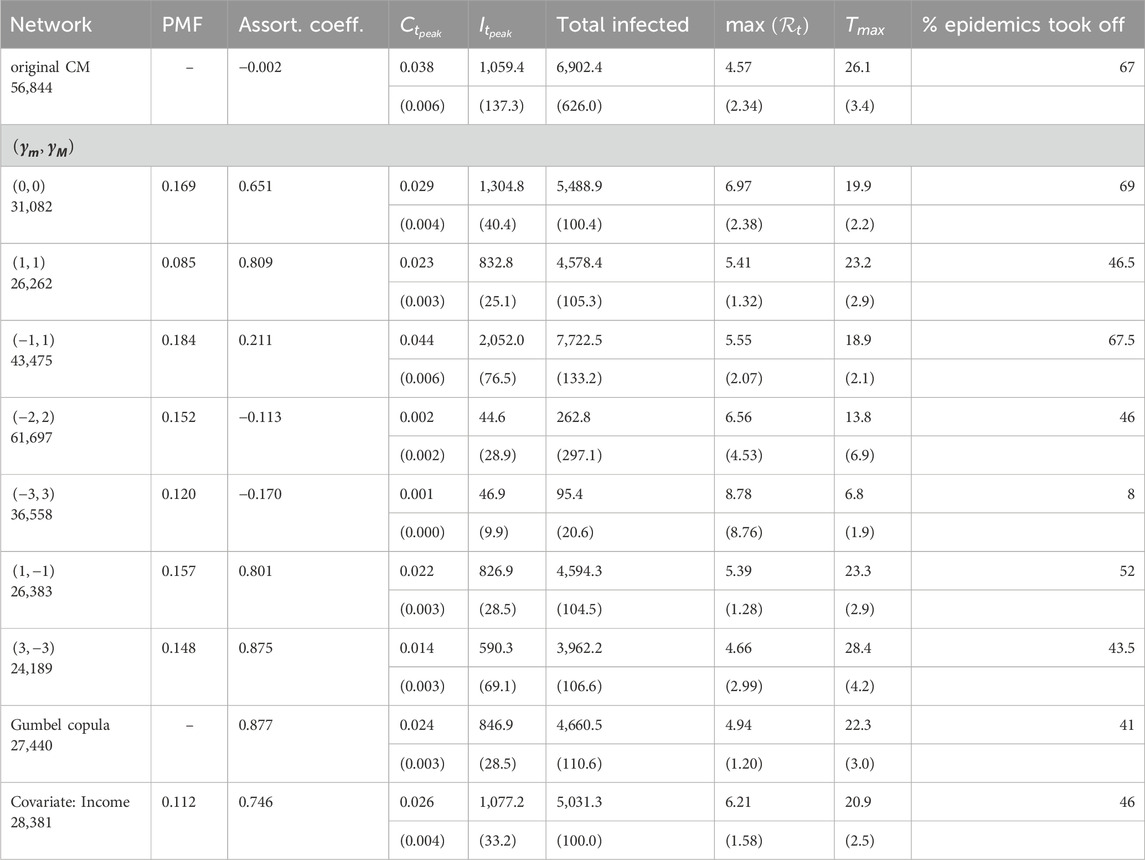
Table 1. SIR epidemic summaries for each network type. Average values are based on 200 replicated epidemics, with standard deviation shown in brackets. Only epidemics that took off were included.
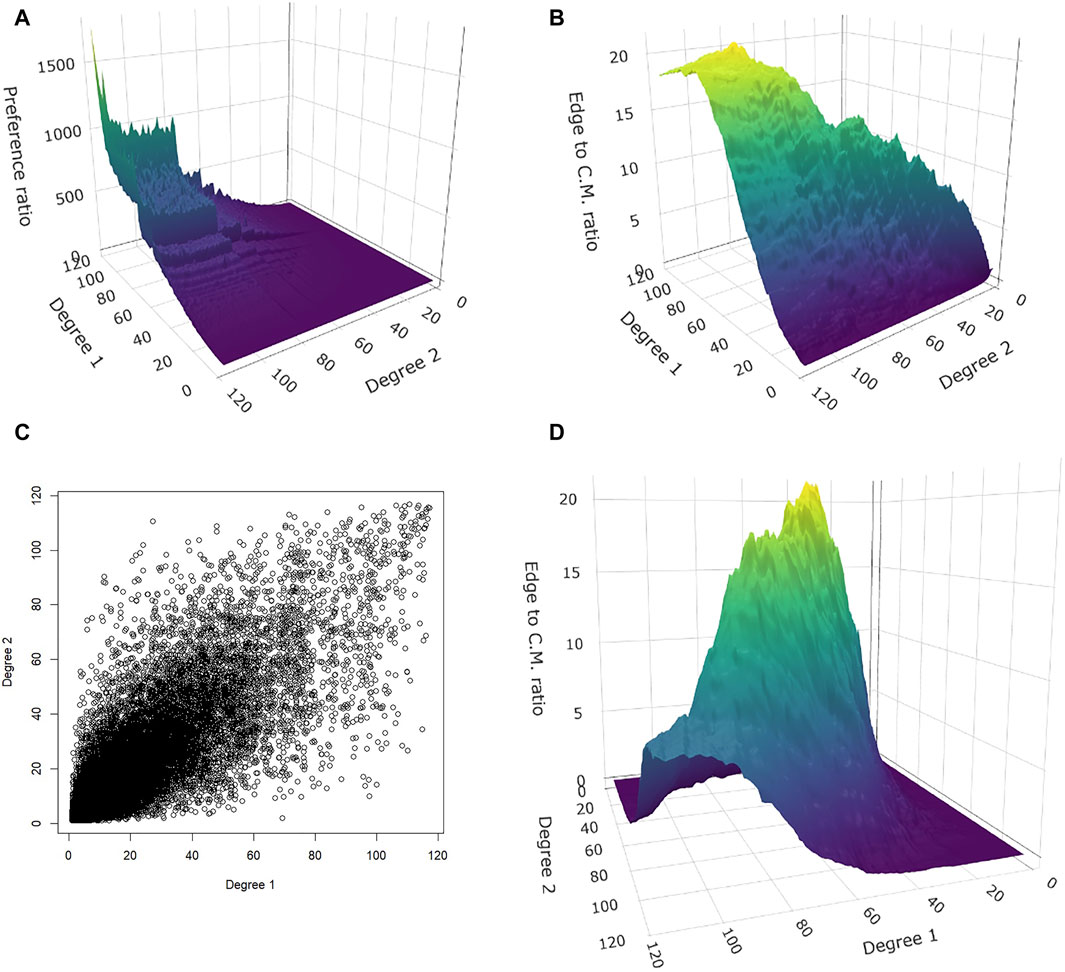
Figure 2. Covariate-induced network (income correlated with degree,
3.2 SIR epidemic results
We run 200 epidemics on each of the generated networks, with transmissibility set at
Figure 3 shows two networks that exhibit qualitatively different epidemic curves. The network with a flat preference function,
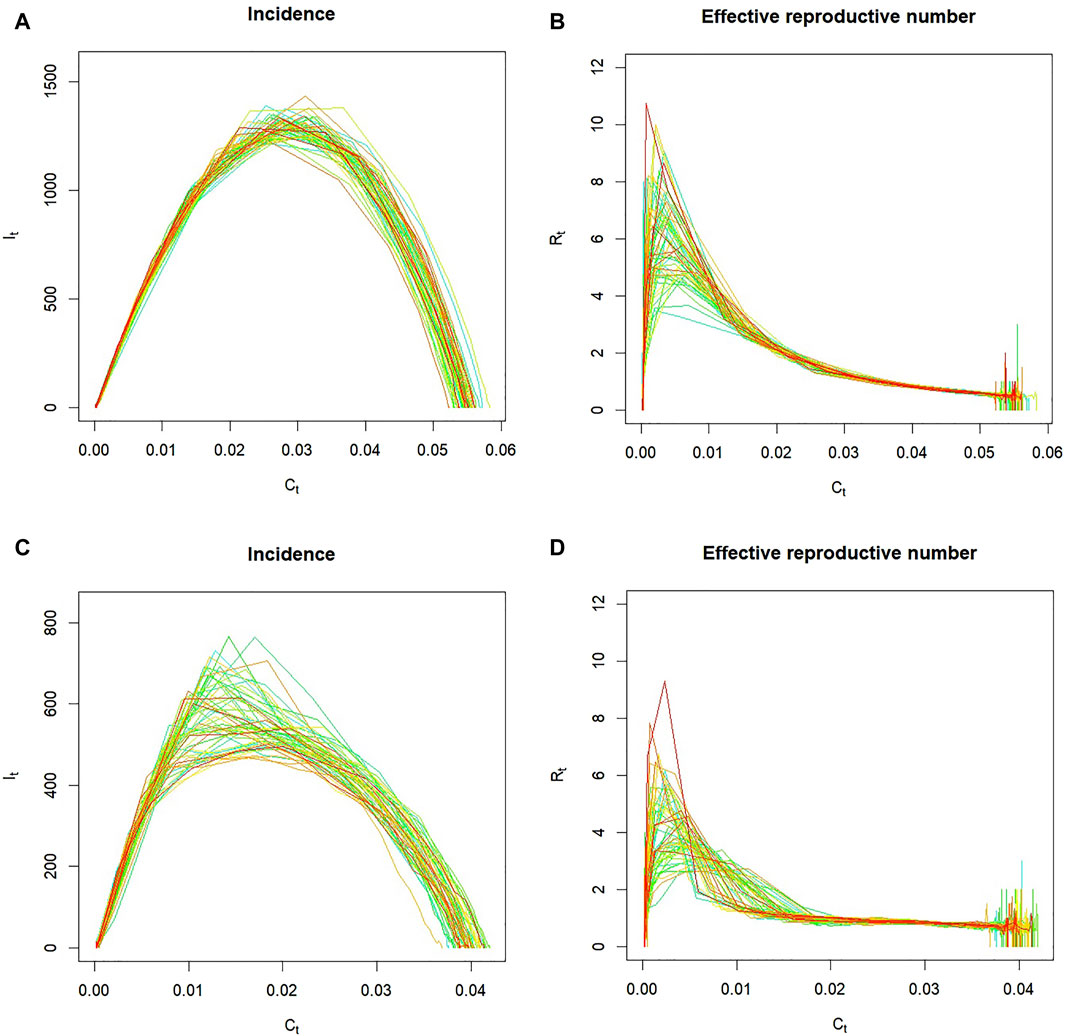
Figure 3. Examples of epidemics over two networks, one having
We record summary statistics from all epidemic experiments in Table 1. In particular, we are interested in the total number of infections, and in the epidemic curve profile, i.e., how long does the epidemic last, the size of the peak, and rate of growth at the beginning (typically indicated by
We also investigate how the total size of an epidemic is affected by changes in transmissibility
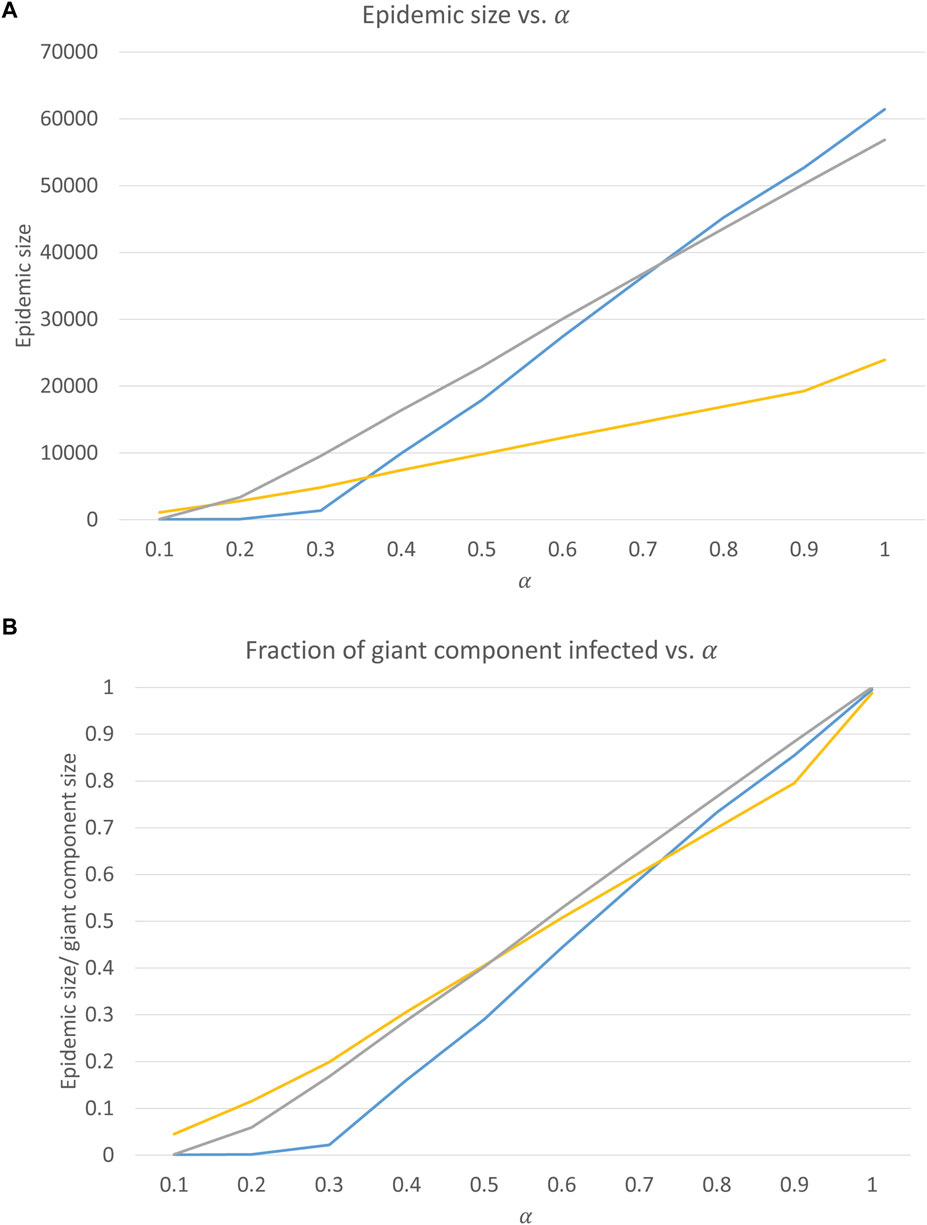
Figure 4. Epidemic sizes as a function of
4 Discussion
In this paper we introduced an algorithm to construct a network, based on the idea of preference to form an edge, given as a parametric function. The main advantage of preference functions is that they allow for a basic underlying mechanism for how the network is built, without being overly subject-specific, such as game-theoretic or ecological networks. This allows for some claim of plausibility or realism when building a network. This algorithm does not intend to replace existing rewiring algorithms, which are efficient when a matrix
We have also investigated the spread of SIR epidemics on these networks, in an attempt to generate hypotheses for future work. The following conclusions and questions emerged:
• The second order structure of the graph (given in matrix
• The effective reproductive number
• While the assortativity coefficient is meaningfully related to diffusion spread, it does not correlate with size of epidemics in a monotonic fashion. The question emerges of whether there is another graph summary that is more directly related to epidemic spread.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
RR: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research received financial support from Research Manitoba, as part of its COVID-19 Research Fund. RR is based at the George and Fay Yee Centre for Healthcare Innovation. Support for CHI is provided by University of Manitoba, Canadian Institutes for Health Research, Province of Manitoba, and Shared Health Manitoba.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1435767/full#supplementary-material
Footnotes
1In Newman’s original definition,
2This corresponds to the 80–20 rule [27].
References
1. Callaway DS, Newman MEJ, Strogatz SH, Watts DJ. Network robustness and fragility: percolation on random graphs. Phys Rev Lett (2000) 85(25):5468–5471. doi:10.1103/PhysRevLett.85.5468
2. Newman MEJ. The structure and function of complex networks. SIAM Rev (2003) 45(2):167–256. doi:10.1137/S003614450342480
3. Romanescu RG, Deardon R. Fast inference for network models of infectious disease spread. Scand J Stat (2017) 44(3):666–83. doi:10.1111/sjos.12270
4. Miller JC, Slim AC, Volz EM. Edge-based compartmental modelling for infectious disease spread. J R Soc Interf (2012) 9(70):890–906. doi:10.1098/rsif.2011.0403
5. Volz E. SIR dynamics in random networks with heterogeneous connectivity. J Math Biol (2008) 56(3):293–310. doi:10.1007/s00285-007-0116-4
6. Moreno Y, Vazquez A. Disease spreading in structured scale-free networks. EPJ B (2002) 31(2):265–271. doi:10.1140/epjb/e2003-00031-9
7. Newman MEJ. Assortative mixing in networks. Phys Rev Lett (2002) 89(20):208701. doi:10.1103/PhysRevLett.89.208701
8. Kiss IZ, Green DM, Kao RR. The effect of network mixing patterns on epidemic dynamics and the efficacy of disease contact tracing. J R Soc Interf (2008) 5(24):791–9. doi:10.1098/rsif.2007.1272
9. Wang Y, Chakrabarti D, Wang C, Faloutsos C. Epidemic spreading in real networks: an eigenvalue viewpoint. In: Proceedings of the IEEE Symposium on Reliable Distributed Systems (2003). p. 25–34. doi:10.1109/RELDIS.2003.1238052
10. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. In: Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 115 (1927). p. 700–721. doi:10.1098/rspa.1927.0118
11. Molloy M, Reed B. A critical point for random graphs with a given degree sequence. Random Struct Algorithms (1995) 6(2–3):161–80. doi:10.1002/rsa.3240060204
12. Anderson I. B. Bollobás, random graphs (London mathematical society monographs, academic press, London, 1985), 447 pp., £52 cloth, £27 paper. In: Proceedings of the Edinburgh Mathematical Society, 30 (1987). p. 329. doi:10.1017/s0013091500028443
13. Barabási AL, Albert R. Emergence of scaling in random networks. Science (1979) (1999) 286(5439):509–12. doi:10.1126/science.286.5439.509
14. Newman MEJ. Mixing patterns in networks. Phys Rev E (2003) 67(2):026126. doi:10.1103/PhysRevE.67.0261269
15. Xulvi-Brunet R, Sokolov IM. Construction and properties of assortative random networks. Phys Rev E (2004) 70(6):066102. doi:10.1103/PhysRevE.70.066102
16. Chang SL, Piraveenan M, Prokopenko M. Impact of network assortativity on epidemic and vaccination behaviour. Chaos Solitons Fractals (2020) 140:110143. doi:10.1016/j.chaos.2020.110143
17. Dipple S, Jia T, Caraco T, Korniss G, Szymanski BK. Assortative mating: encounter-network topology and the evolution of attractiveness. Sci Rep (2017) 7:45107. doi:10.1038/srep45107
18. Avin C, Keller B, Lotker Z, Mathieu C, Peleg D, Pignolet YA. Homophily and the glass ceiling effect in social networks. In: ITCS 2015 - Proceedings of the 6th Innovations in Theoretical Computer Science. Association for Computing Machinery, Inc (2015). p. 41–50. doi:10.1145/2688073.2688097
19. Jiménez-Martínez A, Melguizo-López I. Making friends: the role of assortative interests and capacity constraints. J Econ Behav Organ (2022) 203:431–65. doi:10.1016/j.jebo.2022.09.016
20. Murphy TJ, Swail H, Jain J, Anderson M, Awadalla P, Behl L, et al. The evolution of SARS-CoV-2 seroprevalence in Canada: a time-series study, 2020-2023. CMAJ Can Medical Assoc J (2023) 195(31):E1030–7. doi:10.1503/cmaj.230249
21. Romanescu RG, Hu S, Nanton D, Torabi M, Tremblay-Savard O, Haque MA. The effective reproductive number: modeling and prediction with application to the multi-wave Covid-19 pandemic. Epidemics (2023) 44(Sep):100708. doi:10.1016/j.epidem.2023.100708
22. Wang C, Lizardo O, Hachen D, Strathman A, Toroczkai Z, Chawla NV. A dyadic reciprocity index for repeated interaction networks. Netw Sci (2013) 1(1):31–48. doi:10.1017/nws.2012.5
23. Miller JW, Harrison MT. Exact sampling and counting for fixed-margin matrices. The Ann Stat (2013) 41(3). doi:10.1214/13-aos1131
24. Sklar A. Fonctions de r{é}partition {à} {n} dimensions et leurs marges (Distribution functions of {n} dimensions and their marginals). Publications de l’Institut Statistique de l’Universit{é} de Paris (1959), vol. 8.
25. Geenens G. Copula modeling for discrete random vectors. Dependence Model (2020) 8(1):417–40. doi:10.1515/demo-2020-0022
26. Muñoz-Herrera M, Dijkstra J, Flache A, Wittek R. Collaborative production networks among unequal actors. Net Sci (2021) 9(1): 1–17. doi:10.1017/nws.2020.23
27. Dunford R, Su Q, Tamang E, Wintour A. The Pareto principle. The Plymouth Student Scientist (2014) 7(2):140–148.
Keywords: graphs, degree distribution, edge matrix, assortative mixing, network construction, compartmental epidemic model
Citation: Romanescu RG (2024) Building a network with assortative mixing starting from preference functions, with application to the spread of epidemics. Front. Phys. 12:1435767. doi: 10.3389/fphy.2024.1435767
Received: 21 May 2024; Accepted: 15 July 2024;
Published: 05 August 2024.
Edited by:
Irina Severin, University POLITEHNICA of Bucharest, RomaniaReviewed by:
Konstantin Klemm, Spanish National Research Council (CSIC), SpainElena Corina Cipu, Politehnica University of Bucharest, Romania
Copyright © 2024 Romanescu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Razvan G. Romanescu, cmF6dmFuLnJvbWFuZXNjdUB1bWFuaXRvYmEuY2E=
 Razvan G. Romanescu
Razvan G. Romanescu