Device-independent certification of desirable properties with a confidence interval

In the development of quantum technologies, a reliable means for characterizing quantum devices, be it a measurement device, a state-preparation device, or a transformation device, is crucial. However, the conventional approach based on, for example, quantum state tomography or process tomography relies on assumptions that are often not necessarily justifiable in a realistic experimental setting. Although the device-independent (DI) approach to this problem bypasses the shortcomings above by making only minimal, justifiable assumptions, most of the theoretical proposals to date only work in the idealized setting where independent and identically distributed (i.i.d.) trials are assumed. Here, we provide a versatile solution for rigorous device-independent certification that does not rely on the i.i.d. assumption. Specifically, we describe how the prediction-based ratio (PBR) protocol and martingale-based protocol developed for hypothesis testing can be applied in the present context to achieve a device-independent certification of desirable properties with confidence interval (CI). To illustrate the versatility of these methods, we demonstrate how we can use them to certify—with finite data—the underlying negativity, Hilbert space dimension, entanglement depth, and fidelity to some target pure state. In particular, we provide examples showing how the amount of certifiable negativity and fidelity scales with the number of trials and how many experimental trials one needs to certify a qutrit state space or the presence of genuine tripartite entanglement. Overall, we have found that the PBR protocol and the martingale-based protocol often offer similar performance, even though the latter does have to presuppose any witness (Bell-like inequality). In contrast, our findings also show that the performance of the martingale-based protocol may be severely affected by one’s choice of Bell-like inequality. Intriguingly, a Bell function useful for self-testing does not necessarily give the optimal confidence-gain rate for certifying the fidelity to the corresponding target state.

1 Introduction

The proper analysis of quantum experiments is an indispensable part in the development of quantum technologies. However, it is not trivial to reliably characterize a quantum setup, which may include, e.g., measurement and state-preparation devices. Moreover, imperfections in the experimental setup can easily result in a mismatch [1–3] between the characterization tools developed for an idealized situation and an actual experimental situation. However, we can circumvent this problem by the so-called “device-independent approach” [4, 5]. In quantum information, the term “device-independent” (DI) was first coined [6] in the task of quantum key distribution [7–9], even though the idea was already perceived independently but implicitly in [10, 11].

In a nutshell, the DI approach is a framework for analyzing physical systems without relying on any assumption about the degrees of freedom measured. Its basis is Bell nonlocality [5, 12], which shows that no local-hidden-variable (LHV) theory can reproduce all quantum predictions, even though no further assumption is made about the details of such a theory. For example, it is known that the violation of Bell inequalities [12] obtained by locally measuring a shared state implies [13] shared entanglement [14], which is a powerful resource in many quantum information processing tasks. More generally, many other desirable properties of the underlying state [15–23], measurements [22–28], and channel [21, 29, 30] may be derived directly from the observation of a Bell inequality-violating correlation between measurement outcomes. Recently, the DI approach has also been incorporated into the security analysis of quantum secure direct communication; see, for example, [31] and references therein.

However, due to statistical fluctuations, even when the experimental trials are independent and identically distributed (i.i.d.), relative frequencies of the measurement outcomes obtained from a Bell experiment do not faithfully represent the underlying distribution. In particular, such raw distributions estimated from the experimental results typically [32–34] lead to a violation of the nonsignaling conditions [35, 36], which is a prerequisite for the analysis shown in [16–30]. In other words, statistical fluctuations render many theoretical tools developed for such a purpose inapplicable. To address this issue, some ad hoc methods [32–34] have been proposed to regularize the relative frequencies obtained to ensure that the resulting distribution satisfy the nonsignaling conditions. In [37], a more in-depth discussion was provided, and two better-motivated regularization methods were proposed.

Although these more recent attempts do provide a point estimator that fits within the framework of the usual DI analysis, they are still problematic in two aspects. First, they do not provide any confidence region associated with the estimate. However, any real experiment necessarily involves only a finite number of experimental trials. Therefore a useful analysis should provide not only an estimate but also an indication of the reliability of such an estimate. In many of the Bell experiments reported [38–41], this is achieved by reporting the standard deviations of Bell violations. However, for finite, especially relatively small numbers of trials, the central limit theorem is not warranted, so the usual interpretation of standard deviations may become dubious. Second, these usual approaches and those that provide a DI point estimator [32–34, 37] implicitly assume that the experimental trials are i.i.d. and hence free of the memory effect [42, 43] (see more discussions in [5, 44–46]). Again, in a realistic experimental setting, the i.i.d. assumption may be difficult to justify.

For the tasks of DI randomness expansion [47, 48] and DI quantum key distribution [49, 50], specific tools [51–59] have been developed to overcome the abovementioned problems. Here, we are interested in providing a general solution to other device-independent certification tasks¹ that 1) can provide a confidence region and two) does not a priori require the i.i.d. assumption. Our approach is inspired by the prediction-based ratio (PBR) protocol developed in [60] and the martingale-based method proposed by Gill [43, 61] for performing a hypothesis testing against the assumption of Bell locality. Following [62], we further adapt these earlier methods and illustrate how they can be used for the device-independent certification of various properties of interest, including the underlying amount of entanglement and its fidelity with respect to some target quantum state.

To this end, we structure the rest of this paper as follows. In Section 2.1, we explain the basic concepts relevant to the understanding of DI certification in the ideal setting. After that, we introduce in Section 2.2 our adapted statistical tools for performing a rigorous device-independent certification. Results obtained from these tools are then presented in Section 3.1. Finally, we provide some concluding remarks and future directions in Section 4.

2 Materials and methods

2.1 Preliminaries

2.1.1 Correlations and Bell inequalities

The starting point of the DI approach is a Bell test. To this end, a bipartite Bell scenario was considered, where two observers, Alice and Bob, can choose, respectively, their measurements labeled by $x,y\in \{\mathrm{0,1},\dots \}$ and register outcomes $a,b\in \{\mathrm{0,1},\dots \}$.² In the i.i.d. setting, one can estimate the underlying correlation between measurement outcomes, i.e., $\vec{P}=\{P(ab|xy)\}$, from the registered empirical frequencies. Interestingly, as Bell first showed in [12], highly nontrivial conclusions can be drawn by inspecting $\vec{P}$ alone.

For example, correlations that can be produced in an LHV theory have to satisfy a Bell inequality:

${\displaystyle \sum _{x,y,a,b}}{\beta }_{xy}^{ab}P\left(ab|xy\right)\stackrel{\mathcal{L}}{\le }{B}_{\mathcal{L}}\left(\vec{\beta }\right),(1)$

where the Bell coefficients ${\beta }_{xy}^{ab}\in \mathbb{R}$, $\vec{\beta }≔\{{\beta }_{xy}^{ab}\}$, and $B_{\mathcal{L}}(\{\vec{\beta }\})$ is the so-called local (upper) bound. Here, we use $\mathcal{L}$ to signify that the inequality holds under the assumption that $\vec{P}$ is compatible with the LHV theory. Explicitly, the nature of such a theory demands that $\vec{P}$ is factorizable in the form [5, 12]:

$P\left(ab|xy\right)\stackrel{\mathcal{L}}{=}{\displaystyle \sum _{\lambda }}{q}_{\lambda }{P}_A\left(a|x\lambda \right)P_B\left(b|y\lambda \right),(2)$

where $q_{\lambda }\ge 0$ for all $\lambda$, ${\sum }_{\lambda }{q}_{\lambda }=1$, and $P_A(a|x\lambda ),P_B(b|y\lambda )\in [\mathrm{0,1}]$ are local response functions.

In an actual Bell test, the measurement settings ought to be chosen randomly according to some predetermined distributions $P_{xy}$. To manifest this fact, one may write Equation 1 using the unconditional joint distribution $P(abxy)=P(ab|xy)P_{xy}$ such that $P_{xy}={\sum }_{a,b}P(abxy)$. In turn, we can then write a Bell inequality as a bound on the expectation value of a Bell function $I(\upsilon )$, defined in terms of $\vec{\beta }$ and $P_{xy}$, i.e.,

$⟨I\left(\upsilon \right)⟩≔\frac{⟨{\beta }_{xy}^{ab}⟩}{P_{xy}}\stackrel{\mathcal{L}}{\le }{B}_{\mathcal{L}}\left(\vec{\beta }\right),(3)$

where $\upsilon =(a,b,x,y)$ is the quadruple of random variables for the measurement outcomes $(a,b)$ and settings $(x,y)$. As an example, the famous Clauser–Horne–Shimony–Holt (CHSH) Bell inequality [63] may be specified via

$I_{\text{\hspace{0.17em}CHSH}}:{\beta }_{xy}^{ab}={\left(-1\right)}^{xy+a+b}\text{and}{B}_{\mathcal{L}}=2,(4)$

or equivalently, in terms of the correlator $E_{xy}≔{\sum }_{a,b=\mathrm{0,1}}{(-1)}^{a+b}P(ab|xy)$, as

${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}={\displaystyle \sum _{x,y=\mathrm{0,1}}}{\left(-1\right)}^{xy}{E}_{xy}\stackrel{\mathcal{L}}{\le }2,(5)$

where ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}=⟨I_{\text{\hspace{0.17em}CHSH}}(\mathcal{\upsilon })⟩$.

In contrast, quantum theory allows correlations that cannot be cast in the form of Equation 2. In fact, in a bipartite Bell test, general quantum correlations read as

$P\left(ab|xy\right)\stackrel{\mathcal{Q}}{=}\text{tr}\left(\rho M_{a|x}^{\left(A\right)}\otimes M_{b|y}^{\left(B\right)}\right),(6)$

where $\{M_{a|x}^{(A)}\}$ and $\{M_{b|y}^{(B)}\}$ are, respectively, the local positive-operator-valued measure (POVM) describing Alice and Bob’s local measurements. For the benefits of subsequent discussions, it is also worth noting that both LHV and quantum correlations satisfy the nonsignaling conditions [35, 36]:

$\begin{array}{c}\hfill {\displaystyle \sum _a}P\left(ab|xy\right)={\displaystyle \sum _a}P\left(ab|x^{\prime }y\right)\forall x,x^{\prime },\\ \hfill {\displaystyle \sum _b}P\left(ab|xy\right)={\displaystyle \sum _b}P\left(ab|x{y}^{\prime }\right)\forall y,y^{\prime }.\end{array}(7)$

For the CHSH Bell function, cf. Equation 4, quantum theory dictates the upper bound as

$⟨I_{\text{\hspace{0.17em}CHSH}}\left(\upsilon \right)⟩\stackrel{\mathcal{Q}}{\le }{B}_{\mathcal{Q}}=2\sqrt{2},(8)$

which can be seen as a Bell-like inequality. Other Bell and Bell-like inequalities relevant to this work will be presented in the corresponding sections below.

2.1.2 Examples of properties to be certified

2.1.2.1 Negativity and dimension

As mentioned above, with local measurements on a quantum system, a Bell inequality-violating correlation $\vec{P}\notin \mathcal{L}$ necessarily originates [13] from an entangled state $\rho$. Interestingly, the entanglement of the underlying $\rho$ can also be lower bounded [17, 18, 20, 23] directly from the observed correlation $\vec{P}$. In this work, we focus on negativity [64], but it is worth noting that DI entanglement quantification can also be achieved, e.g., for the linear entropy of entanglement [18], generalized robustness of entanglement [23], and one-shot distillable entanglement [20].

For a bipartite density operator $\rho$, let ${\rho }^{{\text{\hspace{0.17em}T}}_A}$ be its partial transposition [65] with respect to subsystem $A$. Then, the negativity for a bipartite density operator $\rho$ is defined as [64] $\mathcal{N}(\rho )≔{\sum }_{{\lambda }_i<0}|{\lambda }_i({\rho }^{{\text{\hspace{0.17em}T}}_A})|$, i.e., the sum of the absolute value of all negative eigenvalues ${\lambda }_i<0$ of ${\rho }^{{\text{\hspace{0.17em}T}}_A}$. Using a variational characterization of negativity provided in [64], it was shown in [17] that $\mathcal{N}(\rho )$ is lower bounded by the optimum value of the following semidefinite program (SDP):

$\text{min\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\chi }_{\ell }{\left[{\sigma }_{-}\right]}_{\text{tr}},(\mathrm{9a})$

$\text{s.t.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\chi }_{\ell }\left[\rho \right]={\chi }_{\ell }\left[{\sigma }_{+}\right]-{\chi }_{\ell }\left[{\sigma }_{-}\right],{\chi }_{\ell }{\left[{\sigma }_{\pm }\right]}^{{\text{\hspace{0.17em}T}}_{\bar{A}}}⪰0,(\mathrm{9b})$

${\chi }_{\ell }\left[\rho \right]⪰0,{\chi }_{\ell }{\left[\rho \right]}_{\text{tr}}=1,(\mathrm{9c})$

where ${\chi }_{\ell }[\rho ]$ is the moment matrix that can be obtained by applying a particular local map on $\rho$ (see [17] for details), $\bar{A}$ is the output Hilbert space of the local map on $A$, and ${\chi }_{\ell }{[\sigma ]}_{\text{tr}}=\text{tr}[\sigma ]$ represents the trace of the underlying operator $\sigma$. It is worth noting that for every integer $\ell \ge 1$, the constraints of Equation 9c provide a superset characterization of the quantum set $\mathcal{Q}$ of correlations, analogous to those considered in [66–68]. Indeed, all entries from $\vec{P}$ appear somewhere in the moment matrix ${\chi }_{\ell }[\rho ]$; see [17].

As an explicit example, note that an observed violation of the CHSH Bell inequality of Equation 5 gives the following nontrivial negativity lower bound of the underlying state $\rho$:

$\mathcal{N}\left(\rho \right)\ge \frac{{\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}-2}{4\left(\sqrt{2}-1\right)}.(10)$

In addition, it is worth noting that if $\rho$ acts on ${\mathbb{C}}^{d_A}\otimes {\mathbb{C}}^{d_B}$ with $d=\min \{d_A,d_B\}$, then the maximal possible negativity $\mathcal{N}(\rho )$ is upper bounded by ${\mathcal{N}}_{\text{max}}^d≔\frac{d-1}{2}$. Consequently, the observation of a large enough negativity also provides a nontrivial lower bound on the local Hilbert space dimension of the underlying system. More precisely, if the lower bound on $\mathcal{N}(\rho )$ obtained from Equations 9a, 9b and 9c exceeds ${\mathcal{N}}_{\text{max}}^d$, one immediately deduces that $\rho$ must act on a local Hilbert space of dimension $\ge d+1$, thereby giving a dimension witness [15].

From Equations 5, 8 and 10, nonetheless, we see that a violation of the CHSH Bell inequality can never witness a local Hilbert space dimension $>2$. Instead, witnessing a local Hilbert space beyond qubits can be achieved by observing a reasonably strong violation of the three-outcome Collins–Gisin–Linden–Massar–Popescu (CGLMP) Bell inequality [69] (see also [70]), defined by

$I_{\text{\hspace{0.17em}CGLMP}3}:{\beta }_{xy}^{ab}={\left(-1\right)}^{x\left(y-1\right)}\left\{{\delta }_{a-b}^{\left(2\right)}-\left[1-{\delta }_x^{\left(2\right)}{\delta }_{y-1}^{\left(2\right)}\right]{\delta }_{b-a-1}^{\left(3\right)}\right\}-{\delta }_x^{\left(2\right)}{\delta }_{y-1}^{\left(2\right)}{\delta }_{b-a+1}^{\left(3\right)}\text{and}{B}_{\mathcal{L}}\left(\vec{\beta }\right)=2,(11)$

where ${\delta }_f^{(d)}=1$ if $\text{mod}(f,d)=0$ and vanishes otherwise. Denoting the corresponding expectation value by ${\mathcal{S}}_{\text{\hspace{0.17em}CGLMP}3}=⟨I_{\text{\hspace{0.17em}CGLMP}3}(\mathcal{\upsilon })⟩$, the results from [17, 71, 72] suggest a negativity lower bound that increases linearly with ${\mathcal{S}}_{\text{\hspace{0.17em}CGLMP}3}$ from $\frac{1}{2}$ whenever ${\mathcal{S}}_{\text{\hspace{0.17em}CGLMP}3}\ge \frac{3}{\sqrt{2}}+\frac{1}{2}$.

2.1.2.2 Entanglement depth

In a many-body system, entanglement can occur in various forms or structures [73]. In particular, an $n$-partite quantum state that is not fully separable is not necessarily genuinely $n$-partite entangled either. To witness the latter, one could rely on the demonstration of so-called genuine multipartite nonlocality [74]. However, as remarked in [16], it is possible to witness genuine multipartite entanglement without relying on this strong form of multipartite nonlocality. In fact, using the SDP introduced in [17], one can even systematically construct DI witnesses of this kind, starting from a given multipartite Bell function, say $\vec{\beta }=\{{\beta }_{\mathit{xyz}}^{\mathit{abc}}\}$. Later, it was further shown in [19] (see also [75]) that the extent to which a multipartite Bell inequality is violated can be used to witness (lower-bound) the underlying entanglement depth [76, 77], i.e., the extent to which a many-body entanglement is needed to prepare the given multipartite state.

For illustration, consider the expectation value of the Mermin Bell function [78] $I_{\text{\hspace{0.17em}Mermin}}(\upsilon )$ with $\upsilon =(a,b,c,x,y,z)$:

${\mathcal{S}}_{\text{\hspace{0.17em}Mermin}}=⟨I_{\text{Mermin}}\left(\mathcal{\upsilon }\right)⟩=\frac{⟨{\beta }_{\mathit{xyz}}^{\mathit{abc}}⟩}{P_{\mathit{xyz}}}={\displaystyle \underset{x,y,z}{{\sum }^{\prime }}}{\left(-1\right)}^{\mathit{xyz}}{E}_{\mathit{xyz}},(12)$

where $E_{\mathit{xyz}}≔{\sum }_{a,b,c=0}^1{(-1)}^{a+b+c}P(abc|xyz)$ is the tripartite correlator, the restricted sum ${\sum }^{\prime }$ is over all combinations of $x,y,z\in \{\mathrm{0,1}\}$ such that $\text{mod}(x+y+z,2)=1$, $P_{\mathit{xyz}}=\frac{1}{4}$ for the same combinations of $x,y,z$, and the Bell coefficients is

${\beta }_{\mathit{xyz}}^{\mathit{abc}}={\left(-1\right)}^{\mathit{xyz+a+b+c}}{\delta }_{x+y+z-1}^{\left(2\right)}.(13)$

Then, it is known [19] that the following Bell-like inequalities hold, respectively, for fully separable states, 2-producible [76] tripartite quantum states (i.e., quantum states that can be generated using only two-body entanglement), and general tripartite quantum states:

${\mathcal{S}}_{\text{\hspace{0.17em}Mermin}}\stackrel{\mathcal{L}}{\le }2,{\mathcal{S}}_{\text{\hspace{0.17em}Mermin}}\stackrel{2-\text{prod.}}{\le }2\sqrt{2},{\mathcal{S}}_{\text{\hspace{0.17em}Mermin}}\stackrel{\mathcal{Q}}{\le }4.(14)$

2.1.2.3 State fidelity

The strongest form of device certification one can hope for within a DI paradigm is called self-testing [79], which was first proposed in [10]. The key observation behind this feat is that the quantum strategy compatible with certain extremal quantum correlations ${\vec{P}}_{\mathcal{Q}}$ is essentially unique. Hence, with the observation of ${\vec{P}}_{\mathcal{Q}}$ in a Bell test, we can conclude unambiguously that some degree of freedom (DOF) of the measured system must match a specific target state $|\psi \rangle$. Often, one can also self-test the underlying measurements alongside the state (see, however, [80, 81] for some examples of exceptions).

For instance, it is long known [82–85] that the maximal CHSH Bell-inequality violation of ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}=2\sqrt{2}$ can only be obtained (up to local isometry) by measuring the following observables on a shared maximally entangled state (MES):

$|{\psi }_{\text{MES}}\rangle =\frac{1}{\sqrt{2}}\left(|00\rangle +|11\rangle \right),(\mathrm{15a})$

$A_0={\sigma }_z,A_1={\sigma }_x,(\mathrm{15b})$

$B_y=\frac{1}{\sqrt{2}}\left[{\sigma }_z+{\left(-1\right)}^y{\sigma }_x\right],(\mathrm{15c})$

where the respective POVM elements (with $x,y=\mathrm{0,1}$) are

$M_{a|x}^{\left(A\right)}=\frac{\mathbb{1}+{\left(-1\right)}^a{A}_x}{2},M_{b|y}^{\left(B\right)}=\frac{\mathbb{1}+{\left(-1\right)}^b{B}_y}{2}.(16)$

Moreover, to obtain the maximal CHSH Bell-inequality violation for a partially entangled two-qubit state,

$|\psi \left(\theta \right)\rangle =\cos \theta |00\rangle +\sin \theta |11\rangle ,\theta \in \left(0,\frac{\pi }{4}\right],(\mathrm{17a})$

it suffices [72] to consider $A_x$ of Equation 15b but generalize $B_y$ to [86]:

$B_y=\cos \mu {\sigma }_z+{\left(-1\right)}^y\sin \mu {\sigma }_x,\tan \mu =\sin \left(2\theta \right),(\mathrm{17b})$

thereby giving

${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}=2\sqrt{1+{\sin }^{2}2\theta }.(18)$

Interestingly, the resulting correlation also self-tests [86, 87] the corresponding quantum strategy of Equation 17a, b and maximally violate the family of tilted CHSH Bell inequalities for $\alpha =2\sqrt{\frac{{\cos }^{2}2\theta }{1+{\sin }^{2}2\theta }}$:

${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}^{\text{\hspace{0.17em}Tilted}}\left(\alpha \right)={\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}+\alpha {\displaystyle \sum _{a,b=0}^1}{\left(-1\right)}^{a}P\left(ab|0y\right)\stackrel{\mathcal{L}}{\le }2+\alpha ,(19)$

giving ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}^{\text{\hspace{0.17em}Tilted}}(\alpha )=\sqrt{8+2{\alpha }^2}$. Note that in Equation 19, thanks to the nonsignaling [35, 36] property of $\vec{P}$, the expression for ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}^{\text{\hspace{0.17em}Tilted}}(\alpha )$ is, in fact, independent of whether $y=0$ or 1.

In practice, however, due to various imperfections, one can, at best, attain a correlation close to the ideal correlation ${\vec{P}}_{\mathcal{Q}}$. In other words, in a realistic experimental setting, one can only hope to lower bound the similarity of the measured state $\rho$ with respect to the target state $|\psi \rangle$ via a fidelity measure. To this end, a powerful numerical technique known as the SWAP method has been introduced in [88] (see also [86]) for exactly this purpose. More precisely, for any observed quantum correlation $\vec{P}$, the method allows one to lower bound the fidelity:

$\mathcal{F}=\langle \psi |{\rho }_{\text{\hspace{0.17em}SWAP}}|\psi \rangle (20)$

with the help of an SDP outer approximation of the quantum set $\mathcal{Q}$ (e.g., due to [17, 66, 67]). Here, ${\rho }_{\text{\hspace{0.17em}SWAP}}$ is the “swapped” state:

${\rho }_{\text{\hspace{0.17em}SWAP}}={\text{tr}}_{AB}\left[\mathrm{\Phi }{\rho }_{AB}\otimes {\left(|00\rangle \langle 00|\right)}_{A^{\prime }{B}^{\prime }}{\mathrm{\Phi }}^{+}\right],(21)$

which is extracted from the underlying quantum state $\rho$ via some local extraction map $\mathrm{\Phi }$, which is a function of the actual POVM elements. Consequently, $\mathcal{F}$ is a function of the entries of the moment matrix ${\chi }_{\ell }[\rho ]$, as discussed below Equations 9a, b and c. For the details of the method, we refer the readers to [86].

2.1.3 Some general remarks

At this point, it is worth noting that for all the three properties $\mathcal{P}$ discussed above—negativity (and hence dimension), entanglement depth, and reference-state fidelity—their DI certification can be achieved via the characterization of some convex set ${\mathcal{C}}_{\mathcal{P}}$ in the space of correlation vectors $\{\vec{P}\}$. More precisely, for negativity, by turning the objective function of Equations 9a into the constraint [17]

${\chi }_{\ell }{\left[{\sigma }_{-}\right]}_{\text{tr}}\le {\mathcal{N}}_0,(22)$

we obtain an SDP that characterizes the set of correlations attainable by quantum states having a negativity upper-bound by ${\mathcal{N}}_0$. Then, Equation 10 can be understood as a separating hyperplane relevant for witnessing a negativity larger than ${\mathcal{N}}_0$.

On the other hand, if we drop the constraint of Equation 9b, but imposes additional positive-partial-transposition constraints, then we obtain an SDP characterization of the set ${\mathcal{C}}_{\mathcal{P}}$ having a bounded amount of entanglement depth [19] (see constraints of Equations 44b, c and d below). In this case, the first two inequalities of Equation 14 serve as the corresponding witness for entanglement depth. Finally, by demanding $\langle \psi |{\rho }_{\text{\hspace{0.17em}SWAP}}|\psi \rangle \le {\mathcal{F}}_0$ together with Equation 9c, we obtain an SDP characterization of the set ${\mathcal{C}}_{\mathcal{P}}$ associated with a swapped state [86] with a $|\psi \rangle$-fidelity upper bounded by ${\mathcal{F}}_0$. In fact, SDP characterization can also be obtained for a number of other properties, including genuine negativity [17], steering robustness [22], entanglement robustness [23], and (measurement) incompatibility robustness [22, 28].

2.2 Methodologies for hypothesis testing

Having understood how DI certification can be achieved from a given correlation $\vec{P}$, we now proceed to discuss the more realistic setting involving only a finite number of experimental trials. For concreteness, the following presentation assumes an analysis based on the data collected from $N$ trials in a Bell test. Below, we explain our approaches to the problem based on hypothesis testing. Our first step is to formulate a null hypothesis $\mathcal{H}$ based on the desired property to be certified. For example, to certify that the underlying state has a negativity larger than ${\mathcal{N}}_0$, we formulate the (converse) null hypothesis:

Null Hypothesis 1. ${\mathcal{H}}_{\mathcal{N}(\rho )\le {\mathcal{N}}_0}$: In every experimental trial, the underlying state has a negativity less than or equal to ${\mathcal{N}}_0$.

Since such a hypothesis involves a set of (rather than a single) compatible distribution $\vec{P}$, it is called a composite hypothesis [89].

Then, we apply appropriate methods for this kind of hypothesis testing on the collected data to determine an upper bound $\mathfrak{p}$ on the $p$-value associated with the hypothesis $\mathcal{H}$. Since a $p$-value quantifies the plausibility of observing the given data when $\mathcal{H}$ holds, a small value of $\mathfrak{p}$, say less than 5%, provides a strong indication that $\mathcal{H}$ is falsified. It then follows that the desired feature corresponding to the negation of $\mathcal{H}$ is certified with a confidence $\gamma$ of at least $1-\mathfrak{p}$.

Of course, one may also be interested to understand how quickly statistical evidence (against a hypothesis $\mathcal{H}$) can be gathered when we increase the number of trials. To this end, we also consider the so-called (asymptotic) confidence-gain rate [60], defined by

$G^{\left(\text{prot}\right)}≔-\underset{N_{\text{tot}}\to \infty }{\text{lim}}\frac{{\log }_2{p}_{N_{\text{tot}}}^{\left(\text{prot}\right)}}{N_{\text{tot}}},(23)$

where $p^{\left(\text{prot}\right)}$ is the $p$-value (upper bound) deduced from some protocol (abbreviated as “prot”). From the definition, it is evident that asymptotically and in the i.i.d. setting, a fewer number of trials are required to achieve the same level of statistical confidence if the corresponding $G^{\left(\text{prot}\right)}$ is higher. Next, let us elaborate the two hypothesis-testing protocols considered in this work.

2.2.1 Martingale-based protocol

We shall start with the martingale-based protocol, pioneered by Gill in [43, 61], for testing against LHV theories, and further developed in [60, 90]. The protocol relies on the observation of the (super)martingale structure in some random variables of interest. To employ the martingale-based protocol, one has to fix a Bell function $I(\upsilon )$ in advance. Ideally, $I(\upsilon )$ should be chosen such that the Bell-like inequality

$⟨I\left(\upsilon \right)⟩≔⟨\frac{{\beta }_{xy}^{ab}}{P_{xy}}⟩={\displaystyle \sum _{a,b,x,y}}{\beta }_{xy}^{ab}P\left(ab|xy\right)\stackrel{\mathcal{H}}{\le }{B}_{\mathcal{H}}\left(\vec{\beta }\right)(24)$

may be violated by some quantum correlation $\vec{P}={\vec{P}}_{\mathcal{Q}}$ (cf. Equation 6) to be prepared in an experiment.

Let ${\mathcal{\upsilon }}_j=(a_j,b_j,x_j,y_j)$ be the value realized for the random variables of the measurement outcomes and settings at the $j$-th experimental trial and $I({\mathcal{\upsilon }}_j)$, the corresponding value of Bell function for that trial. Moreover, let $\mathbf{v}=\{{\mathcal{\upsilon }}_1,\dots ,{\mathcal{\upsilon }}_i,\dots ,{\mathcal{\upsilon }}_N\}$. Then, from the observed average value of $I(\upsilon )$ over $N$ trials, i.e., $\widehat{I}(\mathbf{v})={\sum }_{j=1}^N\frac{I({\mathcal{\upsilon }}_j)}{N}$, the following $p$-value upper bound is known [90] to hold whenever $\widehat{I}\ge B_{\mathcal{H}}$:

$p^{\left(\text{mart}\right)}\le {\left[{\left(\frac{{\mathfrak{b}}_{+}-B_{\mathcal{H}}}{{\mathfrak{b}}_{+}-\widehat{I}}\right)}^{\frac{{\mathfrak{b}}_{+}-\widehat{I}}{{\mathfrak{b}}_{+}-{\mathfrak{b}}_{-}}}{\left(\frac{B_{\mathcal{H}}-{\mathfrak{b}}_{-}}{\widehat{I}-{\mathfrak{b}}_{-}}\right)}^{\frac{\widehat{I}-{\mathfrak{b}}_{-}}{{\mathfrak{b}}_{+}-{\mathfrak{b}}_{-}}}\right]}^N,(25)$

where, for simplicity, we have suppressed the dependency of $B_{\mathcal{H}}$ on $\vec{\beta }$ (and $\widehat{I}$ on $\mathbf{v}$), whereas the minimum and maximum values of $I(\mathcal{\upsilon })$ over all possible values of $\mathcal{\upsilon }=(a,b,x,y)$ are

${\mathfrak{b}}_{-}≔{\inf }_{\mathcal{\upsilon }}I\left(\mathcal{\upsilon }\right)<B_{\mathcal{H}}\le \widehat{I}<{\mathfrak{b}}_{+}≔{\sup }_{\mathcal{\upsilon }}I\left(\mathcal{\upsilon }\right).(26)$

It is worth noting that the martingale-based $p$-value upper bound of Equation 25 improves over the upper bound given in [48, 60, 61]. In Figure 1, we provide a pseudocode to explain the steps involved in applying the martingale-based protocol for DI certification.

Figure 1

Figure 1. Pseudocode associated with the martingale-based protocol for DI certification. If the $p$-value bound $\mathfrak{p}<1-\gamma$, we reject the null hypothesis ${\mathcal{H}}_{\neg \mathcal{P}}$ and hence certify the desired property $\mathcal{P}$ with confidence $\gamma$.

Let $I_{\mathcal{Q}}$ be the expectation value of $I(\upsilon )$ when we replace $\vec{P}$ by some ${\vec{P}}_{\mathcal{Q}}$ capable of violating the Bell-like inequality in Equation 24. Then, in the i.i.d. setting, where the experimental data follow the distributions given by ${\vec{P}}_{\mathcal{Q}}$, the corresponding asymptotic confidence-gain rate can be deduced from Equation 23 and Equation 25 as

$G^{\left(\text{mart}\right)}=\frac{{\mathfrak{b}}_{+}-I_{\mathcal{Q}}}{{\mathfrak{b}}_{+}-{\mathfrak{b}}_{-}}{\log }_2\frac{{\mathfrak{b}}_{+}-I_{\mathcal{Q}}}{{\mathfrak{b}}_{+}-B_{\mathcal{H}}}+\frac{I_{\mathcal{Q}}-{\mathfrak{b}}_{-}}{{\mathfrak{b}}_{+}-{\mathfrak{b}}_{-}}{\log }_2\frac{I_{\mathcal{Q}}-{\mathfrak{b}}_{-}}{B_{\mathcal{H}}-{\mathfrak{b}}_{-}}.(27)$

2.2.2 The prediction-based ratio (PBR) protocol

The other hypothesis-testing protocol that we consider in this work is based on the so-called PBR protocol proposed in [60] (see also [90]). In contrast with a martingale-based protocol, the PBR protocol does not need to presuppose any Bell-like inequality for determining a $p$-value bound. Instead, for the data $\mathbf{v}$ collected in $N$ trials, one may start by using the first $N_{\text{est}}<N$ trials from $i=\mathrm{1,2},\dots ,N_{\text{est}}$ to estimate the relative frequency

$f\left(ab|xy\right)=\frac{N_{\text{est}}\left(a,b,x,y\right)}{N_{\text{est}}\left(x,y\right)},(28)$

where $N_{\text{est}}(x,y)={\sum }_{a,b}{N}_{\text{est}}(a,b,x,y)$ and $N_{\text{est}}(a,b,x,y)$ counts among these $N_{\text{est}}$ trials the total number of times the specific combination of measurement settings and outcomes $(x,y,a,b)$ occurs.

The key idea of the PBR protocol is to use this relative frequency $\vec{f}=\{f(ab|xy)\}$ to obtain an optimized Bell-like inequality³ and apply that to $v_i$ from $i=\{N_{\text{est}}+1,N_{\text{est}}+2,\dots ,N_{\text{est}}+N_{\text{test}}\}$. To this end, we minimize the Kullback–Leibler (KL) divergence [91] from a regularized relative frequency ${\vec{f}}_{\text{reg}}$ (explained below) to the set ${\mathcal{S}}_{\mathcal{H}}$ of correlations compatible with $\mathcal{H}$:

$D_{\text{KL}}\left({\vec{f}}_{\text{reg}}\Vert {\mathcal{S}}_{\mathcal{H}}\right)≔{\inf }_{\vec{P}\in {\mathcal{S}}_{\mathcal{H}}}{\displaystyle \sum _{a,b,x,y}}{P}_{xy}{f}_{\text{reg}}\left(ab|xy\right)\log \frac{f_{\text{reg}}\left(ab|xy\right)}{P\left(ab|xy\right)}.(29)$

An important point to note now is that if the composite null hypothesis ${\mathcal{S}}_{\mathcal{H}}$ is associated with a convex set that admits an SDP characterization (as discussed in Section 2.1.3) like the kind proposed in [17, 22, 66, 67, 68]; then, Equation 29 is a conic program (see [37]) and thus efficiently solvable using a solver like $\mathsf{M}\mathsf{O}\mathsf{S}\mathsf{E}\mathsf{K}$ [93].

The unique [37] minimizer ${\vec{P}}_{\star }\in {\mathcal{S}}_{\mathcal{H}}$ can then be used to define the non-negative prediction-based ratio (PBR),

$R\left(a,b,x,y\right)≔\frac{f_{\text{reg}}\left(ab|xy\right)}{P_{\star }\left(ab|xy\right)},(30)$

which gives the optimized Bell-like inequality $⟨R(\upsilon )⟩\stackrel{\mathcal{H}}{\le }1$. Next, we compute the test statistic as

$t\left(\mathbf{v}\right)={\displaystyle \underset{j}{\Pi }}R\left(a_j,b_j,x_j,y_j\right),(31)$

where the product is only carried out over the remaining $N_{\text{test}}$ trials. Using arguments completely analogous to those given in [60] for $\mathcal{H}=\mathcal{L}$, it can then be shown that the following upper bound on the $p$-value holds:

$p^{\left(\text{pbr}\right)}\le \text{min}\left\{\frac{1}{t\left(\mathbf{v}\right)},1\right\}.(32)$

Several remarks are now in order. First, if none of the entries in $\vec{f}$ vanishes, one could also use $\vec{f}$ directly in the optimization problem of Equation 29. However, for a small $N_{\text{est}}$, a vanishing entry in $\vec{f}$ is almost bound to happen, we thus follow [60] and mix $\vec{f}$ with the uniform distribution ${\vec{P}}_{\mathbb{1}}$ to obtain

$\vec{f}\to {\vec{f}}^{\prime }≔\frac{N_{\text{est}}}{N_{\text{est}}+1}\vec{f}+\frac{1}{N_{\text{est}}+1}{\vec{P}}_{\mathbb{1}}.(33)$

Next, notice that ${\vec{f}}^{\prime }$ typically cannot be cast in the form of Equation 6. Consequently, we observe empirically that $R$ obtained by solving Equation 29 with ${\vec{f}}^{\prime }$ in place of ${\vec{f}}_{\text{reg}}$ gives evidently suboptimal performance (see, e.g., Supplementary Figures S1, S4 and S6). As such, we shall first regularize [37] ${\vec{f}}^{\prime }$ to some outer approximation of the quantum set ${\mathcal{Q}}_{\ell }$ by solving Equation 29 with ${\mathcal{S}}_{\mathcal{H}}$ replaced by ${\mathcal{Q}}_{\ell }$. In our work, ${\mathcal{Q}}_{\ell }$ is the level-$\ell$ outer approximation of the quantum set $\mathcal{Q}$ introduced in [17]. However, one may also consider other approximations [22, 66]. Since all these outer approximations admit SDP characterization, this regularization process is a conic program (see [37]). The resulting minimizer, which we call the regularized relative frequency, ${\vec{f}}_{\text{reg}}$ is then fed into Equation 29 to obtain the desired PBR.

Another important feature of the PBR protocol is that the optimized inequality characterized by $\vec{R}=\{R(a,b,x,y)\}$ can be updated as more data are incorporated into the analysis. In principle, one can update $\vec{R}$ as frequently as one desires. However, this is neither necessary nor efficient. As such, we work with blocks of $N_{\text{blk}}$ trials. The first block of data is used exclusively for producing the first regularized relative frequency, the first PBR ${\vec{R}}_1$, and by applying to the second block of $\mathbf{v}$, we obtain the first test statistic:

$t_1={\mathrm{\Pi }}_{i=N_{\text{est}}^{\left(1\right)}+1}^{N_{\text{est}}^{\left(1\right)}+N_{\text{test}}^{\left(1\right)}}{R}_1\left(a_i,b_i,x_i,y_i\right),(34)$

where $N_{\text{test}}^{(k)}=N_{\text{blk}}$ for all $k$ (if N_tot is divisible by N_blk). In the next iteration, we determine the PBR ${\vec{R}}_2$ by solving Equation 29 using $\mathbf{v}$ from the first two blocks and apply this updated PBR to the third block of $\mathbf{v}$ to get, for $k=2$,

$t_k=t_{k-1}\times {\mathrm{\Pi }}_{i=N_{\text{est}}^{\left(k\right)}+1}^{N_{\text{est}}^{\left(k\right)}+N_{\text{test}}^{\left(k\right)}}{R}_k\left(a_i,b_i,x_i,y_i\right),(35)$

where $N_{\text{est}}^{(k)}=k{N}_{\text{blk}}$. These steps may then be repeated iteratively until all the data $\mathbf{v}$ have been consumed in one way or another in the computation of $t_k$ for $k=3,\dots ,\frac{N_{\text{tot}}}{N_{\text{blk}}}-1$. For a schematic illustration of this procedure, see Figure 2. Importantly, once the test statistic $t_k$ for each iteration is determined, we can obtain the corresponding $p$-value bound using Equation 32. For the readers’ convenience, we also provide in Figure 3 a pseudocode to explain the steps involved in applying the PBR protocol for DI certification.

Figure 2

Figure 2. Instruction for the PBR method.

Figure 3

Figure 3. Pseudocode associated with the PBR protocol for DI certification. If the $p$-value bound $\mathfrak{p}<1-\gamma$, we reject the null hypothesis ${\mathcal{H}}_{\neg \mathcal{P}}$ and hence certify the desired property $\mathcal{P}$ with confidence $\gamma$.

Finally, note that for an ideal Bell test giving the correlation ${\vec{P}}_{\mathcal{Q}}$ and a composite hypothesis associated with $\mathcal{H}$, the PBR protocol has the asymptotic confidence-gain rate

$G^{\left(\text{pbr}\right)}=D_{\text{KL}}\left({\vec{P}}_{\mathcal{Q}}\Vert {\mathcal{S}}_{\mathcal{H}}\right),(36)$

which may be obtained by solving Equation 29 with ${\vec{f}}_{\text{reg}}$ replaced by ${\vec{P}}_{\mathcal{Q}}$. The proof is again completely analogous to that given for $\mathcal{H}=\mathcal{L}$ in [60] and is thus omitted.

3 Results

3.1 Device-independent certification with a confidence interval

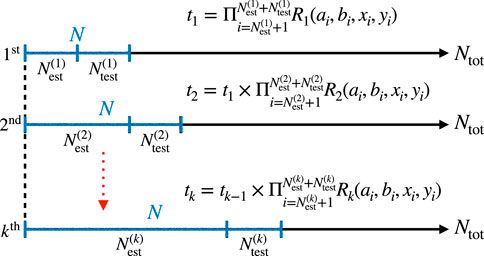
We are now ready to present our simulations results involving a finite number of trials. Throughout this section, the results presented for finite trials consist of an average over 30 complete Bell tests, each involving $N_{\text{tot}}=10^5$ trials, with the trials partitioned into blocks of size $N_{\text{blk}}=500$. Moreover, we always consider a uniform distribution for (possibly a restricted set of) measurement settings. In each Bell test, we then simulate the raw data $\mathbf{v}={\{{\upsilon }_i=(a_i,b_i,x_i,y_i)\}}_{i=1}^{N_{\text{tot}}}$ using the function $\mathsf{s}\mathsf{a}\mathsf{m}\mathsf{p}\mathsf{l}\mathsf{e}\text{\_}\mathsf{hist}$ from the Lightspeed MATLAB toolbox [93]. For the certification with finite data, we set a confidence level of $\gamma =0.99$. We also present some related confidence-gain rates in the respective subsections.

3.1.1 Negativity and dimension certification

3.1.1.1 Negativity certification

Our first example consists of a Bell test based on the quantum strategy presented in Equations 15a, b, c, which leads to a CHSH Bell value of ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}=2\sqrt{2}$. Using Equation 10, we know that the resulting quantum correlation ${\vec{P}}_{\text{CHSH}}$ gives a tight negativity lower bound of $\frac{1}{2}$ for a Bell state. From the numerically simulated data, we then perform composite hypothesis testing for Null Hypothesis 1 with ${\mathcal{N}}_0\in \{\mathrm{0,0.01},\dots ,0.50\}$.

Specifically, for the martingale-based protocol, we use Equation 25 with the CHSH Bell expression of Equation 4. In this case, ${\mathfrak{b}}_{\pm }=\pm 4$ for the chosen $P_{xy}$, while it follows from Equations 4, 10 and 24 that

${\displaystyle \sum _{a,b,x,y}}{\left(-1\right)}^{xy+a+b}4P\left(abxy\right)\stackrel{\mathcal{N}\le {\mathcal{N}}_0}{\le }2+4{\mathcal{N}}_0\left(\sqrt{2}-1\right).(37)$

On the other hand, for the PBR protocol, the optimizing distribution $P_{\star }^{(k)}(a,b|x,y)$ for the $k$-iteration can be obtained by solving (cf. Equation 29)

${\mathrm{argmin}}_{\vec{P}}-{\displaystyle \sum _{a,b,x,y}}{P}_{xy}{f}_{\text{reg}}^{\left(k\right)}\left(ab|xy\right)\log P\left(ab|xy\right),(\mathrm{38a})$

$\text{s.t.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\chi }_{\ell }\left[\rho \right]={\chi }_{\ell }\left[{\sigma }_{+}\right]-{\chi }_{\ell }\left[{\sigma }_{-}\right]⪰0,{\chi }_{\ell }{\left[{\sigma }_{\pm }\right]}^{{\text{\hspace{0.17em}T}}_{\bar{A}}}⪰0,(\mathrm{38b})$

${\chi }_{\ell }{\left[\rho \right]}_{\text{tr}}=1,{\chi }_{\ell }{\left[{\sigma }_{-}\right]}_{\text{tr}}\le {\mathcal{N}}_0,(\mathrm{38c})$

where ${\mathrm{argmin}}_{\vec{P}}$ seeks for the argument minimizing the expression in Equation 38a, ${\vec{f}}_{\text{reg}}^{(k)}$ is the regularized frequency obtained for the same iteration, and each $P(ab|xy)$ also appears as an optimization variable in the moment matrix ${\chi }_{\ell }[\rho ]$. Then, the PBR used in the computation of $t_k$ can be evaluated by replacing $f_{\text{reg}}(ab|xy)$ and $P_{\star }(ab|xy)$ in Equation 30, respectively, by $f_{\text{reg}}^{(k)}(ab|xy)$ and $P_{\star }^{(k)}(ab|xy)$.

Figure 4 shows the average amount of certifiable negativity from these two methods as a function of the number of trials $N$ employed. From the figure, it is clear that for certifying the underlying negativity using the data arising from ${\vec{P}}_{\text{CHSH}}$, the performance of the two protocols is similar. In fact, even though the martingale-based protocol appears to have a slight advantage over the PBR protocol for this certification task for small $N$’s, our computations of the asymptotic gain-rates $G^{\left(\text{pbr}\right)}$ and $G^{\left(\text{mart}\right)}$ show that they, in fact, agree (for all these values of ${\mathcal{N}}_0$ that we have considered), up to a numerical precision of $10^{-7}$. In addition, in both cases, we see that with approximately $5\times 10^3$ and $2\times 10^4$ trials, we can already certify, respectively, more than 80% and 90% of the underlying negativity with a confidence $\gamma \ge 0.99$. In Supplementary Section 1.1, we provide some additional plots showing how the $p$-value bound changes with $N$ for several values of ${\mathcal{N}}_0$.

Figure 4

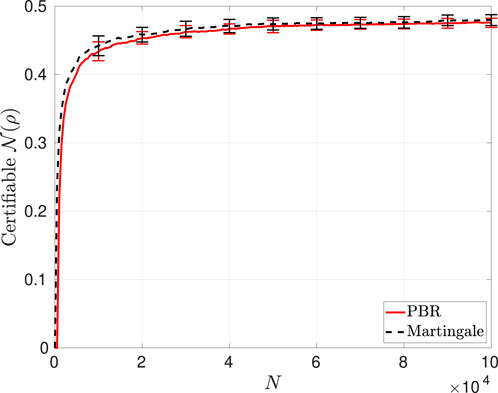
Figure 4. Negativity certifiable from the data observed in a Bell test generating ${\vec{P}}_{\text{CHSH}}$, which arises by locally measuring the Bell state $|{\psi }_{\text{\hspace{0.17em}MES}}\rangle$ of Equation 15a with the observables given in Equations 15b, c. For the martingale-based protocol and any given ${\mathcal{N}}_0$ among ${\mathit{N}}_0=\{\mathrm{0,0.01},\dots ,0.49\}$, we use Equation 37 in Equation 25 to upper-bound $p^{\left(\text{mart}\right)}$ after every block of $N_{\text{blk}}=500$ trials, thereby generating $200\times 50$ upper bounds on $p^{\left(\text{mart}\right)}$ for a complete Bell test. For the PBR protocol and a given ${\mathcal{N}}_0$ from ${\mathit{N}}_0$, we solve Equation 38 by considering the same block size and the level-3 outer approximation of $\mathcal{Q}$ introduced in [17]. Then, we obtain $199\times 50$ upper bounds on $p^{\left(\text{pbr}\right)}$ from Equations 32, 34 and 35. To determine the lower bound on the underlying $\mathcal{N}(\rho )$ with the desired confidence of $\gamma \ge$ 99%, we look for the largest ${\mathcal{N}}_0$ in ${\mathit{N}}_0$ such that ${\mathcal{H}}_{\mathcal{N}(\rho )\le {\mathcal{N}}_0}$ is rejected with a $p$-value bound being less than or equal to 0.01. Each data point shown in the plot is an average over 30 such lower bounds, and the error bar (standard deviation) gives an indication of the spread of the certifiable negativity. To avoid cluttering the plots, in each line, we show only a small number of markers.

These results clearly suggest that the CHSH Bell function of Equation 4 is optimal for certifying the underlying negativity of $|{\psi }_{\text{\hspace{0.17em}MES}}\rangle$ using the martingale-based protocol. Indeed, a separate computation of Equation 29 and Equation 30 using ${\vec{P}}_{\text{CHSH}}$ in place of ${\vec{f}}_{\text{reg}}$ show that, within a precision of $10^{-4}$, the optimized Bell-like inequality for ${\mathcal{N}}_0=\mathrm{0,0.05},\dots ,1$ is equivalent to Equation 10. How would things change if we perform DI negativity certification using the data generated from the partially entangled state $|\psi (\theta )\rangle$, Equation 17a? To this end, consider the quantum strategy of Equations 17a, b, whose resulting correlation ${\vec{P}}_{\theta }$ gives the maximal Bell CHSH violation for $|\psi (\theta )\rangle$, as well as the maximal violation of the tilted CHSH Bell inequality of Equation 19. Then, instead of repeating the same analysis, we show in Figure 5 the confidence-gain rates due to both protocols for certifying several given fractions of the underlying negativity. From the plots shown, it is evident that asymptotically, the martingale-based protocol employing the CHSH Bell function is far from optimal for certifying the underlying negativity of $|\psi (\theta )\rangle$. Indeed, the PBR protocol could identify some other Bell-like inequality that gives a much better confidence-gain rate, especially for the correlations arising from $|\psi (\theta )\rangle$ that is weakly entangled (small $\theta$). To a large extent, this can be understood by noting that the negativity lower bound of Equation 10 due to its CHSH Bell violation is generally far from tight for these states; see Supplementary Figure S3.

Figure 5

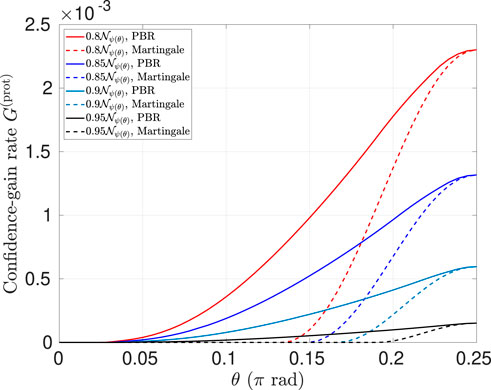
Figure 5. Asymptotic confidence-gain rate $G^{\left(\text{prot}\right)}$ based on the family of quantum correlations ${\vec{P}}_{\theta }$ derived from Equation 17a, b, where $\theta =\frac{k\pi }{180}$ rad, $k=\{\mathrm{1,2},\dots ,45\}$, parametrizes the two-qubit entangled state $|\psi (\theta )\rangle =\cos \theta |00\rangle +\sin \theta |11\rangle$. Here, we again consider Null Hypothesis 1, with ${\mathcal{N}}_0=\{0.8{\mathcal{N}}_{\psi (\theta )},0.85{\mathcal{N}}_{\psi (\theta )},0.9{\mathcal{N}}_{\psi (\theta )},0.95{\mathcal{N}}_{\psi (\theta )}\}$ and ${\mathcal{N}}_{\psi (\theta )}$ being the negativity of $\psi (\theta )$; see Supplementary Figure S3. The gain rate for the martingale-based protocol is computed from Equation 27 using the CHSH Bell-like inequality of Equation 37, whereas that for the PBR protocol is evaluated from Equation 36 using the correlation derived from Equation 17a, b.

3.1.1.2 Dimension certification via negativity certification

As mentioned in Section 2.1.2.1, the correlation ${\vec{P}}_{\text{CHSH}}$ is insufficient to demonstrate any nontrivial dimension bound. Let us consider, instead, a correlation ${\vec{P}}_{\text{CGLMP}}$ derived by locally measuring the partially entangled two-qutrit state:

$|\mathrm{\Psi }\rangle =\frac{1}{\sqrt{2+{\zeta }^2}}\left(|00\rangle +\zeta |11\rangle +|22\rangle \right),\zeta =\frac{1}{2}\left(\sqrt{11}-\sqrt{3}\right),(\mathrm{39a})$

with the local measurements

$\begin{array}{c}\hfill M_{a|x}^{\left(A\right)}=|{a\rangle }_{A,x}\langle a|,M_{b|y}^{\left(B\right)}=|{b\rangle }_{B,y}\langle b|,\hfill \\ \hfill |{a\rangle }_{A,x}={\displaystyle \sum _{j=0}^2}\frac{{\omega }^{j\left({\phi }_x^A+a\right)}}{\sqrt{3}}|j\rangle ,|{b\rangle }_{B,y}={\displaystyle \sum _{j=0}^2}\frac{{\omega }^{j\left({\phi }_y^B-b\right)}}{\sqrt{3}}|j\rangle ,\hfill \end{array}(\mathrm{39b})$

where ${\phi }_x^A=\frac{x}{2}$, ${\phi }_y^B={(-1)}^y\frac{1}{4}$, and $\{|j\rangle \}$ is the set of computational basis states. It is known [67, 71] that this strategy gives the maximal CGLMP Bell-inequality violation of ${\mathcal{S}}_{\text{\hspace{0.17em}CGLMP}3}=1+\sqrt{\frac{11}{3}}\cong 2.91485$. Moreover, the negativity of $|\mathrm{\Psi }\rangle$ can be easily evaluated to yield $\cong 0.98358$.

Next, we use the data numerically simulated from ${\vec{P}}_{\text{CGLMP}}$ to perform hypothesis testing for Null Hypothesis 1 but now with ${\mathcal{N}}_0\in {\mathit{N}}_0=\{0.5,0.51,\dots ,0.98\}$. For the PBR protocol, the computation proceeds in exactly the same way as described above (see the paragraph containing Equation 38). However, for the martingale-based protocol, since we do not have an explicit expression like that shown in Equation 37 for the CGLMP Bell expression, we compute an upper bound on $B_{\mathcal{H}}$ for each given value of ${\mathcal{N}}_0\in {\mathit{N}}_0$ according to

$\text{max}{\displaystyle \sum _{a,b,x,y}}{\beta }_{xy}^{ab}P\left(ab|xy\right),(\mathrm{40a})$

$\text{s.t.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\chi }_{\ell }\left[\rho \right]={\chi }_{\ell }\left[{\sigma }_{+}\right]-{\chi }_{\ell }\left[{\sigma }_{-}\right],{\chi }_{\ell }{\left[{\sigma }_{\pm }\right]}^{{\text{\hspace{0.17em}T}}_{\bar{A}}}⪰0,(\mathrm{40b})$

${\chi }_{\ell }\left[\rho \right]⪰0,{\chi }_{\ell }{\left[\rho \right]}_{\text{tr}}=1,{\chi }_{\ell }{\left[{\sigma }_{-}\right]}_{\text{tr}}\le {\mathcal{N}}_0,(\mathrm{40c})$

where the CGLMP Bell coefficients ${\beta }_{xy}^{ab}$ are defined in Equation 11. Meanwhile, since $P_{xy}=\frac{1}{4}$ and ${\beta }_{xy}^{ab}\in \{-\mathrm{1,0,1}\}$, we again have ${\mathfrak{b}}_{\pm }=\pm 4$ for $I_{\text{\hspace{0.17em}CGLMP}3}$.

Figure 6 shows that with approximately $6\times 10^4$ trials, we can already certify a negativity lower bound of 0.9. On the other hand, if we want to certify that we need at least a two-qutrit state to produce the observed data (arising from ${\vec{P}}_{\text{CGLMP}}$), it suffices to certify that the underlying negativity is strictly larger than 0.50, which happens already with approximately 1,500 trials. Could other two-qutrit states provide a more favorable correlation in this regard? To gain insight into the problem, we consider the following one-parameter family of two-qutrit states

$|\mathrm{\Psi }\left(\tilde{\zeta }\right)\rangle =\frac{1}{\sqrt{2+{\tilde{\zeta }}^2}}\left(|00\rangle +\tilde{\zeta }|11\rangle +|22\rangle \right)(41)$

and numerically maximize their CGLMP Bell-inequality violation using the heuristic algorithm given in [94]. We denote the corresponding correlation by ${\vec{P}}_{\tilde{\zeta }}$, compute the corresponding asymptotic confidence-gain rate for both protocols, and plot the results in Figure 7.

Figure 6

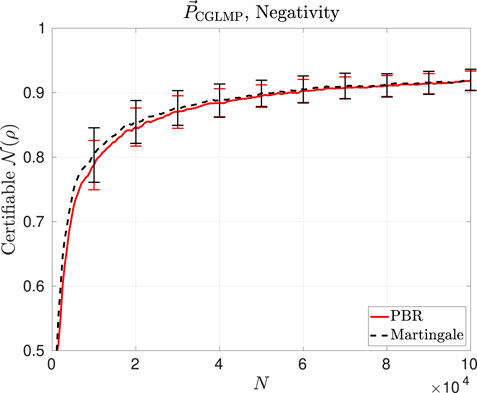
Figure 6. Negativity certifiable from the data observed in a Bell test generating ${\vec{P}}_{\text{CGLMP}}$, which arises by locally measuring the partially entangled state of Equation 39a. For details on how the plot is generated, see the caption of Figure 4, but bearing in mind that for the martingale-based protocol, we now use in Equation 25 the $B_{\mathcal{H}}$ determined from Equation 40.

Figure 7

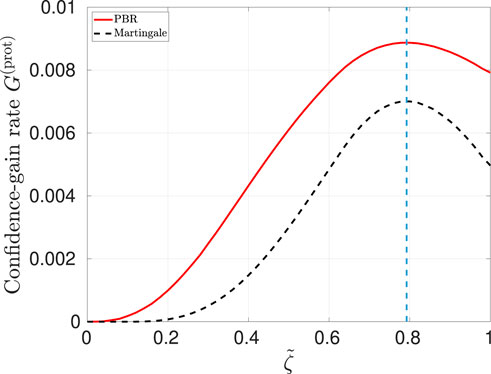
Figure 7. Asymptotic confidence-gain rate $G^{\left(\text{prot}\right)}$ based on the quantum correlation ${\vec{P}}_{\tilde{\zeta }}$ derived from maximizing the CGLMP Bell inequality violation of $|\mathrm{\Psi }(\tilde{\zeta })\rangle$, as shown in Equation 41. Here, we consider $\tilde{\zeta }=\{\mathrm{0,0.02},\dots ,1\}$ and Null Hypothesis 1, with ${\mathcal{N}}_0=0.5$. The gain rate for the martingale-based protocol is computed from Equation 27 using the CGLMP Bell function and the bound $B_{\mathcal{H}}$ determined in Equation 40 whereas that for the PBR protocol is evaluated from Equation 36 and setting ${\vec{P}}_{\mathcal{Q}}$ to ${\vec{P}}_{\tilde{\zeta }}$. The dashed blue line corresponds to the value $\tilde{\zeta }=\zeta$, cf. Equation 39a.

Interestingly, even though Figure 6 suggests that the CGLMP Bell function is very effective in providing a good $p$-value bound against Null Hypothesis 1, Figure 7 clearly shows that, asymptotically, it is not optimal. The results shown in Figure 7 further suggest that among the family of two-qutrit states given in Equation 41, the qutrit signature of $|\mathrm{\Psi }(\zeta )\rangle$, cf. Equation 39a, could even be the most prominent, when it comes to its DI certification using these hypothesis-testing techniques.

3.1.2 Entanglement depth certification

Next, we consider the tripartite correlation ${\vec{P}}_{\text{GHZ}}$ that results from locally measuring the $\pm 1$-eigenvalue observables

$A_0=B_0=C_0={\sigma }_y,A_1=B_1=C_1=-{\sigma }_x(\mathrm{42a})$

on the Greenberger–Horne–Zeilinger (GHZ) state [95, 96]:

$|\text{GHZ}\rangle =\frac{1}{\sqrt{2}}\left(|000\rangle +|111\rangle \right).(\mathrm{42b})$

It is easy to verify that ${\vec{P}}_{\text{GHZ}}$ leads to a violation of the Mermin Bell inequality, as shown in Equations 12 and 14, giving the algebraic maximum of ${\mathcal{S}}_{\text{\hspace{0.17em}Mermin}}=4$. For our simulations, we assume a uniform distribution $P_{\mathit{xyz}}=\frac{1}{4}$ over all measurement settings $x,y,z\in \{\mathrm{0,1}\}$ that satisfy $\text{mod}(x+y+z,2)=1$. Then, we test the data against the following composite hypotheses:

Null Hypothesis 2. ${\mathcal{H}}_{\text{Sep}}$: In every experimental trial, the underlying state is separable (having an entanglement depth of 1).

Null Hypothesis 3. ${\mathcal{H}}_{2-\text{prod}}$: In every experimental trial, the underlying state is 2-producible, i.e., having an entanglement depth of 2 or less.

For the martingale-based method, we use Equation 25 with the Mermin Bell expression of Equation 12 and the bounds given in Equation 14, i.e., $B_{\mathcal{H}}=2$ for Null Hypothesis 2 and $B_{\mathcal{H}}=2\sqrt{2}$ for Null Hypothesis 3. Since ${\beta }_{\mathit{xyz}}^{\mathit{abc}}\in \{-\mathrm{1,0,1}\}$, we again have ${\mathfrak{b}}_{\pm }=\pm 4$. Note that separable states can only generate Bell-local correlations [5], cf. Equation 2. Thus, for the PBR protocol with Null Hypothesis 2, the optimizing distribution $P_{\star }^{(k)}(abc|xyz)$ for the $k$-iteration can be obtained by solving (cf. Equation 29)

${\mathrm{argmin}}_{\vec{P}}-{\displaystyle \sum _{a,b,c,x,y,z}}{P}_{\mathit{xyz}}{f}_{\text{reg}}^{\left(k\right)}\left(abc|xyz\right)\log P\left(abc|xyz\right),(\mathrm{43a})$

$\text{s.t.}\vec{P}={\displaystyle \sum _i}{q}_i{\vec{D}}_i,q_i\ge 0,{\displaystyle \sum _i}{q}_i=1,(\mathrm{43b})$

where ${\vec{D}}_i$ is the $i$-th (local deterministic) extreme points of the set of tripartite Bell-local distributions.

On the other hand, notice that 2-producibility [76] is equivalent to biseparability [14] in the tripartite scenario. Hence, for Null Hypothesis 3, we obtain the corresponding optimizing distribution by solving

${\mathrm{argmin}}_{\vec{P}}-{\displaystyle \sum _{a,b,c,x,y,z}}{P}_{\mathit{xyz}}{f}_{\text{reg}}^{\left(k\right)}\left(abc|xyz\right)\log P\left(abc|xyz\right),(\mathrm{44a})$

$\text{s.t.}{\chi }_{\ell }\left[\rho \right]={\chi }_{\ell }\left[{\rho }_1\right]+{\chi }_{\ell }\left[{\rho }_2\right]+{\chi }_{\ell }\left[{\rho }_3\right],{\chi }_{\ell }\left[\rho \right]⪰0,(\mathrm{44b})$

${\chi }_{\ell }{\left[\rho \right]}_{\text{tr}}=1,{\chi }_{\ell }\left[{\rho }_i\right]⪰0,\forall i\in \left\{\mathrm{1,2,3}\right\},(\mathrm{44c})$

${\chi }_{\ell }{\left[{\rho }_1\right]}^{{\text{\hspace{0.17em}T}}_{\bar{A}}}⪰0,{\chi }_{\ell }{\left[{\rho }_2\right]}^{{\text{\hspace{0.17em}T}}_{\bar{B}}}⪰0,{\chi }_{\ell }{\left[{\rho }_3\right]}^{{\text{\hspace{0.17em}T}}_{\bar{C}}}⪰0,(\mathrm{44d})$

where ${\rho }_i$ with $i=\{\mathrm{1,2,3}\}$ are meant to represent, respectively, the constituent of $\rho$ that is separable with respect to $A|BC$, $B|AC$, and $C|AB$ bipartitions. In evaluating Equations 44a, b, c, d, we use level $\ell =1$ of the hierarchy introduced in [17]. For both hypotheses, we then evaluate

$R\left(a,b,c,x,y,z\right)=\frac{f_{\text{reg}}^{\left(k\right)}\left(abc|xyz\right)}{P_{\star }\left(abc|xyz\right)}(45)$

for the computation of the test statistic $t_k$.

For ${\vec{P}}_{\text{GHZ}}$ and Null Hypothesis 2, the confidence-gain rate $G^{\left(\text{pbr}\right)}$ is already known (see Table I of [89]) to be approximately 0.415037; our computation reproduces this and further shows that for Null Hypothesis 3, the confidence-gain rate is approximately 0.228446. Moreover, to six decimal places, $G^{\left(\text{pbr}\right)}$ and $G^{\left(\text{mart}\right)}$ agree for both hypotheses. What about finite data? Based on the average results from 30 simulations, we find that the $p$-value bounds or, more precisely, $\mathfrak{P}=-{\log }_2{p}^{\left(\text{prot}\right)}$can be very well-fitted into the following straight lines:

${\mathfrak{P}}_{{\mathcal{H}}_{\text{Sep}}}^{\left(\text{pbr}\right)}=0.414958N-204.978,N\in \left[10^3,10^5\right],(46)$

${\mathfrak{P}}_{{\mathcal{H}}_{\text{Sep}}}^{\left(\text{mart}\right)}=0.415037N,N\in \left[\mathrm{0,1}{0}^5\right](47)$

for the separable hypothesis ${\mathcal{H}}_{\text{Sep}}$ in Null Hypothesis 2, and

${\mathfrak{P}}_{{\mathcal{H}}_{2-\text{prod.}}}^{\left(\text{pbr}\right)}=0.22838N-115.22,N\in \left[10^3,10^5\right],(48)$

${\mathfrak{P}}_{{\mathcal{H}}_{2-\text{prod.}}}^{\left(\text{mart}\right)}=0.228447N,N\in \left[\mathrm{0,1}{0}^5\right](49)$

for the 2-producible hypothesis ${\mathcal{H}}_{2-\text{prod.}}$ in Null Hypothesis 3. In all these fits, the coefficient of determination $R^2$ is 1 even if we keep up to 7 significant digits. Consequently, based on this interpolation, even if we only run the Bell test using the strategy of Equation 42a, b for 100 trials, there is already sufficient data to certify genuine tripartite-entanglement with a confidence of at least $1-10^{-6}$.

3.1.3 Fidelity certification

Our last examples concern the DI certification of a lower bound on the fidelity of the swapped state ${\rho }_{\text{\hspace{0.17em}SWAP}}$ with respect to the target state $|\psi (\theta )\rangle$ of Equation 17a. To this end, we use the same set of data generated for the analysis in Section 3.1.1.1 and consider the following null hypothesis:

Null Hypothesis 4. ${\mathcal{H}}_{{\mathcal{F}}_{\theta }({\rho }_{\text{\hspace{0.17em}SWAP}})\le {\mathcal{F}}_0}$: In every experimental trial, the swapped state ${\rho }_{\text{\hspace{0.17em}SWAP}}$ extractable from the underlying state $\rho$ has a $|\psi (\theta )\rangle$-fidelity upper bounded by ${\mathcal{F}}_0$, i.e.,

${\mathcal{F}}_{\theta }\left({\rho }_{\text{\hspace{0.17em}SWAP}}\right)≔\langle \psi \left(\theta \right)|{\rho }_{\text{\hspace{0.17em}SWAP}}|\psi \left(\theta \right)\rangle \le {\mathcal{F}}_0.(50)$

Then, for any given $\theta$ and ${\mathcal{F}}_0\ge \cos \theta$, to apply the PBR protocol, we solve the optimizing distribution $P_{\star }^{(k)}(ab|xy)$ for the $k$-iteration (cf. Equation 29) by

${\mathrm{argmin}}_{\vec{P}}-{\displaystyle \sum _{a,b,x,y}}{P}_{xy}{f}_{\text{reg}}^{\left(k\right)}\left(ab|xy\right)\log P\left(ab|xy\right),(\mathrm{51a})$

$\text{s.t.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\chi }_{\ell }\left[\rho \right]⪰0,{\chi }_{\ell }{\left[\rho \right]}_{\text{tr}}=1,{\mathcal{F}}_{\theta }\left({\rho }_{\text{\hspace{0.17em}SWAP}}\right)\le {\mathcal{F}}_0,(\mathrm{51b})$

where the left-hand side of the last inequality in Equation 51b consists of some specific linear combination of entries of ${\chi }_{\ell }[\rho ]$; see [86] for details. Then, as with negativity certification, we can evaluate the PBR used in the computation of $t_k$ by replacing $f_{\text{reg}}(ab|xy)$ and $P_{\star }(ab|xy)$, respectively, by $f_{\text{reg}}^{(k)}(ab|xy)$ and $P_{\star }^{(k)}(ab|xy)$ in Equation 30. As for the martingale-based protocol, we first solve

$\text{max}{\displaystyle \sum _{a,b,x,y}}{\beta }_{xy}^{ab}P\left(ab|xy\right),(\mathrm{52a})$

$\text{s.t.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\chi }_{\ell }\left[\rho \right]⪰0,{\chi }_{\ell }{\left[\rho \right]}_{\text{tr}}=1,{\mathcal{F}}_{\theta }\left({\rho }_{\text{\hspace{0.17em}SWAP}}\right)\le {\mathcal{F}}_0(\mathrm{52b})$

to determine $B_{\mathcal{H}}$ for Null Hypothesis 4 and then apply Equation 25 to determine the corresponding $p$-value upper bound.

Let us start with the self-testing of a Bell state, corresponding to $\theta =\frac{\pi }{4}$ in Equation 17a. In this case, we use the CHSH Bell function specified in Equation 4 and consider ${\mathcal{F}}_0\in {\mathit{F}}_0=\{0.5,0.51,\dots ,0.99\}$. For both protocols, by systematically evaluating the $p$-value bounds from the data for each of these ${\mathcal{F}}_0$’s, we determine a lower bound on ${\mathcal{F}}_{\theta =\frac{\pi }{4}}({\rho }_{\text{\hspace{0.17em}SWAP}})$ with the desired confidence of at least 99%. The results obtained from both hypothesis-testing protocols are shown in Figure 8.

Interestingly, our results show that the martingale-based protocol with the CHSH Bell function of Equation 4 again performs very well for the self-testing of a Bell state with finite statistics, even though our computation of the corresponding asymptotic confidence-gain rate for ${\mathcal{F}}_0=0.5$ clearly shows that it is suboptimal even for the Bell state; see Figure 9. What about other partially entangled states? To answer this question, we evaluate the confidence-gain rate derived from both protocols for ${\mathcal{F}}_0={\cos }^2\theta$, with $\theta =\{0°,1°,2°,\dots ,45°\}$. Note that a fidelity of ${\cos }^2\theta$ is always achievable even if Alice and Bob do not share any entanglement; they merely have to prepare $|00\rangle$ using local operations and classical communication before the Bell test. This time around, for the martingale-based protocol, we switch to the Bell function of the tilted CHSH Bell inequality of Equation 19, which is known to facilitate the self-testing of all entangled $|\psi (\theta )\rangle$. The corresponding results are shown in Figure 9.

Figure 8

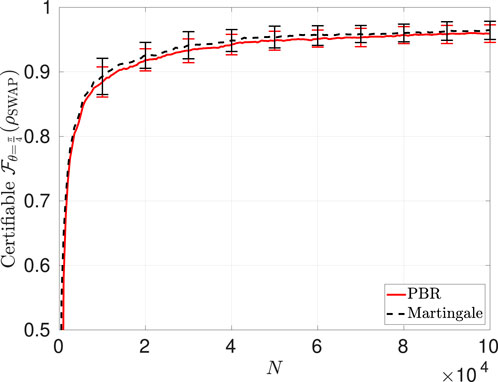
Figure 8. Certifiable fidelity ${\mathcal{F}}_{\theta =\frac{\pi }{4}}({\rho }_{\text{\hspace{0.17em}SWAP}})$ from the data observed in a Bell test generating ${\vec{P}}_{\text{CHSH}}$, which arises by locally measuring the Bell state $|{\psi }_{\text{\hspace{0.17em}MES}}\rangle$, cf. Equations 15a, b, c. For the martingale-based protocol and any given ${\mathcal{F}}_0$ among ${\mathit{F}}_0=\{0.5,0.51,\dots ,0.99\}$, we use $B_{\mathcal{H}}$ determined from Equations 52a, b in Equation 25 to upper-bound $p^{\left(\text{mart}\right)}$ after every block of $N_{\text{blk}}=500$ trials, thereby generating $200\times 50$ upper bounds on $p^{\left(\text{mart}\right)}$ for a complete Bell test. For the PBR protocol and a given ${\mathcal{F}}_0$ from ${\mathit{F}}_0$, we solve Equations 51a, b by considering the same block size and the level-2 outer approximation of $\mathcal{Q}$ introduced in [17]. Then, we obtain $199\times 50$ upper bounds on $p^{\left(\text{pbr}\right)}$ from Equations 32, 34 and 35. To determine the lower bound on the underlying ${\mathcal{F}}_{\theta =\frac{\pi }{4}}({\rho }_{\text{\hspace{0.17em}SWAP}})$ with the desired confidence of $\gamma \ge$ 99%, we look for the largest ${\mathcal{F}}_0$ in ${\mathit{F}}_0$ such that ${\mathcal{H}}_{{\mathcal{F}}_{\theta }({\rho }_{\text{\hspace{0.17em}SWAP}})\le {\mathcal{F}}_0}$ is rejected with a $p$-value upper bound less than or equal to 0.01.

Figure 9

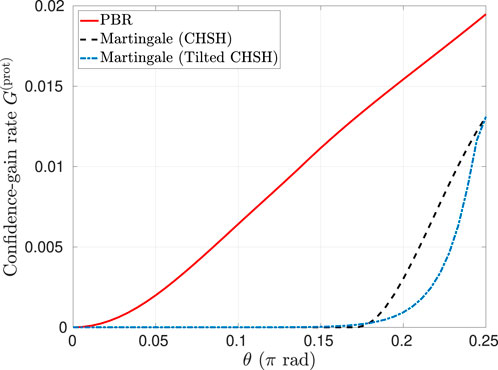
Figure 9. Asymptotic confidence-gain rate $G^{\left(\text{prot}\right)}$ based on the family of quantum correlations ${\vec{P}}_{\theta }$ derived from Equations 17a, b, where $\theta =\frac{k\pi }{180}$ rad, $k=\{\mathrm{1,2},\dots ,45\}$. Here, we consider Null Hypothesis 4, with ${\mathcal{F}}_{\theta }({\rho }_{\text{\hspace{0.17em}SWAP}})={\cos }^2\theta$, the trivial fidelity achievable without shared entanglement. The gain rate for the martingale-based protocol is computed from Equation 27 using the CHSH Bell function of Equation 4 (dashed line, black) and the tilted CHSH Bell function of Equation 19 (dashed-dotted line, blue), whereas that for the PBR protocol is evaluated from Equation 36.

3.1.4 Properties certification via Bell-value certification

The advantage of a fidelity certification based on the SWAP method [86, 88] is that the technique is applicable to a general Bell scenario. However, in the simplest CHSH Bell scenario, it is known that a much tighter lower bound on the Bell-state fidelity can be obtained by considering a more general extraction map. Specifically, Kaniewski showed in [97] that

${\max }_{{\mathrm{\Lambda }}_A,{\mathrm{\Lambda }}_B}{\min }_{{\rho }_{AB}}\mathcal{F}\left.[\left({\mathrm{\Lambda }}_A\otimes {\mathrm{\Lambda }}_B\right)\left({\rho }_{AB}\right),|{\psi }_{\text{MES}}\rangle \langle {\psi }_{\text{MES}}|]\right)\ge \frac{1}{2}+\frac{1}{2}\frac{{\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}-{\beta }^{*}}{2\sqrt{2}-{\beta }^{*}},(53)$

where ${\mathrm{\Lambda }}_A$, ${\mathrm{\Lambda }}_B$ are local extraction maps acting, respectively, on Alice’s and Bob’s subsystem, while ${\beta }^{*}≔\frac{16+14\sqrt{2}}{17}\approx 2.1058$ is the threshold CHSH value, for which the fidelity bound becomes trivial.

To take the advantage of Equation 53, we can first perform hypothesis testing based on the following null hypothesis.

Null Hypothesis 5. ${\mathcal{H}}_{{\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}(\rho )\le {\mathcal{S}}_0}$: In every experimental trial, the underlying state and measurements yield a CHSH value ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$ less than or equal to ${\mathcal{S}}_0$.

Specifically, using the same set of data generated for the analysis in Sections 3.1.1.1 and 3.1.3, we perform composite hypothesis testing for Null Hypothesis 5 with ${\mathcal{S}}_0\in \{\mathrm{2,2}+\mathrm{\Delta }\mathcal{S},2+2\mathrm{\Delta }\mathcal{S},\dots ,2\sqrt{2}-\mathrm{\Delta }S\}$, where $\mathrm{\Delta }\mathcal{S}=\frac{2(\sqrt{2}-1)}{50}$.

In particular, for the martingale-based protocol, we can simply use Equation 25 with ${\mathfrak{b}}_{\pm }=\pm 4$ and $B_{\mathcal{H}}={\mathcal{S}}_0$. Could one also employ the PBR protocol, which does not usually presuppose any Bell-like inequality, for the current hypothesis testing? This is indeed possible. To this end, one may solve the optimizing distribution $P_{\star }^{(k)}(ab|xy)$ for the $k$-iteration (cf. Equation 29) of the PBR protocol by

${\mathrm{argmin}}_{\vec{P}}-{\displaystyle \sum _{a,b,x,y}}{P}_{xy}{f}_{\text{reg}}^{\left(k\right)}\left(ab|xy\right)\log P\left(ab|xy\right),(\mathrm{54a})$

$\text{s.t.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\displaystyle \sum _{a,b,x,y}}{\left(-1\right)}^{xy+a+b}P\left(ab|xy\right)\le {\mathcal{S}}_0,(\mathrm{54b})$

with or without imposing the SDP constraints of Equation 9c. The results obtained from these tests are shown in Figure 10.

Using each lower bound on ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$ certified from the data, Equation 53 immediately translates to a lower bound on the Bell-state fidelity with the desired confidence. For a direct comparison with the efficacy of the SWAP-based approach adopted in Section 3.1.3, we plot in Figure 11 the Bell-state fidelity certifiable using the two approaches. As expected, the tighter Bell-state fidelity lower bound provided by Equation 53 also facilitates a considerably tighter lower bound when one has access to only a finite amount of data.

It is also worth noting that in computing these PBR bounds, the computation may be further simplified by regularizing the relative frequency ${\vec{f}}_{\text{reg}}$ using only the nonsignaling constraint of Equation 7, instead of the quantum approximation using Equation 9c. For the lower bounds on ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$ presented in Figure 10, this further simplification was found to give, unsurprisingly, a worse lower bound but with a deviation bounded by $8\times 10^{-3}$. Of course, the lower bounds on ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$ can also be used to bound other desired properties. For example, Figure 4 can equivalently be obtained by combining Equation 10 with the results shown in Figure 10.

Figure 10

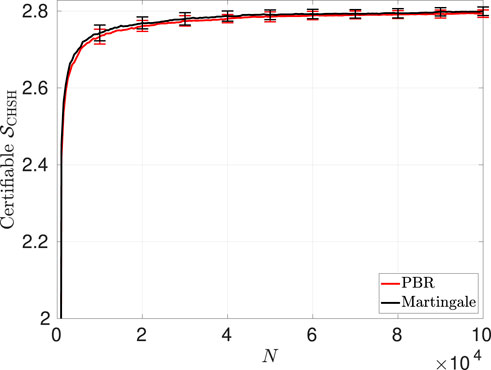
Figure 10. Certifiable Bell-CHSH violation ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$ from the data observed in a Bell test generating ${\vec{P}}_{\text{CHSH}}$, which arises by locally measuring the Bell state $|{\psi }_{\text{\hspace{0.17em}MES}}\rangle$, cf. Equation 15a, b, c. For the martingale-based protocol and any given ${\mathcal{S}}_0$ among ${\mathit{S}}_0={\{2+k\mathrm{\Delta }\mathcal{S}\}}_{k=0}^{49}$, we use Equation 54b in Equation 25 to upper-bound $p^{\left(\text{mart}\right)}$ after every block of $N_{\text{blk}}=500$ trials, thereby generating $200\times 50$ upper bounds on $p^{\left(\text{mart}\right)}$ for a complete Bell test. For the PBR protocol and a given ${\mathcal{S}}_0$ from ${\mathit{S}}_0$, we solve Equations 54a, b by considering the same block size. Then, we obtain $199\times 50$ upper bounds on $p^{\left(\text{pbr}\right)}$ from Equations 32, 34 and 35. To determine the lower bound on the underlying ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$ with the desired confidence of $\gamma \ge 99$ %, we look for the largest ${\mathcal{S}}_0$ in ${\mathit{S}}_0$ such that ${\mathcal{H}}_{{\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}\le {\mathcal{S}}_0}$ is rejected with a $p$-value bound being less than or equal to 0.01. A separate calculation shows that if we impose Equation 9c in addition to Equation 54b, one may find a visually indistinguishable difference $(<5\times 10^{-4})$ in the certifiable ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$.

Figure 11

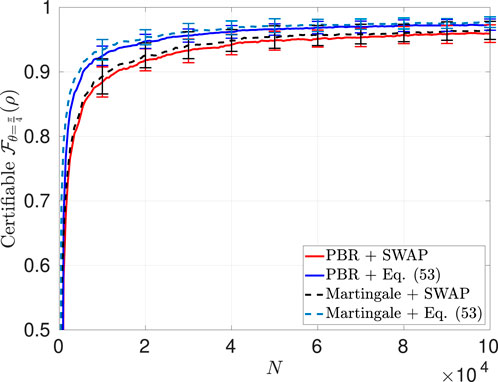
Figure 11. Comparison of the Bell-state fidelity certifiable via the SWAP-based approach presented in Section 3.1.3 and that using Equations 54a, b and ${\mathcal{S}}_{\text{\hspace{0.17em}CHSH}}$-value certification.

4 Discussion

Tomography and witnesses are two commonly employed toolkits for certifying the desirable properties of quantum devices [98]. In recent years, the device-independent paradigm has offered an appealing alternative to these conventional means as it involves only a minimal set of assumptions. Nonetheless, many DI certification schemes, e.g., [16–19, 21–27, 29, 30], implicitly assumes that the underlying quantum correlation ${\vec{P}}_{\mathcal{Q}}$ (or the actual Bell-inequality violation due to ${\vec{P}}_{\mathcal{Q}}$) is known. In practice, this is unrealistic for two reasons: 1) we always have access to only a finite amount of experimental data, and 2) actual experimental trials are typically not independent and identically distributed (i.i.d.).

To this end, very specialized tools have been developed for the task of randomness generation, quantum key distributions, and the self-testing [86, 99, 100] of quantum states. Among them, the possibility of using hypothesis testing (based on the PBR protocol [60]) for self-testing with finite data was first discussed in [86] (see also [99] for a different approach). Meanwhile, it is long known [43, 61, 90] that hypothesis testing in a Bell test can also be carried out using a martingale-based protocol. Here, we demonstrate the viability and versatility of such hypothesis-testing-based approaches for the general problem of DI certification.

Central to our finding is the observation that many desirable quantum properties $\mathcal{P}$ that one wishes to certify can be characterized by (the complement of) some convex set ${\mathcal{C}}_{\mathcal{P}}$ in the space of correlation vectors $\{\vec{P}\}$. In other words, if a given ${\vec{P}}_{\mathcal{Q}}$ lies outside ${\mathcal{C}}_{\mathcal{P}}$, a Bell-like inequality can be provided to witness this fact. This separating hyperplane then provides the basis for our martingale-based protocol for DI certification. On the other hand, if ${\mathcal{C}}_{\mathcal{P}}$ itself admits a semidefinite programming characterization like the kind proposed in [17, 22, 66–68], then the problem of minimizing the statistical distance to ${\mathcal{C}}_{\mathcal{P}}$ can be cast as a conic program, which can readily be solved using existing solvers, such as $\mathsf{M}\mathsf{O}\mathsf{S}\mathsf{E}\mathsf{K}$ [92]. In turn, the PBR protocol provides an optimized Bell-like inequality that facilitates the corresponding hypothesis testing.

In this paper, we explain in detail how the two aforementioned hypothesis-testing protocols can be adapted for the DI certification of desirable properties. Specifically, we illustrate how we can use them to perform the DI certification of the underlying negativity [64], local Hilbert space dimension [15], entanglement depth [76]; [77], and fidelity to some target two-qubit entangled pure state $|\psi (\theta )\rangle$. In each of these examples, we further demonstrate how the certifiable property (with a confidence of 99%) varies with the number of experimental trials involved; see Figures 4, 6, 8. Even though we have focused on certifying desirable properties of quantum states, as explained above, the protocols can also be applied to certify desirable properties of the measurement devices, such as their measurement incompatibility [22, 23, 26, 28] or their similarity to some target measurements [86] or instruments [27], etc. Note, however, that the usefulness of our protocols relies on the possibility of certifying the desired property from a Bell inequality-violating correlation. To this end, we remind that determining the complete list of quantum properties certifiable in a device-independent manner remains, to our knowledge, an open problem.

In the i.i.d. setting, the PBR protocol is known to be asymptotically optimal (in terms of its confidence-gain rate). However, we see from Figures 4, 6, 8 that for a relatively small number of trials and with the right choice of the Bell function, the martingale-based protocol performs equally well, if not better. A similar observation was also noted in [101] where the authors therein compare the PBR method with the Chernoff–Hoeffding bound in determining the success probability of Bernoulli trials. In our case, this is not surprising as the PBR method does not presuppose a Bell-like inequality but rather sacrifices some of the data to determine one. Indeed, if we equip the PBR protocol with the optimized Bell-like inequality right from the beginning, its performance is, as expected, no worse than the martingale-based protocol; see Supplementary Figures S1, S2, S4-S7 for some explicit examples.

Meanwhile, we also see from Figures 5, 7, 9 that for several cases that we have investigated, one’s intuitive choice of the Bell function for the martingale-based method can lead to a relatively poor confidence-gain rate and hence impairs its efficiency to produce a good $p$-value bound; see Supplementary Figures S5 and S7. For example, even though the titled CHSH Bell inequality of Equation 19 is known to self-test all entangled two-qubit pure states $|\psi (\theta )\rangle$, this choice of the Bell function in the martingale-based method leads to a worse performance (for bounding the target-state fidelity) compared with using the CHSH Bell function, which, in turn, gives a suboptimal performance compared with that derived from the PBR protocol; see Figure 9. At this point, it is worth reiterating that both protocols do not require the assumption that the experimental trials are i.i.d., even though we have only given, for simplicity, examples with i.i.d. trials.

Several research directions naturally follow from the present work. First, there are the scalability questions: 1) how do the number of measurement bases and 2) the number of samples scale with the complexity (say, dimension) of the measured system? The former is again closely related to the general viability of the device-independent certification approach, where our understanding is far from complete. As for the latter, we remark that it is indeed one of the goals of the present work to shed light on the sample complexity of our hypothesis-testing-based approaches. In some cases, such as the certification from the GHZ correlation, we see that hundreds of trials suffice, but in some others, several tens of thousands may be required to give a satisfactory level of certification. Still, some general understanding of how the sample size scales with the properties to be certified and the confidence level will be surely welcome.

Second, for experimental trials expected to deviate significantly from being i.i.d., one should choose a much smaller block size $N_{\text{blk}}$ than the size adopted in our analysis using the PBR protocol. Intuitively, we should choose $N_{\text{blk}}$ so that the trials do not differ significantly within each block of data. In fact, for testing against LHV theories, some guidelines have been provided in [60] on how we should choose $N_{\text{blk}}$. A similar analysis for other DI certifications is clearly desirable. Next, even though our hypothesis-testing-based approaches enable rigorous DI certification with a confidence interval, by virtue of the techniques involved, one can only make a relatively weak certification; out of the many experimental trials, we can be sure that at least one consists of a setup that exhibits the desired property (say, with 99% confidence). This is evidently far from satisfactory. A preferable certification scheme should allow one to comment on the general or average behavior of all the measured samples, as has been achieved in [100, 102] for self-testing.

Given that self-testing with a high fidelity is technically challenging, it is still of interest to devise a general recipe for certifying the average behavior of other more specific properties (such as entanglement and steerability), which may already be sufficient for the specific information processing task at hand. However, note that the rejection of a null hypothesis on the average behavior (e.g., average negativity $\overline{\mathcal{N}(\rho )}\le {\mathcal{N}}_0$) necessarily entails the rejection of the corresponding null hypothesis for all trials (e.g., $\mathcal{N}(\rho )\le {\mathcal{N}}_0$ in every trial). Thus, we may expect a tradeoff when switching from the current kind of hypothesis testing to that for an average behavior.

In addition, it is worth noting that if the i.i.d. assumption is somehow granted, then our protocols also certify the quality of the setup for every single runs, including those that have not been measured. In this case, once a sufficiently small $p$-value bound is obtained, one can stop measuring the rest of the systems and use them, instead, for the information processing tasks of interest. Of course, since the i.i.d. assumption is generally not warranted, a protocol that achieves certification for some fraction of the copies while leaving the rest useful for subsequent tasks will be desirable. This has been considered for one-shot distillable entanglement in [20] and the self-testing fidelity in [102]. Again, a general treatment will be more than welcome (see, e.g., [103]).

Data availability statement

The raw data supporting the conclusions of this article are available in the Supplementary Material.

Author contributions

W-GC: data curation, investigation, software, writing–original draft, and writing–review and editing. K-CC: data curation, investigation, software, and writing–original draft. K-SC: data curation, investigation, software, validation, and writing–review and editing. S-LC: investigation, validation, writing–review and editing, formal analysis, and software. Y-CL: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, software, supervision, validation, writing–review and editing, and visualization.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the National Science and Technology Council, Taiwan (Grants Nos 107-2112-M-006-005-MY2, 109-2112-M-006-010-MY3, 112-2628-M-006-007-MY4, 111-2119-M-001-004, 112-2119-M-001-006, and 111-2112-M-005-007-MY4), the Higher Education Sprout Project, Ministry of Education to the Headquarters of University Advancement at the National Cheng Kung University (NCKU), the National Center for Theoretical Sciences, the 2024 Academia Sinica Investigator Award (AS-IA-110-M02), and the Foxconn Research Institute, Taipei, Taiwan.

Acknowledgments

The authors are grateful to Jean-Daniel Bancal, Gelo Tabia, and Yanbao Zhang for many enlightening discussions and to an anonymous referee for helpful suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1434095/full#supplementary-material

Footnotes

¹Note that the same task is called device-independent verification in [102].

²If a third party is involved in the Bell test, as in the case of 2.1.2.2, and 3.1.2, we denote by $z$ and $c$, respectively, its label for the measurement setting and outcome. All other notations generalize accordingly.

³Here, the inequality is optimized in the sense that it provides the largest possible asymptotic confidence-gain rate, cf. Equation 23.

References

1. Rosset D, Ferretti-Schöbitz R, Bancal JD, Gisin N, Liang YC. Imperfect measurement settings: implications for quantum state tomography and entanglement witnesses. Phys Rev A (2012) 86:062325. doi:10.1103/PhysRevA.86.062325

CrossRef Full Text | Google Scholar

2. Moroder T, Kleinmann M, Schindler P, Monz T, Gühne O, Blatt R. Certifying systematic errors in quantum experiments. Phys Rev Lett (2013) 110:180401. doi:10.1103/PhysRevLett.110.180401

PubMed Abstract | CrossRef Full Text | Google Scholar

3. van Enk SJ, Blume-Kohout R. When quantum tomography goes wrong: drift of quantum sources and other errors. New J. Phys (2013) 15:025024. doi:10.1088/1367-2630/15/2/025024

CrossRef Full Text | Google Scholar

4. Scarani V. The device-independent outlook on quantum physics. Acta Phys Slovaca (2012) 62:347. doi:10.2478/v10155-012-0003-4

CrossRef Full Text | Google Scholar

5. Brunner N, Cavalcanti D, Pironio S, Scarani V, Wehner S. Bell nonlocality. Rev Mod Phys (2014) 86:419–78. doi:10.1103/RevModPhys.86.419

CrossRef Full Text | Google Scholar

6. Acín A, Gisin N, Masanes L. From Bell’s theorem to secure quantum key distribution. Phys Rev Lett (2006) 97:120405. doi:10.1103/PhysRevLett.97.120405

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bennett CH, Brassard G. Quantum cryptography: public key distribution and coin tossing. Theor Comput Sci (2014) 560:7–11. doi:10.1016/j.tcs.2014.05.025

CrossRef Full Text | Google Scholar

8. Ekert AK. Quantum cryptography based on Bell’s theorem. Phys Rev. Lett (1991) 67:661–3. doi:10.1103/PhysRevLett.67.661

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Gisin N, Ribordy G, Tittel W, Zbinden H. Quantum cryptography. Rev Mod Phys (2002) 74:145–95. doi:10.1103/RevModPhys.74.145

CrossRef Full Text | Google Scholar

10. Mayers D, Yao A. Quantum cryptography with imperfect apparatus. In: Proceedings 39th annual symposium on foundations of computer science (cat. No.98CB36280) (1998). p. 503–9. doi:10.1109/SFCS.1998.743501

CrossRef Full Text | Google Scholar

11. Mayers D, Yao A. Self testing quantum apparatus. Quan Info Comput (2004) 4:273–86. doi:10.26421/qic4.4-3

CrossRef Full Text | Google Scholar

12. Bell JS. On the Einstein Podolksy Rosen paradox. Physics (1964) 1:195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195

CrossRef Full Text | Google Scholar

13. Werner RF. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys Rev A (1989) 40:4277–81. doi:10.1103/PhysRevA.40.4277

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Horodecki R, Horodecki P, Horodecki M, Horodecki K. Quantum entanglement. Rev Mod Phys (2009) 81:865–942. doi:10.1103/RevModPhys.81.865

CrossRef Full Text | Google Scholar

15. Brunner N, Pironio S, Acin A, Gisin N, Méthot AA, Scarani V. Testing the dimension of Hilbert spaces. Phys Rev Lett (2008) 100:210503. doi:10.1103/PhysRevLett.100.210503

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bancal JD, Gisin N, Liang YC, Pironio S. Device-independent witnesses of genuine multipartite entanglement. Phys Rev Lett (2011) 106:250404. doi:10.1103/PhysRevLett.106.250404

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Moroder T, Bancal JD, Liang YC, Hofmann M, Gühne O. Device-independent entanglement quantification and related applications. Phys Rev Lett (2013) 111:030501. doi:10.1103/PhysRevLett.111.030501

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Tóth G, Moroder T, Gühne O. Evaluating convex roof entanglement measures. Phys Rev Lett (2015) 114:160501. doi:10.1103/PhysRevLett.114.160501

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Liang YC, Rosset D, Bancal JD, Pütz G, Barnea TJ, Gisin N. Family of Bell-like inequalities as device-independent witnesses for entanglement depth. Phys Rev Lett (2015) 114:190401. doi:10.1103/PhysRevLett.114.190401

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Arnon-Friedman R, Bancal JD. Device-independent certification of one-shot distillable entanglement. New J Phys (2019) 21:033010. doi:10.1088/1367-2630/aafef6

CrossRef Full Text | Google Scholar

21. Chen SL, Ku HY, Zhou W, Tura J, Chen YN. Robust self-testing of steerable quantum assemblages and its applications on device-independent quantum certification. Quantum (2021) 5:552. doi:10.22331/q-2021-09-28-552

CrossRef Full Text | Google Scholar

22. Chen SL, Budroni C, Liang YC, Chen YN. Natural framework for device-independent quantification of quantum steerability, measurement incompatibility, and self-testing. Phys Rev Lett (2016) 116:240401. doi:10.1103/PhysRevLett.116.240401

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chen SL, Budroni C, Liang YC, Chen YN. Exploring the framework of assemblage moment matrices and its applications in device-independent characterizations. Phys Rev A (2018) 98:042127. doi:10.1103/PhysRevA.98.042127

CrossRef Full Text | Google Scholar

24. Bancal JD, Sangouard N, Sekatski P. Noise-resistant device-independent certification of Bell state measurements. Phys Rev Lett (2018) 121:250506. doi:10.1103/PhysRevLett.121.250506

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Renou MO, Kaniewski J, Brunner N. Self-testing entangled measurements in quantum networks. Phys Rev Lett (2018) 121:250507. doi:10.1103/PhysRevLett.121.250507

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Quintino MT, Budroni C, Woodhead E, Cabello A, Cavalcanti D. Device-independent tests of structures of measurement incompatibility. Phys Rev Lett (2019) 123:180401. doi:10.1103/PhysRevLett.123.180401

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wagner S, Bancal JD, Sangouard N, Sekatski P. Device-independent characterization of quantum instruments. Quantum (2020) 4:243. doi:10.22331/q-2020-03-19-243

CrossRef Full Text | Google Scholar

28. Chen SL, Miklin N, Budroni C, Chen YN. Device-independent quantification of measurement incompatibility. Phys Rev Res (2021) 3:023143. doi:10.1103/PhysRevResearch.3.023143

CrossRef Full Text | Google Scholar

29. Sekatski P, Bancal JD, Wagner S, Sangouard N. Certifying the building blocks of quantum computers from Bell’s theorem. Phys Rev Lett (2018) 121:180505. doi:10.1103/PhysRevLett.121.180505

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Sekatski P, Bancal JD, Ioannou M, Afzelius M, Brunner N. Toward the device-independent certification of a quantum memory. Phys Rev Lett (2023) 131:170802. doi:10.1103/PhysRevLett.131.170802

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zhou L, Sheng YB, Long GL. Device-independent quantum secure direct communication against collective attacks. Sci Bull (2020) 65:12–20. doi:10.1016/j.scib.2019.10.025

CrossRef Full Text | Google Scholar

32. Bernhard C, Bessire B, Montina A, Pfaffhauser M, Stefanov A, Wolf S. Non-locality of experimental qutrit pairs. J Phys A: Math Theo (2014) 47:424013. doi:10.1088/1751-8113/47/42/424013

CrossRef Full Text | Google Scholar

33. Bancal JD, Sheridan L, Scarani V. More randomness from the same data. New J. Phys (2014) 16:033011. doi:10.1088/1367-2630/16/3/033011

CrossRef Full Text | Google Scholar

34. Schwarz S, Bessire B, Stefanov A, Liang YC. Bipartite Bell inequalities with three ternary-outcome measurements—from theory to experiments. New J. Phys (2016) 18:035001. doi:10.1088/1367-2630/18/3/035001

CrossRef Full Text | Google Scholar

35. Popescu S, Rohrlich D. Quantum nonlocality as an axiom. Found Phys (1994) 24:379–85. doi:10.1007/BF02058098

CrossRef Full Text | Google Scholar

36. Barrett J, Linden N, Massar S, Pironio S, Popescu S, Roberts D. Nonlocal correlations as an information-theoretic resource. Phys Rev A (2005) 71:022101. doi:10.1103/PhysRevA.71.022101

CrossRef Full Text | Google Scholar

37. Lin PS, Rosset D, Zhang Y, Bancal JD, Liang YC. Device-independent point estimation from finite data and its application to device-independent property estimation. Phys Rev A (2018) 97:032309. doi:10.1103/PhysRevA.97.032309

CrossRef Full Text | Google Scholar

38. Aspect A, Dalibard J, Roger G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys Rev Lett (1982) 49:1804–7. doi:10.1103/PhysRevLett.49.1804

CrossRef Full Text | Google Scholar

39. Tittel W, Brendel J, Zbinden H, Gisin N. Violation of Bell inequalities by photons more than 10 km apart. Phys Rev Lett (1998) 81:3563–6. doi:10.1103/PhysRevLett.81.3563

CrossRef Full Text | Google Scholar

40. Weihs G, Jennewein T, Simon C, Weinfurter H, Zeilinger A. Violation of Bell’s inequality under strict einstein locality conditions. Phys Rev Lett (1998) 81:5039–43. doi:10.1103/PhysRevLett.81.5039

CrossRef Full Text | Google Scholar

41. Rowe M, Kielpinski D, Meyer V, Sackett CA, Itano WM, Monroe C, et al. Experimental violation of a Bell’s inequality with efficient detection. Nature (2001) 409:791–4. doi:10.1038/35057215

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Barrett J, Collins D, Hardy L, Kent A, Popescu S. Quantum nonlocality, Bell inequalities, and the memory loophole. Phys Rev A (2002) 66:042111. doi:10.1103/PhysRevA.66.042111

CrossRef Full Text | Google Scholar

43. Gill RD Accardi contra Bell (cum mundi): the impossible coupling, 42. Beachwood, OH: Lecture Notes-Monograph Series (2003). 133–54.

CrossRef Full Text | Google Scholar

44. Hensen B, Bernien H, Dreau AE, Reiserer A, Kalb N, Blok MS, et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature (2015) 526:682–6. doi:10.1038/nature15759

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Shalm LK, Meyer-Scott E, Christensen BG, Bierhorst P, Wayne MA, Stevens MJ, et al. Strong loophole-free test of local realism. Phys Rev Lett (2015) 115:250402. doi:10.1103/PhysRevLett.115.250402

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Giustina M, Versteegh MAM, Wengerowsky S, Handsteiner J, Hochrainer A, Phelan K, et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys Rev Lett (2015) 115:250401. doi:10.1103/PhysRevLett.115.250401

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Colbeck R. Quantum and relativistic protocols for secure multi-party computation. Cambridge, United Kingdom: University of Cambridge (2006). Ph.D. thesis.

Google Scholar

48. Pironio S, Acín A, Massar S, de la Giroday AB, Matsukevich DN, Maunz P, et al. Random numbers certified by Bell’s theorem. Nature (2010) 464:1021–4. doi:10.1038/nature09008

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Acín A, Brunner N, Gisin N, Massar S, Pironio S, Scarani V. Device-independent security of quantum cryptography against collective attacks. Phys Rev Lett (2007) 98:230501. doi:10.1103/PhysRevLett.98.230501

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Pironio S, Acín A, Brunner N, Gisin N, Massar S, Scarani V. Device-independent quantum key distribution secure against collective attacks. New J. Phys (2009) 11:045021. doi:10.1088/1367-2630/11/4/045021

CrossRef Full Text | Google Scholar

51. Pironio S, Massar S. Security of practical private randomness generation. Phys Rev A (2013) 87:012336. doi:10.1103/PhysRevA.87.012336

CrossRef Full Text | Google Scholar

52. Nieto-Silleras O, Bamps C, Silman J, Pironio S. Device-independent randomness generation from several Bell estimators. New J. Phys (2018) 20:023049. doi:10.1088/1367-2630/aaaa06

CrossRef Full Text | Google Scholar

53. Bierhorst P, Knill E, Glancy S, Zhang Y, Mink A, Jordan S, et al. Experimentally generated randomness certified by the impossibility of superluminal signals. Nature (2018) 556:223–6. doi:10.1038/s41586-018-0019-0

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Bourdoncle B, Lin PS, Rosset D, Acín A, Liang YC. Regularising data for practical randomness generation. Quan Sci Technol (2019) 4:025007. doi:10.1088/2058-9565/ab01e8

CrossRef Full Text | Google Scholar

55. Zhang Y, Fu H, Knill E. Efficient randomness certification by quantum probability estimation. Phys Rev Res (2020) 2:013016. doi:10.1103/PhysRevResearch.2.013016

CrossRef Full Text | Google Scholar

56. Knill E, Zhang Y, Bierhorst P. Generation of quantum randomness by probability estimation with classical side information. Phys Rev Res (2020) 2:033465. doi:10.1103/physrevresearch.2.033465

CrossRef Full Text | Google Scholar

57. Metger T, Fawzi O, Sutter D, Renner R. Generalised entropy accumulation. In: 2022 IEEE 63rd annual symposium on foundations of computer science (FOCS) (2022). p. 844–50. doi:10.1109/FOCS54457.2022.00085

CrossRef Full Text | Google Scholar

58. Arnon-Friedman R, Renner R, Vidick T. Simple and tight device-independent security proofs. SIAM J Comput (2019) 48:181–225. doi:10.1137/18m1174726

CrossRef Full Text | Google Scholar

59. Dupuis F, Fawzi O, Renner R. Entropy accumulation. Commun Math Phys (2020) 379:867–913. doi:10.1007/s00220-020-03839-5

CrossRef Full Text | Google Scholar

60. Zhang Y, Glancy S, Knill E. Asymptotically optimal data analysis for rejecting local realism. Phys Rev A (2011) 84:062118. doi:10.1103/PhysRevA.84.062118

CrossRef Full Text | Google Scholar

61. Gill RD Time, finite statistics, and Bell’s fifth position, 5. Växjö, Sweden: Math. Modelling in Phys. Engi., and Cog. Sc. (2003). p. 179–206. Proc. Foundations of Probability and Physics-2 (Växjö: Växjö University Press).

Google Scholar

62. Liang YC, Zhang Y. Bounding the plausibility of physical theories in a device-independent setting via hypothesis testing. Entropy (2019) 21:185. doi:10.3390/e21020185

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Clauser JF, Horne MA, Shimony A, Holt RA. Proposed experiment to test local hidden-variable theories. Phys Rev Lett (1969) 23:880–4. doi:10.1103/PhysRevLett.23.880

CrossRef Full Text | Google Scholar

64. Vidal G, Werner RF. Computable measure of entanglement. Phys Rev A (2002) 65:032314. doi:10.1103/PhysRevA.65.032314

CrossRef Full Text | Google Scholar

65. Peres A. Separability criterion for density matrices. Phys Rev Lett (1996) 77:1413–5. doi:10.1103/PhysRevLett.77.1413

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Navascués M, Pironio S, Acín A. Bounding the set of quantum correlations. Phys Rev Lett (2007) 98:010401. doi:10.1103/PhysRevLett.98.010401

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Navascués M, Pironio S, Acín A. A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations. New J. Phys (2008) 10:073013. doi:10.1088/1367-2630/10/7/073013

CrossRef Full Text | Google Scholar

68. Doherty AC, Liang YC, Toner B, Wehner S. The quantum moment problem and bounds on entangled multi-prover games. 23rd Annu IEEE Conf. Comput Comp 2008, Ccc’08 (2008) 199–210. doi:10.1109/CCC.2008.26

CrossRef Full Text | Google Scholar

69. Collins D, Gisin N, Linden N, Massar S, Popescu S. Bell inequalities for arbitrarily high-dimensional systems. Phys. Rev. Lett. (2002) 88:040404. doi:10.1103/PhysRevLett.88.040404

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Kaszlikowski D, Kwek LC, Chen JL, Żukowski M, Oh CH. Clauser-Horne inequality for three-state systems. Phys Rev A (2002) 65:032118. doi:10.1103/PhysRevA.65.032118

CrossRef Full Text | Google Scholar

71. Acín A, Durt T, Gisin N, Latorre JI. Quantum nonlocality in two three-level systems. Phys Rev A (2002) 65:052325. doi:10.1103/PhysRevA.65.052325

CrossRef Full Text | Google Scholar

72. Liang YC. Correlations, Bell inequality violation and quantum entanglement. Bribsane, Australia: University of Queensland (2008). Ph.D. thesis.

Google Scholar

73. Lu H, Zhao Q, Li ZD, Yin XF, Yuan X, Hung JC, et al. Entanglement structure: entanglement partitioning in multipartite systems and its experimental detection using optimizable witnesses. Phys Rev X (2018) 8:021072. doi:10.1103/PhysRevX.8.021072

CrossRef Full Text | Google Scholar

74. Bancal JD, Barrett J, Gisin N, Pironio S. Definitions of multipartite nonlocality. Phys Rev A (2013) 88:014102. doi:10.1103/PhysRevA.88.014102

CrossRef Full Text | Google Scholar

75. Curchod FJ, Gisin N, Liang YC. Quantifying multipartite nonlocality via the size of the resource. Phys Rev A (2015) 91:012121. doi:10.1103/PhysRevA.91.012121

CrossRef Full Text | Google Scholar

76. Gühne O, Tóth G, Briegel HJ. Multipartite entanglement in spin chains. New J. Phys (2005) 7:229. doi:10.1088/1367-2630/7/1/229

CrossRef Full Text | Google Scholar

77. Sørensen AS, Mølmer K. Entanglement and extreme spin squeezing. Phys Rev Lett (2001) 86:4431–4. doi:10.1103/PhysRevLett.86.4431

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Mermin ND. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys Rev Lett (1990) 65:1838–40. doi:10.1103/PhysRevLett.65.1838

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Šupić I, Bowles J. Self-testing of quantum systems: a review. Quantum (2020) 4:337. doi:10.22331/q-2020-09-30-337

CrossRef Full Text | Google Scholar

80. Jebarathinam C, Hung JC, Chen SL, Liang YC. Maximal violation of a broad class of Bell inequalities and its implication on self-testing. Phys Rev Res (2019) 1:033073. doi:10.1103/PhysRevResearch.1.033073

CrossRef Full Text | Google Scholar

81. Kaniewski J. Weak form of self-testing. Phys Rev Res (2020) 2:033420. doi:10.1103/PhysRevResearch.2.033420

CrossRef Full Text | Google Scholar

82. Summers SJ, Werner R. Maximal violation of Bell’s inequalities is generic in quantum field theory. Commun Math Phys (1987) 110:247–59. doi:10.1007/BF01207366

CrossRef Full Text | Google Scholar

83. Popescu S, Rohrlich D. Which states violate Bell’s inequality maximally? Phys Lett A (1992) 169:411–4. doi:10.1016/0375-9601(92)90819-8

CrossRef Full Text | Google Scholar

84. Braunstein SL, Mann A, Revzen M. Maximal violation of Bell inequalities for mixed states. Phys Rev Lett (1992) 68:3259–61. doi:10.1103/PhysRevLett.68.3259

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Tsirelson BS. Some results and problems on quantum Bell-type inequalities. Hadronic J. Suppl (1993) 8:329–45.

Google Scholar

86. Bancal JD, Navascués M, Scarani V, Vértesi T, Yang TH. Physical characterization of quantum devices from nonlocal correlations. Phys Rev A (2015) 91:022115. doi:10.1103/PhysRevA.91.022115

CrossRef Full Text | Google Scholar

87. Yang TH, Navascués M. Robust self-testing of unknown quantum systems into any entangled two-qubit states. Phys Rev A (2013) 87:050102. doi:10.1103/PhysRevA.87.050102

CrossRef Full Text | Google Scholar

88. Yang TH, Vértesi T, Bancal JD, Scarani V, Navascués M. Robust and versatile black-box certification of quantum devices. Phys Rev Lett (2014) 113:040401. doi:10.1103/PhysRevLett.113.040401

PubMed Abstract | CrossRef Full Text | Google Scholar

89. van Dam W, Gill R, Grunwald P. The statistical strength of nonlocality proofs. IEEE Trans Inf Theor (2005) 51:2812–35. doi:10.1109/TIT.2005.851738

CrossRef Full Text | Google Scholar

90. Zhang Y, Glancy S, Knill E. Efficient quantification of experimental evidence against local realism. Phys Rev A (2013) 88:052119. doi:10.1103/PhysRevA.88.052119

CrossRef Full Text | Google Scholar

91. Kullback S, Leibler RA. On information and sufficiency. Ann Math Stat (1951) 22:79–86. doi:10.1214/aoms/1177729694

CrossRef Full Text | Google Scholar

93. Minka T. The lightspeed Matlab toolbox (2017). Available from: https://github.com/tminka/lightspeed (Accessed October 15 2024).

Google Scholar

94. Liang YC, Doherty AC. Bounds on quantum correlations in Bell-inequality experiments. Phys Rev A (2007) 75:042103. doi:10.1103/PhysRevA.75.042103

CrossRef Full Text | Google Scholar

95. Greenberger DM, Horne MA, Zeilinger A. Bell’s theorem, quantum theory and conceptions of the universe. Dordrecht: Kluwer: Going Beyond Bell’s Theorem (1989). p. 69–72.

CrossRef Full Text | Google Scholar

96. Mermin ND. Quantum mysteries revisited. Am J. Phys (1990) 58:731–4. doi:10.1119/1.16503

CrossRef Full Text | Google Scholar

97. Kaniewski J. Analytic and nearly optimal self-testing bounds for the Clauser-Horne-Shimony-Holt and Mermin inequalities. Phys Rev Lett (2016) 117:070402. doi:10.1103/PhysRevLett.117.070402

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Eisert J, Hangleiter D, Walk N, Roth I, Markham D, Parekh R, et al. Quantum certification and benchmarking. Nat Rev Phys (2020) 2:382–90. doi:10.1038/s42254-020-0186-4

CrossRef Full Text | Google Scholar

99. Tan TR, Wan Y, Erickson S, Bierhorst P, Kienzler D, Glancy S, et al. Chained Bell inequality experiment with high-efficiency measurements. Phys Rev Lett (2017) 118:130403. doi:10.1103/PhysRevLett.118.130403

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Bancal JD, Redeker K, Sekatski P, Rosenfeld W, Sangouard N. Self-testing with finite statistics enabling the certification of a quantum network link. Quantum (2021) 5:401. doi:10.22331/q-2021-03-02-401

CrossRef Full Text | Google Scholar

101. Wills P, Knill E, Coakley K, Zhang Y. Performance of test supermartingale confidence intervals for the success probability of Bernoulli trials. J. Res Natl Inst Stan (2020) 125:125003. doi:10.6028/jres.125.003

CrossRef Full Text | Google Scholar

102. Gočanin A, Šupić I, Dakić B. Sample-efficient device-independent quantum state verification and certification. PRX Quan (2022) 3:010317. doi:10.1103/PRXQuantum.3.010317

CrossRef Full Text | Google Scholar

103. Zhang Y, Seshadri A, Knill E. Confidence-interval construction with non-i.i.d. spot-checking trials and its application in quantum information. Optica Quantum 2.0 Conference and Exhibition. Denver, Colorado: Optica Publishing Group (2023). Technical Digest Series, QTu3A.20. doi:10.1364/QUANTUM.2023.QTu3A.20

CrossRef Full Text | Google Scholar

104. Mosek AS. Mosek conic optimization. MOSEK Model Cookbook (2019).

Google Scholar

105. Lin PS, Vértesi T, Liang YC. Naturally restricted subsets of nonsignaling correlations: typicality and convergence. Quantum (2022) 6:765. doi:10.22331/q-2022-07-14-765

CrossRef Full Text | Google Scholar