Electronic 1/f noise as a probe of dimensional effects on spin-glass dynamics

Over the past decade, spin-glass simulations have improved to the point that they now access time- and length-scales comparable to experiments at the mesoscale. A recent series of thin-film field-cooled/zero-field-cooled magnetization (FC/ZFC) experiments demonstrated activated spin dynamics, with a temperature-independent activation energy proportional to the logarithm of the film thickness and with coefficients in remarkable agreement with the simulation. These measurements require the application of small magnetic fields, which has been shown to affect the spin-glass energy landscape. Measurements of the $1/f$ noise in metallic spin-glasses have been previously shown to be a sensitive probe of the spin dynamics, and the measurements can be made without applying a magnetic field. In this mini-review, we review these techniques and discuss how transport measurements can fit into the current landscape of spin-glass measurements. We compare previous measurements to more recent measurements on similar films, made with ostensibly different cooling protocols, and compare both the previous and recent measurements to the magnetometry. The transport measurements—taken over a wider range of temperature than magnetometry—suggest that the maximum spin-glass energy barrier height is temperature-dependent, not fixed, possibly due to two-dimensional dynamics. We discuss this possibility, along with future measurements, which may be able to resolve this mystery.

Introduction

Spin-glasses are an archetypal complex system. The same rugged energy landscape characteristic to these frustrated magnets can describe polymers, structural glasses, the stock market, and even neural networks. Yet, despite the passage of more than 5 decades since their discovery, accompanied by intensive experimental and theoretical efforts, the underlying physics of the spin-glass state remains a mystery, with even the existence of a single ground state (in three dimensions) being an open question [1].

Experimentally, spin-glass systems are notoriously difficult to study. Spin-glasses are a magnetic system; however, absent the application of a magnetic field (either before or during a measurement), the magnetization will be 0. In order to directly probe the dynamics, an experimenter must apply a small magnetic field, which has been shown to alter the dynamics of the system, reducing the free-energy barriers due to the Zeeman interaction. Indeed, even small fields may fundamentally alter the nature of the system, with the “droplet” model [2, 3] predicting that the spin-glass state is destroyed by any field, no matter how small, although this has proven difficult to distinguish experimentally from the mean-field prediction of a (de Almeida–Thouless) phase transition in a field [4].

Moreover, spin-glass systems rapidly fall out of equilibrium. Their dynamics are slow and exhibit memory: in general, the result of a measurement on a spin-glass will depend on the parameters (e.g., applied field and temperature) at the time of the measurement and on the values of those parameters at all previous time points since cooling into the spin-glass state, although this description is complicated by effects such as temperature chaos. For this reason, for an unambiguous comparison between simulation and experiment, a well-defined cooling protocol should be used.

In this mini-review, we discuss recent spin-glass magnetometry measurements, which have been interpreted through the spin-glass coherence length. The coherence length is defined using a four-spin correlation function, and it is physically the characteristic length-scale of the thermally equilibrated domains within a spin-glass sample. Well below the spin-glass transition temperature, the domains grow very slowly and the system is out-of-equilibrium. In experiments, one way to probe the coherence length is to fabricate devices where the coherence length can increase to the sample thickness. Then, the dynamics should change from three- to two-dimensional, and the apparent freezing temperature is reduced. In simulations, the ground state is never known and may not be unique, so to measure the coherence length, researchers look at the overlap between many replicas of the system [5]. Because the computing power has increased (and costs have decreased) dramatically over the past decades, the JANUS collaboration has been able to design and build an FPGA-based, ultra-parallelized processor optimized specifically for Monte Carlo simulations of spin-glasses [6]. These simulations provide access to the spin-glass coherence length, and for the first time, experiments and simulations on mesoscale systems are able to probe comparable time- and length-scales, allowing direct comparison between the two.

After the discussion of the state-of-the-art conventional measurements and simulation, we will move to the main topic of this review: electronic noise measurements. These measurements are an ideal complement to the more conventional measurements for measurements on mesoscale systems, where dimensional effects play a role. The techniques discussed here are not new, but they are of renewed importance due to the advances in simulation and recent measurements of the spin-glass coherence length.

Magnetometry and spin-glass coherence length

When a spin-glass is quenched from above its glass temperature ${\text{T}}_{\text{g}}$ to a measurement temperature $T$ well below ${\text{T}}_{\text{g}}$, spin-glass correlations grow slowly in time and the system falls out of equilibrium. In order to describe this effect, Kisker et al. simulated Ising spin-glasses and measured a four-spin autocorrelation function [5]. In this way, the authors were able to define an effective coherence length, the fundamental length-scale describing the spatial extent of the spin-glass correlations after waiting time $t$,

$\frac{\xi \left(t,T\right)}{a_0}=c_1{\left(\frac{t}{{\tau }_0}\right)}^{c_{2}T/{\text{T}}_{\text{g}}},(1)$

where $a_0$ is the average spacing between the magnetic dopants, $c_1$ is a prefactor of order unity, ${\tau }_0\approx \hslash /k_{\text{B}}{\text{T}}_{\text{g}}$ is a characteristic timescale of microscopic magnetic fluctuations, and $c_2$ is a constant which can be determined experimentally [5]. On the experimental front, Joh et al. provided the first procedure for determining $\xi (t,T)$ experimentally [7]. One key insight is that after time $t$, the maximum free energy barrier, ${\mathrm{\Delta }}_{\text{max}}$, surmounted will be given by

${\mathrm{\Delta }}_{\text{max}}\left(t\right)\approx k_{\text{B}}T\ln \left(\frac{t}{{\tau }_0}\right),(2)$

according to the Arrhenius law.

Recently, variations on this approach have been employed on Ge:Mn [8, 9], single-crystal Cu:Mn [10–13], polycrystalline Cu:Mn [14], and Cu:Mn thin-films [15, 16]. Moreover, in the decades since the work by Kisker et al., it has become possible to simulate spin-glasses on the same time- and length-scales probed experimentally [10, 11, 17–19]; the agreement between the dynamics of the coherence length extracted experimentally and from simulation has been remarkable [20].

In the Cu:Mn thin-film experiments (e.g., Refs. [15, 16]), the coherence length $\xi (t,T)$ increases in time according to Equation 1 until it reaches the film thickness $\mathcal{L}$, after which it can increase no further in the direction perpendicular to the plane of the film. Neglecting the effects of any in-plane increase in the coherence length on the energy barriers, according to Equation 1 and Equation 2, this will pin the maximum barrier height at

$\frac{{\mathrm{\Delta }}_{\text{max}}\left(\mathcal{L}\right)}{k_{\text{B}}{\text{T}}_{\text{g}}}=\frac{1}{c_2}\left[\ln \left(\frac{\mathcal{L}}{a_0}\right)-\ln c_1\right].(3)$

In the vicinity of ${\text{T}}_{\text{g}}$, the maximum barrier height will be fixed by the film thickness alone and independent of temperature. This implies that, at long times, the thermoremanent magnetization (TRM) and, equivalently, the irreversible magnetizaton (defined as the difference between the FC and ZFC magnetization) should be time-dependent, exhibiting an exponential decay, consistent with activated dynamics over a free energy barrier of height ${\mathrm{\Delta }}_{\text{max}}(\mathcal{L})$. By the same argument, the apparent freezing temperature of a thin spin-glass film will depend on the measurement time $t$ according to

$t\approx {\tau }_0\exp \left[\frac{{\mathrm{\Delta }}_{\text{max}}\left(\mathcal{L}\right)}{k_{\text{B}}{T}_f}\right]\iff T_f\approx \frac{{\mathrm{\Delta }}_{\text{max}}\left(\mathcal{L}\right)}{k_{\text{B}}}{\left[\ln \left(\frac{t}{{\tau }_0}\right)\right]}^{-1}.(4)$

Using this approach, Zhai et al. was able to fit data for multiple film thicknesses (ranging from 4 nm to 20 nm), taken at multiple temperatures, to Equation 3 with $c_1=1.448$ and $c_2=0.104$ [15]. Using the Janus II supercomputer, Baity-Jesi et al. later measured an exponent in quantitative agreement with the $c_2$ from experiment [17], demonstrating the new synergy between experiment and simulation.

Applying a magnetic field will reduce the maximum barrier height, due to the Zeeman interaction. Here,

${\mathrm{\Delta }}_{\text{max}}\left(H,\mathcal{L}\right)={\mathrm{\Delta }}_{\text{max}}\left(0,\mathcal{L}\right)-E_{\text{Z}},(5)$

where the Zeeman energy is given by $E_{\text{Z}}=N_c{\chi }_{\text{FC}}{H}^2$, with $N_c$ the number of correlated spins, ${\chi }_{\text{FC}}$ the per-spin susceptibility, and $H$ the applied field. Repeating the measurements from Ref. [15] on the 20-nm film, over a range of applied fields, Zhai et al. was able to extract the number of spins in a correlated volume and determine that the correlated regions could not be spherical, but must instead be “pancake-like” (though possibly non-compact and fractal) [16]. Partially for this reason, most recent works have focused on single-crystal systems [10–13, 21], where—due to symmetry—the correlated regions will surely be spherical, to facilitate an understanding of the spin-glass state in the bulk.

Thin-film spin-glasses are of intrinsic interest, however from both an academic and practical perspective. For instance, the performance of SQUID-based superconducting circuits—including frequency-tunable qubits enabling fast quantum gates—is limited by anomalous $1/f$ magnetic flux noise at low temperatures, with the magnitude of order $\sim 1{\mathrm{\mu }{\mathrm{\Phi }}_0/\mathrm{H}\mathrm{z}}^{1/2}$ at 1 Hz, essentially independent of the geometry [22]. The weak dependence of the noise on the area of the SQUID loop points to a surface effect, and the most up-to-date work pinpoints adsorbed molecular oxygen as the origin [23]. This adsorbed oxygen—which freezes to the SQUID as it is cooled—appears to undergo a spin-glass transition at a temperature between 50 mK and 2 K, although the details are still not well-understood [22, 24, 25]. Certainly in such a system, dimensional effects play a role in the dynamics.

Transport measurements in spin-glasses

While measurements of the field-cooled, zero-field-cooled, and thermoremanent magnetization, as well as measurements of the AC susceptibility, of mesoscale spin-glass devices have been tremendously successful, they are intrinsically limited due to magnetization being an extrinsic quantity: measurement signal-to-noise (SNR) always decreases with decreasing volume. These measurements require carefully designed systems and multi-layer samples, with many thin spin-glass layers separated by non-magnetic spacing layers [15, 16, 26–28]. Moreover, interesting spin-glass dynamics are the result of a rich energy landscape, consisting of many metastable states, and the application of even weak magnetic fields can alter this landscape [9, 16]. Finally, while this scheme works well for devices “small” in one dimension (thickness), it is difficult to imagine efficiently scaling the process to devices small in two or even three dimensions.

In the 1980s and 1990s, M.B. Weissman et al., demonstrated that transport measurements—specifically, measurements of either the fluctuations of the resistance of a mesoscale spin-glass device or measurements of the fluctuations in the fluctuations of the resistance—can provide similar and complementary information to the more conventional magnetometric probes [29–33]. Despite their non-ergodic nature, the fluctuation-dissipation theorem has been shown to apply to spin-glass dynamics, meaning that these noise measurements provide the same information as direct measurements of the AC susceptibility [34]. However, because resistance fluctuations are not an extrinsic property, going to smaller volumes does not degrade and can even improve the SNR. Additionally, noise measurements allow the spin-glass energy landscape to be probed without any perturbing magnetic field, eliminating any concern over whether the system is in the linear-response regime.

Transport measurements are a proven method of probing spin-glass dynamics. While the resistivity of a spin-glass shows no sharp signature near ${\text{T}}_{\text{g}}$, the magnitude of the resistance fluctuations does exhibit such a signature, increasing by more than an order of magnitude over a temperature range of approximately $0.2{\text{T}}_{\text{f}}$ [30, 31, 33]. For mesoscale dynamics, this can be an ideal probe because the SNR does not directly depend on the volume, which is by definition always small for a mesoscale device.

The observed noise is due to universal conductance fluctuations (UCFs). Here, elastic scattering off of the magnetic dopants dominates over inelastic scattering, and the noise is due to changes in the interference in the Feynman paths of the electrons due to the reorienting of the magnetic moments of the dopants (spins). The UCF theory does result in a temperature-dependent $(\propto T^2)$ coupling between the magnetization and resistance fluctuations, that—along with an additional thermodynamic factor of $T$—must be divided out in our analysis [30, 31, 33].

Measurements of the $1/f^{\gamma }$ $(\gamma \approx 1)$ noise are a relatively direct probe of the zero-field spin-glass energy landscape. Van der Ziel explains $1/f$ noise in terms of a collection of non-interacting two-level fluctuators (TLFs) with a distribution of energy barriers [35]. A single TLF produces a Lorentzian spectrum with a “knee” frequency given by the average switching rate (related to the energy barrier as $f=f_0\exp [-E_B/kT]$ where $E_B$ is the barrier height and $f_0$ is the temperature-independent attempt frequency); the sum of many such spectra with a uniform distribution of energy barriers produces $1/f$ noise.

If the barrier distribution is not uniform, but weighted more heavily at higher (lower) energies, the spectral exponent will not be exactly $\gamma =1$, but will be $\gamma <1$ $(\gamma >1)$. Working within this model, Dutta and Horn noted that additionally, at a given temperature $T$ and for a given bandwidth ($f_{\text{min}}$ to $f_{\text{max}}$), an experiment probes the barrier distribution only within a small domain: $\text{k}\text{T}\ln (f_0/f_{\text{min}})<E_B<\text{k}\text{T}\ln (f_0/f_{\text{max}})$ [36]. In other words, for a fixed bandwidth, reducing the temperature means probing the dynamics set by smaller barriers. Combining these two concepts, one can relate the measured spectral exponent $\gamma$ at a given frequency to the logarithmic derivative of the spectral density S_M with respect to temperature, at that same frequency,

$\gamma \left(f,T\right)=1-\frac{1}{\ln \left(f/f_0\right)}\left[\frac{d\ln S_M}{d\ln T}-1\right].(6)$

This is illustrated in Figure 1. The key assumption here is that the barrier heights are independent of temperature, i.e., that the dynamics are activated. If they are not, one can repeat this analysis, but allow $f_0$ to be a temperature-dependent free parameter rather than a physical attempt frequency. If the barriers are growing with decreasing temperature, but one performs the Dutta–Horn analysis assuming constant barriers, it will appear that the attempt frequency is very large, although this is not physical. To illustrate this, consider a toy model with barriers having a linear temperature dependence, $E_B\to E_{B0}-|\alpha |\text{k}\text{T}$. Inserting this into the Arrhenius law gives $f=f_0\exp (|\alpha |)\exp [-E_{B0}/\text{k}\text{T}]$, which is equivalent to $f_0\to f_0\exp (|\alpha |)$ and removing the temperature dependence from the barriers. Fenimore and Weissman suggested defining cooperativity from noise measurements, given by

$c_{\text{N}}\left(f,T\right)\equiv -\frac{\partial \ln S_R}{\partial \ln T}{\left(1-\gamma \left(f,T\right)\right)}^{-1},(7)$

where we have converted from $S_M$ to the resistance spectral density $S_R$, taking into account the temperature-dependent factors. In the case of temperature-independent barriers, $c_N=\ln (f_0/f)\approx 30$ at all temperatures; the dynamics are activated. If, on the other hand, barriers are growing with decreasing temperature, then $c_N\gg 30$, indicating cooperative dynamics. This definition of cooperativity is analogous to the more traditional definition from magnetometry

$c_{\text{M}}\equiv \frac{\partial \ln T_f}{\partial \ln f},(8)$

but it is defined at all temperatures, including well away from $T_f$.

Figure 1

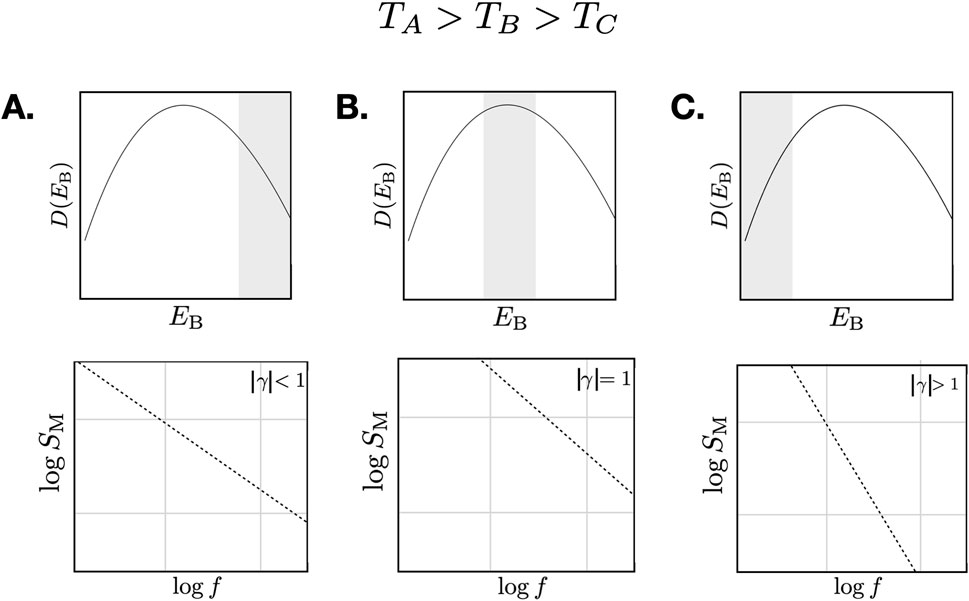
Figure 1. Dutta–Horn picture for a simple barrier distribution. (A) At high temperatures, a measurement will probe larger barriers. If the barrier distribution is weighted to lower energy, as shown, the spectral exponent will be smaller than unity. (B) At a lower temperature, the measurement will probe smaller barriers. Here, the experimental bandwidth is near the peak of the barrier distribution, which is approximately flat. The result is a spectral density with a spectral exponent near unity. The magnitude of the spectral density has also increased due to the larger density of barriers. (C) At a lower temperature still, the measurement will probe barriers below the peak. As the barrier distribution is now weighted to higher energy, the spectral exponent will be larger than unity, and because the barrier distribution is now smaller than at the peak, the magnitude of the noise has also decreased. Temperature-dependent barriers result in deviations from this picture.

We again note that $S_M$ (derived from $S_R$) provides the same information as the imaginary part of the AC susceptibility, ${\chi }^{″}$, according to the FDT [34]:

$S_M\left(f,T\right)=\frac{k_{B}T}{f}{\chi }^{″}\left(f,T\right).(9)$

Discussion

First, we compare recent transport measurements in spin-glasses. The effect of the cooling protocol on spin-glass thin-film measurements is still an open question; it is possible that temperature chaos renders the details of the experimental temperature quench moot, while Ref. [37] suggests that it is critical to rapidly quench from well above the bulk ${\text{T}}_{\text{g}}$ to a measurement temperature $T$ between each measurement. To allow for unambiguous interpretation of the measurements, Harrison et al. employed this well-defined cooling protocol and reported noise measurements on Cu:Mn (13.5 at%) on films ranging in thickness from 10 nm to 80 nm [38]. For these measurements, the devices were patterned using electron-beam lithography to form a balanced bridge, as shown schematically in Figure 2A. Each arm measures $50\text{μ}\text{m}\times 300\mathrm{n}\mathrm{m}$. The measurements are made with a lock-in amplifier. With this configuration, current fluctuations should affect each arm equally and cancel out, and the lock-in moves the signal away from the $1/f$ noise intrinsic to the electronics. The measured voltage fluctuations are then converted to resistance fluctuations, which can in turn be converted to magnetization fluctuations. In Figure 2B, we reproduce Figure 1 from Ref. [38], showing the change in both the shape and magnitude of the resistance spectral density as a function of temperature, while in Figure 2C, we reproduce Figure 2 from Ref. [38], showing the ${\chi }^{″}$ computed from noise measurements. We first note the power of the transport technique here: as noted in Ref. [38], even a witness film 100 ${\mathrm{c}\mathrm{m}}^2$ in the area sputtered simultaneously with the thinnest transport film did not yield enough magnetic material for magnetization measurements in a commercial SQUID magnetometer.

Figure 2

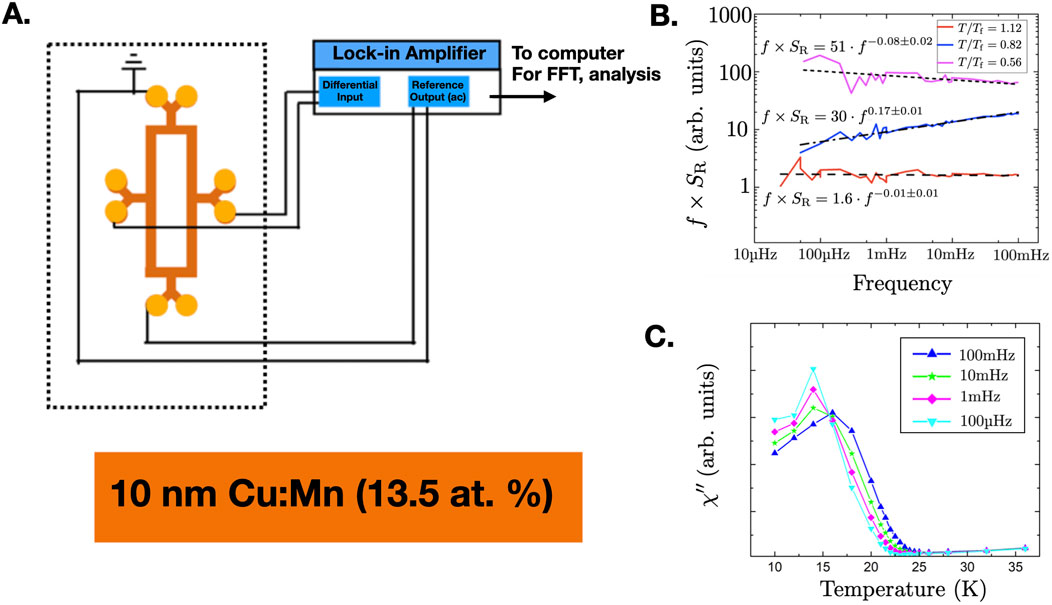
Figure 2. (A) Experimental setup for noise measurements; the dashed box denotes the inside of the cryostat. The spin-glass samples are patterned in a bridge configuration and measured with a lock-in technique. (B) $f\times S_R$ at three temperatures showing the strong dependence of both the spectral magnitude and exponent as a function of temperature. (C) Imaginary part of the AC susceptibility, ${\chi }^{″}$ as computed from the noise measurement. The data are reproduced from Ref. [38].

The analysis by Zhai et al. in Refs. [15, 16] takes the maximum barrier height, which governs the dynamics of a spin-glass, to be fixed once the spin-glass coherence length reaches the film thickness. In other words, the continued increase (if any) in the coherence length in the plane of the sample is taken to have no effect on the maximum barrier height. At this point, the dynamics are activated over fixed (temperature-independent) barriers. As discussed earlier, this implies $c_N\approx 30$. While there is a marked reduction in the cooperativity with decreasing film thickness, the dynamics are always cooperative, never exhibiting simple thermal activation. This is in apparent contrast to the analysis in Refs. [15–17] (on the other hand, the recent measurements are roughly consistent with the earlier thin-film results—both transport and magnetometry from Refs. [27, 28, 31, 33]—suggesting that the cooling protocol does not play a key role, as it was not well-specified in the earlier work and was likely different). More measurements are needed to understand why this is the case. The most obvious explanation for temperature-dependent barrier heights is the growth of in-plane correlations; though it is not yet understood why these manifest more clearly here than in Ref. [15], we note that the transport measurements were all taken over a much broader temperature range than the magnetization measurements, which would have made this effect difficult to see in the latter case.

Fortunately, transport measurements offer a clear path in testing this physics. One possibility would be to fabricate samples small in two dimensions (e.g., 20-nm-wide wires) or in all three dimensions (e.g., 40-nm cubes). In order to get an acceptable SNR for the one-dimensional cubic devices, it would certainly be necessary to fabricate long chains with non-magnetic spacers, and it would be difficult to align and make good contact. However, while daunting, this is well within the limits of modern electron-beam lithography tools. With such devices, there would be only one length scale set by the film geometry, making it possible to rule out in-plane coherence length growth as the cause of temperature-dependent barriers. These measurements would leverage both advantages of transport techniques, which would enable the measurement of devices with such small volume while, and—because they do not rely on a Zeeman energy—would provide an independent confirmation of the previous measurements of in-plane correlation growth.

In addition, measurements of the second spectral density, i.e., the noise in the $1/f$ noise, in mesoscale devices has been shown to provide different information than that accessible from susceptibility measurements [30]. Again, these effects were studied extensively by the Weissman group, but may be worth revisiting, employing the cooling protocol suggested by Ref. [37] and analyzing within the now-fully developed coherence length framework.

Author contributions

DH: writing–original draft and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Newman CM, Stein DL. Ground-state stability and the nature of the spin glass phase. Phys Rev E (2022) 105:044132. doi:10.1103/physreve.105.044132

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fisher DS, Huse DA. Nonequilibrium dynamics of spin glasses. Phys Rev B (1988) 38:373–85. doi:10.1103/physrevb.38.373

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Fisher DS, Huse DA. Equilibrium behavior of the spin-glass ordered phase. Phys Rev B (1988) 38:386–411. doi:10.1103/physrevb.38.386

PubMed Abstract | CrossRef Full Text | Google Scholar

4. de Almeida JR, Thouless DJ. Stability of the Sherrington-Kirkpatrick solution of a spin glass model. J Phys A: Math Gen (1978) 11 (5):983. doi:10.1088/0305-4470/11/5/028

CrossRef Full Text | Google Scholar

5. Kisker J, Santen L, Schreckenberg M, Rieger H. Off-equilibrium dynamics in finite-dimensional spin-glass models. Phys Rev B (1996) 53:6418–28. doi:10.1103/physrevb.53.6418

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Baity-Jesi M, Baños RA, Cruz A, Fernandez LA, Gil-Narvión J, Gordillo-Guerrero A, et al. Comp Phys Comm (2014) 185:550. doi:10.1016/j.cpc.2013.10.019

CrossRef Full Text

7. Joh YG, Orbach R, Wood GG, Hammann J, Vincent E. Extraction of the spin glass correlation length. Phys Rev Lett (1999) 82:438–41. doi:10.1103/physrevlett.82.438

CrossRef Full Text | Google Scholar

8. Guchhait S, Orbach R. Direct dynamical evidence for the spin glass lower critical Dimension2<dℓ<3. Phys Rev Lett (2014) 112:126401. doi:10.1103/physrevlett.112.126401

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Guchhait S, Orbach R. Magnetic field dependence of spin glass free energy barriers. Phys Rev Lett (2017) 118:157203. doi:10.1103/physrevlett.118.157203

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhai Q, Paga I, Baity-Jesi M, Calore E, Cruz A, Fernandez LA, et al. Phys Rev Lett (2020) 125:237202. doi:10.1103/PhysRevLett.125.237202

PubMed Abstract | CrossRef Full Text

11. Paga I, Zhai Q, Baity-Jesi M, Calore E, Cruz A, Cummings C, et al. Phys Rev B (2023) 107:214436. doi:10.1103/PhysRevB.107.214436

CrossRef Full Text

12. Zhai Q, Orbach RL, Schlagel DL. Evidence for temperature chaos in spin glasses. Phys Rev B (2022) 105:014434. doi:10.1103/physrevb.105.014434

CrossRef Full Text | Google Scholar

13. Kenning GG, Schlagel DL, Thompson V. Experimental determination of the critical spin-glass correlation length in single-crystal CuMn. Phys Rev B (2020) 102:064427. doi:10.1103/physrevb.102.064427

CrossRef Full Text | Google Scholar

14. Tennant DM, Orbach RL. Collapse of the waiting time effect in a spin glass. Phys Rev B (2020) 101:174409. doi:10.1103/physrevb.101.174409

CrossRef Full Text | Google Scholar

15. Zhai Q, Harrison DC, Tennant D, Dahlberg ED, Kenning GG, Orbach RL, et al. Phys Rev B (2017) 95:054304. doi:10.1103/PhysRevB.95.054304

CrossRef Full Text

16. Zhai Q, Harrison DC, Orbach RL. Effect of magnetic fields on spin glass dynamics. Phys Rev B (2017) 96:054408. doi:10.1103/physrevb.96.054408

CrossRef Full Text | Google Scholar

17. Baity-Jesi M, Calore E, Cruz A, Fernandez LA, Gil-Narvion JM, Gordillo-Guerrero A, et al. Phys Rev Lett (2018) 120:267203. doi:10.1103/PhysRevLett.120.267203

PubMed Abstract | CrossRef Full Text

18. Fernandez LA, Marinari E, Martin-Mayor V, Parisi G, Ruiz-Lorenzo JJ. An experiment-oriented analysis of 2D spin-glass dynamics: a twelve time-decades scaling study. J Phys A: Math Theor (2019) 52:224002. doi:10.1088/1751-8121/ab1364

CrossRef Full Text | Google Scholar

19. Fernandez LA, Marinari E, Martin-Mayor V, Paga I, Ruiz-Lorenzo JJ Phys Rev B (2019) 100:184412. doi:10.1103/PhysRevB.100.184412

CrossRef Full Text

20. He J, Orbach RL. Spin glass dynamics through the lens of the coherence length. Front Phys (2024) 12. doi:10.3389/fphy.2024.1370278

CrossRef Full Text | Google Scholar

21. Zhai Q, Martin-Mayor V, Schlagel DL, Kenning GG, Orbach RL Phys Rev B (2019) 100:094202. doi:10.1103/PhysRevB.100.094202

CrossRef Full Text

22. Sendelbach S, Hover D, Kittel A, Mück M, Martinis JM, McDermott R. Magnetism in SQUIDs at millikelvin temperatures. Phys Rev Lett (2008) 100:227006. doi:10.1103/physrevlett.100.227006

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Kumar P, Sendelbach S, Beck MA, Freeland JW, Wang Z, Wang H, et al. Phys Rev App (2016) 6:041001. doi:10.1103/PhysRevApplied.6.041001

CrossRef Full Text

24. Faoro L, Ioffe LB. Microscopic origin of low-frequency flux noise in josephson circuits. Phys Rev Lett (2008) 100:227005. doi:10.1103/physrevlett.100.227005

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Sendelbach S, Hover D, Mück M, McDermott R. Complex inductance, excess noise, and surface magnetism in dc SQUIDs. Phys Rev Lett (2009) 103:117001. doi:10.1103/physrevlett.103.117001

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kenning G, Slaughter JM, Cowen JA. Finite-Size effects in a CuMn spin-glass. Phys Rev Lett (1987) 59:2596–9. doi:10.1103/physrevlett.59.2596

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Granberg P, Nordblad P, Svedlindh P, Lundgren L, Stubi R, Kenning GG, et al. Dimensionality crossover in CuMn spin-glass films. J Appl Phys (1990) 67:5252–4. doi:10.1063/1.344627

CrossRef Full Text | Google Scholar

28. Sandlund L, Granberg P, Lundgren L, Nordblad P, Svedlindh P, Cowen JA, et al. Dynamics of Cu-Mn spin-glass films. Phys Rev B (1989) 40:869–72. doi:10.1103/physrevb.40.869

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Weissman MB, Israeloff NE, Alers GB J Magn Magn Mater (1992) 87:114. doi:10.1016/0304-8853(92)90336-M

CrossRef Full Text

30. Weissman MB. Rev Mod Phys (1993) 65:829–39. doi:10.1103/revmodphys.65.829

CrossRef Full Text

31. Israeloff NE, Weissman MB, Nieuwenhuys GJ, Kosiorowska J. Electrical noise from spin fluctuations in CuMn. Phys Rev Lett (1989) 63:794–7. doi:10.1103/physrevlett.63.794

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Israeloff NE, Alers GB, Weissman MB. Spin-fluctuation statistics inCuMn. Phys Rev B (1991) 44:12613–6. doi:10.1103/physrevb.44.12613

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Fenimore PW, Weissman MB. Resistance noise as a technique for measuring finite-size effects in single-layer Cu_Mn spin-glass films. J Appl Phys (1999) 85:8317–21. doi:10.1063/1.370676

CrossRef Full Text | Google Scholar

34. Reim W, Koch RH, Malozemoff AP, Ketchen MP, Maletta H. Magnetic equilibrium noise in spin-glasses: Eu0.4Sr0.6S. Phys Rev Lett (1986) 57:905–8. doi:10.1103/PhysRevLett.57.905

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Van der Ziel A. On the noise spectra of semi-conductor noise and of flicker effect. Physica (1950) 16:359–72. doi:10.1016/0031-8914(50)90078-4

CrossRef Full Text | Google Scholar

36. Dutta P, Horn P. Low-frequency fluctuations in solids:1fnoise. Rev Mod Phys (1981) 53:497–516. doi:10.1103/revmodphys.53.497

CrossRef Full Text | Google Scholar

37. Guchhait S, Kenning GG, Orbach RL, Rodriguez GF. Spin glass dynamics at the mesoscale. Phys Rev B (2015) 91:014434. doi:10.1103/physrevb.91.014434

CrossRef Full Text | Google Scholar

38. Harrison DC, Dahlberg ED, Orbach RL Phys Rev B (2022) 105:014413. doi:10.1103/PhysRevB.105.014413

CrossRef Full Text