
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 15 November 2024
Sec. Fusion Plasma Physics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1425963
This article is part of the Research Topic Proton Boron Nuclear Fusion: From Energy Production to Medical Applications View all 8 articles
Aneutronic p-11B nuclear fusion is promising for clean energy production, as it produces three (3) alpha particles with 8.7 MeV total energy. However, the main difficulty for p-11B fusion ignition (Q = Pfus/PBrems ≥ 1) concerns the nuclear cross section and thus, reactivity efficiency at higher than 200 keV medium temperatures. To overcome this difficulty, the present work emphasizes on the numerical investigation of medium schemes (configurations) with enhanced reactivity. The configurations refer to the addition of energetic protons in a low-density 11boron or proton–11boron medium (n = 1020 m−3), with (np/nB) > 1 for Bremsstrahlung losses optimization and initial temperature in the range of 1 keV ≤ Tin ≤ 400 keV. A self-consistent multi-fluid global particle and energy balance code, including collisions between all medium species (p, 11B, e, α), is used for the description of the temporal evolution of all fusion medium physical parameters and the evaluation of the optimum initial conditions for the obtainment of Q ≥ 1. The numerical simulation results show that the coupling between the 200 keV < Ep,0 ≤ 750 keV energetic protons and the 1 keV ≤ Tin ≤ 400 keV initial fusion medium leads to ignition, 1 ≤ Q < 1.4, below Tin = 100 keV. In all the presented initial medium temperature cases, and especially, the lower (<) than 100 keV, the ignition condition (Pfus/PBrems) > 1 arises, as a consequence of the chain reactions and the related avalanche alpha heating effect.
Energy is the most basic means for the provision of fundamental human needs, such as food and transportation. The relationship between the current global energy consumption and the Earth’s population is approximately square, and it is expected to double by 2050, as a result of the population’s growth from seven billion to nine billion people [1]. Ιn 2015, with a global population of 7.2 billion people and an annual per capita energy consumption of 2.5 kW, the annual global energy consumption reached 18 TW [2].
The nuclear fusion of light elements, from the one proton hydrogen (Z = 1) to the twenty six protons iron (Z = 26), can release a few MeVs of energy per fusion reaction [3]. Fusion is a fundamental process in nature, as the major energy source of the solar system, the Sun, has been based on it via the proton cycle for 13.8 billion years. Fusion developed on Earth could be a clear and inexhaustible energy source [1].
Deuterium–tritium (D–T) fusion is the most feasible fusion reaction on Earth, as it has the highest nuclear cross section (5.0 barn) at the lowest center-of-mass energy (∼65 keV) [3,4]. However, D–T fusion reactors require breeding technologies for tritium production and a thick blanket surrounding the plasma chamber, to prevent its material activation from the intense generated neutron flux (1 neutron of 14.1 MeV energy per D–T fusion reaction) [3,5]. These problems could be overcome through the use of advanced nuclear fusion fuels, amongst which is the p-11B fuel cycle [3,6].
From the 1930s [7], the p-11B nuclear fusion reaction was of interest due to i) Boron’s abundance in nature [5], ii) The lower than 1% neutron generation [8], and iii) the formation of three (3) isoenergetic, non-radioactive alpha particles with 8.7 MeV total energy. The latter energy can be converted into electricity without passing through a thermodynamic cycle, with a 60%–70% efficiency [5, 9, 10]. From the early twenty-first century and until today, there has been a growing interest in the significant re-examination of p-11B fusion, as a potential source of future clean energy production [10, 11]. This interest was greatly enhanced due to the important experiments of [12–18], the theoretical works of [19–23], the numerical simulations of [22–27], and the recent global ignition record at the National Ignition Facility (NIF) (Q = 1.54) [28]. Nonetheless, for the utilization of this nuclear fuel for clean energy production, it is necessary to develop appropriate fusion configurations or schemes, which will allow its ignition (Q = Pfus/PBrems ≥ 1) from considerably lower than 100 keV initial medium temperatures. Due to nuclear cross-section efficiency in the medium temperature range between ∼160 keV (σ ∼ 0.1 barn) and 675 keV (σmax = 1.2 barn) [29], as well as due to boron’s high charge (Z = 5), p-11B fusion devices emit intense Bremsstrahlung radiation. For Bremsstrahlung optimization and fusion ignition {Q = Pfus/PBrems ≥ 1)}, D. C. Moreau in the 1970s [5] concluded that the p-11B fuel must meet certain conditions: i) density ratios (np/nB > 1) between the p, 11B fusion species and ii) temperature ratios: (Ti/Te) ∼ 2 between medium ions and electrons. A major drawback of this work was, however, the fact that the temperature difference between ions and electrons did not arise from self-consistent numerical calculations, but was introduced as an initial condition to obtain fusion ignition.
The first detection of p-11B fusion-produced alpha particles came from the experiment of V. S. Belyaev et al. (2005), which measured 103 alpha particles [12], later corrected by [30] to 105 alpha particles. The next experiments by C. Labaune et al. (2013) [13] and A. Picciotto–D. Margarone et al. (2014, 2015) at Prague Asterix Laser System (PALS) [14, 15] measured 106 alpha particles/sr/laser pulse and 109 alpha particles/sr/laser pulse, correspondingly. After the experiments at PALS, a new series of p-11B experiments led to higher alpha particle yields. However, even the current record in alpha particle yield (≈1011) [18] has not demonstrated ignition conditions (Q ≥ 1), which means that the p-11B fusion reactivity must still be significantly enhanced [31]. A number of approaches in is proposed in the international literature for p-11B fusion reactivity enhancement and the increase of net energy gains. These approaches include the chain reactions alpha heating effect and the related avalanche effect [9, 20, 21], as well as the hybrid burn [32].
The potential processes of the “chain reactions alpha heating effect and the related avalanche effect,” with a model of elastic collisions leading to alpha plasma heating effect, fusion reactivity enhancement, and further increase of the fusion gain [9, 20, 21] were firstly indicated, after the four orders of magnitude increase in the alpha particle yield, between the experiments of [12] and [16, 17]. The increase from 105 to 109 experimentally produced alphas [12–15, 30] was firstly presented in the works of [9, 21, 33], which proposed a specific interpretation model. Their interpretation that the enhancement of the alpha production is directly related to the avalanche effect at the optimum 675 keV resonance, where σmax = 1.2 barn, was followed by the criticism of [34], the consequent answer of [35], and the numerical work of [36]. The latter enabled the proposal of an alternative avalanche model (new evaluation of the avalanche time) at the low cross-section resonance of ∼160 keV. The latter resonance was successfully targeted in the experiment by V. Istokskaia et al. (2023) [37] and showed a generation of 6 × 104 alpha particles per second and 106 alpha particles per second, operating the table-top laser system PERLA-B at 10 Hz and 1 kHz, correspondingly.
Our recent work [38], concerning a low-density p-11B medium (n = 1020 m−3–1021 m−3), presents the necessary conditions for fusion ignition {Q = Pfus/PBrems ≥ 1)} through the chain reactions alpha heating effect and the related avalanche effect. In the context of this work, the “chain reactions alpha heating effect and the related avalanche effect” is used as a terminology for the compact description of a series of time-dependent effects. The latter concern the alpha energy transfer to the fusion species (alpha heating) and its contribution to the enhancement of fusion reactivity <σv> and the fast increase in alpha density production (avalanche effect manifestation). Provided that Bremsstrahlung radiation losses are optimized through the consideration of (np/nB) > 1 [5, 39] and that the initial low-density p-11B medium temperature is in the range of 130 keV ≤ Tin ≤ 400 keV, the avalanche effect is manifested, when the fusion produced alpha particle density is nα ∼ 1018 m–3 (two orders of magnitude lower than the initial p, 11B species density). The avalanche effect manifestation triggers a significant accumulation of alpha heating in the medium, which raises the p-11B fusion species’ temperatures to temperatures corresponding to the optimum fusion reactivity (400 keV–600 keV). Due to reactivity optimization in this area, a higher alpha density is produced and the p-11B medium is ignited: 1 ≤ Q ≤ 1.29, in a time interval of Δt = 10 s (necessary medium trapping time). In this series of numerical calculations, a critical factor for fusion ignition is also the arising temperature decoupling between electrons and p, 11B fusion species after the avalanche manifestation and until the maximum of the Q = (Pfus/PBrems) ratio. At the maximum Q value, TB > Te.
In addition to the chain reactions alpha heating effect and the related avalanche effect, another promising approach for p-11B fusion reactivity enhancement is the so-called “hybrid burn” [32]. Hybrid burn, which is currently being investigated by the private HB11 Energy Company (Sydney, Australia), combines thermonuclear (inertial) fusion ignition with proton-driven fast ignition. Its basic concept involves the implosion of a solid hydrogen–boron target and the injection of a laser-produced energetic proton beam during its maximum compression. The injected energetic protons produce local heating in the inertial fusion plasma and contribute to the direct induction of more p-11B fusion events.
The present numerical study uses the same numerical model as [38, 40] and examines the change in the ignition condition of a low-density p-11B medium (n = 1020 m–3) [38], due to the addition of energetic protons in the medium. For this purpose, two medium configurations are proposed, which refer to the inclusion of additional 100 keV–700 keV energetic protons in a p-11B medium or a 11B medium. The latter are considered with density ratios (np/nB) > 1 between the total protons and boron ions, for Bremsstrahlung losses optimization and initial temperature (Tin) between 1 keV and 400 keV.
The upper-temperature limit of Tin = 400 keV is selected, as in our previous series of low-density numerical results [38], ignition conditions Q = (Pfus/PBrems) ≥ 1 are observed in the temperature range between Tin = 130 keV and Tin = 400 keV. In this temperature range, the optimum ignition condition, Q = 1.29 (Pfus = 0.35 MW/m3), is observed at Tin = 200 keV. According to the current numerical results, the addition of energetic protons (200 keV < Ep,0 ≤ 750 keV) supports enhanced low-density fusion ignition 1 ≤ Q < 1.4 below Tin = 100 keV. Higher proton energies than Ep,0 = 750 keV are not considered, as the numerical simulations showed no significant improvement of the ignition condition (Q) above this energy. Recently, the injection of neutral ion beams for fuel replenishment and plasma burn sustainment was exploited in the Tri Alpha Energy (TAE) Technologies experiment at the compact stellarator Large Helical Device (LHD) in Japan [41], as well as in the ENN’s Helong experiment [42].
In the TAE experiment, the boron target plasma was produced utilizing the boronization system of the plasma-facing components (PFCs) of the LHD [41]. In the context of this PFC technique, boron can be delivered to the plasma in the form of grains of pure boron, boron nitride (BN), or boronized carbon (BC) [42–44]. Although the energy of the injected negative-neutral hydrogen beams was relatively low (∼160 keV) to enable ignition (Q ≥ 1), their interaction with the generated boron plasma led to the first alpha particle measurements from p-11B magnetic confinement fusion (MCF). Near future improvements in negative-neutral beam injection systems, similar to those developed for ITER, will enable p-11B fusion ignition in compact magnetic fusion devices (CMFDs). According to [43–46], boronization can improve confinement time and, thus, alpha particle production from p-11B fusion reactions, through the decrease of recycling and intrinsic impurity content (e.g., C, O, Fe) in the walls of the magnetic confinement vessel. An understanding of the link between these plasma improvements and the wall surface chemistry (PFCs) was established in the experimental and computational studies of [47] in the spherical Tokamak National Spherical Torus Experiment Upgrade (NSTX-U), at the Princeton Plasma Physics Laboratory (PPPL).
In the recent numerical work [38], the necessary conditions for fusion ignition, through the manifestation of the chain reactions alpha heating effect and the related avalanche effect, are presented for a low-density p-11B medium (n = 1020 m–3–1021 m–3). For the performed numerical investigation concerning the evaluation of the temporal evolution of the fusion medium physical parameters (e.g., see Figures 5, 11), a multi-fluid global particle and energy balance code was used [38, 40, 48]. For each fluid medium species, the multi-fluid model includes a separate mass density and power density losses first-order differential equation. This means that the total number of equations is adjusted, accordingly to the considered plasma components. The system of differential equations is solved with a fourth-order Runge–Kutta method. Due to the fact that the multi-fluid model includes only temporal component, not spatial (no plasma expansion), for the justification of the results, we assume that there are no particle losses (including of alpha) for at least t ≤ 10 s. In the case of magnetic confinement fusion (MCF), the plasma may remain trapped in the device without important losses for relatively long time intervals (see, for ex., [41, 42]), in which the alphas can transfer the maximum of their energy to the fusion species.
The temperature/energy of all fluid plasma species, including the alphas, is described by the Maxwellian distribution. The total alpha energy of Eα,tot = 8.7 MeV is used in the context of the numerical simulations, assuming the generation of three (3) isoenergetic alphas. In the international literature, alternative p-11B fusion channels have been proposed, with different alpha spectrums compared to Eα,0 = 2.9 MeV (see the Discussion-conclusions section in [38]). These alternative channels refer to the two-step breakup of 8Be in its ground or first exited state [9, 49], which leads to the generation of alphas in the low-energy resonance (∼0.657 MeV) [49], with a maximum energy up to ∼4–5 MeV. In this alternative scenario, the total alpha energy is also Eα,tot = 8.7 MeV.
The multi-fluid code is self-consistent, including electron power density losses, due to Bremsstrahlung radiation and all the required binary Coulomb collisions between the p-11B fusion medium species (p, 11B, e, α). Bremsstrahlung radiation losses are evaluated for only free-free electron–ion interactions in non-hydrogenic plasmas with Z = Σi ni Zi2/ne > 1 (i: each ion species), considered in the formulations of [39, 50]. Nevertheless, for electron temperatures Te < 150 keV, the simplified expressions of [5, 50–52] could be used. The used collision frequencies (see Equation (B.9) of [38]) employ the formulation of Equation 2.112 of [53], which is similar to Equation (36) of [54].
The most recent evaluations of p-11B nuclear fusion cross-section and reactivity are presented in [55, 56]. In the context of the model, for the optimization of the ignition condition {Q = (Pfus/PBrems)} [38, 57], the p-11B fusion cross section and reactivity calculations exploit the parametric equations of [55], which have been based on the updated data of [56], due to their potentiality to cover energies up to E ≤ 9.76 MeV. Both [55, 56] have used similar mathematical formulation analysis as [29], treating the earlier cross-section results, that are also presented in [4].
Bremsstrahlung radiation losses and ignition conditions are further optimized in [38], considering the optimum density ratio of (np/nB) = 10 between the p, 11B fusion species (Figure 1). Given a p-11B medium initial temperature in the range of 130 keV ≤ Tin ≤ 400 keV, the avalanche effect is manifested when the fusion-produced alpha particle density is two orders of magnitude lower than the initial fusion species’ density. After the avalanche effect manifestation, there is a decoupling between p, 11B and electrons. The p, 11B species’ temperatures increase to values corresponding to the optimum nuclear p-11B fusion reactivity while the electron temperature decreases [38]. The latter fact leads to an additional reduction of Bremsstrahlung radiation losses and, in turn, to p-11B medium ignition, Q ≥ 1. In the case of the optimum density ratio, (np/nB) = 10 (the red curve shown in Figure 1), the maximum ignition condition, Q = 1.29 at the Tin = 200 keV initial p-11B medium temperature, is achieved in a time interval of Δt = 10 s. For this optimum ignition condition, the ratio of the boron species’ temperature to the electron species’ temperature is (TB/Te) ≥ 2, and the fusion power density is Pfus = 0.35 MW/m3.
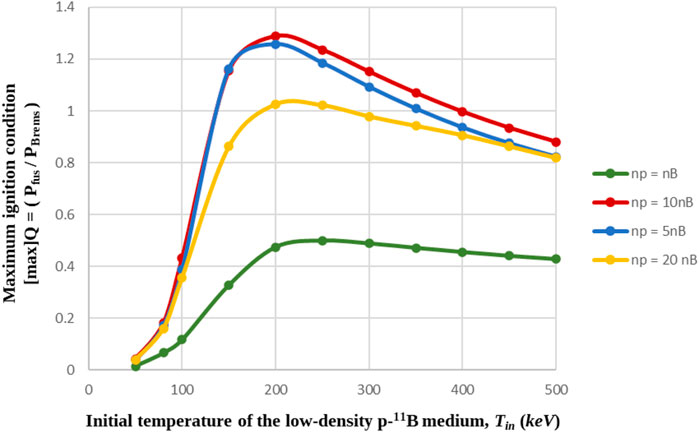
Figure 1. Bremsstrahlung radiation loss optimization in a low-density p-11B medium (n = 1020 m–3) through the consideration of the most common density ratios (np/nB) > 1 between the p, 11B fusion species. The density ratio (np/nB) = 10 leads to the optimum values of the ignition condition: 1 ≤ Q ≤ 1.29 in the initial p-11B medium temperature range of 130 keV ≤ Tin ≤ 400 keV.
As already stated, in a low-density p-11B medium without additional energetic protons, the optimum ignition condition Q = 1.29 is ensured at the initial medium temperature of Tin = Tp = TB = Te = 200 keV (Figure 1). However, in this case, ignition is overshadowed by the challenging p-11B medium heating to Tin = 200 keV. Thus, the main objective of the present work is to investigate, whether the consideration of additional energetic protons in a low-density medium has an important beneficial impact on the initiation of the fusion ignition process (Q ≥ 1) at lower than 130 keV ≤ Tin ≤ 400 keV initial p-11B medium temperatures (Figure 1). Configurations based on the addition of energetic protons in a low-density proton–11boron or 11boron medium (n ∼ 1020 m–3) may seem very promising for this purpose, taking into consideration the proposed scheme of [34] for “hybrid burn” in inertial p-11B fusion. For the performance of our numerical investigation, the differential equations of mass densities and power density losses of the multi-fluid global particle and energy balance code [38, 40] were adjusted, incorporating one (1) extra Maxwellian fluid plasma species, corresponding to the energetic protons in the case of a p-11B medium. The initial energy of the energetic protons is considered favorable in the range of 200 keV < Ep,0 ≤ 750 keV due to the greater capability of the p-11B fusion reactivity (or cross section) to induce fusion events in this region [4, 29, 34, 55, 57].
The maximum ignition condition curves {[max]Q = (Pfus/PBrems)} shown in Figure 1 were reproduced for both examined configurations: i) the low-density 11boron medium with energetic protons and ii) the low-density p-11B medium with additional energetic protons, to spot essential differences. The insertion of the fluid of energetic protons is considered at the time point of t = 0 (starting point of numerical simulations) without pulse duration (it is instantaneous). In case (ii), the additional energetic protons alter (increase) the initial density ratio of the low-density medium as a consequence of 11boron density reduction. For example, if a number density of np,in = 5 × 1019 m–3 energetic protons is added in a p-11B medium with initial proton density np,med = 1020 m–3 and density ratio (np,med/nB) = 10, the arising density ratio is (
In the current section, our numerical study is initiated with the case that the p-11B fusion medium formation is owed to the inclusion of energetic protons in low-density boron (nB ∼ 1019 m–3). As the main objective of the present work is the proposition of p-11B configurations with potentially enhanced fusion ignition conditions at lower than 130 keV initial medium temperatures (see Figure 1), in Figure 2, we initially sketch the maximum ignition condition as a function of the energetic protons’ energy, for the typical representative example of the initial boron medium temperature of Tin,B = TB = Te = 80 keV and final proton-to-boron density ratios (after the inclusion of energetic protons): 5 ≤ (
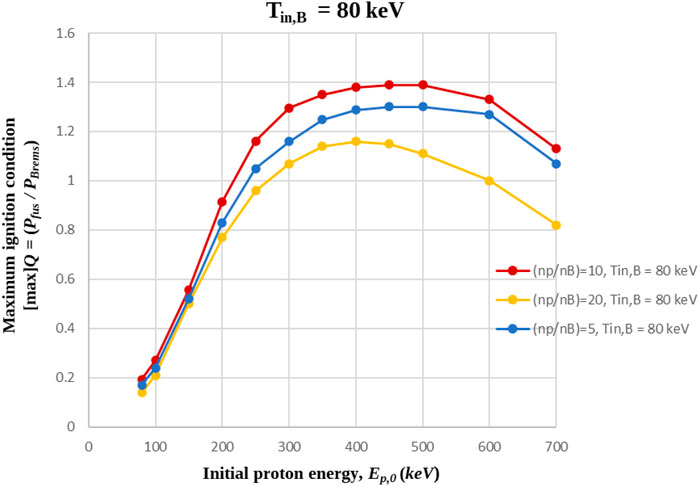
Figure 2. Maximum ignition condition, as a function of initial proton energy, for the Tin,B = 80 keV initial 11boron medium temperature. Bremsstrahlung radiation losses are optimized, considering density ratios between the energetic protons and the 11boron medium ions.
According to the results shown in Figure 2, the ranking of the most common density ratio curves resulting in fusion ignition, remains the same, as in the case of the low-density p-11B medium without energetic protons and with equal proton and boron initial temperatures (Figure 1). However, compared to Figure 1, where ignition 1 ≤ [max] Q = (Pfus/PBrems) ≤ 1.29, requires initial p-11B medium temperatures in the range of 130 keV ≤ Tin ≤ 400 keV, in the present case, equal or even higher maximum ignition conditions can be observed. For example, for the indicative initial 11boron medium temperature of Tin,B = 80 keV and the 220 keV–700 keV energetic protons, ignition conditions may reach 1 ≤ Q ≤ 1.4, in the case of the optimum medium density ratio (
In order to observe the evolution of the maximum ignition condition, the latter was also sketched for initial boron medium temperatures below Tin,B = 80 keV (Figure 3A) and up to Tin,B = 400 keV (Figure 3B). Figure 3A shows that ignition is possible in all the temperature range between Tin,B = 1 keV and Tin,B = 80 keV, with an expected decrease in the required energy of the energetic protons as the total internal energy of the boron medium increases (Figure 3C). For the lowest examined bound of initial boron medium temperature, Tin = 1 keV (yellow curve), for example, ideal ignition, Q = 1, demands 350 keV energetic protons. For the relative cases of Tin.B = 40 keV (light blue curve) and Tin,B = 60 keV (green curve), the required proton energies for ignition are Ep,0 = 285 keV and Ep,0 = 250 keV, correspondingly. The approximate initial boron medium temperature of Tin,B = 80 keV provides the highest (optimum) ignition condition values, {[max]Q}, in the lower than Tin,B = 100 keV temperature range.
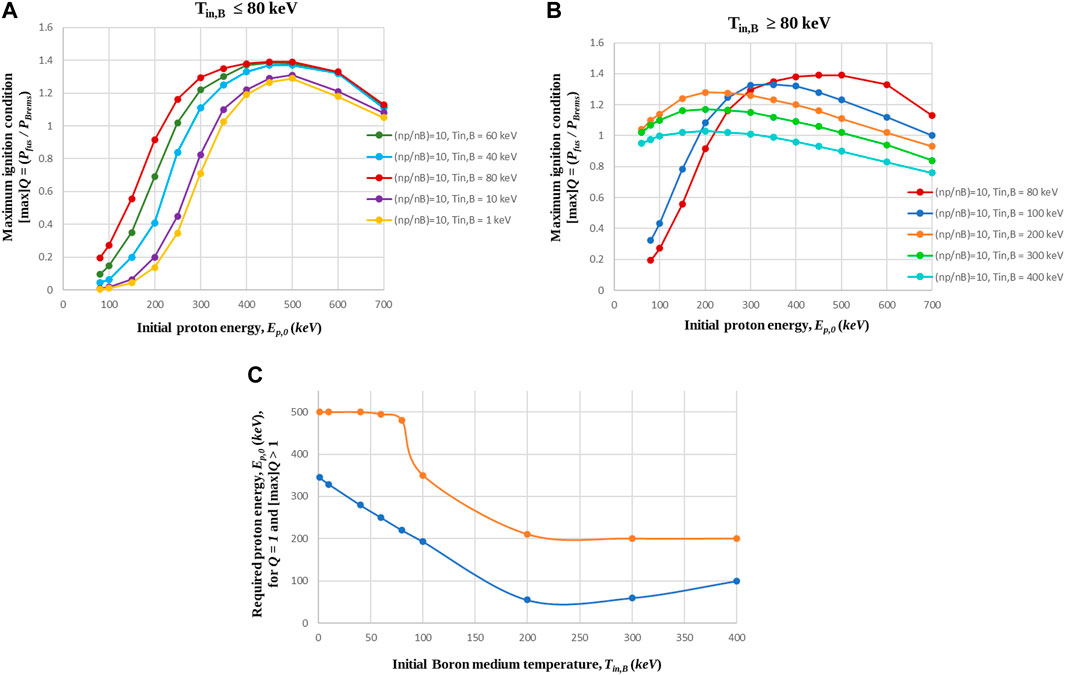
Figure 3. (A) Maximum ignition condition, as a function of the energetic protons’ initial energy, for initial boron medium temperatures ranging between Tin,B = 1 keV (yellow curve) and Tin,B = 80 keV (red curve). The results show boron medium ignition (Q ≥ 1) for all these initial temperatures, provided a minimum initial proton energy of Ep,0 = 220 keV (in the case of Tin,B = 80 keV). (B) Maximum ignition condition as a function of the energetic protons’ initial energy for initial boron medium temperatures in the range of 80 keV ≤ Tin,B ≤ 400 keV. The results show enhanced ignition conditions (Q > 1) for boron medium temperatures up to Tin,B = 300 keV and energetic protons of Ep,0 ≤ 150 keV. (C) Required proton energy for the break-even ignition (Q = 1 in blue) of a boron medium with initial temperature in the range of 1 keV ≤ Tin,B ≤ 400 keV. The intersection of the curve with the Y-axis shows a maximum proton energy of Ep,0 = 350 keV, in the case of Tin,B = 1 keV. In the same figure, the necessary proton energy for the obtainment of the optimum ignition condition {[max]Q > 1 in orange} is also given, as a function of the initial boron medium temperature.
In Figure 3A, it is characteristic that, for the case of Tin,B = 1 keV, the maximum ignition condition results are very close to those of Tin,B = 10 keV. Thus, for the whole initial boron temperature range of 1 keV–10 keV, there are only slight differentiations in the calculated [max]Q > 1 values if energetic protons of 350 keV < Ep,0 < 700 keV are considered. For initial boron temperatures below Tin,B = 1 keV (Tin,B = 0.5 keV, for example), the relevant [max]Q results cannot be clearly distinguished from those of Tin,B = 1 keV. Thus, the presentation was limited to Tin,B = 1 keV.
For the higher than Tin,B = 80 keV initial boron temperature range (Figure 3B), the obtained maximum ignition condition results show an increase by a factor of approximately five between Tin,B = 80 keV and Tin,B = 200 keV (orange curve) or Tin,B = 300 keV (neon green curve) if energetic protons of Ep,0 ≤ 150 keV are added in the medium. For higher proton energies (Ep,0 > 200 keV), however, the ignition condition curves of the higher than Tin,B ≥ 100 keV initial boron temperatures present different profiles. Similar profiles also appear in the fusion power density (Pfus) curves shown in Figure 4A and will be discussed in parallel in the next paragraphs.

Figure 4. (A) Fusion power density, corresponding to the maximum ignition condition curves of a low-density boron medium with energetic protons. The initial boron temperature is considered between Tin,B = 1 keV and Tin,B = 400 keV, while the energetic protons to boron medium density ratio is (
The highest required proton energy for break-even ignition (Q = 1) of a low-temperature boron medium (Tin,B → 0) is Ep,0 = 350 keV–400 keV (Figure 3C). According to the same figure, the necessary proton energy for the manifestation of break-even (Q = 1) presents a well-defined profile as a function of initial boron medium temperature. In contrast, the optimum ignition condition {[max]Q} corresponds to approximately the same energetic proton energies below and above Tin,B = 100 keV. Note that for initial boron medium temperatures Tin,B < 80 keV (Figure 3A), the maximum ignition conditions, [max]Q ∼ 1.3–1.4, correspond to energetic protons in the range of Ep,0 ∼ 450 keV–550 keV. For Tin,B > 80 keV, on the other hand (Figure 3B), the maximum ignition conditions, [max]Q ∼ 1–1.3, shift to lower proton energies, Ep,0 ∼ 200 keV. In Figure 3C, a significant observation concerns the “deviation” of the point, referring to the initial boron medium temperature of Tin,B = 400 keV. This is due to the profile of the presented curves in Figure 3B, where the [max]Q values decrease, as Tin,B increases between 200 keV and 400 keV. Therefore, as Tin,B increases, the value of the ignition condition approaches the value of [max]Q. Thus, for slightly higher boron medium temperatures than Tin,B = 400 keV, the [max]Q curve decreases even more, reaching [max]Q ∼ 1 at Ep,0 ∼ 200 keV, and the blue curve will intersect the orange one (Figures 3B, C).
The numerical results shown in Figures 3A, B show that fusion ignition (Q ≥ 1) can be obtained, considering (i) high-energy protons in a low-temperature boron medium and (ii) low-energy protons in a high-temperature boron medium. In contrast, in the case of a p-11B medium with (np/nB) = 10 and Tin = Tp = TB (red curve shown in Figure 1), fusion ignition appears only for high initial p, 11B fusion species’ temperatures (130 keV ≤ Tin ≤ 400 keV). Therefore, for the same initial proton energies, different results are observed between the two medium cases. The inclusion of energetic protons in a boron medium is a versatile scheme, as it allows the observation of fusion ignition conditions for both high and low boron plasma internal energies. For both medium cases, however, the optimum Q values are similar. Nevertheless, it can be excluded that, the configuration corresponding to the consideration of energetic protons in a low-density boron medium is more efficient.
The correspondence between the maximum ignition condition curves {[max]Q = (Pfus/PBrems)}, shown in Figures 3A, B and fusion power density (Pfus), is given in Figure 4A, as a function of the energetic protons’ initial energy (Ep,0). As it can be observed, the maximum ignition condition, [max]Q = (Pfus/PBrems) = 1.4, corresponding to the initial 11B medium temperature of Tin,B = 80 keV (red curves shown in Figures 3A, B), implies a fusion power density generation of Pfus = 0.44 MW/m3 (Figure 4A).
In Figures 4A, 3B, the corresponding Q and Pfus curves to the higher than Tin,B > 100 keV initial boron medium temperatures present an increasing behavior for energetic protons in the low-energy range (Ep,0 < 250 keV). This increasing behavior does not continue as expected but stops for proton energies above Ep,0 > 250 keV, showing a decreasing behavior. Thus, smaller ignition conditions and fusion power densities are observed, in relation to the [max]Q (Figure 3B) and Pfus (Figure 4A) curves of the lower than Tin,B < 100 keV medium temperatures. The aforementioned behavior is owed to two effects, that are both directly related to the high arising medium species’ temperatures, as a consequence of the chain reactions and the related avalanche effect (see Section 2.1.2). According to [57, 58], the p-11B nuclear fusion reactivity presents a plateau-like maximum of ∼ 500 keV, which decreases for higher energies. The first effect is therefore due to the p, 11B fusion species’ temperature increase to values above the optimum p-11B fusion reactivity. The second effect is due to the severe electron Bremsstrahlung radiation losses at these temperatures. Thus, in Figure 3B, we notice that the ignition condition curve of the Tin,B = 400 keV initial boron medium temperature is below the curve of Tin,B = 200 keV, while in Figure 4A, the fusion power density curve (Pfus) of Tin,B = 400 keV is above the curve of Tin,B = 200 keV.
For the optimum initial 11boron temperature of Tin,Β = 80 keV and the initial proton energy of Ep,0 = 450 keV (see Figures 3, 4), the temporal evolution of the fusion medium species’ (p, 11B, e and α) temperatures is given in Figure 5. According to the latter, at t = 10−1 s, when the fusion-produced alpha particle density is two orders of magnitude lower than the total medium density of energetic protons and boron, the temperature of alphas (Tα) starts to decrease, in contrast to the temperature of the 11B species (TB), which starts to increase. Thus, the time point of t = 10−1 s with its corresponding alpha particle density marks the onset of the avalanche effect and confirms the required lower alpha particle limit for its occurrence, as fully described in [38]. It is significant to mention that, at t = 10−2 s (initial value in the time axis shown in Figure 5), the alpha temperature has decreased below the alpha creation energy of Eα,0 = 2.9 MeV. This is because the alpha temperature diagnostic considers the energy of all alpha particles present, including those that have already transferred energy to the other species (p, 11B, e) through collisions. Between the avalanche effect manifestation at t = 10−1 s and t = 101 s, the 11B species’ temperature increases by a factor of five, as a result of the energetic protons and the alpha heating transfer. Note that, in the relative case of a low-density p-11B medium (n ∼ 1020 m–3) without energetic protons and Tin = 80 keV initial temperature, there is no medium heating due to the chain reactions alpha heating effect and the related avalanche effect [38]. The latter fact is owed to the three orders of magnitude lower alpha particle density, nα = 1017 m–3, than the total, initial p, 11B fusion species’ density at the time of the occurrence of the rapid alpha temperature decrease (t = 10−1 s). In both p-11B medium formation configurations, with and without energetic protons, the number densities of proton and boron are exactly the same, np = 1.0 × 1020 m–3, (np/nB = 10). However, the 450 keV energetic protons correspond to a higher (p-11B) fusion reactivity than the isoenergetic p, 11B fusion species (Tin = Tp = TB = 80 keV) and lead to a higher alpha particle generation at t = 10−1 s. Thus, the required critical alpha density of nα = 1018 m–3 [38] is reached, and the heating of the medium within the optimum reactivity region (300 keV ≤ T ≤ 700 keV) is ensured through the avalanche effect.
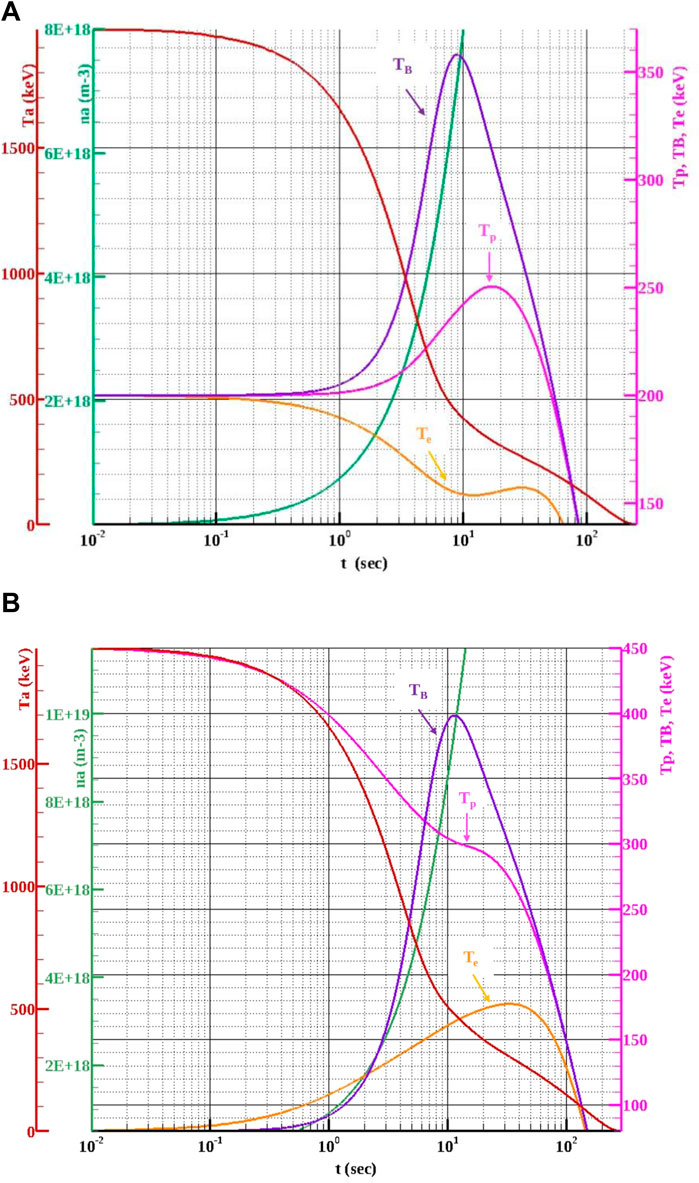
Figure 5. Presentation of the temporal evolution of the fusion medium species (p, 11B, e, α) temperatures and alpha density (nα) at ignition conditions: Q ≥ 1, in the cases of (A) A low-density p-11B medium with (np/nB) = 10 and Tin = 200 keV ([max]Q = 1.29). (B) A low-density 11boron medium of Tin,B = 80 keV initial temperature, with 450 keV energetic protons and (
The main difference between the low-density p-11B medium without energetic protons [38] and the configuration, taking into consideration the presence of energetic protons in a boron medium, concerns the temporal evolution of the temperatures of protons (pink curves) and electrons (orange curves) at ignition conditions (Q ≥ 1). In the case of no energetic protons (Figure 5A), the avalanche effect manifestation is accompanied by a significant temperature difference between p, 11B, and e. The p, 11B species’ temperatures start to increase, while the electron temperature starts to decrease. On the other hand, in the case that the medium consists of energetic protons and boron (Figure 5B), at the avalanche effect manifestation (fast increase in alpha density production) at t = 10−1 s, the electron temperature starts to increase, but at a lower rate, than the 11B temperature. The latter effect may be attributed to the higher energetic transfer from the 450 keV protons to the medium electrons. However, due to Bremsstrahlung radiation losses, the increase rate of the electron temperature is relatively lower than the corresponding one of the 11B species. In both medium cases, at the maximum 11B species’ temperature, where the fusion power density (Pfus) attains its optimum value, the ratio of the 11B temperature to the electron temperature is TB > Te.
In the low-density case without energetic protons and with equal initial proton and boron temperatures (Tin = Tp = TB) (Figure 1), the optimum density ratio, (np/nB) = 10, provides ignition of the p-11B medium, 1 ≤ Q ≤ 1.29, in the initial temperature range of 130 keV ≤ Tin ≤ 400 keV. Due to the manifestation of the avalanche effect, the temperature of the p, 11B ions is raised while the e temperature declines. The optimum ignition condition, Q = 1.29, is observed at the initial medium temperature of Tin = 200 keV and is directly related to i) The temperature increase of the p, 11B ions to Tp,max = 250 keV and TB,max = 360 keV, and ii) The arising temperature difference between the p, 11B ions and e. At the maximum 11B temperature, (TB,max/Te) ∼ 2.3. The mean plasma temperature, corresponding to the maximum p, 11B temperatures, is Tmean,max = 294.2 keV. The relative fusion reactivity is <σv ≥ 3.5 × 10−22 (m3/s).
In the context of this section, the addition of an energetic protons fluid (npin) is considered in a low-density p-11B medium composed of low-energy protons (npmed) and boron, as it may have a potential influence on:
i. The decrease of the lowest required temperature for fusion ignition (Q ≥ 1) below Tin < 100 keV through the chain reactions alpha heating effect and the related avalanche effect.
ii. The targeting of higher mean maximum plasma temperatures (Tmean,max) in the optimum fusion reactivity (<σv>) region, 400 keV–600 keV.
iii. The improvement of the highest ignition criterion value Q, provided that it is observed at an initial p-11B medium temperature below Tin < 100 keV.
The maximum ignition condition is sketched in the following Figures 6A, B as a function of initial p-11B medium temperature, for initial proton densities: np,med = 1 × 1020 m–3 (medium protons) and additional proton number densities (np,in), forming the final density ratios of (
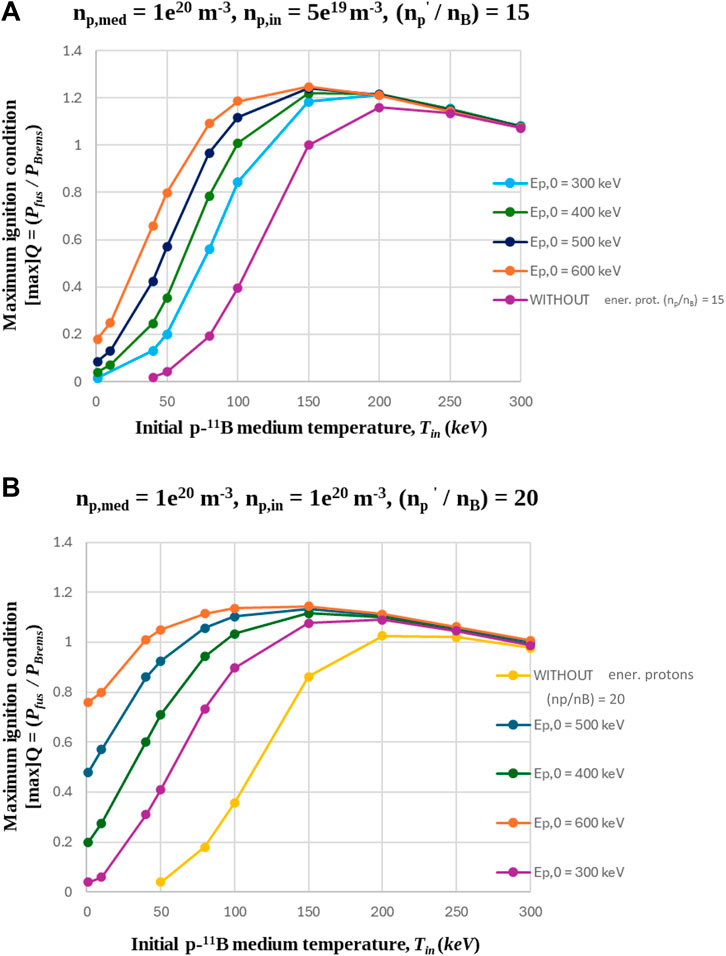
Figure 6. Maximum ignition condition, as a function of initial p-11B medium temperature, for the cases that the additional energetic protons form the total protons to boron density ratio of (A) (
According to Figures 6A, B, if the initial energy of the additional energetic protons is Ep,0 = 500 keV or Ep,0 = 600 keV, the low-density p-11B medium may be ignited (Q ≥ 1) from a lower than Tin = 100 keV initial temperature. In the case of (
In the relative case shown in Figure 6B (
Then, considering the additional fluid of energetic protons in the low-density p-11B medium (np,med = 1020 m–3), so that the final density ratio between total protons and boron ions is (
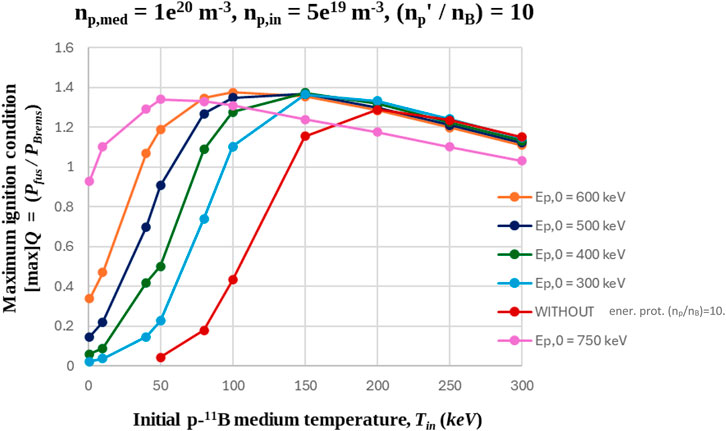
Figure 7. Maximum ignition condition as a function of initial p-11B medium temperature and energetic proton energy. The arising density ratio between total protons and boron is: (
According to the ignition condition curves of Figure 7:
i) The required proton energy for the ignition of a low-temperature p-11B medium (Tin →0), with (np’/nB) = 10, is Ep,0 ∼ 750 keV.
ii) In the case of the initial proton energy of Ep,0 = 600 keV, the optimum ignition condition of the p-11B medium is improved by a factor of approximately 1.12 (from Q = 1.29 to Q ∼ 1.4), compared to the case of (np/nB) = 10 and no energetic protons (red curve shown in Figure 7). Equally good values of the maximum ignition condition are also observed at the initial p-11B medium temperatures of Tin = 40 keV (Q = 1.29) and Tin = 50 keV (Q = 1.34), for energetic protons of Ep,0 = 750 keV (pink curve shown in Figure 7).
iii) The initial proton energy of Ep,0 = 600 keV is responsible for the enlarging of the p-11B medium ignition temperature window from 130 keV ≤ Tin ≤ 400 keV to 30 keV ≤ Tin ≤ 400 keV. The p-11B medium can also be ignited at lower than Tin = 100 keV initial p-11B medium temperatures, ranging between Tin = 10 keV and Tin = 90 keV, if additional energetic protons of 300 keV ≤ Ep,0 ≤ 750 keV are considered.
For the representative case of the Ep,0 = 600 keV initial proton energy and the ignition condition curve of the optimum p-11B medium density ratio, (
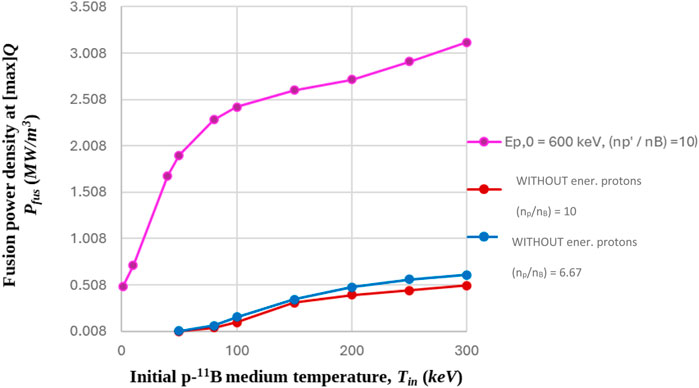
Figure 8. Fusion power density, corresponding to the optimum ignition condition curve shown in Figure 7 for (
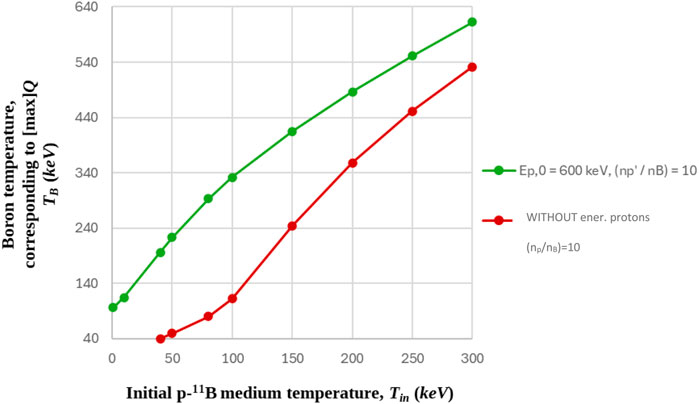
Figure 9. Boron temperature, corresponding to the optimum ignition condition curves of (np/nB) = 10 (without additional energetic protons in the low-density p-11B medium) and (
As shown in Figure 8, the additional 600 keV energetic protons (pink curve) provide a high fusion power density production, especially in the initial temperature range of Tin < 100 keV. We should remind the fact that, in this initial temperature range, there is no ignition of the low-density p-11B medium without energetic protons, due to the relatively low alpha-density production and, consequently, the weak contribution of the induced alpha heating effect.
However, if we consider that the comparison between the two different p-11B mediums, with and without energetic protons (pink curve, red curve), is performed on the basis of initial energy density, we must mention that, the 20 keV–100 keV energy range of the p-11B medium with the additional 600 keV energetic protons has a comparable energy density with the simple 270 keV–400 keV p-11B medium without energetic protons (Tin = Tp = TB). For the aforementioned energy intervals, the corresponding fusion power density (Pfus) ratio varies between 2.3 and 4.5, being in favor of the configuration of the (p, 11B) medium with the additional energetic protons.
The inclusion of the 600 keV energetic protons is considered in a p-11B medium (pink curve), with a medium proton to boron density ratio equal to (
The results shown in Figure 9 show that in the case of the p-11B medium temperature of Tin = 50 keV and no additional energetic protons (Tin = Tp = TB), the boron temperature remains constant at TB = 50 keV (due to the absence of alpha heating). However, if a number density of Ep,0 = 600 keV energetic protons is added in the low-density p-11B medium, and the arising density ratio is (
According to the results shown in Figures 10, 11, at t = 10−1 s, when the fusion produced alpha particle density is two orders of magnitude lower than the initial p-11B medium density, nα = 1 × 1018 m–3, there is a steep alpha temperature decrease, occuring in parallel with a rapid increase in the p, 11B fusion species’ temperatures. Consequently, the time point of t = 10−1 s onsets the manifestation of the avalanche alpha heating effect in a similar manner to the low-density p-11B medium without additional energetic protons (see Figure 5A or [38]). Between t = 10−1 s and t = 5 s, when the 11B species’ temperature is maximized (as is the Q value shown in Figure 7, Q ∼ 1.4), the p, 11B species’ temperatures increase by a factor of approximately 2.4 and 3, correspondingly. Although the medium electron temperature starts to increase after the avalanche effect manifestation, in contrast with the low-density p-11B medium case without energetic protons (Figure 5A), this increase is not high enough compared to the increases in the p, 11B species’ temperatures. At t = 5 s, the ratio of the boron species’ temperature to the electron temperature is (TB/Te) ∼ 2.4. These results confirm our initial findings, presented in [38], concerning the required conditions for the induction of a significant p-11B medium heating and ignition (Q ≥ 1), through the manifestation of the avalanche alpha heating effect. As shown in Figure 11, it is also characteristic that at t = 5 s, the energy of the energetic protons (np,in) is thermalized with the energy of the initial protons of the medium (np,med).
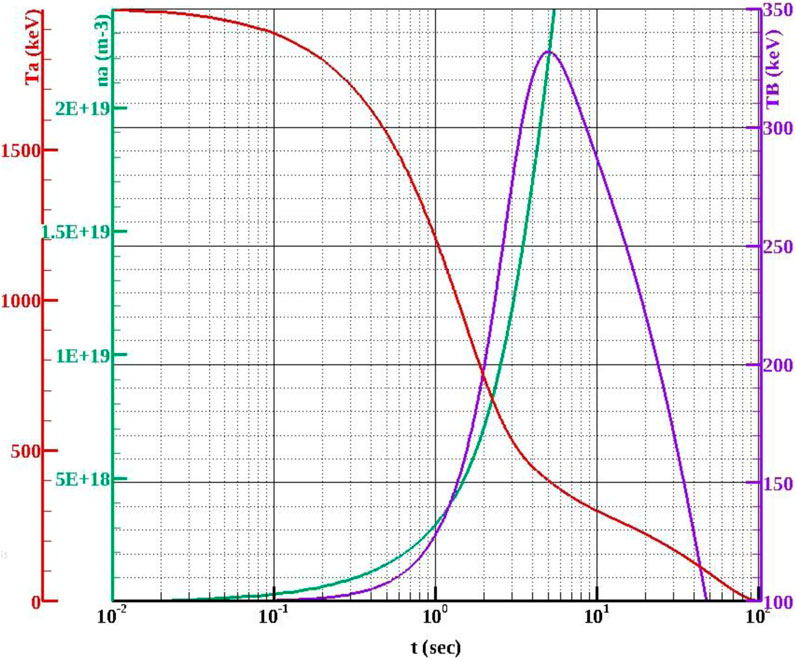
Figure 10. Temporal evolution of alpha density (nα) and the temperatures of boron (ΤΒ) and alphas (Tα) for the initial p-11B medium temperature of Tin = 100 keV, considering the addition of energetic protons in the medium. Due to the presence of energetic protons, the total proton to boron density ratio is formed to (
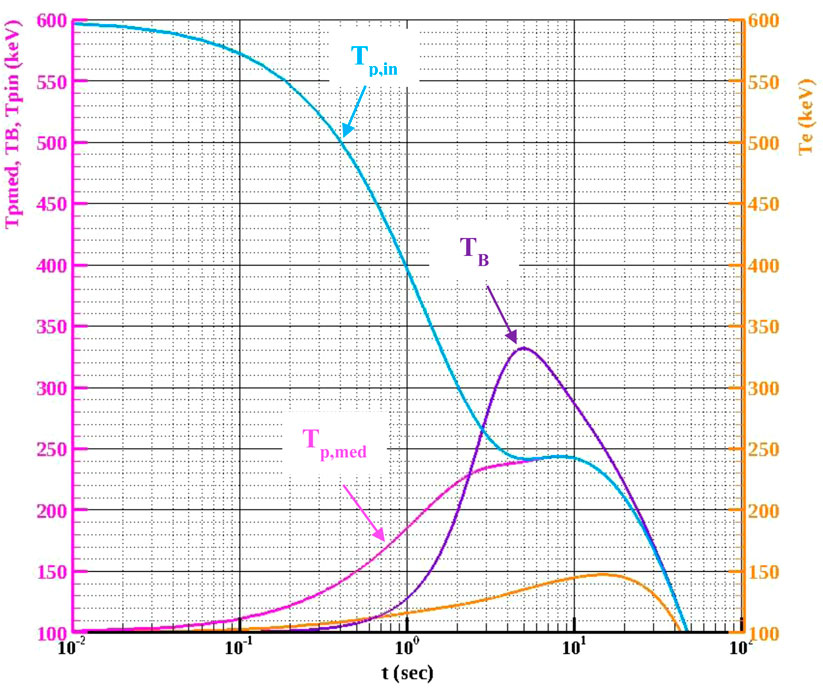
Figure 11. Temporal evolution of the different fusion medium species’ temperature, for the initial p-11B medium temperature of Tin = 100 keV: additional energetic protons (Tp,in), medium protons (Tp,med), boron ions (TB), and electrons (Te). At the time point of t ∼ 5 s, where the maximum ignition condition (Q ∼ 1.4) is obtained, the ratio of boron temperature to electron temperature is (TB/Te) > 2.
The up today numerical studies for a low-density p-11B medium (n ∼ 1020 m–3) without energetic protons (Tin = Tp = TB) show that, fusion ignition {Q = (Pfus/PBrems) ≥ 1} necessitates initial temperatures in the range of 130 keV < Tin < 400 keV and density ratios between the p, 11B fusion species, (np/nB) = 5, 10, or 20 for Bremsstrahlung radiation losses optimization. The maximum Q value, Q = 1.29, is obtained at the high initial temperature of Tin = 200 keV [38].
The employed multi-fluid model [38, 40] enables the investigation of fusion mediums with different initial conditions of density and temperature and the temporal description of the different fusion medium physical parameters (fusion reactivity, reactivity, etc.). The differential equations of species mass densities and power densities are solved with a fourth-order Runge–Kutta method. This method presents significant advantages, amongst which are very good stability and accuracy, as a consequence of the consideration of intermediate time steps. For the intersection of the accuracy of the presented numerical results, each set of numerical calculations was repeated for three different time steps. Figure 12 presents an indicative example of the maximum ignition condition {Q = (Pfus/PBrems)}, as a function of time, for the time steps of dt = 10−5 sec, dt = 10−6 s, and dt = 10−7 sec, confirming the accuracy of the fourth order Runge–Kutta. Our choice to present only the Q parameter is owed to its dependence on various fusion medium physical parameters (species densities and temperatures, reactivity). The results shown in Figures 1–11 correspond to a time step of dt =10−6 sec, for the optimization of the running time.
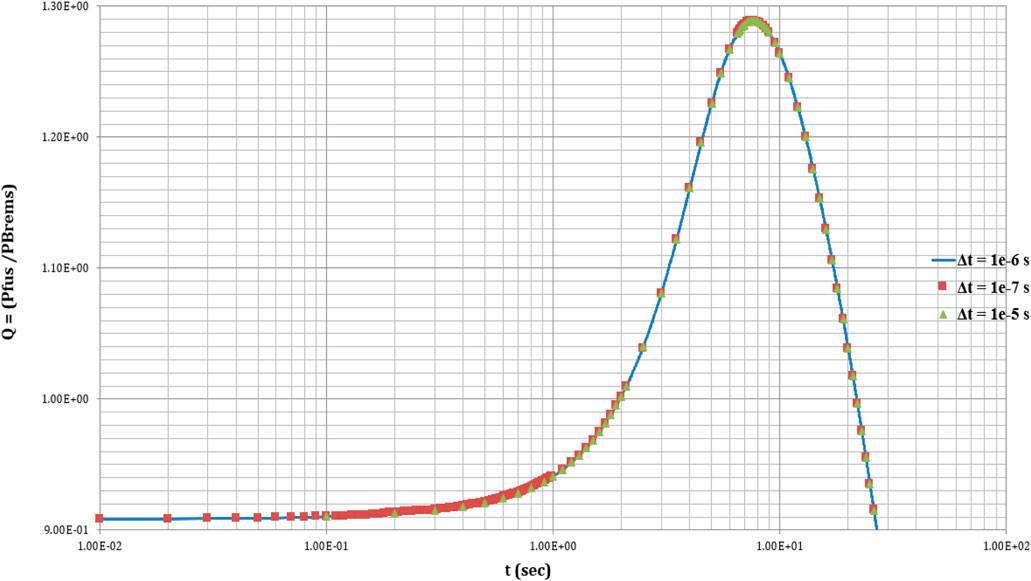
Figure 12. Representative example for the temporal evolution of the maximum ignition condition, for the different used time steps: dt = 10−5 sec, dt = 10−6 s, and dt = 10−7 sec, in the context of the simulations with the multi-fluid model.
The current numerical investigation, using the multi-fluid global particle and energy balance code [38, 40], explores the possibility of achieving further enhanced fusion ignition conditions [Q > 1] at lower than Tin = 100 keV initial medium temperatures, for two different configurations. The first configuration refers to the presence of energetic protons in a low-density boron medium, while the second one to the inclusion of additional energetic protons in a low-density p-11B medium. In both configurations, the density ratio between the fusion species remains at (np/nB) > 1, for Bremsstrahlung radiation losses optimization.
Provided specific initial conditions, the described configurations show not only an increase of the Q value up to 1.4, but also a decrease of the lowest required temperature for fusion ignition to Tin = 1 keV–10 keV. These interesting results make the p-11B fuel competitive with D–T fuel, with the extra advantage of no neutron generation. The fusion ignition possibility from lower than Tin = 100 keV initial medium (11B or p-11B) temperatures is owed to the consideration of energetic protons (200 keV < Ep,0 ≤ 750 keV) in the medium. The latter contribute jointly with the fusion-produced alphas to the increase of the p, 11B fusion species’ temperatures, within the optimum fusion reactivity region (<σv>). This is the main difference between the proposed configurations and the “simple” p-11B medium configuration (without energetic protons), where only the produced alphas contribute to the manifestation of the chain reactions alpha heating effect and the related avalanche effect.
The comparison between the two presented configurations supports the exclusion of following remarks: (i) For both configurations, the results show potential medium fusion ignition from lower than Tin = 100 keV initial temperatures, and (ii) The presence of energetic protons in a11B medium requires less external input energy than the addition of energetic protons (np,in) in a p-11B medium, with initial temperature Tin = Tp,med = TB. Therefore, the first configuration seems more attractive for employment in potential experiments. The second configuration, however, allows the obtainment of high fusion power density values, 0.72 ≤ Pfus ≤ 2.43 MW/m3, in the ignition temperature window of 10 keV ≤ Tin ≤ 100 keV (for the case of 600 keV energetic protons). The latter fact presents certain advantages in the case of laser-oriented experiments, as described in the introduction section.
The rapid increase of the fusion species’ temperatures to temperatures corresponding to the optimum fusion reactivity, shows its direct relationship with the chain reactions alpha heating effect and the related avalanche effect. During the fusion process of the p-11B fuel, the temporal evolution of the medium species’ physical parameters presents significant correlation effects, that connect the p, 11B species’ temperature increase profiles with the density rise of the produced alphas. These effects follow a sequence of time-dependent events [38]. More specifically, the energy profile of the produced alphas presents a significant decline, due to the occurring energy transfer to the fusion species (p, 11B). The fusion species’ temperature increase results in the density rise of the produced alphas, due to the higher corresponding nuclear fusion reactivity. The higher reactivity values lead to a higher alpha particle generation and, thus, to greater alpha energy transfer to the fusion species and fusion ignition (Q ≥ 1). The notable increase in the fusion species’ temperatures occurs when, the p-11B fusion produced alpha particle density is approximately two orders of magnitude lower than the initially formed total medium density. The above energy transfer process also receives the contribution of the energetic protons, which add energy to the fusion species, thus improving alpha density production. For both examined medium configurations, another equally important result concerns the ratio (TB/Te) > 1 at the time point of the maximum 11B species’ temperature, which is also observed in the case of a low-density p-11B medium without energetic protons (Tin = Tp = TB).
The presented numerical results describe the temporal evolution of the fusion medium physical parameters and, thus, could be useful for potential experimental setups or compact magnetic fusion devices, in which the plasma is trapped for a relatively long time without important density losses (expansion losses). The stable alpha production, during the first p-11B fusion-oriented experiment by TAE Technologies, in the compact LHD stellarator with five injected energetic proton beams [41] and the results obtained in the spherical compact Tokamak by the ENN Energy Research Institute in China [42], confirm the efficient plasma trapping without losses for relatively long periods of time.
The parameters of reaction rate (reactions/m3/sec) and/or fusion power density (W/m3) are proportional to fusion reactivity (<σv>). For the p-11B nuclear fuel, reactivity presents a “plateau-like maximum” for fusion species’ temperatures between 400 keV and 600 keV [4, 29, 55, 56], while, for higher temperatures, it decreases. In the performed numerical simulations, the maximum energetic protons’ energy is limited to Ep,0 ∼ 700 keV–750 keV for three main reasons:
(1) The higher than Ep,0 = 700 keV–750 keV energetic protons do not contribute to the further improvement of fusion power density (Pfus) and ignition condition (Q), although the fusion species’ temperature may increase to higher values than those corresponding to the maximum fusion reactivity (TB > 600 keV).
(2) Current laser facilities with TW or PW laser beams allow the generation of a relatively high number of proton and/or boron fluid species (∼1015–1016), with an energy of a few hundred keV. A potential experimental setup for the production of the highest possible number of fusion species with moderate energy (100 keV–750 keV), concerns the illumination of a relatively big target surface with a laser beam, rather than strong laser beam focusing for ultra-high energy species generation. This way, the trapping of a low-density p-11B medium (n ∼ 1020 m–3) for τΕ ∼ 10 s, inside a moderate volume (10−3 m–3–10−4 m–3), may allow the possibility of studying and comparing the results of the proposed configurations.
(3) For higher proton energies (e.g., 3 MeV ≤ Ep,0 ≤ 5 MeV), secondary nuclear reactions with boron can produce a neutron flux. Consequently, we prefer to continue our study for the aneutronic fusion channel of the p-11B fuel.
The important result of the performed numerical investigation concerns the decrease of the lowest required ignition temperature of the p-11B medium, below Tin = 100 keV. The described configurations and initial conditions show ignition conditions up to Q ∼ 1.4, even in the initial medium temperature range of Tin =1 keV–10 keV, which thus places the p-11B fuel in a competitive position, compared to D–T. Although the generation of the initial energy and density of the energetic proton fluid presents particular challenges the current day, significant advantages are also present, which are superior to the ones of the case of the relatively cooler simple p-11B medium (without energetic protons and Tin = Tp = TB) of Tin = 200 keV, for example, where [max]Q = 1.29 (see red curves shown in Figures 1, 7). The advantages of the p-11B medium with the additional energetic protons (np,in) and the total proton to boron density ratio of (
In conclusion, the results of the present work show that, the p-11B fuel could be considered a promising candidate for clean energy production in the near future.
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.
CD: conceptualization, software, writing–review and editing, validation, methodology, visualization, and writing–original draft. SM: software, writing–review and editing, conceptualization, methodology, validation, and supervision. SE: conceptualization, validation, and writing–review and editing. ZH: writing–review and editing. PL: writing–review and editing, methodology, software, and validation. NN: writing–review and editing and validation. YS: writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Wagner F. Physics of magnetic confinement fusion. The Eur Phys J Conferences (2013) 54:01007. doi:10.1051/epjconf/20135401007
2. Ongena J. Nuclear fusion and its large potential for the future world energy supply. Nukleonika (2016) 61:425–32. doi:10.1515/nuka-2016-0070
3. Girka I. One noble goal and a variety of scientific and technological challenges. London: IntechOpen (2019).
4. Atzeni S, Meyer-ter-Vehn J. Nuclear fusion reactions. In: The Physics of inertial fusion. Oxford: Oxford University Press (2004) p. 1–30.
5. Moreau DC. Potentiality of the proton-boron fuel for controlled thermonuclear fusion. Nucl Fusion (1977) 17:13–20. doi:10.1088/0029-5515/17/1/002
6. Hora H, Eliezer S, Nissim N. Elimination of secondary neutrons from laser proton-boron fusion. Laser Part Beams (2021) 2021:e13. doi:10.1155/2021/9978899
7. Oliphant MLE. Rutherford Lord. Experiments on the transmutation of elements by protons. Proc R Soc Lond (1932) 141:843. doi:10.1098/rspa.1933.0117
8. Labaune C, Baccou C, Yahia V, Neuville C, Rafelski J. Laser-initiated primary and secondary nuclear reactions in Boron-Nitride. Scientific Rep (2016) 6:21202. doi:10.1038/srep21202
9. Belloni F, Batani K. Multiplication processes in high-density H-11B fusion fuel. Laser Part Beams (2022) 2022:e11. doi:10.1155/2022/3952779
10. Hora H, Eliezer S, Kirchhoff GJ, Nissim N, Wang JX, Xu YX, et al. Road map to clean energy using laser beam ignition of boron-proton fusion. Laser Part Beams (2017) 35:4. doi:10.1017/S0263034617000799
11. Hora H, Lalousis P, Moustaizis SD. Fiber ICAN laser with exawatt-picosecond pulses for fusion without nuclear radiation problems. Laser Part Beams (2014) 32:63–8. doi:10.1017/S0263034613000876
12. Belyaev VS, Matafonov AP, Vinogradov VI. Observation of neutronless fusion reactions in picosecond laser plasma. Phys Rev E (2005) 72:2. doi:10.1103/PhysRevE.72.026406
13. Labaune C, Deprierraux S, Goyon S, Loisel C, Yahia G, Rafelski J, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun (2013) 4:2506. doi:10.1038/ncomms3506
14. Picciotto A, Margarone D, Velyhan A, Bellini P, Krasa J, Szydlowski A, et al. Boron-proton nuclear-fusion enhancement induced in boron-doped silicon targets by low-contrast pulsed laser. Phys Rev (2014) 4:031030. doi:10.1103/PhysRevX.4.031030
15. Margarone D, Picciotto A, Velyhan A, Krasa J, Kucharik M, Mangione A, et al. Advanced scheme for high-yield laser driven nuclear reactions. Plasma Phys Controlled Fusion (2015) 57:014030. doi:10.1088/0741-3335/57/1/014030
16. Margarone D, Bonvalet J, Giuffrida L, Morace A, Kantarelou V, Tosca M, et al. In-target proton-boron nuclear fusion using a PW-class laser. Appl Sci (2022) 12:1444. doi:10.3390/app12031444
17. Baccou C, Depierreux S, Yahia V, Neuville C, Goyon C, De Angelis R, et al. New scheme to produce aneutronic fusion reactions by laser-accelerated ions. Laser Part Beams (2015) 33:117–22. doi:10.1017/S0263034615000178
18. Giufrida L, Belloni F, Margarone D, et al. High-current stream of energetic alpha particles from laser-driven proton boron fusion. Phys Rev E (2020) 101:1. doi:10.1103/PhysRevE.101.013204
19. Hegelich BM, Labun L, Labun OZ, McCary E, Mehlhorn T. Photon and neutron production as in-situ diagnostics of proton-boron fusion. Laser Part Beams (2023) 2023:e7. doi:10.1155/2023/6924841
20. Eliezer S, Hora H, Korn G, Nissim N, Martinez-Val JM. Avalanche proton-boron fusion based on elastic nuclear collisions. Phys Plasmas (2016) 23. doi:10.1063/1.4950824
21. Eliezer S, Hora H, Korn G, Nissim N, Martinez-Val JM. Avalanche proton-boron fusion based on elastic nuclear collisions. Phys Plasmas (2016) 23:5. doi:10.1063/1.4950824
22. Belloni F. On a fusion chain reaction via super thermal ions in high-density H–11B plasma. Plasma Phys Controlled Fusion (2021) 63:5. doi:10.1088/1361-6587/abf255
23. Gruenwald J. On fusion chain reactions in 11B targets for laser driven aneutronic fusion. J Technol Space Plasmas (2021) 2:104–8. doi:10.31281/jtsp.v2i1.22
24. Lalousis P, Hora H, Eliezer S, Martinez-Val JM, Moustaizis SD, Miley GH, et al. Shock mechanisms by ultrahigh laser accelerated plasma blocks in solid density targets for fusion. Phys Lett A (2013) 377:885–8. doi:10.1016/j.physleta.2013.01.037
25. Lalousis P, Hora H, Moustaizis SD. Optimized boron fusion with magnetic trapping by laser driven plasma block initiation at nonlinear forced driven ultrahigh acceleration. Laser Part Beams (2014) 32:409–11. doi:10.1017/S0263034614000287
26. Hora H, Miley G, Lalousis P, Moustaizis SD, Clayton K, Jonas D. Efficient generation of fusion flames using PW-ps laser pulses for ultrahigh acceleration of plasma blocks by nonlinear (ponderomotive) forces. IEEE Transaction Plasma Sci (2014) 42:640–4. doi:10.1109/TPS.2014.2304558
27. Lalousis P, Moustaizis SD, Hora H, Miley GH. Kilotesla magnetic assisted fast laser ignited Boron11 proton fusion with nonlinear force driven ultrahigh accelerated plasma blocks. J Fusion Energy (2015) 34:1. doi:10.1007/s10894-014-9759-5
28. Shawareb AH, Acree R, Adams P, Adams J. Achievement of target gain larger than unity in an inertial fusion experiment. Phys Rev Lett (2024) 132:6. doi:10.1103/PhysRevLett.132.065102
29. Nevins WM, Swain R. Thee thermonuclear fusion rate coefficient for p-11B reactions. Nucl Fusion (2000) 40:4. doi:10.1088/0029-5515/40/4/310
30. Kimura S, Anzalone A, Bonasera A. Comment on Observation of neutronless fusion reactions in picosecond laser plasmas. Phys Rev A (2009) 79:038401. doi:10.1103/PhysRevE.79.038401
31. McKenzie W, Batani D, Mehlhorn TA, Margarone D, Belloni F, Michael Campbell E, et al. HB11—understanding hydrogen-boron fusion as a new clean energy source. J Fusion Energy (2023) 42:17. doi:10.1007/s10894-023-00349-9
32. Mehlhorn TA, Labun L, Hegelich BM, Margarone D, Gu MF, Batani D, et al. Path to increasing p-B11 reactivity via ps and ns lasers. Laser Part Beams (2022) 2022:e1. doi:10.1155/2022/2355629
33. Hora H, Eliezer S, Nissim N, Lalousis P. Non-thermal laser driven plasma-blocks for proton boron avalanche fusion as direct drive option. Matter Radiat Extremes (2017) 2:177–89. doi:10.1016/j.mre.2017.05.001
34. Shmatov M. Comment on “Avalanche proton-boron fusion based on elastic nuclear collisions” [Phys. Plasmas 23, 050704 (2016)]. Phys Plasmas (2016) 23:9. doi:10.1063/1.4963006
35. Eliezer S, Hora H, Korn G, Nissim N, Martinez Val JM. Response to “Comment on ‘Avalanche proton-boron fusion based on elastic nuclear collisions’” [Phys. Plasmas 23, 094703 (2016)]. Phys Plasmas (2016) 23:9. doi:10.1063/1.4963007
36. Belloni F, Margarone D, Picciotto A, Schillaci F, Giuffrida L. On the enhancement of p-11B fusion reaction rate in laser-driven plasma by a→p collisional energy transfer. Phys Plasmas (2018) 25:2. doi:10.1063/1.5007923
37. Istokskaia V, Tosca M, Giuffrida L, Psikal J, Grepl F, Kantarelou V, et al. A multi-MeV alpha particle source via proton boron fusion driven by a 10-GW tabletop laser. Commun Phys (2023) 6:27. doi:10.1038/s42005-023-01135-x
38. Moustaizis S, Daponta C, Eliezer S, Henis Z, Lalousis P, Nissim N, et al. Alpha heating and avalanche effect simulations for low density proton-boron fusion plasma. J Instrumentation (2024) 19:C01015. doi:10.1088/1748-0221/19/01/C01015
39. Putvinski SV, Ryutov DD, Yushmanov PN. Fusion reactivity of the Pb11 plasma revisited. Nucl Fusion (2019) 59:076018. doi:10.1088/1741-4326/ab1a60
40. Lalousis P (2016). Alpha heating in magnetic and inertial confinement fusion. Proceedings of the 43rd European Plasma Conference (EPS 2016). (Leuven, Belgium). P5.069.pdf (epfl.ch).
41. Magee RM, Ogawa K, Tajima T, Allfrey I, Gota H, McCarroll P, et al. First measurements of p11B fusion in a magnetically confined plasma. Nat Commun (2023) 14:955. doi:10.1038/s41467-023-36655-1
42. ΕΝΝ Energy Research Institute. Helong experiment (2017). Available from: http://en.ennresearch.com/researchfield/Compactfusion/Experiment/ (Accessed September 4, 2024).
43. Nagy A, Bortolon A, Mauzey DM, Wolfe E, Gilson EP, Lunsford R, et al. A multi-species powder dropper for magnetic fusion applications. Rev Scientific Instr (2018) 89. 10K121, doi:10.1063/1.5039345
44. Nespoli F, Ashikawa N, Gilson EP, Lunsford R, Mazuraki S, Shoji M, et al. The LHD experiment group. First impurity powder injection experiments in LHD. Nucl Mater Energy (2020) 25. doi:10.1016/j.nme.2020.100842
45. Skinner CH, Kugel HW, Maingi R, Wampler WR, Blanchard W, Bell MG, et al. Effect of boronization on ohmic plasma in NSTX. Nucl Fusion (2002) 42:3. doi:10.1088/0029-5515/42/3/313
46. Buzhinskij OI, Semenets YM. Review of in situ boronization in contemporary tokamaks. Fusion Sci Technology (1997) 32:1–13. doi:10.13182/FST97-A19875
47. Domínguez-Gutiérrez FJ, Bedoya F, Predrag SK, Allain JP, Irle S, Skinner CH, et al. Unraveling the plasma-material interface with real time diagnosis of dynamic boron conditioning in extreme tokamak plasmas. Nucl Fusion (2017) 57:8. doi:10.1088/1741-4326/aa7b17
48. Friedberg J. Plasma Physics and fusion energy. 1st ed. Cambridge: Cambridge University Press (2007). doi:10.1017/CBO9780511755705
49. Stave S, Ahmed MW, France RH, Henshaw SS, Muller B, Perdue BA, et al. Understanding the 11B (p, α)αα reaction at the 0675 MeV resonance. Phys Lett B (2011) 696. doi:10.1016/j.physletb.2010.12.015
50. Wurzel SE, Scott CH. Progress toward fusion energy breakeven and gain as measured against the Lawson criterion. Phys Plasmas (2022) 29:062103. doi:10.1063/5.0083990
51. Eliezer S, Schweitzer Y, Nissim N, Martinez Val JM. Mitigation of the stopping power effect on proton-boron11 nuclear fusion chain reactions. Front Phys (2020) 8:573694. doi:10.3389/fphy.2020.573694
52. Glasstone S, Lovberg R. Controlled thermonuclear reactions. United States: Krieger Publishing Company Huntington (1975). chapter 2.
53. Callen DJ. Fundamentals of plasma physics (2006). Available from: https://www.scribd.com/document/85976601/fundamentals-of-plasma-physics-2006 (Accessed January 10, 2024).
54. Fundamenski W, Garcia OE. Comparison of Coulomb collision rates in the plasma physics and magnetically confined fusion literature. Efda–jet–r 01 EFDR07001.pdf (euro-fusion.org) (2007).
55. Tentori A, Belloni F. Revisiting p-11B fusion cross section and reactivity, and their analytic approximations. Nucl Fusion (2023) 63:086001. doi:10.1088/1741-4326/acda4b
56. Sikora MH, Weller HR. A new evaluation of the 11B(p, α)αα Reaction Rates. J Fusion Energy (2016) 35:3. doi:10.1007/s10894-016-0069-y
Keywords: proton–boron fusion, low-density plasma, energetic protons in low-density p-11B medium, multi-fluid code, alpha heating effect, chain reactions, avalanche effect
Citation: Daponta C, Moustaizis S, Eliezer S, Henis Z, Lalousis P, Nissim N and Schweitzer Y (2024) Towards p-11B medium configurations with high Pfus/PBrems ratios. Front. Phys. 12:1425963. doi: 10.3389/fphy.2024.1425963
Received: 30 April 2024; Accepted: 15 October 2024;
Published: 15 November 2024.
Edited by:
Alex Robinson, Science and Technology Facilities Council, United KingdomReviewed by:
Francisco Javier Dominguez Gutierrez, National Centre for Nuclear Research, PolandCopyright © 2024 Daponta, Moustaizis, Eliezer, Henis, Lalousis, Nissim and Schweitzer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: C. Daponta, Y2hyeXNvdmFsYW50aWRhcG9udGFAZ21haWwuY29t; Y. Schweitzer, eW9uYS5zY2h3ZWl0emVyQGdtYWlsLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.