Thermal and non-thermal DM production in non-standard cosmologies: a mini review

We provide a short review of some aspects of dark matter (DM) production in non-standard cosmology. Considering the simplest Higgs portal model as a definite particle physics setup, we consider the impact on the parameter space corresponding to the correct relic density and the complementary experimental constraints of the presence, during thermal production, of an exotic component dominating the energy density of the universe. In the second part of the work, we will focus on the case that such an exotic component satisfies the equation of state of matter and can produce DM non-thermally.

1 Introduction

The solution to the dark matter (DM) puzzle is one of the biggest challenges of modern particle physics. The determination of the mechanism for DM production is a key ingredient in solving this puzzle. Thermal freeze-out is one of the most popular proposals as it relates the DM relic density to a single-particle physics input, the so-called thermally averaged DM pair annihilation cross section. Furthermore, the value of the latter quantity, favored by cosmological observations of the DM abundance (see [1]), is characteristic of weak interactions, leading to the so-called weakly interacting massive particle (WIMP) miracle. The thermal freeze-out paradigm is, however, in increasing tension with null results from DM searches, especially the ones based on the principle of direct detection (DD) (see, e.g., [2, 3] for some reviews). In light of this, an alternative production mechanism, dubbed freeze-in [4], is gaining increasing attention as it can accommodate the correct relic density for very small values of the coupling between the DM and standard model (SM) states, encompassing the aforementioned experimental tensions. Both conventional freeze-in and freeze-out mechanisms rely on the hypothesis of a standard cosmological history of the Universe implying, in particular, that the DM is produced in a radiation-dominated epoch. There are no reasons, in addition to minimality, to enforce a priori such an assumption as we have no confirmed experimental evidence about the cosmological history prior to the Big Bang Nucleosynthesis (BBN). It is then interesting to consider the impact on DM production of a non-standard cosmological evolution of the Universe. By this, we intend the possibility that at some epoch, comprised between the primordial inflation and the BBN, the energy budget of the Universe was dominated by an exotic component, i.e., different by ordinary (and dark) matter and radiation. Such an exotic component impacts DM production in a two-fold manner: it affects the Hubble expansion parameter and the evolution of the temperature of the Universe with time during DM thermal production; it might be itself a source of (non-thermal) production of DM. In this work, we will provide a brief review of some aspects of thermal and non-thermal production of DM in a non-standard cosmological history (please refer to [5] for more extensive discussions).

The remainder of this paper is organized as follows: in Section 2, we will describe the general set of equations for DM production in the presence of a single exotic component, to the energy budget of the Universe, characterized by an arbitrary equation of state parameter. Some analytical approximations for the solution of such equations, in the case that the new component is not a direct source of DM, will also be provided. In Section 3, a reference particle physics framework, i.e., the Higgs portal with scalar DM, will be introduced. The findings of Section 2 will be applied to it. Finally, in Section 4, the case of non-thermal production from an exotic matter component will be reviewed. Again, some examples of the solutions of Boltzmann’s equations will be applied to the scalar Higgs portal. The final section will be devoted to the conclusions.

2 Boltzmann equations

Following [6], the most general set of Boltzmann equations describing the scenario under concern can be written as follows¹:

$\begin{array}{ll}\hfill & \frac{d{\rho }_{\varphi }}{dt}+3\left(1+\omega \right)H{\rho }_{\varphi }=-{\mathrm{\Gamma }}_{\varphi }{\rho }_{\varphi }\hfill \\ \hfill & \frac{ds}{dt}+3Hs=\frac{{\mathrm{\Gamma }}_{\varphi }{\rho }_{\varphi }}{T}\left(1-b_{\chi }\frac{E_{\chi }}{m_{\varphi }}\right)+2\frac{E_{\chi }}{T}\langle \sigma v\rangle \left(n_{\chi }^2-n_{\chi ,\mathrm{e}\mathrm{q}}^2\right)\hfill \\ \hfill & \frac{d{n}_{\chi }}{dt}+3H{n}_{\chi }=\frac{b_{\chi }}{m_{\varphi }}{\mathrm{\Gamma }}_{\varphi }{\rho }_{\varphi }-\langle \sigma v\rangle \left(n_{\chi }^2-n_{\chi ,\mathrm{e}\mathrm{q}}^2\right),\hfill \end{array}(1)$

where $E_{\chi }^2\simeq m_{\chi }^2+3T^2$. ρ_ϕ represents the energy density of an exotic component $\varphi$, with an equation of state relating its energy density and pressure, ${\rho }_{\varphi }={\omega \rho }_{\varphi }$. This component can dominate the energy density of the Universe during certain stages. As further detailed in the next section, ω = 0 is the most popularly considered option, corresponding to a so-called “early matter domination period,” due, for example, to heavy metastable particles. On a similar footing, one might consider additional radiation components, i.e., ω = 1/3. Other popular examples are kination (ω = 1)-dominated [7–9] and quintessence (ω = −1)-dominated Universe [10, 11]. Different values of ω can be expected by considering scalar fields with suitable choices for their potentials (refer to [12, 13] for example). Finally, scenarios of braneworld cosmologies [14] and modified gravity theories [15, 16] can be described via the formalism illustrated below. For a more extensive review of the possible origins of non-standard cosmologies, we refer to [17]. The time evolution $\varphi$ is governed by a decay rate Γ_ϕ, which must ensure that it disappears before the onset of BBN. At the moment of decay, the energy stored in $\varphi$ is passed to the primordial plasma, increasing its entropy, and possibly to the DM. As just pointed out, in light of the decay of $\varphi$, the entropy density s of the primordial plasma is not a conserved quantity any longer; consequently, we need to explicitly consider a Boltzmann equation (alternatively one can consider, instead, an equation for the energy density of radiation, refer to [18–21] for example). The last equation in (1) tracks the time evolution of the DM number density n_χ. In addition to the Hubble expansion, it is governed by pair annihilation processes into SM pairs, described by the thermally averaged cross section ⟨σv⟩, which can be computed as shown in detail in [22] or via public available packages as micrOMEGAs [23, 24] or DarkSUSY [25, 26], and, possibly, by a non-thermal production term depending on Γ_ϕ and on a parameter $b_{\chi }$, measuring the fraction of the energy density of $\varphi$, which gets converted into DM. The system written in Eq. 1 should be combined witht the following equation for the Hubble expansion parameter $H$.

$H^2=\frac{8\pi G}{3}\left({\rho }_{\varphi }+{\rho }_R+E_{\chi }{n}_{\chi }\right),$

with

${\rho }_R=\frac{{\pi }^2}{90}{g}_{\text{eff}}\left(T\right)T^4.$

Let us consider the case where $b_{\chi }=0$ so that $\varphi$ influences DM production only indirectly by altering the expansion rate of the Universe. A recent extensive semi-analytical study of the solution of Eq. 1 has been presented in [6], and we summarize below the results. The non-standard cosmology is parameterized mostly via three quantities:

$\omega ,\kappa ={\left.\frac{{\rho }_{\varphi }}{{\rho }_R}\right|}_{T=m_{\chi }},T_{\text{end}},(2)$

where ω is the already mentioned equation of the state parameter; κ indicates, at a reference temperature, the amount of energy density of $\varphi$, compared to the one of radiation, and can be used to set the initial conditions for Eq. 1. $T_{\text{end}}$ is finally the temperature at which the standard radiation domination era starts again after the $\varphi$-dominated epoch. In the so-called instantaneous decay approximation, it can be determined by the following condition:

${\mathrm{\Gamma }}_{\varphi }^2=H{\left(T_{\text{end}}\right)}^2=\frac{8\pi G}{3}{\rho }_R\left(T_{\text{end}}\right)\to T_{\text{end}}^4=\frac{90}{{\pi }^2{g}_{\text{eff}}\left(T_{\text{end}}\right)}{M}_{\text{Pl}}^2{\mathrm{\Gamma }}_{\varphi }^2.(3)$

Such conditions can be used to set Γ_ϕ as a function of $T_{\text{end}}$ without relying on a specific model. To avoid tension with BBN, $T_{\text{end}}$ ≥ 4 MeV is required [27–30]. The system Eq. 1 can be solved as function of the parameters listed in Eq. 2 without referring to a specific model. There are three additional temperature (and hence time) scales.

• The standard freeze-out temperature $T_{f.o.}$, i.e., the temperature at which DM annihilation becomes inefficient and DM starts to decouple from the primordial plasma, in the absence of exotic components in the energy budget of the Universe. The freeze-out temperature can be determined by solving the following equation:

$x_{f.o.}=\frac{m_{\chi }}{T_{\text{f.o.}}}=\log \left[\frac{3}{2}\sqrt{\frac{5}{{\pi }^5{g}_{\text{eff}}}}{g}_{\chi }{m}_{\chi }{M}_{Pl}⟨\sigma v⟩\sqrt{x_{f.o.}}\right],$

with $g_{\chi }$ being the internal degrees of freedom of the DM candidate. For values of ⟨σv⟩ around the thermally favored value, $x_{\text{f.o.}}$ ∼ 20 ÷ 30.

• The temperature $T_{\text{eq}}$ from which, give an initial value for κ, the $\varphi$ components becomes the dominant contribution to $H$.

• The temperature $T_c$ at which the presence of the exotic component starts altering the evolution of the plasma temperature with the scale factor.

Having in mind these relevant scales, one can achieve a semi-analytical determination of the DM abundance in some limiting regimes:

• $T_{\text{eq}}$ ≪ $T_{f.o.}$: DM freeze-out occurs similar to that in the standard radiation domination scenario. The main effect from $\varphi$ is represented by the entropy injection during its decay, causing a dilution of thermal abundance of the DM. In the instantaneous decay approximation, the DM relic density can be written as

$\begin{array}{ll}\hfill & Y_{\chi }=\frac{Y_{\chi }^T}{D}\simeq \frac{15}{2\pi \sqrt{10g_{eff}}}\frac{x_{f.o.}}{m_{\chi }{M}_{Pl}\langle \sigma v\rangle }{\left[\frac{1}{\kappa }{\left(\frac{T_{\text{end}}}{m_{\chi }}\right)}^{1-3\omega }\right]}^{\frac{1}{1+\omega }}\omega \ne -1\hfill \\ \hfill & Y_{\chi }=\frac{Y_{\chi }^T}{D}\simeq \frac{15}{2\pi \sqrt{10g_{eff}}}\frac{x_{f.o.}}{m_{\chi }{M}_{Pl}\langle \sigma v\rangle }{\left[1-\kappa {\left(\frac{m_{\chi }}{T_{\text{end}}}\right)}^4\right]}^{3/4}\omega =-1.\hfill \end{array}$

• $T_c$ ≪ $T_{f.o.}$ ≪ $T_{\text{eq}}$: In such a regime, freeze-out occurs when the Hubble expansion parameter is dominated by the $\varphi$ component.

$H\simeq \frac{\sqrt{{\rho }_{\varphi }}}{3M_{Pl}^2}=\frac{\pi }{3}\sqrt{\frac{g_{\text{eff}}}{10}}\frac{m_{\chi }^2}{M_{\text{Pl}}}\sqrt{\frac{\kappa }{x^{3\left(1+\omega \right)}}}.$

We are, however, far enough from its decay time so that the relation between the temperature and scale factor is the same as in standard cosmology. In such a case, the DM abundance is again given by the ratio of a thermal abundance and the same dilution factor defined in the previous case. However, the thermal abundance differs from the standard computation as a consequence of a different freeze-out time.

$\begin{array}{ll}\hfill & Y_{\chi }=D^{-1}\frac{45}{4\pi }\frac{1-\omega }{m_{\chi }{M}_{\text{Pl}}\langle \sigma v\rangle }\sqrt{\frac{\kappa }{10g_{\text{eff}}}}{\tilde{x}}_{f.o.}^{\frac{3}{2}\left(1-\omega \right)}\omega \ne 1\hfill \\ \hfill & Y_{\chi }=D^{-1}\frac{15}{2\pi }\frac{1}{m_{\chi }{M}_{Pl}\langle \sigma v\rangle }\sqrt{\frac{\kappa }{10g_{\text{eff}}}}{\left[\log \frac{x_{\text{end}}}{{\tilde{x}}_{f.o.}}\right]}^{-1}\omega =1,\hfill \end{array}$

where $x_{\text{end}}=m_x/T_{\text{end}}$ and ${\tilde{x}}_{f.o.}$ refers to a modified freeze-out time, with respect to a standard cosmological history, given by

${\tilde{x}}_{\text{f.o.}}=\log \left[\frac{3}{2}\sqrt{\frac{5}{{\pi }^5{g}_{\text{eff}}}}{g}_{\chi }\frac{m_{\chi }{M}_{Pl}⟨\sigma v⟩}{\sqrt{\kappa }}{\tilde{x}}_{\text{f.o.}}^{3/2\omega }\right].$

• $T_{\text{end}}$ ≪ $T_{f.o}$ ≪ $T_c$: In such a case, DM freeze-out is affected by the different relation between the temperature and scale parameter. The relic density can be approximated, this time, as

$\begin{array}{ll}\hfill & Y_{\chi }=\frac{45\left(1-\omega \right)}{4\pi }\sqrt{\frac{1}{10g_{\text{eff}}}}\frac{1}{M_{\text{Pl}}\langle \sigma v\rangle }{\left[{\bar{T}}_{\text{f.o.}}^{4\left(\omega -1\right)}{T}_{\text{end}}^{3-5\omega }\right]}^{1/\left(1+\omega \right)}\omega \ne 1\hfill \\ \hfill & Y_{\chi }=\frac{45}{8\pi }\sqrt{\frac{1}{10g_{\text{eff}}}}\frac{1}{T_{\text{end}}{M}_{\text{Pl}}\langle \sigma v\rangle }{\left(\log \frac{{\bar{T}}_{\text{f.o.}}}{T_{\text{end}}}\right)}^{-1}\omega =1,\hfill \end{array}$

where the freeze-out temperature is obtained by solving the following equation:

${\bar{x}}_{\text{f.o.}}=\log \left[\frac{3}{2}\sqrt{\frac{5}{{\pi }^5{g}_{\text{eff}}}}{g}_{\chi }\frac{M_{\text{Pl}}⟨\sigma v⟩T_{\text{end}}^2}{m_{\chi }}{\bar{x}}_{\text{f.o.}}^{5/2}\right].$

• $T_{f.o.}$ ≪ $T_{\text{end}}$: the presence of an epoch dominated by the exotic component has no impact on DM production. The relic density is determined as in the standard cosmological model.

3 Results in a specific case of study

As evident from the previous discussion, the framework under consideration can be analyzed in terms of a limited set of parameters without relying on a specific particle physics framework: the initial ratio κ between $\varphi$ and radiation energy densities, the equation of state parameter ω, $T_{\text{end}}$, the DM mass $m_{\chi }$, and the annihilation cross section ⟨σv⟩. However, for a better understanding of the impact of non-standard cosmologies on DM production, it is useful to consider a definite particle model. Our choice falls on the Higgs portal (see [31] for a review) with scalar DM as it allows for maintaining a low number of free parameters. Indeed, the latter model is fully characterized by the following Lagrangian equation:

$\mathcal{L}=-\frac{1}{2}{m_{\chi }^0}^2{\chi }^2-\frac{1}{4}{\lambda }_s{\chi }^2-\frac{1}{4}{\lambda }_{\chi }{\chi }^2{H}^{†}H.$

Here, χ is a real scalar DM candidate² and $H$ is the Higgs doublet. After the Higgs obtains a vacuum expectation value (vev), the Lagrangian function generates a trilinear interaction between the Higgs boson and a pair of DM particles, which allows for DM annihilations into SM fermion, gauge boson, and Higgs boson pairs. In addition to the DM mass,

$m_{\chi }^2={m_{\chi }^0}^2+\frac{1}{4}{\lambda }_{\chi }^2{v}^2,$

the coupling ${\lambda }_{\chi }$ is the only free parameter of the theory. By comparing the DM annihilation rate with the Hubble expansion rate during a radiation-dominated era, one finds that for ${\lambda }_{\chi }$ ≳ 10^–5, the DM was capable of being in thermal equilibrium in the Early Universe. One could then apply the standard freeze-out paradigm and find that the correct relic density, Ω_χh² ≈ 0.12, is matched for O (0.1–1) values of the ${\lambda }_{\chi }$ coupling, with an exception of $m_{\chi }\sim m_H/2$, where the s-channel resonant enhancement of the DM annihilation cross section allows for very small values of the couplings (see Figure 1). For λ_χ ≤ 10^–6, the DM was not capable of thermalizing with the primordial plasma. Nevertheless, the correct relic density can be achieved for λ_χ ∼ O (10^–11) via the freeze-in mechanism³. The parameter space corresponding to thermal freeze-out can be effectively probed experimentally. The most relevant constraints come from DM DD. For our analysis, we have considered the combination of the limits given by XENON1T [33] for $m_{\chi }$ ≤ 10 GeV and by LZ [34] for $m_{\chi }$ ≥ 10, GeV. For $m_{\chi }\le m_H/2$, DD constraints are well-complemented by the bounds from searches of invisible decays of the SM Higgs (refer to [35] for most recent results). In this work, we have adopted the limit $\mathit{Br}(H\to \text{inv})$ ≤ 0.11 and also considered projected increased sensitivities to 0.05 and 0.01 [36, 37].

Figure 1

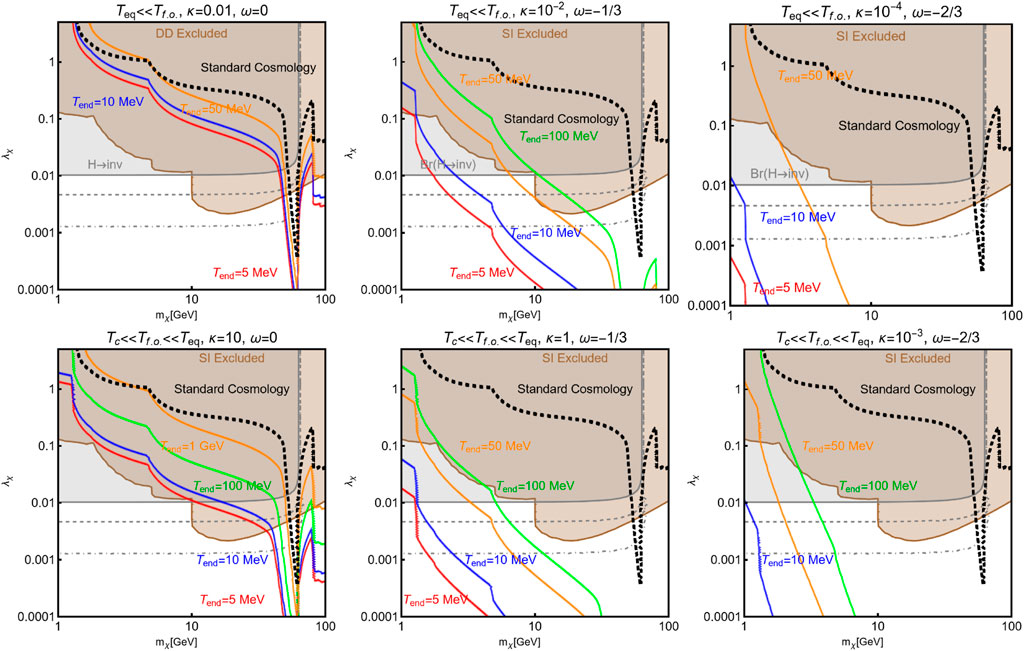
Figure 1. Parameter space of the Higgs portal considering three non-standard cosmological scenarios identified by different assignations of the (ω, κ) pair. The different colored contours correspond to the correct value of the DM relic density for the assignations of $T_{\text{end}}$ reported in the plots. The brown region is excluded by current DD constraints. The gray regions are, instead, ruled out by searches for invisible decays of the Higgs. The dashed gray line corresponds to future hypothetical limits $\mathit{Br}(H\to \text{inv})$ < 0.05, 0.01. For reference, we have shown the result relative to the correct relic density in a standard cosmological scenario as black dashed lines. The upper row refers to the solution in the regime T_end ≪ T_f.o, while the bottom row to T_c ≪ T_f.o. ≪ T_eq (see main text for discussion).

Figure 1 illustrates, via some examples, the impact of a non-standard cosmological history, as illustrated in the previous section, on the parameter space of the scalar Higgs portal, with a focus on the $m_{\chi }$ ≤ 100 GeV region, which is mostly subjected to experimental constraints. The different panels of the figure consider some assignations of the (ω, κ) pair and show, in the ($m_{\chi }$, ${\lambda }_{\chi }$) bi-dimensional plane, isocontours of the correct relic density for different values of $T_{\text{end}}$ ranging from 5 MeV (approximately the lower bound from BBN) to 1 GeV. To be viable, such isocontours should be (at least partially) outside the brown- and gray-colored regions corresponding to, respectively, the exclusion bounds from DD and invisible Higgs decays. For reference, the isocontour corresponding to the standard freeze-out scenario has also been shown. From the outcome of the plots, one notices that non-standard cosmologies sensitively affect the parameter space corresponding to the correct DM relic density, allowing lower values of the DM couplings and, more interestingly, lower values of the mass. In the case of an additional matter component ω = 0, it remains very difficult to overcome experimental constraints for $m_{\chi }\le m_H/2$. To achieve a viable parameter space at low DM masses, one needs to rely on more exotic components with ω = −1/3 and ω = −2/3.

4 Thermal and non-thermal DM in the universe with early matter domination

The most commonly considered scenario with b_χ ≠ 0 is the one in which ϕ is an additional matter component, i.e., ω = 0. In this setup, ϕ can be interpreted as a particle field that is always thermally decoupled from the primordial plasma. The existence of these fields is motivated by several particle physics frameworks (refer to [38–44] for some examples). In more recent times, primordial black holes have been proposed as this exotic matter component [45]. In this kind of setups, $T_{\text{end}}$ is customarily referred to as reheating temperature $T_R$. Although we will adopt the phenomenological determination given by Eq. 3 and use, as well, the parameter κ to fix the initial conditions for the Boltzmann equations, one can determine Γ_ϕ from the model parameters as follows:

${\mathrm{\Gamma }}_{\varphi }=D_{\varphi }\frac{m_{\varphi }^3}{M_{\text{Pl}}^2},$

where $D_{\varphi }$ depends on the specific underlying model and the initial energy density is assigned as ${\rho }_{\varphi ,I}=\frac{1}{2}{m}_{\varphi }^2{M}_{\text{Pl}}^2$. In this setup, $T_R$ can be extrapolated from the numerical solution of the Boltzmann equations (refer to [21] for a discussion). Equation 1 can be solved in the case of a new matter field Φ via the following change of variables [18, 21]:

$\mathrm{\Phi }=\frac{{\rho }_{\varphi }{a}^3}{\mathrm{\Lambda }},N_{\chi }=n_{\chi }{a}^3,a=\frac{A}{a_I}.$

Such a change in variables allows us to gauge out the terms linear with the Hubble expansion rate so that the system of equations can be rewritten as

$\begin{array}{ll}\hfill & \frac{d\mathrm{\Phi }}{dA}=-\frac{{\mathrm{\Gamma }}_{\mathrm{\Phi }}}{\mathcal{H}}{A}^{1/2}{a}_I^{3/2}\mathrm{\Phi }\hfill \\ \hfill & \frac{dN}{dA}=\frac{A^{1/2}{a}_I^{3/2}}{\mathcal{H}}\mathrm{\Lambda }\frac{b_{\chi }}{m_{\varphi }}{\mathrm{\Gamma }}_{\varphi }\mathrm{\Phi }-\frac{\langle \sigma v\rangle }{\mathcal{H}}{A}^{-5/2}{a}_I^{-3/2}\left(N_{\chi }^2-N_{\chi ,\mathrm{e}\mathrm{q}}^2\right)\hfill \\ \hfill & \frac{dT}{dA}={\left(3+T\frac{d{h}_{\text{eff}}}{dT}\right)}^{-1}\left\{-\frac{T}{A}+\frac{{\mathrm{\Gamma }}_{\varphi }\mathrm{\Lambda }}{m_{\varphi }}\left(1-\frac{b_{\chi }{E}_{\chi }}{m_{\varphi }}\right)\frac{T}{s\mathcal{H}}{A}^{-5/2}{a}_I^{-3/2}\mathrm{\Phi }\right.\hfill \\ \hfill & \left.+2\frac{E_{\chi }}{s\mathcal{H}}{A}^{-11/2}{a}_I^{-9/2}\langle \sigma v\rangle \left(N_{\chi }^2-N_{\chi ,\mathrm{e}\mathrm{q}}^2\right)\right\},\hfill \end{array}$

where $\mathcal{H}$ is defined as

$\mathcal{H}\equiv {\left(a_{I}A\right)}^{3/2}H=\left(\frac{\mathrm{\Lambda }\mathrm{\Phi }+{\rho }_R\left(T\right)A^3{a}_I^3+E_{\chi }{N}_{\chi }}{3M_{Pl}^2}\right).$

In the abovementioned equations, $h_{\text{eff}}$ represents the entropy effective degrees of freedom.

In the following, we will present some examples of numerical solutions to the equations above, again adopting the Higgs portal as a model for DM interactions with the SM. A similar scenario has also been considered in [46]. Before doing this, we briefly illustrate some approximate solutions, following the discussion of [20, 21] (detailed studies of Boltzmann’s equations for non-thermal DM production have also been conducted in [47–49]). Assuming that $T_R$ is sufficiently lower than $T_{\text{f.o.}}$ so that the thermally produced component of the DM gets sufficiently diluted to account for Ω_χ to a negligible extent, we distinguish two leading regimes for the solution of Boltzmann’s equations. In the case that interactions between the DM and SM are substantial, non-thermal production of DM can lead to a significant DM annihilation rate, i.e., Γ_ann = ⟨σv⟩$n_{\chi }$, becoming efficient again, compared to the Hubble expansion rate at low temperatures so that there is a compensation between non-thermal production and annihilations. This situation occurs when the number density of non-thermally produced DM exceeds the critical value given by

$n_{\chi }^c\simeq \frac{H}{⟨\sigma v⟩}.$

In the instantaneous decay approximation, the condition $n_{\chi }>n_{\chi }^c$ can be re-expressed as [43]

$\frac{1}{⟨\sigma v⟩}<b_{\chi }\frac{{\pi }^2}{30}{T}_R^{4/3}{M}_{Pl}^{2/3},$

evidencing that for a fixed $b_{\chi }$, as $T_R$ decreases, one would need stronger DM interactions (encoded in ⟨σv⟩) to match this condition.

In this regime, also dubbed as the re-annihilation regime in the literature [15, 50], the DM relic density can be approximated by an analogous expression as in the standard freeze-out case but replacing $T_{\text{f.o.}}$ with $T_R$:

${\mathrm{\Omega }}_{\chi }^{\text{NT}}{h}^2\simeq \frac{T_{f.o.}}{T_{\text{R}}}{\mathrm{\Omega }}_{\chi }^{\text{T}}{h}^2,$

where ${\mathrm{\Omega }}_{\chi }^{\text{T}}$ is the relic density computed according to the conventional freeze-out paradigm assuming standard cosmology (we remember ${\mathrm{\Omega }}_{\chi }^T\propto 1/⟨\sigma v⟩$). If the interactions between the DM and SM states are not efficient enough, a fraction of the energy initially stored in the Φ field, determined by the parameter $b_{\chi }$, is directly transferred into DM particles. In such a regime, the DM relic density is directly proportional to $b_{\chi }$ and reheating temperature $T_R$.

$\begin{array}{ll}\hfill & Y_{\chi }\left(T_{\text{R}}\right)=\frac{n_{\chi }\left(T_{\text{R}}\right)}{s\left(T_{\text{R}}\right)}\simeq \frac{b_{\chi }}{m_{\varphi }}\frac{{\rho }_{\varphi }\left(T_{\text{R}}\right)}{s\left(T_{\text{R}}\right)}\simeq \frac{3}{4}\frac{b_{\chi }}{m_{\varphi }}{T}_{\text{RH}}\hfill \\ \hfill & \to {\mathrm{\Omega }}_{\chi }^{\text{NT}}{h}^2\simeq 0.2\times 10^4{b}_{\chi }\frac{10\text{TeV}}{m_{\varphi }}\frac{T_{\text{R}}}{1\text{MeV}}\frac{m_{\chi }}{100\text{GeV}}\hfill \end{array}$

Figures 2, 3 show some examples of the solution to Boltzmann’s equations for non-thermal production of DM.

Figure 2

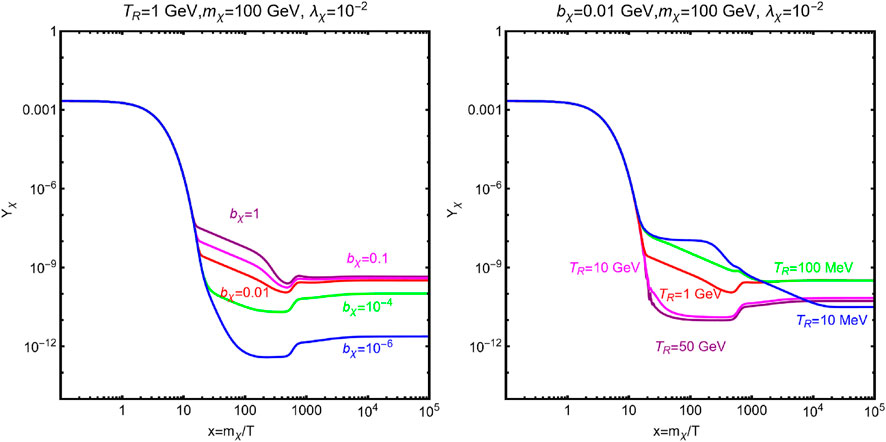
Figure 2. Evolution of the DM co-moving abundance for $m_{\chi }$ = 100 GeV and λ_χ = 10^–2. The left plot considers the assignation T_R = 1 GeV and different values of $b_{\chi }$, ranging from 10^–6 to 1, corresponding to the different colored lines. The right plots consider, instead, the fixed assignation $b_{\chi }$ = 10^–2 and a variation in $T_R$.

Figure 3

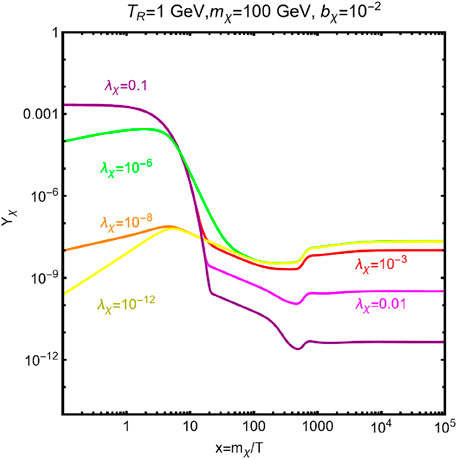
Figure 3. Evolution of the DM co-moving abundance, with respect to x = m_χ/T, for the assignation of the (m_χ, b_χ, T_R) set, reported on the top of the figure. The different colored lines correspond to different assignations for DM coupling λ_χ reported on the plots.

Figure 2 considers the variation in DM abundance as a function of $b_{\chi }$ and $T_R$. In all cases, κ = 10 is considered. As far as the particle physics input is concerned, the values of 100 GeV and 10^–2 have been considered for, respectively, DM mass and coupling. These parameter assignations comply with the constraints from DD and invisible Higgs decay. The left panel of Figure 2 considers a fixed value of the reheating temperature, namely, 1 GeV, and different values of b_χ. The DM abundance is very weakly dependent on the latter parameter for values above 0.01. This is because the latter is generated in the re-annihilation regime. Indeed, when the abundance of the non-thermally produced DM exceeds $n_{\chi }^c$ (or, equivalently, $Y_{\chi }^c$), it is described as the quasi-statical equilibrium (QSE) [50] number density:

$n_{\chi }^{\text{QSE}}={\left(\frac{b_{\chi }{\mathrm{\Gamma }}_{\varphi }{\rho }_{\varphi }}{m_{\chi }⟨\sigma v⟩}\right)}^{1/2},$

until the latter drops below $n_{\chi }^c$ and gets frozen. By further decreasing the value of $b_{\chi }$, the amount of non-thermally produced DM is not sufficient to reactivate annihilation processes; hence, we have $Y_{\chi }$ ∝ $b_{\chi }$. Moving to the right panel of Figure 2, we see that $T_R$ < 1 GeV increases as $T_R$ decreases, while such a trend is reversed for $T_R$ < 100 GeV. In agreement with the discussion of [19], this is due to the transition from the re-annihilation regime, corresponding to ${\mathrm{\Omega }}_{\chi }\propto T_R^{-1}$, occurring at a high reheating temperature, to the regime in which annihilations are not active, corresponding to Ω_χ ∝ T_R.

In Figure 3, we have considered the impact of a variation in the DM coupling λ_χ. Again, Figure 3 show the evolution of Y_χ with DM mass. The values T_R = 1 GeV and $b_{\chi }$ = 0.01 have been considered. For values of ${\lambda }_{\chi }$ > 10^–5, the DM is in thermal equilibrium in the first stages of the evolution of the Universe. For a value of $x\gtrsim 10$, $Y_{\chi }$ starts deviating from the equilibrium value and the two competing effects become relevant: the dilution by the entropy injection due to the late decay of Φ and the non-thermal production process. The final DM abundance is inversely proportional to coupling ${\lambda }_{\chi }$ as the solution tracks the re-annihilation regime. For ${\lambda }_{\chi }$ < 10^–5, the DM is initially produced via freeze-in. Such abundance is diluted away by the decay of the Φ field and replaced by a non-thermal population of DM without re-annihilation as the DM interaction rate is too suppressed. This explains the fact that the DM abundance is independent of the value of ${\lambda }_{\chi }$.

We conclude our analysis with a few remarks about the detection prospects of the scenarios discussed in this paper. On general grounds, distinguishing non-standard cosmological scenarios only via earth-scale experiments, such as the ones based on direct/indirect detection and collider searches, is complicated as they can reconstruct DM particle properties, like the size of the interactions with SM states, while being affected to a negligible extent by the cosmological ones. It is nevertheless evident that, in the presence of a non-standard cosmological history, the parameter space, corresponding to the correct relic density, can vary substantially with respect to the case of thermal freeze-out. Consequently, a hypothetical future signal, for example, at a current or next-generation direct detection facility, possibly incompatible with the expectations of the conventional freeze-out paradigm, would represent a very useful indication (refer to [6] for similar ideas). A conclusive statement would nevertheless require a complementary signal from a probe of pre-BBN cosmology. In this context, gravitational wave (GW) detectors capable of probing the primordial GW background can make a difference [51, 52]. As a final remark, we mention that scenarios of non-thermal production of DM, such as the one discussed in Section 4, in the re-annihilation regime, have already been effectively probed. Indeed, indirect detection experiments (refer to [53, 54]) and CMB probes ([1, 55]) are already sensitive to DM annihilation cross sections of the order of the thermally favored one. Consequently, scenarios of non-thermal production in the reannihilation regime, which reproduce the correct relic density for the annihilation cross section greater than the thermal one, might be strongly constrained or ruled out. Notice anyway that this statement is strictly valid for models with the s-wave-dominated annihilation cross section, i.e., the case in which the value of ⟨σv⟩ at freeze-out and CMB/present times substantially coincides. Finally, structure formation could also provide insights about non-thermal production scenarios as DM properties at that time could deviate from the conventional cold dark matter paradigm, leaving an imprint that could be traced by Lyman-α [56].

5 Conclusion

Thermal freeze-out is a very popular framework, leading to predictive models that are testable via a broad variety of complementary experimental search strategies. It relies, however, on the assumption of standard cosmological history during DM production. There are no a priori reasons to enforce such an assumption. We have provided a brief review of the scenario of thermal and non-thermal production of DM in a non-standard cosmological history, represented by an exotic component, possibly dominating the energy budget of the Universe during DM production and prior to BBN. Although the result might be illustrated in a very general perspective, we have found it convenient to identify a reference model corresponding to the Higgs portal with scalar DM. Assuming only the thermal production of DM, the non-standard cosmological evolution enlarges the parameter spaces complying with constraints from DD and invisible Higgs decays. In the second part of this review, we have focused on non-thermal production, focusing on the case in which the Universe encounters an early matter domination epoch. We have illustrated the relevant Boltzmann’s equations and discussed both numerical and analytical approximations of the solutions.

Author contributions

GA: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The system of Boltzmann’s equations can actually be written in the considered form if the following assumptions hold: i) DM self-interactions influence to a negligible extent its number density (they should ensure anyway thermalization of the DM particle with themselves). Such an assumption can be easily satisfied by a suitable assignation of λ_s. ii) The DM is, during its whole production process, at least in kinetic equilibrium with the primordial plasma.

²The phenomenology would be totally analogous in the case of complex scalar DM.

³Assuming that an initial DM population was produced during inflation, the correct relic density would also be achieved for λ_χ = 0 [32].

References

1. Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. VI. Cosmological parameters. Astron Astrophys (2020) 641:A6. [Erratum: Astron.Astrophys. 652, C4 (2021)]. doi:10.1051/0004-6361/201833910

CrossRef Full Text | Google Scholar

2. Arcadi G, Dutra M, Ghosh P, Lindner M, Mambrini Y, Pierre M, et al. The waning of the WIMP? A review of models, searches, and constraints. Eur Phys J C (2018) 78:203. doi:10.1140/epjc/s10052-018-5662-y

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Arcadi G, Cabo-Almeida D, Dutra M, Ghosh P, Lindner M, Mambrini Y, et al. The waning of the WIMP: endgame? (2024). arXiv:2403.15860.

Google Scholar

4. Hall LJ, Jedamzik K, March-Russell J, West SM. Freeze-in production of FIMP dark matter. JHEP (2010) 03:080. doi:10.1007/JHEP03(2010)080

CrossRef Full Text | Google Scholar

5. Kane GL, Kumar P, Nelson BD, Zheng B. Dark matter production mechanisms with a nonthermal cosmological history: a classification. Phys Rev D (2016) 93:063527. doi:10.1103/PhysRevD.93.063527

CrossRef Full Text | Google Scholar

6. Arias P, Bernal N, Herrera A, Maldonado C. Reconstructing non-standard cosmologies with dark matter. JCAP (2019) 10:047. doi:10.1088/1475-7516/2019/10/047

CrossRef Full Text | Google Scholar

7. Barrow JD. MASSIVE PARTICLES AS A PROBE OF THE EARLY UNIVERSE. Nucl Phys B (1982) 208:501–8. doi:10.1016/0550-3213(82)90233-4

CrossRef Full Text | Google Scholar

8. Ford LH. Gravitational particle creation and inflation. Phys Rev D (1987) 35:2955–60. doi:10.1103/PhysRevD.35.2955

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Visinelli L (Non-)thermal production of WIMPs during kination. Symmetry (2018) 10:546. doi:10.3390/sym10110546

CrossRef Full Text | Google Scholar

10. Salati P. Quintessence and the relic density of neutralinos. Phys Lett B (2003) 571:121–31. doi:10.1016/j.physletb.2003.07.073

CrossRef Full Text | Google Scholar

11. Profumo S, Ullio P. SUSY dark matter and quintessence. JCAP (2003) 11:006. doi:10.1088/1475-7516/2003/11/006

CrossRef Full Text | Google Scholar

12. Choi K String or M theory axion as a quintessence. Phys Rev D (2000) 62:043509. doi:10.1103/PhysRevD.62.043509

CrossRef Full Text | Google Scholar

13. Di Marco A, Pradisi G, Cabella P. Inflationary scale, reheating scale, and pre-BBN cosmology with scalar fields. Phys Rev D (2018) 98:123511. doi:10.1103/PhysRevD.98.123511

CrossRef Full Text | Google Scholar

14. Okada N, Seto O. Relic density of dark matter in brane world cosmology. Phys Rev D (2004) 70:083531. doi:10.1103/PhysRevD.70.083531

CrossRef Full Text | Google Scholar

15. Catena R, Fornengo N, Masiero A, Pietroni M, Rosati F. Dark matter relic abundance and scalar - tensor dark energy. Phys Rev D (2004) 70:063519. doi:10.1103/PhysRevD.70.063519

CrossRef Full Text | Google Scholar

16. Meehan MT, Whittingham IB. Dark matter relic density in Gauss-Bonnet braneworld cosmology. JCAP (2014) 12:034. doi:10.1088/1475-7516/2014/12/034

CrossRef Full Text | Google Scholar

17. Allahverdi R, et al. The first three seconds: a review of possible expansion histories of the early Universe (2020). doi:10.21105/astro.2006.16182

CrossRef Full Text | Google Scholar

18. Giudice GF, Kolb EW, Riotto A. Largest temperature of the radiation era and its cosmological implications. Phys Rev D (2001) 64:023508. doi:10.1103/PhysRevD.64.023508

CrossRef Full Text | Google Scholar

19. Gelmini G, Gondolo P, Soldatenko A, Yaguna CE. Effect of a late decaying scalar on the neutralino relic density. Phys Rev D (2006) 74:083514. doi:10.1103/PhysRevD.74.083514

CrossRef Full Text | Google Scholar

20. Gelmini GB, Gondolo P. Neutralino with the right cold dark matter abundance in (almost) any supersymmetric model. Phys Rev D (2006) 74:023510. doi:10.1103/PhysRevD.74.023510

CrossRef Full Text | Google Scholar

21. Arcadi G, Ullio P. Accurate estimate of the relic density and the kinetic decoupling in non-thermal dark matter models. Phys Rev D (2011) 84:043520. doi:10.1103/PhysRevD.84.043520

CrossRef Full Text | Google Scholar

22. Gondolo P, Gelmini G. Cosmic abundances of stable particles: improved analysis. Nucl Phys B (1991) 360:145–79. doi:10.1016/0550-3213(91)90438-4

CrossRef Full Text | Google Scholar

23. Belanger G, Boudjema F, Pukhov A, Semenov A. MicrOMEGAs 2.0: a Program to calculate the relic density of dark matter in a generic model. Comput Phys Commun (2007) 176:367–82. doi:10.1016/j.cpc.2006.11.008

CrossRef Full Text | Google Scholar

24. Belanger G, Boudjema F, Pukhov A, Semenov A. Dark matter direct detection rate in a generic model with micrOMEGAs 2.2. Comput Phys Commun (2009) 180:747–67. doi:10.1016/j.cpc.2008.11.019

CrossRef Full Text | Google Scholar

25. Gondolo P, Edsjo J, Ullio P, Bergstrom L, Schelke M, Baltz EA. DarkSUSY: computing supersymmetric dark matter properties numerically. JCAP (2004) 0407:008. doi:10.2172/827305

CrossRef Full Text | Google Scholar

26. Bringmann T, Edsjö J, Gondolo P, Ullio P, Bergström L. DarkSUSY 6: an advanced tool to compute dark matter properties numerically. JCAP (2018) 07:033. doi:10.1088/1475-7516/2018/07/033

CrossRef Full Text | Google Scholar

27. Kawasaki M, Kohri K, Sugiyama N. MeV-scale reheating temperature and thermalization of the neutrino background. Phys Rev D (2000) 62:023506. doi:10.1103/PhysRevD.62.023506

CrossRef Full Text | Google Scholar

28. Hannestad S. What is the lowest possible reheating temperature? Phys Rev D (2004) 70:043506. doi:10.1103/PhysRevD.70.043506

CrossRef Full Text | Google Scholar

29. Ichikawa K, Kawasaki M, Takahashi F. Oscillation effects on thermalization of the neutrinos in the universe with low reheating temperature. Phys Rev D (2005) 72:043522. doi:10.1103/PhysRevD.72.043522

CrossRef Full Text | Google Scholar

30. De Bernardis F, Pagano L, Melchiorri A. New constraints on the reheating temperature of the universe after WMAP-5. Astropart Phys (2008) 30:192–5. doi:10.1016/j.astropartphys.2008.09.005

CrossRef Full Text | Google Scholar

31. Arcadi G, Djouadi A, Raidal M. Dark matter through the Higgs portal. Phys Rept (2020) 842:1–180. doi:10.1016/j.physrep.2019.11.003

CrossRef Full Text | Google Scholar

32. Arcadi G, Lebedev O, Pokorski S, Toma T. Real scalar dark matter: relativistic treatment. JHEP (2019) 08:050. doi:10.1007/JHEP08(2019)050

CrossRef Full Text | Google Scholar

33. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro F, et al. Light dark matter search with ionization signals in XENON1T. Phys Rev Lett (2019) 123:251801. doi:10.1103/PhysRevLett.123.251801

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Aalbers J, Akerib D, Akerlof C, Al Musalhi A, Alder F, Alqahtani A, et al. First dark matter search results from the LUX-ZEPLIN (LZ) experiment. Phys Rev Lett (2023) 131:041002. doi:10.1103/PhysRevLett.131.041002

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Aad G, Abbott B, Abeling K, Abidi S, Aboulhorma A, Abramowicz H, et al. Combination of searches for invisible decays of the Higgs boson using 139 fb−1 of proton-proton collision data at s=13 TeV collected with the ATLAS experiment. Phys Lett B (2023) 842:137963. doi:10.1016/j.physletb.2023.137963

CrossRef Full Text | Google Scholar

36. Cepeda M, et al. Report from working group 2: Higgs physics at the HL-LHC and HE-LHC. CERN Yellow Rep Monogr (2019) 7:221–584. doi:10.23731/CYRM-2019-007.221

CrossRef Full Text | Google Scholar

37. de Blas J, Cepeda M, D’Hondt J, Ellis R, Grojean C, Heinemann B, et al. Higgs boson studies at future particle colliders. JHEP (2020) 01:139. doi:10.1007/JHEP01(2020)139

CrossRef Full Text | Google Scholar

38. Moroi T, Randall L. Wino cold dark matter from anomaly mediated SUSY breaking. Nucl Phys B (2000) 570:455–72. doi:10.1016/S0550-3213(99)00748-8

CrossRef Full Text | Google Scholar

39. Allahverdi R, Dutta B, Mohapatra RN, Sinha K. Supersymmetric model for dark matter and baryogenesis motivated by the recent CDMS result. Phys Rev Lett (2013) 111:051302. doi:10.1103/PhysRevLett.111.051302

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Acharya BS, Kumar P, Bobkov K, Kane G, Shao J, Watson S. Non-thermal dark matter and the moduli problem in string frameworks. JHEP (2008) 06:064. doi:10.1088/1126-6708/2008/06/064

CrossRef Full Text | Google Scholar

41. Acharya BS, Kane G, Watson S, Kumar P. Nonthermal “WIMP miracle”. Phys Rev D (2009) 80:083529. doi:10.1103/PhysRevD.80.083529

CrossRef Full Text | Google Scholar

42. Moroi T, Nagai M, Takimoto M. Non-thermal production of wino dark matter via the decay of long-lived particles. JHEP (2013) 07:066. doi:10.1007/JHEP07(2013)066

CrossRef Full Text | Google Scholar

43. Aparicio L, Cicoli M, Dutta B, Muia F, Quevedo F. Light higgsino dark matter from non-thermal cosmology. JHEP (2016) 11:038. doi:10.1007/JHEP11(2016)038

CrossRef Full Text | Google Scholar

44. Chowdhury D, Dudas E, Dutra M, Mambrini Y. Moduli portal dark matter. Phys Rev D (2019) 99:095028. doi:10.1103/PhysRevD.99.095028

CrossRef Full Text | Google Scholar

45. Riajul Haque M, Kpatcha E, Maity D, Mambrini Y. Primordial black hole reheating. Phys Rev D (2023) 108:063523. doi:10.1103/PhysRevD.108.063523

CrossRef Full Text | Google Scholar

46. Hardy E. Higgs portal dark matter in non-standard cosmological histories. JHEP (2018) 06:043. doi:10.1007/JHEP06(2018)043

CrossRef Full Text | Google Scholar

47. Pallis C. Massive particle decay and cold dark matter abundance. Astropart Phys (2004) 21:689–702. doi:10.1016/j.astropartphys.2004.05.006

CrossRef Full Text | Google Scholar

48. Drees M, Hajkarim F. Dark matter production in an early matter dominated era. JCAP (2018) 02:057. doi:10.1088/1475-7516/2018/02/057

CrossRef Full Text | Google Scholar

49. Drees M, Hajkarim F. Neutralino dark matter in scenarios with early matter domination. JHEP (2018) 12:042. doi:10.1007/JHEP12(2018)042

CrossRef Full Text | Google Scholar

50. Cheung C, Elor G, Hall LJ, Kumar P. Origins of hidden sector dark matter I: cosmology. JHEP (2011) 03:042. doi:10.1007/JHEP03(2011)042

CrossRef Full Text | Google Scholar

51. Figueroa DG, Tanin EH. Ability of LIGO and LISA to probe the equation of state of the early Universe. JCAP (2019) 08:011. doi:10.1088/1475-7516/2019/08/011

CrossRef Full Text | Google Scholar

52. Liu L, Chen ZC, Huang QG. Probing the equation of state of the early Universe with pulsar timing arrays. JCAP (2023) 11:071. doi:10.1088/1475-7516/2023/11/071

CrossRef Full Text | Google Scholar

53. Charles E, Sánchez-Conde M, Anderson B, Caputo R, Cuoco A, Di Mauro M, et al. Sensitivity projections for dark matter searches with the fermi large area telescope. Phys Rept (2016) 636:1–46. doi:10.1016/j.physrep.2016.05.001

CrossRef Full Text | Google Scholar

54. McDaniel A, Ajello M, Karwin CM, Di Mauro M, Drlica-Wagner A, Sánchez-Conde MA. Legacy analysis of dark matter annihilation from the Milky Way dwarf spheroidal galaxies with 14 years of Fermi-LAT data. Phys Rev D (2024) 109:063024. doi:10.1103/PhysRevD.109.063024

CrossRef Full Text | Google Scholar

55. Galli S, Iocco F, Bertone G, Melchiorri A. CMB constraints on Dark Matter models with large annihilation cross-section. Phys Rev D (2009) 80:023505. doi:10.1103/PhysRevD.80.023505

CrossRef Full Text | Google Scholar

56. Ballesteros G, Garcia MAG, Pierre M. How warm are non-thermal relics? Lyman-α bounds on out-of-equilibrium dark matter. JCAP (2021) 03:101. doi:10.1088/1475-7516/2021/03/101

CrossRef Full Text | Google Scholar