Fibre bundle models as a framework for the detachment dynamics of soft probabilistic fasteners

Adhesives can be made by patterning surfaces with discrete adhesive elements. Nature uses this approach to provide animals with highly adaptive and robust approaches towards gaining an effective grip on surfaces. The mechanism of patterned surface adhesion involve many different attachment principles, adhesive site interactions, and probabilistic effects, the interplay of which is not understood. This limits our ability to design patterned surface adhesives for engineering applications. In this work, we quantify how a mechanically patterned adhesive based on passive mushroom-shaped elements performs. We explore a range of surface design features and model the mechanical adhesion dynamics with an approach based on the fiber bundle model (FBM). We find that the fiber bundle model can be used to rationalize the observations after modifying it to capture the initial non-linear force response of the adhesives. Additionally, we investigate the behavior of the system’s elastic energy and damage energy, as it is stretched under strain-controlled conditions. Our experimental data indicates that the elastic energy has a maximum that appears after the macroscopic strength $({\sigma }_{\text{c}})$, corresponding to strains where a full rupture of the system can no longer be prevented. Moreover, we observed that below the maximum of the constitutive curve ${\sigma }_{\text{c}}$, the elastic energy consistently exceeds the damage energy. Finally, we found that the derivative of the elastic energy has a maximum, which always appears before ${\sigma }_{\text{c}}$. Therefore, the derivative of the elastic energy would serve as a reliable signal of upcoming catastrophic failure in experiments under stress-controlled conditions.

1 Introduction

Putting two seemingly flat surfaces together does not make a new solid. This proposition is a potentially perplexing observation from the field of interface mechanics, a study of an everyday phenomenon that is surprisingly poorly understood. Two interfaces can be made to adhere via a number of mechanisms, among which the use of discrete adhesive sites. Such attachment styles often use mechanical interlocking of three-dimensional (3D) protruded features and are prevalent in Nature [1]. Inspired by such attachment systems, smart surfaces consisting of micron-millimetric sized attachment features are being developed for many applications, such as climbing robots [2] and grippers [3]. The invention of Velcro^® was originally inspired by burdock seeds [4], and the related “3M dual lock” system [5] has been successfully applied in textile industry and the medical field.

The discrete nature of these adhesive sites and the continuous detachment dynamics that they can generate inspire us to understand the statistical mechanics of attachment and detachment of discrete probabilistic fasteners. Here we analyze a combination of older data [6] and new measurements with precisely such statistical modeling, coming from Fiber Bundle Models (FBM) [7–9].

The surface that we use is described in detail elsewhere [6]. Briefly, we studied a soft surface with soft micrometric mushroom-shaped features, providing mechanical interlocking while leaving no visible damage on attachment features or the surface it attaches to. The pattern of adhesive sites consists of cubic arrays of cylindrical “stems” with hemispherical “caps” which we will refer to as “mushrooms”. We 3D-printed the original “positive” mould and obtain an inverted “negative” version in silicon rubber, which is coated with a perfluorosilane after peeling from the positive mold. A final casting delivers an image, which is peeled from the elastomeric mold. The mushroom arrays deliver robust adhesion to textile, with a significant benefit over high-modulus (MPa-range) Velcro-type attachment systems: the far softer elastomeric system detaches from textile before damage occurs to either part. Thus, the combination of 3D printing and elastomer synthesis offers new approaches to address gaps in the property space of adhesives. However, the difficulty of relating stress to strain inherent to the non-linear mechanics in soft adhesive failure [10] results in a lack of analytical routines to characterize and compare various soft adhesive systems. We, therefore, turn to modeling to understand the adhesive performance of these substrates.

1.1 Fiber bundle models (FBM)

Fiber Bundle Models are fundamental classes of approaches to the fracture problem [7–9]. Despite their simple nature, FBMs exhibit the most essential aspects of material breakdown. In a literal interpretation, they model specimens loaded parallel to the fiber direction and describe the damage evolution after one or several fibers fail. For simplicity, each fiber has the same Young’s modulus $\kappa$. They break if the load acting on them exceeds their threshold value, which is an independent random variable sampled from a distribution $p(\epsilon )$ and cumulative distribution $P(\epsilon )={\int }_0^{\epsilon }p(x)dx$. Once the fibers fail, one can choose among several load transfer rules, usually called load-sharing types. Two limiting types of load sharing correspond to the extreme limits of stress redistribution. In the global load sharing (GLS) approach, the load of a failed fiber is equally redistributed among the active fibers remaining in the system. On the other hand, in local load sharing (LLS), the load of a failed fiber is redistributed among the nearest neighbors’ intact fibers. Moreover, some variable range of interaction models have been developed [11, 12]. The bundle may be stretched either under stress or strain control.

When a collection of $N$ elastic fibers are stretched between two rigid supports, as in a strain-controlled experiment up to stress $\epsilon$, we can relate the work required $E_{\text{T}}$ to the fiber failure distribution $p(\epsilon )$. Following [13], we write,

$E_{\text{T}}\left(\epsilon \right)=E_{\text{e}}\left(\epsilon \right)+E_{\text{d}}\left(\epsilon \right)(1)$

$E_{\text{T}}\left(\epsilon \right)=\left(1-P\left(\epsilon \right)\right)\frac{\kappa {\epsilon }^2}{2}+\frac{\kappa }{2}{\int }_0^{\epsilon }{x}^{2}p\left(x\right)\mathrm{d}x(2)$

The first term in Eqs 1, 2 denotes the elastic (or potential) energy $E_{\text{e}}$ accumulated by the surviving $N(1-P(\epsilon ))$ elements, and the second the sum of all dissipated elastic energy due to $Np(\epsilon )$ broken fibers, denoted $E_{\text{d}}$.

Similarly, the constitutive law that relates the stress $\sigma (\epsilon )$ to the applied strain $\epsilon$ is

$\sigma \left(\epsilon \right)=\left(1-P\left(\epsilon \right)\right)\kappa \epsilon .(3)$

The maximum of the constitutive curve ${\epsilon }_{\text{c}}$, ${\sigma }_{\text{c}}$ indicates the system’s stress ${\sigma }_{\text{c}}$ at its corresponding critical deformation ${\epsilon }_{\text{c}}$. It can be obtained from the maximization of Eq. 3,

$\frac{d\sigma \left(\epsilon \right)}{d\epsilon }=1-P\left(\epsilon \right)-\epsilon \frac{dP\left(\epsilon \right)}{d\epsilon }=0.(4)$

In particular, for a Weibull cumulative distribution $P(\epsilon )=1-\exp \left[-{\left(\frac{\kappa \epsilon }{{\sigma }_0}\right)}^{\rho }\right]$, where ${\sigma }_0$ is a stress parameter that dictates the onset of fracture, the maximum of Eq. 4 lies at ${\epsilon }_{\text{c}}=({\sigma }_o/\kappa ){\rho }^{1/\rho }$ and ${\sigma }_{\text{c}}={\sigma }_0{(\rho e)}^{1/\rho }$. Figure 1 shows the constitutive curves Eq. 3, the elastic energy $E_{\text{e}}$ and its $\mathrm{d}{E}_{\text{e}}/\mathrm{d}\epsilon$ as function of the deformation $\epsilon$, for a Weibull cumulative distribution with $\rho =1$ and ${\sigma }_0=1\frac{\mathrm{N}}{{\mathrm{m}}^2}$. In this work, we apply and extend the FBM’s theoretical framework to examine the statistical detachment process of adhesive surfaces composed of soft micrometre-scale mushroom-shaped features.

Figure 1

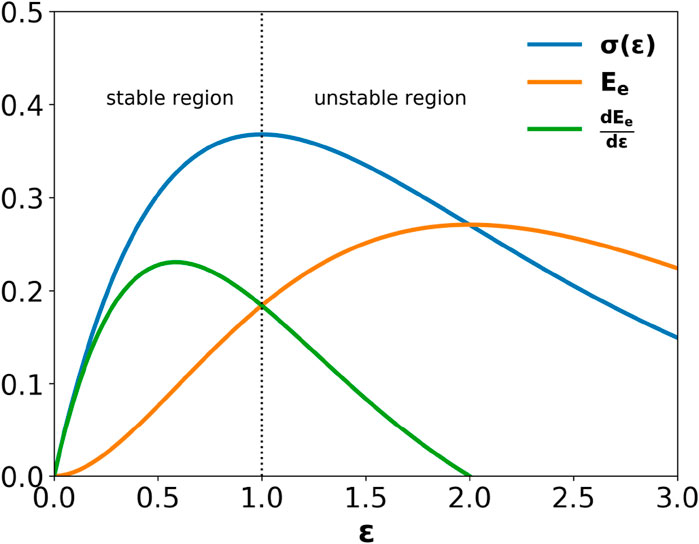
Figure 1. As a bundle of linearly elastic fibers is stretched, the system first accumulates elastic energy $E_{\text{e}}$ at the rate of $N$ times $\kappa$, the per-bond modulus. As bonds start failing, this accumulation slows down. Eventually, $E_{\text{e}}$ peaks and then decreases as more and more bonds fail. Here, we give the stress, elastic energies, and the derivative of the elastic energy as a function of the strain for a fiber bundle model with a Weibull distribution of thresholds and bond failure threshold distribution parameter $\rho =1$.

2 Experimental methods

The experiments have been described in detail elsewhere [6]. Briefly, we studied the adhesive interactions of mushroom-studded surfaces made from poly (dimethyl siloxane) (silicone rubber) with a nylon fabric with the help of a rheometer (Figure 2). A schematic of the mushroom-studded surfaces is given in Figure 3, including the relevant dimensions. In particular, we determined the cross-section of the mushrooms by image analysis with ImageJ, which amounted to $A_{\text{e}}=152\mu {\mathrm{m}}^2$.

Figure 2

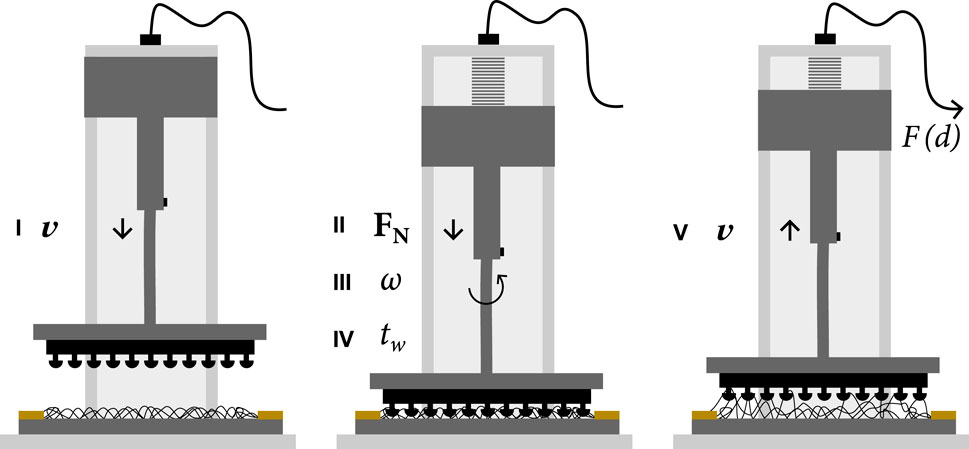
Figure 2. Illustrated rheometry protocol for characterization of the adhesive interaction between nylon fabric and our adhesive devices: i) Approach at constant $v$ until ii) pre-set normal force ${\mathbf{F}}_{\mathbf{n}}$, followed by iii) oscillation at angular frequency $\omega$ and iv) relaxation for $t_{\text{w}}$. Finally, v) the probe holding the adhesive device is retracted with constant $v$ while the normal force $F$ is recorded as function of the gap size $d$.

Figure 3

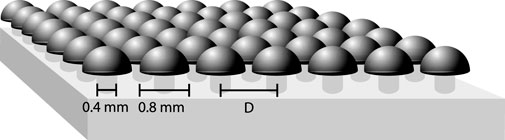
Figure 3. Drawing of a mushroom-covered silicone adhesive surface. The stem and cap diameter are labeled in the figure and identical for all surfaces in the study. We made surfaces with 114, 361 and 441 features by varying the inter-mushroom distance $D$, respectively, 2.3, 1.3, and 1.1 mm. All surfaces measured 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$.

Fabric samples were obtained from a pantyhose using scissors. First, a fabric sample was attached to the base plate of the rheometer by applying scotch tape over its four sides. The silicone mushroom devices were attached to a glass plate using plasma bonding. For testing, we used a five-step protocol, also illustrated in Figure 2: i) mushroom-studded surfaces were pressed onto a fabric up to a given normal force ${\mathbf{F}}_{\mathbf{n}}$ and a constant approach rate of $v=500\mu \mathrm{m}{\mathrm{s}}^{-1}$, ii) the system was allowed to relax for 10 s, iii) the probe to which the mushrooms are attached was rotationally oscillated with $\theta =10$° for 50 cycles, iv) 10 s relaxation, and, (v) the probe was retracted under strain control conditions at a rate equal to that of the approach. While pulling off the adhered surface, the fabric was monitored from below to record the number $N_0$ of mushroom features that had penetrated the surface. We recorded force-distance curves until full detachment of surface to fabric.

3 Results and discussion

3.1 Macroscopic constitutive response: strain hardening

Figure 4 gives the force-strain curves obtained for systems with systematic variations of feature densities and preload intensities ${\mathbf{F}}_{\mathbf{n}}$. The reproducibility of the experimental procedure enable us to use the average of four experimental realizations. The flexibility of the backing layer and variation in feature densities preclude an analysis in terms of global load sharing with strain identical to a stretch value valid across the fibre bundle and between experiments at different feature densities. To avoid introducing a free parameter, we opt to define the strain values based on the experimental conditions, as $\epsilon =l/l_0$. $l$ is the gap size, and we introduce the characteristic length $l_0=10\mathrm{m}\mathrm{m}$ using $l_0=v\times t_{\text{max}}$, with $v$ the retraction velocity and $t_{\text{max}}=$ 20 s, the typical timescale of the experiment. Indeed, the three panels of Figure 4 show that the fabric-device attachments fail around unity, $0.9<\epsilon <1.2$.

Figure 4

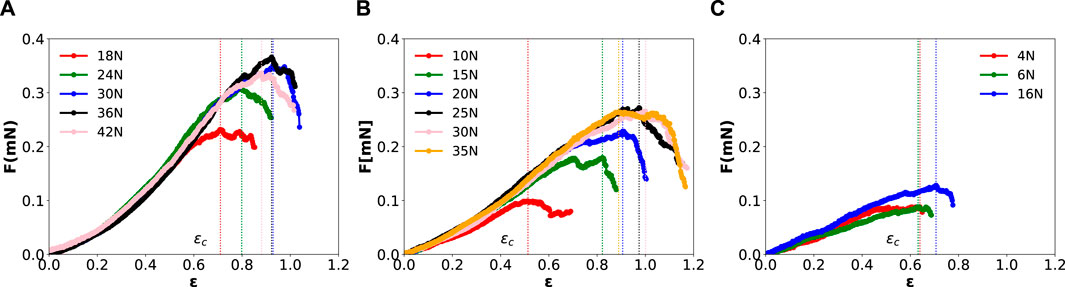
Figure 4. Raw force-distance curves of mushroom-patterned silicone rubber adhesive pads detaching from a textile substrate consisting of nylon fibers. Each of the panels gives data corresponding to devices having (A) 441, (B) 361, and (C) 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$. Keeping the density constant, we provide data for a systematic variation of preload intensity ${\mathbf{F}}_{\mathbf{n}}$.

All the macroscopic constitutive responses in Figure 4 display the two regimes introduced in Ref. [13]. One stable regime for $0\le \epsilon \le {\epsilon }_{\text{c}}$, and an unstable regime, for $\epsilon >{\epsilon }_{\text{c}}$ (see also Figure 1), which lies after the stress peak. At the end of the process, the macroscopic stiffness decreases discontinuously before complete detachment from the elastic fabric substrate occurs. The observability of the unstable regime is in line with the choice of strain-controlled retraction: the detachment process runs continuously, the stress reaches a maximum value ${\sigma }_{\text{c}}$ at ${\epsilon }_{\text{c}}$, and the full detachment of surface to fabric occurs at strain values notably greater than ${\epsilon }_{\text{c}}$. In our experiment, we attribute the macroscopic stiffness changes solely to detachment of fabric-mushroom bonds, rather than to fracture of features or in the fabric, given its reproducibility over five cycles.

Interestingly, for our experimental data, Eq. 3 does not adequately capture the behaviour in the stable regime. Non-linearity in the macroscopic response is apparent in the raw force-strain curves presented in Figure 4. The earlier stage of the curves indicates that the stretching of the textile fibers against our mushroom arrays does not follow a linear force-strain relationship that is characterized by a per mushroom elastic modulus $\kappa$. Instead, the macroscopic stiffness gradually increases, denoting the absence of internal damage (detaching). Only for very low preload intensities and feature densities (see Figure 4C), a single slope characterizes the constitutive curves in the earlier stage.

In all cases, the maximum force indicates the system strength ${\sigma }_{\text{c}}$ and the corresponding stretch value ${\epsilon }_{\text{c}}$, highlighted with vertical lines in the panels of Figure 4. The values ${\epsilon }_{\text{c}}$ are the critical stretch beyond which the system would collapse under an analogous stress-controlled experiment. In our previous work [6] we have observed that ${\sigma }_{\text{c}}$ saturates with increasing ${\mathbf{F}}_{\mathbf{N}}$, which we interpreted as a saturation of the available surface “adhooking” of the features on the fabric. Beyond ${\sigma }_{\text{c}}$, features start to unhook from the fabric. Importantly, the mushrooms do not break; a surface is reusable and this also means that there is only one typical “unhooking” stress scale.

FBMs have been used to rationalise the random damage evolution of fracturing systems, even beyond disordered solids [14–19]. However, the non-linearity of the initial loading regime represents a fundamental challenge to the validity of fiber bundle models, which attempt to capture the microscopic features of the feature-fabric interaction. In a basic form, such a model would feature a linear loading regime $\sigma =\kappa \epsilon$, followed by a failure regime, governed by the survival probability $(1-P(\epsilon ))$ of features at strain $\epsilon$. Our curves disobey linearity at low $\epsilon$, and therefore we propose to use a modified non-linear FBM.[20].

Interestingly, the fabric-mushroom stretching seems to impose a power law on the force-strain curves. Following the theoretical and experimental results [21–24] on other (crosslinked) fibrous networks as present in the fabric, we propose a stress-distance curve, using a strain-hardening ansatz $\sigma \sim E{\epsilon }^{\alpha }$ followed by a probabilistic decay factor:

$\sigma \left(\epsilon \right)=\left(1-P\left(\epsilon \right)\right)A{\epsilon }^{\alpha },(5)$

with $\sigma (\epsilon )$ the stress acting on the surviving $(1-P(\epsilon ))$ element fraction. We also introduce a modified Weibull failure distribution which reads $P(\epsilon )=1-\exp \left[-{\left(\frac{A{\epsilon }^{\alpha }}{{\sigma }_0}\right)}^{\rho }\right]$, Eq. 5 and gives the following strain-stiffening constitutive equation:

$\sigma \left(\epsilon \right)=A{\epsilon }^{\alpha }\exp \left[-{\left(\frac{A{\epsilon }^{\alpha }}{{\sigma }_0}\right)}^{\rho }\right],(6)$

where $A$ is a non-linear stiffness coefficient, $\alpha$ the strain stiffening exponent at low $\epsilon$, ${\sigma }_0$ a stress coefficient that positions the onset of element failure, and $\rho$ the Weibull exponent, which is related to the width of the failure probability distribution.

Subsequently, we fit all curves in Figure 4 to equation Eq. 6. Good fits to the data were accomplished with least squares optimization. We used the powers and pre-factors from Figure 5 to initialize the fits, and ${\sigma }_0$ and $\rho$ were initialized with linear regression on one representative curve using a linearised version of Eq. 6 with $\alpha =1$ (Figure A1 in the Appendix includes the fits).

Figure 5

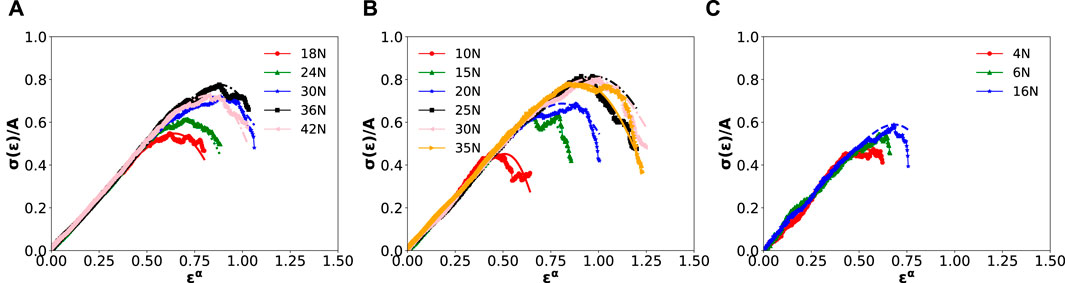
Figure 5. Scaled stress-distance curves $\sigma /A=F/(N_0{A}_{\text{e}}A)$ (-), where $N_0$ is the initial number of connected mushrooms and $A_{\text{e}}$ is the cross-section of a mushroom neck, and $A$ is the non-linear stiffness (see Figure 6; Eq. 5). The panels present processed force-distance data from detachment of nylon fabric against devices numbering (A) 441, (B) 361 and (C) 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$, respectively. Data are colour-coded for the preload intensity after which they were recorded, as listed in the legends.

Figure 5 illustrates the validity of the used strain-hardening ansatz, showing good fits for all strain-stress curves for specimens with 441, 361, and 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$, respectively, and a range of preload intensities. A summary of the fitting parameters $\alpha$, $\rho$, and $A$ are included in Figure 6. In each case, the interlocking characteristic strength ${\sigma }_0$ of the individual features, was analytically obtained in terms of the macroscopic strength ${\sigma }_c$, i.e., ${\sigma }_0={\sigma }_{\text{c}}{\left(\rho e\right)}^{1/\rho }$. The Appendix includes details of the fitting executed in each case.

Figure 6

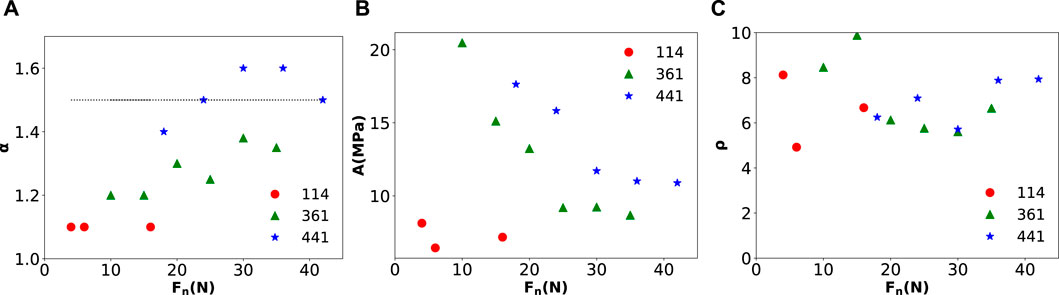
Figure 6. Resulting fitting parameters as a function of the preload intensity ${\mathbf{F}}_{\mathbf{n}}$, in (A) strain hardening $\alpha$ in (B) non-linear stiffness $A$ and (C) the Weibull exponent $\rho$. Details of the self-consistent Weibull fitting appears in the Appendix. Each of the panel includes data corresponding to 441, 361 and 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$.

A surprising result of the present analysis is that the power law exponent $\alpha$ varies between 1 and $\frac{3}{2}$, as seen in Figure 6. We analyze the emergence of a power law with strength $\frac{3}{2}$ as strain hardening caused by the presence of entanglements between the fibers in the cloth substrate (“crosslinks”). Presumably, stretching of the fibers causes a concomitant tensing-up at the intersection points, resulting in a progressively stiffening of the fiber network as more strain is applied. The dependence of the power on preload can be seen as the presence of a critical active fiber density beneath which intersections do not form. At low densities, we simply measure the (linear, at all low strains) elasticity of the nylon strands. We note that strain hardening should originate in the fabric itself [25] and is more likely as more mushrooms are activated. Finally, we note that strain hardening with a power law of strength $\frac{3}{2}$ is a common feature seen on a completely different length scale, in cross-linked polymer networks of semi-flexible polymers [23]. It is worth mentioning, that the existence of the initial non-linear response does not allow to quantify the effective element stiffness of a single element for comparing to the Young modulus of PDMS, which is about 1.8 MPa. However, the non-linear stiffness $A$ plays a similar role, and we obtain values of $A$ in the order of $6.4-20$ MPa as visible in Figure 6B, in terms of the characteristic length $l_0=10$ mm. Surprisingly, for samples with high density of features the parameter $A$ saturates at large $F_N$. We also found that the value of ${\sigma }_0$ is proportional $A$ and also saturate at large $F_N$ – their ratio remains close to unity for all curves treated here.

For a Weibull distribution of bond breaking thresholds, the strength disorder is set by the parameter $\rho$. Regardless of the density of features or the applied preload, the estimation of the Weibull parameter $\rho$ resulted in a narrow domain, $5<\rho <10$ (see Figure 6B). This indicates that neither the density of features nor the applied preload significantly impacts the system local strength disorder.

4 Signal of upcoming catastrophic failure

In the past, several authors have proposed a thermodynamic frameworks of the statistical failure of elastic fiber bundles, using a variety of threshold distributions $P(ϵ)$ [26, 13, 27]. Recently, Pradhan and collaborators showed that the variation of the elastic energy,

$E_{\text{e}}=\left(1-P\left(\epsilon \right)\right)\frac{{\epsilon }^2}{2}(7)$

indicates the upcoming stretching-induced failure [13, 27]. They found that the elastic energy in Eq. 7 has a maximum at a particular value, which we define as ${\epsilon }_{\text{m}}$ (with $\mathrm{m}$ for maximum of the elastic energy), distinct from the critical value of strain ${\epsilon }_{\text{c}}$ (see the example displayed in Figure 1). However, as Figure 1 indicates, the elastic energy typically reaches its maximum in the unstable region of the loading process, i.e., ${\epsilon }_{\text{m}}>{\epsilon }_{\text{c}}$. Consequently, $E_{\text{e}}$ per se is not useful to forecast catastrophic failure [27].

However, the authors obtained analytically that $d{E}_{\text{e}}/d\epsilon$ reaches a maximum at a strain value defined as ${\epsilon }_{\text{I}}$ ($\mathrm{I}$ for inflection) in the stable region of the loading curve, thus ${\epsilon }_{\text{I}}<{\epsilon }_{\text{c}}$ (see Figure 1). The forecasting potential of $d{E}_{\text{e}}/d\epsilon$ is confirmed for several failure threshold distributions $P(ϵ)$, including uniform, power law, and Weibull [27]. The authors have even proposed a prediction window for the ratio between the critical strain ${\epsilon }_{\text{c}}$ and ${\epsilon }_{\text{I}}$, suggesting that $[1.2<{\epsilon }_{\text{c}}/{\epsilon }_{\text{I}}<1.5]$. So far, the prediction has been validated exclusively with numerical results. Following the same procedure, we now confront this theoretical analysis with our experimental outcomes.

We used a strain-hardening ansatz (vide supra) to describe the non-linearity of the initial loading regime. Similarly, we interpret our results by introducing a generalized elastic energy:

$E_{\text{e}}=\left(1-P\left(\epsilon \right)\right)\frac{{\epsilon }^{\alpha +1}}{\alpha +1}=\frac{\sigma \left(\epsilon \right)\epsilon }{\alpha +1}.(8)$

The average damage energy that is lost when each fiber breaks reads as

$E_{\text{d}}\left(\epsilon \right)={\int }_0^{\epsilon }\sigma \left(\epsilon \right)d\epsilon -E_{\text{e}}\left(\epsilon \right),(9)$

where the first term in Eq. 9 accounts for the total average work required to stretch the system.

Figure 7 shows $E_{\text{e}}(\epsilon )$ for specimens with feature densities of, respectively, 441, 361 and 114 mushrooms per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$. Each panel presents data color-coded for the preload intensity after which it was recorded. We mark the stress maxima ${\epsilon }_{\text{c}}$ with vertical lines, also color-coded for preload intensity. In all cases, the data show that the maxima of the elastic energy appear at strains superior to ${\epsilon }_{\text{c}}$. Thus, elastic energy maxima indeed appear in the unstable region, ${\epsilon }_{\text{m}}>{\epsilon }_{\text{c}}$.

Figure 7

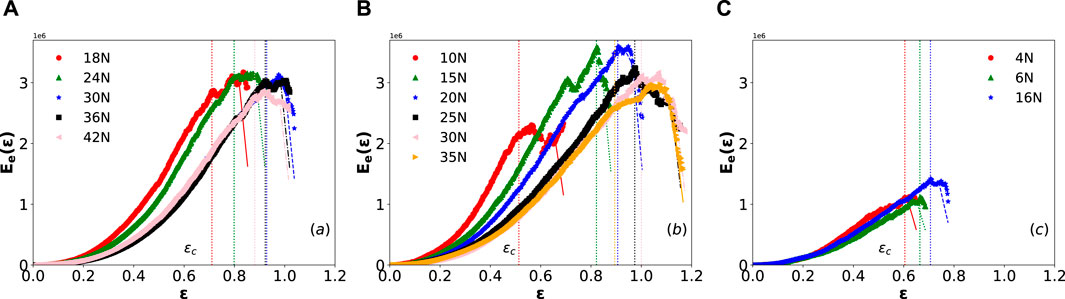
Figure 7. Elastic energy as a function of the system deformation, each of the panels presents data collected with adhesive pads numbering (A) 441, (B) 361, and (C) 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$. Elastic energies were calculated for force-distance curves using Eq. 8. We performed retractions after reaching the indicated preload intensity.

Can the damage energy then be used to forecast failure? We analyze the evolution of the ratio between the damage and the elastic energy $E_{\text{d}}/E_{\text{e}}$ as a function of the system deformation. Figure 8 presents the energy ratios, with arranged and color-coded analogously to Figure 7. The outcomes are very similar, regardless of the area fraction of features or preload intensity. In general, at strains $\epsilon <{\epsilon }_{\text{c}}$, the damage energy $E_{\text{d}}$ is significantly lower than its elastic counterpart. Only after reaching the stress maximum $E_{\text{d}}$ increases significantly. Thus, neither $E_{\text{e}}$ nor $E_{\text{d}}$ are reliable signals of upcoming catastrophic failure in experiments under stress-controlled conditions.

Figure 8

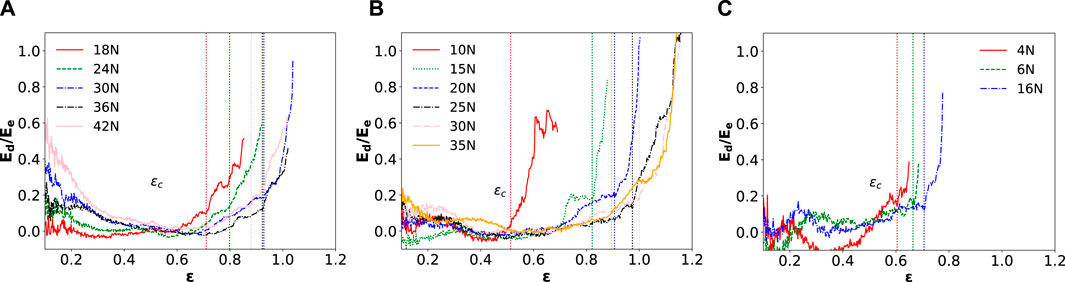
Figure 8. Ratio between the damage and the elastic energy as a function of the system deformation, with systems of (A) 441, (B) 361, and (C) 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$. The elastic and damage energies were calculated on the basis of measured force-distance curves using Eqs 8, 9, respectively.

Finally, we examine the change in elastic energy $d{E}_{\text{e}}/d\epsilon$. Figure 9 shows $d{E}_{\text{e}}/d\epsilon$ graphed against the deformation $\epsilon$, presented analogously to Figure 7, and maximum strain ${\epsilon }_{\text{c}}$ indicated with vertical lines color-coded for preload. The result is robust: for all applied preload intensities, the maximum of $d{E}_{\text{e}}/d\epsilon$ appears at stresses markedly lower than ${\epsilon }_{\text{c}}$, and thus within the stable phase, ${\epsilon }_I<{\epsilon }_m$. Thus, our experimental analysis fully agrees with the hypothesis that $d{E}_{\text{e}}/d\epsilon$ gives a prior indication of upcoming catastrophic failure at $[{\epsilon }_{\text{c}};{\sigma }_{\text{c}}]$, in experiments under stress-controlled conditions.

Figure 9

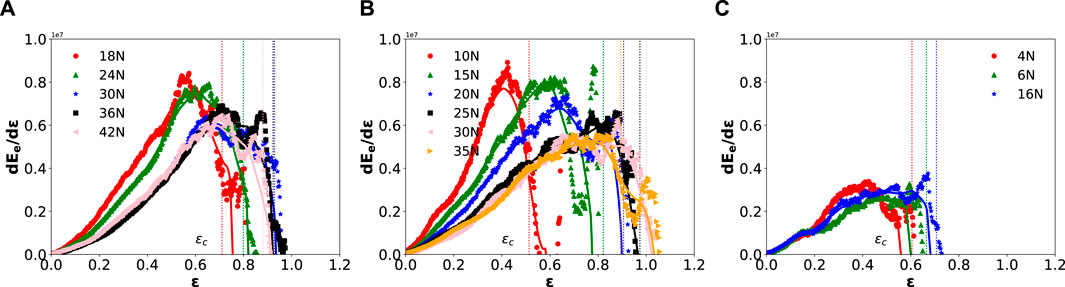
Figure 9. We plotted the numerical derivative of the elastic energy $\frac{d{E}_{\text{e}}}{d\epsilon }$ as a function of the system deformation for all averaged force-distance curves. The panels correspond to (A) 441, (B) 361 and (C) 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$, respectively. The preload after which the data were recorded are indicated as given in the legend.

The previous observations are summarized in Figure 10. On the one hand, Figure 10A shows the stress at elastic energy maximum ${\epsilon }_{\text{m}}$ as a function of ${\epsilon }_{\text{c}}$, plotted as ${\epsilon }_{\text{c}}/{\epsilon }_{\text{m}}$. We include results for all area fractions of features and preload intensities. For all cases ${\epsilon }_{\text{c}}/{\epsilon }_{\text{m}}<1$. Thus, the elastic energy maximum has no predictive power. On the other hand, Figure 10B shows stress at the inflection point of the elastic energy ${\epsilon }_I$ as a function of ${\epsilon }_{\text{c}}$. In general, ${\epsilon }_{\text{c}}/{\epsilon }_{\text{I}}$ results in values notably larger than one: the inflection point of elastic energy occurs before catastrophic failure sets in and thus reliably predicts upcoming failure. It is worth mentioning, that carefully monitoring the evolution of the Kolkata and Gini indexes also serves as an indicator to imminent catastrophic failure at $\sigma ={\sigma }_c$ [28].

Figure 10

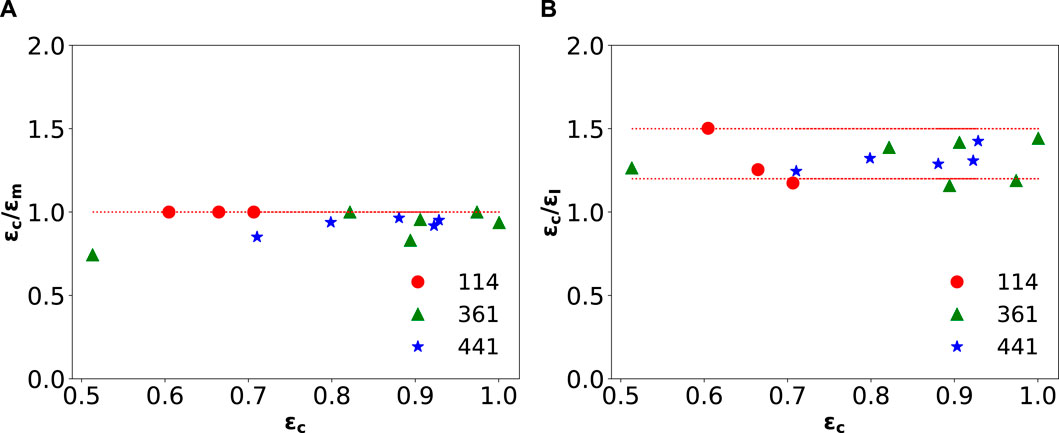
Figure 10. The relative location of the (A) elastic energy maximum ${\epsilon }_{\text{m}}$ and the (B) energy inflection point ${\epsilon }_{\text{I}}$, as a function of ${\epsilon }_{\text{c}}$, for convenience the inverse is illustrated. For comparison, (A) includes the unit and (B) includes the pre-factor window $1.2<{\epsilon }_{\text{c}}/{\epsilon }_{\text{I}}<1.5$ suggested in Ref.Pradhan et al. [27].

Summarising: we quantified the performance of a mechanical adhesive based on a pattern of passive mushroom-shaped structures. We observed that the stretching of fibers induces tension at the intersection points, leading to a progressive stiffening of the fiber network with the stress a power law in strain. We show that an FBM reproduces the experimental results after incorporating adjustments to capture the initial non-linear force response emergent at higher feature densities, $\sigma \sim A{\epsilon }^{\alpha }$. A dependency of the power law exponent $\alpha$ on preload suggests the existence of a critical active fiber density, below which intersections fail to form. At low densities, our measurements reflect the linear elasticity of the nylon strands, especially at lower strains. We emphasize that the origin of strain hardening depends on the fabric [25], yet it becomes more pronounced as more mushrooms are activated. Remarkably, $\alpha$ spans from 1 to $\frac{3}{2}$, which implies the emergence of a power law with a strength of $\frac{3}{2}$, indicative of strain hardening influenced by the presence of entanglements between the fibers, often referred to as “crosslinks”. Even so, the true mechanism behind the strain hardening of the fabric-pattern attachment in this study remains subject of necessary future work, as characterizing that relies on knowledge of many physical parameters in the fabric, such as fiber friction coefficients, density etc [21, 24].

Our work validates the approach to predicting the catastrophic failure of Pradhan and co-authors, which has so far been supported with numerical work [13, 27]. As per the approach, we quantified the elastic and damage energy as the fiber-adhesive assembly is stretched under strain-controlled conditions. Stress-strain curves revealed that the elastic energy reaches a maximum after ${\sigma }_{\text{c}}$, corresponding to the unstable region. Consequently, elastic and damage energy are unreliable signals of upcoming catastrophic failure in experiments under stress-controlled conditions. However, we now confirm experimentally that the derivative of the elastic energy exhibits a maximum before reaching ${\sigma }_{\text{c}}$. This characteristic stands out as a reliable signal of imminent catastrophic failure in experiments conducted under stress-controlled conditions. Our results show the robustness of the theoretical results of Pradhan and collaborators [13, 27] to the reality of finite systems, sample variability, and, notably, non-linearity of the elastic behavior of the fiber bundle.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AF: Conceptualization, Data curation, Investigation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. PS: Data curation, Investigation, Writing–review and editing. FH: Data curation, Writing–review and editing. JD: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Writing–review and editing. RH: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Funding from the 4.TU Federation through the program “Soft Robotics” with grant number 4TU-UIT-335 is gratefully acknowledged. RH acknowledges the Ministerio de Ciencia e Innovación (Spanish Government) Grant PID2020-114839GB-I00 funded by MCIN/AEI/10.13039/501100011033.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Smith CW, Gorb SN, Popov VL. Probabilistic Fasteners with Parabolic Elements: Biological System, Artificial Model and Theoretical Considerations. Philos Trans R Soc Lond Ser A: Math Phys Eng Sci (2002) 360:211–25. doi:10.1098/rsta.2001.0926

CrossRef Full Text | Google Scholar

2. Fiorello I, Tricinci O, Naselli GA, Mondini A, Filippeschi C, Tramacere F, et al. Climbing Plant-Inspired Micropatterned Devices for Reversible Attachment. Adv Funct Mater (2020) 30:2003380. doi:10.1002/adfm.202003380

CrossRef Full Text | Google Scholar

3. Zhang T, Liang T, Yue X, Sameoto D. Integration of Thermoresponsive Velcro-Like Adhesive for Soft Robotic Grasping of Fabrics or Smooth Surfaces. In: 2019 2nd IEEE international Conference on soft Robotics (RoboSoft). Seoul, Republic of Korea: IEEE (2019). p. 120–125. doi:10.1109/ROBOSOFT.2019.8722743

CrossRef Full Text | Google Scholar

4. Mestral Gd. Velvet Type Fabric and Method of Producing Same (Velcro®). U.S. Patent No. 2,717,437 (1955).

Google Scholar

5. Melbye WL, Susan KNE, Wood L, Lindseth MD, Bychinski DA. Mushroom-Type Hook Strip for A Mechanical Fastener. U.S. Patent No. 5,077,870 (2003).

6. Sharma P, Saggiomo V, Van Der Doef V, Kamperman M, A Dijksman J. Hooked on Mushrooms: Preparation and Mechanics of a Bioinspired Soft Probabilistic Fastener. Biointerphases (2021) 16:011002. doi:10.1116/6.0000634

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kun F, Raischel F, Hidalgo R, Herrmann H. Extensions of Fibre Bundle Models. Berlin, Heidelberg: Springer Berlin Heidelberg (2006). 57–92.

Google Scholar

8. Pradhan S, Hansen A, Chakrabarti BK. Failure Processes in Elastic Fiber Bundles. Rev Mod Phys (2010) 82:499–555. doi:10.1103/RevModPhys.82.499

CrossRef Full Text | Google Scholar

9. Hansen A, Hemmer PC, Pradhan S eds. The Fiber Bundle Model: Modeling Failure in Materials. John Wiley and Sons (2015).

Google Scholar

10. Creton C, Ciccotti M. Fracture and Adhesion of Soft Materials: A Review. Rep Prog Phys (2016) 79:046601. doi:10.1088/0034-4885/79/4/046601

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hidalgo RC, Moreno Y, Kun F, Herrmann HJ. Fracture Model with Variable Range of Interaction. Phys Rev E (2002) 65:046148. doi:10.1103/PhysRevE.65.046148

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Batool A, Pál G, Danku Z, Kun F. Transition from Localized to Mean Field Behaviour of Cascading Failures in the Fiber Bundle Model on Complex Networks. Chaos, Solitons and Fractals (2022) 159:112190. doi:10.1016/j.chaos.2022.112190

CrossRef Full Text | Google Scholar

13. Arango-Restrepo A, Rubi JM, Pradhan S. A Thermodynamic Framework for Stretching Processes in Fiber Materials. Front Phys (2021) 9. doi:10.3389/fphy.2021.642754

CrossRef Full Text | Google Scholar

14. Chakrabarti BK. A Fiber Bundle Model of Traffic Jams. Physica A: Stat Mech its Appl (2006) 372:162–6. Common Trends in Traffic Systems. doi:10.1016/j.physa.2006.05.003

CrossRef Full Text | Google Scholar

15. Long R, Hui C-Y, Kim S, Sitti M. Modeling the Soft Backing Layer Thickness Effect on Adhesion of Elastic Microfiber Arrays. J Appl Phys (2008) 104:044301. doi:10.1063/1.2968249

CrossRef Full Text | Google Scholar

16. Halász Z, Kun F. Slip Avalanches in a Fiber Bundle Model. Europhysics Lett (2010) 89:26008. doi:10.1209/0295-5075/89/26008

CrossRef Full Text | Google Scholar

17. Mulla Y, Oliveri G, Overvelde JT, Koenderink GH. Crack Initiation in Viscoelastic Materials. Phys Rev Lett (2018) 120:268002. doi:10.1103/physrevlett.120.268002

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Capelli A, Reiweger I, Schweizer J. Studying Snow Failure with Fiber Bundle Models. Front Phys (2020) 8. doi:10.3389/fphy.2020.00236

CrossRef Full Text | Google Scholar

19. Kádár V, Pál G, Kun F. Record Statistics of Bursts Signals the Onset of Acceleration towards Failure. Scientific Rep (2020) 10:2508. doi:10.1038/s41598-020-59333-4

CrossRef Full Text | Google Scholar

20. Chandreyee R, Manna S. Brittle-to-quasibrittle Transition in Bundles of Nonlinear Elastic Fibers. Phys Rev E (2016) 94:032126. doi:10.1103/PhysRevE.94.032126

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kabla A, Mahadevan L. Nonlinear Mechanics of Soft Fibrous Networks. J R Soc Interf (2007) 4:99–106. doi:10.1098/rsif.2006.0151

CrossRef Full Text | Google Scholar

22. Cranford SW, Tarakanova A, Pugno NM, Buehler MJ. Nonlinear Material Behaviour of Spider Silk Yields Robust Webs. Nature (2012) 482:72–6. doi:10.1038/nature10739

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear Elasticity in Biological Gels. Nature (2005) 435:191–4. doi:10.1038/nature03521

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Picu R. Mechanics of Random Fiber Networks—A Review. Soft Matter (2011) 7:6768–85. doi:10.1039/c1sm05022b

CrossRef Full Text | Google Scholar

25. Hu J, Xin B (2008). “Structure and mechanics of woven fabrics,” in Structure and Mechanics of Textile Fibre Assemblies. 2nd Edn, Editors P. Schwartz (Woodhead Publishing), 27–60. The Textile Institute Book Series. Available at: https://www.sciencedirect.com/science/article/pii/B978008102619900002X. doi:10.1016/B978-0-08-102619-9.00002-X

CrossRef Full Text | Google Scholar

26. Pride SR, Toussaint R. Thermodynamics of Fiber Bundles. Physica A: Stat Mech its Appl (2002) 312:159–71. doi:10.1016/S0378-4371(02)00816-6

CrossRef Full Text | Google Scholar

27. Pradhan S, Kjellstadli JT, Hansen A. Variation of Elastic Energy Shows Reliable Signal of Upcoming Catastrophic Failure. Front Phys (2019) 7. doi:10.3389/fphy.2019.00106

CrossRef Full Text | Google Scholar

28. Soumyaditya D, Soumyajyoti B. Critical Scaling through Gini Index. Phys Rev Lett (2023) 131:157101. doi:10.1103/PhysRevLett.131.157101

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix

Figure A1 shows the non-linear fitting with the power-law-modified FBM of Eq. 6 of our experimental stress–strain data. The obtained Weibull parameters are included as insets. $\rho$ was used to compare the constitutive curves using the scaling ansatz in Figure 5.

FIGURE A1

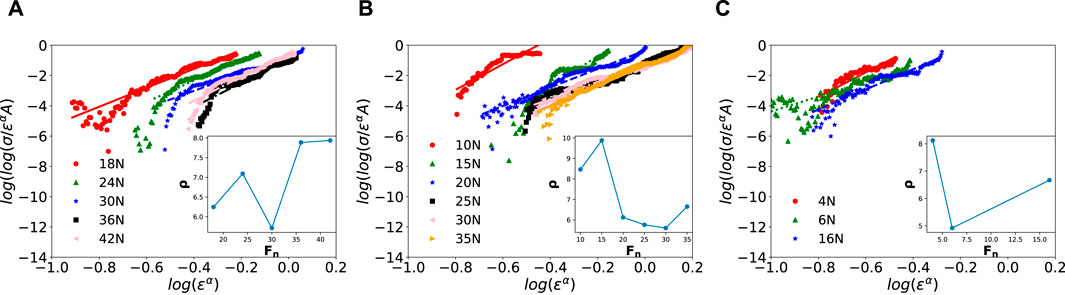
FIGURE A1. Fits of the double-logarithmic stress versus the logarithmic strain to the Weibull distribution given in Eq. 6 with power-law onset. Each panel represents a different feature count: (A) 441, (B) 361, and (C) 114 features per 25$\cdot$25 ${\mathrm{m}\mathrm{m}}^2$. Stress-strain curves are color-coded for preload force, as given in the legend. The insets show the parameter $\rho$ as a function of preload force, as also given in Eq. 6. $\rho$ is a measure of the width of the stress threshold distribution.