
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 25 October 2024
Sec. Fluid Dynamics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1409318
In this work, entropy generation is optimized through the application of the second law of thermodynamics. The slip mechanisms, Brownian diffusions, and thermophoresis are elaborated using the tangent hyperbolic nanomaterial model. Magnetohydrodynamic (MHD) fluid is taken into consideration. To characterize the impact of activation energy, a unique model involving the binary chemical reaction is deployed. The effects of mixed convection that is nonlinear in nature, bioconvection, and Joule effect are all taken into consideration. The key partial differential equations (PDEs) are reduced into ordinary differential equations (ODEs) by utilizing appropriate similarity transformations and then solved numerically with the help of a built-in ‘bvp4c’ technique of MATLAB software. Varied flow parameters’ impacts on the nanoparticle volume concentration, entropy number, microorganism concentration, temperature, and velocity fields are analyzed using graphs. Various flow variables are taken into consideration to calculate the total rate of entropy generation. The obtained results show that concentration irreversibility, Joule effect irreversibility, viscous dissipation, and heat irreversibility all influence the entropy. The numerical outcomes were observed by fixing the physical parameters as
Engineers and scientists have held a longstanding fascination with researching non-Newtonian fluids, primarily because of their behavior on stretched surfaces with heat and mass transfer. This is because of its numerous practicalities, such as paper manufacturing, wire drawing, paper manufacturing, petroleum production, and polymer sheet manufacturing. Because shear rate and shear stress are not linearly related in non-Newtonian fluids, one constitutive equation is insufficient for representing the relationship between shear rates and shear stresses. Owing to this, various frameworks have been presented in the literature, including the Maxwell model, Reiner–Rivlin model, generalized Burgers, Oldroyd-A model, Oldroyd-B model, Oldroyd-8 constants, Carreau model, and the Carreau–Yasuda model. In the current investigation, we took non-Newtonian tangent hyperbolic fluid under consideration. Effects of shear thinning are described by a four-constant pseudoplastic model of fluid, i.e., tangent hyperbolic fluid. When flow decreases, owing to increased shear stress, it is useful to evaluate the inter-particle friction in the fluid. Examples of such liquids include ketchup, paint, blood, nail polish, and whipped cream. [1] presented a numerical approach for the flow of rate-type fluid across the stretchable cylinder using MHD flow. [2] focused on thermal radiation, which is non-linear in nature, to probe the flow by a stretchable surface with Brownian diffusion and thermophoresis. The flow of the two-dimensional rate-type fluid toward a stretchable sheet with the applied magnetic effect was investigated [3]. [4] found solutions in the series form for a tangent hyperbolic fluid that is inclined uniformly in a tube. [5] analyzed the tangent hyperbolic fluid using a stretchable sheet while considering both the impacts of Soret and Dufour in MHD stagnation point flow. [6–13] provided more research articles on non-Newtonian fluids.
Recently, some energy-efficient mechanisms have been designed to minimize the quantity of wasted energy and boost energy utilization capabilities of liquid systems. The transport of heat and viscous dissipation results in energy waste, which aids the irreversibility of the liquid system. Electrochemical and chemical, evaporative cooling, natural convection, solar thermal, microchannels, air separators, chillers, gas turbines, fuel cells, and functionally graded materials are all examples of systems where entropy generation minimization (EGM) is beneficial. [14] recently analyzed the generation of entropy in nanofluids using copper and silver nanoparticles. [15] studied the increase in entropy in a burner model with various energy sources. The optimization of entropy in a nonlinear radiative flow while accounting for Joule effects and dissipation is investigated by [16].
The change in density over a region induces additive rapid movement in self-propelled microorganisms; as a result of this, there is macroscopic movement of the fluid, which is termed as bioconvection. Self-propelled microorganisms have a tendency to enhance the base fluid to create a bio-convective stream in a specific direction. The self-propelled microorganisms are categorized into different types, i.e., gyrotactic, negative gravitaxis, and chemotaxis or oxytactic microorganisms. Compared to self-propelled microorganisms, nanoparticles do not move on their own, and their movement is driven by the effect of Brownian motion and thermophoresis. If there is minimal nanoparticle concentration, then in the nanofluids, bioconvection is supposed to be feasible and it will not result in an essential increase in the thickness of the base fluid. Bioconvection with nanoparticles was originally discussed in [17, 18]. Afterward, combining nanoparticles with gyrotactic microorganisms was proposed by [19] using Buongiornos theory.[20] studied the flow of nanofluids with bioconvection in porous medium numerically. Bioconvective flow with nanoparticles through a symmetric channel was studied by [21], and a bio nanoengineering model was presented. In rapidly changing magnetic lines of force, the clot blood model was also analyzed by [22] using the Jeffrey fluid model with microorganisms and nanoparticles. A magnetized laminar flow of nanofluid along with phototactic microorganisms in a medium that is non-Darcy with pores was observed by [23]. The external magnetic effect and bioconvective flow were researched by [24] with convective boundary conditions and nanoparticles.
In the recent past, as a result of advancements in nanotechnology, the researchers’ focus has shifted to improving heat transport through the nanoparticle interaction. Because of their fascinating thermo-physical aspects, the nanoparticles, which include metallic particles of micro-size, are useful in biological, mechanical, chemical, and other engineering fields. The conductivity of heat energy and the viscosity of the fluid improve not just with the addition of nanoparticles but also with the structure of particle size, and slip features in nanoparticles play an important role as well. [25] developed nanoparticles to improve the product efficiency and fluid thermal conductivity. Heat transfer near a stagnation point in the Maxwell nanofluid flow over a porous rotating disk, highlighting the impact of shear stress and flow field alterations on heat transfer, has been investigated by [26]. Some interesting studies on nanofluids have been discussed in [27–30]. [31] analyzed the magnetohydrodynamic stagnation point flow of Williamson hybrid nanofluid over a porous sheet, considering chemical reactions, energy generation, and boundary conditions. [32] examined the unsteady 2D laminar flow of Williamson hybrid nanoliquid over a convectively heated stretching sheet, focusing on maximizing energy and mass transfer rates. [33] investigated entropy generation in the mixed convection time-dependent flow of cross-hybrid nanoliquid at a stagnation point using engine oil with
Activation energy and chemical reactions have been used in mass transportation phenomena, which have been carried out in the history of food sciences, chemistry, chemical, and mechanical industries. In 1889, Svante Arrhenius engaged in the key observations on activation energy and defined it in terms of the least quantity of energy that is required to begin a chemical process. Geothermal sciences, petroleum engineering applications, oil reserves, heat reactions, and a lot of other fields are part of the activation energy phenomenon. Some major contributions to this subject are discussed in [34–36]. [37] numerically investigated the natural convection boundary-layer flow over a truncated cone with gyrotactic microorganisms in water-based nanofluid, revealing enhanced transport properties and boundary conditions’ effects. [38] explored the bioconvection phenomenon of a nanofluid with gyrotactic microorganisms around a horizontal circular cylinder, utilizing Buongiorno’s model and finite-difference algorithm for the comprehensive analysis of transport phenomena. [39] investigated mixed convection of nanofluid with gyrotactic microorganisms over a permeable vertical surface in a porous medium, which reveals suction/injection effects, with significant impacts on heat and mass transfer. [40] also examined the mixed bio-convective stagnation point flow of a power-law nanofluid over a stretchable surface with passively controlled boundary conditions. [41] explored non-Newtonian nanofluid flow induced by a rotating stretchable disk, analyzing heat and mass transfer with Stefan blowing and Cattaneo–Christov fluxes. He also examined the flow of a non-Newtonian nanofluid in a conical gap between rotating/stationary surfaces, considering heat and mass transfer and a uniform magnetic field [42]. Some of the similar results are discussed in [43–45]. The study of the fluid flow in porous medium is of great importance in fluid mechanics. [46] analyzed the motion of Jeffrey nanofluid in porous medium with motile microorganisms between two revolving stretching disks. The study of different types of fluids in between porous medium is given in [47–50]. Furthermore, heat and mass transfer analysis of nanofluid is numerically scrutinized under the influence of magnetic field subject to marangoni boundary layer [51, 52].
The major goal of this work is to look at the optimization of entropy in the tangent hyperbolic nanofluid flow on a stretchable sheet. The uniqueness of the work under discussion is that it investigates the optimization of entropy generation in a non-Newtonian fluid model with non-linear thermal radiation, non-linear mixed convection, viscous dissipation, bioconvection, and activation energy as additional effects. To characterize activation energy’s effects, we used a unique two-step chemical reaction model. Various flow variables are utilized to compute the rate of total entropy generation. We have used a method called the shooting technique to deal with the nonlinear ordinary system. To examine the behavior of the included variables on fluid properties, graphs and tables are created. Analysis on various methodologies is shown in [53–56].
In tangent hyperbolic nanomaterial flow, we analyzed Bejan numbers and entropy. In the current model, the impacts of non-linear heat radiation, non-linear mixed convection, activation energy, and Joule effect are studied. The stretchable sheet with the stretching rate being a generates the flow.
Following are the flow constraints used with the current flow model:
where
For present flow, suitable transformations Equation 7 are derived from [53]
The governing equations with the aforementioned variables yield these Equations 8–12 in dimensionless forms:
with
where the Hartmann number is denoted by
The following are the mathematical expressions (Equations 13–16) for the motile density number, local Sherwood number, skin friction coefficient, and the local Nusselt number:
with
where
The above quantities are expressed as follows in non-dimensional forms:
where
For tangent hyperbolic fluid, entropy generation is [58]
where
Now Equation 17 becomes using Equation 18
Equation 19 contains five factors: i) viscosity dissipation in the entropy generation for tangent hyperbolic fluid, ii) thermal irreversibility, iii) nanoparticle concentration irreversibility, iv) Joule effect irreversibility, and v) microorganism concentration irreversibility. The dimensionless form are in Equation 20
where Equation 21 represents
It is a well-known observation that a number of physical models contain differential equations which are nonlinear depending on the included constraints that can be solved using numerical approaches. In the suggested numerical approaches, the shooting method is perhaps a more reliable strategy for achieving adequate accuracy. After generating dimensionless forms, the bvp4c built-in package is used to tackle numerically. This approach is reliable and efficient, having an error tolerance of 10−6. As a result, we used this strategy to target Equations 8–12. The collection of these mathematical equations is turned into first-order differential equations using dummy variables as in Equations 24–28:
Then,
The transformed boundary conditions are
This part describes the visual representation of physical characteristics such as velocity distribution
The parameter for the buoyancy ratio
The impacts of the Prandtl number
The effects of the
To examine the changes in concentration distribution
The Peclet number
The streamlines of the flow problem visualize the flow pattern and movement of the molecules, as displayed in Figures 13A–D. The laminar pattern is visible among all profiles, and no intersection is found. These streamlines describe the movement, velocity distribution, heat transport efficiency, and interaction with the surface body.
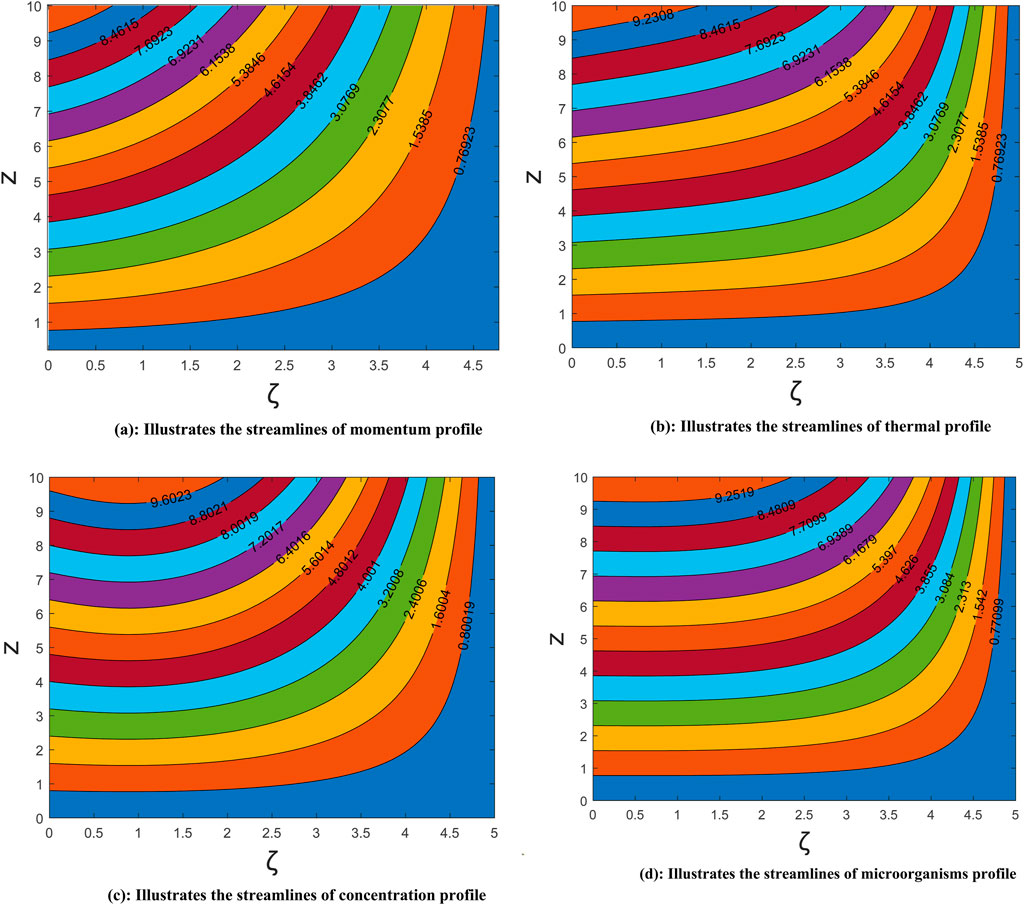
Figure 13. (A) Streamlines of the momentum profile. (B) Streamlines of the thermal profile. (C) Streamlines of the concentration profile. (D) Streamlines of the microorganism profile.
In the tabulated values in Table 1, we see the comparison of our computed results with the already in the tabulated values we see the comparison of our computed results with the already results shows the great accord with available literature.
The aim of this contribution is to study the flow of tangent hyperbolic nanomaterials for entropy optimization, owing to a stretchable surface. Some key findings are as follows:
• For the first-order velocity slip factor, the velocity distribution increases, but the Hartmann number, Weissenberg number, buoyancy ratio constant, and second-order slip parameter show a declining trend.
• The thermal Biot number, parameter for the temperature ratio, Eckert number, and parameter for thermophoresis enhanced the temperature of nanoparticles, while a decreasing trend is noticed for the Prandtl number.
• Activation energy improved the concentration of nanoparticles, while it reduces the concentration for the Prandtl number, Lewis number, and Brownian parameter.
• The distribution for self-propelling gyrotactic microorganisms declines for larger Lewis and Prandtl numbers.
• Entropy generation reduces for a larger power law index and parameters for Brownian motion; however, a negative relationship is observed for larger Weissenberg and Hartmann numbers.
In the future, this approach may be extended to include the various heat and mass flux models, as well as the observation of changes in transport rates due to geometrical changes.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
YW: writing–review and editing and methodology. MC: conceptualization and writing–original draft. NM: software and writing–original draft. MT: data curation and writing–original draft. MB: validation and writing–review and editing. MI: supervision and writing–original draft.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research project is supported by the 2022 university-level scientific research team project, 2018 university-level quality engineering project, and 2023 Project of Natural Science Foundation of Colleges and Universities in Anhui Province (kytd202207; 2018jpkcx17; and 2023AH030085).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Malik MY, Salahuddin T, Hussain A, Bilal S. MHD flow of tangent hyperbolic fluid over a stretching cylinder: using Keller box method. J Magnetism Magn Mater (2015) 395:271–6. doi:10.1016/j.jmmm.2015.07.097
2. Waqas M, Khan MI, Hayat T, Alsaedi A, Khan MI. Nonlinear thermal radiation in flow induced by a slendering surface accounting thermophoresis and Brownian diffusion. The Eur Phys J Plus (2017) 132(6):280–13. doi:10.1140/epjp/i2017-11555-0
3. Akbar NS, Nadeem S, Haq RU, Khan ZH. Numerical solutions of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J Phys (2013) 87(11):1121–4. doi:10.1007/s12648-013-0339-8
4. Nadeem S, Akbar NS. Series solutions for the peristaltic flow of a Tangent hyperbolic fluid in a uniform inclined tube. Z Fr Naturforschung A (2010) 65(11):887–95. doi:10.1515/zna-2010-1101
5. Hayat T, Khan MI, Waqas M, Alsaedi A. Stagnation point flow of hyperbolic tangent fluid with Soret-Dufour effects. Results Phys (2017) 7:2711–7. doi:10.1016/j.rinp.2017.07.014
6. Waqas M, Farooq M, Khan MI, Alsaedi A, Hayat T, Yasmeen T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int J Heat Mass Transfer (2016) 102:766–72. doi:10.1016/j.ijheatmasstransfer.2016.05.142
7. Hayat T, Khan MI, Waqas M, Alsaedi A. Effectiveness of magnetic nanoparticles in radiative flow of Eyring-Powell fluid. J Mol Liquids (2017) 231:126–33. doi:10.1016/j.molliq.2017.01.076
8. Hayat T, Waqas M, Khan MI, Alsaedi A, Shehzad SA. Magnetohydrodynamic flow of burgers fluid with heat source and power law heat flux. Chin J Phys (2017) 55(2):318–30. doi:10.1016/j.cjph.2017.02.004
9. Hayat T, Qasim M, Abbas Z. Radiation and mass transfer effects on the magnetohydrodynamic unsteady flow induced by a stretching sheet. Z fr Naturforschung A (2010) 65(3):231–9. doi:10.1515/zna-2010-0312
10. Sheikholeslami M, Zeeshan A. Numerical simulation of Fe3O4-water nanofluid flow in a non-Darcy porous media. Int J Numer Methods Heat and Fluid Flow (2018) 28(3):641–60. doi:10.1108/hff-04-2017-0160
11. Khan MI, Waqas M, Hayat T, Alsaedi A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J Colloid Interf Sci (2017) 498:85–90. doi:10.1016/j.jcis.2017.03.024
12. Zeeshan A, Shehzad N, Ellahi R. Analysis of activation energy in Couette-Poiseuille flow of nanofluid in the presence of chemical reaction and convective boundary conditions. Results Phys (2018) 8:502–12. doi:10.1016/j.rinp.2017.12.024
13. Hassan M, Zeeshan A, Majeed A, Ellahi R. Particle shape effects on ferrofuids flow and heat transfer under influence of low oscillating magnetic field. J Magnetism Magn Mater (2017) 443:36–44. doi:10.1016/j.jmmm.2017.07.024
14. Hayat T, Khan MI, Qayyum S, Alsaedi A. Entropy generation in flow with silver and copper nanoparticles. Colloids and Surfaces A. Physicochemical Eng Aspects (2018) 539:335–46. doi:10.1016/j.colsurfa.2017.12.021
15. Hayat T, Qayyum S, Khan MI, Alsaedi A. Entropy generation in magnetohydrodynamic radiative flow due to rotating disk in presence of viscous dissipation and Joule heating. Phys Fluids (2018) 30(1):1070–6631. doi:10.1063/1.5009611
16. Rashidi S, Akar S, Bovand M, Ellahi R. Volume of fluid model to simulate the nanofluid flow and entropy generation in a single slope solar still. Renew Energ (2018) 115:400–10. doi:10.1016/j.renene.2017.08.059
17. Kuznetsov AV, Avramenko AA. Effect of small particles on this stability of bioconvection in a suspension of gyrotactic microorganisms in a layer of finite depth. Int Commun Heat Mass Transfer (2004) 31(1):1–10. doi:10.1016/s0735-1933(03)00196-9
18. Geng P, Kuznetsov AV. Settling of bidispersed small solid particles in a dilute suspension containing gyrotactic micro-organisms. Int J Eng Sci (2005) 43(11-12):992–1010. doi:10.1016/j.ijengsci.2005.03.002
19. Kuznetsov AV. Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth. Eur J Mechanics-B/Fluids (2011) 30(2):156–65. doi:10.1016/j.euromechflu.2010.10.007
20. Bég OA, Prasad VR, Vasu B. Numerical study of mixed bioconvection in porous media saturated with nanofluid containing oxytactic microorganisms. J Mech Med Biol (2013) 13(04):1350067. doi:10.1142/s021951941350067x
21. Akbar NS. Bioconvection peristaltic flow in an asymmetric channel filled by nanofluid containing gyrotactic microorganism. Int J Numer Methods Heat and Fluid Flow (2015) 25(2):214–24. doi:10.1108/hff-07-2013-0242
22. Bhatti MM, Zeeshan A, Ellahi R. Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc Res (2017) 110:32–42. doi:10.1016/j.mvr.2016.11.007
23. Abbas IA, Palani G. Effects of magnetohydrodynamic flow past a vertical plate with variable surface temperature. Appl Maths Mech (2010) 31(3):329–38. doi:10.1007/s10483-010-0306-9
24. Chakraborty T, Das K, Kundu PK. Framing the impact of external magnetic field on bioconvection of a nanofluid flow containing gyrotactic microorganisms with convective boundary conditions. Alexandria Eng J (2018) 57(1):61–71. doi:10.1016/j.aej.2016.11.011
25. Choi SUS, Zhang ZG, Yu W, Lockwood FE, Grulke EA. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett (2001) 79(14):2252–4. doi:10.1063/1.1408272
26. Li S, Faizan M, Ali F, Ramasekhar G, Muhammad T, Khalifa HAEW, et al. Modelling and analysis of heat transfer in MHD stagnation point flow of Maxwell nanofluid over a porous rotating disk. Alexandria Eng J (2024) 91:237–48. doi:10.1016/j.aej.2024.02.002
27. Reddy MV, Ajithkumar M, Lone SA, Ali F, Lakshminarayana P, Saeed A. Magneto-Williamson nanofluid flow past a wedge with activation energy: Buongiorno model. Adv Mech Eng (2024) 16(1):16878132231223027. doi:10.1177/16878132231223027
28. Ali F, Zaib A, Faizan M, Zafar SS, Alkarni S, Shah NA, et al. Heat and mass exchanger analysis for Ree-Eyring hybrid nanofluid through a stretching sheet utilizing the homotopy perturbation method. Case Stud Therm Eng (2024) 54:104014. doi:10.1016/j.csite.2024.104014
29. Ali F, Mahnashi AM, Hamali W, Raizah Z, Saeed A, Khan A. Numerical scrutinization of Darcy–Forchheimer flow for trihybrid nanofluid comprising of (GO+ZrO2+SiO2/kerosene oil) over the curved surface. J Therm Anal Calorim (2024) 1–16. doi:10.1007/s10973-024-13103-w
30. Yasmin H, Lone SA, Ali F, Alrabaiah H, Raizah Z, Saeed A. Thermal radiative flow of cross nanofluid due to a stretched cylinder containing microorganisms. Nanotechnology Rev (2023) 12(1):20230147. doi:10.1515/ntrev-2023-0147
31. Vinodkumar Reddy M, Ajithkumar M, Zafar SSB, Faizan M, Ali F, Lakshminarayana P. Magnetohydrodynamic stagnation point flow of Williamson hybrid nanofluid via stretching sheet in a porous medium with heat source and chemical reaction. Proc Inst Mech Eng E: J Process Mech Eng (2024):09544089241239583. doi:10.1177/09544089241239583
32. Ahmed MF, Ali F, Zafar SS, Reddy CS, Aslam M. Irreversibility analysis and thermal radiative of Williamson (ZnO+MOS2/C3H8O2) hybrid nanofluid over a porous surface with a suction effect. Physica Scripta (2023) 98(11):115237. doi:10.1088/1402-4896/acffff
33. Lone SA, Ali F, Saeed A, Bognár G. Irreversibility analysis with hybrid cross nanofluid of stagnation point and radiative flow (TiO2+CuO) based on engine oil past a stretchable sheet. Heliyon (2023) 9(4):e15056. doi:10.1016/j.heliyon.2023.e15056
34. Zhang T, Khan SU, Imran M, Tlili I, Waqas H, Ali N. Activation energy and thermal radiation aspects in bioconvection flow of rate-type nanoparticles configured by a stretching/shrinking disk. J Energ Resour Technol (2020) 142(11):112102. doi:10.1115/1.4047249
35. Alghamdi M. Significance of Arrhenius activation energy and binary chemical reaction in mixed convection flow of nanofluid due to a rotating disk. Coatings (2020) 10(1):86. doi:10.3390/coatings10010086
36. Asma M, Othman WAM, Muhammad T. Numerical study for Darcy- Forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Mathematics (2019) 7(10):921. doi:10.3390/math7100921
37. Khan WA, Rashad AM, Abdou MMM, Tlili I. Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. Eur J Mechanics-B/Fluids (2019) 75:133–42. doi:10.1016/j.euromechflu.2019.01.002
38. Rashad AM, Nabwey HA. Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. J Taiwan Inst Chem Eng (2019) 99:9–17. doi:10.1016/j.jtice.2019.02.035
39. Nabwey HA, El-Kabeir SMM, Rashad AM, Abdou MMM. Gyrotactic microorganisms mixed convection flow of nanofluid over a vertically surfaced saturated porous media. Alexandria Eng J (2022) 61(3):1804–22. doi:10.1016/j.aej.2021.06.080
40. Nabwey HA, A. Khan W, Rashad AM, Mabood F, Salah T. Power-law nanofluid flow over a stretchable surface due to gyrotactic microorganisms. Mathematics (2022) 10(18):3285. doi:10.3390/math10183285
41. Moatimid GM, Mohamed MA, Elagamy K. Heat and mass flux through a Reiner–Rivlin nanofluid flow past a spinning stretching disc: Cattaneo–Christov model. Scientific Rep (2022) 12(1):14468. doi:10.1038/s41598-022-18609-7
42. Moatimid GM, Mohamed MA, Elagamy K. A Casson nanofluid flow within the conical gap between rotating surfaces of a cone and a horizontal disc. Scientific Rep (2022) 12(1):11275. doi:10.1038/s41598-022-15094-w
43. Moatimid GM, Mohamed MA, Gaber AA, Mostafa DM. Numerical analysis for tangent-hyperbolic micropolar nanofluid flow over an extending layer through a permeable medium. Scientific Rep (2023) 13(1):13522. doi:10.1038/s41598-023-33554-9
44. Moatimid GM, Mohamed MA, Elagamy K. Peristaltic transport of Rabinowitsch nanofluid with moving microorganisms. Scientific Rep (2023) 13(1):1863. doi:10.1038/s41598-023-28967-5
45. He JH, Moatimid GM, Mohamed MA, Elagamy K. A stretching cylindrical carreau nanofluid border layer movement with motile microorganisms and variable thermal characteristics. Int J Mod Phys B (2023) 38:2450223. doi:10.1142/s0217979224502230
46. Moatimid GM, Mohamed MA, Elagamy K. A motion of Jeffrey nanofluid in porous medium with motile microorganisms between two revolving stretching discs: effects of Hall currents. J Porous Media (2022) 25(10):83–101. doi:10.1615/jpormedia.2022043529
47. Moatimid GM, Mohamed MA, Elagamy K. A pulsatile Williamson nanofluid flow with motile microorganisms between two permeable walls: effect of modified Darcy's law. J Porous Media (2023) 26(12):57–86. doi:10.1615/jpormedia.2023044143
48. Moatimid GM, Mohamed MA, Elagamy K. Microorganisms peristaltic transport within a Carreau Nanofluid through a modified Darcy porous medium. Spec Top and Rev Porous Media: Int J (2023) 14(5):1–30. doi:10.1615/specialtopicsrevporousmedia.2023046194
49. Moatimid GM, Mohamed MA, Elagamy K. A Williamson nanofluid with motile microorganisms across a vertical exponentially stretching porous sheet with varying thermal characteristics. Spec Top and Rev Porous Media: Int J (2024) 15(1):67–98. doi:10.1615/specialtopicsrevporousmedia.2023046440
50. Mohamed M, Elagamy K. Sutterby nanofluid flow with microorganisms around a curved expanding surface through a porous medium: thermal diffusion and diffusion thermo impacts. J Porous Media (2024) 27:19–48. doi:10.1615/JPorMedia.2024052470
51. Sheikholeslami M, Ganji DD. Influence of magnetic field on CuOH2O nanofluid flow considering Marangoni boundary layer. Int J Hydrogen Energ (2017) 42(5):2748–55. doi:10.1016/j.ijhydene.2016.09.121
52. Pandey AK, Kumar M. Boundary layer flow and heat transfer analysis on Cu-water nanofluid flow over a stretching cylinder with slip. Alexandria Eng J (2017) 56(4):671–7. doi:10.1016/j.aej.2017.01.017
53. Javed MF, Khan MI, Khan NB, Muhammad R, Rehman MU, Khan SW, et al. Axisymmetric flow of Casson fluid by a swirling cylinder. Results Phys (2018) 9:1250–5. doi:10.1016/j.rinp.2018.04.015
54. Khan NB, Ibrahim Z, Khan MI, Hayat T, Javed MF. VIV study of an elastically mounted cylinder having low mass-damping ratio using RANS model. Int J Heat Mass Transfer (2018) 121:309–14. doi:10.1016/j.ijheatmasstransfer.2017.12.109
55. Khan NB, Ibrahim Z, Bin Mohamad Badry AB, Jameel M, Javed MF. Numerical investigation of flow around cylinder at Reynolds number= 3900 with large eddy simulation technique: effect of spanwise length and mesh resolution. J Eng Maritime Environ (2019) 233(2):417–27. doi:10.1177/1475090217751326
56. Javed MF, Waqas M, Khan NB, Muhammad R, Rehman MU, Khan MI, et al. On entropy generation effectiveness in flow of power law fluid with cubic autocatalytic chemical reaction. Appl Nanoscience (2019) 9(5):1205–14. doi:10.1007/s13204-019-01064-8
57. Khan MI, Qayyum S, Hayat T, Khan MI, Alsaedi A, Khan TA. Entropy generation in radiative motion of tangent hyperbolic nanofluid in presence of activation energy and nonlinear mixed convection. Phys Lett A (2018) 382(31):2017–26. doi:10.1016/j.physleta.2018.05.021
58. Ahmed SE, Raizah ZAS, Aly AM. Entropy generation due to mixed convection over vertical permeable cylinders using nanofluids. J King Saud University-Science (2019) 31(3):352–61. doi:10.1016/j.jksus.2017.07.010
Keywords: nanoparticles, magnetohydrodynamic flow, mixed convection, chemical reaction, radiation, bioconvection, inclined sheet
Citation: Wu Y, Chaudhry M, Maqbool N, Tahir M, Basit MA and Imran M (2024) Entropy generation in radiative motion of tangent hyperbolic nanofluid in the presence of gyrotactic microorganisms and activation energy. Front. Phys. 12:1409318. doi: 10.3389/fphy.2024.1409318
Received: 29 March 2024; Accepted: 30 September 2024;
Published: 25 October 2024.
Edited by:
Aurang Zaib, Federal Urdu University of Arts, Sciences and Technology Islamabad, PakistanReviewed by:
Farhan Ali, Federal Urdu University of Arts, Sciences and Technology Islamabad, PakistanCopyright © 2024 Wu, Chaudhry, Maqbool, Tahir, Basit and Imran. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Imran, ZHJtaW1yYW5jaGF1ZGhyeUBnY3VmLmVkdS5waw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.