A qualitative analysis of the artificial neural network model and numerical solution for the nanofluid flow through an exponentially stretched surface

This article aims to analyze the two-dimensional (2D) nanofluid (Ag/C₂H₆O₂) flow past an exponentially stretched sheet. The magnetic field impact, heat source/sink, and convection in the thermal profile are taken into account. The complexity of the problem is reduced by introducing a dimensionless group of functions. The reduced model is transformed into a system of first-order ordinary differential equations (ODEs). This system is further analyzed with the artificial neural network (ANN), which is trained using the Levenberg–Marquardt algorithm. The whole dataset is sub divided into three parts: training ($70\%$), validation ($15\%$), and testing ($15\%$). The impact of nonlinear heat source/sink parameter, magnetic parameter, volume fraction of nanoparticles, and Prandtl number is displayed through graphs. The heat source, volume fraction, and the Prandtl number cause an increase in the thermal profile with its larger values. The magnetic parameter causes a decline in both the thermal and momentum boundary layers with its higher values. The analysis shows that the thermal energy profile is enhanced with the larger values of the volume fraction of silver nanoparticles and heat source. For each case study, the residual error (RE), regression line, and validation of the results are presented. The performance of the proposed methodology is numerically tabulated for the nanoparticle volume fraction shown in Table 3, where the minimum absolute error (AE) is $5.3373e-11$ at $\varphi =0.05$. Based on this, we recommend $\varphi =0.05$ for better performance. The AEs for the ANN and bvp4c are computed for the state variables in Tables for the magnetic parameter $M=\mathrm{5,10}$, and 15. These tables show the overall performance of the ANN and further validate the present study. We have also validated the results of the ANN through the mean squared error graphically, where the accuracy of the proposed methodology is proven.

1 Introduction

Fluids including air, water, and plasma are the most frequently encountered substances in human life. Without a thorough knowledge of these fluids’ transport properties, their industrial utilization is not feasible. Several industrial operations, such as the coating and coloring of constantly moving metal sheets, extrusion of polymer sheets, drawing of copper wires, extrusion of polyvinyl chloride, thin film coating on photographic films, and plastic sheets, include flows over a stretching surface. Due to its practical implications, the study of fluid flows driven by stretching surfaces is a popular topic these days. Byron [1] was the first to investigate the boundary layer flow of a viscous fluid on a continuously moving surface. Lawrence [2] achieved a crowded type solution for a 2D flow, limited by a linear stretching sheet. Numerous assumptions have been taken into consideration when analyzing this ground-breaking research. Andersson [3] investigated how slipping forces affect a stretching surface. The work of Lawrence [2] is expanded upon by Donald [4] for the 3D case. Liu [5] provided the heat transfer analysis for a second-grade electrically conducting fluid across a stretched surface. While discussing the boundary layer flow caused by an exponentially growing surface, Ishak et al. [6] considered the radiation effect. The HNF mixed convective flow phenomenon is examined by Waini et al. [7]. for an exponentially expanding/constricting surface. Gowda et al. [8]. analyzed computationally the Stefan effect for a second-grade fluid flow past a curved stretched sheet. The role of magnetic dipoles in the flow of ferromagnetic NF past a stretching sheet is presented by Gowda et al. [9] in their 2013 investigation. Asghar et al. [10] used the generalized Fourier strategy to analyze the convective heat transfer for Williamson fluid flows past an unstable sheet.

The phrase “nanofluid” was first used by Choi [11] in a study presented at the ASME Winter Annual Meeting. The thermal conductivity of the nanofluids is better than that of water, making them an innovative type of fluid, including small solid particles. Microparticle applications involve heat transfer, according to several recent inventions. Nanofluids are fluids used in conventional heat transfer that dissipate nanoscale flammable particles. Medical uses for nanofluids include the use of gold nanoparticles to treat malignant tumors and the development of tiny explosives to eliminate malignancies. Jacopo [12] investigated the convective heat transmission in nanofluids with a new type of nanofluid model. Nadeem and Lee [13]. examined the boundary layer flow of the nanofluid that flows past an elongated surface. Convective boundary conditions are used by Mustafaa et al. [14] to characterize the boundary layer flow on the exponentially stretched surface. The nanofluid phenomenon across a porous stretched surface is explained by Bhattacharyya and Layek [15]. Waqas et al. [16] studied the thermally radiative MHD nanofluid flow by utilizing the Robin conditions. Ghosh and Mukhopadhyay [17]. reported the fluxes in the NF flow past a stretching sheet. Sulaiman et al. [18] discusses the 3D flow of microorganisms that contain nanofluids. Ghosh and Mukhopadhyay [19]. described the transfer of heat for an NF flow past an exponentially declining sheet. Ali et al. [20] described numerically the nanofluid phenomenon for an exponentially expanding surface by taking non-uniform heat fluxes. The numerical study for the thermal analysis of the new wavy absorber tube within a solar system is provided by Sheikholeslami et al. [21]. They considered the two-phase model of the nanofluids that contain oil and CuO nanoparticles. They concluded that the friction factor is decreased by $28.96\%$ with $180.13\%$ improvement in the heat transfer coefficient by increasing the Reynolds number from 5,000 to 20,000. Sheikholeslami [22] also demonstrated an air conditioner that uses porous media of four-lobed cylinders that contain paraffin and nanoparticles of ZnO. Gowda et al. [23] examined the stretchable disks for the slip effects of the Casson–Maxwell nanofluid flow. Asghar et al. [24] studied numerically the motion of an organism sliding down a slime-shaded surface.

Magnetohydrodynamics (MHD) is the study of how electrically conducting fluids behave under the influence of the applied magnetic field. The terms magneto (which refers to a magnetic field), hydro (which refers to a liquid), and dynamic (which refers to motion) form the term magnetohydrodynamic. This kind of fluid can be found in electrodes, liquid crystals, seawater, and solitons [25]. The conductor develops a potential when an electric field and a magnetic field move in relation to one another, which results in current flowing between the endpoints in accordance with Faraday’s law of electromagnetic induction [26–28]. This law is used to create MHD power. Currents may flow through an electrically conductive fluid that is flowing through magnetic fields, polarizing the fluid and altering the magnetic field in the process. Alfvén [29] referred to such a fluid having magnetohydrodynamics (MHD). The dynamics of the microorganisms for the Carreau–Yasuda layer is analyzed by Asghar et al. [30]. The mechanism and uses of the MHD flow in a variety of industrial processes have been the subject of numerous studies [31–33]. Benos et al. [34] used the Hamilton–Crosser model to theoretically examine the natural convective MHD flow of CNT-based NF. Asghar et al. [35] studied the flow past a wavy curved sheet in the presence of low Reynolds number. In another study, Asghar et al. [36]. analyzed the bacterial motion past a slime with the Oldroyd-4 constant. A more recent survey can be found in Refs. [37–40]. The solution strategy is important for the analysis of the nonlinear problems [41]. Recently, artificial intelligence (AI) methodologies have been broadly used for a variety of nonlinear problems. Among them, Shafiq et al. [42, 43]. used the ANN for the analysis of the exponential distribution. They have analyzed the Weibull distribution through the ANN and compared the results by using a numerical strategy. Bhadauria et al. [44] studied the THNF flow past a cone and disk by using the supervised learning ANN approach. Ali et al. [45] studied the Ostwald–de Waele model for the flow through the cavity by using the ANN based on the Levenberg–Marquardt algorithm. Srilatha et al. [46] studied the nanofluid flow past a porous rotating disk by using the ANN. Brunton et al. [47] explained the applications of machine learning in fluid mechanics. Amini and Mohaghegh [48] analyzed the machine learning in a porous media. They implemented the ANN by considering proxy modeling. Eivazi et al. [49] studied the experimental fluid mechanics under the impact of machine learning. A more recent survey on the nanofluid flow by using the ANN can be found in Refs. [50–52].

The above analysis clarifies that the choice of nanofluids for the transfer of heat is important. In this work, we will use silver (Ag) nanoparticles in the base fluid C₂H₆O₂ to form a new nanofluid and briefly explain the flow of Ag/C₂H₆O₂ past an unstable stretched sheet. The magnetic parameter is applied perpendicular to the sheet along the $y$-axis. The convective impact on the thermal profile is taken into account. The non-uniform flux of heat is considered to analyze the source and sink for thermal energy enhancement or reduction. Including these assumptions, the physical problem is modeled together with the boundary convective conditions. Furthermore, the proposed problem is tackled with a trained ANN that uses the Levenberg–Marquardt algorithm. To the best of our knowledge, this is the first study to report the Ag/C₂H₆O₂ nanofluid by using the ANN-trained approach based on the Levenberg–Marquardt algorithm.

The layout of the article is categorized as follows: Section 2 presents a physical description of the problem together with its mathematical relation. The proposed methodology is briefly explained in Section 3, while the training procedure is explained in Section 3.1. The approximation and impact of various pertinent parameters are explained in Section 4, while the conclusion is provided in Section 5.

2 Problem formulation

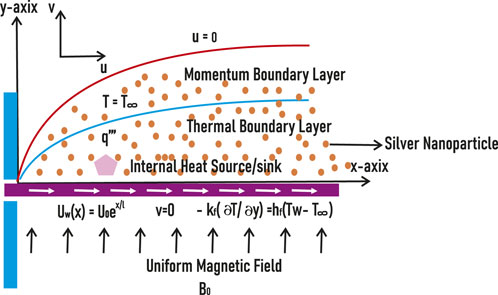
We consider a constant, incompressible, and two-dimensional nanofluid flow past a nonlinear stretching surface. A magnetic field with strength $B_0$ is applied normally to the fluid flow. The impacts of uneven heat transfer and convective boundary conditions are also considered. The geometry is chosen in such a way that the surface is stretched along the $x$-axis, as shown in Figure 1. Since the surface chosen is exponentially stretching, the velocity along the $x-$axis has the form $U_w=U_0{e}^{\frac{x}{l}}$.

Figure 1

Figure 1. Problem geometry.

By assuming the above conditions, we have [20]

$\frac{\partial u}{\partial x}=-\frac{\partial v}{\partial y},(1)$

$u\frac{\partial u}{\partial x}=-v\frac{\partial u}{\partial y}+\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{nf}}{{\rho }_{nf}}{B}_0^{2}u,(2)$

$u\frac{\partial T}{\partial x}=-v\frac{\partial T}{\partial y}+\frac{{\kappa }_{nf}}{{\left(\rho c_p\right)}_{nf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\kappa }_{nf}{U}_w\left(x\right)}{x{v}_{nf}{\left(\rho c_p\right)}_{nf}}\left[A\left(T_w-T_{\infty }\right)f^{\prime }+\left(T-T_{\infty }\right)B\right].(3)$

The boundary conditions from the physical problem can be written as [20, 53]

$\begin{array}{c}\hfill u=U_w\left(x\right),v=0,{\kappa }_f\frac{\partial T}{\partial y}+h_f\left(T_w-T_{\infty }\right)=0,\text{\hspace{0.17em}at\hspace{0.17em}}y=0,\\ \hfill u\to 0,T\to T_{\infty }\text{\hspace{0.17em}as\hspace{0.17em}}y\to \infty .\end{array}(4)$

Here, $(u,v)$ represent the components of velocity; $B_0$ is the applied magnetic field strength; $T$ is the temperature of the fluid, $A$ and $B$ are the heat source and sink, respectively, $T_{\infty }$; and $T_w$ are the ambient and surface temperatures, respectively.

Assume the following [53]:

$\begin{array}{cc}\hfill & \frac{u}{U_0}=\exp \left(\frac{x}{l}\right)f^{\prime }\left(\eta \right),v=-\sqrt{\frac{v_f{U}_0}{2l}}\exp \left(\frac{x}{l}\right)\left(\eta f^{\prime }\left(\eta \right)+f\left(\eta \right)\right),\hfill \\ \hfill & \theta \left(\eta \right)\left(T_w-T_{\infty }\right)=T-T_{\infty },\frac{\eta }{y}=\sqrt{\frac{U_0}{2v_{f}l}}\exp \left(\frac{x}{2l}\right).\hfill \end{array}(5)$

Now, by substituting Equation 5 into Equations 1–4, we obtain

$\frac{A_0}{A_1}{f}^{\prime \prime \prime }+f^{\prime \prime }=\frac{A_2}{A_1}M{f}^{\prime }+2f^{\prime 2},(6)$

${\theta }^{\prime \prime }+\mathrm{Pr}\frac{A_3}{A_4}f{\theta }^{\prime }+\frac{A_1}{A_0}\left(f^{\prime }A+\theta B\right)=0,(7)$

$\begin{array}{cc}\hfill & f^{\prime }\left(\eta \right)=1,f\left(\eta \right)=0,{\theta }^{\prime }\left(\eta \right)+\gamma \left(1-\theta \left(\eta \right)\right)=0\text{\hspace{0.17em}at\hspace{0.17em}}\eta =0,\hfill \\ \hfill & \theta \left(\eta \right)\to 0,f^{\prime }\left(\eta \right)\to 0\text{\hspace{0.17em}as\hspace{0.17em}}\eta \to \infty .\hfill \end{array}(8)$

Here, $A_0=\frac{{\mu }_{nf}}{{\mu }_f}$, $A_1=\frac{{\rho }_{nf}}{{\rho }_f}$, $A_2=\frac{{\sigma }_{nf}}{{\sigma }_f}$, $A_3=\frac{{\left(\rho c_p\right)}_{nf}}{{\left(\rho c_p\right)}_f}$, and $A_4=\frac{{\kappa }_{nf}}{{\kappa }_f}$. All these parameters are defined in Table 1, whose thermophysical properties are defined in Table 2. In addition, $M=\frac{{\sigma }_f{B}_0^2{U}_0}{{\rho }_f}$ and $Pr=\frac{{\mu }_f{(\rho c_p)}_f}{{\rho }_f{k}_f}$ are magnetic and Prandtl numbers, respectively.

Table 1

Table 1. Nanofluid models.

Table 2

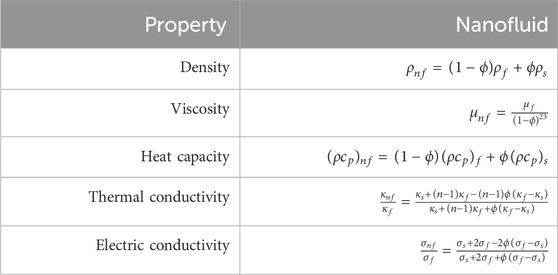
Table 2. Thermo-physical properties of the base fluid and nanoparticles [54].

3 Proposed methodology

This work aims to implement the machine learning strategy known as the artificial neural network (ANN). The ANN is a nature-inspired algorithm that uses the structure of the human brain. It receives the input and trains the neurons in the hidden layers to produce the output. Nowadays, the ANN is widely used for different purposes, including future prediction of economic prosperity, weather prediction, and security purposes. The ANN has opened a new era in machine learning with its wide range of applications see the references [55, 56].

The ANN is also very fault-tolerant and continues its functioning even if some parts stop working. In addition, ANNs are helpful for modeling complicated systems because they can detect nonlinear correlations in data. Finally, ANNs are helpful for many real-world applications because they can accurately map inputs to outputs as suggested in the reference [57]. ANNs are based on interconnected neurons and nodes. They receive the input and perform various operations back and forth to generate the output.

We reduce the system of Equations 6–8 to a first-order system as given below:

$\begin{array}{c}\hfill y_1=f,y_3=f^{\prime \prime },y_2=f^{\prime },y_4=\theta ,y_5={\theta }^{\prime },\\ \hfill y_1^{\prime }=y_2,\\ \hfill y_2^{\prime }=y_3,\\ \hfill y_3^{\prime }=-\frac{A_1}{A_0}\left(y_1{y}_3-2y_2^2-\frac{A_2}{A_1}M{y}_2\right),\\ \hfill y_4^{\prime }=y_5,\\ \hfill y_5^{\prime }=-\left(Pr\frac{A_3}{A_4}{y}_1{y}_5+\frac{A_1}{A_0}\left(A{y}_2+B{y}_4\right)\right.\end{array}(9)$

The corresponding B.Cs are as follows:

$\begin{array}{c}\hfill y_1\left(0\right)=0,y_5\left(0\right)=-\gamma \left(1-y_4\left(0\right)\right),y_2\left(0\right)=1,\\ \hfill y_2\left(\infty \right)=0,y_4\left(\infty \right)=0.\end{array}(10)$

In general, for an unknown function $u_k$, the weight $w_k$ and constant ${\beta }_k$ are given by the following formula for a certain input $t_k$.

$u_j={\displaystyle \sum _{j=1}^k}{w}_j{t}_j-{\beta }_j.(11)$

We introduce the following sigmoid function to obtain the results for $f(\zeta )$ and $\theta (\zeta )$:

$\chi \left(u_j\right)=\frac{1}{1+e^{-\left(w_j{t}_j-{\beta }_j\right)}}.(12)$

3.1 Weight training

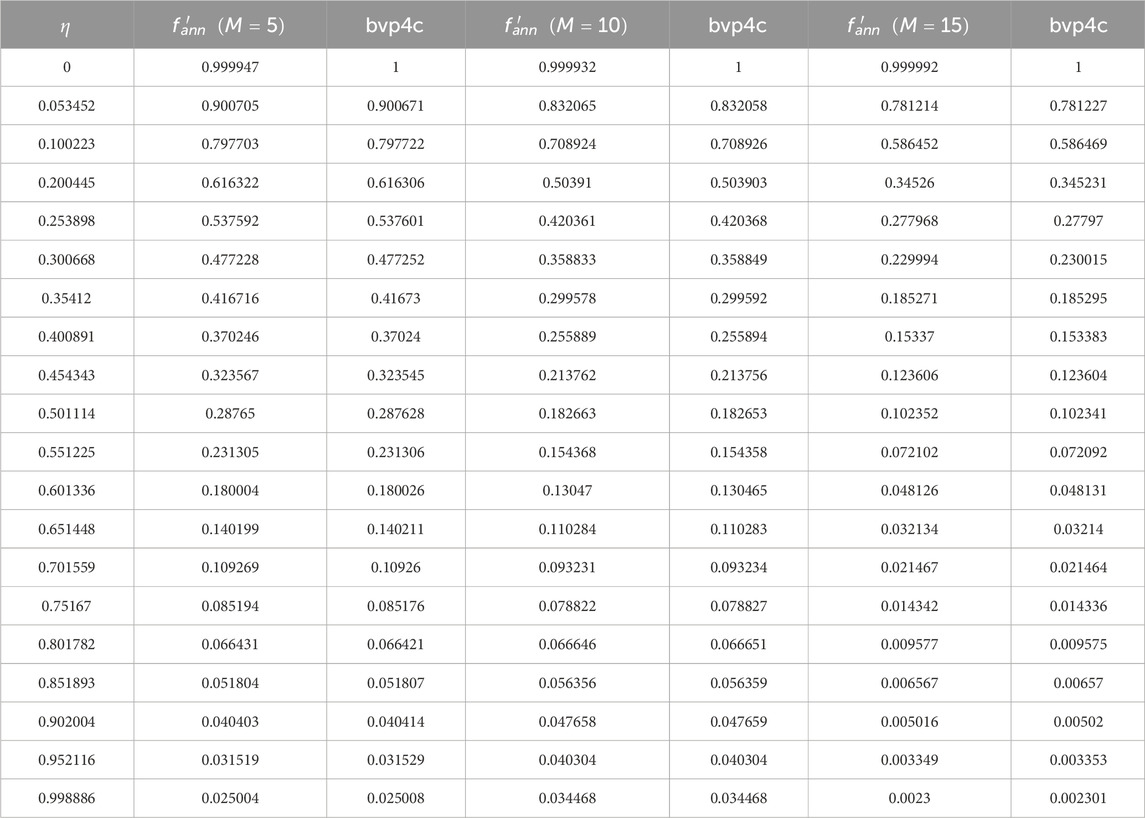
The generation of output results with the training phase in the hidden layer needs to be analyzed in detail. Before the implementation of the ANN, the systems of Equations 9, 10 are solved using the bvp4c. Bvp4c uses the finite difference scheme and implements the Lobatto IIIa formula. This formula is derived from the collection of polynomials that provide a continuous, fourth-order, accurate, and uniform solution. We assume $\eta =3$, step size = 0.01, and tolerance = $e-10$. We approximate the unknown function given in Equation 11 by using the sigmoid function defined in Equation 12. The basic idea of the bvp4c for fluid flow problems is explained by Wang et al. [58]. Ullah et al. [59] recently explained the supervised learning approach for HNF flow problems. We take this result as a dataset and split it into testing, training, and validation datasets for the implementation of the ANN. The ANN assigns different weights to the neurons and produces the optimal result. The solution is discussed with mean squared error, absolute error, and regression $(R^2)$, defined as follows:

$MSE=\frac{1}{j}{\displaystyle \sum _{i=1}^j}{\left(z_i\left(t\right)-{\widehat{z}}_i\left(t\right)\right)}^2,(13)$

$1-R^2=\frac{{\sum }_{i=1}^j{\left({\widehat{z}}_i\left(t\right)-{\bar{x}}_i\left(t\right)\right)}^2}{{\sum }_{i=1}^j{\left(z_i\left(t\right)-{\widehat{z}}_i\left(t\right)\right)}^2},(14)$

and

$AE=|z_i\left(t\right)-{\widehat{z}}_i\left(t\right)|,j=\mathrm{1,2},\dots ,k.(15)$

4 Results and discussions

The results obtained are presented in Figures 2–6 and Table 3. The state variables are displayed under the influence of various pertinent parameters, together with AEs, regression lines, and validation of results given in Equations 13–15. In addition, the results are presented in the form of a table for various choices of the nanofluid volume fraction.

Figure 2

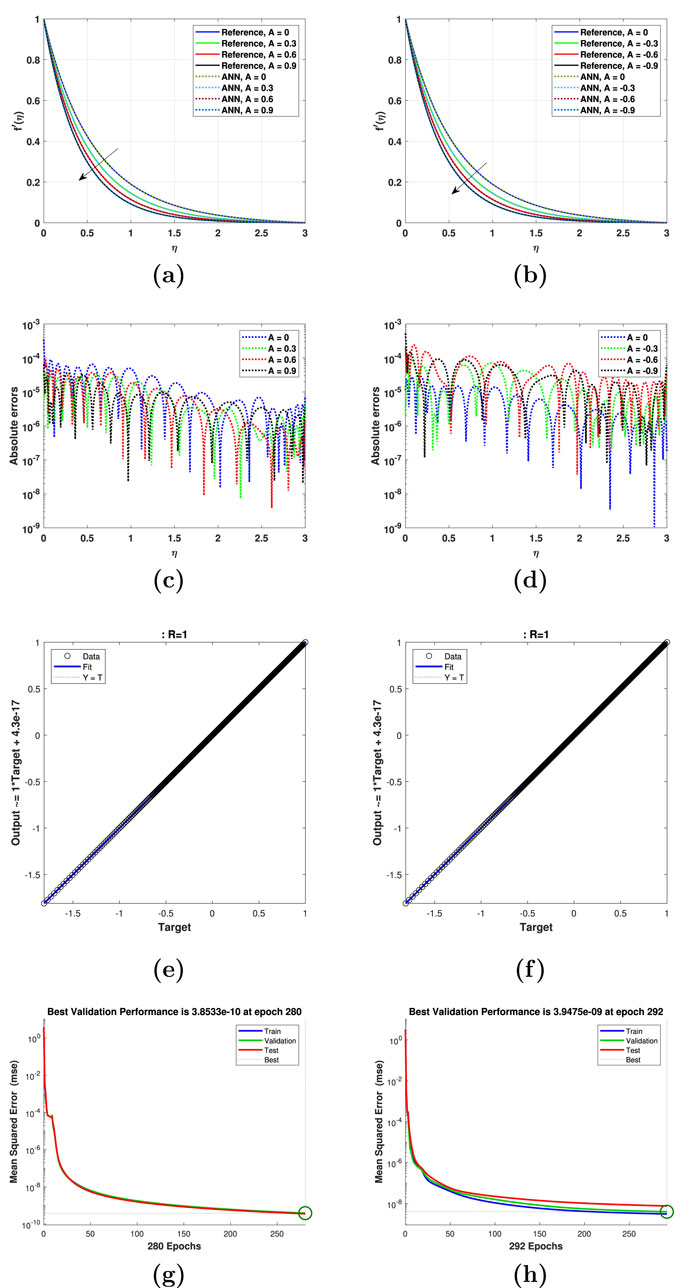
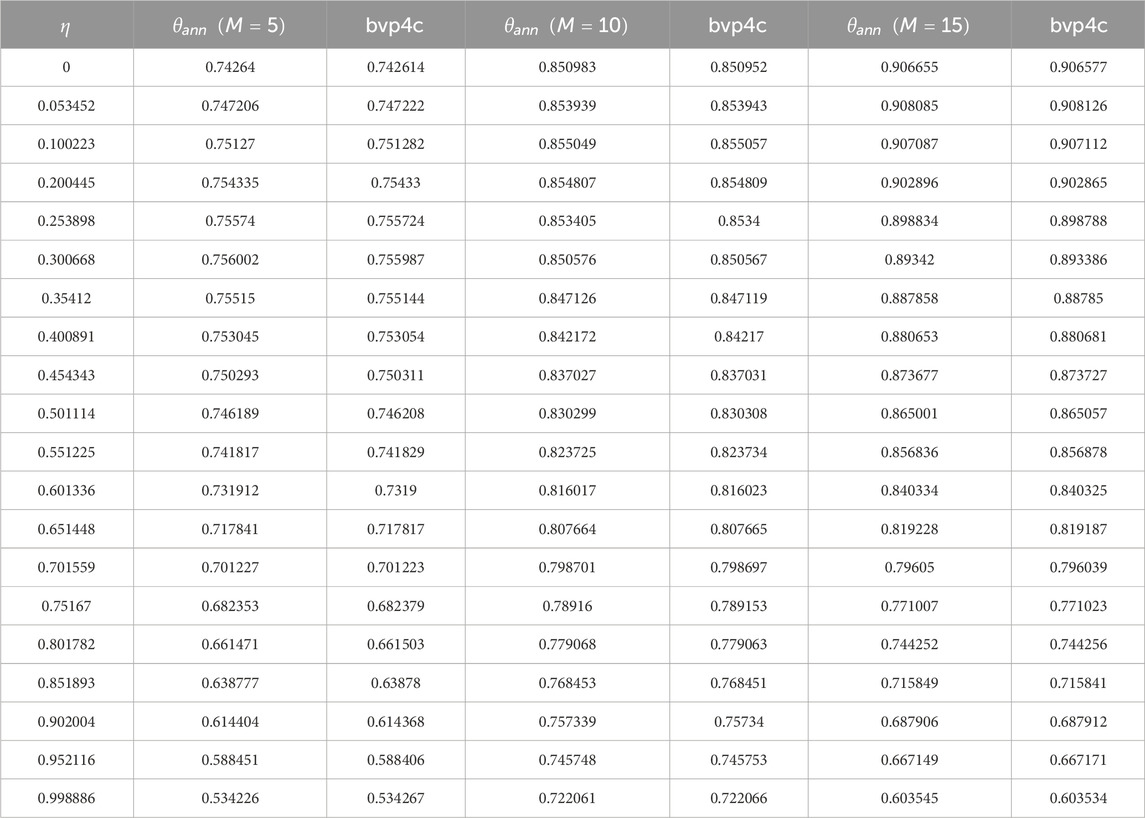
Figure 2. Impact of the space-dependent parameter $(A)$ on $f^{\prime }$ when (A) $A>0$, (B) when $A<0$, (C) absolute error (AE) when $A>0$, (D) absolute error (AE) when $A<0$, (E) regression line when $A>0$, (F) regression line when $A<0$, (G) performance when $A>0$, and (H) performance when $A<0$.

Figure 3

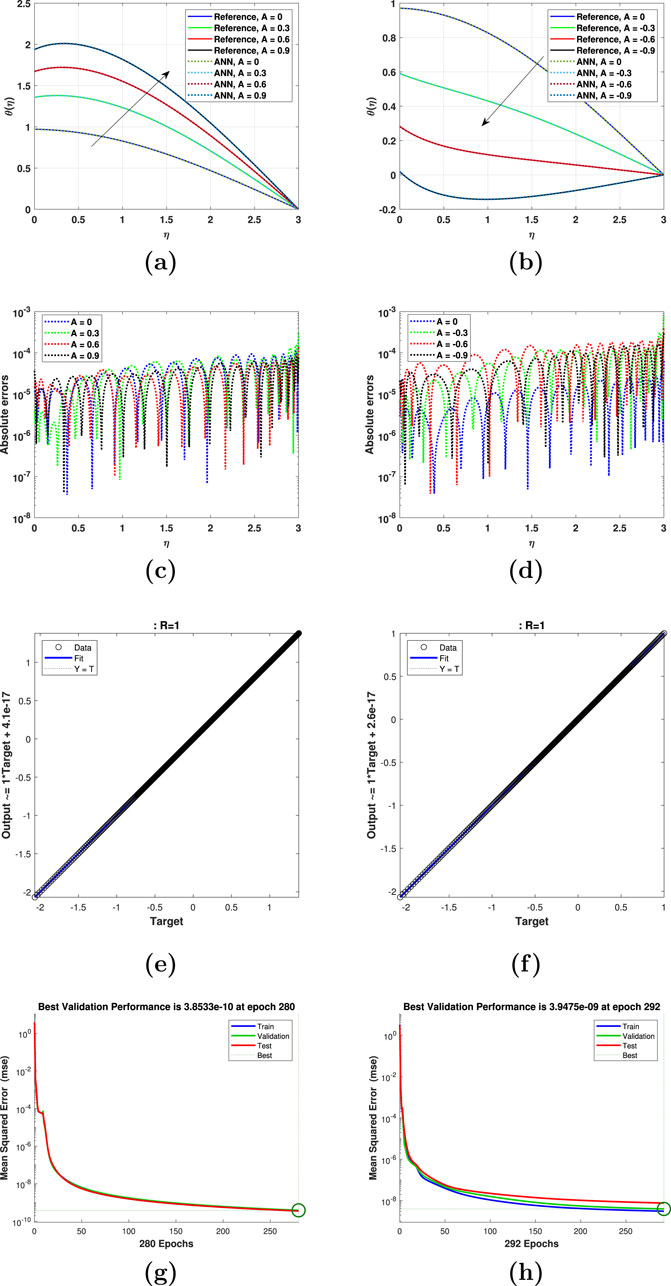
Figure 3. Impact of the space-dependent parameter $(A)$ on $\theta$ when (A) $A>0$, (B) when $A<0$, (C) absolute error (AE) when $A>0$, (D) absolute error (AE) when $A<0$, (E) regression line when $A>0$, (F) regression line when $A<0$, (G) performance when $A>0$, and (H) performance when $A<0$.

Figure 4

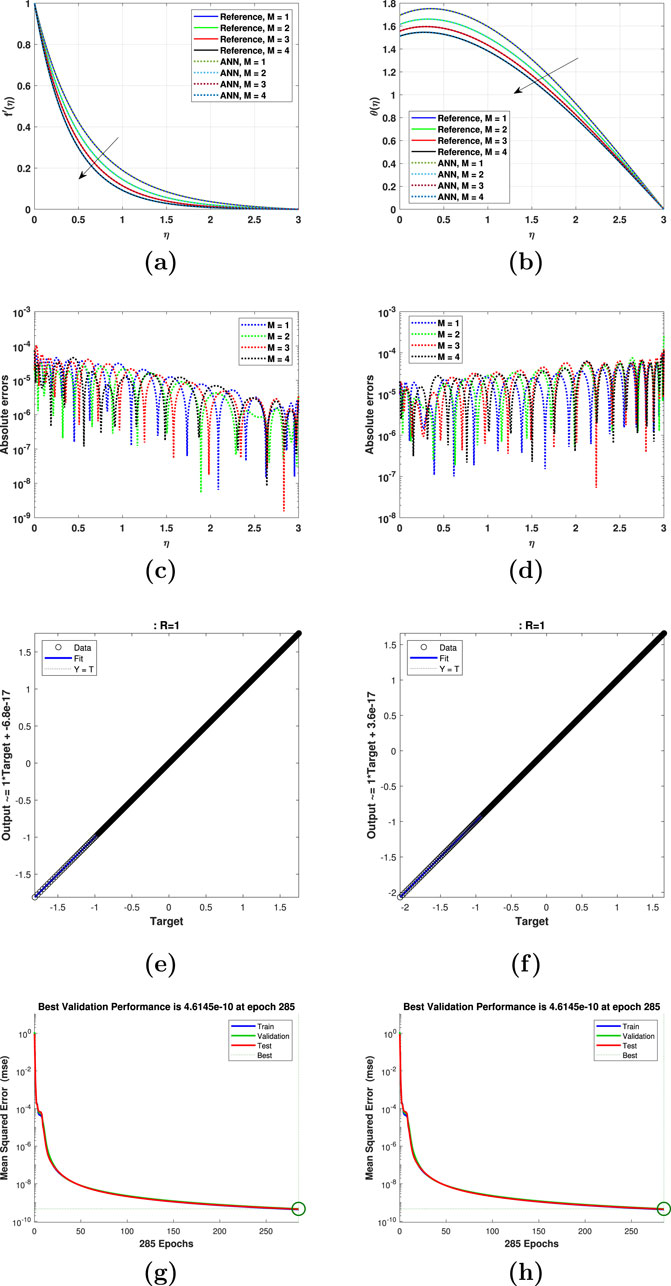
Figure 4. Impact of the magnetic parameter $(M)$ on (A) $f^{\prime }$ and (B) $\theta$, (C) absolute error (AE) for $f^{\prime }$, (D) absolute error (AE) for $\theta$, (E) regression line for $f^{\prime }$, (F) regression line for $\theta$, (G) performance for $f^{\prime }$, and (H) performance for $\theta$.

Figure 5

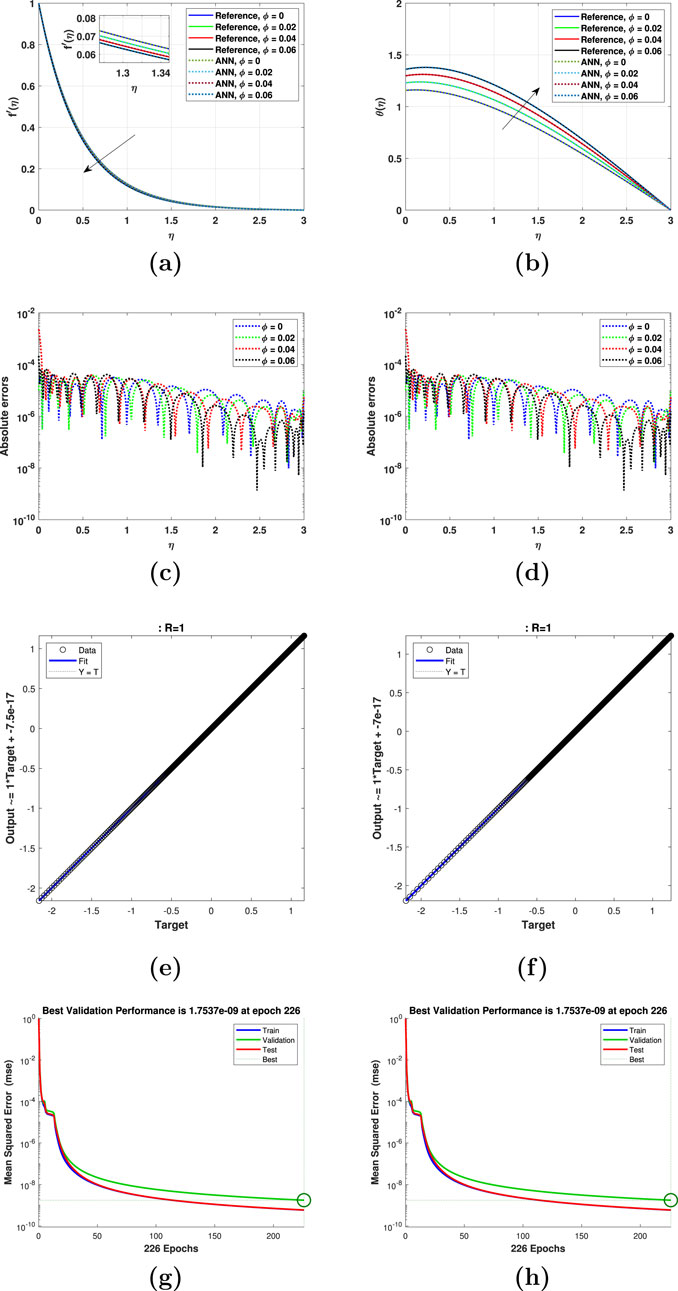
Figure 5. Impact of the nanoparticle volume fraction $(\varphi )$ on (A) $f^{\prime }$ and (B) $\theta$, (C) absolute error (AE) for $f^{\prime }$, (D) absolute error (AE) for $\theta$, (E) regression line for $f^{\prime }$, (F) regression line for $\theta$, (G) performance for $f^{\prime }$, and (H) performance for $\theta$.

Figure 6

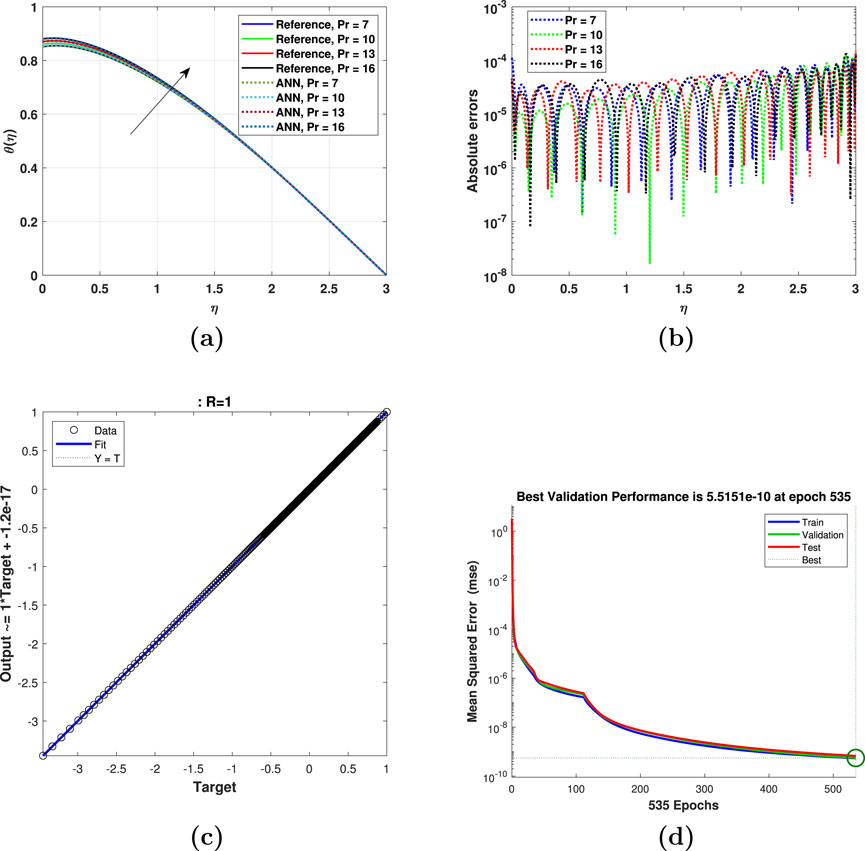
Figure 6. Impact of Prandtl number $Pr$ on (A) $\theta$, (B) AE for $\theta$, (C) regression line for $\theta$, and (D) performance for $\theta$.

Table 3

Table 3. Absolute error (AE) for various values of $\varphi$.

A shown in Figure 2A, the impact of the space-dependent parameter $A>0$ is displayed for the velocity gradient. When increasing the positive $A$ from 0 to 0.9, the velocity gradient decreases from 1 to 0. A quite similar trend is observed in Figure 2B for $A<0$. The AEs for both positive and negative trends of $A$ are displayed in Figures 2C, D. The AEs in both cases vary up to $10^{-9}$. This effect is faster as $\eta$ varies from 0 to 3. The maximum AE occurs at $\eta =2.7$ for $A<0$, while the same trend is observed for $A>0$ when $\eta =2.67$. The maximum AE occurs for $A=0.6$ and $A=0$, as shown by the red and blue lines in Figures 2C, D, respectively. Regression is employed to assess the reliability of the data. As the regression value approaches 1, it implies improved data. Regression is used to assess the validity, training, and testing data. As shown in Figures 2E, F, the regression lines show 1, which proves the best result and recommends that $100\%$ data are available on the linear line. This analysis proves that our proposed methodology has better performance. Furthermore, the surrogate results are presented on the $y-$axis. The total performance in both cases is presented in Figures 2G, H. The best validation performance for $A>0$ is $3.8533e-10$ at $280$ epochs, while for $A<0$, it is $3.9475e-09$ at 292 epochs. The same parameter for both positive and negative values is analyzed for the thermal profile, as shown in Figure 3. When $A>0$, the thermal profile increases and vice versa, as shown in Figures 3A, B. By comparing both figures, we see that the increase is a bit slower as compared to the decline. In the case of $A>0$, the fluid velocity blows, and the thermal profile due to the convection increases. On the other hand, when $A<0$, the suction takes place and the fluid velocity declines. As a result, the migration of the particles decreases, which further decreases the interaction and causes a decline in the thermal profile. The AEs for both $A>0$ and $A<0$ are displayed in 3(c) and 3(d), respectively. The AEs for both cases are bounded in the range $10^{-4}$–$10^{-8}$, which proves the stability of our proposed methodology. The regression and performance of the proposed method are displayed in Figures 3E–H. The regression line shows that $R=1$ proves the total data on the fitting line, while the performance is achieved at $3.8533e-10$ and $3.9475e-09$, respectively. This minimum validation is obtained at 280 and 292 epochs, respectively.

The impact of the magnetic parameter for its increasing values is displayed in Figure 4. Figures 4A, B shows the results for the velocity gradient and thermal profiles, respectively. The larger values of $M$ cause a decline in both the velocity gradient and thermal profiles. The reference solution is represented with bold lines, while the ANN results are displayed with dots. The resemblance in both solutions shows the accuracy of the implemented methodology. As $M$ approaches $M$ and $\eta \to 3$, the velocity gradient and the thermal profiles tend to 0. Physically, the larger values of $M$ are due to the stronger magnetic parameter strength $(B_0)$, which acts perpendicular to the stretching sheet. This force creates a field of spirals in the motion of the velocity field that itself is a function of $x$ only. As a result, the field created acts as a barrier to the velocity field, which causes a decline in the velocity profile. Again, the influence of $B_0$ cannot be ignored on the thermal profile. The field created acts as a barrier to the migration of the nanoparticles. The transfer of heat is due to the minimum convection of these nanoparticles, which becomes very small with larger values of $M$. As a result, the thermal profile decreases. The absolute error shows the total performance of the method applied. As shown in Figures 4C, D, the absolute error varies from $10^{-4}$–$10^{-9}$ and $10^{-4}$–$10^{-7}$, respectively. The fitness of the current data for the magnetic parameter is displayed in Figures 4E, F. The regression line shows $R=1$ in both the cases, which recommends that the $100\%$ data are used in fitting the regression curve. On the $y-$axis, the surrogate results are displayed, which vary by $10^{-17}$ in both cases. The validation for the current analysis is shown in Figures 4G, H. The mean squared error in each case decreases, and the best results in both cases for velocity and thermal profiles are achieved at 285 epochs, which is $4.6145e-10$ for both profiles.

The impact of the volume fraction $\varphi$ on its increasing trend is displayed in Figure 5. As shown in Figures 5A, B, these analyses are carried out for the state variables (velocity gradient and thermal profile). As $\varphi$ increases, the velocity decreases. This decrease is very small. For more clarity, a zoom capture is provided, where the decrease is clearly visible. Physically, the larger volume fraction decreases the convection, and as a result, the velocity profile decreases. As shown n Figure 5B, the temperature profile decreases due to the larger values of the nanofluid volume fraction. The larger volume fraction has the ability to absorb more heat and acts as a source of heat. Thus, the larger the volume fraction, the greater the volume fraction. The reference solution and ANN solution show a similar trend in both profiles. The absolute errors for both cases are plotted in Figures 5C, D. The absolute error for both the velocity and temperature ranges from $10^{-2}$–$10^{-9}$. The regression lines and validations are presented in Figures 5E–H. The regression lines show $R=1$ and the output $10^{-17}$ on the $y-axis$ in both cases. The results are validated at $1.7537e-09$ at 226 epochs, as shown in Figures 5G, H.

The impact of the Prandtl number $Pr$ on the thermal profile is shown in Figure 6. The increasing values of $Pr$ increase the thermal profile. When $Pr$ increases, the specific heat increases, further causing the fluid to lose internal energy. The density $\rho$ is inversely related to $Pr$, and hence the larger values of $Pr$ cause the fluid density to be smaller and the base fluid to become more feasible to flow. The motion of the base fluid and the thermal increase in the specific heat increases the thermal profile. The AE for the $Pr$ variations is plotted in Figure 6B. The absolute error (AE) ranges in $10^{-4}$–$10^{-8}$. This shows the overall performance of our method. The regression line and validations are both presented in Figures 6C, D. The regression line has $R=1$, with the trained output on the $y-$ axis varying up to $10^{-17}$. The validations are achieved at $5.5151e-10$ with 535 epochs. The overall performance shows that the results are validated.

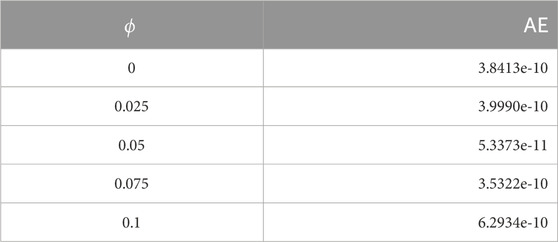
The AEs for various choices of $\varphi$ while keeping other parameters fixed are displayed in Table 3. The AE varies from $10^{-10}$–$10^{-11}$. Best values of AE occur at $\varphi =0.05$. This analysis proves that in the range of 0–0.1, the ideal choice would be 0.05 for $\varphi$. The numerical results for the AEs are presented in Tables 4, 5 for $f^{\prime }$ and $\theta$, respectively. The ANN results are compared with the bvp4c results for various choices of $M$. It is clear from both the tables that when $\eta \to 1$, the convergence of $f^{\prime }$, as compared to bvp4c, is faster. This convergence rate is proved at each step, and the ANN results converge more rapidly toward 0. A quite similar trend is observed in Table 5, where the larger values of $\eta$ push the ANN results for $\theta$ more rapidly toward 0 as compared to bvp4c. The analysis proves that the ANN has better performance as compared to bvp4c.

Table 4

Table 4. Comparison of ANN and bvp4c AEs for $f^{\prime }$.

Table 5

Table 5. Comparison of ANN and bvp4c AEs for $\theta$.

5 Conclusion

This article provides a comprehensive analysis of a new type of ethylene glycol-based nanofluid with silver nanoparticles. The shape of nanoparticles and other important parameters for the thermal as well as the velocity profile are discussed in detail. We observed the following points:

$•$ The thermal profile under the influence of the increasing values of the heat source increases, while the velocity gradient decreases.

$•$ The larger values of the magnetic parameter cause a decline in the thermal and velocity profiles.

$•$ The shape effect of the nanofluid decreases the velocity profiles and increases the thermal profile.

$•$ The minimum AE $5.3373e-11$ is observed at $\varphi =0.05$ in Table 3, and therefore, we recommend nanoparticle shape 0.05 for simulation purposes.

$•$ As shown in Tables 4, 5, the results of the ANN are compared with the bvp4c for different values of $M$, where the efficacy of the ANN is proved.

$•$ For the validity and stability of the proposed methodology, the regression line, MSE, and AE are presented in each case.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

AU: conceptualization, data curation, formal analysis, methodology, software, visualization, and writing–review and editing. HY: conceptualization, formal analysis, project administration, resources, supervision, validation, visualization, and writing–original draft. Waseem: conceptualization, data curation, formal analysis, methodology, resources, software, validation, and writing–original draft. AS: data curation, formal analysis, investigation, methodology, software, validation, and writing–review and editing. FA: data curation, formal analysis, funding acquisition, investigation, project administration, software, visualization, and writing–review and editing. EI: conceptualization, data curation, formal analysis, funding acquisition, investigation, resources, software, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

Researchers Supporting Project Number (RSPD2024R1060), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Byron CS. Boundary-layer behavior on continuous solid surfaces: I. boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J (1961) 7(1):26–8. doi:10.1002/aic.690070108

CrossRef Full Text | Google Scholar

2. Lawrence JC. Flow past a stretching plate. Z für Angew Mathematik Physik ZAMP (1970) 21:645–647. doi:10.1007/BF01587695

CrossRef Full Text | Google Scholar

3. Andersson HI. Slip flow past a stretching surface. Acta Mechanica (2002) 158(1-2):121–5. doi:10.1007/bf01463174

CrossRef Full Text | Google Scholar

4. Donald Ariel P. Generalized three-dimensional flow due to a stretching sheet. ZAMM-Journal Appl Mathematics Mechanics/Zeitschrift für Angew Mathematik Mechanik: Appl Mathematics Mech (2003) 83(12):844–52. doi:10.1002/zamm.200310052

CrossRef Full Text | Google Scholar

5. Liu I-C. Flow and heat transfer of an electrically conducting fluid of second grade in a porous medium over a stretching sheet subject to a transverse magnetic field. Int J Non-Linear Mech (2005) 40(4):465–74. doi:10.1016/j.ijnonlinmec.2004.07.008

CrossRef Full Text | Google Scholar

6. Ishak A, et al. Mhd boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malaysiana (2011) 40(4):391–5.

Google Scholar

7. Waini I, Ishak A, Pop I. Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid. Alexandria Eng J (2020) 59(3):1881–91. doi:10.1016/j.aej.2020.05.030

CrossRef Full Text | Google Scholar

8. Gowda RJP, Mehmet Baskonus H, Kumar RN, Prasannakumara BC, Prakasha DG. Computational investigation of stefan blowing effect on flow of second-grade fluid over a curved stretching sheet. Int J Appl Comput Mathematics (2021) 7(3):109. doi:10.1007/s40819-021-01041-2

CrossRef Full Text | Google Scholar

9. Gowda RJP, Kumar RN, Prasannakumara BC, Nagaraja B, Gireesha BJ. Exploring magnetic dipole contribution on ferromagnetic nanofluid flow over a stretching sheet: an application of stefan blowing. J Mol Liquids (2021) 335:116215. doi:10.1016/j.molliq.2021.116215

CrossRef Full Text | Google Scholar

10. Asghar Z, Kousar M, Waqas M, Irfan M, Bilal M, Khan WA. Heat generation in mixed convected williamson liquid stretching flow under generalized fourier concept. Appl Nanoscience (2020) 10:4439–44. doi:10.1007/s13204-020-01500-0

CrossRef Full Text | Google Scholar

11. Choi SUS, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne, IL (United States): Argonne National Lab.ANL (1995). Technical report.

Google Scholar

12. Jacopo Buongiorno. Convective transport in nanofluids (2006).

Google Scholar

13. Nadeem S, Lee C. Boundary layer flow of nanofluid over an exponentially stretching surface. Nanoscale Res Lett (2012) 7:94–6. doi:10.1186/1556-276x-7-94

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Mustafaa M, Hayat T, Obaidat S. Boundary layer flow of a nanofluid over an exponentially stretching sheet with convective boundary conditions. Int J Numer Methods Heat and Fluid Flow (2013) 23(6):945–59. doi:10.1108/hff-09-2011-0179

CrossRef Full Text | Google Scholar

15. Bhattacharyya K, Layek GC. Magnetohydrodynamic boundary layer flow of nanofluid over an exponentially stretching permeable sheet. Phys Res Int (2014) 2014:1–12. doi:10.1155/2014/592536

CrossRef Full Text | Google Scholar

16. Waqas M, Asghar Z, Khan WA. Thermo-solutal robin conditions significance in thermally radiative nanofluid under stratification and magnetohydrodynamics. The Eur Phys J Spec Top (2021) 230(5):1307–16. doi:10.1140/epjs/s11734-021-00044-w

CrossRef Full Text | Google Scholar

17. Ghosh S, Mukhopadhyay S. Nanofluid flow past an exponentially porous stretching sheet with heat and mass fluxes. Acta Technica (2016) 61:17–29.

Google Scholar

18. Sulaiman M, Ali A, Islam S. Heat and mass transfer in three-dimensional flow of an oldroyd-b nanofluid with gyrotactic micro-organisms. Math Probl Eng (2018) 2018:1–15. doi:10.1155/2018/6790420

CrossRef Full Text | Google Scholar

19. Ghosh S, Mukhopadhyay S. Flow and heat transfer of nanofluid over an exponentially shrinking porous sheet with heat and mass fluxes. Propulsion Power Res (2018) 7(3):268–75. doi:10.1016/j.jppr.2018.07.004

CrossRef Full Text | Google Scholar

20. Ali A, Sajjad A, Asghar S. Thermal-diffusion and diffusion-thermo effects in a nanofluid flow with non-uniform heat flux and convective walls. J Nanofluids (2019) 8(6):1367–72. doi:10.1166/jon.2019.1683

CrossRef Full Text | Google Scholar

21. Sheikholeslami M, Said Z, Jafaryar M. Hydrothermal analysis for a parabolic solar unit with wavy absorber pipe and nanofluid. Renew Energy (2022) 188:922–32. doi:10.1016/j.renene.2022.02.086

CrossRef Full Text | Google Scholar

22. Sheikholeslami M. Modeling investigation for energy storage system including mixture of paraffin and zno nano-powders considering porous media. J Pet Sci Eng (2022) 219:111066. doi:10.1016/j.petrol.2022.111066

CrossRef Full Text | Google Scholar

23. Gowda RJP, Rauf A, Naveen Kumar R, Prasannakumara BC, Shehzad SA. Slip flow of casson–maxwell nanofluid confined through stretchable disks. Indian J Phys (2022) 96(7):2041–9. doi:10.1007/s12648-021-02153-7

CrossRef Full Text | Google Scholar

24. Asghar Z, Ali Shah R, Ali N. A computational approach to model gliding motion of an organism on a sticky slime layer over a solid substrate. Biomech Model Mechanobiology (2022) 21(5):1441–55. doi:10.1007/s10237-022-01600-6

CrossRef Full Text | Google Scholar

25. Wang Y. Multiple positive solutions for mixed fractional differential system with p-laplacian operators. In: Boundary value problems (2019). p. 1–17.

CrossRef Full Text | Google Scholar

26. Zhao Y, Sun Y, Liu Z, Bai Z. Basic theory of differential equations with mixed perturbations of the second type on time scales. In: Advances in difference equations (2019). p. 1–15.

CrossRef Full Text | Google Scholar

27. Mi L. The exact asymptotic behavior of blow-up solutions to a highly degenerate elliptic problem. Boundary Value Probl (2015) 2015:216–2. doi:10.1186/s13661-015-0482-6

CrossRef Full Text | Google Scholar

28. Asghar Z. Enhancing motility of micro-swimmers via electric and dynamical interaction effects. The Eur Phys J Plus (2023) 138(4):357. doi:10.1140/epjp/s13360-023-03963-w

CrossRef Full Text | Google Scholar

29. Alfvén H. On the existence of electromagnetic-hydromagnetic waves. Arkiv Mat Astron Fys (1943).

Google Scholar

30. Asghar Z, Ali Shah R, Ali N. A numerical framework for modeling the dynamics of micro-organism movement on carreau-yasuda layer. Soft Comput (2023) 27(13):8525–39. doi:10.1007/s00500-023-08236-3

CrossRef Full Text | Google Scholar

31. Farooq U, Lu D, Munir S, Ramzan M, Suleman M, Hussain S. Mhd flow of maxwell fluid with nanomaterials due to an exponentially stretching surface. Scientific Rep (2019) 9(1):7312. doi:10.1038/s41598-019-43549-0

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Guo X, Fu Z. An initial and boundary value problem of fractional jeffreys’ fluid in a porous half space. Comput and Mathematics Appl (2019) 78(6):1801–10. doi:10.1016/j.camwa.2015.11.020

CrossRef Full Text | Google Scholar

33. Sharada K, Shankar B. Mhd mixed convection flow of a casson fluid over an exponentially stretching surface with the effects of soret, dufour, thermal radiation and chemical reaction. World J Mech (2015) 5(09):165–77. doi:10.4236/wjm.2015.59017

CrossRef Full Text | Google Scholar

34. Th Benos L, Karvelas EG, Sarris IE. A theoretical model for the magnetohydrodynamic natural convection of a cnt-water nanofluid incorporating a renovated Hamilton-crosser model. Int J Heat Mass Transfer (2019) 135:548–60. doi:10.1016/j.ijheatmasstransfer.2019.01.148

CrossRef Full Text | Google Scholar

35. Asghar Z, Khan MWS, Shatanawi W, Gondal MA, Ghaffari A. An ifdm analysis of low Reynolds number flow generated in a complex wavy curved passage formed by artificial beating cilia. Int J Mod Phys B (2023) 37(19):2350187. doi:10.1142/s0217979223501874

CrossRef Full Text | Google Scholar

36. Asghar Z, Shatanawi W, Hussain S. Biomechanics of bacterial gliding motion with oldroyd-4 constant slime. The Eur Phys J Spec Top (2023) 232(6):915–25. doi:10.1140/epjs/s11734-022-00723-2

CrossRef Full Text | Google Scholar

37. Zi Y, Wang Y. Positive solutions for caputo fractional differential system with coupled boundary conditions. In: Advances in difference equations (2019). p. 1–12.

CrossRef Full Text | Google Scholar

38. ZeinEldin RA, Ullah A, El-Wahed Khalifa HA, Ayaz M. Analytical study of the energy loss reduction during three-dimensional engine oil-based hybrid nanofluid flow by using cattaneo–christov model. Symmetry (2023) 15(1):166. doi:10.3390/sym15010166

CrossRef Full Text | Google Scholar

39. Ullah A, Fatima N, Alharbi KAM, Elattar S, Khan W, Khan W. A numerical analysis of the hybrid nanofluid (ag+ tio2+ water) flow in the presence of heat and radiation fluxes. Energies (2023) 16(3):1220. doi:10.3390/en16031220

CrossRef Full Text | Google Scholar

40. Asghar Z, Khan MWS, Gondal MA, Ghaffari A. Channel flow of non-Newtonian fluid due to peristalsis under external electric and magnetic field. Proc Inst Mech Eng E: J Process Mech Eng (2022) 236(6):2670–8. doi:10.1177/09544089221097693

CrossRef Full Text | Google Scholar

41. Liu Z, Ding Y, Liu C, Zhao C. Existence and uniqueness of solutions for singular fractional differential equation boundary value problem with p-laplacian. Adv Difference Equations (2020) 2020(1):83. doi:10.1186/s13662-019-2482-9

CrossRef Full Text | Google Scholar

42. Shafiq A, Colak AB, Ahmad Lone S, Sindhu TN, Muhammad T. Reliability modeling and analysis of mixture of exponential distributions using artificial neural network. Math Methods Appl Sci (2024) 47(5):3308–28. doi:10.1002/mma.8178

CrossRef Full Text | Google Scholar

43. Shafiq A, Çolak AB, Sindhu TN. Reliability investigation of exponentiated weibull distribution using ipl through numerical and artificial neural network modeling. Qual Reliability Eng Int (2022) 38(7):3616–31. doi:10.1002/qre.3155

CrossRef Full Text | Google Scholar

44. Bhadauria BS, Yaseen M, Kumar Rawat S, Pant M, Pant M. Designing machine learning based intelligent network for assessment of heat transfer performance of ternary hybrid nanofluid flow between a cone and a disk: case of mlp feed forward neural network. Comput and Mathematics Appl (2024) 169:17–38. doi:10.1016/j.camwa.2024.06.003

CrossRef Full Text | Google Scholar

45. Ali AR, Mahmood R, Asghar A, Majeed AH, Behiry MH. Ai-based predictive approach via ffb propagation in a driven-cavity of ostwald de-waele fluid using cfd-ann and levenberg–marquardt. Scientific Rep (2024) 14(1):11024. doi:10.1038/s41598-024-60401-2

CrossRef Full Text | Google Scholar

46. Srilatha P, Gowda RJP, Madhu J, Nagaraja KV, Gamaoun F, Kumar RSV, et al. Designing a solid–fluid interface layer and artificial neural network in a nanofluid flow due to rotating rough and porous disk. J Therm Anal Calorim (2024) 149(2):867–78. doi:10.1007/s10973-023-12706-z

CrossRef Full Text | Google Scholar

47. Brunton SL, Noack BR, Koumoutsakos P. Machine learning for fluid mechanics. Annu Rev Fluid Mech (2020) 52(1):477–508. doi:10.1146/annurev-fluid-010719-060214

CrossRef Full Text | Google Scholar

48. Amini S, Mohaghegh S. Application of machine learning and artificial intelligence in proxy modeling for fluid flow in porous media. Fluids (2019) 4(3):126. doi:10.3390/fluids4030126

CrossRef Full Text | Google Scholar

49. Eivazi H, Wang Y, Vinuesa R. Physics-informed deep-learning applications to experimental fluid mechanics. Meas Sci Technol (2024) 35(7):075303. doi:10.1088/1361-6501/ad3fd3

CrossRef Full Text | Google Scholar

50. Shafiq A, Çolak AB, Sindhu TN. Optimization of bioconvective magnetized walter’s b nanofluid flow towards a cylindrical disk with artificial neural networks. Lubricants (2022) 10(9):209. doi:10.3390/lubricants10090209

CrossRef Full Text | Google Scholar

51. Sheraz Junaid M, Aslam MN, Asim Khan M, Saleem S, Riaz MB. Thermal analysis of a viscoelastic maxwell hybrid nanofluid with graphene and polythiophene nanoparticles: insights from an artificial neural network model. Alexandria Eng J (2024) 94:193–211. doi:10.1016/j.aej.2024.03.029

CrossRef Full Text | Google Scholar

52. Urooj A, Hassan QMU, Raja MAZ, Ayub K, Nisar KS, Shoaib M. Numerical treatment for radiative hybrid nanofluid flow over a stretching sheet. Results Eng (2024) 22:102209. doi:10.1016/j.rineng.2024.102209

CrossRef Full Text | Google Scholar

53. Hussain S, Rasheed K, Ali A, Vrinceanu N, Ahmed A, Shah Z. A sensitivity analysis of mhd nanofluid flow across an exponentially stretched surface with non-uniform heat flux by response surface methodology. Scientific Rep (2022) 12(1):18523. doi:10.1038/s41598-022-22970-y

CrossRef Full Text | Google Scholar

54. Abid N, Ramzan M, Chung JD, Kadry S, Chu Y-M. Comparative analysis of magnetized partially ionized copper, copper oxide–water and kerosene oil nanofluid flow with cattaneo–christov heat flux. Scientific Rep (2020) 10(1):19300. doi:10.1038/s41598-020-74865-5

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Acar Boyacioglu M, Kara Y, Kaan Baykan Ö. Predicting bank financial failures using neural networks, support vector machines and multivariate statistical methods: a comparative analysis in the sample of savings deposit insurance fund (sdif) transferred banks in Turkey. Expert Syst Appl (2009) 36(2):3355–66. doi:10.1016/j.eswa.2008.01.003

CrossRef Full Text | Google Scholar

56. Hamid R, Plaksina T. Application of artificial intelligence techniques in the petroleum industry: a review. Artif Intelligence Rev (2019) 52(4):2295–318. doi:10.1007/s10462-018-9612-8

CrossRef Full Text | Google Scholar

57. Wang D, He H, Liu D. Intelligent optimal control with critic learning for a nonlinear overhead crane system. IEEE Trans Ind Inform (2017) 14(7):2932–40. doi:10.1109/tii.2017.2771256

CrossRef Full Text | Google Scholar

58. Wang J, Ali Shah N, Almutairi B, Kwon OK, Chung JD. Bvp4c approach and duality of hybrid nanofluid over extending and contracting sheet with chemical reaction and cross-diffusion effects. Results Phys (2024) 57:107362. doi:10.1016/j.rinp.2024.107362

CrossRef Full Text | Google Scholar

59. Ullah A, Yao H, Ikramullah NAO, El-Sayed MS. A neuro-computational study of viscous dissipation and nonlinear arrhenius chemical kinetics during the hypodicarbonous acid-based hybrid nanofluid flow past a riga plate. ZAMM-Journal Appl Mathematics Mechanics/Zeitschrift für Angew Mathematik Mechanik:e202400208. doi:10.1002/zamm.202400208

CrossRef Full Text | Google Scholar

Nomenclature

$\mathit{\sigma }$ Electrical conductivity $\frac{S}{m}$

${\mathit{B}}_{\mathbf{0}}$ Magnetic field strength $T$

$\mathit{k}$ Thermal conductivity $\frac{W}{mK}$

$\mathit{P}\mathit{r}$ Prandtl number

${\mathit{U}}_{\mathit{w}}$ Stretching velocity $(\frac{m}{sec})$

${\mathit{U}}_{\mathbf{0}}$ Constant surface velocity $(\frac{m}{sec})$

$\mathit{T}$ Fluid temperature $(K)$

$\mathit{A},\mathit{B}$ Source and sink of heat

$\mathit{\nu }$ Kinematic viscosity $\frac{m^2}{sec}$

$\mathit{\rho }$ Density $(\frac{Kg}{m^3})$

$\mathit{\mu }$ Dynamic viscosity $mPa$

${\mathit{c}}_{\mathit{p}}$ Specific heat $(\frac{J}{KgK})$

$\mathit{x}$,$\mathit{y}$, and$\mathit{z}$ Coordinates $(m)$

$\mathit{\eta }$ Similarity variable

$\mathit{\psi }$ Stream function

${\mathit{h}}_{\mathit{f}}$ Convective heat transfer coefficient

$\mathit{M}$ Magnetic parameter

$\mathit{\varphi }$ Nanofluid volume fraction

$\mathit{f},\mathit{g}$ Dimensionless velocities

$\mathit{l}$ Characteristic length $m$

$\mathit{M}\mathit{S}\mathit{E}$ Mean squared error

$\mathit{R}$ Regression line

$\mathit{R}\mathit{E}$ Residual error

$\mathit{A}\mathit{E}$ Absolute error

$\mathit{b}\mathit{v}\mathit{p}\mathbf{4}\mathit{c}$ Built-in code MATLAB for boundary value problems

$\mathit{\theta }$ Dimensionless temperature

$\mathit{A}\mathit{N}\mathit{N}$ Artificial neural network

$\mathit{\chi }$ Activation function

$\mathit{f}$ Base fluid

$\mathit{N}\mathit{F}$ Nanofluid

$\mathit{H}\mathit{N}\mathit{F}$ Hybrid nanofluid

$\mathit{\infty }$ Condition at infinity

0 Reference condition