
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 24 June 2024
Sec. Quantum Engineering and Technology
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1408429
This article is part of the Research Topic Advancements and Challenges in Quantum Technologies Using Low-Dimensional Systems View all 6 articles
The spin-1/2 Ising-Heisenberg branched chain, inspired by the magnetic structure of three isostructural polymeric coordination compounds [(Tp)2Fe2(CN)6X (bdmap)Cu2(H2O)] ⋅ H2O to be further denoted as Fe2Cu2 (Tp = tris(pyrazolyl)hydroborate, bdmapH = 1,3-bis(dimethylamino)-2-propanol, HX = acetic acid, propionic acid or trifluoroacetic acid), is rigorously studied using the transfer-matrix method. The overall ground-state phase diagram reveals three distinct phases: a quantum antiferromagnetic phase, a quantum ferrimagnetic phase and a classical ferromagnetic phase. In the zero-temperature magnetization curve, two quantum ground states are manifested as intermediate plateaus at zero and half of the saturation magnetization, while the magnetization reaches its saturated value within the classical ferromagnetic phase. The bipartite entanglement between nearest-neighbor Heisenberg spins is more pronounced in the quantum ferrimagnetic phase compared to the quantum antiferromagnetic phase due to a fully polarized nature of the Ising spins. A reasonable agreement between theoretical predictions for the spin-1/2 Ising-Heisenberg branched chain and experimental data measured for a temperature dependence of the magnetic susceptibility and a low-temperature magnetization curve suggests strong antiferromagnetic coupling between nearest-neighbor Cu2+-Cu2+ magnetic ions and moderately strong ferromagnetic coupling between nearest-neighbor Cu2+-Fe3+ magnetic ions in the polymeric compounds Fe2Cu2. A thermal entanglement between nearest-neighbor Cu2+-Cu2+ magnetic ions persists up to a relatively high threshold temperature T ≈ 224 K and undergoes a transient magnetic-field-driven strengthening.
Although one-dimensional (1D) quantum spin models may seem relatively simple at first glance, achieving an exact solution for these lattice-statistical models is often accompanied with formidable mathematical difficulties stemming from noncommuting algebra [1]. As a matter of fact, there exists only a few paradigmatic examples of exactly solved 1D quantum spin models such as the quantum spin-1/2 Heisenberg chain solved by the Bethe-ansatz method [2–5] or the quantum spin-1/2 XY model solved using the Jordan-Wigner fermionization approach [6, 7]. It should be stressed that the exploration of 1D quantum spin models is of particular importance, because several low-dimensional magnetic materials may have negligible exchange interactions in the remaining two spatial dimensions [8]. It has been demonstrated that several 1D spin chains may display intriguing quantum features such quantized magnetization plateaus [9] and quantum entanglement [10].
1D Ising-Heisenberg models featuring regularly alternating Ising and Heisenberg spins are conversely relatively easily exactly solvable using the transfer-matrix method. In spite of their simplicity, these models still offer a plausible framework for theoretical modeling of a certain class of insulating quantum magnetic materials. The first paradigmatic experimental realization of the spin-1/2 Ising-Heisenberg chain composed from regularly alternating Ising spins and Heisenberg spin trimers was found by van den Heuvel and Chibotaru during their analysis of magnetic properties of the trimetallic 3d-4d-4f coordination polymer [{(CuL)2Dy}{Mo(CN)8}]⋅CH3CN⋅H2O, where L2− = N,N′-propylenebis (3-methoxysalicylideneiminato) [11, 12]. A simpler experimental realization of the spin-1/2 Ising-Heisenberg chain, composed from regularly alternating Ising and Heisenberg spins, was discovered in the bimetallic 3d-4f coordination polymer Dy(NO3)(DMSO)2Cu(opba)(DMSO)2 (DMSO = dimethylsulfoxide, opba = orthophenylenebisoxamato) [13–15]. The low-temperature magnetization data of another 3d-4f heterobimetallic coordination polymer [Dy (hfac)2(CH3OH)2Cu(dmg)(Hdmg)2]n (H2dmg = dimethylglyoxime; Hhfac = 1,1,1,5,5,5-hexafluoropentane-2,4-dione) have been successfully interpreted within the spin-1/2 Ising-Heisenberg orthogonal-dimer chain [16, 17]. It is worthwhile to remark that several other exactly solved Ising-Heisenberg spin chains have provided unbiased descriptions of various intriguing quantum phenomena including quantized magnetization plateaus [18, 19], enhanced magnetocaloric effect [19, 20], partition function zeros [21], quantum teleportation [22], unconventional “fire-and-ice” ground states [23], pseudo-transitions [24], quantum coherence [25], quantum nonlocality [26], quantum Fisher information [27] as well as nanostructures [28, 29].
In recent years, considerable attention has been directed towards investigating magnetic and quantum features of Ising-Heisenberg branched chains. Notably, the mixed spin-(1/2,5/2,1/2) Ising-Heisenberg branched chain has demonstrated its utility in theoretical modeling the magnetic characteristics of the heterotrimetallic coordination polymer [CuMn(L)][Fe (bpb)(CN)2]ClO4 ⋅ H2O [30, 31]. The mixed spin-(1/2,5/2,1/2) Ising-Heisenberg branched chain provided a satisfactory explanation of the magnetization and susceptibility behavior of this heterotrimetallic Fe-Mn-Cu coordination polymer. Furthermore, the Fe-Mn-Cu polymeric branched chain has been proposed as a promising platform for realizing quantum teleportation [32, 33], while also exhibiting robust quantum coherence [33] and thermal entanglement [34]. On the other hand, the spin-1/2 Ising-Heisenberg branched chain inspired by the magnetic structure of the bimetallic coordination polymer [(Tp)2Fe2(CN)6(OCH3)(bap)Cu2(CH3OH) ⋅ 2CH3OH ⋅ H2O] (Tp = tris(pyrazolyl)hydroborate, bapH = 1,3-bis(amino)-2-propanol) theoretically predicts an intriguing breakdown of the intermediate one-half magnetization plateau in a low-temperature magnetization curve depending basically on the interaction anisotropy [35, 36].
In the present study, we will introduce a similar but structurally distinct spin-1/2 Ising-Heisenberg branched chain to model the magnetic properties of three isostructural polymeric coordination compounds [(Tp)2Fe2(CN)6X (bdmap)Cu2(H2O)] as reported in Ref. [37] [Tp = tris (pyrazolyl) hydroborate, bdmapH = 1,3-bis(dimetylamino)-2-propanol and HX is acetic acid, propionic acid or trifluoracetic acid]. The magnetic structure of these polymeric coordination compounds, further abbreviated as Fe2Cu2, is shown in Figure 1 and it can be identified as another variant of spin-1/2 Ising-Heisenberg branched chain. This characterization arises from the presence of magnetically isotropic spin-1/2 Cu2+ magnetic ions (S = 1/2) described by the notion of quantum Heisenberg spins, which is in contrast to highly magnetically anisotropic spin-1/2 Fe3+ magnetic ions (σ = 1/2) described by the notion of Ising spins. Consequently, the exchange coupling between nearest-neighbor Cu2+-Cu2+ magnetic ions will be assumed to be of the Heisenberg type, whereas the exchange coupling between nearest-neighbor Fe3+-Cu2+ magnetic ions will be treated as the Ising-type exchange interaction (see Figure 2).
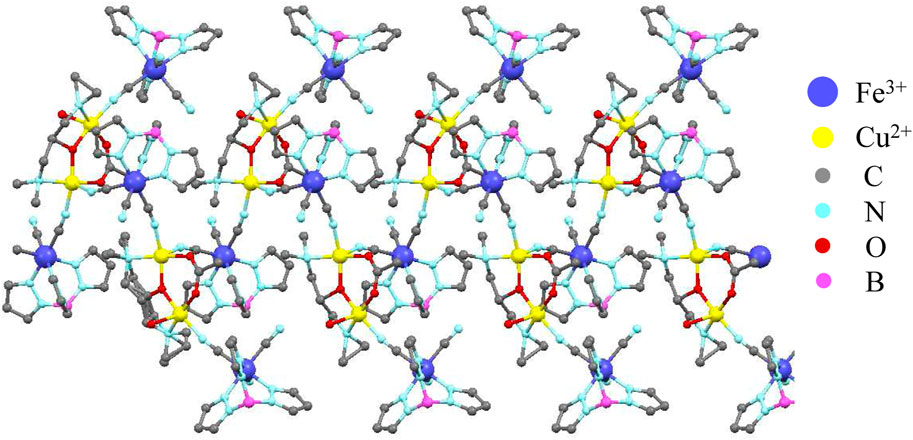
Figure 1. A part of the crystal structure of the polymeric coordination compound [(Tp)2Fe2(CN)6(CH3COO)(bdmap)Cu2(H2O)] depicted according to crystallographic data reported in Ref. [37]. Tp stands for tris(pyrazolyl) hydroborate and bdmapH is 1,3-bis(dimetylamino)-2-propanol.
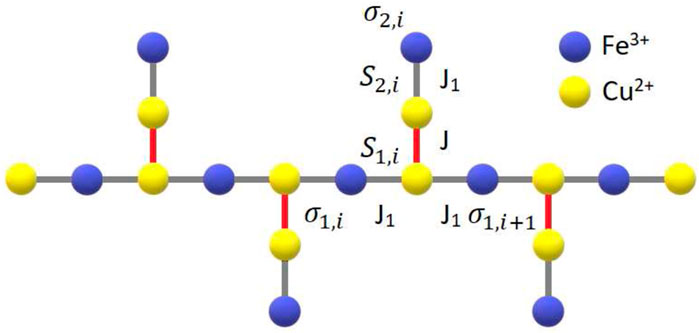
Figure 2. A schematic illustration of the spin-1/2 Ising-Heisenberg branched chain with the isotropic exchange interaction J between nearest-neighbor Heisenberg spins and the anisotropic exchange interaction J1 between the nearest-neighbor Heisenberg and Ising spins, respectively. The Heisenberg spins capture lattice positions of Cu2+ magnetic ions (yellow circles), while the Ising spins capture lattice positions of Fe3+ magnetic ions (blue circles).
The structure of this paper is as follows. In Section 2, we introduce the spin-1/2 Ising-Heisenberg branched chain along with a brief outline of the method employed for its calculation. Section 3 is dedicated to discussing the theoretical findings regarding the ground-state phase diagram, magnetization curves, entropy, and concurrence. In Section 4, we compare the exact theoretical results for the spin-1/2 Ising-Heisenberg branched chain with available experimental data for the magnetization and susceptibility of the polymeric compound Fe2Cu2 together with the respective theoretical prediction for the concurrence. Finally, Section 5 provides a summary of the most important scientific findings obtained in this study.
The spin-1/2 Ising-Heisenberg branched chain schematically illustrated in Figure 2 can be defined through the following Hamiltonian:
where
It is convenient to rewrite the total Hamiltonian (1) as a sum of the cell Hamiltonians
Owing to the fact that the cell Hamiltonians (2) commute with each other
where β = 1/(kBT), kB is the Boltzmann’s constant, T is the absolute temperature, Tri stands for a trace over degrees of freedom of the Heisenberg dimer S1,i − S2,i from the ith unit cell,
where the reduced cell Hamiltonian
The reduced cell Hamiltonian
To perform a trace Tri over degrees of freedom of the spin-1/2 Heisenberg dimer from the ith unit cell in the relevant expression for the partition function (4), it is convenient to proceed to a matrix representation of the reduced cell Hamiltonian (5) in the standard basis:
The state vectors
with the corresponding eigenvectors:
where the probability amplitudes
With the use of the eigenvalues (6) one can further rewrite the partition function (4) into the following simplified form:
where the effective Boltzmann’s factor T (σ1,i, σ1,i+1) is defined as follows:
The effective Boltzmann’s weight (7) depends only on degrees of freedom of two Ising spins σ1,i and σ1,i+1 and it can be alternatively viewed as the transfer matrix:
where Ti (i = 1, 2, 3) denote three different elements of the transfer matrix obtained from Eq. 7 by considering all four available states of two Ising spins σ1,i and σ1,i+1:
In the spirit of the transfer-matrix method, the final expression for the partition function can be finally expressed in terms of the transfer-matrix eigenvalues:
The transfer matrix (8) can be readily diagonalized in order to obtain the eigenvalues λ± defined through the transfer-matrix elements (9):
In the thermodynamic limit N → ∞, the Gibbs free energy of the spin-1/2 Ising-Heisenberg branched chain per unit cell is given by the largest transfer-matrix eigenvalue:
From the Gibbs free energy (10) one can subsequently derive the local magnetization of the Heisenberg and Ising spins as well as the total magnetization (per spin) of the spin-1/2 Ising-Heisenberg branched chain:
From the exact result (10) for the Gibbs free energy one can eventually derive other quantities such as magnetic susceptibility, entropy and specific heat using the standard relations of thermodynamics. Besides, one may also investigate a strength of the bipartite entanglement inside of the Heisenberg dimers using the quantity concurrence [38], which can be calculated from the pair correlation functions and the local magnetization [39, 40]:
Here,
but their explicit form is too cumbersome to write it down here explicitly.
Let us proceed to a discussion of the most interesting results obtained for the spin-1/2 Ising-Heisenberg branched chain by assuming the isotropic antiferromagnetic Heisenberg coupling constant J > 0, while keeping the anisotropy parameter fixed at the constant value of Δ = 1 for illustrative purposes. Throughout this section, the coupling constant J > 0 will serve as an energy unit when defining a relative strength of the magnetic field h/J, the dimensionless temperature kBT/J and the interaction ratio J1/J. To reduce the number of free parameters, the Landé g-factors of the Heisenberg and Ising spins assigned to Cu2+ and Fe3+ magnetic ions were set equal to each other, thereby ensuring that the ‘local’ magnetic fields exert an equal strength h ≡ hH = hI.
By comparing energies of all available eigenstates of the spin-1/2 Ising-Heisenberg branched chain one finds just three different ground states schematically shown in Figure 3 and mathematically given by the eigenvectors:

Figure 3. A schematic illustration of typical configurations realized within all possible ground states of the spin-1/2 Ising-Heisenberg branched chain: (A,B) the quantum antiferromagnetic phases
While the factorized form of the third ground state (15) is consistent with the classical nature of the fully polarized ferromagnetic state
From this perspective, it would be insightful to compare the strength of the bipartite quantum entanglement emerging within the quantum antiferromagnetic (13) and ferrimagnetic (14) phases using the concept of the concurrence (12), which acquires within these two ground states the following values:
It is obvious from Eq. 16 that the bipartite quantum entanglement of the Heisenberg spin pairs is consistently stronger within the quantum ferrimagnetic phase
For the sake of completeness, let us also quote eigenenergies (per unit cell) corresponding to the quantum antiferromagnetic phase
the quantum ferrimagnetic phase
the classical ferromagnetic phase
It should be stressed that the ground states
1. phase boundary
2. phase boundary
3. phase boundary
4. phase boundary
Using these exact expressions, we have plotted in Figure 4A the overall ground-state phase diagram of the spin-1/2 Ising-Heisenberg branched chain in the J1/J − h/J plane. The parameter regions denoted in Figure 4A as I(I′), II(II’) and III correspond to the quantum antiferromagnetic (QAF), the quantum ferrimagnetic (QFI) and the classical ferromagnetic (CF) phase, respectively. Note furthermore that the coexistence lines (20)–(22) correspond to discontinuous magnetic-field-driven phase transitions. All three phases QAF, QFI and CF coexist together in Figure 4A at a triple coexistence point emerging for the specific value of the interaction ratio J1/J ≈ − 0.97. Below this value, the QFI ground state
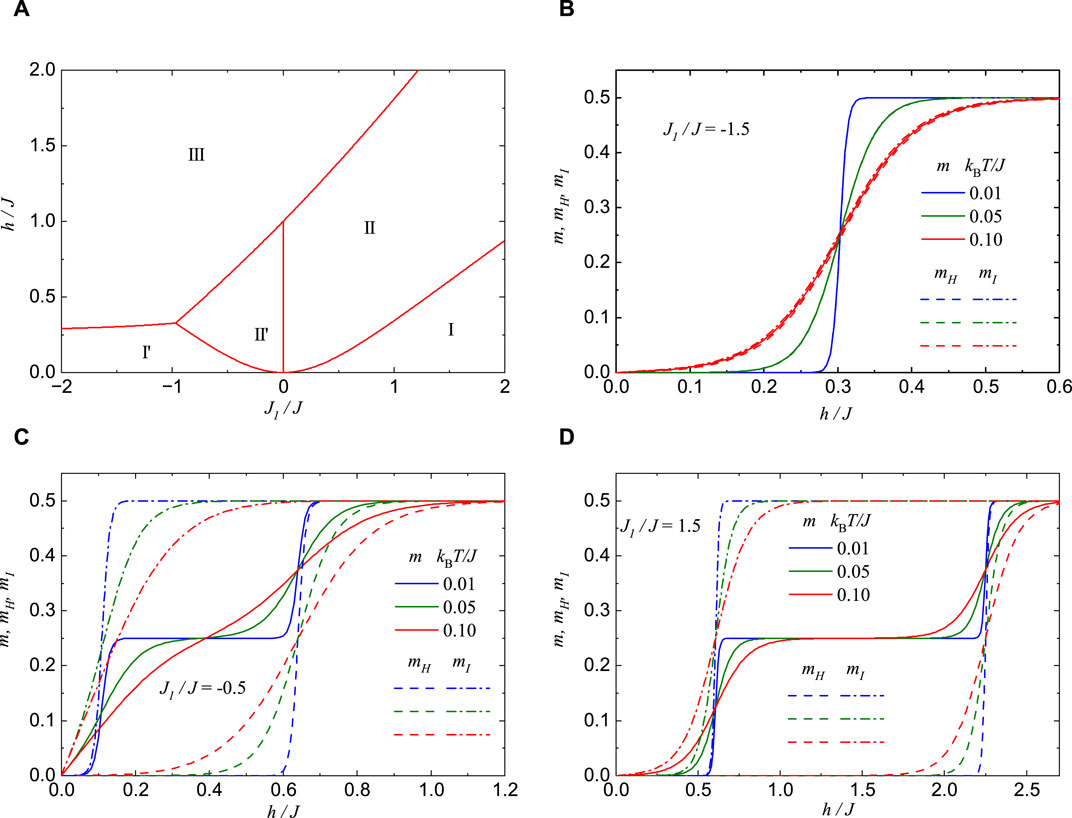
Figure 4. (A) The ground-state phase diagram for the spin-1/2 Ising-Heisenberg branched chain in the J1/J − h/J plane by assuming the isotropic value of the parameter Δ =1. The regions I(I′), II(II’) and III correspond to a quantum antiferromagnetic, a quantum ferrimagnetic and a classical ferromagnetic phase, respectively; (B–D) Magnetic-field dependencies of the local and total magnetization given by Eq. 18 for the spin-1/2 Ising-Heisenberg branched chain at three different temperatures and three selected values of the interaction ratio: (B) J1/J = −1.5; (C) J1/J = −0.5; (D) J1/J = 1.5.
To verify this observation, we present magnetic-field dependencies of the local and total magnetization in Figure 4B for the interaction ratio J1/J = −1.5 and three distinct temperature values. Under this condition, the local magnetization mH and mI defined as a single-site magnetization of the Heisenberg and Ising spins are zero until the saturation field hs/J ≈ 0.3 is reached. This consequently leads to a zero magnetization plateau of the total magnetization m, which is consistent with the antiferromagnetic alignment of the Ising spins and the singlet-like ordering of the Heisenberg spin pairs realized within the QAF ground state
Next, the local and total magnetization of the spin-1/2 Ising-Heisenberg branched chain are plotted against the magnetic field in Figure 4C for another value of the interaction ratio J1/J = −0.5 and three distinct temperatures. The spin-1/2 Ising-Heisenberg branched chain undergoes in this particular case two magnetic-field-driven phase transitions: initially from the QAF ground state
Finally, we illustrate in Figure 4D the local and total magnetization of the spin-1/2 Ising-Heisenberg branched chain for a fixed value of the interaction ratio J1/J = 1.5. The behavior observed here closely resembles that of the previous cases, with two intermediate magnetization plateaus and two magnetic-field-induced transitions: first from the QAF phase
An independent validation of the aforementioned magnetization scenario is provided through a comprehensive analysis of the magnetic entropy, as depicted in Figure 5 in the form of a density plot in the magnetic field versus temperature plane (h/J - kBT/J). The isoentropy lines shown in Figure 5 bring further insight into the adiabatic demagnetization process of the spin-1/2 Ising-Heisenberg branched chain. It is evident from Figure 5 that a sharp decrease (or increase) in temperature is observed upon decreasing (or increasing) the magnetic field above (below) each magnetic-field-driven phase transition. Consistent with this observation, the isoentropy lines tend towards absolute zero temperature at a single magnetic field for the specific case J1/J = −1.5, owing to the absence of the quantum ferrimagnetic phase |II′⟩ at moderate magnetic fields [refer to Figure 5A]. Conversely, for the other two specific cases, J1/J = −0.5 and 1.5, the isoentropy lines approach absolute zero temperature at two distinct magnetic fields due to the presence of the quantum ferrimagnetic phase |II′⟩ at moderate magnetic fields.
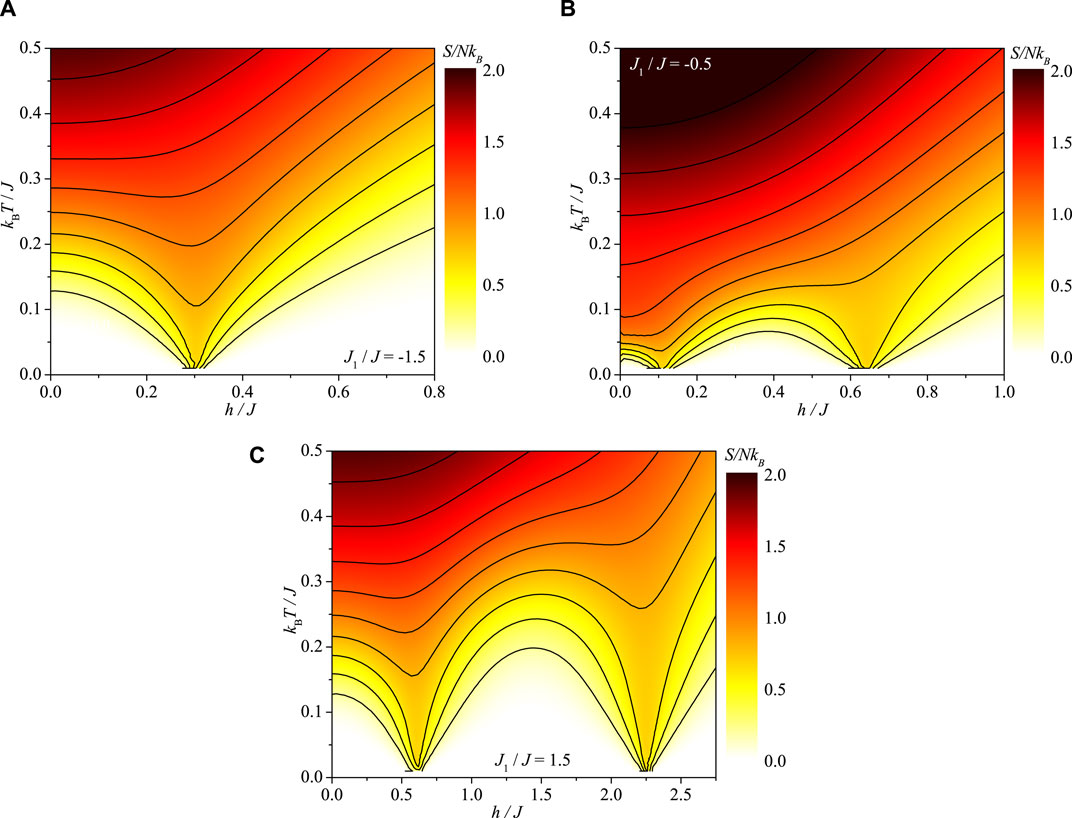
Figure 5. A density plot of the reduced entropy S/NkB of the spin-1/2 Ising-Heisenberg branched chain in the magnetic field versus temperature plane h/J − kBT/J for three selected values of the interaction ratio: (A) J1/J = −1.5, (B) J1/J = −0.5, and (C) J1/J = 1.5.
The temperature dependence of the initial magnetic susceptibility times temperature product is illustrated in Figure 6 for various values of the interaction ratio J1/J. It is noteworthy that the spin-1/2 Ising-Heisenberg branched chain exhibits the quantum antiferromagnetic (QAF) ground state in the zero-field limit for any value of the interaction ratio J1/J [refer to Figure 4A]. This aligns with the vanishing behavior of the susceptibility times temperature product as temperature approaches zero. It is apparent from Figure 6 that the product of susceptibility and temperature gradually tends to zero as temperature decreases for the interaction ratio J1/J = 1.5. For the interaction ratio J1/J = −0.25, the product χT contrarily initially declines, followed by maintaining a nearly constant value below the temperature kBT/J ≲ 0.25, before rapidly decreasing to zero as absolute zero temperature is approached. The notable temperature dependence with a nearly constant value of the susceptibility times temperature product observed at moderate temperatures is attributed to the ferromagnetic nature of the Ising coupling constant J1 < 0, which has opposite tendency of increasing of the product χT upon decreasing of temperature. Indeed, the reinforcement of the ferromagnetic coupling constant J1 leads to an increase in the susceptibility times temperature product as temperature decreases, as evidenced in Figure 6 for specific values of the interaction ratio J1/J = −1.5 and −2.3, where the product χT initially reaches a rounded maximum before ultimately approaching zero as temperature decreases.
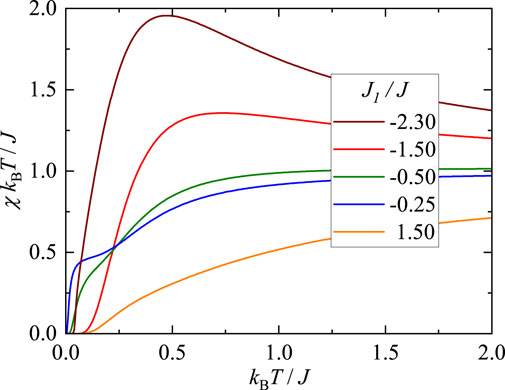
Figure 6. Temperature dependence of the initial magnetic susceptibility times the temperature χkBT/J of the spin-1/2 Ising-Heisenberg branched chain for a few different values of the interaction ratio J1/J.
To better understand the quantum nature of the spin-1/2 Ising-Heisenberg branched chain, we conduct a detailed analysis of the concurrence (12), which quantifies the strength of bipartite entanglement within the Heisenberg spin pairs. In Figure 7A, we illustrate the magnetic-field dependence of the concurrence for a fixed interaction ratio J1/J = −1.5 and three distinct temperatures. At sufficiently low magnetic fields, the concurrence is non-zero due to the presence of the quantum antiferromagnetic (QAF) ground state
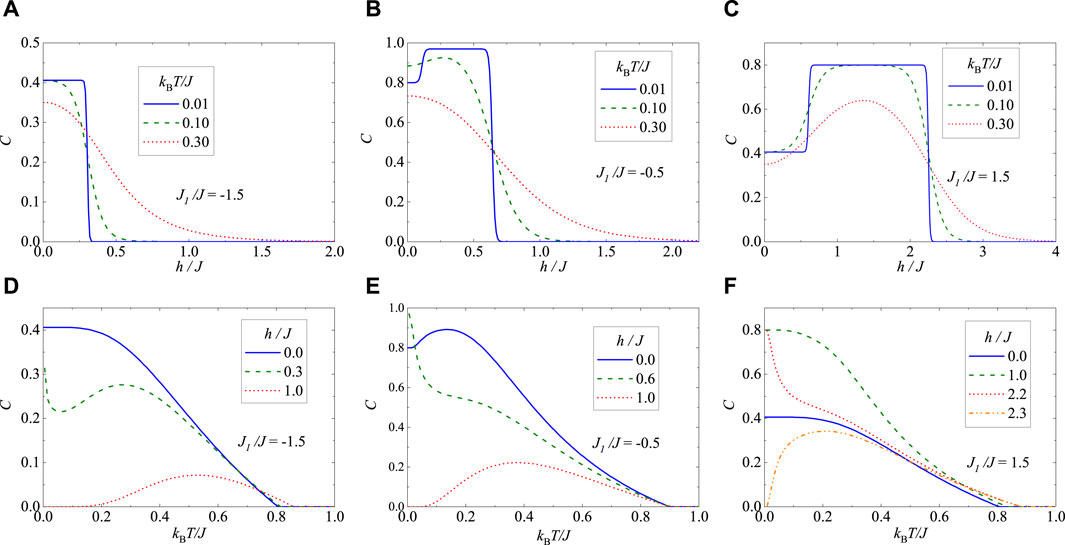
Figure 7. Magnetic-field (A–C) and temperature (D–F) dependencies of the concurrence (19) calculated for the Heisenberg spin pairs of the spin-1/2 Ising-Heisenberg branched chain at three different values of the interaction ratio: (A) and (D) J1/J = −1.5; (B) and (E) J1/J = −0.5; (C) and (F) J1/J = 1.5.
Next, we depict in Figure 7B the concurrence as a function of the magnetic field for a fixed interaction ratio J1/J = −0.5 and three distinct temperatures. In contrast to the previous case, the spin-1/2 Ising-Heisenberg branched chain encompasses at zero temperature all three possible ground states: QAF, QFI, and CF. Consequently, the concurrence initially attains a relatively large value (C ≈ 0.8) due to the QAF ground state
Last but not least, we have depicted in Figures 7C,F the magnetic-field and temperature dependencies of the concurrence for the fixed value of the interaction ratio J1/J = 1.5. It is evident that the results shown in Figures 7C,F are qualitatively very similar to those displayed in Figures 7B,E for the other specific case J1/J = −0.5. The main quantitative difference lies in the strength of bipartite entanglement, i.e., the magnitude of concurrence, which generally weakens with an increase in the absolute value of the interaction ratio |J1|/J. Notably, the concurrence attains the same zero-temperature asymptotic value within the QAF ground states
In this section, we will take advantage of the spin-1/2 Ising-Heisenberg branched-chain model described by the Hamiltonian (1) to theoretically interpret available magnetic data experimentally measured for the heterobimetallic coordination polymer [(Tp)2Fe2(CN)6(CH3COO)(bdmap)Cu2(H2O)] to be further abbreviated as Fe2Cu2, which serves as its experimental realization [37]. The experimental data for the temperature dependence of the magnetic susceptibility times temperature product χMT recorded at a magnetic field of B = 0.2 T [37] are confronted in Figure 8A with the best theoretical fit obtained using the spin-1/2 Ising-Heisenberg branched-chain model. The least-squares fitting procedure yielded a rather strong antiferromagnetic coupling constant J/kB = 247.8 K between nearest-neighbor Cu2+-Cu2+ magnetic ions, a moderately strong ferromagnetic coupling constant J1/kB = −64.2 K between nearest-neighbor Cu2+-Fe3+ magnetic ions, and Landé g-factors gCu = 2.16 and gFe = 2.23 for Cu2+ and Fe3+ magnetic ions, respectively. A moderate value of the interaction ratio J1/J ≈ − 0.26 contributes to a relatively rapid decline in the susceptibility times temperature product as temperature decreases in a high-temperature regime T ≳ 50 K. This is successively followed by a less steep decline observed in a range of moderate temperatures 20 K ≲ T ≲ 50 K before it finally rapidly falls to zero with further temperature reduction. Note furthermore that the steep reduction of the susceptibility times temperature product observed in the low-temperature range is consistent with the quantum antiferromagnetic (QAF) ground state |I′⟩.
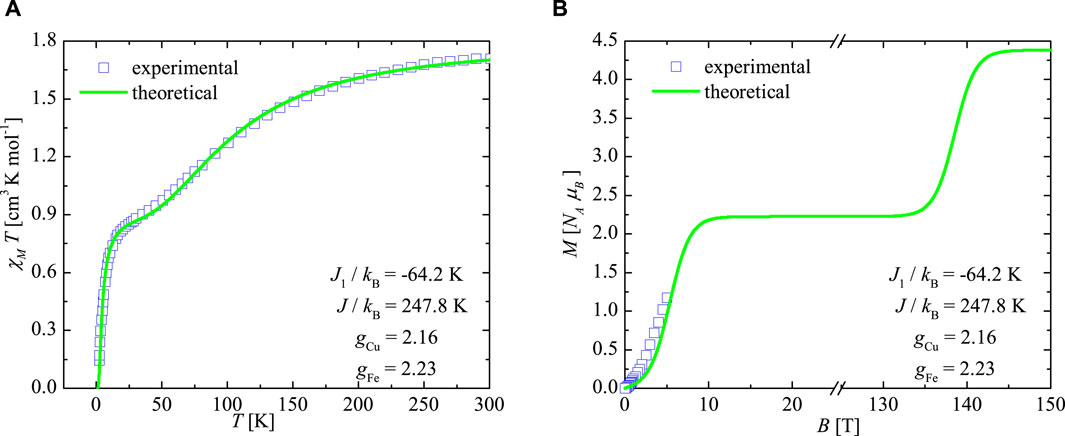
Figure 8. Temperature dependence of the molar magnetic susceptibility χM times temperature T data at the magnetic field B = 0.2 T (A) and the isothermal magnetization curve of the polymeric coordination compound [(Tp)2Fe2(CN)6(CH3COO)(bdmap)Cu2(H2O)] recorded at temperature T = 1.8 K (B). Blue squares represent experimental data reported in Ref. [37], while green curves are the respective theoretical fits obtained with the help of the spin-1/2 Ising-Heisenberg branched chain model.
Utilizing the determined set of fitting interaction parameters, we have also conducted theoretical modeling of the low-temperature magnetization curve of the polymeric compound Fe2Cu2, as reported in Ref. [37], for sufficiently low temperatures T = 1.8 K up to a magnetic field of B = 5 T. The magnetization data recorded for the coordination polymer Fe2Cu2 are confronted in Figure 8B with the corresponding theoretical fit based on the spin-1/2 Ising-Heisenberg branched chain model, calculated up to an ultrahigh magnetic field of 150 T surpassing the saturation field. The spin-1/2 Ising-Heisenberg branched chain model provides a relatively satisfactory fit to the experimental magnetization data. Moreover, an extrapolation to higher magnetic fields predicts the presence of a sizable intermediate one-half magnetization plateau in the magnetic field range between B ≈ 10 T and 140 T. This intermediate magnetization plateau reflects the emergence of the quantum ferrimagnetic phase |II′⟩ accompanied by a stronger bipartite entanglement of the Heisenberg spin pairs. It is worthwhile to mention that a small deviation between the theoretical and experimental data can be attributed to the Ising approximation of a highly (but not infinitely) anisotropic exchange coupling between Cu2+ and Fe3+ magnetic ions.
To shed light on the strength of bipartite entanglement within the Cu2+-Cu2+ dimeric units of the polymeric chain Fe2Cu2, we utilized the determined fitting parameters of the corresponding spin-1/2 Ising-Heisenberg branched chain to calculate the concurrence (12). Temperature dependencies of the concurrence (12) calculated for the Heisenberg spin pairs of the spin-1/2 Ising-Heisenberg branched chain are illustrated in Figure 9A for a few selected values of the magnetic field B. At zero magnetic field, the concurrence exhibits a striking temperature-induced rise almost to its maximum possible value, after which it gradually declines with increasing temperature until it completely vanishes at the threshold temperature T ≈ 224 K. A small magnetic field can be considered as another driving force that may reinforce the strength of bipartite entanglement. Indeed, it turns out that the concurrence approaches almost its maximum value in the zero-temperature asymptotic limit when a small magnetic field is applied. If the magnetic field exceeds the saturation field, a double reentrant behavior of the concurrence is observed.
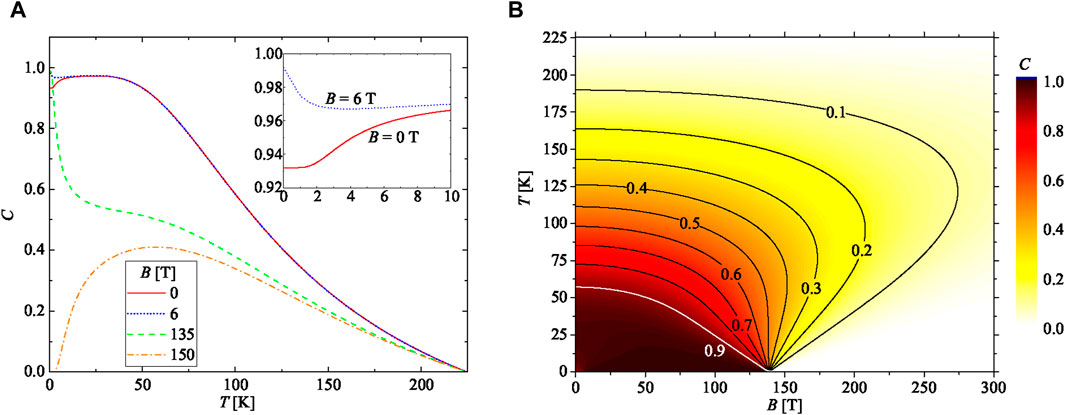
Figure 9. (A) Temperatures dependencies of the concurrence (19) calculated for the Cu2+-Cu2+ dimeric units using the spin-1/2 Ising-Heisenberg branched chain for several values of the magnetic field B (the inset shows a detail from the low-field region); (B) A density plot of the concurrence (19) calculated for the Cu2+-Cu2+ dimeric units of the spin-1/2 Ising-Heisenberg branched chain in the magnetic field vs. temperature plane. Displayed lines correspond to isocontour lines of the concurrence. All calculations are presented for the set of fitting parameters J/kB = 247.8 K, J1/kB = −64.2 K, gCu = 2.16 and gFe = 2.23 obtained for the polymeric coordination compound [(Tp)2Fe2(CN)6(CH3COO)(bdmap)Cu2(H2O)].
Last but not least, a density plot of the concurrence (12) calculated for the Heisenberg spin pairs of the spin-1/2 Ising-Heisenberg branched chain is presented in Figure 9B in the magnetic field versus temperature plane. This density plot can be interpreted as a phase diagram, delineating the entangled parameter region from the disentangled one. Remarkably, the density plot in Figure 9B reveals that a relatively high value of the concurrence (C = 0.1) can still be detected even up to relatively high temperatures of around T ≈ 188 K irrespective of the accessible magnetic-field strength for experimental testing (B < 10 T). This suggests the persistence of significant bipartite entanglement in the system over a wide temperature range, which could be of interest for experimental investigations.
In this paper, we have investigated the ground-state phase diagram, magnetization process, magnetocaloric effect, and bipartite entanglement of the spin-1/2 Ising-Heisenberg branched chain with two different coupling constants using the transfer-matrix method. Our analysis reveals that the spin-1/2 Ising-Heisenberg branched chain exhibits five distinct ground states: two quantum antiferromagnetic phases
It has been demonstrated that the spin-1/2 Ising-Heisenberg branched chain with two different coupling constants provides a satisfactory description of the magnetic behavior observed in the heterobimetallic polymeric chain Fe2Cu2. By fitting available experimental data for the temperature dependence of the susceptibility times temperature product and the low-temperature magnetization curve, we have determined a rather strong coupling constant J/kB = 247.8 K between the Cu2+-Cu2+ magnetic ions and a moderately strong coupling constant J1/kB = −64.2 K between the Cu2+-Fe3+ magnetic ions with subtle differences in the Landé g-factors gCu = 2.16 and gFe = 2.23. Our analysis reveals that the quantum antiferromagnetic phase is realized at sufficiently low magnetic fields (B ≲ 10 T), while the quantum ferrimagnetic phase, characterized by a sizable intermediate one-half magnetization plateau, can be detected in the magnetic-field range between B ≈ 10 T and 140 T. The substantial coupling constant between the Cu2+-Cu2+ dimeric units further implies a robust bipartite entanglement between the nearest-neighbor Cu2+-Cu2+ magnetic ions. This entanglement persists up to a relatively high threshold temperature (T ≈ 224 K) and undergoes a transient magnetic-field-driven strengthening.
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
DS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing–original draft. KK: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation, Writing–review and editing. JS: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Visualization, Writing–original draft, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the grant of the Slovak Research and Development Agency provided under the contract No. APVV-22-0172 and by the grant of The Ministry of Education, Science, Research, and Sport of the Slovak Republic provided under the contract No. VEGA 1/0695/23. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 945380. This project was also supported by the internal grant of Faculty of Science of Pavol Jozef Safarik University in Kosice under the contract number VVGS-2023-2559.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Mattis CD. The many-body problem: an encyclopedia of exactly solved models in one dimension. In: 3rd printing with revisions and corrections. Singapore: World Scientific (1993).
5. Griffiths RB. Magnetization curve at zero temperature for the antiferromagnetic Heisenberg linear chain. Phys Rev (1964) 133:A768–75. doi:10.1103/PhysRev.133.A768
6. Lieb E, Schultz T, Mattis D. Two soluble models of an antiferromagnetic chain. Ann Phys (1961) 16:407–66. doi:10.1016/0003-4916(61)90115-4
7. Katsura S. Statistical mechanics of the anisotropic linear Heisenberg model. Phys Rev (1962) 127:1508–18. doi:10.1103/PhysRev.127.1508
8. Miller JS, Drillon M Magnetism: molecules to materials I: models and experiments. Weinheim: Wiley-VCH Verlag GmbH (2002).
9. Aydiner E. Magnetic properties of one-dimensional ferrimagnetic mixed (1,3/2) spin chain with single-ion anisotropy. Chin Phys Lett (2004) 21:2289–91. doi:10.1088/0256-307X/21/11/059
10. Han SD, Tüfekçi T, Spiller TP, Aydiner E. Entanglement in (1/2,1) mixed-spin XY model with long-range interaction. Int J Theor Phys (2017) 56:1474–83. doi:10.1007/s10773-017-3287-9
11. Van den Heuvel W, Chibotaru LF. Dysprosium-based experimental representatives of an Ising-Heisenberg chain and a decorated Ising ring. Phys Rev B (2010) 82:174436. doi:10.1103/PhysRevB.82.174436
12. Bellucci S, Ohanyan V, Rojas O. Magnetization non-rational quasi-plateau and spatially modulated spin order in the model of the single-chain magnet [(CuL)2DyMo(CN)8]-2CH3CN- H2O. EPL (2014) 105:47012. doi:10.1209/0295-5075/105/47012
13. Strečka J, Hagiwara M, Han Y, Kida T, Honda Z, Ikeda M. Ferrimagnetic spin-1/2 chain of alternating Ising and Heisenberg spins in arbitrarily oriented magnetic field. Condens Matter Phys (2012) 15:43002. doi:10.5488/CMP.15.43002
14. Han Y, Kida T, Ikeda M, Hagiwara M, Strečka J, Honda Z. High-field magnetization of a bimetallic ferrimagnetic chain with alternating Ising and Heisenberg spins. J Korean Phys Soc (2013) 62:2050–3. doi:10.3938/jkps.62.2050
15. Torrico J, Strečka J, Hagiwara M, Rojas O, de Souza SM, Han Y, et al. Heterobimetallic Dy-Cu coordination compound as a classical-quantum ferrimagnetic chain of regularly alternating Ising and Heisenberg spins. J Magn Magn Mater (2018) 460:368–80. doi:10.1016/j.jmmm.2018.04.021
16. Strečka J, Gálisová L, Verkholyak T. Insights into nature of a magnetization plateau f 3d-4f coordination polymer [Dy2Cu2]n from a spin-1/2 Ising-Heisenberg orthogonal-dimer chain. Condens Matter Phys (2020) 23:43708. doi:10.5488/CMP.23.43708
17. Gálisová L. Insight into ground-state spin arrangement and bipartite entanglement of the polymeric coordination compound [Dy2Cu2]n through the symmetric spin-1/2 Ising–Heisenberg orthogonal-dimer chain. J Magn Magn Mater (2022) 561:169721. doi:10.1016/j.jmmm.2022.169721
18. Čanová L, Strečka J, Jaščur M. Geometric frustration in the class of exactly solvable Ising-Heisenberg diamond chains. J Phys Condens Matter (2006) 18:4967–84. doi:10.1088/0953-8984/18/20/020
19. Strečka J, Rojas O, Verkholyak T, Lyra ML. Magnetization process, bipartite entanglement, and enhanced magnetocaloric effect of the exactly solved spin-1/2 Ising-Heisenberg tetrahedral chain. Phys Rev E (2014) 89:022143. doi:10.1103/PhysRevE.89.022143
20. Qi Y, Du A. Magnetocaloric effect in an Ising-Heisenberg diamond chain with direct monomer spin couplings. Phys Status Solidi B (2014) 251:1096–101. doi:10.1002/pssb.201350381
21. Hovhannisyan VV, Ananikian NS, Kenna R. Partition function zeros and magnetization plateaus of the spin-1 Ising-Heisenberg diamond chain. Physica A (2016) 453:116–30. doi:10.1016/j.physa.2016.02.047
22. Rojas M, de Souza SM, Rojas O. Entangled state teleportation through a couple of quantum channels composed of XXZ dimers in an Ising-XXZ diamond chain. Ann Phys (2017) 377:506–17. doi:10.1016/j.aop.2016.12.033
23. Torrico J, Ohanyan V, Rojas O. Non-conserved magnetization operator and ‘fire-and-ice’ ground states in the Ising-Heisenberg diamond chain. J Magn Magn Mater (2018) 454:85–96. doi:10.1016/j.jmmm.2018.01.044
24. Carvalho IM, Torrico J, de Souza SM, Rojas O, Derzhko O. Correlation functions for a spin-1/2 Ising-XYZ diamond chain: further evidence for quasi-phases and pseudo-transitions. Ann Phys (2019) 402:45–65. doi:10.1016/j.aop.2019.01.001
25. Freitas M, Filgueiras C, Rojas M. The effects of an impurity in an ising-XXZ diamond chain on thermal entanglement, on quantum coherence, and on quantum teleportation. Ann Phys (2019) 531:1900261. doi:10.1002/andp.201900261
26. Bhuvaneswari S, Muthuganesan R, Radha R. Spotlighting quantum phase transition in spin-1/2 Ising–Heisenberg diamond chain employing Measurement-Induced Nonlocality. Physica A (2021) 573:125932. doi:10.1016/j.physa.2021.125932
27. Ren YP, Zhao ZJ, Yang X, Wang GH, Leng YD, Gao GJ, et al. Quantum Fisher information at finite temperatures and the critical properties in Ising-Heisenberg diamond chain. Results Phys (2022) 37:105542. doi:10.1016/j.rinp.2022.105542
28. Ma D-C, Du A. The exact solution of the edge-modified kekulene-like nanostructure Ising-Heisenberg spin system. Physica E (2022) 144:115470. doi:10.1016/j.physe.2022.115470
29. Ma D-C, Du A. The exact solution of the edge-modified graphene nanoribbon-like structure Ising-Heisenberg spin (1,1/2) system. Physica E (2023) 147:115569. doi:10.1016/j.physe.2022.115569
30. Souza F, Lyra ML, Strečka J, Pereira MSS. Magnetization processes and quantum entanglement in a spin-1/2 Ising-Heisenberg chain model of a heterotrimetallic Fe-Mn-Cu coordination polymer. J Magn Magn Mater (2019) 471:423–31. doi:10.1016/j.jmmm.2018.09.121
31. Souza F, Veríssimo LM, Strečka J, Lyra ML, Pereira MSS. Exact and density matrix renormalization group studies of two mixed spin-(1/2, 5/2, 1/2) branched-chain models developed for a heterotrimetallic Fe-Mn-Cu coordination polymer. Phys Rev B (2020) 102:064414. doi:10.1103/PhysRevB.102.064414
32. Zheng Y-D, Mao Z, Zhou B. Entanglement teleportation via a couple of quantum channels in Ising-Heisenberg spin chain model of a heterotrimetallic Fe-Mn-Cu coordination polymer. Chin Phys B (2019) 28:120307. doi:10.1088/1674-1056/ab53cc
33. Arian Zad H, Rojas M. Quantum coherence, quantum Fisher information and teleportation in the Ising-Heisenberg spin chain model of a heterotrimetallic Fe–Mn–Cu coordination polymer with magnetic impurity. Physica E (2021) 126:114455. doi:10.1016/j.physe.2020.114455
34. Zheng Y-D, Zhou B. Negativity and quantum phase transition in a mixed spin-(1/2, 5/2, 1/2) Ising–Heisenberg branched chain. Physica A (2022) 603:127753. doi:10.1016/j.physa.2022.127753
35. Karl’ová K, Strečka J, Lyra ML. Breakdown of intermediate one-half magnetization plateau of spin-1/2 Ising-Heisenberg and Heisenberg branched chains at triple and Kosterlitz-Thouless critical points. Phys Rev E (2019) 100:042127. doi:10.1103/PhysRevE.100.042127
36. Strečka J, Karl’ová K, Ghannadan A. Influence of a spatial anisotropy on presence of the intermediate one-half magnetization plateau of a spin-1/2 Ising–Heisenberg branched chain. J Magn Magn Mater (2022) 542:168547. doi:10.1016/j.jmmm.2021.168547
37. Kang L-C, Chen X, Wang H-S, Li Y-Z, Song Y, Zuo J-L, et al. Syntheses, structures, and magnetic properties of two kinds of unique heterometallic chains with mixed-bridging ligands of tricyanometalate and alkoxide. Inorg Chem (2010) 49:9275–82. doi:10.1021/ic100861n
38. Wootters WK. Entanglement of formation of an arbitrary state of two qubits. Phys Rev Lett (1998) 80:2245–8. doi:10.1103/PhysRevLett.80.2245
39. Amico L, Fazio R, Osterloh A, Vedral V. Entanglement in many-body systems. Rev Mod Phys (2008) 80:517–76. doi:10.1103/RevModPhys.80.517
Keywords: Ising-Heisenberg branched chain, quantum and thermal entanglement, Fractional magnetization plateau, magnetocaloric effect, heterobimetallic coordination polymers, exact results
Citation: Sivý D, Karl’ová K and Strečka J (2024) Quantum magnetism in Fe2Cu2 polymeric branched chains: insights from exactly solved Ising-Heisenberg model. Front. Phys. 12:1408429. doi: 10.3389/fphy.2024.1408429
Received: 28 March 2024; Accepted: 09 May 2024;
Published: 24 June 2024.
Edited by:
Nanrun Zhou, Shanghai University of Engineering Sciences, ChinaCopyright © 2024 Sivý, Karl’ová and Strečka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jozef Strečka, am96ZWYuc3RyZWNrYUB1cGpzLnNr
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.