LIF measurement in a partially saturated and partially absorbed regime

The problems of laser-induced fluorescence (LIF) measurements in a partially saturated regime with spatially dependent laser intensity in the sample (caused by absorption) are analyzed. The obtained equations are tested by means of LIF of free tellurium atoms in a plasma of an atmospheric pressure dielectric barrier discharge (DBD) by comparing fluorescence and absorption measurements. The results show a high reliability of LIF measurements.

1 Introduction

Fluorescence, frequently realized as laser-induced fluorescence (LIF), is one of the most important methods for detection of various species in numerous scientific fields [1-3]. It offers in situ measurements with high sensitivity (going to single-molecule detection [4]), versatility, and spatial resolution. Due to these advantages, it is a key method for detection of reactive species in plasmas [5-9], including free atoms, molecular radicals, complete molecules, and ions.

Unfortunately, the phenomena occurring during the fluorescence process can be relatively complicated due to collisions of the excited state [10], laser induced photodissociation [11, 12], invasivity of the method [13, 14], or necessity of calibration of the detection system [5-7]. As a result, the absolute concentrations obtained by LIF sometimes exhibit high uncertainty [15]. Therefore, any validation of the results of the LIF method is valuable. Moreover, the fluorescence process can be complicated by partial saturation, i.e., by deviation of the fluorescence signal from its linear dependence on the energy of laser pulses, which is caused by evident depletion of the investigated ground state, stimulated emission, and eventually by photoionization of the excited state. Therefore, LIF saturation was studied by several works [16-18]. Another complication is that the laser beam may be fully or partially absorbed in the studied sample, which leads to spatially variable energy of laser pulses. In addition, the absorption can be partially saturated from the same reasons which cause the saturation of the fluorescence.

The abovementioned complications were the motivation to derive equations that can be used for evaluation of LIF and that take into account the absorption of the laser beam in the sample (in this case in plasma) and the saturation of both LIF and absorption. This study also aimed to validate the concentration values gained from LIF measurements by absorption. These intentions were realized in atmospheric pressure plasma of a dielectric barrier discharge (DBD) ignited in a so-called atomizer, i.e., in a device that is used for dissociation (atomization) of volatile species in the field of trace element analysis to determine metal concentrations by atomic spectrometry. Particularly, the presented measurement was realized on LIF of free tellurium atoms that were supplied to the plasma in the form of tellurium hydride (TeH₂), which was atomized in the plasma to produce the free Te atoms.

2 Experimental

A volume DBD was ignited inside a DBD atomizer consisting of two parts—an optical and an inlet arm. The DBD was ignited in the optical arm—a 75-mm-long silica vessel with 7 mm × 3 mm internal rectangular cross-section. Two planar copper electrodes (50 mm long, 5 mm wide) were placed on the outer surfaces of the upper and lower bases of the vessel and supplied with a sinusoidal voltage of 26 kHz frequency and 9 kV amplitude. An inlet arm—a silica tube with internal diameter 2 mm—was sealed to the centre of the optical arm and served as the inlet for the working gas mixture from the hydride generator unit. This compartment served for almost quantitative (93% ± 5%) conversion of the Te standard solution (50 ng/mL Te) by chemical reaction, reduction by NaBH₄ to TeH₂. Ar (75 sccm) served as the carrier gas, while 50 sccm H₂ is produced as a by-product of the chemical reaction. After passing through the atomizer, the gases escaped freely through its open ends into the surrounding atmosphere.

The scheme of the whole laser-induced fluorescence setup is shown in Figure 1. Figure 1C shows the energy scheme for the detection of the tellurium atoms. The ground state 5p⁴³P₂ atoms were excited to the 5p³ 6s ⁵S₂ state by absorbing laser photons of wavelength 225.903 nm. The resulting fluorescence photons of wavelength 253.074 nm were emitted while the atoms were depopulated to the 5p⁴³P₁ state. The excitation laser beam was generated by a system consisting of a Q-switched pump laser (Spectra-Physics, Quanta-Ray PRO-270-30), a dye laser (Sirah, PrecisionScan PRSC-D-24-EG with Rhodamine 101/B), and a frequency conversion unit. The output beam with a wavelength of 225.903 nm, spectral width of 0.4 pm, single-pulse duration of 8 ns, and repetition frequency of 30 Hz was divided into two branches by a silica window acting as a beam splitter, which decreased the energy of the laser beam entering the DBD in order to reduce the strong fluorescence saturation. The laser beam was circular with a diameter of approx. 3 mm. Before entering the DBD, a part of its spatial wings was cut by a rectangular (5 × 2 mm) diaphragm so that it could pass through the center of the optical arm of the atomizer without touching the silica walls. The beam was localized at the axis of the optical arm. The energy of both beams was monitored by pyroelectric power meters (Ophir, Vega PE9), providing the information on the laser energy before entering the discharge and after the absorption on tellurium atoms (the ratio between the energy measured by the first power meter and the real energy at the DBD input was obtained from measurements realized when there was no plasma and no absorption in the atomizer). The fluorescence signal was detected perpendicular to the laser beam by using an ICCD camera (Princeton Instruments, PI-MAX). The spatial resolution of the measurements was 0.08 mm. An interference filter (AHF 257/12 BrightLine HC) was mounted on the camera lens to separate the fluorescence signal from the ambient radiation. The signal was temporally integrated over 100 ns, covering the entire laser pulse and the fluorescence decay (only for measurements of the fluorescence decay rate, discussed in Section 4, the signal was integrated only over 0.64 ns, and the delay between the laser pulse and the signal detection was gradually increased by a step 0.5 ns). In order to increase the signal-to-noise ratio, the fluorescence image was accumulated on the ICCD camera chip from typically 300 of laser shots.

Figure 1

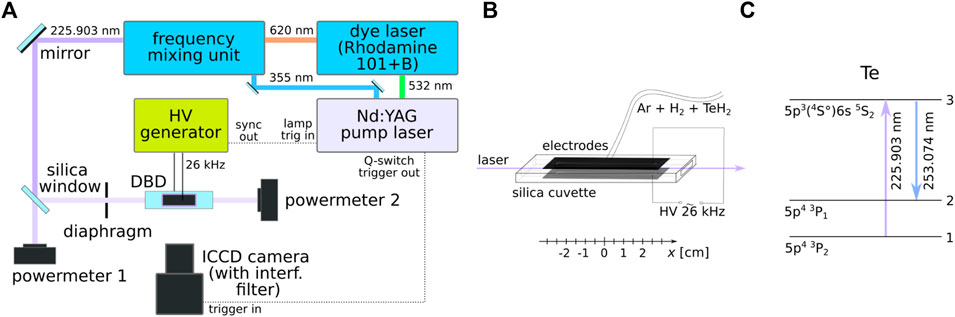
Figure 1. Experimental setup. (A) the whole laser-induced fluorescence setup; (B) the DBD cell; (C) the energy scheme for the detection of the tellurium atoms.

3 Theory

For calculating the LIF signal, we will use the simple three-level model, where atoms or molecules are excited by a laser photon from their ground state (denoted as the level 1) to a higher excited state (level 3). The excitation is followed by a spontaneous radiative decay to a lower excited state (level 2), which is accompanied by emission of a fluorescence photon–this fluorescence radiation is detected, and its intensity is used for determination of the concentration of studied atoms or molecules. Alternatively, the excited atom in the third level can undergo radiative transition to another lower lying state, or its excitation can be non-radiatively quenched by a number of collisional processes. The rate of the desired fluorescence transition to level 2 is described by the Einstein coefficient of spontaneous emission (A₃₂), whereas the total depopulation rate of level 3 can be described by the reciprocal value of the lifetime of the excited level 3 (1/τ). The product A₃₂ τ gives the quantum efficiency of the fluorescence.

In the standard LIF measurement in the linear regime, where the fluorescence signal is directly proportional to the energy of laser pulses, the measured fluorescence signal can be calculated according to [10].

$M_f=a_f{A}_{32}\tau \frac{\kappa B_{13}}{c}n{E}_f\int \underset{V}{\int }\int D_f\frac{\mathrm{\Omega }}{4\pi }s\mathrm{d}V,(1)$

where n is the concentration of studied atoms, E_f is the mean energy of laser pulses, B₁₃ is the Einstein coefficient for excitation from the ground level to the excited level 3, and κ describes the overlap between the spectral profiles of the laser line and the absorption line [19] (for the narrow laser line, κ is simply equal to the ratio between the maximum and integral intensities of the absorption line. M_f in Eq. 1 is the fluorescence signal integrated temporally over the whole fluorescence duration and spectrally over the whole fluorescence transition; it is not spectrally integrated over the excitation line—if it was spectrally integrated also over the excitation line, the factor κ should be left out from the equation). c is the speed of light, and a_f is the number of accumulations used during the collection of the fluorescence signal. D_f is the detector sensitivity for the fluorescence wavelength—this constant includes the quantum efficiency of the ICCD camera (η_f) and the transmission of the used interference filter (T). Ω is the solid angle for detection of fluorescence photons covered by the detector. Finally, s describes the spatial distribution of laser beam energy normalized to 1 (i.e., the surface integral of s over the plane perpendicular to the beam axis is equal to 1). In practice, it is problematic to predict the value of the integral $\int \underset{V}{\int }\int D_f\frac{\mathrm{\Omega }}{4\pi }s\mathrm{d}V$. Therefore, the LIF measurement is often calibrated by Rayleigh scattering, which gives the signal

$M_r=a_r\frac{\mathrm{d}{\sigma }_r}{\mathrm{d}\mathrm{\Omega }}\frac{p_r}{k{T}_r}\frac{E_r}{h{\nu }_r}\int \underset{V}{\int }\int D_r\mathrm{\Omega }s\mathrm{d}V,(2)$

where dσ_r/dΩ is the differential cross-section for Rayleigh scattering on the gas used for calibration; p_r and T_r are the pressure and temperature of the calibration gas, respectively (the gas concentration is equal to n_r = p_r/kT_r); and k is the Boltzmann constant. E_r is the mean energy of laser pulses used for Rayleigh scattering, ν_r is the frequency of laser light, and h is the Planck constant. D_r is the detector sensitivity for Rayleigh wavelength, and this quantity is proportional to the ICCD quantum efficiency η_r. The combination of Eqs 1, 2 enables to calculate the concentration of studied atoms by

$n_0=4\pi \frac{a_r{\eta }_r}{a_f{\eta }_{f}T}\frac{n_r{E}_r}{M_{r}h{\nu }_r}\frac{\mathrm{d}{\sigma }_r}{\mathrm{d}\mathrm{\Omega }}\frac{c{M}_f}{A_{32}\tau \kappa B_{13}{E}_f}.(3)$

When the partially saturated LIF regime is used, the ratio M_f/E_f in Eq. 3 must be replaced by the term $M_f\beta /\mathrm{l}\mathrm{n}\left(1+\beta E_f\right)$ [17], which takes into account the partial saturation of the LIF process quantified by the saturation constant β. In addition, if an appreciable part of the laser beam is absorbed during the measurement, the spatial dependence of the laser pulse energy should be taken into account:

$n\left(x\right)=4\pi \frac{a_r{\eta }_r}{a_f{\eta }_{f}T}\frac{n_r{E}_r}{M_{r}h{\nu }_r}\frac{\mathrm{d}{\sigma }_r}{\mathrm{d}\mathrm{\Omega }}\frac{c{M}_f\left(x\right)\beta }{A_{32}\tau \kappa B_{13}\mathrm{l}\mathrm{n}\left[1+\beta E_f\left(x\right)\right]}.(4)$

This equation must be supplemented by another equation that describes the spatial variation of the laser pulse energy along the direction of the laser beam propagation (x). With no saturation, the variation would be described by $\frac{\mathrm{d}{E}_f}{\mathrm{d}x}=-n(x)\kappa {\sigma }_a{E}_f(x)$, where the absorption cross-section ${\sigma }_a=A_{31}\frac{{\lambda }_{13}^2}{8\pi }\frac{g_3}{g_1}$. A₃₁ is the Einstein coefficient for spontaneous emission from directly excited level 3 to ground level 1, which is connected to the Einstein coefficient for excitation by the relation $B_{13}=A_{31}\frac{{\lambda }_{13}^3}{8\pi h}\frac{g_3}{g_1}$, where g₁ and g₃ are the degenerations of the ground and excited state, respectively. If we take into account the saturation effects (the depletion of the ground state and stimulated emission), we will find that the number of photons lost from the laser pulse is proportional to

$\mathcal{A}=\underset{0}{\overset{\infty }{\int }}\left[n_1\left(t\right)\kappa B_{13}-n_3\left(t\right)\kappa B_{31}\right]I\left(t\right)\mathrm{d}t,(5)$

where n₁ and n₃ are the concentrations of the ground and directly excited states, respectively; B₃₁ is the Einstein coefficient for stimulated emission; and I is the laser intensity. The first term describes excitation, and the second term is the creation of new laser photons by stimulated emission (when laser intensity is small, i.e., in the linear regime, n₃ ≪ n₁ and n₁ ≈ const., which simplifies the integral to $\mathcal{A}\approx n_1\kappa B_{13}\underset{0}{\overset{\infty }{\int }}I(t)\mathrm{d}t$). From the rate equation analysis of a partially saturated fluorescence process, it follows [15, 17] that the number of fluorescence photons is also proportional to the integral $\mathcal{A}$, defined in Eq. 5. Consequently, saturation of both the absorption and fluorescence can be described by the same formula, and the equation for the spatial variation of the laser pulse energy can be rewritten to

$\frac{\mathrm{d}{E}_f}{\mathrm{d}x}=-n\left(x\right)\kappa {\sigma }_a\frac{\mathrm{l}\mathrm{n}\left[1+\beta E_f\left(x\right)\right]}{\beta }.(6)$

The term $\mathrm{l}\mathrm{n}\left[1+\beta E_f(x)\right]/\beta$ in Eq. 6 takes into account the partial saturation of the absorption. For low laser energies, $\mathrm{l}\mathrm{n}\left[1+\beta E_f(x)\right]/\beta \approx E_f(x)$, which is the limit of the linear regime. Of course, in non-homogeneous environments, β (and also the decay time τ) may also depend on the position. When saturation and absorption are strong or when the concentration of measured species strongly varies in the direction perpendicular to x, β may vary along the laser beam (in the x direction) also due to different absorption in various parts of the beam, resulting in changes of the beam profile. It should be noted that fluorescence and absorption processes are characterised by identical saturation constants (β) only if ground state depletion and emission stimulated by laser photons dominate to the saturation mechanisms. In rare situations, when other saturation mechanisms (photoionization of the excited state; emission stimulated by fluorescence photons) play an important role, the saturation constants for absorption and fluorescence may differ.

4 Results

In our study, we applied the equations obtained in Section 3 on the LIF of free Te atoms generated by a DBD. First, let us assess the non-linearity or saturation of the LIF process. Saturation can be revealed when a straight line is fitted to the dependence lnM_f on lnE_f because the slope of the fitted line is equal to 1 for linear LIF and smaller than 1 for saturated LIF, whereas slope higher than 1 indicates some photodissociation ignited by the laser [12]. In our measurement, the slope had the value $\left(0.88\pm 0.01\right)$, indicating a weak saturation (according to [17] caused mainly by the ground state depletion). Therefore, the dependence of the measured fluorescence signal on the energy of laser pulses was fitted by the equation

$M_f=\frac{\alpha }{\beta }\mathrm{l}\mathrm{n}\left(1+\beta E_f\right),(7)$

derived in [17] for Gaussian beams, where β is the above mentioned saturation constant and αE_f gives the hypothetical signal that would be measured if no saturation occurred. Both the data and the fit (with $\beta =\left(8.8\pm 0.2\right)\cdot 10^5$ J⁻¹) are shown in Figure 2, which demonstrates the deviation of the real fluorescence signal from the hypothetical linear dependence shown by the broken cyan line.

Figure 2

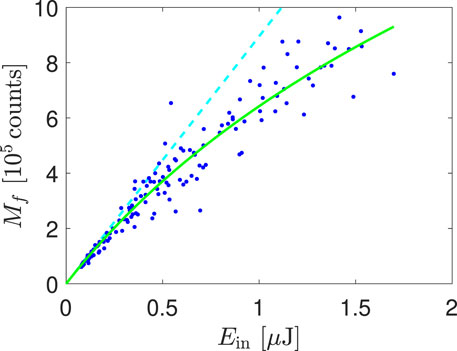
Figure 2. Saturation of the LIF process. The green line shows the fitted curve (Eq. 7), and the cyan broken line shows the hypothetical non-saturated dependence.

Not only fluorescence but also absorption can be affected by saturation processes. Therefore, Eq. 6 should be used instead of the traditional equation $\frac{\mathrm{d}{E}_f}{\mathrm{d}x}=-n\kappa {\sigma }_a{E}_f$ for strong laser intensities. The fact that absorption in our measurements was partially saturated can be demonstrated by Figure 3, which shows the ratio between the energy of laser pulses that enter and leave the DBD reactor. The fact that this ratio is not constant, but it is a slightly decreasing function of the laser pulse energy, is an evidence of the saturation of absorption.

Figure 3

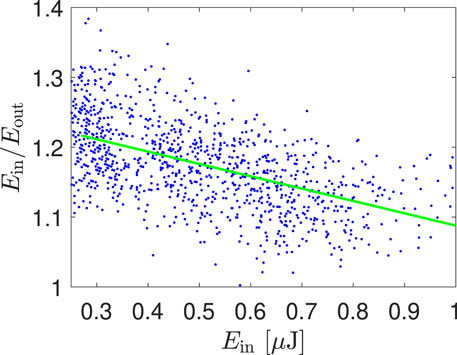
Figure 3. Ratio of the laser pulse energy behind (E_out) and in front of (E_in) the DBD as a function of the energy E_in. The green line is the linear fit of measured points characterized by the slope $\left(-1.77\pm 0.09\right)\cdot 10^5$ J⁻¹.

In order to characterize the fluorescence process, it is necessary to measure the fluorescence decay time (i.e., the lifetime of the excited state) and the spectral profile of the excitation line. The decay time was measured by variation of the delay between the laser pulse and the interval when the ICCD camera collects the fluorescence radiation. In our case, the decay time was significantly shorter than the laser pulse duration, and a weak tail of the laser pulse disturbed the decay process. Consequently, it would not be correct to fit a single exponential through the measured data, and the fluorescence decay was fitted by the convolution $\underset{0}{\overset{t}{\int }}L(t^{\prime }){\mathrm{e}}^{-(t-t^{\prime })/\tau }\mathrm{d}{t}^{\prime }$, where the temporal shape of the laser pulse tail intensity L (strictly speaking, L is the convolution of the temporal profile of the laser pulse and the temporal response of the camera) was determined from the temporally resolved measurement of Rayleigh-scattered laser photons. This procedure led to the value τ = (1.7 ± 0.2) ns. In our case, the fluorescence quantum yield A₃₂ τ = 1.6 ⋅ 10^–3 was low because the choosen fluorescence line was a triplet–quintet transition, and it was weak. The remaining characteristics, the excitation line profile, were measured by the variation of laser wavelength. The measured shape agreed with the Voigt profile with the Gauss parameter σ ≈ 1 ⋅ 10⁹ Hz and Lorentz parameter γ ≈ 5 ⋅ 10⁹ Hz and with the ratio between maximum and spectrally integrated signals κ = (5.6 ± 0.3) Hz⁻¹. Due to the narrow laser linewidth and small Doppler broadening of the relatively heavy atoms in the plasma with a low gas temperature around 550 K [20], the spectral profile of the excitation line is controlled by broadening mechanisms connected with the atmospheric pressure (collisional broadening, van der Waals broadening, event. resonance broadening) [21]. In addition, Stark broadening may play a role in the DBD.

Finally, we can proceed to the calculation of the concentration of free Te atoms realized by Eqs 4, 6. At the beginning of the solution, Eq. 4 is used for the calculation of the Te concentration in one of the discharge edges. When the concentration is known, Eq. 6 is used for the calculation of laser pulse energy in the neighboring point and the alternating use of both these equations continues until the Te concentration and the laser pulse energy are known along the whole beam path in the plasma. The obtained concentration profile for the measurement, where TeH₂ was generated from a solution with Te concentration 50 μg/L, is shown by the black curve in Figure 4 (it should be noted that the wavy structures in the right half of the DBD reactor were caused by an uneven surface of the front silica wall of the atomizer, which deflected part of the fluorescence radiation). The consequences of the concentration profile for the understanding of the TeH₂ atomization are described elsewhere [22]; here, we will only summarize that the presence of free Te atoms in the whole discharge region and the high Te concentration demonstrate a good performance of the DBD in atomization of the hydride. The mean concentration in the left part (not affected by the uneven surface) of the atomizer 3.5 ⋅ 10¹⁸ m⁻³ is in good agreement with the expected value between 3.45 ⋅ 10¹⁸ m⁻³ and 3.83 ⋅ 10¹⁸ m⁻³ (calculated from the TeH₂ supply rate from the hydride generator to the DBD assuming full hydride atomization), indicating reliability of the used measurement and evaluation procedure.

Figure 4

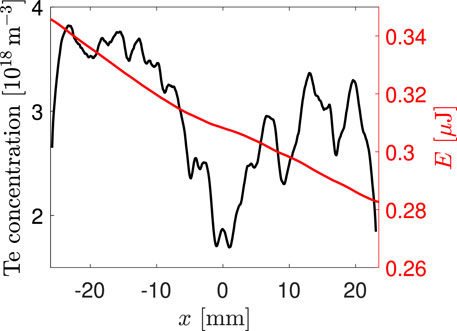
Figure 4. Spatial distributions of Te concentration (black, left axis) and laser pulse energy (red, right axes) in the DBD.

There are several sources of uncertainty of the concentration values: the first is the variability of the measured intensities, which was, in our case, approximately 8%. The second was the uncertainty of LIF parameters, namely, of τ, κ, and β. In our case, the uncertainty of κ and β was only few percent, but the uncertainty of the decay time τ was approximately 10%. All the above listed sources together led in our measurements to an uncertainty below 20%. The third source can be the uncertainty of the Einstein coefficients A₃₂ and B₁₃. Our values were taken from [23]. Unfortunately, we did not find the uncertainty of the used Einstein coefficient in the cited work and in the references therein.

At last, when solving the pair of Eqs 4, 6, one of the results is the spatial development of laser pulse energy. One example of this curve is shown in Figure 4 by the red curve. From such a curve, it is possible to obtain the ratio of the energy of laser pulses at the input and at the output of the DBD reactor, which can be simply compared with the measured value of this ratio. In other words, our experiment enabled comparing the results of fluorescence and absorption measurements. In our experiment, the ratio of laser pulse energies predicted from the intensity of the fluorescence signal by means of Eqs 4, 6 had the value 1.34, whereas the directly measured value was 1.25. The results of the fluorescence and absorption measurements differed only by 7%, which could be attributed to losses caused by the reflection of the fluorescence radiation on the front atomizer wall, which shows a very good agreement.

5 Conclusion

The equations for the evaluation of Rayleigh-calibrated LIF measurements in a partially saturated regime when a detectable part of laser photons is absorbed in the sample, in other words of partially saturated fluorescence measurement with spatially dependent intensity of the excitation radiation, were summarized. LIF measurement evaluated by these equations was tested on free tellurium atoms present in an atmospheric pressure DBD. The results were in a good agreement with both the expected Te concentration and with the measured absorption of laser in the DBD, demonstrating a high reliability of absolute LIF measurements.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PD: writing–review and editing and writing–original draft. MM: writing–review and editing and writing–original draft. JK: writing–review and editing and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research has been supported by the Czech Science Foundation (Contract 23-05974K), Institute of Analytical Chemistry of the Czech Academy of Sciences (RVO: 68081715), and by the Project LM2023039 funded by the Ministry of Education, Youth and Sports of the Czech Republic.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Geddes CD, Lakowicz JR. Reviews in fluorescence 2016. Cham, Switzerland: Springer (2017).

Google Scholar

2. Birch DJS, Chen Y, Rolinski OJ. Photonics: biomedical photonics, spectroscopy, and microscopy. John Wiley and Sons (2015). p. 1–58. chap. fluorescence.

CrossRef Full Text | Google Scholar

3. Stchur P, Yang KX, Hou X, Sun T, G MR. Laser excited atomic fluorescence spectrometry — a review. Spectrochimica Acta B (2001) 56:1565–92. doi:10.1016/s0584-8547(01)00265-8

CrossRef Full Text | Google Scholar

4. Shashkova S, Leak MC. Single-molecule fluorescence microscopy review: shedding new light on old problems. Biosci Rep (2017) 37:BSR20170031. doi:10.1042/bsr20170031

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Amorim J, Baravian G, Jolly J. Laser-induced resonance fluorescence as a diagnostic technique in non-thermal equilibrium plasmas. J Phys D: Appl Phys (2000) 33:R51–65. doi:10.1088/0022-3727/33/9/201

CrossRef Full Text | Google Scholar

6. Niemi K, von der Gathen VS, Döbele H. Absolute calibration of atomic density measurements by laser-induced fluorescence spectroscopy with two-photon excitation. J Phys D: Appl Phys (2001) 34:2330–5. doi:10.1088/0022-3727/34/15/312

CrossRef Full Text | Google Scholar

7. Döbele HF, Mosbach T, Niemi K, Schulz-von der Gathen V. Laser-induced fluorescence measurements of absolute atomic densities: concepts and limitations. Plasma Sourc Sci. Technol. (2005) 14:S31–41. doi:10.1088/0963-0252/14/2/s05

CrossRef Full Text | Google Scholar

8. Freegarde TGM, Hancock G. 23RD international conference on phenomena in ionized J Phys IV France (1997) 7:C4. doi:10.1051/jp4:1997403

CrossRef Full Text | Google Scholar

9. Dilecce G, Martini L, Tosi S, Scotoni M, De Benedictis S. Laser induced fluorescence in atmospheric pressure discharges. Plasma Sourc Sci. Technol. (2015) 18:034007. doi:10.1088/0963-0252/24/3/034007

CrossRef Full Text | Google Scholar

10. Voráč J, Dvořák P, Mrkvičková M. Laser induced fluorescence of hydroxyl (OH) radical in cold atmospheric discharges. In: N. Britun, and A. Nikiforov, editors Photon counting. Rijeka, Croatia. IntechOpen (2017).

Google Scholar

11. Kulatilaka WD, Frank JH, Patterson BD, Settersten TB. Analysis of 205-nm photolytic production of atomic hydrogen in methane flames. Appl Phys B (2009) 97:227–42. doi:10.1007/s00340-009-3474-3

CrossRef Full Text | Google Scholar

12. Dvořák P, Procházka V, Krumpolec R, Zemánek M. Solution to the perturbation of LIF measurements via photodissociation, OH measurement in atmospheric-pressure multihollow DBD. Plasma Process Polym (2020) 17:202000020. doi:10.1002/ppap.202000020

CrossRef Full Text | Google Scholar

13. Ambrico PF, Ambrico M, Šimek M, Colaianni A, Dilecce G, De Benedictis S. Laser triggered single streamer in a pin-to-pin coplanar dielectric barrier discharge. Appl Phys Lett (2009) 94:231501. doi:10.1063/1.3152284

CrossRef Full Text | Google Scholar

14. Mrkvičková M, Ráheľ J, Dvořák P, Trunec D, Morávek T. Fluorescence (TALIF) measurement of atomic hydrogen concentration in a coplanar surface dielectric barrier discharge. Plasma Sourc Sci. Technol. (2016) 25:055015. doi:10.1088/0963-0252/25/5/055015

CrossRef Full Text | Google Scholar

15. Verreycken T, Mensink R, van der Horst R, Sadeghi N, Bruggeman PJ. Absolute OH density measurements in the effluent of a cold atmospheric-pressure Ar–H₂O RF plasma jet in air. Plasma Sourc Sci. Technol. (2013) 22:055014. doi:10.1088/0963-0252/22/5/055014

CrossRef Full Text | Google Scholar

16. Daily JW. Laser induced fluorescence spectroscopy in flames. Prog Energ Combust. Sci. (1997) 23:133–99. doi:10.1016/s0360-1285(97)00008-7

CrossRef Full Text | Google Scholar

17. Mrkvičková M, Dvořák P, Svoboda M, Kratzer J, Voráč J, Dědina J. Dealing with saturation of the laser-induced fluorescence signal: an application to lead atoms. Combustion and Flame (2022) 241:112100. doi:10.1016/j.combustflame.2022.112100

CrossRef Full Text | Google Scholar

18. Voráč J, Dvořák P, Procházka V, Morávek T, Ráhel J. Dependence of laser-induced fluorescence on exciting-laser power: partial saturation and laser – plasma interaction. Eur Phys J Appl Phys (2015) 71:20812. doi:10.1051/epjap/2015150022

CrossRef Full Text | Google Scholar

19. Voráč J, Dvořák P, Procházka V, Ehlbeck J, Reuter S. Measurement of hydroxyl radical (OH) concentration in an argon RF plasma jet by laser-induced fluorescence. Plasma Sourc Sci. Technol. (2013) 22:025016. doi:10.1088/0963-0252/22/2/025016

CrossRef Full Text | Google Scholar

20. Dvořák P, Talába M, Obrusník A, Kratzer J, Dědina J. Concentration of atomic hydrogen in a dielectric barrier discharge measured by two-photon absorption fluorescence. Plasma Sourc Sci. Technol. (2017) 26:085002. doi:10.1088/1361-6595/aa76f7

CrossRef Full Text | Google Scholar

21. Konjević N. Plasma broadening and shifting of non-hydrogenic spectral lines: present status and applications Phys Rep (1999) 316:339. doi:10.1016/S0370-1573(98)00132-X

CrossRef Full Text | Google Scholar

22. Bufková K, Musil S, Kratzer J, Dvořák P, Mrkvičková M, Voráč J, et al. Generation of tellurium hydride and its atomization in a dielectric barrier discharge for atomic absorption spectrometry. Spectrochimica Acta Part B (2020) 171:105947. doi:10.1016/j.sab.2020.105947

CrossRef Full Text | Google Scholar

23. Kramida A, Ralchenko Y, Reader JNIST ASD Team. NIST atomic spectra database (ver. 5.11). Gaithersburg, MD: National Institute of Standards and Technology (2023). Available from: https://physics.nist.gov/asd (Accessed May 22, 2024).

Google Scholar