A novel spreading dynamic based on adoption against the trend

In the spreading dynamics of previous fashion trends, adoption researchers have neglected to consider that some individuals may behave differently from popular tendencies, which is called opposite-trend adoption behavior. To explore the dissemination mechanisms of the behavior, we first establish the adoption-against-trend model. Additionally, an edge division theory based on the adoption of opposite trends was proposed to quantitatively analyze this unique dissemination mechanism. This study presents three different degrees of opposite trends, each highlighting unique spreading scenarios. In the case of a strong opposite trend, no spreading occurs. In the case of a weak opposite trend, limited contact will accelerate information spreading, but it will not alter the mode of spreading. Nevertheless, in the case of a moderately opposite trend, the degree of the opposite trend alters the mode of spreading. Meanwhile, a cross-phase transition occurs. The findings of this paper can be applied to various areas, including social media and commercial trades.

1 Introduction

The theory of spreading dynamics can be used to analyze many aspects of life, including healthy behaviors [1-3], social recommendations [4-9], advertising and promotion [10-11], and fashion trends. The adoption of popular trends is strengthened by the reinforcement effect, which can lead to further expansion. Furthermore, investigators have found that due to the reinforcement effect, individuals showing a higher adoption trend toward certain behaviors are more likely to adopt those behaviors [12]. Additionally, there appears to be a connection between the reinforcement and memory effects. Upon receiving information, individuals accumulate pieces of information, leading to either a full or partial memory effect, as there are accumulative messages present. Moreover, the memory effect is characterized by being non-Markovian [13-15]. Apart from the features mentioned above, investigators discover a lot of elements that affect the infection region, including group heterogeneity [16], network structure [17], and node preference for connection [18].

To harness information spreading, certain researchers have introduced the threshold model [19-20]. Individuals only accept information once they have received messages exceeding a certain threshold. Subsequent studies have proposed the use of a truncated normal distribution due to the varying adoption probabilities of individuals impacted by factors such as age and education level [21-22]. Leng et al. discovered that the acceptance of information by individuals is not only related to the level of intimacy with their neighbors but also to the degree of nodes in the social network [23]. Similarly, Cui et al. proved that the adoption of behavior is influenced by individual interest and not merely by the behavior itself [24]. Some studies have demonstrated that the acceptance and adoption of information and behavior are governed by various influential factors in social networks. Ruan et al. examined the process by which nodes provide inverse feedback upon the receipt of messages, influencing vulnerable nodes [25]. Otherwise, group behaviors should also be observed beyond individual actions. Investigators have grouped networks into two categories: positive and negative [26-27]. Researchers have identified imitative behaviors in society and are studying information propagation laws in double-layered networks by establishing gate-like adoption functions [28]. To comprehend the information dissemination process precisely, Zhu et al. suggested that an individual can only obtain limited information from their finite neighbors due to time and energy constraints [29-34].

Hence, it is crucial to establish a network with limited contact. To date, researchers have rarely studied the dissemination of information against the fashionable trend, which is called the adoption of behavior against the trend. People refrain from adopting their neighbors’ behavior when they lack sufficient information. However, if a few nodes adopt the behavior, individuals are much more likely to adopt it as well. As the number of individuals displaying the behavior increases, the likelihood of additional individuals adopting the behavior decreases significantly. For example, new clothing brands do not immediately form a trend. Initially, only a few unique individuals will purchase them. As the clothing becomes more popular, more people will buy it. However, some individuals may choose to avoid the trend.

Focusing on the aforementioned situation, this paper studies the spreading mechanism among single-layer network neighbors with limited contact. A comparable adoption threshold model is constructed to characterize the spreading characters since the quasi-right triangle is associated with the adoption qualities against neighbors, which have a rapidly increasing character at first and a slowly decreasing character thereafter. Afterward, we propose a general edge compartmental to quantitatively analyze the mechanism of propagation. In addition, our acceptable model has been confirmed through simulations that coincide with theoretical calculations. We note that there is a phase transition present, regardless of whether the network is random or scale-free. In cases of strong opposition, we observe that information is not transmitted. In the weak scenario, limited contact hastens transmission but does not convert the spreading mode. In both networks, the mode of spreading continuously grows with a second-order transition. In the moderate scenario, the dissemination mode changes due to the influence of the opposite adaptive parameter.

The remainder of this paper is divided into five sections. Section 2 introduces a model of opposite trend acceptance with limited contact ability. Section 3 presents evidence to support the validity of the model. Section 4 examines the process of information dissemination across two distinct networks, using both inference and simulation. Section 5 offers a conclusion about the study as a whole.

2 Model description

To investigate the mechanism of individual information sharing within a single-layer social network under the influence of opposite trend adoption and limited contact heterogeneity, a network containing N nodes was designed. The social network is comparable to platforms such as WeChat, Microblog, and Facebook, and thus, a distribution of node degrees p(k) was obtained.

According to the above description of a single-layer network model, we use the traditional SAR model to research information-spreading mechanisms, as shown in Figure 1. In the SAR model, individuals can be in three different stages. Susceptible individuals have the zest to receive information. Adopted nodes have already received information and subsequently transmit it to their neighbors. On the other hand, recovered nodes have received information but have no interest in the message, so they will not participate in the propagation of information.

Figure 1

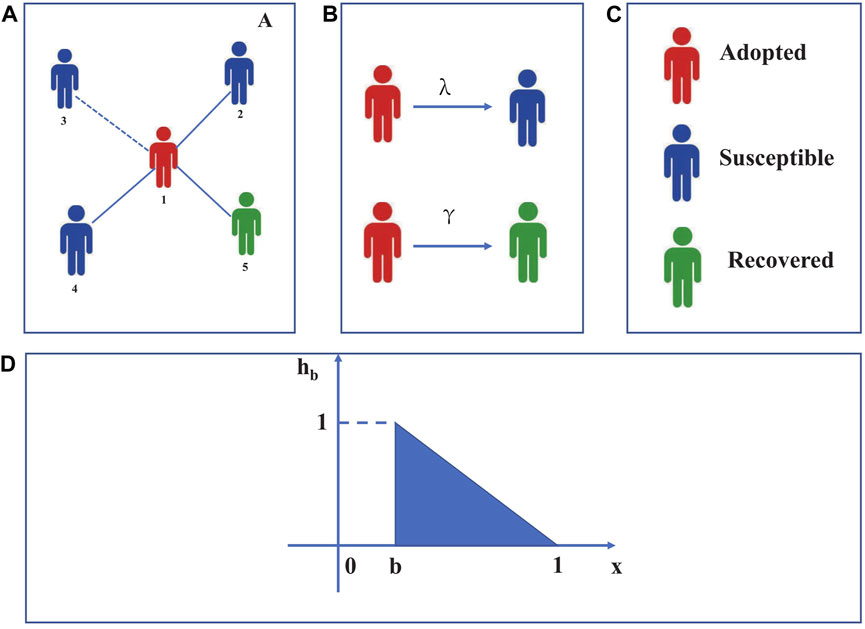
Figure 1. (A) Dissemination of information in a complex network comprising a single layer. Individual 1 has embraced the information, while individuals 2, 3, and 4 are still prone to it. Individual 5 has already regained information. Information was effectively disseminated through the blue dashed line, and node 1 that has received the information has conveyed it to its neighbors through this route. To represent the impact of limited contact, the paper sets the parameters of limited contact at 5 and 20. This means that each node can receive either 5 or 20 pieces of information from its neighbors. (B) Nodes that have embraced the information disseminate it to susceptible nodes with a likelihood of λ. When state nodes transition from adopted to recovered, the probability is represented by γ. (C) Each color represents a dissemination state—red for adopted nodes, blue for susceptible nodes, and green for recovered nodes. (D) Probability of neighbors adopting the opposite trend. Adoption probability is 0 when 0 < x < b, but as soon as b ≤ x < 1, individuals will adopt behavior with a probability of $\frac{1-x}{1-b}$.

We introduced limited contact to represent the contact ability of each node. $f\left(k_j\right)$ denotes the limited contact of nodes, and k_j represents the degree of node j. If $f\left(k_j\right)\ge k_j$, adopted nodes can transmit information to all of their neighbors. However, when $f\left(k_j\right)<k_j$, they can only transmit information to their f(k_j) nodes, resulting in a reduced amount of information that individuals can access. Within a unit of time, the adopted nodes were converted by susceptible nodes with a probability of λ. Additionally, the nodes adopted the practice of spreading messages to all of their neighbors with a probability of $\frac{\lambda f\left(k_j\right)}{k_j}$.

We define m as the accumulation of information by nodes. Information is not transmitted initially, but when a susceptible node receives information, m increases by 1. We present an adoption threshold model that exhibits the characteristic of information spread against trends in a similar manner to a right triangle as Eq. 1.

$\mathrm{h}\left(x,b\right)=\left\{\begin{array}{cc}0\hfill & ,0<x<b\hfill \\ \frac{1-x}{1-b}\hfill & ,b\le x<1\hfill \end{array}\right..(1)$

Here, x represents the ratio of received information to the degree of a susceptible node and b denotes the degree parameter of opposite trend adoption.

• The process of information spreading in a single-layer network with limited contact is outlined as follows: prior to transmission, we randomly select the proportion of ρ₀ adopted nodes. The remaining nodes are deemed susceptible.

• Adopted nodes, which are stochastically chosen f(k_j) times from susceptible nodes, transmit messages along edges with a probability of $\frac{\lambda f\left(k_j\right)}{k_j}$.

• As susceptible nodes receive messages, the number of susceptible nodes decreases by 1.

• The node will reject duplicate information that has been previously received.

• During a unit of time, the adopted nodes have a probability of transitioning into recovered nodes. However, if there are no adopted nodes left, the process will terminate within that time frame.

3 Theoretical analysis

In accordance with the hole theorem in a single-layer network with limited contact, we assume the random selection of node i as the hole state. In this state, node i can merely receive information from its adopted neighbors. The probability of nodes not delivering information to their neighbors is determined as ${\theta }_{k_j}$. We subsequently calculate the probability of node i being unable to accept messages from its neighbors at time t as

$\theta \left(t\right)={\displaystyle \sum _{{\mathrm{k}}_j=0}^{{\mathrm{k}}_{\mathrm{j}}\max }}\frac{k_{j}p\left(k_j\right)}{<k>}{\theta }_{k_j\left(t\right)}.(2)$

At time t, the likelihood of the hole-state node receiving information from multiple neighbors can be represented by Eq. 3.

${\mathrm{\Phi }}_m\left(k_i,t\right)=\left(\begin{array}{c}\hfill k_i\hfill \\ \hfill m\hfill \end{array}\right)\theta {\left(t\right)}^{k_i-m}{\left[1-\theta \left(t\right)\right]}^m.(3)$

Although node i may receive information, it will not transition immediately to the adopted state upon gaining such information. The probability of node i remaining susceptible is defined as $\underset{l=0}{\overset{m}{\Pi }}[1-h(\frac{l}{k},b)]$. We accumulate the probability of the susceptible state at time t. The degree of node i is also defined as k = k_i. Node i is defined to be in one of three states: susceptible, adopted, or recovered. We accumulate the probability of the susceptible state at time t as Eq. 4.

$\begin{array}{c}\tau \left(k_i,t\right)={\displaystyle \sum _{m=0}^{k_i}}{\mathrm{\Phi }}_m\left(k_i,t\right)\underset{l=0}{\overset{m}{\Pi }}\left[1-h\left(\frac{l}{k_i},b\right)\right]\hfill \\ ={\displaystyle \sum _{m=0}^{⌊b{k}_i⌋}}{\mathrm{\Phi }}_m\left(k_i,t\right)+{\displaystyle \sum _{m=⌈b{k}_i⌉}^{k_i}}{\mathrm{\Phi }}_m\left(k_i,t\right)\prod _{l=⌈b{k}_i⌉}^m\left(1-\frac{1-\frac{l}{k_i}}{1-b}\right)\hfill \end{array}.(4)$

In addition, the probability of all the susceptible nodes at time t can be represented by Eq. 5.

$\begin{array}{c}\mathrm{s}\left(k_i,t\right)=\left(1-{\rho }_0\right){\displaystyle \sum _{m=0}^{k_i}}{\mathrm{\Phi }}_m\left(k_i,t\right)\underset{l=0}{\overset{m}{\Pi }}\left[1-h\left(\frac{l}{k_i},b\right)\right]\hfill \\ =\left(1-{\rho }_0\right)\tau \left(k_i,t\right)\hfill \end{array}.(5)$

The probability of susceptible nodes maintaining their current status is represented by Eq. 6.

$\eta ={\displaystyle \sum _{k_i}^{k_i\max }}p\left(k_i\right)\tau \left(k_i,t\right).(6)$

Until time t, the ratio of susceptible nodes in the single-layer network is observed to be as represented by Eq. 7.

$S\left(t\right)={\displaystyle \sum _k}p\left(k\right)s\left(k,t\right)=\left(1-{\rho }_0\right)\eta .(7)$

The probability of node j being in one of the three states and not acquiring any information from its neighboring nodes is represented by Eq. 8.

${\theta }_{k_j}\left(t\right)={\xi }_{S,k_j}\left(t\right)+{\xi }_{A,k_j}\left(t\right)+{\xi }_{R,k_j}\left(t\right).(8)$

However, the probability of node j gaining information as of time t is represented by Eq. 9.

${\mathrm{\Phi }}_m\left(k_{\mathrm{j}}-1,t\right)=\left(\begin{array}{c}{k}_{\mathrm{j}}-1\\ m\end{array}\right)\theta {\left(t\right)}^{k_{\mathrm{j}}-1-m}{\left[1-{\theta }_{k_{\mathrm{j}}}\left(t\right)\right]}^m.(9)$

Susceptible nodes will not transition to adopted state nodes until they receive a certain quantity of messages. Therefore, we define the probability of a node receiving n messages and remaining in the susceptible state as ς(k_j − 1, t). At time t, the probability of a node j with degree k_j remaining in the susceptible state is calculated.

$\begin{array}{c}{\zeta }_n\left(k_j-1,t\right)={\displaystyle \sum _{n=0}^{k_j-1}}{\mathrm{\Phi }}_n\left(k_j-1,t\right)\underset{l=0}{\overset{n}{\Pi }}\left[1-h\left(\frac{l}{k_j},b\right)\right]\hfill \\ ={\displaystyle \sum _{n=0}^{⌊b{k}_j⌋}}{\mathrm{\Phi }}_n\left(k_j,t\right)+{\displaystyle \sum _{n=⌈b{k}_j⌉}^{k_j}}{\mathrm{\Phi }}_n\left(k_j,t\right)\prod _{l=⌈b{k}_j⌉}^n\left(1-\frac{1-\frac{l}{k_j}}{1-b}\right)\hfill \end{array},(10)$

where the likelihood of nodes connecting to neighbors via an edge is determined as $\frac{k_{j}p(k_j)}{<k_j>}$. At time t, the probability of susceptible nodes remaining in their current state as they have not received any information is

${\xi }_{S,k_j}\left(t\right)=\left(1-{\rho }_0\right){\zeta }_n\left(k_j-1,t\right).(11)$

Since the impact is limited by contact, the probabilities of an adopted node j delivering information to its neighbors and transmitting through edges are determined as $\frac{f(k_j)}{k_j}$ and λ, respectively. Therefore, the probability of a node transmitting information to its neighboring nodes via edges is established as $\frac{\lambda f(kj)}{kj}$, and a function can be obtained as Eq. 12:

$\frac{d{\theta }_{k_j}\left(t\right)}{dt}=-\frac{\lambda f\left(k_j\right)}{k_j}{\xi }_{A,k_j}.(12)$

Due to the adopted nodes being converted to a recovered state with a certain probability γ, it is possible to require the function about $\frac{d{\xi }_{R,k_j}(t)}{dt}$, which can be expressed as Eq. 13

$\frac{d{\xi }_{R,k_j}\left(t\right)}{dt}=\gamma {\xi }_{A,k_j}\left(t\right)\left(1-\frac{\lambda f\left(k_j\right)}{k_j}\right).(13)$

By combining Eqs 10, 11, we can derive

${\xi }_{R,k_j}\left(t\right)=\gamma \left[1-{\theta }_{k_j}\left(t\right)\right]\left[\frac{k_j}{\lambda f\left(k_j\right)}-1\right].(14)$

By applying Eqs 11, 14 along with Eq. 10, we derive the following result: ${\xi }_{A,k_j(t)}$. Regarding the initial conditions, information has not been transmitted yet. As a consequence, we can calculate the probability of susceptible nodes not receiving any messages using Eq. 15:

${\theta }_{k_j}\left(0\right)=1.(15)$

At the same time, the network does not have any recovered nodes, providing us with the knowledge that

${\xi }_{R,k_j}\left(0\right)=0.(16)$

Overwriting function

$\frac{d{\theta }_{k_j}\left(t\right)}{dt}=-\frac{\lambda f\left(k_j\right)}{k_j}\left[{\theta }_{k_j}\left(t\right)-{\xi }_{S,k_j}\left(t\right)\right]+\gamma \left[1-{\theta }_{k_j}\left(t\right)\right]\left(1-\frac{\lambda f\left(k_j\right)}{k_j}\right).(17)$

When t → ∞, on the basis of Eq. 20, we obtain

${\theta }_{k_j}\left(\infty \right)={\xi }_{S,k_j}\left(\infty \right)+\gamma \left[1-{\theta }_{k_j}\left(\infty \right)\right]\left[\frac{k_j}{\lambda f\left(k_j\right)}-1\right].(18)$

Substituting Eq. 18 into Eq. 2, we obtain Eq. 19

$\theta \left(\infty \right)={\displaystyle \sum _{k_j=0}}\frac{k_{j}p\left(k_j\right)}{<k>}{\theta }_{k_j}\left(\infty \right)=g\left(\theta \left(\infty \right)\right).(19)$

In order to simplify the process, we consider

$\theta \left(\infty \right)=g\left(\theta \left(\infty \right)\right).(20)$

When Eq. 16 is in tangency with Eq. 17, it can be observed that a value abruptly changes into another value. The implication is that R(∞) increases discontinuously with λ. When θ(∞) < 1, the critical condition for information spreading can be obtained as Eq. 21:

$\frac{\partial g\left(\theta \left(\infty \right)\right)}{\partial \theta \left(\infty \right)}=1.(21)$

4 Results and discussion

In this study, the network comprised a set number of total nodes of 2 × 10⁴ and an average degree of 10. To demonstrate the parameter, experiments were conducted on both the random networks (ER) and scale-free networks (SF). The ER network adheres to a Poisson distribution $p(k)=e^{-<k>\frac{<{k>}^k}{k!}}$ for its node degree, unlike the SF network, which displays a power–law distribution with values of p(k) = ζk^−v and $\zeta =1/{\displaystyle \sum _k}{k}^{-v}$. It was observed that the heterogeneity of the node distribution was negatively correlated with the degree exponent v. To comprehend the complete information transmission process, we establish γ as 1. The specific critical value is denoted by χ, as detailed in Eq. 22.

$\chi =\frac{<{\left(R\left(\infty \right)-<R\left(\infty \right)>\right)}^2>}{<R{\left(\infty \right)>}^2}.(22)$

4.1 Analysis of opposite adoption against neighbors on the ER network

The limited contact that is heterogeneous in nature is observed to impact the ultimate range of propagation for both Figures 2A, B. Additionally, variations in the mode of dissemination are uncovered. The data suggest that the increase in λ eventually leads to universal acceptance $R\left(\infty \right)$. If in a weak opposite trend condition b = 0.01, the growth mode of $R\left(\infty \right)$ continues in a second-order fashion. Notably, $R\left(\infty \right)$ remains unchanged, and information is not disseminated under strong opposite conditions b = 0.15. Under moderate opposite-trend conditions b = 0.10 with limited contact, the transition $R\left(\infty \right)$ is second-order and continuous. However, under strong limited contact, the transition $R\left(\infty \right)$ is first-order and discontinuous. A comparison of the figures reveals that stronger limited contact has a greater impact on the spread of the network than weaker contact.

Figure 2

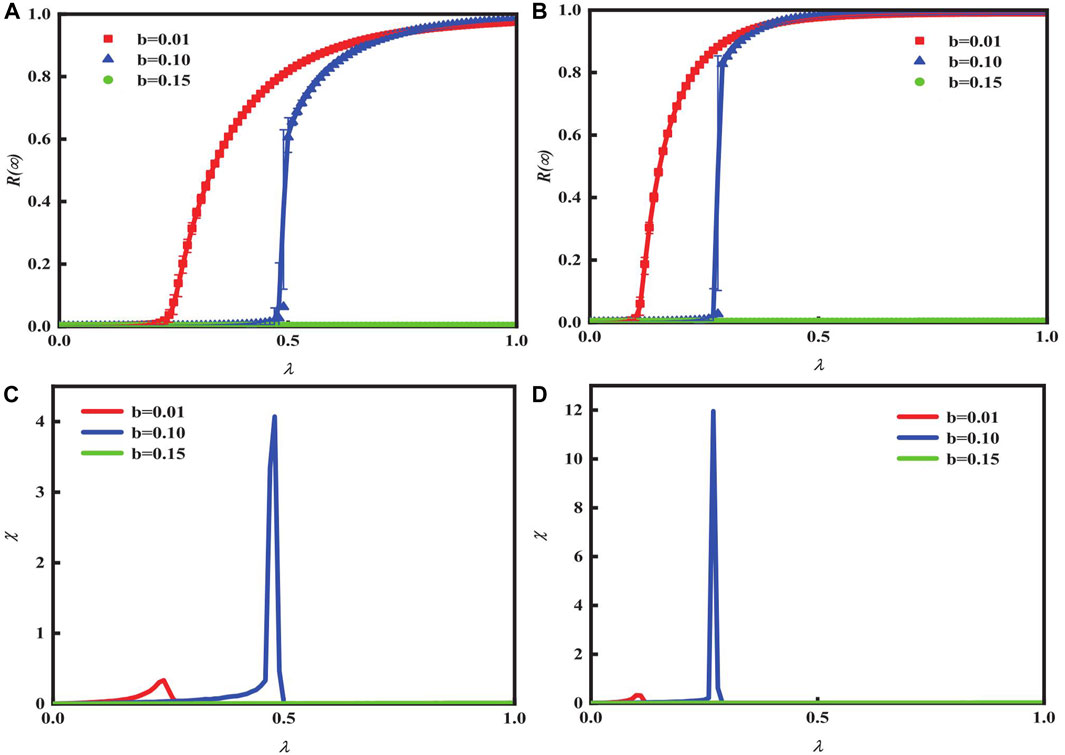
Figure 2. Impact of final spreading scope $R\left(\infty \right)$ on distinct opposite trend degree parameters b and heterogeneous limited contact with unit transmission rates λ in the ER network. Limited contact values of 5 and 20 are shown in (A) and (B) respectively. The ratio of initial infected nodes is also presented ρ₀ = 0.00125. Relative mistakes corresponding to (A) and (B) are depicted in (C) and (D) respectively.

Figures 2C, D indicate the ratio of critical dissemination of information, including relative errors. The highest point of relative errors χ, known as the critical point, demonstrates global adoption. The theoretical (lines) and simulated (symbols) results coincide.

The growth mode about $R\left(\infty \right)$ depends on λ and b (Figure 3). In region I, as λ increases, there is a second-order phase transition of $R\left(\infty \right)$ in continuous forms. In region II, there is a first-order phase transition in discontinuous forms. No information was reported for region III. The condition for the phase transition changes with varying degrees of parameter opposition. It is worth noting that the critical conditions for first- and second-order phase transitions correspond to the continuous and discontinuous growth of propagation, respectively. Additionally, the color temperature chart can elucidate the mechanisms of spreading and analyze the changes in spreading modes.

Figure 3

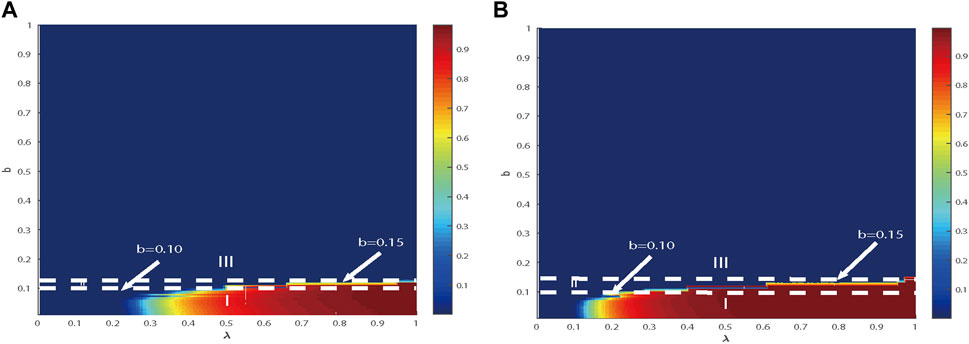
Figure 3. It can be inferred that there is a shared impact $\left(\lambda ,b\right)$ on $R\left(\infty \right)$ in the ER network. Limited contacts are observed at 5 in (A) and 20 in (B), with the ratio of initial infected nodes being ρ₀ = 0.00125. In region I, the increase in $R\left(\infty \right)$ follows a second-order continuous pattern, which distinguishes it from region II, where it increases in a first-order discontinuous pattern. No information propagation is detected in region III.

4.2 Analysis of opposite adoption against neighbors on the SF network

Figures 4A, B demonstrate the relationship between heterogeneous degree distribution and b influence on global adoption $R\left(\infty \right)$. With λ growing, $R\left(\infty \right)$ increase to globally adoption. The findings from Figures 4C, D indicate the ratio of critical dissemination of information, including relative errors. It becomes clear that heterogeneous degree distribution has no effect on the transmission mode of information. In the condition with an opposite middle b = 0.10, phase transitions vary. In a strong opposite situation b = 0.15, the growth pattern of $R\left(\infty \right)$ is first discontinuous. Conversely, in a weak condition b = 0.01, the increment mode about $R\left(\infty \right)$ is continuously second. The maximum value of relative error can indicate an explosion in information propagation at a certain point. Studying the amplitude of relative error can reflect the scale and pattern of propagation bursts during propagation.

Figure 4

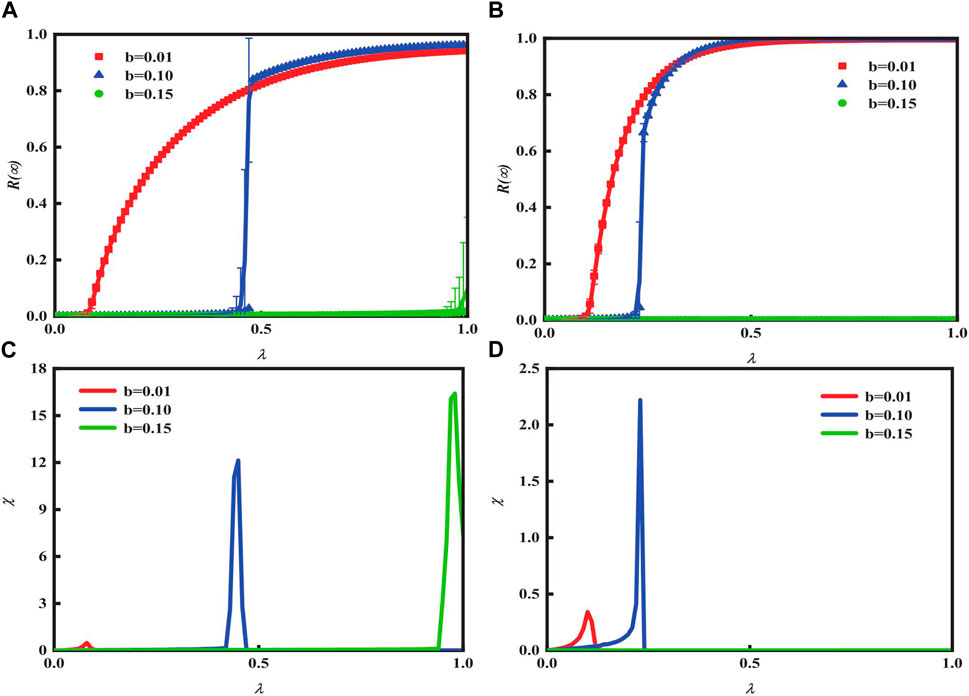
Figure 4. Impact b and heterogeneous limited contact on $R\left(\infty \right)$ with λ in the SF network. Limited contact is 20, while the heterogeneity of degree v is 2.1 in (A) and 4 in (B). The impact of these factors on the phase transition in (A) and (B) is evidenced by b. And we set initial infected nodes ρ₀ = 0.00125. (C) and (F) represent relative discrepancies that correspond to (A) and (B).

In Figure 5, the combination effect of $\left(\lambda ,b\right)$ on the variable $R\left(\infty \right)$ is depicted. In region I, as λ increases, the pattern of $R\left(\infty \right)$ represents a second continuous phase transition. In region II, the mode of increments $R\left(\infty \right)$ represents a first discontinuous phase transition. In region III, there is no explosion of information. Regardless of the scenario shown in Figure 3 or Figure 5, a cross-phase transition occurs at the junction of a discontinuous (in region II) or continuous (in region I) phase transition.

Figure 5

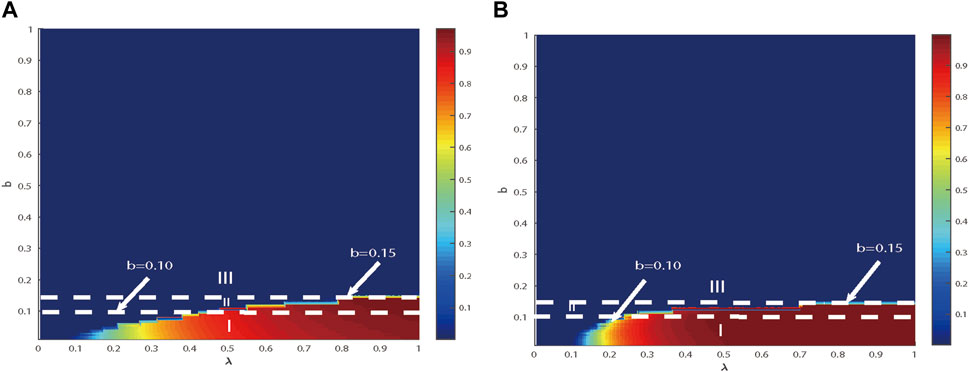
Figure 5. It can be inferred that there is a shared impact $\left(\lambda ,b\right)$ on $R\left(\infty \right)$ in the SF network. It demonstrates that in the scale-free network, there is a common influence about $\left(\lambda ,b\right)$ on $R\left(\infty \right)$ across different heterogeneity parameters, i.e., 2.1 in (A) and 4 in (B), with same limited contact at 20. The ratio of initial infected nodes is specified ρ₀ = 0.00125. In region I, the increase in $R\left(\infty \right)$ follows a second-order continuous pattern, differing from region II, where the increase follows a first-order discontinuous pattern. No information spreading occurs in region III.

5 Conclusion

In this paper, we analyze the mechanism of information spreading in relation to the adoption of opposing views within neighboring communities. We investigate the impact of opposite trend adoption among neighbors in a single-layer network and find that this behavior influences information dissemination to varying degrees. Meanwhile, we propose an adoption threshold function that takes the form of a right triangle with limited contacts.

The results demonstrate that under a strong opposite trend condition (b = 0.15), information will not be disseminated. Moreover, limited contact promotes the dissemination process, and with the increase in $R\left(\infty \right)$, the dissemination scope is second-order continuous under a weak condition (b = 0.01). Interestingly, there is a cross-phase transition in the results of the opposite trend condition in the middle (b = 0.10). The growth mode about $R\left(\infty \right)$ in the ER network shifts from continuous second-order to discontinuous first-order, whereas in the SF network, it transits quite contrarily. These results reveal the significant importance of opposite-trend adoption.

In future research, researchers could investigate the prevalence of counter-trend adoption in new settings. For instance, investigators can study counter-trend adoption in multi-layer networks and even discover information heterogeneity among individuals.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JH: Conceptualization, methodology, software, writing–original draft, writing–review and editing. JM: Conceptualization, methodology, software and writing-review and editing. SL: Validation, writing–review and editing. YT: Validation, writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ji P, Ye J, Mu Y, Lin W, Tian Y, Hens C, et al. Signal propagation in complex networks. Phys Rep (2023) 1017:1–96. doi:10.1016/j.physrep.2023.03.005

CrossRef Full Text | Google Scholar

2. Wang H, Ma C, Chen H-S, Zhang H-F. Effects of asymptomatic infection and self-initiated awareness on the coupled disease-awareness dynamics in multiplex networks. Appl Math Comput (2021) 400:126084. doi:10.1016/j.amc.2021.126084

CrossRef Full Text | Google Scholar

3. Chen X, Gong K, Wang R, Cai S, Wang W. Effects of heterogeneous self-protection awareness on resource-epidemic coevolution dynamics. Appl Math Comput (2020) 385:125428. doi:10.1016/j.amc.2020.125428

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ni Q, Guo J, Wu W, Wang H, Wu J. Continuous influence-based community partition for social networks. IEEE Trans Netw Sci Eng (2021) 9:1187–97. doi:10.1109/tnse.2021.3137353

CrossRef Full Text | Google Scholar

5. Liu S, Yu J, Deng X, Wan S. Fedcpf: an efficient-communication federated learning approach for vehicular edge computing in 6g communication networks. IEEE Trans Intell Transportation Syst (2021) 23:1616–29. doi:10.1109/tits.2021.3099368

CrossRef Full Text | Google Scholar

6. Hu Y, Xiong F, Pan S, Xiong X, Wang L, Chen H. Bayesian personalized ranking based on multiple-layer neighborhoods. Inf Sci (2021) 542:156–76. doi:10.1016/j.ins.2020.06.067

CrossRef Full Text | Google Scholar

7. Zhong C, Xiong F, Pan S, Wang L, Xiong X. Hierarchical attention neural network for information cascade prediction. Inf Sci (2023) 622:1109–27. doi:10.1016/j.ins.2022.11.163

CrossRef Full Text | Google Scholar

8. Ni X, Xiong F, Pan S, Wu J, Wang L, Chen H. Community preserving social recommendation with cyclic transfer learning. ACM Trans Inf Syst (2023) 42:1–36. doi:10.1145/3631115

CrossRef Full Text | Google Scholar

9. Zhu H, Xiong F, Chen H, Xiong X, Wang L. Incorporating a triple graph neural network with multiple implicit feedback for social recommendation. ACM Trans Web (2024) 18:1–26. doi:10.1145/3580517

CrossRef Full Text | Google Scholar

10. Ren Z-M, Zeng A, Zhang Y-C. Structure-oriented prediction in complex networks. Phys Rep (2018) 750:1–51. doi:10.1016/j.physrep.2018.05.002

CrossRef Full Text | Google Scholar

11. Yin H, Wang Q, Zheng K, Li Z, Yang J, Zhou X. Social influence-based group representation learning for group recommendation. In: 2019 IEEE 35th International Conference on Data Engineering (ICDE). IEEE (2019). p. 566–77.

CrossRef Full Text | Google Scholar

12. Zheng M, Lü L, Zhao M. Spreading in online social networks: the role of social reinforcement. Phys Rev E (2013) 88:012818. doi:10.1103/physreve.88.012818

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang W, Liu Q-H, Cai S-M, Tang M, Braunstein LA, Stanley HE. Suppressing disease spreading by using information diffusion on multiplex networks. Scientific Rep (2016) 6:29259. doi:10.1038/srep29259

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang W, Liu Q-H, Liang J, Hu Y, Zhou T. Coevolution spreading in complex networks. Phys Rep (2019) 820:1–51. doi:10.1016/j.physrep.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Juul JS, Porter MA. Hipsters on networks: how a minority group of individuals can lead to an antiestablishment majority. Phys Rev E (2019) 99:022313. doi:10.1103/physreve.99.022313

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Tian Y, Tian H, Cui Y, Zhu X, Cui Q. Influence of behavioral adoption preference based on heterogeneous population on multiple weighted networks. Appl Math Comput (2023) 446:127880. doi:10.1016/j.amc.2023.127880

CrossRef Full Text | Google Scholar

17. Yang M, Wu C, Xie T. Information propagation dynamics model based on implicit cluster structure network. In: 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC). IEEE (2020). p. 1253–7.

CrossRef Full Text | Google Scholar

18. Ren Y, Li L. Sar dynamical mechanism affected by diminishing marginal effect based on personal fashion psychology on multi-layer contacted network. Physica Scripta (2024) 99:035252. doi:10.1088/1402-4896/ad295f

CrossRef Full Text | Google Scholar

19. Kobayashi T. Trend-driven information cascades on random networks. Phys Rev E (2015) 92:062823. doi:10.1103/physreve.92.062823

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Juul JS, Porter MA. Synergistic effects in threshold models on networks. Chaos: Interdiscip J Nonlinear Sci (2018) 28:013115. doi:10.1063/1.5017962

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Tian Z, Zhang G, Yu H, Liu H, Lu D. Negemotion: explore the double-edged sword effect of negative emotion on crowd evacuation. IEEE Trans Comput Soc Syst (2024) 1–14. doi:10.1109/tcss.2023.3344172

CrossRef Full Text | Google Scholar

22. Huo S, Yu Y. The impact of the self-recognition ability and physical quality on coupled negative information-behavior-epidemic dynamics in multiplex networks. Chaos, Solitons and Fractals (2023) 169:113229. doi:10.1016/j.chaos.2023.113229

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Leng H, Zhao Y, Wang D. Message passing approach for social contagions based on the trust probability with multiple influence factors. Physica A: Stat Mech its Appl (2022) 587:126510. doi:10.1016/j.physa.2021.126510

CrossRef Full Text | Google Scholar

24. Cui Y, Wei R, Tian Y, Tian H, Zhu X. Information propagation influenced by individual fashion-passion trend on multi-layer weighted network. Chaos, Solitons and Fractals (2022) 160:112200. doi:10.1016/j.chaos.2022.112200

CrossRef Full Text | Google Scholar

25. Ruan Z, Zhang L, Shu X, Xuan Q. Social contagion with negative feedbacks. Physica A: Stat Mech its Appl (2022) 608:128304. doi:10.1016/j.physa.2022.128304

CrossRef Full Text | Google Scholar

26. Salling MC, Martinez D. Brain stimulation in addiction. Neuropsychopharmacology (2016) 41:2798–809. doi:10.1038/npp.2016.80

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Chen X, Wang N. Rumor spreading model considering rumor credibility, correlation and crowd classification based on personality. Scientific Rep (2020) 10:5887. doi:10.1038/s41598-020-62585-9

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ye J, Chen Y. Social contagion influenced by active-passive psychology of college students. Front Phys (2022) 10:1019118. doi:10.3389/fphy.2022.1019118

CrossRef Full Text | Google Scholar

29. Zhu Y-X, Cao Y-Y, Chen T, Qiu X-Y, Wang W, Hou R. Crossover phenomena in growth pattern of social contagions with restricted contact. Chaos, Solitons and Fractals (2018) 114:408–14. doi:10.1016/j.chaos.2018.06.010

CrossRef Full Text | Google Scholar

30. Du J, Zhao D, Issa RR, Singh N. Bim for improved project communication networks: empirical evidence from email logs. J Comput Civil Eng (2020) 34:04020027. doi:10.1061/(asce)cp.1943-5487.0000912

CrossRef Full Text | Google Scholar

31. Yang D, Xian J, Pan L, Wang W, Zhou T. Effective edge-based approach for promoting the spreading of information. IEEE Access (2020) 8:83745–53. doi:10.1109/access.2020.2992058

CrossRef Full Text | Google Scholar

32. Lv C, Yuan Z, Si S, Duan D, Yao S. Cascading failure in networks with dynamical behavior against multi-node removal. Chaos, Solitons and Fractals (2022) 160:112270. doi:10.1016/j.chaos.2022.112270

CrossRef Full Text | Google Scholar

33. Huo S, Chen S. Rumor propagation model with consideration of scientific knowledge level and social reinforcement in heterogeneous network. Physica A: Stat Mech Its Appl (2020) 559:125063. doi:10.1016/j.physa.2020.125063

CrossRef Full Text | Google Scholar

34. Li W, Li J, Nie Y, Lin T, Chen Y, Liu X, et al. Infectious disease spreading modeling and containing strategy in heterogeneous population. Chaos, Solitons and Fractals (2024) 181:114590. doi:10.1016/j.chaos.2024.114590

CrossRef Full Text | Google Scholar