What do we learn from impurities and disorder in high-Tc cuprates?

A series of experimental studies established that the differing morphologies of the phase diagrams versus hole doping n_h of the various cuprate families are mostly controlled by defects and disorder. In the minimally disordered cuprate Yttrium Baryum Copper Oxide (YBCO) we introduced controlled detfects that allowed us to probe the metallic and superconducting states. We demonstrate that the extent of the spin glass phase and the superconducting dome can be controlled by the concentration of spinless (Zn, Li) impurities substituted on the planar Cu sites. NMR frequency shift measurements establish that these defects induce, in their vicinity, a cloud with a Kondo-like paramagnetic behavior. Its “Kondo” temperature and spatial extent differ markedly between the pseudogap and strange metal regimes. We have performed transport measurements on single crystals with a controlled content of in-plane vacancies introduced by electron irradiation. At high T, the inelastic scattering of the carriers has been found independent of disorder and completely governed by the excitations of the correlated electronic state. The low T upturns in the resistivity associated with single-site Kondo-like scattering are qualitatively in agreement with local magnetism induced by spinless impurities. The apparent metal insulator crossover is only detected for a very large defect content, and part of the large resistivity upturn remains connected with Kondo-like paramagnetism. In the superconducting state, the defect-induced reduction of T_c scales linearly with the increase in residual resistivity induced by disorder. High-field magnetoresistance experiments permit us to determine the paraconductivity due to superconducting fluctuations. The latter vanishes beyond a temperature T’_c and a field H’_c that both decrease with increasing in-plane defect content. In the pseudogap regime, the weaker decrease of T’_c with respect to that of T_c reveals a large loss of superconducting phase coherence in the presence of disorder. In light of our experimental results, we initiate a discussion of its interplay with pair breaking. Our data also permit us to confirm that the differing phase diagrams are due to competing orders or disorders that are family-specific. In the ideal phase diagram of a disorder-free cuprate, 2D superconductivity should persist at low doping. This ensemble of experimental results provides serious challenges for the theoretical understanding of superconductivity in these correlated electron systems.

1 Introduction

Impurities and disorder play a major role in solid state physics, as could be already shown in materials for which an independent electron approximation holds. They govern the mechanical and optical properties of most materials. The chemical nature of impurities determines, for instance, the beautiful colors of gems that are large bandgap insulators. The transport properties of semiconductors were only under control when it became clear that the carrier content is associated with the chemical properties of the impurities and their concentration. The low-temperature electronic and thermal conductivity of metals are limited by the scattering of carriers on impurities and lattice defects. In the metals that display a superconducting state at low T, the disorder favors the type II state and plays a major role in the pinning of vortices and so on.

One does naturally expect then to find that disorder has a strong influence on the original physical properties displayed by materials in which electronic interactions are dominant, such as high-T_c cuprates [1]. These are materials involving a large number of atomic species. They are then likely expected to house a variety of impurities or lattice defects. On the experimental side, they are quasi unavoidable and intrinsic to the growth of the materials. The basic structure of cuprates is a set of layered CuO₂ planes separated by charge reservoir layers. The former is responsible for the original physical properties, while the latter is essential to control the electron or hole doping of the CuO₂ planes. On the theory side, one faces a sufficiently complex theoretical challenge in trying to explain the properties of a single CuO₂ plane with increasing doping. One generally considers impurities and disorder as unwanted complications.

In actual cuprates, defects are always present and, for experimentalists, the real difficulty is to decide whether the observed physical properties are generic, that is, due to the ideal defect-free cuprate plane. Most of the works reported in this article are attempts to isolate those from the extrinsic effects related to the chemical doping procedure. It can altogether be shown as well that defects or impurities injected in a controlled manner can be excellent probes of the properties of the pure material.

An essential approach to reach this aim is to eliminate as much as one can the sources of disorder that smear or influence the measured properties. Improving the sample preparation procedure is an obvious method to achieve this task. An alternative approach is to compare the properties of different cuprate families to sort out the generic properties from those that are specific or marginal. Once this has been performed, that is, a rather disorder-free compound or family has been selected, one might then try to introduce defects in a controlled manner in that pure material. One may then use both thermodynamic and local probes to determine the influence of specific defects on the physical properties. I shall show that those observations sometimes bring new information hardly accessible experimentally on the pure material [2].

I have initiated such an orientation in my research group since the early days of the discovery of high T_c superconductivity and encouraged many researchers in the Orsay-Saclay area to follow this approach over the last 35 years. I summarize here the various important results obtained that allowed some understanding of the experimental properties of cuprates and still raise important questions to be resolved on the theory side.

I shall consider first in Section 2 the (T,n_h) phase diagram of diverse hole doped cuprate families and show that its morphology is driven by the existing disorder, which raises the question about the actual phase diagram which should represent the hypothetical disorder-free cuprate. This will further allow me to categorize the cuprate families with increasing disorder. I shall then show that the Yttrium Baryum Copper Oxide (YBCO) family is among the cleanest cases where one could investigate the influence of an increasing content of defects. This allowed me to present in Section 3 the local NMR studies of the magnetic properties induced by Zn and Li spinless impurities in the metallic state of the CuO₂ planes. Using highly energetic electron irradiation allowed one to control the introduction of vacancies in the CuO₂ planes in cuprate single crystals. Their influence on the transport properties was identical to that produced by Zn chemical substitutions. We could, therefore, perform a refined comparison of the evolution with the defect content of the normal state transport and magnetic properties. In Section 4, I shall then present results on the corresponding modifications of the SC properties such as the decrease of T_c. Similarly, I shall describe a detailed investigation of the evolution with a disorder of the superconducting fluctuation range, using high magnetic fields when necessary. The importance of the loss of phase coherence in the 2D SC state in the presence of disorder will be underlined. A discussion of this ensemble of results, done in Section 5, will permit to summarize that one cannot any more consider disorder effects as unnecessary complications. They rather permit to raise many essential questions and give useful guidance for theory.

2 Cuprate phase diagrams and disorder

Let me perform first a small historical survey about the discovery of cuprates and of their phase diagram and discuss hereafter my present understanding of the influence of disorder.

2.1 Early phase diagrams of cuprates

The first cuprate discovered by Bednorz and Muller has been the family of 124 compounds [3]. The parent La₂CuO₄ is an AF Mott insulator with T_N = 240 K that can be doped by substitution of a concentration x of La³⁺ by Ba²⁺ or Sr²⁺ [4]. The long-range ordered AF state is destroyed for x = 2%, and an SC dome appears for 0.07 < x < 0.3 with a maximum T_c = 38 K for x ∼ 0.19. From simple chemical arguments, the concentration of holes in the CuO₂ planes is merely n_h = x and most researchers have immediately considered that this (T,n_h) phase diagram is generic of the cuprate plane. One noticed as well that the material displays in the intermediate range 0.02 < x < 0.07 a low T disordered frozen spin state of the Cu 3d⁹ magnetic sites labeled as spin glass (SG).

A year later, the YBa₂Cu₃O_6+x family has been discovered [5], with a parent AF state as well with T_N = 410 K for x = 0 and part of a SC dome with a maximum T_c = 93 K. This compound involves two CuO₂ layers with an intermediate Y³⁺ layer. Successive bilayers are separated by a square lattice layer of non-magnetic Cu⁺ for x = 0. The hole doping for x > 0 results from the extra oxygen atoms introduced in this intermediate Cu layer. The relation between x and n_h is not straightforward as the Cu²⁺-O^2-- Cu²⁺ chain segments formed do not transfer charge in the CuO₂ planes. The phase diagram displayed in Figure 1 is quite similar to that of La₂CuO₄, but the AF phase is contiguous to the SC phase [7]. An important difference is therefore the absence of an intermediate SG regime. Although this is a very important distinction, many researchers mostly interested by the SC properties considered that as a minor difference and mapped the n_h ranges in the 124 and YBCO phase diagrams by an artificial parabolic fit of the SC domes [8].

Figure 1

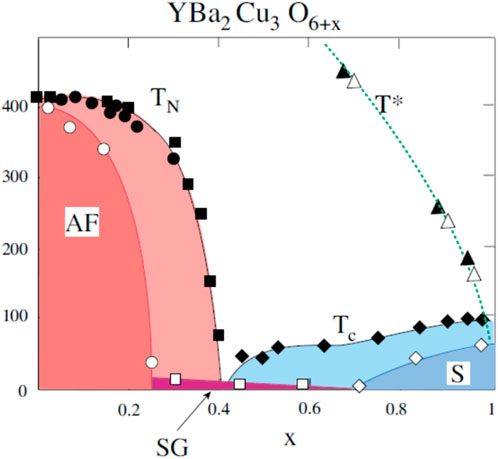
Figure 1. Phase diagrams of the AF Néel temperature T_N, spin glass transition T_SG, SC transition T_c, and pseudogap T* for pure YBCO samples (filled symbols) and for 4% Zn substitution (empty symbols). From Ref. [6].

In our preliminary experiments with Zn impurities in YBa₂Cu₃O_6+x, we immediately found that the reduction of T_c was larger in the underdoped regime than in the optimally doped case. This Zn induced in plane disorder has then led us to notice changes in the morphology of the phase diagram (PD), as displayed in Figure 1 [9]. Then, we plotted together the PD versus oxygen content x for pure samples and for 4% Zn substitution [6]. One can see that both extents of the AF phase and the SC dome shrink and disclose a wide SG regime. The morphology of the PD resembles then markedly that of the 124 family upon this introduction of disorder. The latter, therefore, plays a major role in defining the extent of the SG regime in the cuprates. This observation also implied that the n_h mapping between phase diagrams is not accurate.

This occurred at the very time of the PG discovery in the underdoped pure YBCO using ⁸⁹Y NMR shift data [10]. I initiated these Zn substitution experiments mostly to try to understand whether the PG had any relation with superconductivity. With 4% Zn substitution, our ⁸⁹Y NMR data immediately convinced us that T* unchanged even for the underdoped YBCO_6.6 sample, for which SC is fully suppressed [9]. This total independence of the two effects suggested that the PG is a phenomenon that competes with the SC state. This powerful indication revealed by introduction of Zn impurities does not, however, allow to conclude whether T* corresponds to a phase transition in the defect-free compound. The actual disorder introduced by the Zn substitution might indeed prevent a long-range ordering.

We were, at that time, most concerned by an important question concerning the PG. What could explain the large T_c difference at optimal doping between the 124 and YBCO families? Could that be associated with an intrinsic difference between compounds with single CuO₂ layers and those with bilayers in the unit cell? We completely cleared that question by performing the first study of powder samples of the single-layer Hg1201 cuprate family, for which the optimum T_c is approximately 85 K. We could synthesize samples covering a large range of doping from the underdoped to the overdoped regime. The comparison of ¹⁷O NMR shift data with that taken in the YBCO family allowed us to demonstrate that PG T* are, in all aspects, quantitatively identical in both families [11].

In this Hg cuprate family, doping proceeds again from an increase in the O content in the Hg layer that is far from the CuO₂ plane so that the dopant-induced disorder should be weaker than in the 124 family. These experiments confirmed, therefore, that the PG is a robust phenomenon independent not only on the number of CuO₂ layers but also on the disorder induced by dopants or substitutions.

2.2 A 3D phase diagram

The Zn substitution experiments of Figure 1 indicate that the SC dome shrinks with increasing plane disorder. This was shown as well using electron irradiation to increase progressively the in-plane defect content (see Section 3). These experiments have led us altogether to understand that the morphology of the PD evolves with the increase in disorder induced by the increase in the Zn content. We could then propose the 3D phase diagram of Figure 2, in which the third axis represents the increase in the Zn content [12]. Transport experiments given in detail in Section 3 allowed to follow the iso-n_h red lines plotted in Figure 2 that confirm the average displacement of the SC dome to the right in the PD while the SG range broadens and the PG T* is unchanged.

Figure 2

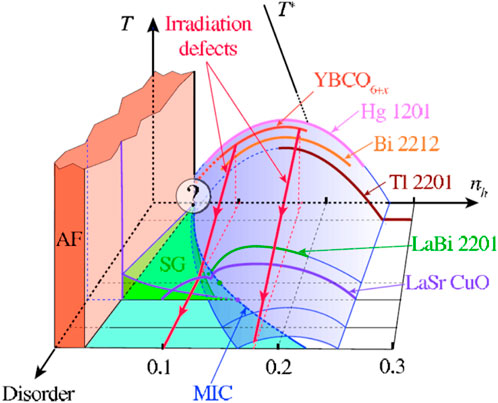
Figure 2. Variation in the (T,n_h) phase diagram for increasing disorder. The red lines represent the T_c variation with disorder induced by electron irradiation in YBCO (See Section 3 in the text). The doping range of the AF state slightly shrinks with increasing disorder for instance with Zn content, or with Ca content in Y_1-y Ca_yBCO₆ (see text in Section 2.2). The T_c domes reported for the various cuprate families are limited to the experimentally accessible doping ranges. Their positions on the disorder axis are chosen in order to roughly match their SG ranges with those expected with increasing Zn-induced disorder in YBCO. From Ref. [12].

We shall consider hereafter the various cuprate families and try to anticipate where their phase diagram could be located on such a 3D scheme. We discarded there the PD for homovalent substitutions of rare earths on the Y³⁺ sites in YBCO_6+x as they do not significantly modify T_c and the PD. We did not consider either the peculiar case of Pr that was shown to display a 4+ valence that changes the oxygen content and hole doping for both AF and SC [13, 14]. For heterovalent substitutions, one can assume that the disorder due to the Coulomb interaction with the dopants decreases as their distance to the CuO₂ planes increases.

For all the single-layer or bilayer cuprate families, the PG T* variation observed by various experimental techniques were found to match with those observed for YBCO. For those families that display T_c ∼ 90 K at optimal doping, the dopants are located in the interlayers. So for these families, the mapping of the (T_c, n_h) SC domes usually assumed by parabolic fits might be acceptable. In Figure 2, their SC domes are located very near that of YBCO.

Let me point out that a weak dopant-induced disorder remains in those actual compounds, for which the optimum T_c value is approximately 90 K. The AF and SG domains for those families could not be probed except for YBCO as they could not be sufficiently underdoped experimentally. We cannot say, at this stage, whether in the absence of disorder, the T_c dome would reach T_c = 0 before the onset of the AF state. Would the clean phase diagram display a first-order transition from the AF to the SC state? In Figure 2, we introduced, therefore, the question mark near the 2D phase diagram for vanishing disorder.

The heterovalent substitutions in (LaSr)124 and (La-Bi)2201 families occur on sites adjacent to the CuO₂ planes. We assumed that the disorder is large in these systems, and we consequently located their 2D PD along the “disorder” axis at points for which their SG ranges approximately match those for YBCO + Zn.

We also considered another PD for Y_1-y Ca_yBCO₆, in which the n_h doping proceeds from a partial substitution of Ca²⁺ on the Y³⁺ site inserted between the CuO₂ layers in the parent YBCO₆ [15]. We again found that the AF state disappears for a Ca content y = 2n_h of about 7%. A SG range was disclosed for 0.03< n_h < 0.09, and a maximum T_c value of approximately 30 K is reached for y = 0.25 that unfortunately appears to be the Ca chemical solubility limit. Here, the large disorder induced by the substitution site between the CuO₂ planes again generates a PD that maps even quantitatively that of (LaSr)124 for n_h < 0.15. We did not plot it in Figure 2 to keep the figure clear.

In our proposed 3D PD, the quantitative definition of the disorder for a given family is, of course, rather rough. The disorder magnitude depends on the defect types and even evolves with doping inside many cuprate families. The data for a given family should be on a distorted surface in Figure 2 rather than on parallel flat planes.

The 3D representation, however, gives a reliable indication on the actual trend followed in the real materials. The systematic analysis conducted allows us to conclude that the disorder governs the morphology of the (T, n_h) phase diagram by opening the spin glass regime.

This 3D phase diagram even suggests that the disorder governs the optimal T_c value of the diverse cuprate families. In-plane disorder produced by Zn leads to a subsequent decrease in optimum T_c. The out-of-plane disorder also has an influence on T_c values, as illustrated for instance within the 124 family. Then, T_c ∼ 45 K are obtained by electrochemical intercalation of excess oxygen [16] that induces less disorder than Sr²⁺ substitution on the La³⁺ sites.

From the above phase diagram analysis, we cannot, however, conclude whether the difference of optimal T_c is solely due to the existing disorder. Further data will allow us to discuss again that point later in Section 5.

Here, I did not discuss so far the interesting low T-phases detected well below T* that have been thoroughly studied during the last decades. Soon, after the cuprate discovery, a stripe charge order has been highlighted in the 124 phase [17]. It is strongly pinned for Ba²⁺ substitution on the La³⁺ site and fully depresses the SC state for x = 0.12. For Sr²⁺ substitution, this stripe phase is less pinned and only seen as a small dip in the T_c (n_h) variation.

In YBCO, many unexpected phenomena were detected at low T in high-quality samples with x ∼ 0.6, starting by quantum oscillations on the resistivity [18], corresponding to a small Fermi surface orbit and a negative Hall effect [19]. Then, NMR in a high applied field allowed to show a charge ordering below T_c = 60 K [20]. The latter could possibly be associated with the 2D CDW order detected for T as high as 150 K by RIXS experiments in zero field [21]. Extension of these measurements in high field [22] provide final evidence that the 2D CDW transforms below 60 K into the 3D CDW seen by NMR. The present understanding is that a reconstruction of the Fermi surface occurs below the SC dome, in a narrower dome-shaped region of the phase diagram [19] centered at about x = 0.6. This original coexistence of SC and CDW order parameters has been underlined and has justified extensive theoretical studies [23, 24].

Independently of the originality of this situation, I anticipated early on that these electronic orders occurred well below T* and, therefore, could not be responsible for the pseudogap that is highly related to Mott physics [25]. Nowadays, an emerging consensus is that the cuprates can display diverse low T electronic orders in the PG regime [19]. These compete with SC and are somewhat distinct in the diverse cuprate families, as found in 124 and YBCO_6.6 families.

I have always suggested that the actual disorder or the order introduced by the hole dopants plays a great role in selecting the ground states [25]. The CDW dome in YBCO occurs for a hole doping nearby that for which a slight singularity occurs in the T_c(x) variation, as shown in Figure 1. Structural studies have also shown that in this range of oxygen contents in YBCO, a Cu-O chain ordering occurs in the interlayer Cu plane [26]. I am, however, not aware of any careful experimental effort to search whether some correlation holds between the oxygen structural order and the CDW. In any case, I still suggest that these competing charge orders are, therefore, not generic of the ideal CuO₂ plane conceived by theoreticians.

3 Point defects in the pseudogapped and strange metals

The d-wave superconductivity, PG, and strange metal with a T linear behavior of the resistivity for optimal doping are the actual generic physical properties of cuprates still requiring a thorough understanding. Experimentally, one still needs to gather all possible information on the cleanest materials, which, from the above analysis, should be among the families with the highest optimal T_c value.

The family of YBCO_6+x appears to be a favorable case as the full range from the AF to the slightly overdoped regime is accessible without the occurrence of the intermediate SG phase. This indicates that disorder effects are minimal as we anticipated from NMR studies of the various nuclei of the unit cell [27].

For some specific oxygen content, the disorder might even be rather weak. The AF state for x = 0 is undoped with a half-filled Cu level in the CuO₂ planes and is not modified by a weak excess oxygen content. For x = 1, the unit cell is stoichiometric with filled ordered chains. It is situated in the slightly overdoped regime with T_c = 92 K, approximately 1 K below that at optimal doping. In the PG regime, we found out that sample reproducibility is extremely good with a large T* ∼ 350 K value for x = 0.6. This slightly exceeds the composition 0.5 with alternative full and empty chains, but one anticipates again that the excess Cu²⁺-O^2-- Cu²⁺ chain segments do not contribute significantly to the charge transfer, hence the flat part of the T_c(x) curve in the phase diagram in Figure 1. We have subsequently considered for years that these three oxygen contents were among the purest references for the AF, strange metal, and large PG metal phases of the cuprates. The highly overdoped regime has been mostly accessible in the Tl2201 family [28]. We concluded, therefore, for long, that one might then use these starting materials to introduce controlled defects and study in some detail their influence on the physical properties.

Why should we introduce defects? In classical physics, when we perfectly know the properties of a material, we might anticipate the influence of the defects introduced. For instance, if one drops a stone on a pond of a given liquid, one knows that a set of waves is created and propagates as circles on the surface. Their period and damping explains about the viscosity of the liquid of the pond. Similarly, introducing an impurity in a metal gives the Friedel charge density oscillations [29] or RKKY oscillations of spin density if the impurity is magnetic [30, 31]. If one considers now a poorly understood correlated electron compound, one may not anticipate the disturbance created. Then, the study of the response to the impurity is all the more important as it provides information on the properties of the pure material [2]. This is what we have been performing for years in cuprates. I shall summarize hereafter first in Section 3.1 the information on the magnetic properties gained mostly by NMR techniques using impurity substitutions. In Section 3.2, I shall present the influence on the transport properties of impurities and vacancies in the CuO₂ planes. The latter, obtained in a controlled manner by electronic irradiation of single crystals, allowed us to probe the properties of the distinct metallic regimes.

3.1 Magnetic properties induced by spinless impurities

In the 2D cuprates, the largest perturbations are induced, of course, by defects located in the CuO₂ planes. The substitution of Cu²⁺ by Zn²⁺ performed from the early days of HTSC introduces a spin vacancy without any charge defect. In the AF state of YBCO₆, these spinless defects only suppress spins on the AF lattice. This spin dilution effect is sufficient to explain the reduction of T_N with the increasing Zn content [32].

For a given Zn content, the introduction of oxygen on the intermediate Cu plane leads to the same hole doping, as for the pure material. Apart from the appearance of the SG phase, we could immediately detect an increase in the ⁸⁹Y NMR linewidth that increases with decreasing T down to T_c. Such broadening can only be associated with the appearance of local magnetic moments [9].

In that regime when the oxygen content is large enough, the spin glass temperature T_SG becomes negligible above x = 0.6, as shown in Figure 1. Spinless impurities never induce such paramagnetic local states in standard independent electron metals. SQUID measurements of the spin susceptibility allowed a determination of an upper limit of its magnitude [33]. An increase in the NMR experimental sensitivity enabled us then to reveal for x = 0.6 weak ⁸⁹Y NMR signals shifted from the main ⁸⁹Y NMR line, with a T-dependent NMR shift. We could attribute those “satellite” lines to ⁸⁹Y nuclei located near the Zn substitution site [34].

The characteristic pseudogap T dependence of the NMR shift has been found unmodified for sites at some distance from the Zn impurities, up to 4% Zn content. This suggests that the establishment of a robust PG behavior requires at most a sample size of about 25 unit cells. The Zn-induced paramagnetic moments appear then as a cloud of Cu sites around Zn with at most a similar spatial extent. They are characteristic of the correlated electronic nature of the PG regime.

In the slightly overdoped YBCO₇ samples, a weak broadening of the Y NMR line has been detected but no satellite could be resolved in this strange metal regime above T* and T_c so that the magnitude and/or the spatial extent of the moments is weaker/smaller.

We then performed an important step in order to test the eventual influence of a charged defect. We used Li⁺ substitution on the Cu²⁺ site of the CuO₂ planes and surprisingly discovered that the ⁸⁹Y NMR spectra were identical for 1% substitution of Li or Zn [35]. Both types of defects induced the same paramagnetism in their vicinity. The extra electron given by Li, therefore just fills a hole state in the bath band. This only slightly modifies the overall hole content for dilute Li substitution. This experimental result allowed us to show that the dominant defect in the CuO₂ plane is the spin vacancy associated with the substituent rather than its local charge.

As this was remarkable, we performed a similar comparison in another correlated electron system, Y₂BaNiO₅, in which Ni²⁺ is ordered in chains of S = 1 spins that constitute a prototype of the Haldane chain [2]. Here, the substitutions on the Ni site disrupt the chains, a staggered paramagnetism occurs near the chain ends, and the ⁸⁹Y NMR then displays many satellite lines [36, 37]. These were identical for Zn, Cu, and Mg substitutions so that any disruption of the spin chain always induces the same staggered paramagnetism on the chain ends. The NMR data allowed a measure of the extension ξ_imp of this staggered perturbation. Its T dependence accurately fits the theoretically computed magnetic correlation length ξ for the pure chain.

Assuming a similar staggered local 2D paramagnetic cloud with an exponential correlation length for the cuprates, we have estimated that ξ_imp would increase from about two to five lattice constants in the PG range from T* to T_c for x = 0.6 [38]. The intrinsic width of the ⁸⁹Y NMR forbids any accurate fit with such a model for the x = 1 strange metal, but ξ_imp would not exceed two lattice constants and would be roughly T-independent. Such a model-dependent determination is rough but establishes a qualitative difference between the PG and strange metal regimes. These ξ_imp(T) would also agree with evaluations of the magnetic correlation length ξ determined from inelastic neutron scattering experiments in single crystals of pure YBCO [39, 40]. Therefore the staggered response detected around spinless impurities monitors the actual correlation length of pure cuprates, as found for the Haldane chain from both theory and experiments [2, 37].

We disclosed a further advantage of the Li substitution as the ⁷Li NMR signal magnitude and intrinsic resolution are larger than those for ⁶⁴Zn. We could, therefore, detect its NMR shift ⁷K for the Li content as small as 1%, regardless of the hole doping in the metallic range of YBCO_6+x. This NMR shift ⁷K results from the transferred hyperfine coupling from the four Cu nearest neighbors of Li in the CuO₂ plane. These are the Cu sites exhibiting the largest paramagnetic response, in an exponentially staggered paramagnetic cloud model. We could measure accurately the T variation in ⁷K for any hole doping [35]. As shown in Figure 3A, it can be fitted quite accurately with a Curie Weiss dependence ⁷K-K₀ = C (T+Θ)⁻¹.

Figure 3

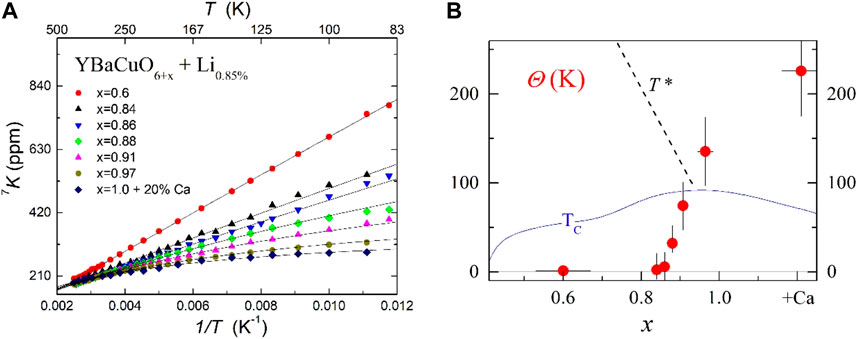
Figure 3. (A) ⁷Li NMR shift ⁷K plotted versus 1/T for increasing doping in YBCO_6+x, up to the overdoped regime with 20% Ca. The full lines are least square Curie Weiss fits. (B) Comparison of the Θ values deduced from the fits with the T_c and T* data from Figure 1. From Ref. [35].

The effective moment given by C is found independent of hole doping within experimental accuracy. The Weiss temperature Θ shown in Figure 3B exhibits a large change from the PG to the strange metal regime. Although Θ is very small in the PG regime, it abruptly increases through the PG “critical” doping point.

We did notice that this T dependence of the local magnetic response is somewhat analogous to that known for Kondo magnetic impurities in classical Fermi liquid metals. The evolution with hole doping of the apparent Kondo temperature Θ is similar to that found when changing 3d impurities in pure copper metal, for which the Kondo temperature T_K changes from a few mK for Mn to 30 K for Fe [41].

Let me point out that all these data given in Figure 3A were taken above T_c and that for x = 0.6, they do not show any singularity at 150 K, the onset temperature of the 3D CDW detected by RIXS experiments [21]. The variation in Θ with hole doping of Figure 3B is obvious even from the data taken above 150 K so that the magnetic response is not influenced by this charge order, if present in our samples. This response to Li impurities is, therefore probing a specific property of the PG regime. Similar studies in other cuprate families have not been performed so far as an intrinsic disorder due to chemical doping complicates the experimental situation. More material research efforts on Li substitutions in favorable cases such as BiSCO2212 or Hg1201 would be required.

I believe that this paramagnetic response to spinless impurity substitutions characterizes an abrupt evolution of the metallic state from the PG to the strange metal regime in cuprates. It remains an important challenge for any theoretical interpretation of the correlated electronic properties of cuprate physics. ¹⁷O NMR experiments show that this paramagnetic behavior persists in the superconducting state of the PG phase, while the Kondo-like screening is quite reduced in the SC state of the strange metal [42].

3.2 Influence of in-plane defects on the normal state transport

I shall consider hereafter the influence of impurities and vacancies in the CuO₂ plane on the transport properties in YBCO_6+x single crystals.

3.2.1 Experimental techniques

F. Rullier-Albenque had been using homogeneous irradiation with a highly energetic (2Mev) electron beam to produce defects in classical metallic superconductors [43]. She has extended her expertise to create vacancies in controlled content in thin cuprate crystal platelets. She checked first that the dominant defects acting on the planar transport are the vacancies produced in the CuO₂ planes by ejecting atoms out of these planes. A comparison with initial work conducted with Zn substitutions established that both resistivity and Hall effect are similarly modified in these two cases [44, 45].

I present in Figure 4 clear evidence for the important advantages of this electron irradiation technique. Herein, the resistivity curves ρ(T) are taken on YBCO₇ [46], YBCO_6.6, and Tl2201 [47] samples, in which the damage created by electron irradiation is progressively increased. One notices immediately on these ρ(T) data some important features that will be discussed in detail hereafter:

(1) The data are accurately parallel to each other at high T.

(2) Low T upturns appear with increasing damage. They suggest metal insulator crossovers (MICs).

(3) The SC transition can be suppressed by disorder down to T_c = 0.

(4) A downturn of ρ(T) onsets above T_c at a temperature T’_c that signals the extension of the superconducting regime.

Figure 4

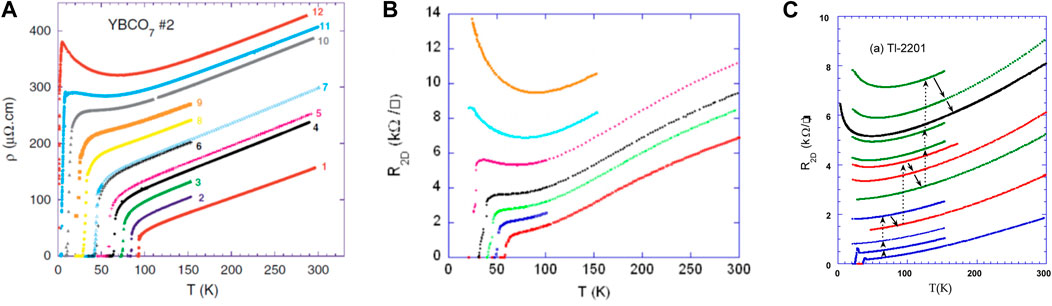
Figure 4. Planar resistivity data taken (A) on a virgin YBCO₇ (curve 1) and after steps of in situ electron irradiation at 20 K. The curves from 2 to 12 are data taken while cooling after annealing at 150 K or 300 K (B) on a YBCO_6.6 sample. The two upper data curves correspond to special heat treatments (see text) (C) on an overdoped sample of Tl2201 with T_c = 31 K. The arrows trace the thermal path followed during the experiment. The final black curve is a record after a long room T annealing. Figures respectively from Refs. [46, 47].

I shall analyze first, in detail, hereafter, points (1) and (2) related to the normal state properties. Experiments performed with large pulse field did allow us to suppress fully the superconducting fluctuations (SCFs) and follow the variation in the normal state resistivity below T_c. This also allowed us then to evaluate the contribution of the SCF to the conductivity, as described in Section 4.

The 12 ρ(T) curves reported in Figure 4A had been measured in situ on a single YBCO₇ crystal within the cryostat where electron irradiation was performed at 20 K. After recording a first cooling curve, ρ(T) was measured after each irradiation step. The defects created at 20 K are stable up to 150 K, and the resistivity curves are reversible, but heating to room T produces a partial annealing of some vacancies. The procedure was similar for the YBCO_6.6 sample of Figure 4B. Before recording the upper data curve, the sample was annealed at 400 K to achieve a clustering of the defects and a new irradiation was performed to fully suppress superconductivity. For the overdoped Tl2201 sample of Figure 4C, the last curve has been taken in a distinct cryostat after a long room T annealing.

As detailed in Section 4, high fields allow us to suppress the SC contributions (3) and (4) to the conductivity, once T_c has been highly reduced for a large enough defect content. We could then separate three contributions to the normal state resistivity:

${\mathit{\rho }}_{\mathit{n}}\left(\mathit{T}\right)={\mathit{\rho }}_0+\Delta \rho \left(\mathit{T}\right)+{\mathit{\rho }}_{\mathit{pn}}\left(\mathit{T}\right).(1)$

Here, ρ_pn(T) is the normal state resistivity measured for the pure sample. Both the T independent increase of “residual” resistivity ρ₀ and the low T upturn Δρ(T) depend on the concentration of defects. The “Matthiessen-like” rule, especially the robustness of the high T variation in ρ_n(T) with increasing defect content, is a totally unexpected observation.

3.2.2 Resistivity of the “pure” samples

In YBCO_6.6, the S-shaped contribution to ρ_pn(T) is linked with the existence of the pseudogap, and application of fields as large as 60 T was not sufficient to suppress SC, except when T_c has been decreased by irradiation. The inflection point at high T has been found to occur approximately at T*/2 and is seen to be independent of defect content. This confirms the independence of the PG on the disorder established by NMR for Zn substitution, as recalled in Figure 1, but also points out that the hole carrier content n_h in the CuO₂ planes is not modified by the irradiation damage, at least in the high T range.

This conclusion is therefore valid for the slightly overdoped YBCO₇ as well in as much as the T linear strange metal behavior is independent of disorder. Similarly, in the overdoped regime of Tl2201, the variation in ρ_pn(T) = bT^P with p ∼ 1.5 applies rather well, which supports an approach toward a Fermi liquid behavior.

In all three cases, as will be shown in Section 4, a 60-T field is sufficient to suppress the SCF contributions to the conductivity but does not allow a direct determination of ρ_pn(T) below T_c down to T = 0. In some cuprate families with low optimal T_c, the linearity with T apparently extends down to rather low T without an applied field. We found that linear fits of our high T data in our best pure YBCO₇ samples would imply a negative value of ρ_pn(0). The T linear dependence of the strange metal behavior would, therefore, break down at low T. For the Tl2201, extending the bT^p fit at low T would be compatible with ρ_pn (0) = 0. On the contrary, for YBCO_6.6, one does get a residual resistivity of about ρ_pn (0) = 1kΩ/□. The symbol square should be introduced as for the vertical scale in Fig4B or 4C.

3.2.3 Metal insulator crossover (MIC)

We have taken data in large enough applied field to suppress the SCF contribution to the conductivity for many defect contents. After subtracting the measured or extrapolated ρ_pn(T) values, we have determined the ρ₀ and Δρ(T) values defined in Equation 1. As ρ₀ was found to be a good measure of the defect content, the ratio Δρ(T)/ρ₀ has been reported versus T, as shown in Figure 5A [12].

Figure 5

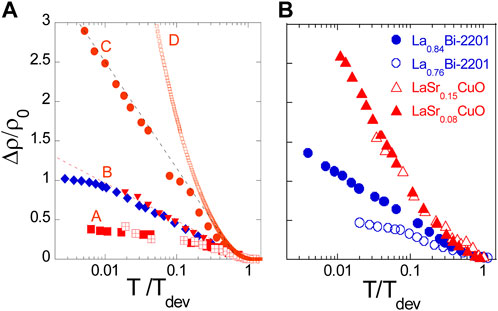
Figure 5. Low T upturn Δρ normalized by the increase in residual resistivity ρ₀ plotted versus T on a log scale. To permit quantitative comparisons, T is referred to T_dev, the onset T of Δρ whose values are between 100 and 150 K [12] (A) for YBCO_6.6 (red curves A to D) and YBCO₇ (blue diamonds). (B) Similarly analyzed data for (LaSr)124 and (LaBi)2201 that are cuprates with low optimal T_c (see Ref. [12] and text).

We have displayed there the analyzed data of Figure 4B for the YBCO_6.6 sample for limiting defect concentrations. For the lower defect contents A and B, a metallic behavior persists. When the SC state has been nearly completely suppressed (C and D), the data still suggest an insulating state. For the optimally doped YBCO₇ of Figure 4A, this procedure was not applicable [46] except after the final irradiation that lowered T_c to 1.9 K. In that case, a metallic behavior persists, as seen in Figure 5A (blue diamonds).

We have similarly analyzed some published data taken on low-T_c compounds (LaSr)124 [48, 49]and (LaBi)2201 [50]. Those presented in Figure 5B show that the resistivity upturns for these “pure” samples are quite similar to those found for YBCO after heavy electron irradiation. This analogy implies that a large disorder affects the physical properties even in the optimally doped (LaSr)124 family [49], as anticipated from the phase diagrams in Section 2.

Let us further note that in Figure 5A, the “insulating” behavior in the PG regime occurs only for very high in-plane defect contents exceeding 5% per Cu. The disorder is then indeed at the origin of the apparent MIC. Contrary to conclusions taken from data on some low T_c cuprates [49], large applied fields do not induce the MIC. They only usefully suppress SC and reveal the underlying MIC associated with the specific intrinsic or extrinsic disorder.

3.2.4 Resistivity upturns for low defect content

We have shown that sizable resistivity upturns revealed by the applied field remain, however, for 1.6% defect content (curve A in Figure 5A). In that case, Δρ(T) onsets at T_dev of approximately 100 K and saturates at low T. An enlarged presentation of this low-defect content regime is displayed in Figure 6. Herein, we display data taken on a sample in zero field, for which the SC contributions cannot be corrected, so that only ρ₀ and ρ_pn(T) have been subtracted (five blue square curves). They are shown together with data taken on two distinct samples in pulse fields that allowed us to suppress the SC contribution. One can see that the upturn of Δρ(T)/ρ₀ is reproducible, weakly depends on the field used to suppress SC, increases initially as -logT with decreasing T, and appears nearly independent of defect content. This trend toward single impurity scattering behavior resembles the initial observations performed in dilute Cu–Mn alloys that revealed the occurrence of Kondo effect in simple metallic states [51].

Figure 6

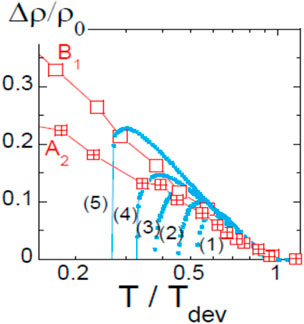
Figure 6. Detailed high T behavior of Δρ(T)/ρ₀ of Figure 5A taken for moderate point defect content on three distinct YBCO_6.6 samples. The five small blue square curves involving the SC contribution are zero-field data taken in situ for the same sample with increasing vacancy content from (1) to (5). Those for samples B1 and A2 taken in 60T pulse field allowed to suppress the contribution of SCF to the conductivity (see text Section 4). From Ref. [12].

The ⁷Li NMR experiments provide evidence for a paramagnetic response with a Curie Weiss Θ value that also resembles the case of Kondo effect for magnetic impurities in metals. These similar findings on the transport and magnetism give a strong weight to this analogy.

The absence of variation in T* with defect content has led us to conclude that the doping n_h is not modified upon introduction of disorder. We might assume that n_h is T-independent as well. In a single carrier band model with ρ_n(T) = m*(n_he²τ)⁻,¹ the T dependence would exclusively be due to the carrier’s scattering rate. With this assumption, the experimental results imply that the data involve two contributions τ⁻¹ = τ_el⁻¹ + τ_in⁻¹. The elastic rate τ_el⁻¹ responsible for ρ₀ scales with the defect content. The inelastic rate τ_in⁻¹ would be the sum of the inelastic rate of the pure compound τ_in,p⁻¹ and of the Kondo-like Δρ(T) contribution that also initially scales with the defect content.

One does expect changes in the latter contribution for a large defect content, due to the modification of their nanostructure. The interactions between impurities yield changes in scattering rates. Our estimate of a correlation length ξ_imp of five lattice constants at low T in YBCO_6.6 would indicate that a departure from the isolated defect regime should already occur for about 1% vacancy content.

Similarly, in YBCO₇, an upturn of ρ(T) is only seen in Figure 4A for an estimated defect content of about 8%. Even if ξ_imp is about two lattice constants, one would expect strong interactions between the defects. The observed saturation at low T of Δρ(T)/ρ₀ seen in Figure 5A has been found independent of applied field in the initial experiments of Ref. [12]. An analogy with the Kondo effect would suggest a Θ value much smaller than that of approximately 100 K found by ⁷Li NMR in the strange metal regime for a low Li concentration. For Kondo alloys, such as CuFe, clusters of Fe impurities acquire a lower Kondo temperature than T_K = 30 K of isolated impurities [52]. The resistivity upturns for a high defect content in YBCO₇ would again appear quite similar to the situation encountered in CuFe alloys.

In Figure 4, the resistivity upturns are much larger in the YBCO samples than in the overdoped Tl2201 sample. A thorough analysis permitted us to show that weak localization induced by purely elastic scattering explains quantitatively the resistivity upturns in that case [47]. This is again a good indication that the electronic properties approach a Fermi liquid behavior for highly overdoped cuprates.

3.3 Conclusion on the normal state properties

We have been able to disclose the influence of dilute in-plane point defects in the three considered “clean” materials that allowed us to probe, respectively, the PG, strange metal, and Fermi liquid regimes. The Curie–Weiss magnetic perturbation induced by spinless defects and the low T saturation of the carriers scattering behave quite similarly with Kondo effect in classical Fermi liquids. The sharp increase in the Kondo-like temperature Θ through the pseudogap line is a striking generic feature of cuprates.

For large concentrations of defects, their mutual interactions might induce a MIC. We could enhance defect clustering and show the importance played by the defect morphology in driving the insulating state. The comparison with data taken on “pure” lower T_c compounds demonstrates that the dopant out-of-plane disorder induces similar upturns of the resistivity and an apparent MIC. This confirms our anticipations performed from simple comparisons of the phase diagrams in Section 2.

Can we reduce the disorder effects to study the metal insulator transition in the small doping part of the phase diagram? Within our study of in-plane defects, we have shown that this disorder is well-quantified by the residual resistivity ρ₀, but we do not know accurately the action of out-of-plane defects. The present results prove that those play an overwhelming role for low doping. The organization of the dopants certainly drives the stabilization of the family-specific low T-competing phases in the PG regime as well.

4 Influence of disorder on the superconducting state

From the 3D phase diagrams proposed in Section 2, we have noticed the existence of a correlation between the optimum T_c value and the morphology of the phase diagram for the various cuprate families. It is then important to analyze the evolution with an increasing disorder of the superconducting properties that are available in our data given in Figure 4. Such data could give indications on the actual origin of the pair condensed state, which is still poorly understood. In these 2D metallic compounds with low superfluid density, superconducting fluctuations are expected to persist above T_c. It has even been suggested that superconducting pair formation could occur at T*, while T_c would be the onset of phase coherence between superconducting pairs. For me, this did not appear to be the case as our early experiments with Zn substitutions revealed that T* is not affected by disorder.

I shall consider hereafter in Section 4.1, the evolution of T_c with controlled disorder that can be followed here until T_c = 0. In Section 4.2, I shall address the evolution of pairing strength through a study of the T-range of the superconducting fluctuations. This will allow me to discuss if there is any influence on the SC properties of the Kondo-like induced magnetism or of the resistivity upturns in the metallic PG regime.

4.1 Variation in T_c with in-plane disorder

Magnetic point defects usually induce pair breaking in classical superconductors. Here, YBCO₇ exhibits a strange metal behavior with nearly zero residual resistivity in its normal state. Electron irradiation allowed us a full suppression of superconductivity, although a metallic state persists. As displayed in Figure 7, we found that T_c scales linearly with the residual resistivity ρ₀ that scales itself with n_d, the defect content [46]. Such a behavior disagrees qualitatively with the Abrikosov–Gorkov (AG) variation [53] expected for pair breaking that implies a sharp downturn of T_c(n_d) before reaching T_c = 0.

Figure 7

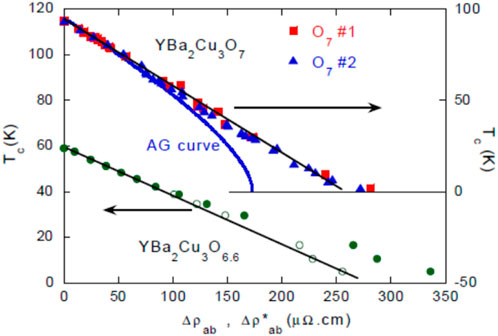
Figure 7. Variation in T_c with the excess residual resistivity ρ₀ induced by electron irradiation The upper curve is for YBCO₇. There, ρ₀ =Δρ_ab is a measure of the defect content n_d. For comparison, the full line reports the expected pure pair breaking (AG) theoretical dependence. The lower data curves for YBCO_6.6 are plotted for two distinct estimates of the defect resistivity Δρ_ab (full circles) and Δρ_ab* (empty circles). From Ref. [46].

We provided further evidence for the inadequacy of AG from the low magnitude of the ΔT_c/ρ₀ slope and the observed variation in the width of the SC transition. The latter, being due to the inhomogeneous distribution of defects, remains narrow and does not broaden when approaching T_c = 0.

The quasi linear measured variation in T_c (ρ₀) is a somewhat unexpected result. One would hardly obtain it as accurately by other means, such as impurity substitutions. It surprisingly applies also for the underdoped YBCO_6.6 samples, as shown also in Figure 7, provided one takes for ρ₀, the high T-value of the extra resistivity.

Emery and Kivelson (EK) have proposed [54] that a peculiarity of the cuprates is their weak superconducting carrier density. They suggested that in such a case, phase fluctuations of the superconducting order parameter could be the source of T_c reduction. The phase coherent SC transition should then occur when the resistivity reaches a critical value [55].

In [46], we provided a detailed discussion indicating that such a correlation between T_c and ρ(T_c) might be compatible with the quasi-linear variation. We were led, however, to conclude that the experimental situation probably requires taking both pair breaking and phase fluctuations into account. The influence of phase fluctuations should be more important for large defect contents and in the underdoped PG regime, but the existence of a single slope of ΔT_c/ρ₀ at all defect contents appears awkward. I shall show hereafter that more information is available from quantitative studies of the magnitude of the SCF.

4.2 Superconducting fluctuations and disorder

Nernst effect [56], diamagnetism [57, 58], or paraconductivity [59, 60] measurements have been used to study the SCF above T_c. The main difficulty in such experiments resides in subtracting the normal state or spurious contributions from the data. Nernst effect data involve vortex motion contributions, while spurious paramagnetic phases can counterbalance the diamagnetic signal.

4.2.1 Paraconductivity experiments

We have rather preferred to use magnetoresistance (MR) measurements. As shown first in [59], it permits us to obtain the paraconductivity accurately. Using 60T pulse fields on an YBCO_6.6 sample, we demonstrated that the H² field dependence of the normal state MR known at high T extends at temperatures well below T_c.

Low-field departures from the H² dependence progressively appear for decreasing T, when SC fluctuations contribute to the low-field conductivity, as shown in Figures 8A, B respectively for a pure YBCO_6.95 and an irrradiated YBCO_6.6 sample. Such departures appear below an onset temperature T’_c. At each T, the normal state H² variation is recovered at a field H’_c(T) [60].

Figure 8

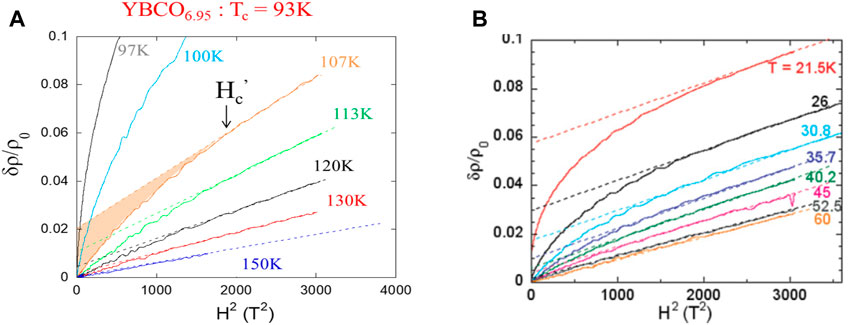
Figure 8. Plot of the magnetoresistance [ρ(H)- ρ (0) ]/ρ (0) versus H² at various temperatures (A) for pure YBCO_6.95. Here, the orange area indicates the SCF contribution to the conductivity. (B) Data taken on YBCO_6.6 after decreasing T_c to 5 K by electron irradiation. Here, the SCF appear below an onset of T’_c = 60 K and are suppressed at fields H’_c (T) that increase with decreasing T. From Ref. [60].

The increase in conductivity Δσ(T) associated with the SCF in zero applied field is easily obtained from the decrease of ρ(T) with respect to the extrapolated normal state behavior. Typical results for Δσ(T) and H’_c(T) are displayed, respectively, in Figures 9A,B for pure and irradiated YBCO samples. As shown there, both T’_c and H’_c decrease after reduction of T_c by electron irradiation. Although the critical field H’_c(T) cannot be determined at low T for most samples, we could show that H’_c(0) can be estimated using the “usual” variation

$\mathit{H}’\mathit{c}\left(\mathit{T}\right)=\mathit{H}’\mathit{c}\left(0\right)\left[1-{\left(\mathit{T}/\mathit{T}’\mathit{c}\right)}^2\right](2)$

that fits the data for low-T’_c samples (see Figure 9B and Ref. [59]).

Figure 9

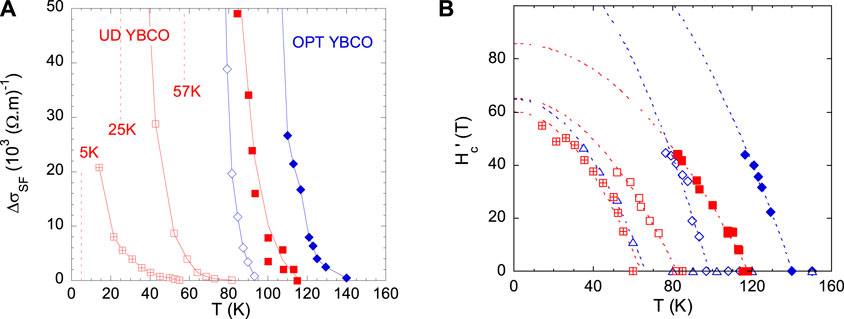
Figure 9. (A) Zero-field paraconductivity Δσ(T) reported for pure and irradiated YBCO₇ and YBCO_6.6. It vanishes for distinct T’_c values. (B) H’_c(T) data for the same samples. H’_c(0) is estimated from the parabolic fits with Equation 2 shown as dotted lines. From Ref. [60].

4.2.2 SCF range and disorder

The onset value T_ν of the SCF that we obtained on the same samples by Nernst effect [61] was smaller than T’_c deduced from the paraconductivity. The onset values obtained by a given technique are somewhat determined by the experimental sensitivity. Here, they would decrease by approximately 10–20 K for one order of magnitude decrease in the cutoff sensitivity. To the best of our knowledge, the T’_c values given here are among the highest reported in YBCO. More importantly, our experimental approach benefits of a significant technical advantage. Using a single sample and identical criteria for all defect contents ensures the reliability in the T’_c data comparisons.

We report in Figure 10 the results for T’_c and H’_c(0) versus T_c obtained from the data on Figure 9 for the YBCO_6.95 and YBCO_6.6 “pure” samples and after electron irradiation. One can easily notice that the SCF temperature range is quite similar for the different defect contents but does not scale with the actual T_c values. The ratio T’_c/T_c increases steadily with defect content so that the range of SCF increases markedly with respect to T_c in samples with in-plane disorder. In the underdoped PG regime, T’_c remains as large as 60 K for the YBCO_6.6 sample with T_c = 5 K, and a large ratio T’_c/T_c ∼ 14 persists for the YBCO₇ sample in the strange metal regime for T_c = 1.5 K.

Figure 10

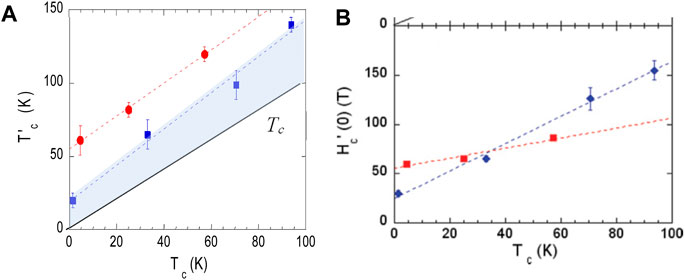
Figure 10. Variation with in-plane disorder of the SCF in the PG (red) and strange metal (blue) regimes. (A) Onset temperature T’_c plotted versus T_c. The blue range is the SCF range for the YBCO₇ sample. (B) Critical field value H’_c(0) plotted versus T_c. It remains large for an increasing disorder for underdoped YBCO_6.6. From Ref. [60].

From these simple observations, it appears quite clearly that the increase of in-plane disorder does not reduce T’_c as much as T_c. The fact that SCF remain important even if T_c is highly depressed implies that superconducting pairs remain above T_c, while full 3D SC is not established. This suggests that phase fluctuations become more important in the presence of disorder, as suggested by EK in “bad metals” [55]. A full quantitative study of the magnitude of the SCF conductivity helps better clarify that point.

4.2.3 Amplitude and phase fluctuations in YBCO

In an applied field H, the SCF paraconductivity is obtained by subtracting the normal state conductivity Δσ_SF(T,H) = ρ ⁻¹(T,H)-ρ_n⁻¹(T,H). Assuming that YBCO samples were among the cleanest cuprates, we have studied the T and H dependences of Δσ_SF in [60] for four samples from the PG to the slightly overdoped regime. We have analyzed first the zero field data reported in Figure 9A in the Ginzburg–Landau framework. The SCF is associated with pair braking in that approach, and the paraconductivity reflects the T dependence of the superconducting coherence length

$\xi \mathit{s}\left(\mathit{T}\right)=\xi \mathit{s}\left(0\right)/{\mathit{\epsilon }}^{1/2},(3)$

with ε= ln(T/T_c) ∼ (T- T_c)/T_c for T > T_c. This 3D paraconductivity should diverge at T_c on a very small T-range inaccessible experimentally, which evolves for a 2D compound toward a 2D Aslamazov Larkin (AL) regime [62] for which

${\mathit{\sigma }}_{\text{SF}}\left(\mathit{T},0\right)={\mathit{e}}^2/\left(16\mathit{\hslash }\mathit{s}\mathit{\epsilon }\right).(4)$

Here, s is the interlayer spacing. The AL expression has been extended by Laurence and Doniach (LD) [63] to include a c direction coherence length ξ_c(0). One can see in Figure 11A that assuming ξ_c(0) = 0.9 Å, the LD/ AL analysis of Equation 4 applies for three of the YBCO samples in the range 0.01<T/T_c < 1.1. The T dependence of Δσ_SF(T,0) for the YBCO_6.6 sample is shifted to the right in Figure 11A but coincides with the other if T_c is replaced by T_c0 = 72 K. I point out here that in [59] the normal state resistivity displays a T dependence with a non-zero residual resistivity ρ₀ for that “pure” sample, as can be seen also in Figure 4B. Considering the linear relation between T_c and Δρ_ab of Figure 7, this ρ₀ value corresponds to a 10 K decrease of T_c so that a defect-free sample could indeed have a critical temperature ∼T_c0.

Figure 11

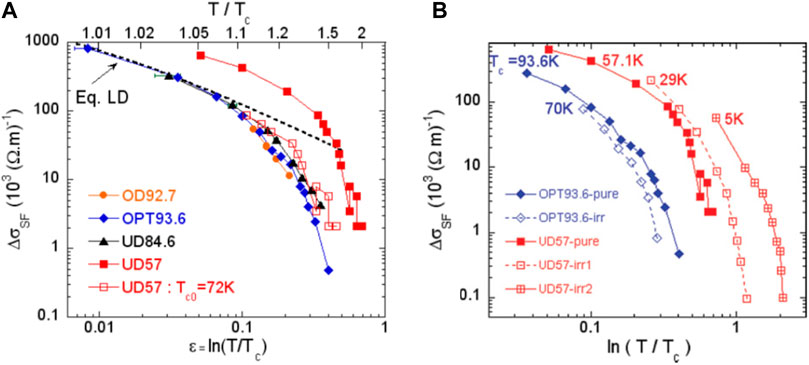
Figure 11. (A) Paraconductivity σ_SF(T,0) is plotted versus ε= ln(T/T_c) for the four “pure” YBCO samples with the indicated T_c values. The dashed line represents the expected variation for the LD Gaussian fluctuations assuming ξ_c(0) = 0.9 Å. For the underdoped sample UD57 with T_c = 57 K, the data are also plotted by replacing T_c by T_c0 = 72 K (see text). (B) Similar plots for pure optimal (OPT) and underdoped (UD) samples and after electron irradiation that reduced T_c to 70 K for the OPT sample and to 29 and 5 K for the UD sample. From Ref. [60].

As underlined in [59], these data allowed us to point out that the existing uncontrolled disorder leads to an intermediate SCF regime between T_c and ∼T_c0. Phase fluctuations initially suppress T_c in that T range, while amplitude fluctuations of the superconducting order parameter take over beyond ∼T_c0.

The similar plots shown in Figure 11B for the underdoped UD irradiated samples provide evidence that systematic shifts to the right occur and increase with increasing defect content. Here, again, one could use values of T_c0 > T_c to obtain rough estimates of the increasing T range, for which phase fluctuations are dominant. For the optimally doped sample, the T variation in the SCF does follow the same pair breaking behavior, as for the pure sample even though T_c has been reduced from 93.6 K to 70 K.

These results indicate in the “pure” YBCO_6.6 sample the small T-range of phase fluctuation is presumably due to the residual native disorder. It broadens markedly with increasing in-plane defect content. The GL amplitude fluctuations only become dominant at high temperatures in this PG regime. A totally coherent conclusion has been drawn from a quantitative comparison of the Nernst effect and σ_SF(T,0) data, as detailed in [60]. It fully supports a disorder-induced large phase fluctuations range in the PG regime and the applicability of Gaussian fluctuations for the strange metal regime even in the presence of disorder.

Let us consider now the case of the clean samples beyond the applicability of the LD amplitude fluctuations regime that applies up to 1.1 T_c in Figure 11A. Beyond that temperature, σ_SF(T,0) decreases markedly and vanishes quite sharply at T’_c that might be assigned to a cutoff in the pairing. From Equation 2, the latter might be linked with a minimal superconducting coherence length, as discussed in [60].

We are still lacking a full theoretical approach, in which the influence of disorder on both phase and amplitude fluctuations would be treated on an equal footing. One can anticipate that the interplay between these two depends on the microscopic sources of superconductivity and disorder. However, the present qualitative experimental information implies that T’_c is a sharp temperature beyond which pair formation is energetically prohibited. T’_c appears, therefore, as one of the best determinations of the upper limit of the superconducting regime.

4.2.4 Magnetoconductance and superconducting gap

Another important thermodynamic entity that characterizes the superconducting state is the field H’_c(T) beyond which the SCF is suppressed. The highest measurable value of H’_c is so far about 45T in the experimentally available 60T applied pulse fields. We have proposed that a natural extension down to T = 0 may apply using Equation 2 as usually done below T_c for the H_c2 of classical 3D superconductors. This choice is supported by the data given in Figure 9B taken on an OD sample with T_c reduced to 5 K by electron irradiation, for which we obtained H’_c(0) = 60T.

In the LD Gaussian fluctuation analysis, one expects an independent determination of H_c2 from the low field behavior of the magnetoconductance Δσ_H(T,H)= σ_SF(T,H)- σ_SF(T,0). We have reported in [60] an analysis of such data that surprisingly establishes that H_c2(0) and H’_c(0) are identical within experimental accuracy for the four pure samples considered in [60].

For a large applied field, Δσ_H(T,H) is also found to depart from the LD behavior and displays then a sharp exp[–(H/H₀)²] decay. This provides evidence that H’_c(T) is a field beyond which pair formation is inhibited in analogy with the finding conducted for T’_c. This applies in the disordered cases, and the validity of this evaluation of H’_c(0) is a confirmation of the reliability of the extrapolation of Equation 2.

The important conclusion drawn from this detailed analysis is that H_c2(0) or equivalently H’_c(0) increases with doping. H_c2(0), being a measure of ξ(0)⁻², one finds that the superconducting gap Δ_SC, which scales with ξ(0)⁻¹, also increases with hole doping. From the H’_c(0) data displayed in Figure 10B, the influence of disorder on the gap is found much smaller for the underdoped sample than for the optimally doped one. This appears in accordance with the corresponding data for T’_c on Figure 10A and with a dominance of phase fluctuations in the PG regime.

4.3 Disorder in the 3D YBCO phase diagram

Although we have clearly shown that the underdoped YBCO_6.6 sample is not a perfectly clean cuprate, we have still confirmed that the YBCO family is not far from being clean enough to yield important conclusions on the differences between the PG and strange metal regimes. The detailed investigation of the SCF conducted in [60] and reported here allowed us to determine reliably the temperature T’_c beyond which superconducting pairing is suppressed as the coherence length becomes presumably very small.

As seen in Figure 12A, T’_c only displays a small decrease below optimal doping but follows T_c and not the pseudogap T*. We have also shown that the latter crosses the T’_c versus doping line (Figure 12A). This again confirms that the pseudogap is not a precursor to SC, as anticipated from the Zn experiments. The SC gap, as determined by H’_c from thermodynamic arguments, increases steadily with hole content up to optimal doping. This appears in line with the doping dependence of the small gap observed by some spectroscopic experiments in other cuprate families [64, 65].

Figure 12

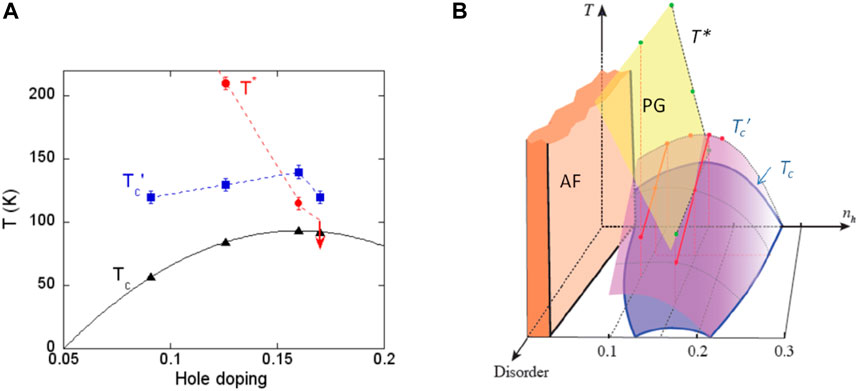
Figure 12. (A) Doping dependence of the 3D T_c, pseudogap T*, and SCF onset T’_c for four “pure” YBCO samples and (B) 3D phase diagram displaying the evolution of these temperatures with the concentration of in-plane defects. The red lines are actual data for T’_c of underdoped and optimally doped YBCO. In the overdoped range, T_c are those for Tl2201 and the T’_c variations are anticipated by extrapolation of the optimally doped behavior (see text). From Ref. [60].

Our studies of the SCF in the “pure” samples also allowed us to point out that in the PG regime of YBCO_6.6, the native disorder slightly reduces T_c that should be 10–15 K higher in a “cleaner” sample.

The detailed investigations with increasing controlled disorder allow us, by analogy with Figure 2, to propose the 3D phase diagram of Figure 12B specific to YBCO with in-plane disorder. Here, the disorder axis is better monitored than in Figure 2, using the concentration of defects introduced by electron irradiation or equivalently the increase of residual resistivity ρ₀, for instance at optimal doping. In this phase diagram, one should consider that T’_c is a better identifier of the 2D pairing than T_c that marks the 3D coherent superconducting state.

The analysis of the SCF conducted in [60] and shortly reviewed here has further allowed us to differentiate the influence of disorder on the SCF in the PG and strange metal regimes. In the latter, the disorder induces essentially a pair breaking so that T’_c, T_c, and H’_c decrease markedly altogether, as seen in Figure 10. In the PG regime of underdoped YBCO_6.6, a large T_c decrease is observed, while T’_c and H’_c are only moderately reduced. This indicates that pairing remains while a loss of phase coherence suppresses 3D superconductivity. The disorder induces in the PG phase a large SCF range that extends from the reduced T_c up to T’_c.

These conclusions about the phase diagram in the PG to strange metal regime are quite important as they result from experimental studies on the YBCO family that is a clean cuprate family, as discussed in Section 2. For lower hole content n_h<0.1, the 3D T_c decreases until the interplay between SC and AF occurs, as displayed in Figure 1. In that range, the doping n_h is, however, not easy to control as it depends on the formation in the intermediate Cu⁺ layer of Cu²⁺ - O^2- - Cu²⁺ segments that do not produce any charge transfer in the CuO₂ planes. The metal insulator transition could only be investigated with significant native out-of-plane disorder in YBCO_6+x for x < 0.45 or in YBCO₆ with Ca²⁺ substitution on the Y³⁺ site. Unfortunately, the investigation of the overdoped range cannot be performed either in the YBCO family as it can only be reached by Ca²⁺ substitution that also introduces a sizable disorder. In Figure 12B, we have reported in that range a T_c variation analogous to that observed for Tl2201 and assumed that amplitude fluctuations remain dominant to anticipate the T’_c variation.

5 Discussion

I shall summarize first hereafter the various results concerning the phase diagram and underline the experimental questions that remain open. I shall analyze then the important information disclosed by using controlled defects as probes of the original properties of the distinct states of the phase diagram.

5.1 Phase diagrams and low T_c cuprates

We have conducted systematic investigations of the evolution of the cuprate phase diagrams with increasing controlled disorder in the CuO₂ planes. Our initial Zn substitution experiments demonstrated that the disorder opens a large spin glass regime, as displayed in the 3D phase diagram of Figure 2. The controlled increase in the vacancy content in single crystals allowed us then to show that SCF persist above T_c up to a temperature T’_c that decreases less than T_c with increasing disorder. The normal state residual resistivity ρ₀ increases markedly altogether and low T upturns appear mostly in the underdoped regime for large disorder.

All these features had been observed in the “pure” singular low-T_c cuprate families such as LSCO [48] or (LaBi)2201 [50]. Large residual resistivity ρ₀ was clearly apparent in the data for those cuprate families, for which the large fields applied to suppress T_c disclosed resistivity upturns even at optimum T_c [49]. Nernst effect data revealed a large range of SCF above T_c in the underdoped rPG regime as well [56]. In LSCO, THz conductivity experiments have also been performed to probe the SCF range [66]. The maximum range of 10–20 K is smaller than that found by Nernst effect all-over the SC dome. All these results confirm our initial guess that had led us to propose the 3D phase diagram of Figure 2 and to anticipate the presence of a large disorder that diminishes T_c in those specific cuprate families.

Comparing ρ₀ of these low-T_c compounds with those induced by electron irradiation in our YBCO samples even suggests that the linear relation, as shown in Figure 7, between T_c and ρ₀ might have an extended validity. Choosing then to use the ρ₀ value at optimal doping to fix the position of the PD of the diverse cuprate families on the disorder axis in Figure 2 would not modify it significantly [67]. In the phase fluctuation scenario, a relationship between T_c and ρ(T_c) is indeed expected. This ensemble of arguments therefore leads me to conclude that the dopant disorder is mostly at the origin of the reduced T_c values in the cuprate families with anomalously low optimal T_c.

5.2 Toward disorder-free cuprates?

Once we have considered that we should put aside the low-T_c cuprates, the question raises as to whether we can decide what family better represents clean cuprates. For YBCO, Bi2212, Hg1201, and Tl2201 that display the highest T_c ∼ 90 K, we noticed that the extrapolated ρ₀ is nearly zero at optimal doping [67]. These families are therefore nearly equivalent in that doping range. We could indeed initially establish the universality of the transition T* between the PG and the strange metal regimes in YBCO and Hg1201 [11].

Our phase diagram of Figure 2 provides evidence that determination of the hole contents n_h by mapping the SC “domes” between different cuprate families is certainly incorrect, except for the higher T_c families. Unfortunately, it appears difficult to underdope the Tl2201 family that is the only “clean” cuprate, for which the overdoped to non-SC transition is accessible. As indicated in Section 4, we have not been able so far to perform a full study of the variation in the thermodynamic properties of the SC state through that transition.

YBCO_6+x is similarly the only family on which the metal-to-insulator transition occurs without a spin glass intermediate regime. We have, however, seen here that for x = 0.6, native disorder effects already appear as T’_c remains large with respect to T_c. Low T upturns of the resistivity occur for oxygen contents x < 0.4 [12], but we do not know how the insulator state sets in. We do not have any reliable control on the influence of the oxygen disorder during this crossover. One cannot anticipate whether a first-order SC insulator transition would occur in a disorder-free cuprate, hence the question mark we have introduced in the 3D phase diagram in Figure 2.

So although huge progress has been performed since the discovery of the cuprates, we only have, at hand, a limited number of cuprates that allow us to explore independently some characteristic clean compositions in the phase diagram of Figure 2. We were not able to discover so far a batch that would play for the cuprates a similar role to that played by silicon single-crystal wafers for semiconductors.

I like to point out that the present critical concern is even more pertinent if one considers the actual disorder that occurs on the sample surfaces. The latter are investigated using novel techniques restricted to easily cleavable single crystals. ARPES [68] and STM [69] experiments allow to thoroughly study the doping dependence of the k-space surface band structures of Bi2212 crystals. One can beautifully see there the dopant disorder in the spatially resolved STM spectra [69] that have been helpful to correlate electronic structure with the local order. This unavoidable dopant disorder probably limits the energy resolution in ARPES spectra. The bulk and surface dopant disorder are not necessarily identical so that refined comparisons between bulk thermodynamic properties and surface energy spectra might be misleading. Local STM and NMR experiments have been achieved on Zn substituted cuprates. NMR could give information mostly on the bulk YBCO normal state properties, while STM permitted to probe the SC local states on the Bi2212 surface [70].

5.3 Point defects in the normal state

The change in the normal state transport properties has initially revealed the difference between the PG, strange metal, and quasi Fermi liquid regimes in the “pure” cuprates. The introduction of point defects has allowed us to highlight those differences by providing clear evidence that the scattering of the carriers splits into two distinct contributions. The contribution observed in the pure compound is totally unmodified by the defects introduced. It adds to the specific scattering of the carriers by the dilute impurities. An unexpected difference with the situation encountered in classical metals is that in the latter case, the scatterings are associated with two different processes, an elastic scattering on the defects and an inelastic one mediated by phonon modes. In the cuprates, both processes deal with electronic states controlled by the correlated electronic properties of the pure compound.

This stems from the fact highlighted by the NMR experiments that the impurity substitutions or vacancies in the CuO₂ planes induce a modification in their vicinity, which has a significant spatial extension that varies with temperature and doping [38]. This is certainly unambiguous evidence that the cuprates are strongly correlated electron systems.

We gave evidence for low T upturns of the resistivity as well when introducing in-plane vacancies by electron irradiation. These correspond to scattering rates on the defects similar to those observed for Kondo magnetic impurities in classical metals. As recalled in Section 3, these upturns scale with defect content as long as their concentration is small enough to avoid overlaps between the clouds induced by the vacancies.

We have shown, both by NMR and transport, that a sharp modification of the defect state occurs when the hole doping of YBCO is switched from the PG to the strange metal regime. We assign that to a reduction of the paramagnetism similar to a large increase in the Kondo-like temperature. In the strange metal regime, the cloud size does not exceed two lattice constants and the resistivity upturns decrease, in agreement with an increased “Kondo” temperature. We assume that paramagnetism should disappear when reaching the pure Fermi liquid regime for large hole doping. This crossover still needs, however, to be carefully studied for instance on the Tl2201 cuprate family.

5.4 Disorder in the SC state

The data analysis of Section 4 reports an original study of the destruction of the 2D superconductivity by a controlled disorder. The GL or Lawrence–Doniach pair breaking approach explains rather well the 2D SCF up to 1.1 or 1.2 T_c in the pure or disordered YBCO near-optimal doping. This would apparently also hold for very clean underdoped samples.

In that PG regime, any disorder native or produced by electron irradiation, induces a large SCF range as compared to T_c that mostly originates from a loss of phase coherence [60]. [55] had proposed a major importance of phase fluctuations for SC with either a low superfluid density or a large resistivity at T_c. Our study indicates that the disorder is mainly responsible for the phase fluctuations in underdoped YBCO. I therefore suggest that the Kondo-like inelastic defect scattering of the hole carriers is the main player in the T_c reduction that occurs before the SC insulator transition.

One should notice finally that our study of the field dependence of the SCF gives a measure of H’_c(0), the critical 2D magnetic field. Thermodynamic arguments allow us to connect it with Δ_SC, the SC gap magnitude. In clean YBCO, Δ_SC increases with doping up to the optimum T_c, and correspondingly, the coherence length ξ(0) diminishes. One would expect to reach a cutoff value of ξ(0) and then a decrease in the gap in the overdoped regime. One should still probe that experimentally in the Tl2201 family and altogether whether the transition at the endpoint of the SC dome is smeared out by disorder.

6 Conclusion

We have recalled here that the cuprates are correlated electron systems in which native disorder occurs naturally due to chemical doping. This disorder has introduced great difficulties in the understanding of the very phase diagram of the hypothetically clean cuprate plane. Immediately after the discovery of YBCO, we have highlighted that the pseudogap to strange metal transition is robust to disorder at high temperatures. We have given evidence that it is generic, which means identical for all hole doped cuprate families. A long time has been required although [25] to see that fact accepted by the community.

Wide attention has been devoted to the original and interesting ground states discovered, such as stripes in the 124 family and later on CDW in YBCO. This diversity of ground states in the cuprate families testifies the richness of the underlying physics of these correlated electron systems. Meanwhile, we have been performing with collaborators an extensive work on Na_xCoO₂ [71, 72] that demonstrated that the physical properties of the CoO₂ layers were highly influenced in these compounds by their interactions with the Na dopants. Although similar detailed investigations haves not been achieved so far in the cuprates, I got convinced that, there too, the order of the dopants may analogously play a great role in stabilizing the different ground states. The fact that these states compete with SC complicated our understanding of the variety of cuprate phase diagrams.

As recalled here, we proposed the 3D phase diagram of Figure 2 with some Orsay-Saclay colleagues. We suggested that the AF insulator, PG, strange metal, and Fermi liquid metallic regimes were the actual phases that characterize the high T part of the disorder free cuprate phase diagram. Among those, all the metallic states display a superconducting ground state except for large doping in the Fermi liquid range. On experimental grounds, the less understood part of the phase diagram is the transition from the metallic PG regime to the insulating state, presumably because even the weak native disorder has a strong influence there on the physical properties.

In my research group, we have always considered that the intentional introduction of controlled impurities or defects allowed us to disclose physical properties of the cleanest phases. The original “Kondo-like” magnetic and transport responses induced by spinless impurities are strong signs for a connection with Mott physics. The step change of its characteristic temperature Θ has been somewhat overlooked so far by the community, although it characterizes a generic part of the clean cuprate phase diagram.

This sharp transition at a doping p* recalled in Figure 3B is so abrupt that it is legitimate to wonder whether it marks a phase transition rather than a crossover. Although T* is not modified by disorder, it could still correspond to a transition that would only be slightly smeared by the weak native disorder always present in the cleanest compounds. The sharp drop of the T* line versus n_h near-optimal doping with a quantum critical point could agree with such a possibility. Whether orbital currents [73, 74] appear at T* remains an open question, and one should like to understand how such a collective state would induce a Kondo-like magnetic cloud around spinless defects. Any further experimental input on such a matter would certainly require extremely clean samples.

If I consider now the SC state, we have shown that the onset of 2D superconducting pair formation occurs rather sharply at a higher temperature T’_c than the 3D superconductivity at T_c. Most researchers considered that the T_c(n_h) dome shape is universal for the cuprates, with differing T_c magnitudes. In contrast, we have shown that T’_c is always large, even in the anomalous cuprate families, for which the disorder (or order) imposes a low T_c value. As shown in Figure 12A, we have even demonstrated that one might hardly define a dome for the T’_c (n_h) variation for the cleanest cuprates.

This study of the influence of defects has, therefore, disclosed two apparently contradictory observations. The PG line marks a high T transition between different electronic states, while the low T pairing energy is nearly unaffected by the opening of the pseudogap, which does not therefore compete directly with SC. Our SCF experiments with controlled disorder allowed us to show that the main difference in the SC states appears to be the influence of in-plane defects. They induce pair breaking in the strange metal while they furthermore enhance phase fluctuations in the PG regime. As recalled previously, we do not know whether T’_c would decrease and vanish before reaching the SC to insulator transition in a “clean” cuprate.

It has been suggested [54] that the low carrier density and the associated low phase stiffness is a possible source of phase fluctuations and T_c reduction in cuprates. Our data rather imply that large impurity-induced carrier scattering rates are required to promote a bad metal behavior. This leads me to speculate that the distinct influences of disorder on SC could be due to the actual difference in the normal state Kondo-like response. This would qualitatively be consistent with the decrease in the 3D T_c on the left of the dome-like SC regime in the supposedly pure cuprate families.

I noticed more than 10 years ago [25] that the occurrence of the pseudogap and the SC states in the cuprates finds some theoretical justification in computations conducted by Cluster DMFT within the simple one-band Hubbard model [75]. Within the three-band Emery model [76], similar computations give analogous results and introduce realistic extra parameters, such as the charge transfer gap or the hole occupancies of the oxygen and copper orbitals. These are considered nowadays to try to justify the difference of optimum T_c between the diverse cuprate families [77]. Our work establishes that disorder is a dominant factor in this differentiation of the low T_c cuprates, while T_c only marginally differs for cleaner cuprate families with low residual resistivity. The actual influence of the planar structure is therefore less important on the optimal T_c than might be anticipated from the data. Given the numerical computations being conducted on clean models, it would appear quite interesting to see if the three-band parameters have any influence on the SC dome shape for the clean compounds. Such computations could help suggest a behavior for the SC–insulator transition that is at present obscured by disorder in the real materials.

As for the relation between the normal and SC state properties, I hope that the present experimental results will stimulate extensions of the thermodynamic developments taking into account random disorder, amplitude, and phase fluctuations on the same footing. This could permit hopefully to relate the normal state scattering properties with T’_c or T_c and to open a route toward an understanding of the microscopic origin of the pairing energy.

Author contributions

HA: writing–original draft and writing–review and editing.

Funding

The author declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The author would like to acknowledge here his collaborators and students who have participated in the large set of experiments mentioned here. Florence Rullier-Albenque (FRA), from CEA (Saclay) has been responsible for most experimental work on transport properties and would have been a co-author on this article if she did not pass away too early in 2016. P. Mendels has been an efficient collaborator on the NMR experiments done during many years after the cuprate discovery, and J. Bobroff has done essential contributions for his PhD and well after with A. Mac Farlane and with his student S. Ouazi. Collaborations with G. Collin, J. F. Marucco (ICMO Orsay), N. Bamchard, D. Colson, and A. Forget (CEA Saclay) have been essential for all the preparation and characterization of the NMR and single-crystal samples. F. Balakirev initiated us to perform the first pulsed high-field transport measurements achieved at the NHMFL in Los Alamos. FRA and the author complemented them by many runs performed at the SNCI (Toulouse), with the help of B. Vignolles, D. Vignolles, and C. Proust. Over the years, the author has benefited of numerous exchanges on the experiments with K. Behnia, P. Bourges, and Y. Sidis and on theoretical matters with M. Civelli, M. Gabay, A. Georges, M. Héritier, P. Hirschfeld, C. Pépin, H. Schulz, G. Sordi, and A. M. Tremblay.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lee PA, Nagaosa N, Wen X-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev Mod Phys (2006) 78:p17–85. doi:10.1103/revmodphys.78.17

CrossRef Full Text | Google Scholar

2. Alloul H, Bobroff J, Gabay M, Hirschfeld P. Defects in correlated metals and superconductors. Rev Mod Phys (2009) 81:45–108. doi:10.1103/revmodphys.81.45

CrossRef Full Text | Google Scholar

3. Bednorz JG, Müller KA. Possible high Tc superconductivity in the Ba-La-Cu-O system. Condensed Matter (1986) 64:p189–93. doi:10.1007/bf01303701

CrossRef Full Text | Google Scholar

4. Shirane G, Birgeneau RJ. In: DM Ginsberg, editor. Physical properties of high temperature superconductor. Singapore: World Scientific (1989). p. p151.

Google Scholar

5. Wu MK, Ashburn JR, Torng CJ, Hor PH, Meng RL, Gao L, et al. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys Rev Lett (1987) 58:p908–10. doi:10.1103/physrevlett.58.908

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Alloul H, Bobroff J, Mac Farlane WA, Mendels P, Fullier-Albenque F. Impurities and defects as probes of the original magnetic properties of the cuprates. J Phys Soc Jpn suppl B (2000) 59:p114.

Google Scholar

7. Rossat-Mignod J, Buffet P, Jurgens MJ, Vettier C, Regnault LP, Henry JY, et al. Antiferromagnetic order and phase diagram of Yba2Cu3O6+x. J Phys (Paris) (1988) C8:2119.

Google Scholar

8. Tallon JL, Obertelli SD, Cooper JR. Systematics in the thermoelectric power of high-T, oxides. Phys Rev B (1992) 46:14928–31. doi:10.1103/physrevb.46.14928

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Alloul H, Mendels P, Casalta H, Marucco JF, Arabski J. Correlations between magnetic and superconducting properties of Zn substituted YBa2Cu3O6+x. Phys Rev Lett (1991) 67:3140–3. doi:10.1103/physrevlett.67.3140

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Alloul H, Ohno T, Mendels P. 89Y NMR evidence for a fermi-liquid behavior in YBa2Cu3O6+x. Phys Rev Lett . (1959) 63:1700–3. doi:10.1103/PhysRevLett.63.1700

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bobroff J, Alloul H, Mendels P, Viallet V, Marucco J-F, Colson D. 17O NMR evidence for a pseudogap in the monolayer HgBa2CuO4+d. Phys Rev Lett (1997) 78:3757–60. doi:10.1103/physrevlett.78.3757

CrossRef Full Text | Google Scholar

12. Rullier-Albenque F, Alloul H, Balakirev F, Disorder CP. Disorder, metal-insulator crossover and phase diagram in high-T _c cuprates. Europhysics Lett.ers. (2008) 81:37008. doi:10.1209/0295-5075/81/37008

CrossRef Full Text | Google Scholar

13. Maple MB, Lee BW, Neumeier JJ, Nieva G, Paulius LM, Seaman CL. Extraordinary behaviour of the Y_1−x Pr_x Ba₂Cu₃O_7−δ system. J Alloys Compd (1992) 181:135–52. doi:10.1016/0925-8388(92)90305-s

CrossRef Full Text | Google Scholar

14. Mac Farlane WA, Bobroff J, Mendels P, Collin G, Marucco JF, Cyrot L, et al. Planar 17O NMR study of PryY1-yBa2Cu3O6+x. Phys Rev B (2002) 66:024508.

Google Scholar

15. Casalta H, Alloul H, Marucco JF. Measurement of the Néel temperature of (Y1yCay)Ba2Cu3O6 versus Calcium content: evidence for the importance of charge dynamics in the destruction of TN. Physica C (1993) 204:331–40. doi:10.1016/0921-4534(93)91017-p

CrossRef Full Text | Google Scholar

16. Johnston DC, Borsa F, Canfield PC, Cho JH, Chou FC, Miller LL, et al. In: E Sigmund, and KA M¨uller, editors. Phase separation in cuprate superconductors. Heidelberg: Springer-Verlag (1994). p. p82.

Google Scholar

17. Tranquada JM, Sternlieb BJ, Axe JD, Nakamura Y, Uchida S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature (1995) 375:561–3. doi:10.1038/375561a0

CrossRef Full Text | Google Scholar

18. Doiron-Leyraud N, Proust C, LeBoeuf D, Levallois J, Bonnemaison JB, Liang R, et al. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature (2007) 447:565–8. doi:10.1038/nature05872

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Proust C, Tailllefer L. The remarkable underlying ground states of cuprate superconductors. Annu Rev Condens Matter Phys (2019) p10409.

CrossRef Full Text | Google Scholar

20. Wu T, Maya H, Kramer S, Horvatic M, Berthier C, Hardy WN, et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy. Nature (2011) 477:p191–4. doi:10.1038/nature10345

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Blanco-Canosa S, Frano A, Schierle E, Porras J, Loew T, Minola M, et al. Resonant x-ray scattering study of charge-density wave correlations in YBa2Cu3O6+x. Phys Rev B (2014) 90:054513. doi:10.1103/physrevb.90.054513

CrossRef Full Text | Google Scholar

22. Gerber S, Jang H, Nojiri H, Matsuzaw S, Yasumura H, Bonn DA, et al. Three-Dimensional charge density wave order in YBa2Cu3O6.67 at high magnetic fields. Science (2015) 350:949–52. doi:10.1126/science.aac6257

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Meier H, Einenkel M, Pépin C, Efetov KB. Effect of magnetic field on the competition between superconductivity and charge order below the pseudogap state. Phys.Rev B (2013) 88:020506. doi:10.1103/physrevb.88.020506

CrossRef Full Text | Google Scholar

24. Hayward LE, Hawthorn DG, Melko RG, Sachdev S Angular fluctuations of a multicomponent order describe the pseudogap of YBa₂ Cu₃ O₆ + x. Science (2014) 343:1336–9. doi:10.1126/science.1246310

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Alloul H. What is the simplest model which captures the basic experimental facts of the physics of underdoped cuprates? C R Physique (2014) 15:519–24. doi:10.1016/j.crhy.2014.02.007

CrossRef Full Text | Google Scholar

26. Zimmermann Mv., Schneider JR, Frello T, Andersen NH, Madsen J, Ka¨ll M, et al. Oxygen-ordering superstructures in underdoped YBa2Cu3O 6¿x studied by hard x-ray diffraction. Phys Rev B. (2003) 68:104515. doi:10.1103/physrevb.68.104515

CrossRef Full Text | Google Scholar

27. Bobroff J, Alloul H, Ouazi S, Mendels P, Mahajan A, Blanchard N, et al. Absence of static phase separation in the high Tc cuprate YBa2Cu3O6+x. Phys Rev Lett (2002) 89:157002. doi:10.1103/physrevlett.89.157002

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kubo Y, Shimakawa Y, Manako T, Igarashi H. Transport and magnetic properties of TlzBa2Cu06+d showing a d -dependent gradual transition from an 85-K superconductor to a non superconducting metal. Phys Rev B (1991) 43:7875–82. doi:10.1103/physrevb.43.7875

CrossRef Full Text | Google Scholar

29. Friedel J. On some electrical and magnetic properties of metallic solid solutions. Can J Phys (1956) 34:1190–211. doi:10.1139/p56-134

CrossRef Full Text | Google Scholar

30. Yosida K. Magnetic properties of Cu-Mn alloys. Phys Rev (1957) 106:893–8. doi:10.1103/physrev.106.893

CrossRef Full Text | Google Scholar

31. Alloul H. From Friedel oscillations and Kondo effect to the pseudogap in cuprates. Jsupercond Nov Mag (2012) 25:585–608. doi:10.1007/s10948-012-1472-x

CrossRef Full Text | Google Scholar

32. Mendels P, Alloul H, Marucco JF, Arabski J, Collin G. Antiferromagnetism in YBa2Cu3O6+x: Ga and Zn substitutions II. zero field NMR of the Cu magnetic sites. Physica C (1990) 171:p429–37. doi:10.1016/0921-4534(90)90252-a

CrossRef Full Text | Google Scholar

33. Mendels P, Bobroff J, Collin G, Alloul H, Gabay M, Marucco JF, et al. Normal-state magnetic properties of Ni and Zn substituted in YBa ₂ Cu ₃ O _{6 + <i>x</i>}: hole-doping dependence. Europhysics Lett (1999) 46:678–84. doi:10.1209/epl/i1999-00319-x

CrossRef Full Text | Google Scholar

34. Mahajan AV, Alloul H, Collin G, Marucco JF. 89Y NMR probe of Zn induced local moments in YBa2(Cu1-yZny)3O6+x. Phys Rev Lett (1994) 72:3100–3. doi:10.1103/PhysRevLett.72.3100

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Bobroff J, Mac Farlane A, Alloul H, Mendels P, Blanchard N, Collin G, et al. Spinless impurities in high Tc cuprates: Kondo like behaviour. Phys Rev Lett (1999) 83:4381–4. doi:10.1103/physrevlett.83.4381

CrossRef Full Text | Google Scholar

36. Tedoldi F, Santachiara R, Horvatic M. Y89 NMR imaging of the staggered magnetization in the doped Haldane chain Y2BaNi1-xMgxO5. Phys Rev Lett (1999) 83:412–5. doi:10.1103/physrevlett.83.412

CrossRef Full Text | Google Scholar

37. Das J, Mahajan AV, Bobroff J, Alloul H, Alet F, Sorensen E. Comparison of S=0 and S=1/2 impurities in the Haldane chain compound Y2BaNiO5. Phys Rev B (2004) 69:144404. doi:10.1103/physrevb.69.144404

CrossRef Full Text | Google Scholar

38. Ouazi S, Bobroff J, Alloul H, MacFarlane WA. Correlation length in cuprate superconductors deduced from impurity-induced magnetization. Phys Rev B (2004) 70:104515. doi:10.1103/physrevb.70.104515

CrossRef Full Text | Google Scholar

39. Balatsky AV, Bourges P. Linear dependence of peak width in $χ(\bq, ω)$ vs T_c for YBCO superconductors. Phys Rev Lett (1999) 82:5337–40. doi:10.1103/physrevlett.82.5337

CrossRef Full Text | Google Scholar

40. Sidis Y, Bourges P, Hennion B, Regnault LP, Villeneuve R, Collin G, et al. Zinc-induced modification of the dynamical magnetic susceptibility in the superconducting state of YBa2 Cu3 O61x as revealed by inelastic neutron scattering. Phys Rev B (1996) 53:p6811–8. doi:10.1103/physrevb.53.6811

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Alloul H. Hyperfine studies of the static and dynamic susceptibilities of Kondo systems. Physica (1977) 86-88B:449–54. doi:10.1016/0378-4363(77)90382-5

CrossRef Full Text | Google Scholar

42. Bobroff J, Alloul H, Mac Farlane WA, Mendels P, Blanchard N, Collin G, et al. Persistence of Li induced Kondo moments in the superconducting state of cuprates. Phys Rev Lett (2001) 86:4116–9. doi:10.1103/physrevlett.86.4116

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Rullier-Albenque F, Quéré Y. An experimental argument — in Nb3Ge — for the Labbé-Barisic-Friedel theory of A-15 superconductors. Phys Lett A (1981) 81:232–4. doi:10.1016/0375-9601(81)90248-6

CrossRef Full Text | Google Scholar

44. Legris A, Rullier-Albenque F, Radeva E, Lejay P. Effects of electron irradiation on YBa[Formula: see text]CU[Formula: see text]0[Formula: see text] superconductor. J Phys (France) (1993) 3:1605–15. doi:10.1051/jp1:1993203

CrossRef Full Text | Google Scholar

45. Mizuhashi K, Takenaka K, Fukuzumi Y, Uchida S. Effect of Zn doping on charge transport in YBa2Cu307-d. Phys Rev B (1995) 52:R3884–7. doi:10.1103/physrevb.52.r3884

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Rullier-Albenque F, Alloul H, Tourbot R. Influences of pair breaking and phase fluctuations in disordered high Tc cuprates. Phys Rev Lett (2003) 91:047001. doi:10.1103/physrevlett.91.047001

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Rullier-Albenque F, Alloul H, Tourbot R. Disorder and transport in cuprates: weak localization and magnetic contributions. Phys Rev Lett (2001) 8:157001. doi:10.1103/physrevlett.87.157001

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Ando Y, Boebinger GS, Passner A, Kimura T, Kishio K. Logarithmic divergence of both in-plane and out-of-plane normal-state resistivities of superconducting La2−xSrxCuO4 in the zero-temperature limit. Phys Rev Lett (1995) 75:4662–5. doi:10.1103/physrevlett.75.4662

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Boebinger GS, Ando Y, Passner A, Kimura T, Okuya M, Shimoyama J, et al. Insulator-to-Metal crossover in the normal state of of La 22xSrxCuO4 near optimum doping. Phys Rev Lett (1996) 77:5417–20. doi:10.1103/physrevlett.77.5417

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Ono S, Ando Y, Murayama T, Balakirev FF, Betts JB, Boebinger GS. Metal-to-Insulator crossover in the low-temperature normal state of Bi2Sr2−xLaxCuO6+δ. Phys Rev Lett (2000) 85:638–41. doi:10.1103/physrevlett.85.638

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Daybell MD, Steyert WA. Localized magnetic impurity states in metals: some experimental relationships. Rev Mod Phys (1968) 40:380–9. doi:10.1103/revmodphys.40.380

CrossRef Full Text | Google Scholar

52. Tholence JL, Tournier R. One-impurity and interaction effects on the Cu:Fe magnetization. Phys.Rev.Letters (1970) 25:867–71. doi:10.1103/physrevlett.25.867

CrossRef Full Text | Google Scholar

53. Borkowski LS, Hirschfeld PJ. Distinguishing d-wave superconductors from highly anisotropic s-wave superconductors. Phys Rev B (1994) 49:15404–7. doi:10.1103/physrevb.49.15404

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Emery VJ, Kivelson SA. Importance of phase fluctuations in superconductors with small superfluid density. Nature (London) (1995) 374:434–7. doi:10.1038/374434a0

CrossRef Full Text | Google Scholar

55. Emery VJ, Kivelson SA. Superconductivity in bad metals. Phys Rev Lett (1995) 74:3253–6. doi:10.1103/physrevlett.74.3253

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Wang Y, Li L, Ong NP. Nernst effect in high-T c superconductors. Phys Rev B (2006) 73:024510. doi:10.1103/physrevb.73.024510

CrossRef Full Text | Google Scholar

57. Wang Y, Lu L, Naughton MJ, Gu GD, Uchida S, Ong NP. Field-enhanced diamagnetism in the pseudogap state of the cuprate Bi2Sr2CaCu2O8+δ superconductor in an intense magnetic field. Phys Rev Lett (2005) 95:247002. doi:10.1103/physrevlett.95.247002

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Li L, Wang Y, Komiya S, Ono S, Ando Y, Gu GD, et al. Diamagnetism and Cooper pairing above T c in cuprates. Phys Rev B (2010) 81:054510. doi:10.1103/physrevb.81.054510

CrossRef Full Text | Google Scholar

59. Rullier-Albenque F, Alloul H, Proust C, Lejay P, Colson D, Forget A. Total suppression of superconductivity by high magnetic fields in YBa2Cu3O6.5. Phys Rev Lett (2007) 99:027003. doi:10.1103/physrevlett.99.027003

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Rullier-Albenque F, Alloul H, Rikken G. High field studies of superconducting fluctuations in high-Tc cuprates: evidence for a small gap distinct from the large pseudogap. Phys Rev B (2011) 84:014522. doi:10.1103/physrevb.84.014522

CrossRef Full Text | Google Scholar

61. Rullier-Albenque F, Tourbot R, Alloul H, Lejay P, Colson D, Forget A. Nernst effect and disorder in the normal state of high-Tc_cuprates. Phys Rev Lett (2006) 96:067002. doi:10.1103/physrevlett.96.067002

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Larkin A, Varlamov AA. Theory of fluctuations in superconductors. Oxford: Oxford University Press (2005).

Google Scholar

63. Lawrence WE, Doniach S. In: E Kanda, editor. Proceedings 12th international conference on low temperature physics, kyoto 1970. Tokyo: Kaigaku (1971). p. 361.

Google Scholar

64. Le Tacon M, Sacuto A, Georges A, Kottliar G, Gallais Y, Colson D, et al. Two energy scales and two distinct quasiparticle dynamics in the superconducting state of underdoped cuprates. Nat Phys (2006) 2:537–43. doi:10.1038/nphys362

CrossRef Full Text | Google Scholar

65. Kondo T, Khasanov R, Takeuchi T, Schmalian J, Kaminski A. Competition between the pseudogap and superconductivity in the high-Tc copper oxides. Nature (London) (2009) 457:296–300. doi:10.1038/nature07644

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Bilbro LS, Valdés Aguiolar R, Logvenov G, Pelleg O, Bo˘zovi´c I, Armitage NP. Temporal correlations of superconductivity above the transition temperature in La2-xSrxCuO4 probed by terahertz spectroscopy. Nat Phys (2011) 7:p302.

CrossRef Full Text | Google Scholar

67. Rullier'Albenque F. Unpublished private communication (2024).

Google Scholar

68. Damascelli A, Hussain Z, Shen ZX. Angle-resolved photoemission studies of the cuprate superconductors. Rev Mod Phys (2003) 75:473–541. doi:10.1103/revmodphys.75.473

CrossRef Full Text | Google Scholar

69. Hoffman JE, McElroy K, Lee D-H, M Lang K, Eisaki H, Uchida S, et al. Imaging quasiparticle interference in Bi ₂ Sr ₂ CaCu ₂ O _8+δ. Science (2002) 297:1148–51. doi:10.1126/science.1072640

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Pan SE, Hudson EW, Lang KM, Eisaki H, Uchida S, Davis J. Imaging the effects of individual zinc impurity atoms on superconductivity in Bi2Sr2CaCu2O8+δ. Nature (London) (2000) 403:746–50. doi:10.1038/35001534

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Alloul H, Mukhamedshin IR, Platova TA, Dooglav AV. Na ordering imprints a metallic kagomé lattice onto the Co planes of Na2/3CoO2. Europhysics Lett (2009) 85:47006. doi:10.1209/0295-5075/85/47006

CrossRef Full Text | Google Scholar

72. Gilmutdinov IF, Schonemann R, Vignolles D, Proust C, Mukhamedshin IR, Balicas L, et al. Interplay between strong correlations and electronic topology in the underlying kagome lattice of Na2/3CoO2. Phys Rev B (2021) 104:L201103. doi:10.1103/physrevb.104.l201103

CrossRef Full Text | Google Scholar

73. Varma CM. Pseudogap phase and the quantum-critical point in copper-oxide metals. Phys Rev Lett (1999) 83:3538–41. doi:10.1103/physrevlett.83.3538

CrossRef Full Text | Google Scholar

74. Bourges P, Sidis Y. Novel magnetic order in the pseudogap state of high-T c copper oxidessuperconductors. Comptes Rendus Physique (2011) 12:461–79. doi:10.1016/j.crhy.2011.04.006

CrossRef Full Text | Google Scholar

75. Séùmon P, Haule K, Tremblay AMS. Strong coupling superconductivity, pseudogap, and Mott transition. Phys Rev Lett (2012) 108:216401. doi:10.1103/physrevlett.108.216401

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Fratino L, S´emon P, Sordi G, Tremblay A-MS. Pseudogap and superconductivity in two-dimensional doped charge transfer insulators. Phys Rev B. (2016) 93:245147. doi:10.1103/physrevb.93.245147

CrossRef Full Text | Google Scholar

77. Kowalski N, Dash SS, Sémon P, Sénéchal D, Tremblay AM. Oxygen hole content, charge-transfer gap, covalency, and cuprate superconductivity. PNAS (2021) 118:2106476118. doi:10.1073/pnas.2106476118

PubMed Abstract | CrossRef Full Text | Google Scholar