On the ignition of H11B fusion fuel

We have revisited recent results on the ideal ignition of H¹¹B fuel, in the light of the latest available reactivity, an alternative self-consistent calculation of the electron temperature, an increased extent of the suprathermal effects and the impact of plasma density. At high density, we find that the ideal ignition temperature is appreciably relaxed (e.g., $T_i\simeq 150\text{\hspace{0.17em}keV}$ for $n_i\sim {10}^{26}{\text{cm}}^{-3}$ and an optimal ¹¹B/H concentration $\epsilon =0.15$) and burn becomes substantial. We have then investigated central hot-spot ignition in both isobaric and isochoric inertial confinement configurations. Although implosion-driven ignition appears to be unfeasible, the isochoric self-heating conditions foster favourable preliminary conclusions on the utilization of proton fast ignition. In the isochoric case, we find a broad minimum in the ignition energy at $\rho R\simeq 8.5\mathrm{g}/{\text{cm}}^2$ and $220\lesssim T_i\lesssim 340\text{\hspace{0.17em}keV}$ (80 $\lesssim$ $T_e\lesssim 95\text{\hspace{0.17em}keV}$), for $\epsilon =0.15$.

1 Introduction

The ¹¹B(p,3α) fusion reaction, with a Q-value of 8.6 MeV, is experiencing a renewed interest for energy production purposes, in the light of recent experimental and theoretical findings [1–11]. The reaction is aneutronic and involves only abundant and stable isotopes. Moreover, the α particles in its final state may release all their energy to the fusion plasma. The reaction is also of interest for studies in stellar evolution, where relative abundances of ¹¹B, Li and Be provide insight into stellar processes [12]. Proposed approaches for energy production span magnetic [13], magneto-inertial [14, 15] and laser-driven [5, 16, 17] fusion. The exploitation of H¹¹B fuel, however, remains extremely challenging because of its low reactivity and high radiative losses at temperatures attainable in present-day fusion devices.

The existence of ideal ignition conditions has been demonstrated only lately by Putvinski et al. [6], who have used a recent fusion cross section dataset [4] for the calculation of the thermal reactivity and added to this latter a contribution coming from kinetic (particularly, suprathermal) effects, calculated self-consistently. Suprathermal effects are due to elastic collisions between the fusion-born α′s and background thermal protons [6, 18], which develop a bolder tail in the proton energy spectrum compared to the Maxwell-Boltzmann distribution [19–21]. Putvinski et al. [6] have found fusion power to overcome bremsstrahlung losses only marginally, for $250\lesssim T_i\lesssim 380\text{\hspace{0.17em}keV}$, in a dilute plasma ($n_i=n_p+n_B=$ 10¹⁴ cm^-3) at the optimal ¹¹B/H ion concentration $\epsilon \equiv n_B/n_p=0.15$, with $T_e$ calculated self-consistently (standard notation is used).

In this Brief Research Report, we first revisit those findings in the light of the latest available reactivity, an alternative self-consistent calculation of $T_e$ as well as the actual extent of the suprathermal effects. We then show how ideal ignition conditions vary depending on the plasma density regime, the extent of suprathermal effects and the boron-to-hydrogen concentration. We find a relaxed ignition temperature and a significantly larger fusion-to-bremsstrahlung power ratio at high density. Consequently, we study ignition in actual isobaric and isochoric hot-spot fuel configurations, and draw preliminary conclusions on fast ignition.

We recall that hot-spot fuel configurations are relevant to laser-driven inertial confinement, which is a promising method to achieve fusion energy [22]. Ignition of DT fuel has recently been achieved at the US National Ignition Facility [23], by exploiting an indirect-drive scheme based on a nearly isobaric fuel configuration [24]. Fast ignition is a technique alternative to hot-spot ignition and is based on the ignition of precompressed fuel by means of an external trigger. Laser-driven fast ignition was proposed by Tabak et al. [25] 30 years ago and it is today the subject of significant theoretical and experimental investigation [26, 27].

2 Ideal ignition

The ideal ignition conditions of Putvinski et al. [6] have been recalculated and plotted in Figure 1A (blue curve) in terms of the ratio $P_f/P_b$, where

$P_f\left(T_i\right)=\left(1+s\right)P_{th}\left(T_i\right)(1)$

is the fusion power (per unit volume), $P_{th}$ is the thermal fusion power, s is a parameter expressing the suprathermal contribution, and $P_b\left(T_e\right)$ is the bremsstrahlung power (see Appendix A for formulas). While $s=0.1$ has been found by Putvinski et al., large-angle scattering, particularly by the effect of the nuclear (strong) interaction, does not appear to have been taken into account in their α-p collision calculations. One of us has shown [20] that in a H¹¹B plasma at high density ($n_e$∼10²⁶ cm^-3) and electron temperature ($T_e\gtrsim$50 keV), suprathermal effects calculated on the basis of the complete elastic α-p cross section can be approximately two times higher than those found upon the assumption of a pure Coulomb scattering. Accordingly, we put forward that s is very likely to reach 0.2. This assumption is in line with the earliest findings of Weaver et al. [19], who calculated a suprathermal increase of the H¹¹B reaction rate up to 15% at high plasma density and temperature, based on kinetic simulations that included both Coulomb and nuclear large-angle scattering (but that were biased by the poor knowledge of the relevant elastic and fusion cross sections at that time).

Figure 1

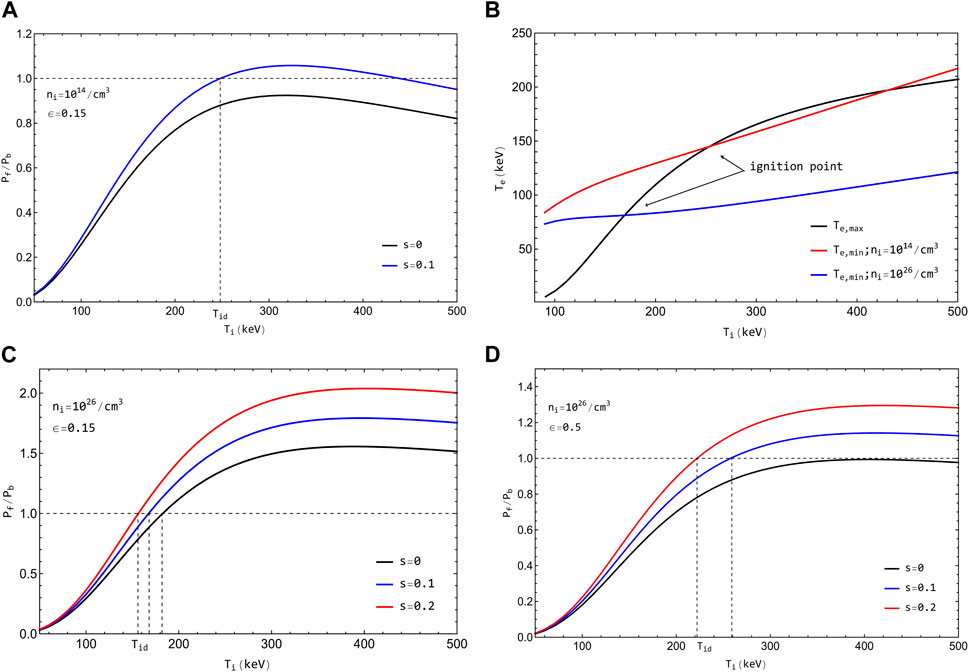
Figure 1. (A) Revisit of Putvinski et al’s ideal ignition and burn conditions [6], at low plasma density. (B) $T_e-T_i$ characteristic curves, calculated self-consistently at low and high plasma density ($s=0.1$). (C, D) High-density case: $P_f/P_b$ vs. $T_i$ and ideal ignition temperature at low and high ¹¹B concentration ($\epsilon =0.15,0.5$), for representative values of s.

From Figure 1A, we note that ignition is not possible if the suprathermal contribution is not accounted for ($s=0$, black curve). We also note that the region where $P_f/P_b\ge 1$ extends to higher values of $T_i$ (up to $440\text{\hspace{0.17em}keV}$) compared to Ref. [6], which is very likely due to the fact that we have used a more accurate (and appreciably higher) reactivity [28] in the calculation of $P_{th}$.

As for the self-consistent calculation of $T_e$, we recall that in the $T_i-T_e$ plane of an ideal plasma, the self-burn region is bounded by the solutions of the steady-state power balance equations (29)

$P_f-P_b=0(2)$

${\eta }_i{P}_f-P_{ie}=0(3)$

where ${\eta }_i$ is the fraction of the fusion power transferred to the ions by the α particles and $P_{ie}$ is the power transferred from the ions to the electrons (see Appendix A). Eq. 2 is the balance equation for the entire system and gives the maximum possible $T_e$, $T_{e,\mathit{max}}$, at any $T_i$ higher than the ideal ignition temperature, $T_{id}$, while Eq. 3 holds for the ion fluid only and gives the minimum possible $T_e$, $T_{e,\mathit{min}}$ (Figure 1B). All the possible trajectories of the system during burn, which are determined by the time-dependent power flow equations (and their initial conditions) for the ion and electron fluids, lie between the $T_{e,\mathit{min}}$ and $T_{e,\mathit{max}}$ curves. We have used Eq. 3 to obtain the $T_e\left(T_i\right)$ relationship (blue curve in Figure 1B), whereas Putvinski et al. have used the power balance equation for the electron fluid, i.e.,

$\left(1-{\eta }_i\right)P_f+P_{ie}-P_b=0(4)$

which yields slightly higher values of $T_e$. Those result in a lower $P_f/P_b$ ratio compared to Figure 1A as $P_b$ increases with $T_e$.

While ignition and self-burn appear less marginal than previously found, low-density plasmas remain of a primary interest for magnetic confinement approaches, which can operate at sub-ignition. More meaningful conclusions can be drawn for ignition-based schemes, at high density. While the explicit square-density dependence of the P-terms cancels out in Eqs 2, 3, a residual dependence on density remains in Eq. 3 through the Coulomb logarithms of $P_{ie}$ −cp. Eqs A3, A4. Typical values of $\mathit{ln}{\mathrm{\Lambda }}_{ie}$ at $T_e=100\text{\hspace{0.17em}keV}$ are: $\mathit{ln}{\mathrm{\Lambda }}_{pe}\simeq 24$, $\mathit{ln}{\mathrm{\Lambda }}_{Be}\simeq 22$ for $n_e={10}^{14}{\text{cm}}^{-3}$, and $\mathit{ln}{\mathrm{\Lambda }}_{pe}\simeq 8,\mathit{ln}{\mathrm{\Lambda }}_{Be}\simeq 6$ for $n_e={10}^{26}{\text{cm}}^{-3}$. The change of the Coulomb logarithms upon density causes the $T_{e,\mathit{min}}$ curve in Figure 1B to shift downward while moving from a dilute to a dense plasma. As a consequence, $T_{id}$ decreases and the self-burn region enlarges. At high density, ignition and burn are quite substantial for H¹¹B fuel. Note that this effect is amplified by the strong decoupling between $T_e$ and $T_i$, without which $P_{ie}\simeq 0$.

As $P_b$ is minimum, throughout the burn region, along $T_e=T_{e,\mathit{min}}\left(T_i\right)$, this latter condition also yields the maximum $P_f/P_b$ ratio attainable at a given $T_i$. This has been plotted in Figure 1C for $n_i={10}^{26}{\text{cm}}^{-3}$ (corresponding to a mass density $\rho \simeq 250\mathrm{g}/{\text{cm}}^3$ for $\epsilon =0.15$) and representative values of s. For s = 0.2, $T_{id}$ lowers to about 150 keV, while $P_f/P_b$ overcomes 2. Moving to $n_i={10}^{27}{cm}^{-3}$ does not change $T_{e,\mathit{min}}\left(T_i\right)$ substantially and decreases T_id only by a few keV. On another note, $T_{e,\mathit{min}}$ and $T_{e,\mathit{max}}$ are mildly sensitive to s, for $s\ll 1$. For instance, it is easy to see that $T_{e,\mathit{max}}$ scales approximately as ${\left(1+s\right)}^2$.

The high $P_f/P_b$ ratio of Figure 1C encourages the analysis of ignition conditions in hot-spot configurations, where additional loss terms come into play, and shows the potential to withstand fuel depletion and bremsstrahlung emission due to the α-particle ash [30, 31]. It also opens the possibility of working at increased ¹¹B concentration. Figure 1D shows $P_f/P_b$ curves for the case of $\epsilon =$ 0.5. Ideal ignition can still be achieved, however subject to the suprathermal contribution and at the expenses of higher values of $T_{id}$. Ignition at equimolarity, i.e., $\epsilon =1$, is confirmed to be impossible, at least for $s\le 0.2$.

3 Hot-spot ignition

The power balance condition for a hot spot of radius R and density ρ at the ignition threshold reads

$P_f-P_b-P_h-P_m=0(5)$

where $P_h$ is the power density lost through heat conduction and $P_m$ that lost through mechanical work ($P_m=0$ in the isobaric case); see Appendix A. All fusion born α′s are assumed to remain inside the hot spot. Eq. 5 results in a quadratic equation for $\rho R$ which coefficients, in general, are functions of $T_i$ and $T_e$, and depend on $\epsilon$ and s. Eq. 5 is coupled to either of the power balance equations for ions and electrons −analogue to Eqs. 3, 4 for the ideal case− through which the variable $T_e$ can be eliminated. It is convenient to work with the power flow equation for the ion fluid, i.e.,

${\eta }_i{P}_f-P_{ie}-P_{m,i}=0(6)$

where $P_{m,i}$ is the component of $P_m$ exerted by the ions. In the isobaric case, the fact that $P_{m,i}=0$ enables the use of the same characteristic curve given by Eq. 3, in blue in Figure 1B. This self-consistent relationship can be retained also in the isochoric case, inasmuch as $P_{m,i}\ll P_{ie}$. The isochoric ignition boundary has been generated upon this assumption (Figure 2). As a term of reference, the contour corresponding to $P_{m,i}/P_{ie}=0.3$ has also been plotted, which shows that the condition $P_{m,i}\ll P_{ie}$ is reasonably consistent with the large $\rho R$ values entailed by the isochoric curve, due to the ${\left(\rho R\right)}^{-1}$ dependency of $P_{m,i}$.

Figure 2

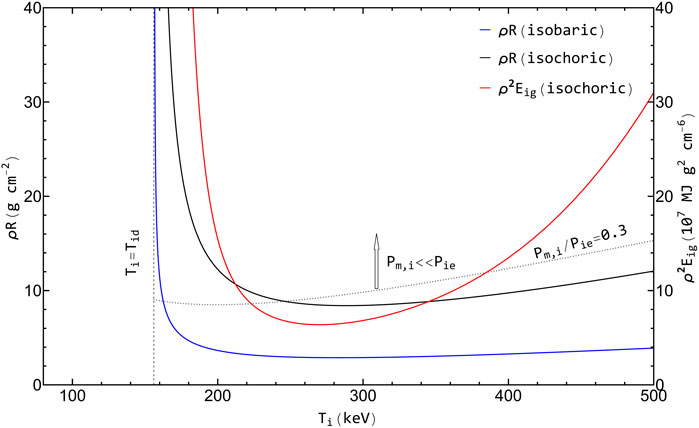
Figure 2. Left-hand ordinate: Confinement parameter vs. ${\mathit{T}}_{\mathit{i}}$ for self-heating of isobaric and isochoric H¹¹B fuel assemblies. Right-hand ordinate: ${\mathit{\rho }}^2$-weighed ignition energy for the isochoric configuration. Calculations are made for ${\mathit{n}}_{\mathit{i}}={10}^{26}/{\mathit{c}\mathit{m}}^3$, $\mathit{\epsilon }=0.15$ and $\mathit{s}=0.2$.

By analogy with the DT and DD cases, we expect that 1D simulations of pre-assembled fuel would actually show a lower branch of the ignition curves in the proximity of and after their knee, due to a cooling/re-heating mechanism of the hot spot for initial points located just below the analytic curves [32–35]. In the case of isochoric DT, for instance, $\rho R$ reduces by a factor of 1.5 when $T_i$ is twice the minimum of the analytic curve, and the gap increases with $T_i$ [35]. The difference is even more dramatic in the case of isobaric DT [33–35].

Although the confinement parameter is high at the minimum of ignition curves, we have checked that the plasma is still optically thin, i.e., the Planck mean free path, $l_P$, is much larger than R. This is due to the high electron temperature. Indeed, one has $l_P={\left(\rho {\kappa }_p\right)}^{-1}$, where

${\kappa }_p=0.43\left(<Z><Z^2>/{<A>}^2\right)\rho T_e^{-7/2}{\text{cm}}^2/\mathrm{g}(7)$

is the free-free Planck mean opacity [35], with

$〈X〉=\frac{n_p{X}_p+n_B{X}_B}{n_i}=\frac{X_p+\epsilon X_B}{1+\epsilon }(8)$

For instance, $\rho l_P\simeq 9000\mathrm{g}/{\text{cm}}^2$ at $T_i=200\text{\hspace{0.17em}keV}$ ($T_e=80\text{\hspace{0.17em}keV}$), $\rho =1000\mathrm{g}/{\text{cm}}^3$ and $\epsilon =0.15$.

The ignition energy, $E_{ig}$, has been calculated as the internal (thermal) energy of the hot spot in the ideal gas approximation, i.e.,

$E_{ig}=\frac{3}{2}pV=2\pi \left({\Gamma }_i{T}_i+{\Gamma }_e{T}_e\right)\frac{{\left(\rho R\right)}^3}{{\rho }^2}(9)$

where V is the volume of the plasma sphere and p is its pressure, as given by

$p=p_i+p_e(10)$

$p_{i\left(e\right)}={\Gamma }_{i\left(e\right)}\rho T_{i\left(e\right)}(11)$

${\Gamma }_i=k/〈A〉m_p,{\Gamma }_e=〈Z〉{\Gamma }_i(12)$

The quantity ${\rho }^2{E}_{ig}$ has been plotted vs. T_i in Figure 2 only for the isochoric case, which is expected to enable the higher gain. The curve shows a broad minimum for $220\lesssim T_i\lesssim 340\text{\hspace{0.17em}keV}$, which corresponds to $\rho R\approx 8.5$ g/cm². One can estimate that at ρ as high as 4,000 g/cm³, $E_{ig}$ at its minimum is still considerably large (∼3 MJ).

4 Discussion and conclusion

Despite the fact that self-heating is possible in a pre-formed hot spot, we have verified that implosion-driven formation of the hot spot is hydrodynamically impossible, on the basis of the same argument preventing it in pure D fuel [34], i.e., a cooling timescale shorter than the hot-spot confinement time $t_c\sim R/c_s$, being $c_s$ the isothermal sound velocity. Even without this issue, considerations on the required implosion velocity and hydrodynamic instabilities would prevent this scheme from being viable. These circumstances point toward fast ignition as possibly the only scheme to ignite inertially confined H¹¹B fuel, apart from the trivial, low-gain case of volume ignition. Nevertheless, isochoric self-heating conditions provide a preliminary estimate of fast ignition requirements [35].

Proton fast ignition [36] is particularly suited to H¹¹B fuel, not only because of its superior ballistic properties in the energy deposition and the potential capability of inducing the hot-ion mode, but also because of the additional heating provided by the in-flight fusion reactions of the proton beam [21, 37]. It has been put forward [21] that in a fully degenerate ¹¹B plasma, under certain conditions, this contribution could become as large as the initial kinetic energy of the proton beam. Such an effect could then appreciably reduce the ignitor energy required in a H¹¹B mixture. Taking also into account the reduction of $E_{ig}$ because of the abovementioned lowering of the higher-$T_i$ branch of the isochoric curve −note that $E_{ig}$ scales as ${\left(\rho R\right)}^3$ − ignitor energies of a few hundreds kJ can be expected at densities around $4000\mathrm{g}/{\text{cm}}^3$. The laser energy required to drive the implosion is estimated at about 1.3 MJ per mg of fuel, by assuming an overall laser-target coupling efficiency of 15% (direct drive), a unit isentrope parameter, and $\epsilon =0.15$.

The ignitor pulse will have to be delivered to the compressed target within a timescale shorter than $t_c$; e.g., $t_c\simeq 6\text{\hspace{0.17em}ps}$ for $T_i=220\text{\hspace{0.17em}keV}$ ($T_e=85\text{\hspace{0.17em}keV}$), $\rho R=10$ g/cm² and ρ = 4,000 g/cm³. Due to the progressive heating induced, the protons in the bunch will experience rapidly and drastically changing plasma conditions upon their arrival onto the hot spot, and even during their slowing down [38]. Plasma degeneracy will shift from strong at the onset of the ignitor pulse to very weak on its tail. Matching the proton range to the hot spot confinement parameter along the evolving plasma conditions will require a suitably tailored proton spectrum. The determination of such spectrum can only be carried out upon a self-consistent approach to the ignitor-fuel interaction, through accurate simulations. While this task is beyond the scope of the present study, here we estimate, for instance, that 2.5 MeV protons have a 10 g/cm² range at the ignition conditions which have been used to calculate $t_c$ and which correspond to the last stage of the hot-spot heating process (see Appendix A for details on the stopping power). At the early stage of hot-spot heating, for e.g., $T_i=T_e=10\text{\hspace{0.17em}keV}$, the 10 g/cm² range corresponds to a much higher proton energy, about 200 MeV. In practice, protons with a mean energy of a few tens MeV will most probably be needed. Assuming a 300 kJ ignitor, an overall number of protons of the order of 10¹⁶–10¹⁷ is estimated accordingly. As a term of comparison, a highly directional beam of 10¹³ protons with an approximately Maxwellian spectrum at an effective temperature of 6 MeV has been produced under intense laser irradiation (600 J, 0.5 ps, 3 × 10²⁰ W/cm²) of thin foils, through the Target Normal Sheath Acceleration (TNSA) mechanism [39]. Driving a TNSA-based proton ignitor for H¹¹B fuel will therefore require a multiple-beam laser firing scheme and a suitably engineered foil target (e.g., multi-spot designed, heavily H-loaded, convex-shaped for focusing the ignitor beam). The placement of such an extended foil target sufficiently close to the hot spot to limit time-of-flight dispersion of the ignitor power will require cone-guiding through the fuel capsule [40], with a wide cone aperture. A conically guided capsule will also limit the implosion driver energy while largely preserving the gain [40].

With a 300 kJ ignitor and the highest reported laser-to-proton energy conversion efficiency, 15% [41, 42], an overall laser energy of 2 MJ will be needed to drive the ignitor. This energy will have to be delivered to the foil target over a timescale of 1 ps. Suitable laser amplifiers and laser architectures will have to be developed to this extent as well as for the ns-scale implosion of the fuel, where driver energies above 10 MJ are expected. Both Diode-Pumped Solid-State Laser (DPSSL) and excimer laser systems show the potential to be scaled up to the large energy outputs required for compression and fast ignition of H¹¹B fuel, on both the ns and ps timescales [43, 44].

We finally recall that within the frame of a very specific fast ignition scheme, based on a laser-driven relativistic shock wave, Eliezer et al. [45] have found that a laser pulse with intensity of 1.6 × 10²⁵ W/cm², duration of 1 ps and energy of 21 MJ impinging on fuel pre-compressed at 4,800 g/cm³ can generate a side, cylindrical hot spot with a depth of 8.3 g/cm², $T_i\simeq 200\text{\hspace{0.17em}keV}$, $T_e\simeq 50\text{\hspace{0.17em}keV}$, where ignition is achieved. Such a laser pulse is judged impracticable in the near term.

On the contrary, our preliminary analysis shows that proton fast ignition of isochoric H¹¹B fuel requires compression and ignitor performances which, though challenging, are in line with near-future laser capabilities. We plan to devote further work to demonstrate burn propagation, better quantify ignition parameters and calculate gain in such scheme, considering actual target configurations.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

EG: Formal Analysis, Writing–original draft, Writing–review and editing, Data curation, Investigation, Software, Visualization. FB: Formal Analysis, Writing–original draft, Writing–review and editing, Conceptualization, Methodology, Supervision, Validation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. HB11 Energy Ltd. Pty. has supported this work through the consultancy contract of the first author and the payment of the publishing fee. This work has been carried out under the Collaborative Science Program of HB11 Energy.

Acknowledgments

The authors wish to thank D Batani, S Pikuz, E Turcu and D Margarone for useful discussions. The authors are indebted with I Morozov for an independent verification of their results. FB is grateful to F Ladouceur for hosting his fellowship at UNSW Sydney.

Conflict of interest

Author EG was affiliated to HB11 Energy Holdings Ltd Pty.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from HB11 Energy Pty. Ltd. The funder was involved in the discussion of the results and in the decision to submit the manuscript for publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Belyaev VS, Matafonov AP, Vinogradov VI, Krainov VP, Lisitsa VS, Roussetski AS, et al. Observation of neutronless fusion reactions in picosecond laser plasmas. Phys Rev E (2005) 72:026406. doi:10.1103/physreve.72.026406

CrossRef Full Text | Google Scholar

2. Stave S, Ahmed MW, France RH, Henshaw SS, Müller B, Perdue BA, et al. Understanding the B11(p,α)αα reaction at the 0.675 MeV resonance. Phys Lett B (2011) 696:26–9. doi:10.1016/j.physletb.2010.12.015

CrossRef Full Text | Google Scholar

3. Labaune C, Baccou C, Depierreux S, Goyon C, Loisel G, Yahia V, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun (2013) 4:2506. doi:10.1038/ncomms3506

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sikora MH, Weller HR. A new evaluation of the ¹¹B(p, α) α α reaction rates. J Fusion Energ (2016) 35:538–43. doi:10.1007/s10894-016-0069-y

CrossRef Full Text | Google Scholar

5. Hora H, Eliezer S, Kirchhoff G, Nissim N, Wang J, Lalousis P, et al. Road map to clean energy using laser beam ignition of boron-hydrogen fusion. Laser Part Beams (2017) 35:730–40. doi:10.1017/s0263034617000799

CrossRef Full Text | Google Scholar

6. Putvinski S, Ryutov D, Yushmanov P. Fusion reactivity of the pB¹¹ plasma revisited. Nucl Fusion (2019) 59:076018. doi:10.1088/1741-4326/ab1a60

CrossRef Full Text | Google Scholar

7. Giuffrida L, Belloni F, Margarone D, Petringa G, Milluzzo G, Scuderi V, et al. High-current stream of energetic α particles from laser-driven proton-boron fusion. Phys Rev E (2020) 101:013204. doi:10.1103/PhysRevE.101.013204

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Magee RM, Ogawa K, Tajima T, Allfrey I, Gota H, McCarroll P, et al. First measurements of p¹¹B fusion in a magnetically confined plasma. Nat Commun (2023) 14:955. doi:10.1038/s41467-023-36655-1

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ning X, Liang T, Wu D, Liu S, Liu Y, Hu T, et al. Laser-driven proton-boron fusions: influences of the boron state. Laser Part Beams (2022) 2022:e8. doi:10.1155/2022/9868807

CrossRef Full Text | Google Scholar

10. Margarone D, Bonvalet J, Giuffrida L, Morace A, Kantarelou V, Tosca M, et al. In-target proton–boron nuclear fusion using a PW-class laser. Appl Sci (2022) 12:1444. doi:10.3390/app12031444

CrossRef Full Text | Google Scholar

11. Turcu ICE, Margarone D, Giuffrida L, Picciotto A, Spindloe C, Robinson APL, et al. Borane (B_mH_n), Hydrogen rich, Proton Boron fusion fuel materials for high yield laser-driven Alpha sources. JINST (2024) 19:C03065. doi:10.1088/1748-0221/19/03/C03065

CrossRef Full Text | Google Scholar

12. Boesgaard AM, Deliyannis CP, Steinhauer A. Boron depletion in F and G dwarf stars and the beryllium-boron correlation. Astrophys J (2005) 621:991–8. doi:10.1086/427687

CrossRef Full Text | Google Scholar

13. Rostoker N, Binderbauer MW, Monkhorst HJ. Colliding beam fusion reactor. Science (1997) 278:1419–22. doi:10.1126/science.278.5342.1419

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ghorbanpour E, Ghasemizad A, Khoshbinfar S. Non-equilibrium ignition criterion for p^-11B advanced fuel in magnetized target fusion. Phys Part Nucl Lett (2020) 17:809–20. doi:10.1134/S1547477120060126

CrossRef Full Text | Google Scholar

15. Lerner EJ, Hassan SM, Karamitsos-Zivkovic I, Fritsch R. Focus fusion: overview of progress towards p-B11 fusion with the dense plasma focus. J Fusion Energ (2023) 42:7. doi:10.1007/s10894-023-00345-z

CrossRef Full Text | Google Scholar

16. McKenzie W, Batani D, Mehlhorn TA, Margarone D, Belloni F, Campbell EM, et al. HB11—understanding hydrogen-boron fusion as a new clean energy source. J Fusion Energ (2023) 42:17. doi:10.1007/s10894-023-00349-9

CrossRef Full Text | Google Scholar

17. Ruhl H, Korn G. Uniform volume heating of mixed fuels within the ICF paradigm (2023). arXiv:2302.06562.

Google Scholar

18. Belloni F, Margarone D, Picciotto A, Schillaci F, Giuffrida L. On the enhancement of p-11B fusion reaction rate in laser-driven plasma by α → p collisional energy transfer. Phys Plasmas (2018) 25:020701. doi:10.1063/1.5007923

CrossRef Full Text | Google Scholar

19. Weaver T, Zimmerman G, Wood L. Preprint UCRL-74938. Livermore, CA, USA: Lawrence Livermore Laboratory (1973).

Google Scholar

20. Belloni F. On a fusion chain reaction via suprathermal ions in high-density H–¹¹B plasma. Plasma Phys Control Fusion (2021) 63:055020. doi:10.1088/1361-6587/abf255

CrossRef Full Text | Google Scholar

21. Belloni F. Multiplication processes in high-density H^-11B fusion fuel. Laser Part Beams (2022) 2022:3952779. doi:10.1155/2022/3952779

CrossRef Full Text | Google Scholar

22. Meier WR, Dunne AM, Kramer KJ, Reyes S, Anklam TM. Fusion technology aspects of laser inertial fusion energy (LIFE). Fusion Eng Des (2014) 89(9–10):2489–92. doi:10.1016/j.fusengdes.2013.12.021

CrossRef Full Text | Google Scholar

23. Abu-Shawareb H, Acree R, Adams P, Adams J, Addis B, Aden R, et al. Achievement of target gain larger than unity in an inertial fusion experiment. Phys Rev Lett (2024) 132:065102. doi:10.1103/physrevlett.132.065102

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Patel PK, Springer PT, Weber CR, Jarrott LC, Hurricane OA, Bachmann B, et al. Hotspot conditions achieved in inertial confinement fusion experiments on the National Ignition Facility. Phys Plasmas (2020) 27:050901. doi:10.1063/5.0003298

CrossRef Full Text | Google Scholar

25. Tabak M, Hammer J, Glinsky ME, Kruer WL, Wilks SC, Woodworth J, et al. Ignition and high gain with ultrapowerful lasers. Phys Plasmas (1994) 1(5):1626–34. doi:10.1063/1.870664

CrossRef Full Text | Google Scholar

26. Zhang J, Wang WM, Yang XH, Wu D, Ma YY, Jiao JL, et al. Double-cone ignition scheme for inertial confinement fusion. Philos Trans R Soc A (2020) 378:20200015. doi:10.1098/rsta.2020.0015

CrossRef Full Text | Google Scholar

27. Xu Z, Wu F, Jiang B, Kawata S, Zhang J. Formation of hot spots at end-on pre-compressed isochoric fuels for fast ignition. Nucl Fusion (2023) 63:126062. doi:10.1088/1741-4326/ad08e6

CrossRef Full Text | Google Scholar

28. Tentori A, Belloni F. Revisiting p-¹¹B fusion cross section and reactivity, and their analytic approximations. Nucl Fusion (2023) 63:086001. doi:10.1088/1741-4326/acda4b

CrossRef Full Text | Google Scholar

29. Moreau DC. Potentiality of the proton-boron fuel for controlled thermonuclear fusion. Nucl Fusion (1977) 17:13–20. doi:10.1088/0029-5515/17/1/002

CrossRef Full Text | Google Scholar

30. Nevins WM. A review of confinement requirements for advanced fuels. J Fusion Energ (1998) 17:25–32. doi:10.1023/a:1022513215080

CrossRef Full Text | Google Scholar

31. Chirkov AY, Kazakov KD. Radiation limit for the energy gain of the p–11B reaction. Plasma (2023) 6:379–92. doi:10.3390/plasma6030026

CrossRef Full Text | Google Scholar

32. Gus’kov SY, Krokhin ON, Rozanov VB. Similarity solution of thermonuclear burn wave with electron and α-conductivities. Nucl Fusion (1976) 16:957–62. doi:10.1088/0029-5515/16/6/007

CrossRef Full Text | Google Scholar

33. Atzeni S, Caruso A. Inertial confinement fusion: ignition of isobarically compressed D-T targets. Nuovo Cim B (1984) 80:71–103. doi:10.1007/bf02899374

CrossRef Full Text | Google Scholar

34. Basko M. Spark and volume ignition of DT and D₂microspheres. Nucl Fusion (1990) 30:2443–52. doi:10.1088/0029-5515/30/12/001

CrossRef Full Text | Google Scholar

35. Atzeni S, Meyerter VJ. The physics of inertial fusion. Oxford: Oxford University Press (2004).

Google Scholar

36. Roth M, Cowan TE, Key MH, Hatchett SP, Brown C, Fountain W, et al. Fast ignition by intense laser-accelerated proton beams. Phys Rev Lett (2001) 86:436–9. doi:10.1103/PhysRevLett.86.436

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Mehlhorn TA, Labun L, Hegelich BM, Margarone D, Gu MF, Batani D, et al. Path to increasing p-B11 reactivity via ps and ns lasers. Laser Part Beams (2022) 2022:2355629. doi:10.1155/2022/2355629

CrossRef Full Text | Google Scholar

38. Honrubia JJ, Murakami M. Ion beam requirements for fast ignition of inertial fusion targets. Phys Plasmas (2015) 22:012703. doi:10.1063/1.4905904

CrossRef Full Text | Google Scholar

39. Snavely R, Key MH, Hatchett SP, Cowan TE, Roth M, Phillips TW, et al. Intense high-energy proton beams from Petawatt-laser irradiation of solids. Phys Rev Lett (2000) 85:2945–8. doi:10.1103/PhysRevLett.85.2945

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Temporal M, Honrubia JJ, Atzeni S. Numerical study of fast ignition of ablatively imploded deuterium–tritium fusion capsules by ultra-intense proton beams. Phys Plasmas (2002) 9:3098–107. doi:10.1063/1.1482375

CrossRef Full Text | Google Scholar

41. Brenner C, Robinson APL, Markey K, Scott RHH, Gray RJ, Rosinski M, et al. High energy conversion efficiency in laser-proton acceleration by controlling laser-energy deposition onto thin foil targets. Appl Phys Lett (2014) 104:081123. doi:10.1063/1.4865812

CrossRef Full Text | Google Scholar

42. Zimmer M, Scheuren S, Ebert T, Schaumann G, Schmitz B, Hornung J, et al. Analysis of laser-proton acceleration experiments for development of empirical scaling laws. Phys Rev E (2021) 104:045210. doi:10.1103/physreve.104.045210

PubMed Abstract | CrossRef Full Text | Google Scholar

43. US DoE Office of Science. Report of the fusion energy sciences workshop on inertial fusion energy (2022). Available from: https://science.osti.gov/-/media/fes/pdf/workshop-reports/2023/IFE-Basic-Research-Needs-Final-Report.pdf. (Accessed January, 2024)

Google Scholar

44. Mehlhorn TA. From KMS fusion to HB11 energy and xcimer energy, a personal 50 year IFE perspective. Phys Plasmas (2024) 31:020602. doi:10.1063/5.0170661

CrossRef Full Text | Google Scholar

45. Eliezer S, Henis Z, Nissim N, Pinhasi SV, Val JM. Introducing a two temperature plasma ignition in inertial confined targets under the effect of relativistic shock waves: the case of DT and pB¹¹. Laser Part Beams (2015) 33:577–89. doi:10.1017/s0263034615000701

CrossRef Full Text | Google Scholar

46. Svensson R. Electron-positron pair equilibria in relativistic plasmas. Astrophys J (1982) 258:335. doi:10.1086/160082

CrossRef Full Text | Google Scholar

47. Spitzer L. Physics of fully ionized gases. New York: Interscience Publishers (1956).

Google Scholar

48. Levush B, Cuperman S. On the potentiality of the proton-boron fuel for inertially confined fusion. Nucl Fusion (1982) 22:1519–25. doi:10.1088/0029-5515/22/11/005

CrossRef Full Text | Google Scholar

49. Corman EG, Loewe WE, Cooper GE, Winslow AM. Multi-group diffusion of energetic charged particles. Nucl Fusion (1975) 15:377–86. doi:10.1088/0029-5515/15/3/003

CrossRef Full Text | Google Scholar

Appendix A: Formalism

Power density terms

Explicit expressions for the power density terms in Eqs 1–6 are given hereafter (electrostatic cgs units are used):

$P_{th}=n_p{n}_B〈\sigma v〉Q(\mathrm{A1})$

where $〈\sigma v〉$ is the Maxwellian reactivity [28];

$P_b=8.511W_0{\widehat{T_e}}^{1/2}\left\{{\mathrm{Z}}_{eff}\left(1+1.78{\widehat{T_e}}^{1.34}\right)+2.12\widehat{T_e}\left(1+1.1\widehat{T_e}+{\widehat{T_e}}^2-1.25{\widehat{T_e}}^{2.5}\right)\right\}(\mathrm{A2})$

where $\widehat{T_e}=k{T}_e/m_e{c}^2$ and $W_0=e^6{n}_e^2/m_e{c}^2ħ$ [6, 46];

$P_{ie}=\frac{3}{2}\left(n_p{\nu }_{pe}+n_B{\nu }_{Be}\right)k\left(T_i-T_e\right)(\mathrm{A3})$

where ${\nu }_{ie}={\nu }_{ie}^{*}∆$,

${\nu }_{ie}*=\frac{{\left(4\pi \right)}^2{n}_e{e}^4{Z}_i^2\mathit{ln}{\mathrm{\Lambda }}_{ie}}{3\sqrt{2}{\pi }^{3/2}{m}_i{m}_e}{\left(\frac{m_e}{k{T}_e}\right)}^{3/2}(\mathrm{A4})$

is the classical heat exchange rate [29],

$∆=\frac{\left(1+2\widehat{T_e}+2{\widehat{T_e}}^2\right)\sqrt{\pi {\widehat{T_e}}^3/2}}{{\int }_0^{\infty }\exp \{-\left(\sqrt{1+x^2}-1\right)/\widehat{T_e}\}{x}^{2}dx}(\mathrm{A5})$

is its relativistic correction [6], and

$\mathit{ln}{\mathrm{\Lambda }}_{ie}=\frac{3}{2Z_i{e}^3}\sqrt{\frac{4.2\times {10}^{5}k}{\pi n_e}}k{T}_e(\mathrm{A6})$

according to Spitzer [47];

$P_h=-ϵ\left(Z_i\right)\kappa \nabla T_{e}S/V(\mathrm{A7})$

where $-\nabla T_e\simeq T_e/R$, S is the area of the hot-spot surface ($S/V=3/R$),

$\kappa =20{\left(\frac{2}{\pi }\right)}^{3/2}\frac{{\left(kT\right)}^{5/2}k}{m_e^{1/2}{e}^4{Z}_i\mathit{ln}{\mathrm{\Lambda }}_{ie}}\delta T\left(Z_i\right)(\mathrm{A8})$

is the Spitzer thermal conductivity, with $Z_i\to Z_{eff}$ for a multi-Z plasma, and the correction factors $ϵ$ and $\delta T$ have been calculated through interpolation ($ϵ=0.407$, $\delta T=0.426$) [47];

$P_m=P_{m,i}+P_{m,e}(\mathrm{A9})$

$P_{m,i\left(e\right)}=3\frac{p_{i\left(e\right)}}{R}u(\mathrm{A10})$

where $u\simeq \sqrt{3p/4\rho }$ is the velocity of the material behind a strong shock in isochoric fuel [35] and the pressures $p$, $p_i$, $p_e$ are given by Eqs 10–12.

Fusion energy partition and stopping power

The fusion power fraction to ions, ${\eta }_i$, has been calculated according to Levush and Cuperman [48] (Figure A1). A stopping power of the form

$dE/dt=E/t_E+\gamma /\sqrt{E}(\mathrm{A11})$

has been used for the fusion-born α particles, with $t_E$ and $\gamma$ given by Corman et al. [49]. A simplified α spectrum has been utilised, as explained in Ref. [20]. ${\eta }_i$ approaches or even overcomes 90% at values of $T_i$ and $T_e$ of interest for ignition and burn. The same stopping power model of Eq. A11 has been utilised for energy-range calculations for the ignitor protons.

FIGURE A1

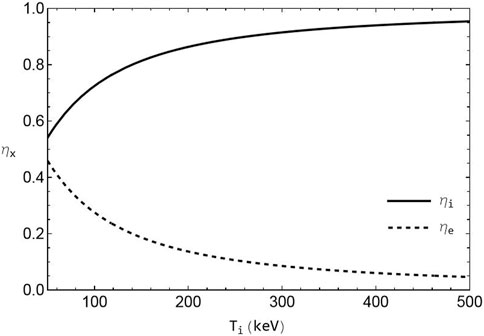
FIGURE A1. Fusion power fraction to ions (electrons) as a function of $T_i$, with $T_e=T_i/2$. Calculations are made for $n_i={10}^{26}/{cm}^3$, $\epsilon =0.15$, and depend on density weakly.

Useful relations

The densities $n_p$ and $n_B$ are linked to $n_e$ and ρ by the obvious relations

$n_p=n_e/\left(Z_p+{\epsilon Z}_B\right)(\mathrm{A12})$

$n_B={\epsilon n}_e/\left(Z_p+{\epsilon Z}_B\right)(\mathrm{A13})$

$n_e=〈Z〉n_i(\mathrm{A14})$

$\rho =n_i〈A〉m_p(\mathrm{A15})$

with $〈Z〉$ and $〈A〉$ given by Eq. 8.