Generation and analysis of the chaos phenomenon in the molecular-distillation-Navier–Stokes (MDNS) nonlinear system

Introduction: For the Navier-Stokes equation, one of the most essential tasks should be to study its completeness of the complex nonlinear systems. Also, its nature and physical practical applications would be depth explored. Moreover, as one of the routes to chaos, this equation with an external force has been investigated numerically in 1989. Recently, some information is worth noting that when the high symmetry was imposed on the velocity field, the complex nonlinear motions should occur even lead to the chaos phenomenon. However, most of the published papers are based on theoretical studies and rarely deal with the above results, which lost of the match between them and the integrity of the scientific system.

Methods: This study analyzed the molecular distillation process in detail based on the basic theory of nonlinear chaotic systems. Then, the mathematical model for the process of molecular distillation with one brushless DC motor (BLDCM) is built and named the Molecular-Distillation-Navier-Stokes (MDNS) equation. Also, its complex and potentially chaotic behaviors and chaotic processes are first discovered and demonstrated, such as chaotic attractors, chaotic co-attractors, phase portraits, time-domain waveforms, Lyapunov exponent spectrums, Poincare maps, the bifurcation diagrams, and so on.

Results: The good agreement among theoretical analysis, simulation and experimental results verifies the practicability and flexibility of the configured model.

Discussion: The related conclusions have supplemented and improved the theoretical system for the Navier Stokes equations. Also, it reflects the significance in molecular distillation processes. Meanwhile, the novel research direction for the fields of the chaotic nonlinear and complex industrial systems have been explored and discovered.

1 Introduction

The Navier–Stokes equation is the partial differential equation that is used to get the motion of viscous fluid substances and was discovered by both physicists Claude-Louis Navier and George Gabriel Stokes [1]. This model mathematically defined momentum balance for Newtonian fluids and showed the relationship among pressure, temperature, and density with the multidimensional equation of state. As one of the important theories to describe the physics for a series of phenomena of scientific and engineering interest, plenty of related results have been obtained and published. Also, it has attracted a large number of peers to explore engineering applications. For example, the full and simplified form of the Navier–Stokes equations could be used to study and analyze blood flow, the weather, ocean currents, neural networks, magnetohydrodynamics, and some other problems [2–4]. Subsequently, some scholars have worked to seek the algorithms for solving these equations [5] and find the route to chaos and complexity [1] based on the basis of nonlinear chaotic dynamics. In other words, the great interest in a purely mathematical sense for this equation has been shown for quite some time. However, some rigorous and real scientific results have been obtained, which belonged to theory, rarely to practical engineering. Moreover, the high symmetry is one of the distinctive features of some devices in the field of industry [6], such as the brushless DC motor (BLDCM). Recently, existing relevant results on brushless DC motors have also been progressively biased toward modeling and analyzing nonlinear behaviors.

For example, in 2004, Zheng-Ming Ge and his workers studied the dynamic model of the three-time scale brushless DC motor system and its chaos anticontrol algorithm [6]. In addition, they used some numerical results, such as phase diagrams, bifurcation diagrams, and Lyapunov exponents (LEs), to present the complex chaotic motions. In 2017, G. Qi presented the energy cycle of brushless DC motors and analyzed the generation route to chaos [7]. In that paper, the symmetry vector field in the BLDCM system has been investigated, and it has been pointed out that this vector field has been regarded as the force field of a pure mechanical system. Both four types of torque (namely, inertial, internal, dissipative, and generalized external torque) and four forms of energy (namely, kinetic, potential, dissipative, and generalized external) have been decomposed and investigated. In addition, the generation conditions of a chaotic attractor for one BLDCM system have been proposed and given. In 2018, Ramon L. V. Medeiros introduced a novel approach to quantifying the chaotic behavior and failure detection for brushless DC motors, which has been named signal analysis based on chaos using density of maxima (SAC-DM) [8]. To demonstrate the potential of the proposed SAC-DM, one experiment has been presented, and the conclusion is that the proposed approach has been able to detect the speed of the brushless DC motors in 99.16% of cases and identify the unbalanced system in 99.79% of cases when the speed is at 50%. It can be seen that the novel approach demonstrated fully shows the important role of chaotic phenomena in motor nonlinear systems. In addition, some valuable findings have demonstrated their importance and necessity in practical engineering, such as the oscillation and chaos control methods for the fractional- and order-integer brushless DC motor system [9–11], the multi-stability, hidden chaos, and transient chaos in the brushless DC motor [12], just to name a few.

As a short-path vacuum distillation, wiped-film molecular distillation could be used to separate, purify, and concentrate natural products and complex and thermally sensitive molecules (such as vitamins and polyunsaturated fatty acids). During the entire operation, the BLDCM has embodied important applications and become one of the core components, which has been used to drive the rotating film scraper. It ensures that a uniformly distributed liquid film can be retained on the evaporating surface of the device for efficient evaporation and separation. Therefore, for the whole molecular distillation process, the BLDCM plays a crucial role, which could be obtained through stable operation and precise control of the position of this device. Meanwhile, the analysis of its nonlinear behaviors, oscillator, and chaos phenomenon is so important and necessary. Turbulence and chaotic phenomena have always existed in the field of molecular distillation. In addition, some research results have been published [13–15]. Rarely the result presents nonlinearity and chaotic oscillators in molecular distillation with the BLDCM. In order to explore the role and significance of chaos theory in the field of molecular distillation, some existing related results and analysis methods could be introduced [16–28].

With these aims in mind, this paper is organized as follows. In Section 2, the molecular distillation process is given. Then, the mathematical model for the process of molecular distillation with one BLDCM is built and named as the molecular-distillation-Navier–Stokes (MDNS) equation. In Section 3, its complex and potentially chaotic behaviors and chaotic oscillators are first discovered and demonstrated, such as chaotic attractors, chaotic co-attractors, phase portraits, time-domain waveforms, Lyapunov exponent spectra, Poincare maps, and bifurcation diagrams. In Section 4, the coexisting chaotic attractors are shown and analyzed. Finally, this paper is summarized in Section 5.

2 Molecular distillation process and molecular-distillation-Navier–Stokes equation

2.1 Molecular distillation process

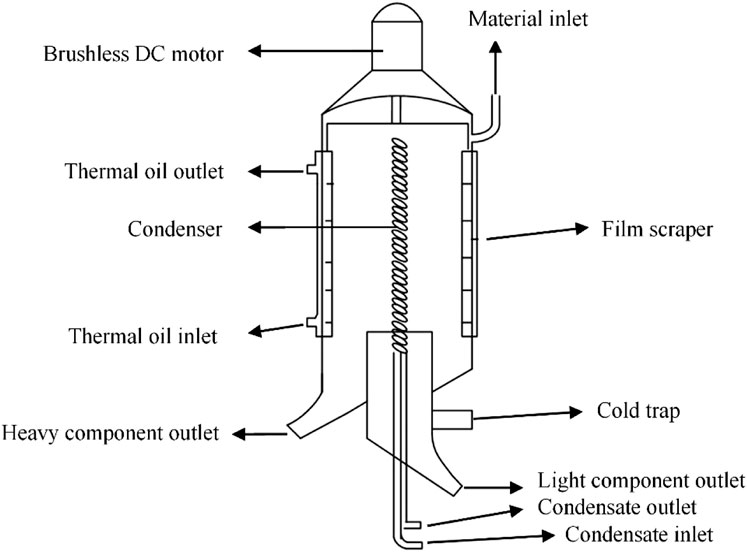
As the third generation of molecular distillation, the structure of one wiped-film molecular distillation is to install a rotating film scraper inside the traditional equipment (see Figure 1, structure of wiped-film molecular distillation).

Figure 1

Figure 1. Structure of wiped-film molecular distillation.

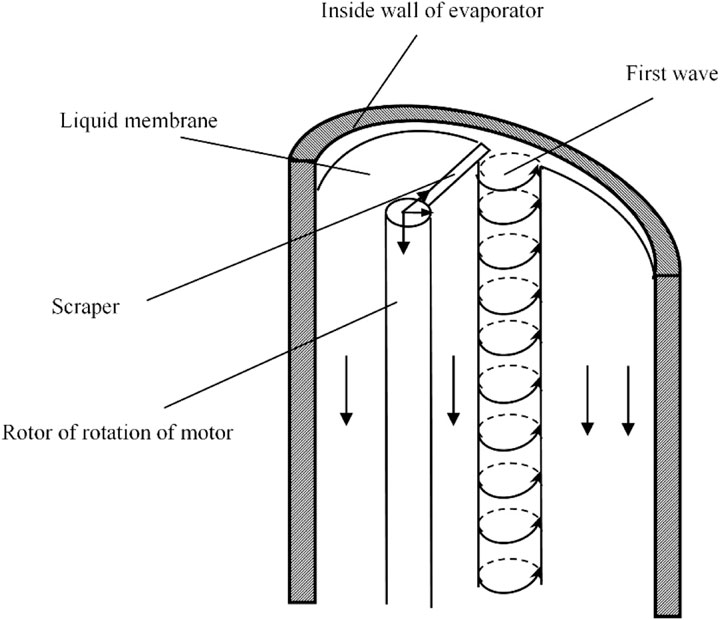
From Figure 1, the wiped-film molecular distillation system has the following advantages: 1) the continuous uniform liquid film could be formed using the scraper and effectively avoid the generation of hot spots, preventing the decomposition of the material and the splash phenomenon; 2) due to the thin liquid film, the equipment has a high efficiency with heat transfer, fast flow of the material, and a short residence time; and 3) it has a simple structure, inexpensive equipment, and high efficiency, which are widely required in laboratory and industrial production. However, some shortcomings should also be mentioned: 1) the speed of the brushless DC motor and material downstream are closely related to the improper speed; otherwise, inappropriate speed ratios could lead to material tumbling, and 2) due to the motor rotation driving the scraper motion, some behaviors (i.e., the flow of material, heat, and mass transfer processes) could become very complex, even leading to chaos and turbulence phenomena. Moreover, the mechanism and operating rules for the entire molecular distillation process could become too difficult to be accurately understood. In order to have a clear and complete understanding of the working principal diagram for the molecular distillation process, the liquid film flow in the evaporator is shown in Figure 2, after the material is put into the evaporator.

Figure 2

Figure 2. Schematic diagram of liquid film flow in the evaporator.

The film scraper and the evaporator work together to make the material uniformly distributed on the evaporator surface (see Figure 3, section of a scraper driven by the motor). After a period of time, under full stirring using the film scraper, the distribution state of the liquid film on the evaporating surface and its thickness could be kept stable for a long time. Then, the continuous input of materials causes the head wave to constantly update the composition of the liquid film, which increases the ability of heat and mass transfer in turn. As the core component, the brushless DC motor is commonly used to drive the rotating film scraper. Furthermore, this motor makes sure that a uniformly distributed liquid film is retained on the evaporating surface of the device for efficient evaporation and separation. It can be seen that the stable operation and precise control of the position of the brushless DC motor play a crucial role.

Figure 3

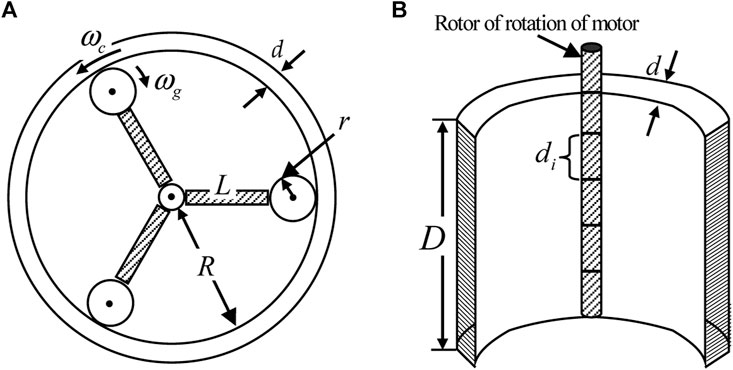
Figure 3. Transverse sections of a scraper driven by the motor: (A) transverse sections of the film scraper and (B) longitudinal sections of the film scraper.

From Figure 3, the meanings of the variables are as follows: ω_c represents the angular velocity of the inner material membrane rotation, ω_g represents the angular velocity of the scraper driven by the stator of the DC brushless motor, L represents the length of each sub-scraper from the center, R represents the radius of the inner material membrane; r represents the radius of the membrane scraper, d represents the thickness of the inner membrane of the material, D represents the height of the inner membrane, and d_i represents the height of each small portion of the membrane scraper driven by the rotating stator.

2.2 Molecular-distillation-Navier–Stokes equation

The five-mode Navier–Stokes equations in Fourier series on a torus have been built [25, 29–31]. As the movement of the film scrape is driven by the rotor of the BLDCM, there are no other force controls. According to the characteristics of the Navier–Stokes equations and BLDCM model, and the process of the wiped-film molecular distillation, the novel molecular-distillation-Navier–Stokes (MDNS) model is introduced, which expands the existing studies while expressing the role of the scraper being driven by the stator. The mathematical model of the proposed MDNS could be given as Eq. 1:

$\left\{\begin{array}{l}\frac{\mathit{d}\mathit{x}}{\mathit{d}\mathit{t}}=-\mathit{x}+{\mathit{\alpha }}_{\mathbf{1}}\mathit{y}+{\mathit{\alpha }}_{\mathbf{2}}\\ \frac{\mathit{d}\mathit{y}}{\mathit{d}\mathit{t}}=-\left(\mathit{\alpha }-\mathit{\delta }\right)\mathit{x}-\mathit{y}-\mathit{\gamma }\mathit{x}\mathit{z}+{\mathit{\alpha }}_{\mathbf{3}}\\ \frac{\mathit{d}\mathit{z}}{\mathit{d}\mathit{t}}=\mathit{x}\mathit{y}-\mathit{\beta }\mathit{z}-{\mathit{\alpha }}_{\mathbf{4}}+\mathit{n}\mathit{v}\\ \frac{\mathit{d}\mathit{w}}{\mathit{d}\mathit{t}}=-\mathit{w}+\mathit{a}\mathit{u}+\mathit{m}\\ \frac{\mathit{d}\mathit{u}}{\mathit{d}\mathit{t}}=-\left(\mathit{e}-\mathit{a}\right)\mathit{w}-\mathit{c}\mathit{u}-\mathit{w}\mathit{v}\\ \frac{\mathit{d}\mathit{v}}{\mathit{d}\mathit{t}}=\mathit{w}\mathit{u}-\mathit{b}\mathit{v}\end{array}\right.,(1)$

where both variants x and y represent the stator currents for the straight-axis and cross-axis of the BLDCM, respectively; both variants w and u represent the driven currents for the straight-axis and cross-axis of the scraper, respectively; both variants z and v represent the angular velocity of the BLDCM and driven scraper, respectively; both parameters α₂ and α₃ are the voltages for the straight-axis and cross-axis, respectively; α₄ means the external torque; n represents one relationship parameter between the motor and the scraper; α₁, α, c, b, e, δ, γ, and a mean system parameters; β means the ratio of the damping coefficient to the moment of inertia for the BLDCM; and m means the driven torque by the BLDCM.

The Jacobian matrix J evaluated at O (0, 0, 0, 0, 0, 0) is as Eq. 2.

${\mathit{J}}_{\mathbf{1}}=\left[\begin{array}{cccccc}-\mathbf{1}& {\mathit{\alpha }}_{\mathbf{1}}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ -\left(\mathit{\alpha }-\mathit{\delta }\right)& -\mathbf{1}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& -\mathit{\beta }& \mathbf{0}& \mathbf{0}& \mathit{n}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& -\mathbf{1}& \mathit{a}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& -\left(\mathit{e}-\mathit{a}\right)& -\mathit{c}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& -\mathit{b}\end{array}\right].(2)$

The characteristic equation of J is as follows:

$\mathit{det}\left(\mathit{\lambda }\mathit{I}-\mathit{J}\right)=\left(\mathit{\lambda }+\mathit{\beta }\right)\left(\mathit{\lambda }+\mathit{b}\right)\left[{\left(\mathit{\lambda }+\mathbf{1}\right)}^{\mathbf{2}}+{\mathit{\alpha }}_{\mathbf{1}}\left(\mathit{\alpha }-\mathit{\delta }\right)\right]\left[\left(\mathit{\lambda }+\mathbf{1}\right)\left(\mathit{\lambda }+\mathit{c}\right)+\mathit{a}\left(\mathit{e}-\mathit{a}\right)\right]=\mathbf{0}.(3)$

Eq. 3 is composed of the product of four polynomials. Its characteristic values Λ = {λ₁, λ₂, λ₃, λ₄, λ₅, λ₆} have two negative real roots (λ₁ and λ₂) and two pairs of complex conjugate roots with no real part (λ_3,4 and λ_5,6) to ensure that the equilibrium points are four hyperbolic saddle points (or simple, saddle points). The six eigenvalues are resolved as Eq. 4.

$\left\{\begin{array}{l}{\mathit{\lambda }}_{\mathbf{1}}=-\mathit{\beta }\\ {\mathit{\lambda }}_{\mathbf{2}}=-\mathit{b}\\ {\mathit{\lambda }}_{\mathbf{3},\mathbf{4}}=-\mathbf{1}\mp \mathit{i}\sqrt{{\mathit{\alpha }}_{\mathbf{1}}\left(\mathit{\alpha }-\mathit{\delta }\right)}\\ {\mathit{\lambda }}_{\mathbf{5},\mathbf{6}}=-\frac{\mathbf{1}}{\mathbf{2}}\mp \frac{\mathbf{1}}{\mathbf{2}}\mathit{i}\sqrt{\mathbf{4}\mathit{a}\left(\mathit{e}-\mathit{a}\right)-{\left(\mathbf{1}-\mathit{c}\right)}^{\mathbf{2}}}\end{array}\right..(4)$

According to the eigenvalues, the Routh–Hurwitz criterion, and the dissipation, the conditions are obtained as Eq. 5.

$\left\{\begin{array}{l}\begin{array}{cc}\begin{array}{cc}\begin{array}{cc}\mathit{\beta }>\mathbf{0},& \mathit{b}\end{array}>\mathbf{0},& \mathit{\alpha }>\mathit{\beta }\end{array},& \mathit{c}>-\mathbf{3}\end{array}\\ \mathbf{1}-\mathbf{2}\sqrt{\mathit{a}\left(\mathit{e}-\mathit{a}\right)}<\mathit{c}<\mathbf{1}+\mathbf{2}\sqrt{\mathit{a}\left(\mathit{e}-\mathit{a}\right)}\end{array}\right..(5)$

The characteristic values Λ = {λ₁, λ₂, λ₃, λ₄, λ₅, λ₆} of Eq. 3 have two negative real roots (λ₁ and λ₂) and two pairs of complex conjugate roots with no real part (λ_3,4 and λ_5,6) to ensure that all the equilibrium points are four hyperbolic saddle points (or simple, saddle points). Intuitively, when the parameters are set as follows: α₁ = 25, α₂ = α₃ = 0.12, α = 38, δ = 10, e = 16, b = 3.68, c = 16, γ = 1, a = 35, and m= 0.04, the initial condition of the state variable is (x, y, z, w, u, v) = (0.01, 0.01, 0.01, 0, 0, 0). The plots of the strange attractors and time-domain waveforms of the MDNS model are illustrated in Figure 4.

Figure 4

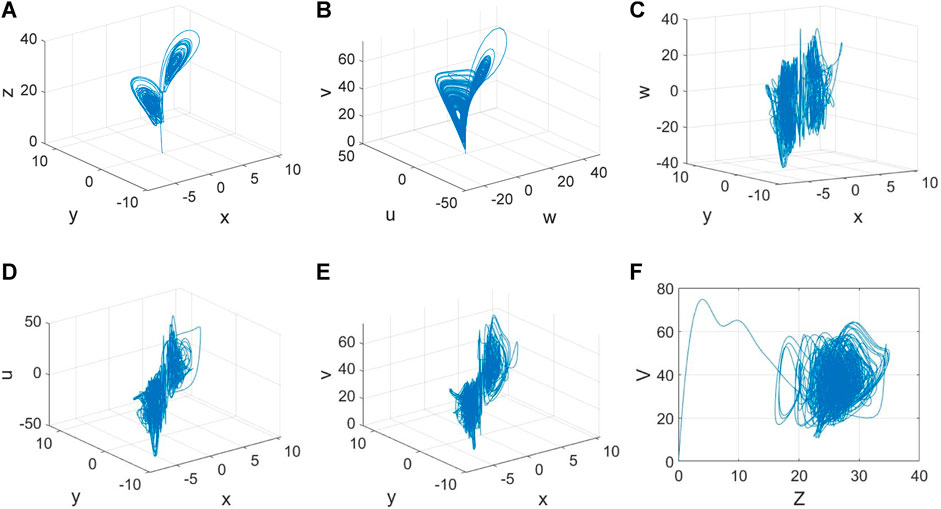
Figure 4. Strange attractors of the MDNS model: (A) phase portrait in x-y-z; (B) phase portrait in x-y-w; (C) phase portrait in x-y-u; (D) phase portrait in x-y-v; (E) phase portrait in w-u-v; and (F) phase portrait in z-v.

From Figure 4A, the chaotic phenomenon has been confirmed [8–12] and observed in molecular distillation, which was induced by its internally fixed motor. Then, the behavior of the key element (i.e., the scraper), which is driven by this motor, must appear chaotic (see Figure 4B). As the movement of the scraper is driven only by the motor, both of them are similar. Then, from Figures 4C–E, both variants x and y stand for the stator currents for the straight-axis and cross-axis of this motor, respectively, which are the source of the forces on the straight and cross-axes of the scraper below. It is evident that when the state of the stator currents presents nonlinearity, the scraper follows nonlinearity; that is, all chaotic phenomena could be observed. From Figure 4F, it exhibits the nonlinear behavior of the scraper, whose angular velocity follows the angular velocity of the motor. Both of them are chaotic and show one attractor.

From Figures 5A,B, double irregular nonlinear regions, that is, two chaotic attractors, could be observed. Then, the obvious nonlinear behaviors of driven scrapers (see Figures 5C,D) could have occurred, but there were two unclear irregular regions. Finally, comparing Figures 5E,F, chaotic motor angular velocity control occurs with chaotic scraper angular velocity.

Figure 5

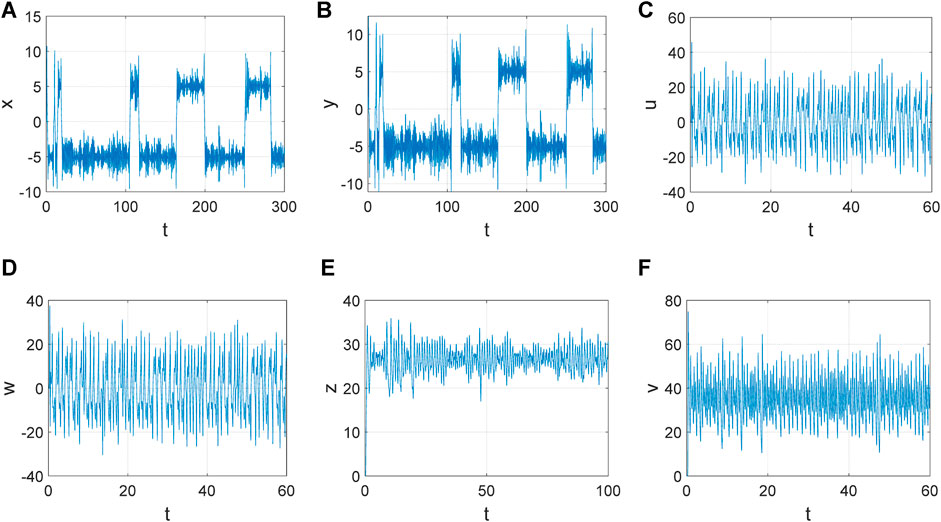
Figure 5. Time-domain waveforms of the MDNS model: (A) x(t); (B) y(t); (C) z(t); (D) w(t); (E) u(t); and (F) u(t).

From both Figure 4 and Figure 5, the models of the proposed MDNS are chaos systems. Exploring and analyzing their chaotic phenomenon could not only reveal the nature of the proposed model in a deeper way but also lay the theoretical foundation for further research on its synchronous control algorithm and accurate prediction.

3 Chaotic behaviors analysis

In this subsection, the chaotic behaviors of the proposed model are studied separately from the aspects of the Lyapunov exponent spectrum, bifurcation diagram, and Poisson map in detail.

3.1 Lyapunov exponent spectrum and Poisson map

The Lyapunov exponent (LEs) is the most important and necessary basis to directly judge a chaotic system and show complexity. Hereby, the maximum LEs could be computed with the above parameters, as follows: LE1 = 18.2261, LE2 = 11.7351, LE3 = -2.6446, LE4 = -3.7106, LE5 = -18.8391, and LE6 = -18.876. In addition, the Hausdorff (Lyapunov) dimension is calculated as DL = 5.2525. As two positive numbers in the Lyapunov exponent and the Hausdorff (Lyapunov) dimension are nonintegers, the proposed model is a hyperchaotic system, which is more complex than a chaotic system. It can be seen that the molecular-distillation process is so complex. It is worth it to study and explore it.

Moreover, taking the parameters (i.e., a, b, and c) for the driven scraper as examples, the LEs spectrum is shown using Wolf’s method in Figure 6.

Figure 6

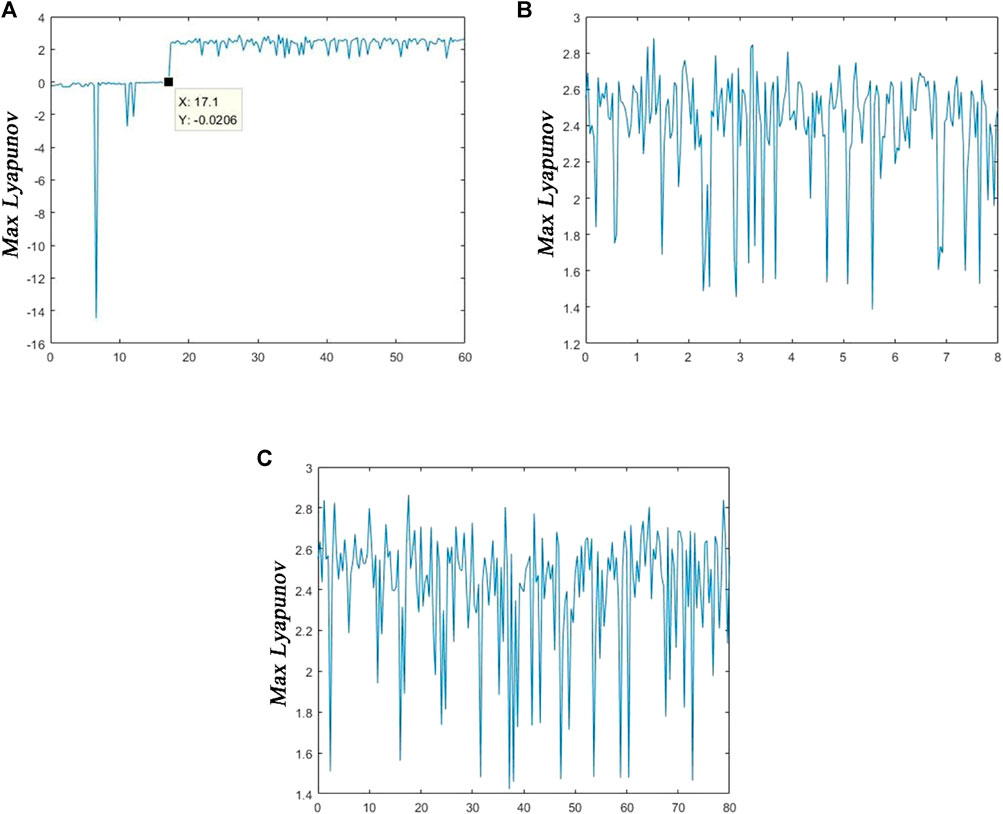
Figure 6. Lyapunov exponents of the proposed MDNS model: (A) LEs with a; (B) LEs with b; and (C) LEs with c.

Observing Figure 6A, when the value of parameter a is greater than 12.3, the system enters the critical chaotic state, that is, LE = 0; when the value of parameter a is greater than 17.1, the system enters the chaotic or hyperchaotic state completely, that is, LE > 0. However, different movements could be obtained in both Figures 6B,C. They immediately enter a state of chaos or hyperchaos. It can be seen that the proposed system is indeed a hyperchaotic system.

Furthermore, the Poincare mappings are depicted in Figure 7, which is another direct and effective method to determine the complex chaos or hyperchaos dynamic behavior of system 1. It can be seen that they consist of a series of isolated points, which means that the system is manifestly chaotic.

Figure 7

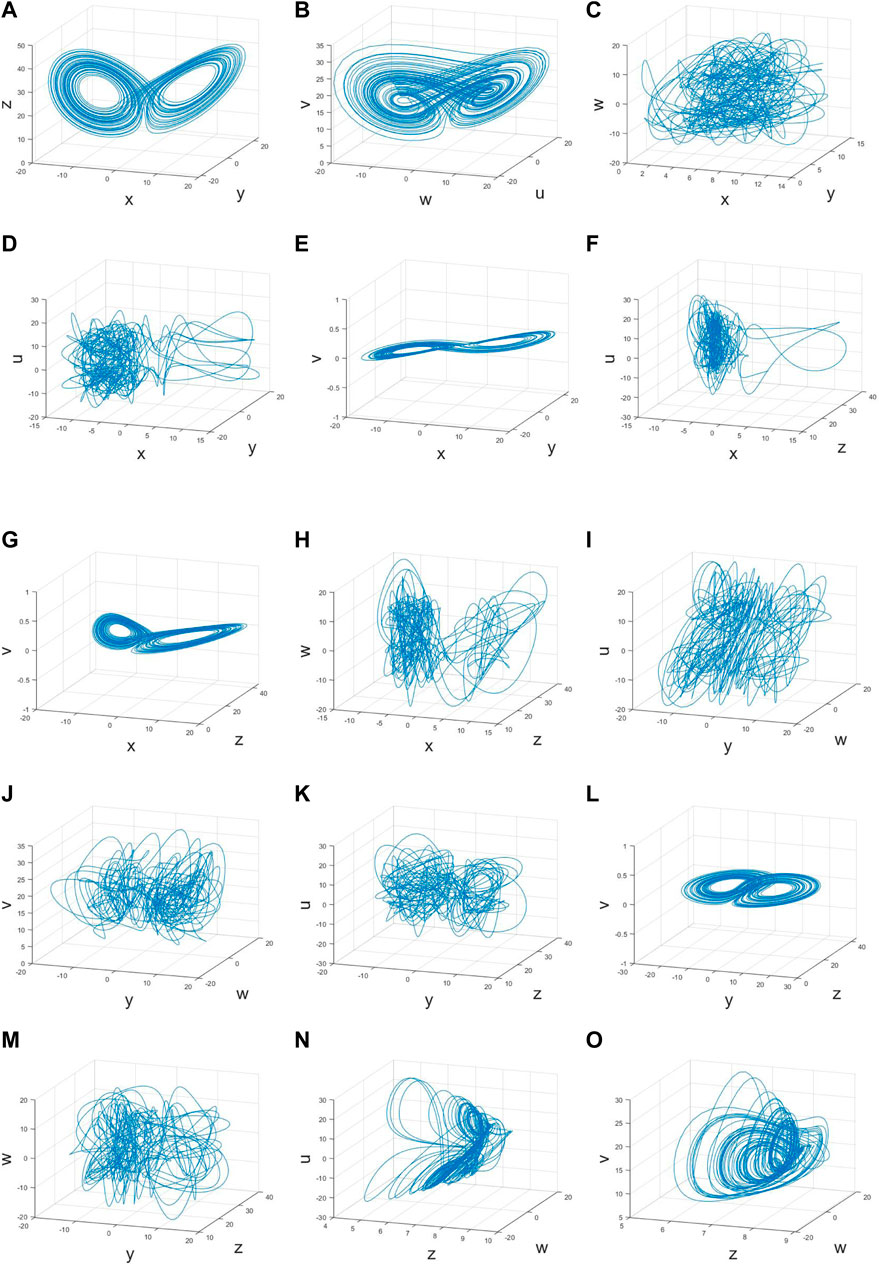
Figure 7. Poincare maps of the proposed MDNS model: (A) X = 0, Y = 0, Z = 0; (B) W = 0, U = 0, V = 0; (C) Z = 0, U = 0, V = 0; (D) Z = 0,W = 0,V = 0; (E) Z = 0,W = 0,U = 0; (F) Y = 0, W = 0, V = 0; (G) Y = 0, W = 0, U = 0; (H) Y = 0, U = 0, V = 0; (I) X = 0, Z = 0, V = 0; (J) X = 0, Z = 0, U = 0; (K) X = 0, W = 0, V = 0; (L) X = 0, W = 0, U = 0; (M) X = 0, U = 0, V = 0; (N) X = 0, Y = 0, V = 0; and (O) X = 0, Y = 0, U = 0.

Notably, the proposed system is a six-dimensional system, which belongs to the field of high-dimensional nonlinearity. In order to describe its complex nonlinear features in detail, the chaotic and attractor behaviors for each variable are shown in the form of three-dimensional diagrams.

Correspondingly, both the LEs and the Poincare mapping diagrams consisting of a series of isolated points are evidence that the proposed system is hyperchaotic.

3.2 Bifurcation diagrams

The bifurcation is one key factor that helps us clearly understand the instability of the proposed system. In this subsection, the bifurcation diagrams with parameters (i.e., a, b, and c) are given and discussed in Figure 8.

Figure 8

Figure 8. Lyapunov exponents of the proposed MDNS model: (A) a ϵ [0,80]; (B) b ϵ [0,8]; and (C) b ϵ [0,60].

It is observed from Figure 8A that the region of parameter a can be divided into three subregions when fixing the parameters α1 = 25, α2 = α3 = 0.12, δ = 10, e = 16, b = 3.68, c = 25, γ = 1, a = 35, and m= 0.04, as follows: 1) for the first part, a ϵ [0, 2.01] illustrates period-1 motion; 2) for the second part, a ϵ (20.1, 67.14] eventually leads to chaos and chaotic oscillation; and 3) for the last part, a ϵ (67.14, 80), represents period-1 motion. Then, Figure 8B presents the chaos region of parameter b when fixing the parameters α1 = 25, α2 = α3 = 0.12, δ = 10, e = 16, a = 16, c = 25, γ = 1, a = 35, and m= 0.04. Finally, Figure 8C presents the chaos region of parameter c when fixing the parameters α1 = 25, α2 = α3 = 0.12, δ = 10, e = 16, a = 16, b = 3.68, γ = 1, a = 35, and m= 0.04. Because there are several key parameters (i.e., a, b, and c for the driven scraper) to determine the proposed system, it could appear to have chaotic and hyperchaotic behaviors. Therefore, the analysis of its bifurcation diagrams could not rely on the processes of period-1, period-2, and period-3, and then on chaotic phenomena as some simple ones did. A more detailed study and description of the bifurcation mechanism of the proposed system would be the next step.

4 Coexisting attractors

It is well known that initial value sensitivity is one of the most significant features of a chaotic system and could represent its complexity. It refers to the chaotic attractors because they give different initial values to the system, which could occur in completely different states of motion. When different values are given to the same system, the different starting points could lead to coexisting attractors and more complex behaviors. This phenomenon could only be discovered in a few chaotic systems. Furthermore, coexisting attractors help us to fully grasp the nonlinear characteristics of the system and design optimal controllers when studying chaotic control and anticontrol algorithms. Especially, in the molecular distillation process, fully exploiting the features of the BLDCM could reduce error accumulation, clearly define system behaviors, and improve the efficiency.

In this subsection, when different initial values are assigned to the proposed MDNS model, the system could observe the coexisting attractors phenomenon, setting the initial condition (x, y, z, w, u, v) = (0.01, 0.01, 0.01, 0.01, 0.01, 0.01) (blue solid curve) and (−0.01, −0.01, −0.01, −0.01, −0.01, −0.01) (red solid curve), respectively. The coexisting attractors are given in Figure 9.

Figure 9

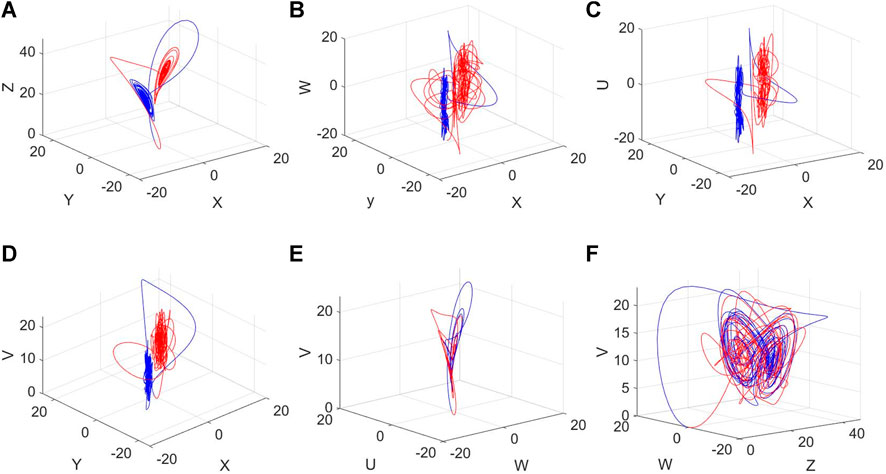
Figure 9. Strange coexisting attractors of the MDNS model: (A) phase portrait in x-y-z; (B) phase portrait in x-y-w; (C) phase portrait in x-y-u; (D) phase portrait in x-y-v; (E) phase portrait in w-u-v; and (F) phase portrait in z-w-v.

For the molecular distillation process, the generation and existence of coexisting attractors could help us to analyze the motion of the configured BLDCM and the driven scraper from another viewpoint, which affects the efficiency of the whole process. Comparing Figures 9A,E, quite different initial motion directions and trajectories exist, but similar phenomena could be observed over a period of time. In other words, the efficiency and results of the molecular distillation process are determined by the motor that drives the movement of the scraper, and when the motor has a stable working condition, the results of molecular distillation are also stable.

5 Conclusion

In mathematics and industry, analyzing and exploring the process of molecular distillation could improve the productivity. It can also provide important theoretical support for improving related equipment and proposing stable control algorithms. In this paper, the study on molecular distillation processes and the BLDCM has been investigated based on the Navier–Stokes theoretical framework, and a novel MDNS equation has been built. In addition, the generation of complex nonlinearity phenomena has been first discovered and displayed in detail, including phase portraits, time-domain waveforms, Lyapunov exponent spectra, Poincare maps, and bifurcation diagrams. Based on the LEs, the hyperchaos could be determined and observed. Moreover, the co-attractors have become another perspective to manifest the complexity and hyperchaos. It would play a potential role in chaotic and hyperchaotic dynamic analysis and engineering applications in molecular distillation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

WQ: conceptualization, methodology, software, validation, writing–original draft, and writing–review and editing. HL: investigation, validation, and writing–review and editing. ZJ: software, validation, and writing–review and editing. ML: validation and writing–review and editing. SC: validation and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Department of Science and Technology of Jilin Province (grant number: 20210401098YY) and the Jilin Province Development and Reform Commission (grant number: 2023C042-3).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kida S, Yamada M, Ohkitani K. Route to chaos in a Navier-Stokes flow. North-Holland Maths Stud (1989) 31–47. doi:10.1016/s0304-0208(08)70505-x

CrossRef Full Text | Google Scholar

2. Bistafa SR. On the development of the Navier-Stokes equation by Navier. Revista Brasileira de Ensino de Física (2017) 40:40 :e2603. doi:10.1590/1806-9126-RBEF-2017-0239

CrossRef Full Text | Google Scholar

3. Alfonsi G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl Mech Rev (2009) 62(4):040802. doi:10.1115/1.3124648

CrossRef Full Text | Google Scholar

4. Jin X, Cai S, Li H, Karniadakis GE. NSFNETS (Navier-Stokes flow nets): physics-informed Neural Networks for the incompressible Navier-Stokes equations. J Comput Phys (2021) 426:109951. doi:10.1016/j.jcp.2020.109951

CrossRef Full Text | Google Scholar

5. Ershkov SV, Prosviryakov EY, Burmasheva NV, Christianto V. Towards understanding the algorithms for solving the Navier–Stokes equations. Fluid Dyn Res (2021) 53:044501. doi:10.1088/1873-7005/ac10f0

CrossRef Full Text | Google Scholar

6. Ge ZM, Cheng JW, Chen YS. Chaos anticontrol and synchronization of three time scales brushless DC Motor System. Chaos. Solitons & Fractals (2004) 22:1165–82. doi:10.1016/j.chaos.2004.03.036

CrossRef Full Text | Google Scholar

7. Qi G Energy cycle of brushless DC motor chaotic system. Appl Math Model (2017) 51:686–97. doi:10.1016/j.apm.2017.07.025

CrossRef Full Text | Google Scholar

8. Medeiros RL, Filho AC, Ramos JG, Nascimento TP, Brito AV. A novel approach for speed and failure detection in brushless DC motors based on Chaos. IEEE Trans Ind Electron (2019) 66:8751–9. doi:10.1109/tie.2018.2886766

CrossRef Full Text | Google Scholar

9. Luo S, Li S, Tajaddodianfar F, Hu J. Anti-oscillation and chaos control of the fractional-order brushless DC motor system via adaptive echo state networks. J Franklin Inst (2018) 355:6435–53. doi:10.1016/j.jfranklin.2018.07.004

CrossRef Full Text | Google Scholar

10. Li ZB, Lu W, Gao LF, Zhang JS. Nonlinear state feedback control of chaos system of brushless DC motor. Proced Comput Sci (2021) 183:636–40. doi:10.1016/j.procs.2021.02.108

CrossRef Full Text | Google Scholar

11. Abro KA, Atangana A, Gómez-Aguilar JF. Chaos control and characterization of brushless DC motor via integral and differential fractal-fractional techniques. Int J Model Simulation (2022) 43:416–25. doi:10.1080/02286203.2022.2086743

CrossRef Full Text | Google Scholar

12. Faradja P, Qi G. Analysis of multistability, hidden chaos and transient chaos in brushless DC motor. Solitons & Fractals (2020) 132:109606. doi:10.1016/j.chaos.2020.109606

CrossRef Full Text | Google Scholar

13. Wang S, Gu Y, Liu Q, Yao Y, Guo Z, Luo Z, et al. Separation of bio-oil by molecular distillation. Fuel Process Technol (2009) 90:738–45. doi:10.1016/j.fuproc.2009.02.005

CrossRef Full Text | Google Scholar

14. Ketenoglu O, Tekin A. Applications of molecular distillation technique in food products. Ital J Food Sci (2015) 27:277–81. doi:10.14674/1120-1770/ijfs.v269

CrossRef Full Text | Google Scholar

15. Mahrous EA, Farag MA. Trends and applications of molecular distillation in pharmaceutical and Food Industries. Separat Purif Rev (2021) 51:300–17. doi:10.1080/15422119.2021.1924205

CrossRef Full Text | Google Scholar

16. Hikihara T, Holmes P, Kambe T, Rega G. Introduction to the focus issue: fifty Years of chaos: applied and theoretical. Chaos: Interdiscip J Nonlinear Sci (2012) 22:047501. doi:10.1063/1.4769035

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Younesian D, Norouzi H. Chaos prediction in nonlinear viscoelastic plates subjected to subsonic flow and external load using extended Melnikov’s method. Nonlinear Dyn (2015) 84:1163–79. doi:10.1007/s11071-015-2561-8

CrossRef Full Text | Google Scholar

18. Alonso LM. Nonlinear resonances and multi-stability in simple neural circuits. Chaos: Interdiscip J Nonlinear Sci (2017) 27:013118. doi:10.1063/1.4974028

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Liu Y, Guan J, Ma C, Guo S. Generation of 2N + 1-scroll existence in new three-dimensional chaos systems. Chaos: Interdiscip J Nonlinear Sci (2016) 26:084307. doi:10.1063/1.4958919

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liu Y, Guo S. Generation and dynamics analysis of N-scrolls existence in new translation-type chaotic systems. Chaos: Interdiscip J Nonlinear Sci (2016) 26:113114. doi:10.1063/1.4967181

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Sharma V, Sharma BB, Nath R. Nonlinear unknown input sliding mode observer based chaotic system synchronization and message recovery scheme with uncertainty. Chaos. Solitons & Fractals (2017) 96:51–8. doi:10.1016/j.chaos.2017.01.006

CrossRef Full Text | Google Scholar

22. Zhou L, Wang C, Zhang X, Yao W. Various attractors, coexisting attractors and antimonotonicity in a simple fourth-order memristive twin-T oscillator. Int J Bifurcation Chaos (2018) 28:1850050. doi:10.1142/s0218127418500505

CrossRef Full Text | Google Scholar

23. Liu Y, Iu HH. Antimonotonicity, Chaos and multidirectional scroll attractor in autonomous odes chaotic system. IEEE Access (2020) 8:77171–8. doi:10.1109/access.2020.2988915

CrossRef Full Text | Google Scholar

24. Liu Y, Iu HH, Li H, Zhang X. Bounded orbits and multiple scroll coexisting attractors in a dual system of Chua System. IEEE Access (2020) 8:147907–18. doi:10.1109/access.2020.3015865

CrossRef Full Text | Google Scholar

25. Lai Q, Kamdem Kuate PD, Liu F, Iu HH. An extremely simple chaotic system with infinitely many coexisting attractors. IEEE Trans Circuits Syst Express Briefs (2020) 67:1129–33. doi:10.1109/tcsii.2019.2927371

CrossRef Full Text | Google Scholar

26. Kong X, Yu F, Yao W, Cai S, Zhang J, Lin H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: image encryption and FPGA implementation. Neural Networks (2024) 171:85–103. doi:10.1016/j.neunet.2023.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Fei Y, Kong X, Yao W, Zhang J, Cai S, Lin H, et al. Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor. Chaos, Solitons & Fractals (2024) 179:114440. doi:10.1016/j.chaos.2023.114440

CrossRef Full Text | Google Scholar

28. Kong X, Fei Y, Yao W, Xu C, Zhang J, Cai S, et al. A class of 2n+1 dimensional simplest Hamiltonian conservative chaotic systems and fast image encryption schemes. Appl Math Model (2024) 125:351–74. doi:10.1016/j.apm.2023.10.004

CrossRef Full Text | Google Scholar

29. Pasini A, Pelino V. A unified view of Kolmogorov and Lorenz Systems. Phys Lett A (2000) 275:435–46. doi:10.1016/s0375-9601(00)00620-4

CrossRef Full Text | Google Scholar

30. Wang H. A five-mode system of the Navier-Stokes equations on a torus. J Appl Maths Phys (2016) 04(04):1245–53. doi:10.4236/jamp.2016.47130

CrossRef Full Text | Google Scholar

31. Zhang F, Liao X, Zhang G. Qualitative behavior of the Lorenz-like chaotic system describing the flow between two concentric rotating spheres. Complexity (2016) 21:67–72. doi:10.1002/cplx.21784

CrossRef Full Text | Google Scholar