Thermal conductivity of nonunitary triplet superconductors: application to UTe2

Considerable evidence shows that the heavy fermion material UTe₂ is a spin-triplet superconductor, possibly manifesting time-reversal symmetry breaking, as measured by Kerr effect below the critical temperature, in some samples. Such signals can arise due to a chiral orbital state or possible nonunitary pairing. Although experiments at low temperatures appear to be consistent with point nodes in the spectral gap, the detailed form of the order parameter and even the nodal positions are not yet determined. Thermal conductivity measurements can extend to quite low temperatures, and varying the heat current direction should be able to provide information on the order parameter structure. Here, we derive a general expression for the thermal conductivity of a spin-triplet superconductor and use it to compare the low-temperature behavior of various states proposed for UTe₂.

1 Introduction

The uranium-based superconductor UTe₂ has stimulated a large number of experimental and theoretical studies, initially because of its apparent role as a paramagnetic end point of a family of ferromagnetic superconductors [1–3] and later as evidence for spin-triplet superconductivity accumulated. The nuclear magnetic resonance (NMR) Knight shift measurements on the earlier samples did not show any change in the superconducting state [4], although recent Knight shift measurements on high-quality samples show a small reduction along all three axes [5]. Both measurements support spin–triplet pairing; however, the spin structure of Cooper pairs remains unclear. Another piece of evidence that indicates spin–triplet pairing is the size of the upper critical field H_c2 that exceeds the Pauli limit for all field directions [1, 6]. Measured power–law temperature dependence in NMR relaxation, specific heat [1], and thermal conductivity [7, 8] was found to be consistent with point nodes, as expected for a triplet superconductor in a system with strong spin–orbit coupling (SOC) [9–11]. Finally, a reentrant superconducting phase was shown to be stabilized at high magnetic fields [12].

A second set of measurements relevant to the nature of the superconducting state purports to exhibit evidence for time-reversal symmetry breaking (TRSB) below T_c, suggesting that UTe₂ may support the long-sought chiral p-wave state that may serve as a quantum computing platform [13–17]. Initially, the polar Kerr effect [18] experiments suggested that TRSB occurred in the superconductor, implying the existence of a multicomponent spin-triplet order parameter. According to group theoretical classifications of the one-dimensional (1D) irreducible representations (irreps) allowed in orthorhombic symmetry, order parameters corresponding to single irreps must be unitary triplet states, meaning that any TRSB must arise from a nonunitary multicomponent state. Such combinations of 1D representations were discussed intensively, particularly because a double specific heat transition was sometimes observed in early samples, recalling the specific heat experiments in multicomponent UPt₃.

More recently, measurements of a new generation of high-quality UTe₂ crystals grown in molten salt flux have challenged this characterization of UTe₂ as a chiral triplet state breaking time-reversal symmetry (TRS). The Kerr effect was observed in a sample showing two specific heat jumps, but as the quality of the samples improved, only a single transition was observed [19, 20]. A recent investigation of the Kerr effect on both the old- and new-generation UTe₂ single crystals displaying a single specific heat jump found no evidence for TRSB superconductivity [21]. Similarly, muon spin relaxation (μSR) measurements of the molten salt flux-grown samples found no evidence of TRSB [22]. Finally, sound velocity changes across T_c [23] and recent NMR Knight shift measurements on similar samples [5] both point to a single-component, odd parity-order parameter, i.e., inconsistent with the previous hypothesis of nonunitary pairing.

The thermal conductivity κ(T) is an important probe of the gap structure of unconventional superconductors, reflecting the ability of the superconductor to carry heat current in various directions. The theory of thermal conductivity in unitary triplet superconductors is quite similar to the well-known theory developed for singlet superconductors [24, 25]. Most of the popular model triplet states in the literature, including the ³He-A phase, belong to this class. In that case, the triplet quasiparticle energies are $E_{\mathbf{k}}=\sqrt{{\xi }_{\mathbf{k}}^2+|\mathbf{d}(\mathbf{k}){|}^2}$, where d(k) is the triplet-order parameter vector defining its structure in spin space via ${\mathrm{\Delta }}_{\sigma {\sigma }^{\prime }}={\left[\mathbf{d}(\mathbf{k})\cdot \mathit{\sigma }(i{\sigma }_y)\right]}_{\sigma {\sigma }^{\prime }}$. Here, σ is the Pauli vector in the spin space spanned by the Pauli matrices σ_x, σ_y, and σ_z. Since the thermal current response depends only on the quasiparticle energies, the same expressions can be used for triplet superconductors [26–28] with |Δ(k)|² replaced by |d(k)|². As shown below, however, in the nonunitary state, additional terms involving the spin moment q ≡ id(k) ×d*(k) carried by quasiparticles of momentum k occur in both the quasiparticle energies and the weights of scattering processes. Furthermore, in nonunitary triplet superconductors, the zeros of |d(k)|² differ from those of E_k, even when k is on the Fermi surface (“spectral nodes”). This distinction may be important; it was suggested by Ishihara et al. [29] that in UTe₂, complex linear combinations of 1D irreducible representations could support spectral nodes pointing in generic directions in the orthorhombic Brillouin zone and thereby explain early experiments exhibiting TRSB and relative isotropy of the low-temperature penetration depth. On the other hand, order parameters corresponding to a single 1D irrep must be real, with nodes along high-symmetry axes.

In this paper, we derive a general form of the thermal conductivity of a triplet superconductor in the presence of nonmagnetic pointlike impurities and evaluate it for various types of triplet states that have been proposed for UTe₂. The aim is to see whether there are qualitative distinctions between the thermal conductivity temperature and heat current direction dependence of unitary and nonunitary states and whether or not predictions of low-temperature behavior can be used, by comparison with experiments, to identify the ground state of UTe₂.

2 Model and formalism

2.1 Superconducting state

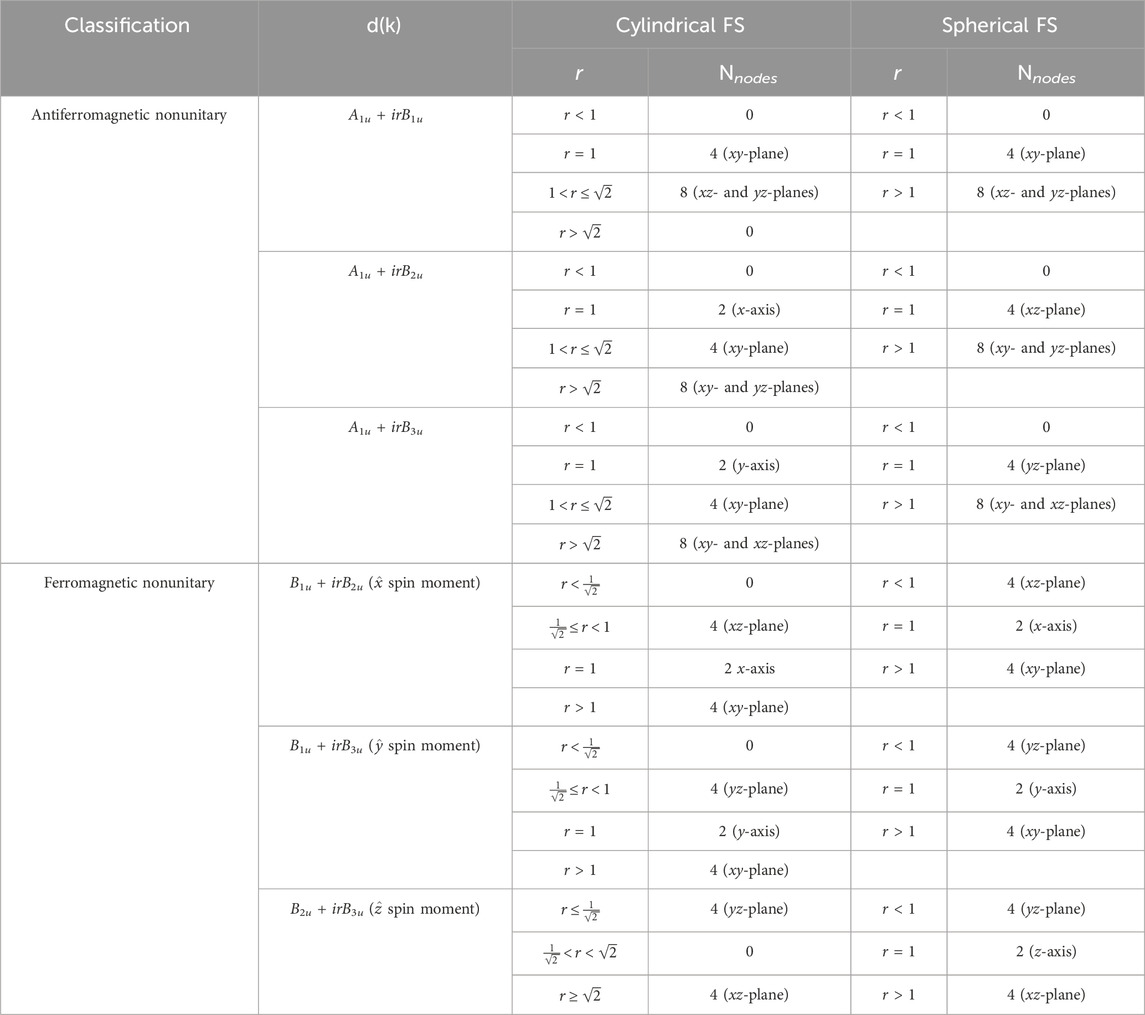
In a general triplet superconductor, the spin structure of the superconducting order parameter is constrained by the underlying crystal symmetries. The structure of the UTe₂ crystals corresponds to the orthorhombic point group D_2h, and the symmetry of the odd-parity pairing states can be deduced according to the irreducible representations of the D_2h point group [30–32]. Table 1 shows the odd-parity triplet superconducting states considered in this article. Here, we do not consider the even-parity states for the D_2h point group, and we further assume strong SOC due to heavy atoms like U and Te. Due to strong SOC, orbital and spin degrees of freedom do not transform independently; instead, each space group rotation involves a rotation in spin and spatial spaces of the order parameter. In the weak SOC limit, the odd-parity states for the D_2h point group come with line nodes that are not consistent with experimental measurements.

Table 1

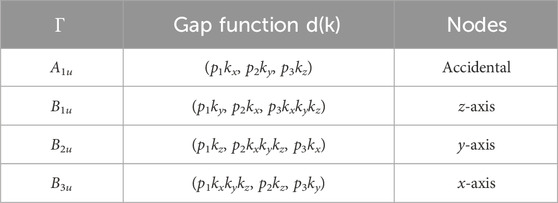
Table 1. List of possible spin-triplet superconducting states for an orthorhombic crystal with strong spin–orbit coupling. Here, p_i=1,..,3 are constants, and ∀p_i ∈ R.

The d-vector is real for the superconducting states listed in Table 1; hence, these states preserve TRS. These states are unitary triplet states, i.e., ${\widehat{\mathrm{\Delta }}}^{†}\widehat{\mathrm{\Delta }}\propto \widehat{\mathbb{1}}$. We denote a 2 × 2 matrix in the spin space with and a 4 × 4 matrix in the Nambu-spin space with . A TRSB state is not possible with a single-component order parameter, noting that the D_2h group has only one-dimensional irreducible representations. We construct the TRSB superconducting state with a combination of two irreducible representations, and all such possible combinations are shown in Table 2. In principle, a combination of two different irreducible representations involves six real constants; however, we introduce a single-parameter model for the TRSB states. The effective d-vector is $({\mathbf{d}}_1+ir{\mathbf{d}}_2)/\sqrt{1+r^2}$, where r is the mixing parameter that determines the relative strength of the individual order parameter. The individual d-vectors are listed in Table 1 with all the coefficients p_i=1,2..3 set to unity.

Table 2

Table 2. Six possible mixed IR states.

In the Nambu-spin basis, the mean field Hamiltonian reads

$\check{\mathbf{H}}=\left(\begin{array}{cc}\hfill {\xi }_{\mathbf{k}}{\sigma }_0\hfill & \hfill i{\mathrm{\Delta }}_0\left(\mathbf{d}\cdot \mathit{\sigma }\right){\sigma }_y\hfill \\ \hfill -i{\mathrm{\Delta }}_0{\sigma }_y\left({\mathbf{d}}^{*}\cdot \mathit{\sigma }\right)\hfill & \hfill -{\xi }_{\mathbf{k}}{\sigma }_0\hfill \end{array}\right),(1)$

where ξ_k is the electronic dispersion, Δ₀ is the superconducting gap energy scale, and σ₀ is the identity matrix in the spin space. We adopt a model where the electronic dispersion reads

${\xi }_{\mathbf{k}}=\frac{{\hslash }^2{k}_x^2}{2m_a}+\frac{{\hslash }^2{k}_y^2}{2m_b}-\mu -2t_{\perp }\cos k_z,(2)$

where m_a/b is the effective masses along $\widehat{x}/\widehat{y}$ directions, t_⊥ is the hopping energy that controls the $\widehat{z}$ velocity, and μ is the chemical potential. We further assume that t_⊥≪ μ. An alternate dispersion with a closed Fermi surface is considered in the Supplementary Material. The bare Green’s function is

${\check{G}}_0={\left(\check{\mathbb{1}}\omega -\check{\mathbf{H}}\right)}^{-1}=\left(\begin{array}{cc}\hfill {\widehat{G}}_{11}\hfill & \hfill {\widehat{G}}_{12}\hfill \\ \hfill {\widehat{G}}_{21}\hfill & \hfill {\widehat{G}}_{22}\hfill \end{array}\right).(3)$

Here, ω is the quasiparticle energy. The Matsubara Green’s function can be obtained by ω → iω_n. The 2 × 2 matrices in the spin space are

${\widehat{G}}_{11}=\frac{\left(\omega +\xi \right)}{D}\left[\left({\omega }^2-{\xi }^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right){\sigma }_0+{\mathrm{\Delta }}_0^2\mathbf{q}\cdot \mathit{\sigma }\right],(4)$

${\widehat{G}}_{12}=\left[\left({\omega }^2-{\xi }^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right){\sigma }_0+{\mathrm{\Delta }}_0^2\mathbf{q}\cdot \mathit{\sigma }\right]\frac{i{\mathrm{\Delta }}_0\left(\mathbf{d}\cdot \mathit{\sigma }\right){\sigma }_y}{D},(5)$

${\widehat{G}}_{21}=-\left[\left({\omega }^2-{\xi }^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right){\sigma }_0+{\mathrm{\Delta }}_0^2\mathbf{q}\cdot {\mathit{\sigma }}^T\right]\frac{{\mathrm{\Delta }}_{0}i{\sigma }_y\left({\mathbf{d}}^{*}\cdot \mathit{\sigma }\right)}{D},(6)$

${\widehat{G}}_{22}=\frac{\left(\omega -\xi \right)}{D}\left[\left({\omega }^2-{\xi }^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right){\sigma }_0+{\mathrm{\Delta }}_0^2\mathbf{q}\cdot {\mathit{\sigma }}^T\right].(7)$

Here, q = i (d ×d*), and the denominator D is

$D={\left({\omega }^2-{\xi }^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right)}^2-{\mathrm{\Delta }}_0^4|\mathbf{q}{|}^2=\left({\xi }^2-{\omega }^2+{\mathrm{\Delta }}_{+}^2\right)\left({\xi }^2-{\omega }^2+{\mathrm{\Delta }}_{-}^2\right).(8)$

Here, we introduce ${\mathrm{\Delta }}_{\pm }^2={\mathrm{\Delta }}_0^2(|\mathbf{d}{|}^2\pm |\mathbf{q}|)$. For the unitary case, q = 0; therefore, there is only a single energy scale. In contrast, for the TRSB nonunitary states, q ≠ 0, which leads to non-degenerate excitation energies. For single-component order parameters, q vanishes. However, for a mixture of multiple irreducible representations, q remains finite, and it can be interpreted as the spin moment of the Cooper pairs. The average of q over the Fermi surface may or may not vanish. The nonunitary states can therefore be further divided into anti-ferromagnetic (AF) and ferromagnetic (FM) states, where the average of q vanishes over the Fermi surface for the former and remains finite for the latter [9]. The six possible nonunitary states are shown in Table 2, with the possibility of nodes on a spherical or a cylindrical Fermi surface open along the $\widehat{z}$ axis. For a cylindrical Fermi surface, we adopt cylindrical coordinates with k_z dependence of the gap functions replaced with sin (k_zd/2), where d is the z-axis. The factor of 1/2 is added to ensure only a single pair of point nodes in the first Brillouin zone in the unitary limit. However, this does not have any qualitative effect on our results.

2.2 Impurity scattering and thermal transport

In order to calculate the thermal conductivity, we need to include the effect of impurity scattering that dominates all other relaxation mechanisms at low temperatures. We consider elastic impurity scattering due to pointlike defects and include its effect through a disorder-averaged self-energy. The impurity self-energy is calculated within the self-consistent T-matrix approximation. The momentum-integrated Green’s function $\widehat{g}$ has both vector and scalar components for the normal Green’s functions:

${\widehat{g}}_{11}=\pi N_0\left(g_0+\mathbf{g}\cdot \mathit{\sigma }\right),(9)$

${\widehat{g}}_{22}=\pi N_0\left(g_0+\mathbf{g}\cdot {\mathit{\sigma }}^T\right),(10)$

and the anomalous Green’s functions ${\widehat{g}}_{12}$ and ${\widehat{g}}_{21}$ vanish because the odd-parity order parameter averages to 0. In Eqs 9, 10, g is directly related to the Fermi surface average of the spin moment q and remains finite for the chiral nonunitary states, only. Using these integrated Green’s functions, we can write the T-matrix self-energy for the non-magnetic impurities as

$\check{\mathrm{\Sigma }}={\check{\tau }}_3\cdot \left(\begin{array}{cc}\hfill {\mathrm{\Sigma }}_3+{\mathbf{\Sigma }}_{\mathbf{3}}\cdot \mathit{\sigma }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Sigma }}_3+{\mathbf{\Sigma }}_{\mathbf{3}}\cdot {\mathit{\sigma }}^T\hfill \end{array}\right)+{\check{\tau }}_0\cdot \left(\begin{array}{cc}\hfill {\mathrm{\Sigma }}_0+\mathbf{\Sigma }\cdot \mathit{\sigma }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Sigma }}_0+\mathbf{\Sigma }\cdot {\mathit{\sigma }}^T\hfill \end{array}\right),(11)$

${\mathrm{\Sigma }}_3={\mathrm{\Gamma }}_u\frac{\cot {\delta }_s\left[{\cot }^2{\delta }_s-\left(g_0^2+\mathbf{g}\cdot \mathbf{g}\right)\right]}{D_{\mathit{imp}}},(12)$

${\mathbf{\Sigma }}_{\mathbf{3}}={\mathrm{\Gamma }}_u\frac{2\cot {\delta }_s{g}_0\mathbf{g}}{D_{\mathit{imp}}},(13)$

${\mathrm{\Sigma }}_0={\mathrm{\Gamma }}_u\frac{g_0\left[{\cot }^2{\delta }_s-\left(g_0^2-\mathbf{g}\cdot \mathbf{g}\right)\right]}{D_{\mathit{imp}}},(14)$

$\mathbf{\Sigma }={\mathrm{\Gamma }}_u\frac{\mathbf{g}\left[{\cot }^2{\delta }_s+\left(g_0^2-\mathbf{g}\cdot \mathbf{g}\right)\right]}{D_{\mathit{imp}}},(15)$

$D_{\mathit{imp}}={\cot }^4{\delta }_s-2{\cot }^2{\delta }_s\left(g_0^2+\mathbf{g}\cdot \mathbf{g}\right)+{\left(g_0^2-\mathbf{g}\cdot \mathbf{g}\right)}^2,(16)$

where δ_s ≡ tan⁻¹ (πN₀V_imp) is the s-wave scattering phase shift; Γ_u = n_imp/(πN₀); and n_imp and V_imp are the impurity concentration and impurity potential, respectively. Here, ${\check{\tau }}_3$ is the Pauli matrix in the Nambu space. The τ₃ component of the self-energy that renormalizes the electronic dispersion is ignored. It can be absorbed in the chemical potential. The impurity-dressed Green’s function reads

$\begin{array}{ll}\hfill {\check{\mathbf{G}}}^{-1}& ={\check{G}}_0^{-1}-\check{\mathrm{\Sigma }}=\left(\begin{array}{cc}\hfill \tilde{\omega }-\xi {\sigma }_0-\mathrm{\Sigma }\cdot \mathit{\sigma }\hfill & \hfill -\widehat{\mathrm{\Delta }}\hfill \\ \hfill -{\widehat{\mathrm{\Delta }}}^{†}\hfill & \hfill \tilde{\omega }+\xi {\sigma }_0-\mathrm{\Sigma }\cdot {\mathit{\sigma }}^T\hfill \end{array}\right),\hfill \\ \hfill \check{\mathbf{G}}& =\left(\begin{array}{cc}\hfill {\widehat{\mathbf{G}}}_{11}\hfill & \hfill {\widehat{\mathbf{G}}}_{12}\hfill \\ \hfill {\widehat{\mathbf{G}}}_{21}\hfill & \hfill {\widehat{\mathbf{G}}}_{22}\hfill \end{array}\right).\hfill \end{array}(17)$

Here, impurity-renormalized $\tilde{\omega }=\omega -{\mathrm{\Sigma }}_0$, which is obtained self-consistently. Unlike unitary superconductors, the impurity-dressed nonunitary Green’s function acquires a different structure from that of the bare Green’s function, in particular the structure in spin space for the normal component. The individual components of the Green’s function $\check{\mathbf{G}}$ are

${\widehat{\mathbf{G}}}_{11}=\frac{L_0+{\mathbf{L}}_1\cdot \mathit{\sigma }}{\tilde{\mathbf{D}}},(18)$

${\widehat{\mathbf{G}}}_{22}=\frac{L_0\left(\xi \to -\xi \right)+{\mathbf{L}}_1\left(\xi \to -\xi \right)\cdot {\mathit{\sigma }}^T}{\tilde{\mathbf{D}}},(19)$

$\begin{array}{l}\hfill {\widehat{\mathbf{G}}}_{12}=[2\xi \left(\mathbf{\Sigma }\cdot \mathbf{d}\right)+\left({\tilde{\omega }}^2-{\xi }^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2+\mathbf{\Sigma }\cdot \mathbf{\Sigma }\right)\mathbf{d}\cdot \mathit{\sigma }+i{\mathrm{\Delta }}_0^2\left(\mathbf{q}\times \mathbf{d}\right)\cdot \mathit{\sigma }-2\left(\mathbf{\Sigma }\cdot \mathbf{d}\right)\mathbf{\Sigma }\cdot \mathit{\sigma }\\ +2i\tilde{\omega }\left(\mathbf{\Sigma }\times \mathbf{d}\right)\cdot \mathit{\sigma }]\frac{i{\sigma }_y{\mathrm{\Delta }}_0}{\tilde{\mathbf{D}}},\hfill \end{array}(20)$

$\begin{array}{l}\hfill {\widehat{\mathbf{G}}}_{21}=[-2\xi \mathbf{\Sigma }\cdot {\mathbf{d}}^{*}+\left({\tilde{\omega }}^2-{\xi }^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2+\mathbf{\Sigma }\cdot \mathbf{\Sigma }\right){\mathbf{d}}^{*}\cdot {\mathit{\sigma }}^T-i{\mathrm{\Delta }}_0^2\left(\mathbf{q}\times {\mathbf{d}}^{*}\right)\cdot {\mathit{\sigma }}^T-2\mathbf{\Sigma }\cdot {\mathbf{d}}^{*}\mathbf{\Sigma }\cdot {\mathit{\sigma }}^T\\ -2i\tilde{\omega }\left(\mathbf{\Sigma }\times {\mathbf{d}}^{*}\right)\cdot {\mathit{\sigma }}^T]\frac{i{\sigma }_y{\mathrm{\Delta }}_0}{\tilde{\mathbf{D}}},\hfill \end{array}(21)$

where

$L_0=X_0{a}_0-{\mathrm{\Delta }}_0^2{b}_0|\mathbf{d}{|}^2-{\mathrm{\Delta }}_0^2\mathbf{q}\cdot \mathbf{\Sigma },(22)$

${\mathbf{L}}_1=\left(X_0+{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right)\mathbf{\Sigma }+{\mathrm{\Delta }}_0^2{b}_0\mathbf{q}-{\mathrm{\Delta }}_0^2\mathbf{\Sigma }\cdot \mathbf{d}{\mathbf{d}}^{*}-{\mathrm{\Delta }}_0^2\mathbf{\Sigma }\cdot {\mathbf{d}}^{*}\mathbf{d}.(23)$

Here, $a_0/b_0=\tilde{\omega }\mp \xi$, $X_0=b_0^2-\mathbf{\Sigma }\cdot \mathbf{\Sigma }$, and the denominator $\tilde{\mathbf{D}}=({\xi }^2+{\tilde{Q}}_{+}^2)({\xi }^2+{\tilde{Q}}_{-}^2)$, where ${\tilde{Q}}_{\pm }$ is

${\tilde{Q}}_{\pm }^2={\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2-{\tilde{\omega }}^2-\mathbf{\Sigma }\cdot \mathbf{\Sigma }\pm \sqrt{{\mathrm{\Delta }}_0^4\mathbf{q}\cdot \mathbf{q}+4{\tilde{\omega }}^2\mathbf{\Sigma }\cdot \mathbf{\Sigma }+4{\mathrm{\Delta }}_0^2\tilde{\omega }\mathbf{q}\cdot \mathbf{\Sigma }-4{\mathrm{\Delta }}_0^2\left(\mathbf{\Sigma }\cdot \mathbf{d}\right)\left(\mathbf{\Sigma }\cdot {\mathbf{d}}^{*}\right)}.(24)$

For the unitary states, the nodes are symmetry-imposed, and for the nonunitary states, nodes may shift away from the high-symmetry directions, and their positions remain protected against disorder as long as the Σ component of the impurity self-energy vanishes. Σ can be interpreted as impurity-induced magnetization. For the chiral states, this term remains finite and gives rise to non-degenerate quasiparticle spin density and, in principle, can change the nodal positions. Here, the nodes do not refer to the zeros of the gap or the order parameter; instead, they are the zeros in the quasiparticle spectrum on the Fermi surface. In the unitary states, the gap nodes and the spectral nodes are same, unlike the nonunitary states. There are some additional triplet terms Σ ⋅σ and (Σ ×d) ⋅σ in Eq. 20, which reflect the impurity-induced modification of the spin structure of the Cooper pairs. It is worth mentioning that there is an impurity-induced odd-frequency pairing for the chiral nonunitary states, which is spin singlet and odd parity in nature.

After obtaining the impurity-dressed Green’s function, we calculate the electronic thermal conductivity κ using the Kubo formula that relates the thermal conductivity to the heat–current response [24]. We ignore the vertex corrections and restrict ourselves to the bare thermal–current response function. The vertex corrections are small in the strong scattering limit that is focused on in this article [33]. The diagonal thermal conductivity for a general triplet superconductor reads

$\frac{{\kappa }_{ii}}{T}={\int }_{-\infty }^{\infty }d\omega \frac{{\omega }^2}{T^2}\left(-\frac{d{n}_F\left(\omega \right)}{d\omega }\right){⟨N_0{v}_{Fi}^2\frac{\left(-c_1{c}_4+c_2{c}_3\right)+c_3{b}_1+c_1{b}_2+b_3\left(-c_3+c_1{c}_2\right)/c_4}{\left(c_3^2+c_1^2{c}_4-c_1{c}_2{c}_3\right)}⟩}_{FS}.(25)$

Here, $c_1=-2\mathrm{R}\mathrm{e}({\tilde{Q}}_{+}+{\tilde{Q}}_{-})$, $c_2=|{\tilde{Q}}_{+}{|}^2+|{\tilde{Q}}_{-}{|}^2+4\mathrm{R}\mathrm{e}({\tilde{Q}}_{+})\mathrm{R}\mathrm{e}({\tilde{Q}}_{-})$, $c_3=-2|{\tilde{Q}}_{+}{|}^2\mathrm{R}\mathrm{e}({\tilde{Q}}_{-})-2|{\tilde{Q}}_{-}{|}^2\mathrm{R}\mathrm{e}({\tilde{Q}}_{+})$, and $c_4=|{\tilde{Q}}_{+}{|}^2|{\tilde{Q}}_{-}{|}^2$, and the coefficients b_i=1,.,3 are

$b_1=\left(|\tilde{\omega }{|}^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2+|\mathbf{\Sigma }{|}^2\right)+\mathrm{R}\mathrm{e}\left[{\tilde{Q}}_{+}^2+{\tilde{Q}}_{-}^2\right],(26)$

$\begin{array}{ll}\hfill b_2& =\frac{1}{4}|{\tilde{Q}}_{+}^2+{\tilde{Q}}_{-}^2{|}^2+\left(|\tilde{\omega }{|}^2+|\mathbf{\Sigma }{|}^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right)\mathrm{R}\mathrm{e}\left[{\tilde{Q}}_{+}^2+{\tilde{Q}}_{-}^2\right]+3{\mathrm{\Delta }}_0^4\mathbf{q}\cdot \mathbf{q}+4|\mathbf{\Sigma }{|}^2\left(|\tilde{\omega }{|}^2+\mathrm{R}\mathrm{e}\left[{\tilde{\omega }}^2\right]\right)\hfill \\ \hfill & -4{\mathrm{\Delta }}_0^2\left(|\mathbf{\Sigma }\cdot \mathbf{d}{|}^2+|\mathbf{\Sigma }\cdot {\mathbf{d}}^{*}{|}^2+\mathrm{R}\mathrm{e}\left[\left(\mathbf{\Sigma }\cdot \mathbf{d}\right)\left(\mathbf{\Sigma }\cdot {\mathbf{d}}^{*}\right)\right]\right)\hfill \\ \hfill & +4|\tilde{\omega }{|}^2\mathrm{R}\mathrm{e}\left[\mathbf{\Sigma }\cdot \mathbf{\Sigma }\right]+4{\mathrm{\Delta }}_0^2\mathrm{R}\mathrm{e}\left[\tilde{\omega }\mathbf{q}\cdot {\mathbf{\Sigma }}^{*}+2\tilde{\omega }\mathbf{q}\cdot \mathbf{\Sigma }\right],\hfill \end{array}(27)$

$b_3=\left(|\tilde{\omega }{|}^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right)\left[|{\alpha }_{+}{|}^2+{\mathrm{\Delta }}_0^4\mathbf{q}\cdot \mathbf{q}\right]-2{\mathrm{\Delta }}_0^4\mathbf{q}\cdot \mathbf{q}\mathrm{R}\mathrm{e}\left[{\alpha }_{+}\right]+\mathcal{Y}\left(\mathbf{\Sigma }\right),(28)$

$\begin{array}{ll}\hfill \mathcal{Y}\left(\mathbf{\Sigma }\right)& =\left\{|\left({\tilde{\omega }}^2+{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2-\mathbf{\Sigma }\cdot \mathbf{\Sigma }\right){|}^2-{\mathrm{\Delta }}_0^4\mathbf{q}\cdot \mathbf{q}\right\}|\mathbf{\Sigma }{|}^2-2{\mathrm{\Delta }}_0^2\mathrm{R}\mathrm{e}\left[\left({\alpha }_{-}-{\alpha }_{-}^{*}\right)\tilde{\omega }\mathbf{q}\cdot {\mathbf{\Sigma }}^{*}\right]\hfill \\ \hfill & -4{\mathrm{\Delta }}_0^2\left(|\tilde{\omega }{|}^2+|\mathbf{\Sigma }{|}^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right)\mathrm{R}\mathrm{e}\left[\tilde{\omega }\mathbf{q}\cdot {\mathbf{\Sigma }}^{*}\right]+2{\mathrm{\Delta }}_0^4\mathrm{R}\mathrm{e}\left[|\mathbf{q}\cdot \mathbf{\Sigma }{|}^2-{\left(\mathbf{q}\cdot \mathbf{\Sigma }\right)}^2+\mathbf{\Sigma }\cdot \mathbf{\Sigma }\mathbf{q}\cdot \mathbf{q}\right]\hfill \\ \hfill & +2{\mathrm{\Delta }}_0^2\mathrm{R}\mathrm{e}\left[\left(|\tilde{\omega }{|}^2-{\tilde{\omega }}^2\right)-\left(|\mathbf{\Sigma }{|}^2-\mathbf{\Sigma }\cdot \mathbf{\Sigma }\right)\right]\left(|\mathbf{\Sigma }\cdot \mathbf{d}{|}^2+|\mathbf{\Sigma }\cdot {\mathbf{d}}^{*}{|}^2\right)-4{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2|\tilde{\omega }{|}^2|\mathbf{\Sigma }{|}^2\hfill \\ \hfill & +4{\mathrm{\Delta }}_0^2\mathrm{R}\mathrm{e}\left[{\alpha }_{+}\left({\mathbf{\Sigma }}^{*}\cdot {\mathbf{d}}^{*}\right)\left({\mathbf{\Sigma }}^{*}\cdot \mathbf{d}\right)\right]-4{\mathrm{\Delta }}_0^2\mathrm{R}\mathrm{e}\left[\left({\tilde{\omega }}^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\right){\mathbf{\Sigma }}^{*}\cdot {\mathbf{\Sigma }}^{*}\right],\hfill \end{array}(29)$

where ${\alpha }_{\pm }={\tilde{\omega }}^2-{\mathrm{\Delta }}_0^2|\mathbf{d}{|}^2\pm \mathbf{\Sigma }\cdot \mathbf{\Sigma }$. The derivation of thermal conductivity is provided in Supplementary Material. We calculate the full temperature dependence of thermal conductivity using the self-consistently determined superconducting gap using an effective pairing potential to obtain a single transition temperature (see Supplementary Material).

3 Results and discussion

3.1 T = 0 limit of the density of states and thermal conductivity

We start with the single-component states based on four irreducible representations of the D_2h point group symmetry. The basis functions for these four states are listed in Table 1, where the A_1u state remains gapped unless the coefficient of one of the basis functions is set to zero. We exclude that possibility and choose the same coefficients for all three basis functions, and this choice of coefficients is adopted for the other states as well, which is a reasonable choice for a qualitative understanding of the low-energy properties. In principle, it is also possible to generate line nodes with an appropriate choice of basis function coefficients, but those possibilities are excluded considering the recent experimental results on UTe₂. Apart from the A_1u state, the B_1u state also remains gapped because the open Fermi surface along the $\widehat{z}$-axis forbids the nodes for this state. For the B_2u and B_3u states, a pair of point nodes exists along the $\widehat{y}$-axis and $\widehat{x}$-axis, respectively. Figures 1A–D show the disorder dependence of the thermal conductivity normalized to the normal state value at the transition as a function of relative reduction in the transition temperature δt_c ≡ = 1 − T_c/T_c0, where T_c0 is the transition temperature in the clean limit. For a clean system, δt_c = 0, and δt_c reaches unity as the impurity scattering kills superconductivity. The normalized residual thermal conductivity κT_c/κ_NT in the zero-temperature limit remains 0 up to a threshold value of disorder Γ_th for all four states; this Γ_th corresponds to a threshold level of T_c suppression $\delta t_c^{th}$. This threshold value of disorder depends on the superconducting gap structure and the strength of the impurity potential [27]. For the gapped states A_1u and B_1u, the residual thermal conductivity remains 0 for slightly higher values of disorder compared to the other two states B_2u and B_3u as expected due to the presence of impurity-induced quasiparticle states near the nodes. The normalized thermal conductivity remains very isotropic for the A_1u and B_1u states. However, for the nodal states, the residual thermal conductivity is enhanced for thermal current along the nodal directions. This trend in anisotropy in thermal conductivity continues even at finite temperatures, as shown in the temperature evolution of κT_c/κ_NT for the four single-component states in Figures 1E–H for tan θ_s = 2 and in Figures 1I–L for tan θ_s = 5, which represents the stronger scatterers. For both impurity strengths, δt_c is 0.02. In the presence of the point nodes, the thermal conductivity shows a weak maximum at very low temperature along the nodal direction for the weak scatterers, which disappears as the scattering rate increases. This is a known behavior for the superconducting states with point nodes [28], which is not present for the stronger impurity potentials.

Figure 1

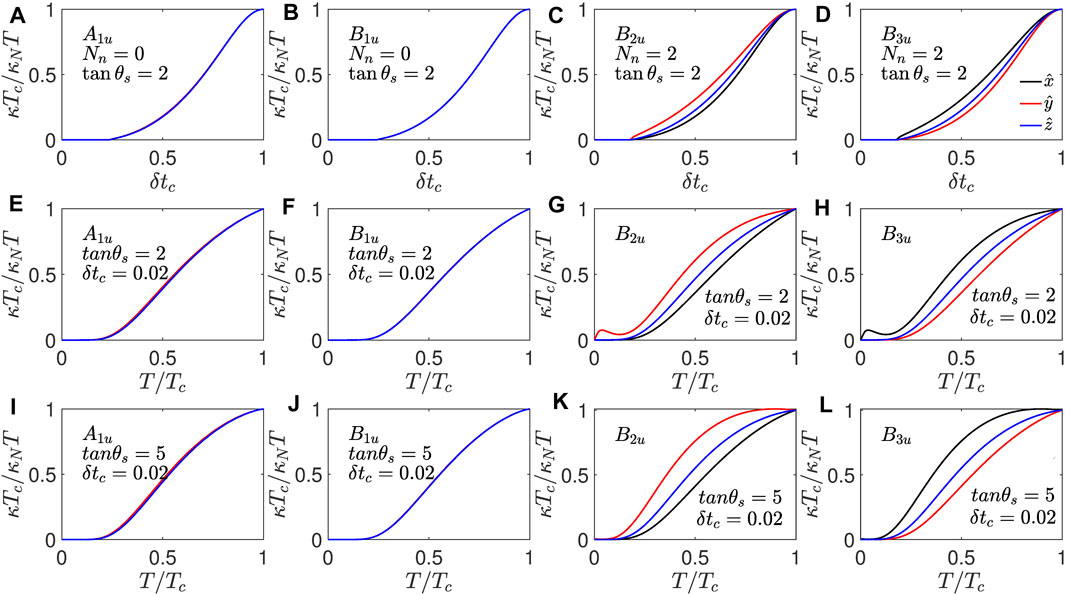
Figure 1. Thermal conductivity for the single-component unitary states allowed by the D_2h point group. The thermal conductivity normalized to its value at T_c for the four irreducible representations of the D_2h point group shown column-wise for the A_1u, B_1u, B_2u, and B_3u representations from (A–D), respectively. The first row shows the residual thermal conductivity in the zero-temperature limit as a function of relative reduction in the transition temperature δt_c. (E–H) in the second row show κT_c/κ_NT for the weak scatterers with tan θ_s = 2 and for the intermediate-strength scatterers with tan θ_s = 5 from (I–L) in the third row. For the temperature dependence, the T_c is reduced by 2% (δt_c = 0.02) with respect to the clean limit.

It is useful to examine the density of states (DOS) and the structure of the low-energy quasiparticle states before discussing the thermal transport for the nonunitary states. We first report the average density of states per spin for the nonunitary states on a cylindrical Fermi surface that is open along the $\widehat{z}$-axis. Figure 2A shows the DOS for the A_1u + irB_2u state, which is a chiral state, and Figures 2B–D show Δ₋ for this state. In the gapped phase (r < 1), this state has minima near the $\widehat{x}$-axis, and a small gap is visible in the DOS. For r = 1, a pair of point nodes appear along the $\widehat{x}$-axis, and the low-energy DOS shows ω² behavior that is expected for linear point nodes. Here, and in subsequent discussions, a “node” refers to spectral nodes, not the gap nodes. However, in contrast to a unitary state, the low-energy quadratic behavior remains confined to a very low energy scale, as compared to the unitary B_3u state. For r > 1, the nodes move away from the $\widehat{x}$-axis, and the positions of four nodes are determined by $\tan \varphi =\pm \sqrt{r^2-1}$, where ϕ is the polar angle on the cylindrical Fermi surface. As the mixing parameter r increases, additional pairs of nodes appear in the yz plane at $\sin (k_z/2)=\pm 1/\sqrt{r^2-1}$. In the r → ∞ limit, only two point nodes along the $\widehat{y}$-axis survive, as expected for a pure B_2u state. The low-energy DOS remains quadratic in all these cases. For $1\le r<\sqrt{2}$, the nodes remain closer to the $\widehat{x}$-axis, and for $r\ge \sqrt{2}$, the nodes move closer to the $\widehat{y}$-axis. The A_1u + irB_3u state also shows similar DOS to the A_1u + irB_2u state, but it has a different nodal structure. It has gap minima in the quasiparticle spectrum near the $\widehat{y}$-axis, and nodes appear along the $\widehat{y}$-axis. For r > 1, a set of four nodes appear near the $\widehat{y}$-axis at $\varphi =\pm {\cot }^{-1}\sqrt{r^2-1}$ and move toward the $\widehat{x}$-axis in the xy-plane as the value of r increases. For $r>\sqrt{2}$, four more nodes appear at $k_z=\pm 2{\sin }^{-1}(1/\sqrt{r^2-1})$ in the xz-plane. Both these states are chiral and show finite quasiparticle spin density along $\widehat{y}$ and $\widehat{x}$ directions in the spin space. The last AF nonunitary state is A_1u + irB_1u, which is not a chiral state. It has nodes along the $\widehat{x}$ and $\widehat{y}$ directions for r = 1, a set of four point nodes in the xz-plane and another set of four point nodes in the yz-plane, where the k_z for the nodal position is determined by $\sin (k_z/2)=\pm \sqrt{r^2-1}$. The DOS shows quadratic behavior at low energies (see Supplementary Material).

Figure 2

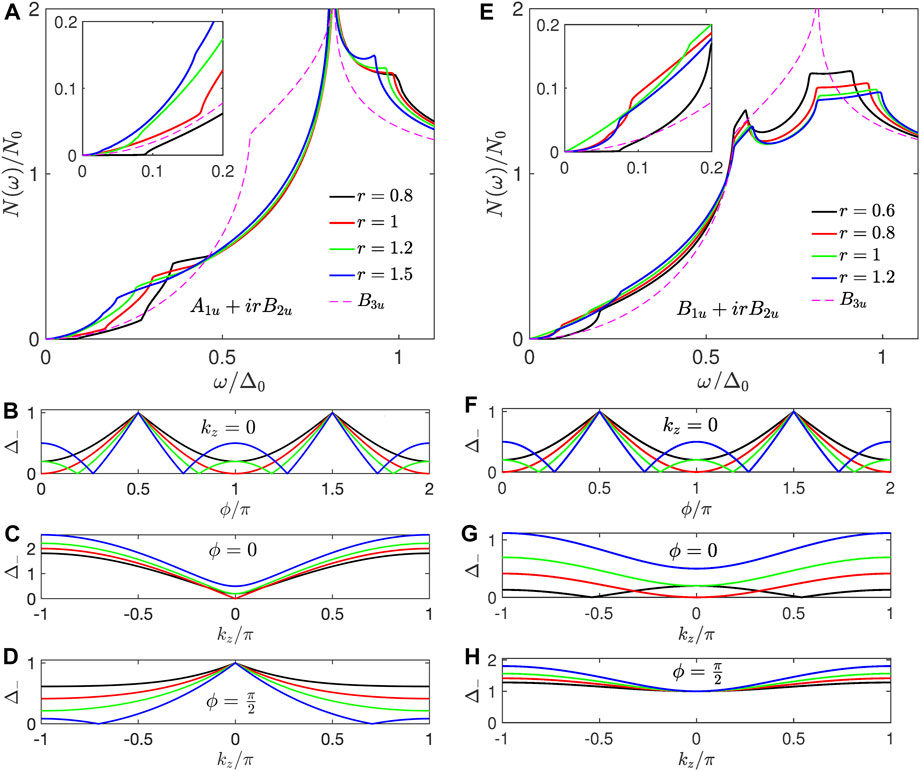
Figure 2. Density of states: (A) shows the density of states (DOS) per spin for the A_1u + irB_2u state for different values of the mixing parameter r. The inset shows the energy dependence of the DOS at low energies. A dashed line illustrating the DOS for the unitary B_3u state is shown for comparison. (B–D) show the variation in Δ₋ for different values of r in the xy, xz, and yz-planes, respectively. (E) shows the DOS per spin for the B_1u + irB_2u state, and Δ₋ in the xy, xz, and yz-planes is shown in panels (F–H), respectively.

Next, we consider the ferromagnetic nonunitary states on the cylindrical Fermi surface, which are chiral states with finite Cooper pair spin moment. Figure 2D shows the DOS for the B_1u + irB_2u state along with the Δ₋ in Figures 2E–F. This state is gapped for $r<1/\sqrt{2}$, and a set of four point nodes appear in the yz-plane for $1/\sqrt{2}\le r<1$, whose positions are determined by $\sin (k_z/2)=r/\sqrt{1-r^2}$. For r > 1, a set of four point nodes appear in the xy-plane at $\varphi =\pm {\tan }^{-1}\sqrt{r^2-1}$ close to the $\widehat{x}$-axis and move toward the $\widehat{y}$-axis as r increases. These states show quadratic DOS at low energies. For r = 1, this state shows point nodes along the $\widehat{x}$-axis, but these are the quadratic point nodes. The first derivative of Δ₋ vanishes at the nodes for quadratic or second-order point nodes. This leads to linear DOS at low energies, as shown in Figure 2D. Similarly, for B_1u + irB_3u, a twin pair of quadratic point nodes appear along the $\widehat{y}$-axis and shows linear DOS at low energies for r = 1. For $1/\sqrt{2}\le r<1$, four point nodes appear at $\sin (k_z/2)=\pm \sqrt{1-r^2}/r$ in the yz-plane, and for r > 1, a set of four point nodes appear in the xy-plane at $\cot \varphi =\pm \sqrt{r^2-1}$, closer to the $\widehat{y}$-axis for r ≥ 1, which move toward the $\widehat{x}$-axis for r ≫ 1. The DOS remains quadratic, as expected. For the B_2u + irB_3u state, four point nodes are either located in the yz-plane at $\sin (k_z/2)=\pm r/\sqrt{1-r^2}$ for $r\le 1/\sqrt{2}$ or in the xz-plane at $\sin (k_z/2)=\pm 1/\sqrt{r^2-1}$ for $r\ge \sqrt{2}$. These states show ω² behavior in the low-energy DOS. For $1/\sqrt{2}<r<\sqrt{2}$, a gap exists in the quasiparticle spectrum due to lack of nodes (see Supplementary Material). In contrast to the AF nonunitary states on the cylindrical Fermi surface, the FM nonunitary states can have at most four nodes and are expected to be more anisotropic.

We now discuss the zero-temperature limit of the thermal conductivity, which is very sensitive to the gap structure. We compare the normalized κT_c/Tκ_N along three principal directions, where the thermal conductivity along a particular direction is normalized to its normal state value at T_c along that direction. This suppresses the intrinsic anisotropy present in the electronic structure and accentuates the effect of order parameter anisotropy. Figures 3A–D show κT_c/Tκ_N in the zero-temperature limit for the A_1u + irB_1u state as a function of the relative reduction in the transition temperature δT_c. For a weakly disordered system, κ/T vanishes in the zero-temperature limit, but as the disorder level increases and crosses Γ_th, κ/T|_T→0 becomes finite and reaches the normal-state value as the superconductivity vanishes. For the A_1u + irB_1u state, κT_c/κ_NT shows isotropic behavior in the xy-plane. Note that for this state, the nodes are always along the $\widehat{x}$ and $\widehat{y}$ axes at the same k_z value. In contrast, the B_2u + irB_3u state shows relatively weaker level anisotropy than a unitary state. Figures 3E–G show κT_c/κ_NT for the B_2u + irB_3u state, while Figure 3H shows κT_c/κ_NT for the unitary B_3u state with nodes along the $\widehat{x}$-axis. As shown in Figure 3E, with nodes in the yz-plane κ_yy and κ_zz exceeding κ_xx, and this behavior reverses as the nodes move to the xz-plane for the B_2u + irB_3u state, as depicted in Figure 3H. As the value of r increases, the anisotropy also reduces, and for r = 1, the superconducting state becomes fully isotropic, as shown in Figure 3F. This is a special case, which has a four-fold symmetric Δ₋, leading to a very isotropic normalized thermal conductivity along the three principal directions. As r becomes larger than unity, the κ_xx starts to dominate.

Figure 3

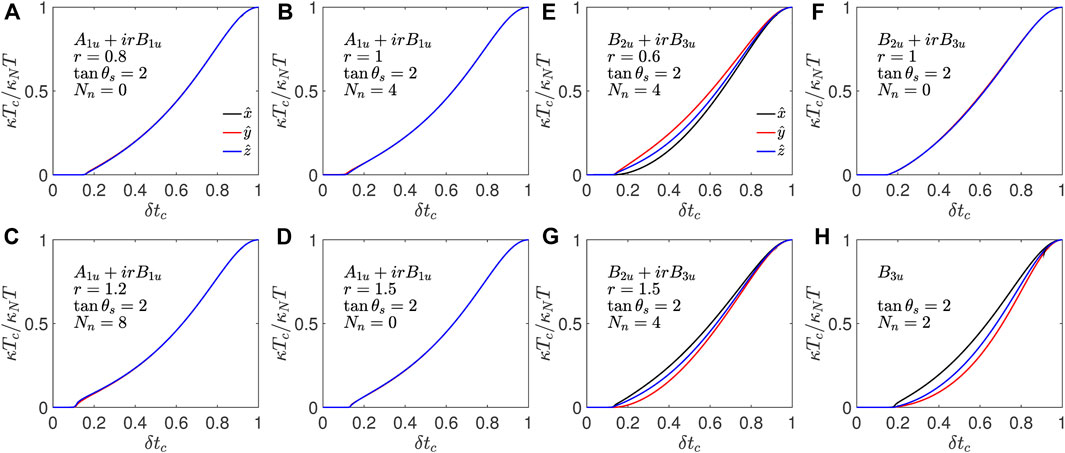
Figure 3. Residual thermal conductivity. Zero-temperature limit κT_c/κ_NT for the A_1u + irB_1u in (A–D) and for the B_2u + irB_3u state in (E–G) for various values of mixing parameter r. (H) shows κT_c/κ_NT|_T→0 for the unitary B_3u state. The s-wave scattering phase shift is θ_s = tan⁻¹ (2) for all the panels. The number of nodes N_n is indicated for each case.

Next, we look at the zero-temperature limit thermal conductivity for the A_1u + irB_2u state for two different impurity potential strengths. Figures 4A–D show κT_c/κ_NT for s-wave scattering phase shift tan⁻¹ (2), and panels Figures 4E–H show κT_c/κ_NT for θ_s = tan⁻¹ (5). κ/T|_T→0 becomes finite above a threshold disorder level, as in earlier cases. This threshold scattering rate is smaller for the stronger impurity potentials. This state has a minimum and maximum along the xz-plane, the energy gap is small in the yz-plane, and a weak maximum exists along the $\widehat{y}$-axis in the xy-plane. This excitation energy spectrum is reflected in the thermal conductivity. As κ/T becomes finite, the in-plane anisotropy is very weak with a slightly larger value along the $\widehat{x}$-axis as long as there is no node in the yz-plane. As the impurity-induced quasiparticles overcome the minima along the $\widehat{y}$-axis, the thermal conductivity along the $\widehat{y}$-axis starts to dominate. In the case of eight nodes, with four in the xy-plane and another four in the yz-plane, the thermal conductivity is always larger along the $\widehat{y}$-axis. The $\widehat{z}$-axis thermal conductivity remains close to the $\widehat{x}$-axis thermal conductivity. For the A_1u + irB_3u state, the thermal conductivity along the $\widehat{x}$-axis and $\widehat{y}$-axis shows the same behavior as κ_yy/T and κ_xx/T in the A_1u + irB_2u state, respectively.

Figure 4

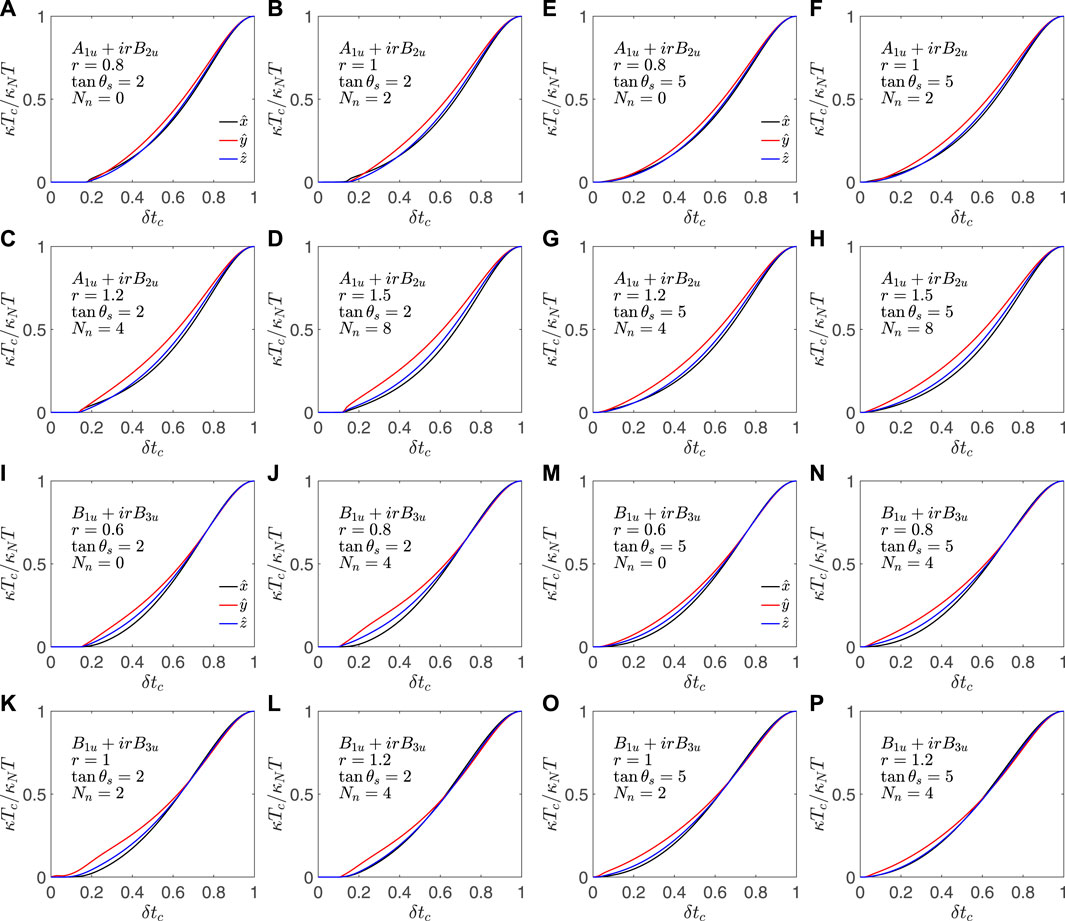
Figure 4. Residual thermal conductivity: (A–H) show κ/T in the zero-temperature limit normalized to κ_N/T at T_c as a function of relative T_c reduction δt_c for the A_1u + irB_2u state for different values of the mixing parameter r. The s-wave scattering phase for (A–D) is θ_s = tan⁻¹ (2) and for panels (E–H) is θ_s = tan⁻¹ (5). For the B_2u + irB_3u state, κT_c/κ_NT|_T→0 is shown for various values of parameter r for the s-wave scattering phase shift θ_s = tan⁻¹ (2) in (I–L) and with θ_s = tan⁻¹ (5) in (M–P). The number of nodes N_n is indicated for each case.

For the B_1u + irB_3u state, in the gapped phase, i.e., $r<1/\sqrt{2}$, the spectral gap on the Fermi surface is small in the yz-plane and near the $\widehat{y}$-axis in the xy-plane, which leads to larger κ/T|_T→0 along the $\widehat{y}$-axis, followed by the $\widehat{z}$ direction, as shown in Figures 4I–M, for tan θ_s = 2 and tan θ_s = 5, respectively. As a set of four nodes appear in the yz-plane, the relative anisotropy remains the same, as shown in Figures 4J–N. This state also shows an elusive quadratic node for r = 1 along the $\widehat{y}$-axis. Unlike the other states with linear point nodes, for this case, κ/T|_T→0 term remains finite along the nodes, and for other directions, residual thermal conductivity remains 0 below the threshold disorder level. This state shows linear DOS at low energies, like superconductors with line nodes. Finally, the nodes appear in the xy-plane for this state as r exceeds unity and remains closer to the $\widehat{y}$-axis, and thermal conductivity along the $\widehat{y}$-axis becomes dominant, while the other two directions show very similar κT_c/κ_NT. As r increases, the in-plane anisotropy decreases, and the $\widehat{x}$-axis κ increases and becomes stronger along the $\widehat{y}$ direction in the r ≫ 1 limit. For the B_1u + irB_2u state, the in-plane anisotropy found for the B_1u + irB_3u state gets interchanged.

3.2 Finite T electronic thermal conductivity

Now, we look at the temperature evolution of the normalized thermal conductivity for the nonunitary states. At very low temperatures, the elastic scattering by the impurities is the main mechanism of relaxation. However, as the temperature increases, the inelastic scattering also becomes important, which we discuss in the subsequent section. Apart from the electron contribution to thermal conductivity, phonon thermal conductivity can also become significant. Here, we focus on electronic thermal conductivity and the effect of impurity scattering on it and the effect of underlying spectral nodes on the anisotropy in the thermal conductivity. As shown in Figure 1, the thermal conductivity shows a weak maximum as a function of temperature at very low temperatures along the nodal directions. There is no evidence for such a feature in the experimental measurements [7, 34]; therefore, we set θ_s = tan⁻¹ (5) for the rest of our discussion (see Supplementary Material for the weaker impurity scatterers). We first consider the A_1u + irB_1u state, which shows very isotropic residual thermal conductivity, and the thermal conductivity remains isotropic as a function of temperature, as shown in Figures 5A–D. For the clean system with δt_c = 0.02, at very low temperatures, the thermal conductivity remains negligibly small, and as the temperature increases, κ/T increases T² at very low temperatures. This behavior is observed for both nodal and gapped systems. Note that in superconductors with point nodes, there are very few states available at the Fermi energy, as shown in Figure 2. For dirtier systems such as δt_c = 0.15, there are sufficient quasiparticle states at the Fermi level to provide nonzero thermal conductivity, which is depicted in Figures 5E–H. At low temperatures, κ/T remains independent of temperature, and as it increases, once more, quasiparticles become relevant for transport as the temperature increases.

Figure 5

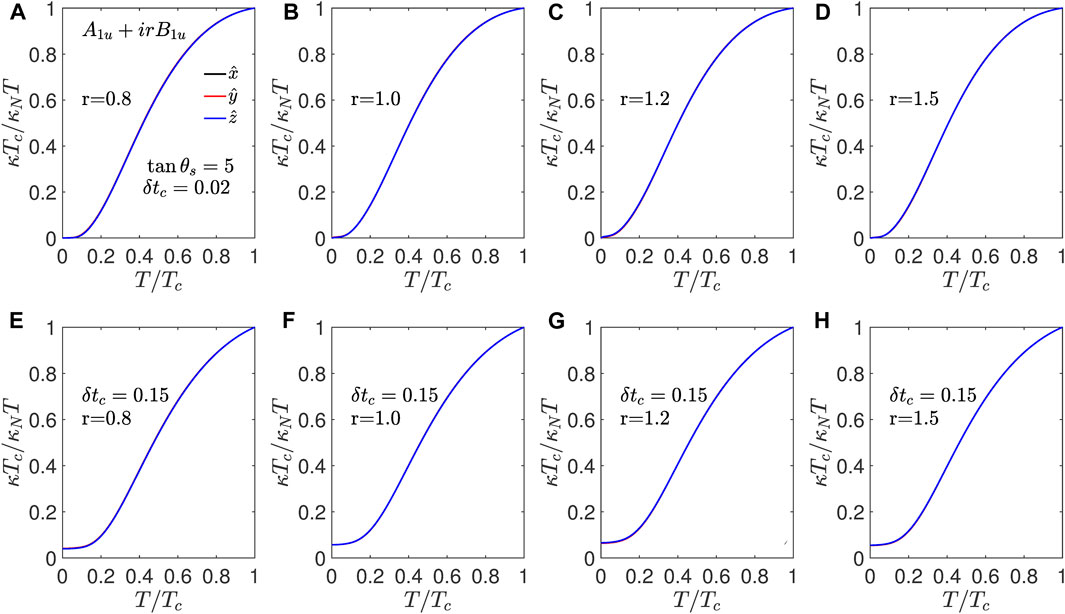
Figure 5. A_1u + irB_1u: Thermal conductivity normalized to its normal state value at T_c for A_1u + irB_1u shown as a function of temperature normalized to T_c for scatterers with tan θ_s = 5 for δt_c = 0.02 from (A–D) and for δt_c = 0.15 in (E–H) for various values of mixing parameter r.

Next, we consider the A_1u + irB_2u state, which shows enhanced thermal conductivity along the $\widehat{y}$-axis. The zero-temperature trends in anisotropy continue as the temperature increases, as shown in Figure 6. For δt_c = 0.02, κ/T is close to 0 and increases as temperature increases beyond a critical value. For the gapped case (r < 1) and for the $\widehat{x}$-axis nodes (r = 1), κ/T is slightly larger than that in the other two directions, but as the temperature increases, the other two directions begin to increase and dominate because the temperature overcomes the gap minima in the yz-plane. For r > 1, there are four point nodes that move toward the $\widehat{y}$ axis, and it is reflected as a larger κ/T along the $\widehat{y}$-axis. For $r>\sqrt{2}$, four more nodes in the yz-plane make κ/T along $\widehat{y}$ and $\widehat{z}$ directions larger than that in the $\widehat{x}$ direction. For dirtier systems, thermal conductivity becomes finite and T-independent at very low temperatures, as in the earlier case, but the anisotropy remains similar to its zero-temperature limit. For A_1u + iB_3u, the behavior of $\widehat{x}$ and $\widehat{y}$ directions gets interchanged (see Supplementary Material).

Figure 6

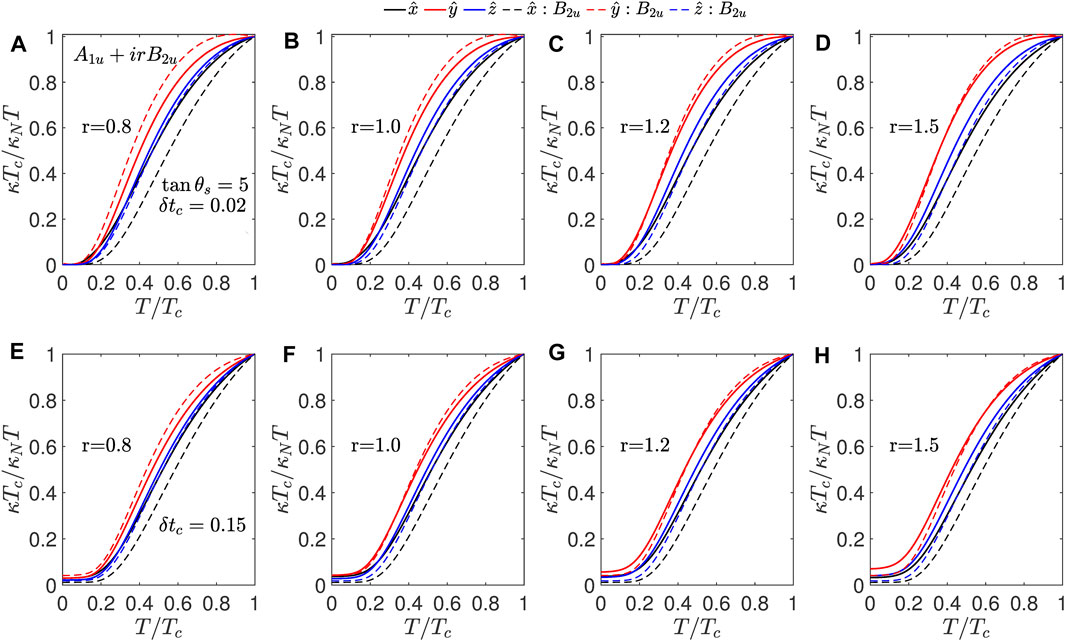
Figure 6. A_1u + irB_2u: Thermal conductivity normalized to its normal state value at T_c for A_1u + irB_2u shown as a function of temperature normalized to T_c for scatterers with tan θ_s = 5 for δt_c = 0.02 from (A–D) and for δt_c = 0.15 in (E–H) for various values of mixing parameter r. The dashed lines show the normalized thermal conductivities for the B_2u state with the same impurity parameters.

Next, we consider the B_2u + irB_3u state, which is one of the FM nonunitary chiral states. For this state, there are four point nodes in the yz-plane for $r<1/\sqrt{2}$, and for $r>\sqrt{2}$, there is a set of four point nodes in the xz-plane. Figure 7 shows the thermal conductivity as a function of temperature, and as expected, κ/T along the nodal directions dominates. For r < 1, the thermal conductivity is enhanced along the $\widehat{y}$ and $\widehat{z}$ directions, and as r increases, the system becomes gapped with enhanced thermal conductivity in the $\widehat{y}$ and $\widehat{z}$ directions, but the anisotropy reduces. The state r = 1 shows completely isotropic behavior, and as r exceeds unity, this state shows a $\widehat{x}$-axis-dominated thermal response, as the nodes reappear in the xz-plane. The anisotropy remains qualitatively same as the temperature increases. Finally, we consider the B_1u + irB_3u state, which is another possible FM nonunitary state that shows enhanced thermal conductivity along the $\widehat{y}$ direction, as shown in Figure 8. Here, the anisotropy changes significantly as the temperature increases. At low temperatures, the $\widehat{y}$-axis dominates due to its vicinity to the point nodes; however, as the temperature increases, κT_c/κ_NT increases along the $\widehat{x}$ directions. This happens because at lower temperatures, the lower-energy branch of the quasiparticle excitations $\sqrt{{\xi }_{\mathbf{k}}^2+{\mathrm{\Delta }}_{-}^2}$ dominates, which has more quasiparticle states along the $\widehat{y}$ directions, but at higher temperatures, the $\sqrt{{\xi }_{\mathbf{k}}^2+{\mathrm{\Delta }}_{+}^2}$ branch of the quasiparticle excitations begins to contribute, which, for this state, has minima along the $\widehat{x}$-axis. The overall anisotropy for this state is relatively less compared to other states, except those that show fully isotropic behavior as a function of temperature or disorder. For the B_1u + irB_2u state, κ/T along the $\widehat{x}$ and $\widehat{y}$ directions gets interchanged by the anisotropy shown by the B_1u + irB_3u state.

Figure 7

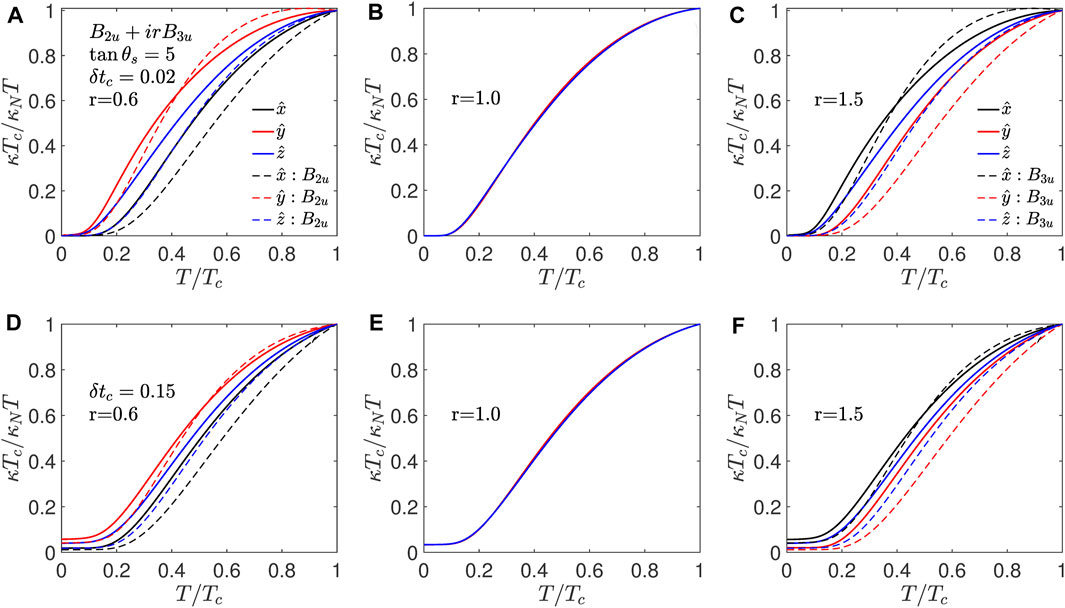
Figure 7. B_2u + irB_3u: Thermal conductivity normalized to its normal state value at T_c for B_2u + irB_3u shown as a function of temperature normalized to T_c for scatterers with tan θ_s = 5 for δt_c = 0.02 from (A–C) and for δt_c = 0.15 in (D–F) for various values of mixing parameter r. The dashed lines show the normalized thermal conductivities for the B_2u state in (A,D) and for the B_3u state in (C,F). The impurity parameters are the same for the single-component superconducting states.

Figure 8

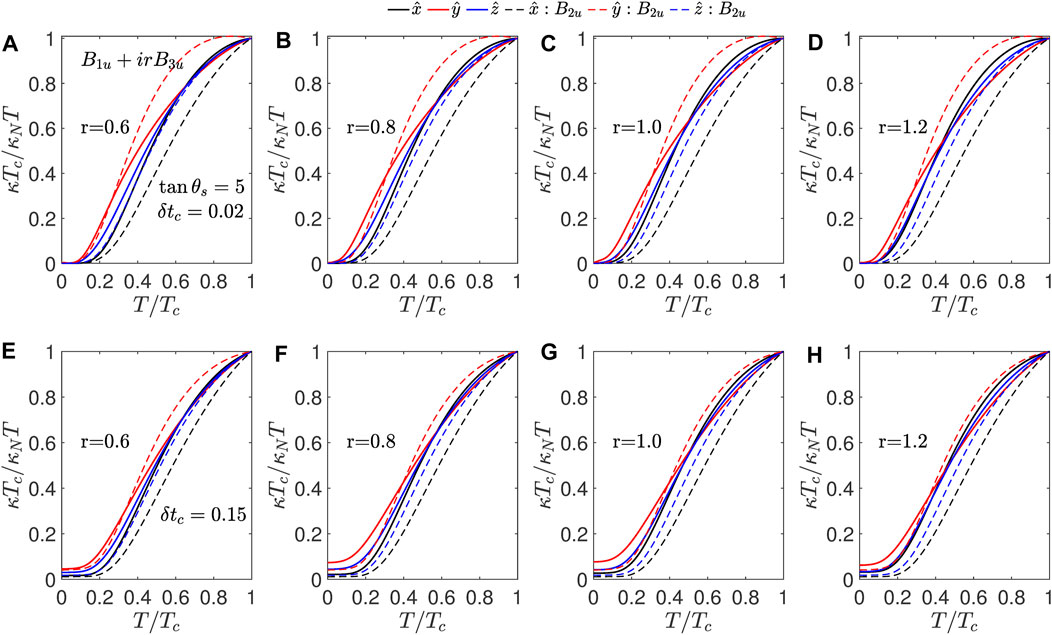
Figure 8. B_1u + irB_3u: Thermal conductivity normalized to its normal state value at T_c for B_1u + irB_3u shown as a function of temperature normalized to T_c for scatterers with tan θ_s = 5 for δt_c = 0.02 from (A–D) and for δt_c = 0.15 in (E–H) for various values of mixing parameter r. The dashed lines show the normalized thermal conductivities for the B_2u state with same impurity parameters.

3.3 Inelastic scattering effects

As mentioned in the previous section, at very low temperatures, i.e., T ≪ T_c, the elastic scattering from impurities is the only mechanism that determines the scattering rate. However, at higher temperature, inelastic scattering from a bosonic mode is possible. We consider a simple scenario where there is a dispersionless bosonic mode that couples with the fermions with an effective coupling constant g_fb. We further assume that the coupling does not depend on the spin degree of freedom of the fermion. The lowest-order self-energy for the fermions reads

${\mathrm{\Sigma }}_{in}\left(i{\omega }_n,\mathbf{k}\right)=g_{fb}^{2}T{\displaystyle \sum _{m,\mathbf{q}}}G\left(i{\omega }_n-i{\mathrm{\Omega }}_m,\mathbf{k}-\mathbf{q}\right)D\left(i{\mathrm{\Omega }}_m,\mathbf{q}\right).(30)$

Here, D is the bosonic Green’s function and ω_n and Ω_m are the fermionic and bosonic Matsubara frequencies, respectively. After performing the Matsubara summation, we obtain

${\mathrm{\Sigma }}_{in}\left(\omega \right)=-\frac{g_{fb}^2}{2\pi }{\int }_{-\infty }^{\infty }dx{\int }_{-\infty }^{\infty }dy\frac{N\left(y\right)D^{\prime \prime }\left(x\right)}{x+y-\omega -i\eta }\left(\coth \left(\beta x/2\right)+\tanh \left(\beta y/2\right)\right).(31)$

Here, the real part of the self-energy contributes to mass renormalization, and the imaginary part modifies the scattering rate, which is a function of quasiparticle energy and temperature. Noting that UTe₂ has very high effective mass, we ignore the real part of the self-energy. The imaginary part of the self-energy is

${\mathrm{\Sigma }}_{in}^{\prime \prime }\left(\omega \right)=-\frac{g_{fb}^2}{2}{\int }_{-\infty }^{\infty }dxN\left(\omega -x\right)D^{\prime \prime }\left(x\right)\left(\coth \left(\beta x/2\right)+\tanh \left(\beta \left(\omega -x\right)/2\right)\right),(32)$

where $D^{\prime \prime }(x)\equiv x/(x^2+{\mathrm{\Omega }}_0^2)$ is the bosonic DOS and Ω₀ is the characteristic energy scale associated with the bosonic mode. In the context of UTe₂, we expect Ω₀ ≫ T_c; therefore, we approximate the bosonic DOS as $D^{\prime \prime }(x)\approx x/{\mathrm{\Omega }}_0^2$. In the zero-temperature limit, ${\mathrm{\Sigma }}_{in}^{\prime \prime }\propto {\omega }^{n+2}$, where the DOS for the superconducting state behaves like ωⁿ at low energies. For linear point nodes, ${\mathrm{\Sigma }}_{in}^{\prime \prime }\propto {\omega }^4$, and for quadratic point nodes or line nodes, it behaves like ω³. Similarly, in the static limit (ω → 0), the imaginary part of the inelastic self-energy reads

${\mathrm{\Sigma }}_{in}^{\prime \prime }\left(\omega =0,T\right)=-2g_{fb}^2{\int }_0^{\infty }dx\frac{N\left(x\right)D^{\prime \prime }\left(x\right)}{\sinh \beta x}.(33)$

Since the thermal response integrand is peaked at ω = 0, we only retain the temperature dependence of the inelastic self-energy at ω = 0. At very low temperatures, the inelastic scattering rate behaves likes T⁴ for the point nodes and T³ for the line nodes in the static limit. This is sufficient to understand the qualitative effect of inelastic scattering. The prefactor in Eq. 33 is fixed by the value of the inelastic scattering rate at T_c.

Figure 9 shows the effect of inelastic scattering on the electronic thermal conductivity. We show the results for two cases as the rest of the cases are qualitatively similar. The first row of Figures 9A–D shows the normalized thermal conductivity for the A_1u + irB_2u state, which shows enhanced thermal conductivity along the $\widehat{y}$-axis. Note that the normal state thermal conductivity includes the inelastic scattering. We fixed the value of r at 1.2, which leads to four point nodes in the xy-plane. The primary effect of inelastic scattering is the formation of a peak below T_c. This peak appears first for the directions that have larger thermal conductivity, as shown in Figure 9A for δ = 0.02. As the system becomes dirtier, the peaks get smeared, as depicted in Figure 9B for δt_c = 0.15. If the strength of inelastic scattering increases, the peaks also strengthen, as shown in Figure 9C, and it may survive in dirtier systems, as illustrated in Figure 9D. Similar trends continue for the other states as well. Figures 9E–H show the normalized thermal conductivity for the B_1u + irB_3u state, which shows the same qualitative behavior as a function of disorder and inelastic scattering strength. However, this state shows a nonmonotonic variation of anisotropy, and the peaks for different directions remain quite close to each other.

Figure 9

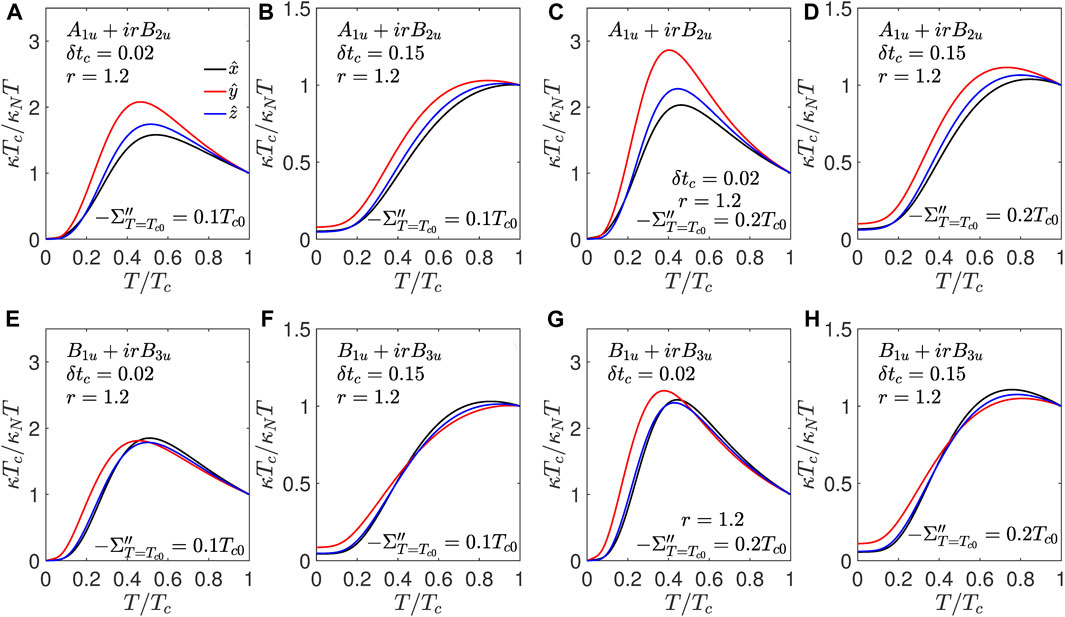
Figure 9. Effect of inelastic scattering: (A–D) show the temperature dependence of normalized thermal conductivity for the A_1u + irB_2u state for r = 1.2. (E–H) show the temperature dependence of the normalized thermal conductivity for the B_1u + irB_3u state. The imaginary part of the inelastic self energy at $T=T_{c0}$ and relative reduction in $T_c$ are indicated in each panel. For brevity, we denote ${\mathrm{\Sigma }}_{in}^{\prime \prime }(T=T_{c0})$ as ${\mathrm{\Sigma }}_{T=T_{c0}}^{\prime \prime }$ The s-wave scattering phase is tan⁻¹ (5). The relative reduction in T_c is indicated in each of the panels.

4 Summary and concluding remarks

We studied low-energy quasiparticle excitations and thermal transport for the single-component and two-component pairing states allowed by the irreducible representations of the D_2h point group symmetry, which is relevant for the orthorhombic UTe₂ crystals. Since D_2h has only one-dimensional representations, the four single-component pairing states corresponding to the irreducible representations cannot break the time-reversal symmetry and describe unitary triplet pairing states. Therefore, we also considered the pairing states that are combinations of two of the four irreducible representations using a single mixing parameter r. We examined all six two-component superconducting states as a function of r on a cylindrical Fermi surface, which describe either gapped states or states with spectral point nodes depending on the value of the mixing parameter. The spectral point nodes are not necessarily the zeros of order parameters, but they are the points on the Fermi surface hosting quasiparticle excitations. The spectral nodes are identical to the gap nodes in the case of single-component or unitary states. These six states can be divided into AF or FM categories depending on the Fermi surface average of the Cooper pair spin moment, which vanishes for the AF states and remains finite for the FM states. Except for the A_1u + irB_1u state, all other states are chiral on the cylindrical Fermi surface as the average angular momentum of the Cooper pairs remains finite.

After introducing the single-parameter model for the two-component states, we calculated the effect of impurity scattering within the self-consistent T-matrix approximation. One of the new findings is the spin-dependent impurity scattering rate for the chiral states. This happens due to finite quasiparticle spin densities for the chiral states. This can be interpreted as accumulation of magnetization near the impurity sites and this leads to qualitative changes in the quasiparticle excitation spectrum. For the two-component states, the nodes are accidental, not symmetry-imposed, like the single-component states, and the spin-dependent self-energy or the impurity-pinned magnetization can change the position of the spectral nodes. In principle, the removal of spectral point nodes by impurity scattering is possible in the chiral superconducting states, but we have not found such an effect for the cases that we considered. Next, we calculate the thermal conductivity using the Kubo formula for the thermal–current response function. Due to spin-dependent impurity self-energies, the thermal conductivity significantly differs from the thermal conductivity reported for the unitary states. We examine the thermal transport for all the single- and double-component states that are possible for the D_2h point group.

We have considered a single band with a cylindrical Fermi surface in our theoretical calculations. The quantum oscillation experiment reports two cylindrical Fermi surfaces, where one is an electron-like and the other is a hole-like Fermi surface with comparable effective masses [35]. However, we expect our analysis to be valid for a two-band system as well because interband scattering is always pair-breaking due to odd-parity order parameters. The impurity will renormalize the quasiparticle energies, and there will not be any off-diagonal impurity self-energy. Therefore, multiple bands will lead to a higher impurity scattering rate; this should not affect the anisotropy of the thermal transport. There are also some speculations about a closed Fermi surface near the Z point; therefore, we also considered a spherical Fermi surface (see Supplementary Material). The key qualitative difference is the possibility of nodes along the $\widehat{z}$-axis and strong thermal conductivity along that direction; however, there are no experimental data available to support that scenario.

Based on our thermal transport study and some recent experimental data, we can identify some states that could possibly describe the gap structure in UTe₂. Definitive conclusions are not possible at this time due to a lack of sufficient direction-dependent data on the newer samples, but we can make some qualitative statements and rule out some states. For the A_1u + irB_1u state on a cylindrical Fermi surface, the normalized thermal conductivity shows isotropic behavior as a function of impurity scattering in the zero-temperature limit and in its temperature dependence for a fixed disorder level. The limited data that are available for the thermal conductivity indicate weak in-plane anisotropy, but not absolute isotropic behavior [7]. The thermal conductivity measurements obtained by [34] claim a fully gapped superconducting state. In contrast, another independent thermal conductivity measurement obtained by Hayes et al. shows evidence for point nodes without finding any residual thermal conductivity in the zero-temperature limit [8]. Therefore, the absence of finite zero-temperature limit thermal conductivity in high-quality samples is not sufficient to rule out point nodes. Other probes such as the field dependence of specific heat suggest a superconducting state with nodes closer to the $\widehat{y}$-axis [36]. The superfluid density measurement indicates stronger low-energy quasiparticle excitations along the $\widehat{y}$ directions and weakest along the $\widehat{x}$-axis [29]. The relative anisotropy in the penetration depth measurements is weaker than that in the single-component states. We find that the A_1u + irB_2u, B_2u + irB_3u state with a dominant B_2u component and the B_1u + irB_3u state show stronger quasiparticle excitations along the $\widehat{y}$-axis. The B_1u + irB_3u state shows a change in anisotropy as a function of temperature, which can be used to distinguish it from the other two states. This state also shows a quadratic point node for r = 1, which shows linear DOS at low energies; hence, it can also be ruled out. The two ferromagnetic states show higher thermal conductivity along the $\widehat{y}$ direction than the B_2u state, which has point nodes along the $\widehat{y}$-axis.

As mentioned earlier, the phonon thermal conductivity could be significant, especially in the low T_c samples. At very low temperatures, the scattering of phonons from defects dictates the phonon mean free path, and hence the phonon thermal conductivity [37–39]. Phonon thermal conductivity is expected to be insignificant in the high-quality samples due to the low concentration of defects. Therefore, a systematic measurement of thermal conductivity along all three directions in the samples with high residual resistivity ratios is highly desirable. One common feature among all these superconducting phases is zero κ/T in the zero-temperature limit in clean samples. For sufficient disorder, even point nodal states acquire a very small residual κ/T, which would require very careful low-T measurements to detect.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

VM: writing–original draft and writing–review and editing. GW: writing–original draft and writing–review and editing. PH: writing–original draft and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. PH was supported by the NSF under DMR-2231821.

Acknowledgments

The authors thank S. Anlage, I. Hayes, T. Metz, J.P. Paglione, and T. Shibauchi for useful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1397524/full#supplementary-material

References

1. Ran S, Eckberg C, Ding QP, Furukawa Y, Metz T, Saha SR, et al. Nearly ferromagnetic spin-triplet superconductivity. Science (2019) 365:684–7. doi:10.1126/science.aav8645

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Aoki D, Ishida K, Flouquet J. Review of U-based ferromagnetic superconductors: comparison between UGe₂, URhGe, and UCoGe. J Phys Soc Jpn (2019) 88:022001. doi:10.7566/JPSJ.88.022001

CrossRef Full Text | Google Scholar

3. Aoki D, Brison JP, Flouquet J, Ishida K, Knebel G, Tokunaga Y, et al. Unconventional superconductivity in UTe₂. J Phys Condensed Matter (2022) 34:243002. doi:10.1088/1361-648X/ac5863

CrossRef Full Text | Google Scholar

4. Fujibayashi H, Nakamine G, Kinjo K, Kitagawa S, Ishida K, Tokunaga Y, et al. Superconducting order parameter in ute2 determined by knight shift measurement. J Phys Soc Jpn (2022) 91:043705. doi:10.7566/JPSJ.91.043705

CrossRef Full Text | Google Scholar

5. Matsumura H, Fujibayashi H, Kinjo K, Kitagawa S, Ishida K, Tokunaga Y, et al. Large reduction in the a-axis knight shift on UTe₂ with T_c = 2.1 k. J Phys Soc Jpn (2023) 92:063701. doi:10.7566/JPSJ.92.063701

CrossRef Full Text | Google Scholar

6. Aoki D, Nakamura A, Honda F, Li D, Homma Y, Shimizu Y, et al. Unconventional superconductivity in heavy fermion ute2. J Phys Soc Jpn (2019) 88:043702. doi:10.7566/JPSJ.88.043702

CrossRef Full Text | Google Scholar

7. Metz T, Bae S, Ran S, Liu IL, Eo YS, Fuhrman WT, et al. Point-node gap structure of the spin-triplet superconductor ute₂. Phys Rev B (2019) 100:220504. doi:10.1103/PhysRevB.100.220504

CrossRef Full Text | Google Scholar

8. Hayes IM, Metz TE, Frank CE, Saha SR, Butch NP, Mishra V, et al. Robust nodal behavior in the thermal conductivity of superconducting UTe₂. arXiv:2402 (2024):19353. doi:10.48550/arXiv.2402.19353

CrossRef Full Text | Google Scholar

9. Volovik GE, Gorkov LP. Superconducting classes in heavy-fermion systems. Zh Eksp Teor Fiz (1985) 88:1412–28.

Google Scholar

10. Ueda K, Rice TM. p-wave superconductivity in cubic metals. Phys Rev B (1985) 31:7114–9. doi:10.1103/PhysRevB.31.7114

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Blount EI. Symmetry properties of triplet superconductors. Phys Rev B (1985) 32:2935–44. doi:10.1103/PhysRevB.32.2935

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Ran S, Liu IL, Eo YS, Campbell DJ, Neves PM, Fuhrman WT, et al. Extreme magnetic field-boosted superconductivity. Nat Phys (2019) 15:1250–4. doi:10.1038/s41567-019-0670-x

CrossRef Full Text | Google Scholar

13. Wang Z, Rodriguez JO, Jiao L, Howard S, Graham M, Gu GD, et al. Evidence for dispersing 1D Majorana channels in an iron-based superconductor. Science (2020) 367:104–8. doi:10.1126/science.aaw8419

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kitaev AY. Unpaired majorana fermions in quantum wires. Physics-Uspekhi (2001) 44:131–6. doi:10.1070/1063-7869/44/10S/S29

CrossRef Full Text | Google Scholar

15. Wilczek F. Majorana returns. Nat Phys (2009) 5:614–8. doi:10.1038/nphys1380

CrossRef Full Text | Google Scholar

16. Ivanov DA. Non-abelian statistics of half-quantum vortices in p-wave superconductors. Phys Rev Lett (2001) 86:268–71. doi:10.1103/PhysRevLett.86.268

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chung SB, Zhang HJ, Qi XL, Zhang SC. Topological superconducting phase and majorana fermions in half-metal/superconductor heterostructures. Phys Rev B (2011) 84:060510. doi:10.1103/PhysRevB.84.060510

CrossRef Full Text | Google Scholar

18. Hayes IM, Wei DS, Metz T, Zhang J, Eo YS, Ran S, et al. Multicomponent superconducting order parameter in UTe₂. Science (2021) 373:797–801. doi:10.1126/science.abb0272

CrossRef Full Text | Google Scholar

19. Rosa PFS, Weiland A, Fender SS, Scott BL, Ronning F, Thompson JD, et al. Single thermodynamic transition at 2 k in superconducting UTe₂ single crystals. Commun Mater (2022) 3:33. doi:10.1038/s43246-022-00254-2

CrossRef Full Text | Google Scholar

20. Sakai H, Opletal P, Tokiwa Y, Yamamoto E, Tokunaga Y, Kambe S, et al. Single crystal growth of superconducting ute₂ by molten salt flux method. Phys Rev Mater (2022) 6:073401. doi:10.1103/PhysRevMaterials.6.073401

CrossRef Full Text | Google Scholar

21. Ajeesh MO, Bordelon M, Girod C, Mishra S, Ronning F, Bauer ED, et al. The fate of time-reversal symmetry breaking in UTe₂. Phys. Rev. X (2023) 13:041019. doi:10.1103/PhysRevX.13.041019

CrossRef Full Text | Google Scholar

22. Azari N, Yakovlev M, Rye N, Dunsiger SR, Sundar S, Bordelon MM, et al. Absence of Spontaneous magnetic fields due to time-reversal symmetry breaking in Bulk superconducting UTe₂. Phys. Rev. Lett. (2023) 131:226504. doi:10.1103/PhysRevLett.131.226504

CrossRef Full Text | Google Scholar

23. Theuss F, Shragai A, Grissonnanche G, Hayes IM, Saha SR, Eo YS, et al. Single-component superconductivity in UTe₂ at ambient pressure. Nat. Phys. (2024). doi:10.1038/s41567-024-02493-1

CrossRef Full Text | Google Scholar

24. Ambegaokar V, Griffin A. Theory of the thermal conductivity of superconducting alloys with paramagnetic impurities. Phys Rev (1965) 137:A1151–67. doi:10.1103/PhysRev.137.A1151

CrossRef Full Text | Google Scholar

25. Kadanoff LP, Martin PC. Hydrodynamic equations and correlation functions. Ann Phys (1963) 24:419–69. doi:10.1016/0003-4916(63)90078-2

CrossRef Full Text | Google Scholar

26. Schmitt-Rink S, Miyake K, Varma CM. Transport and thermal properties of heavy-fermion superconductors: a unified picture. Phys Rev Lett (1986) 57:2575–8. doi:10.1103/PhysRevLett.57.2575

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Hirschfeld P, Vollhardt D, Wölfle P. Resonant impurity scattering in heavy fermion superconductors. Solid State Commun (1986) 59:111–5. doi:10.1016/0038-1098(86)90190-0

CrossRef Full Text | Google Scholar

28. Hirschfeld PJ, Wölfle P, Einzel D. Consequences of resonant impurity scattering in anisotropic superconductors: thermal and spin relaxation properties. Phys Rev B (1988) 37:83–97. doi:10.1103/PhysRevB.37.83

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ishihara K, Roppongi M, Kobayashi M, Imamura K, Mizukami Y, Sakai H, et al. Chiral superconductivity in UTe₂ probed by anisotropic low-energy excitations. Nat Commun (2023) 14:2966. doi:10.1038/s41467-023-38688-y

CrossRef Full Text | Google Scholar

30. Marchenko VI. On the theory of gauge symmetry of superconductors. Zh Eksp Teor Fiz (1986) 93:583–9.

Google Scholar

31. Sigrist M, Rice TM. Symmetry classification of states in high temperature superconductors. Z Phys B (1987) 68:9–14. doi:10.1007/BF01307857

CrossRef Full Text | Google Scholar

32. Annett JF. Symmetry of the order parameter for high-temperature superconductivity. Adv Phys (1990) 39:83–126. doi:10.1080/00018739000101481

CrossRef Full Text | Google Scholar

33. Fledderjohann A, Hirschfeld P. Thermal conductivity anisotropy in superconducting UPt₃. Solid State Commun (1995) 94:163–7. doi:10.1016/0038-1098(95)00050-X

CrossRef Full Text | Google Scholar

34. Suetsugu S, Shimomura M, Kamimura M, Asaba T, Asaeda H, Kosuge Y, et al. Fully gapped pairing state in spin-triplet superconductor UTe₂. Sci Adv. (2024) 10: eadk3772. doi:10.1126/sciadv.adk3772

CrossRef Full Text | Google Scholar

35. Aoki D, Sakai H, Opletal P, Tokiwa Y, Ishizuka J, Yanase Y, et al. First observation of the de haas–van alphen effect and fermi surfaces in the unconventional superconductor UTe₂. J Phys Soc Jpn (2022) 91:083704. doi:10.7566/JPSJ.91.083704

CrossRef Full Text | Google Scholar

36. Lee S, Woods AJ, Rosa PFS, Thomas SM, Bauer ED, Lin SZ, et al. Anisotropic field-induced changes in the superconducting order parameter of ute2. arXiv:2310.04938. (2023). doi:10.48550/arXiv.2310.04938

CrossRef Full Text | Google Scholar

37. Klemens PG. The scattering of low-frequency lattice waves by static imperfections. Proc Phys Soc London, Sect A (1955) 68:1113–28. doi:10.1088/0370-1298/68/12/303

CrossRef Full Text | Google Scholar

38. Bardeen J, Rickayzen G, Tewordt L. Theory of the thermal conductivity of superconductors. Phys Rev (1959) 113:982–94. doi:10.1103/PhysRev.113.982

CrossRef Full Text | Google Scholar

39. Uher C Thermal conductivity of high-tcsuperconductors. J Superconductivity (1990) 3:337–89. doi:10.1007/BF00617463

CrossRef Full Text | Google Scholar