Insensitivity of Tc to the residual resistivity in high-Tc cuprates and the tale of two domes

One of the few undisputed facts about hole-doped high-T_c cuprates is that their superconducting gap Δ has d-wave symmetry. According to ‘dirty’ d-wave BCS theory, even structural (non-magnetic) disorder can suppress Δ, the transition temperature T_c and the superfluid density ρ_s. The degree to which the latter is affected by disorder depends on the nature of the scattering. By contrast, T_c is only sensitive to the total elastic scattering rate (as estimated from the residual resistivity ρ₀) and should follow the Abrikosov-Gor’kov pair-breaking formula. Here, we report a remarkable robustness of T_c in a set of Bi2201 single crystals to large variations in ρ₀. We also survey an extended body of data, both recent and historical, on the LSCO family which challenge key predictions from dirty d-wave theory. We discuss the possible causes of these discrepancies, and argue that either we do not understand the nature of disorder in cuprates, or that the dirty d-wave scenario is not an appropriate framework. Finally, we present an alternative (non-BCS) scenario that may account for the fact that the superconducting dome in Tl2201 extends beyond that seen in Bi2201 and LSCO and suggest ways to test the validity of such a scenario.

1 Introduction

Over the past decade or so, overdoped (OD) cuprates, i.e., those with a carrier density beyond optimal doping, have become the central focus of efforts to elucidate the origin of high-T_c superconductivity. This shift of focus has emerged from two seemingly contradictory standpoints. The first is the perceived simplicity of the nature of the OD regime; the normal state pseudogap (on the hole-doped side) having been suppressed and with it, many of the associated ordering tendencies [1]. The second is the realization that this region of the cuprate phase diagram also hosts its own highly anomalous properties, both in the normal and superconducting (SC) states [2–14]. Chief among these is the report of a robust linear-in-T dependence of the superfluid stiffness ρ_s as T_c → 0 on the overdoped side [5]. Prior to this discovery, the observed reduction in T_c and ρ_s with overdoping had been attributed to a combination of a diminishing pairing interaction and the pair-breaking effects of impurities treated within a ‘dirty d-wave’ extension of BCS theory. The robustness of the T-linear form of ρ_s(T), a hallmark of clean d-wave superconductivity, was inconsistent with theoretical predictions and thus presented a challenge to the pre-existing consensus of what drives the reduction of T_c and ρ_s with overdoping.

In response to this challenge, a thorough examination of the viability of the dirty d-wave scenario was carried out on two very different OD cuprates–La_2−xSr_xCuO₄ (LSCO) and Tl₂Ba₂CuO_6+δ (Tl2201)–using realistic parameterisations of their respective electronic structures and treating the scattering potentials generated by out-of-plane defects with ab initio DFT calculations [15–19]. The conclusions of this work were that many facets of the SC state in both families, including the dependence of ρ_s on T and p [5], the THz optical conductivity (in LSCO) [7], the residual specific heat [20, 21] and the residual thermal conductivity [22–25] could be successfully captured within the existing framework. In order to account for the robustness of the T-linearity of ρ_s(T) down to low-T, the total scattering potential was argued to consist almost exclusively of weak (Born) scatterers–due to the out-of-plane defects–combined with a small amount of strong (unitarity-limit) scatterers located within the CuO₂ plane (see also Ref. [26]).

Within the same picture, the suppression of T_c from its disorder-free value T_c0 does not depend on the nature of the scatterer, only on the absolute magnitude of the normal-state scattering rate Γ_n, as described by the Abrikosov-Gorkov pair-breaking formula [27]. In the work of Broun, Hirschfeld and co-workers [15–19], estimates for Γ_n were deduced from the residual resistivity ρ₀ (essentially an extrapolation of the normal-state in-plane resistivity ρ_ab(T) down to zero temperature). These estimates for Γ_n (≈20 K in OD Tl2201 and ≈55 K in OD LSCO) were then found to generate T_c(p) domes with realistic values for the maximum T_c $(T_c^{\text{max}})$ as well as the doping level (p_sc) at which superconductivity vanishes in both families. Initially, these T_c(p) domes were derived from a single T_c0(p) dome [17]. The later, more refined ab initio treatment required two T_c0(p) domes to reproduce the experimental results though the difference between them was only slight [18].

One of the most consequential aspects of dirty d-wave theory, largely overlooked until now, is the strong dependence of T_c on Γ_n, irrespective of the nature of the scattering potential. As a rough guide, an increase in ρ₀ by 10 μΩcm corresponds to a decrease in both Γ_n and T_c of order 10 K. (More details of this correspondence will be presented later). Such modest variations in ρ₀ are not uncommon in samples from different growth batches or in samples synthesized in different laboratories and thus one might expect a notable variation in reported T_c values. Yet, throughout almost 4 decades of cuprate research, the SC domes reported in the literature for a particular cuprate family have been, to all intents and purposes, identical, both in terms of their $T_c^{\text{max}}$ values and the doping extent of the dome itself.

The aim of this article is to highlight this insensitivity of T_c to changes in ρ₀ in different OD cuprates through a combination of new measurements and analysis of existing data. The article itself is divided into three parts. The first is an in-house transport study of one of the most inhomogeneous cuprate families–Pb/La-doped Bi₂Sr₂CuO_6+δ (Bi2201)–that exhibits a remarkable robustness of T_c to marked changes in ρ₀. The second is a survey of recent transport data on LSCO crystals and films which, when combined with multiple reports of the T_c(x) dome in LSCO spanning several decades, represent a notable challenge to the applicability of dirty d-wave BCS theory to OD cuprates. In the final section, we present a simple (two-fluid) scenario for OD cuprates which offers an alternative explanation as to why p_sc (Tl2201) $>p_{sc}$(Bi2201/LSCO). While incorporating disorder-induced pair-breaking in some capacity, this scenario considers the strange metallic nature of OD cuprates [28] as its defining feature. The corollary of this study is that either we do not understand the nature of disorder in cuprates, or that the dirty d-wave scenario, at least in its present guise, is not an appropriate framework to describe the suppression of superconductivity in OD cuprates as p → p_sc.

2 Results and discussion

2.1 Robustness of T_c to variations of ρ₀ in Bi2201

Large single crystals of Pb/La-doped Bi2201 were taken from boules grown independently at two sites via the floating-zone technique. The doping level of the crystals used in this study (p = 0.215 ± 0.005) was estimated from the measured T_c using the Presland relation $1-T_c/T_c^{\text{max}}=82.6{(p-0.16)}^2$ [29], with $T_c^{\text{max}}$ = 36 K. Recently, it was shown that when using this relation, normalized ρ_ab(T) curves for Bi2201 and LSCO single crystals of the same p (or T_c) value collapse on top of one another [30]. The crystals were cleaved along the ab-plane and cut into shape along the c-axis using a wire saw which leaves no burring of the edges. Typical sample dimensions were approximately 1,000 × 200 × 8–40 μm³ (the thicknesses having been determined by a scanning electron microscope).

For the resistivity measurements, electrical contacts were made using 25 μm Au wire and fixed using Dupont 6838 paint before being annealed in flowing oxygen for 10 min at 450°C. Typical contact resistances were between 1 and 10 Ω. All samples were cooled using a ⁴He flow cryostat and their in-plane resistivity measured using a standard four-point ac lock-in detection technique. While the dimensions of the samples could be determined to a high degree of accuracy, the absolute magnitudes of ρ_ab(T) were subject to an uncertainty of ±25% due to the uncertainty in estimating the distance between the voltage electrodes. Complementary magnetization measurements were carried out in a commercial SQUID magnetometer.

Figure 1 shows ρ_ab(T) curves for 6 Pb/La-doped Bi2201 crystals grown in Amsterdam (top panel) and Sendai (bottom panel). For both sets of crystals T_c ≃ 27 K and p ≃ 0.20. According to a recent combined transport and angle-resolved photoemission spectroscopy (ARPES) study [30], this doping level lies very close to the doping level p* at which the pseudogap regime terminates in Bi2201. Correspondingly, all ρ_ab(T) curves display a quasi-T-linear dependence from room temperature down to T_c albeit shifted with respect to each other due to the difference in their respective ρ₀ values.

Figure 1

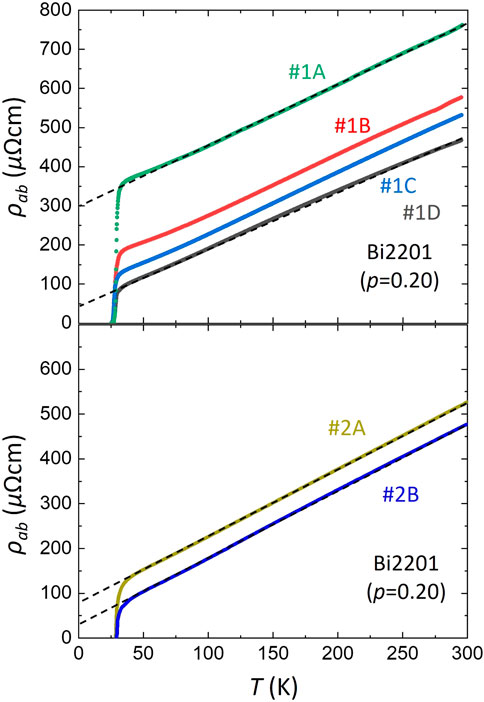
Figure 1. In-plane resistivity versus temperature ρ_ab(T) for several Bi2201 single crystals with a doping level p ≈0.20. The crystals in the two panels were grown at two distinct sites: those labeled ♯1 (top panel) were grown in Amsterdam, while those labeled ♯2 (bottom panel) were grown in Sendai. The dashed lines are extrapolations of a fit to ρ_ab(T) between 50 and 150 K to allow a better estimate of the residual resistivity (ρ₀) values for each crystal. Note that the ρ_ab(T) curves have been normalised such that their high-T T-linear slopes are equivalent. The adjustments required to normalise these slopes were of the order of the geometrical uncertainty (±25%) in each panel.

In certain crystals (labelled ♯1B and ♯1C in Figure 1A), ρ_ab(T) displays a small upward deviation from T-linearity below around 75 K. One possible origin for this upward deviation is contamination of the signal from c-axis mixing, whereby a proportion of the current flows between the CuO₂ planes. The anisotropy in the resistivity ρ_c/ρ_ab is extremely large in Bi2201 (≈10⁵–10⁶) [31] and ρ_c(T) is known to exhibit only weakly metallic behaviour in the OD regime. Hence, any c-axis mixing would lead to a marked increase in the absolute value of the as-measured resistivity relative to the intrinsic ab-plane response as well as a different T-dependence. In order to minimise this possibility, each sample was mounted in a ‘floating’ configuration, i.e., elevated above the substrate with the silver paint fully extending across the sample thickness, in order to isolate the in-plane current response and avoid any contamination from current along the c-axis. Using only samples in which the resistivities on opposite sides of the crystal were identical, we obtained a series of ρ_ab(T) curves that exhibit the same T-linear slope between 75 K and 300 K (to within our geometrical uncertainty), suggesting that c-axis mixing is indeed negligible in these crystals.

The most striking feature of Figure 1 is the invariance of T_c (= 27 ± 1 K), irrespective of the magnitude of ρ₀, that itself varies by over 250 μΩcm. (For each crystal, ρ₀ is obtained by extrapolating a fit to ρ_ab(T) between 50 K and 150 K). Moreover, any small variations in the value of T_c do not appear to be correlated with ρ₀. As we will discuss in the following section, this level of impurity scattering should be enough to destroy superconductivity many times over. Such robustness is contrary to expectations within dirty d-wave theory in which changes in T_c and ρ₀ are strongly correlated (via Γ_n).

2.2 Comparison with dirty d-wave theory

Dirty d-wave theory, as applied to cuprate superconductivity, is an extension of an original treatment of paramagnetic impurities in a conventional (s-wave) BCS superconductor [27]. Due to the sign change of the SC order parameter Δ occurring at the nodes, even non-magnetic impurities can induce pair breaking in a d-wave superconductor. This in turn leads to a residual density of zero-energy states and a suppression of both T_c and the superfluid density n_s. More quantitatively, Δ closes at a T_c value that is reduced in the presence of disorder from its optimal value T_c0 according to the Abrikosov-Gor’kov (AG) equation:

$\mathrm{l}\mathrm{n}\frac{T_{c0}}{T_c}={\psi }_0\left(\frac{1}{2}+\frac{\hslash {\mathrm{\Gamma }}_n}{2\pi k_B{T}_c}\right)-{\psi }_0\left(\frac{1}{2}\right),(1)$

where ψ₀ is the usual digamma function, Γ_n is the normal-state impurity scattering rate, and ℏ and k_B are the reduced Planck constant and Boltzmann constant, respectively.

As mentioned in the Introduction, a recent series of studies based on the self-consistent T-matrix approximation (SCTMA) have indicated that a number of experimental observations in LSCO and Tl2201 can be successfully accounted for by carefully treating the scattering potentials arising from different types of out-of-plane disorder within the dirty d-wave formalism [15–19]. Within their picture, the momentum relaxation rate is assumed to be the same as the single-particle scattering rate, as deduced, for example, from ARPES. Accordingly, Γ_n can be estimated from the Drude expression for the (residual) dc resistivity:

${\rho }_0=\frac{m^{*}}{n{e}^2}{\mathrm{\Gamma }}_n.(2)$

Here m* is the effective mass, n is the carrier density and e is the electronic charge. Within the SCTMA, Born and unitarity scattering contribute additively to Γ_n and thus, from the perspective of Eq. 1, the suppression of T_c is largely independent of the impurity phase shift. Note too that the above expression does not take into account the effects of small-angle scattering, which can cause the momentum relaxation rate to be substantially smaller than the single-particle scattering rate. Hence, the estimate of Γ_n from Eq. 2 is in fact a lower bound for input into Eq. 1.

Figure 2 reproduced from Ref. [17]–shows how different T_c(p) domes for LSCO (red line) and Tl2201 (blue line) can be derived from a singular form of T_c0(p) using estimates for Γ_n that are consistent with experimental observations. The quoted values of Γ_n = 6π (18π) K correspond to ρ₀ = 6 (20) μΩcm for Tl2201 (LSCO), respectively. (As mentioned above, in a subsequent study [18], slightly modified T_c0(p) domes for Tl2201 and LSCO were incorporated into the model, though the differences were only minor.) The essential feature of Figure 2 is that the reduction in T_c of ∼ 20 K (60 K) from its inferred T_c0 value in optimally doped Tl2201 (LSCO) is attributed to a normal state scattering rate of approximately the same magnitude. At the same time, the extent of the SC dome in LSCO (on the overdoped side) is reduced by Δp ≈ 0.06 for the same level of impurity scattering.

Figure 2

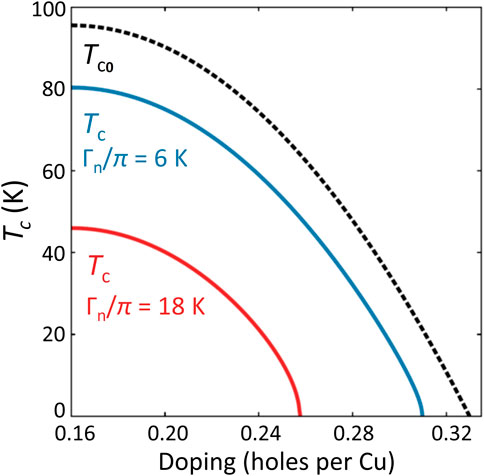
Figure 2. Predictions of dirty d-wave theory. For a single parabolic doping dependence of the underlying T_c0(p), different choices of Γ_n result in superconducting domes T_c(p) reminiscent of Tl2201 and LSCO. The quoted values of Γ_n = 6π (18π) K correspond to ρ₀ values of 6 (20) μΩcm for Tl2201 (LSCO), respectively. For Bi2201, ρ₀ = 50 μΩcm corresponds to Γ_n ∼ 90 K or 30π K. Reproduced with kind permission from Ref. [17].

In order to link these estimates for Γ_n to ρ₀, we must also derive estimates for m* and n = (1 + p)/V_cell into Eq. 1, where V_cell is the volume of the unit cell. First, let us consider LSCO. For p = x = 0.20, we obtain m* ∼ 10 m_e (the bare electron mass) from the electronic specific heat [32] and n = 1.3 × 10²⁸ m⁻³ (using 1 + p instead of p). Hence, Γ_n = 55 K corresponds to ρ₀ ∼ 20 μΩcm, as quoted above. Similarly for Tl2201 (p = 0.27), m* ∼ 5 m_e [33, 34], n = 7.4 × 10²⁷ m⁻³ and Γ_n = 18 K, giving ρ₀ ∼ 6 μΩcm.

2.3 Application of dirty d-wave theory to Bi2201

For Bi2201, m* ∼ 7–10 m_e for p ∼ 0.23 (T_c = 18 K) [35] and n = 7.0 × 10²⁷ m⁻³. Hence, the spread in ρ₀ shown in Figure 1 (40–290 μΩcm) corresponds to 70 K ≲ Γ_n ≲ 500 K. In other words, while the impurity scattering rate deduced from ρ₀ varies on the scale of 500 K, the superconducting transition temperature is found to be constant to within 1 K. Such extreme inequality is clearly at odds with expectations from dirty d-wave theory but is likely, at least in part, to reflect the presence of some form of defect that contributes to an enhanced ρ₀ while creating, by itself, little or no pair-breaking. Before addressing the viability of the BCS pair-breaking picture, therefore, let us first consider alternative explanations for this surprising finding. (Recall that we have already dismissed c-axis mixing in the current flow as a possible cause of this variation in ρ₀.)

In this present study, T_c values are quoted based on ρ_ab(T) measurements. Resistivity is effectively a one-dimensional probe of superconductivity, in the sense that a transition to zero resistivity requires only a single, filamentary SC path to be realized. Hence, if a sliver of nominally pristine Bi2201 (i.e., with minimal disorder) permeates each crystal, the apparent robustness of T_c may be illusory. In the normal state, by contrast, the current distribution will be sensitive to all regions of the sample and indeed, if the SC filament is sufficiently thin, it will be dominated by those non-SC regions with higher ρ₀. Such a scenario may help explain why T_c is so insensitive to marked variations in ρ₀.

Simulations presented in Supplementary Appendix SA indicate that for such a scenario to be applicable, the SC region must occupy ∼ 1% of the total volume of the sample; otherwise the T-dependence of ρ_ab(T) will visibly deviate downwards from its intrinsic (T-linear) behaviour, which is not observed. In order to estimate the SC volume fraction of our crystals, we measured the dc magnetisation of two of them (with ρ₀ values of 80 μΩcm (ρ(T) data not shown) and 300 μΩcm (Sample #1A in Figure 1), respectively) using a SQUID magnetometer with the magnetic field applied parallel to the ab-plane (where the demagnetisation factor is minimised). The results are shown in Supplementary Appendix SB and reveal an estimated volume fraction in both crystals of ∼ 100%. Thus, it seems unlikely that the presence of a filamentary SC path (which would have to be very similar in form in all crystals studied) can account for the observed robustness of the SC transition.

A more plausible origin of this insensitivity of T_c on ρ₀ is the presence of specific (extended) forms of microstructural defects (e.g., dislocations, columnar defects, grain boundaries, etc., … ) that adversely affect ρ₀ while contributing minimally to pair breaking. An example of such extended defects having a profound effect on ρ_ab(T) but a minimal effect on T_c can be found in the infinite-layer nickelates [36, 37]. Structural and electronic nanoscale inhomogeneity is a well-known feature of Bi-based cuprates [14, 38], but this inhomogeneity tends to be more point-like than extended and as such, should also have a similar effect on both T_c and ρ₀. Larger defects, such as microcracks, could also cause an increased resistivity though in this case, one might expect to see Arrhenius-type behaviour (ρ(T) ∝ exp(−Δ/k_BT)) due to tunneling across the crack, as one finds in polycrystalline samples with multiple grain boundaries. While we noted earlier that there were small upturns observed in the ρ_ab(T) curves of some of our Bi2201 crystals, there did not appear to be any correlation between the value of ρ₀ and the presence of an upturn.

A dedicated transmission electron microscopy (TEM) study is currently underway to look for evidence for the type of defect that might cause this dichotomy between T_c and ρ₀, the results of which will be published elsewhere. Although we cannot rule out the presence of such extended defects affecting ρ₀ without impacting T_c, in the following section we present a body of evidence on the LSCO family that provides arguably a greater challenge to the viability of the dirty d-wave scenario to cuprates within the strange metal regime.

2.4 Review of T_c dependence on ρ₀ in LSCO

It is well known that superconductivity in cuprates is strongly suppressed upon Zn substitution on the planar Cu site. In LSCO, for example, 4% Zn substitution can destroy superconductivity entirely while at the same time raising ρ₀ by ∼ 50 μΩcm [39]. The origin of this suppression is not entirely clear. Despite being a non-magnetic impurity, Zn dopants appear to influence strongly the magnetic environment within the CuO₂ plane as well as act as unitarity-limit scatterers [39].

Mahmood et al. [40] recently reported a study on OD LSCO thin films irradiated using 1 MeV oxygen ions. Ion irradiation is believed to create narrow columnar defect tracks throughout the film. Figure 3A shows a series of ρ_ab(T) curves obtained on an optimally doped LSCO film exposed to different fluences using a flux gradient to produce a spread in defect density. Irradiation leads to a maximal increase in ρ₀ of 36–40 μΩcm without the T-dependence or the slope of the ρ_ab(T) curves changing. Such adherence to Matthiessen’s rule, coupled with accompanying measurements of the low-frequency Drude response, suggests that the irradiation is simply creating additional elastic scattering centres. According to the calculations in Section 2.2, the magnitude of Δρ₀ corresponds to ΔΓ_n > 100 K, and given that Eqs 1, 2 predict a ∼ 1 K drop in T_c for every 1 K increase in Γ_n, clearly such a level of disorder should be sufficient to remove all vestiges of superconductivity in the film. Yet T_c itself is found to drop by less than 5 K.

Figure 3

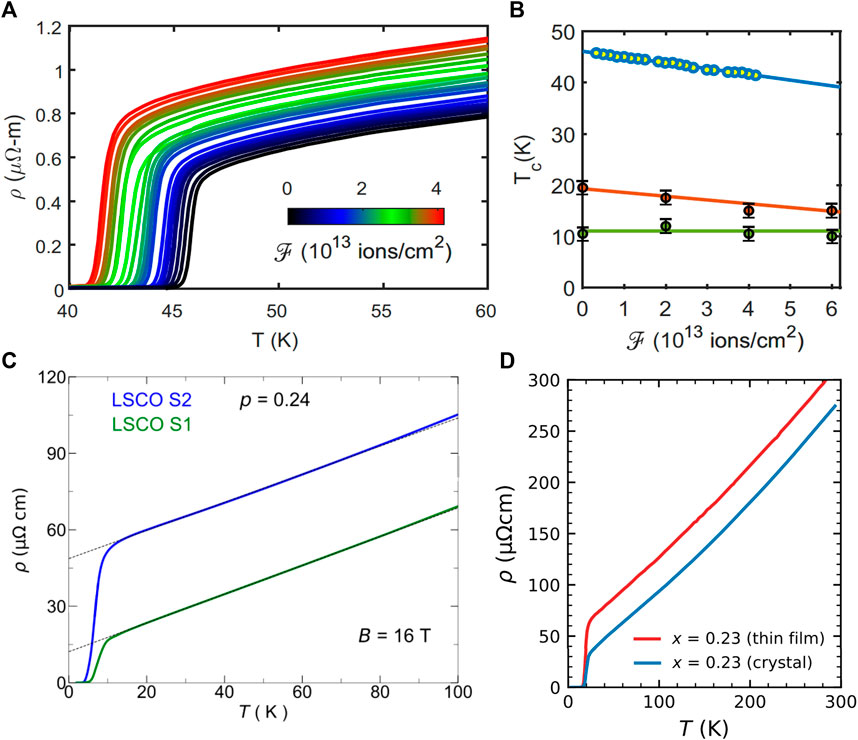
Figure 3. Examples of the robustness of T_c to changes in ρ₀ in LSCO. (A) ρ_ab(T) of an optimally doped LSCO thin film (x = 0.16) irradiated with 1 MeV oxygen ions, but with a total fluence that varies across the devices between 0 and 4 × 10¹³ ions/cm², as indicated by the inset color bar. Reproduced with kind permission from Ref. [40]. (B) T_c as a function of irradiation fluence $\mathcal{F}$ for an optimally doped film (blue dots) and two overdoped LSCO films with different initial T_c values (red and green dots). Solid lines are guides to the eye. Reproduced with kind permission from Ref. [40]. (C) ρ_ab(T) of two different crystals of LSCO (x = 0.24) with ρ₀ values differing by 36 μΩcm, corresponding to ΔΓ_n ∼ 100 K. Despite this large value of ΔΓ_n, the respective T_c values differ by only 1.5 K (Note that these ρ_ab(T) curves were obtained in a magnetic field of 16 T applied perpendicular to the CuO₂ planes). Reproduced with kind permission from Ref. [41]. (D) Comparison of ρ_ab(T) of a LSCO single crystal (x = 0.23, blue curve) and a LSCO thin film (x = 0.23, red curve). Reproduced from Ref. [43]. The ρ_ab(T) data for the thin film has been divided by two in order to normalize the slopes. The corresponding ρ₀ values are 20 and 50 μΩcm respectively, corresponding to ΔΓ_n ∼ 85 K.

One expects that an optimally doped film will possess a more robust SC state than those at a higher doping level with a lower T_c. In reality, Mahmood et al. observed the opposite trend. As shown in Figure 3B, for a pristine film with T_c ∼ 10 K, there was no discernible change in T_c for the same level of fluence that induced a ∼ 5 K reduction in T_c in the optimally-doped film. It seems that the more overdoped the pristine film is and the lower its initial superfluid density, the more robust is the superconductivity to similar levels of irradiation.

Two further examples of the insensitivity of T_c to changes in ρ₀ in OD LSCO are shown in Panels C and D of Figure 3. Panel C shows ρ_ab(T) curves for two single crystals (x = 0.24) whose ρ₀ values differ by ∼ 35 μΩcm, corresponding to ΔΓ_n ∼ 100 K [41], yet the difference in T_c in the two crystals is less than 2 K. Panel D shows ρ_ab(T) for a single crystal [2] and thin film [42] with x = 0.23. Note that the form of ρ_ab(T), as well as their derivatives [43], are the same, implying that their doping levels are essentially equivalent. The difference in ρ₀ of the two samples (after normalising their slopes [43]) is such that ΔΓ_n ∼ 85 K, but yet again, their T_c values are almost indistinguishable.

In the previous section, we discussed the possibility that in Bi2201, the insensitivity of T_c on ρ₀ reflects the fact that elastic scattering is dominated by extended defects that contribute largely to ρ₀ but do not, by themselves, break pairs and thereby cause a suppression in T_c. In the study by Mahmood et al., extended (columnar) defects were found to cause an increase in scattering, as deduced from the width of the Drude conductivity peak. We note too that the superfluid density also decreased, implying that such defects do indeed cause pair breaking, yet T_c itself remained remarkably robust.

According to Figure 2 and the corresponding relation between Γ_n and ρ₀, dirty d-wave theory predicts that for every 1 μΩcm increase in ρ₀, T_c in optimally doped LSCO should decrease by around 2.5 K [17], irrespective of the phase shift of the dominant scattering process. At the same time, the full extent of the SC dome diminishes by Δp ∼ 0.0075 per 1 μΩcm increase in ρ₀. This extreme sensitivity of the T_c(p) dome to small changes in ρ₀ represents arguably the greatest challenge to the theory’s applicability. Indeed, one of the most striking and largely overlooked features of cuprate research is the immutability of the T_c(p) dome.

The six panels in Figure 4 reproduce full T_c(p) domes for bulk LSCO reported over a period of 2 decades (1989–2009) [44–49]. The samples in question are both poly- and single crystalline and were prepared by various techniques, including flux and travelling-solvent floating-zone growth of single crystals and spray-drying or powder-mixing procedures for the ceramic powders. Note that all T_c values, bar those in panel (E), were determined by magnetisation or susceptibility measurements. The dashed green line in each panel represents the Presland formula [29] with $T_c^{\text{max}}$ = 38 K and assuming p = x (the Sr content). The consistent overlap between the dashed lines and the data indicates that the T_c(p) dome in bulk, as-grown LSCO is invariant, independent of the quality of the starting materials or the way in which the samples have been synthesized. Moreover, as highlighted by the single horizontal line spanning all six panels, $T_c^{\text{max}}$ is the same for all series of samples to within 1 K. For such consistency to be accounted for within the dirty d-wave scenario, ρ₀ would have to be identical to within 0.4 μΩcm $(<2\%)$ for every sample at every single doping level.

Figure 4

Figure 4. Superconducting domes in LSCO over the decades. T_c(x) as measured on (A–C) polycrystalline pellets grown via various techniques [44–46]; (D) flux-grown single crystals [47]; (E,F) travelling-solvent floating-zone crystals [48, 49]. For all panels except (E), T_c was determined from the onset of the Meissner (diamagnetic) signal. For panel (E), T_c was determined from the onset of zero resistivity. The dashed line in each panel is the Presland formula T_c = $T_c^{\text{max}}$(1–82.6 (x - 0.16)²) with $T_c^{\text{max}}$ = 38 K. All T_c(x) domes appear to follow the same trajectory with the same $T_c^{\text{max}}$ value (±1 K) and most remarkably, the same beginning (x = 0.05) and end (x = 0.27) points.

Such extreme levels of reproducibility are clearly beyond all reasonable expectations (requiring as it does that all LSCO samples have identical values of Γ_n to within 1 K) and highlight a key feature of the superconductivity in LSCO that remains unresolved. It appears that the T_c(p) dome in bulk LSCO is not, as has been argued [15], set by the level of disorder in the material, but by some other driving mechanism, such as the strength of next-nearest hopping [50, 51]. Certainly, it would be remarkable if the drop from T_c0(p) to T_c(p) for LSCO in Figure 2 were due to a scattering rate Γ_n whose magnitude is fixed and commensurate with a ρ₀ value equivalent to 20 μΩcm and that all other contributions to ρ₀, e.g., flux or crucible inclusions, were extraneous and had no further pair-breaking effect. A similar fundamental limit to ρ₀ would also have to exist for Bi2201, despite the fact that Bi2201 may contain multiple elements (e.g., Bi/Pb, La/Sr) in its formula unit.

Although a number of SC properties of OD LSCO and Tl2201 have been successfully modeled by considering the differences in the impurity potential, its phase shift and its location relative to the CuO₂ plane [15–19], the relation between T_c and Γ_n is, by and large, independent of these details and as such, should be a robust test of the theory’s applicability. The inability of dirty d-wave theory to account for the remarkable insensitivity of T_c to changes in ρ₀–highlighted in Figures 1, 4 – thus implies that either we do not understand the true causes of residual resistivity in cuprates (i.e., that the correspondence between Γ_n and ρ₀ is somehow lost), or that the basis of the theory is not the right framework to describe the transition from strange metal to superconductor.

Motivated by these findings, we present below an alternative (non-BCS) scenario for the robust T_c(p) domes in OD cuprates in which the non-FL nature of the cuprate strange-metal plays a central role. In the process, we offer an alternative explanation as to why the SC dome in cleaner Tl2201 extends to a higher p-value than in Bi2201 and LSCO and suggest ways to test the validity of such a scenario.

2.5 A tale of two domes

In the previous section, we highlighted various types of extended defects that could, in principle, enhance ρ₀ without necessarily inducing substantial pair breaking within the CuO₂ plane. In order to investigate whether such defects are indeed the root cause of this behaviour, more detailed microstructural studies of each of the relevant cuprate families are strongly advocated. Certainly, it is something that has been largely overlooked by the community. Until such time, however, it is worthwhile to at least consider alternative explanations for the demise of superconductivity on the overdoped side.

Franz et al. [52] have argued that the predicted drop in T_c with disorder is higher than observed experimentally due to the fact that within AG theory, the order parameter is spatially averaged, an assumption that may not be applicable to high-T_c cuprates by virtue of their short coherence lengths. Allowing for the spatial variation of the order parameter within a Bogoliubov-de Gennes formalism leads to a suppression of T_c that is indeed weaker than that predicted by the AG theory, but only by a factor of 2. Moreover, naively, one would expect the coherence length to diverge as p → p_sc, yet according to the study of Mahmood et al., T_c becomes even more robust at higher doping levels [40].

The SCTMA used by Lee-Hone et al. [15] treats disorder using an effective medium theory in which the SC state is also assumed to be homogeneous. Other treatments, however, have considered inhomogeneity or granularity in the SC state [53, 54]. When the Cooper pair coherence length becomes comparable to the correlation length of the disorder potential, the order parameter is found to vary spatially while the superconductor segregates into regions of high and low superfluid density, that in turn enhances the propensity for SC phase fluctuations. Indeed, evidence has emerged for both granular superconductivity [14, 55] and enhanced SC phase fluctuations [56] in OD cuprates.

While the granular model described in Ref. [54] captures a number of key observations, it cannot be the complete picture. What this model–and indeed the majority of disorder models that consider this problem–assumes it that the OD cuprates are essentially Fermi-liquids that transition into a BCS superconductor (homogeneous or otherwise) below T_c. Yet, as stressed elsewhere, there is now mounting evidence that OD cuprates are in fact strange metals, with a dominant non-FL T-linear resistivity extending over the entire doping region [2]. Moreover, this strange metal is claimed to exhibit dual character [9, 10] with coexisting but spatially separated regions with FL and non-FL character, respectively [57].

The natural question that arises is whether the non-FL sector possesses the necessary qualities to preserve the size of the pairing amplitude in the presence of disorder. While there is currently no microscopic picture that addresses this, we consider here a simple ‘patchwork’ model for OD cuprates in which intrinsic superconductivity emerges uniquely from the non-FL sector and is resilient to large changes in Γ_n. Figure 5A shows a schematic of such a patchwork cuprate comprising distinct regions of non-FL (in blue) and FL (in red). In a related article [59], we applied both effective medium theory and random resistor networks to a binary mixture of FL and non-FL patches to capture the evolution of the low-T resistivity from purely T² at high dopings to T-linear near p* (≈0.19) with an increasing fraction f of non-FL sector. The same model also explains the correlation between the T-linear resistivity coefficient and the slope of the H-linear magnetoresistance [59]. In Figure 5A, the doping level is set such that there is no percolation path available for the non-FL component. Supercurrent could, in principle, flow through the FL regions via the proximity effect and thus maintain the SC state. In inhomogeneous systems like LSCO and Bi2201, however, the FL sector will be susceptible to strong pair-breaking effects due to scattering off such inhomogeneities, thereby inhibiting the flow of supercurrent between the SC patches. Hence, as soon as the percolation limit is exceeded, the zero-resistance state is lost. For LSCO and Bi2201, this percolation limit is assumed to coincide with the end of the SC dome at p_sc = 0.27.

Figure 5

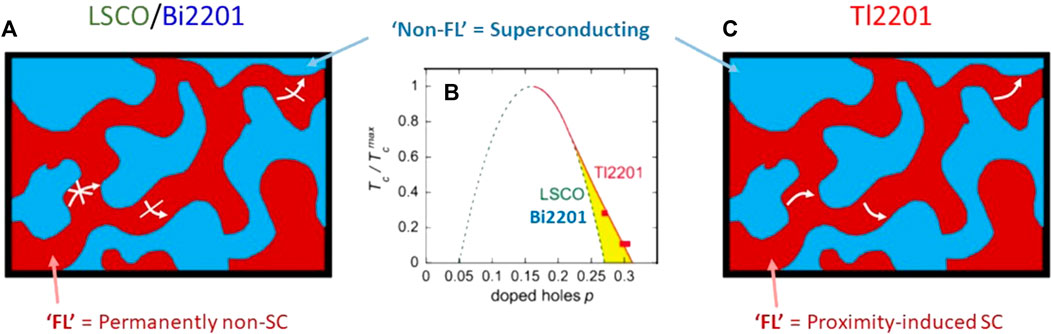
Figure 5. A tale of two superconducting domes. (A) Patchwork model for a hole-doped cuprate comprising distinct regions of non-FL (in blue) and FL (in red). Here, the doping level is such that there is no percolation path available for the non-FL sector. In LSCO and Bi2201, supercurrent could, in principle, flow through the FL sectors via the proximity effect (and thus maintain superconductivity. Due to the presence of strong inhomogeneities, however, pair-breaking effects inhibit the formation of proximity-induced superconductivity within the FL sectors. (B) Normalized T_c(p) domes for LSCO and Bi2201 (dashed line) and Tl2201 (solid line and squares). Reproduced from Ref. [58]. The yellow shaded area represents the proposed region of suppressed superconductivity in OD LSCO and Bi2201. (C) Patchwork model for Tl2201 with the same concentration (and distribution) of non-FL sectors. Due to its lower levels of disorder, superconductivity can survive beyond the percolation limit because the supercurrent is now able flow through the FL sectors via the proximity effect. Once the non-FL sector vanishes at p = 0.31, however, then all traces of superconductivity are lost.

According to Pelc et al., percolation emerges when the fraction of SC patches reaches a critical value of 0.3 (assuming SC and non-SC patches of equivalent size) [60]. Related to this, α₁–the coefficient of the low-T T-linear resistivity in OD cuprates–is found to grow linearly from p = 0.31 up to its maximum value ${\alpha }_1^{\text{max}}$ at p* ∼ 0.20 where the pseudogap opens. Thus, at p = 0.27, ${\alpha }_1/{\alpha }_1^{\text{max}}\sim$ 0.35. In a recent high-field transport study [59], we argued that ${\alpha }_1/{\alpha }_1^{\text{max}}$ is a measure of the fraction of Planckian carriers that are present at a particular doping. If these carriers, and only these carriers, form the superfluid condensate in LSCO and Bi2201, then the reason for the onset of superconductivity at p = p_sc becomes self-evident–it is the point at which the supercurrent can travel percolatively between adjacent patches.

Figure 5B compares the normalised T_c dome for LSCO and Bi2201 (dashed line) with that of Tl2201 (solid line and squares). The yellow shaded area in Figure 5B represents the region of the phase diagram where the superconductivity in Tl2201 is enhanced relative to that seen in LSCO and Bi2201. (This extended region of superconductivity is essentially the same as that shown in Figure 2.) Tl2201 is known to be more homogeneous than LSCO and Bi2201 and possess longer mean-free-paths (as manifest in lower ρ₀ values) [34]. According to the above picture, the level of disorder scattering in Tl2201 is low enough to allow supercurrent to traverse the FL sectors via the proximity effect (see Figure 5C) and for superconductivity to persist beyond the percolation limit. Once the non-FL sector vanishes at p = 0.31, however, then all traces of superconductivity are lost.

This picture represents a marked departure from the extended BCS description for a disordered d-wave superconductor, yet is clearly nothing more than a toy model at present. Before closing, therefore, let us consider some of the consequences of the proposed picture and how it might be tested experimentally. One such consequence may in fact have been tested already. In an earlier electron irradiation study on OD Tl2201 (T_c = 31 K) [61], an increase in ρ₀ by 70 μΩcm was found to cause a reduction of 20 K in T_c. Using the values quoted in Section 2.2, we find that ΔΓ_n ∼ 210 K $>$ 10 ΔT_c. Despite this level of T_c reduction being far smaller than expected by modified AG theory (ΔT_c = -(π/4)Γ_n [61]), it is still more than is seen in LSCO or in Bi2201. (In Ref. [61], the authors used p, rather than 1 + p, for the carrier density, making the agreement with their expectations from AG theory appear reasonable.). If superconductivity within the FL sector is susceptible to disorder (in accordance with dirty d-wave theory) but is resilient within the non-FL sector, electron radiation might induce pair-breaking predominantly or uniquely within the FL sector. Moreover, if the doping level sits close to the percolation threshold, superconductivity will be appreciably suppressed. Further irradiation, on the other hand, would not cause a further deterioration in T_c due to the resilience of the superfluid residing the non-FL sector. A more dedicated irradiation study, over a range of dopings and to higher fluences, could thus serve as a robust test of the validity of this proposal.

The other corollary of this picture is the presence of SC droplets beyond p_sc = 0.27. According to Ref. [59], signatures of superconductivity are intimately tied to the existence of the T-linear component in ρ(T) that itself indicates the fraction of carriers that are not standard Landau quasiparticles. Hence, for 0.27 $\le p\le$ 0.31, one expects SC patches to survive, fluctuating or otherwise. A recent STM study [14] observed gap features persisting in nominally non-SC Bi2201, albeit with a low filling fraction, consistent with this picture. In order to test this idea more rigorously, however, one would need to track the evolution of these features in combination with ρ(T) measurements up to p = 0.31 and beyond.

3 Conclusion

The measurements, reproductions and analysis presented in this article serve to highlight serious shortcomings in our understanding of the normal and SC properties of overdoped cuprates. The fundamental problem can be expressed as follows; either we do not understand the relation between Γ_n and ρ₀ and the origins of residual resistivity in OD cuprates, or dirty d-wave theory, at least in its present guise, is not the appropriate framework to describe OD cuprates. The reality is probably a combination of the two. The robustness of the T_c(p) domes in LSCO is particularly challenging for scenarios based on standard pair-breaking effects in d-wave superconductors. At the same time, there clearly needs to be a more concerted effort to understand the nature of defects and their contribution to pair-breaking and to ρ₀.

In the absence of a consistent picture, we have introduced here an alternative explanation for the robustness of T_c in different OD cuprates, based on a ‘patchwork’ model that recognises the dual character and non-FL nature of the strange metal regime and the importance of the latter for pair condensation. Within this model, dirty d-wave theory is still found to play some role, accounting for difference in the extent of the T_c(p) domes in LSCO, Bi2201 and Tl2201. Further irradiation studies on samples located at the edge of the SC dome may allow us to differentiate between the different explanations for these striking effects.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

DJ: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. JA: Data curation, Investigation, Validation, Writing–review and editing, Writing–original draft. RN: Data curation, Investigation, Validation, Writing–review and editing. NH: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Netherlands Organisation for Scientific Research (NWO) Grant No. 16METL01 “Strange Metals” (MB), the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 835279-Catch-22) (DJ, JA and NH) and the Engineering and Physical Sciences Research Council (United Kingdom) grant EP/V02986X/1 (NEH). JA acknowledges the support of a Leverhulme Trust Early Career Fellowship.

Acknowledgments

We acknowledge stimulating discussions with W. A. Atkinson, A. Carrington, C. Duffy, P. Chudzinski, A. Ghosh and M. Grüning. We also acknowledge T. Kondo, T. Takeuchi and Y. Huang for synthesising the Bi2201 single crystals used in this study, as well as M. Berben for preparation of some of the single crystals for transport measurements.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1396463/full#supplementary-material

References

1. Keimer B, Kivelson SA, Norman MR, Uchida S, Zaanen J. From quantum matter to high-temperature superconductivity in copper oxides. Nature (2015) 518:179–86. doi:10.1038/nature14165

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Cooper RA, Wang Y, Vignolle B, Lipscombe OJ, Hayden SM, Tanabe Y, et al. Anomalous criticality in the electrical resistivity of La_2−xSr_xCuO₄. Science (2009) 323:603–7. doi:10.1126/science.1165015

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Jin K, Butch NP, Kirshenbaum K, Paglione J, Greene RL. Link between spin fluctuations and electron pairing in copper oxide superconductors. Nature (2011) 476:73–5. doi:10.1038/nature10308

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Chang J, Månsson M, Pailhes S, Claesson T, Lipscombe OJ, Hayden SM, et al. Anisotropic breakdown of Fermi-liquid quasiparticle excitations in overdoped La_2−xSr_xCuO₄. Nat Commun (2015) 4:2559. doi:10.1038/ncomms3559

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Božović I, He X, Wu J, Bollinger AT. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature (2016) 510:309–11. doi:10.1038/nature19061

CrossRef Full Text | Google Scholar

6. Giraldo-Gallo P, Galvis JA, Stegen Z, Modic KA, Balakirev FF, Betts JB, et al. Scale-invariant magnetoresistance in a cuprate superconductor. Science (2018) 361:479–81. doi:10.1126/science.aan3178

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Mahmood F, He X, Božović I, Armitage NP. Locating the missing superconducting electrons in the overdoped cuprates La_2−xSr_xCuO₄. Phys Rev Lett (2019) 122:027003. doi:10.1103/PhysRevLett.122.027003

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Legros A, Benhabib S, Tabis W, Laliberté F, Dion M, Lizaire M, et al. Universal T-linear resistivity and Planckian dissipation in overdoped cuprates. Nat Phys (2019) 15:142–7. doi:10.1038/s41567-018-0334-2

CrossRef Full Text | Google Scholar

9. Putzke C, Benhabib S, Tabis W, Ayres J, Wang Z, Malone L, et al. Reduced Hall carrier density in the overdoped strange metal regime of cuprate superconductors. Nat Phys (2021) 17:826–31. doi:10.1038/s41567-021-01197-0

CrossRef Full Text | Google Scholar

10. Ayres J, Berben M, Čulo M, Hsu YT, van Heumen E, Huang Y, et al. Incoherent transport across the strange-metal regime of overdoped cuprates. Nature (2021) 595:661–6. doi:10.1038/s41586-021-03622-z

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Grissonnanche G, Fang Y, Legros A, Verret S, Laliberté F, Collignon C, et al. Linear-in temperature resistivity from an isotropic Planckian scattering rate. Nature (2021) 595:667–72. doi:10.1038/s41586-021-03697-8

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Smit S, Mauri E, Bawden L, Heringa F, Gerritsen F, van Heumen E, et al. Momentum-dependent scaling exponents of nodal self-energies measured in strange metal cuprates and modelled using semi-holography (2021). arXiv:2112.06576 [cond-mat].

Google Scholar

13. Yuan J, Chen Q, Jiang K, Feng Z, Lin Z, Yu H, et al. Scaling of the strange-metal scattering in unconventional superconductors. Nature (2022) 602:431–6. doi:10.1038/s41586-021-04305-5

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Tromp WO, Benschop T, Ge JF, Battisti I, Bastiaans KM, Chatzopoulos D, et al. Puddle formation, persistent gaps, and non-mean-field breakdown of superconductivity in overdoped (Pb,Bi)₂Sr₂CuO_6+δ. Nat Mater (2023) 22:703–9. doi:10.1038/s41563-023-01497-1

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Lee-Hone NR, Dodge JS, Broun DM. Disorder and superfluid density in overdoped cuprate superconductors. Phys Rev B (2017) 96:024501. doi:10.1103/PhysRevB.96.024501

CrossRef Full Text | Google Scholar

16. Lee-Hone NR, Mishra V, Broun DM, Hirschfeld PJ. Optical conductivity of overdoped cuprate superconductors: application to La_2−xSr_xCuO₄. Phys Rev B (2018) 98:054506. doi:10.1103/PhysRevB.98.054506

CrossRef Full Text | Google Scholar

17. Lee-Hone NR, Özdemir HU, Mishra V, Broun DM, Hirschfeld PJ. Low energy phenomenology of the overdoped cuprates: viability of the Landau-BCS paradigm. Phys Rev Res (2020) 2:013228. doi:10.1103/PhysRevResearch.2.013228

CrossRef Full Text | Google Scholar

18. Özdemir HU, Mishra V, Lee-Hone NR, Kong X, Berlijn T, Broun DM, et al. Effect of realistic out-of-plane dopant potentials on the superfluid density of overdoped cuprates. Phys Rev B (2022) 106:184510. doi:10.1103/PhysRevB.106.184510

CrossRef Full Text | Google Scholar

19. Broun DM, Özdemir HU, Mishra V, Lee-Hone NR, Kong X, Berlijn T, et al. Optical conductivity of overdoped cuprates from ab initio out-of-plane impurity potentials (2023). arXiv:2312.16632 [cond-mat].

Google Scholar

20. Loram JW, Mirza KA, Wade JM, Cooper JR, Liang WY. The electronic specific heat of cuprate superconductors. Physica C (1994) 235–240:134–7. doi:10.1016/0921-4534(94)91331-5

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang Y, Yan J, Shan L, Wen HH, Tanabe Y, Adachi T, et al. Weak-coupling d-wave BCS superconductivity and unpaired electrons in overdoped La_2−xSr_xCuO₄ single crystals. Phys Rev B (2007) 76:064512. doi:10.1103/PhysRevB.76.064512

CrossRef Full Text | Google Scholar

22. Takeya J, Ando Y, Komiya S, Sun XF. Low-temperature electronic heat transport in La_2−xSr_xCuO₄ single crystals: unusual low-energy physics in the normal and superconducting states. Phys Rev Lett (2002) 88:077001. doi:10.1103/physrevlett.88.077001

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Sutherland M, Hawthorn DG, Hill RW, Ronning F, Wakimoto S, Zhang H, et al. Thermal conductivity across the phase diagram of cuprates: low-energy quasiparticles and doping dependence of the superconducting gap. Phys Rev B (2003) 67:174520. doi:10.1103/PhysRevB.67.174520

CrossRef Full Text | Google Scholar

24. Proust C, Boaknin E, Hill RW, Taillefer L, Mackenzie AP. Heat transport in a strongly overdoped cuprate: Fermi liquid and a pure d-wave BCS superconductor. Phys Rev Lett (2002) 89:147003. doi:10.1103/PhysRevLett.89.147003

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Hawthorn DG, Li SY, Sutherland M, Boaknin E, Hill RW, Proust C, et al. Doping dependence of the superconducting gap in Tl₂Ba₂CuO_6+δ from heat transport. Phys Rev B (2007) 75:104518. doi:10.1103/PhysRevB.75.104518

CrossRef Full Text | Google Scholar

26. Wang D, Xu JQ, Zhang HJ, Wang QH. Anisotropic scattering caused by apical oxygen vacancies in thin films of overdoped high-temperature cuprate superconductors. Phys Rev Lett (2022) 128:137001. doi:10.1103/PhysRevLett.128.137001

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Abrikosov AA, Gor’kov LP Methods of quantum field theory in statistical physics. New York, NY: Dover (1975).

Google Scholar

28. Hussey NE, Licciardello S, Buhot J. A tale of two metals: contrasting criticalities in the pnictides and hole-doped cuprates. Rep Prog Phys (2018) 81:052501. doi:10.1088/1361-6633/aaa97c

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Presland MR, Tallon JL, Buckley RG, Liu RS, Flower NE. General trends in oxygen stoichiometry effects on T_c in Bi and Tl superconductors. Physica C (1991) 176:95–105. doi:10.1016/0921-4534(91)90700-9

CrossRef Full Text | Google Scholar

30. Berben M, Smit S, Duffy C, Hsu YT, Bawden L, Heringa F, et al. Superconducting dome and pseudogap endpoint in Bi2201. Phys Rev Mater (2022) 6:044804. doi:10.1103/PhysRevMaterials.6.044804

CrossRef Full Text | Google Scholar

31. Ono S, Ando Y. Evolution of the resistivity anisotropy in Bi₂Sr_2−xLa_xCuO_6+δ single crystals for a wide range of hole doping. Phys Rev B (2003) 67:104512. doi:10.1103/PhysRevB.67.104512

CrossRef Full Text | Google Scholar

32. Momono N, Matsuzaki T, Oda M, Ido M. Superconducting condensation energy and pseudogap formation in La_2−xSr_xCuO₄: new energy scale for superconductivity. J Phys Soc Jpn (2002) 71:2832–5. doi:10.1143/JPSJ.71.2832

CrossRef Full Text | Google Scholar

33. Wade JM, Loram JW, Mirza KA, Cooper JR, Tallon JL. Electronic specific heat of Tl₂Ba₂CuO_6+δ from 2 K to 300 K for 0 ≤ δ ≤ 0.1. J Supercond (1994) 7:261–4. doi:10.1007/BF00730408

CrossRef Full Text | Google Scholar

34. Rourke PMC, Bangura AF, Benseman TM, Matusiak M, Cooper JR, Carrington A, et al. A detailed de Haas–van Alphen effect study of the overdoped cuprate Tl₂Ba₂CuO_6+δ. New J Phys (2010) 12:105009. doi:10.1088/1367-2630/12/10/105009

CrossRef Full Text | Google Scholar

35. Girod C, LeBoeuf D, Demuer A, Seyfarth G, Imajo YSamd K, Kohama Y, et al. Normal state specific heat in the cuprate superconductors La_2xSr_xCuO₄ and Bi_2+ySr_2−x−yLa_xCuO_6+δ near the critical point of the pseudogap phase. Phys Rev B (2022) 103:214506. doi:10.1103/PhysRevB.103.214506

CrossRef Full Text | Google Scholar

36. Lee K, Goodge BH, Li D, Osada M, Wang BY, Cui Y, et al. Aspects of the synthesis of thin film superconducting infinite-layer nickelates. APL Mater (2020) 8:041107. doi:10.1063/5.0005103

CrossRef Full Text | Google Scholar

37. Lee K, Wang BY, Osada M, Goodge BH, Wang TC, Lee Y, et al. Linear-in-temperature resistivity for optimally superconducting (Nd,Sr)NiO₂. Nature (2023) 619:288–92. doi:10.1038/s41586-023-06129-x

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Pan SH, O’Neal JP, Badzey RL, Chamon C, Ding H, Engelbrecht JR, et al. Microscopic electronic inhomogeneity in the high-T_c superconductor Bi₂Sr₂CaCu₂O_8+x. Nature (2001) 413:282–5. doi:10.1038/35095012

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Fukuzumi Y, Mizuhashi K, Takenaka K, Uchida S. Universal superconductor-insulator transition and T_c depression in Zn-substituted high-T_c cuprates in the underdoped regime. Phys Rev Lett (1996) 76:684–7. doi:10.1103/PhysRevLett.76.684

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Mahmood F, Ingram D, He X, Clayhold JA, Božović I, Armitage NP. Effect of radiation-induced defects on the superfluid density and optical conductivity of overdoped La_2−xSr_xCuO₄. Phys Rev B (2022) 105:174501. doi:10.1103/PhysRevB.105.174501

CrossRef Full Text | Google Scholar

41. Ataei A, Gourgout A, Grissonnanche G, Chen L, Baglo J, Boulanger ME, et al. Electrons with Planckian scattering obey standard orbital motion in a magnetic field. Nat Phys (2022) 18:1420–4. doi:10.1038/s41567-022-01763-0

CrossRef Full Text | Google Scholar

42. Ando Y, Boebinger GS, Passner A, Wang NL, Geibel C, Steglich F, et al. Normal-state Hall effect and the insulating resistivity of high-T_c cuprates at low temperatures. Phys Rev B (1997) 56:R8530–4. doi:10.1103/PhysRevB.56.R8530

CrossRef Full Text | Google Scholar

43. Čulo M, Duffy C, Ayres J, Berben M, Hsu YT, Hinlopen RDH, et al. (2021) Possible superconductivity from incoherent carriers in overdoped cuprates, Scipost Phys 11:012. doi:10.21468/SciPostPhys.11.1.012

CrossRef Full Text | Google Scholar

44. Takagi H, Ido T, Ishibashi S, Uota M, Uchida S, Tokura Y. Superconductor-to-nonsuperconductor transition in La_2−xSr_xCuO₄ as investigated by transport and magnetic measurements. Phys Rev B (1989) 40:2254–61. doi:10.1103/PhysRevB.40.2254

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Nagano T, Tomioka Y, Nakayama Y, Kishio K, Kitazawa K. Bulk superconductivity in both tetragonal and orthorhombic solid solutions of La_2−xSr_xCuO₄. Phys Rev B (1993) 48:9689–96. doi:10.1103/PhysRevB.48.9689

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Radaelli PG, Hinks DG, Mitchell AW, Hunter BA, Wagner JL, Dabrowski B, et al. Structural and superconducting properties of La_2−xSr_xCuO₄ as a function of sr content. Phys Rev B (1994) 49:4163–75. doi:10.1103/PhysRevB.49.4163

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Matsuzaki T, Momono N, Oda M, Ido M. Electronic specific heat of La_2−xSr_xCuO₄: pseudogap formation and reduction of the superconducting condensation energy. J Phys Soc Jpn (2004) 73:2232–8. doi:10.1143/JPSJ.73.2232

CrossRef Full Text | Google Scholar

48. Komiya S, Chen HD, Zhang SC, Ando Y. Magic doping fractions for high-temperature superconductors. Phys Rev Lett (2005) 94:207004. doi:10.1103/PhysRevLett.94.207004

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Adachi T, Omori K, Tanabe Y, Koike Y. Magnetic-susceptibility and specific-heat studies on the inhomogeneity of superconductivity in the underdoped La_2−xSr_xCuO₄. J Phys Soc Jpn (2009) 78:114707. doi:10.1143/JPSJ.78.114707

CrossRef Full Text | Google Scholar

50. Pavarini E, Dasgupta I, Saha-Dasgupta T, Jepsen O, Andersen OK. Band-structure trend in hole-doped cuprates and correlation with T_c^max. Phys Rev Lett (2001) 87:047003. doi:10.1103/PhysRevLett.87.047003

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Eberlein A, Metzner W. Superconductivity in the two-dimensional t − t′-Hubbard model. Phys Rev B (2014) 89:035126. doi:10.1103/PhysRevB.89.035126

CrossRef Full Text | Google Scholar

52. Franz M, Kallin C, Berlinsky AJ, Salkola MI. Critical temperature and superfluid density suppression in disordered high-T_c cuprate superconductors. Phys Rev B (1997) 56:7882–5. doi:10.1103/PhysRevB.56.7882

CrossRef Full Text | Google Scholar

53. Atkinson WA, Hirschfeld PJ, MacDonald AH. Gap inhomogeneities and the density of states in disordered d-wave superconductors. Phys Rev Lett (2000) 85:3922–5. doi:10.1103/PhysRevLett.85.3922

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Li ZX, Kivelson SA, Lee DH. Superconductor-to-metal transition in overdoped cuprates. npj Quant Mater (2021) 6:36. doi:10.1038/s41535-021-00335-4

CrossRef Full Text | Google Scholar

55. Li Y, Sapkota A, Lozano PM, Du Z, Li H, Wu Z, et al. Strongly overdoped La_2−xSr_xCuO₄: evidence for Josephson-coupled grains of strongly correlated superconductor. Phys Rev B (2022) 106:224515. doi:10.1103/PhysRevB.106.224515

CrossRef Full Text | Google Scholar

56. Rourke PMC, Mouzopoulou I, Xu XF, Panagopoulos C, Wang Y, Vignolle B, et al. Phase-fluctuating superconductivity in overdoped La_2−xSr_xCuO₄. Nat Phys (2011) 7:455–8. doi:10.1038/nphys1945

CrossRef Full Text | Google Scholar

57. Ayres J, Katsnelson MI, Hussey NE. Superfluid density and two-component conductivity in hole-doped cuprates. Front Phys (2022) 10:1021462. doi:10.3389/fphy.2022.1021462

CrossRef Full Text | Google Scholar

58. Bangura AF, Rourke PMC, Benseman TM, Matusiak M, Cooper JR, Hussey NE, et al. Fermi surface and electronic homogeneity of the overdoped cuprate superconductor Tl₂Ba₂CuO_{6+δ} as revealed by quantum oscillations. Phys Rev B (2010) 82:140501. doi:10.1103/PhysRevB.82.140501

CrossRef Full Text | Google Scholar

59. Ayres J, Berben M, Duffy C, Hinlopen RDH, Hsu YT, Cuoghi A, et al. Universal correlation between H-linear magnetoresistance and T-linear resistivity in high-temperature superconductors (2023). Submitted.

Google Scholar

60. Pelc D, Vučković M, Grbić MS, Požek M, Yu G, Sasagawa T, et al. Emergence of superconductivity in the cuprates via a universal percolation process. Nat Commun (2018) 9:4327. doi:10.1038/s41467-018-06707-y

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Rullier-Albenque F, Vieillefond PA, Alloul H, Tyler AW, Lejay P, Marucco JF. Universal T_c depression by irradiation defects in underdoped and overdoped cuprates? Europhys Lett (2000) 50:81–7. doi:10.1209/epl/i2000-00238-x

CrossRef Full Text | Google Scholar