How fear emotion impacts collective motion in threat environment

Introduction: The emergence of collective behavior often depends on the adequate interaction of individuals through self-organization and the exchange of local information. When facing external threats, communication among individuals requires both rapid and effective information exchange to characterize sudden events. In this paper, we introduce the mechanism of emotions into the modeling of dynamics to study collective avoidance behavior in response to threats.

Methods: A scenario involving a hidden dynamic threat is constructed to test the avoidance and survival capabilities of the collective when faced with a lack of effective information. By employing the activation and spread of emotion in modeling, the collective may self-organized and adeptly mitigate risks and enhance their own benefits.

Results: Through adjustments to the intensity of emotional activation, spread, and decay, rich behaviors emerge. Relying on the regulation of emotion, the collective exhibits different response strategies and action patterns when facing threats, in which the optimal performance from the macroscopic level is expectable.

Discussion: By analyzing these phenomena, it can enhance our understanding of the emotional states of collective in response to threats and the methods of controlling in intelligent collective motion.

1 Introduction

The influence of information exchange on the regulation of collective motion is significant, affecting animals’ perceptions of situations, decision-making processes, and the selection of appropriate movement patterns. In previous studies on collective movement, such as those involving bird flocks Cavagna et al. [1]; Bialek et al. [2]; Nagy et al. [3]; Lei et al. [4], researchers have predominantly modeled micro-scale interactions among individuals based on the acquisition of relative velocity information through observations of local neighbors, such as Vicsek model Vicsek et al. [5]. In the study of singular, homogeneous collective such as locusts Buhl et al. [6]; Yates et al. [7], mosquitoes Attanasi et al. [8], ants Beekman et al. [9]; Couzin and Franks [10], and even pedestrian with social force models Johansson et al. [11]; Jiang et al. [12], researchers often focus on the process of motion information spread within the group and its impact on the patterns of collective motion.

In addition, multiple population systems Duan and Zhang [13]; Krause et al. [14]; Hoare et al. [15], such as those involving prey and predators Kamimura and Ohira [16]; Angelani [17]; Colombo et al. [18], have also been extensively analyzed. However, within the scope of these researches, individual movement is also primarily influenced by the movement information of neighbors and predators.

It is evident that in most predatory encounters, the fleeing prey animals are unable to accurately discern the exact position and velocity of their pursuers. This suggests that models simulating prey movement with an omniscient perspective may not accurately reflect reality. Documentaries and videos from African wildlife hunts, often show prey species with limited awareness of their pursuers during escape. They tend to run long distances before reassessing their situation or rely on the cries of captured companions to gauge immediate danger. This case illustrates that in natural environments, animals prioritize communication founded on inherent biological characteristics de Waal [19]; Pérez-Manrique and Gomila [20] over precise observation of the location and velocity of the predators behind them. Most animals can only release limited information, usually in the form of abnormal postures or behavior Pinho et al. [21], facial expressions Davila Ross et al. [22]; Palagi et al. [23], pheromone Speedie and Gerlai [24]; Diaz-Verdugo et al. [25] and so on, which contain primitive emotional information Preston and de Waal [26]; Kikusui et al. [27]; Decety et al. [28]; Oliveira and Faustino [29] in urgent situations.

Emotion in animals is a rapid response to stressors encountered in natural environments and during abrupt events. This rapid and efficient response mechanism plays a crucial role in augmenting an individual’s likelihood of survival in environments fraught with multifaceted threats. Moreover, the expressions of emotions are often the first piece of information generated in response to external stimuli. Hence, the empathy-driven processes in animal collective facilitate a primary qualitative discernment of events, even in the absence of complete situational awareness. This interactive model of information exchange is instrumental in enhancing the survival prospects of the entire collective.

Researchers have conducted numerous studies on the emotional responses of various animals in nature, including the mechanism of emotion activation Young and Wang [30]; Smith and Wang [31]; Lamm et al. [32], as well as related experiments Davila Ross et al. [22]; Faustino et al. [33]; Pinho et al. [21]. Building upon this foundation, there have also been researches exploring the impact of emotional mechanisms on collective behavior Zhu and Li [34]; Goldenberg et al. [35], as well as studies on collective behavior under states of panic Lemasson et al. [36]; Calvão and Brigatti [37]; Zanette and Clinchy [38]; Diaz-Verdugo et al. [25]. However, the study of collective emotions, particularly fear, requires further investigation into aspects such as the interplay of emotions among collectives, the expression of emotional feedback regarding external events, the influence of emotions on the collective’s survival capabilities, and the regulation of collective dynamics through collective emotions.

To address aforementioned issues, we constructed a corresponding scenario based on the phenomenon of hidden threats encountered during collective migration, where the threats are concealed and individuals cannot perceive specific information about them. In such situation, the exchange of emotional information between individuals becomes crucial. We propose a dynamic model regulated by fear emotion, where fear are activated based on external event feedback and can spread among neighbors. By adjusting the intensity of emotional activation and contagion, a rich variety of simulated behaviors in collective motion can be observed. Notably, for specific optimal configuration, the collective can exhibit intelligent behavior to effectively avoid harm.

2 Scenario and model

Every June, in the eastern regions of Africa, thousands upon thousands of wildebeests and zebras form herds, migrating from Tanzania’s Serengeti National Park northward to Kenya’s Maasai Mara National Reserve, creating the spectacular East African Great Migration. Besides evading terrestrial predators, wildebeests and zebras encounter the challenge of crossing the Mara River, where they must contend with the hidden threat of Nile crocodiles lurking beneath the water’s surface Subalusky et al. [39].

Inspired by these phenomena, we established a similar abstract scenario, wherein a collective, unaware of the location of the threat, endeavors to reach their destination while avoiding harm from the potential danger. Accordingly, we investigated how collective could maximize their entry into their destination and survive for a longer duration through emotional communication and dynamic interaction in facing a lack of information.

The scenario is shown in Figure 1, the inner red circle with a radius of $r_a$ represents the effective area, it is the destination of the collective. Each individual initializes with a health value of $H=100$ and will suffer losses in the injury area. The red sector representing the injury area will rotate within the black circle with a radius of $r_d$ and damage individuals located within the sector until they are removed from the system due to a decrease in health to 0. The damage suffered by individuals within the injury area per unit of time is:

$D_i^{\ast }\left(\mathrm{\Delta }{\theta }_i,d_i\right)=D{\left(1-\frac{d_i}{r_d}\right)}^{\frac{1}{2}}\exp \left(-\frac{|\mathrm{\Delta }{\theta }_i|}{2\sigma }\right).(1)$

In Eq. 1, the coefficients $D$ and $\sigma$ respectively represent damage intensity and coverage. As shown in Figure 2A, $\mathrm{\Delta }{\theta }_i$ is the angle between the direction $-{\widehat{d}}_i$ and the current orientation of the injury area. ${\widehat{d}}_i$ means the direction from unit $i$’s position to its destination, and $d_i$ is the length of the vector ${\vec{d}}_i$. This equation indicates that the further an individual is from the destination and the injury area, the less damage it will suffer.

Figure 1

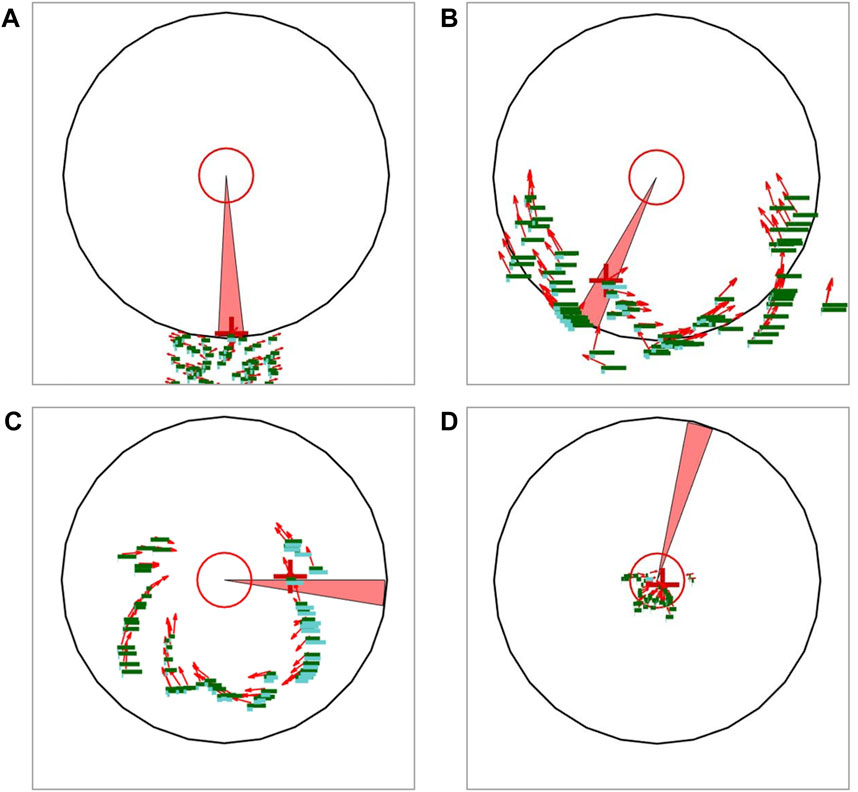
Figure 1. Schematic diagram of scenario. The red arrows represent the positions and velocity vectors of individuals, while the green bars represent their health values, and the cyan bars represent their current fear values. Individuals will lose health in the injury area (red sector) and gain scores in the innermost red circle. The red crosshair represents the current target of the injury area. (A) The collective begins to move towards their destination. (B) Driven by the spread of fear, the collective disperses towards the flanks of the threat area. (C) Owing to the scattered spatial distribution of individuals, which also forms a surrounding formation, individuals under attack continuously disperse due to fear, while the remaining individuals have the opportunity to advance safely towards their destination. (D) Almost all remaining individuals have entered the effective area.

Figure 2

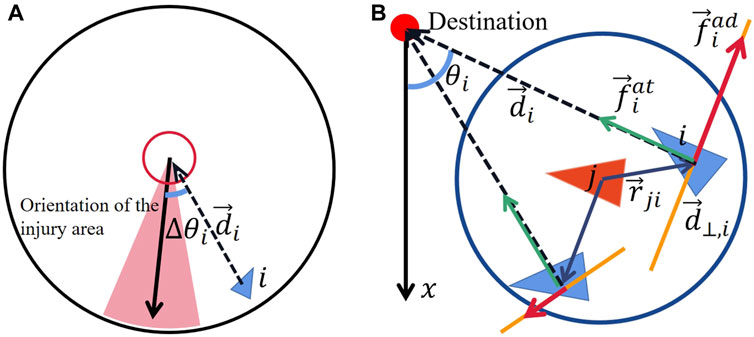
Figure 2. (A) Diagram of the included angle between the orientation of injury area and the direction of $-{\vec{d}}_i$. (B) Schematic diagram of avoidance and attraction, individuals experience attraction from their destination and repulsion from high fear individuals, such as unit $j$.

The injury area approaches the selected individual with the maximum angular velocity of ${\omega }_d$ until the selected target is eliminated. The injury area will choose the individual with the maximum weight as the target selection from each surviving individuals within the black circle. The expression for weight is:

$W_i=1/\left(\mathrm{\Delta }{\theta }_i+\left(d_i-\frac{\mathrm{\Delta }{\theta }_i}{{\omega }_d}{v}_{p,i}\right)\right).(2)$

In Eq. 2, $v_{p,i}$ is the projection of the individual’s current velocity on ${\widehat{d}}_i$. The weight expression means that the injury area can cleverly consider both the individual nearest to its current orientation and the individual that will be closest to the destination in the future as target selections.

When an individual enters the effective area (its destination) the system will record its effective survival time. The accumulative effective survival time (AEST) that an individual and the entire collective can obtain in effective area can be expressed as:

$AEST={\int }_0^{end}\kappa N_{ra}\mathrm{d}t.(3)$

In Eq. 3, $N_{ra}$ represents the number of all remaining individuals currently alive in the effective area, and in order to amplify the difference in scores, we set $\kappa =\ln (e{N}_{ra})$.

The entire simulation process constitutes a complete cycle from the initialization of the collective to the death of all individuals. Throughout the simulation, individuals cannot identify or perceive which unit is targeted by the injury area, nor the current orientation of the injury area. The individuals can only sense the event of being harmed themselves.

The next step is to establish a dynamic model for individuals. Self-propulsion, target preference, and collision avoidance are typical characteristics used in modeling collective dynamic, such as in the social force model Johansson et al. [40]. Our emotion-regulated dynamic model will also be built upon these features.

The individuals in our model are self-driven agents, the velocity of individuals $i$ is ${\vec{v}}_i=v_0{\widehat{v}}_i$(where $v_0$ means the absolute speed and ${\widehat{v}}_i$ is the unit vector of individual velocity). The other forces can only change individual’s direction of motion.

Migratory collective are also influenced by the attractive force of target preference from the direction of their destination as shown in Figure 2B. This force is defined as:

${\vec{F}}_i^{at}=c_{at}\left(\arctan \left(\left(d-r_a\right)/2\right)+\arctan \left(r_a/2\right)\right){\widehat{d}}_i,(4)$

In Eq. 4, $c_{at}$ denotes the intensity of attractive force, which is strong when the unit is far from the destination $(d>r_a)$, and it rapidly decreases when $d\le r_a$.

Typical collective could spontaneously avoid collisions among individuals, thereby activating mutual repulsion within a certain range. Moreover, when individuals encounter or perceive potential threats, they would immediately choose to move away from the location of the dangerous source, just like zebrafish perceive surrounding alarm pheromone from the others Speedie and Gerlai [24]; Diaz-Verdugo et al. [25]. This can be regarded as individuals being driven by the repulsive force exerted by the dangerous source. In this paper, individuals are unable to directly recognize dangers or obtain information about the source of the threat. When an individual is harmed, it triggers fear and manifests this fearful emotion to the others. For the surrounding neighboring individuals, the location near the fearful individual is perceived as filled with danger and threat. The highly frightened individual serves as a signal to nearby individuals, indicating the presence of predators. Consequently, other individuals will choose to move away from the fearful individual, which can also be considered as being driven by the repulsive force. Therefore, the fear value influences the effect of the repulsive. The avoidance force shown in Figure 2, which is defined as:

${\vec{F}}_i^{ad}={\displaystyle \sum _{j\in C_i}}{c}_{ad}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(P^{*}\right)e^{-|P^{*}|}\left(1-e^{-S_j}\right){\widehat{d}}_{\perp ,i}.(5)$

In Eq. 5, $c_{ad}$ represents the intensity of the avoidance interaction, while $P^{*}={\widehat{d}}_{\perp }\cdot {\widehat{r}}_{ji}$ denotes the dot product between the unit vector ${\widehat{d}}_{\perp }$ and the unit vector ${\widehat{r}}_{ji}$ (direction of the relative position from individual $j$ to individual $i$). Avoidance interaction acts on the perpendicular direction$({\widehat{d}}_{\perp })$ relative to the direction $\widehat{d}$ or ${\widehat{d}}_{\Vert }$, causing nearby individuals to repel each other. The interaction occurs within a neighboring set $C_i$, which consists of units located within a radius of $r_n$ centered around the unit $i$. $S_j$ means the fear value of individual $j$. To ensure a rapid decay in the marginal effect of the expansion size as $S_j$ increases, the expansion relationship is defined as $1-e^{-S_j}$.

Then, we will consider the dynamic process of individual fear states. The emotions of biological individuals typically evoke due to specific sudden events, or may be continuously generated when the individual is in a certain specific situation. Intense emotions also decay as the individual becomes more familiar with the scene and as the sudden event dissipates over time Nanda et al. [11]. Meanwhile, emotions can also be transmitted to peers through abnormal postures or panicked shouting Zanette and Clinchy [38]; Pinho et al. [21]. Therefore, the dynamics of emotion should take into account the activation component based on the environment, the contagion component, and as well as a component that decays with time. Its differential form is as follows:

$\frac{\mathrm{d}{S}_i}{\mathrm{d}t}=\alpha \frac{D_i^{\ast }}{D}+\beta {\displaystyle \sum _{j\in C_i,S_j>S_i}}\left(S_j-S_i\right)-\gamma S_i.(6)$

In Eq. 6, $\alpha$, $\beta$ and $\gamma$ are the intensity coefficient. The contagion occurs within a neighboring set $C_i$ either and only takes place from the unit with a high emotion value to the lows. An individual in an extremely excitement may experience weakened perception of pain and injury, indicating that the individual’s own fear will rapidly dissipate. Therefore, when an individual approaches their destination, the decay coefficient $\gamma$ will increase accordingly, ${\gamma }_i=\exp (3r_a/d_i)$.

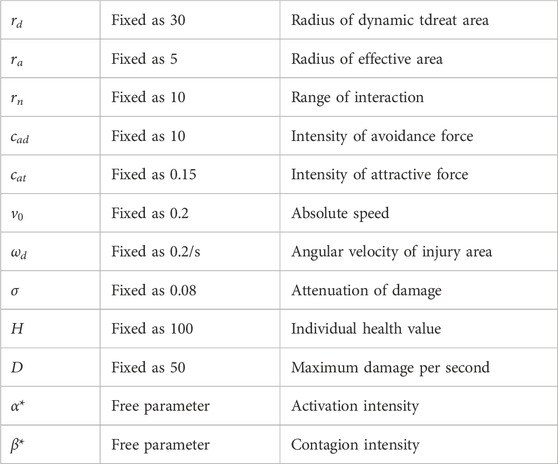
The system parameters in the model are shown in Table 1. This study focuses on the influence of fear emotion on the activation and contagion of the collective. To better demonstrate the effects of different intensities, we choose ${\alpha }^{*}={\log }_2(100\alpha )$ and ${\beta }^{*}={\log }_{1.5}(10\beta )$ for simulation and parameter scanning.

Table 1

Table 1. A summary of the parameters used in our model.

3 Results

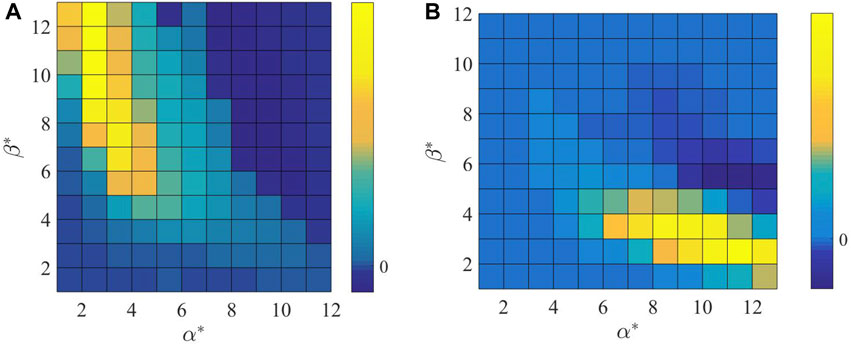
Statistical results of the AEST for ${\alpha }^{*}$ and ${\beta }^{*}$ ranging from 1 to 13 are shown in Figure 3A. It can be clearly observed that there exists an optimal configuration for both the activation and spread intensity under the current environmental parameter settings, located approximately at ${\beta }^{*}=5$ and ${\alpha }^{*}=9$. Furthermore, in most situations, when one parameter (For example, ${\alpha }^{*}$) remains constant, the impact of the another parameter on the system exhibits non-monotonic behavior. As shown in Figure 3B, the results of the simulation duration are intuitive, with low activation and spread coefficients, the impact of fear is too weak, and the collective exhibits a “reckless” behavior of crowding together, which will be quickly eliminated in the dynamic injury area because they failed to disperse in time. Conversely, with strong activation and contagion, the collective will hover around the periphery of the black circle, hesitating to move forward, since it prolong the duration being attacked. It is evident that excessively high or low levels of fear do not enhance the efficiency of the collective in reaching their destination.

Figure 3

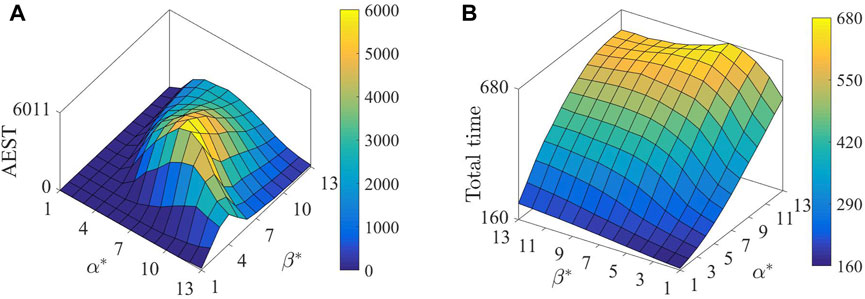
Figure 3. Statistical results of (A) accumulative effective survival time (AEST) and (B) total simulative duration, changing with ${\alpha }^{*}$ and ${\beta }^{*}$.

It can be seen in Figure 4 that when $\alpha$ is small and $\beta$ is large, $\mathrm{\Delta }AEST/\mathrm{\Delta }\alpha$ will increase rapidly with the increase of $\alpha$, indicating that even a slight increase of fear can greatly enhance the survival ability of the collective which has no fear or has very little fear. The effect of $\beta$ on $\mathrm{\Delta }AEST/\mathrm{\Delta }\alpha$ is more like a threshold relationship, that is, when $\beta$ exceeds this threshold, the adjustment of AEST for small $\alpha$ will have a very sensitive change. The effects of $\alpha$ and $\beta$ on $\mathrm{\Delta }AEST/\mathrm{\Delta }\beta$ are exactly opposite to those on $\mathrm{\Delta }AEST/\mathrm{\Delta }\alpha$, which means that for collective that cannot transmit emotions or empathize with others, even a slight increase in emotion spread intensity can cause AEST to increase dramatically, and $\alpha$ provides a certain threshold effect for this increase. This indicates that for a collective, whether it can activate fear according to the environment and whether it can transmit and receive emotions from other individuals are very important for their survival. Although these two mechanisms have different features, they have similar complementary affects and are indispensable. When $\alpha$ is greater than eight and $\beta$ is greater than five, the sensitivity of the entire collective’s AEST will rapidly decrease, which further illustrates that for the collective, whether there is a certain degree of fear activation and fear contagion is relatively important, and increasing its intensity further has little meaning for the survival of the collective, and may even have a negative effect. Therefore, for a collective, there must be a stress mechanism such as fear, and once the corresponding threshold is reached, its effect can be well exerted.

Figure 4

Figure 4. Sensitivity analysis of (A) $\mathrm{\Delta }AEST/\mathrm{\Delta }\alpha$ and (B) $\mathrm{\Delta }AEST/\mathrm{\Delta }\beta$.

Accordingly, we conducted a statistical analysis about how the collective with optimal parameters could achieve maximum survival of collective intelligent emergent behavior when facing threat. In order to visually demonstrate the emergence of the primary and the other disparate states in collective motions, video materials are provided in the Supplementary Material.

As shown in Figure 5A, in the beginning, the collective began to enter the threat area (black circle), individuals were rapidly diffusing at the edge of the threat area, and the loss rate is relatively stable. When simulation time reached $t=367$ (black dashed line in Figure 5A), individuals began to enter the effective area, the AEST score (red solid line) and the proportion of the collective enter the effective area started to increase. The red dot represents the average survival rate when the first individual entered the effective area, indicating that the lower this proportion is, the less AEST score the collective could obtain in the following time. As the collective continued to enter the effective area, the occupancy rate will approach 100%, and the AEST would continue to increase. When the proportion reached 100%, the rate of AEST accumulation also reached the maximum, and the subsequent growth rate of the overall AEST would became more flattened.

Figure 5

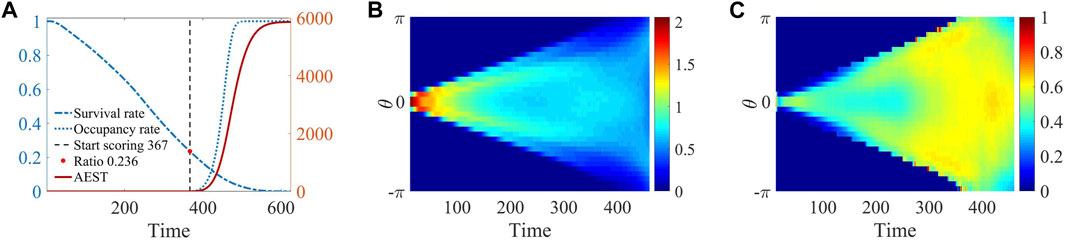
Figure 5. The simulation results of system statistics evolving over time are presented. (A) The results include the collective survival rate $(({\sum }_{i=1}^N{H}_i(t))/(NH))$, occupancy rate $(N_{ra}/N_{rest})$ and AEST. The black dash line means the average time of the first individual enters the effective area, accordingly, the red dot means the survival rate at the same time. (B) Presents the distribution of density around the destination from different angles. (C) Shows the distribution of the projection of the speed $v_p/v_0$ in the direction from the destination to the unit at various angles. The direction angle $\theta$ of vertical axis in (B) and (C) takes the center of the effective area as the origin, and the downward direction of the simulated scene as the polar axis.

In Figures 5A, B clear bimodal distribution pattern is evident during the period spanning from 100 to 300. This observation signifies a remarkably distinct and intriguing phenomenon characterized by spontaneous self-organization, resulting in the emergence of two distinct teams, as visually illustrated in Figure 1C. This formation enables the collective to influence the direction of dynamic injury area, thereby creating opportunities for collective to make a dash toward the destination. The two-wings structure greatly enhances the overall survival capability of the collective, reduces the actual coverage of the dynamic injury area, and thus helps to avoids damage. As the collective gradually approaches the effective area, the excitement level begins to surge, leading to an increase in the fear attenuation coefficient, which causes the fear value to remain at a small level. The repulsive force affected by fear will decrease, which making the collective overall “fearless.” Driven by emotional changes, the transition of behavioral strategies induced by varying environmental conditions is the mechanism behind the emergence of such a novel self-organizing behavior and achieving optimal scores.

Here, the formation process of a more obvious bimodal structure can be seen in the distribution of the projection of collective velocity (Figure 5C), the colors indicate the ratio of velocity projection to the maximum speed. The velocity projection on both sides is generally higher than that in the middle, implying that the individuals in the middle are constantly moving apart towards both sides during the swing phase period. Similarly, at around $t=300$, the suppressive effect of excitement on fear begins to emerge, and the speed of the entire collective transitions from a swing state to a dash state in all directions.

Eight parameter points around the optimal parameter configuration are selected to represent various possible extreme choices of ${\alpha }^{*}$ and ${\beta }^{*}$¹ to fully illustrate the characteristics of different parameter configurations and their non-monotonic parameter transformations.

As shown in Figure 3B, the prolonged simulative duration can be predominantly attributed to the activation intensity ${\alpha }^{*}$. Activation markedly elevates fear levels, thereby amplifying the extent of repulsion among neighboring individuals. This heightened repulsion prompts rapid diffusion and effectively aids in harm avoidance, consequently extending the collective survival time (non-AEST). Likewise, as depicted in Figure 6, the influence of ${\beta }^{*}$ on this duration appears to be relatively minor. The spread process does not generate fear value that surpasses the threshold of the damage event. Instead, it only affects other individuals at a certain level of fear, thereby promoting a more homogeneous approach within their neighbors. Although, when contrasting various ${\beta }^{*}$ values under constant ${\alpha }^{*}$, an elevation in ${\beta }^{*}$ does indeed lead to a partial increase in the overall fear level, its impact remains relatively modest.

Figure 6

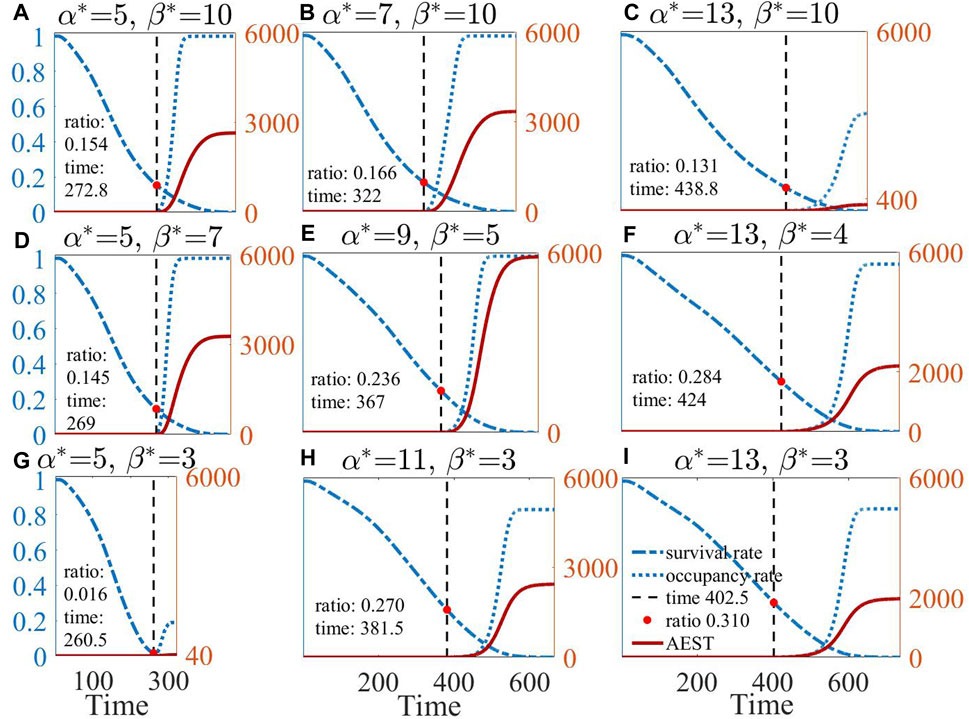
Figure 6. The results of the survival rate, occupancy rate, and AEST over time for the optimal parameter configuration (E) and eight neighboring parameter configurations (A–D) and (F–I).

In the top-left panel of Figures 6A, B, D, E, the ratio of surviving individuals entering the effective area to the remaining individuals (occupancy rate) can attain 100%. This observation, in turn, implies that an excessive ${\alpha }^{*}$ or a small ${\beta }^{*}$ can disrupt overall pace consistency, where some individuals enter the effective area while others remain outside. These parameter configurations will lead to an increased disparity in the fear level among the entire collective, resulting in a longer duration for individuals to enter the effective area in succession.

Comparing AEST with different parameters reveals that, although the score is associated with the survival rate of individuals during their initial entry into the effective area, the primary determinant influencing the final AEST is the growth rate of the subsequent occupancy rate. A reduced growth in the occupancy rate signifies that fewer individuals remain alive when all surviving individuals eventually access the effective area, resulting in diminished score accumulation.

In Figure 7, it is evident that as ${\beta }^{*}$ increases, the tendency of the collective to encircle the destination becomes more pronounced. A low ${\beta }^{*}$ leads to insufficient dispersion of the collective, significantly diminishing its overall survival capability when encountering the injury area. A higher ${\beta }^{*}$ facilitates the rapid contagion of fear among attacked, covering a broader range and directly influencing the diffusion behavior of the entire collective. However, the drawback of a high ${\beta }^{*}$ are also apparent, as even during the stage when the collective should transition to dash state, the collective remains engaged in dispersion behavior. In comparison, the optimal parameter configuration exhibits clear strategy switching behavior over time.

Figure 7

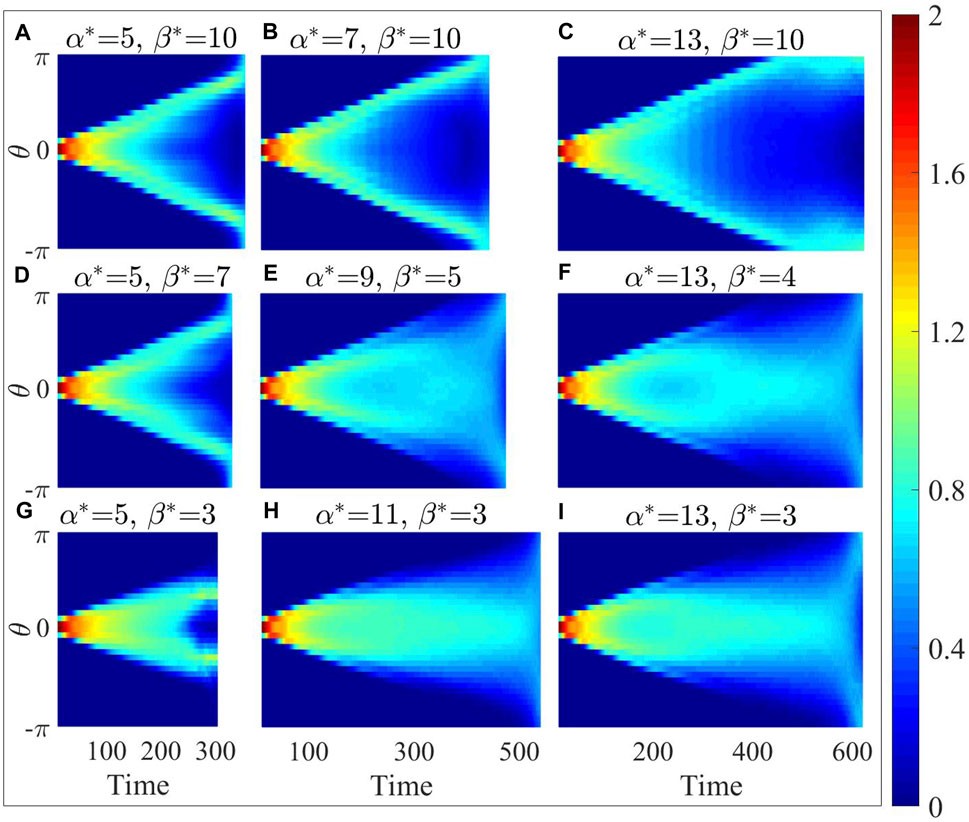
Figure 7. In polar coordinates with the destination as the origin, the distribution of particle number density at different angles for the optimal parameter configuration (E) and its eight neighboring parameter configurations (A–D) and (F–I).

The distribution of velocity projection is shown in Figure 8. A smaller ${\alpha }^{*}$ value results in a considerably reduced fear level within the entire collective, prompting individuals in a state of “recklessness” to exhibit reduced swing movements, driving them closer to the destination and resulting in a higher proportion of their projected velocity. From the four graphs in the bottom-right panel in Figures 8E, F, H, I, it can be observed that larger ${\alpha }^{*}$ and smaller ${\beta }^{*}$ facilitate the dispersion of the collective towards both sides, taking advantage of the unlocked gaps to approach the destination.

Figure 8

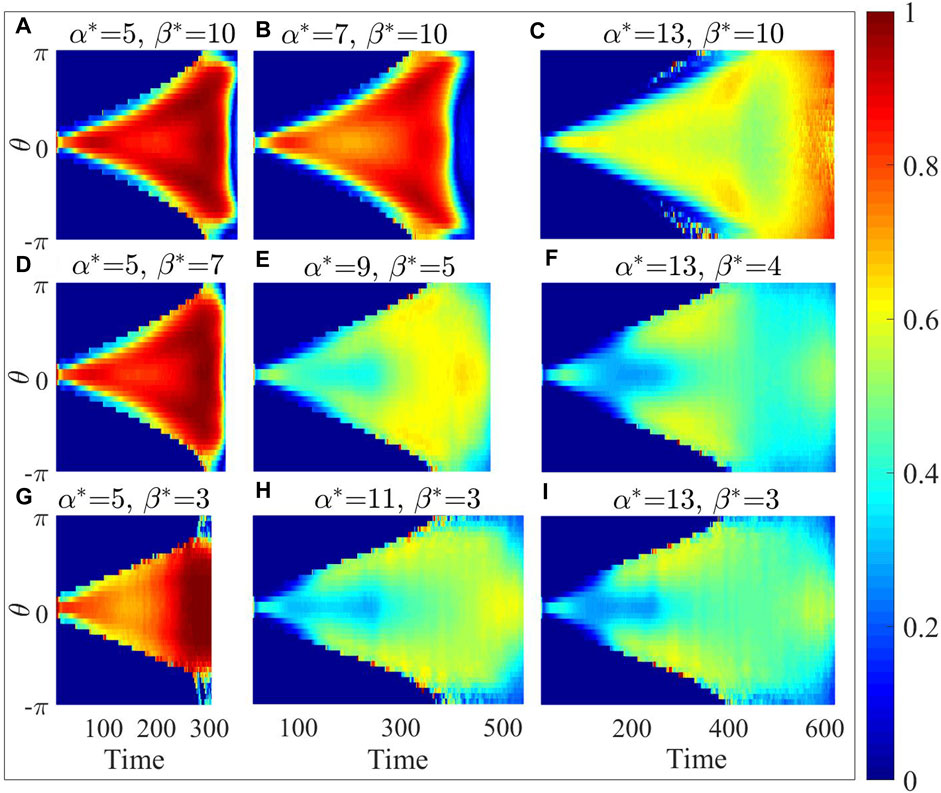
Figure 8. In polar coordinates with the destination as the origin, the distribution of velocity projection at different angles for the optimal parameter configuration (E) and its eight neighboring parameter configurations (A–D) and (F–I).

Compared to the density map (Figure 7), the velocity projection map (Figure 8) with higher ${\beta }^{*}$ displays a distinct concave pattern on the upper and lower edges. The concave region corresponds to the part of highest density in density map. This phenomenon suggests that individuals situated at the high-density edges, whose predominant movement directions are nearly perpendicular to $\widehat{d}$, contribute minimally to velocity projection towards the destination. The observation once again indicate that individuals with higher ${\beta }^{*}$ or lower ${\alpha }^{*}$ situated at the outer periphery of the collective tend to prioritize encircling the destination rather than advancing effectively towards it.

In contrast, as depicted in the bottom-right panel of Figures 7E, F it becomes evident that at the low-density edges on both sides of the density map, the corresponding positions in the velocity projection map show notably higher speed. This observation implies that the scattered individuals positioned on the outermost periphery can detect the absence of immediate danger in their surroundings. Whenever an opportunity arises, individuals spread to the farthest tend to choose to approach the destination. However, individuals only adopt evasive actions solely in the vicinity of damage events for larger ${\alpha }^{*}$ and smaller ${\beta }^{*}$, leading to an inadequate overall diffusion.

From Figures 7, 8, the optimal parameter configuration strikes a balance between the dispersion and its capability to approach the destination promptly. This configuration enables the collective to secure sufficient evasion space while also discerning opportunities to safely approach the destination, even in the absence of information regarding the location of the injury area.

As shown in Figure 9, the collective size $N$ and threat level $D$ have been taken into account. It can be observed that the optimal parameter configuration for obtaining the AEST score varies nonlinearly with the increase of $N$ and $D$. Specifically, as the collective size increases, the marginal increment of the collective’s ability to counter increasing threats exhibits a diminishing trend. When the damage capability $D$ of the injury area increases to a certain level, the effective survival capacity of a fixed number of collective exhibits a decline by an order of magnitude. This is because the increase in damage capability of the injury area causes a faster reduction in the number of individuals, and the individuals often cannot disperse and evade in time while standing in the vicinity of a new locked target of injury area. In the situations with high threat levels and low scores, the performance of the optimal parameter configuration is more prominent. In challenging scenarios, it is difficult for individuals to enter the effective area, and each additional individual entering the effective area greatly increases the overall AEST score. Therefore, the disparities between different parameter configurations are further magnified.

Figure 9

Figure 9. The impact of different collective sizes $N$ and threat levels $D$ on AEST.

It is evident that when the challenge difficulty decreases, even in the case of excessive recklessness (both lower ${\alpha }^{*}$ and ${\beta }^{*}$), the collective achieves a certain balance between approach efficiency and incurred losses, resulting in scores comparable to the pattern of two-wing containment. Nevertheless, the manifestation of time-wasting wandering behavior demonstrates a less dramatic relationship with variations in environmental parameters (the scores would not directly drop to 0 when difficulty increase). Regardless of changes in environmental difficulty, fear-driven individuals consistently expend substantial time diffusing near the vicinity of black circle. The collective consistently prioritizes diffusion before gradually converging towards the destination. On one hand, the damage incurred within the vicinity of the black circle is relatively minimal across all difficulty levels. On the other hand, the extensive diffusion of the collective provides individuals with ample space. Consequently, the more widely distributed collective is not significantly affected by the extent of range damage within the injury area, and as $D$ increases, the number of individuals entering the effective area will only decrease moderately. In contrast, reckless collective are significantly more vulnerable when facing area damage. In extreme cases, if the collective are entirely engulfed by the dynamic injury area, increasing its quantity does not affect the overall time it takes for the collective to be completely annihilated. As a consequence, once the level of threat escalates, a rapid decline of the associated configuration parameters’ scores to zero ensues.

As an additional study, we have calculated the probability of individuals entering the effective area with varying spread intensity under a fixed activation intensity. The Figure 10 illustrates the mean probability of individuals, with ${\beta }^{*}$ takes a random value from [1–9], entering in their destination. It is evident that the survival rate of individuals decreases significantly with the increase of the spread intensity. This brings a very interesting result. Our simulation analysis has revealed that the system’s overall AEST is maximized when the activation intensity is nine and the spread intensity is five. Nevertheless, the individual survival rate suggests that those who refrain from spreading fear and do not empathize with their neighbors have a better chance of survival. This suggests that individuals who are deeply embedded in empathetic collective can acquire more environmental information. However, when an individual is located in threat and screaming in fear, the others will choose to stay away from the individual. This indicates that empathetic individuals, after experiencing fear emotion, transmit threatening information through their own fear, but end up being isolated. Therefore, the most advantageous strategy for individuals is to leave away from high-threat and high-fear neighbors, while refraining from or minimizing the spread of fear, to prevent driving others away and to remain in a state of being able to acquire information. Based on the AEST, only appropriate empathetic behavior is advantageous for the survival of the collective. Calm and self-interested individuals (with small spread intensity) can achieve higher survival abilities in the collective with empathy and cooperation. However, the more such self-interested individuals there are in the collective, the worse the overall survival ability of the collective, which represents a typical group game process.

Figure 10

Figure 10. Probability of individuals with ${\beta }^{*}$ randomly assigned arriving at their destination.

4 Discussion

In this paper, we establish corresponding scenario based on the phenomenon of potential threat encountered during collective migration and investigates how collective, through emotional interaction, particularly fear, avoid harm in threat environments. We propose a dual-layer control model comprising an emotional interaction layer and a dynamic interaction layer, where emotions could regulate the dynamic behaviors of individuals. Through simulations, a rich variety of collective motion can be found.

From the simulative results of time series and statistical scoring, it can be found that the fear mechanism would be too weak in the situation of small activation and contagion intensities, resulting in reckless behavior of the collective, which would be rapidly removed from the injury area due to dense standing. This emphasizes the critical role of fear regulation within the collective, facilitating swift dispersion and evasion from harm, thus underscoring the importance of emotions in bolstering the collective’s adaptability in threat environments. Conversely, excessive activation and contagion intensities may induce hesitancy and wandering along the periphery of the threat area, leading to the eventual exhaustion of the collective over an extended period of attrition. High contagion and low activation will lead to a synergy of fear emotion and movements for all collective. On the contrary, localized and substantial fear fluctuations can lead to the emergence of a two-wing formation in low contagion and high activation configuration.

The optimal parameter configuration enables the collective to exhibit a dispersed behavior at the low-damage edge of the threat area and form a two-wing formation during the subsequent approach and enclosure process. Through the continuous alternation of the two-wing approach, it effectively influencing the locked units of the injury area, the swinging process significantly diminishes the injury area’s capacity to inflict damage upon the collective while enhancing the collective’s overall survival capacity. The entire process demonstrates how the collective, lacking global information and devoid of knowledge about the identity of the locked unit and the location of the injury area, spontaneously transition from surrounding diffusion to two-wing containment and finally achieve the switch of the strategies from avoidance to concentrated rush. Within the effective area, a very wonderful phenomenon of sacrificing oneself for the others should be mentioned that the locked units will spontaneously move away from the collective, exhibiting intelligent behaviors resembling self-sacrifice for the collective protection in Supplementary Material.

As the number of individuals increases, the marginal increment of the difficulty that they can cope with shows a diminishing trend. In more dangerous environments, in order to obtain the same score, it is necessary to exceed a corresponding proportion to increase the size of the collective. Just as the African Great Migration poses multiple challenges, where millions of wildebeests confront numerous obstacles, hundreds of thousands among them ultimately fail to return alive to the migration’s origin Hopcraft et al. [41].

Calm and self-interested individuals may obtain higher survival probability in empathetic and cooperative collective. However, The increase of selfish individuals will also reduce the collective survival. How to induce cooperation is one of our future research topics.

In conclusion, fear emotions can help a collective enhance its survival capacity through emotional interactions when facing unknown threats. It is well known that fear emotions are stress response mechanisms that have been selected over generations through survivorship genetics in individuals facing crises. However, if this mechanism only benefits individuals and proves detrimental to the collective, it cannot be inherited. Through our modeling research, it becomes evident that a certain degree of empathy or emotional communication abilities, particularly the appropriate transmission of fear emotions, can significantly enhance the overall survival capacity of the entire collective. It is worth noting that typical studies on collective dynamics often builds upon individual interactions in terms of movement information. Our model illustrates the interaction processes within the emotional layer of a collective and the modulation of individual dynamics by biological emotions. As a novel model of collective dynamics, its rich simulative phenomena demonstrate how individuals, in an information deficiency environment, utilize the dual-layer interaction structure of emotion and movement to enhance their fitness. By regulating the intensity of emotional activation and contagion, collective can find optimized configurations for environmental adaptation. This not only reveals the behavioral mechanisms of collective in information deficiency environments but also provides design insights for controlling techniques in artificial intelligence agent clusters within complex environments.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Y-XL: Conceptualization, Formal Analysis, Methodology, Visualization, Writing–original draft. S-PZ: Formal Analysis, Methodology, Writing–original draft. G-YM: Investigation, Writing–review and editing. B-HG: Conceptualization, Writing–review and editing. X-LL: Conceptualization, Writing–review and editing. Z-XW: Validation, Writing–review and editing. Z-GH: Funding acquisition, Project administration, Resources, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key R&D Program of China (Grant 2021ZD0201300), Natural Science Foundation of China under Grants (No. 12105213 and No. 12247101), Natural Science Basic Research Program of Shaanxi (Nos.2021JQ-007, 2023-JC-YB-071), Shaanxi Fundamental Science Research Project for Mathematics and Physics (Grant No.22JSQ037).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1394983/full#supplementary-material

Footnotes

¹Based on the results obtained from Figure 3A, take into account the larger and smaller values of ${\alpha }^{*}$ and ${\beta }^{*}$, we selected four typical parameter configurations as the extreme situations. In addition, the parameter positions of maximum AEST between each pair of these extreme configurations are either selected.

References

1. Cavagna A, Cimarelli A, Giardina I, Parisi G, Santagati R, Stefanini F, et al. Scale-free correlations in starling flocks. Proc Natl Acad Sci U S A (2010) 107:11865–70. doi:10.1073/pnas.1005766107

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Bialek W, Cavagna A, Giardina I, Mora T, Silvestri E, Viale M, et al. Statistical mechanics for natural flocks of birds. Proc Natl Acad Sci U S A (2012) 109:4786–91. doi:10.1073/pnas.1118633109

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Nagy M, Ákos Z, Biro D, Vicsek T. Hierarchical group dynamics in pigeon flocks. Nature (2010) 464:890–3. doi:10.1038/nature08891

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lei L, Escobedo R, Sire C, Theraulaz G. Computational and robotic modeling reveal parsimonious combinations of interactions between individuals in schooling fish. PLOS Comput Biol (2020) 16:e1007194. doi:10.1371/journal.pcbi.1007194

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. Novel type of phase transition in a system of self-driven particles. Phys Rev Lett (1995) 75:1226–9. doi:10.1103/PhysRevLett.75.1226

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Buhl J, Sumpter DJT, Couzin ID, Hale JJ, Despland E, Miller ER, et al. From disorder to order in marching locusts. Science (2006) 312:1402–6. doi:10.1126/science.1125142

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yates CA, Erban R, Escudero C, Couzin ID, Buhl J, Kevrekidis IG, et al. Inherent noise can facilitate coherence in collective swarm motion. Proc Natl Acad Sci U S A (2009) 106:5464–9. doi:10.1073/pnas.0811195106

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Attanasi A, Cavagna A, Del Castello L, Giardina I, Melillo S, Parisi L, et al. Collective behaviour without collective order in wild swarms of midges. Plos Comput Biol (2014) 10:e1003697. doi:10.1371/journal.pcbi.1003697

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Beekman M, Sumpter DJT, Ratnieks FLW. Phase transition between disordered and ordered foraging in pharaoh’s ants. Proc Natl Acad Sci U S A (2001) 98:9703–6. doi:10.1073/pnas.161285298

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Couzin ID, Franks NR. Self-organized lane formation and optimized traffic flow in army ants. Proc R Soc B-biol Sci (2003) 270:139–46. doi:10.1098/rspb.2002.2210

CrossRef Full Text | Google Scholar

11. Nanda P, Patnaik S, Patnaik S. Modelling of multi-agent coordination using crocodile predatory strategy. Int J Reasoning-based Intell Syst (2016) 8:119–31. doi:10.1504/IJRIS.2016.082963

CrossRef Full Text | Google Scholar

12. Jiang Y-Q, Chen B-K, Wang B-H, Wong W-F, Cao B-Y. Extended social force model with a dynamic navigation field for bidirectional pedestrian flow. Front Phys (2017) 12:124502. doi:10.1007/s11467-017-0689-3

CrossRef Full Text | Google Scholar

13. Duan H, Zhang X. Phase transition of vortexlike self-propelled particles induced by a hostile particle. Phys Rev E (2015) 92:012701. doi:10.1103/PhysRevE.92.012701

CrossRef Full Text | Google Scholar

14. Krause J, Hoare D, Krause S, Hemelrijk CK, Rubenstein DI. Leadership in fish shoals. Fish Fish (2000) 1:82–9. doi:10.1111/j.1467-2979.2000.tb00001.x

CrossRef Full Text | Google Scholar

15. Hoare DJ, Couzin ID, Godin J-GJ, Krause J. Context-dependent group size choice in fish. Anim Behav (2004) 67:155–64. doi:10.1016/j.anbehav.2003.04.004

CrossRef Full Text | Google Scholar

16. Kamimura A, Ohira T. Group chase and escape. New J Phys (2010) 12:053013. doi:10.1088/1367-2630/12/5/053013

CrossRef Full Text | Google Scholar

17. Angelani L. Collective predation and escape strategies. Phys Rev Lett (2012) 109:118104. doi:10.1103/physrevlett.109.118104

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Colombo EH, Martínez-García R, López C, Hernández-García E. Spatial eco-evolutionary feedbacks mediate coexistence in prey-predator systems. Scientific Rep (2019) 9:18161. doi:10.1038/s41598-019-54510-6

CrossRef Full Text | Google Scholar

19. de Waal FB. Putting the altruism back into altruism: the evolution of empathy. Annu Rev Psychol (2008) 59:279–300. doi:10.1146/annurev.psych.59.103006.093625

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Pérez-Manrique A, Gomila A. Emotional contagion in nonhuman animals: a review. Wiley Interdiscip Rev.-Cogn Sci (2022) 13:e1560. doi:10.1002/wcs.1560

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Pinho JS, Castilho M, Sollari JS, Oliveira RF. Innate chemical, but not visual, threat cues have been co-opted as unconditioned stimulus for social fear learning in zebrafish. Genes Brain Behav (2020) 19:e12688. doi:10.1111/gbb.12688

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Davila Ross M, Menzler S, Zimmermann E. Rapid facial mimicry in orangutan play. Biol Lett (2007) 4:27–30. doi:10.1098/rsbl.2007.0535

CrossRef Full Text | Google Scholar

23. Palagi E, Celeghin A, Tamietto M, Winkielman P, Norscia I. The neuroethology of spontaneous mimicry and emotional contagion in human and non-human animals. Neurosci Biobehav Rev (2020) 111:149–65. doi:10.1016/j.neubiorev.2020.01.020

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Speedie N, Gerlai R. Alarm substance induced behavioral responses in zebrafish (danio rerio). Behav Brain Res (2008) 188:168–77. doi:10.1016/j.bbr.2007.10.031

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Diaz-Verdugo C, Sun GJ, Fawcett CH, Zhu P, Fishman MC. Mating suppresses alarm response in zebrafish. Curr Biol (2019) 29:2541–6.e3. doi:10.1016/j.cub.2019.06.047

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Preston SD, de Waal FBM. Empathy: its ultimate and proximate bases. Behav Brain Sci (2002) 25:1–20. doi:10.1017/S0140525X02000018

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kikusui T, Winslow JT, Mori Y. Social buffering: relief from stress and anxiety. Philos Trans R Soc B (2006) 361:2215–28. doi:10.1098/rstb.2006.1941

CrossRef Full Text | Google Scholar

28. Decety J, Norman GJ, Berntson GG, Cacioppo JT. A neurobehavioral evolutionary perspective on the mechanisms underlying empathy. Prog Neurobiol (2012) 98:38–48. doi:10.1016/j.pneurobio.2012.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Oliveira RF, Faustino AI. Social information use in threat perception: social buffering, contagion and facilitation of alarm responses. Commun Integr Biol (2017) 10:e1325049. doi:10.1080/19420889.2017.1325049

CrossRef Full Text | Google Scholar

30. Young LJ, Wang Z. The neurobiology of pair bonding. Nat Neurosci (2004) 7:1048–54. doi:10.1038/nn1327

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Smith AS, Wang Z. Hypothalamic oxytocin mediates social buffering of the stress response. Biol Psychiatry (2014) 76:281–8. doi:10.1016/j.biopsych.2013.09.017

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Lamm C, Rütgen M, Wagner IC. Imaging empathy and prosocial emotions. Neurosci Lett (2019) 693:49–53. doi:10.1016/j.neulet.2017.06.054

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Faustino AI, Tacão-Monteiro A, Oliveira RF. Mechanisms of social buffering of fear in zebrafish. Sci Rep (2017) 7:44329. doi:10.1038/srep44329

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhu Y-B, Li J-S. Collective behavior simulation based on agent with artificial emotion. Cluster Comput (2019) 22:5457–65. doi:10.1007/s10586-017-1288-3

CrossRef Full Text | Google Scholar

35. Goldenberg A, Garcia D, Halperin E, Gross JJ. Collective emotions. Curr Dir Psychol Sci (2020) 29:154–60. doi:10.1177/0963721420901574

CrossRef Full Text | Google Scholar

36. Lemasson BH, Anderson JJ, Goodwin RA. Motion-guided attention promotes adaptive communications during social navigation. Proc R Soc B: Biol Sci (2013) 280:20122003. doi:10.1098/rspb.2012.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Calvão AM, Brigatti E. Collective movement in alarmed animals groups: a simple model with positional forces and a limited attention field. Physica A: Stat Mech its Appl (2019) 520:450–7. doi:10.1016/j.physa.2019.01.029

CrossRef Full Text | Google Scholar

38. Zanette LY, Clinchy M. Ecology of fear. Curr Biol (2019) 29:R309–13. doi:10.1016/j.cub.2019.02.042

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Subalusky AL, Dutton CL, Rosi EJ, Post DM. Annual mass drownings of the serengeti wildebeest migration influence nutrient cycling and storage in the mara river. Proc Natl Acad Sci (2017) 114:7647–52. doi:10.1073/pnas.1614778114

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Johansson A, Helbing D, Shukla PK. Specification of the social force pedestrian model by evolutionary adjustment to video tracking data. Adv Complex Syst (2007) 10:271–88. doi:10.1142/S0219525907001355

CrossRef Full Text | Google Scholar

41. Hopcraft JGC, Holdo RM, Mwangomo E, Mduma SA, Thirgood SJ, Borner M, et al. Why are wildebeest the most abundant herbivore in the serengeti ecosystem. In: Serengeti IV: sustaining biodiversity in a coupled human-natural system 125. Chicago: University of Chicago Press (2015).

Google Scholar