Nuclear magnetic resonance studies in a model transverse field Ising system

The suppression of ferroquadrupolar order in TmVO₄ in a magnetic field is well-described by the transverse field Ising model, enabling detailed studies of critical dynamics near the quantum phase transition. We describe nuclear magnetic resonance measurements in pure and Y-doped single crystals. The non-Kramers nature of the ground state doublet leads to a unique form of the hyperfine coupling that exclusively probes the transverse field susceptibility. Our results show that this quantity diverges at the critical field, in contrast to the mean-field prediction. Furthermore, we find evidence for quantum critical fluctuations present near Tm-rich regions in Y-doped crystals at levels beyond which long-range order is suppressed, suggesting the presence of quantum Griffiths phases.

1 Introduction

Unconventional superconductivity tends to emerge in the vicinity of a quantum critical point (QCP), where some form of long-range ordered state is continually suppressed to T = 0 [1–9]. This observation suggests that there may be an important relationship between the superconducting pairing mechanism and the strong quantum fluctuations associated with the QCP, however there are major challenges to understanding the fundamental physics at play in these systems. In practice various approaches can be utilized to tune the ordered state to the QCP. Hydrostatic pressure or magnetic field are thermodynamic variables that are homogeneous throughout the material and can be varied continuously. Doping, on the other hand, offers a convenient method to apply “chemical pressure” or introduce charge carriers, but can introduce electronic heterogeneity at the nanoscale which can complicate interpretation [10, 11]. In such cases it can be difficult to disentangle what experimental observations to ascribe to fundamental properties of a quantum phase transition versus extrinsic effects arising from the long-range effects of the dopants.

In order to better understand the influence of doping in strongly interacting system near a quantum phase transition, it is valuable to study a model system in the absence of superconductivity. TmVO₄ is as material that has attracted interest recently because its low temperature properties are well-described by the transverse field Ising model (TFIM), an archetype of quantum criticality [12, 13]. TmVO₄ exhibits long-range ferroquadrupolar order in which the Tm 4f orbitals spontaneously align in the same direction, as illustrated in Figure 1. The Tm³⁺ ions (4f ¹² with L = 5, S = 1, J = 6) experience a tetragonal crystal field interaction, and the ground state is well separated by a gap of $\sim 77$ K to the lowest excited state [15, 16]. The ground state is a non-Kramers doublet, so the first order Zeeman interaction vanishes for in-plane fields (i.e., g_c ∼ 10 while g_a = g_b = 0). This doublet can be described by a spin-1/2 pseudospin in which one component, σ_z, corresponds to a magnetic dipole moment oriented along the c-axis, while the other two components σ_x and σ_y correspond to electric quadrupole moments with B_2g (xy) and B_1g (x² − y²) symmetry, respectively [17]. The two quadrupole moments couple bilinearly to lattice strains ɛ_xx − ɛ_yy and ɛ_xy, which gives rise to an effective interaction between the moments and leads to a cooperative Jahn-Teller distortion at a temperature, T_Q [18]. TmVO₄ spontaneously undergoes a tetragonal to orthorhombic distortion with B_2g symmetry below T_Q = 2.15 K with orthorhombicity δ ≈ 0.01, as illustrated in Figure 1B. Because there are two distinct orientations of the quadrupolar moments, the ferroquadrupolar order has Ising symmetry that can be described as a coupling between neighboring pseudospins. On the other hand, a magnetic field oriented along the c-axis couples to the pseudospin in a direction that is transverse to the ferroquadrupolar order [19]. This field mixes the two degenerate ground state quadrupolar states, enhancing the fluctuations of the pseudospins and suppressing T_Q at a quantum phase transition with critical field $H_c^{*}\approx 0.5$ T [12]. This interpretation has been strengthened by the recent observation of a quantum critical fan emerging from the QCP that extends to temperatures above T_Q [20].

Figure 1

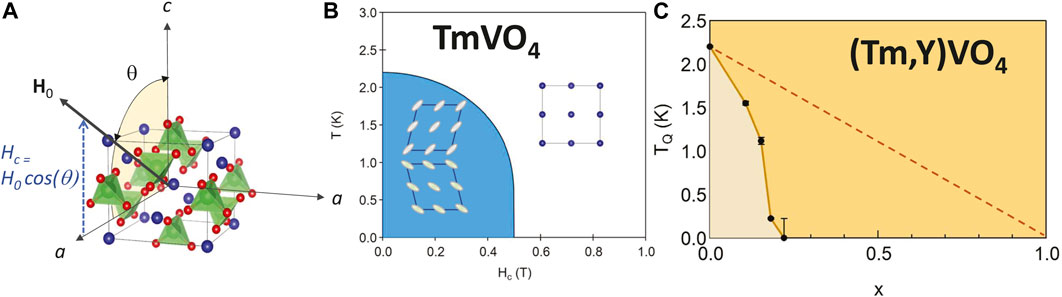
Figure 1. (A) Crystal structure of TmVO₄ (I41/amd) with Tm atoms in blue, V atoms lie at the center of green tetrahedra, and oxygen atoms in red. For the studies discussed here, the magnetic field, H₀, was rotated in the ac-plane, with an angle θ between H₀ and the c axis. The projection of the field along the c-axis is H₀ cos θ. (B) Schematic phase diagram of TmVO₄ as a function of magnetic field H_c along the c-axis, illustrating the B_2g orthorhombic distortion in the ferroquadrupolar state. (C) Phase diagram for Tm_1−xY_xVO₄, reproduced from [14]. The dashed line represents the mean-field result expected purely from dilution.

LiHoF₄ is another important material whose physics is well described by the TFIM [21]. There are important differences, however, between LiHoF₄ and TmVO₄. Although the physics of both systems derives from non-Kramers doublets, the former is a ferromagnet with Ho moments ordering along the c-axis, whereas the latter has ferroquadrupolar order with quadrupolar moments ordering in the plane. As a result, the transverse field direction for LiHoF₄ is perpendicular to the c-axis, whereas in TmVO₄ the transverse field direction is parallel to c. This fact is crucial for TmVO₄ because it also has profound consequences for the hyperfine coupling to neighboring nuclear spins and enables unique measurements of the quantum fluctuations directly. Moreover, since the quadrupolar moments couple to strain fields, long-range order in TmVO₄ is particularly sensitive to dopants. Therefore substituting with Y in TmVO₄ offers a unique opportunity to investigate how the quantum phase transition changes in response to the disorder and random fields introduced by the dopant atoms.

2 Couplings to non-Kramers doublet

2.1 Lattice interaction

2.1.1 Ground state wavefunctions

The ground state wavefunctions of the Tm in the D_4h point group symmetry of the TmVO₄ lattice are given by:

$|{\psi }_{\mathrm{1,2}}\rangle ={\alpha }_1|\pm 5\rangle +{\alpha }_2|\pm 1\rangle +{\alpha }_3|\mp 3\rangle$

in the |J_z⟩ basis, where the α_i coefficients are determined by the details of the crystal field Hamiltonian [16, 19]. Is is straightforward to show that J_x,y operators vanish in the subspace spanned by these states. On the other hand, there are three other operators that do not vanish:

$J_x^2-J_y^2\sim {\sigma }_x,J_x{J}_y+J_y{J}_x\sim {\sigma }_y,\text{and}{J}_z\sim {\sigma }_z,$

where the σ_α are the Pauli matrices. Physically, the first two operators represent quadrupolar moments with B_1g and B_2g symmetries, respectively, and the third represents a magnetic moment along the z direction. The conjugate fields to these moments are strain ϵ_B1g = ϵ_xx − ϵ_yy, ϵ_B2g = ϵ_xy, and magnetic field H_z, respectively. Here the strain tensor is defined as ϵ_ij = (∂u_i/∂x_j − ∂u_j/∂x_i)/2, where u(x) is the displacement from the equilibrium lattice positions.

2.1.2 Cooperative Jahn-Teller effect

Because the quadrupolar moments have non-uniform charge distributions, they can interact with a strained lattice via a bilinear coupling of the form −η_iɛ_iσ_i, where η_i is an electron-lattice coupling constant. This coupling renormalizes the elastic constant, leading to a softening in both the B_1g and B_2g channels, but is strongest for the B_2g channel for TmVO₄. It can be shown that this leads to an effective coupling between the quadrupolar moments:

${\mathcal{H}}_{ex}={\displaystyle \sum _{l\ne l^{\prime }}}J\left(l-l^{\prime }\right){\sigma }_y\left(l\right){\sigma }_y\left(l^{\prime }\right)(1)$

where the sum is over the lattice sites, and J(l − l′) is an Ising interaction between the Tm quadrupolar moments [17, 18]. The coupling depends on the details of the lattice, and because it is mediated by strain fields, it can extend well beyond just nearest neighbor sites. This interaction leads to long-range order in the three-dimensional TmVO₄ lattice below a temperature T_Q = 2.15 K, with finite expectation values of ±⟨σ_y⟩. This ferroquadrupolar order is accompanied by a B_2g lattice distortion as illustrated in Figure 1B [22].

2.2 Zeeman interaction

The interaction between a non-Kramers doublet in a tetragonal environment and a magnetic field is given by:

${\mathcal{H}}_Z=g_z{\mu }_B{H}_z{\sigma }_z+\frac{1}{2}{\left(g_J{\mu }_B\right)}^{2}b\left[\left(H_x^2-H_y^2\right){\sigma }_x+2H_x{H}_y{\sigma }_y\right],(2)$

where H_x,y is a magnetic field along the (x, y) direction, g_J = 7/6 for Tm³⁺ and g_c and b depend on the crystal field Hamiltonian [23]. These parameters have been measured for TmVO₄ to be g_c = 10.21 and b/k_B = 0.082 K⁻¹ [16]. Note that H couples quadratically in the x and y directions, rather than linearly for a Kramers doublet. A field in the z direction splits the doublet linearly, and acts as a transverse field for the Ising interaction in Eq. 1.

2.2.1 Induced moments for perpendicular fields

The Zeeman interaction can also be written as ${\mathcal{H}}_Z=\mu \cdot \mathbf{H}$, where the magnetic moment along z is μ_z = g_‖μ_Bσ_z, and the perpendicular fields H_x,y can couple with quadrupolar moments giving rise to effective magnetic moments:

${\mu }_{x,y}=\frac{1}{2}{\left(g_J{\mu }_B\right)}^{2}b\left(H_x{\sigma }_{y,x}\pm H_y{\sigma }_{x,y}\right).$

For sufficiently low perpendicular fields, H_x,y ≤ 3 T, the second order Zeeman interaction in the perpendicular direction will be less than 0.1k_BT_Q, and can be safely ignored. At higher fields, H_x and H_y can also act as either longitudinal or transverse fields for the Ising order, and can in fact be used to detwin the ferroquadrupolar order [24].

2.3 Transverse field Ising model for ferroquadrupolar order

The low temperature degrees of the Tm electronic degrees of freedom are thus captured by the sum ${\mathcal{H}}_{ex}+{\mathcal{H}}_Z$, which maps directly to the TFIM:

${\mathcal{H}}_{Tm}={\displaystyle \sum _{l\ne l^{\prime }}}J\left(l-l^{\prime }\right){\sigma }_y\left(l\right){\sigma }_y\left(l^{\prime }\right)+g_z{\mu }_B{H}_c{\displaystyle \sum _l}{\sigma }_z\left(l\right),(3)$

where the sum is over the Tm lattice sites. Here we have ignored the small contribution from the perpendicular component of the magnetic field. Mean field theory predicts a QCP for a c-axis field of T_Q/g_cμ_B ≈ 0.3 T, which is close to the experimental value of $H_c^{*}=0.5$ T. Note that if there is a perpendicular field oriented such that H_x or H_y is zero, the system can still be described by the TFIM, because ${\mathcal{H}}_Z$ does not couple to the longitudinal order in pseudospin space (σ_y). Rather, there is an effective transverse field in the x-z plane of pseudospin space leading to a different value of the critical field [24].

2.4 Coupling to nuclear spins

2.4.1 Hyperfine coupling to ⁵¹V

In most insulators the hyperfine coupling between a localized electron spin and a nearby nucleus arises due to the direct dipolar interaction and can be described as ${\mathcal{H}}_{\mathit{hyp}}=\mathbf{I}\cdot \mathbb{A}\cdot \mathbf{J}$, where I is the nuclear spin, A is the (traceless) hyperfine tensor, and J is the electron spin. For temperatures well below the crystal field excitations, J should be replaced by the ground state pseudospin operators and $\mathbb{A}$ should be renormalized. For a non-Kramers doublet, there can be no coupling along the x or y directions because the magnetic field of the nucleus does not interact with the doublet. Rather, the hyperfine coupling has the form:

${\mathcal{H}}_{\mathit{hyp}}=A_{zz}{I}_z{\sigma }_z+C\left(H_x{I}_x-H_y{I}_y\right){\sigma }_x+C\left(H_x{I}_y+H_y{I}_x\right){\sigma }_y,(4)$

where A_zz and C are constants [23]. In the absence of magnetic field, there is only a coupling along the z direction, corresponding to the transverse field direction. To determine the values of the coupling C, note that Eq. 4 can be re-written in terms of the effective magnetic moments:

${\mathcal{H}}_{\mathit{hyp}}=\frac{2C}{{\left(g_J{\mu }_B\right)}^{2}b}\left(I_x{\mu }_x+I_y{\mu }_y\right)+\frac{A_{zz}}{g_z{\mu }_B}{I}_z{\mu }_z(5)$

$=\gamma \hslash \left(h_x{I}_x+h_y{I}_y+h_z{I}_z\right),$

where h_α are the hyperfine fields at the nucleus created by the Tm moments. Using the measured values of h_x/μ_x = −0.0336 T/μ_B and h_z/μ_z = 0.0671 T/μ_B obtained by comparing the Knight shift versus susceptibility, we can then identify:

$C=\frac{1}{2}\gamma \hslash {\left(g_J{\mu }_B\right)}^{2}b\left(\frac{h_x}{{\mu }_x}\right)\approx -0.37\mu \mathrm{K}/\mathrm{T}$

$A_{zz}=\gamma \hslash g_z{\mu }_B\left(\frac{h_z}{{\mu }_z}\right)\approx 368\mu \mathrm{K}.$

these values of the hyperfine fields were obtained via direct Knight shift measurements, but agree well with the calculated direct dipolar fields in the TmVO₄ lattice [25].

2.4.2 Quadrupolar coupling to ⁵¹V

⁵¹V has spin I = 7/2 and a nuclear quadrupolar moment Q = 0.052 barns. Note that this moment is several orders of magnitude smaller than the electronic quadrupolar moment of the Tm 4f orbitals that undergo the ferroquadrupolar ordering at T_Q. Nevertheless, the extended charge distribution of the latter can contribute to the electric field gradient (EFG) tensor at the V nuclear site, which in turn couples to Q. As a result, the nuclear spins can couple to the pseudospin via the nuclear quadrupolar interaction [23]:

${\mathcal{H}}_Q=B_1\left(I_x^2-I_y^2\right){\sigma }_x+B_2\left(I_x{I}_y+I_y{I}_x\right){\sigma }_y+P\left[3I_z^2-I\left(I+1\right)\right]\mathbf{1}.$

Note that B₂ = B₁, and corresponds to a 45° rotation of the principal axes of the EFG. The last term, P, is determined by the local charge distribution in the VO₄ tetrahedra, and is independent of the 4f orbitals. The EFG asymmetry parameter is given by B₁⟨σ_x⟩/P, and can be measured through detailed spectral measurements as a function of angle in the ordered state. We estimate P ≈ 15 μK and B₁ = B₂ ≈ 0.22 μK [24].

Of all the terms in ${\mathcal{H}}_{\mathit{hyp}}+{\mathcal{H}}_Q$, A_zz is several orders of magnitude larger than any other, even for perpendicular fields of several tesla. Thus the coupling between the ⁵¹V and the Tm 4f orbitals is essentially only along the transverse field direction.

2.4.3 Hyperfine coupling to ¹⁶⁹Tm

¹⁶⁹Tm has a spin of I = 1/2, and experiences a hyperfine coupling but no quadrupolar interaction. By symmetry, the form of the hyperfine coupling must also be described by Eq. 5. In this case, however, the coupling A_zz ≈ 160 mK is nearly three orders of magnitude larger than that for the ⁵¹V due to the on-site coupling [26]. As a result, the spin lattice relaxation rate in the paramagnetic state is so fast that the ¹⁶⁹Tm resonance has not been observed. On the other hand, Bleaney and Wells reported ¹⁶⁹Tm in the ferroquadrupolar state, where they found a large shift of the resonance frequency for fields applied in the perpendicular direction [16]. In this case, the shift is due to the induced moments from the ordered Tm quadrupoles. The shift exhibited a two-fold rotation symmetry as the field was rotated in the perpendicular direction, which they attributed to the second order Zeeman interaction and the induced magnetization. The two-fold rotation reflects the orthorhombic crystal structure in the ferroquadrupolar state.

3 Nuclear magnetic resonance studies

Recently several studies have been conducted of the ⁵¹V NMR in TmVO₄ in order to better understand the nature of the quantum phase transition [19, 24, 25]. In principle, one could perform zero-field NMR (or nuclear quadrupolar resonance, NQR) and gradually apply a c-axis field to investigate the behavior as the field is tuned to the QCP. In this case, the NMR resonance frequency is given by |γH + nν_zz|, where γ = 11.193 MHz/T is the gyromagnetic ratio, ν_zz = 0.33 MHz, and n = −3, … , + 3. Thus the highest transition frequency at H = 0 is only 1 MHz, but experiments below 1 MHz are difficult because the signal-to-noise ratio varies as f ^3/2, where f is frequency [27]. To overcome this challenge, a perpendicular field of 3.3 T was applied along the [100] direction of the crystal (corresponding to the x or y directions in Eq. 2), and the crystal was rotated to project a small component along the c-axis, as illustrated in Figure 1A.

Spectra for several different values of H_c are shown in Figure 2A. For H_c = 0, the spectra consist of seven transitions separated by a quadrupolar interaction P ∼ 300 kHz, as seen in Figure 2A. As H_c increases, the anisotropic Knight shift and EFG tensors alter the frequencies of the various quadrupolar satellites in a well-controlled fashion, shown in Figure 2B. The separation between the seven peaks gradually reduces and vanishes at the magic angle (where $H_c=H_0/\sqrt{3}\approx 1.8$ T), and all the peaks shift to higher frequency, reflecting the strong magnetic anisotropy. Surprisingly, the integrated area of the spectra is dramatically suppressed in the vicinity of the QCP, as shown in Figure 2C. This suppression of intensity has been interpreted as evidence for quantum critical fluctuations of the transverse field, due to an increase in $T_2^{-1}$, the decoherence rate of the nuclear spins [20]. The relative area shown in the figure is proportional to signal size $L(t)\sim e^{-t/T_2}$, which depends on the time evolved, t, since the nuclear spins are prepared in their initial superposition state. In this experiment t is a fixed quantity determined by the pulse spacing in the experiment. An increase in $T_2^{-1}$ thus drives a suppression of the area. If L(t) decays faster than the minimum time to perform an experiment, then the signal intensity will be suppressed, or “wiped out.” The data in Figure 2C suggests that $T_2^{-1}$ reaches a maximum at the QCP.

Figure 2

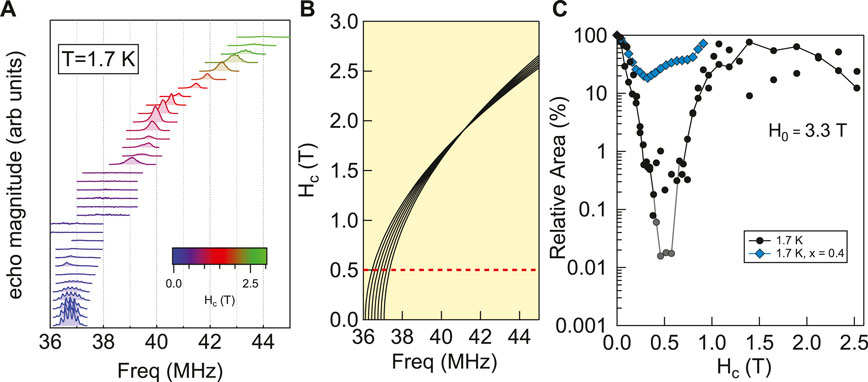
Figure 2. (A) Spectra of ⁵¹V for several different values of H_c as the crystal is rotated (see Figure 1A). (B) Calculated frequencies of the seven transitions as a function of H_c. The transitions merge at the magic angle, and then separate at higher values of H_c. The dashed red line corresponds to the critical field, $H_c^{*}$. (C) The spectral area versus H_c for several different values of temperature. The blue diamonds correspond to Tm_1−xY_xVO₄ with x = 0.4.

3.1 Transverse field susceptibility

The decoherence of an NMR signal can often be extended by applying refocusing pulses [28]. The simplest such pulse sequence consists of a spin echo, in which a single π pulse at time t/2 reverses the direction of precession and refocuses static field inhomogeneities. Noise fluctuations at time scales shorter than t/2, however, will lead to decoherence and loss of signal. In general, the decay envelope, L(t), of a spin-echo can be related to the noise fluctuations of the environment. In TmVO₄, this quantity can be written as:

$\log \left[L\left(t\right)/L\left(0\right)\right]=-\frac{A_{zz}^2}{{\hslash }^2}{\int }_0^{\infty }{S}_{zz}\left(\omega \right)\frac{F\left(\omega t\right)}{\pi {\omega }^2}d\omega ,$

where S_zz is the dynamical structure factor for the transverse field fluctuations:

$S_{zz}\left(\omega \right)={\int }_0^{\infty }⟨{\sigma }_z\left(\tau \right){\sigma }_z\left(0\right)⟩e^{i\omega \tau }d\tau ,$

and F(x) = 8 sin⁴(x/4) is a filter function for the spin echo pulse sequence, which takes into account the refocusing nature of the spin echo π pulse [29, 30]. The spectral area, shown in Figure 2C, is proportional to L(t) at fixed t corresponding to the pulse spacing in the spin echo experiment. Because the hyperfine coupling in TmVO₄ is solely along the transverse field direction, the nuclei are invisible to the longitudinal degrees of freedom. Only S_zz(ω), the noise spectrum in the transverse direction, contributes to the decoherence of the nuclear spins. This anisotropic coupling is highly unusual, but it enables us to probe the transverse fluctuations without any contamination from the longitudinal fluctuations, which diverge strongly at the QCP. The filter function acts to remove the static or low frequency (ω ≤ 10⁵ Hz) components of the fluctuations, which are dominated by thermal fluctuations [19, 31]. The remaining contributions to S_zz(ω), and hence to the decay of L(t), is from quantum fluctuations, which exist at finite frequency. This is because they arise from the intrinsic time evolution due to the many-body Hamiltonian, which has a finite gap except at the QCP. The fact that L(t) reaches a minimum at the QCP indicates that these quantum fluctuations are largest here. Importantly, these extend to finite temperature, even exceeding T_Q. These results thus imply that there is a broad region of phase space, a “quantum critical fan,” where quantum fluctuations are present.

An open question is how does the transverse susceptibility behave in the vicinity of the quantum phase transition? In mean-field theory at T = 0, χ_zz remains constant in the ordered state, and vanishes for $H_c>H_c^{*}$, as shown in Figure 3A. The NMR data are inconsistent with the mean field picture, since the relative area under the spectra decreases dramatically at the QCP, indicating that χ_zz must be strongly field-dependent in this range. Numerical calculations that are based on high and low field series expansions indicate that χ_zz diverges logarithmically on both sides of the QCP for various 3D lattices [32]. At T = 0 the enhancement is in a very narrow region but it should widen into a quantum critical fan at finite temperatures. Indeed we find significant differences between numerical calculations for small finite clusters and mean field theory at finite temperatures with enhancement in the general vicinity of the QCP, as seen in Figure 3B. We expect the differences to be much larger and centered at the critical point in the thermodynamic limit. These calculations, however, assume only a nearest neighbor interaction [e.g., J(l = l′) = 0 if l, l′ are not nearest neighbors in Eq. 3]. The interaction is expected to be long-range in TmVO₄, which could tend to stabilize mean-field behavior.

Figure 3

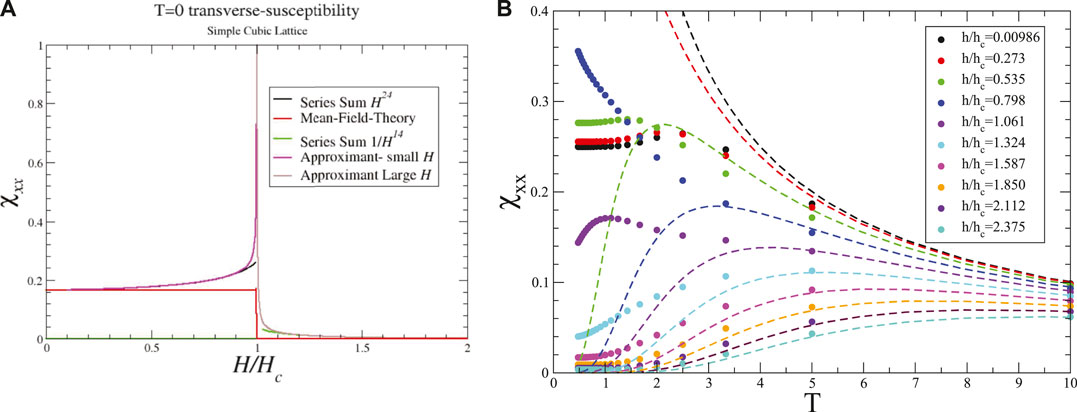
Figure 3. (A) Transverse susceptibility as a function of field for a simple cubic lattice at T = 0 in mean-field theory and in 3D short-range models. (B) Temperature dependence of the transverse field susceptibility at several different values of the transverse field calculated numerically for small periodic clusters of the square-lattice. The dashed lines are the mean field result, and the solid points of the same color are the results of numerical calculations.

3.2 Fidelity susceptibility

Understanding the mechanisms of decoherence is a key problem for quantum computing, and the behavior of a central spin coupled to a well-controlled environment is an important theoretical model that has been studied extensively [31, 33]. In the case where the central spin (or qubit) is coupled to a 1D TFIM via a hyperfine coupling along the transverse field direction, the decoherence of the qubit can be elegantly expressed in terms of the overlap of the wavefunction of the environment at different times and values of the transverse field. In fact, the ⁵¹V spins coupled to the ferroquadrupolar ordering in TmVO₄ maps well to this model, but with a 3D lattice for the environment. Although the central spin model was originally developed for a single spin coupled to an environment, it is straightforward to generalize to an ensemble of nuclear spins in a lattice, each with its own identical coupling [20]. Thus, TmVO₄ offers a unique opportunity to experimentally study this model.

Importantly, this connection offers a new approach to understanding NMR decoherence in terms of the quantum fidelity of the environment, which is defined as the modulus of the overlap between two states: F = |⟨Ψ′|Ψ⟩|. In the case of the central spin model, the two states are ${\mathrm{\Psi }}_{\lambda }^{\prime }(t=0)$ and Ψ_λ+ϵ(t), where λ corresponds to the transverse field, and ϵ corresponds to the small hyperfine field. Two ground states of the TFIM at different values of the transverse field may initially be very similar, but will evolve strongly away from one another in the vicinity of the QCP. At T = 0, the intensity of the NMR free induction decay is proportional to F², thus the qubit experiences a strong decoherence as the transverse field approaches the critical value. This tendency can be captured by the fidelity susceptibility: χ_F = −∂²F/∂ϵ². At finite temperatures, the fidelity can be expressed in terms of the density matrix [31]. A related quantity is the Quantum Fisher Information which quantifies the sensitivity of density matrices to small changes in parameters [34]. Because the fidelity susceptibility tends to diverge at a QCP, this quantity has been exploited theoretically to identify quantum and topological phase transitions [35, 36].

On the surface, this picture differs from the conventional NMR picture in which decoherence arises due to the presence of stochastic fluctuations of the hyperfine field, which can be quantitatively measured via Bloch-Wangsness-Redfield theory: $T_2^{-1}=A_{zz}^2{S}_{zz}(\omega =0)/2{\hslash }^2$ [28, 37, 38]. However, χ_F in fact can be related to the transverse field susceptibility, χ_zz = S_zz/k_BT [39]. This remarkable connection offers new insights and connections between NMR and quantum information theory. For example, NMR wipeout is ubiquitous in strongly correlated systems, and has been observed in the high temperature superconducting cuprates and the iron based superconductors [40–44]. In these cases, this phenomenon has been attributed to electronic inhomogeneity introduced because of the dopant atoms. However, the behavior in TmVO₄ suggests that it might be valuable to considering the wipeout in these other systems as a consequence of their proximity to a QCP.

4 NMR studies of Y substitution

Replacing Tm with Y suppresses the long range ferroquadrupolar order in Tm_1−xY_xVO₄ to zero at x_c ≈ 0.22, as illustrated in Figure 1C [14]. Y has no 4f electrons and thus lacks any magnetic or quadrupolar moments, so it acts to dilute the interactions between the Tm quadrupolar moments. The rapid suppression with doping is surprising because mean-field theory predicts a much weaker doping dependence: T_Q ∼ 1 − x. Y doping also suppresses ferromagnetic order in LiHoF₄, however in this case long-range order persists until x = 0.95 [45]. The reason for the difference between the TmVO₄ and LiHoF₄ is that the Y creates strain fields that couple to the ferroquadrupolar order in the former. Y is slightly larger than Tm, thus it creates local distortions in the lattice that couple to the Tm quadrupolar moments [14]. This behavior is similar to that of a random field Ising model (RFIM), and causes T_Q to be suppressed much faster with Y doping [46]. The local strain fields may have components with B_1g symmetry, which couples to σ_x and is a transverse field, as well as fields with B_2g symmetry, which couples to σ_y and is a longitudinal field.

Y substitution offers an opportunity to test whether the decoherence observed in the pure TmVO₄ is due to quantum critical fluctuations. Figure 2C shows that for x = 0.40, which has no long-range ferroquadruplar order, the relative spectral area does not change significantly at $H_c^{*}$, in contrast to x = 0. This observation indicates that the quantum fluctuations are suppressed in the x = 0.40 sample.

4.1 NMR spectra

NMR spectra in doped systems are generally broader than in undoped materials because the dopants often give rise to inhomogeneity. As seen in Figure 4A, the spectra of the pure TmVO₄ and YVO₄ consist of seven clear resonances with small linewidths, but these resonances grow progressively broader with doping. Each of the seven resonances broadens equally between 0 ≤ x ≤ 0.1. This behavior indicates that the broadening mechanism is not quadrupolar inhomogeneity, but rather a Knight shift inhomogeneity. The red dotted lines in Figure 4A are fits to the spectra, and the data in panel (e) show how the Gaussian width, σ, varies with doping for the spectra that can be clearly fit. It is surprising that even though random strain fields are clearly present and rapidly suppressing T_Q, they apparently do not significantly alter the local EFG at the V sites. In many other strongly-correlated systems, doping usually causes significant quadrupolar broadening [47–50]. In Tm_1−xY_xVO₄, the larger Y atoms slightly displace the O and V in their vicinity [14]. On the other hand, it is possible that the VO₄ tetrahedra may not be significantly distorted upon Y substitution. Also, there are two main contributions to the EFG: a lattice term arising from the arrangement of charges, and an on-site term that is determined by the electronic configuration of the local electronic orbitals [28]. It is reasonable that the latter term dominates the EFG at the V, and that the electronic configuration of the V and O orbitals remain relatively unperturbed by Y doping.

Figure 4

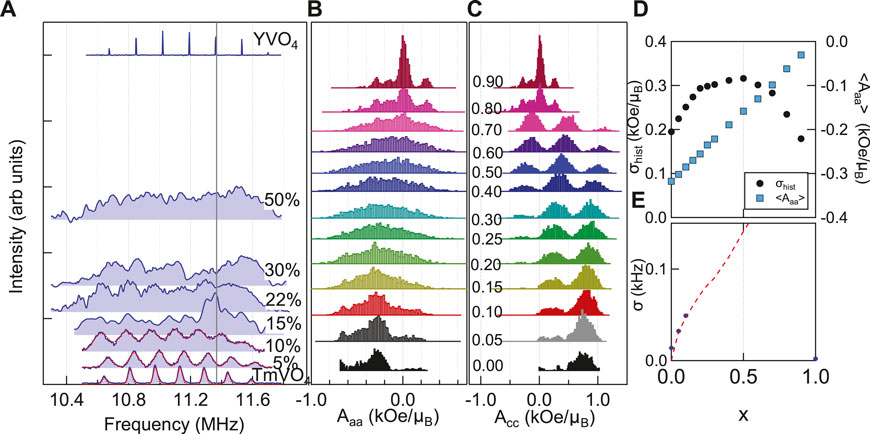
Figure 4. (A) Spectra for several values of x measured in an external field H₀ = 1 T oriented perpendicular to the c-axis at 1.8 K for all but the x = 1 case. For YVO₄ the spectrum was measured at 4.5 T and 10 K, but has been shifted to lower frequency by γΔH (ΔH = 3.9 T) to coincide with the other spectra. The red dotted lines are fits as described in the text. (B,C) Histograms of the hyperfine coupling constants, A_aa and A_cc, respectively, for a series of Y dopings for simulations as described in the text. (D) Average ⟨A_aa⟩ and standard deviation, σ, of the distributions shown in (B) as a function of Y doping, x. (E) The measured Gaussian linewidth of the spectra shown in (A) as a function of Y doping. The dashed red line was calculated using the computed standard deviation, as discussed in the text.

4.1.1 Numerical simulations

To investigate the inhomogeneity of the magnetic environments, we computed the direct dipolar hyperfine couplings, A_aa and A_cc, to the V sites in a 9 × 9 × 9 superlattice in which a fraction of the Tm sites are randomly removed. Histograms of these couplings are shown in Figures 4B, C for different Y concentrations. The sum is dominated by the two nearest neighbor Tm sites along the c-axis direction (see Figure 1A). The distribution for the perpendicular direction (A_aa) broadens with doping, but does not exhibit any structure. Figure 4D shows how the mean, ⟨A_aa⟩, and standard deviation, σ_hist, of the histograms vary with Y concentration. The standard deviation increases linearly with doping, which agrees with the experimental observation of the linewidth. The dashed red line in Figure 4E represents the expected magnetic linewidth in a field of H₀ = 1 T, as in the experiment. This quantity is given by σ(x)|K|γH₀/⟨A_aa⟩, where K = −0.66%. Here we have subtracted (in quadrature) the standard deviation of the histogram of the pure TmVO₄ case, which includes boundary effects: $\sigma (x)=\sqrt{{\sigma }_{\mathit{hist}}^2(x)-{\sigma }_{\mathit{hist}}{(0)}^2}$. The simulated linewidth agrees well with the measured linewidth, indicating that for low Y concentrations the magnetic environment of the remaining Tm is not significantly altered, despite the presence of the strain fields surrounding the Y sites. At higher doping levels, the magnetic broadening becomes comparable to the quadrupolar splitting, and the spectra become too broad to extract any information.

4.1.2 Effect of c-axis field

Figure 5A shows how the spectra for the x = 0.40 sample vary as the crystal is rotated in a fixed field, similar to the data shown in Figure 2A for the x = 0 case. As H_c increases, there is no significant wipeout at $H_c^{*}$, as expected since there is no long range order at this doping level and therefore no quantum critical behavior. The integrated area for these spectra are shown in Figure 2C as a function of H_c. However, there are three peaks that emerge as H_c increases beyond $\sim 1.5$ T, labelled A, B, and C, that are not present in the undoped sample. In fact, these extra peaks are consistent with the simulated histograms of the c-axis hyperfine couplings shown in Figure 4C. The three peaks correspond to V sites with 0, 1 or 2 nearest neighbor Tm atoms, respectively.

Figure 5

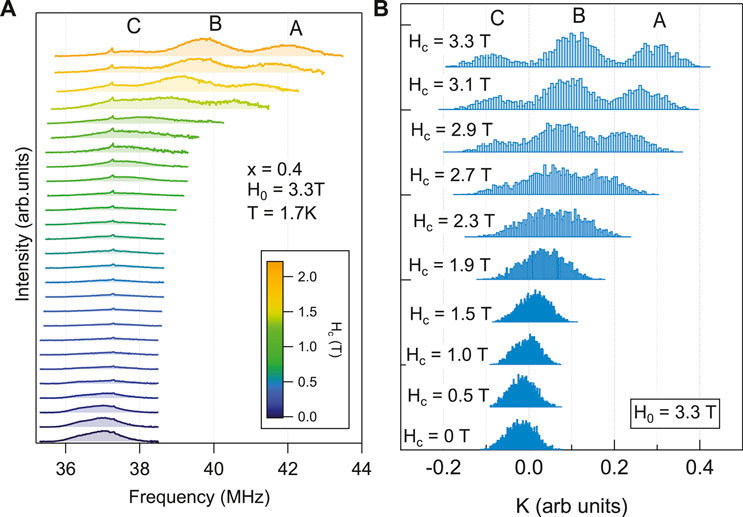
Figure 5. (A) Spectra of Tm_1−xY_xVO₄ with x = 0.40 for several different values of H_c. For H_c ≳ 1.5 T, three peaks are discernable, A, B, and C. (B) Computed spectra based on the histograms of hyperfine couplings shown in Figures 4B, C for several different values of H_c for x = 0.40.

As seen in Figure 4B these different V sites should not be discernible for a field H₀ ⊥ c. On the other hand, as H₀ rotates towards the c-axis, three distinct peaks should emerge. This behavior is demonstrated in Figure 5B, which displays the histograms of the Knight shift, K(θ) = A_aaχ_aa sin²θ + A_ccχ_cc cos²θ, for several different values of H_c = H₀ cos θ. Here χ_αα is the static susceptibility, and we assume χ_cc/χ_aa = 3 for concreteness. The three sites are indeed discernible for sufficiently large H_c, which agrees well with the observations shown in panel (a). Moreover, the relative intensity of the peaks (A: B: C = 0.32 : 0.49: 0.18) also agrees well with the observed spectra (0.33 ± 0.01 : 0.51 ± 0.01 : 0.16 ± 0.01). We therefore conclude that site A corresponds to V with 2 n.n. Tm, site B with 1 n.n. Tm, and site C with 0 n.n. Tm. This property enables us to learn about the electronic inhomogeneity by measuring the relaxation at the different sites.

4.2 Spin lattice relaxation rate

Figure 6A displays ${(T_{1}T)}^{-1}$ versus temperature for several different doping levels, measured for field perpendicular to the c-axis. Note that for this field orientation the resonance frequencies of sites A, B, and C overlap, and thus we are unable to discern if these spin fluctuations are spatially inhomogeneous. We do not see any evidence for stretched relaxation for x < 0.1, which would indicate the presence of inhomogeneity. In this range the different quadrupolar satellites are clearly resolved, and the relaxation was measured at all transitions to extract both the magnetic and quadrupolar relaxation channels, although just the magnetic contribution is shown [24]. For higher doping levels where the spectra no longer show any structure, we are unable to determine if there is any stretched relaxation behavior. There is a clear peak for the pure TmVO₄ at T_Q reflecting the critical slowing down at the thermal phase transition. As the doping level increases this peak is suppressed to lower temperatures, yet ${(T_{1}T)}^{-1}$ increases and reaches a broad maximum around x ≈ 0.10. In fact, the spin fluctuations appear to be enhanced near the vicinity of the critical doping level, x_c, possibly reflecting quantum critical fluctuations at this doping. At higher doping levels, the fluctuations gradually are suppressed and eventually disappear. For the pure YVO₄, there are no magnetic moments present anymore, and ${(T_{1}T)}^{-1}$ is several orders of magnitude smaller.

Figure 6

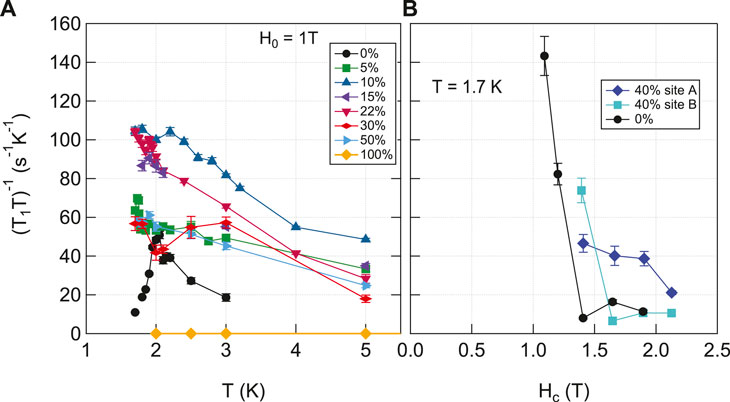
Figure 6. (A) ${(T_{1}T)}^{-1}$ versus temperature for several different Y doping levels, measured at H₀ = 1 T (except for the 100%, measured at 4.5 T), for θ = 90°. In this case, all three sites overlap. This data corresponds to the magnetic relaxation channel, as described in [51]. (B) ${(T_{1}T)}^{-1}$ versus the c-axis field component, H_c, for the pure TmVO₄, and for the A and B sites in the 40% sample.

Sites A, B and C can be discerned when there is a finite H_c component present. Figure 6B compares ${(T_{1}T)}^{-1}$ versus H_c in pure TmVO₄ with Tm_0.6Y_0.4VO₄ for the A and B sites. The strong field dependence of the pure system reflects the growth of the gap as the system is tuned away from the QCP at $H_c^{*}$: ${(T_{1}T)}^{-1}\sim \exp (-\mathrm{\Delta }(H_c)/T)$ [20]. As H_c is tuned beyond the QCP, the gap increases and ${(T_{1}T)}^{-1}$ decreases. It is surprising that in the x = 0.40 sample, which has no long range order, the A and B sites exhibit behavior that is qualitatively similar to that in the pure system. In other words, they each increase with decreasing field as H_c approaches the critical value. This behavior suggests that there are still localized clusters of Tm which continue to exhibit behavior reminiscent of the undoped lattice. Statistically there are regions of the disordered lattice with connected Tm atoms, and these may continue to exhibit correlations despite the absence of long-range order, giving rise to Griffiths phases [52]. An interesting open question is how such disconnected clusters may be affected by the presence of random strain fields.

Inhomogeneous dynamics in the disordered lattice may also explain the fact that the spectra in Figure 5A appear to exhibit an increasing intensity for H_c ≳ 1.5 T once the A and B peaks emerge. If local clusters of Tm continue to exhibit quantum critical fluctuations at these sites, then $T_2^{-1}$ will be large, suppressing the signal from these sites. In other words, the A and B sites may experience partial wipeout in the vicinity of $H_c^{*}$. Overall these sites contribute 84% of the total area, and the relative area under the spectra decreases by approximately the same value near $H_c^{*}$ in Figure 2C. These observations further support the argument that the A and B sites are locally unperturbed by the Y dopants, and may exhibit behavior consistent with quantum Griffiths phases.

5 Conclusion

TmVO₄ offers a unique new experimental platform to investigate quantum critical phenomena and the effects of doping. The unique properties of the non-Kramers doublet in this system not only gives rise to the unusual Ising ferroquadrupolar order, but also ensures that the nuclear spins in this system only couple to the transverse field degrees of freedom. Studies of the Tm_1−xY_xVO₄ uncovered several unexpected results. First, despite the presence of random strain fields, the EFG at the V sites remains unperturbed, at least for low doping concentrations. As the doping level increases and the long range ferroquadrupolar order vanishes, the spin lattice relaxation rate for the V sites is enhanced, before decreasing for doping levels that exceed the critical concentration. However, we find evidence that quantum critical fluctuations remain present for V sites that belong to Tm-rich clusters, even beyond the critical doping level, suggesting the presence of quantum Griffiths phases in the Y-doped system. It is unclear whether such isolated Tm clusters also experience random transverse or longitudinal strain fields. Further studies of this doped system will shed important light on how quantum fluctuations are destroyed by disorder.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Y-HN: Data curation, Investigation, Writing–review and editing. IV: Data curation, Investigation, Writing–review and editing. CC: Investigation, Writing–review and editing. YL: Resources, Writing–review and editing. MZ: Resources, Writing–review and editing. PM: Resources, Writing–review and editing. RS: Conceptualization, Formal Analysis, Investigation, Writing–review and editing. IF: Conceptualization, Resources, Writing–review and editing. NC: Conceptualization, Writing–original draft, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. Work at UC Davis was supported by the NSF under Grants No. DMR-1807889 and DMR-2210613, as well as the UC Laboratory Fees Research Program ID LFR-20-653926. Crystal growth performed at Stanford University was supported by the Air Force Office of Scientific Research under award number FA9550-20-1-0252.

Acknowledgments

We thank P. Klavins for support with cryogenic operations at UC Davis, and A. Albrecht and R. Fernandes for enlightening discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Balakirev FF, Betts JB, Migliori A, Ono S, Ando Y, Boebinger GS. Signature of optimal doping in Hall-effect measurements on a high-temperature superconductor. Nature (2003) 424:912–5. doi:10.1038/nature01890

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Coleman P, Schofield AJ. Quantum criticality. Nature (2005) 433:226–9. doi:10.1038/nature03279

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Park T, Ronning F, Yuan HQ, Salamon MB, Movshovich R, Sarrao JL, et al. Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn₅. Nature (2006) 440:65–8. doi:10.1038/nature04571

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Park T, Sidorov VA, Ronning F, Zhu JX, Tokiwa Y, Lee H, et al. Isotropic quantum scattering and unconventional superconductivity. Nature (2008) 456:366–8. doi:10.1038/nature07431

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Shibauchi T, Carrington A, Matsuda Y. A quantum critical point lying beneath the superconducting dome in iron pnictides. Annu Rev Condens Matter Phys (2014) 5:113–35. doi:10.1146/annurev-conmatphys-031113-133921

CrossRef Full Text | Google Scholar

6. Kuo HH, Chu JH, Palmstrom JC, Kivelson SA, Fisher IR. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science (2016) 352:958–62. doi:10.1126/science.aab0103

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lederer S, Schattner Y, Berg E, Kivelson SA. Enhancement of superconductivity near a nematic quantum critical point. Phys Rev Lett (2015) 114:097001. doi:10.1103/PhysRevLett.114.097001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Schuberth E, Tippmann M, Steinke L, Lausberg S, Steppke A, Brando M, et al. Emergence of superconductivity in the canonical heavy-electron metal YbRh₂Si₂. Science (2016) 351:485–8. doi:10.1126/science.aaa9733

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Paschen S, Si Q. Quantum phases driven by strong correlations. Nat Rev Phys (2020) 3:9–26. doi:10.1038/s42254-020-00262-6

CrossRef Full Text | Google Scholar

10. Alloul H, Bobroff J, Gabay M, Hirschfeld PJ. Defects in correlated metals and superconductors. Rev Mod Phys (2009) 81:45–108. doi:10.1103/RevModPhys.81.45

CrossRef Full Text | Google Scholar

11. Seo S, Lu X, Zhu JX, Urbano RR, Curro N, Bauer ED, et al. Disorder in quantum critical superconductors. Nat Phys (2014) 10:120–5. doi:10.1038/nphys2820

CrossRef Full Text | Google Scholar

12. Massat P, Wen J, Jiang JM, Hristov AT, Liu Y, Smaha RW, et al. Field-tuned ferroquadrupolar quantum phase transition in the insulator TmVO₄. Proc Natl Acad Sci (2022) 119:e2119942119. doi:10.1073/pnas.2119942119

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sachdev S Quantum phase transitions. Cambridge University Press (2001).

Google Scholar

14. Li Y, Zic MP, Ye L, Meese WJ, Massat P, Zhu Y, et al. Disorder-induced local strain distribution in Y-doped TmVO₄ (2024). doi:10.48550/ARXIV.2402.17049

CrossRef Full Text | Google Scholar

15. Knoll KD. Absorption and fluorescence spectra of Tm³⁺ in YVO₄ and YPO₄. Physica Status Solidi (B) (1971) 45:553–9. doi:10.1002/pssb.2220450218

CrossRef Full Text | Google Scholar

16. Bleaney B, Wells MR. Radiofrequency studies of TmVO₄. Proc R Soc Lond Ser A, Math Phys Sci (1980) 370:131–53.

Google Scholar

17. Melcher RL The anomalous elastic properties of materials undergoing cooperative Jahn Teller phase transisions (Elsevier), chap. The anomalous elastic properties of materials undergoing cooperative Jahn Teller phase transisions (1976). p. 1–77. doi:10.1016/B978-0-12-477912-9.50006-0

CrossRef Full Text | Google Scholar

18. Gehring GA, Gehring KA. Co-operative Jahn-Teller effects. Rep Prog Phys (1975) 38:1–89. doi:10.1088/0034-4885/38/1/001

CrossRef Full Text | Google Scholar

19. Maharaj AV, Rosenberg EW, Hristov AT, Berg E, Fernandes RM, Fisher IR, et al. Transverse fields to tune an Ising-nematic quantum phase transition. Proc Natl Acad Sci (2017) 114:13430–4. doi:10.1073/pnas.1712533114

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Nian YH, Vinograd I, Green T, Chaffey C, Massat P, Singh RRP, et al. Spin-echo and quantum versus classical critical fluctuations in TmVO₄. Phys. Rev. Lett (2024) 132:216502. doi:10.1103/PhysRevLett.132.216502

CrossRef Full Text | Google Scholar

21. Bitko D, Rosenbaum TF, Aeppli G. Quantum critical behavior for a model magnet. Phys Rev Lett (1996) 77:940–3. doi:10.1103/PhysRevLett.77.940

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Melcher RL, Pytte E, Scott BA. Phonon instabilities in TmVO₄. Phys Rev Lett (1973) 31:307–10. doi:10.1103/PhysRevLett.31.307

CrossRef Full Text | Google Scholar

23. Washimiya S, Shinagawa K, Sugano S. Effective Hamiltonian for non-Kramers doublets. Phys Rev B (1970) 1:2976–85. doi:10.1103/physrevb.1.2976

CrossRef Full Text | Google Scholar

24. Vinograd I, Shirer KR, Massat P, Wang Z, Kissikov T, Garcia D, et al. Second order Zeeman interaction and ferroquadrupolar order in TmVO₄. npj Quan Mater (2022) 7:68. doi:10.1038/s41535-022-00475-1

CrossRef Full Text | Google Scholar

25. Wang Z, Vinograd I, Mei Z, Menegasso P, Garcia D, Massat P, et al. Anisotropic nematic fluctuations above the ferroquadrupolar transition in TmVO₄. Phys Rev B (2021) 104:205137. doi:10.1103/PhysRevB.104.205137

CrossRef Full Text | Google Scholar

26. Schwab G, Hillmer W. Epr of non-kramers rare-earth ions in tetragonal crystals. physica status solidi (b) (1975) 70:237–44. doi:10.1002/pssb.2220700122

CrossRef Full Text | Google Scholar

27. Hoult D, Richards R. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J Magn Reson (1969) (1976) 24:71–85. doi:10.1016/0022-2364(76)90233-x

CrossRef Full Text | Google Scholar

28. Slichter CP Principles of nuclear magnetic resonance. 3rd ed. Springer-Verlag (1992).

Google Scholar

29. Cywiński Ł, Lutchyn RM, Nave CP, Sarma SD. How to enhance dephasing time in superconducting qubits. Phys Rev B (2008) 77:174509. doi:10.1103/physrevb.77.174509

CrossRef Full Text | Google Scholar

30. Yang W, Ma WL, Liu RB. Quantum many-body theory for electron spin decoherence in nanoscale nuclear spin baths. Rep Prog Phys (2016) 80:016001. doi:10.1088/0034-4885/80/1/016001

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Chen SW, Jiang ZF, Liu RB. Quantum criticality at high temperature revealed by spin echo. New J Phys (2013) 15:043032. doi:10.1088/1367-2630/15/4/043032

CrossRef Full Text | Google Scholar

32. Weihong Z, Oitmaa J, Hamer CJ. Series expansions for the 3D transverse Ising model at T=0. J Phys A: Math Gen (1994) 27:5425–44. doi:10.1088/0305-4470/27/16/010

CrossRef Full Text | Google Scholar

33. Quan HT, Song Z, Liu XF, Zanardi P, Sun CP. Decay of Loschmidt echo enhanced by quantum criticality. Phys Rev Lett (2006) 96:140604. doi:10.1103/physrevlett.96.140604

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Hauke P, Heyl M, Tagliacozzo L, Zoller P. Measuring multipartite entanglement through dynamic susceptibilities. Nat Phys (2016) 12:778–82. doi:10.1038/nphys3700

CrossRef Full Text | Google Scholar

35. König EJ, Levchenko A, Sedlmayr N. Universal fidelity near quantum and topological phase transitions in finite one-dimensional systems. Phys Rev B (2016) 93:235160. doi:10.1103/PhysRevB.93.235160

CrossRef Full Text | Google Scholar

36. Tang HK, Marashli MA, Yu WC. Unveiling quantum phase transitions by fidelity mapping. Phys Rev B (2021) 104:075142. doi:10.1103/PhysRevB.104.075142

CrossRef Full Text | Google Scholar

37. Wangsness RK, Bloch F. The dynamical theory of nuclear induction. Phys Rev (1953) 89:728–39. doi:10.1103/PhysRev.89.728

CrossRef Full Text | Google Scholar

38. Redfield AG. On the theory of relaxation processes. IBM J Res Dev (1957) 1:19–31. doi:10.1147/rd.11.0019

CrossRef Full Text | Google Scholar

39. Gu SJ. Fidelity approach to quantum phase transitions. Int J Mod Phys B (2010) 24:4371–458. doi:10.1142/S0217979210056335

CrossRef Full Text | Google Scholar

40. Curro N, Hammel P. The Cu NMR echo decay in stripe ordered La_1.65Eu_0.2Sr_0.15CuO₄. Phys C (2000) 341:1797–8. doi:10.1016/S0921-4534(00)01084-4

CrossRef Full Text | Google Scholar

41. Curro N, Hammel P, Suh B, Hücker M, Büchner B, Ammerahl U, et al. Inhomogeneous low frequency spin dynamics in La_1.65Eu_0.2Sr_0.15CuO₄. Phys Rev Lett (2000) 85:642–5. doi:10.1103/PhysRevLett.85.642

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Hunt A, Singer P, Thurber K, Imai T. ⁶³Cu NQR measurement of stripe order parameter in La_2−xSr_xCuO₄. Phys Rev Lett (1999) 82:4300–3. doi:10.1103/PhysRevLett.82.4300

CrossRef Full Text | Google Scholar

43. Julien MH, Campana A, Rigamonti A, Carretta P, Borsa F, Kuhns P, et al. Glassy spin freezing and NMR wipeout effect in the high-T_c superconductor La_1.90Sr_0.10CuO₄ critical discussion of the role of stripes. Phys Rev B (2001) 63:144508. doi:10.1103/PhysRevB.63.144508

CrossRef Full Text | Google Scholar

44. Dioguardi AP, Crocker J, Shockley AC, Lin CH, Shirer KR, Nisson DM, et al. Coexistence of cluster spin glass and superconductivity in Ba(Fe_1−xCo_x)₂As₂ for 0.060 ≤ x ≤ 0.071. Phys Rev Lett (2013) 111:207201. doi:10.1103/PhysRevLett.111.207201

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Babkevich P, Nikseresht N, Kovacevic I, Piatek JO, Dalla Piazza B, Kraemer C, et al. Phase diagram of diluted Ising ferromagnet LiHo_xy_1−xf₄. Phys Rev B (2016) 94:174443. doi:10.1103/PhysRevB.94.174443

CrossRef Full Text | Google Scholar

46. Nattermann T Theory of the random field ising model (world scientific) (1997). p. 277–98. doi:10.1142/9789812819437_0009

CrossRef Full Text | Google Scholar

47. Imai T, Slichter CP, Yoshimura K, Kosuge K. Low frequency spin dynamics in undoped and Sr-doped La₂CuO₄. Phys Rev Lett (1993) 70:1002–5. doi:10.1103/PhysRevLett.70.1002

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Lang G, Grafe HJ, Paar D, Hammerath F, Manthey K, Behr G, et al. Nanoscale electronic order in iron pnictides. Phys Rev Lett (2010) 104:097001. doi:10.1103/PhysRevLett.104.097001

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Kissikov T, Dioguardi AP, Timmons EI, Tanatar MA, Prozorov R, Bud’ko SL, et al. NMR study of nematic spin fluctuations in a detwinned single crystal of underdoped Ba(Fe_2−xCo_x)₂As₂. Phys Rev B (2016) 94:165123. doi:10.1103/PhysRevB.94.165123

CrossRef Full Text | Google Scholar

50. Menegasso P, Souza JC, Vinograd I, Wang Z, Edwards SP, Pagliuso PG, et al. Hyperfine couplings as a probe of orbital anisotropy in heavy-fermion materials. Phys Rev B (2021) 104:035154. doi:10.1103/physrevb.104.035154

CrossRef Full Text | Google Scholar

51. Vinograd I, Edwards SP, Wang Z, Kissikov T, Byland JK, Badger JR, et al. Inhomogeneous Knight shift in vortex cores of superconducting FeSe. Phys Rev B (2021) 104:014502. doi:10.1103/physrevb.104.014502

CrossRef Full Text | Google Scholar

52. Vojta T. Disorder in quantum many-body systems. Annu Rev Conden Ma P (2019) 10:233–52. doi:10.1146/annurev-conmatphys-031218-013433

CrossRef Full Text | Google Scholar