A dynamic beam switching metasurface based on angular mode-hopping effect

Fast and versatile beam forming and steering technologies are now crucial for various emerging applications, including wireless optical communications and optical switches. However, these technologies often rely on expensive components, such as spatial light modulators (SLMs) and optical phase arrays (OPAs), which come with complex and power-consuming control systems. In response to this challenge, we propose a dynamic beam-switching method inspired by the mode-hopping effect of lasers. As a proof of concept, we introduce the dynamic beam switching metasurface (DBSM) design, featuring an in-plane mechanical actuation system. Our numerical analyses, based on the finite element method (FEM), demonstrate that the proposed DBSM exhibits versatile beam forming and steering functionalities. These include beam splitting and omnidirectional beam steering. Moreover, we anticipate that the tuning speed of the DBSM will reach the kilohertz (kHz) range or even higher when utilizing a microelectromechanical systems (MEMS) actuator, building upon pioneering research in this field. We envision it holds promising applications in areas such as light detection and ranging (LiDAR), optical wireless communication devices, and optical switches.

1 Introduction

The precision control of optical beams is of paramount importance for numerous emerging applications, encompassing light detection and ranging [1–3], free space optical communications (FSO) [4–7], optical multiple-input multiple-output (MIMO) [8, 9], optical switches [10–12], structured light [13, 14] and beyond. Emerging technologies now demand more versatile beam steering techniques beyond merely controlling the propagation direction of individual beams. For example, multiple beams and structured light have now been widely applied to LiDARs and 3D scanners. Optical MIMO utilizes beam steering to guide beams emitted by individual light sources in various directions. This relies on fast beam-switching technologies, which enable spatial multiplexing, facilitating simultaneous data transmission across multiple spatial channels. Similarly, multiple-beam steering technology is now required to switch the optical signal not only from one channel to another (one to one) but also from one-to-multiple and multiple-to-multiple channels. These prospective applications motivate the development of optical beam generation and steering devices towards vast functionalities with merits, such as high deflection speed, good directivity, ultra-compactness, lightweight, and more.

Two key technologies, i.e., spatial light modulators [15–19] and optical phase arrays [20–22], have been intensively studied for achieving multiple beam generation and steering, enabling diverse applications in fields such as communications, imaging, and sensing. SLMs manipulate the diffraction pattern of the output beam by introducing pixel-by-pixel variations in the amplitude, phase, or both of the incident light beams, relying on a sophisticated control system to modulate each pixel individually. In the present day, compact and high-speed spatial light modulator (SLM) devices predominantly rely on liquid crystal on silicon (LCoS) technology [23, 24]. These devices utilize the nonlinear behavior of liquid crystals (LCs) to drive phase and amplitude shifters on a silicon chip. However, LCoS SLMs face several challenges, including cost, complexity, slow deflection speeds, limited deflection angles, and temperature sensitivity. Efforts to mitigate these limitations, such as incorporating angle amplifiers, often introduce additional system complexity and optical losses. Similarly, OPAs encounter technological challenges due to the use of optical antennas that are significantly smaller than the operational wavelength. These limitations impact the performance and design of OPAs, necessitating innovative solutions to address their unique constraints, e.g., the development of tunable optical delay lines [25–27]. Micro-/nanoelectromechanical systems (MEMS/NEMS) provide another conventional method, steering light beams through the rotation of micromirrors. Nevertheless, their applicability is confined to specific deflection angles due to the limited working states of the micromirrors, restricting their use in diverse fields [28]. Therefore, a simple and yet efficient method for generating and steering multiple optical beams remains elusive.

Metasurfaces, which can be categorized into metallic metasurfaces and dielectric metasurfaces, leverage various physical phenomena. These include Mie resonance [29, 30], toroidal moment [31], bound states in the continuum [32, 33], topological effects [34], and other phenomena. These effects are harnessed through precise manipulation of the amplitude, phase, and polarization of incident waves. Leveraging their remarkable ability to manipulate light, metasurfaces exhibit extraordinary phenomena such as perfect focusing [35, 36], high-efficiency holography [37–39], beam forming and steering [40–44], and flat lenses [45–47]. Leveraging mechanical motion, a recent demonstration of cascaded metasurfaces highlights several advantages, including low cost, ease of fabrication, simple control systems, compactness, and high modulation speed [48]. In comparison to other beam steering methods, this approach emerges as a cost-effective and efficient solution for dynamic beam control. Conversely, the widely recognized mode-hopping effect in tunable cavity lasers reveals that the laser’s output frequency is influenced by the overlap between the gain spectrum and the cavity modes in the frequency domain [49, 50]. This mechanism can be extended to the angular domain by leveraging the design flexibility of metasurfaces, resulting in a versatile yet concise approach for multiple-beam generation and steering. Supplementary Table S1 provides an overview of the advantages and disadvantages of various beamforming and steering technologies, including LCoS SLMs, OPAs, and reconfigurable metasurfaces. Among these, reconfigurable metasurfaces exhibit promising benefits such as low cost, energy efficiency, rapid tuning speeds (ranging from milliseconds to microseconds), and feasibility for on-chip integration.

Here, we introduce a cascaded metasurface comprising a converter array and a tuner array. This innovative design leverages the angular mode hopping effect to enable seamless switching of the output angular mode by translating the tuner array. The cascaded metasurface’s design flexibility empowers us to artificially control critical parameters of beam steering devices, including the maximum beam deflection angle, the number of array elements, and the mode switching function. To validate this concept, we have meticulously designed and numerically demonstrated a translation-controlled cascaded metasurface for beam switching, operating at a wavelength of 1,550 nm. Remarkably, this metasurface allows for mode switching among single-angular-mode (SAM), dual-angular-mode (DAM), and four-angular-mode (FAM), while consistently maintaining a sidelobe suppression ratio (SSR) below −9 dB. Compared with the LCoS SLMs [23, 24] and OPA-based [20–22] beam generation and steering technologies, the DBSM exhibits remarkably versatile functionalities, all while being controlled by a system with only two degrees of freedom. Therefore, our proposed translation-controlled cascaded metasurface offers a concise pathway to realize dynamic multiple-beam generation and steering across various applications, including FSO communication, LiDAR, optical MIMO, and optical switching.

2 The angular mode-hopping effect

The mode-hopping effect in lasers was first observed in the 1960s, which is a sudden jump in output optical frequency associated with transitions between different modes of the laser’s cavity [51–54]. The mode-hopping effect is a complex nonlinear process introduced by external influences during the laser operation, such as temperature drift, laser cavity vibration, and random noises, et.al. Nevertheless, the basic principle of laser mode hopping can be simplified based on the mode competition theory of the laser, as shown in Figure 1A. The laser’s output frequency is governed by the overlapping between the spectrum of the gain medium and the cavity modes. As a result, the output laser mode can be tuned by the variation of either the gain medium or the laser cavity.

Figure 1

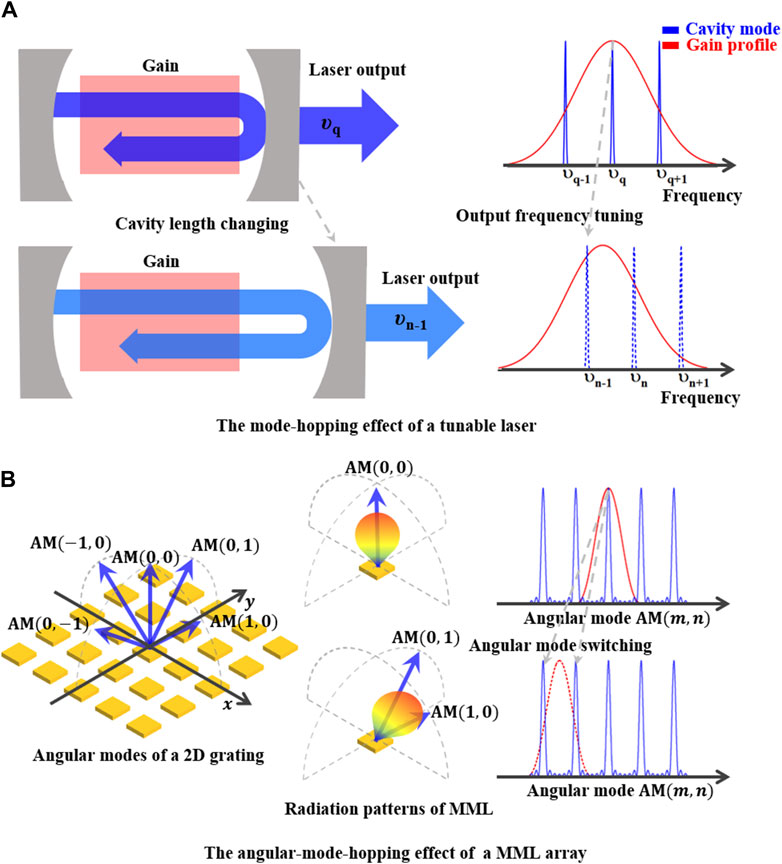
Figure 1. Schematics of mode-hopping effects in tunable lasers and MML arrays. (A) The mode-hopping effect of a tunable laser where the output frequency is tuned by changing the resonance cavity length. The output frequency is governed by the mode competition process, which can be tuned by the overlapping of the gain profile (red lines) and cavity modes (blue lines) in the frequency domain. (B) The angular-mode-hopping effect of an MML array where the radiation patterns of metasurface mirrors are tuned. The angular modes, i.e., the deflection angles of the output beams, are governed by the overlapping of the MML radiation patterns (red lines) and the 2D grating angular modes (blue lines).

The principle of the laser’s mode-hopping effect can also be applied to a two-dimensional (2D) grating consisting of an array of micro-sized metalens (MML), as shown in Figure 1B. The 2D grating is a periodical array along both x- and y-directions, resulting in diffraction orders oriented in both directions. Here, we define those diffraction orders as the angular modes (AMs) of the MML array, which is the counterpart of the cavity modes of the lasers. The mode number of AM(m, n) is defined according to the diffraction orders of the 2D gratings where m and n are the diffraction orders along x- and y-directions, respectively. For example, the angular mode is expressed as AM(0, 0) when the diffracted beam is the 0th-order diffraction along both x- and y-directions. Therefore, the diffraction angles DA(θ, φ) of an output beam can be expressed by AM(m, n) which is predefined by the period and effective refractive indices of the MML array. Here, θ and φ are the elevation and azimuth angles, respectively, which can be derived by the wavevector matching conditions along x- and y-directions as,

$k_0\mathit{cos}\theta \mathit{cos}\phi =K_x=\frac{2\pi m}{d_x}(1)$

$k_0\mathit{cos}\theta \mathit{sin}\phi =K_y=\frac{2\pi n}{d_y}(2)$

where k₀ is the wave number of the output beam and d_x and d_y are the MML period along x- and y-directions, respectively. K_x and K_y denote the modulus of grating vectors along x- and y-directions, respectively.

The radiation pattern RP(θ, φ) of an MML is determined by its phase and amplitude profile, i.e., P(x, y) and A(x, y), and the incident electromagnetic (EM) field, i.e., P_i(x, y) and A_i(x, y). The RP(θ, φ) can be expressed based on plane-wave expansion method as,

$RP\left(\mathrm{\theta },\mathrm{\phi }\right)={\int }_{-\frac{P_{cy}}{2}}^{\frac{P_{cy}}{2}}y{\int }_{-\frac{P_{cx}}{2}}^{\frac{P_{cx}}{2}}xA\left(x,y\right)A_i\left(x,y\right)e^{i\left(\omega t+P\left(x,y\right)+P_i\left(x,y\right)-\overrightarrow{k}\bullet \overrightarrow{r}\right)}dxdy(3)$

where P_cy and P_cx are the diameters of the MML along x and y-directions, respectively. A(x, y) and P(x, y) are the amplitude and phase of the MML unit cell transmission coefficient, respectively. P_i (x, y) and A_i(x, y) are the phase and amplitude of the incident EM wave, respectively. $\overrightarrow{k}$ is the wavevector of the output beam, which is a function of θ, φ and k0 and $\overrightarrow{r}$ is the displacement of the unit cell from the center of the MML which is set as the reference plane for the output phase profile.

Similar to the laser mode-hopping effect, the angular mode of the output beam can be selected when the maximum intensity of the MML radiation is superimposed with one of the angular modes A (m, n) in the angular domain. Therefore, the phase and amplitude profiles of the MML can be derived by substituting Eqs 1, 2 to Eq. 3 with given mode numbers m and n. In other words, the MML can be rationally designed to control the angular mode of the output beam.

3 Design of the DBSM

The working principles of the DBSM are shown in Figure 2. The DBSM is an MML array composed of a converter array and a tuner array. The converter array is to convert the incident wavefront to a reconfigurable wavefront. The tuner array can be actuated within the x-y plane with a displacement denoted as D (x, y). The insert shows the working principle of an MML composed of two cascade metasurfaces. Each layer of the cascaded metasurface consists of unit cells composed of a silicon cylinder patterned on a silica substrate. The optical response of a single unit cell can be obtained through numerical simulation using the finite element method. We considered periodic boundary conditions around a single unit cell in both directions to simulate an infinite size of the array. Furthermore, perfectly matched layers (PML) were assumed at the top and bottom of the structure, preventing any light reflection that does not happen in a real scene. A normal incident wave with linear polarization along x-direction was used as the excitation of an injection port and the reflection and transmission coefficient were calculated using additional ports. A parameter sweep of the single unit cell with fixed height 900 nm and fixed unit cell period 665 nm under x polarization at a wavelength of 1,550 nm was carried out to obtain the phase and amplitude of the different structural parameters as shown in Supplementary Figure S1. The phase of the transmitted light can be modulated from 0 to 2π while maintaining the transmittance of the amplitude above 90% with the variation of cylinder diameter d. Here, the MMLs are chosen to be rectangular with side length P_c = P_cx = P_cy = 40 μm. The output wavefront of the MML can be dynamically controlled by the tuning of D (x, y), which control the radiation pattern of the MML and thus tuning the angular mode of the output beam. As a result, we can design a metasurface with a dynamic beam switching function, i.e., tunable output angular mode, based on the angular-mode-hopping effect.

Figure 2

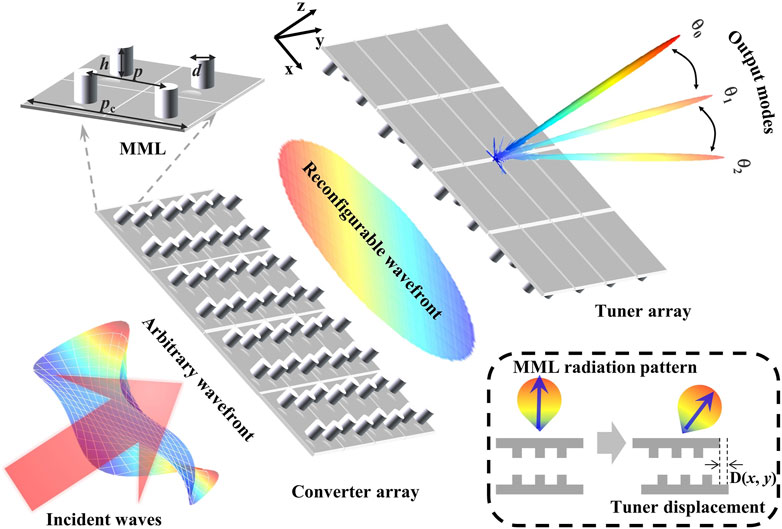
Figure 2. The working principles of the DBSM. The DBSM is an MML array composed of a converter array and a tuner array. The converter array is to covert the incident wavefront to a reconfigurable wavefront. The tuner array can be actuated within the x-y plane with a displacement denoted as D(x, y). The insert shows the working principle of an MML composed of two cascade metasurfaces. The radiation pattern of an MML is governed by the tuner displacement D(x, y). As a result, the output mode of the DBSM is selected among the 2D grating modes of the MML array by actuating the tuner array.

The performances of the dynamic beam-switching metasurface are governed by quite a few parameters, including the design of the tuner and converter, their spacing G, MML period p_c, the MML array size N × N, etc. Therefore, the optimization of the DBSM is a multiple-target process with multiple variations, which requires vast computation resources. To accelerate the optimization process, we first simplify the converter metasurface to a parabolic lens with a numerical aperture NA as shown in Figure 3A. The design parameters were reduced to N, ms, and NA. Here the ms is defined as the ratio between the diameter of the spot size on the tuner p_t and the MML period p_c which represents the filling ratio of the output beam.

Figure 3

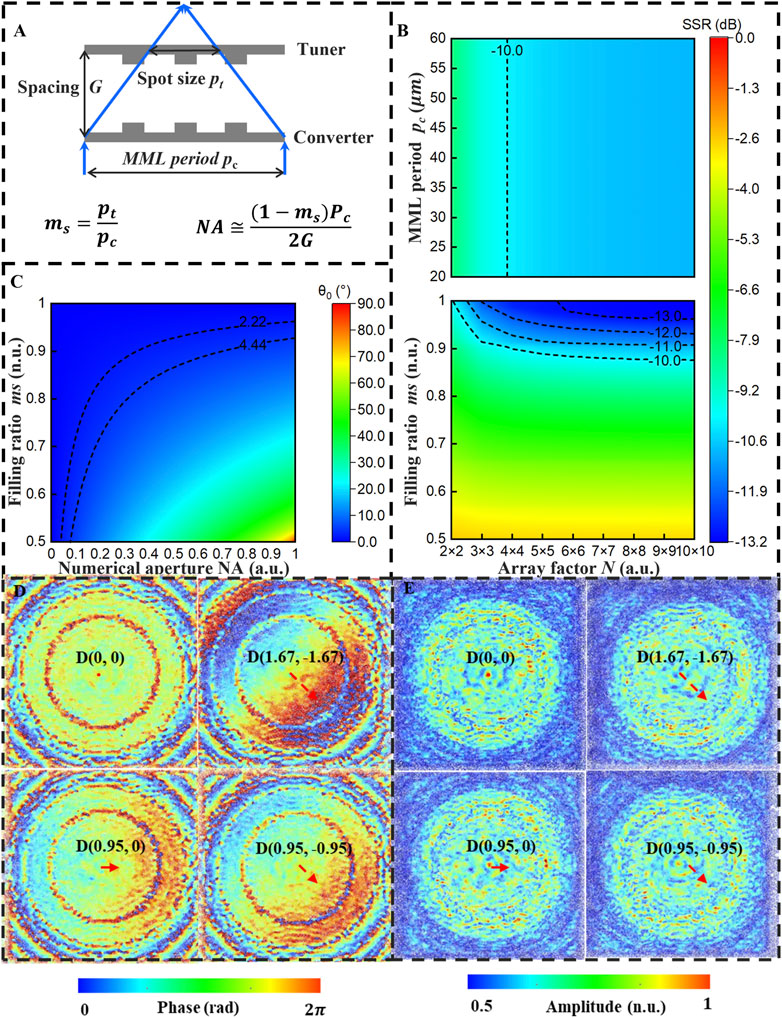
Figure 3. The optimization of the DBSM. (A) The optimization parameters of the DBSM. (B) the SRR as functions of p_c, ms and N. (C) The deflection angle θ₀ as a function of ms and NA. The electric field distributions of DBSM at the tuner’s surface with different displacement D (x, y) are shown in (D,E), which represent the phase and amplitude distributions, respectively. The phase distributions show a linear gradient along the displacement direction while the amplitude distribution is diffusive within the illumination area.

Then the far-field radiation pattern of the DBSM can be estimated by the product of the MML radiation and the space factor of the periodical lattice [55]. The Side-lobe suppression ratio (SSR) as functions of p_t, p_c, and N are shown in Figure 3B. The filling factor ms has the most significant influence on SSR, while N has a marginal impact, and p_c demonstrates negligible influence on SSR. Supplementary Figure S2A shows the SSRs as the functions of N and p_c at different ms. The effects of N and ms on the SSR with different p_c are shown in Supplementary Figure S2B. Again, the MML period p_c shows negligible influence on SSR. The side lobe is suppressed by the interferences of the MML in the DBSM array. The SSR’s increasing saturates when N continues increasing. The filling factor governs the interference between adjacent MMLs and thus dominates the SSR, which approaches −5.9 dB when ms is below 0.7.

Therefore, ms and NA are optimized for the deflection angles θ₀, i.e., the angle between the output beam and the metasurface norm. Figure 3C shows θ₀ under different NA and ms values. To achieve optimization goals with SSR less than −10 dB and θ₀ greater than 2.22°, and considering the optimization relationship diagram, we selected final design parameters as follows, p_c = 40 μm, N = 10, ms = 0.9, and NA = 0.4. In this configuration, the theoretical value of SSR reaches −10.81 dB, and θ₀ is 2.55°. It should be pointed out that the deflection angle can be greatly improved by reducing the filling ratio ms while increasing the NA, e.g., θ₀=36.9° when ms = 0.5 and NA = 0.6.

The radiation pattern of an MML is governed by the tuner displacement D(x, y). As a result, the output mode of the DBSM is selected among the 2D grating modes of the MML array by actuating the tuner array. The phase profiles of the tuner and converter metasurfaces are optimized to maximize the average directivities during the beam-switching process based on the reversed Rayleigh-Sommerfeld method which is detailed in [45]. The design flow chart of the DBSM is shown in Supplementary Figure S3, which can be divided into two major steps. One is to optimize the configuration of the MML array, i.e., the NA of the converter, the filling factor, and the array factor. The other is to further optimize the metasurface phase profiles. The optimization targets vary corresponding to the DBSM functionalities.

4 Numerical characterizations of the DBSM

The numerical characterization of the beam-switching function based on DBSM is conducted by using the finite element method (FEM). Here the numerical characterization is conducted in two steps since the DBSM is too large compared with the incident wavelength and thus requires too much computation resources. Therefore, we first obtain the electrical and magnetic field distribution of MMLs based on periodical boundary conditions, as shown in Figures 3D, E. The phase and amplitude distributions of electrical fields with different tuner displacements D (x, y) are shown in Figures 3D, E respectively. D (x, y) represents a tuner displacement of x μm along the x-direction and y μm along the y-direction. The cutting plane of the electrical fields is on the surface of the tuner metasurface. The electrical field distribution clearly shows a phase gradient along the direction of the tuner displacement, indicating a deflection of the MML’s radiation patterns. The amplitude distributions of the MML is diffusive due to the cutting plane being too close to the unit cell structures. The optical resonances of the unit cells in the near-field region still have nontrivial effects on the output wavefront.

Figure 4 shows the radiation intensity of different angular modes with different tuner displacements. Here, the radiation intensity is derived using the Fourier transformation of the MML’s electrical and magnetic field distributions. The inserted tables show the angular modes AM(m, n), the tuner displacement D(x, y), and the diffraction angles DA(θ,φ). Figure 4A shows the initial state of the proposed DBSM with a single angular mode output beam propagating along the norm of the metasurface, i.e., DA = (90°, 0°), with an SSR of −9.41 dB. The output beam is switched to AM(−1, 1) mode when the tuner is actuated 1.67 μm along both the negative x-direction and positive y-direction, i.e., D (x, y) = (−1.67, 1.67). The output beam remains in single mode but the DA is switched to (86.9°, 135°), as shown in Figure 4B. The dual-mode output beam, i.e., AM (0, 0) and AM (−1, 0), can be achieved with a tuner displacement D = (−0.95, 0). The output beam is now split into two, pointing at DA = (90°, 0°) and DA = (87.8°, 180°) simultaneously, as depicted in Figure 4C. A four-mode output beam can be achieved with a tuner displacement D = (−0.95, 0.95). The radiation pattern of MML overlaps four adjacent angular modes, i.e., AM (0, 0), AM (0, 1), AM (−1, 0), and AM (−1, 1), in the angular domain and splits the incident beam into four, as shown in Figure 4D.

Figure 4

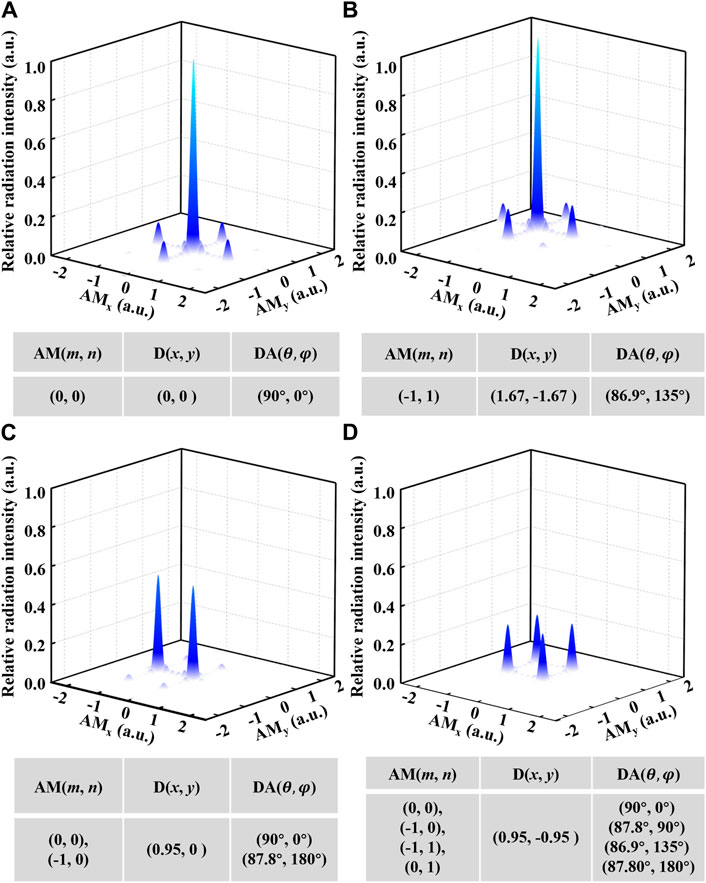
Figure 4. The beam switching processes of the DBSM. (A) and (B) the single beam switching function by exciting one angular mode at a time. (C) Dual-mode output and (D) Four-mode output by exciting multiple angular mode simultaneously. The inserted tables show detailed information of angular modes, tuner displacement and the diffraction angles.

Supplementary Figure S4 shows another DBSM design with dual-mode output at the initial state. In this design, higher angular modes and a larger tuning range of elevation angle are achieved by decreasing the filling factor. The maximum deflection angle θ0 is increased to 7.18° by decreasing the ms to 0.8. Supplementary Figure S4D shows that the SSR increased to −6.8 dB when the DBSM is switched to single mode output. However, the SSRs have minor changes when the DBSM is working at dual-mode or four-mode output. This is due to that the span of the MML radiation pattern is limited in the frequency domain thus suppressing the angular modes far away from the main slob of the radiation pattern in the angular domain. The dynamic angular mode switching of DBSM is shown in the movie S5 of the Supplementary Material. The DBSM demonstrates versatile beam forming and switching functionalities pre-coded in the MML’s design

5 Conclusion and prospects

We proposed a dynamic beam forming and steering method inspired by the mode-hopping effect of the lasers. As a proof of concept, we introduce the Dynamic Beam Switching Metasurface, pre-coded with functionalities for both beam forming and steering. Remarkably, the DBSM achieves these functions with a tuner’s displacement of less than 2 μm, facilitated by a two-degree-of-freedom in-plane mechanical actuation system. Our proposed translation-controlled cascaded metasurface provides a succinct approach for achieving dynamic multiple-beam generation and steering. Compared with the state-of-the-art technologies based on SLMs and OPAs, the DBSM shows versatile functionalities, including single-to-multiple-mode output switching and dynamic beam steering. It should be pointed out that our optimization process for the design parameters of the DBSM primarily relies on parameter sweeping. We determine the sweeping range based on our physics model and practical experience. However, this optimization process involves multiple variables and targets specific applications. For instance, when optimizing a DBSM, we consider parameters like unit cell structures, filling factors, spacing, and phase profiles of the two metasurfaces. Simultaneously, our optimization targets encompass aspects such as working bandwidth, angular modes as functions of displacements, and side-lobe suppression ratios. It is expected that the optimal design of DBSM can be achieved more effectively when combining our physics model with deep learning methods, such as neural networks and particle swarm optimization (PSO) algorithms. More importantly, pioneer research indicates that the DBSM can achieve impressive tuning speeds, reaching the kilohertz (kHz) range with a piezo actuator [48], and even the megahertz (MHz) regime when integrated within a MEMS system [43]. Furthermore, the streamlined control system is poised to facilitate effortless fabrication and cost-effectiveness for devices based on DBSMs. Applications include LiDAR, optical wireless communication devices, and optical switches, making it a promising solution for next-generation optical systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.

Author contributions

DH: Writing–original draft, Visualization, Validation, Software, Methodology, Investigation, Formal Analysis, Data curation. SH: Writing–review and editing, Visualization, Validation, Funding acquisition. SL: Writing–review and editing, Resources, Methodology, Funding acquisition, Formal Analysis. WZ: Writing–review and editing, Visualization, Supervision, Methodology, Investigation, Funding acquisition, Formal Analysis, Conceptualization.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Grant Nos 61975026 and 61875030) and Creative Research Groups of the National Natural Science Foundation of Sichuan Province (2023NSFSC1973).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1392115/full#supplementary-material

References

1. Marinov E, Martins RJ, Ben Youssef MA, Kyrou C, Coulon P-M, Genevet P. Overcoming the limitations of 3d sensors with wide field of view metasurface-enhanced scanning lidar. Adv Photon (2023) 5(4):046005. doi:10.1117/1.Ap.5.4.046005

CrossRef Full Text | Google Scholar

2. Chen R, Shu H, Shen B, Chang L, Xie W, Liao W, et al. Breaking the temporal and frequency congestion of lidar by parallel chaos. Nat Photon (2023) 17(4):306–14. doi:10.1038/s41566-023-01158-4

CrossRef Full Text | Google Scholar

3. Meng Z, Xia X, Xu R, Liu W, Ma J. Hydro-3d: hybrid object detection and tracking for cooperative perception using 3d lidar. IEEE T Intell Vehicl (2023) 8(8):4069–80. doi:10.1109/tiv.2023.3282567

CrossRef Full Text | Google Scholar

4. Xu G, Zhang N, Xu M, Xu Z, Zhang Q, Song Z. Outage probability and average ber of uav-assisted dual-hop fso communication with amplify-and-forward relaying. IEEE T Veh Technol (2023) 72(7):8287–302. doi:10.1109/tvt.2023.3252822

CrossRef Full Text | Google Scholar

5. Bekkali A, Hattori M, Hara Y, Suga Y. Free space optical communication systems for 6g: a modular transceiver design. IEEE Wirel Commun (2023) 30(5):50–7. doi:10.1109/mwc.006.2300118

CrossRef Full Text | Google Scholar

6. Wan Z, Shen Y, Wang Z, Shi Z, Liu Q, Fu X. Divergence-degenerate spatial multiplexing towards future ultrahigh capacity, low error-rate optical communications. Light Sci Appl (2022) 11(1):144. doi:10.1038/s41377-022-00834-4

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Feng F, Hu J, Guo Z, Gan J-A, Chen P-F, Chen G, et al. Deep learning-enabled orbital angular momentum-based information encryption transmission. ACS Photon (2022) 9(3):820–9. doi:10.1021/acsphotonics.1c01303

CrossRef Full Text | Google Scholar

8. Chen J, Liang Y-C, Cheng HV, Yu W. Channel estimation for reconfigurable intelligent surface aided multi-user mmwave mimo systems. IEEE T Wirel Commun (2023) 22(10):6853–69. doi:10.1109/twc.2023.3246264

CrossRef Full Text | Google Scholar

9. Wen F, Shi J, Gui G, Gacanin H, Dobre OA. 3-D positioning method for anonymous uav based on bistatic polarized mimo radar. IEEE Internet Things (2023) 10(1):815–27. doi:10.1109/jiot.2022.3204267

CrossRef Full Text | Google Scholar

10. Lou B, Rodriguez JA, Wang B, Cappelli M, Fan S. Inverse design of optical switch based on bilevel optimization inspired by meta-learning. ACS Photon (2023) 10(6):1806–12. doi:10.1021/acsphotonics.3c00113

CrossRef Full Text | Google Scholar

11. Jiang Y, Han X, Li Y, Xiao H, Huang H, Zhang P, et al. High-speed optical mode switch in lithium niobate on insulator. ACS Photon (2023) 10(7):2257–63. doi:10.1021/acsphotonics.2c01364

CrossRef Full Text | Google Scholar

12. Zhang Y, Chen J, Liu S, Jin W, Cheng S, Zhang Y, et al. All-fiber nonvolatile broadband optical switch using an all-optical method. Opt Lett (2022) 47(14):3604–7. doi:10.1364/ol.462200

PubMed Abstract | CrossRef Full Text | Google Scholar

13. He C, Shen Y, Forbes A. Towards higher-dimensional structured light. Light Sci Appl (2022) 11(1):205. doi:10.1038/s41377-022-00897-3

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Shen Y. Rays, waves, su(2) symmetry and geometry: toolkits for structured light. J Opt (2021) 23(12):124004. doi:10.1088/2040-8986/ac3676

CrossRef Full Text | Google Scholar

15. Li W, Hu X, Wu J, Fan K, Chen B, Zhang C, et al. Dual-color terahertz spatial light modulator for single-pixel imaging. Light Sci Appl (2022) 11(1):191. doi:10.1038/s41377-022-00879-5

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Mansha S, Moitra P, Xu X, Mass TWW, Veetil RM, Liang X, et al. High resolution multispectral spatial light modulators based on tunable fabry-perot nanocavities. Light Sci Appl (2022) 11(1):141. doi:10.1038/s41377-022-00832-6

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Park J, Jeong BG, Kim SI, Lee D, Kim J, Shin C, et al. All-solid-state spatial light modulator with independent phase and amplitude control for three-dimensional lidar applications. Nat Nanotechnol (2021) 16(1):69–76. doi:10.1038/s41565-020-00787-y

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kwon H, Zheng T, Faraon A. Nano-electromechanical spatial light modulator enabled by asymmetric resonant dielectric metasurfaces. Nat Commun (2022) 13(1):5811. doi:10.1038/s41467-022-33449-9

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Panuski CL, Christen I, Minkov M, Brabec CJ, Trajtenberg-Mills S, Griffiths AD, et al. A full degree-of-freedom spatiotemporal light modulator. Nat Photon (2022) 16(12):834–42. doi:10.1038/s41566-022-01086-9

CrossRef Full Text | Google Scholar

20. Han R, Sun J, Hou P, Ren W, Cong H, Zhang L, et al. Multi-dimensional and large-sized optical phased array for space laser communication. Opt Express (2022) 30(4):5026–37. doi:10.1364/oe.447351

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kjellman JO, Prost M, Marinins A, Tyagi HK, Kongnyuy TD, Dwivedi S, et al. Densely integrated phase interrogators for low-complexity on-chip calibration of optical phased arrays. J Light Technol (2022) 40(16):5660–7. doi:10.1109/jlt.2022.3179437

CrossRef Full Text | Google Scholar

22. Yu L, Ma P, Luo G, Cui L, Zhou X, Wang P, et al. Adoption of large aperture chirped grating antennas in optical phase array for long distance ranging. Opt Express (2022) 30(15):28112–20. doi:10.1364/oe.464358

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhu Z, Wen Y, Li J, Chen Y, Peng Z, Li J, et al. Metasurface-enabled polarization-independent lcos spatial light modulator for 4k resolution and beyond. Light Sci Appl (2023) 12(1):151. doi:10.1038/s41377-023-01202-6

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhang Z, You Z, Chu D. Fundamentals of phase-only liquid crystal on silicon (lcos) devices. Light Sci Appl (2014) 3:e213. doi:10.1038/lsa.2014.94

CrossRef Full Text | Google Scholar

25. Capmany J, Domenech D, Munoz P. Silicon graphene reconfigurable crows and scissors. IEEE Photon J (2015) 7(2):1–9. doi:10.1109/jphot.2015.2407314

CrossRef Full Text | Google Scholar

26. Brunetti G, Conteduca D, Dell’Olio F, Ciminelli C, Armenise MN. Design of an ultra-compact graphene-based integrated microphotonic tunable delay line. Opt Express (2018) 26(4):4593–604. doi:10.1364/OE.26.004593

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Margallo-Balbás E, Pandraud G, French P. Thermo-optical delay line for optical coherence tomography. Proc SPIE (2007) 6717:30–8. doi:10.1117/12.754324

CrossRef Full Text | Google Scholar

28. Pribosek J, Bainschab M, Sasaki T. Varifocal mems mirrors for high-speed axial focus scanning: a review. Microsyst Nanoeng (2023) 9(1):135. doi:10.1038/s41378-022-00481-0

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Cheng Y, Zhou C, Yuan BG, Wu DJ, Wei Q, Liu XJ. Ultra-sparse metasurface for high reflection of low-frequency sound based on artificial Mie resonances. Nat Mater (2015) 14(10):1013–9. doi:10.1038/nmat4393

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Barsukova MG, Shorokhov AS, Musorin AI, Neshev DN, Kivshar YS, Fedyanin AA. Magneto-optical response enhanced by Mie resonances in nanoantennas. ACS Photon (2017) 4(10):2390–5. doi:10.1021/acsphotonics.7b00783

CrossRef Full Text | Google Scholar

31. Conteduca D, Brunetti G, Barth I, Quinn SDD, Ciminelli C, Krauss TFF. Multiplexed near-field optical trapping exploiting anapole states. Acs Nano (2023) 17(17):16695–702. doi:10.1021/acsnano.3c03100

PubMed Abstract | CrossRef Full Text | Google Scholar

32. He Y, Guo G, Feng T, Xu Y, Miroshnichenko AE. Toroidal dipole bound states in the continuum. Phys Rev B (2018) 98(16):161112. doi:10.1103/PhysRevB.98.161112

CrossRef Full Text | Google Scholar

33. Kupriianov AS, Xu Y, Sayanskiy A, Dmitriev V, Kivshar YS, Tuz VR. Metasurface engineering through bound states in the continuum. Phys Rev Appl (2019) 12(1):014024. doi:10.1103/PhysRevApplied.12.014024

CrossRef Full Text | Google Scholar

34. Song Q, Odeh M, Zuniga-Perez J, Kante B, Genevet P. Plasmonic topological metasurface by encircling an exceptional point. Science (2021) 373(6559):1133–7. doi:10.1126/science.abj3179

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Papaioannou M, Plum E, Rogers ETF, Zheludev NI. All-optical dynamic focusing of light via coherent absorption in a plasmonic metasurface. Light Sci Appl (2018) 7:17157. doi:10.1038/lsa.2017.157

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Taghvaee H, Liu F, Diaz-Rubio A, Tretyakov S. Perfect-lens theory enables metasurface reflectors for subwavelength focusing. Phys Rev Appl (2023) 19(1):014004. doi:10.1103/PhysRevApplied.19.014004

CrossRef Full Text | Google Scholar

37. So S, Kim J, Badloe T, Lee C, Yang Y, Kang H, et al. Multicolor and 3d holography generated by inverse-designed single-cell metasurfaces. Adv Mater (2023) 35(17):2208520. doi:10.1002/adma.202208520

CrossRef Full Text | Google Scholar

38. Ren H, Fang X, Jang J, Buerger J, Rho J, Maier SA. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat Nanotechnol (2020) 15(11):948–55. doi:10.1038/s41565-020-0768-4

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Qu G, Yang W, Song Q, Liu Y, Qiu C-W, Han J, et al. Reprogrammable meta-hologram for optical encryption. Nat Commun (2020) 11(1):5484. doi:10.1038/s41467-020-19312-9

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Komar A, Paniagua-Dominguez R, Miroshnichenko A, Yu YF, Kivshar YS, Kuznetsov AI, et al. Dynamic beam switching by liquid crystal tunable dielectric metasurfaces. ACS Photon (2018) 5(5):1742–8. doi:10.1021/acsphotonics.7b01343

CrossRef Full Text | Google Scholar

41. Li S-Q, Xu X, Veetil RM, Valuckas V, Paniagua-Dominguez R, Kuznetsov AI. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science (2019) 364(6445):1087–90. doi:10.1126/science.aaw6747

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Liu S, Ma S, Shao R, Zhang L, Yan T, Ma Q, et al. Moire metasurfaces for dynamic beamforming. Sci Adv (2022) 8(33):eabo1511. doi:10.1126/sciadv.abo1511

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Meng C, Thrane PCV, Ding F, Bozhevolnyi SI. Full-range birefringence control with piezoelectric mems-based metasurfaces. Nat Commun (2022) 13(1):2071. doi:10.1038/s41467-022-29798-0

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Shirmanesh GK, Sokhoyan R, Wu PC, Atwater HA. Electro-optically tunable multifunctional metasurfaces. ACS Nano (2020) 14(6):6912–20. doi:10.1021/acsnano.0c01269

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Badloe T, Kim I, Kim Y, Kim J, Rho J. Electrically tunable bifocal metalens with diffraction-limited focusing and imaging at visible wavelengths. Adv Sci (2021) 8(21):2102646. doi:10.1002/advs.202102646

CrossRef Full Text | Google Scholar

46. Ossiander M, Meretska ML, Hampel HK, Lim SWD, Knefz N, Jauk T, et al. Extreme ultraviolet metalens by vacuum guiding. Science (2023) 380(6640):59–63. doi:10.1126/science.adg6881

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wang S, Wu PC, Su V-C, Lai Y-C, Chen M-K, Kuo HY, et al. A broadband achromatic metalens in the visible. Nat Nanotechnol (2018) 13(3):227–32. doi:10.1038/s41565-017-0052-4

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Deng W, Jiang S, Shi Y, Liu Z, Zang G, Qin J, et al. Mid-infrared dynamic wavefront transformer based on a two-degrees-of-freedom control system. Laser Photon Rev (2022) 16(10):2200152. doi:10.1002/lpor.202200152

CrossRef Full Text | Google Scholar

49. Muduli PK, Heinonen OG, Akerman J. Decoherence and mode hopping in a magnetic tunnel junction based spin torque oscillator. Phys Rev Lett (2012) 108(20):207203. doi:10.1103/PhysRevLett.108.207203

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Kosulnikov S, Zalipaev V, Shchelokova A, Melchakova I, Glybovski S, Slobozhanyuk A, et al. Mode hopping in arrays of resonant thin wires over a dielectric interface. Phys Rev B (2018) 98(17):174302. doi:10.1103/PhysRevB.98.174302

CrossRef Full Text | Google Scholar

51. Tang CL, Statz H. Nonlinear effects in the resonant absorption of several oscillating fields by a gas. Phys Rev (1962) 128(3):1013–21. doi:10.1103/PhysRev.128.1013

CrossRef Full Text | Google Scholar

52. Isenor NR. Polarization and mode hopping in a gas laser. J Appl Phys (1967) 38(1):417–8. doi:10.1063/1.1708999

CrossRef Full Text | Google Scholar

53. Shen Y, Meng Y, Fu X, Gong M. Wavelength-tunable hermite-Gaussian modes and an orbital-angular-momentum-tunable vortex beam in a dual-off-Axis pumped Yb:calgo laser. Opt Lett (2018) 43(2):291–4. doi:10.1364/ol.43.000291

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Shen Y, Yang X, Fu X, Gong M. Periodic-trajectory-controlled, coherent-state-phase-switched, and wavelength-tunable su(2) geometric modes in a frequency-degenerate resonator. Appl Opt (2018) 57(32):9543–9. doi:10.1364/AO.57.009543

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Stutzman WL, Thiele GA. Antenna theory and design. United States: Wiley (1981).

Google Scholar