- 1College of Advanced Interdisciplinary Studies, National University of Defense Technology, Changsha, China
- 2Nanhu Laser Laboratory, National University of Defense Technology, Changsha, China
In this manuscript, an automated optimization neural network is applied in Hadamard single-pixel imaging (H-SPI) and Fourier single-pixel imaging (F-SPI) to improve the imaging quality at low sampling ratios which is called AO-Net. By projecting Hadamard or Fourier basis illumination light fields onto the object, a single-pixel detector is used to collect the reflected light intensities from object. The one-dimensional detection values are fed into the designed AO-Net, and the network can automatically optimize. Finally, high-quality images are output through multiple iterations without pre-training and datasets. Numerical simulations and experiments demonstrate that AO-Net outperforms other existing widespread methods for both binary and grayscale images at low sampling ratios. Specially, the Structure Similarity Index Measure value of the binary reconstructed image can reach more than 0.95 when the sampling ratio is less than 3%. Therefore, AO-Net holds great potential for applications in the fields of complex environment imaging and moving object imaging.
1 Introduction
With the rapid development of computer hardware and optoelectronic devices, computational imaging (CI) has gained increasing attention. As a novel CI technique, single-pixel imaging (SPI) is characterized by using a single-pixel detector (SPD) without spatial resolution to reconstruct image. The SPD, such as avalanche photodiode or photon multiplier, can be made of germanium, silicon and other materials with board working waveband and low cost. Therefore, SPI can be widely applied in the non-visible waveband imaging, such as infrared imaging [1], X-ray [2] and terahertz light [3, 4]. Additionally, the SPD also has the advantages of high quantum efficiency and detection sensitivity, making SPI widely used in remote sensing [5], 3D imaging [6], weak light detection [7] and other areas.
In SPI, the object is illuminated by the modulated light fields generated from a variety of devices, including rotating ground glass plate [8, 9], Digital Micromirror Devices (DMD) [6, 10, 11], liquid crystal spatial light modulator (LC-SLM) [12–14], LED-based array [15–17], multimode fiber (MMF) [18], Silicon-based optical phased array (OPA) [19], fiber laser array [20] and so on. And the transmitted or reflected light intensities from the object are measured by the SPD. Combining the illumination light fields and light intensities, the images can be reconstructed by a variety of algorithms [21–24]. Therefore, researchers improve the imaging quality and efficiency of SPI by designing light fields with specific distributions and optimizing reconstruction algorithms.
The earliest light field used in SPI is random speckle [25]. It often requires a large number of samples to reconstruct an image, resulting in very low efficiency. Subsequently, orthogonal basis patterns are introduced into SPI as the illumination light field to improve the sampling efficiency, such as Hadamard basis patterns [10, 26], Fourier basis patterns [10, 11, 27], Discrete cosine basis patterns [28], Zernike basis patterns [29, 30]. Among of them, Hadamard single-pixel imaging (H-SPI) and Fourier single-pixel imaging (F-SPI) are two typical SPI techniques [10]. They obtain spectral information of the object through corresponding orthogonal basis transformation and efficiently reconstruct the target image by inverse transformation [31]. It has been proven that both H-SPI and F-SPI can achieve theoretically perfect reconstruction in full sampling without the noise or other distractions. Besides, due to the sparse representation in Hadamard and Fourier domains of natural images, they can obtain a large amount of low-frequency information to achieve clear imaging in under-sampling conditions. However, it also has been shown that when the sampling ratio is too low, both H-SPI and F-SPI introduce observable noise and artifacts that damage image quality. Specifically, H-SPI introduces the mosaic artifacts, while F-SPI introduces the ringing artifacts [10]. These artifacts need to be eliminated in the practical application of H-SPI and F-SPI. Additionally, there are also some theoretical differences between them. For example, H-SPI obtains the spatial information of objects in Hadamard domain by Hadamard transform and reconstructs the image by inverse Hadamard transform, while F-SPI extracts the image information in the Fourier domain. Reference [10] gives a detailed description. Moreover, it analyzed and compared the performance of H-SPI and F-SPI, indicating that F-SPI is more efficient than H-SPI and H-SPI is more noise-robust than F-SPI. In practice, the difference between the binary Hadamard and the grayscale Fourier basis will also affect the sampling efficiency.
With the advancement of deep learning (DL), numerous studies have demonstrated its effectiveness in enhancing the image quality of SPI [9, 32–36]. In 2017, the deep learning ghost imaging (GIDL) was first proposed by Lyu et al. [33]. They trained a deep neural network (DNN) using reconstructed images from traditional computational ghost imaging algorithm and ground truths which cost lots of time. Another approach is an end-to-end deep-learning method based on convolutional neural network (CNN) presented by Wang et al. [34]. This method takes the single-pixel detection signal sequence as the input and directly outputs the reconstructed image, significantly improving imaging efficiency. Recently, Ulyanov et al. introduced the concept of deep image prior (DIP) for image processing, which has the advantages of not requiring advance training and large data sets [35]. They demonstrated that a randomly-initialized neural network has a subtle focus on natural images and can be used to solve the image inverse problem. Inspired by DIP, Liu et al. proposed a computational ghost imaging method based on an untrained neural network [36]. They combined DGI and DNN to obtain high-quality image without requiring data sets. In 2022, Wang et al. improved upon this algorithm with a method called Deep neural network Constraint (GIDC) which achieved far-field super-resolution ghost imaging [9]. This advancement presents a new perspective for applying deep learning in the SPI system.
Inspired by the development of DL, we introduce an automated optimization neural network (AO-Net) into H-SPI and F-SPI to achieve high imaging quality at low sampling ratios. Firstly, we employ Hadamard or Fourier inverse transformation to obtain rough images that suffer from significant artifacts and noise due to the low sampling ratios. Subsequently, they are fed into the AO-Net for automated iterative optimization and obtaining high-quality images. Through numerical simulations and experimental demonstrations, AO-Net can effectively eliminate the introduced artifacts and noise with better image details, outperforms other existing widespread methods. It holds great potential for applications in fields of complex environment imaging and moving object imaging.
2 Model and theory
Initially, a mathematical model is developed based on the principle of SPI. The object
where
2.1 Basic model of H-SPI and F-SPI
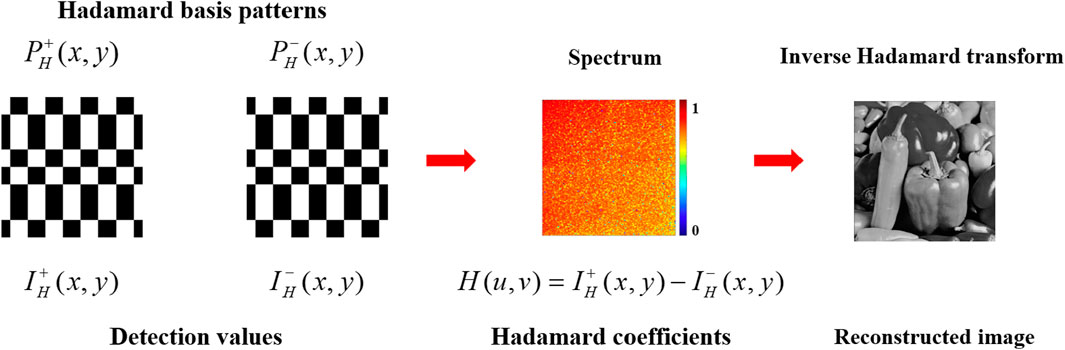
H-SPI is an efficient single-pixel imaging technique utilizes Hadamard transform [10]. In this approach, as mentioned in Eq. 1, the Hadamard basis patterns
where
Eq. 2 reveals that the presence of −1 elements in the Hadamard matrix prevents its direct loading onto SLM in the SPI system. To maintain the orthogonality of the Hadamard matrix, a differential H-SPI approach is employed to obtain the Hadamard coefficients. As depicted in Figure 1, the pattern
The corresponding detection values are
Therefore, to reconstruct an image with N pixels, it is necessary to acquire 2N measurements. Besides, H-SPI can employ a specific sampling sequence to enhance the sampling efficiency and prioritize important coefficients. This method makes the more important coefficients are ranked in front to obtain most of the information of target image in real time, such as zigzag [10], Russian Doll [26], Cake Cutting [37] and so on.
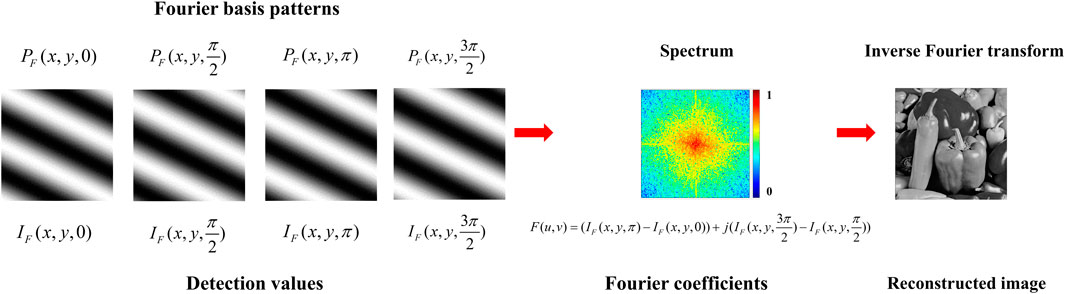
F-SPI is another efficient method based on Fourier transform [10]. Similarly, this method obtains the Fourier spectrum of object and reconstruct the image using inverse Fourier transform [11]. The method generates Fourier basis patterns
where
Due to the conjugate symmetry of the Fourier spectrum of real-valued images,
2.2 The process of AO-Net
Based on the above model, we introduce an automated optimization neural network into H-SPI and F-SPI which is called AO-Net. It combines the powerful feature extraction capabilities of DNN and SPI physical model to obtain high-quality images at low sampling ratios. The reconstruction process is illustrated in Figure 3 and the details are expressed as follows:
[1] Reconstructing the rough images R by using the inverse transformation in H-SPI (
[2] Loading the rough images R into the randomly initialized automated optimization neural network Uθ and obtaining the output image O (x,y), as shown in Eq. 10.
[3] Calculating the estimated values sequence Ii (as shown in Eq. 11, i is the iteration number) with the network output O (x,y) and the basis patterns Pn(x,y) according to Eq. 1.
[4] Evaluating the root-mean-square error (RMSE) between Ii and Ir as the loss function to automatically guide network parameter θ optimization, aiming to obtain the optimal AO-Net model
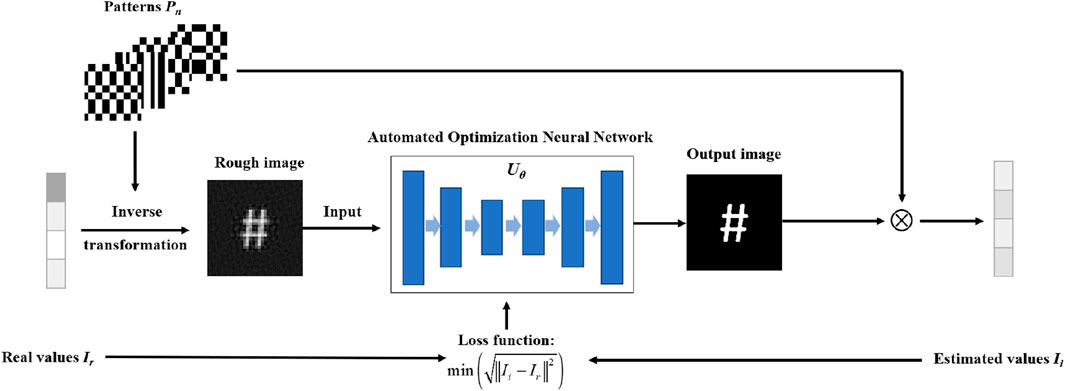
Figure 3. The basic process of AO-Net. Uθ is the network, θ is the parameter of the network and
Moreover, the network Uθ is based on the U-net deep neural network architecture, which consists of encoder, decoder and skip connection [38], as depicted in Figure 4. The input image has a resolution of 128 × 128 pixels. This structure includes four downsampling layers, one double convolutional layer and four upsampling layers. The downsampling layer involves two convolutional layers (Conv2D) to extract image features with a 3 × 3 kernel size of filters, one max-pooling layer to reduce dimensions and remove redundant information, batch normalization and the active function leaky_relu with the alpha = 0.2 to prevent the “vanishing gradient” problem. The upsampling layer contains one transposed convolutional layer to restore the image resolution, two convolutional layers, batch normalization and the active function leaky_relu. Additionally, the skip connection connects the downsampling path features with the corresponding upsampling layers to address the boundary pixel loss issue. Furthermore, the “Adam” optimizer [39] is used to better optimize the neural network parameters, which are initially set as follows: beta1 = 0.5, beta2 = 0.9 and epsilon = 1e-8. We also use the dynamic learning rate to make the algorithm can converge quickly, the initial learning rate is set to 0.01. Ultimately, the output is a high-quality image with a resolution of 128 × 128 pixels. The processes are run in Python environment and accelerated by NVIDIA GeForce GTX4060 GPU.
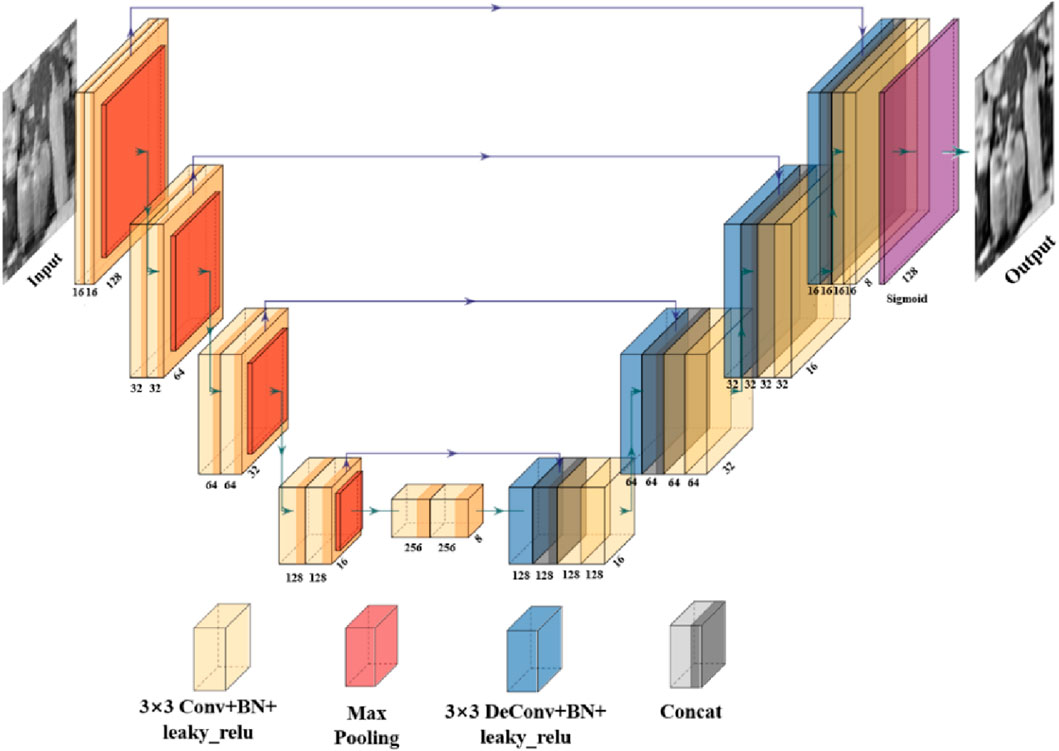
Figure 4. The architecture of the U-net. It contains encoder, decoder and skip connection. The input is a rough image and a high-quality image is used as the output.
3 Numerical simulation
In this section, without loss of generality, we consider two binary images (a number symbol and a Chinese character) and a typical grayscale image called ‘Peppers’ (128 × 128 pixels) as objects for analysis. Normally, if an N-pixel image is reconstructed with M measurements, then β = M/N is defined as the sampling ratio. Firstly, the rough images of objects are reconstructed by using H-SPI and F-SPI at various sampling ratios (specifically, 1%, 3%, 5%, 8%, and 10%). Besides, in the process, we adopt “zigzag” sampling strategy in H-SPI and “circular” sampling path in F-SPI to improve sampling efficiency [10]. The rough images and corresponding basis patterns serve as the prior information for AO-Net. And the one-dimensional detection values obtained from the inner product of the basis patterns with the object are used as data-driven model. AO-Net outputs high-quality images through iterative optimization. Figure 5 shows the reconstructed images of H-SPI and AO-Net (H-SPI). Figure 6 depicts the F-SPI images and corresponding AO-Net (F-SPI) images. As the sampling ratio increases from 1% to 10%, a common feature observed is that the reconstructed images exhibit clearer details and improved image quality. However, the H-SPI introduces numerous mosaic artifacts and the F-SPI introduces obvious ringing artifacts and noise, which compromise image quality and reduce resolution. In contrast, AO-Net can effectively eliminate the introduced artifacts and noise. The reconstructed images of AO-Net with enhanced resolution approximate the original image. When the sampling ratio is about 10%, the image quality obtained by the two methods is similar, and the advantage of AO-Net is not obvious. However, when the sampling ratio is less than 3%, the image obtained by AO-Net has more clearer details, higher resolution and better quality than the traditional method, showing obvious advantages. Therefore, AO-Net demonstrates significant improvement in the quality of H-SPI and F-SPI images at extremely low sampling ratios.

Figure 5. Simulation results with Hadamard patterns for binary and grayscale objects with different SPI reconstruction methods at low sampling ratios. The resolution of images is 128 × 128 pixels and the iterations of AO-Net are 100.

Figure 6. Simulation results with Fourier patterns for binary and grayscale objects with different SPI reconstruction methods at low sampling ratios. The resolution of images is 128 × 128 pixels and the iterations of AO-Net are 100.
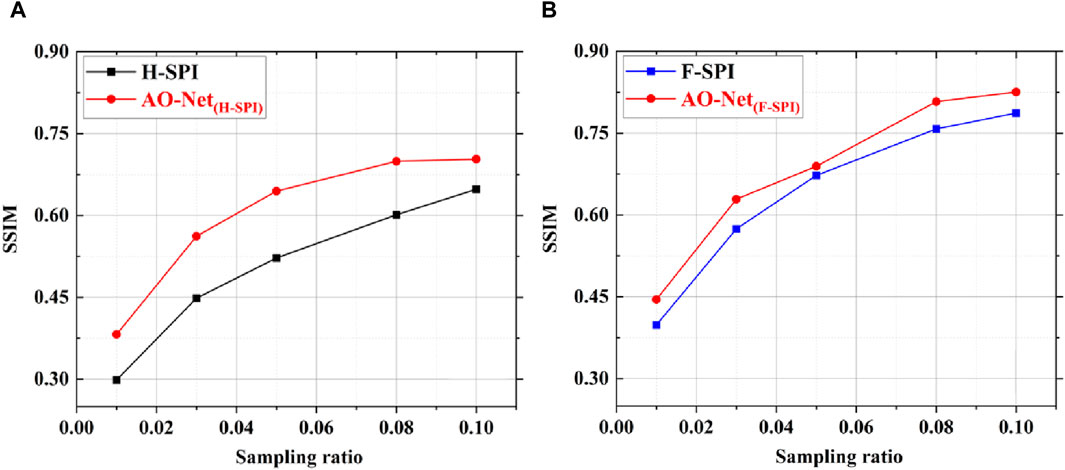
To further quantitatively analyze the advantages of the AO-Net over the traditional H-SPI and F-SPI, we employ the Structure Similarity Index Measure (SSIM) as an evaluation parameter. A larger SSIM value indicating that the reconstructed image is closer to the original image and has better image quality. Typically, the SSIM values of grayscale image “Peppers” are analyzed and compared. Figures 7A,B respectively show the change trend of SSIM values of H-SPI, F-SPI and AO-Net reconstructed images with the increasing of sampling ratios. The black and blue lines represent H-SPI and F-SPI respectively, and the red lines represent AO-Net. Generally, as the sampling ratio increases, the SSIM values of the images also increase. Moreover, all AO-Net images exhibit higher SSIM values compared to the corresponding H-SPI and F-SPI images at the same sampling ratio, indicating better image quality. This demonstrates the effectiveness of AO-Net and the significant improvement in reconstruction efficiency. The above results illustrate that AO-Net can obtain high-quality clear images at low sampling ratios, outperforms the existing traditional methods. Besides, F-SPI has better image quality than H-SPI. And AO-Net results based on Fourier patterns have highest SSIM values and best image quality at each sampling ratio.
On the other hand, we make a simple comparison with other deep learning algorithms. Firstly, compared with the traditional training-based deep learning methods, in theory, this algorithm has stronger generalization and adaptability without large data sets and pre-training, which has been expressed in part of introduction. It has unique advantages in terms of applicability. Additionally, we also add a comparison to the simulation results based on Hadamard patterns of a typical untrained reconstruction algorithm (GIDC) proposed by Wang et al [9]. Figure 8 shows the comparison results. The number of iterations of both algorithms is 100. The object is grayscale image “peppers” and the reconstruction algorithm are GIDC and AO-Net, respectively. We also calculate the SSIM value of each image. The part marked in red shows that the image has a larger SSIM value at the same conditions, indicating the better image quality. Visually, the AO-Net images have clearer details, less noise and artifacts. The results show that the proposed AO-Net has greater potential to solve the above problems than GIDC. Therefore, we only verify the performance of AO-Net in the follow-up experiment comparison. And in the future, we will carry out more in-depth research and comparison.
4 Experimental results
In order to further validate the feasibility of the aforementioned method, a SPI system was assembled as depicted in Figure 9. The setup involved the emission of laser light from a solid-state laser with a wavelength of 532 nm (LSR-532NL). Subsequently, the laser was collimated and expanded by using a beam expander (BE), resulting in a spot size ten times larger than the original. The expanded laser was directed onto the DMD 1 screen, and its reflected light was then projected onto DMD 2 through a projection lens (PL) with a focal length of 200 mm. Both DMDs (Texas Instruments DLP V-650L) featured a 1280 × 800 micro-mirror array for loading modulation patterns. DMD 1 was utilized to load the generated basis pattern sequence (Hadamard basis patterns and Fourier basis patterns), while DMD 2 was employed to load the object (binary and grayscale images). Furthermore, DMD 1 and DMD 2 needed to be positioned at conjugate positions of PL to obtain a clear image. Therefore, based on the focal length of PL and the Gaussian imaging formula, the distance from DMD 1 to PL and the distance from PL to DMD 2 were both set to 400 mm. Subsequently, the reflected light from DMD 2 was collected by the single-pixel detector (SPD, Thorlabs PDA-10A2) after passing through the collecting lens (CL). The light intensities were recorded by a data acquisition card (DAC, ART USB-2872D) connected to a computer. This entire process was facilitated by self-developed data synchronization acquisition software (LABVIEW).
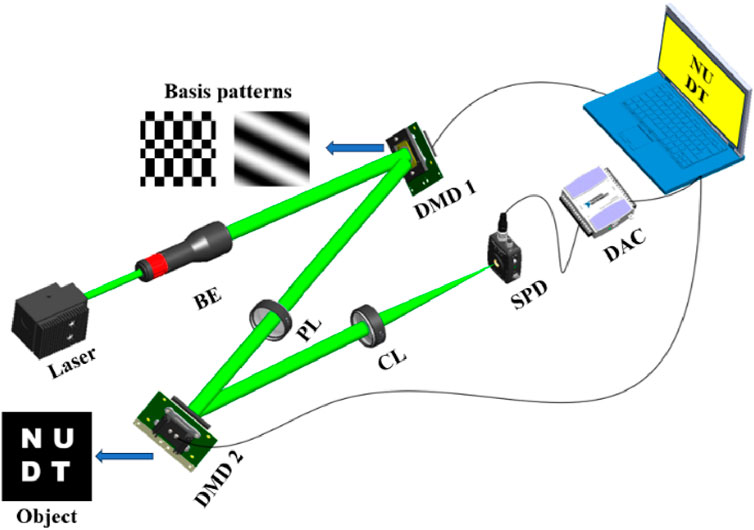
Figure 9. The diagram of experimental setup. BE (beam expander), PL (projection lens), CL (collecting lens), SPD (single-pixel detector), DAC (data acquisition card).
In this experiment, the resolution of 128 × 128 pixels basis patterns were sequentially loaded into DMD 1 to implement SPI. When loading the binary Hadamard basis patterns, the refresh rate of DMD could reach up to 22.4 kHz. Therefore, the projection interval was set to 2 ms, with each frame being projected for 1 ms to accommodate the response rate of the detector and acquisition card. When the grayscale Fourier basis patterns were loaded, the DMD refresh rate was only 258 Hz, so the projection internal was set to 20 ms and the projection duration of each frame was 10 ms. Additionally, DMD 2 loaded binary images representing a simple “drone”, the letter combination “NUDT”, and the grayscale image “Peppers” as imaging objects. All of them were also 128 × 128 pixels. Moreover, in order to achieve optimal modulation, the 128 × 128 pixels images were enlarged to 512 × 512 pixels, occupying the central portion of the DMD by combining each set of 4 × 4 pixels into a single resolution cell. The images were reconstructed by H-SPI, F-SPI and AO-Net. And the SSIM was employed for quantitative and comparative analysis. The sampling ratios were also set to 1%, 3%, 5%, 8% and 10% to align with the simulations.
Figure 10 and Figure 11 show the experimental results of H-SPI, F-SPI and AO-Net at different sampling ratios, respectively. As the sampling ratio increased, the details of the reconstructed images became more discernible. However, a notable difference was observed in the images generated by H-SPI, which exhibited numerous noise points and mosaic artifacts. And there were also obvious ringing artifacts and noise in F-SPI reconstructed images. On the contrary, the AO-Net results could eliminate these interferences, resulting in higher-quality images that were closer to the original more than traditional methods. For binary images, it could be intuitively seen that the advantage of AO-Net was particularly pronounced, enabling clear imaging at a low sampling ratio less than 3%. And the AO-Net results based on Fourier patterns were best among these images.

Figure 10. Experimental results with Hadamard patterns for binary and grayscale objects with different SPI reconstruction methods at low sampling ratios. The iterations of AO-Net are 300.

Figure 11. Experimental results with Fourier patterns for binary and grayscale objects with different SPI reconstruction methods at low sampling ratios. The iterations of AO-Net are 300.
In order to further illustrate the advantages of AO-Net, we analyzed the SSIM value of the grayscale reconstructed images. Figures 12A,B respectively depict the SSIM values of H-SPI, F-SPI and AO-Net reconstructed images. Similarly, the black and blue lines represented H-SPI and F-SPI results respectively, and the red lines represented AO-Net. Intuitively, the SSIM values increased with the increase of sampling ratio for every method, indicating better image quality. It was apparent that the SSIM values of the AO-Net images were noticeably higher than those of the H-SPI and F-SPI images, suggesting a closer resemblance to the original image. The above results showed that AO-Net can achieve higher-quality imaging at low sampling ratios. Therefore, combined with simulation results, we could choose the appropriate basis patterns according to different application scenes to ensure maximum efficiency.
5 Discussion and conclusion
In conclusion, we introduce an automated optimization neural network into H-SPI and F-SPI called AO-Net to obtain high-quality reconstructed images at low sampling ratios. One-dimensional detection values are obtained by SPI process and fed into the designed AO-Net. The network parameters are automatically optimized and outputs high-quality images without pre-training and datasets. Through the numerical simulations and experimental demonstrations, we validate that H-SPI and F-SPI introduce unavoidable artifacts and noise in the reconstructed images at low sampling ratios. On the contrary, AO-Net can effectively eliminate these disturbances for both binary and grayscale objects. Consequently, the reconstructed images of AO-Net have better image quality, enhanced contrast and clearer details. Furthermore, the advantages for binary reconstructed images are particularly evident. It is obvious that the reconstructed images have clearer details and higher image quality which are close to the original image at a sampling ratio less than 3%. For grayscale images, the ability of the algorithm to extract image information needs to be improved. Meanwhile, the process of synchronous data acquisition in the experiment needs to be further optimized. The above results indicate that the proposed AO-Net has the potential to solve the above problems. Therefore, by leveraging the high detection efficiency of SPD and the fast modulation speed of DMD, AO-Net can find applications in the fields of moving object imaging, recognition and tracking.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
GL: Formal Analysis, Investigation, Methodology, Validation, Writing–original draft. WL: Software, Validation, Writing–review and editing. QM: Investigation, Validation, Writing–review and editing. WC: Supervision, Writing–review and editing. HL: Supervision, Writing–review and editing. YW: Methodology, Supervision, Writing–review and editing. KH: Conceptualization, Methodology, Supervision, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Edgar MP, Gibson GM, Bowman RW, Sun B, Radwell N, Mitchell KJ, et al. Simultaneous real-time visible and infrared video with single-pixel detectors. Scientific Rep (2015) 5(1):10669. doi:10.1038/srep10669
2. Klein Y, Schori A, Dolbnya IP, Sawhney K, Shwartz S. X-ray computational ghost imaging with single-pixel detector. Opt Express (2019) 27(3):3284. doi:10.1364/oe.27.003284
3. Chan WL, Charan K, Takhar D, Kelly KF, Baraniuk RG, Mittleman DM. A single-pixel terahertz imaging system based on compressed sensing. Appl Phys Lett (2008) 93(12). doi:10.1063/1.2989126
4. Lu Y, Wang X-K, Sun W-F, Feng S-F, Ye J-S, Han P, et al. Reflective single-pixel terahertz imaging based on compressed sensing. IEEE Trans Terahertz Sci Technology (2020) 10(5):495–501. doi:10.1109/tthz.2020.2982350
5. Jianwei M. A single-pixel imaging system for remote sensing by two-step iterative Curvelet Thresholding. IEEE Geosci Remote Sensing Lett (2009) 6(4):676–80. doi:10.1109/lgrs.2009.2023249
6. Jiang W, Yin Y, Jiao J, Zhao X, Sun B. 2,000,000 fps 2D and 3D imaging of periodic or reproducible scenes with single-pixel detectors. Photon Res (2022) 10(9):2157. doi:10.1364/prj.461064
7. Morris PA, Aspden RS, Bell JEC, Boyd RW, Padgett MJ. Imaging with a small number of photons. Nat Commun (2015) 6(1):5913. doi:10.1038/ncomms6913
8. Gong W, Zhao C, Yu H, Chen M, Xu W, Han S. Three-dimensional ghost imaging lidar via sparsity constraint. Scientific Rep (2016) 6(1):26133. doi:10.1038/srep26133
9. Wang F, Wang C, Chen M, Gong W, Zhang Y, Han S, et al. Far-field super-resolution ghost imaging with a deep neural network constraint. Light: Sci Appl (2022) 11(1):1. doi:10.1038/s41377-021-00680-w
10. Zhang Z, Wang X, Zheng G, Zhong J. Hadamard single-pixel imaging versus Fourier single-pixel imaging. Opt Express (2017) 25(16):19619. doi:10.1364/oe.25.019619
11. Zhang Z, Ma X, Zhong J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat Commun (2015) 6(1):6225. doi:10.1038/ncomms7225
12. Bromberg Y, Katz O, Silberberg Y. Ghost imaging with a single detector. Phys Rev A (2009) 79(5):053840. doi:10.1103/PhysRevA.79.053840
13. Huang J, Shi D. Multispectral computational ghost imaging with multiplexed illumination. J Opt (2017) 19(7):075701. doi:10.1088/2040-8986/aa72ff
14. Sun S, Liu W-T, Lin H-Z, Zhang E-F, Liu J-Y, Li Q, et al. Multi-scale adaptive computational ghost imaging. Scientific Rep (2016) 6(1):37013. doi:10.1038/srep37013
15. Xu Z-H, Chen W, Penuelas J, Padgett M, Sun M-J. 1000 fps computational ghost imaging using LED-based structured illumination. Opt Express (2018) 26(3):2427. doi:10.1364/oe.26.002427
16. Salvador-Balaguer E, Latorre-Carmona P, Chabert C, Pla F, Lancis JS, Ejoe T. Low-cost single-pixel 3D imaging by using an LED array. Opt Express (2018) 26(12):15623–31. doi:10.1364/oe.26.015623
17. Zhao W, Chen H, Yuan Y, Zheng H, Liu J, Xu Z, et al. Ultrahigh-speed color imaging with single-pixel detectors at low light Level. Phys Rev Appl (2019) 12(3):034049. doi:10.1103/PhysRevApplied.12.034049
18. Fukui T, Kohno Y, Tang R, Nakano Y, Tanemura T. Single-pixel imaging using multimode fiber and silicon photonic phased array. J Lightwave Technology (2021) 39(3):839–44. doi:10.1109/JLT.2020.3008968
19. Kohno Y, Komatsu K, Tang R, Ozeki Y, Nakano Y, Tjoe T. Ghost imaging using a large-scale silicon photonic phased array chip. Opt Express (2019) 27(3):3817–23. doi:10.1364/oe.27.003817
20. Lai W, Lei G, Meng Q-S, Wang Y, Ma Y, Liu H, et al. Efficient single-pixel imaging based on a compact fiber laser array and untrained neural network. Front Optoelectron (2024) 17:9. doi:10.1007/s12200-024-00112-8
21. Bian L, Suo J, Dai Q, Chen F. Experimental comparison of single-pixel imaging algorithms. J Opt Soc America A (2017) 35(1):78. doi:10.1364/josaa.35.000078
22. Ferri F, Magatti D, Lugiato LA, Gatti A. Differential ghost imaging. Phys Rev Lett (2010) 104(25):253603. doi:10.1103/PhysRevLett.104.253603
23. Sun B, Welsh SS, Edgar MP, Shapiro JH, Padgett MJ. Normalized ghost imaging. Opt Express (2012) 20(15):16892. doi:10.1364/oe.20.016892
24. Duarte MF, Davenport MA, Takhar D, Laska JN, Sun T, Kelly KF, et al. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag (2008) 25(2):83–91. doi:10.1109/msp.2007.914730
26. Sun M-J, Meng L-T, Edgar MP, Padgett MJ, Radwell N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Scientific Rep (2017) 7(1):3464. doi:10.1038/s41598-017-03725-6
27. Zhang Z, Wang X, Zheng G, Zhong J. Fast Fourier single-pixel imaging via binary illumination. Scientific Rep (2017) 7(1):12029. doi:10.1038/s41598-017-12228-3
28. Liu B-L, Yang Z-H, Liu X, Wu L-A. Coloured computational imaging with single-pixel detectors based on a 2D discrete cosine transform. J Mod Opt (2016) 64(3):259–64. doi:10.1080/09500340.2016.1229507
29. Lei G, Lai W, Meng Q, Liu H, Shi D, Cui W, et al. Efficient and noise-resistant single-pixel imaging based on Pseudo-Zernike moments. Opt Express (2023) 31(24):39893. doi:10.1364/oe.506062
30. Lai W, Lei G, Meng Q, Shi D, Cui W, Ma P, et al. Single-pixel imaging using discrete Zernike moments. Opt Express (2022) 30(26):47761. doi:10.1364/oe.473912
31. Lu T, Qiu Z, Zhang Z, Zhong J. Comprehensive comparison of single-pixel imaging methods. Opt Lasers Eng (2020) 134:106301. doi:10.1016/j.optlaseng.2020.106301
32. Song K, Bian Y, Wu K, Liu H, Han S, Li J, et al. Single-pixel imaging based on deep learning. 2023.
33. Lyu M, Wang W, Wang H, Wang H, Li G, Chen N, et al. Deep-learning-based ghost imaging. Scientific Rep (2017) 7(1):17865. doi:10.1038/s41598-017-18171-7
34. Wang F, Wang H, Wang H, Li G, Situ G. Learning from simulation: an end-to-end deep-learning approach for computational ghost imaging. Opt Express (2019) 27(18):25560. doi:10.1364/oe.27.025560
35. Ulyanov D, Vedaldi A, Lempitsky V. Deep image prior. Int J Computer Vis (2020) 128(7):1867–88. doi:10.1007/s11263-020-01303-4
36. Liu S, Meng X, Yin Y, Wu H, Jiang W. Computational ghost imaging based on an untrained neural network. Opt Lasers Eng (2021) 147:106744. doi:10.1016/j.optlaseng.2021.106744
37. Yu W-K Super Sub-Nyquist single-pixel imaging by means of Cake-Cutting Hadamard basis Sort. Sensors (2019) 19(19):4122. doi:10.3390/s19194122
38. Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for Biomedical image Segmentation. Med Image Comput Computer-Assisted Intervention – MICCAI (2015) 2015:234–41. Chapter Chapter 28 (Lecture Notes in Computer Science). doi:10.1007/978-3-319-24574-4_28
Keywords: Hadamard single-pixel imaging, Fourier single-pixel imaging, low sampling, high imaging quality, deep neural network, automated optimization
Citation: Lei G, Lai W, Meng Q, Cui W, Liu H, Wang Y and Han K (2024) Low-sampling high-quality Hadamard and Fourier single-pixel imaging through automated optimization neural network. Front. Phys. 12:1391608. doi: 10.3389/fphy.2024.1391608
Received: 26 February 2024; Accepted: 29 April 2024;
Published: 15 May 2024.
Edited by:
Mario Alan Quiroz-Juarez, National Autonomous University of Mexico, MexicoReviewed by:
Lu Rong, Beijing University of Technology, ChinaArmando Perez.Leija, University of Central Florida, United States
Alfred U’Ren, National Autonomous University of Mexico, Mexico
Copyright © 2024 Lei, Lai, Meng, Cui, Liu, Wang and Han. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan Wang, d2FuZ3lhbjEwMTcxMkAxNjMuY29t; Kai Han, aGFua2FpMDA3MUBudWR0LmVkdS5jbg==
 Guozhong Lei
Guozhong Lei Wenchang Lai
Wenchang Lai Qi Meng1
Qi Meng1 Wenda Cui
Wenda Cui Hao Liu
Hao Liu Kai Han
Kai Han