
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 26 April 2024
Sec. Medical Physics and Imaging
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1390439
This article is part of the Research TopicPhysical, Biological, Clinical, and Methodological Advances in Particle TherapyView all 7 articles
Radiation therapy, one of the most effective methods for cancer treatment, is still limited by the tolerances of normal tissues surrounding the tumor. Innovative techniques like spatially fractionated radiation therapy (SFRT) have been shown to increase normal tissue dose resistance. Heavy ions also offer high-dose conformity and increased relative biological effectiveness (RBE) when compared to protons and X-rays. The alliance of heavy ions and spatial fractionation of the dose has the potential to further increase the therapeutic index for difficult-to-treat cases today. In particular, the use of β-delayed multiple-particle emitters might further improve treatment response, as it holds the potential to increase high linear energy transfer (LET) decay products in the valleys of SFRT (low-dose regions) at the end of the range. To verify this hypothesis, this study compares β-delayed multiple-particle emitters (8Li, 9C, 31Ar) with their respective stable isotopes (7Li, 12C, 40Ar) to determine possible benefits of β-delayed multiple-particle emitters minibeam radiation therapy (β-MBRT). Monte Carlo simulations were performed using the GATE toolkit to assess the dose distributions of each ion. RBE-weighted dose distributions were calculated and used for the aforementioned comparison. No significant differences were found among carbon isotopes. In contrast, 8Li and 31Ar exhibited improved RBE-weighted dose distributions with an approximately 12–20% increase in the Bragg-peak-to-entrance dose ratio (BEDR) for both peaks and valleys, which favors tissue sparing. Additionally, 8Li and 31Ar exhibited a lower peak-to-valley dose ratio (PVDR) in normal tissues and higher PVDR in the tumor than 7Li and 40Ar. Biological experiments are needed to conclude whether the differences observed make β-delayed multiple-particle emitters advantageous for MBRT.
The last decades have witnessed significant advances in tumor dose conformation in radiation therapy (RT) [1]. However, normal tissue tolerances continue to represent an important challenge, especially for the treatment of radioresistant tumors or pediatric cancer. New RT approaches, therefore, need to overcome the barrier of normal tissue tolerances. To this end, one possible strategy involves employing distinct dose delivery methods, such as spatially fractionated radiation therapy (SFRT). SFRT strategically delivers high radiation doses exclusively to specific tissue volumes by employing multiple narrow beamlets. The resulting dose distribution showcases a succession of areas of high dose (peaks) and areas of low dose (valleys) [2]. The scale and geometry of the irradiation patterns are a key distinction among the four main SFRT techniques. GRID therapy [3] utilizes pencil-shaped beamlets ranging from 1 to 2 cm2, LATTICE therapy (LRT) [4] focuses small beams to create hot spots (of 1–2 cm2) in the target, minibeam radiation therapy (MBRT) [5] uses planar beamlets with widths of 0.5–1 mm, and microbeam radiation therapy (MRT) [6] employs beamlets ranging from 50 to 100 µm. GRID and LRT impose restrictions on normal tissue dose tolerances and offer modest potential for safe dose escalation in very radioresistant tumors. MRT is confined to low energy X-rays [2]. MBRT represents the ideal compromise between the thick beams employed in GRID and LRT and the extreme conditions associated with MRT. MBRT can be implemented in small animal irradiators [7] and permits the use of higher beam energies compared to MRT while employing a beam sufficiently narrow to achieve a significant increase in normal tissue tolerances [5, 8–10]. A significant tumor control effectiveness has also been observed in glioma-bearing rats treated with MBRT [8, 11, 12]. Additionally, the immune system has recently been shown to play a crucial role in the anti-tumor response of MBRT [13].
Recent studies offer evidence that the high therapeutic index of MBRT could be further increased by combining MBRT with (heavy) charged particles [14–20]. Charged particles are characterized by superior relative biological effectiveness (RBE) and more targeted dose deposition in depth as compared with photons. Research into combining MBRT with charged particles started with proton minibeams [21, 22]. The biological experiments conducted with proton minibeams have shown remarkable normal tissue sparing, both for the skin [23, 24] and brain [24, 25], along with an even higher tumor control effectiveness than standard therapy [14, 26]. Previous studies have also explored the combination of helium [15] and heavy ions [16–20] with MBRT. Notably, there are indications that heavy ions, such as carbon, could enhance the immune response more effectively than photons or proton beams [27]. This finding suggests the possibility of synergistic effects between the immune response enhancement associated with heavy ions and the observed effective immune priming in MBRT [13].
A useful step in researching the combination of MBRT with heavy ions involves exploring possible advantages of radioactive ion beams (RIB), in particular β-delayed multiple-particle emitters in radiotherapy. The use of RIB for therapeutical application was proposed at the heavy ion medical accelerator in Chiba (HIMAC) [28]. Studies conducted at HIMAC with 9C showed advantages in terms of the distributions of biologically effective dose and cell survival along the beam penetration as compared with stable 12C [29–31]. In the case of MBRT, the nuclear fragments resulting from the β-delayed multiple-particle breakup reaching the valleys regions might be biologically very relevant [17, 18, 20], particularly for tumor control [32].
β-delayed multiple-particle emission has been studied for a long time and more than 400 β-delayed particle precursors have been identified [33]. The parent nucleus (precursor) decays via β emission to excited levels of the emitter nucleus. The emitter will, almost immediately, emit particles (protons, alpha particles, etc.) to reach a stable state. The half-life of the β decay is much longer than that of the nuclear excitation, so the half-life of the process is given by the β decay. The energy and intensity of the emitted particle are directly related to the position of the nuclear state in the daughter nucleus and to the intensity of the feeding of the β decay. However, energy and momentum conservation do not entirely determine the emission mechanism of three or more particles, such as in 9C. The emission can proceed sequentially (via resonances in the binary subsystems), directly to the continuum (democratic decay), or via both mechanisms. The resulting particles, mostly protons and alpha particles, are emitted with energies ranging from hundreds of keV to tens of MeV. For example, the protons emitted after the β decay of 9C have energies ranging from 0.17 MeV up to 12 MeV which correspond to a range in water of 0.002–2 mm. Assuming that every primary ion will decay only at the end of the range, the resulting lighter nuclear products will be produced at the target region.
The products of the β-delayed multiple-particle emission may significantly affect the dose distribution in MBRT and selectively increase the valley doses. In heavy ion therapy with stable beams, primary ion fragmentation typically results in one heavy and one lighter fragment, predominantly forward-directed. On the contrary, in the case of multiple-particle breakup at the end of the range, the resulting fragments are (much) lighter than the primary ion and will be scattered in a more isotropic way. Hence, high-linear energy transfer (LET) particles may reach the valley regions while remaining mostly confined to the target volume due to their short ranges (∼mm). This could boost the local biological effect and might further improve treatment outcomes.
In this work, we therefore perform a preliminary dosimetric exploration of β-delayed multiple-particle emitters minibeam radiation therapy (β-MBRT). Considering the strong correlation between valley dose, normal tissue sparing, and life span in MBRT [32], our investigation focuses on understanding how β-MBRT influences the composition of the valley dose in terms of secondary particles. The primary goal is to conduct a comparative analysis between radioactive ions and their stable isotopes to determine whether a potential advantage of β-MBRT might be expected.
To the best of our knowledge, this is the first in-depth dosimetric evaluation of the combination of β-delayed multiple-particle emitters and MBRT.
Monte Carlo simulations were performed to assess dose and LET distributions for three different ion types: lithium, carbon, and argon.
The studied ion species have been chosen based on two criteria. Firstly, production feasibility was considered. As discussed in previous studies [34–36], RIB used for therapy are produced through fragmentation of the stable primary beam in thin targets and subsequent magnetic separation of the produced fragments. The secondary particles are immediately directed with relativistic energies to the target, where they subsequently undergo decay. Secondly, favorable dosimetric and decay characteristics for treating deep-seated tumors were sought. A key requirement was that the heavy ion had a radioactive isotope whose decay leads to β-delayed multiple-particle emission with a half-life sufficiently long to prevent in-flight decay (>ms).
Lithium MBRT was initially proposed by Dilmanian et al. [37] who suggested that its ability to spare normal tissue at shallow depths, coupled with the potential for dose homogenization in the target, could enhance the treatment of deep-seated tumors and facilitate hypofractionated radiation therapy. 7Li and its radioactive isotope 8Li were chosen for our investigation. The β− decay of 8Li generates high-energy electrons and 8Be, which immediately (t1/2 = 8.19 × 10−17s) breaks up into two alpha particles.
12C stands as the most widely employed and extensively studied heavy ion for radiotherapy [38]. Carbon MBRT was explored in a first biological experiment [16] where a rabbit brain was irradiated with several arrays of 300-µm-wide carbon beams interlacing at the target, showing a reduced impact on the non-targeted tissues. Theoretical and experimental dosimetric evaluations of carbon MBRT have been conducted by Gonzalez et al. [20] and Martinez-Rovira et al. [19], respectively, showing favorable dose distributions. The chosen radioactive ion for our evaluation was 9C, a drip-line nucleus. 9C was extensively used in the biological studies conducted at HIMAC to assess possible advantages of radioactive heavy-ion therapy [29, 30]. 9C decays via three different branches: via β+ in 9B (branching ratio = 0.6), via β+, p in 8Be (branching ratio = 0.23) and via β+, α in 5Li (branching ratio = 0.17). The produced ions are not stable: 9B breaks up into one proton and two alpha particles, 8Be breaks up into two alpha particles and 5Li breaks up into one proton and one alpha particle. The emitted alpha particles, having a range in water r ∈ [0.01–0.08] mm, are confined to the peak regions. The emitted protons, having a mm range in water, might contribute to a higher RBE in the valley regions.
Argon was used in pioneering radiobiological evaluations in the late 70 s [39] which indicated that resistant cells of hypoxic tumors could be effectively destroyed with very heavy ion beams (neon, silicon, argon, etc.). However, clinical results with a few patients performed with argon in 1979 and with silicon in 1982 led to adverse late tissue results, causing treatments with these beams to be discontinued [39]. Argon MBRT, relying on the normal tissue-sparing effect of the spatial fraction of the dose, could lead to a renewed use of argon in radiotherapy [40]. Characterized by a high LET and an oxygen enhancement ratio of ∼ 1, argon could provide new hope for aggressive hypoxic tumors, which currently have very few treatment options. Theoretical dosimetric characterizations of argon MBRT were performed by Peucelle et al. [17] and by Gonzalez et al. [20] showing advantageous dose distributions favoring normal tissue preservation. The radioactive ion chosen for our evaluation was 31Ar, a drip-line nucleus. 31Ar decays via four different branches: via β+ in 31Cl (branching ratio = 0.22), via β+, p in 30S (branching ratio = 0.68), via β+, 2p in 29P (branching ratio = 0.09) and via β+, 3p in 28Si (branching ratio = 0.0007). For the first three mentioned decay branches, the produced heavy ions are not stable and will continue to emit positrons (isobaric chain) until they reach a stable state. The final products of the isobaric chain, stable isotopes of silicon and phosphorus, will mainly be confined to the peak regions due to their short ranges (<µm). However, the β-delayed emitted protons, having a mm range in water, might contribute to a higher RBE in the valley regions.
The decay modes, products, and emission energies of the described isotopes are summarised in Table 1. The decay schemes are shown in Supplementary Table S1.
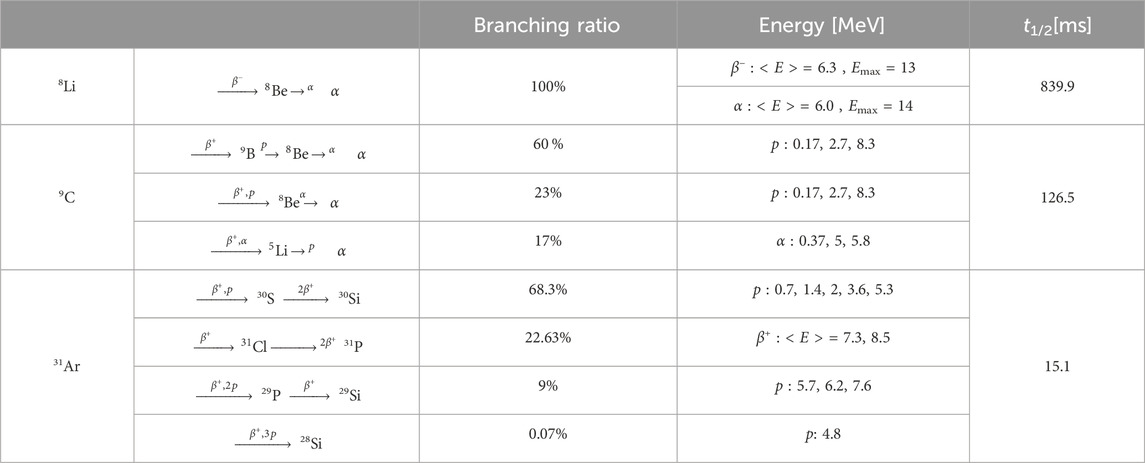
Table 1. Decay table, energy of the emitted fragments and half-lives for 8Li,9C and 31Ar. When in a discrete form, the reported proton/alpha energies are relative to the highest peaks populating the emission spectra. From IAEA-Nuclides Chart [41,42].
The simulations presented in this work were performed with version 9.0 of the GATE toolkit. GATE is an open-source Monte Carlo (MC) simulation platform based on GEANT4 enabling the modeling of emission and transmission tomography, and radiotherapy [43]. The physics lists recommended for hadrontherapy were used [44], specifically the QGSP_BERT_HP_EMY list for hadronic processes and standard option 3 for electromagnetic processes. GATE provides a TPS Pencil Beam source designed to simulate treatment plans for active beam scanning delivery techniques. The TPS source was used specifying one field. The field, defined by a gantry angle, consisted of a collection of magnetically collimated pencil minibeams having the same energies, directions, and weights. The total number of primary particles simulated was 108, leading to a global uncertainty of less than 1%. The mono-energetic beams impinged on a cylindrical water phantom whose size (height and diameter of 16 cm) mimics the human head. Similar phantom dimensions have been used in previous dosimetric studies [17, 18, 20]. A virtual tumor (2 cm × 2 cm × 2 cm) placed at 7 cm depth constituted the target region. A range cut value of 50 µm was used for all particles in the water phantom.
Six different ions were simulated: 7Li, 8Li, 9C, 12C, 31Ar, 40Ar. The energies of the primary beams, summarized in Table 2, were chosen to have a range in water of ∼ 7 cm. Energy spreads of 0.1% MeV of the total energy were simulated in all cases. Two different irradiation geometries were considered: a one-dimensional array of elongated, rectangular minibeams (referred to as MBRT hereafter) and a two-dimensional grid arrangement of square minibeams (hereafter GRT). The two geometries are illustrated in Figure 1. The sources were located at the water phantom entrance. A Gaussian angular distribution with a realistic standard deviation of 3 mrad was considered for the divergence of the minibeams. The lateral beam dimensions were 1 mm × 1 cm for MBRT and 1 mm × 1 mm for GRT.
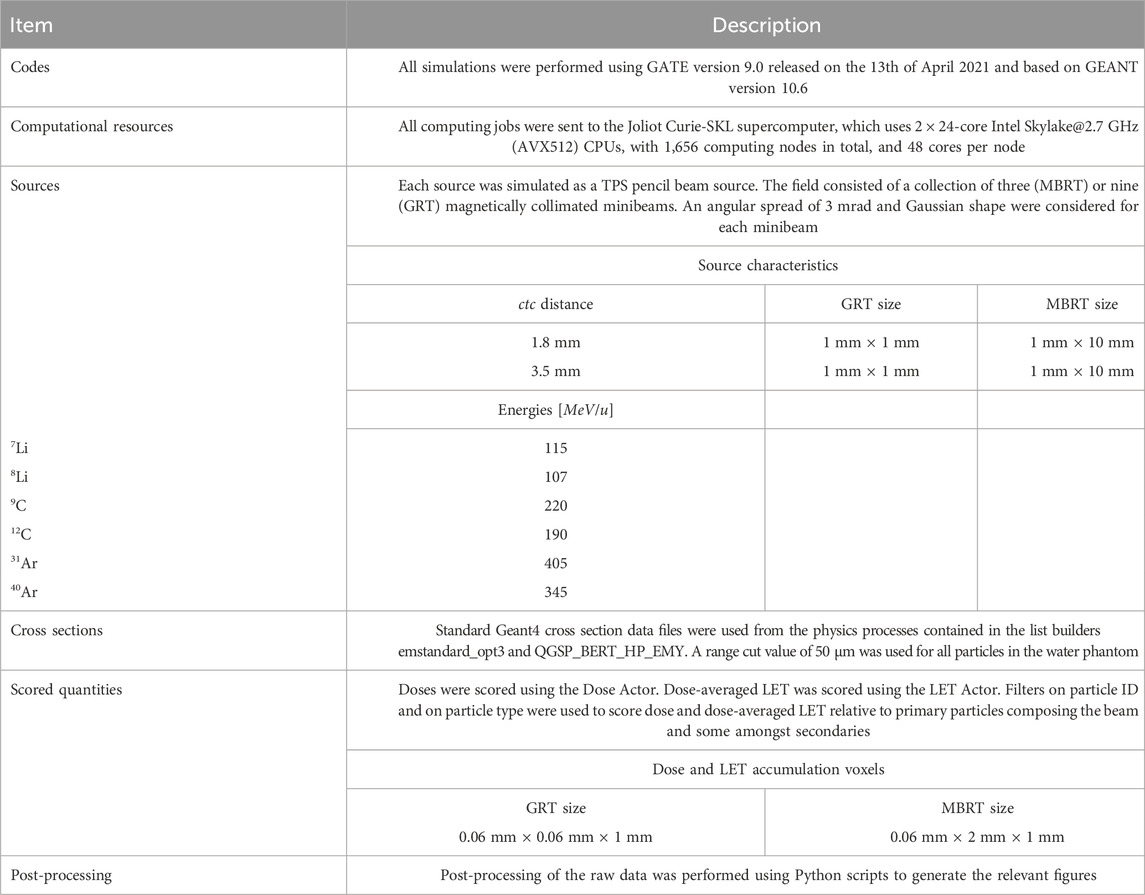
Table 2. Summary of the main details of the MC simulations, in accordance with the recommendation of AAPM TG-268 [45].
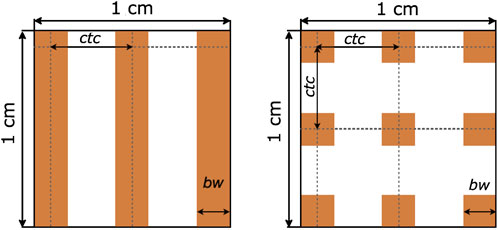
Figure 1. Schematic illustration representing the geometrical parameters in MBRT (left) and in GRT (right). Abbreviations correspond to center-to-center distance (ctc) and beam width (bw). Adapted from Gonzalez et al. [18].
Two different values were evaluated for the center-to-center (ctc) distance between adjacent minibeams (see Figure 1), based on the following rationale. A ctc of 3.5 mm was used in previous experimental studies of charged particle MBRT [17, 21, 46] and has been shown to minimize the contribution of heavy nuclear fragments to the valleys in the first centimeters [17, 18, 20], favoring normal tissue sparing. Additionally, a significant gain in brain sparing has been observed in proton MBRT with a ctc of 3.5 mm [46]. A second ctc value of 1.8 mm was simulated to investigate LET homogeneity in the target, primarily influenced by the presence of high LET secondaries in the valley region. Homogeneous LET distribution implies that radiobiological LET-dependent effects are comparable in both peak and valley regions.
Dose and dose-averaged LET were scored in the water phantom. While the LET of a pure beam of ions with a fixed energy is well-defined, the LET of a mixed radiation field has to be averaged over the different ions contributing. This is often done using the so-called dose-averaged LET, where the LET of each particle is weighted according to its dose contribution [47, 48]. Additionally, to evaluate the number, type and energy of secondary particles in the peaks and valleys, three phase space files were recorded at 30 mm (normal tissue position), 70 mm (pristine Bragg peak), and 90 mm (fragmentation tail) depth in the water phantom. LET profiles and recorded phase space files are presented in Supplementary Material. Further details concerning the characteristics of the MC simulations are provided in Table 2 in accordance with the recommendation from AAPM TG268 [45] which attempts to standardize the reporting of MC simulations.
The simulated 3D dose distribution was integrated over a rectangular region of interest (ROI) corresponding to the peak and valley regions, resulting in the peak and valley depth dose profiles. The peak-to-valley dose ratio (PVDR) was assessed as a function of depth for each ion and irradiation configuration. Dose-averaged LET was evaluated in both the peak and valley regions as a function of depth and used to determine RBE values. RBE values were used to compute the RBE-weighted dose distributions. The RBE model proposed by Parisi et al. [49] was chosen because it has the advantage of directly correlating RBE with dose-weighted LET, while other models typically correlate RBE with mean lineal energy.
This section compares stable ion species (7Li, 12C,40Ar) and their radioactive counterparts (8Li,9C, 31Ar). Two irradiation schemes and ctc values were evaluated for each ion species. Firstly, an overview of the dose profiles for the different configurations is provided. Subsequently, a detailed analysis of the contribution of selected secondary products is presented. Lastly, the RBE-weighted dose is discussed, offering insights into the radiobiological impact of the administered doses.
Figure 2 shows the evolution of the central peak and central valley percentage depth dose (PDD) curves for all the simulated ion species and irradiation configurations. Each curve is normalized by the peak dose value at the BP position, providing a standardized basis for comparison. The valley doses increase as a function of depth until the proximal edge of the BP. This phenomenon can be ascribed to the secondary particle production, the scattering of primaries, and the source divergence (3 mrad). Gonzalez et al. [18] measured a 10% full width at half maximum (FWHM) increase at the BP due to beam divergence for a carbon beam in water. In addition, the larger the ctc, the lower the valley dose since a lower proportion of secondary species will have an energy and an angular aperture large enough to reach the center of the valley region.
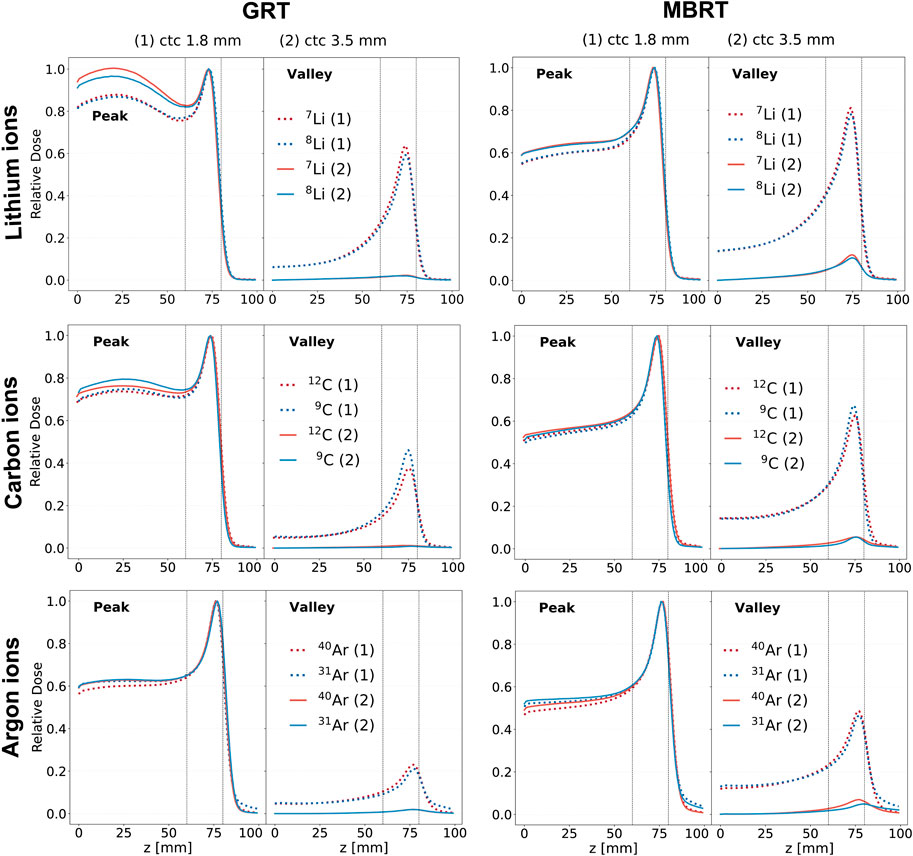
Figure 2. Depth dose curves resulting from the irradiation with mono-energetic beams of three ion species (rows). The red curves correspond to stable ions, while the blue curves correspond to unstable ones. Two irradiation schemes are considered: GRT (left column) and MBRT (right column). Two values of ctc distance are considered for each irradiation schemes: 1.8 mm (dashed line) and 3.5 mm (solid line). The first column corresponds to the GRT setup, while the second one corresponds to the MBRT setup. The region between the two vertical dotted lines corresponds to the target region.
The secondaries present in the valleys are produced by two main processes: electromagnetic interaction and nuclear interactions. As the primary beam traverses the medium, an increasing amount of energy is deposited through collisions with atomic electrons, with some δ-rays able to travel into the valleys. On the other hand, nuclear fragments resulting from nucleus-nucleus collisions become more significant with increasing penetration depth. These fragments are primarily forward-directed but exhibit a broader spread than the lateral distribution of the primary ions due to multiple Coulomb scattering. In the case of β-delayed multiple-particle emitters, radioactive decay is an additional source of secondaries. The emitted light fragments, mainly protons, have high enough energies to reach the valleys and, being high LET particles, might contribute to increasing the RBE in the valley regions.
The irradiation geometry (GRT or MBRT) significantly influences the shape of the depth dose curve. MBRT exhibits a more favorable Bragg-peak-to-entrance dose ratio (BEDR) in the peaks. This can be explained by the ratio of particles scattering away from and into the peak region: the elongated beamlets of the MBRT geometry can provide more particles scattering into the peak region than the smaller square beams of the GRT geometry [17, 50]. The BEDR ranges from 60% to 90% in GRT and from 50% to 60% in MBRT. When all other parameters (ctc, widths, etc.) are constant, the BEDR increases with increasing atomic number.
Regarding lithium isotopes, 8Li provides a more favorable BEDR then 7Li when the GRT setup with a ctc of 3.5 mm is employed. For carbon, the BEDR in the valley regions of 9C is better than that of 12C when GRT setup with ctc of 1.8 mm is employed. For argon, no significant differences are observed in the depth dose profiles for both peaks and valleys independently from the ctc distance and the lateral beam dimensions.
Figure 3 illustrates the PVDR for the simulated ions and irradiation configurations. PVDR values increase with ctc distance, inversely to the valley dose behavior (see Figure 2). The differences in PVDR between RIB and stable ions depend on the ctc employed.
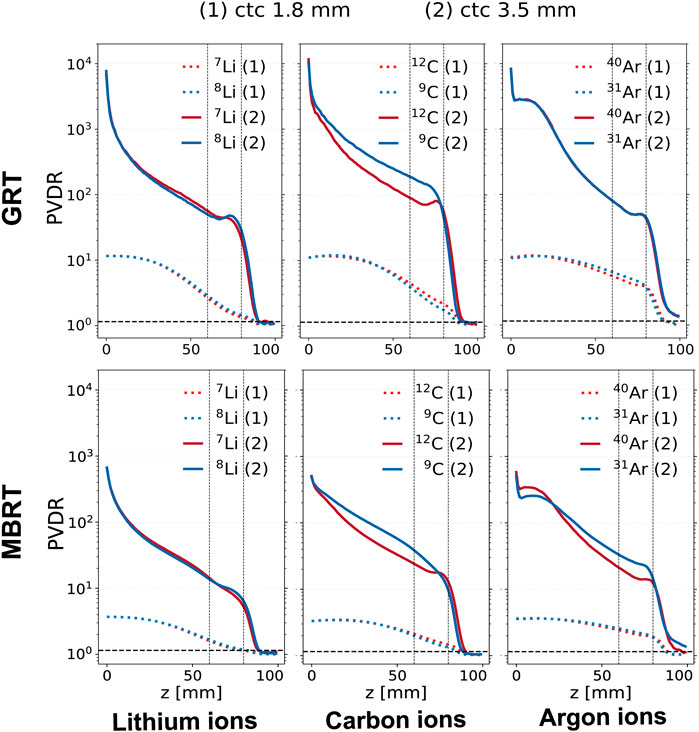
Figure 3. PVDR evolution in depth for different ion species (columns) and irradiation configurations (rows). The red curves correspond to stable ions, while the blue curves correspond to unstable ones. The upper row corresponds to the GRT setup and the lower one to the MBRT setup. Two values of ctc distance are shown for each ion: 1.8 mm (dashed line) and 3.5 mm (solid line). The region between the two vertical dotted lines corresponds to the target region.
In the case of lithium isotopes, and when a ctc of 1.8 mm is used, the PVDR of the radioactive ion is 10% lower than that of the stable ion. In contrast, for a ctc of 3.5 mm, the PVDRs for both isotopes are equivalent in the normal tissues, while 8Li presents a 10% higher PVDR in the target.
For carbon and a ctc of 1.8 mm, the stable ion beam exhibits a 10% higher PVDR in the target for both GRT and MBRT. On the contrary, for ctc = 3.5 mm the PVDR relative to the stable ion is 20% lower than the radioactive ion in the normal tissue and 50% lower in the target.
The PVDR values are equal for the two argon isotopes evaluated when the GRT setup with a ctc of 3.5 mm is employed. On the contrary, when the MBRT setup is used, the radioactive isotopes present a 10% lower PVDR at shallow depths and a 50% higher PVDR in the target. The argon PVDR curves present a kink at the phantom entrance. This behavior may be explained by the dose deposited in the valley regions by secondary electrons (δ-rays) as reflected in the respective secondary depth-dose curves (see Figure 4; Figure 5). The electron valley depth dose profile is characterized by a build-up region (visible in Figure 5, third row, third column): δ-rays liberated at the surface travel up to several millimeters into the irradiated object before stopping.
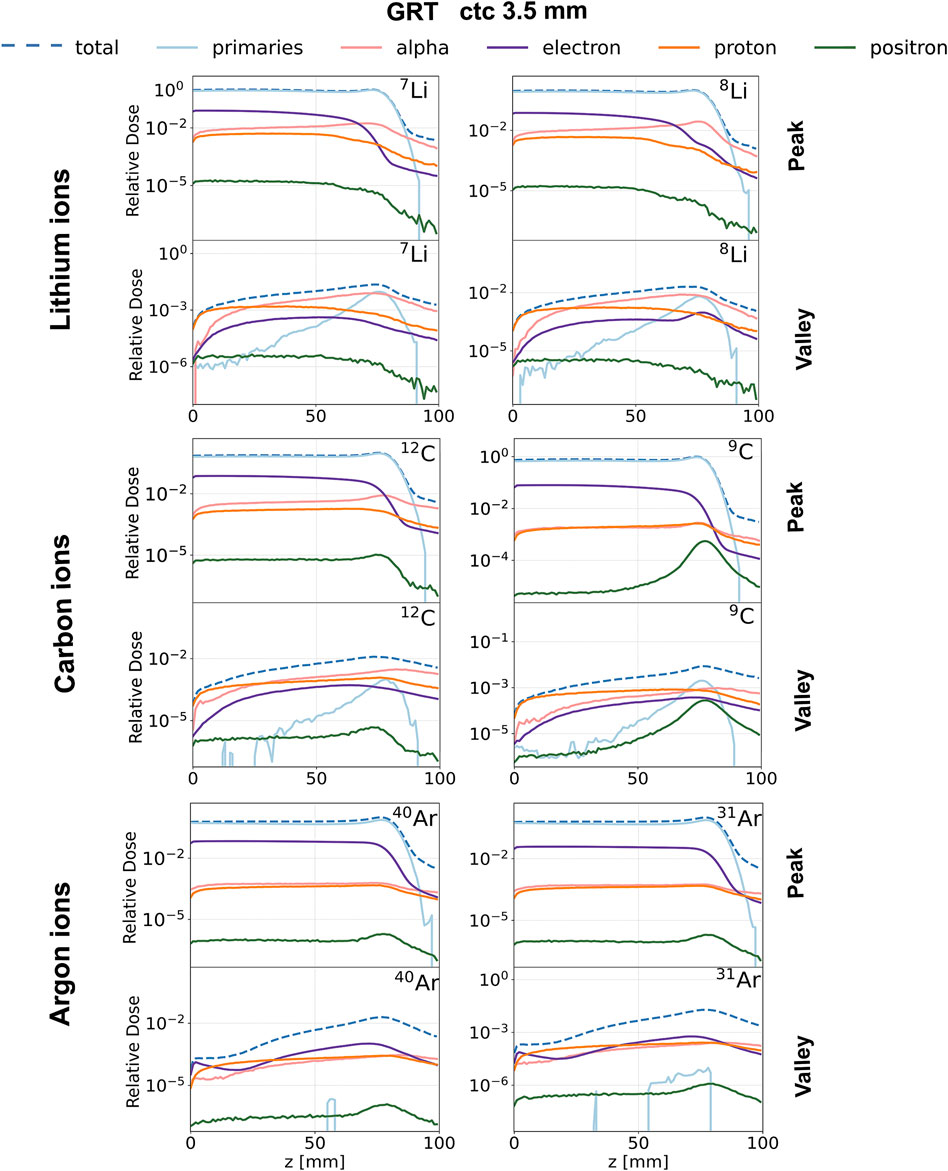
Figure 4. Relative depth dose profiles for the studied ion species (rows) and the chosen isotopes (columns). GRT irradiation setup with ctc = 3.5 mm. Contribution of primaries (light blue), alpha particles (pink), electrons (purple), protons (orange) and positrons (green) to total dose in the peak (top row) and valley (bottom row) regions. Each curve is normalized to the total dose deposited in the peak region at the BP position.
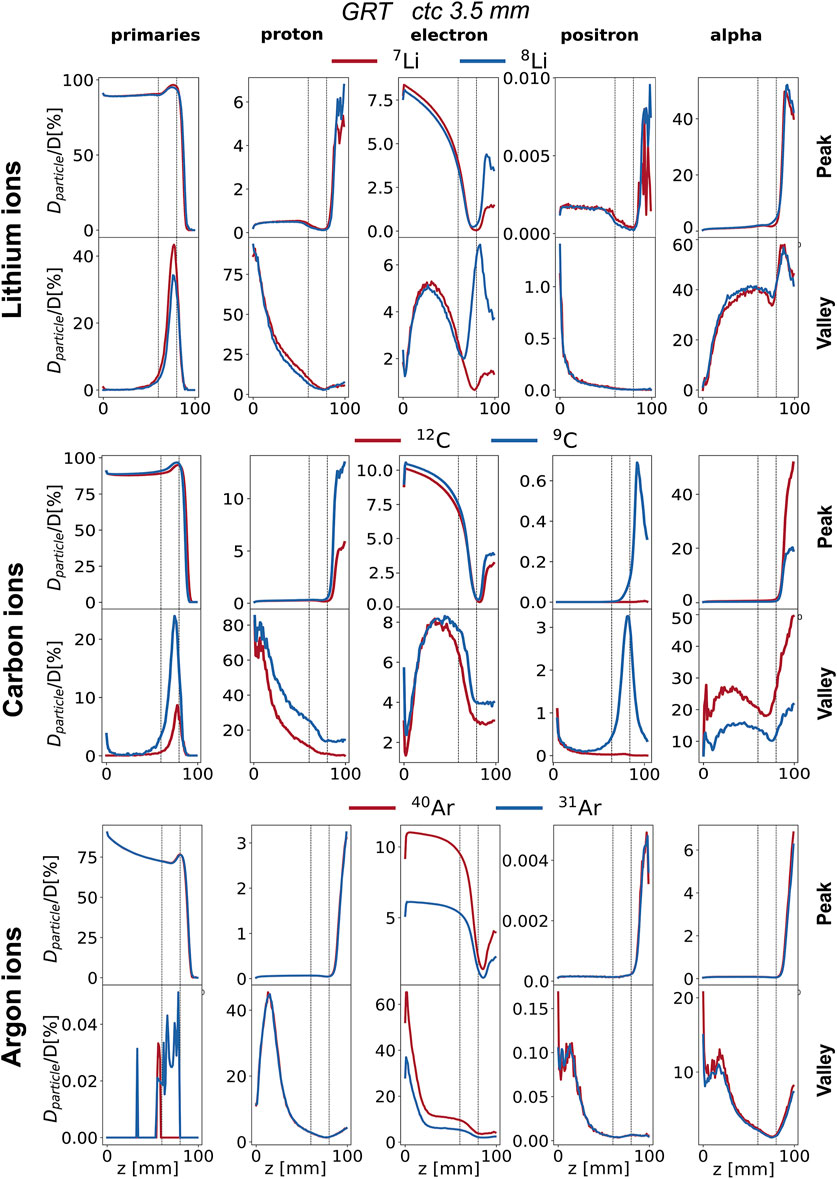
Figure 5. Percentage depth dose profiles of primary particles, electrons, protons, positrons, and alpha particles (columns) for the studied ion species (rows). GRT irradiation setup with ctc = 3.5 mm. Peak depth dose profile (top) and valley depth dose profile (bottom) are presented for each ion species. Each curve is normalized to the total dose. The region between the two vertical dotted lines corresponds to the target region.
It should be noted that the kink can also be appreciated by looking at the carbon PVDR curves, although less pronounced. As the velocity of the δ-rays increases with the Z of the primary ions, the build-up related kink is shifted to greater depths [17]. Then, the reduction of the primary beam velocity leads to a subsequent decrease of the δ-rays energy, which explains the fall-off of valley dose in the first centimeters [17].
This analysis will focus on the configuration with ctc = 3.5 mm, as it has been shown to minimize the contribution of heavy nuclear products coming from the primary ion fragmentation to the valleys [17]. This might facilitate the observation of the contribution of the lighter nuclear products coming from the β-delayed multiple-particle emission. Only GRT results are presented since no significant differences were found with MBRT.
Figure 4 compares the normalized depth dose distributions (normalized to the BP dose) of both primaries and (selected) secondary particles for the several primary ions considered. Figure 5 shows the same data but presents it as the relative contributions of the individual particle categories to the total dose. Primary particles account for more than 70% of the dose in the peak regions for argon and more than 85% for lithium and carbon across the entire phantom depth. The primary dose contribution in the valley decreases as the ion becomes heavier, in agreement with previous studies [17].
The analysis of secondary particles focuses on alpha particles, electrons, protons, and positrons, as examining their spatial and energy distribution can reveal potential differences between stable ion beams and RIB.
Electrons: The peak depth dose profiles (see the purple profiles in Figure 4) present a rapid fall-off after the BP for all simulated ions expect 8Li. This is in agreement with the findings of Peucelle et al. [17]. The rapid fall-off is explained by the complete stop of the primary beam at the BP, resulting in a reduction of secondary electron (δ-rays) emissions. In the case of 8Li, the β− decay mitigates the rapid fall-off, and the electron peak depth dose profile exhibits a local maximum at the BP position (see the purple profile in Figure 4). The electron spectrum recorded at the BP for 8Li ranges from 0 to 13 MeV (refer to Supplementary Figure S3) and coincides with the β− decay spectrum of 8Li [41]. Additionally, for 7Li, the electron spectrum shows a significant component only at energies smaller than 1 MeV, consistent with the energy of the δ-rays. Thus, we can infer that (part of) the recorded electrons originate from the radioactive decay of 8Li. The electrons resulting from the β− decay at the BP (
No significant differences are found in the dose deposited by electrons between the two carbon isotopes. As for argon, the electron dose for 40Ar is 50% higher than that of 31Ar for both peak and valley regions starting from the phantom entrance until the BP. This contribution can be attributed to δ-rays produced in the peaks with an energy high enough to reach the valley.
Positrons: The contribution of positrons plays a different role in the total deposited dose in the valleys and the peaks as a function of the primary ion. The contribution of positrons to the peak and valley doses is negligible for both lithium and argon. As for carbon, the contribution of positrons to the total dose (see green profiles in Figure 5) is very similar between the two isotopes from the entrance to the proximal edge of the BP. At the BP, the dose deposited by positrons for the radioactive ion is 60 times higher in the peaks and 30 times higher in the valleys than in the case of the stable isotope. The positron spectrum recorded at the BP position for 9C ranges from 0 to 14 MeV (refer to Supplementary Figure S4) and coincides with the β+ decay spectrum of 9C [41]. On the contrary, for 12C, the positron spectrum shows a significant component only at energies smaller than 1 MeV. Thus, we can infer that (part of) the recorded positrons originate from the radioactive decay of 9C.
Protons: The contribution of protons plays a different role in the total deposited dose in the valleys and the peaks as a function of the considered primary ion. No significant differences were found between lithium isotopes. The dose deposited by protons in the valley region goes from 75% of the total dose at the phantom entrance down to 5% at the BP. Also for carbon, the contribution of protons dominates the valley dose at shallow depths, ranging from 75% at the phantom entrance to 10–5% at the BP. Additionally, starting from the BP position, the proton valley dose resulting from the radioactive isotope is twice that of the stable one. This also holds for the peak dose. As for argon, protons deposit a significant amount of the total valley dose at shallow depths, ranging from 10% at the phantom entrance to 50% at 20 mm depth. No significant differences between radioactive argon and stable argon can be appreciated in terms of the contribution of protons in the valleys.
Alpha particles: The contribution of alpha particles is significantly different between 12C and 9C. The alpha contribution to the total peak dose is negligible between 0 and 8 cm for both radioactive and stable ions (see Figure 5). However, after the target region, the dose deposited by alpha particles reaches 55% of the total dose for 12C and is three times higher when compared to 9C. As for the valley depth dose, the alpha contribution for 12C is twice that of 9C across the whole range and in particular at the BP position. This suggests that the β-delayed alpha particles (E = 0.4 MeV, 5.8 MeV, etc.), emitted once the beam reaches the BP, deposit a negligible dose in comparison to the dose deposited by alpha particles resulting from projectile and target fragmentation. For 12C, the dose deposited by alpha particles becomes the primary contribution to the total valley dose from 7 cm depth onward, constituting about 20% of the total dose at the BP and increasing to 60% in the fragmentation tail. However, this pattern differs for the radioactive isotope, where the valley dose at BP is dominated by the contribution of primary particles and protons.
The analysis performed thus far takes into account only the absolute physical dose. To get a better idea of the actual biological effect, one can consider the RBE-weighted dose. For this purpose, dose-averaged LET distributions were simulated and used to approximate the RBE (see Supplementary Figure S1). Utilizing the RBE model detailed in [49], the RBE values corresponding to the simulated beams can be extrapolated and used to calculate biological doses (obtained by multiplying dose × RBE). Figure 6 illustrates the RBE-weighted depth dose profiles and the RBE-weighted PVDRs for the studied ions at two different ctc distances in the case of the GRT irradiation setup.
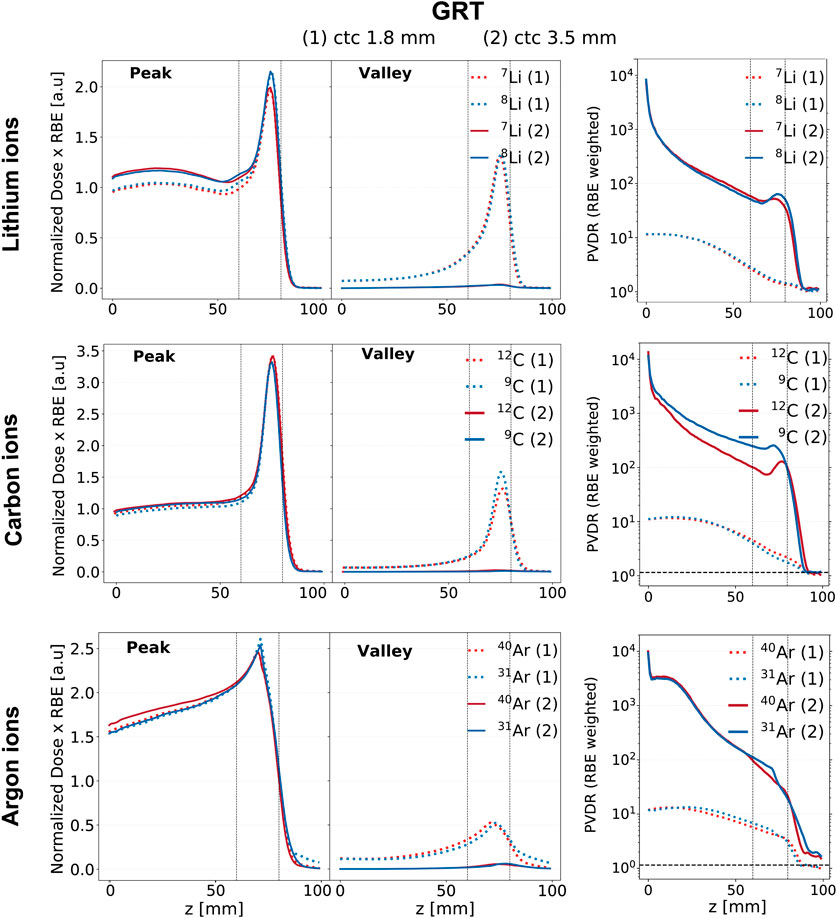
Figure 6. RBE-weighted dose evolution in depth for the GRT irradiation setups across the studied ion species (rows) and ctc distances, 1.8 mm (dashed line) and 3.5 mm (solid line). The red curves correspond to stable ions, while the blue curves correspond to unstable ones. The first column corresponds to the peak depth RBE-weighted dose profile, the second column to the valley depth RBE-weighted dose profile, and the third column to the RBE-weighted PVDR. The region between the two vertical dotted lines corresponds to the target region.
The RBE-weighted valley dose profiles are significantly lower when a ctc of 3.5 mm is employed for all the studied ions. This effect, already noticeable when comparing physical doses (see Figure 2), is enhanced when considering RBE-weighted values. A ctc of 3.5 mm corresponds, in fact, to lower RBE values in the valleys, mainly due to the substantially lower LET values. Specifically, LET values in the valleys relative to a ctc of 3.5 mm are a factor of 2 smaller than those relative to a ctc of 1.8 mm (refer to Supplementary Figure S1).
The top row of Figure 6 presents the RBE-weighted dose profiles for lithium. An enhanced BEDR is obtained when considering RBE-weighted doses as compared to physical doses. Comparing the two ions for ctc = 3.5 mm, 8Li shows a more favorable Bragg-peak-to-entrance RBE-weighted dose ratio than its stable counterpart. The RBE-weighted PVDR exhibits an inflection point coinciding with the rising edge of the BP for both isotopes. At the BP, the RBE-weighted PVDR of 8Li is 25% higher than that of 7Li. While a higher PVDR in normal tissue can enhance tissue sparing, a lower PVDR (and therefore more homogeneous dose distribution) in the target is generally preferable. However, MBRT preclinical in-vivo experiments suggest that good tumor control can be obtained even with distinctly heterogeneous target doses [14, 51].
The middle row of Figure 6 presents the profiles for carbon ions. An enhanced BEDR is obtained when considering RBE-weighted doses as compared to physical doses across both ctc distances and for both carbon isotopes. No differences are found among the two isotopes when comparing the BEDR obtained using RBE-weighted doses. The RBE-weighted PVDR relative to 9C is higher than that of 12C across the entire range, reaching values up to three times higher in the target region. Additionally, the RBE-weighted PVDR of 12C is not monotonic in the target region and exhibits an increase at the BP position. This effect is much less pronounced for 9C whose RBE-weighted PVDR presents an almost steady decline with depth. Therefore, the advantages of 9C linked to a favorable trend and a favorable PVDR in the normal tissues might be counterbalanced by a less favorable PVDR in the target.
The bottom row of Figure 6 presents the profiles for argon ions. The RBE-weighted dose profile of 31Ar exhibits a lower entrance dose value than that of 40Ar when a ctc of 3.5 mm is employed in both the peak and valley regions. Additionally, 31Ar exhibits a higher RBE-weighted dose value at the BP in the peak region, independently of the ctc. This results in an improved BEDR for both the peak and valley regions. In particular, in the peak region, the BEDR relative to 31Ar is 20% higher than that of 40Ar for both ctc distances. However, the unstable ion exhibits a less favorable PVDR in the target region, being 50% higher than the stable isotope in the case of ctc = 3.5 mm and 20% higher in the case of ctc = 1.8 mm.
Spatially fractionated radiation therapy is an innovative therapeutic approach that has shown great promise to widen the therapeutic window for radioresistant tumors [2, 52]. The alliance of SFRT with the benefits of heavy ion therapy can further increase the therapeutic index, as suggested by previous works [17–20]. Our study aimed to investigate whether the alliance between SFRT and heavy ions could be further exploited when using RIB (in particular β-delayed multiple-particle emitters), capitalizing on the radiobiological effects obtained in the valley regions through radioactive decay.
RIB, such as 9C, have already been used for therapy in the past [28] eliciting a lot of interest because of the β-delayed decay of low-energy (densely ionizing) particles. The potential increase in RBE attributed to the decay products is not yet clear [31, 35]. Given the distinct dose distributions in MBRT, it was crucial to investigate whether the use of RIB could lead to a potential increase in RBE in the valley regions which play a significant role in both normal tissue sparing and tumor response [32].
Concerning physical doses, no major differences were observed between stable and unstable isotopes either in the peak or in the valley regions. The contribution of primaries and selected secondary particles to the total physical dose was investigated for the GRT setup and a ctc distance of 3.5 mm. A comparative analysis of the secondary particle contributions between stable and radioactive isotopes aimed to assess the impact of β-delayed products on the total valley physical dose. In the case of lithium, protons are the principal contributors to the total valley physical dose at shallow depths while primaries and alpha particles are the principal contributors at the BP. The equal contribution of alpha particles for stable and radioactive lithium suggests that the dose deposited at the BP by β-delayed emitted alpha particles is negligible when compared to the dose deposited by alpha particles resulting from projectile and target fragmentation. Similarly, for carbon, protons are the principal contributors to the total valley physical dose at shallow depths in agreement with the results of Gonzalez et al. [18]. The valley physical dose at the BP position is dominated by alpha particles for the stable ion and by primaries for the unstable one. In particular, the contribution of alpha particles to the total valley physical dose is 50% lower for 9C compared to 12C. This suggests that the dose deposited by β-delayed emitted alpha particles at the BP is negligible when compared to the dose deposited by alpha particles resulting from projectile and target fragmentation. For argon, the contribution of δ-rays dominates the total valley physical dose at the phantom entrance, in agreement with the findings of Peucelle et al. [17]. Differently from lithium and carbon, primaries do not significantly contribute to the total valley physical dose at the BP for the two argon isotopes. Furthermore, the cumulative contribution of all selected secondaries (protons, positrons, electrons, alpha particles) constitutes only 20% of the total valley physical dose at the BP indicating that heavier nuclear fragments play a dominant role in the valleys. The contribution of protons to the total valley physical dose is equal for the two argon isotopes across the entire range. This suggests that the dose deposited by β-delayed protons at the BP is negligible compared to that deposited by protons resulting from projectile and target fragmentation.
To go further we employed LET-average dose values to estimate the RBE according to the model proposed by Parisi et al. [49]. Concerning RBE-weighted dose curves for lithium and argon isotopes, RIB leads to an increased BEDR in the peak regions (12% for 8Li and 20% for 31Ar) when compared to their stable counterparts and for the two ctc distances evaluated. Additionally, in the case of argon, a 10% increase in BEDR is also evident in the valley region. Higher BEDR is associated with better normal tissue sparing. As for carbon MBRT, no differences were observed among the two isotopes concerning the BEDR of the RBE-weighted doses.
All the studied radioactive isotopes exhibit an increased RBE-weighted PVDR in the tumor compared to their stable counterparts for the two ctc distances evaluated. In particular, the RBE-weighted PVDR of radioactive lithium, carbon and argon is 25%, 100% and 50% higher than the stable counterpart when a ctc of 3.5 mm is employed. Although MBRT experiments showed that good treatment outcomes can be achieved even with considerable dose heterogeneity in the tumor [14], excessively high PVDR might be unfavorable for tumor control. For carbon, the radioactive ion also shows a 100% increase in RBE-weighted PVDR in the normal tissue which could favor normal tissue sparing. Which of the two factors is predominant is yet to be established by biological experiments.
It is crucial to note that the RBE model used to weight the simulated dose distributions refers to broad beam irradiation conditions and has been benchmarked on in-vitro data [49]. Additionally, the model only describes stable isotopes. For the purpose of this study and due to the lack of more specific data, we used the same RBE-vs-LET curves for both the stable and radioactive isotopes. These assumptions constitute a limitation of this study. The radiobiological characteristics of MBRT differ significantly from those of standard charged ion therapy (broad beam irradiation). The biological response to MBRT may involve non-targeted effects, abscopal effects, and immune responses [53]. Biological experiments are therefore needed to establish the validity of RBE in the context of MBRT.
Even if no advantages were to be found in terms of biologically effective doses, RIB remains the ideal bullet for image-guided particle therapy, offering advantages for both β+ imaging [54] and optical imaging [55]. The use of RIB for in-beam range verification was proposed more than 40 years ago at Lawrence Berkeley Laboratory [56] to tackle the range uncertainty problem. RIB featuring β+ decay can increase the signal intensity in online PET improving the count rate by an order of magnitude, they can reduce the shift between measured activity and dose, and mitigate the washout blur of the image with short-lived isotopes and in-beam acquisition [57]. In the context of MBRT, those capabilities could be exploited to visualize the minibeam paths.
Concerning the feasibility of preclinical experiments, it should be highlighted that over the last years, the Yamaya laboratory conducted several preclinical studies [58, 59] at the HIMAC facility to investigate the washout of RIB in animal targets using an online PET. Preclinical studies are also currently ongoing at GSI to demonstrate the potential of RIB therapy in animal models [36]. Moreover, research is ongoing to address RIB production limitations, such as low beam intensity. NIRS [60] and CERN [61] are studying RIB sources compatible with medical synchrotrons with the aim of facilitating RIB translation into clinics.
This work constitutes the first in-depth evaluation of the dosimetric characteristics of β-MBRT with a focus on lithium, carbon, and argon.
Radioactive ions exhibit a more favorable RBE-weighted dose profile than their stable counterparts characterized by an equal (carbon) or superior (lithium and argon) BEDR across all the simulated irradiation configurations. Moreover, they exhibit either equal (lithium and argon) or higher (carbon) RBE-weighted PVDR at shallow depths and a higher RBE-weighted PVDR in the target. While higher BEDR and RBE-weighted PVDR at shallow depths are known to favor normal tissue sparing [9], it needs to be experimentally investigated how the higher PVDR could influence tumor control. The insights provided by this study could guide the design of future biological experiments.
The raw data supporting the conclusion of this article will be made available upon reasonable request to corresponding author.
AC: Data curation, Formal Analysis, Investigation, Software, Visualization, Writing–original draft, Supervision, Writing–review and editing. TS: Methodology, Software, Supervision, Visualization, Writing–review and editing. YP: Conceptualization, Funding acquisition, Resources, Supervision, Validation, Writing–review and editing, Project administration.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No 817908). It was granted access to the Joliot Curie-SKL (France) computational cluster under TGCC (Très grand centre de calcul) from the European High Performance Computing Joint Undertaking (EuroHPC number EHPC-REG-2022R02-177) and from the Grand Equipement National de Calcul Intensif (GENCI project A0130313736 and A0150314559).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1390439/full#supplementary-material
1. Garibaldi C, Jereczek-Fossa BA, Marvaso G, Dicuonzo S, Rojas DP, Cattani F, et al. Recent advances in radiation oncology. Ecancermedicalscience (2017) 11:785. doi:10.3332/ecancer.2017.785
2. Prezado Y. Divide and conquer: spatially fractionated radiation therapy. Expert Rev Mol Med (2022) 24:e3. doi:10.1017/erm.2021.34
3. Köhler A. Theorie einer methode, bisher unmöglich unanwendbar hohe dosen röntgenstrahlen in der tiefe des gewebes zur therapeutischen wirksamkeit zu bringen ohne schwere schäden des patienten, zugleich eine methode des schutzes gegen röntgenverbrennungen überhaupt. Fortschritte auf dem Gebiete der Röntgenstrahlen und der Nuklearmedizin (1909) 14:27–9.
4. wu X, Ahmed M, Pollack A. On modern technical approaches of 3d high-dose lattice radiotherapy (lrt). Fuel Energ Abstr (2009) 75:S723. doi:10.1016/j.ijrobp.2009.07.1647
5. Dilmanian FA, Zhong Z, Bacarian T, Benveniste H, Romanelli P, Wang R, et al. Interlaced x-ray microplanar beams: a radiosurgery approach with clinical potential. Proc Natl Acad Sci USA (2006) 103:9709–14. doi:10.1073/pnas.0603567103
6. Slatkin D, Spanne P, Dilmanian A, Sandborg M. Microbeam radiation therapy. Med Phys (1992) 19:1395–400. doi:10.1118/1.596771
7. Hopewell J, Trott K. Volume effects in radiobiology as applied to radiotherapy. Radiother Oncol J Eur Soc Ther Radiol Oncol (2000) 56:283–8. doi:10.1016/S0167-8140(00)00236-X
8. Deman P, Vautrin M, Edouard M, Stupar V, Bobyk L, Farion R, et al. Monochromatic minibeams radiotherapy: from healthy tissue-sparing effect studies toward first experimental glioma bearing rats therapy. Int J Radiat Oncol Biol Phys (2012) 82:e693–e700. doi:10.1016/j.ijrobp.2011.09.013
9. Prezado Y, Deman P, Varlet P, Jouvion G, Gil S, Le C’HC, et al. Tolerance to dose escalation in minibeam radiation therapy applied to normal rat brain: long-term clinical, radiological and histopathological analysis. Radiat Res (2015) 184:314–21. doi:10.1667/RR14018.1
10. Prezado Y, Dos Santos M, Gonzalez W, Jouvion G, Guardiola C, Heinrich S, et al. Transfer of minibeam radiation therapy into a cost-effective equipment for radiobiological studies: a proof of concept. Scientific Rep (2017) 7:17295. doi:10.1038/s41598-017-17543-3
11. Prezado Y, Sarun S, Gil S, Deman P, Bouchet A, Le Duc G. Increase of lifespan for glioma-bearing rats by using minibeam radiation therapy. J Synchrotron Radiat (2012) 19:60–5. doi:10.1107/S0909049511047042
12. Sotiropoulos M, Brisebard E, Le Dudal M, Jouvion G, Juchaux M, Crépin D, et al. X-rays minibeam radiation therapy at a conventional irradiator: pilot evaluation in f98-glioma bearing rats and dose calculations in a human phantom. Clin Translational Radiat Oncol (2021) 27:44–9. doi:10.1016/j.ctro.2021.01.001
13. Bertho A, Iturri L, Brisebard E, Juchaux M, Gilbert C, Ortiz R, et al. Evaluation of the role of the immune system response after minibeam radiation therapy. Int J Radiat Oncol Biol Phys (2023) 115:426–39. doi:10.1016/j.ijrobp.2022.08.011
14. Prezado Y, Jouvion G, Guardiola C, Gonzalez W, Juchaux M, Bergs J, et al. Tumor control in rg2 glioma-bearing rats: a comparison between proton minibeam therapy and standard proton therapy. Int J Radiat Oncol Biol Phys (2019) 104:266–71. doi:10.1016/j.ijrobp.2019.01.080
15. Schneider T, De Marzi L, Patriarca A, Prezado Y. Monte Carlo comparison of proton and helium-ion minibeam generation techniques. Front Phys (2021) 9:595721. doi:10.3389/fphy.2021.595721
16. Dilmanian FA, Rusek A, Fois GR, Olschowka J, Desnoyers NR, Park JY, et al. Interleaved carbon minibeams: an experimental radiosurgery method with clinical potential. Int J Radiat Oncol Biol Phys (2012) 84:514–9. doi:10.1016/j.ijrobp.2011.12.025
17. Peucelle C, Martínez-Rovira I, Prezado Y. Spatial fractionation of the dose using neon and heavier ions: a Monte Carlo study. Med Phys (2015) 42:5928–36. doi:10.1118/1.4930960
18. González W, Peucelle C, Prezado Y. Theoretical dosimetric evaluation of carbon and oxygen minibeam radiation therapy. Med Phys (2017) 44:1921–9. doi:10.1002/mp.12175
19. Martínez-Rovira I, González W, Brons S, Prezado Y. Carbon and oxygen minibeam radiation therapy: an experimental dosimetric evaluation. Med Phys (2017) 44:4223–9. doi:10.1002/mp.12383
20. González W, Prezado Y. Spatial fractionation of the dose in heavy ions therapy: an optimization study. Med Phys (2018) 45:2620–7. doi:10.1002/mp.12902
21. Prezado Y, Fois GR. Proton-minibeam radiation therapy: a proof of concept. Med Phys (2013) 40:031712. doi:10.1118/1.4791648
22. Zlobinskaya O, Girst S, Greubel C, Hable V, Siebenwirth C, Walsh DWM, et al. Reduced side effects by proton microchannel radiotherapy: study in a human skin model. Radiat Environ Biophys (2013) 52:123–33. doi:10.1007/s00411-012-0450-9
23. Girst S, Greubel C, Reindl J, Siebenwirth C, Zlobinskaya O, Walsh DW, et al. Proton minibeam radiation therapy reduces side effects in an in vivo mouse ear model. Int J Radiat Oncol Biol Phys (2016) 95:234–41. doi:10.1016/j.ijrobp.2015.10.020
24. Prezado Y, Jouvion G, Hardy D, Patriarca A, Nauraye C, Bergs J, et al. Proton minibeam radiation therapy spares normal rat brain: long-term clinical, radiological and histopathological analysis. Scientific Rep (2017) 7:14403. doi:10.1038/s41598-017-14786-y
25. Lamirault C, Doyère V, Juchaux M, Pouzoulet F, Labiod D, Dendale R, et al. Short and long-term evaluation of the impact of proton minibeam radiation therapy on motor, emotional and cognitive functions. Scientific Rep (2020) 10:13511. doi:10.1038/s41598-020-70371-w
26. Bertho A, Ortiz R, Juchaux M, Gilbert C, Lamirault C, Pouzoulet F, et al. First evaluation of temporal and spatial fractionation in proton minibeam radiation therapy of glioma-bearing rats. Cancers (Basel) (2021) 13:4865. doi:10.3390/cancers13194865
27. Tinganelli W, Durante M. Carbon ion radiobiology. Cancers (Basel) (2020) 12:3022. doi:10.3390/cancers12103022
28. Li Q, Kanai T, Kitagawa A. The potential application of β-delayed particle decay beam 9c in cancer therapy. Phys Med Biol (2004) 49:1817–31. doi:10.1088/0031-9155/49/9/016
29. Li Q, Furusawa Y, Kanazawa M, Kanai T, Kitagawa A, Aoki M, et al. Enhanced efficiency in cell killing at the penetration depths around the bragg peak of a radioactive 9C-ion beam. Int J Radiat Oncol Biol Phys (2005) 63:1237–44. doi:10.1016/j.ijrobp.2005.08.006
30. Li Q, Furusawa Y, Kanazawa M, Kanai T, Kitagawa A, Aoki M, et al. Enhanced biological effect induced by a radioactive 9c-ion beam at the depths around its bragg peak. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2006) 245:302–5. doi:10.1016/j.nimb.2005.11.119
31. Tian L, Li Q, Liu X, Dai Z, Fu T, He P, et al. Theoretical substantiation of biological efficacy enhancement for beta-delayed particle decay (9C) beam: a Monte Carlo study in combination with analysis with the local effect model approach. Med Phys (2016) 43:1200–21. doi:10.1118/1.4941310
32. Fernandez-Palomo C, Chang S, Prezado Y. Should peak dose be used to prescribe spatially fractionated radiation therapy? a review of preclinical studies. Cancers (Basel) (2022) 14:3625. doi:10.3390/cancers14153625
33. Borge MJG. Beta-delayed particle emission. Physica Scripta (2013) T152:014013. doi:10.1088/0031-8949/2013/T152/014013
34. Chacon A, James B, Tran L, Guatelli S, Chartier L, Prokopvich D, et al. Experimental investigation of the characteristics of radioactive beams for heavy ion therapy. Med Phys (2020) 47:3123–32. doi:10.1002/mp.14177
35. Mancusi D, Sihver L, Niita K, Li Q, Sato T, Iwase H, et al. Calculation of energy-deposition distributions and microdosimetric estimation of the biological effect of a 9c beam. Radiat Environ Biophys (2009) 48:135–43. doi:10.1007/s00411-008-0206-8
36. Durante M, Parodi K. Radioactive beams in particle therapy: past, present, and future. Front Phys (2020) 8:00326. doi:10.3389/fphy.2020.00326
37. Dilmanian FA, Eley JG, Krishnan S. Minibeam therapy with protons and light ions: physical feasibility and potential to reduce radiation side effects and to facilitate hypofractionation. Int J Radiat Oncol Biol Phys (2015) 92:469–74. Epub 2015 Mar 11. doi:10.1016/j.ijrobp.2015.01.018
38. Okada T, Kamada T, Tsuji H, Mizoe J, Baba M, Kato S, et al. Carbon ion radiotherapy: clinical experiences at national institute of radiological science (nirs). J Radiat Res (2010) 51:355–64. doi:10.1269/jrr.10016
39. Castro JR, Linstadt DE, Bahary JP, Petti PL, Daftari I, Collier JM, et al. Experience in charged particle irradiation of tumors of the skull base: 1977–1992. Int J Radiat Oncol Biol Phys (1994) 29:647–55. doi:10.1016/0360-3016(94)90550-9
40. Prezado Y, Hirayama R, Matsufuji N, Inaniwa T, Martínez-Rovira I, Seksek O, et al. A potential renewed use of very heavy ions for therapy: neon minibeam radiation therapy. Cancers (2021) 13:1356. doi:10.3390/cancers13061356
41. Iaea. Iaea - nuclear data section. ensdf database (2014). Available at: https://nds.iaea.org/relnsd/vcharthtml/VChartHTML.html (Accessed January, 2014).
42. Axelsson L, Äystö J, Borge M, Fraile L, Fynbo H, Honkanen A, et al. Beta decay of 31ar. Nucl Phys A (1998) 634:475–96. doi:10.1016/S0375-9474(98)00172-9
43. Jan S, Benoit D, Becheva E, Carlier T, Cassol F, Descourt P, et al. Gate v6: a major enhancement of the gate simulation platform enabling modelling of ct and radiotherapy. Phys Med Biol (2011) 56:881–901. doi:10.1088/0031-9155/56/4/001
44. Grevillot L, Frisson T, Zahra N, Bertrand D, Stichelbaut F, Freud N, et al. Optimization of geant4 settings for proton pencil beam scanning simulations using gate. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2010) 268:3295–305. doi:10.1016/j.nimb.2010.07.011
45. Sechopoulos I, Rogers DWO, Bazalova-Carter M, Bolch WE, Heath EC, McNitt-Gray MF, et al. Records: improved reporting of Monte Carlo radiation transport studies: report of the aapm research committee task group 268. Med Phys (2018) 45:e1–e5. doi:10.1002/mp.12702
46. Y P, Gonzalez-Infantes W, Heinrich S Proton minibeam radiation therapy increases normal tissue resistance. Med Phys (2016) 43:3675–6. doi:10.1118/1.4957089
47. Wilkens JJ, Oelfke U. Analytical linear energy transfer calculations for proton therapy. Med Phys (2003) 30:806–15. doi:10.1118/1.1567852
48. Grün R, Friedrich T, Traneus E, Scholz M. Is the dose-averaged let a reliable predictor for the relative biological effectiveness? Med Phys (2019) 46:1064–74. doi:10.1002/mp.13347
49. Parisi A, Sato T, Matsuya Y, Kase Y, Magrin G, Verona C, et al. Development of a new microdosimetric biological weighting function for the rbe10 assessment in case of the v79 cell line exposed to ions from 1h to 238u. Phys Med Biol (2020) 65:235010. doi:10.1088/1361-6560/abbf96
50. Martínez-Rovira I, Fois G, Prezado Y. Dosimetric evaluation of new approaches in grid therapy using nonconventional radiation sources. Med Phys (2015) 42:685–93. doi:10.1118/1.4905042
51. Prezado Y, Jouvion G, Patriarca A, Nauraye C, Guardiola C, Juchaux M, et al. Proton minibeam radiation therapy widens the therapeutic index for high-grade gliomas. Scientific Rep (2018) 8:16479. doi:10.1038/s41598-018-34796-8
52. Yan W, Khan MK, Wu X, Simone CB, Fan J, Gressen E, et al. Spatially fractionated radiation therapy: history, present and the future. Clin Translational Radiat Oncol (2019) 20:30–8. doi:10.1016/j.ctro.2019.10.004
53. Cho YB, Yoon N, Suh JH, Scott JG. Radio-immune response modelling for spatially fractionated radiotherapy. Phys Med Biol (2023) 68:165010. doi:10.1088/1361-6560/ace819
54. Mohammadi A, Yoshida E, Tashima H, Nishikido F, Inaniwa T, Kitagawa A, et al. Production of an 15o beam using a stable oxygen ion beam for in-beam pet imaging. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2017) 849:76–82. doi:10.1016/j.nima.2016.12.028
55. Kang HG, Yamamoto S, Takyu S, Nishikido F, Mohammadi A, Horita R, et al. Optical imaging for the characterization of radioactive carbon and oxygen ion beams. Phys Med Biol (2019) 64:115009. doi:10.1088/1361-6560/ab1ccf
56. Llacer J, Chatterjee A, Alpen EL, Saunders W, Andreae S, Jackson HC. Imaging by injection of accelerated radioactive particle beams. IEEE Trans Med Imaging (1984) 3:80–90. doi:10.1109/TMI.1984.4307660
57. Augusto RS, Bauer J, Bouhali O, Cuccagna C, Gianoli C, Kozłowska WS, et al. An overview of recent developments in fluka pet tools. Phys Med (2018) 54:189–99. Epub 2018 Jul 2. doi:10.1016/j.ejmp.2018.06.636
58. Hirano Y, Takuwa H, Yoshida E, Nishikido F, Nakajima Y, Wakizaka H, et al. Washout rate in rat brain irradiated by a 11C beam after acetazolamide loading using a small single-ring openpet prototype. Phys Med ‘I&’ Biol (2016) 61:1875–87. doi:10.1088/0031-9155/61/5/1875
59. Toramatsu C, Yoshida E, Wakizaka H, Mohammadi A, Ikoma Y, Tashima H, et al. Washout effect in rabbit brain: in-beam pet measurements using 10C, 11C and 15O ion beams. Biomed Phys ‘I&’Engineering Express (2018) 4:035001. doi:10.1088/2057-1976/aaade7
60. Katagiri K, Noda A, Nagatsu K, Nakao M, Hojo S, Muramatsu M, et al. A singly charged ion source for radioactive ¹¹C ion acceleration. Rev Scientific Instr (2016) 87:02B509. doi:10.1063/1.4935899
Keywords: minibeam radiation therapy, Monte Carlo simulations, β-delayed multiple-particle emitters, radioactive heavy-ions, spatially fractionated radiation therapy, normal tissue sparing
Citation: Corvino A, Schneider T and Prezado Y (2024) β-delayed multiple-particle emitters minibeam radiation therapy: first dosimetric evaluation with Monte Carlo simulations. Front. Phys. 12:1390439. doi: 10.3389/fphy.2024.1390439
Received: 23 February 2024; Accepted: 02 April 2024;
Published: 26 April 2024.
Edited by:
Dousatsu Sakata, Osaka University, JapanReviewed by:
Christopher John Hall, Australian Nuclear Science and Technology Organisation, AustraliaCopyright © 2024 Corvino, Schneider and Prezado. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yolanda Prezado, eW9sYW5kYS5wcmV6YWRvQGN1cmllLmZy
†Present address: Tim Schneider, Laboratoire d’Imagerie Biomédicale Multimodale, BIOMAPS, Université Paris-Saclay, Service Hospitalier Frédéric Joliot, Orsay, France
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.