
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 11 July 2024
Sec. Social Physics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1387312
This article is part of the Research Topic Real-World Applications of Game Theory and Optimization View all 17 articles
This paper investigates the decision-making behaviors of opinion leaders and netizens in the context of uncertain information dissemination with the aim of effectively managing online public opinion crises triggered by major sudden events. The decision-making behaviors of opinion leaders are categorized into positive and negative guidance, while those of netizens are classified into acceptance and nonacceptance. Using an evolutionary game model, this study introduces random factors to examine their influence on the decision-making processes of both groups. A stochastic evolutionary game model is constructed to analyze the behaviors of opinion leaders and netizens in the context of uncertain information dissemination. The evolutionary stability strategies and stochastic evolutionary processes of the model are analyzed based on the theory of Itô stochastic differential equations. The impacts of key variables such as random disturbances, the degree of psychological identification of netizens with opinion leaders, and the intensity of government penalties for those spreading negative information are examined through numerical simulations. The findings indicate that opinion leaders evolve to make stable strategies more rapidly than netizens do; random disturbances slow the evolution of stable strategies for both groups but do not alter their strategic choices; a higher degree of psychological identification increases the likelihood of netizens adopting the views of opinion leaders; and as punitive measures intensify, both opinion leaders and netizens are inclined to choose strategies of positive guidance and acceptance. The results of this study offer theoretical insights and decision-making guidance for future government strategies for managing similar online collective behaviors.
The emergence of major emergencies can cause great damage to the lives and property of governments and the public. For example, the 6.2 magnitude earthquake that struck Gansu Province, China, on 18 December 2023 and the 7.4 magnitude earthquake that struck off the west coast of Honshu, Japan, on 1 January 2024 resulted in a considerable loss of life and extensive property damage. The harm caused by major emergencies is not only limited to the impact of the event itself but also to the various secondary impacts it causes, which can also hinder the smooth operation of society. Sometimes, the damage caused by secondary impacts may even exceed the damage caused by the major emergency itself. With the continuous iteration of internet technologies, the internet is gradually emerging as the predominant conduit through which the general public obtains information. Individuals within society can conveniently access platforms such as Facebook, X (Twitter), TikTok, Weibo, and WeChat through computers or mobile devices at any time and from any location to acquire information of interest and engage in real-time communication and interaction with others. Therefore, when a major emergency occurs in a certain place, netizens can obtain all kinds of related information quickly andonduct information exchange around it. However, because major emergencies are characterized by randomness, wide coverage, uncertain duration and a large degree of harm, relevant departments are unable to publish all the information related to major emergencies in a timely and effective manner, resulting in a large amount of unsubstantiated and uncertain information on social platforms. If opinion leaders choose to guide netizens negatively for certain purposes, netizens will make incorrect judgments after adopting the information, thus spreading panic and even triggering online public opinion crises resulting in mass incidents. This will not only cause great obstacles to relevant government departments in dealing with major emergencies, but also have a negative impact on the prosperity and stability of society. Therefore, analyzing the decision-making behaviors of opinion leaders and netizens in the dissemination of uncertain information to identify strategic choices that can contribute to the smooth operation of society are highly important for preventing and controlling online public opinion crises triggered by major emergencies.
Based on the summary and combination of previous studies, to analyze the decision-making behaviors of opinion leaders and netizens in uncertain information dissemination after major emergencies occur, this paper combines stochastic analysis theory with an evolutionary game model. First, we take opinion leaders and netizens as research objects and construct an evolutionary game model between them. Second, considering that random factors from the internal or external environment affect decision-making behavior, Gaussian white noise is introduced on the basis of the evolutionary game model to construct a stochastic evolutionary game model between opinion leaders and netizens. Again, the stochastic evolutionary game model is solved, the conditions when the model reaches a stable state are analyzed, and the numerical solution of the equilibrium solution of the model is solved using stochastic Taylor expansion. Finally, the model is numerically simulated using MATLAB 2017b to analyze the effects of different variables on the model evolution process.
The main contributions of the research reported in this paper are as follows: 1) Considering that after the occurrence of major emergencies, opinion leaders and netizens are the main actors in the dissemination of uncertain information in social platforms. Therefore, we study the decision-making behavior of opinion leaders and netizens. 2) When constructing the model, we took into account that netizens may not fully trust the statements released by opinion leaders. Therefore, we included netizens’ psychological identification with opinion leaders in the model. 3) Compared to other scholars’ research on the decision-making behaviors of different groups in the process of uncertain information dissemination, this paper incorporates random disturbance factors into the model construction. The random disturbance factors not only includes the bounded rationality of opinion leaders and netizens but also reflects the complexity of the real world and the impact of random interference factors on their decision-making process. This paper introduces Gaussian white noise into the construction of the evolutionary game model of opinion leaders and netizens. In this way, this paper depictes the evolution of decision-making behaviors of opinion leaders and netizens in the process of uncertain information dissemination more realistically. The research in this paper provides the corresponding theoretical basis and decision-making reference for the future exploration of the decision-making behavior of opinion leaders and netizens in uncertain information dissemination in the context of major emergencies.
The embryonic form of evolutionary game theory was initially applied by biologists in research pertaining to the species evolution of animals and plants. It was not until 1973 that the evolutionary stability strategy proposed by Smith et al. [1] marked the formalization of evolutionary game theory. Evolutionary game theory is widely used in sociology, management, cybernetics, biology and other disciplines because it does not require game subjects to be completely rational, and the information between game subjects is not fully disclosed. Wölfl et al. [2] used the evolutionary game model to study the evolution of cancer. Li et al. [3] analyzed the decision-making behaviors of the government, online media and netizens in the process of disinformation dissemination by constructing a three-party evolutionary game model. Wang et al. [4] analyzed the decision-making behaviors of workers, platforms and requesters in spatial crowdsourcing based on an evolutionary game model. Wu et al. [5] studied the behavior of enterprises facing energy transition in the carbon trading market. Shi et al. [6] studied decision-making behaviors among the government, service providers and elderly people in a smart aging system. Sun et al. [7] studied the decision-making behavior of civil aviation and high-speed rail under a carbon trading price. Shi et al. [8] studied the behavior of the government, automotive suppliers and logistics companies in the context of green transition. As Perc et al. [9] and Tanimoto et al. [10] explored whether the emergence of random disturbances will affect the payoffs of the game system. Different game subjects in a real environment are affected by the uncertainties they experience or by the external environment, which results in great uncertainty in decision-making behavior among game subjects. Therefore, some scholars have combined stochastic analysis theory with evolutionary game theory, introduced Gaussian white noise into the construction of models, and constructed stochastic evolutionary game models. For example, Mo et al. [11] suggested that random factors interfere with the decision-making behavior of game subjects and constructed a stochastic evolutionary game model to study the decision-making behavior of different game subjects in the online car market. Kang et al. [12] constructed a stochastic evolutionary game model among multinational corporations, international dealers and the government. Xie et al. [13] contructed the model to study the behavior of market regulators and risky units in electricity markets. Du et al. [14] constructed an evolutionary game model between e-commerce firms and banks without considering the interference of stochastic factors and a stochastic evolutionary game model considering the interference of stochastic factors. Scatà et al. [15] used the stochastic evolutionary game model to investigate the cooperation mechanism between humans.
Scholars in various countries have carried out related research from various perspectives against the background of major emergencies. Among them, some scholars have studied the impact of major emergencies. Mos et al. [16] believe that major emergencies can cause enormous financial risks and economic losses. Cheng et al. [17] analyzed the oil price data of the month when major emergencies occurred from 2009 to 2020 and found that major emergencies in major economies around the world would seriously affect international oil prices. Some other scholars, studied the behavior of different types of actors after major emergencies. For example, Jia et al. [18] constructed a stochastic evolutionary game model based on the Moran process to study the effects of different game actors on prevention and control behavior in public health emergencies. Using game theory, Özkaya et al. [19] investigated the effect of self-isolation on the spread of COVID-19. Salarpour et al. [20] used COVID-19 as a background for a game-theoretic study of the behavior of countries in the supply of medical supplies at different stages. Wang et al. [21] studied the dispatching behavior of relief supplies after a major emergency. Meanwhile, some scholars conducted research about online public opinion caused by major emergencies. Wei [22] used the theory of heat conduction to study the propagation behavior of online public opinion after major emergencies. Chen et al. [23] argue that the topics that are widely discussed over time will generate new sub topics which will combine with existing public opinion to form multidimensional new public opinion. Lu et al. [24] argue that netizens pay limited attention to different events occurring at the same time and do not pay attention to all the information. Apuke et al. [25] argued that factors such as altruism, quality of information, and netizens’ thirst for information determine whether false information will be spread on social media. Chew et al. [26] argued that relevant government departments can utilize online social media platforms to disseminate truthful information related to major emergencies, thereby reducing public panic. Yu et al. [27] argued that when there is a major emergency, spreading false information related to the event will increase public panic. Zhang et al. [28] argued that in major emergencies, the identity and social influence of opinion leaders have a positive effect on the efficiency of crisis information dissemination. Guan et al. [29] argued that information released by opinion leaders with a certain social status is more likely to be adopted by netizens, and in most cases, the gender factor does not affect netizens’ decision-making behavior. Alvarez-Galvez [30] argues that even if a message is not adopted by the majority of netizens, they will choose to adopt the message when a central opinion leader supports the message. Parsegov et al. [31] argue that netizens are able to discuss topics of interest in social networks and form clusters of different types of networks.
In past research on different actors after major emergencies occurred, few scholars have studied decision-making behavior in the process of uncertain information dissemination. Based on previous research, this paper combines stochastic analysis theory with evolutionary game models to analyze the decision-making behavior of opinion leaders and netizens in uncertain information dissemination after major emergencies occur. Considering that random factors from internal or external environments can affect the decision-making behavior of both parties, we construct a stochastic evolutionary game model between 2 research objects, opinion leaders and netizens, by introducing Gaussian white noise. This study provides theoretical basis and decision-making reference for exploring the decision-making behavior of opinion leaders and netizens in uncertain information dissemination under the background of major emergencies in the future.
The workflow comprises four key steps: 1) Defining game subjects and their decision-making behaviors; 2) Constructing the model; 3) Computing equilibrium solutions; 4) Analyzing evolutionary stability strategies. Organizational diagram of the current study as shown in Figure 1.
In the era of new media, the public can use social platforms to obtain information triggered by major emergencies worldwide, but due to the diverse forms, large quantities and rich content of network information, it is impossible for the public to grasp all the information. Therefore, the public can watch the audio and video of video bloggers, live broadcasts of anchors, and information organized by self-media to obtain rapid access to relevant information. This paper defines video bloggers, anchors, self-media outlets and other people who have a certain degree of discourse power and are able to influence and shape the opinions of others through their own speech or behavior as opinion leaders. The members of the public who can use online social media platforms to obtain information are defined as netizens. Based on this, this paper defines opinion leaders and netizens as the main actors in the process of disseminating uncertain information after major emergencies. Both of them are limited rational participants with learning ability; in the case of incomplete information, they cannot judge whether the choices they make can maximize the benefits the first time, but due to their learning ability, they can make choices toward the strategy of maximizing the benefits in the process of learning continuously.
After major emergencies occur, opinion leaders need to integrate and sort out the relevant information related to major emergencies and propose their own views for netizens to adopt to gain attention. Since opinion leaders have the right to speak, which leads to their remarks being able to guide netizens’ thoughts, the gaming strategy of opinion leaders can include positive guidance (by investigating the relevant events and releasing the real information about the events) or negative guidance (by rumor mongering, releasing unconfirmed and false information, stirring up the netizens’ emotions, and other means to make profits). The netizens’ game strategies include adopting or not adopting the opinions published by opinion leaders. Upon combinations of the above game strategies, the resultant scenarios encompass: (positive guidance, adoption), (negative guidance, adoption), (positive guidance, nonadoption), and (negative guidance, nonadoption).
This paper is based on the literature [32]. The following assumptions are made for this evolutionary game model:
(1) The probability that an opinion leader chooses posotive guidance or negative one is x and 1-x; the probability that a netizen chooses to adopt or not is y and 1-year, respectively.
(2) Neitziens’ psychological identification with opinion leaders is λ(0 < λ < 1). In this paper, it is argued that netizens’ psychological identity toward opinion leaders is a kind of trust relationship formed after netizens pay attention to the remarks of opinion leaders for a long time; when the identity degree is zero, it means that netizens have no trust in opinion leaders; and when the identity degree is one, it means that netizens have complete trust in opinion leaders.
(3) When the opinion leader provides positive guidance, they will investigate and collect evidence on a series of uncertain information triggered by major emergencies, the cost of investigation will be C1, and the public speech from the opinion leader will be M1; if the netizens adopt the speech from the opinion leader’s positive guidance, then the opinion leader will receive the benefit of I1. When the opinion leader leads negatively, since he or she publishes false information and does not verify the uncertain information, he or she does not pay investigation costs, and the published speech is M2. However, since negative guidance is more capable of stirring up netizens’ emotions, leading to netizens’ panic or increasing conflict between netizens and the government, there is a probability of π for the opinion leader to be punished by the government, and the punishment is L2. If the netizen adopts the speech published by the opinion leader under negative guidance, the opinion leader receives the benefit of I2. As long as negatively guided speech is not adopted, the opinion leader loses L1 due to a decrease in his or her popularity.
(4) When netizens agree with the opinion leader’s speech, they will pay the cost of time and energy C3 and the cost of judging the relevant speech (1-λ) C4. Meanwhile, they will also have a certain sense of satisfaction and participation, I3 and I4, respectively, and I4 > I3 because the speech in negative steering was more appealing. If netizens adopt positively guided speech, they will have a positive gain λM1; if netizens adopt negatively guided speech, they will have a negative gain λM2 because the speech is not true but false and harmful information (recorded as
The above parameters C1, C2, C3, C4, I1, I2, I3, I4, L1, L2, M1, M2, π, λ are all greater than 0, where
Based on the assumptions above, we can examine that when netizens adopt the positive guidance of opinion leaders, the total profit of the opinion leader is composed of their own investigation cost C1 and the profit obtained from netizens’ adoption I1, the gain of opinion leaders is
Combining the benefit matrix in Table 1, let the expected benefit of opinion leaders choosing positive guidance be U11, the expected benefit of opinion leaders choosing negative guidance be U12, and the average benefit of opinion leaders be
Based on Eqs 1–3, it can be obtained that, the replication dynamic equation for opinion leaders’ choice of positive guidance strategy is:
Similarly, let the expected benefit of the netizen’s choice to adopt be U21, the expected benefit of the netizen’s choice not to adopt be U22, and the average benefit of the netizen be
Based on Eqs 5–7, it can be obtained that, the replication dynamic equation for netizens’ choice of adoption strategy is:
Due to limitations, the above Eq. 4 considers only the expected and overall benefits of opinion leaders adopting positive guidance strategies and does not take into account the difference between the benefits of opinion leaders adopting positive guidance and the benefits of adopting negative guidance; therefore, the above Eq. 4 adjusted to:
The above Eq. 8 considers only the expected and overall benefits of adopting an adoption strategy by netizens and does not take into account the difference between the benefits of adopting and the benefits of not adopting by netizens; therefore, the above Eq. 8 adjusted to:
Considering that in the real world, opinion leaders and netizens are influenced by uncertain factors caused by their own or external environment, making their decision-making behavior highly uncertain. Therefore, to better understand the influence of the random perturbation term on the decision-making behavior of the game subjects, this section combines stochastic analysis theory and introduces Gaussian white noise into the replication dynamic equation of the evolutionary game between opinion leaders and netizens Eqs 9, 10 in the game, i.e.,
where
The above equation is a one-dimensional Itô stochastic differential equation containing a Gaussian random disturbance term, which represents the replicated dynamic equations for opinion leaders and netizens subjected to random perturbations.
Compared with the evolutionary game model between opinion leaders and netizens constructed in literature [32], the stochastic evolutionary game model between opinion leaders and netizens constructed in this paper not only takes into account the impact of known factors on both parties when making behavioral choices but also considers the influence of uncertainties caused by themselves or the external environment. After introducing Gaussian white noise, the stochastic evolutionary game model differs from the ordinary evolutionary game model in the calculation of equilibrium solutions. The ordinary evolutionary game is mathematically expressed based on ordinary differential equations, while the stochastic evolutionary game model is mathematically expressed based on stochastic differential equations.
Analyze the existence and stability of equilibrium solutions for stochastic evolutionary game models separately. Firstly, evaluate the existence of equilibrium solutions. Lemma 1 below is a sufficient condition for the solutions of stochastic differential equations to satisfy existence and uniqueness.
Lemma 1. There is a stochastic process
If
(1) The measurability condition, i.e.,
(2) The Lipschitz condition, i.e., the existence of a constant H such that
(3) Linear growth bounded condition: There exists a positive constant P such that
(4) Initial conditions:
Then, there exists a unique process
Proposition 1. A stochastic differential equation has a unique solution under
Proof:
(1) Measurability condition
Rewrite the equations as
Clearly,
(2) Lipschitz condition
Due to
where
(3) Linear growth bounded condition
For any
where
(4) Initial conditions
The initial condition (4) clearly holds.
Thus, Proposition 1 is proved.
From Proposition 1, we can see that there is an equilibrium solution in the stochastic evolution game model of opinion leaders and netizens; i.e., under the premise of no Gaussian white noise interference, opinion leaders and netizens can reach a consensus with each other at the beginning and choose a strategy that meets their own interests. However, in reality, with the passage of time and changes in the internal or external environment, opinion leaders and netizens may be affected by random interference, which changes their decision-making behavior. For example, after a period of time after a major emergency, as relevant investigations are conducted, an increasing number of details are reported, and netizens are able to obtain more information, which makes netizens quickly choose whether to adopt or not to adopt the comments released by opinion leaders. This random factor plays an important role in the original decision-making behavior, and the random factor plays a crucial role in the selection of the final stabilization strategies of opinion leaders and netizens. Therefore, fully considering random factors is more conducive to understanding the decision-making behaviors of opinion leaders and netizens in real society.
Next, the stability of the equilibrium solution is analyzed based on Lemma 2 below:
Lemma 2. Let the stochastic differential equation
There exist continuous differentiable functions
(1) If there exists a positive constant γ such that
(2) If there exists a positive constant γ such that
Among others,
Proposition 2. For the Eq. 11, when
(1) The exponential stability condition for the zero solution moment of the stochastic evolution equation satisfying the opinion leader is DL1.
When
(2) The zero-solution moment-exponential instability condition for a stochastic evolutionary equation satisfying the opinion leader is DL2.
When
Proof: For Eq. 11, when
(1) When the zero-solution moment exponent is stabilized, the equation is required to satisfy
(2) When the zero-solution moment exponent is unstable, the equation is required to satisfy
Proposition 2 suggests that the stabilizing strategy of opinion leaders will be influenced by their own factors as well as by random factors. When condition DL1 is satisfied, opinion leaders will eventually choose the strategy of negative guidance; i.e., over time, no matter what the initial state is, opinion leaders will eventually reach a stable state under the strategy of negative guidance after continuously adjusting their decision-making behavior. When condition DL2 is met, the opinion leader will eventually choose the strategy of positive guidance; that is, over time, regardless of the initial state, the opinion leader will eventually reach a stable state under the strategy of positive guidance after constantly adjusting his or her decision-making behavior.
From condition DL1 and condition DL2 of Proposition 2, it is clear that opinion leaders are more inclined to choose a strategy that is in their own interest. That is, opinion leaders adopt the strategy of negative steering when the expected benefit of choosing negative steering is greater than the expected benefit of choosing positive steering; conversely, they adopt the strategy of positive steering. This finding is consistent with the actual situation because the decision-making behavior of opinion leaders is influenced by factors such as penalties from regulatory agencies and the traffic generated by the attention of netizens, and which strategy is adopted is determined by the expected benefit of that strategy. However, random factors from internal or external sources can also have an impact on the final decision-making behavior of opinion leaders. For example, to smear the public image of China, hostile forces force opinion leaders to make negatively guided choices by means of coercion and enticement when major emergencies occur. In addition, to help the government reduce the impact of major emergencies as soon as possible, opinion leaders always choose to guide them positively, regardless of their own interests. All of these random factors may affect the decision-making behavior of opinion leaders, causing the final stabilization strategy to fluctuate or change.
Proposition 3. For Eq. 12, when
(1) The exponential stability condition for the zero-solution moment of the stochastic evolutionary equation that satisfies the netizen is
DW1 when
DW2 when
(2) The zero-solution moment-exponential instability condition for the stochastic evolutionary equations that satisfy the netizens is
DW3 when
DW4 when
Proof: For Eq. 12, when
(1) When the zero-solution moment exponent is stabilized, the equation is required to satisfy
In the case when
In the case when
Based on this, one can obtain Eq. 12 The exponential stability condition for the zero solution moment is:
When
(2) When Eq. 12 The zero solution moment exponent is unstable, the equation needs to satisfy
In the case when
In the case when
Based on this, one can obtain Eq. 12 The exponential instability condition for the zero solution moment is:
When
Proposition 3 suggests that netizens’ stabilizing strategies are influenced by their own factors as well as by random factors. When
From the condition and the condition of Proposition 3, it is clear that netizens are more inclined to choose a strategy that is in their own interest. That is, when the expected benefit of not adopting is greater than the expected benefit of adopting, netizens will choose to not adopt; in contrast, they will adopt the strategy of adopting. Because netizens’ decision-making behavior is influenced by the degree to which they pay attention to major emergencies and by their psychological recognition of opinion leaders, which strategy to adopt is determined by the expected benefit of the strategy. Moreover, random factors from internal or external sources may also have an impact on netizens’ final decision-making behavior. For example, at the early stage of major emergencies, the investigation of major emergencies by relevant departments has just begun, and specific real information has not yet been released in time; in these cases, netizens can only pay attention to major emergencies through the remarks released by opinion leaders. In this case, netizens can only pay attention to the comments of opinion leaders. Or for other reasons, the attention of netizens may be drawn to other events and they may give up paying attention to major emergencies. All of these random factors may affect the decision-making behavior of netizens, which may lead to fluctuations or shifts in the final stabilization strategy.
Based on Proposition 3 in Proposition 4, the final evolutionary stability strategies of the random evolutionary game between opinion leaders and netizens can be described by the following four scenarios:
(1) When
(2) When
(3) When
(4) When
Among the above four scenarios, the strategy most conducive to the society stablity is (positive guidance, adoption). In this scenario, opinion leaders and netizens will cooperate together. Opinion leaders publish positive guidance statements, and netizens choose to believe the truthful information released by opinion leaders. Both parties work together to clarify uncertain information, which can greatly reduce the adverse effects caused by the dissemination of uncertain information. The strategy least conducive to the stable operation of society is (negative guidance, adoption). In this situation, opinion leaders, for some purpose, publish negative guidance statements on social platforms, inciting panic among netizens who believe in negative guidance statements, which will directly exacerbate the adverse effects caused by the dissemination of uncertain information.
Since Eqs 11, 12 is a nonlinear Itô stochastic differential equation, it is impossible to find its analytical solution directly, so it needs to be solved numerically; in the next part of this paper, we use the stochastic Taylor expansion and Itô’s formula to solve Eqs 11, 12 In the next part of this paper, the stochastic Taylor expansion and Itô’s formula are applied to numerically solve Eq.
For the following Itô stochastic differential equation:
where
Let the step size
where R is the remainder term of the expansion,
Based on the Formula 20, the random Taylor expansions for Eqs 11, 12 are:
where R1 and R2 are the remainder of the expansion of Eqs 21, 22.
In real-world applications, the model can be simulated numerically using Euler’s method or Milstein’s method, which involves partial term interception of the stochastic Taylor expansion and subsequent numerical solution. In this paper, the numerical solution is based on Milstein’s method, taking Eq. 20 For example, the intercept format of the Milstein method is shown in Eq. 23:
This paper investigates the decision-making behavior of opinion leaders and netizens on online social media platforms in the process of uncertain information dissemination after a major emergency. A two-party stochastic evolutionary game model of opinion leaders and netizens is constructed considering random interference factors. The evolutionary stability strategy of the model and the stochastic evolution process are solved and analyzed, and the effects of different variables on the decision-making behavior of the two parties are discussed.
To more accurately reflect the influence of the interference strength of random factors, the strength of the regulatory body on the negative guidance of opinion leaders and the psychological identity of opinion leaders toward the decision-making behavioral choices and stochastic evolutionary process of opinion leaders and netizens should be considered. In the following, MATLAB 2017b software is used to numerically simulate the behavioral evolution process of the above two game subjects and verify the theoretical analysis above.
To better analyze the influence of random interference factors on opinion leaders and netizens in making decision-making behavioral choices, i.e., to analyze the evolutionary stabilization process of the game system after the introduction of Gaussian white noise. The other parameters in the model are randomly assigned, and the evolutionary processes in the absence of random interference factors (
(1) Analysis of the stochastic evolutionary process of opinion leaders’ and netizens’ choices (negative guidance, nonadoption).
The relevant parameters of the model are assigned as follows: I1 = 10, I2 = 3, I3 = 2, I4 = 4, L1 = 8, L2 = 10, C1 = 9, C2 = 6, C3 = 10, C4 = 10, M1 = 3, M2 = 3, λ = 0.35, and π = 0.2. The initial values of the opinion leaders’ choice of the positive steering strategy and the netizens’ choice of the adoption strategy are set to x (0) = 0.5 and y (0) = 0.5, respectively, and the simulation step size is h = 0.01. The random evolutionary trend of opinion leaders and netizens can be obtained as shown in Figure 2 below. 0.01. Under the premise of ensuring that the values of the remaining parameters remain unchanged, the stochastic evolution trend graphs of opinion leaders and netizens at
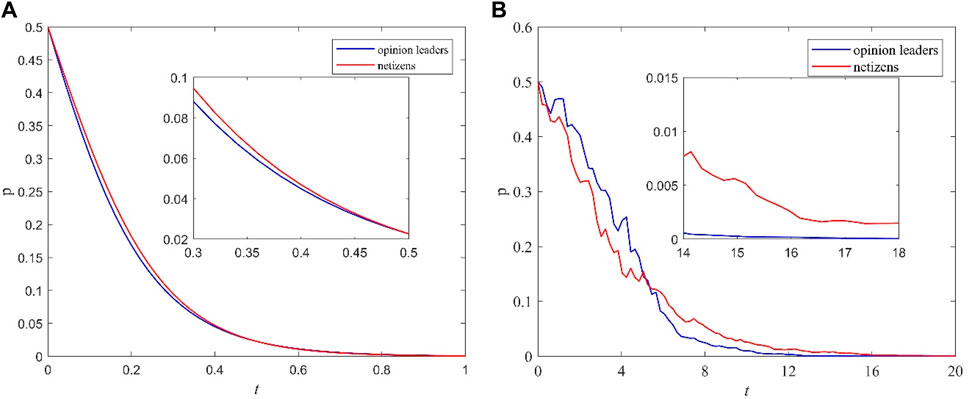
Figure 2. Stochastic evolutionary trend of opinion leaders and netizens’ choices (negative guidance, nonadoption). (A)
The blue line in Figure 2 represents the probability curve of opinion leaders choosing the positive guidance strategy, and the red line represents the probability curve of netizens choosing the adoption strategy. Figure 2 shows that after a period of evolution, opinion leaders and netizens gradually converge to 0. That is, no matter what the initial values of opinion leaders choosing the positive guidance strategy and netizens choosing the adoption strategy are, opinion leaders and netizens will ultimately choose the strategy of negative guidance or nonadoption over time, and opinion leaders tend to converge to 0 at a slightly faster rate than netizens. This is because, after major emergencies, opinion leaders can obtain more information from multiple sources and are able to adjust more quickly after gaming behavior has begun. This is because after a major emergency occurs, opinion leaders can obtain more information from multiple sources and make faster adjustments after the game behavior begins. When the benefits of negative guidance strategies are discovered due to positive guidance, opinion leaders can quickly choose negative guidance strategies.
By comparing Figures 2A, B, it can be found that at
(2) Analysis of the stochastic evolutionary process of opinion leaders’ and netizens’ choices (positive guidance, adoption).
The relevant parameters of the model are assigned as follows: I1 = 10, I2 = 3, I3 = 2, I4 = 4, L1 = 8, L2 = 20, C1 = 6, C2 = 6, C3 = 6, C4 = 4, M1 = 3, M2 = 3, λ = 0.5, and π = 0.5. The initial values of the opinion leaders’ choice of the positive steering strategy and the netizens’ choice of the adoption strategy are set as x (0) = 0.5 and y (0) = 0.5, and the simulation step size is h = 0.01. The random evolutionary trends of opinion leaders and netizens can be obtained as shown in Figure 3. 0.01. Under the premise of ensuring that the values of the remaining parameters remain unchanged, the stochastic evolution trend graphs of opinion leaders and netizens at

Figure 3. Stochastic evolutionary trend of opinion leaders’ and netizens’ choices (positive guidance, adoption). (A)
The blue line in Figure 3 represents the probability curve of opinion leaders choosing the positive guidance strategy, and the red line represents the probability curve of netizens choosing the adoption strategy. Figure 3 shows that after a period of evolution, opinion leaders and netizens gradually converge to 1. That is, no matter what the initial values are for opinion leaders to choose the positive guidance strategy and for netizens to choose the adoption strategy, opinion leaders and netizens will ultimately choose the strategy of positive guidance adoption over time, and the speed at which opinion leaders converge to 1 is slightly faster than that of netizens.
By comparing Figures 3A, B, it can be observed that the speed at which opinion leaders and netizens evolve to a stable strategy is relatively slow. This is because both are subject to interference from internal or external random factors during the decision-making process, resulting in oscillations during the evolution to a stable state. Therefore, in a nonidealized situation, opinion leaders and netizens will be partially limited by random factors in their decision-making, and they will slow their decision-making speed when thinking about the pros and cons of random factors.
To analyze the influence of netizens’ psychological identity toward opinion leaders on the stochastic evolution process, other parameters in the model are randomly assigned, and the evolution process is simulated. The influence of changes in psychological identity on the decision-making behavior of opinion leaders and netizens should be observed.
The relevant parameters of the model were assigned as I1 = 10, I2 = 3, I3 = 2, I4 = 4, L1 = 8, L2 = 20, C1 = 6, C2 = 6, C3 = 6, C4 = 4, M1 = 3, M2 = 3, π = 0.5, and σ = 1. Setting the initial value of the opinion leader’s choice of the positive steering strategy, the netizen’s choice of the adoption strategy is set to x (0) = 0.5, y (0) = 0.5, and the simulation step size h = 0.01. Under the premise of ensuring that the values of the remaining parameters remain unchanged, we change the value of λ and set λ = 0.1, 0.5, and 0.8. We can construct a stochastic evolution trend graph of opinion leaders and netizens, as shown in Figure 4 below.
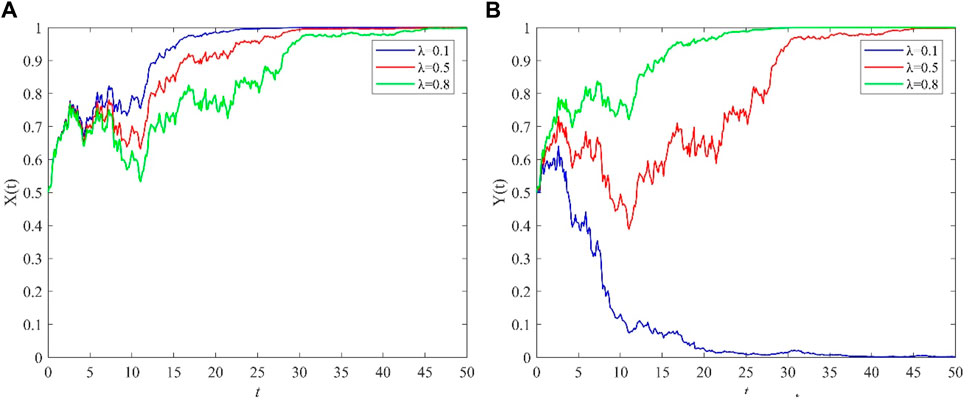
Figure 4. The effect of psychological identity λ on the evolutionary strategies of opinion leaders and netizens. (A) opinion leaders (B) netizens.
The blue line in Figure 4A represents the probability curve of opinion leaders choosing the positive guidance strategy when the psychological identity λ = 0.1, the red line represents the probability curve when the psychological identity λ = 0.5, and the green line represents the probability curve when the psychological identity λ = 0.8. The three lines in Figure 4B are the probability curves of netizens choosing the adoption strategy. Figure 4A shows that the netizens’ psychological identity λ of the opinion leader does not affect the final strategy choice of the opinion leader; however, the smaller the value of psychological identity λ is, the faster the opinion leader equals 1. This is because, in reality, the less value a netizen places on the opinions of the opinion leader, the less likely it is that the opinion leader’s published speech will be adopted by the netizens. To increase their influence among netizens, opinion leaders need to make strategic choices as early as possible to attract netizens’ attention. The more content an opinion leader publishes, the more netizens will pay attention to it, and the more likely it is to increase netizens’ psychological identification with it.
Figure 4B shows that as netizens’ recognition of opinion leaders gradually increases, they gradually convert from converging to 0 to converging to 1; that is, netizens convert from not adopting the remarks released by opinion leaders to adopting the remarks released by opinion leaders. This is because the more netizens trust opinion leaders, the easier it is for them to believe their statements. However, the psychological recognition of opinion leaders by netizens is a double-edged sword. Due to their limited understanding, it is difficult to accurately distinguish whether the statements made by opinion leaders are true. This leads to the fact that when opinion leaders provide positive guidance, they can largely maintain the stable operation of society, but when they provide negative guidance, it is easy to exacerbate the spread of panic and greatly increase the difficulty of government work.
To analyze the influence of the government’s punishment strength on those who propagate and spread negative information on the stochastic evolution process, the other parameters in the model are randomly assigned values, and the evolution process is simulated. The influence of changes in punishment strength on the decision-making behavior of opinion leaders and netizens should be observed.
Since both π and L2 in the model can affect the punishment strength, for the convenience of analysis, only the government’s punishment probability π for those who propagate and spread negative information is selected for analysis. The relevant parameters of the model are assigned as follows: I1 = 10, I2 = 3, I3 = 2, I4 = 4, L1 = 8, L2 = 20, C1 = 6, C2 = 6, C3 = 6, C4 = 4, M1 = 3, M2 = 3, λ = 0.35, and σ = 1. The initial values of the opinion leaders’ choice of the positive guidance strategy and the netizens’ choice of the adoption strategy are set as x (0) = 0.5 and y (0) = 0.5, respectively, and the simulation step size is set as h = 0.01. Under the premise of ensuring that the values of the remaining parameters remain unchanged, changing the value of π and setting π = 0.2, 0.5, and 0.8, we can obtain the stochastic evolution trend graph of opinion leaders and netizens, which is shown in Figure 5 below.
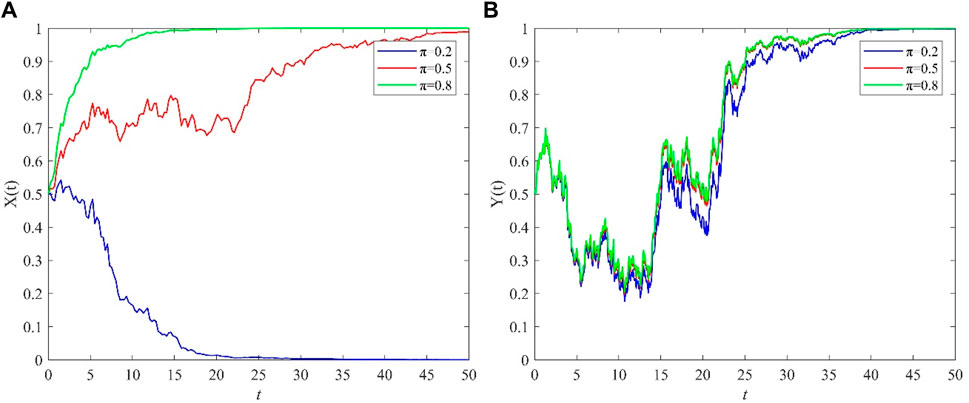
Figure 5. Impact of punishment probability π on the evolutionary strategies of opinion leaders and netizens. (A) opinion leaders (B) netizens.
The blue line in Figure 5A represents the probability curve of opinion leaders choosing the positive guidance strategy when the penalty probability is π = 0.2, the red line represents the probability curve when the penalty probability is π = 0.5, and the green line represents the probability curve when the penalty probability is π = 0.8. The three lines in Figure 5B are the probability curves of netizens choosing the adoption strategy. From Figure 5A, it can be seen that when the government’s punishment for propagandizing and spreading negative information gradually increases, the opinion leader gradually changes from 0 to 1, i.e., the opinion leader converts from negative guidance to positive guidance. This is because when the government’s punishment gradually exceeds the range that opinion leaders can bear, to avoid being punished, such as through banning, blocking or administrative punishment, opinion leaders will switch from negative guidance to positive guidance. Therefore, when there are major emergencies, the government should increase punishment for those who publicize and disseminate negative information to encourage opinion leaders to choose a positive guidance strategy.
Figure 5B shows that the government’s punishment strength for those who publicize and spread negative information does not affect netizens’ final strategy choice; however, the stronger the punishment is, the faster the netizens tend to 1. This is because, in netizens’ thinking, the more the government punishes opinion leaders for spreading negative statements, the more correct the statements spread by the possible opinion leaders will be; therefore, the netizens will adopt the strategy more quickly.
This study has certain limitations: 1) this paper assumes that the ability of opinion leaders to disseminate statements is the same and does not distinguish the ability of opinion leaders to disseminate statements, but in reality, the statements released by different opinion leaders are all different; 2) the vague relationship between opinion leaders and netizens has not been clearly distinguished; In the real world, opinion leaders can be natural persons or institutional accounts; 3)This paper uses MATLAB for numerical simulation of the model without combining real-world data.
In future work, we will conduct separate research on opinion leaders with different dissemination capabilities based on different network structures [33, 34] by combining complex networks with stochastic evolutionary game models. Furthermore, we will refine the differences between opinion leaders and netizens, incorporate more detailed decision-making behaviors, and include more accurate assumptions in the construction of the model. Additionally, we will try to combine real-world data and use real cases to simulate the model.
This paper takes the decision-making behavior of opinion leaders and netizens in the process of uncertain information dissemination on online social media platforms after major emergencies as the research background. In the real world, opinion leaders and netizens are subject to random interference from their own internal factors or external environmental factors in the decision-making process. Based on the traditional evolutionary game model, Gaussian white noise is introduced to construct a stochastic evolutionary game model based on uncertain information dissemination behavior between opinion leaders and netizens. Using the theory of Itô stochastic differential equations and stochastic Taylor expansion, the evolutionary stability strategy and stochastic evolution process of the model are analyzed, and the numerical solution of the equilibrium solution of the model is found. Finally, through numerical simulation software, we analyze the influence of the interference intensity of random factors, the punishment strength of regulatory agencies when opinion leaders spread false or negative information, and the opinions of netizens toward opinion leaders on the stochastic evolution process. The results of this paper can be summarized as follows:
(1) Random disturbances will not change the strategic choices of opinion leaders or netizens during the process of stochastic evolution to a stable state. However, due to the emergence of random interference, opinion leaders and netizens will think about the advantages and disadvantages of random factors in the process of decision-making, which leads to the slowing of their progression to a stable state and the occurrence of oscillations in the process of evolution. After a major emergency occurs, opinion leaders can obtain more information from multiple sources and make faster adjustments after the game behavior begins. The speed at which opinion leaders reach a stable state is faster than the speed at which netizens reach a stable state.
(2) A change in the netizens’ psychological identity λ will not affect the final strategy choice of opinion leaders, but it will affect the speed at which opinion leaders reach a stable state; the smaller the value of λ is, the faster the opinion leaders reach a stable state. A change in psychological identity λ has a greater impact on netizens and even changes their final strategy choice. Under the premise that the other variables remain unchanged, when the value of λ gradually increases, the netizens’ final stable state will be converted from nonadoption to adoption of the speech released by opinion leaders.
(3) Changes in the government’s punishment of those who publicize and disseminate negative information will not affect netizens’ final strategic choices but will affect the speed at which netizens reach a stable state; the greater the punishment is, the more quickly netizens reach a stable state. A change in punishment intensity has a greater impact on opinion leaders and even changes their final strategy choice. Under the premise that other variables remain unchanged, when the punishment intensity gradually increases, the final stable state of opinion leaders will be converted from negative guidance to positive guidance.
Therefore, when major emergencies occur again, government regulators can encourage opinion leaders to make positive decisions by increasing punishment for those who publicize and disseminate negative information, accelerating the investigation of major emergencies and releasing the real situation in a timely manner, and improving the channels for opinion leaders to obtain information. Opinion leaders can attract the attention of netizens by increasing their psychological recognition and improving and enriching the content of the real information they publish to encourage netizens to adopt positive statements.
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
LM: Writing–review and editing, Writing–original draft, Conceptualization. BL: Writing–review and editing, Writing–original draft, Validation, Software, Methodology, Formal Analysis, Conceptualization. JW: Writing–review and editing, Validation, Supervision, Software, Data curation.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research was supported by the Project of Liaoning Provincial Federation Social Science Circles of China (No. L20BGL047).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Smith JM, Price GR. The logic of animal conflict. Nature (1973) 246(5427):15–8. doi:10.1038/246015a0
2. WöLFL B, Te Rietmole H, Salvioli M, Kaznatcheev A, Thuijsman F, Brown JS, et al. The contribution of evolutionary game theory to understanding and treating cancer. Dynamic Games Appl (2022) 12(2):313–42. doi:10.1007/s13235-021-00397-w
3. Li XY, Li QZ, Du YJ, Fan Y, Chen X, Shen F, et al. A novel tripartite evolutionary game model for misinformation propagation in social networks. Security Commun Networks (2022) 2022:1–13. doi:10.1155/2022/1136144
4. Wang H, Liu W, Liu AF, Wang T, Song H, Zhang S. SQCS: a sustainable quality control system for spatial crowdsourcing via three-party evolutionary game: theory and practice. Expert Syst Appl (2024) 238:122132. doi:10.1016/j.eswa.2023.122132
5. Wu ZQ, Yang C, Zheng RJ. An analytical model for enterprise energy behaviors considering carbon trading based on evolutionary game. J Clean Prod (2024) 434:139840. doi:10.1016/j.jclepro.2023.139840
6. Shi QN, Yang SM, Wang N, Zhang SE, Wang Y, Wu B, et al. An evolutionary game-based simulation study of a multi-agent governance system for smart senior care services in China. Bmc Geriatr (2023) 23(1):871. doi:10.1186/s12877-023-04521-w
7. Sun B, Xu ZH, Wei M. Evolutionary game model of civil aviation and high-speed rail interaction strategies based on the passenger ticket and carbon trading prices. J Adv Transportation (2023) 2023:1–16. doi:10.1155/2023/7675900
8. Shi WQ, Hu QD, Zhou YM. Evolutionary game analysis of vehicle procurement in the courier industry from the perspective of green supply chain. Int J Ind Eng Computations (2024) 15(1):223–34. doi:10.5267/j.ijiec.2023.10.002
9. Perc M. Coherence resonance in a spatial prisoner's dilemma game. New J Phsyics (2006) 8(3):22. doi:10.1088/1367-2630/8/2/022
10. Tanimoto J. Promotion of cooperation by payoff noise in a 2x2 game. Physical review E, Statistical, nonlinear. soft matter Phys (2007) 76(4 Pt 1):041130. doi:10.1103/physreve.76.041130
11. Mo D, Chen X, Zhu Z, Liu C, Xie N. A stochastic evolutionary dynamic game model for analyzing the ride-sourcing market with limited platform reputation. Transportmetrica B-Transport Dyn (2023) 11(1). doi:10.1080/21680566.2023.2248399
12. Kang K, Bai L, Zhang J. A tripartite stochastic evolutionary game model of complex technological products in a transnational supply chain. Comput Ind Eng (2023) 186:109690. doi:10.1016/j.cie.2023.109690
13. Xie JD, Guan BW, Yao Y, Li R, Shi Q. Market power risk prevention mechanism of China's electricity spot market based on stochastic evolutionary game dynamics. Front Energ Res (2023) 11. doi:10.3389/fenrg.2023.1270681
14. Du J, Li JJ, Li JX, Li W. Competition-cooperation mechanism of online supply chain finance based on a stochastic evolutionary game. Oper Res (2023) 23(3):55. doi:10.1007/s12351-023-00792-8
15. Scata M, Di Stefano A, La Corte A, Liò P, Catania E, Guardo E, et al. Combining evolutionary game theory and network theory to analyze human cooperation patterns. Chaos Solitons and Fractals (2016) 91:17–24. doi:10.1016/j.chaos.2016.04.018
16. Mo TC, Xie C, Li KL, Ouyang Y, Zeng Z. Transmission effect of extreme risks in China?s financial sectors at major emergencies: empirical study based on the GPD-CAViaR and TVP-SV- VAR approach. Electron Res Archive (2022) 30(12):4657–73. doi:10.3934/era.2022236
17. Cheng A, Chen TH, Jiang GG, Han X. Can major public health emergencies affect changes in international oil prices? Int J Environ Res Public Health (2021) 18(24):12955. doi:10.3390/ijerph182412955
18. Jia FJ, Wang DD, Li LS. The stochastic evolutionary game analysis of public prevention and control strategies in public health emergencies. Kybernetes (2023) 52(6):2205–24. doi:10.1108/k-10-2021-0988
19. Özkaya M, Izgi B. Effects of the quarantine on the individuals' risk of Covid-19 infection: game theoretical approach. Alexandria Eng J (2021) 60(4):4157–65. doi:10.1016/j.aej.2021.02.021
20. Salarpour M, Nagurney A. A multicountry, multicommodity stochastic game theory network model of competition for medical supplies inspired by the Covid-19 pandemic. Int J Prod Econ (2021) 236:108074. doi:10.1016/j.ijpe.2021.108074
21. Wang HC, Ma XY. Research on multiobjective location of urban emergency logistics under major emergencies. Math Probl Eng (2021) 2021:1–12. doi:10.1155/2021/5577797
22. Wei Y. Network public opinion propagation control model of major emergencies based on heat conduction theory. Wireless Commun Mobile Comput (2022) 2022:1–14. doi:10.1155/2022/1476231
23. Chen TG, Yin XH, Yang JJ, Cong G, Li G. Modeling multi-dimensional public opinion process based on complex network dynamics model in the context of derived topics. Axioms (2021) 10(4):270. doi:10.3390/axioms10040270
24. Lu P, Chen DH, Zhang G, Ding J. Online attention dynamics: the triangle framework of theory, big data and simulations. Expert Syst Appl (2023) 233:120900. doi:10.1016/j.eswa.2023.120900
25. Apuke OD, Omar B. Fake news and COVID-19: modelling the predictors of fake news sharing among social media users. Telematics Inform (2021) 56:101475. doi:10.1016/j.tele.2020.101475
26. Chew C, Eysenbach G. Pandemics in the age of twitter: content analysis of tweets during the 2009 H1N1 outbreak. Plos One (2010) 5(11):e14118. doi:10.1371/journal.pone.0014118
27. Yu LA, Li L, Tang L, Dai W, Hanachi C. A multi-agent-based online opinion dissemination model for China's crisis information release policy during hazardous chemical leakage emergencies into rivers. Online Inf Rev (2017) 41(4):537–57. doi:10.1108/oir-04-2015-0126
28. Zhang L, Wang X, Wang J, Yang P, Zhou P, Liao G. A study on predicting crisis information dissemination in epidemic-level public health events. J Saf Sci Resilience (2023) 4(3):253–61. doi:10.1016/j.jnlssr.2023.02.003
29. Guan WQ, Gao HY, Yang MM, Li Y, Ma H, Qian W, et al. Analyzing user behavior of the micro-blogging website Sina Weibo during hot social events. Physica a-Statistical Mech Its Appl (2014) 395:340–51. doi:10.1016/j.physa.2013.09.059
30. Alvarez-Galvez J. Network models of minority opinion spreading: using agent-based modeling to study possible scenarios of social contagion. Soc Sci Comp Rev (2016) 34(5):567–81. doi:10.1177/0894439315605607
31. Parsegov SE, Proskurnikov AV, Tempo R, Friedkin NE. Novel multidimensional models of opinion dynamics in social networks. Ieee Trans Automatic Control (2017) 62(5):2270–85. doi:10.1109/tac.2016.2613905
32. Li B, Li H, Sun Q, Lv R, Zhao J. Evolutionary game analysis of the dissemination of false information by multiple parties after major emergencies. Complexity (2022) 2022:1–14. doi:10.1155/2022/3527674
33. Li H-J, Feng Y, Xia C, Cao J. Overlapping graph clustering in attributed networks via generalized cluster potential game. ACM Trans Knowledge Discov Data (2023) 18(1):1–26. doi:10.1145/3597436
Keywords: stochastic evolution game, opinion leaders, psychological identification, random disturbance, netizens
Citation: Ma L, Li B and Wang J (2024) Dynamic evolutionary analysis of opinion leaders’ and netizens’ uncertain information dissemination behavior considering random interference. Front. Phys. 12:1387312. doi: 10.3389/fphy.2024.1387312
Received: 17 February 2024; Accepted: 11 June 2024;
Published: 11 July 2024.
Edited by:
Dun Han, Jiangsu University, ChinaCopyright © 2024 Ma, Li and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bowen Li, ZHJfbGJ3QDE2My5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.