Quantum-enhanced photoprotection in neuroprotein architectures emerges from collective light-matter interactions

Background: Superradiance is the phenomenon of many identical quantum systems absorbing and/or emitting photons collectively at a higher rate than any one system can individually. This phenomenon has been studied analytically in idealized distributions of electronic two-level systems (TLSs), each with a ground and excited state, as well as numerically in realistic photosynthetic nanotubes and cytoskeletal architectures.

Methods: Superradiant effects are studied here in idealized toy model systems and realistic biological mega-networks of tryptophan (Trp) molecules, which are strongly fluorescent amino acids found in many proteins. Each Trp molecule acts as a chromophore absorbing in the ultraviolet spectrum and can be treated approximately as a TLS, with its $1L_a$ excited singlet state; thus, organized Trp networks can exhibit superradiance. Such networks are found, for example, in microtubules, actin filaments, and amyloid fibrils. Microtubules and actin filaments are spiral-cylindrical protein polymers that play significant biological roles as primary constituents of the eukaryotic cytoskeleton, while amyloid fibrils have been targeted in a variety of neurodegenerative diseases. We treat these proteinaceous Trp networks as open quantum systems, using a non-Hermitian Hamiltonian to describe interactions of the chromophore network with the electromagnetic field. We numerically diagonalize the Hamiltonian to obtain its complex eigenvalues, where the real part is the energy and the imaginary part is its associated enhancement rate. We also consider multiple realizations of increasing static disorder in either the site energies or the decay rates.

Results: We obtained the energies and enhancement rates for realistic microtubules, actin filament bundles, and amyloid fibrils of differing lengths, and we use these values to calculate the quantum yield, which is the ratio of the number of photons emitted to the number of photons absorbed. We find that all three of these structures exhibit highly superradiant states near the low-energy portion of the spectrum, which enhances the magnitude and robustness of the quantum yield to static disorder and thermal noise.

Conclusion: The high quantum yield and stable superradiant states in these biological architectures may play a photoprotective role in vivo, downconverting energetic ultraviolet photons—absorbed from those emitted by reactive free radical species—to longer, safer wavelengths and thereby mitigating biochemical stress and photophysical damage. Contrary to conventional assumptions that quantum effects cannot survive in large biosystems at high temperatures, our results suggest that macropolymeric collectives of TLSs in microtubules, actin filaments, and amyloid fibrils exhibit increasingly observable and robust effects with increasing length, up to the micron scale, due to quantum coherent interactions in the single-photon limit. Superradiant enhancement and high quantum yield exhibited in neuroprotein polymers could thus play a crucial role in information processing in the brain, the development of neurodegenerative diseases such as Alzheimer’s and related dementias, and a wide array of other pathologies characterized by anomalous protein aggregates.

1 Introduction

Superradiance is a quantum coherent phenomenon first explored in detail by Robert Dicke [1] in 1954. Superradiance arises from the interaction of a collective of quantum systems with the external electromagnetic field. Thus, the theoretical formalism that describes superradiance is given frequently in the language of open quantum systems. In collectives of quantum systems with discrete energy levels, collective superradiant states are characterized by the collective decay rate $\mathrm{\Gamma }$ of the state being much larger than the single-system decay rate $\gamma$. An eigenstate with a larger decay is more short-lived than an eigenstate with a small decay rate. In other words, an absorbed photon in an eigenstate with a larger decay rate will be very quickly re-emitted into the environment. The reason that the decay rate can larger for a collective of quantum systems than one system is that in a collective, the excitation is delocalized across the collective, rather than being incoherently concentrated on a single system. In this work, we consider the weak-excitation limit (more specifically, the single-photon limit), in which only a single excitation is shared coherently across the collective.

Superradiant effects in the ultraviolet region of the electromagnetic spectrum have been studied for biosystems [2–4] and emerge largely due to collective light-matter interactions involving tryptophan (Trp), which is a strongly fluorescent amino acid found in many proteins. It has many notable photophysical properties, such as its strong ultraviolet absorption, significant absorption-emission Stokes shift, and large transition dipole moment. Trp can be modeled as a two-level system (TLS), which has a ground and an excited state. The TLS approximation for Trp can be derived from the pioneering experiments of Patrik Callis’s group [5, 6], where it has been proven to be an extraordinarily good approximation in several theoretical, computational, and experimental studies [2–4, 7]. Its validity is further supported by experimental quantum yield values obtained in [3] that match closely with theoretical predictions based on this approximation. Other amino acids such as tyrosine, phenylalanine, and cysteine also absorb in the ultraviolet, but much more weakly than Trp. The fact that Trp networks absorb in the ultraviolet means that the excitation wavelengths are frequently shorter than the characteristic length scales of the biological scaffolds in which such networks lie $(\lambda \lesssim L)$, a sharp distinction from the longer visible wavelengths that excite smaller photosynthetic light-harvesting complexes. This implies that long-range interactions in the ultraviolet-excited system will play a more prominent role in the light-matter dynamics.

Coherent quantum phenomena arising from organized networks of chromophores in protein scaffolds have been shown to play a role in the efficiency of photosynthetic complexes [8–12] and of other light-harvesting structures (see [2, 13–16] and references therein). More recently, superradiance arising from single photon-excited superposition states has been experimentally confirmed in solvated microtubules at the micron scale and theoretically predicted in centrioles¹ and neuronal axons [3]. In this work, we study the role of superradiance in a wider class of neuroprotein polymers, including cytoskeletal filaments and pathological aggregates, thereby demonstrating the generalizability of our prior experimental results and theoretical predictions for a novel group of chromophore architectures with significant implications for a host of neurodegenerative and other complex diseases.

2 Background

2.1 Cytoskeleton: microtubules and actin filaments

The cytoskeleton is a dynamic structure in eukaryotic cells that provides structural support and acts as a transport mechanism for molecules inside the cell. It has three main components: microtubules, actin filaments, and intermediate filaments. In this work, we specifically focus on microtubules and actin filaments.

Microtubules (pictured in the leftmost structure of Figure 1), spiral-cylindrical structures made of tubulin dimers, play a role in cell communication and mitosis. They are a dynamic part of the cytoskeleton, being able to quickly grow and shrink via polymerization or depolymerization, respectively. Microtubules also make up the internal structure of external appendages such as flagella and cilia, which are important for locomotion and movement. Intra-cell communication is also facilitated by microtubules, as well as the whole cytoskeleton in general. Microtubules are a primary constituent of axons in the brain. They have been shown to play an important role in transport along axonal processes in neurons [24], so disruption of microtubule transport processes in neurons has been linked to several neurodegenerative diseases.

Figure 1

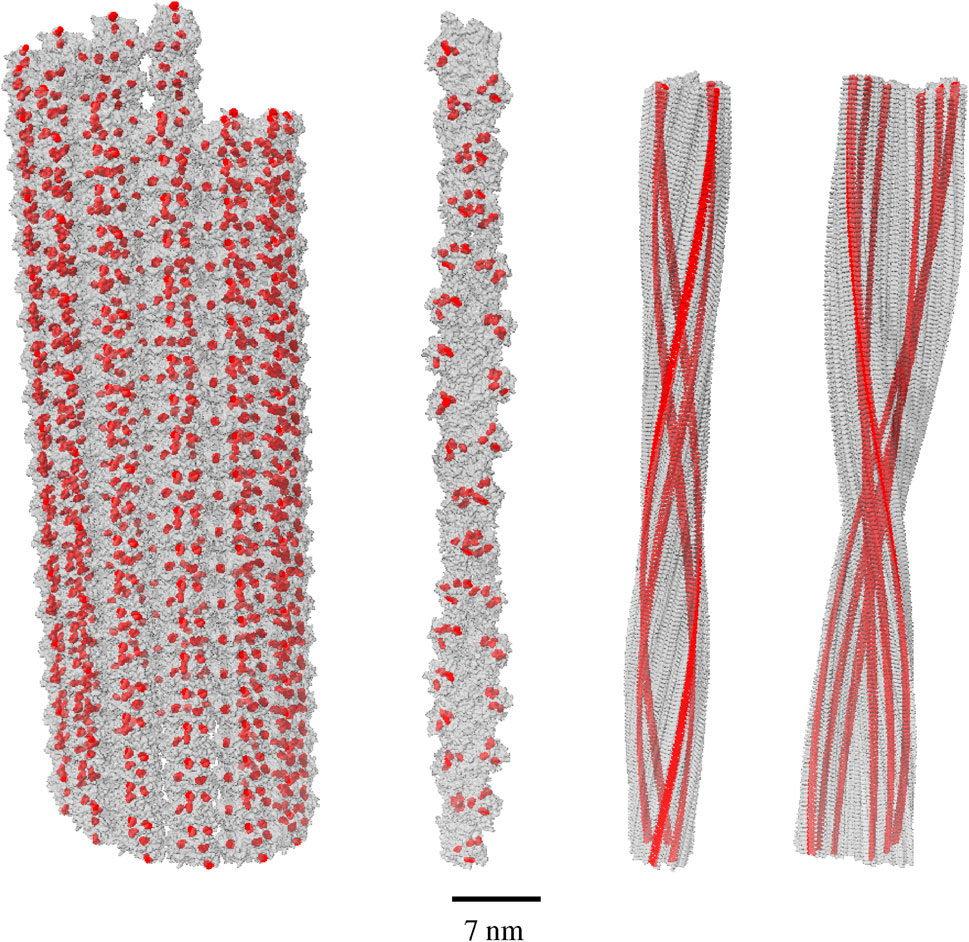
Figure 1. Tryptophan (Trp) network geometries in model biological structures. From left to right, the structures are the following: an 80-nm microtubule (built from tubulin dimer PDB entry 1JFF), a 90-nm actin filament (built from actin subunit PDB entry 6BNO), an 86.4-nm human amyloid fibril (built from amyloid subunit PDB entry 6MST), and an 86.4-nm mouse amyloid fibril (built from amyloid subunit PDB entry 6DSO). The Trp molecules are colored in red and have been enlarged for ease of viewing, within each gray protein lattice. Scale bar is valid for the entire figure.

Actin filaments (pictured in the second from left structure in Figure 1) are strandlike structures that play an important role in the cytoskeleton. Within the context of the cytoskeleton, they are known as microfilaments, reflecting their small diameter generally less than one-third that of microtubules (see Figure 1 for comparison). Actin filaments can bundle together to form hexagonal arrangements [25], which we also analyze in this work. They provide contractile and protrusive forces to stabilize the cytoskeleton and assist with the mobility of the cell. Like microtubules, they assist in transport from outside the cell to the inside. Actin also plays a role in the contractile apparatus of muscle cells, in the form of so-called thin filaments, and helps to maintain the structure of dendritic spines, tiny protrusions from dendrites that form functional contacts with neighboring axons of other neurons in the brain. Dendritic spines play a significant role in plasticity and processing of memory. Therefore, the role of actin has been investigated in synaptic failure in neurodegenerative diseases such as Alzheimer’s [26].

2.2 Pathological aggregates: amyloid fibrils

Amyloid fibrils (pictured in the rightmost and second from right structures of Figure 1) are helical aggregates of amyloid proteins. Amyloids, the building blocks of amyloid fibrils, are a class of self-assembling proteins that fold in a $\beta$-sheet structure. The $\beta$-sheet structure, originally discovered by Herman Branson, Linus Pauling, and collaborators [27], consists of so-called $\beta$-strands, each of which forms a zig-zag pattern, and which are connected laterally to each other via hydrogen bonding to form a pleated sheet. The $\beta$-sheet has a twist (i.e., the zig-zag sheet is not confined to undulations in a single plane). Multiple $\beta$-sheets stacked on top of one another form amyloid fibrils, which are also called $\beta$-helices. An image of a human amyloid subunit (PDB entry 6MST) is pictured in Figure 2A. In Figure 2B, we can see how a human amyloid subunit forms a $\beta$-sheet structure. Typical amyloid fibrils can grow up to several micrometers in length [28–30]. Many different proteins can form amyloids, such as amyloid-beta (A$\beta$) [31], islet amyloid polypeptide (IAPP) [32], lysozyme [33], and insulin [34], and they are all associated with different pathological diseases. A$\beta$ is associated with Alzheimer’s disease, while IAPP, lysozyme, and insulin are associated with type II diabetes, lysozyme amyloidosis, and injection-localized amyloidosis, respectively [35]. There are three main models that were proposed for how amyloids are created from the original protein fold: the refolding, natively disordered, and gain-of-interaction models [36]. The most well-known of these is the refolding model, in which the protein folds from its native state to an amyloid state. Through such a mechanism, amyloids form amyloid fibrils, which can further aggregate and form clumps known as amyloid plaques. Amyloid, amyloid fibrils, and amyloid plaques are a hallmark of neurodegenerative diseases, such as Alzheimer’s and related dementias.

Figure 2

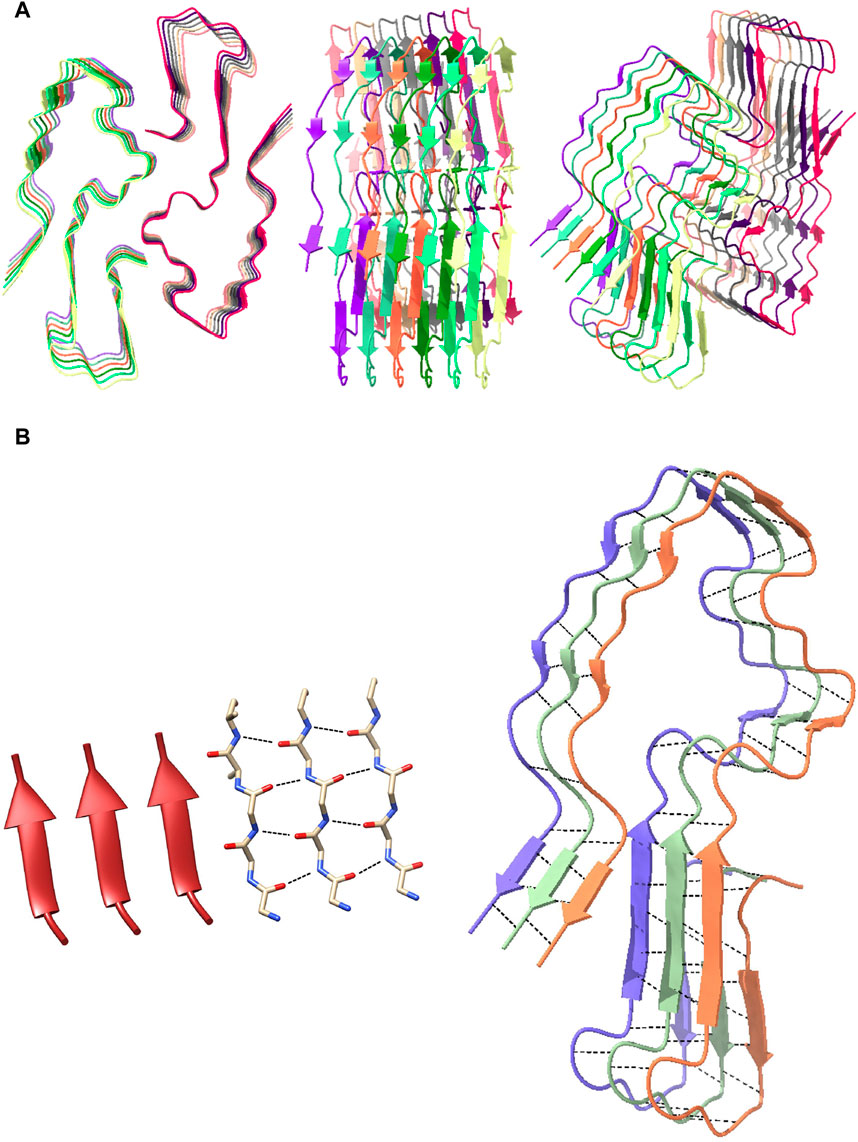
Figure 2. Structure of a single human amyloid subunit and its distinctive parallel β-sheet structure. (A) The structure of a human amyloid subunit (PDB entry 6MST) in cartoon/ribbon from a top-down view (left), side-on view (middle), and angled view (right). (B) Visual of parallel β-sheet structure of the human amyloid subunit. The left image is the structure of a parallel beta sheet, both in ribbon form and molecular form, with black dashed lines indicating hydrogen bonds. The right image is three chains from a human amyloid subunit, again with the hydrogen bonds shown with black dashed lines, showing the similarity with the left image.

Another indicator of Alzheimer’s disease is the formation of neurofibrillary tangles, abnormal aggregates of the tau protein. The tau protein aids in structural support of microtubules in the brain [37], which start to disintegrate in Alzheimer’s disease. The tau proteins undergo hyperphosphorylation and thus dissociate from microtubules, which causes tau to transition from an unfolded state to a folded state capable of aggregating into threadlike structures inside neurons, called tangles [38]. Tangles block transport and inhibit communication between neurons. The population density of tangles is strongly linked to the severity of cognitive decline in Alzheimer’s disease [38, 39].

2.3 Toy models of cylindrical geometries of ultraviolet-excited transition dipoles

First, we present a preliminary analysis of some toy models, in order to gain physical intuition and insight on how transition dipole vector orientations affect the photophysical properties of prototypical biological structures with cylindrical symmetry. We consider two idealized architectures of molecules based on the ones studied in [40]. Each molecule has the photophysical parameters of tryptophan (Trp; excitation wavelength of 280 nm and decay rate of $\sim 2.73\times 10^{-3}{\text{\hspace{0.17em}cm}}^{-1}$), but different transition dipole geometries. The architectures consist of multiple rings of radius $R$ parallel to the $x$-$y$ plane, each stacked on top of one another and separated by a distance $L$ in the $z$-direction. The first dipole vector arrangement is the case in which all vectors point in the $+z$ direction. We call this the parallel dipole (PD) arrangement. The next arrangement is where the dipoles are all pointing in the $x$-$y$ plane tangent to the ring, the so-called tangent dipole (TD) arrangement. See the insets from Figure 3 for a visual representation of the structures. We solve for the eigenstates of the PD and TD arrangements under the effective Hamiltonian Eq. 1.

Figure 3

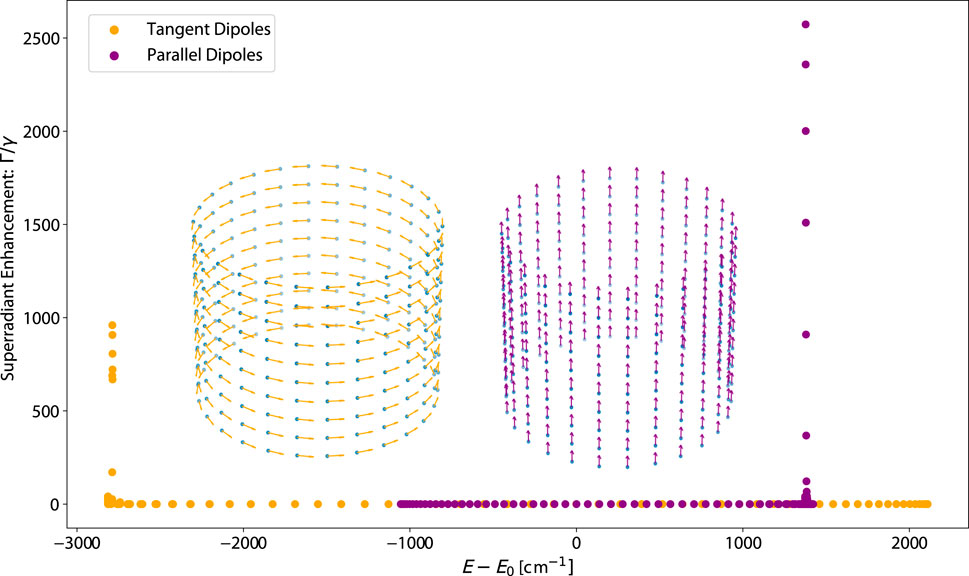
Figure 3. Plot of the eigenvalue spectrum (superradiant enhancement rate vs. energy) of idealized ring structures, with the transition dipole vectors of each cylinder plotted inset in their corresponding colors. Each transition dipole has the photophysical parameters of a tryptophan (Trp) chromophore: an excitation wavelength of 280 nm and a fluorescence decay rate of $\sim 2.73\times 10^{-3}{\text{\hspace{0.17em}cm}}^{-1}$. Each ring has a radius of 11.2 nm, corresponding to the inner radius of a microtubule. We see that, for these idealized structures, the superradiant states arise at only a very few specific energies.

Figure 3 shows the eigenspectrum of the TD and PD arrangements of an idealized ring structure with $R=11.2$ nm (the inner radius of a microtubule) and $L=8$ nm (the spacing between spirals of a microtubule helix). An interesting feature of the spectrum is that both the TD and PD structures have superradiant states at a few specific energies, rather than being distributed across many energies. This feature arises from a specific property of the transition dipole vector arrangements: each vector’s orientation is only slightly deformed from its nearest neighbors (or, in the case of the PD arrangement, not modified at all). This symmetrical geometry of the transition dipole vectors creates a selection for a very small range of energies that contain superradiant states. We also see that, for microtubule parameters, the PD arrangement has a large positive energy shift, while the TD arrangement has a large negative energy shift.

The spectrum having this unique property is significant because it influences the quantum yield (QY), defined as the ratio of the number of photons emitted to the number of photons absorbed, as well as its thermal average (${⟨\text{QY}⟩}_{th}$; see Eqs 13–16 and surrounding text in Section 6 (Methods) for more details on the quantum yield. A spectrum with the majority of superradiant states lying at the lower end of the energy spectrum will have a higher ${⟨\text{QY}⟩}_{th}$, since lower energies are weighted higher in a thermal Gibbs distribution, while a spectrum with superradiant states only near the high-energy portion will have a lower ${⟨\text{QY}⟩}_{th}$.

To show how the Trp packing density affects the superradiance and thermally averaged quantum yield, we present the eigenspectra and quantum yields of our toy models, varying the number of TLSs per ring or the number of rings per unit length. These results are shown in Figure 4, 5, respectively. Figure 4A shows the eigenvalue spectrum of both PD and TD structures, with increasing number of TLSs per ring. If the energy shifts of the most superradiant states are positive, the shifts become more positive, and if the energy shifts of the most superradiant states are negative, they become more negative. In both the PD and TD structures, the maximum superradiance increases with the number of TLSs. However, the QY as displayed in Figure 4B decreases for the PD structure and increases for the TD structure. We can understand this by looking at Figure 4C, which plots the numerator $\left({⟨\mathrm{\Gamma }⟩}_{th}Z={\sum }_{j=0}^{N-1}{\mathrm{\Gamma }}_j\exp (-\beta E_j)\right)$ and denominator $\left(Z={\sum }_{j=0}^{N-1}\exp (-\beta E_j)\right)$ of the expression for the thermally averaged decay rate, which is given by Eq. 15. For the TD model, the numerator and denominator get closer together as the number of TLSs increases, so the QY increases, due to the increasingly negative collective energy shifts in the maximally superradiant states by three orders of magnitude. For the PD model, the numerator increases, but the denominator increases faster, which dampens the QY. This shows that high packing density, while very important for enhanced superradiance, does not always lead to a high QY.

Figure 4

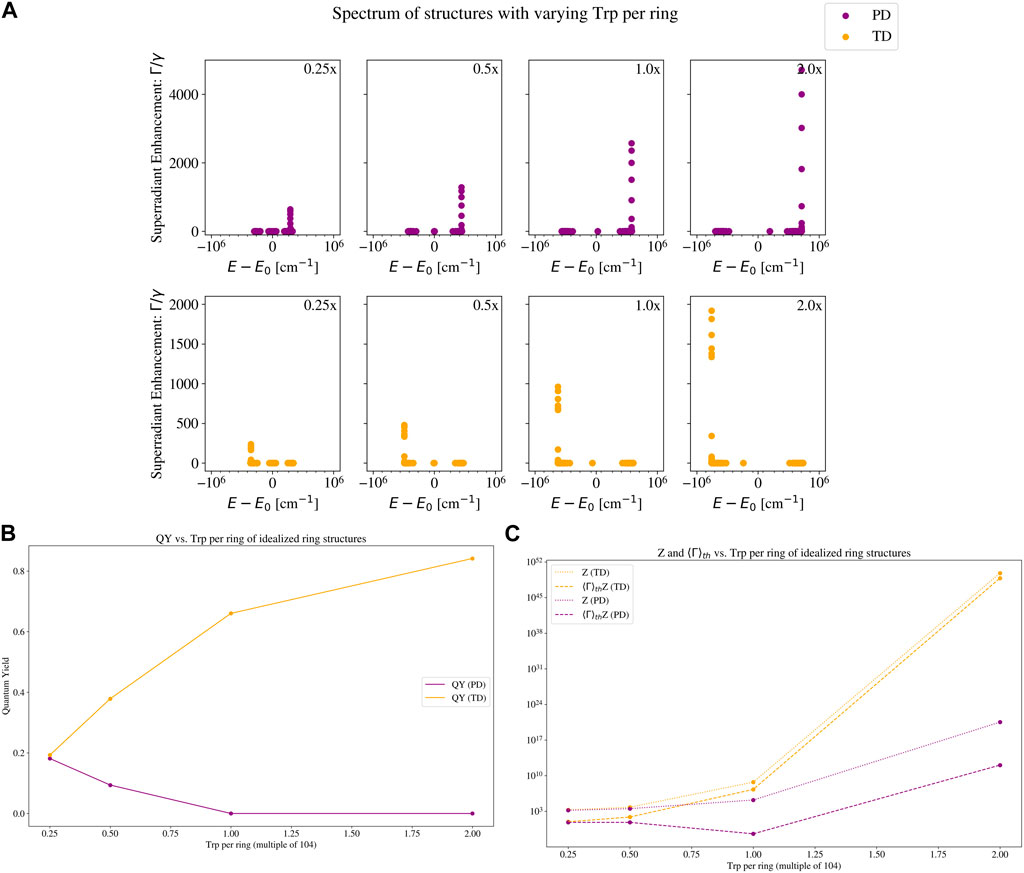
Figure 4. Eigenvalue spectrum and quantum yield plots of a set of idealized ring structures with varying number of two-level systems (TLSs) per ring. The two structures are the ones with a parallel-dipole (PD; purple color) arrangement, and a tangent-dipole (TD; orange color) arrangement. See Section 2.3 for a description of these models, and the insets in Figure 3 for a visual picture of each. Each TLS has the photophysical parameters of a tryptophan (Trp) chromophore: an excitation wavelength of 280 nm and a fluorescence decay rate of $\sim 2.73\times 10^{-3}{\text{\hspace{0.17em}cm}}^{-1}$. (A) Eigenvalue spectrum plots. The number on the top right hand corner of each subplot is the multiple of the number of TLSs per spiral in a microtubule (104), e.g., the leftmost subplots have $0.25\times 104=26$ TLSs per ring. (B) Thermally averaged quantum yield (QY) vs. number of TLSs (dipoles) per ring for the TD and PD structures. The QY is calculated using Eq. 16. The QY for the TD structures increases with dipoles per ring, while it decreases for PD structures. (C) Partition function $Z$ (dotted lines) and ${⟨\mathrm{\Gamma }⟩}_{th}Z$ (dashed lines) vs. number of TLSs (dipoles) per ring. The QY is proportional to ${⟨\mathrm{\Gamma }⟩}_{th}$, which is the ratio of the values on the dashed lines to the values on the dotted lines (see Eq. 15). As the values of ${⟨\mathrm{\Gamma }⟩}_{th}Z$ and $Z$ get closer to each other in the TD model, ${⟨\mathrm{\Gamma }⟩}_{th}$ approaches its maximum value of unity, so the QY increases. In the PD model, the values of ${⟨\mathrm{\Gamma }⟩}_{th}Z$ and $Z$ increasingly separate, so the QY decreases.

Figure 5

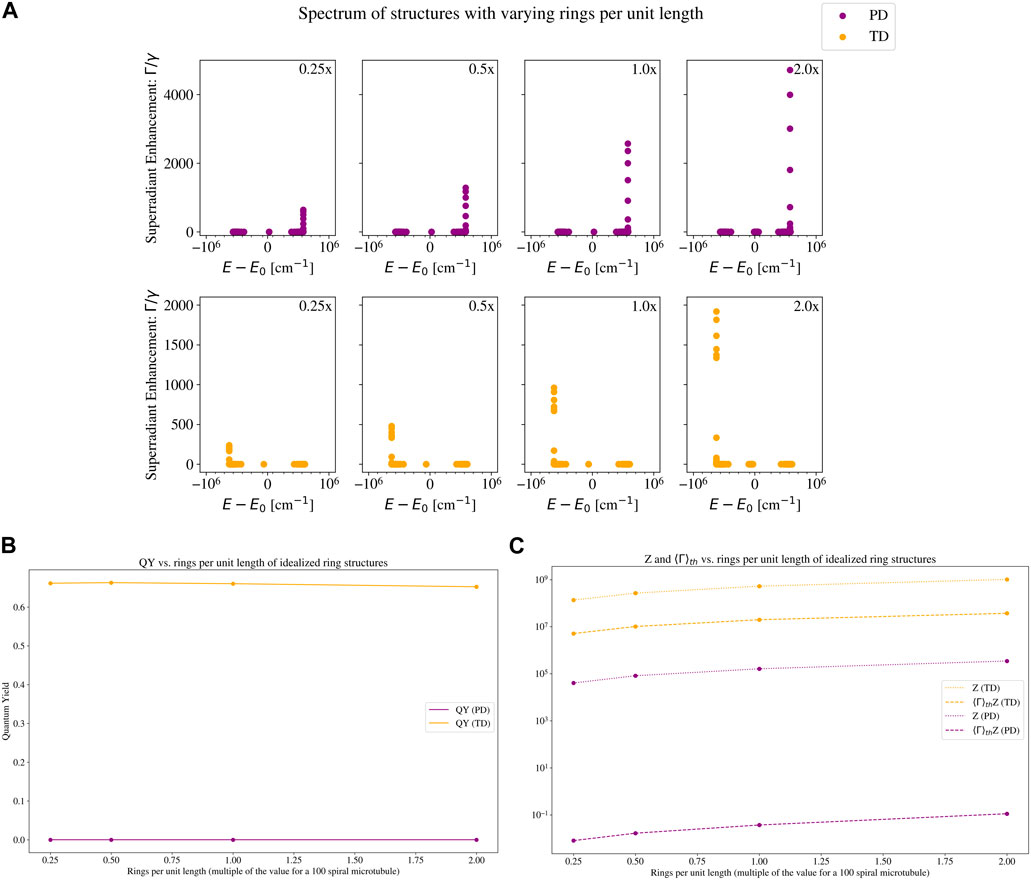
Figure 5. Eigenvalue spectrum and quantum yield plots of a set of idealized ring structures with varying number of rings per unit length. The two structures are the ones with a parallel-dipole (PD; purple color) arrangement, and a tangent-dipole (TD; orange color) arrangement. See Section 2.3 for a description of these models, and the insets in Figure 3 for a visual picture of each. Each TLS has the photophysical parameters of a tryptophan (Trp) chromophore: an excitation wavelength of 280 nm and a fluorescence decay rate of $\sim 2.73\times 10^{-3}{\text{\hspace{0.17em}cm}}^{-1}$. (A) Eigenvalue spectrum plots. The number on the top right hand corner of each subplot is the multiple of the number of spirals per unit length in a microtubule (100 spirals in an 80 nm microtubule). So, the leftmost subplots, for example, have $0.25\ast 100=25$ rings (since the structures all have the same length). (B) Thermally averaged quantum yield (QY) vs. number of rings per unit length for the TD and PD structures. The QY is calculated using Eq. 16. The QY for both structures is almost constant, although the QY for the TD structure decreases slightly. (C) Partition function $Z$ (dotted lines) and ${⟨\mathrm{\Gamma }⟩}_{th}Z$ (dashed lines) vs. number of TLSs (dipoles) per ring. The QY is proportional to ${⟨\mathrm{\Gamma }⟩}_{th}$, which is the ratio of the values on the dashed lines to the values on the dotted lines (see Eq. 15). For both the TD and PD models, $Z$ and ${⟨\mathrm{\Gamma }⟩}_{th}Z$ increase similarly, so ${⟨\mathrm{\Gamma }⟩}_{th}$ and thus the QY remain relatively constant in both cases.

Figure 5 shows the eigenspectra and quantum yields of our toy models, varying the number of rings per unit length. In Figure 5A, we can see that the maximum superradiance increases by an order of magnitude, but the energy shift of the maximally superradiant states remains almost constant. The QY on the other hand, displayed in Figure 5B, is almost unchanged for the PD structure, and slightly decreases for the TD structure. At first glance, this may seem surprising based on the spectra, especially for the TD case. To understand this, compare the leftmost (0.25x the microtubule value) and rightmost (2.0x the microtubule value) subplots of the TD structure in Figure 5A. There are only 7 states in the rightmost subplot that have a higher superradiance than the maximum superradiance in the leftmost subplot. In the thermal average (which is relevant for the QY plotted in Figure 5B), these 7 states are negligible compared to the partition function, which normalizes the thermal average (see Eq. 16). The partition function of the 2.0x TD structure is an order of magnitude larger than the partition function of the 0.25x TD structure. Since the 0.25x TD structure has fewer TLSs (and a smaller partition function), each state has more weight in the thermal average. Thus, the states with the highest superradiance in the 0.25x TD structure enhance the QY more than the states with highest superradiance in the 2.0x TD structure. This is why the QY of the 0.25x TD structure is slightly higher than the QY of the 2.0x TD structure.

We can see how the partition function affects the thermally averaged decay rate (and in turn, the QY) in Figure 5C. The bright superradiant states at the low-energy portion of the spectrum increase the numerator of Eq. 15, but the denominator (partition function) increases more due to the additional number of TLSs, and the net effect is a slight QY decrease. This further demonstrates that neither a high maximum collective decay rate nor a high packing density is sufficient on its own to elicit a high QY.

This analysis is different from the analysis done in [40] in significant ways. Our analysis uses the parameters for the Trp chromophore, which has an absorption peak at $\sim 280$ nm and a decay rate of $\sim 2.73\times 10^{-3}{\text{\hspace{0.17em}cm}}^{-1}$, while in [40], the photosynthetic chromophores absorb in the visible ($\sim 650$ nm) and have a smaller decay rate of $\sim 1.821\times 10^{-4}{\text{\hspace{0.17em}cm}}^{-1}$. The physics changes in a critical way when the excitation wavelength changes from the visible to the ultraviolet: the biosystem sizes considered generally become comparable to or larger than the excitation wavelength, as can be the case for characteristic microtubules, actin filaments, and amyloid fibrils in the brain. Thus, we employ a widely used effective Hamiltonian for the light-matter interactions that couples the Trp chromophores at long range due to their collective interactions with the electromagnetic field. This Hamiltonian is non-Hermitian because the large number of degrees of freedom of the electromagnetic field are traced out to give an effective description of the (collective) open quantum system, whose probability amplitude decays to the field with time. For further details on the non-Hermitian formalism, please see [41–44], as well as Eqs 4–12 in Section 6 (Methods).

3 Results

We present the eigensolutions of the effective Hamiltonian given in Eq. 1 for microtubules, actin filaments, and amyloid fibrils of varying lengths. For details on the geometry of these structures, see the Methods in Section 6. For a visual image, see Figure 1. For the transition dipole orientations, see Figure 6. We also consider the thermal average of the quantum yield (see Section 6: Methods for further details), its dependence on system size, and its robustness to static disorder. The effective Hamiltonian is non-Hermitian, and can be written as the sum of a Hermitian part and a non-Hermitian part

$H_{\text{eff}}=H_0+\mathrm{\Delta }-\frac{i}{2}G,(1)$

where $H_0$, $\mathrm{\Delta }$, and $G$ are real matrices. Because of the non-Hermitian part $-\frac{i}{2}G$, the eigenvalues of this matrix are complex numbers. Assuming that the dimension of the matrix is $N$, then the (right) eigenvectors $|{\mathcal{E}}_j\rangle$ and their associated eigenvalues ${\mathcal{E}}_j$ are

$H_{\text{eff}}|{\mathcal{E}}_j\rangle ={\mathcal{E}}_j|{\mathcal{E}}_j\rangle ;{\mathcal{E}}_j=E_j-\frac{i}{2}{\mathrm{\Gamma }}_j,(2)$

where $E_j$ is the energy (real part of eigenvalue) and ${\mathrm{\Gamma }}_j$ is the decay rate ($-2$ times imaginary part of eigenvalue) of the eigenvector $|{\mathcal{E}}_j\rangle$. The decay rate in Eq. 2 tells us how quickly the probability amplitude of the eigenvector in Eq. 2 dies out. For further details, please see the Methods in Section 6.

Figure 6

Figure 6. Transition dipole vector geometries of tryptophan (Trp) in the realistic biological structures considered in this paper. The blue dots represent the Trp molecules. The relative size of structures with respect to one another is not to scale. For illustrative purposes, the size of vectors has been enlarged for viewing. (A) Angled longitudinal view of microtubule (built from tubulin dimer PDB entry 1JFF; length 45 nm, radius 22.4 nm). (B) Cross-sectional view of the microtubule. (C) Angled longitudinal view of actin filament (built from actin subunit PDB entry 6BNO; length 112.5 nm, radius ∼6 nm). (D) Cross-sectional view of the actin filament. (E) Angled longitudinal view of human amyloid fibril (built from amyloid subunit PDB entry 6MST; length 20.2 nm, radius ∼4.5 nm). (F) Cross-sectional view of human amyloid fibril. (G) Angled longitudinal view of mouse amyloid fibril (built from amyloid subunit PDB entry 6DSO; length 20.2 nm, radius ∼5 nm). (H) Cross-sectional view of mouse amyloid fibril.

3.1 Microtubules

We study single microtubules of varying length constructed as spiral-cylindrical collectives of tubulin dimers (PDB entry 1JFF). One tubulin dimer contains 8 tryptophan (Trp) molecules, and one spiral of the microtubule contains 13 tubulin dimers (so one spiral contains $8\times 13=104$ Trp molecules). For example, a 100-spiral microtubule contains $104\times 100=10400$ Trp molecules.

Shown in Figure 7 is the thermal average of the quantum yield (QY) as a function of the length of the microtubule, reported as the number of Trp molecules. Each color represents a differing static disorder strength, with red being the smallest $(W=0{\text{\hspace{0.17em}cm}}^{-1})$ and blue being the largest $(W=1000{\text{\hspace{0.17em}cm}}^{-1})$, which is approximately five times larger than static disorder in a room-temperature environment $(W=200{\text{\hspace{0.17em}cm}}^{-1})$. Let us now define $\%\mathrm{\Delta }\text{QY}(W:W_i\to W_f)$ as the percent change in quantum yield when the static disorder goes from $W_i{\text{\hspace{0.17em}cm}}^{-1}$ to $W_f{\text{\hspace{0.17em}cm}}^{-1}$ for a set system size. Using this notation for a system size of 20,800 Trp molecules (200 spirals; the rightmost data points in Figure 7), $\%\mathrm{\Delta }\text{QY}(W:0\to 1000)=-3.08\%$. The quantum yield dampening by only $3.08\%$ when the static disorder is five times that of room temperature demonstrates its robustness. Such quantum yield robustness to static disorder has recently been experimentally confirmed for microtubules at room temperature [3] (also see Figures 6 and 4 of [3] for theoretical predictions of the enormous superradiant enhancements for axonal microtubule bundles, and of the quantum yield robustness for centrioles, respectively). This suggests that quantum yield robustness can be observed for similar biological structures, once realized experimentally.

Figure 7

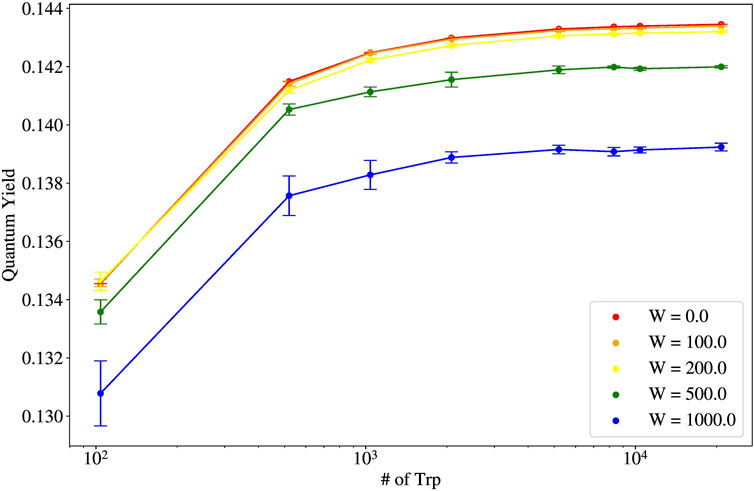
Figure 7. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for single microtubules (pictured in the leftmost structure in Figure 1). $W$ (in units of ${\text{cm}}^{-1}$) represents the strength of static disorder applied to Eq. 1, where each diagonal element of the effective Hamiltonian $H_{\text{eff},ii}$ is replaced by a random value in the range $[H_{\text{eff},ii}-W/2,H_{\text{eff},ii}+W/2]$. See Section 6.3.1 (specifically, Eq. 17 and surrounding text) for more details. The Hamiltonian is then diagonalized to find the eigenvalues, and from the eigenvalues the thermal average of the quantum yield is obtained. This is repeated ten times, and the mean is taken to obtain a data point. The error bars on each point represent one standard deviation of the ten QY values calculated for that point.

The robustness of the quantum yield for microtubules (and their bundled architectures) is explainable from the shape of the spectrum of eigenvalues of the non-Hermitian Hamiltonian Eq. 1. The spectrum of single microtubules has been studied in [2]. Specifically, in Figure 2C of [2], the spectrum of a 100-spiral microtubule (10,400 Trp molecules) is shown. It can be seen that the most superradiant states lie in the low-energy portion of the spectrum. Examining Eq. 15, if a large ${\mathrm{\Gamma }}_j$ is associated with a smaller $E_j$, then the term ${\mathrm{\Gamma }}_j\exp (-\beta E_j)$ in the Gibbs thermal ensemble will be weighted more strongly, thereby augmenting the quantum yield.

In the case of microtubules, the dependence of the thermal average of the quantum yield on system size also highlights that collective light-matter interactions can enhance quantum effects beyond the length scales normally associated with quantum behavior. Let us define $\%\mathrm{\Delta }\text{QY}(N:N_i\to N_f)$ to be the percent change in the quantum yield at a fixed static disorder strength, when the structure goes from $N_i$ Trp molecules to $N_f$ Trp molecules. The QY has been determined experimentally to be 0.124 for Trp alone in BRB80 aqueous buffer solution [3]. For microtubules, when $W=0{\text{\hspace{0.17em}cm}}^{-1}$, $\%\mathrm{\Delta }\text{QY}(N:1\to 20800)=15.76\%$. With a static disorder of $W=1000{\text{\hspace{0.17em}cm}}^{-1}$, $\%\mathrm{\Delta }\text{QY}(N:1\to 20800)=12.31\%$. So, even with extremely large static disorder strengths, at thermal equilibrium, the quantum yield for microtubules is enhanced as the system size grows.

We also study the effects of mechanical/vibrational degrees of freedom on the superradiant states of microtubules (see Supplementary Figures S1, S2 in the Supplementary Material), within the Born-Oppenheimer approximation. As seen in these figures, the superradiance is dynamically altered by nuclear geometry and changes when microtubules are mechanically deformed in different ways. Purely longitudinal modes (only deforming along the microtubule main axis) have higher superradiance than modes with purely twisting motions around the microtubule main axis, which have higher superradiance than bending motions off the microtubule main axis. Mode 15 has purely longitudinal stretching/contracting motions, which still preserve a $\mathrm{\Gamma }/\gamma$ factor of greater than 27. This mode has the highest superradiance of any mode in Supplementary Figures S1, S2. The mode with the next highest superradiance is mode 9, with a 180-degree twisting motion along the microtubule axis. Some of the large bending motions displayed in modes 12, 13, and 17 dampen the superradiance down to a $\mathrm{\Gamma }/\gamma$ factor of less than 10. These results show that the superradiance is modified depending on not only the biological type of structure, but its intrinsic mechanical modes. Microtubules form long, straight, packed bundles in neuronal axons, which would mostly have longitudinal stretching/contracting modes. From this analysis, we show that longitudinal vibrational modes would not dampen superradiance as much as other modes, suggesting that highly stable structures such as axons may actively be exploiting quantum coherent effects based on their architecture and which mechanical modes are allowed. Although we only conduct this analysis for microtubules, the modulation of superradiant effects with vibrational state can be extended to other structures.

The vibrational modes studied have a mechanical frequency in the low gigahertz range [45], corresponding to a timescale on the order of nanoseconds. As a microtubule oscillates mechanically, any superradiant states supported by the given atomic/nuclear configuration can vary from their enhancement factors reported in both the left and right columns of Supplementary Figures S1, S2, to enhancement factors one or two orders of magnitude higher near the amplitude node of each vibration (see middle panels), where the structure is closest to a “straight” longitudinal configuration. From Table 1, we can see that the lifetimes for the superradiant states of microtubules and of many other structures are on the order of picoseconds. Thus, the photophysical effect of superradiance is operating on a timescale at least three orders of magnitude faster than the mechanical motion of the microtubule, which can be considered more or less static in this ultrafast regime. However, even though our predictions have all been calculated within the Born-Oppenheimer approximation, it is clear from Tables 1, 2 that the most subradiant states—and even a few of the superradiant states—supported by these neuroprotein architectures are extremely long-lived, suggesting potential influence and interaction across electronic and nuclear degrees of freedom in these structures.

Table 1

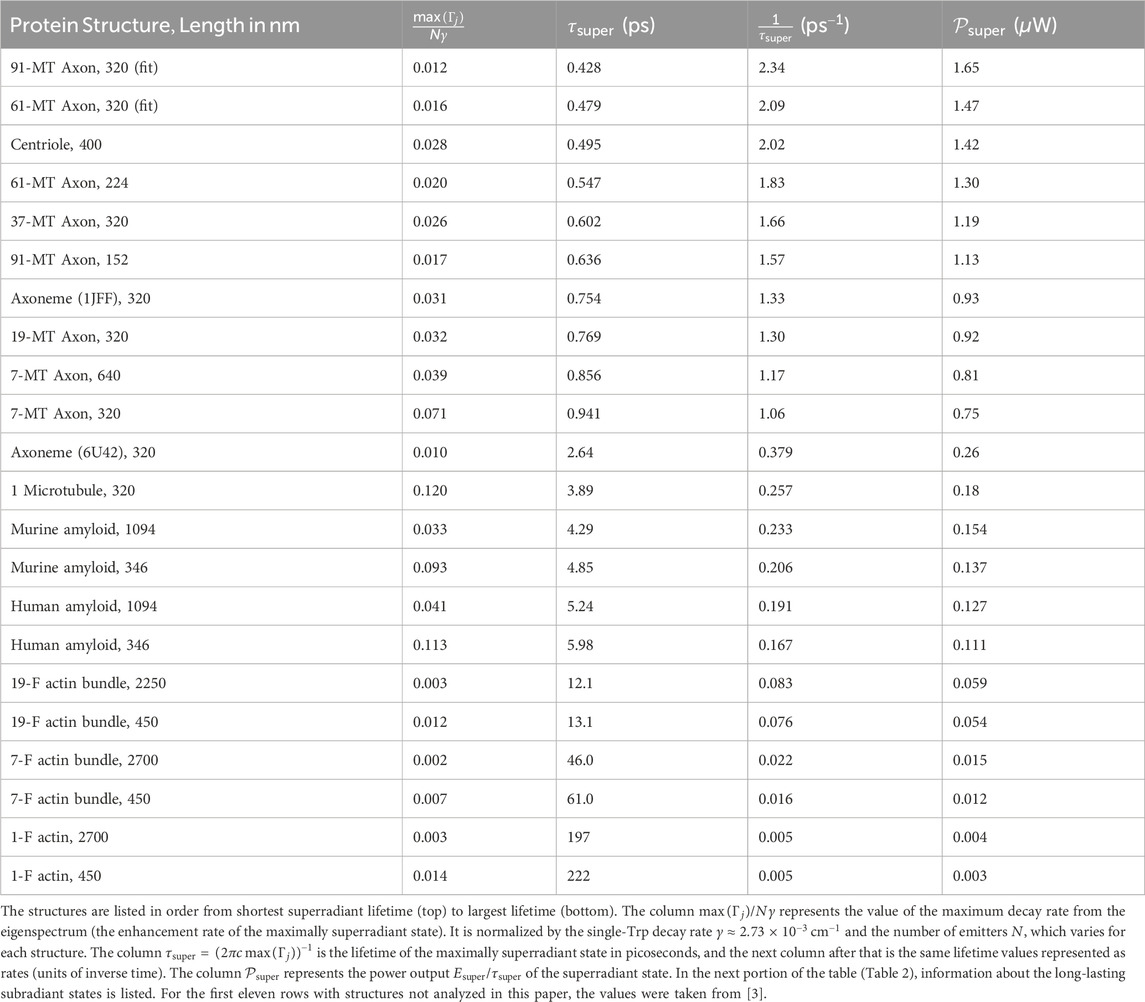
Table 1. Values for the maximum superradiant decay rates calculated by diagonalizing the non-Hermitian Hamiltonian in Eq. 1 for the tryptophan (Trp) network in each protein structure.

Table 2

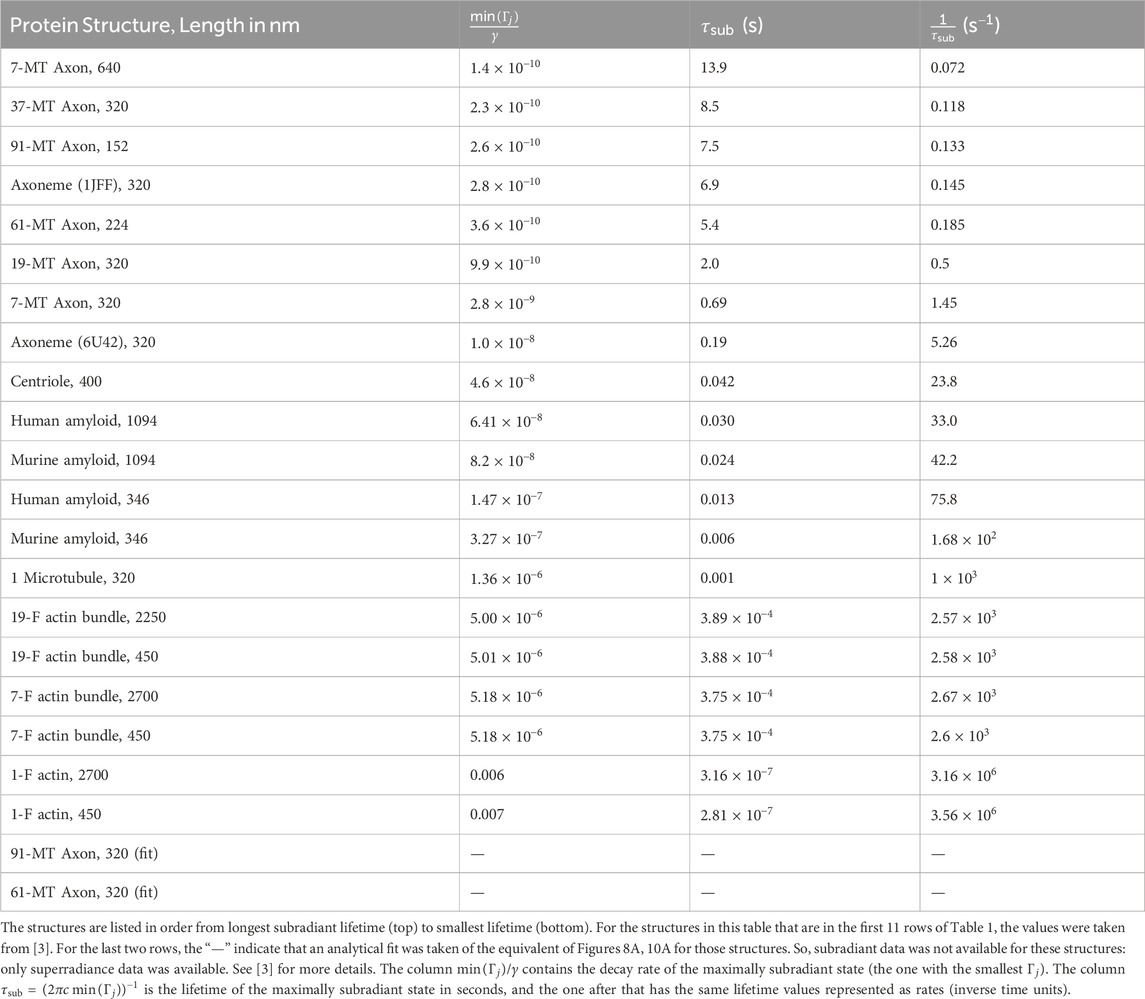
Table 2. Values for the minimum subradiant decay rates calculated by diagonalizing the non-Hermitian Hamiltonian in Eq. 1 for the tryptophan (Trp) network in each protein structure.

In many of the middle columns of Supplementary Figures S1, S2, we can see high exciton probabilities near the ends of the structures, despite the mode being symmetric. This could be a biological manifestation of topological edge states, which have been previously studied in paradigmatic non-Hermitian systems [46, 48].

3.2 Actin filaments

We study two different types of actin collectives: actin filaments and actin bundles. An actin filament is made from a concatenation of bare actin subunits (PDB entry 6BNO), each of which is a homo-octamer (protein consisting of eight identical chains) about 22.5 nm long. We then study two sizes of actin bundles corresponding to the smallest hexagonal configurations: 7-filament bundles, and 19-filament bundles (a top-down view of both of these are pictured in the inset of Figure 8A). One bare actin subunit contains 32 Trp molecules. So, for example, a 19-filament bundle comprised of single-subunit actin filaments contains $32\times 19=608$ Trp molecules. Also, the Trp network in actin filaments forms a helical structure, which repeats approximately every 40 nm.

Figure 8

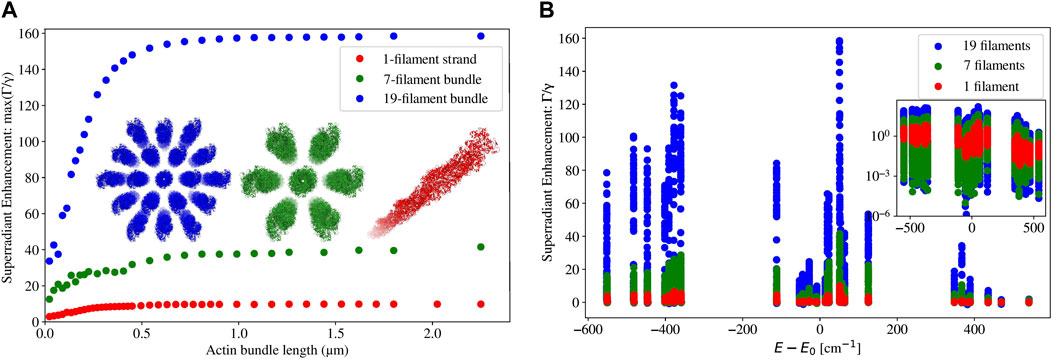
Figure 8. (A) Plot of the maximum superradiance $\max ({\mathrm{\Gamma }}_j/\gamma )$ vs. structure length for model actin filament structures. Filaments have diameters of $\sim 7$ nm, and the hexagonal bundles have filaments spaced 12 nm from each other center-to-center. Sample images of 1-filament (3200 tryptophan), 7-filament (22,400 tryptophan), and 19-filament (60,800 tryptophan) actin structures are shown inset to the plot with their corresponding colors. (B) The eigenvalue spectrum (${\mathrm{\Gamma }}_j/\gamma$ vs. $E-E_0$) of 2.25-$\mu \text{m}$ actin structures with 1 filament, 7 filaments, and 19 filaments in their corresponding colors. Inset is the same spectrum plotted with the $y$ axis on a semi-log scale.

Figure 8A shows the enhancement rate of the maximally superradiant state against the length of an actin filament or of a bundle of actin filaments. Similarly to the case of microtubules, the maximum superradiant enhancement rate increases with length at first, and then eventually saturates when the length approaches or exceeds the excitation wavelength. This feature is most pronounced in the 19-filament actin bundles. In the single filament and the 7-filament bundle, saturation of the maximum enhancement rate starts to occur when the length of the actin structure is around the length scale of excitation (280 nm). However, in the 19-filament bundle, saturation occurs at about twice that length. This is an interesting difference between microtubules/microtubule bundles [2, 3], which saturate in their maximum superradiant enhancement (in the single-photon limit) at about three or more times the excitation wavelength, and actin filaments/bundles.

In Figure 8B, we can see that the maximally superradiant states of 2.25 $\mu$m-long actin structures are not close to the lowest exciton state. This impacts the quantum yield of actin bundles and filaments, as seen in Figure 9. With zero static disorder, $\%\mathrm{\Delta }\text{QY}(N:1\to 60800)=62.31\%$ and with $W=1000{\text{\hspace{0.17em}cm}}^{-1}$, $\%\mathrm{\Delta }\text{QY}(N:1\to 60800)=55.14\%$. Even though the QY of actin bundles is enhanced for large structures with respect to Trp alone in solution, it can be seen in Figure 9 that all curves show a very slight decrease in the QY. Specifically, $\%\mathrm{\Delta }\text{QY}(N:608\to 60800)=-1.11\%$ for $W=0{\text{\hspace{0.17em}cm}}^{-1}$. For room-temperature static disorder of $W=200{\text{\hspace{0.17em}cm}}^{-1}$, such a decrease is still present, although for $W=1000{\text{\hspace{0.17em}cm}}^{-1}$, the change is within the error bars of the static disorder. Despite this decrease being small, its existence means that once a 19-filament bundle of single-subunit actin filaments is created, increasing the filament length further does not enhance the QY at all, contrary to the microtubule case. For the dependence of the QY of actin bundles with static disorder, we calculated $\%\mathrm{\Delta }\text{QY}(W:0\to 1000)=-4.17\%$ for a 60800-Trp actin bundle $(60800\text{\hspace{0.17em}Trp}=2.25\mu \text{m})$. This means that, at thermal equilibrium, the QY for large actin structures is dampened only slightly more than the QY for single microtubules.

Figure 9

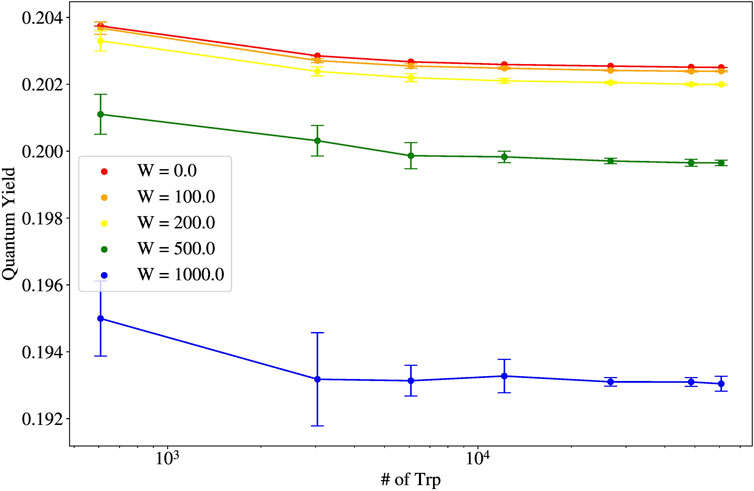
Figure 9. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for 19-filament bundles of actin (one actin filament is pictured in the second from the left structure in Figure 1, and a 19-filament bundle is pictured inset in blue in Figure 8A). $W$ (in units of ${\text{cm}}^{-1}$) represents the strength of static disorder applied to Eq. 1, where each diagonal element of the effective Hamiltonian $H_{\text{eff},ii}$ is replaced by a random value in the range $[H_{\text{eff},ii}-W/2,H_{\text{eff},ii}+W/2]$. See Section 6.3.1 (specifically, Eq. 17 and surrounding text) for more details. The Hamiltonian is then diagonalized to find the eigenvalues, and from the eigenvalues the thermal average of the quantum yield is obtained. This is repeated ten times, and the mean is taken to obtain a data point. The error bars on each point represent one standard deviation of the ten QY values calculated for that point.

Comparing Figure 8 to the analogous spectrum for microtubules (see Figure 2 of [2]), and by examining the entries of Table 1, we see that microtubules have brighter superradiant states than those for all actin structures. However, 19-filament actin bundles still have higher predicted QY values (see Figure 9) than those for microtubules (see Figure 7). We can understand this by revisiting Eq. 15. Each decay rate ${\mathrm{\Gamma }}_j$ is weighted by a Boltzmann factor $\exp (-\beta E_j)$. If the energy $E_j$ is sufficiently less than the single-Trp excitation energy (our “zero” reference) and has a relatively large absolute value, as is the case for the collective Lamb shift in certain actin bundles, this can compensate for the collective decay rate being small. Figure 8 shows that the lowest energy states are shifted about $-600{\text{\hspace{0.17em}cm}}^{-1}$, while for microtubules the lowest energy states are shifted only about $-100{\text{\hspace{0.17em}cm}}^{-1}$. This is due to the average Trp-Trp couplings in actin filaments being much larger than the average Trp-Trp couplings in microtubules. For a 35-spiral microtubule (280-nm length), the average Trp-Trp interaction is $0.0311{\text{\hspace{0.17em}cm}}^{-1}$, with a standard deviation of $0.898{\text{\hspace{0.17em}cm}}^{-1}$. The nearest-neighbor Trp-Trp interaction is $62.82{\text{\hspace{0.17em}cm}}^{-1}$, which is small compared to room temperature $(k_{B}T\approx 200{\text{\hspace{0.17em}cm}}^{-1})$. An actin filament of 13 subunits $(292.5\text{\hspace{0.17em}nm})$, on the other hand, has an average Trp-Trp interaction of $0.683{\text{\hspace{0.17em}cm}}^{-1}$, with a standard deviation of $14.06{\text{\hspace{0.17em}cm}}^{-1}$. The nearest-neighbor Trp-Trp interaction for an actin filament is $537.2{\text{\hspace{0.17em}cm}}^{-1}$, much larger than room temperature. The strength of the Trp-Trp couplings in actin compared to microtubules explains the larger collective Lamb shift for lower-energy states in actin, thereby explaining its high quantum yield despite having dimmer superradiant states than microtubules.

These results show that although the absolute values of the QYs for 19-filament actin bundles are larger than that of single microtubules, these QYs for actin bundles decrease with system size after even a single twist (608 Trp). However, 19-filament actin bundles are comparable to microtubules in their QY robustness to static disorder. Although such actin bundles do exhibit observable and important superradiant effects via the QY, our results imply that their role in cytoskeletal dynamics may be restricted, more so than microtubules, to their conventional mechanical roles rather than having significant photophysical enhancements at long length scales. Experiments in vitro to detect superradiant QY enhancements (from Trp in solution) in actin bundles would be warranted, as has been demonstrated with microtubules [3].

3.3 Amyloid fibrils

Figure 10 presents the same data as in Figure 8, but for single amyloid fibrils in human and in mouse. We will refer to the length of an amyloid fibril by its absolute length (in $\mu$m), and/or the number of subunits it is made of. The subunit of human (mouse) amyloid is given by the PDB entry 6MST (6DSO), contains 24 (36) Trp molecules, and is 2.88 nm in length. The Trp network of amyloid forms a helical pattern, which repeats approximately every 40 subunits (every 115.2 nm).

Figure 10

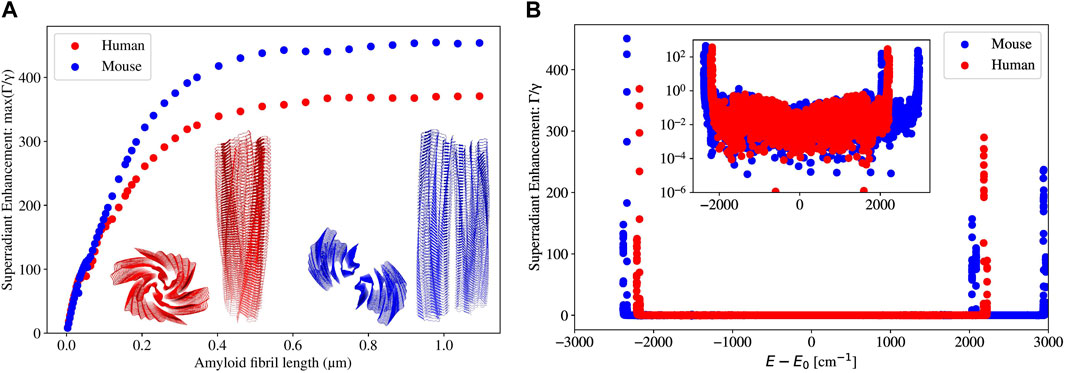
Figure 10. (A) Plot of the maximum superradiance $\max ({\mathrm{\Gamma }}_j/\gamma )$ vs. structure length for model amyloid fibrils. Sample images of amyloid structures built from PDB files 6MST (Homo sapiens) and 6DSO (Mus musculus) are shown inset to the plot with their corresponding colors, both in a cross-sectional view and a longitudinal view. (B) The eigenvalue spectrum (${\mathrm{\Gamma }}_j/\gamma$ vs. $E-E_0$) of 864-$\text{nm}$ 6MST (7,200 tryptophan) and 6DSO (10,800 tryptophan) amyloid fibrils. Inset is the same spectrum plotted with the $y$ axis on a semi-log scale.

In Figure 10A, it can be seen that for both human and mouse amyloid fibrils, the maximum superradiant enhancement $\text{max}(\mathrm{\Gamma }/\gamma )$ reaches a saturating value at large lengths. For 1.09-$\mu$m human (mouse) amyloid fibrils, $\text{max}(\mathrm{\Gamma }/\gamma )=371.21(453.14)$, far surpassing that of even a 2.2-$\mu$m 19-filament actin bundle, which has $\text{max}(\mathrm{\Gamma }/\gamma )=160.93$. This is despite the Trp network in the amyloid fibrils being comprised of significantly fewer chromophores than that in actin. In fact, if one considers a human amyloid fibril and a 19-filament actin bundle that have the same number of Trp molecules (e.g., picking 1824 Trp molecules), the actin bundle has $\text{max}(\mathrm{\Gamma }/\gamma )=37.70$, while the human amyloid fibril has $\text{max}(\mathrm{\Gamma }/\gamma )=270$. This shows that the density of Trp chromophores within a unit volume and the transition dipole orientations of amyloid are much more suited for maintaining bright superradiant states than the Trp density and transition dipole orientations of actin bundles.

In Figure 10B, we can see that superradiant states emerge at very specific bands in both the low- and high-energy portions of the spectrum, and at all other energies, the superradiant enhancement rate is very close to 0. For the human amyloid fibril (built from PDB file 6MST), the superradiant states are only present near the smallest and largest energies, and every other state is subradiant (${\mathrm{\Gamma }}_j<\gamma$, close to zero enhancement rate). The emergence of superradiant states only at a few energies arises due to the structure of the Trp networks in question, as discussed with the toy models in Section 2.3. Both amyloid fibril structures have dipole vector orientations that vary more smoothly from one dipole to its nearest neighbor, as compared with microtubules and actin filaments, which do not exhibit this feature (Figure 6). The presence of a large proportion of superradiant states in the low-energy portion of the amyloid fibril spectrum gives it a very large QY, as seen in Figures 11, 12. Specifically, for system sizes of 864 Trp or above, the human (mouse) amyloid has a quantum yield between 0.55 and 0.60 (0.44 and 0.49) for all considered values of static disorder up to 1,000 ${\text{cm}}^{-1}$; these quantum yields are about two to three times that of actin filaments, and more than three to four times that of microtubules.

Figure 11

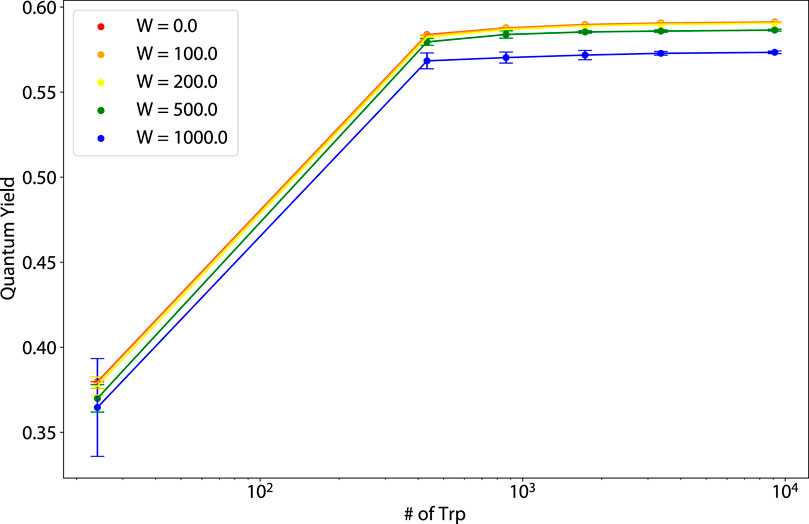
Figure 11. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for human amyloid fibrils (pictured in the second from the right structure of Figure 1). $W$ (in units of ${\text{cm}}^{-1}$) represents the strength of static disorder applied to Eq. 1, where each diagonal element of the effective Hamiltonian $H_{\text{eff},ii}$ is replaced by a random value in the range $[H_{\text{eff},ii}-W/2,H_{\text{eff},ii}+W/2]$. See Section 6.3.1 (specifically, Eq. 17 and surrounding text) for more details. The Hamiltonian is then diagonalized to find the eigenvalues, and from the eigenvalues the thermal average of the quantum yield is obtained. This is repeated ten times, and the mean is taken to obtain a data point. The error bars on each point represent one standard deviation of the ten QY values calculated for that point.

Figure 12

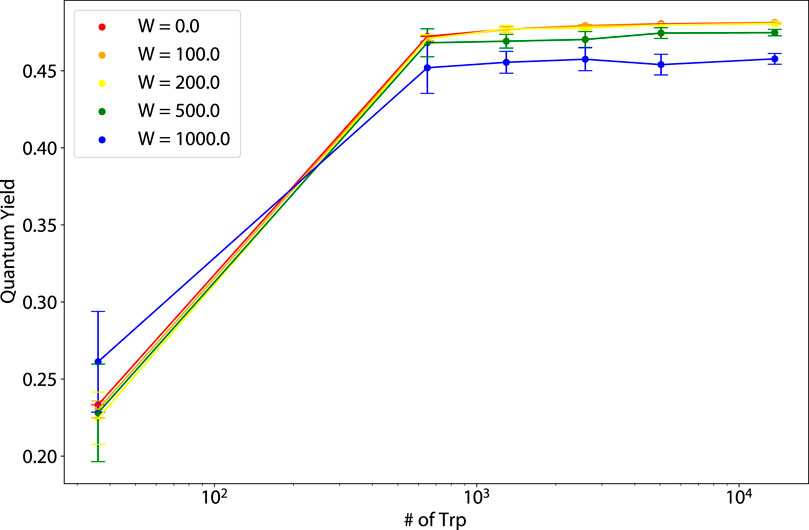
Figure 12. Thermal average of the quantum yield (QY) vs. number of tryptophan (Trp) molecules for varying static disorder strengths for murine amyloid fibrils (pictured in the rightmost structure of Figure 1). $W$ (in units of ${\text{cm}}^{-1}$) represents the strength of static disorder applied to Eq. 1, where each diagonal element of the effective Hamiltonian $H_{\text{eff},ii}$ is replaced by a random value in the range $[H_{\text{eff},ii}-W/2,H_{\text{eff},ii}+W/2]$. See Section 6.3.1 (specifically, Eq. 17 and surrounding text) for more details. The Hamiltonian is then diagonalized to find the eigenvalues, and from the eigenvalues the thermal average of the quantum yield is obtained. This is repeated ten times, and the mean is taken to obtain a data point. The error bars on each point represent one standard deviation of the ten QY values calculated for that point.

For the dependence of the amyloid fibril QY on static disorder, for 864 nm structures, $\%\mathrm{\Delta }\text{QY}(W:0\to 1000)=-3.05\%$ for human, and $\%\mathrm{\Delta }\text{QY}(W:0\to 1000)=-5.01\%$ for mouse, making these fibrils at least as robust to static disorder as microtubules and actin filament bundles, and potentially more so. The QY of amyloid is also strongly enhanced with system size, with $\%\mathrm{\Delta }\text{QY}(N:1\to 9120)=130.65\%$ for human and $\%\mathrm{\Delta }\text{QY}(N:1\to 13680)=118.05\%$ for mouse, at zero static disorder. For $W=1000{\text{\hspace{0.17em}cm}}^{-1}$, $\%\mathrm{\Delta }\text{QY}(N:1\to 9120)=128.88\%$ for human and $\%\mathrm{\Delta }\text{QY}(N:1\to 13680)=114.73\%$ for mouse. Thus, amyloid displays a very high QY that increases with system size, up to a certain point at which it begins to saturate: at zero static disorder, $\%\mathrm{\Delta }\text{QY}(N:432\to 9120)=1.26\%$ for human amyloid fibrils and $\%\mathrm{\Delta }\text{QY}(N:648\to 13680)=1.87\%$ for mouse amyloid fibrils, a clear indication of flattening of the monotonically increasing QY, as compared with the initial more-than-doubling and more-than-tripling of the QY from Trp alone in solution. For a human (mouse) amyloid fibril with greater than or equal to 432 (648) Trp molecules, the QY stays constant when $W=1000{\text{\hspace{0.17em}cm}}^{-1}$ (any variation is within the error bars, i.e., random fluctuations caused by the static disorder).

It should be noted that for both amyloid fibrils, some inter-Trp distances are as small as $\sim 5\text{Å}$. In the Hamiltonian Eq. 1, the point dipole approximation is made. But, in reality, the Trp molecule extends over space: the distance from the oxygen atom to the furthest carbon atom (CZ2) in Trp is $\sim 7.7\text{Å}$. The nearest-neighbor Trp distances being smaller than the Trp molecules themselves means that orbitals of different Trp molecules may overlap, and this can lead to the formation of charge-transfer states, which are intermediate between an exciton and an electron donor-acceptor complex. Such charge-transfer states in biomolecular complexes with closely spaced chromophores have previously been described in DNA [48–50], proteins [51–53], and photosynthetic complexes [54]. In the case of our amyloid fibrils, strictly speaking, the point dipole approximation for Trp would break down. Also, ultrafast electron-transfer effects such as those between Trp and carbonyl-containing groups on the picosecond timescale [55] and those between Trp and thymine on the sub-picosecond timescale [56] can occur for structures with closely-packed residues such as in amyloid fibrils. Since these ultrafast quenching effects occur on timescales faster than some of the superradiant states that we study, they may degrade the quantum yield. However, these effects only apply to nearest-neighbor Trp-Trp interactions. For Trp molecules that are not as closely spaced (the vast majority of Trp-Trp pairs), the long-range terms that go as $r^{-1}$ in Eq. 8 and Eq. 9 are dominant over the $r^{-2}$ and $r^{-3}$ terms. Superradiance is greatly enhanced by this type of long-range interaction, and for these Trp molecules the aforementioned approximations remain valid.

Due to the close Trp-Trp spacings in amyloid fibrils, we would expect the Trp-Trp couplings to be very high, and indeed they are. The average Trp-Trp coupling strength for a 100-subunit human (mouse) amyloid fibril, which has a length of 288 nm, is $0.971{\text{\hspace{0.17em}cm}}^{-1}$ $(0.741{\text{\hspace{0.17em}cm}}^{-1})$ with a standard deviation of $26.6{\text{\hspace{0.17em}cm}}^{-1}$ $(24.6{\text{\hspace{0.17em}cm}}^{-1})$. The nearest-neighbor Trp-Trp coupling for human (mouse) amyloid fibril is $1012{\text{\hspace{0.17em}cm}}^{-1}$ $(1306{\text{\hspace{0.17em}cm}}^{-1})$. As we expected, this leads to much larger magnitude collective Lamb shifts for the lowest exciton states of amyloid fibrils, which can be seen in Figure 10B at about $-2500{\text{\hspace{0.17em}cm}}^{-1}$. This explains the very high quantum yield for amyloid fibrils (see Figures 11, 12): they have their brightest superradiant states at large negative shifts from the single-Trp excitation energy, thereby increasing the weight of these states in the thermal ensemble beyond those in either microtubules or actin bundles.

3.4 Energy gaps in the complex plane, and thermal robustness

We create plots of the energy gap $(\mathrm{\Delta }\mathcal{E})$ in the complex plane for all the biological structures we study in this work. Let each complex eigenvalue of the non-Hermitian Hamiltonian Eq. 1 be denoted by ${\mathcal{E}}_j$, where the real and imaginary parts of ${\mathcal{E}}_j$ are $E_j$ and $-\frac{i}{2}{\mathrm{\Gamma }}_j$, respectively. The energy gap in the complex plane is defined as

$\mathrm{\Delta }\mathcal{E}\equiv |{\mathcal{E}}_1-{\mathcal{E}}_0|,(3)$

where $|\cdot |$ represents the complex norm, ${\mathcal{E}}_0$ is the state with the lowest energy and ${\mathcal{E}}_1$ is the state with the second lowest energy (i.e., $E_0<E_j\forall j\ne 0$ and $E_1<E_j\forall j\ne \mathrm{0,1}$). This energy gap can be considered a measure of how “quantum mechanical” the system is and has been associated with robustness to thermal noise and supertransfer processes [2, 3, 39]. If the classical limit is taken for a quantum system (the limit $\hslash /S_{\text{sys}}\to 0$, where $S_{\text{sys}}$ is the characteristic scale of the action of the system), then the spacing between the energy levels will approach 0. Therefore, as the system size increases, it would be conventionally expected that the system would become more classical, and thus exhibit a decrease in the energy gap.

In Figure 13, $\mathrm{\Delta }\mathcal{E}$ is plotted against structure length for single microtubules, 19-filament actin bundles, human amyloid fibrils, and mouse amyloid fibrils. In microtubules, we can observe an increase in the energy gap from around 100 nm–280 nm. Since 280 nm is the excitation wavelength of Trp, this means that the system increases its energy gap up to this characteristic length scale induced by matter interacting with the electromagnetic field. This observation has been made in [2]. Interestingly, we do not see this behavior for any of the other structures in Figure 13. For both amyloids (panels (C) and (D) in Figure 13), there is a huge peak of the energy gap around 10–25 nm, and then a smooth dropoff that tends to 0. The maximum energy gap of human (mouse) amyloid is $40.32{\text{\hspace{0.17em}cm}}^{-1}$ $(60.47{\text{\hspace{0.17em}cm}}^{-1})$, which is about 47 (71) times larger than the maximum energy gap of microtubules around 280 nm, which is $0.85{\text{\hspace{0.17em}cm}}^{-1}$. Even though the energy gap of amyloid is decreasing at the excitation wavelength of Trp (280 nm), its value for human (mouse) amyloid fibrils at this length is $0.278{\text{\hspace{0.17em}cm}}^{-1}$ $(0.344{\text{\hspace{0.17em}cm}}^{-1})$, which is on the same order as the energy gap of microtubules. This is consistent with the robustness of amyloid fibrils compared with microtubules.

Figure 13

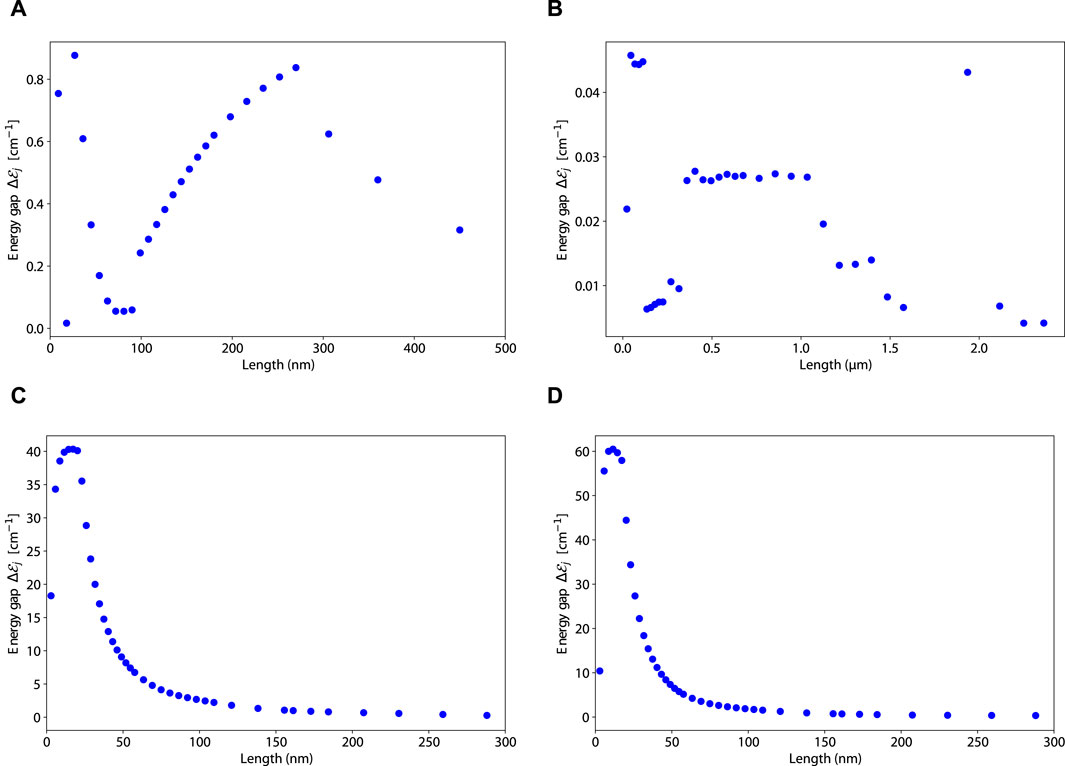
Figure 13. Plots of the energy gap $\mathrm{\Delta }\mathcal{E}$ in the complex plane, given by Eq. 3, vs. length. The energy gap is calculated using the eigenspectrum obtained by diagonalizing the non-Hermitian Hamiltonian Eq. 1 for the tryptophan networks in biological structures. (A) Energy gap plot for single microtubules (pictured in the leftmost structure in Figure 1). (B) Energy gap plot for 19-filament actin bundles. A top-down view of a 19-filament actin bundle is pictured inset in Figure 8A, and a single filament is pictured in the second from left structure in Figure 1. (C) Energy gap plot for human amyloid fibrils (pictured in the second from right structure in Figure 1). (D) Energy gap plot for murine amyloid fibrils (pictured in the rightmost structure in Figure 1).

The energy gap behavior of 19-filament actin bundles (panel (B) from Figure 13) is vastly different from all the other structures. It has a sporadic behavior that does not trend upward with increasing system size. The maximum energy gap for 19-filament actin bundles is at $\sim 0.045\mu$m, and it is $0.046{\text{\hspace{0.17em}cm}}^{-1}$, which is a whole order of magnitude below the maximum energy gap of microtubules, and three orders of magnitude less than the maximum energy gap of amyloid. The sporadic behavior and low values for the energy gap for actin may reflect the more strictly mechanical nature of actin bundles compared with the other structures studied in this work. However, a more comprehensive analysis of these energy gaps averaged over multiple realizations of different static disorder strengths is warranted, to understand better how the transition to classicality in these structures is affected by a thermal environment.

3.5 Static disorder in the single tryptophan decay rate

We also implement static disorder in the single-Trp decay rate $(\gamma )$, to see how it affects the superradiance and QY for a 100-spiral microtubule structure. See Section 6.3.2 for a detailed description. Plotted in Figure 14 is the thermally averaged QY vs. the static disorder strength in $\gamma$ for a 100-spiral microtubule. We find that the QY slightly increases (by around 0.1%) when a distribution of $\gamma$ values are chosen. The fact that the QY does not dampen when a distribution of decay rates are chosen demonstrates that our approximation of a constant single-Trp decay rate is justified.

Figure 14

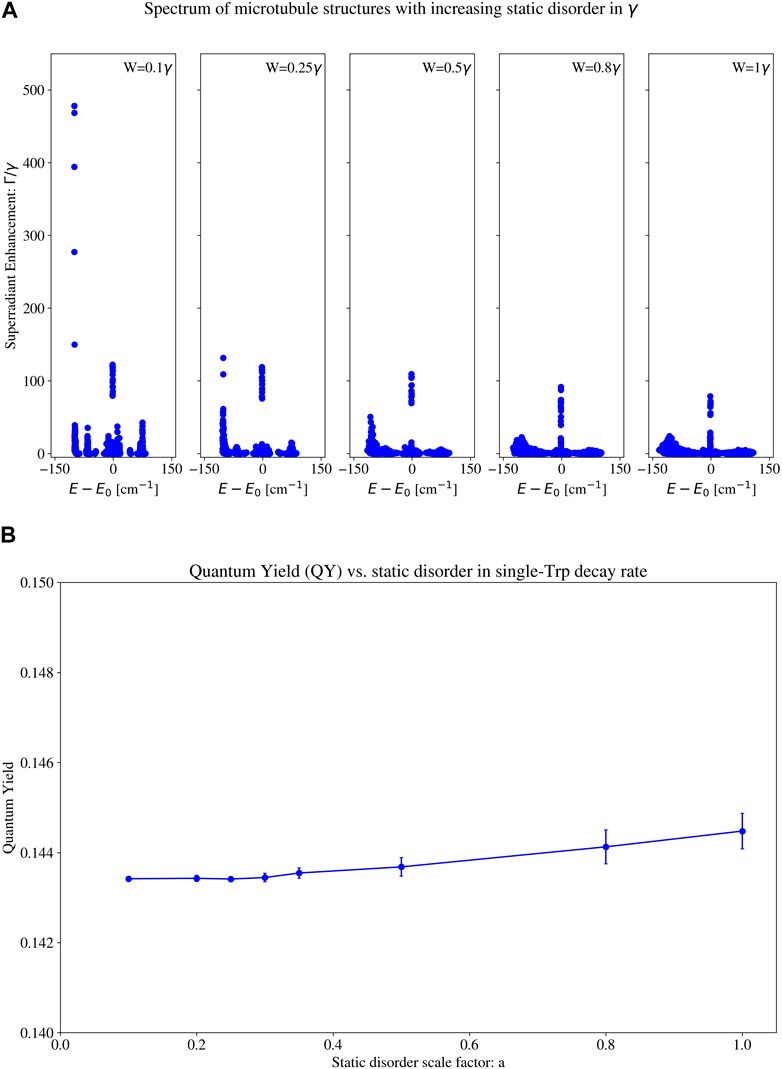
Figure 14. (A) Eigenspectra and (B) thermally averaged quantum yield (QY) with increasing static disorder in the single-tryptophan (Trp) decay rate for a 100 spiral microtubule (pictured in the leftmost structure in Figure 1). Each subplot in (A) contains the eigenvalues of the Hamiltonian for a different static disorder strength. The static disorder in the single-Trp decay rate is implemented as follows (see Section 6.3.2 (specifically, Eqs 18, 19 and surrounding text) for a more detailed description): each on-site $\gamma$ in the Hamiltonian (i.e., diagonal element) is replaced by a random value in the range $[-a\gamma /2,a\gamma /2]$, where $a$ is the dimensionless static disorder scale factor plotted on the $x$-axis of the plot. Each off-diagonal $\gamma$ is replaced by the mean of the corresponding on-site $\gamma$ values. The Hamiltonian is then diagonalized to find the complex eigenvalues, and from these eigenvalues the thermal average of the quantum yield is obtained. This is repeated ten times for different realizations of the static disorder. The error bars in (B) represent one standard deviation above and below the mean from the 10 realizations. Note that the QY for $a=1.0$, at the $1\sigma$ level of significance, is statistically larger than the QY for $a=0.1$.

4 Discussion

We discuss here the implications of our findings of high quantum yield and robustness for microtubules, actin bundles, and amyloid fibrils. In Alzheimer’s disease and related dementias, the prevailing theory is that amyloid plaque formation is a direct cause of the onset of the disease [39]. Based on our results we propose an alternative hypothesis to these previous observations on amyloid. By definition, if the QY of a structure was 1, then every photon that it absorbed would be re-emitted into the environment. We have predicted here that the QY of even small human amyloid fibrils $<1\mu$m is over 0.5. Given the significant absorption-emission Stokes shift of Trp, every photon that is re-emitted will be redshifted to a much lower energy than the UV photon that was absorbed, indicating that amyloid may serve a photoprotective role that downconverts dangerous UV photons in the brain to lower-energy photons which can be safely managed. Lower QY structures like microtubules and actin may assist with this process as well.

It is important to emphasize that the QY increases we predict here do not have any classical interpretation. If an analogous classical system, such as a classical antenna, could be used to describe these biosystems, it would not include the transition dipole moment of tryptophan (Trp), which is a genuinely quantum (electronic) transition. Even if such a classical collective effect were operative, large numbers of photons (e.g., in a Glauber coherent state) constituting a semi-classical light source would be required to excite such an antenna. In the single-photon regime, only a quantum mechanical interpretation is possible.

Tables 1, 2 show the decay rate values of the most superradiant and most subradiant states, along with other key observables associated with these diverse neuroprotein architectures. One trend we can see in Table 1—and according to which it is organized—is that the maximum superradiance of the axon bundles is the highest $({\tau }_{\text{super}}\propto 1/\text{max}({\mathrm{\Gamma }}_j))$, and as we go down the table, this value decreases for the other protein structures, with the smallest maximum superradiance (longest superradiant lifetime) belonging to the single actin filament. Large bundles of long, stably configured, straight microtubules in axons can exhibit enhanced, robust superradiance several thousands of times the single-Trp decay rate [3], suggesting possible routes for quantum information processing in the brain that would be at least nine orders of magnitude faster than Hodgkin-Huxley chemical signaling at the millisecond scale in spiking neurons.

After the microtubule-based structures, amyloid fibrils in both humans and mice have the next largest superradiant power outputs $(E_{\text{super}}/{\tau }_{\text{super}})$, both due to their high-energy clustering of superradiant states and their picosecond-scale superradiant lifetimes. Interestingly, among the protein structures we consider in Table 1, the maximum superradiant density $(\text{max}({\mathrm{\Gamma }}_j)/N\gamma )$ is the highest for a single microtubule of 320 nm (0.120) and a human amyloid fibril of 346 nm (0.113). Protein aggregates supporting such superradiant states with high power outputs could dissipate high-energy UV photons in an intensely oxidative cellular environment more quickly, and mitigate any potential damage. This is especially important in neuropathological conditions such as Alzheimer’s, but also in a host of other complex diseases characterized by high allostatic load and oxidative stress, where high-energy photons can be produced due to metabolic photon emissions. Our prediction of high power outputs for amyloid fibrils supports the hypothesis that amyloid fibrils and plaques could actually serve as photoprotective entities in the brain.

We also see in Tables 1, 2 the general trend of highly subradiant long-lived states correlated with highly superradiant short-lived states. (${\tau }_{\text{sub}}$ strictly decreases down Table 2, while ${\tau }_{\text{super}}$ strictly increases down Table 1.). Subradiant states have been predicted with high excitonic occupation probabilities on the inner lumen surface of microtubules, while superradiant states have more delocalized occupation probabilities but with a preference for the external microtubule surface (see Figure 4 of [2]). The lifetime of such superradiant states is faster than thermal noise from the aqueous environment surrounding the microtubule, whereas the lumen surface of the microtubule is exposed to a more ordered, gel-like matrix, and is thus subjected to far less thermal fluctuation. Such a locally protected environment could enable the potential exploitation of subradiant states (which are not particularly robust to noise) by living systems, possibly serving as a collective quantum mechanism for synchronizing behavior and information processing over long periods. (${\tau }_{\text{sub}}$ values in Table 2 are on the order of microseconds to tens of seconds.). In quantum information applications, the long lifetime of subradiant states in qubit architectures has been used to create very long-lived quantum memories [57], implement mechanisms for lossless transport of photons [58], and generate phase-imprinting for potential quantum storage of multiphotonic qubits in two-level systems [59].

The mechanism that makes superradiance possible is the delocalization of the excitation across many chromophores. The delocalization of a superradiant state in microtubules has been shown and visualized in Figure 4 of Ref. [2]. It has also been shown that in supramolecular dye [60] and photosynthetic nanotubes [13], superradiant states are delocalized across many chromophores. This delocalization is a clear sign of quantum coherence in the site basis. Although the study of a specific coherence measure is beyond the scope of this work, we do study the energy gap in the complex plane (Figure 13), which has been associated with cooperative robustness and supertransfer processes [2, 39], indicating quantum coherence. We have also studied coherence indirectly through cooperative robustness in Figure 5 of Ref. [3]. A detailed study of the off-diagonal elements of the density matrix and their dynamics is planned for future work.

An upper bound for the scaling of the decay rate of the maximally superradiant state in the single-excitation limit is $N\gamma$ ($\gamma$ is the single-system decay rate). While the buildup over time of macroscopic coherence through, for example, a laser pump-probe experiment is beyond the scope of our work here, Figures 8A, 10A demonstrate the scaling of the maximum decay rate with the length of the system (equivalently, the number of chromophores). These plots show how superradiance scales with the number of chromophores in these protein systems, due to long-range interactions and persistent delocalization across the network.

An important and subtle point to consider is the individual addressability of states (as either superradiant or subradiant states), versus the thermal average of the ensemble. In physical environments which are in thermal equilibrium, the thermal average should be used. In these cases, the behavior of the superradiant states dominates the thermal average, while the effect of subradiant states is negligible in the Gibbs ensemble. However, in environments which are not in thermal equilibrium, such as the interior of microtubules, the thermal average does not strictly apply, so subradiant states which are weighted negligibly in the Gibbs ensemble may take on a more pronounced importance.

Significantly, the structures we study in this work contain other aromatic amino acids, such as tyrosine and cysteine, but their transition dipole moments are much smaller than that of Trp at its peak excitation wavelength. Incorporating other amino acids into the network at close range to Trp would in principle change the non-radiative decay rates, especially as ultrafast electron-transfer effects emerge on the sub-picosecond timescale, competing with superradiance and potentially degrading the quantum yield. However, it is known that photoexcited tyrosine resonantly transfers its excitation energy to Trp on ultrafast timescales [61], enhancing the transition dipole strength of Trp rather than quenching it, and thus would increase the superradiant effect.²

It is of particular note that electron transfers from photoexcited Trp to peptide carbonyl groups occur on the 100 ps timescale, but electron transfers from photoexcited Trp to sulfur-containing residues within van der Waals (vdW) contact (∼5–6 Å) occur on the 10 ps timescale [55]. In a tubulin dimer, only $\sim 1.2\%$ of the Trp-Cys pairs are within vdW contact of each other, and so these ultrafast electron transfer effects are relatively minor in this system. Thus, the timescale for superradiant states in microtubules (few ps and below) is generally orders of magnitude faster than the operative electron-transfer phenomena. In actin, none of the Trp-Cys pairs are within 7Å of each other. The amyloid we studied in this work does not have any Cys residues, so electron transfers to sulfur-containing residues would be practically negligible in these systems. However, the extremely close Trp-Trp spacing in the amyloids we studied does warrant further ultrafast studies (like in [55]) to elucidate the timescale, role, and interplay of superradiant states and electron-transfer states [62, 63] in rapidly absorbing, dissipating, and downconverting UV photoexcitations.

In addition to other aromatic amino acids, there are other objects that may enhance superradiant emission even further. For example, in the $\beta$-sheets of amyloid displayed in Figure 2B, we can see that there are so-called short hydrogen bonds (SHBs) that connect the $\beta$-strands side-by-side. Even in the absence of aromatic chromophores like Trp, networks of these SHBs have been observed to absorb strongly in the UV band through proton transfer events, and emit in the visible band [64, 65]. It has been suggested that $n\to {\pi }^{*}$ transitions on amide groups [66] or blocking the vibrational mode associated with carbonyl elongation [67] stimulates such non-aromatic fluorescence. This means that, like with Trp, networks of SHBs in amyloid fibrils may exhibit their own bright superradiant states and enhance or modulate the QY of amyloid even beyond what we predict in this work.

Due to the incredibly high QY of amyloid fibrils and its potential for photoprotection, rather than being a cause of pathological conditions, amyloid fibrils could be a response to them, and to the highly oxidative environments that characterize them. Therapies that target amyloid in the brain for elimination could therefore exacerbate such diseases rather than ameliorating them.

There are at least 37 known proteins that form pathological amyloids [35]. We have found that the amyloids 6MST and 6DSO, which are associated with systemic AA amyloiosis [68], exhibit extremely robust QY. Since amyloids are a geometric class of protein architectures characterized by helical superstructures made of $\beta$-sheets, it is likely that amyloids formed from other proteins (such as lysozyme, insulin, and IAPP) will have similar transition dipole networks as discussed in Section 2.3, and thus may also exhibit the high QYs that would play a strongly photoprotective role in the pathological cellular environment.

Furthermore, the formation of structures called cofilin-actin rods from pools of actin and the cofilin protein have also been studied [69–71], with recent suggestions of potentially quantum behavior being disrupted in Alzheimer’s pathogenesis [71]. Cofilin-actin rods do have a helical structure: every subunit that is added to the rod comes with an approximate $5°$ twist [70]. Therefore, without having conducted any of the detailed analyses presented here for microtubules, actin bundles, and amyloid fibrils, we would hypothesize that cofilin-actin rods exhibit significant superradiance that may translate into robust, observable quantum yield effects based on the symmetry and interactions of their helical Trp networks. This is yet another instance in which a cylindrically or helically symmetric structure is created in the context of neurodegeneration, further stressing the importance of chromophore network geometry in protein lattices as the source of these robust superradiant effects.

As the microtubule results in the Supplementary Material and in Section 3.1 attest, the morphology and mechanical deformations of protein structures are crucial to understanding the modulation of superradiant effects. For example, amyloid fibrils are known to aggregate into macroscopic structures called amyloid plaques, together with glial and neuritic debris [72]. They are found in the grey matter of the brain in the areas associated with memory and cognition. Amyloid plaques can form spherically symmetric aggregates of amyloid fibrils with very dense cores [73]. Plaques have also been observed to form symmetric superarchitectures such as bundles, as well as mesh-like and star-like geometries [74]. Given these observations, amyloid plaques may exhibit even higher, more robust superradiance and quantum yield values than those of single fibrils, which would strengthen the argument of amyloid’s photoprotective role and of the mitigating effect of plaque formation in neurodegenerative pathology.

Our predictions of robust, observable increases in the QY for Trp networks in large protein polymeric architectures has implications for many other diseases outside the neurodegenerative context. For example, sickle-cell anemia results from a $\text{Glu}\to \text{Val}$ mutation of the amino acid at the sixth position on the beta chain of normal hemoglobin (HbA). The resulting deoxygenated hemoglobin (HbS) is known to aggregate in erythrocytes (red blood cells without nuclei) [75, 76] and form helical structures. These helical hemoglobin strands, commonly known as Wishner-Love helices, would then manifest helical Trp networks. We have found that helical Trp networks exhibit superradiance in three distinct cases (in microtubules, actin filaments, and amyloid fibrils), so hemoglobin’s helical Trp network may also exhibit significant superradiance and/or quantum yield. If these hemoglobin aggregates are indeed found to exhibit superradiance and robust increases in QY with increasing size, then quantum-enhanced photoprotection may also play an important role in the onset, progression, and treatment of hemoglobinopathies like sickle-cell, which are also associated with intensely oxidative and damaging cellular environments.

Our results pose opportunities for a paradigm shift in the theory of neuronal information processing and signaling. The role of microtubules in information processing in the brain has been studied extensively [24, 76–79]. Also, classical energy scalings cannot account for the sub-neuronal information processing capacity of the brain [80], given its extremely low input power of around 20 W. There must be another physical mechanism that enables the human brain to achieve the computational efficiency that it does, at orders of magnitude lower power consumptions than high-performance hardware systems. A tantalizing possibility is that extended protein architectures, such as those described here and elsewhere [2, 3], including axons in the brain, may form a highly interconnected, ultrafast quantum-optical network that gives rise to incredibly efficient transfer and processing of information. This mechanism would be much faster than chemical Hodgkin-Huxley-type transport based on neuronal sodium-potassium gradients firing at the millisecond timescale, which is currently used as a standard paradigm in neuroscience.

5 Conclusion and future plans

We analyze the interaction of the electromagnetic field with networks of tryptophan (Trp) chromophores. Geometrical information on these networks and the orientations of the Trp transition dipoles are extracted from realistic simulations of three types of neuroprotein architectural elements: microtubules, actin filaments/bundles, and amyloid fibrils. The Trp chromophores are modeled as two-level systems and exhibit superradiant behavior as a collective when coherently superposed in the single-excitation limit. We see this by diagonalizing the non-Hermitian Hamiltonian used to describe the collective light-matter interaction of such a weakly photoexcited system. All three structures were found to exhibit bright superradiant states due to symmetry and long-range couplings, which support robustness of the quantum yield as a figure of merit with increasing static disorder even up to five times room-temperature energy. In the case of microtubules and amyloid fibrils, the brightest superradiant states are clustered near the lowest-energy portion of their spectra, and these photophysical properties result in a large quantum yield that counterintuitively increases with system size and has been experimentally confirmed for microtubules [3].

Our results display the observable and important consequences that quantum coherent effects have on neuroprotein architectures. These analyses could strengthen our understanding of the etiology of neurodegenerative and other complex diseases, which are frequently characterized by anomalous protein polymers. Furthermore, our investigations of superradiance and subradiance in these neuroproteins are revealing an ultrafast mechanism that our brains may use to process information, which is paired with an extremely long-lived mechanism for coordinating biological function. This work contributes significantly to our understanding of how quantum biology can speed up, enhance, and optimize behavior in the “wetware” environments of living systems. Acknowledging the wide body of research that has been conducted on ultraweak and metabolic photon emissions in the cell, we have incorporated the interaction of neuroprotein Trp lattices with the electromagnetic field via the equations of quantum optics, giving us a totally different lens with which to view biology. Such a paradigm shift can greatly enhance our understanding of nature, to visualize biological architectures as chromophore lattices synchronized by long-range interactions, and imbued with unique and specific photophysical properties that are enhanced by collective light-matter interactions governed by the equations of quantum optics. Such a shift reflects a return to understanding, in the (paraphrased) words of Richard Feynman and with the ancients, how external light from the fiery sun causes trees and plants to grow from the carboniferous air; and in parallel symbiosis how oxygen-metabolizing organisms may have evolved their protein architectures to exploit “internal” photonic emissions for information processing and to mitigate potentially damaging wavelengths in the cell.

Future work will include performing experiments in order to verify the quantum yield predictions that we have made here. Analogous to prior work [3], where the increased quantum yield in microtubules from tubulin dimers in solution was unambiguously associated with the increased radiative rate due to superradiance, we now have a clear path and approach to experimental validation of collective quantum optical behavior in a wide class of protein polymeric aggregates in solution. We hope that this work will stimulate further experimental efforts in this regard.

6 Methods

6.1 Physical model

In this work we model tryptophan (Trp), a strongly fluorescent amino acid in the ultraviolet (UV) band, as a two-level system [5] with transition energy $e_0\approx 280\text{\hspace{0.17em}nm}=3.57\times 10^4{\text{\hspace{0.17em}cm}}^{-1}$ and decay rate $\gamma \approx 2.73\times 10^{-3}{\text{\hspace{0.17em}cm}}^{-1}$ [4, 78]. Trp has a large transition dipole moment of $\sim 6.0$ debye. We use a non-Hermitian Hamiltonian to describe the interaction of a $N$-dimensional Trp network with the electromagnetic field [79–85].

$H_{\text{eff}}=H_0+\mathrm{\Delta }-\frac{i}{2}G(4)$

where.

$H_0={\displaystyle \sum _{n=0}^{N-1}}\hslash {\omega }_0|n\rangle \langle n|(5)$

$\mathrm{\Delta }={\displaystyle \sum _{n\ne m}^N}{\mathrm{\Delta }}_{nm}|n\rangle \langle m|(6)$

$G={\displaystyle \sum _{n=0}^{N-1}}\gamma |n\rangle \langle n|+{\displaystyle \sum _{n\ne m}^N}{G}_{nm}|n\rangle \langle m|(7)$

$\begin{array}{ll}\hfill {\mathrm{\Delta }}_{nm}& =\frac{3\gamma }{4}\left[\left(-\frac{\cos \left({\alpha }_{nm}\right)}{{\alpha }_{nm}}+\frac{\sin \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^2}+\frac{\cos \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^3}\right){\widehat{\mu }}_n\cdot {\widehat{\mu }}_m\right.\hfill \\ \hfill & \left.-\left(-\frac{\cos \left({\alpha }_{nm}\right)}{{\alpha }_{nm}}+3\frac{\sin \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^2}+3\frac{\cos \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^3}\right)\left({\widehat{\mu }}_n\cdot {\widehat{r}}_{nm}\right)\left({\widehat{\mu }}_m\cdot {\widehat{r}}_{nm}\right)\right]\hfill \end{array}(8)$

$\begin{array}{ll}\hfill G_{nm}& =\frac{3\gamma }{2}\left[\left(\frac{\sin \left({\alpha }_{nm}\right)}{{\alpha }_{nm}}+\frac{\cos \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^2}-\frac{\sin \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^3}\right){\widehat{\mu }}_n\cdot {\widehat{\mu }}_m\right.\hfill \\ \hfill & \left.-\left(\frac{\sin \left({\alpha }_{nm}\right)}{{\alpha }_{nm}}+3\frac{\cos \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^2}-3\frac{\sin \left({\alpha }_{nm}\right)}{{{\alpha }_{nm}}^3}\right)\left({\widehat{\mu }}_n\cdot {\widehat{r}}_{nm}\right)\left({\widehat{\mu }}_m\cdot {\widehat{r}}_{nm}\right)\right]\hfill \end{array}(9)$

where ${\alpha }_{nm}\equiv k_0{r}_{nm}$. The constants $k_0$ and ${\omega }_0$ are defined in terms of $e_0$ by $k_0=2\pi e_0\times 10^{-8}$ and ${\omega }_0=2\pi e_{0}c/n_r\times 10^{-8}$ where $n_r\approx \sqrt{{\epsilon }_r}$ is the refractive index assuming that relative permeability is 1. The vector ${\widehat{r}}_{nm}$ is the unit vector pointing from the $n^{\text{th}}$ site to the $m^{\text{th}}$ site in physical space, and $r_{nm}$ is the distance between the $n^{\text{th}}$ and $m^{\text{th}}$ sites. The unit vector ${\widehat{\mu }}_n$ is the transition dipole moment of the $n^{\text{th}}$ site.

The dynamics of the system is governed by the Schrödinger equation with the non-Hermitian Hamiltonian

$i\hslash \frac{\partial }{\partial t}|\psi \left(t\right)\rangle =H_{\text{eff}}|\psi \left(t\right)\rangle .(10)$

This means that the evolution of the state vector is not unitary, representing a leakage of probability into the envirnonment. Utilizing a non-Hermitian Hamiltonian with the Schrödinger equation is completely equivalent to using a Lindblad master-equation approach, in which the environment is modeled by a set of Lindblad operators (not necessarily Hermitian). This means that all the same approximations that go into the Lindblad equation (Born-Markov approximation, rotating wave approximation, weak interaction with environment, etc.) apply to our model. The non-Hermiticity of the Hamiltonian also means that there are two sets of eigenvectors: the right and left eigenvectors, which are given by

$H_{\text{eff}}|\psi \rangle ={\mathcal{E}}_j|{\mathcal{E}}_j^R\rangle (11)$

$\langle \psi |H_{\text{eff}}^{†}=\langle {\mathcal{E}}_j^L|{\mathcal{E}}_j.(12)$

Since the Hamiltonian is symmetric, the left and right eigenvectors are transposes of each other.

6.2 Quantum yield

The quantum yield (QY) is a dimensionless number from 0 to 1 that is defined to be the ratio of the number of photons emitted to the number of photons absorbed. Equivalently, it can be written as

$\text{QY}\equiv \frac{\mathrm{\Gamma }}{\mathrm{\Gamma }+{\mathrm{\Gamma }}_{nr}}(13)$

where $\mathrm{\Gamma }$ is the collective radiative decay rate, and ${\mathrm{\Gamma }}_{nr}$ is the non-radiative decay rate. The QY ranges from 0 to 1. If the QY is close to 1, that means that most photons that get absorbed get re-emitted, and if the QY is close to 0, that means that most photons that get absorbed do not get re-emitted. Trp is known to have a significant absorption-emission Stokes shift [3], so photons will be re-emitted at a lower energy than that of their absorption. Therefore, if a Trp network has a high QY, it can be inferred that the Trp network will act in a photoprotective role against high-energy UV photons: absorbing them and then “downconverting” (red-shifting) them to a lower energy.

Since biological structures exist in a warm and wet environment, we take the thermal average of our quantities. Firstly, the partition function $Z$ is given by

$Z={\displaystyle \sum _{j=0}^{N-1}}\exp \left(-\beta E_j\right)(14)$

where $\beta \equiv {(k_{B}T)}^{-1}$. The thermal average of the decay rate is then

${⟨\mathrm{\Gamma }⟩}_{th}=\frac{1}{Z}{\displaystyle \sum _{j=0}^{N-1}}{\mathrm{\Gamma }}_j\exp \left(-\beta E_j\right).(15)$

This allows us to calculate the thermal average of the QY

${\langle \text{QY}\rangle }_{th}=\frac{{\langle \mathrm{\Gamma }\rangle }_{th}}{{\langle \mathrm{\Gamma }\rangle }_{th}+{\langle {\mathrm{\Gamma }}_{nr}\rangle }_{th}}.(16)$

We take ${⟨{\mathrm{\Gamma }}_{nr}⟩}_{th}={\gamma }_{nr}=1.93\times 10^{-2}$, where ${\gamma }_{nr}$ is the non-radiative decay rate of a single Trp in BRB80 buffer solution [3]. This non-radiative decay rate takes into account the average effect of non-radiative processes, such as those due to decoherence, potential photodamage, etc. We can see that ${\gamma }_{nr}$ is approximately an order of magnitude larger than $\gamma$ (equivalently, the timescale of the non-radiative processes are a factor of 10 larger than the radiative lifetime, assuming exponential decay). However, superradiant enhancement studied in this work can increase the radiative decay rate by more than a factor of 100, which means that the radiative processes in this case occur much faster than non-radiative processes, in the weak excitation limit. We can take the collective non-radiative decay rate as equal to the single-Trp non-radiative decay rate, assuming conservatively that there is no reduction in the non-radiative decay rate leading to an increase in the QY. This represents the assumption that Trp network formation in protein introduces no change in the non-radiative decay channels, as compared with Trp alone in solution. Recent experimental evidence [3] indicates that Trp network formation in tubulin actually increases the non-radiative decay rate, suggesting that the protein environment competes with superradiant enhancements to modulate the observed QY.

6.3 Static disorder

6.3.1 Site energies

In addition to taking the thermal average of the QY, we also consider the effects of random fluctuations in the site energies, i.e., static disorder, on our model Hamiltonian. We do this by modifying the $H_0$ term Eq. 5 of our Hamiltonian as follows:

$H_0\to H_0+{\displaystyle \sum _{n=0}^{N-1}}{ϵ}_n\left(W\right)|n\rangle \langle n|,(17)$

where $W$ is the strength of the static disorder in units of ${\text{cm}}^{-1}$, and ${ϵ}_n(W)$ is a uniform random number (also units of ${\text{cm}}^{-1}$) in the range $[-\frac{W}{2},\frac{W}{2}]$.

We then diagonalize the Hamiltonian with the new $H_0$, and calculate QY with the new eigenvalues. We do this 10 times, and calculate the QY in each run. Then, we calculate the average of these 10 QYs, to determine the average effect of the random fluctuations in the site energies.

Note that we do not study the dynamics of our systems, and thus do not consider dynamical instabilities in this work. However, the structures we study are stable for extraordinarily long times (up to years) in mammalian neurons and eukaryotic cells that are not undergoing mitosis. We also obtain all of our results in the steady-state (thermal equilibrium), so dynamical instabilities are not as significant as the static disorder that we take into account.

6.3.2 Single-tryptophan decay rate

We also implement static disorder in the single-Trp decay rate $\gamma$ as follows. For each $\gamma$ value on the diagonal (i.e., on-site $\gamma$ values):

$\gamma \to \gamma \left(n,n\right)=\gamma +\delta {\gamma }_{nn}\left(a\right),(18)$

where $\delta {\gamma }_{nn}(a)$ is a random number in the range $[-\frac{a\gamma }{2},\frac{a\gamma }{2}]$, and $a$ is a dimensionless, positive real number not greater than 2 ($a\le 2$ since $\gamma$ must be non-negative). Note that the new $\gamma$ values are different for each Trp site (as indicated by the dependence on the index $n$). For each off-diagonal $\gamma$, it is changed to the mean of the corresponding on-diagonal $\gamma$ values:

$\gamma \to \gamma \left(n,m\right)=\frac{\gamma \left(n,n\right)+\gamma \left(m,m\right)}{2}.(19)$

Note that by Eq. 19, $\gamma (n,m)=\gamma (m,n)$, which keeps the Hamiltonian symmetric. Once this procedure is done for the Hamiltonian, we diagonalize it andfind new decay rates and energy shifts. We repeat this process 10 times, calculate the QY for each of the 10 realizations, and take the average of the QY.

6.4 Biological structures

We model three sets of biological structures in this paper: microtubules, actin filaments, and amyloid fibrils. Python scripts that implement all the following procedures and generate all PDB files for structures of a given length can be found in this GitHub repository link in the Data Availability Statement.

6.4.1 Microtubules

We construct models of microtubules of varying length from the tubulin dimer stored in the Protein Data Bank (PDB) entry 1JFF [86] as per the methods given in Appendix A of [2] and Section S3 in [3]. We briefly summarize the procedure here.

Many identical 1JFF tubulin dimers are laid next to one another to form a left-handed helical microtubule structure with a diameter of 22.4 nm. The initial orientation of one tubulin dimer is such that the $\alpha$ and $\beta$ chains lie both along the protofilament direction. Let this be the x-axis. Then, each tubulin dimer is acted on by the following initial operations: (1) rotated by −55.38$°$ about its longitudinal axis, (2) rotated by 11.7$°$ about the $\beta$-tubulin Trp346 CD2 atom, and (3) translated by 11.2 nm in the y-direction and 0.3 nm in the z-direction. After applying operations (1)–(3) to each tubulin dimer, a set of operations is applied $N$ times to the $N$th dimer to form a single spiral (one spiral consists of 13 tubulin dimers, so $N\le 13$): (4) rotation of 27.69$°$ about the x-axis and (5) translation of 0.9 nm in the x-direction. This generates a 13-dimer spiral. To create microtubules with multiple spirals, each spiral is translated multiples of 80 nm in the x-direction from the initial spiral. This procedure creates microtubules with a radius of $\sim 11.2$ nm (from the microtubule longitudinal axis to the tubulin dimer center-of-mass), approximately intermediate between the outer (cytoplasm-surface) radius of $\sim 13.5$ nm and the inner (lumen-surface) radius of $\sim 9.5$ nm.

After creating a microtubule, the positions and transition dipole moments of the eight Trp residues in each tubulin dimer are extracted. The position of a Trp molecule is given by the midpoint of the positions of the CD2 and CE2 carbon atoms in it. The transition dipole moment of a Trp molecule is taken as the well-known¹$L_a$ transition of Trp [5, 7], which is the vector pointing 46.2$°$ above the axis joining the midpoint between the CD2 and CE2 carbons and carbon CD1, in the plane of the indole ring (i.e., towards nitrogen NE1).

6.4.2 Actin filaments and actin filament bundles

We construct models of actin filaments of varying length from the PDB entry 6BNO as per the description of the structure given in [87]. The procedure to generate actin filaments of a specified length is summarized below.

Many identical 6BNO bare actin subunits are laid next to one another to form a right-handed helical filament. Let the logitudinal direction of the filament be defined as the x-axis. Then, the following operations are applied $N$ times to the $N$th subunit: (1) translation of 22.488 nm in the x-direction and (2) rotation by −253.2$°$ about its own axis (the x-axis). This creates actin filaments consisting of any number of 6BNO subunits. Extraction of Trp positions and transition dipole moments is performed in the same manner as outlined in Section 6.4.1.

We also take many actin filaments constructed in this way, and pack them together in concentric hexagons, forming actin bundles. This creates bundles containing $3N^2-3N+1$ filaments, where $N$ is the number of concentric hexagons, including the center. We create and study 7-filament $(N=2)$ and 19-filament $(N=3)$ bundles.

6.4.3 Amyloid fibrils

We construct models of human (mouse) amyloid fibrils of varying length from the PDB entries 6MST (6DSO), respectively, as per the descriptions of the structures given in [68]. The procedure to generate amyloid fibrils of a specified length is summarized below. For both human and mouse amyloid, each subunit is characterized by a six-strand $\beta$-sheet structure, where each $\beta$ strand is joined to its neighbor via hydrogen bonds. The entire fibril is also known as a $\beta$ helix.

Many identical 6MST (6DSO) amyloid subunits are laid next to one another to form a right (left)-handed helical fibril. Before applying the necessary operations, we find that a preliminary translation is required for each 6MST (6DSO) subunit: -14.0474 (−14.1715) nm in the x-direction, −14.0376 (−14.1595) nm in the y-direction, and −14.0039 (−11.8823) nm in the z-direction. This moves the center of mass of the amyloid subunit to the origin, so that subsequent rotations are performed along the axis parallel to the would-be fibril direction that passes through the center of mass. Let this axis be defined as the x-axis. Then, the following operations are applied $N$ times to the $N$th subunit for 6MST: (1) translation of 2.88 nm in the x-direction and (2) rotation by 9.24$°$ about its own axis (the x-axis). For 6DSO, the translation is the same, but the rotation is −6.90$°$ about its own axis. This procedure ensures that the beta strands in both the human and mouse amyloid are separated 4.8 Å from each other along the main fibril axis, consistent with the spacings observed in the crystal structures. This procedure creates amyloid fibrils consisting of any number of amyloid subunits. Extraction of Trp positions and dipole moments is performed in the same manner as outlined in Section 6.4.1.

6.5 Matrix diagonalization

For all systems, we utilized Python’s eig() function from the NumPy library to calculate the eigensolutions for the non-Hermitian symmetric Hamiltonian matrices. The eig() function, according to the NumPy documentation (https://numpy.org/doc/stable/reference/generated/numpy.linalg.eig.html) is implemented using the standard _geev LAPACK Fortran routines which calculate eigensolutions for general complex square matrices. In our case, the specific routine of interest is zgeev. The zgeev routine could handle even the largest Hamiltonian matrices we have studied in this work and in our previous work [3], of dimension $\sim 10^5\times 10^5$. All matrices were diagonalized on a system with a Dual Intel^® Xeon^® Gold 6248 Processor, with multi-threading enabled for the eigenvalue calculation. With these specifications, diagonalizing a $60800\times 60800$ matix took approximately 13.3 h ($\sim 47900$ seconds). The complex-valued matrix was stored in $\sim 30$ GB of memory, using 8 bytes for each complex number (4 for the real part and 4 for the imaginary part).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. The GitLab repository which contains all the code used by the authors can be found at this link: https://gitlab.com/superradiance/superradiance_in_tryptophan_architectures.

Author contributions

HP: Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. NB: Data curation, Investigation, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. PK: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in parts by the Alfred P. Sloan Foundation, Guy Foundation (United Kingdom), and Chaikin-Wile Foundation.

Acknowledgments

This research used resources of the Argonne Leadership Computing Facility, a U.S. Department of Energy (DOE) Office of Science user facility at Argonne National Laboratory supported by the U.S. DOE Office of Science-Advanced Scientific Computing Research Program, under Contract No. DE-AC02-06CH11357. The authors thank the Howard University RCMI program for supporting publication charges to make this article open access. Portions of the manuscript were drafted and discussed during PK’s 2023 residency as a Fellow of the Kavli Institute for Theoretical Physics (KITP), which was supported in part by grant NSF PHY-1748958 to KITP.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer AH declared a past co-authorship with the author(s) PK to the handling editor.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1387271/full#supplementary-material

Footnotes

¹Centrioles are cylindrically symmetric organelles formed from nine triplets of microtubules exhibiting a pinwheel-like structure (see [17] for more specifics on their geometry). They are highly conserved in most eukaryotic cells, but notably absent in yeast and higher plants, among others [17]. Centrioles play an important role in forming the spindle complex in cell division, where they help ensure that the correct number of chromosomes are present in each daughter cell after replication [18, 19]. They have also been shown, in several studies by Guenter Albrecht-Buehler [20–23], to aid orientation of the cell to an external light stimulus.

²The number of Trp-Tyr pairs within van der Waals contact (∼$5$-6Å) in a tubulin dimer is $\sim 2.5\%$ of the total number of Trp-Tyr pairs. This means that in microtubules, while the enhancement of the Trp dipole strength due to Tyr may be small, it may be more significant than quenching effects due to other residues (see paragraph below).

References

1. Dicke RH. Coherence in spontaneous radiation processes. Phys Rev (1954) 93:99–110. doi:10.1103/PhysRev.93.99

CrossRef Full Text | Google Scholar

2. Celardo GL, Angeli M, Craddock TJA, Kurian P. On the existence of superradiant excitonic states in microtubules. New J Phys (2019) 21:023005. doi:10.1088/1367-2630/aaf839

CrossRef Full Text | Google Scholar

3. Babcock NS, Montes-Cabrera G, Oberhofer KE, Chergui M, Celardo GL, Kurian P. Ultraviolet superradiance from mega-networks of tryptophan in biological architectures. J Phys Chem B (2024) 128:4035–46. doi:10.1021/acs.jpcb.3c07936

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kurian P, Obisesan T, Craddock TJ. Oxidative species-induced excitonic transport in tubulin aromatic networks: potential implications for neurodegenerative disease. J Photochem Photobiol B: Biol (2017) 175:109–24. doi:10.1016/j.jphotobiol.2017.08.033

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Callis PR. [7] 1La and 1Lb transitions of tryptophan: applications of theory and experimental observations to fluorescence of proteins. Fluorescence Spectroscopy (Academic Press). Methods Enzymol (1997) 278:113–50. doi:10.1016/S0076-6879(97)78009-1

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Vivian JT, Callis PR. Mechanisms of tryptophan fluorescence shifts in proteins. Biophysical J (2001) 80:2093–109. doi:10.1016/s0006-3495(01)76183-8

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Schenkl S, van Mourik F, van der Zwan G, Haacke S, Chergui M. Probing the ultrafast charge translocation of photoexcited retinal in bacteriorhodopsin. Science (2005) 309:917–20. doi:10.1126/science.1111482

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Engel GS, Calhoun TR, Read EL, Ahn TK, Mančal T, Cheng YC, et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature (2007) 446:782–6. doi:10.1038/nature05678

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Panitchayangkoon G, Hayes D, Fransted KA, Caram JR, Harel E, Wen J, et al. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc Natl Acad Sci USA (2010) 107:12766–70. doi:10.1073/pnas.1005484107

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Collini E, Wong CY, Wilk KE, Curmi PM, Brumer P, Scholes GD. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature (2010) 463:644–7. doi:10.1038/nature08811

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Strümpfer J, Sener M, Schulten K. How quantum coherence assists photosynthetic light-harvesting. J Phys Chem Lett (2012) 3:536–42. doi:10.1021/jz201459c

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Jang SJ, Mennucci B. Delocalized excitons in natural light-harvesting complexes. Rev Mod Phys (2018) 90:035003. doi:10.1103/RevModPhys.90.035003

CrossRef Full Text | Google Scholar

13. Doria S, Sinclair TS, Klein ND, Bennett DI, Chuang C, Freyria FS, et al. Photochemical control of exciton superradiance in light-harvesting Nanotubes. ACS Nano (2018) 12:4556–64. doi:10.1021/acsnano.8b00911

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Mattiotti F, Kuno M, Borgonovi F, Jankó B, Celardo GL. Thermal decoherence of superradiance in lead halide perovskite nanocrystal superlattices. Nano Lett (2020) 20:7382–8. doi:10.1021/acs.nanolett.0c02784

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mattiotti F, Sarovar M, Giusteri GG, Borgonovi F, Celardo GL. Efficient light harvesting and photon sensing via engineered cooperative effects. New J Phys (2022) 24:013027. doi:10.1088/1367-2630/ac4127

CrossRef Full Text | Google Scholar

16. Werren N, Brown W, Gauger EM. Light harvesting enhanced by quantum ratchet states. PRX Energy (2023) 2:013002. doi:10.1103/prxenergy.2.013002

CrossRef Full Text | Google Scholar

17. Winey M, O’Toole E. Centriole structure. Philos Trans R Soc B: Biol Sci (2014) 369:20130457. doi:10.1098/rstb.2013.0457

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Fırat-Karalar EN, Stearns T. The centriole duplication cycle. Philos Trans R Soc B: Biol Sci (2014) 369:20130460. doi:10.1098/rstb.2013.0460

CrossRef Full Text | Google Scholar

19. Rodrigues-Martins A, Riparbelli M, Callaini G, Glover DM, Bettencourt-Dias M. From centriole biogenesis to cellular function: centrioles are essential for cell division at critical developmental stages. Cell Cycle (2008) 7:11–6. doi:10.4161/cc.7.1.5226

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Albrecht-Buehler G. Rudimentary form of cellular “vision”. Proc Natl Acad Sci USA (1992) 89:8288–92. doi:10.1073/pnas.89.17.8288

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Albrecht-Buehler G. Cellular infrared detector appears to be contained in the centrosome. Cell Motil Cytoskeleton (1994) 27:262–71. doi:10.1002/cm.970270307

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Albrecht-Buehler G. Autofluorescence of live purple bacteria in the near infrared. Exp Cell Res (1997) 236:43–50. doi:10.1006/excr.1996.3688

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Albrecht-Buehler G. Phagokinetic tracks of 3T3 cells: parallels between the orientation of track segments and of cellular structures which contain actin or tubulin. Cell (1977) 12:333–9. doi:10.1016/0092-8674(77)90109-x

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ahmad FJ, He Y, Myers KA, Hasaka TP, Francis F, Black MM, et al. Effects of dynactin disruption and dynein depletion on axonal microtubules. Traffic (2006) 7:524–37. doi:10.1111/j.1600-0854.2006.00403.x

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Matsudaira P, Mandelkow E, Renner W, Hesterberg LK, Weber K. Role of fimbrin and villin in determining the interfilament distances of actin bundles. Nature (1983) 301:209–14. doi:10.1038/301209a0

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Pelucchi S, Stringhi R, Marcello E. Dendritic spines in Alzheimer’s disease: how the actin cytoskeleton contributes to synaptic failure. Int J Mol Sci (2020) 21:908. doi:10.3390/ijms21030908

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pauling L, Corey RB, Branson HR. The structure of proteins: two hydrogen-bonded helical configurations of the polypeptide chain. Proc Natl Acad Sci USA (1951) 37:205–11. doi:10.1073/pnas.37.4.205

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Eves BJ, Doutch JJ, Terry AE, Yin H, Moulin M, Haertlein M, et al. Elongation rate and average length of amyloid fibrils in solution using isotope-labelled small-angle neutron scattering. RSC Chem Biol (2021) 2:1232–8. doi:10.1039/d1cb00001b

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Toyama BH, Weissman JS. Amyloid structure: conformational diversity and consequences. Annu Rev Biochem (2011) 80:557–85. doi:10.1146/annurev-biochem-090908-120656

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Segers-Nolten I, van Raaij M, Subramaniam V. “Biophysical analysis of amyloid formation,” in Comprehensive Biomaterials. Elsevier (2011). p. 347–59. doi:10.1016/b978-0-08-055294-1.00086-6

CrossRef Full Text | Google Scholar

31. Findeis MA, Musso GM, Arico-Muendel CC, Benjamin HW, Hundal AM, Lee JJ, et al. Modified-peptide inhibitors of amyloid β-peptide polymerization. Biochemistry (1999) 38:6791–800. doi:10.1021/bi982824n

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Akter R, Cao P, Noor H, Ridgway Z, Tu LH, Wang H, et al. Islet amyloid polypeptide: structure, function, and pathophysiology. J Diabetes Res (2016) 2016:1–18. doi:10.1155/2016/2798269

CrossRef Full Text | Google Scholar

33. Kyle RA. Amyloidosis: a convoluted story. Br J Haematol (2001) 114:529–38. doi:10.1046/j.1365-2141.2001.02999.x

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Nielsen L, Khurana R, Coats A, Frokjaer S, Brange J, Vyas S, et al. Effect of environmental factors on the kinetics of insulin fibril formation: elucidation of the molecular mechanism. Biochemistry (2001) 40:6036–46. PMID: 11352739. doi:10.1021/bi002555c

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Chiti F, Dobson CM. Protein misfolding, amyloid formation, and human disease: a summary of progress over the last decade. Annu Rev Biochem (2017) 86:27–68. doi:10.1146/annurev-biochem-061516-045115

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Nelson R, Eisenberg D. Recent atomic models of amyloid fibril structure. Curr Opin Struct Biol (2006) 16:260–5. doi:10.1016/j.sbi.2006.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Brion JP, Hanger DP, Bruce MT, Couck AM, Flament-Durand J, Anderton BH. Tau in Alzheimer neurofibrillary tangles. N- and C-terminal regions are differentially associated with paired helical filaments and the location of a putative abnormal phosphorylation site. Biochem J (1991) 273:127–33. doi:10.1042/bj2730127

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Binder LI, Guillozet-Bongaarts AL, Garcia-Sierra F, Berry RW. Tau, tangles, and Alzheimer’s disease. Biochim Biophys Acta (Bba) - Mol Basis Dis (2005) 1739:216–23. doi:10.1016/j.bbadis.2004.08.014

CrossRef Full Text | Google Scholar

39. Ow S, Dunstan DE. A brief overview of amyloids and Alzheimer’s disease. Protein Sci (2014) 23:1315–31. doi:10.1002/pro.2524

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gullì M, Valzelli A, Mattiotti F, Angeli M, Borgonovi F, Celardo GL. Macroscopic coherence as an emergent property in molecular nanotubes. New J Phys (2019) 21:013019. doi:10.1088/1367-2630/aaf01a

CrossRef Full Text | Google Scholar

41. Moiseyev N. Non-hermitian quantum mechanics. Cambridge University Press (2011). doi:10.1017/cbo9780511976186

CrossRef Full Text | Google Scholar

42. Breuer HP, Petruccione F. The theory of open quantum systems. Oxford University Press (2007). doi:10.1093/acprof:oso/9780199213900.001.0001

CrossRef Full Text | Google Scholar

43. Manzano D. A short introduction to the Lindblad master equation. AIP Adv (2020) 10:025106. doi:10.1063/1.5115323

CrossRef Full Text | Google Scholar

44. Lindblad G. On the generators of quantum dynamical semigroups. Commun Math Phys (1976) 48:119–30. doi:10.1007/BF01608499

CrossRef Full Text | Google Scholar

45. Havelka D, Deriu MA, Cifra M, Kučera O. Deformation pattern in vibrating microtubule: structural mechanics study based on an atomistic approach. Scientific Rep (2017) 7:4227. doi:10.1038/s41598-017-04272-w

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Yao S, Wang Z. Edge states and topological invariants of non-hermitian systems. Phys Rev Lett (2018) 121:086803. doi:10.1103/physrevlett.121.086803

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Song F, Yao S, Wang Z. Non-hermitian topological invariants in real space. Phys Rev Lett (2019) 123:246801. doi:10.1103/physrevlett.123.246801

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Bauer B, Sharma R, Chergui M, Oppermann M. Exciton decay mechanism in DNA single strands: back-electron transfer and ultrafast base motions. Chem Sci (2022) 13:5230–42. doi:10.1039/d1sc06450a

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Renaud N, Berlin YA, Lewis FD, Ratner MA. Between superexchange and hopping: an intermediate charge-transfer mechanism in poly(A)-Poly(T) DNA hairpins. J Am Chem Soc (2013) 135:3953–63. doi:10.1021/ja3113998

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Bittner ER. Lattice theory of ultrafast excitonic and charge-transfer dynamics in DNA. J Chem Phys (2006) 125:094909. doi:10.1063/1.2335452

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Spata VA, Matsika S. Role of excitonic coupling and charge-transfer states in the absorption and CD spectra of adenine-based oligonucleotides investigated through QM/MM simulations. J Phys Chem A (2014) 118:12021–30. doi:10.1021/jp507520c

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Jong KH, Azar YT, Grisanti L, Stephens AD, Jones STE, Credgington D, et al. Low energy optical excitations as an indicator of structural changes initiated at the termini of amyloid proteins. Phys Chem Chem Phys (2019) 21:23931–42. doi:10.1039/c9cp04648h

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Oakley MT, Hirst JD. Charge-transfer transitions in protein circular dichroism calculations. J Am Chem Soc (2006) 128:12414–5. doi:10.1021/ja0644125

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Andrea Rozzi C, Maria Falke S, Spallanzani N, Rubio A, Molinari E, Brida D, et al. Quantum coherence controls the charge separation in a prototypical artificial light-harvesting system. Nat Commun (2013) 4:1602. doi:10.1038/ncomms2603

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Qiu W, Li T, Zhang L, Yang Y, Kao YT, Wang L, et al. Ultrafast quenching of tryptophan fluorescence in proteins: interresidue and intrahelical electron transfer. Chem Phys (2008) 350:154–64. doi:10.1016/j.chemphys.2008.01.061

CrossRef Full Text | Google Scholar

56. Kao YT, Guo X, Yang Y, Liu Z, Hassanali A, Song QH, et al. Ultrafast dynamics of nonequilibrium electron transfer in photoinduced redox cycle: solvent mediation and conformation flexibility. J Phys Chem B (2012) 116:9130–40. doi:10.1021/jp304518f

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Asenjo-Garcia A, Moreno-Cardoner M, Albrecht A, Kimble HJ, Chang DE. Exponential improvement in photon storage fidelities using subradiance and “selective radiance” in atomic arrays. Phys Rev X (2017) 7:031024. doi:10.1103/physrevx.7.031024

CrossRef Full Text | Google Scholar

58. Gutiérrez-Jáuregui R, Asenjo-Garcia A. Directional transport along an atomic chain. Phys Rev A (2022) 105:043703. doi:10.1103/physreva.105.043703

CrossRef Full Text | Google Scholar

59. Jen HH. Phase-imprinted multiphoton subradiant states. Phys Rev A (2017) 96:023814. doi:10.1103/physreva.96.023814

CrossRef Full Text | Google Scholar

60. Eisele DM, Cone CW, Bloemsma EA, Vlaming SM, van der Kwaak CGF, Silbey RJ, et al. Utilizing redox-chemistry to elucidate the nature of exciton transitions in supramolecular dye nanotubes. Nat Chem (2012) 4:655–62. doi:10.1038/nchem.1380

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Li H, Jiang G, Jia M, Cao S, Zhang S, Chen J, et al. Ultrafast Förster resonance energy transfer between tyrosine and tryptophan: potential contributions to protein–water dynamics measurements. Phys Chem Chem Phys (2022) 24:18055–66. doi:10.1039/d2cp02139k

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Gregory WE, Sharma B, Hu L, Raghavendra AJ, Podila R. Interfacial charge transfer with exfoliated graphene inhibits fibril formation in lysozyme amyloid. Biointerphases (2020) 15(3):031010. doi:10.1116/6.0000019

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Cha W, Heo C, Lee S, Yun SJ, Cho BW, Ha T, et al. Probing interfacial charge transfer between amyloid-β and graphene during amyloid fibrillization using Raman Spectroscopy. ACS Nano (2023) 17(5):4834–4842. doi:10.1021/acsnano.2c11428

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Grisanti L, Pinotsi D, Gebauer R, Kaminski Schierle GS, Hassanali AA. A computational study on how structure influences the optical properties in model crystal structures of amyloid fibrils. Phys Chem Chem Phys (2017) 19:4030–40. doi:10.1039/c6cp07564a

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Stephens AD, Qaisrani MN, Ruggiero MT, Díaz Mirón G, Morzan UN, González Lebrero MC, et al. Short hydrogen bonds enhance nonaromatic protein-related fluorescence. Proc Natl Acad Sci USA (2021) 118:e2020389118. doi:10.1073/pnas.2020389118

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Grisanti L, Sapunar M, Hassanali A, Došlić N. Toward understanding optical properties of amyloids: a reaction path and nonadiabatic dynamics study. J Am Chem Soc (2020) 142:18042–9. doi:10.1021/jacs.0c07134

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Mirón GD, Semelak JA, Grisanti L, Rodriguez A, Conti I, Stella M, et al. The carbonyl-lock mechanism underlying non-aromatic fluorescence in biological matter. Nat Commun (2023) 14:7325. doi:10.1038/s41467-023-42874-3

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Liberta F, Loerch S, Rennegarbe M, Schierhorn A, Westermark P, Westermark GT, et al. Cryo-EM fibril structures from systemic AA amyloidosis reveal the species complementarity of pathological amyloids. Nat Commun (2019) 10:1104–10. doi:10.1038/s41467-019-09033-z

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Jang DH, Han JH, Lee SH, Lee YS, Park H, Lee SH, et al. Cofilin expression induces cofilin-actin rod formation and disrupts synaptic structure and function in Aplysia synapses. Proc Natl Acad Sci USA (2005) 102:16072–7. doi:10.1073/pnas.0507675102

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Bamburg JR, Bernstein BW. Actin dynamics and cofilin-actin rods in Alzheimer disease. Cytoskeleton (2016) 73:477–97. doi:10.1002/cm.21282

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Nichols TW, Berman MH, Tuszynski JA. Is Alzheimer’s disease a manifestation of brain quantum decoherence resulting from mitochondrial and microtubular deterioration? J Multiscale Neurosci (2023) 2 (1):141–158. doi:10.56280/1564010613

CrossRef Full Text | Google Scholar

72. Bazan NG, Halabi A, Ertel M, Petasis NA. Chapter 34 - Neuroinflammation. In: ST Brady, GJ Siegel, RW Albers, and DL Price, editors. Basic neurochemistry. 8th ed. New York: Academic Press (2012). p. 610–20. doi:10.1016/B978-0-12-374947-5.00034-1

CrossRef Full Text | Google Scholar

73. Merz PA, Wisniewski HM, Somerville RA, Bobin SA, Masters CL, Iqbal K. Ultrastructural morphology of amyloid fibrils from neuritic and amyloid plaques. Acta Neuropathologica (1983) 60:113–24. doi:10.1007/bf00685355

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Han S, Kollmer M, Markx D, Claus S, Walther P, Fändrich M. Amyloid plaque structure and cell surface interactions of β-amyloid fibrils revealed by electron tomography. Scientific Rep (2017) 7:43577. doi:10.1038/srep43577

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Mu XQ, Makowski L, Magdoff-Fairchild B. Analysis of the stability of hemoglobin S double strands. Biophysical J (1998) 74:655–68. doi:10.1016/s0006-3495(98)77825-7

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Henry ER, Cellmer T, Dunkelberger EB, Metaferia B, Hofrichter J, Li Q, et al. Allosteric control of hemoglobin S fiber formation by oxygen and its relation to the pathophysiology of sickle cell disease. Proc Natl Acad Sci (2020) 117:15018–27. doi:10.1073/pnas.1922004117

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Craddock TJ, Tuszynski JA, Hameroff S. Cytoskeletal signaling: is memory encoded in microtubule lattices by CaMKII phosphorylation? PLoS Comput Biol (2012) 8:e1002421. doi:10.1371/journal.pcbi.1002421

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Craddock TJA, Friesen D, Mane J, Hameroff S, Tuszynski JA. The feasibility of coherent energy transfer in microtubules. J R Soc Interf (2014) 11:20140677. doi:10.1098/rsif.2014.0677

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Craddock TJ, Kurian P, Tuszynski JA, Hameroff SR. Quantum processes in neurophotonics and the origin of the brain’s spatiotemporal hierarchy. In: RR Alfano, and L Shi, editors. Neurophotonics and biomedical spectroscopy. Elsevier (2019). p. 189–213. Nanophotonics. doi:10.1016/B978-0-323-48067-3.00009-3

CrossRef Full Text | Google Scholar

80. Penrose R. Shadows of the mind (Oxford University Press) (1996).

Google Scholar

81. Grad J, Hernandez G, Mukamel S. Radiative decay and energy transfer in molecular aggregates: the role of intermolecular dephasing. Phys Rev A (1988) 37:3835–46. doi:10.1103/PhysRevA.37.3835

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Spano FC, Mukamel S. Superradiance in molecular aggregates. J Chem Phys (1989) 91:3835–3846. doi:10.1063/1.457174

CrossRef Full Text | Google Scholar

83. Bienaimé T, Bachelard R, Piovella N, Kaiser R. Cooperativity in light scattering by cold atoms. Fortschritte der Physik (2013) 61:377–92. doi:10.1002/prop.201200089

CrossRef Full Text | Google Scholar

84. Giusteri GG, Mattiotti F, Celardo GL. Non-Hermitian Hamiltonian approach to quantum transport in disordered networks with sinks: validity and effectiveness. Phys Rev B (2015) 91:094301. doi:10.1103/PhysRevB.91.094301

CrossRef Full Text | Google Scholar

85. Akkermans E, Gero A, Kaiser R. Photon localization and Dicke superradiance in atomic gases. Phys Rev Lett (2008) 101:103602. doi:10.1103/PhysRevLett.101.103602

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Löwe J, Li H, Downing K, Nogales E. Refined structure of αβ-tubulin at 3.5 Å resolution. J Mol Biol (2001) 313:1045–57. doi:10.1006/jmbi.2001.5077

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Gurel PS, Kim LY, Ruijgrok PV, Omabegho T, Bryant Z, Alushin GM. Cryo-EM structures reveal specialization at the myosin VI-actin interface and a mechanism of force sensitivity. eLife (2017) 6:e31125. doi:10.7554/eLife.31125

PubMed Abstract | CrossRef Full Text | Google Scholar