Insight into the thermal transport by considering the modified Buongiorno model during the silicon oil-based hybrid nanofluid flow: probed by artificial intelligence

This work aims to analyze the impacts of the magnetic field, activation of energy, thermal radiation, thermophoresis, and Brownian effects on the hybrid nanofluid (HNF) (Ag++silicon oil) flow past a porous spinning disk. The pressure loss due to porosity is constituted by the Darcy–Forchheimer relation. The modified Buongiorno model is considered for simulating the flow field into a mathematical form. The modeled problem is further simplified with the new group of dimensionless variables and further transformed into a first-order system of equations. The reduced system is further analyzed with the Levenberg–Marquardt algorithm using a trained artificial neural network (ANN) with a tolerance, step size of 0.001, and 1,000 epochs. The state variables under the impacts of the pertinent parameters are assessed with graphs and tables. It has been observed that when the magnetic parameter increases, the velocity gradient of mono and hybrid nanofluids (NFs) decreases. As the input of the Darcy–Forchheimer parameter increases, the velocity profiles decrease. The result shows that as the thermophoresis parameter increases, temperature and concentration increase as well. When the activation energy parameter increases, the concentration profile becomes higher. For a deep insight into the analysis of the problem, a statistical approach for data fitting in the form of regression lines and error histograms for NF and HNF is presented. The regression lines show that $100\%$ of the data is used in curve fitting, while the error histograms depict the minimal zero error $-7.1e6$ for the increasing values of $Nt$. Furthermore, the mean square error and performance validation for each varying parameter are presented. For validation, the present results are compared with the available literature in the form of a table, where the current results show great agreement with the existing one.

1 Introduction

A new generation of hybrid nanofluids (HNFs) has been created as a result of emerging technologies [1]. Unlike nanofluids (NFs), which only contain one metal nanoparticle, HNFs contain many metallic nanoparticles. A simple NF is created when water is added to ${\mathrm{A}\mathrm{l}}_2{\mathrm{O}}_3$ nanoparticles [2]. However, combining water, aluminum oxide, silicon oil, and copper metallic nanoparticles results in the formation of a HNF. The thermal conductivity of HNFs is much higher than that of the common fluids, which is one of the reasons behind the interest of numerous scientists and academicians in this area. Nadeem et al. [3] analyzed the important properties like transfer of heat for the 3D HNF flow. Suresh et al. [4] studied the hybrid NF’s mobility and heat transport features. Gorla et al. [5] employed the source or sink impact on the Cu-${\mathrm{A}\mathrm{l}}_2{\mathrm{O}}_3$/${\mathrm{H}}_2$O to explore natural convection in conjunction with heat transmission. Once they moved the heat sources to achieve hybrid prohibition, the Nusselt number decreased dramatically. Tayebi et al. [6] presented a comparative study of the HNFs Cu-${\mathrm{A}\mathrm{l}}_2{\mathrm{O}}_3$/water and NFs ${\mathrm{A}\mathrm{l}}_2{\mathrm{O}}_3$/water through monocular elliptic cylinders by taking the convective effects. Acharya [7] studied the radiative natural convective HNF flow patterns and thermal transport through a square object with variable heated walls. The heat transmission of a HNF through the pores of a cylindrical shape is covered by Tayebi et al. [8]. Using a rotating apparatus, Chamkha et al. [9] analyzed the magnetohydrodynamic HNF flow for heat transfer. Asghar et al. [10] studied the ooze slime for examining the gliding motility of bacteria. The kinetic control of the rod-like swimmers past a sinusoidal object is explained by Asghar et al. [11]. A more recent survey on micro-swimmers and bacteria can be found in [12–16]. Acharya [17] considered the particle size and the solid–liquid interface by investigating the magnetic field effects for ferrofluid flow through a rotating disk. Yarmand et al. [18] studied the accelerated heat transport for the HNF flow. Abbasi et al. [19] investigated the thermal expansion coefficient for HNF of alumina and carbon nanotubes. Both theoretical and experimental studies for the thermophysical characteristics of the HNF flow through nanotubes are presented by Sajid et al. [20]. Kada et al. [21] studied the Carreau–Yasuda model for the waves of cilia in a micro-channel. Asghar et al. [22] used the numerical approach for simulating the flow in a micro-channel using the Carreau–Yasuda layer.

Rotating machinery is a vital component of numerous industries. The rotating disk has many industrial applications, and therefore, its analysis is very important. An increasing variety of industries, including the aviation, automotive, and marine sectors, are using these rotating objects in various parts [23, 24]. The use of irregularly thickened disks is growing, mostly due to financial limitations and the requirement to improve mechanical properties. Rotating disks are necessary for the operation of many pieces of industrial equipment. As a result, researchers working on this subject have recently launched a number of initiatives. Shah et al. [25] investigated the Hall current for the 3D NF flow extending surface by considering the Cattaneo–Christov (C.C.) heat flux model. For example, the analysis of NF flow resulting from rotating disks with different thicknesses and relatively uniform responses was done by Hayat et al. [26]. In a different work, Hayat et al. [27] investigated the flow between two stretchable rotating disks in a porous medium using the C.C. heat flux simulation. The analysis of heat and mass for the 3D NF flow past an elastic sheet is investigated by Khan et al. [28]. Qayyum et al. [29] studied the entropy and dissipation of the MHD Williamson fluid between two rotating disks. Jyothi et al.’s investigation deals with the effect that magnetic fields and heat radiation have on CNT convection in NF within rotating elastic disks [30]. Pourmehran et al. [31] used the Patel model and Brownian motion to study heat exchange and NF flow between two rotating disks. A more recent work on rotating surfaces can be found in [32–35].

The applications of artificial intelligence (AI) cannot be denied. AI covered all areas of research, including medical, engineering, and technology [36–40]. The engineering applications of AI are briefly reviewed by Nti et al. [41]. Jang et al. studied the AI applications for the recognition of pathways and enzymes in metabolic engineering. Sofos et al. [42] reviewed the applications of AI in the field of fluid mechanics. Kartik et al. [43] analyzed the inviscid flow field by using AI. Amini and Mohaghegh [44] used AI by analyzing the fluid flow in a porous medium. The squeezing model with the help of AI is analyzed by Almalki et al. [45]. The irreversibility impact of considering the carbon nanotubes during the viscous fluid flow is analyzed by Zubair et al. [46]. They used a supervised learning-based AI approach to analyze the fluid flow. The MHD HNF flow during the rotating frame for heat and mass transfer is investigated by Shoaib et al. [47]. They used the numerical result as a reference solution for the neural network and analyzed the problem for various impacts of the pertinent parameters and related statistical analysis. The thermal slip and absorption impacts on the HNF flow during the rotating disk are investigated by Shoaib et al. [48]. They used AI for computational purposes. Ali et al. [49] used the Levenberg–Marquardt backpropagation search path for training the neural network for the analysis of the water-based CNT HNF fluid past an unstable spinning disk.

The magnetization of conducting fluids is the subject of research in the field known as magnetohydrodynamics (MHD). MHD engagement detects the interaction of ferromagnetic or fluid metal particles in the presence of an electromagnetic field and current. The MHD model connects the electrohydrodynamic Maxwell equations and fluid computations with the Lorentz force as a result of magnetism. The processes that generate Lorentz force and capacitive electric charge generally seem to be completely opposite to one another. Due to a decrease in concentration, there is an increase in temperature, growing velocity, and Joule heating as the joule number increases. Babu and Sandeep [50] studied the 3D slip effects for the MHD NF flow past an unstable sheet. Ghadikolaei et al. [51] studied the MHD stagnant-point flow of a ${\mathrm{T}\mathrm{i}\mathrm{O}}_2$–Cu–water hybrid NF across such a stretched sheet. The ${\mathrm{T}\mathrm{i}\mathrm{O}}_2$ nanoparticles in a porous medium were studied in the boundary layer of a micropolar hazy fluid medium by Ghadikolaei et al. [52] in order to take into consideration the effects of magnetization and heat radiation. The flow of thin fluid films with different thermophysical properties in a two-dimensional boundary layer in a three-dimensional environment was studied by Palwasha et al. [53].In light of the above, we assume the following.

$•$ The HNF (Ag+${\mathrm{T}\mathrm{i}\mathrm{O}}_2$/silicon oil) flow past a spinning disk is considered.

$•$ The impacts of porosity, the Darcy–Forchheimer (DF) parameter, thermal radiation, and energy activation are considered in the flow field.

$•$ The modification in the Buongiorno model (MBM) is considered to analyze the flow behavior in depth.

$•$ Silicon oil is used as a base fluid for Ag and ${\mathrm{T}\mathrm{i}\mathrm{O}}_2$ nanoparticles.

$•$ The thermal transport for the hybrid and mono NFs is investigated using the Levenberg–Marquardt algorithm (LMA).

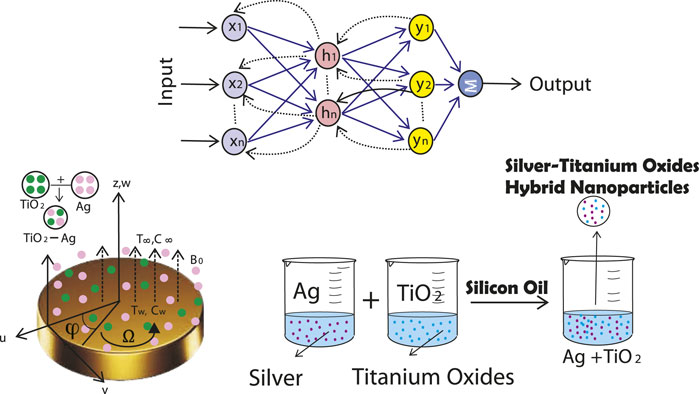
A comparative analysis of the HNF and NF is carried out by implementing the neural network. A graphical abstract is presented in Figure 1.

Figure 1

Figure 1. Graphical abstract.

2 Problem formulation

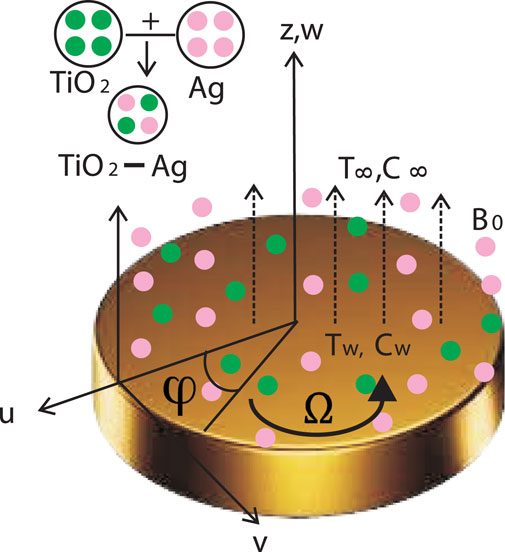
Assume a steady HNF flow past a spinning disk that is axially symmetric along the $\phi$ direction in the $(r,\phi ,z)$ coordinates. The disk is half-filled with HNF and rotates with angular velocity $\mathrm{\Omega }$. The surface and the surrounding temperatures are $T_w$ and $T_{\infty }$, respectively. A magnetic field $B$ is acting normal to the $z$-direction. Since the flow is axially symmetric, the implications along $\phi$ are not considered, as shown in Figure 2.

Figure 2

Figure 2. Problem geometry.

Considering the Buongiorno model with modifications, we have the following basic equations for the fluid flow [54, 55]:

$u_r+\frac{u}{r}+w_z=0,(1)$

$\begin{array}{c}\hfill {\rho }_{hnf}\left(u{u}_r-\frac{{\upsilon }^2}{r}+w{u}_z\right)=-P_r+{\mu }_{hnf}\left(u_{rr}+\frac{1}{r}{u}_r-\frac{u}{r^2}+u_{zz}\right)\\ \hfill -{\sigma }_{hnf}{B}_0^{2}u-\frac{{\mu }_{hnf}}{k^{*}}u-F{u}^2,\end{array}(2)$

$\begin{array}{c}\hfill {\rho }_{hnf}\left(u{u}_r-\frac{u\upsilon }{r}+w{\upsilon }_z\right)={\mu }_{hnf}\left({\upsilon }_{rr}+\frac{1}{r}{\upsilon }_r-\frac{\upsilon }{r^2}+{\upsilon }_{zz}\right)\\ \hfill -{\sigma }_{hnf}{B}_0^{2}v-\frac{{\mu }_{hnf}}{k^{*}}\upsilon -F{\upsilon }^2,\end{array}(3)$

$\begin{array}{c}\hfill {\rho }_{hnf}\left(u{w}_r+w{w}_r\right)=-P_z+{\mu }_{hnf}\left(w_{rr}+\frac{1}{r}{w}_r+w_{zz}\right),\end{array}(4)$

$\begin{array}{c}\hfill u{T}_r+w{T}_z={\alpha }_{hnf}\left(T_{rr}+\frac{1}{r}{T}_r+T_{zz}\right)+\tau [D_B\left(T_r{C}_r+T_z{C}_z\right)\\ \hfill \left.+\frac{D_T}{T_{\infty }}\left({\left(T_r\right)}^2+{\left(T_z\right)}^2\right)\right]+\frac{16{\sigma }^{†}{T}_{\infty }^3}{3{\left(\rho c_p\right)}_{hnf}k}{T}_{zz},\end{array}(5)$

$\begin{array}{c}\hfill u{C}_r+w{C}_z=D_B\left(C_{rr}+\frac{1}{r}{C}_r+C_{zz}\right)+\frac{D_T}{T_{\infty }}\left(T_{rr}+\frac{1}{r}{T}_r+T_{zz}\right)\\ \hfill -K_r^2{\left(\frac{T}{T_{\infty }}\right)}^n\exp \left(-\frac{Ea}{kT}\right)\left(C-C_{\infty }\right),\end{array}(6)$

with the B.Cs [56].

$\begin{array}{c}\hfill \text{at}z=0:w=0,u=L_1{u}_z,\upsilon =r\mathrm{\Omega },C=C_w,T=T_w,\\ \hfill \text{as}z\to \infty :T\to T_{\infty },u\to 0,C\to C_{\infty },P\to P_{\infty }.\end{array}(7)$

Here, $u,v$, and $w$ are the velocity components along $r,\phi$, and $z$ directions, respectively. In addition, ${\upsilon }_f,T,D_T,D_B,C,P,{\alpha }_{hnf},\tau ,{\rho }_f,k^{*},F,L_1$ are the kinematic viscosity of the fluid, fluid temperature, thermophoretic and Brownian diffusion coefficients, nanoparticle concentration, pressure, thermal diffusivity of the hybrid NF, the ratio of specific heat to the nanoparticle element, density, porous medium permeability, porous medium inertial coefficient, and the wall slip parameter, respectively.Introducing the following dimensionless transformations [31, 55]:

$\begin{array}{c}\hfill \left(P,C,T\right)=\left(P_{\infty }-\mathrm{\Omega }{\mu }_{f}P\left(\eta \right),C_{\infty }+\left(C_w-C_{\infty }\right)\varphi \left(\eta \right),T_{\infty }+\left(T_w-T_{\infty }\right)\theta \left(\eta \right)\right),\\ \left(u,w,\upsilon \right)=\left(\mathrm{\Omega }r{f}^{\prime }\left(\eta \right),-\sqrt{2\mathrm{\Omega }{\upsilon }_f}f\left(\eta \right),\mathrm{\Omega }rg\left(\eta \right)\right),\eta =\sqrt{\frac{2\mathrm{\Omega }}{v_f}}z.\hfill \end{array}(8)$

Applying Eq. 8 to Eqs 1–6, we obtain [55]:

$f^{\prime \prime \prime }+\left(\frac{\frac{{\rho }_{\mathit{hnf}}}{{\rho }_f}}{\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}}\right)\left(f^{\prime \prime }f-\frac{1}{2}{f}^{\prime 2}+\frac{1}{2}{g}^2\right)-\left(\frac{\frac{{\rho }_{\mathit{hnf}}}{{\rho }_f}}{\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}}\right)f^{\prime 2}Fr-\delta f^{\prime }-M\left(\frac{\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}}{\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}}\right)f^{\prime }=0,(9)$

$g^{\prime \prime \prime }-\left(\frac{\frac{{\rho }_{\mathit{hnf}}}{{\rho }_f}}{\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}}\right)\left(\frac{1}{2}{f}^{\prime 2}f-\frac{1}{2}{f}^{\prime }g-f{g}^{\prime }\right)-M\left(\frac{\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}}{\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}}\right)g-\left(\frac{\frac{{\rho }_{\mathit{hnf}}}{{\rho }_f}}{\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}}\right)g^{2}Fr-\delta g=0,(10)$

$\frac{1}{Pr}\left(\frac{\frac{k_{hnf}}{k_f}}{\frac{{\left(\rho Cp\right)}_{\mathit{hnf}}}{{\left(\rho Cp\right)}_f}}+\frac{4}{3}Rd\right){\theta }^{\prime \prime }+{\theta }^{\prime }f+Nt{\theta }^{\prime 2}+{\theta }^{\prime }Nb{\varphi }^{\prime }=0,(11)$

${\varphi }^{\prime \prime }+Scf{\varphi }^{\prime }+\frac{Nt}{Nb}{\theta }^{\prime \prime }-{\sigma }_{1}Sc{\left(1+\tilde{\delta }\theta \right)}^n\exp \left(-\frac{E}{1+\tilde{\delta }\theta }\right)\varphi =0,(12)$

$\begin{array}{c}\hfill \text{\hspace{0.17em}as\hspace{0.17em}}\eta =0:f^{\prime }=\alpha f^{\prime \prime },g=1,f=0,\theta =1,\varphi =1,\\ \hfill \text{\hspace{0.17em}as\hspace{0.17em}}\eta \to \infty :f^{\prime }\to 0,g\to 0,f=0,\theta \to 0,\varphi \to 0.\end{array}(13)$

Here, $Rd=\frac{4\sigma T_{\infty }^3}{k{k}_f}$ is the radiation parameter, $M=\frac{{\sigma }_f{B}_0^2}{2{\rho }_f\mathrm{\Omega }}$ is the magnetic parameter, $Sc=\frac{v_f}{D_B}$ is the Schmidt number, $Nb=\frac{\tau D_B{C}_{\infty }}{v_f}$ is the Brownian motion parameter, $E=\frac{E_a}{k{T}_{\infty }}$ is the energy activation parameter, $Fr=\frac{C_b}{\sqrt{k^{*}}}$ represents the DF number, $\tilde{\delta }=\frac{T_w-T_{\infty }}{T_{\infty }}$ is the temperature difference parameter, $\alpha =L_1\sqrt{\frac{2\mathrm{\Omega }}{v_f}}$ is the velocity slip parameter, $Pr=\frac{v_f}{{\alpha }_f}$ is the Prandtl number, ${\sigma }_1=\frac{K_r^2}{\mathrm{\Omega }}$ is the chemical reaction parameter, $\delta =\frac{v_f}{k^{*}\mathrm{\Omega }}$ is the porosity parameter, and $Nt=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{T_{\infty }{v}_f}$ is the thermophoresis parameter.It is clear from Eq. 4 that we can obtain the pressure by integrating it. The torque resistance on the disk having radius $R$ is given as follows [55]:

$T=-{\left.{\int }_0^R{\mu }_{hnf}{v}_z\right|}_{z=0}2\pi r^{2}dr=-\frac{\pi {\rho }_{hnf}\mathrm{\Omega }}{2}\sqrt{2{\upsilon }_f\mathrm{\Omega }}{R}^4{g}^{\prime }\left(0\right).(14)$

In addition, the tangential ${\tau }_0$ and radial ${\tau }_r$ stresses are given as follows [55]:

$\begin{array}{c}\hfill {\tau }_r={\mu }_{hnf}{\left(u_z+w_r\right)}_{z=0}=r\mathrm{\Omega }{\mu }_{hnf}\sqrt{\frac{2\mathrm{\Omega }}{{\upsilon }_f}}{f}^{\prime \prime }\left(0\right),\\ \hfill {\tau }_{\theta }={\mu }_{hnf}{\left({\upsilon }_z+w_r\right)}_{z=0}=r\mathrm{\Omega }{\mu }_{hnf}\sqrt{\frac{2\mathrm{\Omega }}{{\upsilon }_f}}{g}^{\prime }\left(0\right),\end{array}(15)$

or

$C_f=\frac{\sqrt{{\tau }_r^2+{\tau }_{\theta }^2}}{{\rho }_{hnf}{\left(r\mathrm{\Omega }\right)}^2}=\frac{{\left(\frac{2\mathrm{\Omega }{r}^2}{{\upsilon }_f}\right)}^{-\frac{1}{2}}{\left(f^{\prime \prime }{\left(0\right)}^2+g^{\prime }{\left(0\right)}^2\right)}^{\frac{1}{2}}}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}.(16)$

The local Nusselt number $N{u}_r$ is computed as follows [55]:

$N{u}_r=\frac{r{q}^{\prime \prime }}{k_f\left(T_w-T_{\infty }\right)},(17)$

where $q^{\prime \prime }=-k_{\text{hnf\hspace{0.17em}}}{T}_z+{\left.\frac{16{\sigma }^{†}{T}_{\infty }^3}{3k}{T}_z\right|}_{z=0}$ is the heat flux. The wall heat flux can be eliminated by choosing the zero wall mass flux; thus, with Eq. 8, we have from (17)

$N{u}_r=-r\sqrt{\frac{2\mathrm{\Omega }}{{\upsilon }_f}}\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}Rd\right){\theta }^{\prime }\left(0\right).(18)$

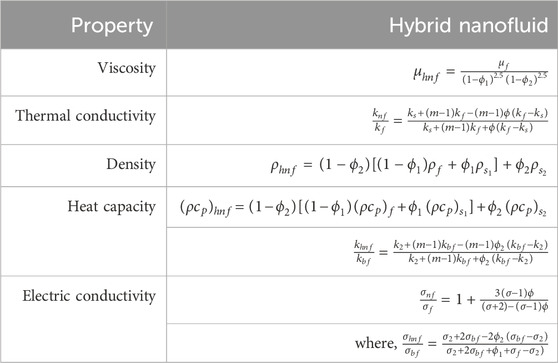
The HNF models and physical properties of the NFs used in this study are displayed in Tables 1,2.

Table 1

Table 1. HNF models [55, 57].

Table 2

Table 2. Some important properties of silicon oil, ${\mathrm{T}\mathrm{i}\mathrm{O}}_2$, and $Ag$ [58, 59].

3 Proposed methodology

Artificial neural networks (ANNs) are computer models that simulate the human brain structure. The human system, from a neurological point of view, is very complex. ANNs are made up of nodes, which are interconnected to form layers with varying degrees of processing depth. Nodes are connected processing components. These combine to create intricate processing circuits that identify input patterns and generate responses. By training layers that correlate responses with incoming data with specific pattern knowledge, the patterns can be learned. The network gains knowledge through practice, and when linked to other networks, it gains knowledge through information sharing. The only layers in an ANN’s structure are the input layer, a hidden layer that is introduced first, and the output layer. Applications of neural networks are being used across numerous industries to address issues with security, the economy, and other factors. In the data-intensive era, neural networks have created new opportunities for study and application [60, 61]. The more recent trends in other disciplines of AI can be found in [61–63]. For a solution of Eqs 9–13, we first transform the given system into a first-order system. For this, we have [55]

$\begin{array}{c}\hfill y_1=f,y_2=f^{\prime },y_6=\theta ,y_7={\theta }^{\prime },y_3=f^{\prime \prime },y_4=g,y_5=g^{\prime },y_8=\varphi ,y_9={\varphi }^{\prime }\\ \hfill y_1^{\prime }=y_2,\\ \hfill y_2^{\prime }=y_3,\\ \hfill y_3^{\prime }=-\left(A0/A1\right)\left(y_1{y}_3-0.5y_2^2+0.5y_4^2-Fr{y}_2^2\right)+\delta y_2+\left(A2/A1\right)M{y}_2,\\ \hfill y_4^{\prime }=y_5,\\ \hfill y_5^{\prime }=\left(A0/A1\right)\left(0.5y_2^2{y}_1-0.5y_2{y}_4-y_1{y}_5+Fr{y}_4^2\right)+\left(A2/A1\right)M{y}_4+\delta y_4,\\ \hfill y_6^{\prime }=y\left(7\right),\\ \hfill y_7^{\prime }=-\left(Pr\left(y_1{y}_7+Nb{y}_7{y}_9+Nt{y}_7^2\right)\right)/\left(A3/A4+\left(4/3\right)Rd\right),\\ \hfill y_8^{\prime }=y\left(9\right),\\ \hfill y_9^{\prime }=-\left(Sc{y}_1{y}_9+\left(Nt/Nb\right)y{\left(7\right)}^{\prime }-\sigma 1Sc\left(\left(1+\delta 1y_6^m\right)y_{8}exp\left(-E/\left(1+\delta 1y_6\right)\right)\right.\right.\end{array}(19)$

The B.Cs are as follows [55]:

$\begin{array}{c}\hfill y_1\left(0\right)=0,y_2\left(0\right)-\alpha y_3\left(0\right)=0,y_4\left(0\right)-1=0,y_6\left(0\right)-1=0,y_8\left(0\right)-1=0,\\ \hfill y_2\left(\infty \right)=0,y_6\left(\infty \right)=0,y_4\left(\infty \right)=0,y_8\left(\infty \right)=0.\end{array}(20)$

The two important steps of ANN are shown in Figure 3. During the process, after providing the input, the weights are trained for $t_k$ inputs, and the required result is obtained as an output. Mathematically, we have [64, 65]

$u_j={\displaystyle \sum _{j=1}^k}{w}_j{t}_j-{\beta }_j.(21)$

The results for the state variables can be obtained by introducing the sigmoid function $\chi (\eta )=\frac{1}{1+e^{-\eta }}$. The obtained output is given by [66]

$\chi \left(u_j\right)=\frac{1}{1+e^{-\left(w_j{t}_j-{\beta }_j\right)}}.(22)$

Figure 3

Figure 3. ANN structure.

3.1 Training of the weights

This section explains how the neural network is trained to find the output. The system given in Eq. 19, 20 is solved with the bvp4c, which is a well-known MATLAB built-in code for solving boundary value problems. The infinity is set at $\eta =8$ with a tolerance of $e^{-6}$ and a step size of 0.001. The neural network takes this solution as an input and produces an optimized solution by minimizing the fitness function. The result is discussed with ms, absolute error, error histogram, and regression line [67, 68].

$MSE=\frac{1}{j}{\displaystyle \sum _{i=1}^j}{\left(z_i\left(t\right)-{\widehat{z}}_i\left(t\right)\right)}^2,(23)$

$1-R^2=\frac{{\sum }_{i=1}^j{\left({\widehat{z}}_i\left(t\right)-{\bar{x}}_i\left(t\right)\right)}^2}{{\sum }_{i=1}^j{\left(z_i\left(t\right)-{\widehat{z}}_i\left(t\right)\right)}^2},(24)$

and

$AE=|z_i\left(t\right)-{\widehat{z}}_i\left(t\right)|,j=\mathrm{1,2},\dots ,k.(25)$

4 Results and discussions

The impact of the silicon oil-based HNF (${\mathrm{T}\mathrm{i}\mathrm{O}}_2$+Ag) flow past a rotating disk using the Buongiorno modified model has been analyzed with the trained AI method. In this section, the results are given under the influence of various pertinent parameters. For simplicity, we choose $0\le M\le 3,\mathrm{P}\mathrm{r}=6.2,0\le \delta \le \mathrm{1,0}\le Rd\le \mathrm{3,0}\le Nt\le \mathrm{1,0}\le Nb\le \mathrm{2,0}\le E\le 2,\tilde{\delta }=\mathrm{1,0}\le Fr\le 5,Sc=1$, $0\le \alpha \le 1$, and $n=3$.

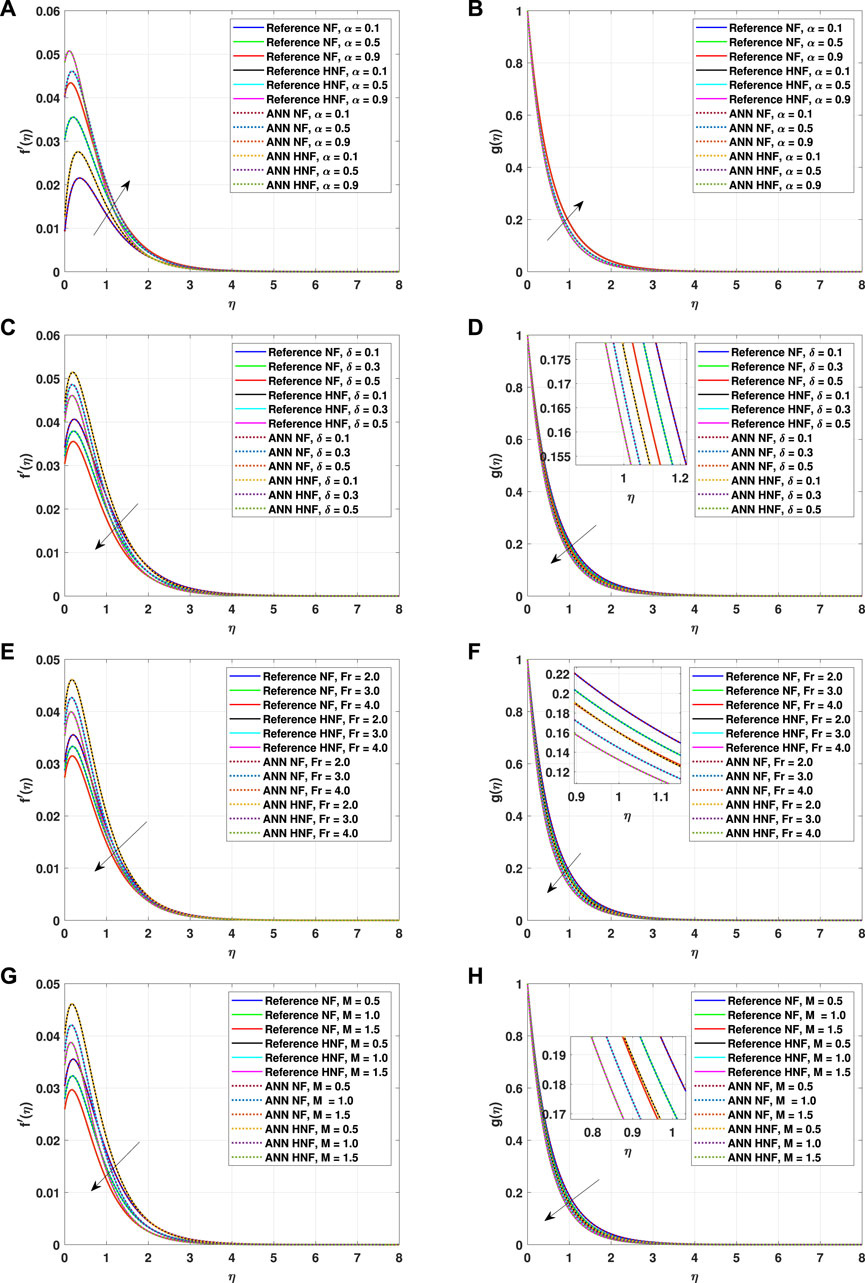
The effect of various parameters on the radial and axial velocities is described in Figure 4A–H. The larger values of the velocity slip parameter $\alpha$ increase both the axial and the radial velocities, as depicted in Figures 4A,B. The variations are very prominent for the HNFs, as compared to the NFs. The HNFs and the NFs behave the same after $\eta =3$. Physically, the greater values of $\alpha$ shift the fluid toward the rotating wall of the disk, which further enhances the fluid flow in both the axial and radial directions. In addition, $\alpha$ is directly related to the spinning factor, which plays a key role in the increasing trends of the fluid flow. The porosity parameter $\delta$ impact is displayed in Figures 4C,D. The larger values of $\delta$ decrease both the axial and radial velocities. The larger values of $\delta$ increase the kinematic viscosity and further decline the rotational effects, which, as a result, causes a decline in both profiles. In addition, the larger values of $\delta$ decrease the rotational velocity of the surface that plays a key role in the decline of the velocity profiles. These variations are much faster for HNFs than those for NFs. The impact of $M$ and the DF parameter $Fr$ is displayed in Figure 4E–H. Both profiles decline with the increasing values of these parameters. These variations are due to the permeability parameter that acts oppositely to the larger trends of $Fr$. On the other hand, $M$ produces the Lorentz force that acts in the opposite direction to the fluid flow and, as a result, decreases the velocity profile, as shown in Figures 4G,H. When $M$ increases, the rotational velocity of the disk declines, which further declines the axial and radial velocities.

Figure 4

Figure 4. Impact of (A) $\alpha$ on $f^{\prime }$, (B) $\alpha$ on $g$, (C) $\delta$ on $f^{\prime }$, (D) $\delta$ on $g$, (E) $Fr$ on $f^{\prime }$, (F) $Fr$ on $g$, (G) $M$ on $f^{\prime }$, and (H) $M$ on $g$.

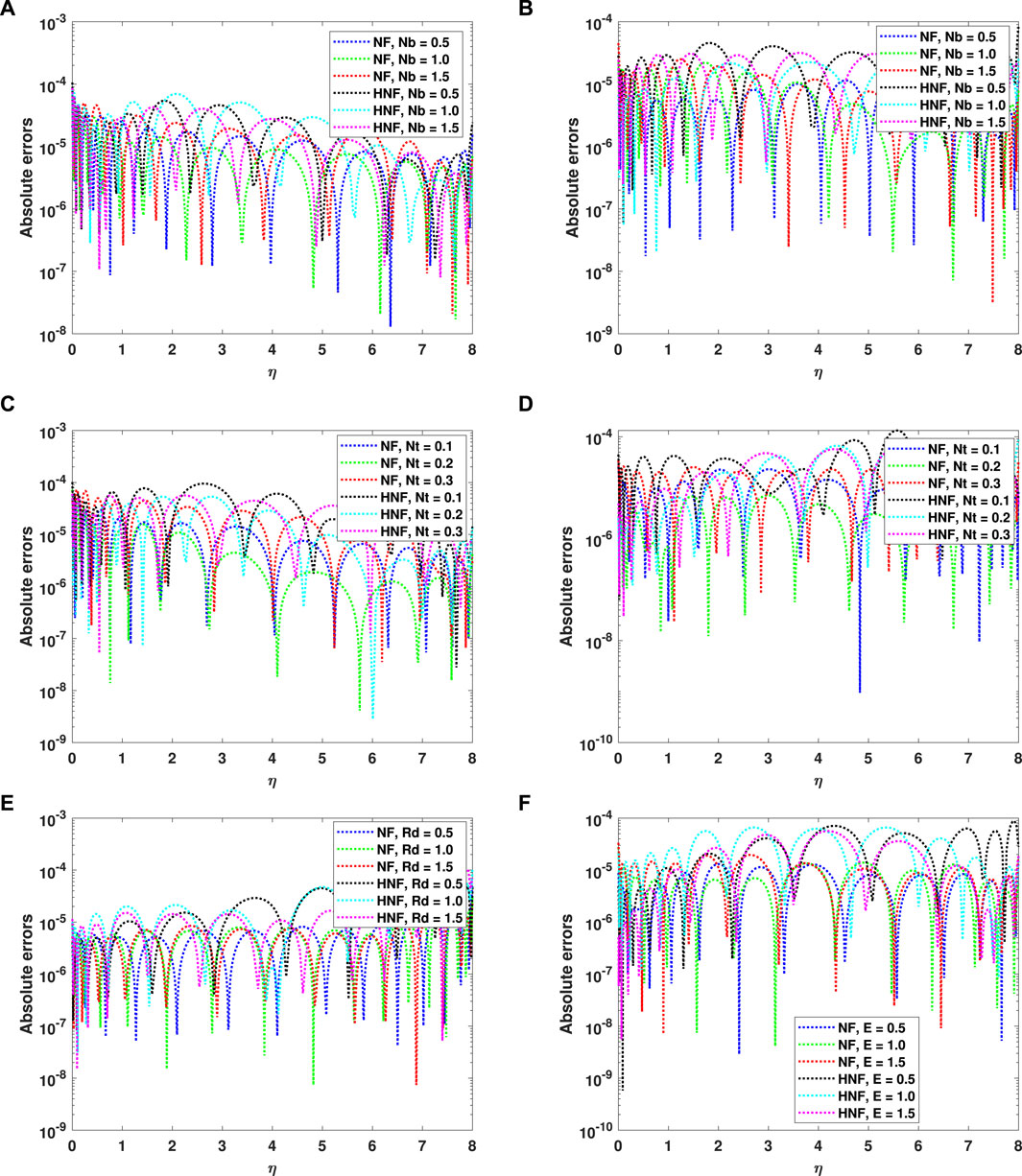
The absolute errors (AEs) to minimize the $L_2-$norm are displayed for all the variations in the above-mentioned parameters in Figure 5A–H. The axial velocity AEs lie in the range $10^{-4}$ to $10^{-8}$, while the radial velocity lies in the range $10^{-3}$ to $10^{-9}$. The best and minimum occur in both variations for $\alpha =0.9$ at $\eta =2.4$ and $\eta =2.2$, respectively, as depicted in Figure 5A,B. The AEs for $\delta$ and $Fr$ are displayed in Figure 5C–F. The range for both variations is $10^{-4}$ to $10^{-9}$. The minimum threshold for both parameters is obtained at $\delta =0.5$ and $Fr=3.0$. The axial velocity AE varies in the range of $10^{-4}$ to $10^{-10}$ for $M$, while the radial velocity ranges from $10^{-4}$ to $10^{-9}$. The minimum value achieved for the radial and axial velocities was at $M=0.5$ and $M=1$, respectively.The error histograms for each parameter with its varying values are presented in 6(a)–(h). The bar graphs are presented with the errors vs the instances with the minimum bins at which the required threshold is achieved. The zero error occurs at the midpoint of the range $-3.8e-6$-$2.52e-6$ for the radial velocity, while the same result occurs at $2.3e-6$ for the axial velocity with the varying values of $\alpha$. The zero error for 4,000 and 8,000 instances is depicted in Figures 6C,D at errors $-3.3e-6$ and $-6.9e-6$ for the radial and axial velocities with varying values of $\delta$, respectively. The Darcy’s parameter impact on the radial velocity shows zero error at the midpoint of $-7.6e-6$-$5.09e-6$ for 3,500 instances. This result is achieved at 20 bins, as shown in Figure 6E. This result for the axial velocity with the varying values of $Fr$ is obtained at $-3.19e-6$ with 6,000 instances, as depicted in Figure 6F. The effect of $M$ on both the velocities is displayed through error histograms in Figure 6G,H. For the radial velocity, the zero error occurs at the midpoint of $-1.2e-5$-$6.19e-6$, while for the axial velocity, the same result is obtained at $-4.7e-6$ with greater $M$.

Figure 5

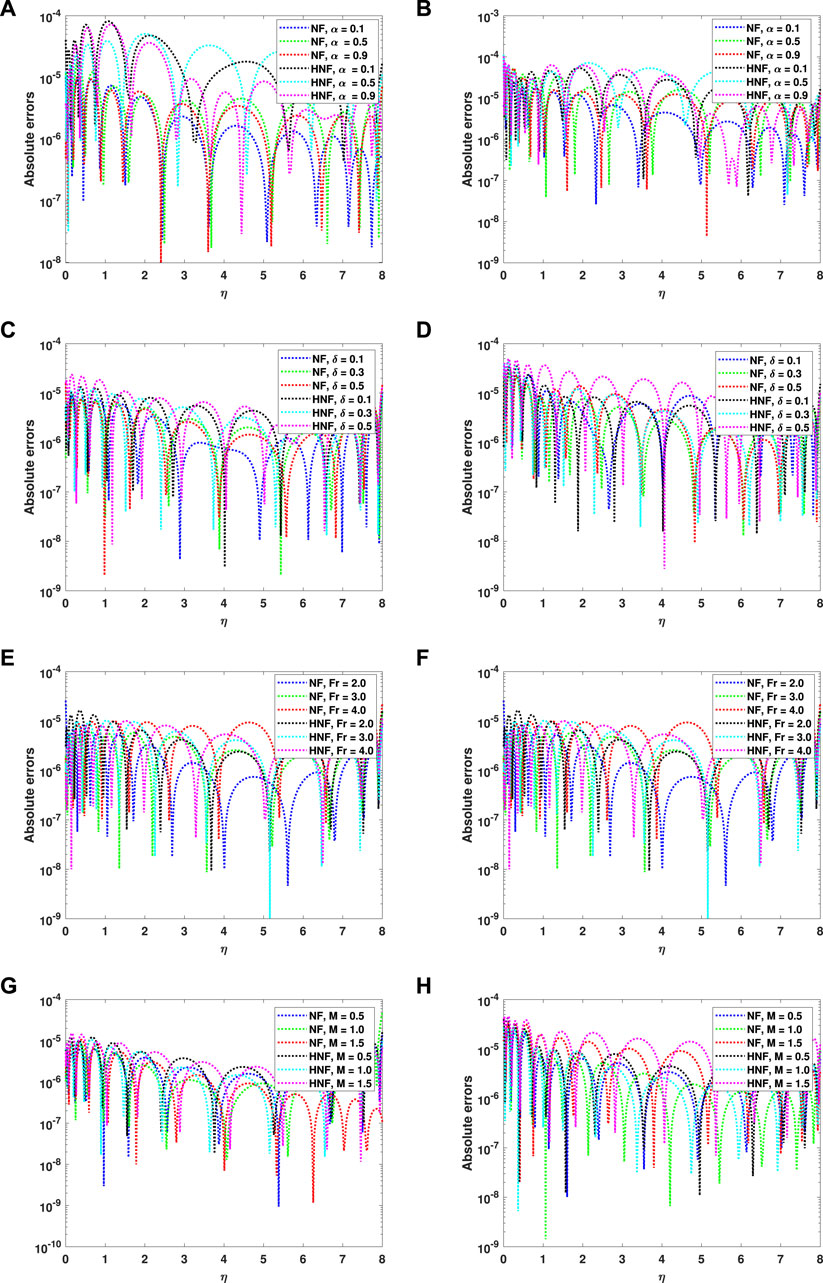
Figure 5. Absolute error for the impact of (A) $\alpha$ on $f^{\prime }$, (B) $\alpha$ on $g$, (C) $\delta$ on $f^{\prime }$, (D) $\delta$ on $g$, (E) $Fr$ on $f^{\prime }$, (F) $Fr$ on $g$, (G) $M$ on $f^{\prime }$, and (H) $M$ on $g$.

Figure 6

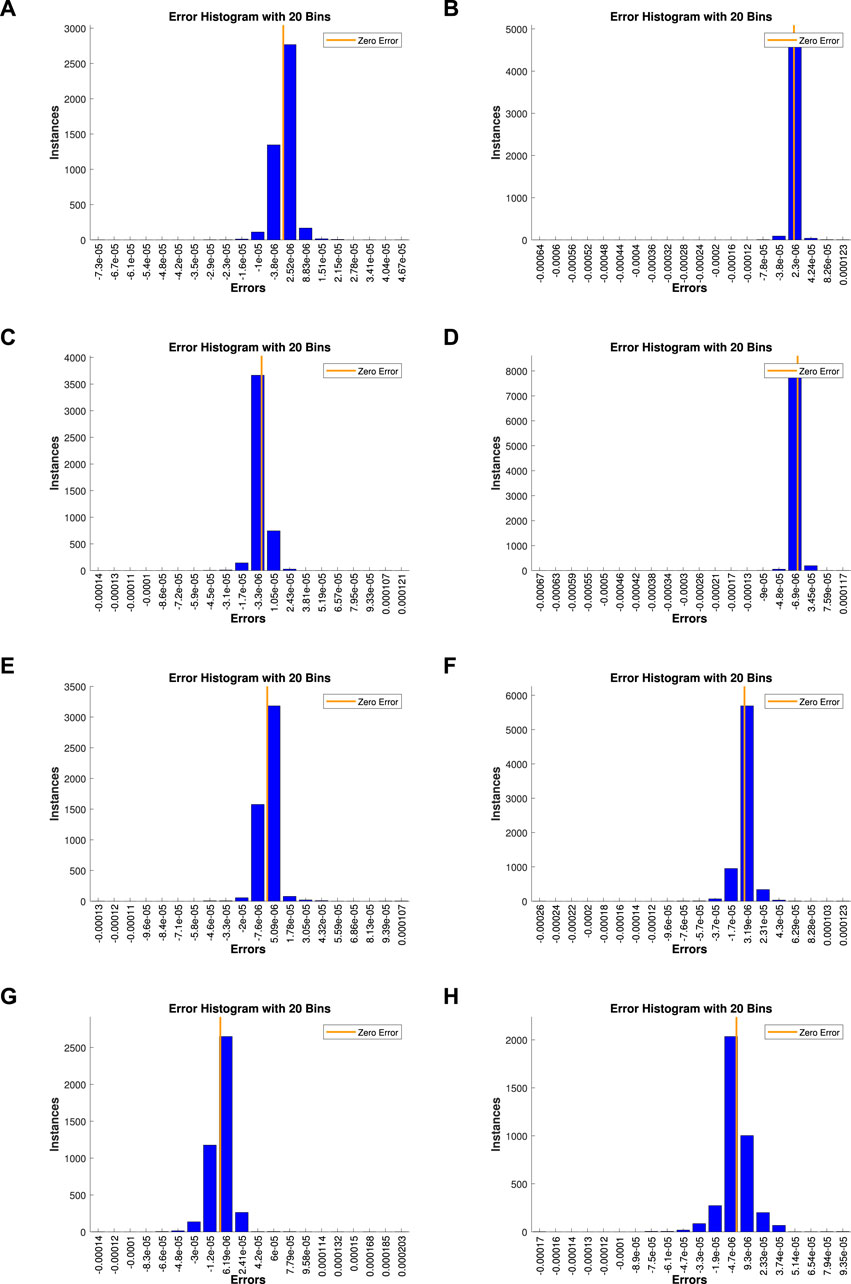
Figure 6. Error histogram for the impact of (A) $\alpha$ on $f^{\prime }$, (B) $\alpha$ on $g$, (C) $\delta$ on $f^{\prime }$, (D) $\delta$ on $g$, (E) $Fr$ on $f^{\prime }$, (F) $Fr$ on $g$, (G) $M$ on $f^{\prime }$, and (H) $M$ on $g$.

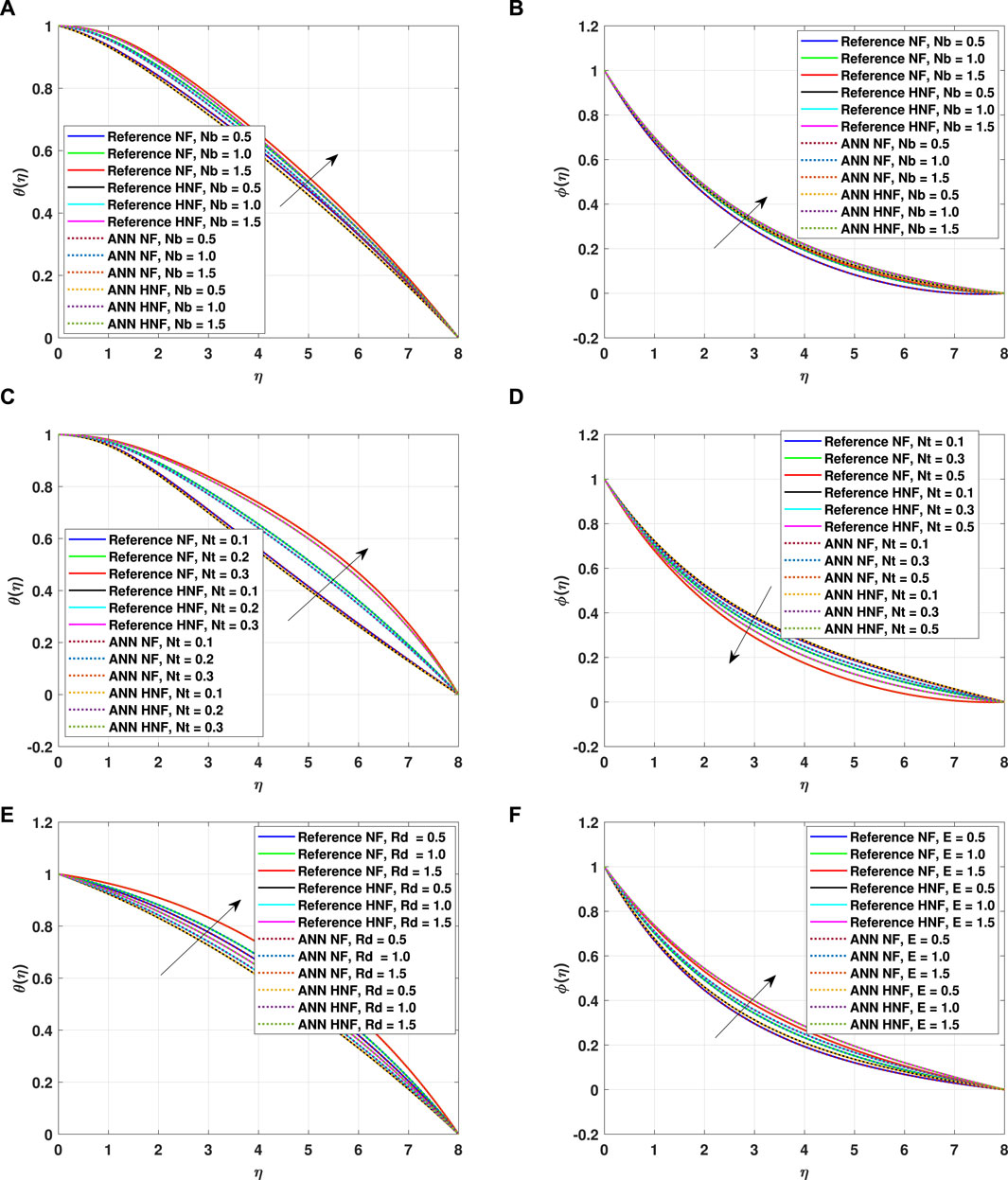
The effect of $\alpha$ for both radial and axial velocities is displayed through the regression lines in Figure 7A–D. The regression lines are used for the fitted data that are displayed with a linear line. Here, the target is taken at the $x$-axis, while the output is considered at the axis perpendicular to it. The first three horizontal boxes in row one from left to right show the fitted data for the NFs with $\alpha =0.1,0.5,0.9$. The value of $R$ in each case is 1, which shows that $100\%$ of the data is fitted. The same results are observed for the HNFs in row two, where $R=1$, as shown in Figure 7A, which is the collective data fitting for the radial and axial velocities with varying values of $\alpha$. The regression lines for the porosity parameter $\delta$, Darcy’s parameter $Fr$, and magnetic parameter $M$ are displayed in Figure 7B–D. The results show that $100\%$ data are fitted for the total data considered, as shown with hollow circles. The output range for the HNFs is smaller than the NF range. The fitted data are displayed with various colors (blue, red, green, and black) displayed with circles on the linear line. The minimum output is obtained for the magnetic parameter $M$ for the HNFs.

Figure 7

Figure 7. Regression lines for (A) $\alpha$ on $f^{\prime }$ and $g$, (B) $\delta$ on $f^{\prime }$ and $g$, (C) $Fr$ on $f^{\prime }$ and $g$, and (D) $M$ on $f^{\prime }$ and $g$.

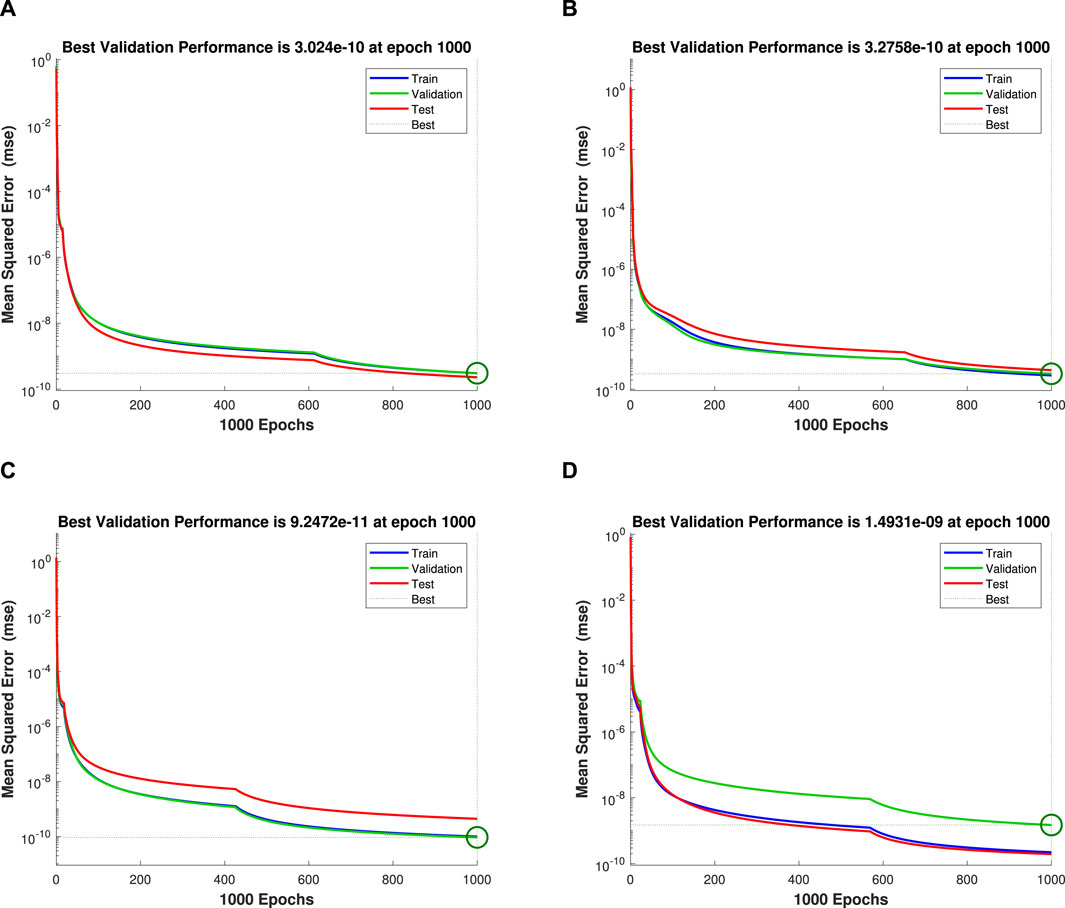
The validations for the total performance of each parameter are presented in Figure 8A–D. These figures demonstrate the mean square error (ms) vs the total iterations performed. Four different curves are used for the trained, validated, tested, and best data. The performance for $\alpha$ and $\delta$ is displayed in Figure 8A,B. The mean square error at the best point occurs near $10^{-10}$ displayed with the green circle. This point is achieved at $3.024e-10$ and $3.2758e-10$ for both $\alpha$ and $\delta$, respectively. In addition, the performance for $Fr$ and $M$ is displayed in Figure 8C,D. The best performance is achieved at $9.2472e-11$ and $1.4931e-09$ for these two parameters, respectively.

Figure 8

Figure 8. Validation performance for (A) $\alpha$ on $f^{\prime }$ and $g$, (B) $\delta$ on $f^{\prime }$ and $g$, (C) $Fr$ on $f^{\prime }$ and $g$, and (D) $M$ on $f^{\prime }$ and $g$.

The impact of $Nb$, $Nt$, $Rd$, and $E$ is analyzed on the thermal and concentration profiles in Figure 9A–F. The varying values of $Nb$ on the thermal and concentration profiles are described in Figure 9A,B. The increasing values of $Nb$ increase both profiles and vary in the range of 0–1. Physically, when $Nb$ increases, the kinematic viscosity decreases and the ambient concentration jumps, which, as a result, increases the number of suspended particles. When these particles increase, the interaction between them also becomes faster and more random, which, as a result, enhances energy transfer from one point to another. These interactions play a key role in energy transfer, either by convection or conduction. The thermophoresis parameter effect shows an opposite trend for both profiles, as shown in Figure 9C,D. The larger values of $Nt$ also increase the temperature difference and reduce the kinematic viscosity. The larger the $Nt$, the higher the difference in temperatures, and the greater the thermal profile, as depicted in Figure 9C. The concentration profile falls due to increase in the density of the fluid with larger values of $Nt$. Furthermore, the diffusion coefficient increases with larger values of $Nt$, but this phenomenon occurs at a very small scale that cannot interrupt the profile mechanism, as displayed in Figure 9D. Both the radiation parameter and the energy activation parameter enhance the thermal and concentration profiles, respectively, as shown in Figure 9E,F. The larger values of $Rd$ increase the inner temperature due to an increase in the ambient temperature. The activation energy also enhances the concentration profile, as shown in Figure 9D.

Figure 9

Figure 9. Effect of (A) $Nb$ on $\theta$, (B) $Nb$ on $\varphi$, (C) $Nt$ on $\theta$, (D) $Nt$ on $\varphi$, (E) $Rd$ on $\theta$, and (F) $E$ on $\varphi$.

The corresponding mean square error for the varying values of $Nb,Nt,Rd$, and $E$ is depicted in Figure 10A–F. It is clear from Figure 10A,B that when $Nb$ varies from 0.5 to 1.5, the corresponding $L-$norm achieves its minimum values of $10^{-8}$ and $10^{-9}$ for $\theta$ and $\varphi$, respectively. A very similar trend for the errors for their minimal values occurs in Figure 10C–F for the remaining parameters. The ms for the activation of the energy parameter $E$ is approaching $10^{-10}$. This shows the total performance of the impact of $E$ on the concentration profile with its increasing values, as depicted in Figure 10F.

Figure 10

Figure 10. Absolute error for (A) $Nb$ on $\theta$, (B) $Nb$ on $\varphi$, (C) $Nt$ on $\theta$, (D) $Nt$ on $\varphi$, (E) $Rd$ on $\theta$, and (F) $E$ on $\varphi$.

The error histograms for all these parameters $(Nb,Nt,Rd,E)$ are displayed in Figure 11A–F. The zero error for $Nb$ of $\theta$ occurs at $-7.6e-6$, while for the concentration profile, it occurs in the range $-1.5e-5$ –$6.85e-6$. All these results are obtained at 20 bins by using 6,000 and 2000 instances, respectively. The zero error for $Nt$ by computing the thermal and concentration profiles falls in the range $-7.1e-6$ –$9.7e-6$ and $-2.4e-5$ –$2.82e-5$, respectively, as presented in Figure 11C,D. In addition, for the impact of the radiation and the activation parameters, the zero errors are obtained at $5.08e-6$ and in the range of $-2.1e-5$ –$2.97e-5$, respectively.

Figure 11

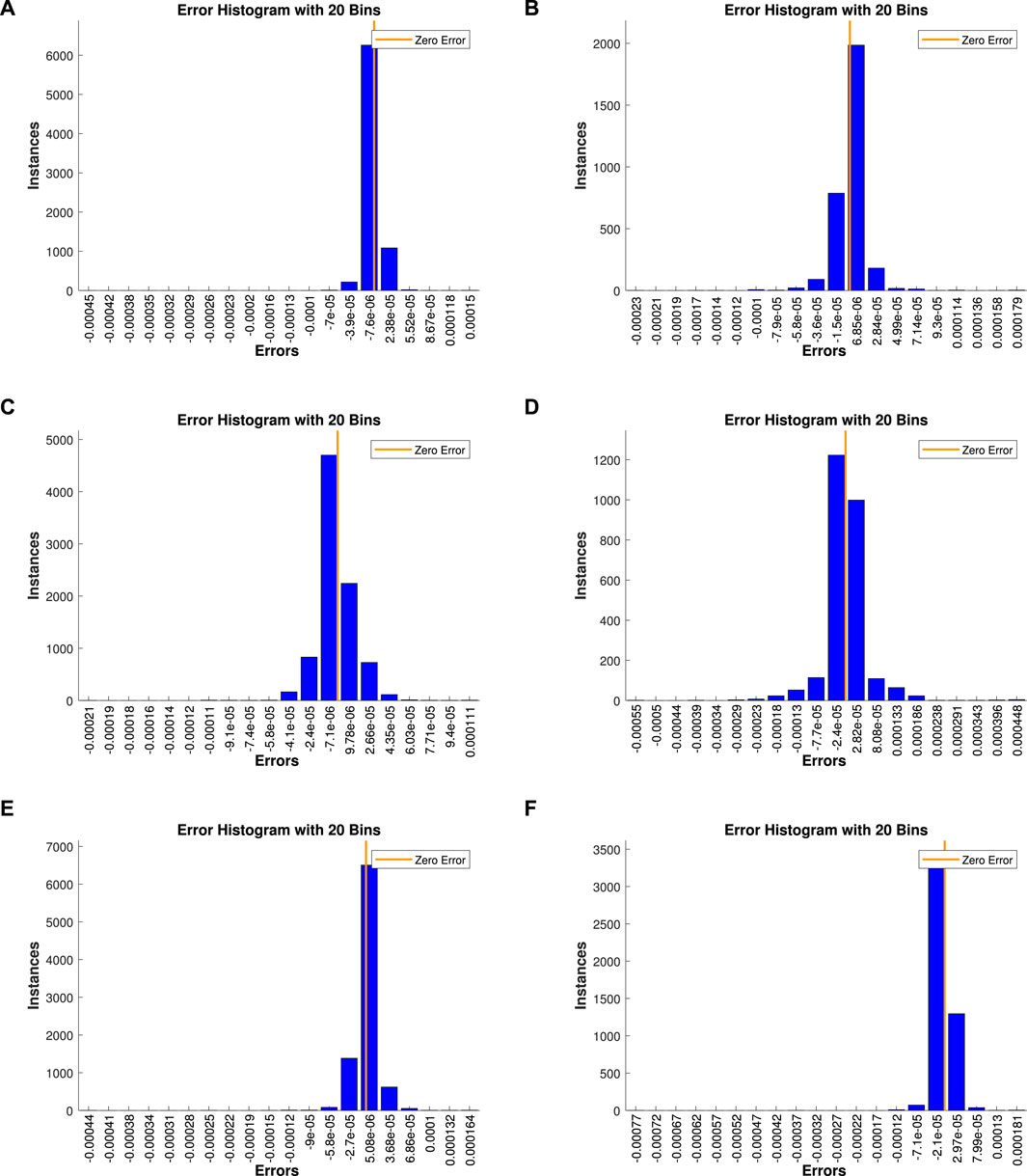
Figure 11. Error histogram for the effect of (A) $Nb$ on $\theta$, (B) $Nb$ on $\varphi$, (C) $Nt$ on $\theta$, (D) $Nt$ on $\varphi$, (E) $Rd$ on $\theta$, and (F) $E$ on $\varphi$.

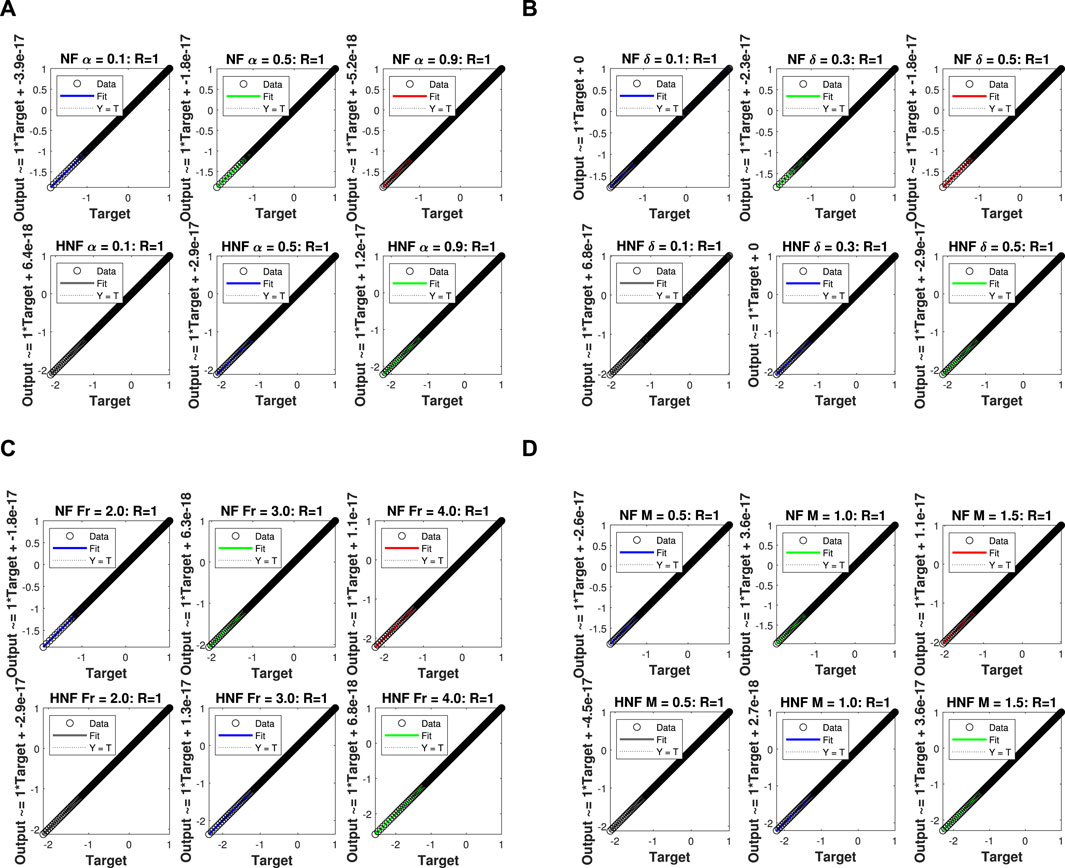
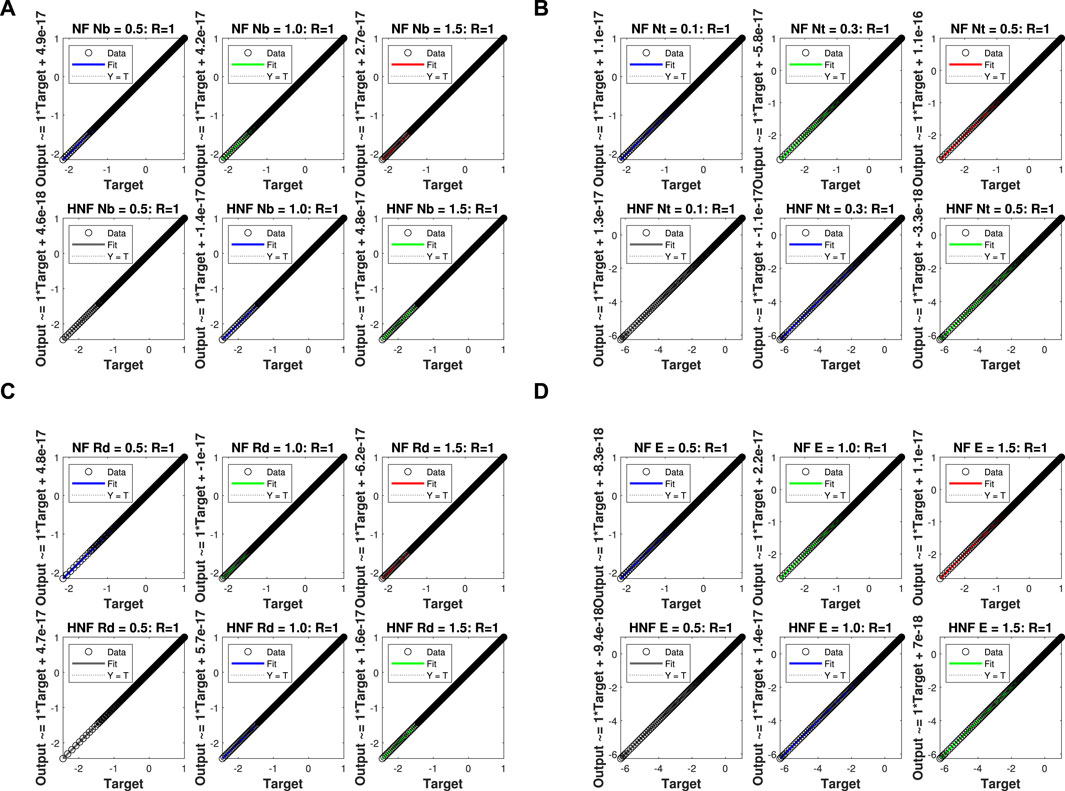
The regression lines for the impact of the parameters $(Nb,Nt,Rd,E)$ are dispayed in Figure 12A–D. The results for the increasing trends are presented for the NFs and HNFs separately in two rows. The output is presented on the $y$-axis, while the target points are chosen along the $x$-axis. In each case, the regression shows $R=1$, which proves that $100\%$ of the data is used in the fitting line. The minimum output for all the cases ranges up to $10^{-18}$, which proves the accuracy of the performed analysis. The fitted data are displayed in various colors (red, blue, green, and black).

Figure 12

Figure 12. Regression line for the effect of (A) $Nb$ on $\theta$, (B) $Nt$ on $\varphi$, (C) $Rd$ on $\theta$, and (D) $E$ on $\varphi$.

The validation performance for the impacts of $Nb,Nt,Rd$, and $E$ is displayed in Figure 13A–D. In Figure 13A,B, the performance for $Nb$ on $\theta$ and $Nt$ on $\varphi$ is presented. The best and minimal mean square errors are achieved at $2.1447e-10$ and $3.2913e-9$ for the parameters, respectively, using 1,000 epochs. Similarly, for $Rd$ and $E$, the same results for the mean square error are achieved at $4.638e-10$ and $4.1829e-9$, respectively.

Figure 13

Figure 13. Validation performance for the effect of (A) $Nb$ on $\theta$, (B) $Nt$ on $\varphi$, (C) $Rd$ on $\theta$, and (D) $E$ on $\varphi$.

4.1 Validation of results

The current approach is validated by considering the numerical values of Nusselt number and skin friction for $Pr=6.2$. These values show a good agreement with the available literature, as depicted in Table 3.

Table 3

Table 3. Numerical values of $f^{\prime }(0)$ and $-{\theta }^{\prime }(0)$ when $Pr=6.2$.

5 Conclusions

This article covers the neural network applications of the silicon-oil based HNF flow past a spinning disk using the Buongiorno model modifications. The impacts of various pertinent parameters for the thermal, concentration, and the velocity profiles are briefly described. We conclude the following:

$•$ The thermal profiles of nano and HNF increase with increasing values of $Rd$, $Nt$, $M$, and $Nb$.

$•$ For both mono and hybrid situations, both velocity profiles increased as the input of porosity $\delta$ and velocity slip $\alpha$ parameters increased, while diminishing as $M$ and DF, and $Fr$ parameters increased.

$•$ With higher $Nt$ and $E$ inputs, the concentration curves get better. Conversely, concentration profiles show declining tendencies when the magnetic and Brownian motion parameters $(M,Nb)$ increase.

$•$ The pace at which heat is transferred by HNF is faster than that of NF.

$•$ The regression graphs depict that $100\%$ of the data is used by the ANN.

$•$ The mean square error, error histogram, and performance validation depict its minimal values: $e-9$, $-7.1e-6$, and $e-11$, respectively, for 1,000 epochs.

$•$ For validity and stability of this work, the results achieved are compared with the available literature, where the proposed methodology shows good agreement. These results are tabulated for Nusselt number and skin friction, as shown in Table 3.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

AU: writing–original draft, validation, software, resources, methodology, investigation, formal analysis, and conceptualization. HY: writing–original draft, visualization, supervision, software, resources, project administration, methodology, and formal analysis. FU: writing–original draft, validation, software, methodology, investigation, and data curation. HA: writing–original draft, validation, software, resources, methodology, investigation, and formal analysis. EI: writing–original draft, visualization, validation, software, methodology, investigation, funding acquisition, and formal analysis. FA: writing–original draft, visualization, software, project administration, methodology, investigation, funding acquisition, and data curation. AS: writing–original draft, visualization, software, formal analysis, and data curation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

Researchers Supporting Project number (RSPD2024R1060), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kumar Devendiran D, Amirtham VA. A review on preparation, characterization, properties and applications of nanofluids. Renew Sust Energ Rev (2016) 60:21–40. doi:10.1016/j.rser.2016.01.055

CrossRef Full Text | Google Scholar

2. Choi SUS, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Technical report. Argonne, IL (United States): Argonne National Lab.ANL (1995).

Google Scholar

3. Nadeem S, Abbas N, Khan AU. Characteristics of three dimensional stagnation point flow of hybrid nanofluid past a circular cylinder. Results Phys (2018) 8:829–35. doi:10.1016/j.rinp.2018.01.024

CrossRef Full Text | Google Scholar

4. Suresh S, Venkitaraj KP, Selvakumar P, Chandrasekar M. Effect of al2o3–cu/water hybrid nanofluid in heat transfer. Exp Therm Fluid Sci (2012) 38:54–60. doi:10.1016/j.expthermflusci.2011.11.007

CrossRef Full Text | Google Scholar

5. Subba Reddy Gorla R, Siddiqa S, Mansour MA, Rashad AM, Salah T. Heat source/sink effects on a hybrid nanofluid-filled porous cavity. J Thermophys Heat Transfer (2017) 31(4):847–57. doi:10.2514/1.t5085

CrossRef Full Text | Google Scholar

6. Tayebi T, Ali JC. Free convection enhancement in an annulus between horizontal confocal elliptical cylinders using hybrid nanofluids. Numer Heat Transfer, A: Appl (2016) 70(10):1141–56. doi:10.1080/10407782.2016.1230423

CrossRef Full Text | Google Scholar

7. Acharya N. On the flow patterns and thermal control of radiative natural convective hybrid nanofluid flow inside a square enclosure having various shaped multiple heated obstacles. The Eur Phys J Plus (2021) 136(8):889. doi:10.1140/epjp/s13360-021-01892-0

CrossRef Full Text | Google Scholar

8. Tayebi T, Ali JC. Natural convection enhancement in an eccentric horizontal cylindrical annulus using hybrid nanofluids. Numer Heat Transfer, Part A: Appl (2017) 71(11):1159–73. doi:10.1080/10407782.2017.1337990

CrossRef Full Text | Google Scholar

9. Ali JC, Dogonchi AS, Ganji DD. Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and joule heating. AIP Adv (2019) 9(2). doi:10.1063/1.5086247

CrossRef Full Text | Google Scholar

10. Asghar Z, Shatanawi W, Ali Shah R, Gondal MA. Impact of viscoelastic ooze slime on complex wavy gliders near a solid boundary. Chin J Phys (2023) 81:26–36. doi:10.1016/j.cjph.2022.10.013

CrossRef Full Text | Google Scholar

11. Asghar Z, Ali Shah R, Ali Pasha A, Rahman MM, Khan MWS. Controlling kinetics of self-propelled rod-like swimmers near multi sinusoidal substrate. Comput Biol Med (2022) 151:106250. doi:10.1016/j.compbiomed.2022.106250

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Asghar Z, Shatanawi W, Hussain S. Biomechanics of bacterial gliding motion with oldroyd-4 constant slime. Eur Phys J Spec Top (2023) 232(6):915–25. doi:10.1140/epjs/s11734-022-00723-2

CrossRef Full Text | Google Scholar

13. Asghar Z, Ahmed E, Shatanawi W, Gondal MA. An exact solution for directional cell movement over jeffrey slime layer with surface roughness effects. Phys Fluids (2023) 35(4). doi:10.1063/5.0143053

CrossRef Full Text | Google Scholar

14. Asghar Z, Ali Shah R, Shatanawi W, Ali N. Fene-p fluid flow generated by self-propelling bacteria with slip effects. Comput Biol Med (2023) 153:106386. doi:10.1016/j.compbiomed.2022.106386

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Asghar Z, Shah RA, Shatanawi W, Ali N. A theoretical approach to mathematical modeling of sperm swimming in viscoelastic ellis fluid in a passive canal. Archive Appl Mech (2023) 93(4):1525–34. doi:10.1007/s00419-022-02343-7

CrossRef Full Text | Google Scholar

16. Asghar Z, Khan MWS, Shatanawi W, Gondal MA, Ghaffari A. An ifdm analysis of low Reynolds number flow generated in a complex wavy curved passage formed by artificial beating cilia. Int J Mod Phys B (2023) 37(19):2350187. doi:10.1142/s0217979223501874

CrossRef Full Text | Google Scholar

17. Acharya N. Framing the impacts of highly oscillating magnetic field on the ferrofluid flow over a spinning disk considering nanoparticle diameter and solid–liquid interfacial layer. J Heat Transfer (2020) 142(10):102503. doi:10.1115/1.4047503

CrossRef Full Text | Google Scholar

18. Yarmand H, Zulkifli NWBM, Gharehkhani S, Shirazi SFS, Alrashed AAAA, Ali MAB, et al. Convective heat transfer enhancement with graphene nanoplatelet/platinum hybrid nanofluid. Int Commun Heat Mass Transfer (2017) 88:120–5. doi:10.1016/j.icheatmasstransfer.2017.08.010

CrossRef Full Text | Google Scholar

19. Mesgari Abbasi S, Rashidi A, Nemati A, Arzani K. The effect of functionalisation method on the stability and the thermal conductivity of nanofluid hybrids of carbon nanotubes/gamma alumina. Ceramics Int (2013) 39(4):3885–91. doi:10.1016/j.ceramint.2012.10.232

CrossRef Full Text | Google Scholar

20. Usman Sajid M, Ali HM. Thermal conductivity of hybrid nanofluids: a critical review. Int J Heat Mass Transfer (2018) 126:211–34. doi:10.1016/j.ijheatmasstransfer.2018.05.021

CrossRef Full Text | Google Scholar

21. Kada B, Ali Pasha A, Asghar Z, Khan MWS, Bin Aris I, Shaikh MS. Carreau–yasuda fluid flow generated via metachronal waves of cilia in a micro-channel. Phys Fluids (2023) 35(1). doi:10.1063/5.0134777

CrossRef Full Text | Google Scholar

22. Asghar Z, Ali Shah R, Ali N. A numerical framework for modeling the dynamics of micro-organism movement on carreau-yasuda layer. Soft Comput (2023) 27(13):8525–39. doi:10.1007/s00500-023-08236-3

CrossRef Full Text | Google Scholar

23. Hayat T, Khan MI, Qayyum S, Khan MI, Alsaedi A. Entropy generation for flow of sisko fluid due to rotating disk. J Mol Liquids (2018) 264:375–85. doi:10.1016/j.molliq.2018.05.022

CrossRef Full Text | Google Scholar

24. Sajid M, Sadiq MN, Ali N, Javed T. Numerical simulation for homann flow of a micropolar fluid on a spiraling disk. Eur J Mechanics-B/Fluids (2018) 72:320–7. doi:10.1016/j.euromechflu.2018.06.008

CrossRef Full Text | Google Scholar

25. Sha Z, Dawar A, Alzahrani EO, Kumam P, Khan AJ, Saeed I. Hall effect on couple stress 3d nanofluid flow over an exponentially stretched surface with cattaneo christov heat flux model. IEEE Access (2019) 7:64844–55. doi:10.1109/access.2019.2916162

CrossRef Full Text | Google Scholar

26. Hayat T, Rashid M, Imtiaz M, Ahmed A. Nanofluid flow due to rotating disk with variable thickness and homogeneous-heterogeneous reactions. Int J Heat Mass Transfer (2017) 113:96–105. doi:10.1016/j.ijheatmasstransfer.2017.05.018

CrossRef Full Text | Google Scholar

27. Hayat T, Qayyum S, Imtiaz M, Ahmed A. Flow between two stretchable rotating disks with cattaneo-christov heat flux model. Results Phys (2017) 7:126–33. doi:10.1016/j.rinp.2016.12.007

CrossRef Full Text | Google Scholar

28. Khan AS, Nie Y, Shah Z, Dawar A, Khan W, Islam S. Three-dimensional nanofluid flow with heat and mass transfer analysis over a linear stretching surface with convective boundary conditions. Appl Sci (2018) 8(11):2244. doi:10.3390/app8112244

CrossRef Full Text | Google Scholar

29. Qayyum S, Khan MI, Hayat T, Alsaedi A, Tamoor M. Entropy generation in dissipative flow of williamson fluid between two rotating disks. Int J Heat Mass Transfer (2018) 127:933–42. doi:10.1016/j.ijheatmasstransfer.2018.08.034

CrossRef Full Text | Google Scholar

30. Jyothi K, Reddy PS, Suryanarayana Reddy M. Influence of magnetic field and thermal radiation on convective flow of swcnts-water and mwcnts-water nanofluid between rotating stretchable disks with convective boundary conditions. Powder Tech (2018) 331:326–37. doi:10.1016/j.powtec.2018.03.020

CrossRef Full Text | Google Scholar

31. Pourmehran O, Sarafraz MM, Rahimi-Gorji M, Ganji DD. Rheological behaviour of various metal-based nano-fluids between rotating discs: a new insight. J Taiwan Inst Chem Eng (2018) 88:37–48. doi:10.1016/j.jtice.2018.04.004

CrossRef Full Text | Google Scholar

32. Jalili P, Ahmadi Azar A, Jalili B, Ganji DD. A novel technique for solving unsteady three-dimensional brownian motion of a thin film nanofluid flow over a rotating surface. Scientific Rep (2023) 13(1):13241. doi:10.1038/s41598-023-40410-3

CrossRef Full Text | Google Scholar

33. Allehiany FM, Bilal M, Alfwzan WF, Ali A, Eldin SM. Numerical solution for the electrically conducting hybrid nanofluid flow between two parallel rotating surfaces subject to thermal radiation. AIP Adv (2023) 13(7). doi:10.1063/5.0154720

CrossRef Full Text | Google Scholar

34. Yasir M, Khan M, Alqahtani AS, Malik MY. Mass transpiration effect on rotating flow of radiative hybrid nanofluid due to shrinking surface with irregular heat source/sink. Case Stud Therm Eng (2023) 44:102870. doi:10.1016/j.csite.2023.102870

CrossRef Full Text | Google Scholar

35. Weerasiri L, Krishna Reddy Duvvuru S, Das S. Numerical simulation of a thin liquid film over a heated rotating disc and cone. Int J Therm Sci (2024) 196:108730. doi:10.1016/j.ijthermalsci.2023.108730

CrossRef Full Text | Google Scholar

36. Strong AI. Applications of artificial intelligence and associated technologies. Science (2016) 5(6).

Google Scholar

37. Shukla AK, Janmaijaya M, Abraham A, Muhuri PK. Engineering applications of artificial intelligence: a bibliometric analysis of 30 years (1988–2018). Eng Appl Artif Intelligence (2019) 85:517–32. doi:10.1016/j.engappai.2019.06.010

CrossRef Full Text | Google Scholar

38. Shahzad H, Sadiq MN, Li Z, Algarni S, Alqahtani T, Irshad K. Scientific computing of radiative heat transfer with thermal slip effects near stagnation point by artificial neural network. Case Stud Therm Eng (2024) 54:104024. doi:10.1016/j.csite.2024.104024

CrossRef Full Text | Google Scholar

39. Chen Y, De Luca G. Technologies supporting artificial intelligence and robotics application development. J Artif Intelligence Tech (2021) 1(1):1–8. doi:10.37965/jait.2020.0065

CrossRef Full Text | Google Scholar

40. Ghalambaz S, Abbaszadeh M, Sadrehaghighi I, Younis O, Ghalambaz M, Ghalambaz M. A forty years scientometric investigation of artificial intelligence for fluid-flow and heat-transfer (aifh) during 1982 and 2022. Eng Appl Artif Intelligence (2024) 127:107334. doi:10.1016/j.engappai.2023.107334

CrossRef Full Text | Google Scholar

41. Kofi Nti I, Felix Adekoya A, Weyori BA, Nyarko-Boateng O. Applications of artificial intelligence in engineering and manufacturing: a systematic review. J Intell Manufacturing (2022) 33(6):1581–601. doi:10.1007/s10845-021-01771-6

CrossRef Full Text | Google Scholar

42. Sofos F, Stavrogiannis C, Exarchou-Kouveli KK, Akabua D, George C, Karakasidis TE. Current trends in fluid research in the era of artificial intelligence: a review. Fluids (2022) 7(3):116. doi:10.3390/fluids7030116

CrossRef Full Text | Google Scholar

43. Karthik PC, Sasikumar J, Baskar M, Poovammal E, Kalyanasundaram P. Field equations for incompressible non-viscous fluids using artificial intelligence. The J Supercomputing (2022) 78(1):852–67. doi:10.1007/s11227-021-03917-y

CrossRef Full Text | Google Scholar

44. Amini S, Mohaghegh S. Application of machine learning and artificial intelligence in proxy modeling for fluid flow in porous media. Fluids (2019) 4(3):126. doi:10.3390/fluids4030126

CrossRef Full Text | Google Scholar

45. Mabrook Almalki M, Salem Alaidarous E, Adnan Maturi D, Raja MAZ, Shoaib M. Intelligent computing technique based supervised learning for squeezing flow model. Scientific Rep (2021) 11(1):19597. doi:10.1038/s41598-021-99108-z

CrossRef Full Text | Google Scholar

46. Zubair G, Shoaib M, Khan MI, Naz I, Ali A, Raja MAZ, et al. Intelligent supervised learning for viscous fluid submerged in water based carbon nanotubes with irreversibility concept. Int Commun Heat Mass Transfer (2022) 130:105790. doi:10.1016/j.icheatmasstransfer.2021.105790

CrossRef Full Text | Google Scholar

47. Shoaib M, Raja MAZ, Rehman Khan MA, Tauseef Sabir M, Sooppy Nisar K, Iltaf I, et al. Investigation of heat and mass transfer for an mhd hybrid nanofluid flow over a rotating disk: a numerical investigation with supervised neural network. Waves in Random and Complex Media (2022) 1–24. doi:10.1080/17455030.2022.2128228

CrossRef Full Text | Google Scholar

48. Shoaib M, Raja MAZ, Touseef Sabir M, Sooppy Nisar K, Jamshed W, Felemban BF, et al. Mhd hybrid nanofluid flow due to rotating disk with heat absorption and thermal slip effects: an application of intelligent computing. Coatings (2021) 11(12):1554. doi:10.3390/coatings11121554

CrossRef Full Text | Google Scholar

49. Ali F, Awais M, Ali A, Vrinceanu N, Shah Z, Tirth V. Intelligent computing with levenberg–marquardt artificial neural network for carbon nanotubes-water between stretchable rotating disks. Scientific Rep (2023) 13(1):3901. doi:10.1038/s41598-023-30936-x

CrossRef Full Text | Google Scholar

50. Jayachandra Babu M, Sandeep N. Three-dimensional mhd slip flow of nanofluids over a slendering stretching sheet with thermophoresis and brownian motion effects. Adv Powder Tech (2016) 27(5):2039–50. doi:10.1016/j.apt.2016.07.013

CrossRef Full Text | Google Scholar

51. Ghadikolaei SS, Yassari M, Sadeghi H, Hosseinzadeh K, Ganji DD. Investigation on thermophysical properties of tio2–cu/h2o hybrid nanofluid transport dependent on shape factor in mhd stagnation point flow. Powder Technol (2017) 322:428–38. doi:10.1016/j.powtec.2017.09.006

CrossRef Full Text | Google Scholar

52. Ghadikolaei SS, Hosseinzadeh K, Yassari M, Sadeghi H, Ganji DD. Boundary layer analysis of micropolar dusty fluid with tio2 nanoparticles in a porous medium under the effect of magnetic field and thermal radiation over a stretching sheet. J Mol Liquids (2017) 244:374–89. doi:10.1016/j.molliq.2017.08.111

CrossRef Full Text | Google Scholar

53. Palwasha Z, Saeed Khan N, Shah Z, Islam S, Bonyah E. Study of two-dimensional boundary layer thin film fluid flow with variable thermo-physical properties in three dimensions space. AIP Adv (2018) 8(10). doi:10.1063/1.5053808

CrossRef Full Text | Google Scholar

54. Kumar M, Mondal PK. Irreversibility analysis of hybrid nanofluid flow over a rotating disk: effect of thermal radiation and magnetic field. Colloids Surf A: Physicochemical Eng Aspects (2022) 635:128077. doi:10.1016/j.colsurfa.2021.128077

CrossRef Full Text | Google Scholar

55. Fawad Malik M, Ali Shah SA, Bilal M, Mohamed H, Mahmood I, Ali A, et al. New insights into the dynamics of heat and mass transfer in a hybrid (ag-tio2) nanofluid using modified buongiorno model: a case of a rotating disk. Results Phys (2023) 53:106906. doi:10.1016/j.rinp.2023.106906

CrossRef Full Text | Google Scholar

56. Miklavčič M, Wang CY. The flow due to a rough rotating disk. Z für Angew Mathematik Physik ZAMP (2004) 55:235–46. doi:10.1007/s00033-003-2096-6

CrossRef Full Text | Google Scholar

57. Awan AU, Ali B, Shah SAA, Oreijah M, Guedri K, Eldin SM. Numerical analysis of heat transfer in ellis hybrid nanofluid flow subject to a stretching cylinder. Case Stud Therm Eng (2023) 49:103222. doi:10.1016/j.csite.2023.103222

CrossRef Full Text | Google Scholar

58. Bhatti MM, Öztop HF, Ellahi R, Sarris IE, Doranehgard MH. Insight into the investigation of diamond (c) and silica (sio2) nanoparticles suspended in water-based hybrid nanofluid with application in solar collector. J Mol Liquids (2022) 357:119134. doi:10.1016/j.molliq.2022.119134

CrossRef Full Text | Google Scholar

59. Zhang J, Cui H, Han S, Li Z, Lu J. Research on the rheological properties of a silicone oil-based ferrofluid. Korea-Australia Rheology J (2023) 35(3):179–90. doi:10.1007/s13367-023-00065-y

CrossRef Full Text | Google Scholar

60. Acar Boyacioglu M, Kara Y, Kaan Baykan Ö. Predicting bank financial failures using neural networks, support vector machines and multivariate statistical methods: a comparative analysis in the sample of savings deposit insurance fund (sdif) transferred banks in Turkey. Expert Syst Appl (2009) 36(2):3355–66. doi:10.1016/j.eswa.2008.01.003

CrossRef Full Text | Google Scholar

61. Hamid R, Plaksina T. Application of artificial intelligence techniques in the petroleum industry: a review. Artif Intelligence Rev (2019) 52(4):2295–318.

Google Scholar

62. Haykin S, Network N. A comprehensive foundation. Neural networks (2004) 2(2004):41.

Google Scholar

63. Wang D, He H, Liu D. Intelligent optimal control with critic learning for a nonlinear overhead crane system. IEEE Trans Ind Inform (2017) 14(7):2932–40. doi:10.1109/tii.2017.2771256

CrossRef Full Text | Google Scholar

64. Raza J, Raza M, Mustaq T, Qureshi MI. Supervised machine learning techniques for optimization of heat transfer rate of cu-h2o nanofluid flow over a radial porous fin. Multidiscipline Model Mater Structures (2023) 19(4):680–706. doi:10.1108/mmms-08-2022-0153

CrossRef Full Text | Google Scholar

65. Tizakast Y, Kaddiri M, Lamsaadi M, Makayssi T. Machine learning based algorithms for modeling natural convection fluid flow and heat and mass transfer in rectangular cavities filled with non-Newtonian fluids. Eng Appl Artif Intelligence (2023) 119:105750. doi:10.1016/j.engappai.2022.105750

CrossRef Full Text | Google Scholar

66. Bhattacharya A, Majumdar P. Artificial intelligence-machine learning algorithms for the simulation of combustion thermal analysis. Heat Transfer Eng (2024) 45(2):176–93. doi:10.1080/01457632.2023.2178282

CrossRef Full Text | Google Scholar

67. Aylı E, Kocak E. Supervised learning method for prediction of heat transfer characteristics of nanofluids. J Mech Sci Tech (2023) 37(5):2687–97. doi:10.1007/s12206-023-0442-5

CrossRef Full Text | Google Scholar

68. Hemmat M, Toghraie D, Amoozad F. Prediction of viscosity of mwcnt-al2o3 (20: 80)/sae40 nano-lubricant using multi-layer artificial neural network (mlp-ann) modeling. Eng Appl Artif Intelligence (2023) 121:105948. doi:10.1016/j.engappai.2023.105948

CrossRef Full Text | Google Scholar

69. Yin C, Zheng L, Zhang C, Zhang X. Flow and heat transfer of nanofluids over a rotating disk with uniform stretching rate in the radial direction. Propulsion Power Res (2017) 6(1):25–30. doi:10.1016/j.jppr.2017.01.004

CrossRef Full Text | Google Scholar

70. Acharya N, Bag R, Kundu PK. Influence of hall current on radiative nanofluid flow over a spinning disk: a hybrid approach. Physica E: Low-dimensional Syst Nanostructures (2019) 111:103–12. doi:10.1016/j.physe.2019.03.006

CrossRef Full Text | Google Scholar