Investigating the properties of octane isomers by novel neighborhood product degree-based topological indices

A topological index is a real number calculated from the structure of a chemical compound to describe its topology. The use of molecular descriptors has been increasing in recent years, helping to determine the physicochemical and biological properties of drugs. The main purpose of this article is to investigate the properties of the octane isomers using the theoretical method. To study the structures of octane isomers, we have introduced a new approach called “neighborhood product degree” to calculate all the classical degree-based topological indices. The np-degree approach is applied to approximate eight properties of octane isomers, such as the acentric factor, density, refractive index, critical volume, molar volume, radius of curvature, critical pressure, and LogP. The np-degree-based topological indices are the estimated values of the properties of octane structures, so the linear and quadratic regression models and correlation coefficients are applied to check the validity of the estimated results. The quantitative structure property relation are obtained by using the linear, quadratic, exponential, logarithmic and sinusoidal regression methods with the help of SPSS. Two models are applied to all the compuations and three regression models are applied to the np-degree Randic index. The computation showed that quadratic regression model is suitable for study octane isomers and np-degree based graph invariants. If the values of the correlation coefficient r ⩾ 0.7, p-values ⩽ 0.05, and F-values ⩾ 2.5, then the results are significant. The results of np-degree-based topological indices satisfy all the criteria for being significant, so these newly introduced indices are valid to study octane isomers. The information determined in this article is beneficial for chemists and pharmacists.

1 Introduction

Octane isomers are hydrocarbons that have different molecular structures but the same chemical formula. These isomers have several uses in industries such as oil and gas, automotive, and chemical manufacturing. They can improve engine performance and reduce harmful emissions. For example, iso-octane has a high resistance to knocking in engines, while n-heptane has a low resistance to knocking. Blending these two isomers together produces gasoline with an octane rating that matches the needs of a specific engine. In addition to improving engine performance, using octane isomers can also lead to more efficient fuel usage and decreased carbon monoxide emissions. One of the main uses of octane isomers is as a reference point for measuring the quality of gasoline. Gasoline with higher octane ratings burns more efficiently and produces fewer emissions. Octane isomers are also used in the production of solvents, plastics, and detergents. Octane isomers are valuable tools in organic chemistry, serving as model compounds for studying chemical reactions and mechanisms. They are used in laboratory settings and research to investigate molecular structure and function and to develop new synthetic methodologies. They also have applications in aerospace engineering, serving as reference fuels for evaluating jet and rocket engine performance and combustion characteristics, ensuring safety and reliability in aviation and space exploration. Additionally, some isomers of octane have medical applications, such as in the treatment of cancer and as an anesthetic. With the versatile properties of octane isomers, they continue to have a significant impact on various industries and fields [1].

Chemical graph theory is a fascinating and important field of study that has significant applications in a variety of fields. Its use of graph theory to model chemical phenomena has led to significant advancements in drug design, material science, and nanotechnology. Isomers of a chemical compound rely on graph theory as they have the same chemical formula but are distinguished by their structures. Graph theory helps understand the isomers of octane. A chemical graph is a labeled graph whose vertices correspond to the atoms of the compound and whose edges correspond to chemical bonds. This branch of mathematics applies chemical graph theory to model molecules and study their various physical properties. Chemical graph theory is a critical tool for understanding molecular structure, designing compounds, understanding reaction mechanisms, and guiding computational simulations in various chemistry fields, contributing to advancements in theoretical understanding and practical applications in drug discovery, materials science, and environmental remediation. The study of chemical graph theory is essential to understanding molecules’ behavior of molecules and their interactions with other molecules, making it a critical area of research in the field of chemistry. QSPR modeling employs graph theory to predict a drug’s properties based on its molecular structure. Researchers develop QSPR models using statistical and mathematical methods to quantify the relationship between the molecular structure and the properties of interest [2–5].

Topological indices are essential mathematical descriptors that provide valuable insights into the structure of chemical compounds. These indices provide quantitative information about various structural features such as size, shape, branching, symmetry, and connectivity, derived from the compound’s molecular graph. Degree-based indices are used in various fields, including quantitative structure-activity relationship (QSAR), chemical reactivity, drug design and discovery, material science, network analysis, predictive modeling, toxicity prediction, and graph theory applications. They help to correlate the structure of molecules with their biological activities, predict chemical reactivity, aid in drug design and discovery, characterize material structure-property relationships, analyze complex systems, train predictive models in machine learning, and predict chemical toxicity profiles in chemicals. They also contribute to graph theory applications in computer science, mathematics, and sociology. Chemists commonly use various topological indices in their field, such as the Wiener index, the Randic index, and the Zagreb index. Each of these indices calculates a different aspect of the molecular structure, providing a unique perspective on the compound’s properties. Topological indices are an important tool for understanding the structure and properties of chemical compounds, allowing chemists to make predictions about a compound’s behavior without having to perform time-consuming experimental measurements. For more information about the significance and applications of the TIs, see [6–8].

The octane isomers are analyzed by different types of numerical descriptors. The atom bond connectivity index and forgotten index are the numerical descriptors that are introduced for the determination of the properties of octane isomers. Researchers mostly use a new index to understand the characteristics of alkanes, benzene derivatives, and octane isomers. Due to the simple nature and great importance of the octane isomers, we applied the newly introduced approach to explore these structures. Below are the main points of our contribution to this article.

• This manuscript studies the physical and chemical characteristics of the octane isomers. There are eight properties, such as acentric factors, density, refractive index, critical volume, molar volume, radius of curvature, critical pressure, and logP. The np-degree approach theoretically analyzes these properties.

• The experimental values of these characteristics of the octane isomers have already been calculated with lab experiments and some theoretical techniques. Computing properties through lab experiments is challenging, time-consuming, expensive, and demands expertise. So, we provide an easy method using a numerical descriptor and some statistical tools.

• Six numerical descriptors are used to determine the properties of octane. The edge partition technique is used for the determination of the results of TIs. The np-degree TIs are the calculated or approximated values of the octane isomers, and the validity of these calculations is checked by the linear and quadratic regression models.

• SPSS software computes the correlation values, p-test values, and F-test values, making it an amazing tool for statistical computations. The correlation coefficients are positive and negative.

• Line graphs graphically represent the data. This is another method to analyze and compare the correlation coefficients. We draw the graphs in MS Excel. Line graphs are a valuable tool for visually representing data. They provide a clear and concise way to analyze and compare correlation coefficients. Plotting data points on a graph allows for easy identification and interpretation of trends and patterns.

The purpose of this article is to explore the characteristics of octane isomers using a theoretical method. A large number of chemical structures have already been examined using topological indices and regression analysis. This work has motivated us to further investigate the properties of octane structures using np-degree indices and regression analysis. Regression analysis is an effective way to determine the suitability of topological indices for specific properties of chemical structures’ properties.

The first topological index was a distance-based index; however, degree-based indices are more useful and applicable to graph invariants. Today, researchers have introduced many types of degree-based numerical descriptors. The degree of vertex work is increasing day by day. The np-degree-based indices will also prove to be a good addition to the progress of degree-based indices. In 2017, Chellali et al. proposed two new degree concepts in topological indices, called ve-degree and ev-degree [9]. The concepts of ev-degree and ve-degree are very simple yet beneficial. These indices showed a very good correlation with the benzene derivatives. In chemistry, benzene derivatives have a very important chemical structure. Rauf et al. investigated the properties of benzene derivatives using six ev-degree and ve-degree numerical descriptors [10]. These indices showed an excellent correlation with experimental values. The multi-linear regression model is used to check the significance of the results. These indices proved to be equally effective for organic and inorganic compounds, such as silicon carbides. In 2020, Jamil et al. introduced a different degree-based index called the face index [11]. It is computed by adding the internal and external degrees of the graphs. This index analyzes the structures of benzene derivatives. It observed from the computations that the new topological index can be use multiple linear regression to accurately predict the pi-electron energy and boiling points of benzenoid hydrocarbons, with a correlation coefficient of r > 0.99. The correlation of face index for some structures was approximately 1, which is a very strong correlation. Mahboob et al. [12] proposed a novel concept related to the degree known as “bi-distant.” In this concept, two edges are considered to be one edge, and we count their degrees using the classical method. The eigenvalue indices have recently been used to explore the properties of COVID-19 drug structures [13]. Entropy, first introduced in Shannon’s paper, measures the uncertainty of information content in probability distributions [14]. It was later applied to graphs and chemical networks to measure structural information. It has been widely applied in fields like chemistry, biology, ecology, and sociology. Graph entropy measures, which associate probability distributions with graph elements, can be classified as intrinsic and extrinsic measures. There are a variety of graph entropy measures. The ve-degree of end vertices of each edge-based entropy index is first proposed to investigate the two-dimensional structure of breast cancer drugs [15]. The QSPR was established using linear and cubic regression methods with SPSS, revealing a strong correlation between entropy indices and the physical properties of the drugs. The results show that the entropy indices under study have a strong correlation with the physical characteristics. All the degree-based indices are proposed to analyze the different structures. There are different types of chemical structures. To get more and more information about the properties of different structures, researchers are using more and more indices with the passage of time. The graph invariants reinforce the connection between chemistry and mathematics.

Recently, Huang et al. studied the characteristics of Lyme drugs using three types of regression models and degree-related TIs [16]. They examined six properties of lyme drugs using ten degree-related TIs, which were degree-based. Our article, however, focuses on np-degree-based indices. Rasheed et al. used TIs and regression analysis to study the properties of heart attack drugs [17]. They calculated the boiling point, enthalpy of vaporization, flash point, and molar refractivity of heart attack drugs based on a strong correlation greater than 0.8 with these properties. Hui et al. examined the physicochemical properties of antiemetics used to treat nausea or vomiting [18]. They investigated six properties of anti-emetics drugs using 13 degree-related TIs and analyzed the results using simple and multi-linear regression models. Mahboob et al. investigated the two-dimensional structures of blood cancer drugs using the newly introduced degree-based topological indices [19]. Three different types of regression models, including linear, logarithmic, and exponential regression, analyze the results. Multiple times, researchers have evaluated and studied octane isomers multiple times to introduce new numerical descriptors. These articles are based on degree-based topological indices as well as the verification of results by different regressions. The advancement of theoretical work in the field of chemical graph theory motivated us to write and explore the various chemical structures with the help of numerical descriptors.

The article divides into nine sections. Section 1 introduces the topic and provides basic definitions, including an overview of np-degree. Section 2 delves into the methods and software used for computations, as well as the procedure for estimating the properties of octane isomers. Section 3 explores the experimental and calculated values of parameters, while Section 4 explains the validity of the two-regression model. Section 5 examines the graphical approach for understanding the results and compares them with those in the literature. Section 6 consists of the data related to the three regression models and analyzes the results. Section 7 provides a detailed analysis of the results obtained from both linear and quadratic regressions, whereas Section 8 highlights the various applications of numerical descriptors in different fields and in describing the properties of octane structures. Finally, Section 9 discusses the conclusion and future scope of our work. A list of references at the end of the article provides readers with access to all relevant information.

1.1 Basic definitions and literature review

Let G = (V, E) be a simple, planar, and connected graph representing the structures of octane isomers. In chemical graphs, atoms are indicated by nodes, and bonds are represented by lines. The structures of octane isomers do not have cycles. There are two concepts related to degrees discussed in this article. The first one is the simple degree of any node v that is formed by counting the number of edges attached to it. The degree of a node v is represented by d_v. This is the classical degree of the nodes of chemical graphs. The neighborhood product degree of a node v is the product of the degrees of vertices attached to v. It is denoted by P_v. Various formulas of np-degree-based topological indices are defined in Eqs 1–8.

The general definition of np-degree-related indices is:

$TI\left(G\right)={\displaystyle \sum _{\left\{u,v\right\}\subseteq V\left(G\right)}}F\left(P_u,P_v\right),(1)$

where P_u and P_v are the inputs, and F is a function. The terms P_u and P_v are not simple vertex degrees, but these are neighborhood product degrees. The np-degree of vertex u is given below.

$P_u=\prod _{uv\in E\left(G\right)}{d}_v(2)$

Milan Randic, a chemist from Croatia, dedicated his efforts to constructing a mathematical model in 1975 that could accurately describe the degree of branching in organic compounds, specifically in the carbon-atom skeleton of alkanes [20]. Randic proposed a branching index, which has since been named after him in recognition of his exceptional contributions to the field. Chemists use the R-index, one of the oldest degree-related indices, to estimate the properties of many chemical structures. Randic proposed replacing the simple vertex degrees with the np-degrees P_v and P_u. A new version of the R-index calculated by np-degree is given below.

${}^{np}R\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\frac{1}{\sqrt{P_u\times P_v}}(3)$

A large number of structures and their properties are estimated by the Randic index. Zhou et al. approximate the seven properties of the narcotic drugs by the R-index [21]. Parveen et al. applied the R-index to study the information about the drugs used to treat blood cancer [22]. The significance of the R-index can be measured by the fact that it is the most useful index for understanding chemical structures theoretically. Gayathri et al. applied the different indices, particularly the R-index, to study the properties of the circumcoronene series of benzenoid [23]. The Randic index is a tool that provides structural information about molecules, enabling understanding of their properties and activities. It correlates well with physicochemical properties, making it useful in QSPR studies. In medicinal chemistry, it aids in drug design and discovery by quantifying molecular branching patterns. It also aids in toxicity prediction by identifying structural features that correlate with toxicological endpoints. The index also provides insights into chemical reactivity, helping predict reaction outcomes. It also finds applications in graph theory and network analysis.

Lingping Zhong introduced a formula to study the properties of trees and general graphs in 2013, named the harmonic index [24]. The formula for the H-index is formed by the inspiring Randic and sum connectivity indices. Zhong introduced this index in graph theory, but it was first studied by Fajtlowicz to study the computer program [25]. The np-degree form of H-index is defined as:

${}^{np}H\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\frac{2}{\left(P_u+P_v\right)}.(4)$

The H-index is very easy to calculate and is highly significant because of its applications in various fields. Due to its success, many approaches have been taken to take advantage of this index. The harmonic index is very simple and easy to calculate. First, it did not catch the attention of many researchers, but with the passage of time, its applications are increasing day by day. The harmonic index is utilized to study the characteristics of asthma drugs [26]. There are different forms and approaches to the classical degree-based indices that are being introduced due to the success of these indices. Applying the np-degree approach to the harmonic index has led to its success. Khan et al. examine the drugs used to treat skin cancer by degree-related TIs, especially H-index [27]. The harmonic index measures a molecule’s structural complexity by considering the distances between atoms. Higher indices indicate more complex molecules. The index correlates with physicochemical properties, making it useful in QSPR studies. By identifying patterns associated with biological activities, medicinal chemistry, it aids in drug design and discovery by identifying patterns associated with biological activities. It also helps predict toxicity by comparing structural features with endpoints. The index also provides insights into chemical reactivity, helping predict reactions.

Gutman and Trinajstic introduced a formula to study hydrocarbons in 1972, represented by M₁ [28]. The parameter M₂ was introduced by Gutman et al. to study acyclic polyenes in 1975 [29]. These parameters are collectively called Zagreb indices due to the name of the city where the authors introduce them. The first index involves the sum of the vertex degrees of an edge, and the second index is formed by the product of the vertex degrees of an edge. The np-degree version of these indices is given below.

${}^{np}M_1\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\left(P_u+P_v\right)(5)$

${}^{np}M_2\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\left(P_u\times P_v\right)(6)$

Shanmukha et al. recently analyzed the 11 properties of the octane isomers by using different types of Zagreb indices and three regression models [30]. After 1 year, Tamilarasi increased the progress of Zagreb indices to study the octane isomers [31]. Parveen et al. use Zagreb indices [32] to determine the QSPR modeling of the structures of diabetes drugs for the treatment of this fatal disease.

Ivan Gutman proposed the Reciprocal Randic Index (RR) and introduced three indices in his 2014 paper [33]. These indices were initially utilized to estimate the characteristics of alkanes, a group of hydrocarbons. The results showed that the indices were highly effective in this regard. The RR index has proven to be a valuable tool for predicting the properties of various chemical compounds, and its applications are in different fields. The np-degree-based RR index is defined as:

${}^{np}RR\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\sqrt{P_u\times P_v}.(7)$

In 2010, Vukicevic proposed the inverse sum index [34]. The IS index includes both the product and sum of the terminal degrees of an edge. The np-degree inverse sum index is defined as:

${}^{np}IS\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\frac{\left(P_u\times P_v\right)}{\left(P_u+P_v\right)}.(8)$

Researchers have conducted limited research on this index; however, it remains a highly effective tool for approximating the characteristics of various chemical structures. Das and Mondal recently applied the IS index and neighborhood IS index to a study of trees and unicyclic graphs [35]. For more information on how to determine the properties of different chemical structures using TIs and regression models, see [36, 37]. Definition of np-degree and its comparison with vertex degree and sum neighborhood degree based topological indices.

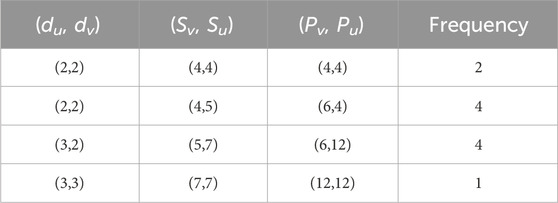
The term “np-degree-based topological indices” refers to neighborhood product degree-based topological indices. The np-degree of a vertex “v” is defined as the product of the neighborhood degrees of vertex “v.” The np-degree of a vertex v is the product of the degrees of two other vertices, u and w, to which v is connected. The np-degree of an edge e = uv is defined by the separate product degrees of u and v. The np-degree method is a simple approach to finding the topological indices using a new method. The concept of neighborhood sum degree is similar to that of neighborhood product degree. Researchers use both methods to estimate the properties of chemical structures. Figure 1 shows the np-degrees of the naphthalene structure.

Figure 1

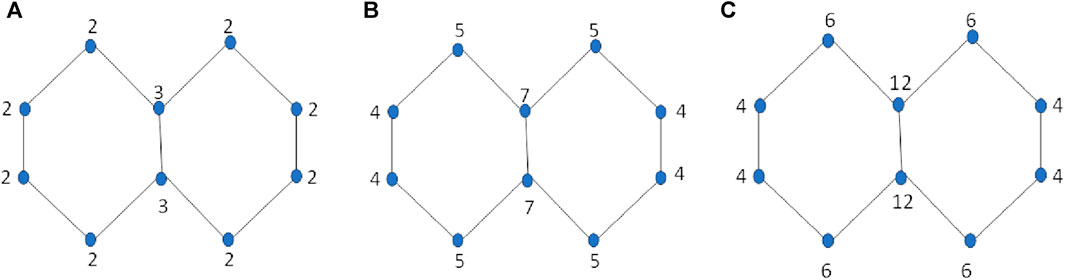
Figure 1. Computation of three types of degrees for Naphthalene. (A) Simple vertex degrees. (B) Sum Neighborhood degrees. (C) Neighborhood product degrees.

The comparison of the different approaches to calculating the topological indices for a particular structure of naphthalene is given in Table 1, and degrees are mentioned in Figure 1. The simple degree of a vertex v is the number of edges connected to it, denoted by d_v. The sum neighborhood degree of a vertex v is the sum of all degrees of the vertices attached to v, denoted by S_v. The neighborhood product degree of a vertex v is the product of the degrees of vertices attached to v and is denoted by P_v. The concept of simple degree-related TIs was introduced in 1972 with the introduction of the first degree-related indices, called Zagreb indices. The concept of sum neighborhoods related to TIs was introduced in 2019. The idea of neighborhood product-related TIs is introduced in the present article and applied to six classical numerical descriptors.

Below are the values of the first Zagreb index computed for the structure of naphthalene using three different types of degree approaches.

$\begin{array}{ll}\hfill M_1\left(G\right)& =6\left(2+2\right)+4\left(3+2\right)+1\left(3+3\right)=24+20+6=50\hfill \\ \hfill {}^{sn}M_1\left(G\right)& =2\left(4+4\right)+4\left(4+5\right)+4\left(5+7\right)+1\left(7+7\right)=16+36+48+14=114{}^{np}M_1\left(G\right)\hfill & =2\left(4+4\right)+4\left(6+4\right)+4\left(6+12\right)+1\left(12+12\right)=16+40+72+24=152\hfill \end{array}$

Table 1

Table 1. Comparison of three types of degrees.

2 Method and material used for computations

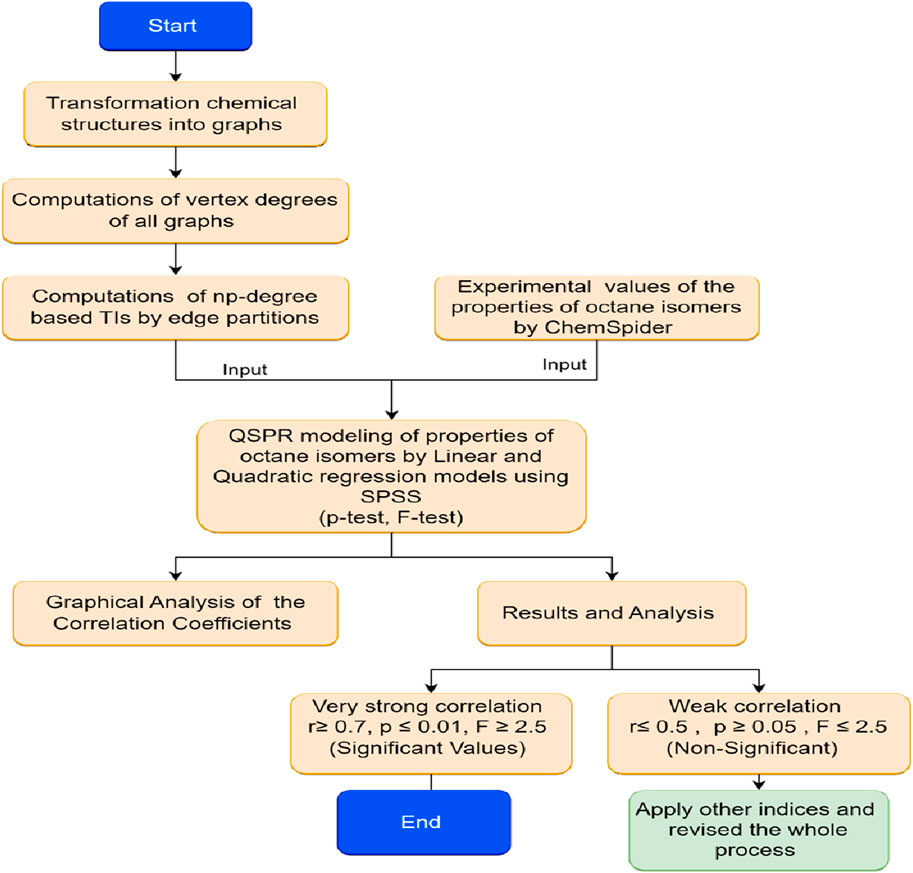
There are two types of computations done here: computation of numerical descriptors and statistical computations. The degree-counting technique is used to count the degrees and np-degrees. Vertex partitioning, np-degree edge partitioning, and computational techniques are used to calculate the estimated values (np-degree TIs). The calculations are done using a scientific calculator and verified by MATLAB software. The software SPSS uses for statistical computations such as regression equations and statistical parameters The 2D graphs of comparison and correlation are drawn by Microsoft Excel. The experimental data is taken from chemSpider. The procedure for estimating the properties of octane isomers by np-degree-based TIs is given below in Figure 2.

Figure 2

Figure 2. Procedure for estimating the octane properties.

3 Determination of results for octane isomers

The values of T-indices are the estimated values of the properties of octane isomers. The accuracy of these numerical values is predicted by using correlation coefficients. A strong relationship between estimated values and the values calculated by experiments shows the validity of T-indices. There are two types of computations included in the section. The first part discusses the experimental values that are taken from ChemSpider and Stenutz. The second part deals with the computation of degree-related T-indices for the 18 structures of the octane isomers.

3.1 Experimental values for properties of octane isomer

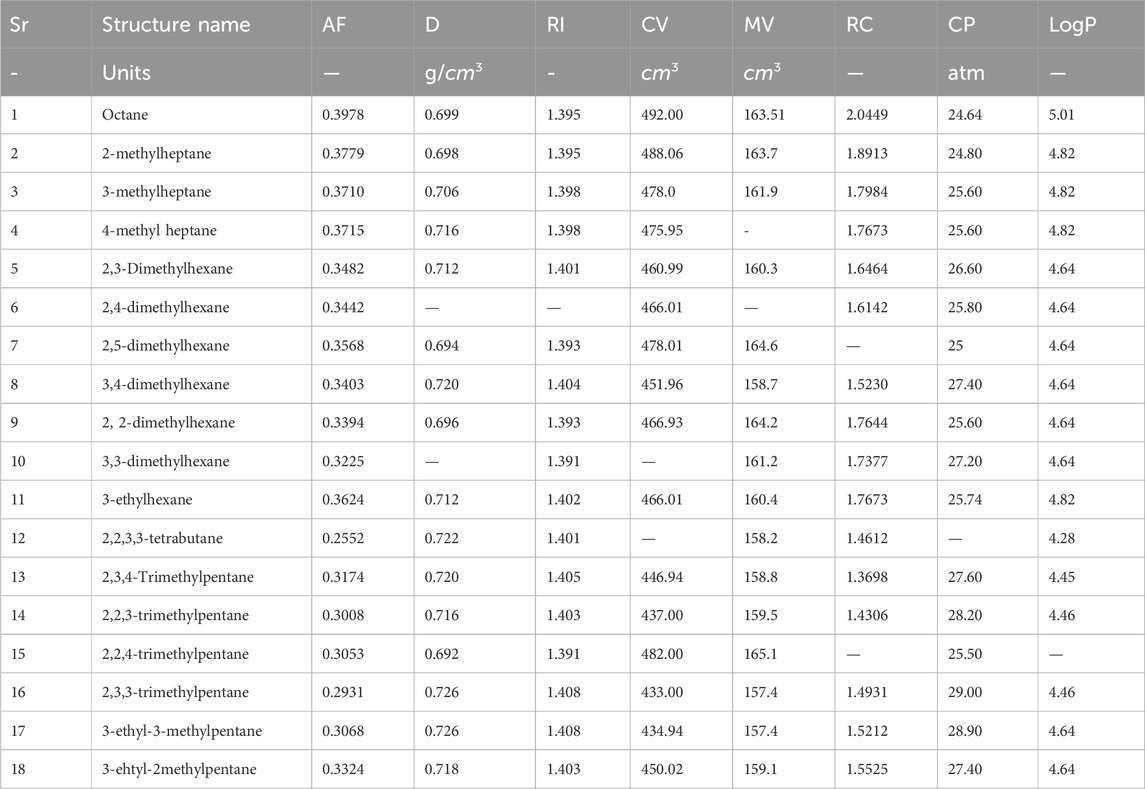
There are eight properties of octane isomers that are predicted by using six np-degree-related indices. All eight characteristics for all octane isomers are given in Table 2. A parameter can be calculated in different units, so the units of the parameters are also mentioned in Table 2. The acentric factor (AF) is a crucial metric that measures the extent to which a substance’s thermodynamic properties deviate from the predictions of the Principle of Corresponding States. The acentric factor is a dimensionless quantity that characterizes a substance’s molecular structure and its ability to interact with other molecules. Density (D) is a physical characteristic that can be calculated by dividing an object’s mass by its volume. It is a constant property that remains the same regardless of the size of the sample. There are different units used to measure density, but we use g/cm³ in this manuscript. The refractive index (RI) is a fundamental property of a material that describes how much the speed of light is reduced when it passes through it. It is calculated by dividing the speed of light in a vacuum by the speed of light in a medium with a higher density. Interestingly, this ratio has no units, making it a dimensionless quantity. The critical volume (CV) refers to the volume occupied by 1 mol of gas at a specific critical temperature and pressure. It is important to note that the critical volume is not a fixed value and varies depending on the gas being studied. The eight properties that are determined with the help of np-degree related T-indices are acentric factor (AF), density (D), refractive index (RI), critical pressure (CP), molar volume (MV), radius of curvature (RC), critical pressure (CP), and LogP. The chemical structures of octane isomers are given in Figure 3.

Table 2

Table 2. Characteristics of octane isomers.

Figure 3

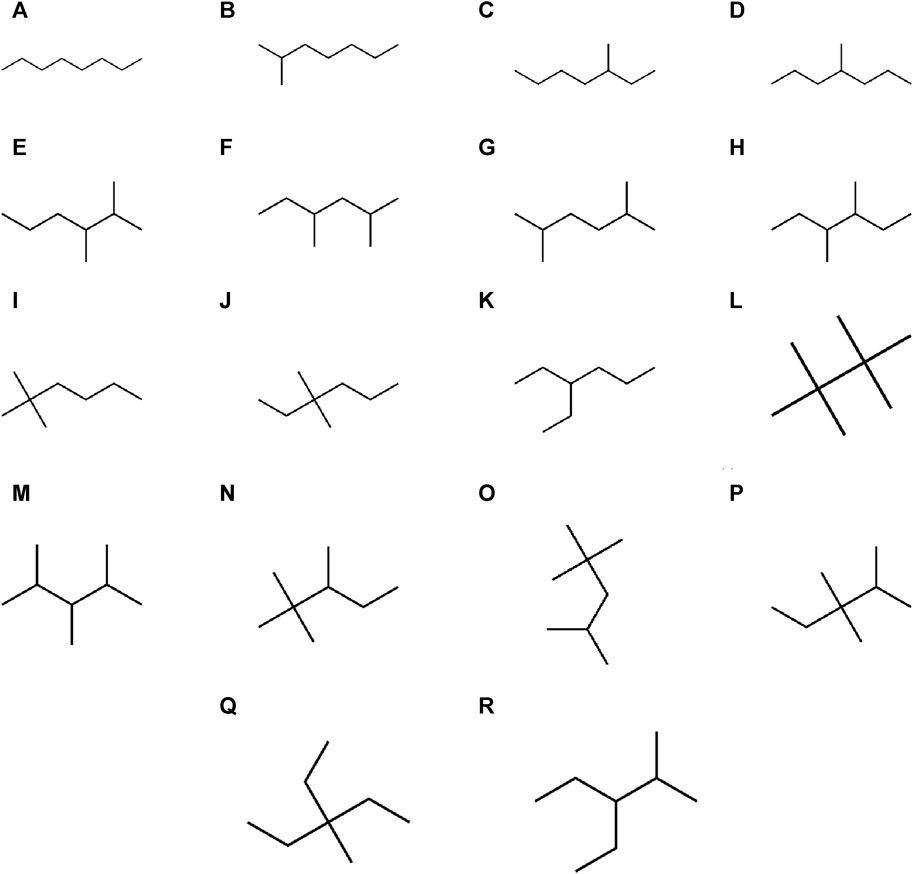
Figure 3. Chemical graphs of octane isomers. (A) Octane. (B) 2-Methylheptane. (C) 3-methylheptane. (D) 4-Methylheptane. (E) 2,3-Dimethylhexane. (F) 2,4-Dimethylhexane. (G) 2,5-Dimethylhexane. (H) 3,4-Dimethylhexane. (I) 2,2-dimethylhexane. (J) 3,3-Dimethylhexane. (K) 3-Ethylhexane. (L) 2,2,3,3-tetramethylbutane. (M) 2,3,4-trimethylpentane. (N) 2,2,3-Trimethylpentane. (O) 2,2,4-trimethylpentane. (P) 2,3,3-trimethylpentane. (Q) 3-Ethyl-3-methylpentane. (R) 2-methyl-3-ethylpentane.

3.2 Estimated values for properties of octane isomers

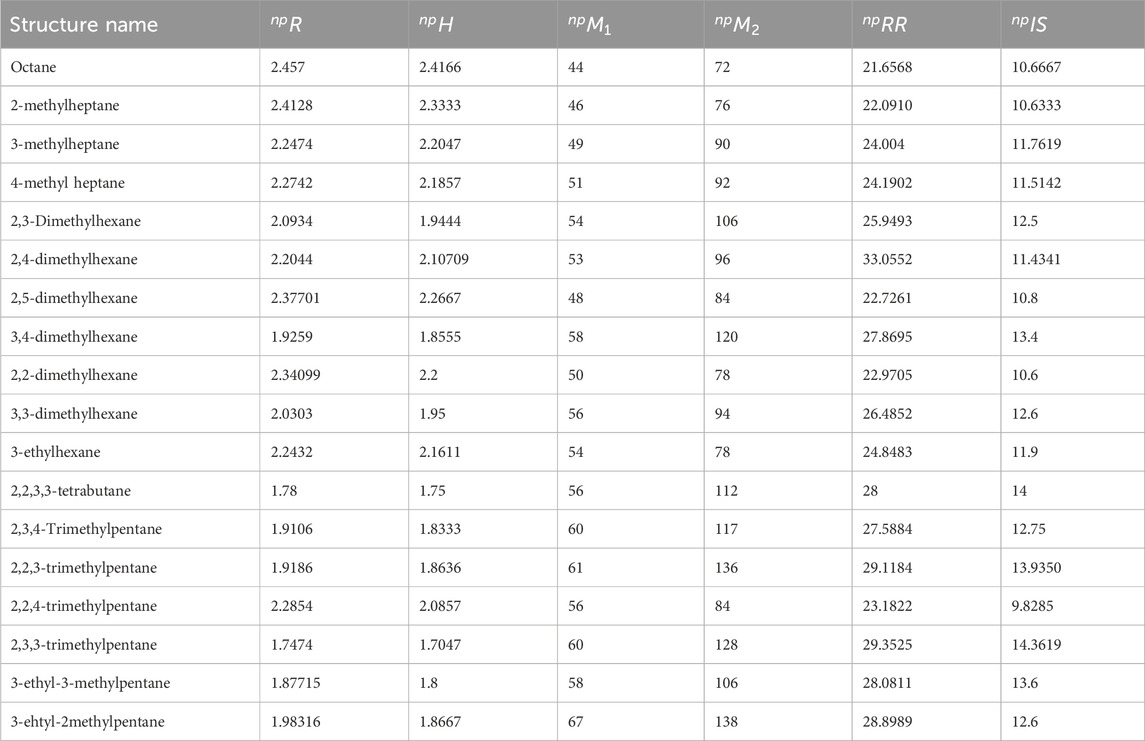
There are six estimated or calculated values used for the study of octane isomers. These numerical values are computed by using simple degree edge partitions and np-degree edge partitions. According to vertex degree, there are eight edge divisions according to the vertex degree. The six numerical descriptors used for estimation of properties of octane structures are np-degree Randic index $({}^{np}R)$, np-harmonic index $({}^{np}H)$, np-degree first Zagreb index $({}^{np}M_1)$, np-degree second Zagreb index $({}^{np}M_2)$, np-degree reciprocal Randic index $({}^{np}RR)$, np-degree inverse sum inverse $({}^{np}IS)$. The maximum and minimum degrees of graph G are four and one, respectively. The edge bundles are:

$E\left(G\right)=\left\{\left(\mathrm{1,2}\right),\left(\mathrm{1,3}\right),\left(\mathrm{1,4}\right),\left(\mathrm{2,2}\right),\left(\mathrm{2,3}\right),\left(\mathrm{2,4}\right),\left(\mathrm{3,3}\right),\left(\mathrm{3,4}\right)\right\}.$

There are 19 possible edge bundles of chemical graphs of the octane isomer according to the np-degree. The highest and lowest possible np-degrees are 12 and 2, respectively.

$\begin{array}{ll}\hfill S\left(G\right)& =\left\{\left(\mathrm{2,2}\right),\left(\mathrm{2,3}\right),\left(\mathrm{2,4}\right),\left(\mathrm{2,6}\right),\left(\mathrm{2,8}\right),\left(\mathrm{2,9}\right),\left(\mathrm{2,12}\right),\left(\mathrm{3,3}\right),\left(\mathrm{3,3}\right),\left(\mathrm{3,6}\right),\left(\mathrm{3,8}\right),\left(\mathrm{3,9}\right),\left(\mathrm{3,12}\right),\right.\hfill \\ \hfill & \left.\left(\mathrm{4,4}\right),\left(\mathrm{4,6}\right),\left(\mathrm{4,8}\right),\left(\mathrm{4,9}\right),\left(\mathrm{6,6}\right),\left(\mathrm{6,8}\right)\right\}\hfill \end{array}$

3.2.1 Example for explanation of computations

To determine all the vertex degrees and np-degrees is a very lengthy process. So we just mentioned the results of these indices in Table 3. Here we discuss the process of finding the np-degree topological indices for the structure of octane. The structure of octane is very simple. There are eight vertices and seven edges in this structure. The graph of octane consists of only two edge parcels with cardinality |E_(1,2)| = 2, and |E_(2,2)| = 5. There are three edge bundles in the octane graph according to the np-degrees. The cardinalities of these bundles are |E_(2,2)| = 2, |E_(2,4)| = 2, and |E_(4,4)| = 3. By using these values, the np-degree T-indices are computed as:

$\begin{array}{ll}\hfill {}^{np}R\left(G\right)& ={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\frac{1}{\sqrt{P_u\times P_v}}=\frac{2}{\sqrt{2\times 2}}+\frac{2}{\sqrt{2\times 4}}+\frac{3}{\sqrt{4\times 4}}\hfill \\ \hfill & =\frac{2}{2}+\frac{2}{\sqrt{8}}+\frac{3}{4}=2.457\hfill \end{array}$

$\begin{array}{ll}\hfill {}^{np}H\left(G\right)& ={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\frac{2}{\left(P_u+P_v\right)}=\frac{4}{\left(2+2\right)}+\frac{4}{\left(2+4\right)}+\frac{6}{\left(4+4\right)}\hfill \\ \hfill & =\frac{4}{4}+\frac{4}{6}+\frac{6}{8}=2.4166\hfill \end{array}$

${}^{np}M_1\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\left(P_u+P_v\right)=2\left(2+2\right)+2\left(2+4\right)+\hspace{0.17em}3\left(4+4\right)=44$

${}^{np}M_2\left(G\right)={\displaystyle \sum _{uv\epsilon E\left(G\right)}}\left(P_u\times P_v\right)=2\left(2\times 2\right)+2\left(2\times 4\right)+\hspace{0.17em}3\left(4\times 4\right)=72$

Table 3

Table 3. Estimated values of the physicochemical parameters of octane structures.

All the computations related to the 18 structures and 6 np-degree-based indices are done using the similar method given in Table 3.

4 Statistical computations

The np-degree T-indices values and the experimental values of the octane isomer properties are what both linear and quadratic regression models use as inputs. The main difference between regression and correlation is that in regression, one parameter is dependent and the other is independent, whereas in correlation, no parameter depends on the other.

4.1 Linear and quadratic regressions

Linear regression is a powerful statistical tool that allows us to model the relationship between a dependent variable and one or more independent variables. This method assumes that the relationship between the two variables is linear, meaning that as one variable increases, the other increases or decreases proportionally. On the other hand, quadratic regression is a type of nonlinear regression that models the relationship between a dependent variable and one independent variable using a quadratic equation. This method is particularly useful when the relationship between the variables is curved rather than linear. Both linear and quadratic regression can be used to analyze data and make predictions, but the choice between them depends on the nature of the data and the research question at hand. Linear regression is appropriate when the relationship between the variables is linear, while quadratic regression is used when the relationship is curved. The equations of the linear and quadratic regressions are given below Eqs 9, 10.

$Y\left(Properties\right)=a+bX\left(linear\right)(9)$

$Y\left(Properties\right)=a+b_{1}X+b_2{X}^2\left(quadratic\right)(10)$

Where Y is dependent and X is an independent variable. There are two coefficients used in linear regression as “a” and “b,” but three coefficients are used in quadratic regression as “a,” “b,” and “c.” The variable Y stands for the chemical or physical properties of the octane isomers, and the variable X stands for the estimated or calculated values of the octane isomers. The regression equations for all the np-degree indices are computed by the SPSS software. The regression equations of six np-degree indices and eight properties of octane isomers are given below.

• Randic Index ${}^{np}R(G)$

$\begin{array}{llll}\hfill & AF=0.06688+0.127\left[{}^{np}R\left(G\right)\right]\hfill & \hfill A& F=-\hspace{0.17em}0.0870{\left[{}^{np}R\left(G\right)\right]}^2+0.4931\left[{}^{np}R\left(G\right)\right]-0.3142\hfill \\ \hfill & D=0.8029-0.04348\left[{}^{np}R\left(G\right)\right]\hfill & \hfill D& =-\hspace{0.17em}0.0209{\left[{}^{np}R\left(G\right)\right]}^2+0.0443\left[{}^{np}R\left(G\right)\right]+0.7116\hfill \\ \hfill & RI=1.438-0.0183\left[{}^{np}R\left(G\right)\right]\hfill & \hfill R& I=0.0080{\left[{}^{np}R\left.\left(G\right)\right)\right]}^2-0.0519\left[{}^{np}R\left(G\right)\right]+1.473\hfill \\ \hfill & CV=287.5755+81.8287\left[{}^{np}R\left(G\right)\right]\hfill & \hfill C& V=4.7580{\left[{}^{np}R\left(G\right)\right]}^2+61.7003\left[{}^{np}R\left(G\right)\right]+308.6415\hfill \\ \hfill & MV=139.1422+10.3399\left[{}^{np}R\left(G\right)\right]\hfill & \hfill M& V=0.3951{\left[{}^{np}R\left(G\right)\right]}^2+8.6735\left[{}^{np}R\left(G\right)\right]+140.8788\hfill \\ \hfill & RC=0.09655+0.7426\left[{}^{np}R\left(G\right)\right]\hfill & \hfill R& C=0.7897{\left[{}^{np}R\left(G\right)\right]}^2-2.5765\left[{}^{np}R\left(G\right)\right]+3.5466\hfill \\ \hfill & CP=40.0549-6.3408\left[{}^{np}R\left(G\right)\right]\hfill & \hfill C& P=2.5369{\left[{}^{np}R\left(G\right)\right]}^2-17.0873\left[{}^{np}R\left(G\right)\right]+51.3235\hfill \\ \hfill & LogP=3.3459+0.6192\left[{}^{np}R\left(G\right)\right]\hfill & \hfill L& ogP=-\hspace{0.17em}0.3388{\left[{}^{np}R\left(G\right)\right]}^2+2.0464\left[{}^{np}R\left(G\right)\right]+1.8596\hfill \end{array}$

• Harmonic Index ${}^{np}H(G)$

$\begin{array}{llll}\hfill & AF=0.05325+0.1392\left[{}^{np}H\left(G\right)\right]\hfill & \hfill A& F=-\hspace{0.17em}0.0235{\left[{}^{np}H\left(G\right)\right]}^2+0.2355\left[{}^{np}H\left(G\right)\right]-0.0443\hfill \\ \hfill & D=0.7978-0.04288\left[{}^{np}H\left(G\right)\right]\hfill & \hfill D& =0.0416{\left[{}^{np}H\left(G\right)\right]}^2-0.2132\left[{}^{np}H\left(G\right)\right]+0.9701\hfill \\ \hfill & RI=1.4359-0.01807\left[{}^{np}H\left(G\right)\right]\hfill & \hfill R& I=0.0360{\left[{}^{np}H\left(G\right)\right]}^2-0.1656\left[{}^{np}H\left(G\right)\right]+1.5853\hfill \\ \hfill & CV=292.4997+83.0917\left[{}^{np}H\left(G\right)\right]\hfill & \hfill C& V=-\hspace{0.17em}35.7886{\left[{}^{np}H\left(G\right)\right]}^2+230.0309\left[{}^{np}H\left(G\right)\right]+143.2175\hfill \\ \hfill & MV=140.1762+10.2738\left[{}^{np}H\left(G\right)\right]\hfill & \hfill M& V=-\hspace{0.17em}13.7998{\left[{}^{np}H\left.\left(G\right)\right)\right]}^2+66.8823\left[{}^{np}H\left(G\right)\right]+82.7858\hfill \\ \hfill & RC=0.08263+0.7789\left[{}^{np}H\left(G\right)\right]\hfill & \hfill R& C=0.5910{\left[{}^{np}H\left(G\right)\right]}^2-1.6407\left[{}^{np}H\left(G\right)\right]+2.5319\hfill \\ \hfill & CP=39.6266-6.414\left[{}^{np}H\left(G\right)\right]\hfill & \hfill C& P=6.1231{\left[{}^{np}H\left(G\right)\right]}^2-31.5812\left[{}^{np}H\left(G\right)\right]+65.2349\hfill \\ \hfill & LogP=3.328+0.6528\left[{}^{np}H\left(G\right)\right]\hfill & \hfill L& ogP=-\hspace{0.17em}0.0319{\left[{}^{np}H\left(G\right)\right]}^2+0.7832\left[{}^{np}H\left(G\right)\right]+3.196\hfill \end{array}$

• First Zagreb Index ${}^{np}M_1(G)$

$\begin{array}{llll}\hfill & AF=0.5602-0.004118\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill A& F=0.0003{\left[{}^{np}M_1\left(G\right)\right]}^2+-0.0377\left[{}^{np}M_1\left(G\right)\right]+1.4703\hfill \\ \hfill & D=0.6401+0.00129\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill D& =0.0000{\left[{}^{np}M_1\left(G\right)\right]}^2+0.0066\left[{}^{np}M_1\left(G\right)\right]+0.497\hfill \\ \hfill & RI=1.3678+0.0005786\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill R& I=0.0000{\left[{}^{np}M_1\left(G\right)\right]}^2+0.001\left[{}^{np}M_1\left(G\right)\right]+1.3564\hfill \\ \hfill & CV=600.6549-2.5347\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill C& V=0.0867{\left[{}^{np}M_1\left(G\right)\right]}^2-12.0473\left[{}^{np}M_1\left(G\right)\right]+858.4125\hfill \\ \hfill & MV=177.8294-0.3093\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill M& V=0.0082{\left[{}^{np}M_1\left(G\right)\right]}^2-1.2051\left[{}^{np}M_1\left(G\right)\right]+202.0213\hfill \\ \hfill & RC=3.0882-0.02626\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill R& C=0.0014{\left[{}^{np}M_1\left(G\right)\right]}^2-0.1758\left[{}^{np}M_1\left(G\right)\right]+7.145\hfill \\ \hfill & CP=16.1077+0.1911\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill C& P=-\hspace{0.17em}0.0055{\left[{}^{np}M_1\left(G\right)\right]}^2+0.7889\left[{}^{np}M_1\left(G\right)\right]-0.0874\hfill \\ \hfill & LogP=5.6722-0.01877\left[{}^{np}M_1\left(G\right)\right]\hfill & \hfill L& ogP=0.0015{\left[{}^{np}M_1\left(G\right)\right]}^2-0.1785\left[{}^{np}M_1\left(G\right)\right]+9.9999\hfill \end{array}$

• Second Zagreb Index ${}^{np}M_2(G)$

$\begin{array}{llll}\hfill & AF=0.4394-0.001032\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill A& F=0.0000{\left[{}^{np}M_2\left(G\right)\right]}^2-0.0063\left[{}^{np}M_2\left(G\right)\right]+0.7052\hfill \\ \hfill & D=0.6703+0.0004008\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill D& =0.0000{\left[{}^{np}M_2\left(G\right)\right]}^2+0.0023\left[{}^{np}M_2\left(G\right)\right]+0.5731\hfill \\ \hfill & RI=1.3805+0.0001876\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill R& I=0.0000{\left[{}^{np}M_2\left(G\right)\right]}^2+0.0005\left[{}^{np}M_2\left(G\right)\right]+1.3641\hfill \\ \hfill & CV=535.8533-0.7282\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill C& P=0.007{\left[{}^{np}M_2\left(G\right)\right]}^2-2.2813\left[{}^{np}M_2\left(G\right)\right]+613.6575\hfill \\ \hfill & MV=170.3758-0.09389\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill M& V=0.0018{\left[{}^{np}M_2\left(G\right)\right]}^2-0.4756\left[{}^{np}M_2\left(G\right)\right]+189.4157\hfill \\ \hfill & RC=2.4096-0.007425\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill R& C=0.0001{\left[{}^{np}M_2\left(G\right)\right]}^2-0.0368\left[{}^{np}M_2\left(G\right)\right]+3.8847\hfill \\ \hfill & CP=21.0528+0.05468\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill C& P=-\hspace{0.17em}0.0008{\left[{}^{np}M_2\left(G\right)\right]}^2+0.2136\left[{}^{np}M_2\left(G\right)\right]+13.0657\hfill \\ \hfill & LogP=5.2306-0.005723\left[{}^{np}M_2\left(G\right)\right]\hfill & \hfill L& ogP=0.0001{\left[{}^{np}M_2\left(G\right)\right]}^2-0.0336\left[{}^{np}M_2\left(G\right)\right]+6.6328\hfill \end{array}$

• Reciprocal Randic Index ${}^{np}RR(G)$

$\begin{array}{llll}\hfill & AF=0.5021+-0.006371\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill A& F=0.0013{\left[{}^{np}RR\left(G\right)\right]}^2-0.0769\left[{}^{np}RR\left(G\right)\right]+1.4289\hfill \\ \hfill & D=0.6134+0.003797\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill D& =-\hspace{0.17em}0.0003{\left[{}^{np}RR\left(G\right)\right]}^2+0.0217\left[{}^{np}RR\left(G\right)\right]+0.3865\hfill \\ \hfill & RI=1.3568+0.001657\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill R& I=0.0001{\left[{}^{np}RR\left(G\right)\right]}^2-0.003\left[{}^{np}RR\left(G\right)\right]+1.4163\hfill \\ \hfill & CV=576.2378-4.3601\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill C& V=0.913{\left[{}^{np}RR\left(G\right)\right]}^2-53.1661\left[{}^{np}RR\left(G\right)\right]+1218.2376\hfill \\ \hfill & MV=183.9676-0.895\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill M& V=0.0278{\left[{}^{np}RR\left(G\right)\right]}^2-2.3166\left[{}^{np}RR\left(G\right)\right]+201.9522\hfill \\ \hfill & RC=2.8989-0.04715\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill R& C=0.0077{\left[{}^{np}RR\left(G\right)\right]}^2-0.4604\left[{}^{np}RR\left(G\right)\right]+8.3567\hfill \\ \hfill & CP=18.4598+0.3094\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill C& P=-\hspace{0.17em}0.0726{\left[{}^{np}RR\left(G\right)\right]}^2+4.1847\left[{}^{np}RR\left(G\right)\right]-32.5319\hfill \\ \hfill & LogP=5.5737-0.03512\left[{}^{np}RR\left(G\right)\right]\hfill & \hfill L& ogP=0.0058{\left[{}^{np}RR\left(G\right)\right]}^2-0.3444\left[{}^{np}RR\left(G\right)\right]+9.6434\hfill \end{array}$

• Inverse Sum Index ${}^{np}IS(G)$

$\begin{array}{llll}\hfill & AF=0.5396-0.01676\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill A& F=-\hspace{0.17em}0.0103{\left[{}^{np}IS\left(G\right)\right]}^2+0.2338\left[{}^{np}IS\left(G\right)\right]-0.9683\hfill \\ \hfill & D=0.6189+0.007549\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill D& =-\hspace{0.17em}0.0012{\left[{}^{np}IS\left(G\right)\right]}^2+0.0377\left[{}^{np}IS\left(G\right)\right]+0.4375\hfill \\ \hfill & RI=1.3595+0.003269\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill R& I=-\hspace{0.17em}0.0002{\left[{}^{np}IS\left(G\right)\right]}^2+0.0079\left[{}^{np}IS\left(G\right)\right]+1.3319\hfill \\ \hfill & CV=617.3717-12.8461\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill C& P=-\hspace{0.17em}1.2483{\left[{}^{np}IS\left(G\right)\right]}^2+17.4586\left[{}^{np}IS\left(G\right)\right]+435.5996\hfill \\ \hfill & MV=182.5088-1.7665\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill M& V=0.1682{\left[{}^{np}IS\left(G\right)\right]}^2-5.8533\left[{}^{np}IS\left(G\right)\right]+207.0113\hfill \\ \hfill & RC=3.1837-0.1239\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill R& C=0.0181{\left[{}^{np}IS\left(G\right)\right]}^2-0.5725\left[{}^{np}IS\left(G\right)\right]+5.9378\hfill \\ \hfill & CP=14.6394+0.9845\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill C& P=0.1575{\left[{}^{np}IS\left(G\right)\right]}^2-2.8353\left[{}^{np}IS\left(G\right)\right]+37.5364\hfill \\ \hfill & LogP=5.8915-0.1009\left[{}^{np}IS\left(G\right)\right]\hfill & \hfill L& ogP=-\hspace{0.17em}0.0210{\left[{}^{np}IS\left(G\right)\right]}^2+0.4173\left[{}^{np}IS\left(G\right)\right]+2.7203\hfill \end{array}$

4.2 Computations of statistical parameters

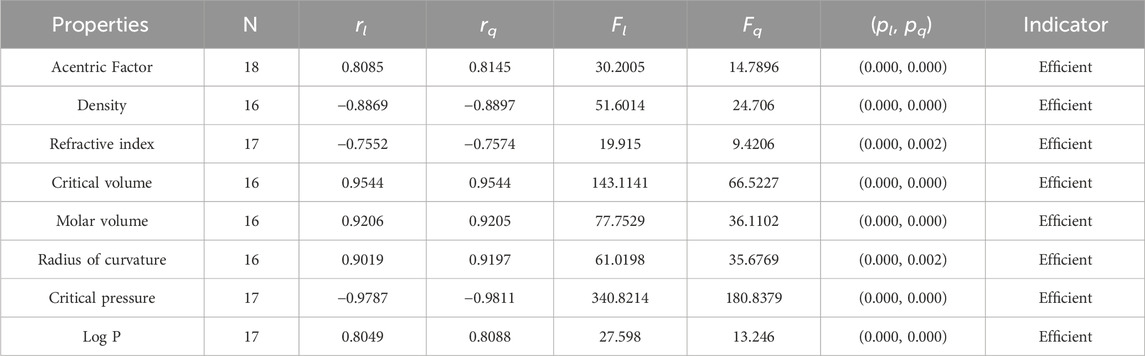
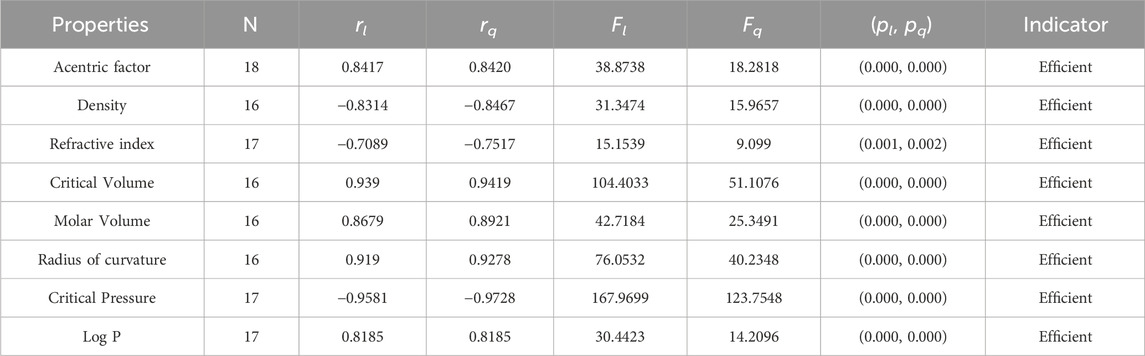
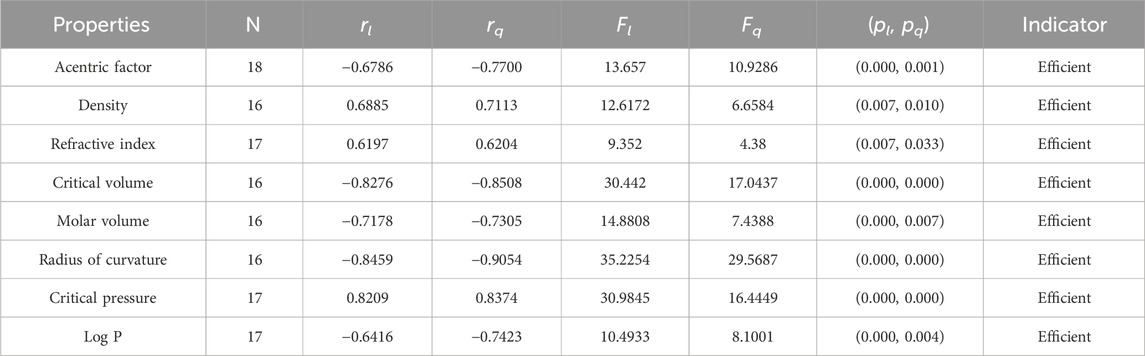
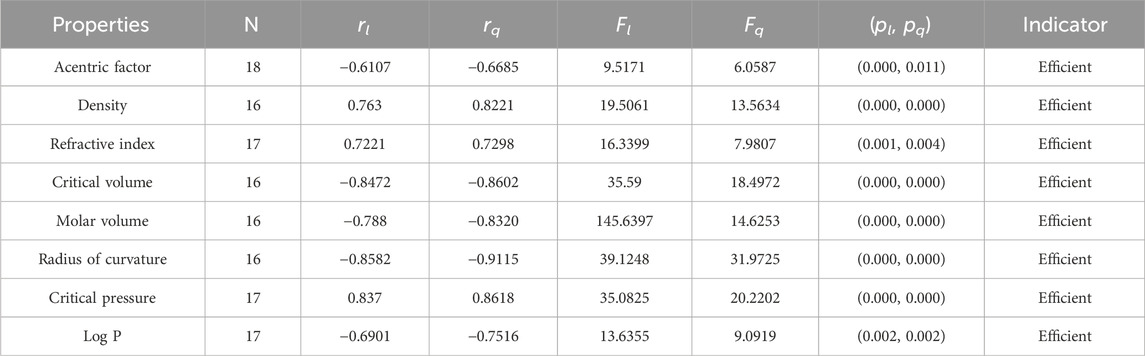
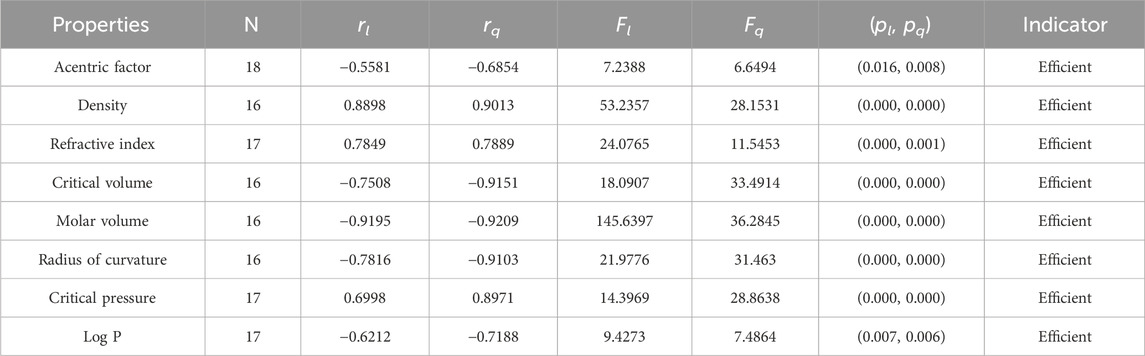
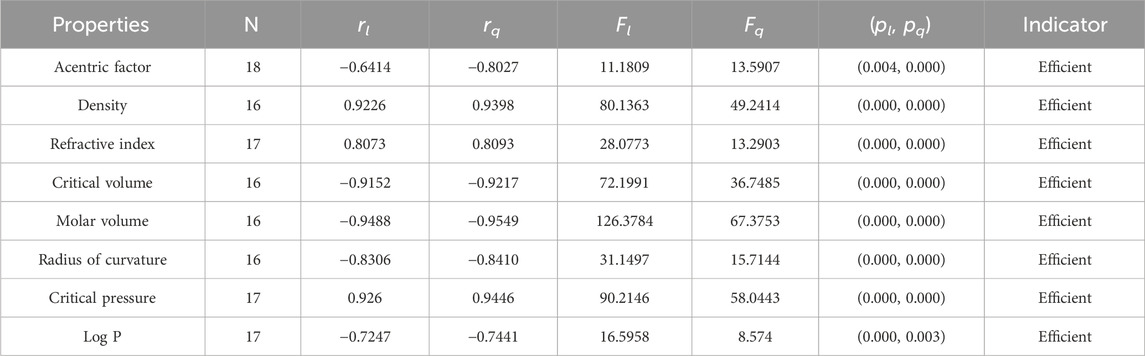
Statistical parameters summarize and describe data, making inferences about the population from which it was drawn. There are four main statistical parameters used in this article. The first one is N, which represents the sample’s population of the sample. In our work, the value of N is 18, 17, or 16 in our work. There are two types of regression models used to get accurate results, so there are two correlation coefficients, r_l and r_q. The parameters r_l, F_l, and p_l stand for the linear correlation, F-values, and p-values, and r_q, F_q, and p_q are the quadratic parameters. Correlation coefficients are statistical measures that determine the relationship between two variables. They range from −1 to 1, with −1 indicating a perfect negative correlation, 0 indicating no correlation, and 1 indicating a perfect positive correlation. Professionals in fields like economics, mathematics, and chemistry use them to analyze the strength and direction of relationships between different variables.

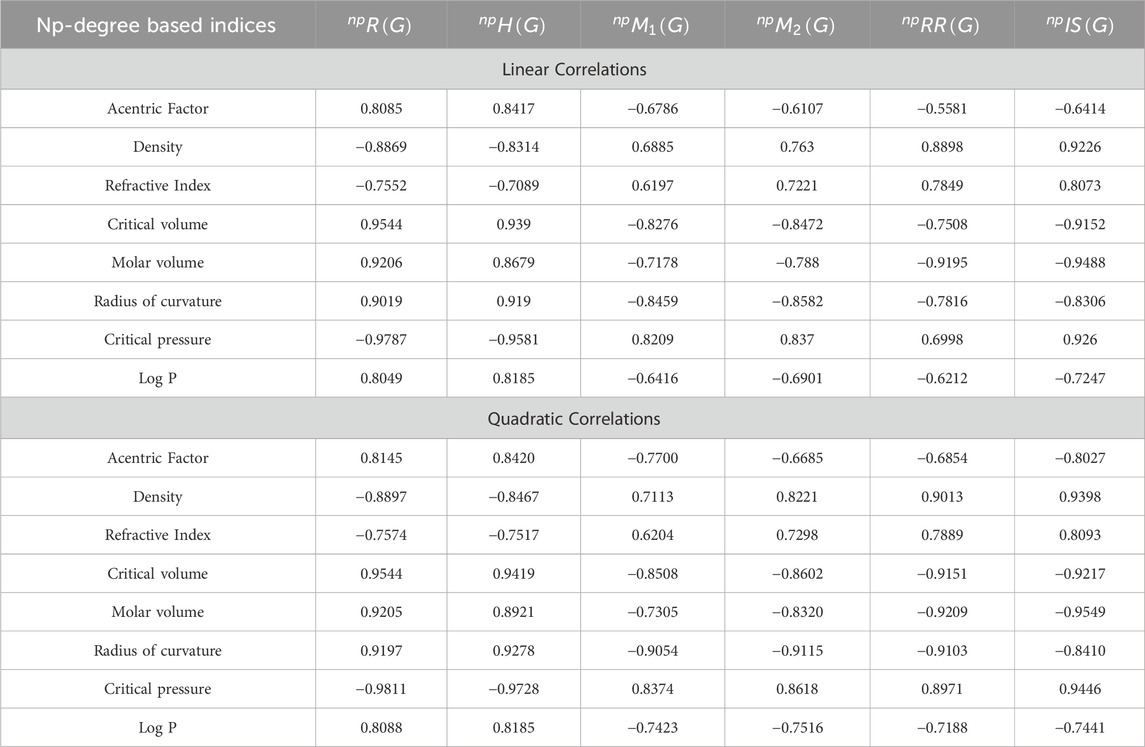
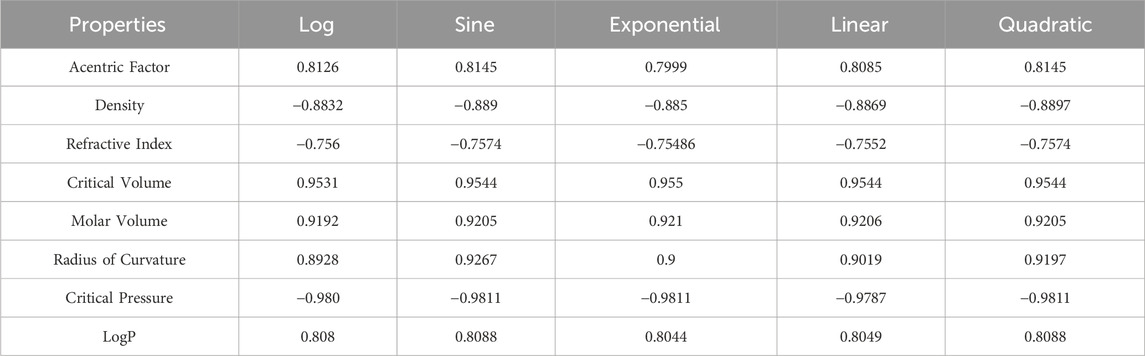
It is clear from Tables 4–9 that the magnitude of all the correlation values is greater than 0.5581 and less than 0.9811. The correlation values, both positive and negative, show the nature of the relationship, but strength is independent of the sign of correlation. The p-test and F-test values of all the indices and properties of the octane isomers are also mentioned in Tables 4–9. These tests are used to reject the null hypothesis. If the value of p is less than 0.05 and the value of F is greater than 2.5, then the results will be valid and significant. The minimum and maximum values of the F-test are 4.38 and 340.8214, respectively. The highest and lowest values of the linear correlations are | − 0.5581| = 0.5581 and | − 0.9787| = 0.9787 respectively. The highest and lowest values of the quadratic correlations are | − 0.6854| = 0.6854 and | − 0.9811| = 0.9811, respectively. All the indicators are significant; the significant values are useful to understand the structures of octane isomers, so we do not include the non-significant results.

Table 4

Table 4. Statistical parameters of linear and quadratic QSPR model for ${}^{np}R$ index.

Table 5

Table 5. Statistical parameters of linear and quadratic QSPR model for ${}^{np}H$ index.

Table 6

Table 6. Statistical parameters of linear and quadratic QSPR model for ${}^{np}M_1(G)$

Table 7

Table 7. Statistical parameters of linear and quadratic QSPR model for ${}^{np}M_2(G)$

Table 8

Table 8. Statistical parameters of linear and quadratic QSPR model for ${}^{np}RR(G)$

Table 9

Table 9. Statistical parameters of linear and quadratic QSPR model for ${}^{np}IS(G)$

5 Numerical and graphical analysis of correlation coefficients

This section deals with the graphical representation of the correlation coefficients. A graph is a unique type of diagram that is commonly used to visually represent collected data. Graphs can serve a multitude of purposes, as they can be used to display both quantitative and qualitative data. There are different types of graphs, according to the nature of the data and the required representations. The line graphs with points are used for the representation and comparison of the correlations. There are two types of regression models that are used for the computations and get accurate results. So there are two lines in all the graphs. Bar graphs and scatter point graphs can also be used for the analysis of the relationship between estimated and experimental values. Eight graphs are formed for the eight properties of octane isomers, and the ninth graph shows the relationship between these physicochemical properties. The values of the correlation coefficients are taken on the y-axis, and the names of the np-degree-based indices are shown on the x-axis.

The correlation of the acentric factor with all six properties of both linear and quadratic compounds is shown in (a) part of Figure 4. The correlation is negative as well as positive, representing the inverse and direct relationship between the estimated and experimental values of the octane isomers. The graphs of the positive correlations are above the x-axis, and the graphs of the negative correlations are below the x-axis. The green and blue color graphs in (b) part of Figure 4 represent the quadratic and linear correlations. The np-degree Randic and harmonic indices have an inverse relationship with the density, and the other four indices have a direct relationship with the density of octane isomers. The blue and dark brown color graphs in the (c) part of Figure 4 represent the variation of correlations between np-degree T-indices and refractive index. The correlation of critical volume is indicated by the orange and sky blue colors in (d) part of Figure 4. The np-degree Randic and harmonic indices have a direct relationship with the molar volume, and other indices have an inverse relationship with the molar volume, as shown in (e) part of Figure 4. The red and green color lines represent the quadratic and linear correlations between T-indices and the radius of curvature. The correlation between the critical pressure and LogP is represented in the (g) and (h) parts of Figure 4. The comparison of all the correlations is given in (i) part of Figure 4. In all the graphs, it is important to note that all the properties have a direct and inverse relationship with the np-degree-related indices. The numerical data is given in Table 10.

Figure 4

Figure 4. Graphical comparison of calculations. (A) Correlation of acentric factor. (B) Correlation of density. (C) Correlation of refractive index. (D) Correlation of critical volume. (E) Correlation molar volume. (F) Correlation of radius of curvature. (G) Correlation of critical pressure. (H) Correlation of LogP. (I) Correlation of all indices.

Table 10

Table 10. Numerical data.

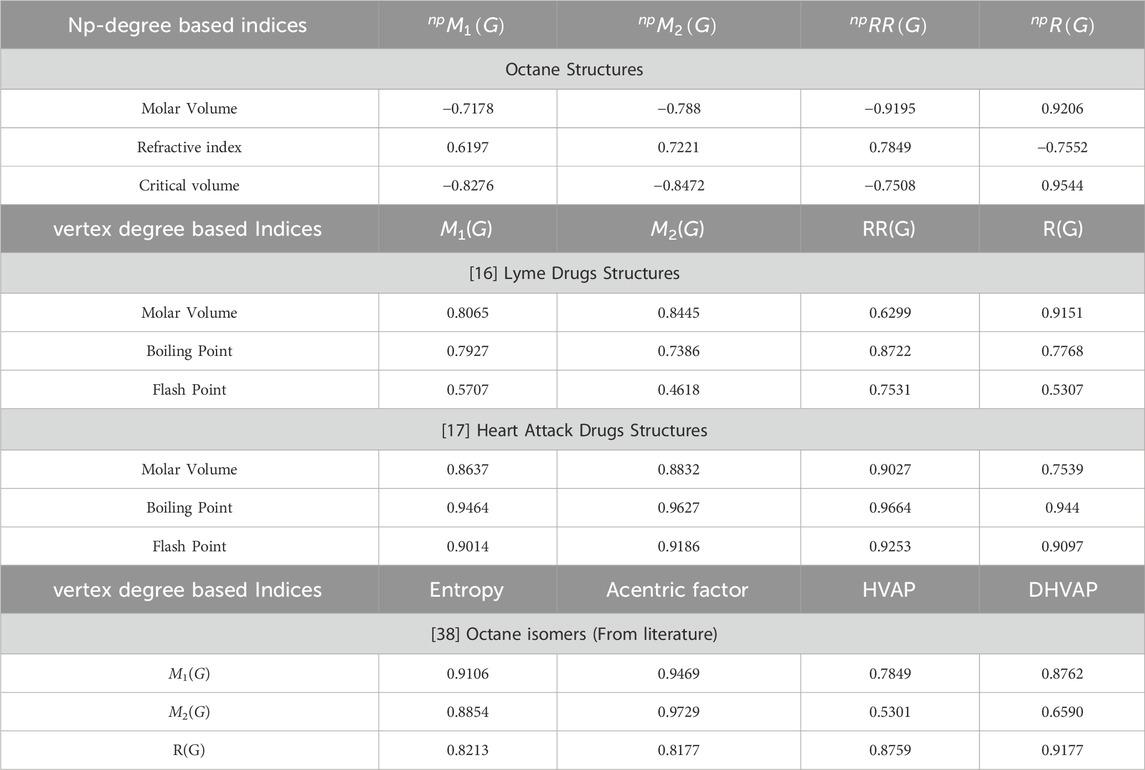
5.1 Comparison of results with literature

In this section, we compare the results of octane structures with the structures of different drugs. The comparison is also based on the simple vertex degree and np-degree topological indices. There are a large number of calculations done in these articles, but we just compare the common ones to show the validity and significance of the present results. The validity of the correlations depends on the values of the correlation coefficients, the F-test, and the p-test. Here, the comparison is performed between the correlation coefficients. The correlations are significant if they are higher than 0.7. We used the most commonly used and powerful indices for the comparison of results, such as the first Zagreb index, the second Zagreb index, the reciprocal Randic index, and the Randic index. The lyme structures gave high as well as moderate correlation values. The maximum and minimum values of correlation for Lyme drugs in Table 11 are 0.9151 and 0.4618, respectively. The correlation values of the heart attack drugs vary from 0.7539 to 0.9664, as given in Table 11. The range of correlation for octane structures changes from 0.6197 to 0.9544. It is important to observe that the correlation in this manuscript is negative as well as positive.

Table 11

Table 11. Comparison of results with literature.

The last section of Table 11 compares the vertex degree-based indices and np-degree-based indices. Researchers have extensively analyzed the properties of octane isomers. When researchers propose a new topological index or formula, they often apply it to octane isomers or alkane structures due to their simplicity in two dimensions. The octane isomers discussed in the last part of the table have four properties, namely, entropy, acentric factor, enthalpy of vaporization (HVAP), and standard enthalpy of vaporization (DHVAP). The correlation for the vertex degree indices ranges from 0.6590 to 0.9729. The correlation for the np-degree indices ranges from 0.6197 to 0.9544. Both types of indices show a good correlation with the properties of octane isomers, so both are effective for determining the results.

6 Analysis of np-Randic index by different regression models

There are two types of regression models are used to check the significance of the calculated values. Three type of more models are applied to check the best line fit with the results. It is clear from Table 12 that quadratic regression is best for the computation of the properties of octane isomers. A type of regression called logarithmic regression is used to model situations in which growth or decay starts quickly and then slows down over time. The logarithmic regression Eq. 11 is defined as:

$Y=a+b\ln \left(X\right).(11)$

Where X and Y are parameters, X represents the input or independent variable, and Y represents the output or dependent variable. The constant a stands for the line or curve that always passes through a point, and b represents the control rate of growth.

$\begin{array}{lll}\hfill & AF=0.1371+0.2667\ln \left({}^{np}R\right)\hfill & \hfill MV=144.9467+21.6152\ln \left({}^{np}R\right)\\ \hfill & D=0.7781-\left(-0.0905\right)\ln \left({}^{np}R\right)\hfill & \hfill RC=0.5265+1.5336\ln \left({}^{np}R\right)\\ \hfill & RI=1.4278-\left(-0.0383\right)\ln \left({}^{np}R\right)\hfill & \hfill CP=36.5907-\left(-13.3679\right)\ln \left({}^{np}R\right)\\ \hfill & CV=332.9448+171.7005\ln \left({}^{np}R\right)\hfill & \hfill LogP=3.6891+1.2996\ln \left({}^{np}R\right)\end{array}$

Table 12

Table 12. Statistical data of five regressions.

Sinusoidal regression is a mathematical model that utilizes trigonometric functions to determine the curve that best fits a set of data points. This regression’s resulting graph of this regression takes the form of a sine function. This method is similar to linear regression in that it aims to find the best-fitting curve, but instead of a straight line, it seeks a sinusoidal curve. The regression equation for sinusoidal data Eq. 12 is provided below.

$Y=a\sin \left(bX+c\right)+d(12)$

The parameters X and Y are variables; X is used for the np-degree Randic index, and Y is used for the eight properties of the octane isomers. The sine curve is repeated over time in different forms of linear regression, in which a is amplitude, c is phase shift, and d is vertical shift.

$\begin{array}{llll}\hfill & AF=571.3861\sin \left[0.0175\left({}^{np}R\right)+1.5213\right]-571.0014\hfill & \hfill M& V=2660.0651\sin \left[0.0175\left({}^{np}R\right)-1.3831\right]+2754.2168\hfill \\ \hfill & D=136.936\sin \left[0.0175\left({}^{np}R\right)+1.5523\right]-136.2007\hfill & \hfill R& C=5184.9395\sin \left[0.0175\left({}^{np}R\right)-1.5993\right]+5186.3846\hfill \\ \hfill & RI=52.45\sin \left[0.0175\left({}^{np}R\right)-1.6276\right]+53.8385\hfill & \hfill C& P=16656.0955\sin \left[0.0175\left({}^{np}R\right)-1.6296\right]+16678.6483\hfill \\ \hfill & CV=31600.7587\sin \left[0.0175\left({}^{np}R\right)-1.4587\right]+31711.0218\hfill & \hfill L& ogP=2224.9915\sin \left[0.0175\left({}^{np}R\right)+1.5181\right]-2220.0421\hfill \end{array}$

Exponential regression is considered one of the most simple nonlinear regression models. It represents scenarios where growth starts slowly and then rapidly accelerates without limit, or where decay initiates quickly and then gradually decelerates towards zero. The general equation of exponential regression is given below Eq. 13.

$Y=a.b^X(13)$

In this equation, Y represents the eight properties, while X represents the np-degree Randic index. When the value of b exceeds 1, exponential growth occurs. An exponential decay model occurs when b is between 0 and 1.

$\begin{array}{llll}\hfill & AF=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill & \hfill M& V=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill \\ \hfill & D=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill & \hfill R& C=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill \\ \hfill & RI=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill & \hfill C& P=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill \\ \hfill & CV=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill & \hfill L& ogP=0.1474\times 1.4714^{\left({}^{np}R\right)}\hfill \end{array}$

Sections four and five present the correlation coefficients of polynomial regression (both linear and quadratic) for all six neighborhood product-based topological indices. Three nonlinear regression models—logarithmic, exponential, and sinusoidal—apply to the np-degree Randic index and eight properties of octane isomers. Table 12; Figure 5 clearly demonstrate that the results of quadratic regression are the most favorable among the regression models, with logarithmic regression also yielding impressive results. However, the outcomes of the other regression models are less satisfactory.

Figure 5

Figure 5. Correlations of different regression models.

7 Discussion

In this section, we discuss the results about octane structures and their significance. The QSPR modeling of the octane structures is done by using two regression models, namely, linear and quadratic. The np-degree-related T-indices are computed by using the edge partitions. The results are extracted from Tables 4–9. The isomers of octane are used in many industries to make drugs and other chemicals. To make useful products from octane, it is necessary to understand the characteristics of these structures. To understand these physicochemical properties, we applied the np-degree-based topological indices. These numerical descriptors are an easy and effective way to understand the properties of many chemicals and drugs.

• According to the linear regression model, the np-degree Randic index is most suitable for the estimation of the critical pressure and critical volume of the octane isomers, with correlation values of 0.9544 and −0.9787, respectively. This index is also called the branching index and is one of the oldest degree-related indices used to study chemical structures. The Randic index is a useful tool when conducting QSPR studies. It has been found to have a minimum correlation coefficient for octane refractive index and a maximum correlation coefficient for octane critical pressure. The correlation coefficient value for the linear model ranges from 0.7552 to 0.9787, indicating a strong inverse relationship between the Randic index and these properties. This information can be valuable in predicting the physical properties of octane isomers and can aid in the development of new materials and compounds. The quadratic model exhibits a correlation coefficient value that falls within the range of −0.7574 to −0.9811 given in Table 4. The refractive index has the minimum correlation coefficient value, while the critical pressure of octane has the maximum correlation value. These correlation coefficient values indicate the strength of the relationship between the variables. A negative sign signifies an inverse correlation, while a positive sign indicates a direct relationship. The relationship of np-degree R-index with all six properties is strong enough to estimate their values theoretically.

• The np-degree harmonic index is useful for the QSPR study of the acentric factor, radius of curvature, and LogP, with the values of the correlations being 0.8417, 0.919, and 0.8185. The np-degree harmonic index is a suitable predictor for the properties of isomers of octanes. The correlation ranges from −0.7089 to −0.9581 for the linear model, with the refractive index of octanes having the lowest correlation coefficient value and the critical pressure of octanes having the highest. Similarly, the correlation coefficient varies from −0.7517 to −0.9728 for the quadratic model, with the refractive index of octanes having the lowest correlation coefficient value and the critical pressure of octanes having the highest. The quadratic regression yields significantly better results as it is a modified version of the linear regression.

• The M₁ index is an amazing degree-based index that has been used for many years in QSPR modeling of drugs and medicines. This work shows that the np-degree-based index is useful in predicting the properties of octane isomers. Specifically, this index has a direct relationship with three properties of octane isomers: density, refractive index, and critical pressure. However, the np-degree-based M1 index has an inverse relationship with five other characteristics of octane structures, including AF, CV, MV, RC, and LogP. These correlations are quite strong, with values ranging from −0.6786 to −0.8459. While the Zagreb indices are generally effective in estimating physical and chemical parameters, they are not nearly as accurate when it comes to predicting the properties of octane isomers. Instead, the harmonic and Randic indices proved to be much more effective in this regard. In fact, when using a quadratic model, the correlation coefficient values can range from 0.6204 to −0.9054, with the refractive index and radius of curvature of octane showing the highest and lowest correlation values, respectively, given in Table 6.

• The np-degree second Zagreb index is a valuable tool in predicting the properties of organic compounds. In analyzing its correlation with various properties, we found that it has the highest correlation with the radius of curvature (−0.8582) and the lowest correlation with the acentric factor (−0.6107). It is important to note that a correlation above 0.7 is considered strong, while a correlation above 0.5 is moderate. Upon further analysis, it was discovered that the M₂ index shows a moderate correlation with the acentric factor and logP. However, for the other six properties analyzed, it shows a stronger correlation above the 0.7 given in Table 8. The correlation value for the quadratic model varies from −0.6685 to −0.9115, with the acentric factor of octane having the lowest correlation value and the radius of curvature of octanes having the highest correlation value.

• The reciprocal Randic Index is an advanced version of the Randic Index, which is widely used in the field of chemistry. While the results of the RR-index may not be as strong as those of the Randic Index for octane structures, it has a range of correlation that varies from −0.5581 to −0.9195. This index is particularly useful for estimating density and molar volume due to its higher correlations. In the case of the quadratic model, three properties, critical volume, molar volume, and radius of curvature, have correlation coefficients greater than 0.9, indicating an excellent relationship between these properties and the np-degree-based RR-index. The correlation coefficient for the quadratic model ranges from −0.6854 to −0.9209, with the acentric factor of octane showing the least correlation coefficient and the molar volume of octane showing the highest correlation coefficient.

• The np-degree inverse sum index is the most suitable index for approximating the properties of octane isomers. This index shows the highest correlation values with three key properties: density (0.9226), refractive index (0.8073), and molar volume (−0.9488). However, the quadratic model surpasses the np-degree inverse sum index in terms of correlation values, with a correlation of 0.9398, 0.8093, and −0.9549 for density, refractive index, and molar volume, respectively. The correlation values for the linear model range from −0.6414 to −0.9488. The acentric factor of octane has the lowest correlation value, while the molar volume of octane has the highest correlation value. In contrast, the correlation coefficient for the quadratic model ranges from −0.8027 to −0.9549. The acentric factor of octane and the molar volume of octanes have the lowest and highest correlation coefficient values, respectively.

8 Applications and significance of work

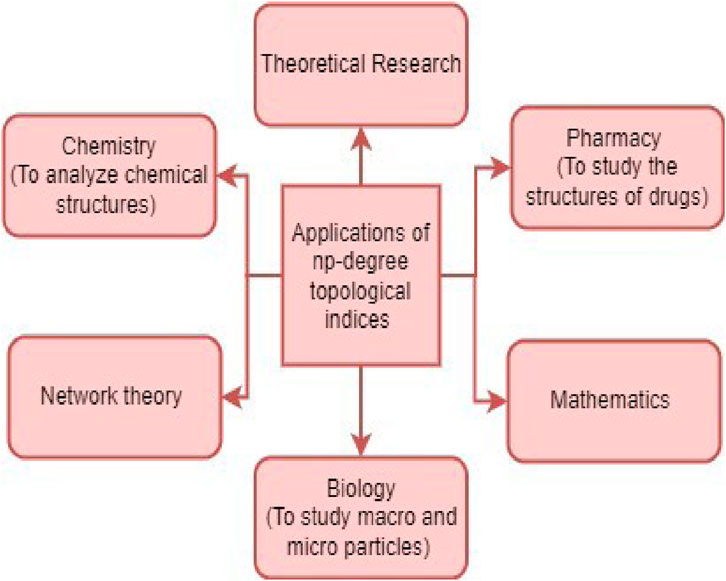
This manuscript numerically explains how to estimate the properties of the octane isomers. Octane isomers are highly useful hydrocarbons with a wide range of applications in the chemical industry, particularly in petrochemicals. The data in this manuscript is applicable to chemistry researchers. Various industries utilize octane isomers, such as fuel additives (fuel industry), solvents (paint industry), research and testing, chemical intermediates (plastics, pharmaceutical), refrigerants (to decrease ozone depletion), standardization, and cosmetics. Various fields utilizing octane isomers can benefit from understanding their properties. This article presents a theoretical method for estimating the properties of octane isomers, making it a valuable resource for researchers in the field of chemistry. This article introduces a new approach to finding the topological indices to explore the properties of octane isomers. The results of np-degree-based topological indices are good. These indices can be used to determine the properties of other chemical structures using numerical methods. Some properties of the drugs used to treat many diseases, such as asthma or malaria, can be analyzed with the help of np-degree-based topological indices, which can help progress the pharmacological industry. The np-degree-based indices can be used in different fields, as given in Figure 6.

The results and their significance demonstrate that the newly defined approach to determining the degree-related TIs is very useful for understanding the properties of octane structures. Tables 4–9 show that critical pressure and critical volume exhibit the strongest correlation with the np-degree Randic index, leading to its utilization in calculating these parameters. The np-degree harmonic index is also the best way to find out about three important features of octane isomers: the acentric factor, the radius of curvature, and logP. Meanwhile, the np-degree inverse sum index is a valuable tool for predicting the density, refractive index, and molar volume of octane isomers. The remaining three indices also provide valuable insights into the compounds’ structures of these compounds. The quadratic regression model is more suitable than the linear model for studying octane isomers. These indices have the potential to be useful in understanding the structures of other chemical compounds and medicines. The np-degree harmonic and IS index are highly significant due to their strong correlation with three essential properties. The np-degree Randic is also important, as it shows the strongest correlation with two properties. Although the remaining three indices do not demonstrate the highest correlation with any physicochemical property of the octane structure, their correlations are still reliable in approximating the values of octane isomers. To better understand the sequence of np-degree indices according to their importance, refer to Figure 7, which presents a flow chart.

Figure 6

Figure 6. Applications of np-degree based in different fields.

Figure 7

Figure 7. Sequence of np-degree TIs according to their significance.

9 Conclusion

This article investigates the eight properties of the isomers of octane by using six np-degree topological indices. We introduced a new approach for determination of the classic vertex degree based indices. The main objective of the research is to use topological indices to quickly and cheaply gather information about the topology of structures. It can be observed from Tables 4–9 that all the correlation coefficients are good and most of the correlations are higher than 0.7 indicating a very strong relationship between newly introduced indices and eight properties of isomers of octanes. Due to great importance and use of the octane isomers, we applied the newly introduced indices to study these structures. There are two tests are also used to check the validity of the results. All the p-values are less than 0.05 and F-values greater than 2.5, which indicates that all estimated values are significant. Some properties have direct relationship with the np-degree indices and some indices have inverse relationship with these indices. This paper can help chemists, pharmacists, and industrialists use the octane isomers and study their properties theoretically.

The np-degree sum connectivity index is not suitable for studying the properties of octane isomers due to their low correlation values and non-significant p-test and F-test values. The indices used in this article are not enough to determine the critical temperature, flash point, heat of formation, heat of vaporization, surface tension, or entropy of octane isomers. To accurately study these properties, alternative indices must be utilized. The results of these properties are not mentioned in this article due to low correlation values.

9.1 Future work

The distinct characteristics of the chemical compounds presented in the paper [39] can be investigated using our proposed method, which would be helpful for chemists in further research.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

MR: Conceptualization, Methodology, Writing–original draft, Writing–review and editing. AM: Supervision, Writing–original draft, Writing–review and editing. IH: Formal Analysis, Software, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chamua M, Buragohain J, Bharali A. Machine learning, a powerful tool for the prediction of BiVO₄ nanoparticles efficiency in photocatalytic degradation of organic dyes. Int.J.QuantumChem. (2024) 124:1–10. doi:10.1080/10934529.2024.2319510

CrossRef Full Text | Google Scholar

2. Hasani M, Ghods M. Topological indices and QSPR analysis of some chemical structures applied for the treatment of heart patients. Int.J.QuantumChem. (2024) 124:256–67. doi:10.1002/qua.27234

CrossRef Full Text | Google Scholar

3. Arockiara M, Greeni AB, Kalaam AA. Comparative analysis of reverse degree and entropy topological indices for drug molecules in blood cancer treatment through QSPR regression models. PolycyclAromatCompd (2023) 24:1–18. doi:10.1080/10406638.2023.2271648

CrossRef Full Text | Google Scholar

4. Hakeem A, Muhammad KN, Muhammad F, Ahmed N. QSPR analysis of some important drugs used in heart attack treatment via degree-based topological indices and regression models. PolycyclAromatCompd (2023) 25:1–10. doi:10.1080/10406638.2023.2262697

CrossRef Full Text | Google Scholar

5. Zhang X, Saif MJ, Idrees N, Kanwal S, Parveen S, Saeed F. QSPR analysis of drugs for treatment of schizophrenia using topological indices. ACSomega (2023) 8:41417–41426. doi:10.1021/acsomega.3c05000

CrossRef Full Text | Google Scholar

6. Mahboob A, Rasheed MW, Dhiaa AM, Hanif I, Amin L. On quantitative structure-property relationship (QSPR) analysis of physicochemical properties and anti-hepatitis prescription drugs using a linear regression model. Heliyon (2024) 10:e25908. doi:10.1016/j.heliyon.2024.e25908

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Mahboob A, Waheed RM, Hanif I, Siddique I. Approximating the properties of some chemical solvents by two-dimensional molecular descriptors. Int.J.QuantumChem. (2024) 124:27–35. doi:10.1002/qua.27305

CrossRef Full Text | Google Scholar

8. Mahboob A, Rasheed MW, Hanif I, Amin L, Alameri A. Role of molecular descriptors in quantitative structure-property relationship analysis of kidney cancer therapeutics. Int.J.QuantumChem. (2024) 124:24–9. doi:10.1002/qua.27241

CrossRef Full Text | Google Scholar

9. Chellali M, Haynes TW, Hedetniemi s.T, Lewis TM. On ve-degree and ev-degree in graphs. Discrete J.Math. (2017) 340:31–8. doi:10.1016/j.disc.2016.07.008

CrossRef Full Text | Google Scholar

10. Rauf A, Naeem M, Bukhari SU. Quantitative structure–property relationship of Ev-degree and Ve-degree based topological indices: physico-chemical properties of benzene derivatives. Int.J.QuantumChem (2022) 122:53–61. doi:10.1002/qua.26851

CrossRef Full Text | Google Scholar

11. Jamil MK, Imran M, Abdul SK. Novel face index for benzenoid hydrocarbons. J.Math. (2020) 8:312–9. doi:10.3390/math8030312

CrossRef Full Text | Google Scholar

12. Mahboob A, Rasheed MW, Bayati JH, Hanif I, Alam SM. Bi-distance approach to determine the topological invariants of silicon carbide. BaghdadSci.J. (2024) 21:0174. doi:10.21123/bsj.2023.8178

CrossRef Full Text | Google Scholar

13. Rauf A, Naeem M, Hanif A. Quantitative structure–properties relationship analysis of Eigen-value-based indices using COVID-19 drugs structure. Int.J.QuantumChem (2023) 123:e27030–121. doi:10.1002/qua.27030

CrossRef Full Text | Google Scholar

14. Shannon CE. A mathematical theory of communication. BellSyst.tech.j. (1948) 27:379–423. doi:10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

15. Rauf A, Naeem M, Rahman J, Saleem AV. QSPR study of Ve-degree based end Vertice edge entropy indices with physio-chemical properties of breast cancer drugs. PolycyclAromatCompd (2023) 43:4170–83. doi:10.1080/10406638.2022.2086272

CrossRef Full Text | Google Scholar

16. Huang R, Mahboob A, Rasheed MW, Alam SM, Siddiqui MK. On molecular modeling and QSPR analysis of lyme disease medicines via topological indices. Eur.Phys.J.Plus (2023) 138:243–50. doi:10.1140/epjp/s13360-023-03867-9

CrossRef Full Text | Google Scholar

17. Rasheed MW, Mahboob A, Hanif I. An estimation of the physicochemical properties of heart attack treatment medicines by using molecular descriptors. S.Afr.J.Chem.Eng (2023) 45:20–9. doi:10.1016/j.sajce.2023.04.003

CrossRef Full Text | Google Scholar

18. Hui ZH, Naeem M, Rauf A, Aslam A. Estimating the physicochemical properties of antiemetics using degree-based topological descriptors. Mol.Phys (2023) 121:201–7. doi:10.1080/00268976.2023.2189491

CrossRef Full Text | Google Scholar

19. Mahboob A, Rasheed MW, Amin L, Hanif I. A study of novel molecular descriptors and quantitative structure–property relationship analysis of blood cancer drugs. Eur.Phys.J.Plus (2023) 138:856–60. doi:10.1140/epjp/s13360-023-04499-9

CrossRef Full Text | Google Scholar

20. Randic M. Characterization of molecular branching. J.Am.Chem.Soc. (1975) 97:6609–15. doi:10.1021/ja00856a001

CrossRef Full Text | Google Scholar

21. Zhou H, Abid M, Rasheed MW, Ali O, Siddiqui MK, Imran Z, et al. On QSPR analysis of molecular descriptor and thermodynamic features of narcotic drugs. PolycyclAromatCompd (2023) 20:1–21. doi:10.1080/10406638.2023.2230336

CrossRef Full Text | Google Scholar

22. Parveen S, Awan UH, Farooq NB, Hussain S. Topological descriptors and QSPR models of drugs used in blood cancer. PunjabUniversityJournalofMathematics (2023) 55:27–43. doi:10.52280/pujm.2023.550103

CrossRef Full Text | Google Scholar

23. Gayathri A, Narasimhan D, Fathima M, Vincy F. Computation of neighbourhood degree based topological indices for circumcoronene series of benzenoid. J.Sci.Multidiscip (2024) 6:2024ss0112–99. doi:10.31893/multiscience.2024ss0112

CrossRef Full Text | Google Scholar

24. Zhong L. The harmonic index for graphs. Appl.Math.Lett (2012) 25:561–6. doi:10.1016/j.aml.2011.09.059

CrossRef Full Text | Google Scholar

25. Fajtlowicz S. On conjectures of Graffiti-II. Congr.Numer. (1987) 60:187–97. doi:10.1016/S0167-5060(08)70776-3

CrossRef Full Text | Google Scholar

26. Balasubramaniyan D, Chidambaram N. On some neighbourhood degree-based topological indices with QSPR analysis of asthma drugs. Eur.Phys.J.Plus (2023) 138:823–30. doi:10.1140/epjp/s13360-023-04439-7

CrossRef Full Text | Google Scholar

27. Khan AR, Awan NU, Ghani MU, Eldin SM, Karamti H, Jawhari AH, et al. Fundamental aspects of skin cancer drugs via degree-based chemical bonding topological descriptors. Molecules (2023) 28:3684–90. doi:10.3390/molecules28093684

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gutman I, Trinajstic N. Graph theory and molecular orbitals. Total fi-electron energy of alternant hydrocarbons. Chem.Phys.Lett (1972) 17:535–8. doi:10.1016/0009-2614(72)85099-1

CrossRef Full Text | Google Scholar

29. Gutman I, Ruscic B, Trinajstic N, Charles F. Graph theory and molecular orbitals. XII. Acyclic polyenes. J.Chem.Phys. (1975) 62:3399–405. doi:10.1063/1.430994

CrossRef Full Text | Google Scholar

30. Shanmukha MC, Basavarajappa NS, Anilkumar KN. Predicting physicochemical properties of octane isomers using QSPR approach. MalayaJournalofMathematik (2020) 8:104–16. doi:10.26637/MJM0504/0018

CrossRef Full Text | Google Scholar

31. Tamilarasi C. The pivotal role of degree-based and neighborhood degree-sum-based topological indices in predicting the physico-chemical properties of N-octane isomers. Ann.RomanianSoc.CellBiol (2021) 25:4481–9.

Google Scholar

32. Parveen S, Hassan A, Mohammed NU, Farooq M, Iqbal N. Topological indices of novel drugs used in diabetes treatment and their QSPR modeling. JournalofMathematics (2022) 2022:1–17. doi:10.1155/2022/5209329

CrossRef Full Text | Google Scholar

33. Gutman I, Furtula B, Elphick C. Three new/old vertex-degree-based topological indices. MATCHCommun.Math.Comput.Chem. (2014) 72:617–32. https://api.semanticscholar.org/CorpusID:123768940.

Google Scholar

34. Gasperov VDM. Bond aditive mdelling 1. Ariatic indices. Croat.Chem.Acta (2010) 83:243–60. https://api.semanticscholar.org/CorpusID:35024968.

Google Scholar

35. Das KC, Mondal S. On neighborhood inverse sum indeg index of molecular graphs with chemical significance. Inf.Sci (2023) 623:112–31. doi:10.1016/j.ins.2022.12.016

CrossRef Full Text | Google Scholar

36. Zaman S, Yaqoob HSA, Ullah A, Sheikh M. QSPR analysis of some novel drugs used in blood cancer treatment via degree based topological indices and regression models. PolycyclAromatCompd (2023) 3:1–17. doi:10.1080/10406638.2023.2217990

CrossRef Full Text | Google Scholar

37. Arockiaraj M, Greeni AB, Kalaam AA. Linear versus cubic regression models for analyzing generalized reverse degree based topological indices of certain latest corona treatment drug molecules. Int.J.QuantumChem. (2023) 123:22–32. doi:10.1002/qua.27136

CrossRef Full Text | Google Scholar

38. Ediz S. Predicting some physicochemical properties of octane isomers: a topological approach using ev-degree and ve-degree Zagreb indices (2017). p. 1–12. arXiv preprint arXiv:1701.02859. doi:10.48550/arXiv.1701.02859s

CrossRef Full Text | Google Scholar

39. Arockiaraj M, Paul D, Clement J, Tigga S, Jacob K, Balasubramanian K. Novel molecular hybrid geometric-harmonic-Zagreb degree based descriptors and their efficacy in QSPR studies of polycyclic aromatic hydrocarbons. SAR QSAR Environ Res (2023) 34(7):569–89. doi:10.1080/1062936x.2023.2239149

PubMed Abstract | CrossRef Full Text | Google Scholar