- 1School of Computer Science, Sichuan University Jinjiang College, Meishan, China
- 2Network and Data Security Key Laboratory of Sichuan Province, School of Information and Software Engineering, University of Electronic Science and Technology of China (UESTC), Chengdu, China
The socialist millionaires' problem, emanating from the millionaires’ problem, allows two millionaires to determine whether they happen to be equally rich while remaining their riches undisclosed to each other. Most of the current quantum solutions to the socialist millionaires’ problem have lower efficiency and are theoretically feasible. In this paper, we introduce a practical quantum secure protocol for the socialist millionaires’ problem based on single photons, which can be easily implemented and manipulated with current technology. Our protocol necessitates the involvement of a semi-honest third party (TP) responsible for preparing the single-photon sequences and transmitting them to Alice who performs Identity or Hadamard operations on the received quantum sequences via her private inputs and the secret keys, producing new quantum sequences that are subsequently sent to Bob. Similarly, Bob encodes his private inputs into the received quantum sequences to produce new quantum sequences, which are then sent to TP. By conducting single-particle measurements on the quantum sequences received from Bob, TP can ascertain the equality of private inputs between Alice and Bob, and subsequently communicate the comparison result to them. To assess the feasibility, the proposed protocol is simulated on IBM Quantum Cloud Platform. Furthermore, security analysis demonstrates that our protocol can withstand attacks from outsiders, such as eavesdroppers, and from insider participants attempting to grab the private input of another participant.
1 Introduction
Since Bennett and Brassard [1] introduced the pioneering quantum key distribution (QKD) protocol in 1984, leveraging the distinctive properties of quantum mechanics instead of relying on computational complexity problems and demonstrating its unconditional security, a multitude of quantum cryptographic protocols have since been developed. These include quantum secret sharing [2–4], quantum secure direct communication [5–7], and quantum key agreement [8, 9], aiming to address various cryptographic tasks. Quantum cryptography offers significant security advantages compared to classical cryptography, which is vulnerable to attacks from quantum algorithms (e.g., Shor’s algorithm [10]).
In 1982, Andrew Yao [11] proposed the concept of the millionaires’ problem, with the aim of solving the following task: two millionaires, each possessing their own wealth, seek to ascertain the wealthier party without revealing their financial status. Boudot et al. [12] introduced an efficient scheme for the socialist millionaires’ problem, relying on three standard assumptions: discrete logarithm, the Diffie–Hellman, and the Decision Diffie–Hellman. In this problem, two millionaires aim to ascertain the equality of their wealth. Nevertheless, as noted by Lo [13], securely evaluating an equality function in a two-party setting is deemed impossible. Consequently, the involvement of a third party (TP) becomes imperative to address the millionaires’ problem. Indeed, addressing the socialist millionaires’ problem is tantamount to formulating a private comparison protocol for confidentially comparing secrets. The reliability of the third party (TP) can be categorized into three types: completely honest, semi-honest, and dishonest. Since completely honest TP involvement in real life is hard to find, and implementing dishonest TP is difficult, semi-honest TP, who may misbehave but cannot collude with the participants, is a more reasonable and widely used approach in designing private comparison protocols up to now.
Quantum private comparison (QPC), which combines quantum mechanics and classical private comparison, can be used to solve the socialist millionaires’ problem that achieves the comparison of the equality or inequality of two secrets while ensuring the security of information transmission. The first QPC protocol, incorporating EPR pairs and decoy photons, was suggested by Yang et al. [14] in 2009, which allows the equality relationship of two secrets to be determined by involving a TP who is barred from accessing either the comparison result or the private inputs. To conserve quantum resources, Chen et al. [15] introduced a QPC protocol using triplet entangled states. In this protocol, the classical message can be divided into multiple groups, and comparison results can be obtained even if not all data are completely compared. Lin et al. [16] identified vulnerabilities in the protocol described in Ref. [15], noting its susceptibility to intercept-resend attacks and emphasizing the need for improvements. Afterward, several QPC protocols were proposed using different quantum states as carriers of quantum information, such as single photons [17], Bell states [18, 19], multi-qubit entangled states [20–24], and multi-qubit cluster states [25–28]. In addition, Ye [29] proposed a QPC protocol using cavity quantum electrodynamics (QED), which requires two-atom product states as carriers of quantum information, and one two-atom product state can be utilized to perform the equality comparison of 1 bit in each round. Chen et al. [30] introduced a QPC protocol utilizing quantum walks on a circle. This protocol requires a two-particle quantum walk state and a quantum walk operator, and it can improve efficiency by allowing private inputs to be compared all at once rather than bit by bit. In order to compare the relationship of arbitrary single-qubit states, Huang et al. [31] constructed a QPC protocol by utilizing the special property of rotation encryption and swap test.
The QPC protocols mentioned above mainly utilize low-dimensional quantum states as carriers of quantum information, with the classical message encoded on these quantum states. In most quantum states, a single quantum state can only convey 1 bit of information, limiting the transmission efficiency of quantum states. To address the issue, some scholars have focused on developing QPC protocols based on high-dimensional quantum states instead of low-dimensional quantum states since high-dimensional quantum states can encode a greater amount of information. In 2011, Jia et al. [32] introduced d-level GHZ states to solve the millionaire problem. The private inputs are encoded into the phase of the initial quantum entangled states by performing local operations, and the phase information can be obtained by performing collective measurements. In 2013, Yu et al. [33] introduced d-level single particles to construct the QPC protocol, with the aim of comparing the size relationship of private inputs. Guo et al. [34] used entanglement swapping of d-level Bell states to determine the equality and size relationship of two secrets. Since the particles can be used multiple times, the scheme has an advantage in efficiency. After that, Li and Shi [35] proposed a QPC protocol utilizing quantum Fourier transforms, wherein the encoding of private inputs into the phase of the quantum state sent from the third party is employed. This protocol achieves higher communication efficiency by employing secret-by-secret comparisons rather than bit-by-bit comparisons. Ji et al. [36] used (n+1)-qubit GHZ states as quantum resources to compare the participants’ secrets, and the requirement of quantum devices can be reduced as the protocol only employs quantum states and quantum measurements without the need for any entanglement swapping and unitary operations. Wu and Zhao [37] proposed a QPC based on d-level Bell states to determine the equality and size relationship of two secrets.
Based on the analysis of the aforementioned protocols, it can be deduced that QPC protocols utilizing low-dimensional quantum states as quantum information carriers, have lower transmission efficiency. In contrast, implementing high-dimensional quantum states-based QPC protocols poses challenges with current quantum technologies. In this paper, we introduce a practical QPC protocol to address the socialist millionaires’ problem utilizing single photons, as they are easier to implement and manipulate with current technology. This protocol utilizes single photons as carriers of quantum information, with TP tasked with preparing groups of quantum sequences and transmitting them to Alice who performs Identity or Hadamard operations on the received quantum sequences via her private inputs and the secret keys to obtain new quantum sequences, which are then sent to Bob. Similarly, Bob encodes his private inputs into the received quantum sequences to produce new quantum sequences, which are then sent to TP. By conducting single-particle measurements on the quantum sequence received from Bob, TP can ascertain the equality of private inputs between Alice and Bob, and subsequently communicate the comparison results to them. Two simulation experiments are conducted on IBM Quantum Experience to showcase the feasibility of the proposed protocol. Additionally, the incorporation of decoy photons enables the detection of any potential eavesdropping during the eavesdropping detection process.
The remaining sections of this paper are structured as follows: Section 2 introduces preliminary knowledge, Section 3 outlines the detailed steps of the proposed quantum secure protocol for the socialist millionaires’ problem, Section 4 conducts two simulation experiments, and Section 5 provides the corresponding analysis for the proposed protocol. Finally, Section 6 concludes the paper.
2 Preliminary knowledge
In this section, we will primarily introduce the Identity and Hadamard operations, which are equivalent to two quantum gates. In essence, a quantum gate can be represented as a unitary matrix. When performing a quantum gate on an n-qubit quantum state, the unitary matrix is of size
For a single qubit, performing the Identity operation will not change its state, while the state will change when performing the Hadamard operation. That is
Theorem 1. When using the Z-basis to measure
Proof. The measurement operators of Z-basis can be represented as
When performing the measurement on
When performing the measurement on
When performing the measurement on
When performing the measurement on
From Eqs 3–6, we can conclude that when using the Z-basis to measure
Theorem 2. When using the X-basis to measure
Proof. The measurement operators of X-basis can be represented as
When performing the measurement on
When performing the measurement on
When performing the measurement on
When performing the measurement on
From Eqs 12–15, we can also conclude that when using the X-basis to measure
3 Quantum secure protocol for the socialist millionaires’ problem
The quantum secure protocol for the socialist millionaires’ problem is run between two participants, each of whom possesses two secret inputs, A and B, respectively. The two participants aim to determine the equality relationship between A and B. The binary representations of A and B in
The detailed steps of the proposed protocol are described in the following procedure.
Step 1. TP prepares
Step 2. Upon receiving
Step 3. Alice discards the decoy photons to get
Step 4. Upon receiving
Step 5. Upon receiving
Step 6. TP communicates the comparison results to both Alice and Bob. If all measurement results in
4 Simulation experiments
Since single photons are easier to implement and manipulate compared to low-dimensional and high-dimensional quantum states, we simulate the aforementioned protocol on IBM Quantum Experience using two concrete examples to demonstrate its feasibility and correctness. The specifics of two simulation experiments are outlined below.
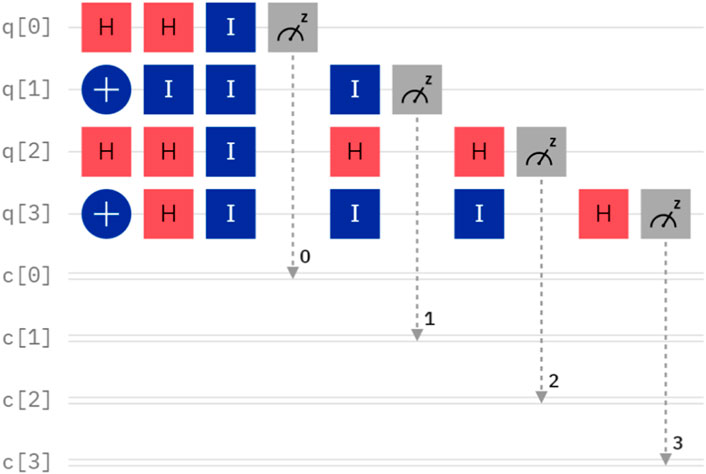
4.1 Simulation I. Alice and Bob desire to compare their private inputs, with A = 12 and B = 12, respectively
A and B can be denoted as
Suppose that the initial quantum sequence prepared by TP is
The quantum circuit for Case I is depicted in Figure 1. By executing the quantum circuit on IBM Quantum Experience, we can obtain the measurement results shown in Figure 2. In Figure 2, the string on the horizontal axis represents the measurement outcome, corresponding to q [0]-q [3] from right to left. The value on the vertical axis represents the quasiprobability. It is important to note that both the measurement bases selected in q [2] and q [3] are the X basis, and the measurement outcome 1 and 0 are considered as
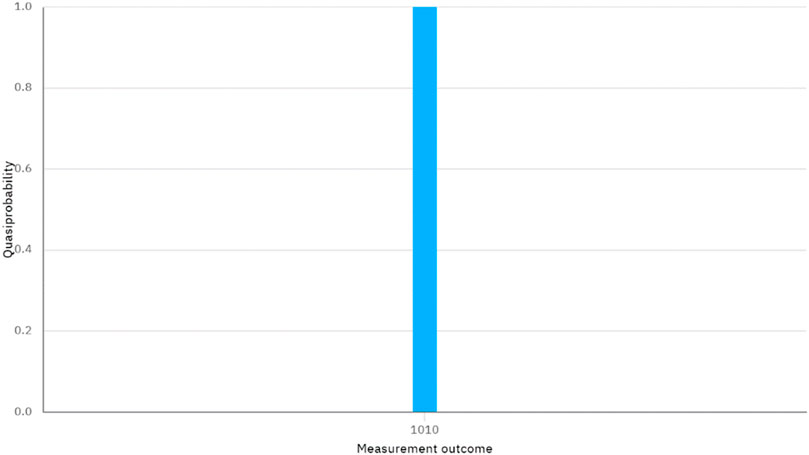
FIGURE 2. The measurement outcome in Figure 1.
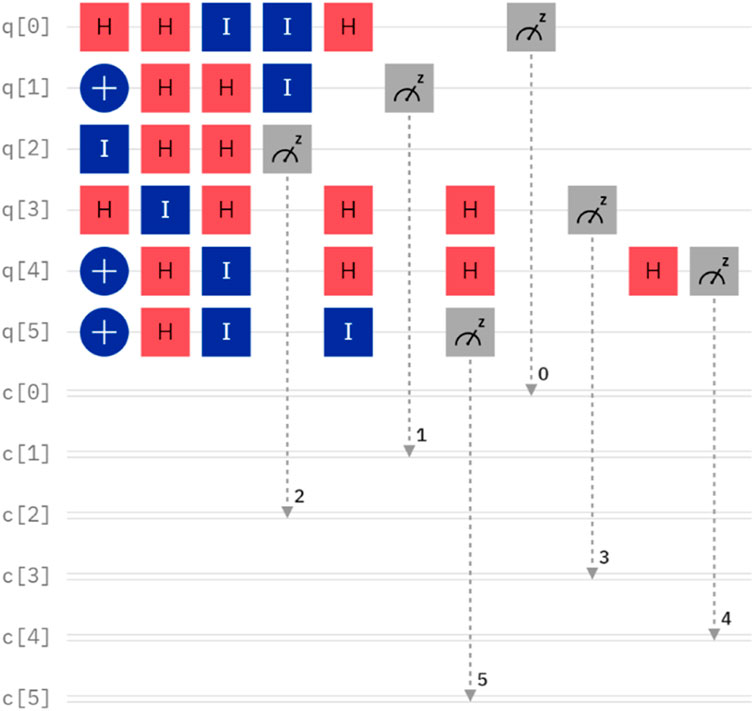
4.2 Simulation II. Alice and Bob desire to compare their private inputs, with A = 55 and B = 22, respectively
A and B can be represented as
Suppose that the initial quantum sequence prepared by TP is
The quantum circuit for Case II is depicted in Figure 3. By executing the quantum circuit on IBM Quantum Experience, we can obtain the measurement results shown in Figure 4. It is important to note that the measurement basis selected in q [0], q [3], and q [4] are all based on the X basis. The measurement outcome 1 and 0 can be considered as
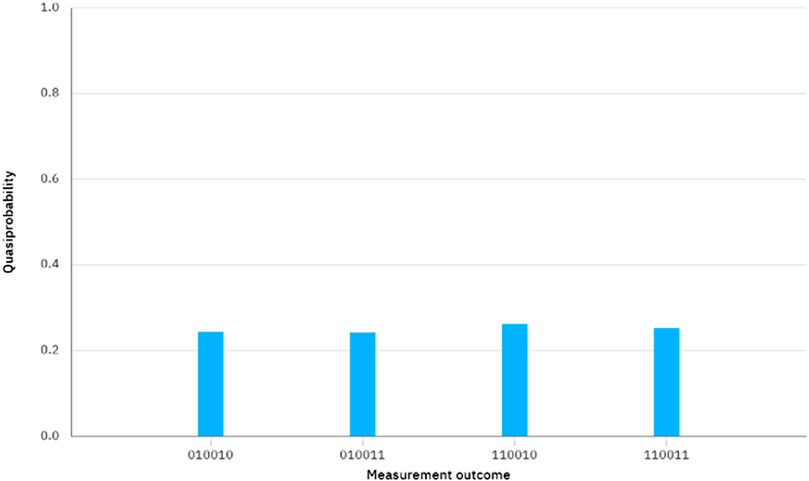
FIGURE 4. The measurement outcome in Figure 3.
5 Analysis
5.1 Correctness analysis
In the proposed protocol, TP prepares
After that,
After that,
There are four cases that should be considered.
Case I: If
When TP measures each group of quantum states in
Case II: If
When TP measures each group of quantum states in
Case III: If
We can see that
Case IV: If
Similarly, we can also observe that
Therefore, the above results reveal that our protocol is correct.
5.2 Security analysis
5.2.1 External attacks
External attacks involve an outsider eavesdropper, Eve, who may attempt to obtain valuable information about Alice’s or Bob’s private inputs during the transmission of the quantum sequence between the participants. Unfortunately, decoy photons are used during the transmission of each quantum sequence. Both the sender and receiver of the quantum sequences will perform the eavesdropping detection to verify the presence of any eavesdropper. This technique guarantees the security of the quantum sequence transmission, and any external attacks including intercept-resend attack, auxiliary particle attack, the man-in-the-middle attack and denial-of-service (Dos) attacks are invalid. In this context, we primarily delve into the security aspects of the proposed protocol concerning intercept-resend attacks, entanglement-measure attacks, and Trojan-Horse attacks in detail.
5.2.1.1 The intercept-resend attack
The intercept-resend attack refers to the outsider eavesdropper, Eve, intercepting the sequence sent from the previous participant during the transmission of each quantum sequence. Once Eve obtains the quantum sequence that carries the private inputs, she has the option to measure them using the Z-basis and send a fake sequence whose states match the measurement results instead of the initial quantum sequences to the original receiver. We assume that when a sender’s initial quantum state is
5.2.1.2 The entanglement-measure attack
The entanglement-measure attack involves an outsider eavesdropper, Eve, intercepting the sequence sent from the previous participant during the transmission of each quantum sequence. She then performs unitary operations to entangle the prepared auxiliary particle sequence
Moreover, the parameters a, b, c, and d satisfy the condition, e.g.,
When Substituting Eq. 31 and
From Eqs 32–35, we can easily see that the auxiliary particles are not related to the intercepted ones. No matter what the intercept particles are, the auxiliary particles will always be in
5.2.1.3 The Trojan-Horse attacks
The Trojan-Horse attacks [38] mainly include the delay-photon attack and the invisible photon eavesdropping attack. These attacks may occur in a two-way communication protocol where quantum states are returned to the sender. Since our protocol is a two-way communication protocol, the initial quantum sequence prepared by TP is returned to TP and the quantum sequence is transmitted in a circular mode. Therefore, the Trojan-Horse attacks should be considered. In order to prevent these attacks, both the Wavelength Quantum Filter (WQF) and the Photons Number Splitter (PNS) should be equipped to remove invisible photons and separate legitimate photons from delayed photons, respectively.
5.2.2 Participants’ attack
Since the participants have the legal capacity to access more information compared to an outside eavesdropper, the dishonest individual has a high probability of obtaining the private input of the dishonest participant without being detected. Therefore, participants’ attack as high security risk should be prevented by taking appropriate measures. Here, we analyze three types of attacks by participants that are aimed at obtaining the private input of the participants.
5.2.2.1 The attack from TP
As a semi-honest party, TP may exhibit improper behavior, but she cannot collude with either Alice or Bob. If TP intends to usurp the private input of Alice or Bob, she may perform external attacks similar to Eve. Unfortunately, this action will be detected, as discussed in Section 5.2.1, and TP cannot avoid detection by eavesdropping. Although TP has some advantages in generating the initial quantum sequences used for information transmission and receiving the sequences encoded with private inputs and secret keys, TP can only gain knowledge about the comparison result. In other words, TP is able to determine whether a bit of Alice and Bob is identical or not, but it will not disclose whether the bit of Alice or Bob is 0 or 1. In addition, both
5.2.2.2 The attack from Alice
When TP sends
5.2.2.3 The attack from Bob
When Alice sends
In summary, the proposed protocol remains resilient against attacks from the participants, ensuring that the secrets of both Alice and Bob are not compromised.
5.3 Efficiency analysis and comparison
In most of QPC protocol, the qubit efficiency is an important indicator for evaluating the utilization rate of quantum states. However, it does not take into account the decoy photons used in eavesdropping detection, which can be considered as an independent process.
The qubit efficiency [39]
Where
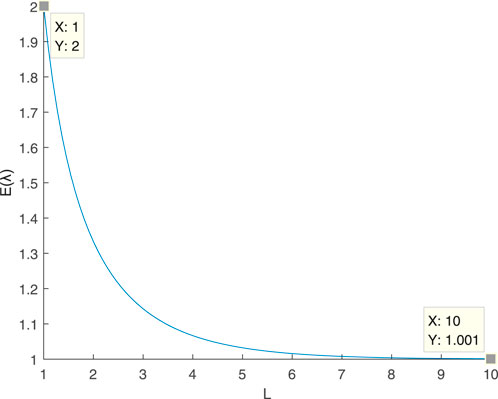
Next, we will discuss the value of
When L is large, we can obtain
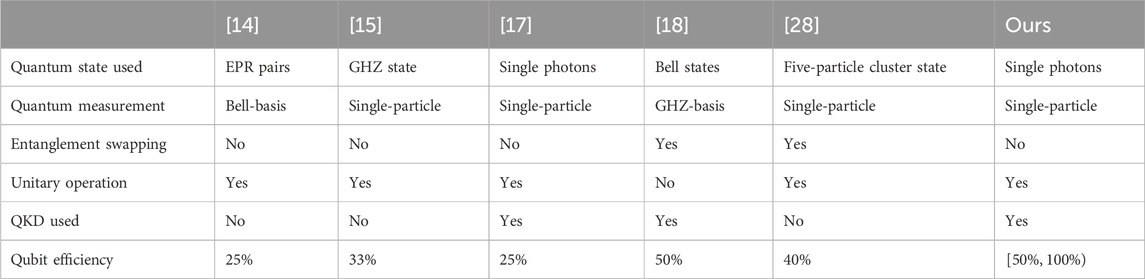
Table 1 illustrates a comparison between the proposed protocol and previous two-party QPC protocols.
Table 1 reveals that our protocol utilizes single photons as carriers of quantum information, which is more feasible than Bell states and multi-particle states. Although both Ref. [17] and our protocol utilize single photons as quantum resources, the qubit efficiency in Ref. [17] is only 25%, which is lower with our protocol with the qubit efficiency of
6 Conclusion
A single-photon-based quantum secure protocol for the socialist millionaires’ problem is presented in this article. By utilizing single photons as quantum information carriers, encoding the private input through Identity or Hadamard operations, and obtaining the classical outcome via single-particle measurement, the protocol is easier to implement and manipulate compared to other existing protocols. By executing the protocol, TP can ascertain the equality of Alice and Bob’s private inputs and subsequently communicates the result to them. Furthermore, the protocol’s feasibility is tested through simulation on IBM Quantum Cloud Platform. Security analysis demonstrates that any attempt by eavesdroppers or insider parties to grab the private input of another participant is invalid. Currently, the quantum protocols for the socialist millionaires’ problem are primarily designed assuming that all users, including TP, have complete quantum capabilities. In the future, we aim to investigate the development of a quantum protocol that accommodates classical users who can only reflect or measure the received quantum states.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
MH: Formal Analysis, Investigation, Methodology, Writing–original draft. YW: Funding acquisition, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Gongga Plan for the “Double World-class Project”.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bennett CH, Brassard G. Quantum cryptography: public key distribution and coin tossing. Theor Comput Sci (2014) 560:7–11. doi:10.1016/j.tcs.2014.05.025
2. Hillery M, Bužek V, Berthiaume A. Quantum secret sharing. Phys Rev A (1999) 59(3):1829–34. doi:10.1103/PhysRevA.59.1829
3. Li F, Hu H, Zhu S, Yan J, Ding J. A verifiable (k, n)-threshold dynamic quantum secret sharing schemen-threshold dynamic quantum secret sharing scheme. Quan Inf Process (2022) 21(7):259. doi:10.1007/s11128-022-03617-3
4. Kuo SY, Tseng KC, Yang CC, Chou YH. Efficient multiparty quantum secret sharing based on a novel structure and single qubits. EPJ Quan Tech (2023) 10(1):29. doi:10.1140/epjqt/s40507-023-00186-x
5. Sheng YB, Zhou L, Long GL. One-step quantum secure direct communication. Sci Bull (2022) 67(4):367–74. doi:10.1016/j.scib.2021.11.002
6. Zhou L, Sheng YB. One-step device-independent quantum secure direct communication. Sci China Phys Mech Astron (2022) 65(5):250311. doi:10.1007/s11433-021-1863-9
7. Huang X, Zhang S, Chang Y, Yang F, Hou M, Chen W. Quantum secure direct communication based on quantum homomorphic encryption. Mod Phys Lett A (2021) 36(37):2150263. doi:10.1142/S0217732321502631
8. Yang YG, Gao S, Li D, Zhou YH, Shi WM. Two-party quantum key agreement over a collective noisy channel. Quan Inf Process (2019) 18:74–17. doi:10.1007/s11128-019-2187-8
9. Huang X, Zhang SB, Chang Y, Qiu C, Liu DM, Hou M. Quantum key agreement protocol based on quantum search algorithm. Int J Theor Phys (2021) 60:838–47. doi:10.1007/s10773-020-04703-x
10. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev (1999) 41(2):303–32. doi:10.1137/S0036144598347011
11. Yao AC. Protocols for secure computations. In: 23rd annual symposium on foundations of computer science (sfcs 1982); 03-05 November 1982; Chicago, IL, USA. IEEE (1982). p. 160–4. doi:10.1109/SFCS.1982.38
12. Boudot F, Schoenmakers B, Traore J. A fair and efficient solution to the socialist millionaires’ problem. Discrete Appl Maths (2001) 111(1-2):23–36. doi:10.1016/S0166-218X(00)00342-5
13. Lo HK. Insecurity of quantum secure computations. Phys Rev A (1997) 56(2):1154–62. doi:10.1103/PhysRevA.56.1154
14. Yang YG, Wen QY. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J Phys A: Math Theor (2009) 42(5):055305. doi:10.1088/1751-8113/42/5/055305
15. Chen XB, Xu G, Niu XX, Wen QY, Yang YX. An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement. Opt Commun (2010) 283(7):1561–5. doi:10.1016/j.optcom.2009.11.085
16. Lin J, Tseng HY, Hwang T. Intercept–resend attacks on Chen et al.'s quantum private comparison protocol and the improvements. Opt Commun (2011) 284(9):2412–4. doi:10.1016/j.optcom.2010.12.070
17. Huang W, Wen QY, Liu B, Gao F, Sun Y. Robust and efficient quantum private comparison of equality with collective detection over collective-noise channels. Sci China Phys Mech Astron (2013) 56:1670–8. doi:10.1007/s11433-013-5224-0
18. Huang X, Zhang SB, Chang Y, Hou M, Cheng W. Efficient quantum private comparison based on entanglement swapping of bell states. Int J Theor Phys (2021) 60:3783–96. doi:10.1007/s10773-021-04915-9
19. Liu W, Wang YB, Cui W. Quantum private comparison protocol based on Bell entangled states. Commun Theor Phys (2012) 57(4):583–8. doi:10.1088/0253-6102/57/4/11
20. Lin S, Guo GD, Liu XF. Quantum private comparison of equality with χ-type entangled states. Int J Theor Phys (2013) 52(11):4185–94. doi:10.1007/s10773-013-1731-z
21. Ye TY, Ji ZX. Two-party quantum private comparison with five-qubit entangled states. Int J Theor Phys (2017) 56:1517–29. doi:10.1007/s10773-017-3291-0
22. Ji ZX, Zhang HG, Fan PR. Two-party quantum private comparison protocol with maximally entangled seven-qubit state. Mod Phys Lett A (2019) 34(28):1950229. doi:10.1142/S0217732319502298
23. Ji Z, Zhang H, Wang H. Quantum private comparison protocols with a number of multi-particle entangled states. IEEE Access (2019) 7:44613–21. doi:10.1109/ACCESS.2019.2906687
24. Fan P, Rahman AU, Ji Z, Ji X, Hao Z, Zhang H. Two-party quantum private comparison based on eight-qubit entangled state. Mod Phys Lett A (2022) 37(05):2250026. doi:10.1142/S0217732322500262
25. Sun Z, Long D. Quantum private comparison protocol based on cluster states. Int J Theor Phys (2013) 52:212–8. doi:10.1007/s10773-012-1321-5
26. Zha XW, Yu XY, Cao Y, Wang SK. Quantum private comparison protocol with five-particle cluster states. Int J Theor Phys (2018) 57:3874–81. doi:10.1007/s10773-018-3900-6
27. Xu GA, Chen XB, Wei ZH, Li MJ, Yang YX. An efficient protocol for the quantum private comparison of equality with a four-qubit cluster state. Int J Quan Inf (2012) 10(04):1250045. doi:10.1142/S0219749912500451
28. Chang Y, Zhang WB, Zhang SB, Wang HC, Yan LL, Han GH, et al. Quantum private comparison of equality based on five-particle cluster state. Commun Theor Phys (2016) 66(6):621–8. doi:10.1088/0253-6102/66/6/621
29. Ye TY. Quantum private comparison via cavity QED. Commun Theor Phys (2017) 67(2):147. doi:10.1088/0253-6102/67/2/147
30. Chen FL, Zhang H, Chen SG, Cheng WT. Novel two-party quantum private comparison via quantum walks on circle. Quan Inf Process (2021) 20(5):178. doi:10.1007/s11128-021-03084-2
31. Huang X, Chang Y, Cheng W, Hou M, Zhang SB. Quantum private comparison of arbitrary single qubit states based on swap test. Chin Phys B (2022) 31(4):040303. doi:10.1088/1674-1056/ac4103
32. Jia HY, Wen QY, Song TT, Gao F. Quantum protocol for millionaire problem. Opt Commun (2011) 284(1):545–9. doi:10.1016/j.optcom.2010.09.005
33. Yu CH, Guo GD, Lin S. Quantum private comparison with d-level single-particle states. Physica Scripta (2013) 88(6):065013. doi:10.1088/0031-8949/88/06/065013
34. Guo FZ, Gao F, Qin SJ, Zhang J, Wen QY. Quantum private comparison protocol based on entanglement swapping of d-level Bell states. Quan Inf Process (2013) 12(8):2793–802. doi:10.1007/s11128-013-0536-6
35. Li L, Shi R. A novel and efficient quantum private comparison scheme. J Korean Phys Soc (2019) 75:15–21. doi:10.3938/jkps.75.15
36. Ji Z, Fan P, Zhang H, Wang H. Greenberger-Horne-Zeilinger-based quantum private comparison protocol with bit-flipping. Physica Scripta (2020) 96(1):015103. doi:10.1088/1402-4896/abc980
37. Wu WQ, Zhao YX. Quantum private comparison of size using d-level Bell states with a semi-honest third party. Quan Inf Process (2021) 20(4):155. doi:10.1007/s11128-021-03059-3
38. Gisin N, Fasel S, Kraus B, Zbinden H, Ribordy G. Trojan-horse attacks on quantum-key-distribution systems. Phys Rev A (2006) 73(2):022320. doi:10.1103/PhysRevA.73.022320
Keywords: single photons, quantum secure protocol, the socialist millionaires’ problem, semi-honest third party, quantum cryptography
Citation: Hou M and Wu Y (2024) Single-photon-based quantum secure protocol for the socialist millionaires’ problem. Front. Phys. 12:1364140. doi: 10.3389/fphy.2024.1364140
Received: 01 January 2024; Accepted: 20 February 2024;
Published: 06 March 2024.
Edited by:
Yuanyuan Huang, Chengdu University of Information Technology, ChinaReviewed by:
Peilin He, University of Pittsburgh, United StatesTingting Song, Jinan University, China
Copyright © 2024 Hou and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Min Hou, aG91bWluQHNjdWpqLmVkdS5jbg==
 Min Hou
Min Hou Yue Wu1
Yue Wu1