Theoretical investigation of the Co-occurrence of superconductivity and antiferromagnetism in iron-based high-temperature superconductors

In this research work, the Co-occurrence of superconductivity and antiferromagnetism in ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ iron-based high-temperature superconductors have been investigated. Based on the multi-band nature of ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ iron-based superconductors, a two-band model Hamiltonian that contains intra- and inter-bands is developed. By employing the matrix form of the temperature-dependent Green’s function formalism with the two-band Hamiltonian, the mathematical expressions of superconducting transition temperature as functions of the superconducting order parameter and antiferromagnetism translational temperature as a function of the magnetic order parameter are obtained, respectively. The plotted graph of the superconducting and magnetic temperature as a function of the magnetic order parameter indicates a clear possibility of Co-occurrence of superconductivity and the antiferromagnetism order parameter in ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ iron-based superconductors in the range of magnetic order parameters between 2.3 meV and 6.07 meV, which is in good agreement with experimental observations. This research contributes to understanding the complex behavior of high-temperature superconductors and provides valuable technological applications for other fields.

1 Introduction

Current research in the field of condensed matter physics is dedicated to characterizing the properties of materials based on their structure and electronic behavior. While most metal systems have weaker Coulomb interaction energies compared to electron kinetic energies, the interaction between electrons, whether direct or indirect, significantly influences the physical properties of strongly correlated electron systems. These systems include unconventional superconductors, Mott insulators, and heavy fermions. On the other hand, superconductivity is a complex phenomenon that requires extensive experimental and theoretical efforts across a wide range of materials such as oxides, magnetic compounds, and organic compounds with their wide range of modern technological and industrial applications like MRI, Maglev train, and electronic device. This particular subfield remains one of the most challenging areas to understand fully.

The phenomenon of superconductivity, initially observed in high-purity mercury by H. Kamerlingh Onnes in April 1911, is characterized by a sudden drop in electrical resistance to zero at 4.2 K [1, 2]. This discovery led to the subsequent identification of elemental and binary superconductors with critical temperature (T_c) values up to 23.2 K [3, 4], which remained unbeaten for over 50 years. Extensive experimental and theoretical efforts were made to understand the underlying microscopic mechanisms and the perfect diamagnetism exhibited by superconductors. In 1933, W. Meissner and R. Ochsenfeld discovered that a superconductor, when cooled in the presence of a static magnetic field, expels the magnetic field from its interior [3–6]. The theoretical breakthrough came in 1957 with the formulation of the BCS theory by John Bardeen, Leon Neil Cooper, and John Robert Schrieffer, which provided a microscopic explanation for superconductivity [6–8]. In the late 1970s and early 1980s, superconductivity was discovered in heavy fermion and nearly magnetic systems despite their lower critical temperatures [8]. Researchers began seeking new pairing interactions to eventually achieve high-temperature superconductivity. The pivotal moment came in 1986 when J. G. Bednorz and K. A. Muller discovered La_(1-x) Ba_x CuO₄ with a T_c of 30 K, sparking intense and continuous research in the field of high-temperature superconductivity [4, 9–11].

The emergence of LaO_(1-x) F_x FeAs, a novel superconductor with a transition temperature of 26 K, marked a significant milestone in superconductivity research [11]. This breakthrough led to a shift in focus from high-temperature cuprates (HTSC or CuSC) to iron-based superconductors (FeSC), as evidenced by the redirection of researchers and funding. Observed as the second family of unconventional High-T_c superconductors, the FeSC exhibits several similarities to cuprate superconductors. These similarities include a layered crystal structure, relatively high critical temperature (T_c), superconductivity occurring near a magnetic phase induced by parameter adjustments like chemical doping or pressure, and notably, a highly comparable temperature-concentration (T - x) phase diagram. Moreover, it is commonly accepted that electronic conduction in the FeAs/FeSe layers is linked, while cuprates have charge carriers that are delocalized in the basal copper oxide planes [11]. However, there are some significant differences: in the edge-sharing tetrahedron, the pnictogen anions are arranged above and below the Fe plane instead of at the same height as in the copper oxide plane [12], and the superconductivity of cuprates is derived from doping a Mott insulator. However, the parent compound of FeSC is a poor metal due to partial gapping around the Fermi surface (FS) at low temperatures [13–15], which does not initiate an insulating state. Doping the two-dimensional (2D) copper oxide plane of cuprate superconductors causes a sharp decline in T_c. The cuprates exhibit a predominantly s-wave gap symmetry, whereas the FeSC are generally immune to this effect [14]. This change is reflected in the early reviews, and FeSC research is now a major area of condensed matter physics, as evidenced by the more than 3000 citations that show its active pursuit [16–18].

The microscopic pairing process for superconductivity has been the subject of extensive research since the discovery of Fe-pnictides, a novel class of high-temperature superconductors [12, 19–22]. However, still, the microscopic pairing process of superconductivity (SC) has to be the main issue in unconventional high-temperature superconductors. The main objective of this theoretical study of the co-occurrence of antiferromagnetism (AFM) and superconductivity in a Co-doped Ca_0.73La_0.27FeAs₂ (Co-CaLa112) high-temperature superconductor is to provide insight on the superconductivity pairing process. FeSC holds great interest for several compelling reasons. Firstly, it offers the opportunity to explore fascinating physics arising from the Co-occurrence of superconductivity and magnetism. Secondly, the wide range of compounds available for study, coupled with the multi-band electronic structure, holds the potential for uncovering the elusive mechanism behind high-temperature superconductivity and discovering methods to enhance it (T_c). Lastly, FeSC shows promise for practical applications due to their higher critical field (H_c) compared to cuprates, as well as their strong and isotropic critical currents. Based on these reasons make them appealing for electrical power and magnetic applications, while the Co-occurrence of magnetism and superconductivity makes them interesting for spintronic [23, 24]. Therefore, FeSC offers a valuable opportunity to explore the influence of structural and electronic factors on the physical properties and pairing mechanism of high-temperature superconductivity (T_c). In the study of FeSC, there is a significant focus on investigating the interplay between antiferromagnetism (AFM) and superconductivity (SC). This attention is driven by the belief that spin fluctuations play a crucial role in the pairing mechanism [6–8, 25].

Since the groundbreaking discovery of LaO_(1-x) F_x FeAs (1111-family), a novel superconductor with a transition temperature of 26 K [11], significant progress has been made in the field of superconductivity research in Fe-pnictides. Includes the 1111-family REFeAs (O, F) (RE = rare-earth elements) [19, 20], the 122 families AeFe₂ As₂ (Ae = alkaline earth metals such as Ca, Sr, Ba) [21, 22], the 111-family AFeAs (A = alkali metals like Li, Na) [26, 27], the 11 family-FeSe [28, 29], and the 10-n-8 family Ca₁₀ (Pt_n As₈) (Fe₂ As₂)₅ (A = Pt, Pd, Ir; n = 3, 4) [27]. Obtaining a deeper understanding of the superconductivity mechanism in iron-based compounds and striving for advancements in Tc (critical temperature) necessitate the crucial discovery of new families of iron-based superconductors. Recently, the 112 family of iron-based superconductors, specifically the Ca_(1-x) A_x FeAs₂ (A = Rare Earth metal, such as La, Ce, Pr, Nd, etc.), has been experimentally confirmed [30, 31]. From this 112 family, the Ca_(1-x) La_x FeAs₂ (CaLa112) is one of the parent compounds with T_c up to 43K, crystalizes in a monoclinic lattice with the $\text{FeAs}-\left(\text{Ca}/\text{La}\right)-\text{As}-\left(\text{Ca}/\text{La}\right)-\text{FeAs}$ layer stacking [28]. CaLa112 is distinctive in several aspects due to the presence of zig-zag chains made of As layers alongside the prototypical FeAs layers consisting of edge-sharing FeAs₄ tetrahedra. This combination of As chains and FeAs layers sets CaLa112 apart from other crystals. By introducing electron over doping in the parent compound of CaLa112 FeSC, the dual nature of moveable and local magnetism in FeSC is exemplified. This electron-doped CaLa112 FeSC undergoes a structural phase transition from monoclinic to triclinic at 58K, while a paramagnetic to stripe antiferromagnetic phase transition occurs at 54 K [32]. In addition to hole-like carriers introduced by Ca doping, electron-like carriers are incorporated through Co substitution on the iron sites, which contributes to the stabilization of superconductivity in Ca _0.73 La _0.27 FeAs₂ [32]. The structure and magnetic phase transitions in Co-doped Ca_0.73La_0.27 FeAs₂ (Co-CaLa112) are suppressed, leading to the emergence of bulk superconductivity with a critical temperature (Tc) of up to 20 K [30]. Doping experiments reveal the microscopic coexistence of AFM and SC in Co-doped samples with doping concentrations of x = 0.025 and 0.033 [30]. To explore the microscopic coexistence of AFM and SC in the 112 material, we utilize a simplified two-band model commonly used in the study of the relation between AFM and SC of FeSC [33–35]. This model consists of a hole pocket located at the center of the Brillouin zone (BZ) and an electron pocket situated at the corner of the Brillouin zone as shown in Figure 1 Refs. [32, 33]. By studying the interplay between these phenomena, their connections can be uncovered, providing an empirical foundation for developing a comprehensive theoretical model.

FIGURE 1

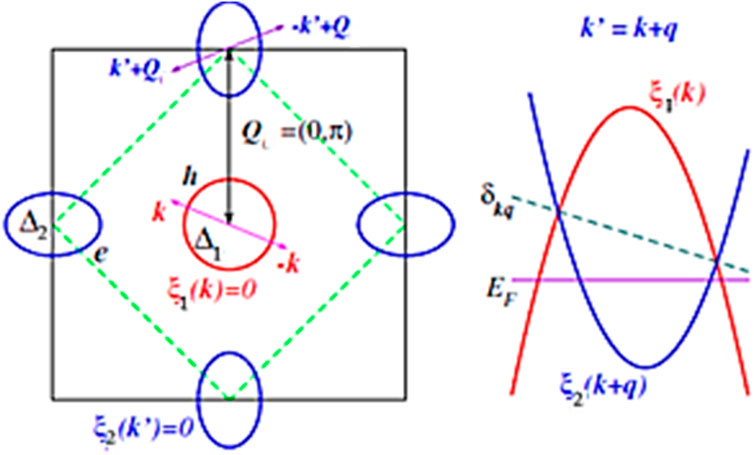
FIGURE 1. Left: modified electronic band dispersion of the two-band model reflected in this paper, in the unfolded Brillouin zone. The circular hole-like FS is in the center, with SC order parameter ${∆}_1$, and the elliptical electron-like FSs are at $=\left(0,\pi \right)and=\left(\pi ,0\right)$ with SC order parameter ${∆}_2$. The magnetic order with momentum $Q=\left(\pi ,0\right)$ hybridizes hole and electron FSs separated by Q but leaves FSs at $=\left(\pm \pi ,0\right)$ intact. Right: by doping one may adjust the size and shape of hole and electron bands, and also magnetic order parameter can be incommensurate, with momentum Q_+q Ref. [33].

This study, which is based on an experimental perspective, focuses on the theoretical analysis of the interplay between superconductivity and antiferromagnetism in Ca _{(0.74 (1))} La _{(0.26 (1))} (Fe_(1-x) Co_x) As ₍₂₎ iron-based high-temperature superconductors by considering intra and inter bands that the system incorporates two computing phenomena involving electron-hole-like pairing and electron-electron pairing. The mathematical expression for the superconducting order parameter, magnetic order parameter, superconducting transition temperature, and AFM transition temperature is found using the matrix form of the temperature-dependent Green’s function formalism with the two-band model Hamiltonian. Our research’s findings determine that AFM and SC are established over specific order parameter ranges, which will give clues for the mystery of high-temperature superconductors.

2 Formulation of the problem

Clarifying the origin of superconductivity in iron-based superconductors requires an understanding of their phase diagram. Spin density wave (SDW) with antiferromagnetism (AFM) is observed in parent compounds of iron-based superconductors below the Neel temperature. Superconductivity arises when hole or electron doping is applied, suppressing magnetization. The close relationship between AFM and SC phases suggests that spin fluctuation mediates the formation of a Cooper pair, leading to s^+-wave order [34], where the gap function sign on hole Fermi surfaces (FSs) centered at momentum k = (0,0) is opposite to that on electron FSs at k = (0,π) and (π,0). Conversely, it is suggested that superconductivity arises from orbital fluctuation and takes the form of s⁺⁺ wave order, where the two signs are the same [36]. s^+-and s⁺⁺ are possible candidates for SC symmetry in iron-based superconductors. Given the proximity of the AFM and SC phases, insights into the superconductivity of iron-based superconductors may be gained from examining their boundary.

Numerous experimental and computational investigations employing Density Functional Theory (DFT) have provided evidence that the Fermi surface of iron-based superconductors comprises two hole surfaces near the Γ point and two electron surfaces near the M point within the Brillouin zone of the Fe/cell [34, 35]. Additionally, these studies highlight the multi-band character of the band structure of FeScs. Calculations of the band structure have further revealed that the Fe 3d orbitals make significant contributions to the spectral weight in the vicinity of the Fermi energy. Neutron diffraction, X-ray diffraction, and NMR investigations all support the microscopically coexisting phase of AFM and SC orders in the Co-CaLa112 high-temperature superconductor [30]. An exploration of the coexistence phase has been conducted theoretically [34]. In the Co-CaLa112 high-temperature superconductor phase, it is generally believed that paramagnetic FSs are made up of a nearly circular hole pocket located at k= (0,0), along with an elliptical electron pocket at k=(π,0) and (0, π) as illustrated the model in Figure 1. The introduction of AFM order with a wave vector Q=(π,0) combines the hole and electron dispersions, resulting in the opening of an SDW gap [32]. There is an additional electron pocket at the edge of the Brillouin zone and a hole-like pocket at the center of the doped Brillouin zone, as observed experimentally in Fe pnictides, in addition to the appearance of an elliptical electron pocket at the corner and a circular hole pocket at the center. Since the fundamental properties of the SC and antiferromagnetic interactions and their interplay should not be significantly affected by the number of bands, we investigate a simple model with one circular hole and one elliptical electron band. In the case of pnictides, the twofold degeneracy of hole and electron states at the center and corners of the Brillouin zone is omitted since it seems to not affect magnetic order or superconducting [37–41]. By utilizing 4 × 4 matrix representations of single particle normal and anomalous thermal Green’s functions within a two-band model Hamiltonian, along with appropriate mean-field approximations, the simultaneous occurrence of superconductivity and antiferromagnetism becomes a highly plausible scenario. This section focuses on investigating the coexistence of superconductivity and antiferromagnetism in the multi-band iron-based superconductor Ca _{(0.74 (1))} La _{(0.26 (1))} (Fe_(1-x) Co_x) As ₍₂₎, as well as examining the influence of magnetic ordering on both the superconducting order parameter $\left(\overline{∆}\right)$ and the transition temperature (T_c) within the framework of the multi-band model Hamiltonian. Based on the multi-band nature of ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ iron-based superconductors, a two-band model Hamiltonian which contains hole and electron bands is developed. The two-band model Hamiltonian includes the free fermion part $H_0$, and the fermion interactions in superconducting and antiferromagnetic channels,

$H=H_0+H_{∆}+H_{AFM}$

The free fermion channel of the Hamiltonian is

$H_0={\displaystyle \sum _{k\sigma }}{\epsilon }_1\left(k\right)c_{1k\sigma }^{+}{c}_{1k\sigma }+{\displaystyle \sum _{k^{\prime }\sigma }}{\epsilon }_2\left(k^{\prime }\right)c_{2k^{\prime }\sigma }^{+}{c}_{2k^{\prime }\sigma }$

Where ${\epsilon }_1\left(k\right)and{\epsilon }_2\left(k^{\prime }\right)$ measured from the Fermi energy $\mu \left(chemicalpotential\right),{i.e,\epsilon }_{ik}={\epsilon }_{ik}-\mu i=1,2$, the $k$ are momentum measured from center of BZ and $k^{\prime }$ are deviations from Q₀, we assume an inversion symmetry ${\epsilon }_{1,2}\left(k\right)={\epsilon }_{1,2}\left(-k\right)$.

The interaction that involves the exchange of electron pairs between the hole and electron pockets is the dominant term in the pairing interaction. However, there exist several other pair-scattering interactions that also contribute to the overall pairing mechanism [40, 42]. The pairing interactions in the superconducting channel for band 1 is

$H_{{\overline{∆}}_{1k}}=-{\displaystyle \sum _{k{k}^{\prime }}}{V}_{11}^{SC}\left(k,k^{`}\right)c_{1k\uparrow }^{+}{c}_{1-k\downarrow }^{+}{c_{1-k\downarrow }c}_{1k\uparrow }-{\displaystyle \sum _{k{k}^{\prime }}}{V}_{12}^{SC}\left(k,k^{\prime }\right)\left(c_{1k\uparrow }^{+}{c}_{1-k\downarrow }^{+}{c}_{2-k\downarrow }{c}_{2k\uparrow }+{c_{2k\uparrow }^{+}{c}_{2-k\downarrow }^{+}{c}_{1-k\downarrow }c}_{1k\uparrow }\right)$

For band 2 is

$H_{{\overline{∆}}_{2k}}=-{\displaystyle \sum _{k{k}^{\prime }}}{V}_{22}^{SC}\left(k,k^{`}\right)c_{2k\uparrow }^{+}{c}_{2-k\downarrow }^{+}{c_{2-k\downarrow }c}_{2k\uparrow }-\frac{1}{2}{\displaystyle \sum _{k{k}^{\prime }}}{V}_{21}^{SC}\left(k,k^{\prime }\right)\left({{c_{2k\uparrow }^{+}{c}_{2-k\downarrow }^{+}{c}_{1-k\downarrow }c}_{1k\uparrow }+c^{+}}_{1k\uparrow }{c}_{1-k\downarrow }^{+}{c}_{2-k\downarrow }{c}_{2k\uparrow }\right)$

We introduce a mean-field equation with order parameter in a self-consistent manner, in the superconducting state for band 1 and 2 as stated by;

${∆}_{11}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{11}^{SC}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{1k\uparrow }〉and{∆}_{12}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{12}^{SC}\left(k,k^{`}\right)〈{c_{2-k\downarrow }c}_{2k\uparrow }〉$

${∆}_{22}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{22}^{SC}\left(k,k^{`}\right)〈{c_{2-k\downarrow }c}_{2k\uparrow }〉and{∆}_{21}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{21}^{SC}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{1k\uparrow }〉$

where the ${∆}_{11}$ and ${∆}_{12}$ are intra and inter-band superconducting order parameter for band 1, and ${∆}_{22}$ and ${∆}_{21}$ are intra and inter-band superconducting order parameter for band 2, respectively

To consider the AFM state, we assume the following intra and interband Coulomb interactions:

$H_{AFM}=-\frac{1}{2}{\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{1,2}^{AFM}\left(k,k^{\prime }\right)\left(c_{1k+Q\uparrow }^{+}{c}_{1-k\downarrow }{c}_{1-k\downarrow }^{+}{c_{1k+Q\uparrow }+c_{2k\uparrow }^{+}c}_{2-k\downarrow }{c}_{2-k\uparrow }^{+}{c}_{2k+Q\uparrow }\right)-\frac{1}{2}{\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{12}^{AFM}\left(k,k^{\prime }\right)\left({c_{2k+Q\downarrow }^{+}{c}_{1-k\downarrow }{c}^{+}}_{1-k\uparrow }{c}_{2k+Q\uparrow }+c_{1-k\uparrow }^{+}{c}_{2k+Q\uparrow }{c}_{2k+Q\downarrow }^{+}{c}_{1-k\downarrow }\right)$

where the first and second terms are intra-band and inter-band Coulomb repulsions, respectively. ${\alpha }_{1,2}^{AFM}$ and ${\alpha }_{12}^{AFM}$ are the parameters of intra and inter-band Coulomb interaction, respectively. We solve a mean-field equation with order parameter in a self-consistent manner, in the AFM state with ordering vector Q, as stated by;

${∆}_{intra-AFM}={\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{11}^{AFM}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{1k+Q\uparrow }〉={\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{22}^{AFM}\left(k,k^{`}\right)〈{c_{2-k\downarrow }c}_{2k+Q\uparrow }〉$

And

${∆}_{inter-AFM}={\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{12}^{AFM}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{2k+Q\uparrow }〉={\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{21}^{AFM}\left(k,k^{`}\right)〈c_{2k+Q\uparrow }{c}_{1-k\downarrow }〉$

where ${∆}_{intra-AFM}$ and ${∆}_{inter-AFM}$ are intra-band and inter-band AFM order parameters, respectively, and take wave vector Q=(π,0). Note that in this calculation the interband AFM order parameter is neglected because very small and insignificant [34, 43].

The two-band model mean field Hamiltonian can be rewritten as;

$H={\displaystyle \sum _{k\sigma }}{\epsilon }_{1k}{c}_{1k\sigma }^{+}{c}_{1k\sigma }-{\overline{∆}}_{1k}{\displaystyle \sum _{k{k}^{\prime }}}{c}_{1k\uparrow }^{+}{c}_{1-k\downarrow }^{+}+{{\displaystyle \sum _{k\sigma }}{\epsilon }_{2k}{c}_{2k\sigma }^{+}{c}_{2k\sigma }}_{-}{\overline{∆}}_{2k}{\displaystyle \sum _{k{k}^{\prime }}}{c}_{2k\uparrow }^{+}{c}_{2-k\downarrow }^{+}-{\overline{∆}}_{Mk}{\displaystyle \sum _{k{k}^{\prime }}}\left(c_{1k+Q\uparrow }^{+}{c}_{1-k\downarrow }^{+}+c_{1-k\downarrow }^{+}{c}_{2k+\mathrm{Q}\uparrow }^{+}\right)+h.c(1)$

Where ${\epsilon }_{1k}$ and ${\epsilon }_{2k}$ are the $\text{quasi}-\text{particle}$ energies for bands 1 and 2, respectively, operators $c_{ik\sigma }^{+}\left(c_{ik\sigma }\right)$ annihilation (creation) or operator for hole and electron bands, respectively, and spin-$\sigma$ electron of momentum- $k$ and band $i=1,2$, summation represents sum over all the -k and $h.c$ is the hopping parameters which are insignificant for this superconducting pairing terms. Within the fermionic basis, there are numerous approaches to decoupling the interacting Hamiltonian, we use mean-field approximation to decouple our assumed interacting orbitals to develop the mean-field Hamiltonian described in Eq. 1 [44], and to define order parameters. The mean field approximation assumes that the average interaction can be approximated by their average values, ignoring the individual fluctuations beyond the mean field, which helps to investigate the stability of superconductivity and magnetism in HTSC specifically in FeBSC, and understand the interplay between these two phenomena. As is typically practiced in mean-field theory, one substitutes a specific operator with its average value multiplied by a small fluctuating term. To provide a concrete example, consider the bilinear term, $c_{ik\uparrow }^{+}{c}_{i-k\downarrow }^{+}{c_{i-k^{`}\downarrow }c}_{i{k}^{`}\uparrow }$ and replaced by ${〈{c_{i-k^{`}\downarrow }c}_{i{k}^{`}\uparrow }〉c^{+}}_{ik\uparrow }{c}_{i-k\downarrow }^{+}$. From Eq. $1,$ the following effective order parameters are obtained. Thus,

${\overline{∆}}_{1k}={∆}_{11}+{∆}_{12}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{11}^{SC}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{1k\uparrow }〉+{\displaystyle \sum _{k{k}^{\prime }}}{V}_{12}^{SC}\left(k,k^{`}\right)〈{c_{2-k\downarrow }c}_{2k\uparrow }〉(2)$

${\overline{∆}}_{2k}={∆}_{22}+{∆}_{21}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{22}^{SC}\left(k,k^{`}\right)〈{c_{2-k\downarrow }c}_{2k\uparrow }〉+{\displaystyle \sum _{k{k}^{\prime }}}{V}_{21}^{SC}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{1k\uparrow }〉(3)$

${\overline{∆}}_{Mk}={\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{11}^{AFM}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{1k+Q\uparrow }〉+{\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{12}^{AFM}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{2k+Q\uparrow }〉(4)$

Where ${\overline{∆}}_{1k}\left({\overline{∆}}_{2k}\right)$ are the effective superconducting order parameters for bands 1 and 2, respectively, with their first and second terms are intra-band and inter-band Coulomb repulsions, respectively and ${\overline{∆}}_{Mk}$ is antiferromagnetic exchange interaction for intra and inter-band pair hopping. In the following calculation we use the terms as; V₁₁^SC = V₁₁, V₁₂^SC = V₁₂, V₂₂^SC = V₂₂, V₂₁^SC = V₂₁, and α₁₁^AFM = α₁₁, α₁₂^AFM = α₁₂. Each band has its proper pairing interaction. $V_{11}$ and $V_{22}$. While pair interchanges between the two bands are assured by $V_{12}$ = $V_{21}$ term.

By introducing the $\tau -$ dependent quantum operators to study the system, we need to transform to the Heisenberg picture [33].

$c_{k\sigma }\left(\tau \right)=e^{\tau H}{c}_{k\sigma }{e}^{-\tau H}(5)$

$c_{k\sigma }^{+}\left(\tau \right)=e^{\tau H}{c}_{k\sigma }^{+}{e}^{-\tau H}(6)$

This satisfies the Heisenberg equation of motion.

$\frac{\partial c_{k\sigma }\left(\tau \right)}{\partial \tau }=\left[H,c_{k\sigma }\left(\tau \right)\right](7)$

$\frac{\partial c_{k\sigma }^{+}\left(\tau \right)}{\partial \tau }=\left[H,c_{k\sigma }^{+}\left(\tau \right)\right](8)$

Inserting Eq. 1 into the right-hand side of the equation Eq. 7 and Eq. 8 we obtain the system of differential equations for the time-dependent quantum operator [45].

$\frac{\partial c_{1k\uparrow }\left(\tau \right)}{\partial \tau }={-\epsilon }_{1k}{c}_{1k\uparrow }+{\overline{∆}}_{1k}{c}_{1-k\downarrow }^{+}(9)$

$\frac{\partial c_{2k\uparrow }\left(\tau \right)}{\partial \tau }={-\epsilon }_{2k}{c}_{2k\uparrow }+{\overline{∆}}_{2k}{c}_{2-k\downarrow }^{+}+{\overline{∆}}_{Mk}{c}_{1-k\downarrow }^{+}(10)$

$\frac{\partial c_{1-k\downarrow }^{+}\left(\tau \right)}{\partial \tau }={\epsilon }_{1k}{c}_{1-k\downarrow }^{+}+{\overline{∆}}_{1k}^{+}{c}_{1k\uparrow }^{+}+{\overline{∆}}_{Mk}^{+}{c}_{2+Qk\uparrow }^{+}(11)$

$\frac{\partial c_{2-k\downarrow }^{+}\left(\tau \right)}{\partial \tau }={\epsilon }_{2k}{c}_{2-k\downarrow }^{+}+{\overline{∆}}_{2k}^{+}{c}_{2k\uparrow }^{+}(12)$

Using Eqs 9–12 can drive a system of differential equations for the thermal, Green function techniques and solution for the equation of motion for both operators. In the state of superconductors, the Nambu-Gorkov formalism characterizes it as a state where symmetry is broken [46, 47]. To grip these equations handily, $\text{Nambu}$ proposed the following a four-component space spanned by the four-component operators;

$a_k\left(\tau \right)=\left(\begin{array}{l}{c}_{1k\uparrow }\left(\tau \right)\\ \begin{array}{c}\begin{array}{c}{c}_{1-k\downarrow }^{+}\left(\tau \right)\\ c_{2k\uparrow }\left(\tau \right)\end{array}\\ c_{2-k\downarrow }^{+}\left(\tau \right)\end{array}\end{array}\right)(13)$

And its corresponding conjugate

$a_k^{+}\left({\tau }^{,}\right)=\left(\begin{array}{cccc}{c}_{1k\uparrow }^{+}\left({\tau }^{,}\right)& c_{1-k\downarrow }\left({\tau }^{,}\right)& c_{2k\uparrow }^{+}\left({\tau }^{,}\right)& c_{2-k\downarrow }\left({\tau }^{,}\right)\end{array}\right)(14)$

Where $a_k\left(\tau \right)and{a^{+}}_k\left({\tau }^{,}\right)$ are nowadays commonly called $\text{Nambu}-\text{Gorkov}$ operators.

2.1 Green’s functions

From the $\text{Nambu}-\text{Gorkov}$ operators, we define the single particle $4\times 4$ matrix of Green’s functions in $\text{Nambu}$ space.

$G_{TS}\left(k,\tau -{\tau }^{,}\right)=-〈\mathbb{T}{a_k\left(\tau \right)a}_k^{+}\left({\tau }^{,}\right)〉(15)$

Where $\mathbb{T}$ is the time ordering operator and the subscript $TS$ shows the elements of the 4 × 4 matrices by substituting $\text{Nambu}$ operators the explicit yields,

$G_{TS}\left(k,\tau -{\tau }^{,}\right)=-\left(\begin{array}{cccc}〈\mathbb{T}{c_{1k\uparrow }\left(\tau \right)c}_{1k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{1k\uparrow }\left(\tau \right)c_{1-k\downarrow }\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{1k\uparrow }\left(\tau \right)c_{2k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{1k\uparrow }\left(\tau \right)c_{2-k\downarrow }\left({\tau }^{,}\right)〉\\ 〈\mathbb{T}{c_{1-k\downarrow }^{+}\left(\tau \right)c}_{1k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{1-k\downarrow }^{+}\left(\tau \right)c_{1-k\downarrow }\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{1-k\downarrow }^{+}\left(\tau \right)c_{2k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{1-k\downarrow }^{+}\left(\tau \right)c_{2-k\downarrow }\left({\tau }^{,}\right)〉\\ 〈\mathbb{T}{c_{2k\uparrow }\left(\tau \right)c}_{1k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{2k\uparrow }\left(\tau \right)c_{1-k\downarrow }\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{2k\uparrow }\left(\tau \right)c_{2k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{2k\uparrow }\left(\tau \right)c_{2-k\downarrow }\left({\tau }^{,}\right)〉\\ 〈\mathbb{T}{c_{2-k\downarrow }^{+}\left(\tau \right)c}_{1k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{2-k\downarrow }^{+}\left(\tau \right)c_{1-k\downarrow }\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{2-k\downarrow }^{+}\left(\tau \right)c_{2k\uparrow }^{+}\left({\tau }^{,}\right)〉& 〈\mathbb{T}{c}_{2-k\downarrow }^{+}\left(\tau \right)c_{2-k\downarrow }\left({\tau }^{,}\right)〉\end{array}\right)(16)$

To study the physical properties, we must define the following thermal Green’s functions;

$G_{ij}\left(k,\tau -{\tau }^{,}\right)=-〈\mathbb{T}{c_{ik\uparrow }\left(\tau \right)c}_{jk\uparrow }^{+}\left({\tau }^{,}\right)〉(17)$

$F_{ij}\left(k,\tau -{\tau }^{,}\right)=-〈\mathbb{T}{c}_{ik\uparrow }\left(\tau \right)c_{j-k\downarrow }\left({\tau }^{,}\right)〉(18)$

$F_{ij}^{+}\left(k,\tau -{\tau }^{,}\right)=-〈\mathbb{T}{c_{i-k\downarrow }^{+}\left(\tau \right)c}_{jk\uparrow }^{+}\left({\tau }^{,}\right)〉(19)$

And

$G_{ij}^T\left(k,\tau -{\tau }^{,}\right)=-〈\mathbb{T}{c}_{i-k\downarrow }^{+}\left(\tau \right)c_{j-k\downarrow }\left({\tau }^{,}\right)〉(20)$

The correlation functions $G_{ij}\left(k,\tau -{\tau }^{,}\right)$ and $F_{ij}\left(k,\tau -{\tau }^{,}\right)$ are the normal and anomalous one-particle Green functions, which are elements of the Green function matrix $G_{TS}$. $i,j$ indicates the band index 1 or 2. $F_{ij}^{+}\left(k,\tau -{\tau }^{,}\right)$ implies the complex conjugate of $F_{ij}$. We will often suppress the spin index. The anomalous green functions, $F_{ij}^{+}\left(k,\tau -{\tau }^{,}\right)$, and $G_{ij}^T\left(k,\tau -{\tau }^{,}\right)$ assumed that singlet pairing. As the creation and annihilation operators of electrons are fermionic, and with these specifications, the Green function matrix $G_{TS}\left(k,\tau -{\tau }^{,}\right)$ can be written in a more compact form;

${\mathrm{G}}_{\text{TS}}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)=-\left(\begin{array}{cccc}{\mathrm{G}}_{11}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{F}}_{11}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{G}}_{12}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{F}}_{12}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)\\ {\mathrm{F}}_{11}^{+}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{G}}_{11}^{\mathrm{T}}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{F}}_{21}^{+}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{G}}_{12}^{\mathrm{T}}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)\\ {\mathrm{G}}_{21}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{F}}_{21}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{G}}_{22}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{F}}_{22}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)\\ {\mathrm{F}}_{12}^{+}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{G}}_{21}^{\mathrm{T}}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{F}}_{22}^{+}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)& {\mathrm{G}}_{22}^{\mathrm{T}}\left(\mathrm{k},\mathrm{\tau }-{\mathrm{\tau }}^{,}\right)\end{array}\right)(21)$

Where $T,s$ = 1,2,3,4, and $G_{11}\left(k,\tau -{\tau }^{,}\right)$, $G_{22}\left(k,\tau -{\tau }^{,}\right)$ are the intraband Green’s functions for electrons of up spin, $G_{11}^T\left(k,\tau -{\tau }^{,}\right)$, $G_{22}^T\left(k,\tau -{\tau }^{,}\right)$, are the $\text{intraband}$ Green’s functions for holes with spin down while $G_{12}\left(k,\tau -{\tau }^{,}\right),$ $G_{21}\left(k,\tau -{\tau }^{,}\right)$, are interpreted to be $\text{interband}$ Green’s functions for electrons of up spin and $G_{12}^T\left(k,\tau -{\tau }^{,}\right),G_{21}^T\left(k,\tau -{\tau }^{,}\right)$ are taken to be $\text{interband}$ Green’s functions for holes with spin down. $F_{11}\left(k,\tau -{\tau }^{,}\right)$, $F_{22}\left(k,\tau -{\tau }^{,}\right)$ are the anomalous $\text{intraband}$ Green’s functions while $F_{12}\left(k,\tau -{\tau }^{,}\right)$, $F_{21}\left(k,\tau -{\tau }^{,}\right)$ represent the interband anomalous thermal Green. s functions involving electrons in different bands and $F_{11}^{+}\left(k,\tau -{\tau }^{,}\right),$ $F_{22}^{+}\left(k,\tau -{\tau }^{,}\right)$, are the complex conjugate of the anomalous $\text{intraband}$ thermal Green’s function, while $F_{12}^{+}\left(k,\tau -{\tau }^{,}\right),F_{21}^{+}\left(k,\tau -{\tau }^{,}\right)$ are the complex conjugate of the anomalous $\text{interband}$ thermal Green’s function.

In the four-component language, the sixteen equations of motion for the propagators lead to the energy matrix equation.

$K_O\left(\tau \right)G_{TS}\left(k,\tau -{\tau }^{,}\right)={\delta }_O\left(\tau -{\tau }^{,}\right)(22)$

Where the operator $K_O\left(\tau \right)$ is $4x4$ energy matrix and ${\delta }_O\left(\tau -{\tau }^{,}\right)$ is $4x4$ unit matrix given by

$K_O\left(\tau \right)=\left(\begin{array}{cccc}\left(-\frac{\partial }{\partial \tau }-{\epsilon }_{1k}\right)& {\overline{∆}}_{1k}& 0& 0\\ {\overline{∆}}_{1k}^{+}& \left(-\frac{\partial }{\partial \tau }+{\epsilon }_{1k}\right)& {\overline{∆}}_{Mk}^{+}& 0\\ 0& {\overline{∆}}_{Mk}& \left(-\frac{\partial }{\partial \tau }-{\epsilon }_{2k}\right)& {\overline{∆}}_{2k}\\ 0& 0& {\overline{∆}}_{2k}^{+}& \left(-\frac{\partial }{\partial \tau }+{\epsilon }_{2k}\right)\end{array}\right)(23)$

And

${\delta }_O\left(\tau \right)=\left(\begin{array}{cccc}{\delta }_O\left(\tau -{\tau }^{,}\right)& 0& 0& 0\\ 0& {\delta }_O\left(\tau -{\tau }^{,}\right)& 0& 0\\ 0& 0& {\delta }_O\left(\tau -{\tau }^{,}\right)& 0\\ 0& 0& 0& {\delta }_O\left(\tau -{\tau }^{,}\right)\end{array}\right)(24)$

Eq. 22 is obtained from the results of Eqs. 9–12 by differentiating $\tau -$ order products. We use the common way of Fourier transforming the correlation function, transitioning it from k-space to momentum space according to its established definition [48];

$G_{ij}\left(k,\tau -{\tau }^{,}\right)=\frac{1}{\beta }{\displaystyle \sum _{{\omega }_n}}{{е}^{{-i\omega }_n\tau }G}_{ij}\left({p,i\omega }_n\right),G_{ij}\left({p,i\omega }_n\right)={\displaystyle \underset{0}{\overset{\beta }{\int }}}d\tau {е}^{{i\omega }_n\tau }{G}_{ij}\left(k,\tau -{\tau }^{,}\right)(25)$

$F_{ij}\left(k,\tau -{\tau }^{,}\right)=\frac{1}{\beta }{\displaystyle \sum _{{\omega }_n}}{{е}^{{-i\omega }_n\tau }F}_{ij}\left({p,i\omega }_n\right),F_{ij}\left({p,i\omega }_n\right)={\displaystyle \underset{0}{\overset{\beta }{\int }}}d\tau {е}^{{i\omega }_n\tau }{F}_{ij}\left(k,\tau -{\tau }^{,}\right)(26)$

and

$G_{ij}^T\left(k,\tau -{\tau }^{,}\right)=\frac{1}{\beta }{\displaystyle \sum _{{\omega }_n}}{{е}^{{-i\omega }_n\tau }{G}^T}_{ij}\left({p,i\omega }_n\right),G_{ij}^T\left({p,i\omega }_n\right)={\displaystyle \underset{0}{\overset{\beta }{\int }}}d\tau {е}^{{i\omega }_n\tau }{G}_{ij}^T\left(k,\tau -{\tau }^{,}\right)(27)$

where ${\omega }_n=\left(2n+1\right)\pi /\beta$, is Matsubara frequencies, $\beta =\frac{1}{K_{B}T}$ with $K_B$ as the Boltzmann constant, $T$ is the temperature, summation represent sum over all the ${\omega }_n$, and $i,j$ show the band index. These transformations to momentum-dependent make the mathematics easily manageable. After performing the Fourier transformations of the correlation function and for the $\tau ={\tau }^{,}$, the matrix product in Eq. 22 becomes;

$\left(\begin{array}{cccc}\left({i\omega }_n-{\epsilon }_{1k}\right)& {\overline{∆}}_{1k}& 0& 0\\ {\overline{∆}}_{1k}^{+}& \left({i\omega }_n+{\epsilon }_{1k}\right)& {\overline{∆}}_{Mk}^{+}& 0\\ 0& {\overline{∆}}_{Mk}& \left({i\omega }_n-{\epsilon }_{2k}\right)& {\overline{∆}}_{2k}\\ 0& 0& {\overline{∆}}_{2k}^{+}& \left({i\omega }_n+{\epsilon }_{2k}\right)\end{array}\right)\times \left(\begin{array}{cccc}{G}_{11}\left({p,i\omega }_n\right)& F_{11}\left({p,i\omega }_n\right)& G_{12}\left({p,i\omega }_n\right)& F_{12}\left({p,i\omega }_n\right)\\ F_{11}^{+}\left({p,i\omega }_n\right)& G_{11}^T\left({p,i\omega }_n\right)& F_{21}^{+}\left({p,i\omega }_n\right)& G_{12}^T\left({p,i\omega }_n\right)\\ G_{21}\left({p,i\omega }_n\right)& F_{21}\left({p,i\omega }_n\right)& G_{22}\left({p,i\omega }_n\right)& F_{22}\left({p,i\omega }_n\right)\\ F_{12}^{+}\left({p,i\omega }_n\right)& G_{21}^T\left({p,i\omega }_n\right)& F_{22}^{+}\left({p,i\omega }_n\right)& G_{22}^T\left({p,i\omega }_n\right)\end{array}\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)(28)$

From the matrix Eq. 28, we obtain the inverse of the Fourier transformed 4 × 4 Green’s function matrix in momentum space as

$G_{T,S}^{-1}\left({p,i\omega }_n\right)=\left(\begin{array}{cccc}\left({i\omega }_n-{\epsilon }_{1k}\right)& {\overline{∆}}_{1k}& 0& 0\\ {\overline{∆}}_{1k}^{+}& \left({i\omega }_n+{\epsilon }_{1k}\right)& {\overline{∆}}_{Mk}^{+}& 0\\ 0& {\overline{∆}}_{Mk}& \left({i\omega }_n-{\epsilon }_{2k}\right)& {\overline{∆}}_{2k}\\ 0& 0& {\overline{∆}}_{2k}^{+}& \left({i\omega }_n+{\epsilon }_{2k}\right)\end{array}\right)(29)$

and gives the components of the inverse Green function for ${\overline{∆}}_{Mk}=M$ where magnetic order parameter and suppressing $k$. To study the order parameters, therefore the equation of motions is;

$F_{11}\left({p,i\omega }_n\right)=〈{c_{1-k\downarrow }c}_{1k\uparrow }〉=\frac{1}{D\left({\omega }_n\right)}\left({\overline{∆}}_1\left({{\omega }_n}^2+{{\epsilon }_2}^2+{{\overline{∆}}_2}^2\right)+M^2{\overline{∆}}_2\right)(30)$

$F_{12}\left({p,i\omega }_n\right)=〈{c_{1-k\downarrow }c}_{2k+Q\uparrow }〉=-\frac{1}{D\left({\omega }_n\right)}\left(M\left(E\left(K\right)-{\epsilon }_2\right)\left({i\omega }_n+{\epsilon }_1\right)+{\overline{∆}}_1{\overline{∆}}_{2}M-M^3\right)(31)$

And

$F_{22}\left({p,i\omega }_n\right)=〈{c_{2-k\downarrow }c}_{2k\uparrow }〉=\frac{1}{D\left({\omega }_n\right)}\left({\overline{∆}}_2\left({{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)-M^2{\overline{∆}}_1\right)(32)$

$F_{21}\left({p,i\omega }_n\right)=〈{c_{2-k\downarrow }c}_{1k\uparrow }〉=-\frac{1}{D\left({\omega }_n\right)}\left(M\left(E\left(K\right)-{\epsilon }_1\right)\left({i\omega }_n+{\epsilon }_2\right)+{\overline{∆}}_1{\overline{∆}}_{2}M-M^3\right)(33)$

$D\left({\omega }_n\right)=\left({{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)\left({{\omega }_n}^2+{{\epsilon }_2}^2+{{\overline{∆}}_2}^2\right)+2M^2{{\omega }_n}^2+2M^2{\epsilon }_1{\epsilon }_2+M^4-2M^2{\overline{∆}}_1{\overline{∆}}_2(34)$

The spectrum of the excitation energies of the $\text{quasi}-\text{particles}$ in a superconductor is given by the poles of both the normal and anomalous thermal Green’s functions $G_{ij}\left({p,i\omega }_n\right)$ and $F_{ij}\left({p,i\omega }_n\right)$ at $T=0$. These poles are the denominators that vanish. $E\left(k\right)$ is the $\text{quasi}-\text{particle}$ excitation energy given as in Eq. 35. For the generalized two-band model the $E\left(k\right)$ , which does not include the hopping parameters can be [49]; .

$E\left(K\right)=\pm {[\frac{1}{2}\left\{\left({{\epsilon }_1}^2+{{\epsilon }_2}^2+{{\overline{∆}}_1}^2+{{\overline{∆}}_2}^2+2M^2\right)\pm {\left[{\left({{\epsilon }_1}^2+{{\overline{∆}}_1}^2-{{\epsilon }_2}^2-{{\overline{∆}}_2}^2\right)}^2+4M^2\left\{{\left({{\epsilon }_1}^2-{{\epsilon }_2}^2\right)}^2+{\left({\overline{∆}}_1+{\overline{∆}}_2\right)}^2\right\}\right]}^{\frac{1}{2}}\right\}]}^{\frac{1}{2}}(35)$

It is of interest to also evaluate the parameters ${\overline{∆}}_1,{\overline{∆}}_2,$ and ${\overline{∆}}_M$ for the case two-band model. They are related to the anomalous Green’s functions by self-consistency conditions Eqs 2–4.

${\overline{∆}}_{1k}={∆}_{11}+{∆}_{12}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{11}\left(k,k^{`}\right)F_{11}\left({p,i\omega }_n\right)+{\displaystyle \sum _{k{k}^{\prime }}}{V}_{12}\left(k,k^{`}\right)F_{22}\left({p,i\omega }_n\right)(36)$

${\overline{∆}}_{2k}={∆}_{22}+{∆}_{21}={\displaystyle \sum _{k{k}^{\prime }}}{V}_{22}\left(k,k^{`}\right)F_{22}\left({p,i\omega }_n\right)+{\displaystyle \sum _{k{k}^{\prime }}}{V}_{21}\left(k,k^{`}\right)F_{11}\left({p,i\omega }_n\right)(37)$

${\overline{∆}}_{Mk}=M={\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{11}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{1k+Q\uparrow }〉+{\displaystyle \sum _{k{k}^{\prime }}}{\alpha }_{12}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{2k+Q\uparrow }〉(38)$

2.2 Physical properties

2.2.1 Superconductor order parameter

The gap parameter $\overline{∆}$ is a superconducting order parameter, which can be determined self-consistently from the gap equations Eq 36 and Eq 37. In matrix form, the order parameter for the superconducting state is given by;

${\overline{∆}}_i={\sum }_j{V}_{ij}{F}_{ij}\left({p,i\omega }_n\right){\overline{∆}}_j(39)$

Where $\left|V_{ij}\right|$ is the pairing interaction constants and functions $F_{ij}\left({p,i\omega }_n\right)$ is anomalous green functions in a superconducting state are defined as above and $D\left({\omega }_n\right)=\left({{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)\left({{\omega }_n}^2+{{\epsilon }_2}^2+{{\overline{∆}}_2}^2\right)$, ${\omega }_n=\left(2n+1\right)\pi /\beta$ and ${{\epsilon }_1}^2+{{\overline{∆}}_1}^2=E_1^2$ and ${{\epsilon }_2}^2+{{\overline{∆}}_2}^2=E_2^2$ energy excitation for the band 1 and 2. Upon substitution, the equation of motion becomes

$〈{c_{1-k\downarrow }c}_{1k\uparrow }〉=\frac{\left({{\omega }_n}^2+E_2^2\right)}{\left({{\omega }_n}^2+E_1^2\right)\left({{\omega }_n}^2+E_2^2\right)}(40)$

$〈{c_{2-k\downarrow }c}_{2k\uparrow }〉=\frac{\left({{\omega }_n}^2+E_1^2\right)}{\left({{\omega }_n}^2+E_1^2\right)\left({{\omega }_n}^2+E_2^2\right)}(41)$

Let ${\displaystyle \sum _{k,n}}(\frac{1}{{\left(2n+1\right)}^2{\pi }^2+x^2})=\frac{\tanh \frac{x}{2}}{2x}$ where $x={\beta E}_1$, by substituting the result

$F_{11}\left({p,i\omega }_n\right)=\frac{{\beta }^2\tanh \frac{{\beta E}_1}{2}}{2{\beta E}_1}(42)$

And

$F_{22}\left({p,i\omega }_n\right)=\frac{{\beta }^2\tanh \frac{{\beta E}_2}{2}}{2{\beta E}_2}(43)$

By substituting these two equations, Eq. 42 and Eq. 43 in Eq. 36 and Eq. 37, respectively, the two gape equations in the superconducting state become;

${\overline{∆}}_1={∆}_{11}+{∆}_{12}=\frac{1}{\beta }{\sum }_k{V}_{11}\frac{{\beta }^2\tanh \frac{{\beta E}_1}{2}}{2{\beta E}_1}{\overline{∆}}_1+\frac{1}{\beta }{\sum }_k{V}_{12}\frac{{\beta }^2\tanh \frac{{\beta E}_2}{2}}{2{\beta E}_2}{\overline{∆}}_2(44)$

${\overline{∆}}_2={∆}_{22}+{∆}_{21}=\frac{1}{\beta }{\sum }_k{V}_{22}\frac{{\beta }^2\tanh \frac{{\beta E}_2}{2}}{2{\beta E}_2}{\overline{∆}}_2+\frac{1}{\beta }{\sum }_k{V}_{21}\frac{{\beta }^2\tanh \frac{{\beta E}_1}{2}}{2{\beta E}_1}{\overline{∆}}_1(45)$

Where $V_{11}$ and $V_{22}$ are pairing interactions for 1 and 2 bands, respectively, while the pair interchange between the two bands is assured by the $V_{12}$ term. The quantity $V_{12}$ has been supposed to be operative and constant in the energy interval for the higher band and the lower band, keeping in mind the integration range, the gap order parameter satisfies the system. If the intraband interactions are missing, i.e., $V_{11}=V_{22}=0$, the interband interaction solely induces the transition is $V_{12}=V_{21}.$ Therefore, Eq. 44 and Eq. 45 Become

${\overline{∆}}_1={∆}_{12}={\sum }_k{V}_{12}\frac{\tanh \frac{{\beta E}_2}{2}}{2E_2}{\overline{∆}}_2(46)$

${\overline{∆}}_2={∆}_{21}={\sum }_k{V}_{21}\frac{\tanh \frac{{\beta E}_1}{2}}{2E_1}{\overline{∆}}_1(47)$

Converting the summation over $k$ values into an integral with the cut-off energy from $\pm ћ{\omega }_D$, ${\omega }_D$ the boson cut-off frequency measured from the Fermi level and introducing the density of state at the Fermi level $N_1\left(0\right)$ and $N_2\left(0\right)$, and by applying identity ${\sum }_1=2N_1\left(0\right)\int$ and ${\sum }_2=2N_2\left(0\right)\int$, then Eq. 46 and Eq. 47 become;

${\overline{∆}}_1={∆}_{12}=2N_1\left(0\right)V_{12}{\int }_{-ћ{\omega }_D}^{ћ{\omega }_D}{\overline{∆}}_2\frac{\tanh \frac{{\beta E}_2}{2}}{2E_2}d{ϵ}_2(48)$

${\overline{∆}}_2={∆}_{21}=2N_2\left(0\right)V_{21}{\int }_{-ћ{\omega }_D}^{ћ{\omega }_D}{\overline{∆}}_1\frac{\tanh \frac{{\beta E}_1}{2}}{2E_1}d{ϵ}_1(49)$

Now, let’s study these two equations by considering different cases.

Case 1; When $T\to 0\beta \to \infty$ which implies, $\tanh {\beta E}_2/2\to 1\text{and}\tanh {\beta E}_1/2\to 1$, then integral becomes

${\overline{∆}}_1={∆}_{12}=N_1\left(0\right)V_{12}{\int }_0^{ћ{\omega }_D}\frac{{\overline{∆}}_2}{{\left({{\epsilon }_2}^2+{{\overline{∆}}_2}^2\right)}^{\frac{1}{2}}}d{\epsilon }_2(50)$

${\overline{∆}}_2={∆}_{21}=N_2\left(0\right)V_{21}{\int }_0^{ћ{\omega }_D}\frac{{\overline{∆}}_1}{{\left({{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)}^{\frac{1}{2}}}d{\epsilon }_1(51)$

Equation 50 and Eq. 51 can be

${\overline{∆}}_1={∆}_{12}=N_1\left(0\right)V_{12}{\overline{∆}}_2\ln \frac{2ћ{\omega }_D}{{\overline{∆}}_2}(52)$

${\overline{∆}}_2={∆}_{21}=N_2\left(0\right)V_{21}{\overline{∆}}_1\ln \frac{2ћ{\omega }_D}{{\overline{∆}}_1}(53)$

Now substitution Eq. 53 into Eq. 52

${\overline{∆}}_1={∆}_{12}={\mathrm{N}}_1\left(0\right){\mathrm{V}}_{12}{\mathrm{N}}_2\left(0\right){\mathrm{V}}_{21}{\overline{∆}}_1\ln \frac{2\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}{{\overline{∆}}_1}\ln \frac{2\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}{{\overline{∆}}_2}(54)$

For the integral ${\int }_0^{\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}\frac{1}{{\left({{\mathrm{\epsilon }}_1}^2+{{\overline{∆}}_1}^2\right)}^{\frac{1}{2}}}\mathrm{d}{\mathrm{\epsilon }}_1=\ln \frac{2\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}{{\overline{∆}}_1}$ and ${\int }_0^{\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}\frac{1}{{\left({{\mathrm{\epsilon }}_2}^2+{{\overline{∆}}_2}^2\right)}^{\frac{1}{2}}}\mathrm{d}{\mathrm{\epsilon }}_2=\ln \frac{2\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}{{\overline{∆}}_2}$ ,

If $V_{12}=V_{21}⟹{\overline{∆}}_1={∆}_{12}={∆}_{21}={\overline{∆}}_2=\overline{∆}$. From this, Eq. 54 becomes,

$\overline{∆}={\mathrm{N}}_1\left(0\right){\mathrm{N}}_2\left(0\right){{\mathrm{V}}_{21}}^2\overline{∆}{\left(\ln \frac{2\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}{\overline{∆}}\right)}^2(55)$

By rearranging, $1/V_{21}\sqrt{N_1\left(0\right)N_2\left(0\right)}=\left(\ln 2ћ{\omega }_D/\overline{∆}\right)$ taking the exponent

$\overline{∆}=2ћ{\omega }_D\mathit{exp}\left[-\frac{1}{\left|V_{12}\sqrt{N_1\left(0\right)N_2\left(0\right)}\right|}\right](56)$

From the BCS theory we have,

$3.5K_B{T}_C=2\overline{∆}$

Therefore, Eq. 56 for the $\text{interband}$ coupling constant of ${\lambda }_{12}=\left|V_{12}\sqrt{N_1\left(0\right)N_2\left(0\right)}\right|$ becomes;

$K_B{T}_C=1.14ћ{\omega }_D\mathit{exp}\left[-\frac{1}{{\lambda }_{12}}\right](57)$

This expression for the superconducting transition temperature $\left(Tc\right)$ is like the well-known BCS [7].

Case 2: To obtain a temperature-dependent superconductivity energy gap, we use the expression from Eq. 48 at $T=T_c$ and $\overline{∆}=0$ it gives

$\frac{1}{\left|V_{12}\sqrt{N_1\left(0\right)N_2\left(0\right)}\right|}=\frac{1}{{\lambda }_{12}}={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{\sqrt{\left({\epsilon }^2+{\overline{∆}}^2\right)}}\tanh \frac{\beta \sqrt{\left({\epsilon }^2+{\overline{∆}}^2\right)}}{2}dϵ(58)$

By using the same techniques as above, this equation becomes

$\frac{1}{{\lambda }_{12}}=\ln 1.14\frac{\mathrm{ћ}{\omega }_D}{K_{B}T}-{\left(\frac{\overline{∆}}{\pi K_{B}T}\right)}^{2}1.05(59)$

From Eq. 57

$\frac{1}{{\lambda }_{12}}=\ln 1.14\frac{\mathrm{ћ}{\omega }_D}{K_B{T}_c}(60)$

By substituting Eq. 60 into Eq. 59 and by rearranging

$\ln \left(\frac{\mathrm{T}}{T_c}\right)=-{\left(\frac{\overline{∆}}{\pi K_{B}T}\right)}^{2}1.05(61)$

Using the relation $\ln \left(1-\mathrm{x}\right)=1-\mathrm{x}-{\left(\frac{\mathrm{x}}{2}\right)}^2+---$

$\overline{∆}\left(\mathrm{T}\right)=3.06K_B{T}_c{\left(1-\frac{\mathrm{T}}{T_c}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}(62)$

Equation 62 demonstrates how the superconducting order parameter $\left(\overline{∆}\left(\mathrm{T}\right)\right)$ varies with temperature when the magnetic order parameter is zero and is analogous to the BCS model. From Eq. 62 at T = 0, the superconducting order parameter $\overline{∆}\left(0\right)=3.06K_B{T}_c$ using the experimental values $T_c=20K$ for ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ FeSC [30], the superconducting order parameter is $\overline{∆}\left(0\right)=3.02\text{mev}$.

2.2.2 The effect of magnetism on the transition temperature (T_c)

From Eq. 36 and Eq. 37, the interchange interaction between the two bands in the two-band model is assured by $V_{12}$ term. The interband interaction can induce the transition temperature ($T_C$) in both antiferromagnetism and superconducting states. Kristoffele et al. [43] have shown that interband pairing is very efficient in enhancing $T_C$. This is the characteristic feature of the band model. Therefore, the band equations can be

${\overline{∆}}_1={∆}_{12}={\displaystyle \sum _{k{k}^{`}}}{V}_{12}(k,k^{`})F_{22}\left({p,i\omega }_n\right)(63)$

${\overline{∆}}_2={∆}_{21}={\displaystyle \sum _{k{k}^{`}}}{V}_{21}(k,k^{`})F_{11}\left({p,i\omega }_n\right)(64)$

From this, to study the band gap, one can write these two equations in simultaneous equations as

${\overline{∆}}_1+{\overline{∆}}_2={∆}_{12}+{∆}_{21}=2\overline{∆}=V_{12}\left({\displaystyle \sum _k}{F}_{22}\left({p,i\omega }_n\right)+{\displaystyle \sum _k}{F}_{11}\left({p,i\omega }_n\right)\right)(65)$

Where ${∆}_{12}={∆}_{21}$, ${∆}_{12}+{∆}_{21}=2\overline{∆}$ for $V_{12}=V_{21}$, using the two Green’s functions from equations Eq. 30–32 $\text{and\hspace{0.17em}with\hspace{0.17em}energy\hspace{0.17em}in}$ Eq. 34 after some mathematical steps, By applying the identity ${\sum }_1=2N_1\left(0\right)\int$ and ${\sum }_2=2N_2\left(0\right)\int$ and simplify Eq. 65 gives;

$\frac{1}{{\lambda }_{12}^{\prime }}={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{\sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}\tanh \frac{\beta \sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}{2}dϵ-{\int }_0^{\mathrm{ћ}{\omega }_D}\frac{M}{\overline{∆}\sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}\tanh \frac{\beta \sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}{2}dϵ(66)$

Where ${\lambda }_{12}^{\prime }=V_{12}\left(N_1+N_2\right)couplingconstant$.

At $T=T_C,\overline{∆}=0$ using Laplace’s Transform, ${\omega \to \omega }_n$ Matsubara frequency and proceeding through all the necessary steps, the first integral of Eq. 66 becomes

$I_1={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{\sqrt{\left({ϵ}^2+M^2\right)}}\tanh \frac{\beta \sqrt{\left({ϵ}^2+M^2\right)}}{2}dϵ={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{2}{\beta }{\displaystyle \sum _{n=-\infty }^{\infty }}\frac{1}{{{\omega }_n}^2+{ϵ}^2+M^2}dϵ(67)$

Where ${\left(2n+1\right)}^2{\pi }^2/{\beta }^2={{\omega }_n}^2$, the Matsubara frequency Eq. 67 becomes

${\mathrm{I}}_1={\int }_0^{\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}\frac{2}{\mathrm{\beta }}{\displaystyle \sum _{\mathrm{n}=-\infty }^{\infty }}\frac{1}{{{\left(2\mathrm{n}+1\right)}^2\frac{\mathrm{\pi }}{{\mathrm{\beta }}^2}}^2+{ϵ}^2+{\mathrm{M}}^2}\mathrm{d}ϵ={\int }_0^{\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}\frac{1}{ϵ}\tan \mathrm{h}\frac{\mathrm{\beta }ϵ}{2}\mathrm{d}ϵ-{\int }_0^{\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}{\mathrm{M}}^2\frac{4}{\mathrm{\beta }}{\displaystyle \sum _{\mathrm{n}=0}^{\infty }}\frac{1}{{{\mathrm{a}}^4\left(1+{\mathrm{x}}^2\right)}^2}\mathrm{d}ϵ$

${\mathrm{I}}_1=\ln 1.14\frac{\mathrm{ћ}{\mathrm{\omega }}_{\mathrm{D}}}{{\mathrm{K}}_{\mathrm{B}}{\mathrm{T}}_{\mathrm{C}}}-{\left(\frac{\mathrm{M}}{\mathrm{\pi }{\mathrm{K}}_{\mathrm{B}}{\mathrm{T}}_{\mathrm{C}}}\right)}^{2}1.05(68)$

The second integral in Eq. 66, $I_2$ also can be evaluated as

$I_2=-{\int }_0^{\mathrm{ћ}{\omega }_D}\frac{M}{\overline{∆}\sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}\tanh \frac{\beta \sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}{2}dϵ(69)$

Applying the L’ HOPITAL rule for the $\overline{∆}\to 0$ Eq. 69 can be written as

$I_2=-{\int }_0^{\mathrm{ћ}{\omega }_D}\underset{\overline{∆}\to 0}{\mathrm{Lim}}\left(\frac{M}{\overline{∆}\sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}\tanh \frac{\beta \sqrt{\left({ϵ}^2+{\left(\overline{∆}-M\right)}^2\right)}}{2}\right)dϵ(70)$

This equation also gives the limit.

$I_2=-\frac{M\beta }{2}{\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{\sqrt{\left({ϵ}^2+{\left(M\right)}^2\right)}}{\mathrm{sech}}^2\frac{\beta \sqrt{\left({ϵ}^2+{\left(M\right)}^2\right)}}{2}dϵ(71)$

Using ${\mathrm{sech}}^{2}x=1-{\tanh }^{2}x$

${\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{\sqrt{\left({ϵ}^2+{\left(M\right)}^2\right)}}dϵ-{\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{\sqrt{\left({ϵ}^2+{\left(M\right)}^2\right)}}{\tanh }^2\frac{\beta \sqrt{\left({ϵ}^2+{\left(M\right)}^2\right)}}{2}dϵ(72)$

By applying part techniques of integration and using Laplace’s transformation, the Matsubara frequency Eq. 72 gives

$\frac{1}{2}\ln \frac{\mathrm{M}+\mathrm{ћ}{\omega }_D}{\mathrm{M}-\mathrm{ћ}{\omega }_D}(73)$

Substituting this result in Eq. 71 and then Eq. 66 for the value of the two integration results (${\mathrm{I}}_1\text{and}{\mathrm{I}}_2$) become

$\frac{1}{{\lambda }_{12}^{\prime }}=\ln 1.14\frac{\mathrm{ћ}{\omega }_D}{K_B{T}_C}-{\left(\frac{M}{\pi K_B{T}_C}\right)}^{2}1.05-\frac{M\mathrm{\beta }}{4}\ln \frac{\mathrm{M}+\mathrm{ћ}{\omega }_D}{\mathrm{M}-\mathrm{ћ}{\omega }_D}(74)$

Neglecting the $M^2$ from the expression because it is very small, the transition temperature $T_C$ is

$T_C=1.14\frac{\mathrm{ћ}{\omega }_D}{K_B}{e}^{-\left[\frac{1}{{\lambda }_{12}^{\prime }}+aM\right]}(75)$

Where $a=\mathrm{\beta }/4\ln \left(\mathrm{M}+\mathrm{ћ}{\omega }_D/\mathrm{M}-\mathrm{ћ}{\omega }_D\right)$

2.2.3 Antiferromagnetic transition temperature

We solve a mean-field equation self-consistently with an order parameter in the $\text{antiferromagnetism}$ (AFM) state with ordering vector $\left(\mathrm{Q}\right)$, as defined above in Eq. 38 with M as the antiferromagnetic order parameter, ${\alpha }_{11,}\text{\hspace{0.17em}and}$ ${\alpha }_{12}\left(k,\stackrel{`}{k}\right)$ intraband and interband coupling constant of the antiferromagnetic order parameter, respectively, and in the first Brillouin zone of the paramagnetic phase, we take the order vector $\mathrm{Q}=\left(\mathrm{\pi },0\right)$. Note that to study Co-occurrence, we neglect the inter-orbital order parameter ${\displaystyle \sum _{k{k}^{`}}}{\alpha }_{12}\left(k,k^{`}\right)〈{c_{1-k\downarrow }c}_{2k+Q\uparrow }〉\left(1\ne 2\right)$. Because these values are almost zero for the present orbital models [34]. The anomalous green’s function for the mean-field equation of the intraband pairing interaction from the inverse matrices;

$〈{c_{1-k\downarrow }c}_{1k+Q\uparrow }〉=\frac{1}{\beta }{\displaystyle \sum _{{\omega }_n}}{{\mathrm{е}}^{{-i\omega }_n\tau }F}_{ij}\left({p,i\omega }_n\right)(76)$

The green function for the antiferromagnetic order parameter

$F_{11}\left({p,i\omega }_n\right)=〈{c_{1-k\downarrow }c}_{1k+Q\uparrow }〉=\frac{1}{D\left({\omega }_n\right)}\left({\overline{∆}}_1\left({{\omega }_n}^2+{{\epsilon }_2}^2+{{\overline{∆}}_2}^2\right)\right)(77)$

Where $D\left({\omega }_n\right)=\left({{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)\left({{\omega }_n}^2+{{\epsilon }_2}^2+{{\overline{∆}}_2}^2\right).$ Substituting Green’s function in the mean-field equation, the antiferromagnetic order parameter as a function of the superconducting order parameter becomes;

$M={\displaystyle \sum _{kk`}}{\alpha }_{11}(k,k^{`})〈{c_{1-k\downarrow }c}_{1k+Q\uparrow }〉=\frac{{\alpha }_{11}(k,k^{`})}{\beta }{\displaystyle \sum _{{\omega }_n}}\frac{{\overline{∆}}_1}{\left({{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)}(78)$

Changing the summation into integration and introducing the density of states, N (0), we get

$M=\frac{{\alpha }_{11}(k{k}^{`})2N_1\left(0\right)}{\beta }{\int }_0^{\mathrm{ћ}{\omega }_D}\frac{{\overline{∆}}_1}{\left({{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)}dϵ(79)$

Using the Matsubara frequency ${\left(2n+1\right)}^2{\pi }^2/{\beta }^2={{\omega }_n}^2$ and $1/{\left(2n+1\right)}^2{\pi }^2+x^2=\tanh \left(x/2\right)/2x$ where $x={\beta E}_1$ Eq. 79 become

$M={\lambda }_{ATM}{\int }_0^{\mathrm{ћ}{\omega }_D}\frac{{\overline{∆}}_1}{\sqrt{\left({{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)}}\tanh \frac{\beta \sqrt{\left({{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)}}{2}dϵ(80)$

Where ${\lambda }_{ATM}={\alpha }_{11}\left(k,k^{`}\right)N_1$ (0) coupling constant, and ${E_1}^2=\left({{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)$.

Now, let us first solve the integral.

${\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{\sqrt{\left({{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)}}\tanh \frac{\beta \sqrt{\left({{\epsilon }_1}^2+{{\overline{∆}}_1}^2\right)}}{2}dϵ={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{2}{\beta }{\displaystyle \sum _{n=-\infty }^{\infty }}\frac{1}{{{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2}dϵ(81)$

Using the Laplace transformation and Matsubara frequency, Eq. 81 become

${\int }_0^{\mathrm{ћ}{\omega }_D}\frac{2}{\beta }{\displaystyle \sum _{n=-\infty }^{\infty }}\frac{1}{{{\omega }_n}^2+{{\epsilon }_1}^2+{{\overline{∆}}_1}^2}dϵ={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{2}{\beta }{\displaystyle \sum _{n=-\infty }^{\infty }}\frac{1}{{{\left(2n+1\right)}^2\frac{\pi }{{\beta }^2}}^2+{ϵ}^2+{{\overline{∆}}_1}^2}dϵ={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{ϵ}\tanh \frac{\beta ϵ}{2}dϵ-{\int }_0^{\mathrm{ћ}{\omega }_D}{{\overline{∆}}_1}^2\frac{4}{\beta }{\displaystyle \sum _{n=0}^{\infty }}\frac{1}{{a^4\left(1+x^2\right)}^2}dϵ(82)$

The two integrations give

$I_1={\int }_0^{\mathrm{ћ}{\omega }_D}\frac{1}{ϵ}\tanh \frac{\beta ϵ}{2}dϵ=-\ln 1.14\frac{\mathrm{ћ}{\omega }_D}{K_B{T}_{ATM}}$

$I_2={\int }_0^{\mathrm{ћ}{\omega }_D}{{\overline{∆}}_1}^2\frac{4}{\beta }{\displaystyle \sum _{n=0}^{\infty }}\frac{1}{{a^4\left(1+x^2\right)}^2}dϵ\approx {\left(\frac{{\overline{∆}}_1}{\pi K_B{T}_{ATM}}\right)}^{2}1.05$

Substituting the $I_1$ and $I_2$ in Eq. 82 and Eq. 80 gives

$M=-{\lambda }_{ATM}\overline{∆}\left(\ln 1.14\frac{\mathrm{ћ}{\omega }_D}{K_B{T}_{ATM}}+{\left(\frac{\overline{∆}}{\pi K_B{T}_{ATM}}\right)}^{2}1.05\right)(83)$

Neglecting ${\overline{∆}}^2$ because very small for $\overline{∆}={\overline{∆}}_1$ the antiferromagnetic order parameter is

$M=-{\lambda }_{ATM}\overline{∆}\ln 1.14\frac{\mathrm{ћ}{\omega }_D}{K_B{T}_{ATM}}(84)$

This equation also gives the antiferromagnetic transition temperature ($T_{ATM}$)

$T_{ATM}=1.14\frac{\mathrm{ћ}{\omega }_D}{K_B}{e}^{\left[\frac{M}{{\lambda }_{ATM}\overline{∆}\left(0\right)}\right]}(85)$

3 Result and discussion

In this section, we have examined the results obtained from analyzing the normal and anomalous one-particle thermal Green’s functions in a two-band model of superconductivity. The analysis takes into account the potential intraband and interband superconducting interaction terms, which decouple both bands in the mean field approximation. We have derived expressions for the superconducting order parameters (${\overline{∆}}_1$ and ${\overline{∆}}_2$) for the two bands, the superconducting transition temperature ($T_C$) in the pure superconducting state, and the superconducting transition temperature with a magnetic order parameter. Additionally, we have obtained the antiferromagnetic transition temperature ($T_{ATM}$).

Using Eq. 57, we have calculated the theoretical value of $T_C$ to be 20.35K, while the experimental value is 20 K [30] for the iron-based superconductor ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$. Additionally, we have employed reasonable approximations for various parameters. For instance, we set the interband coupling constant (λ₁₂) to 0.25 and assumed a substantial boson energy of 84meV within the multi-band model. The electron-phonon coupling constant in FeSC is estimated to be in the range of λ∼0.17–0.21 [50]. Our theoretical prediction is in agreement with the experimental results, providing further evidence that supports their agreement [44, 51]. This observation offers valuable insights into the underlying mechanism responsible for the pairing in superconductivity. Interestingly, it is possible to obtain $T_C$ even when all the intraband and interband interactions correspond to repulsion between carriers, as long as the relation $\left({\lambda }_{11}{\lambda }_{22}-{\lambda }_{12}{\lambda }_{21}\right)>0$ is satisfied [52]. This relation is often used for Fe-based superconductors. To visualize the relationship between $T_C$ and the interband coupling constant (${\lambda }_{12}$), we have plotted $T_C$ against ${\lambda }_{12}$ in Figure 2A. From the figure, it can be observed that as ${\lambda }_{12}$ increases, the superconducting temperature ($T_C$) for the ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ superconductor exponentially increases, and vice versa. As the interband coupling constant increases, Tc also increases, supporting the commonly accepted pairing scenario for iron pnictids, which involves SFs mediating pairing.

FIGURE 2

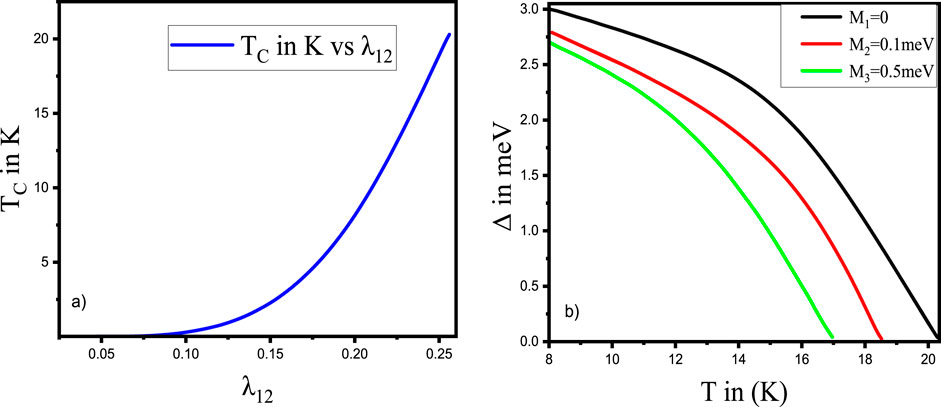
FIGURE 2. (A) Interband coupling constant (${\mathrm{\lambda }}_{\mathbf{12}}$) versus superconducting temperature $\left({\mathit{T}}_{\mathbf{C}}\right)$ for ${\text{Ca}}_{\mathbf{0.74}\left(\mathbf{1}\right)}{\text{La}}_{\mathbf{0.26}\left(\mathbf{1}\right)}\left({\text{Fe}}_{\mathbf{1}-\mathbf{x}}{\text{Co}}_{\mathbf{x}}\right){\text{As}}_{\mathbf{2}}$ Superconductor for $\mathbf{ћ}{\mathit{\omega }}_{\mathit{D}}=\mathbf{84}\mathit{m}\mathit{e}\mathit{v}$ (B) Phase diagram of superconducting order parameter versus temperature for various values of the magnetic order parameter for ${\text{Ca}}_{\mathbf{0.74}\left(\mathbf{1}\right)}{\text{La}}_{\mathbf{0.26}\left(\mathbf{1}\right)}\left({\text{Fe}}_{\mathbf{1}-\mathbf{x}}{\text{Co}}_{\mathbf{x}}\right){\text{As}}_{\mathbf{2}}$ Superconductor by fixing ${\mathbf{T}}_{\mathbf{c}}$

In the study, the expression for the superconducting order parameter as a function of temperature (Eq. 62) and magnetic ordering was obtained (Eq. 85), and the phase diagram of the superconducting order parameter versus temperature for different values of the magnetic order parameter was plotted (Figure 2B). The results showed that the superconducting order parameter is suppressed when magnetic ordering is present, and this suppression becomes more significant as the value of the magnetic order parameter increases. The impact of magnetic ordering on superconductivity depends on the details of the magnetic structure and the electron bands. The phase diagram of the transition temperature (Tc) versus magnetic ordering was also plotted (Figure 3A) using Eq. 85, and it was observed that magnetic ordering suppresses the superconducting transition temperature. This suppression is likely due to the coupling between localized and conduction electrons, which is strong enough to break up the Cooper pairs. The effect of magnetic ordering on superconductivity depends on the details of the magnetic structure and the electron bands [34].

FIGURE 3

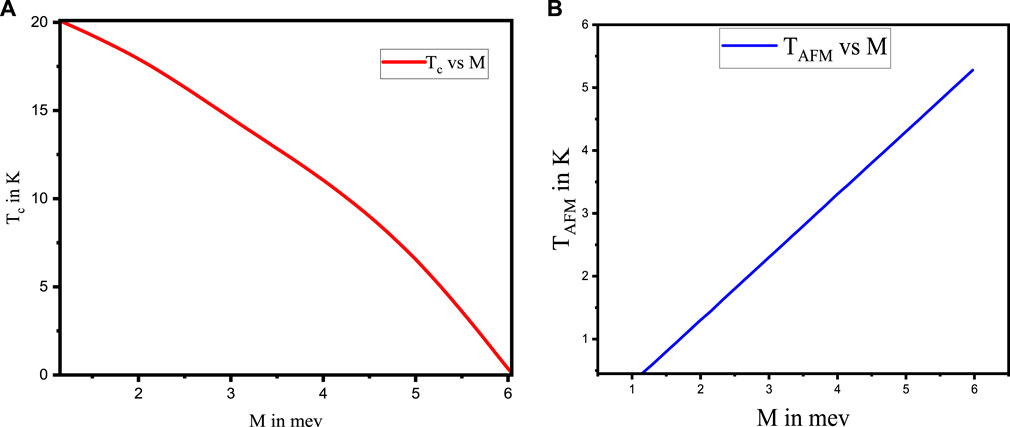
FIGURE 3. (A) Phase diagram of superconducting transition temperature versus magnetic order Parameter for ${\text{Ca}}_{\mathbf{0.74}\left(\mathbf{1}\right)}{\text{La}}_{\mathbf{0.26}\left(\mathbf{1}\right)}\left({\text{Fe}}_{\mathbf{1}-\mathbf{x}}{\text{Co}}_{\mathbf{x}}\right){\text{As}}_{\mathbf{2}}$ Superconductor for $\mathbf{ћ}{\mathit{\omega }}_{\mathit{D}}=\mathbf{84}\mathit{m}\mathit{e}\mathit{v}$ and ${\mathit{\lambda }}_{\mathbf{12}}=\mathbf{0.25}$. (B) Phase diagram of antiferromagnetic order temperature versus magnetic order Parameter (Eq. 85) for ${\text{Ca}}_{\mathbf{0.74}\left(\mathbf{1}\right)}{\text{La}}_{\mathbf{0.26}\left(\mathbf{1}\right)}\left({\text{Fe}}_{\mathbf{1}-\mathbf{x}}{\text{Co}}_{\mathbf{x}}\right){\text{As}}_{\mathbf{2}}$ Superconductor for ${\mathit{\lambda }}_{\mathbf{12}}=\mathbf{0.25}$, $\mathbf{ћ}{\mathit{\omega }}_{\mathit{D}}=\mathbf{84}\mathit{m}\mathit{e}\mathit{v}$ and $\overline{∆}$ (0) = 3.02mev.

The quantum mechanical interaction between the spins of localized electrons and the atomic magnetic moments of the system is the underlying cause of magnetic ordering, suppressing superconductivity. Below the transition temperature ($T_C$), the exchange interaction attempts to align the Cooper pairs, imposing strict limits on the existence of superconductivity. Additionally, we have plotted the phase diagram of $T_{ATM}$ (transition temperature to antiferromagnetism) versus M (Figure 3B). It can be observed that magnetic ordering enhances the Neel temperature ($T_{ATM}$). This implies that the antiferromagnetic moment lies in the basal plane for all values of M. By combining Figures 3A, B, we have identified the region between (2.3 < M < 6.07) for M, the magnetic order parameter where superconductivity and antiferromagnetic coexist, as depicted in Figure 4. Our findings are broadly consistent with experimental observations [30]. This also gives additional information for the physics of superconductivity. Based on our discovery, we have found that incorporating the interaction between intra-band and inter-band terms in the two-band model Hamiltonian leads to a multi-band dispersion at the Fermi surface. This is achieved through the utilization of the matrix form of thermal Green function formalism, which holds significance for further comprehensive investigations. By employing mean-field decoupling, it becomes possible to establish the order parameters for superconductivity and magnetism. These order parameters, along with the critical temperatures associated with superconductivity and magnetism, allow us to construct a phase diagram. In mean-field theory, the absence of fluctuations can lead to an overestimation of phase stability, allowing phases that would normally exist in competition to coexist. It is crucial to recognize that mean-field theory has its limits and might not precisely capture the phase boundaries or quantitative characteristics. Still, by encapsulating the fundamental qualitative features of the phase diagram, mean-field theory can offer insightful information. In short, superconducting (SC) and antiferromagnetism (AFM) phases coexist within a certain range of increasing magnetic order parameter values. At lower temperatures, the width of the coexistence region expands as the magnetic order parameter increases, indicating that the coexistence of these phases is influenced by the ellipticity of the electron bands.

FIGURE 4

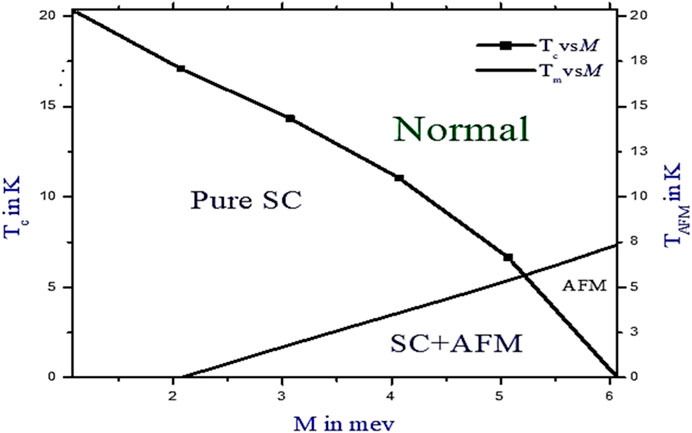
FIGURE 4. Phase diagram of SC transition temperature and antiferromagnetic transition temperature versus magnetic order parameter. The figure demonstrates the Co-occurrence of superconductivity and antiferromagnetism (SC + AFM) region between $\left(\mathbf{2.3}<\mathit{M}<\mathbf{6.07}\right)$ for $\mathit{M}$ the magnetic order parameter.

4 Conclusion

In the present work, the possible interplay of superconductivity and antiferromagnetic in ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ superconductor was studied. Based on the electronic band structure of the iron-based superconductor, we have developed the two-band model Hamiltonian for the system, which consists of intra and interband pairing interactions, and inter-orbital pair hopping. Using the normal and anomalous thermal Green function technique with the two-band model Hamiltonian, the self-consistent gap equations and the expressions for the transition temperatures and order parameters have been obtained. With this mathematical expression and relevant parameters numerically solved the results have been presented in the figure. Figure 2A shows that the interband coupling constant increases as the transition temperature increases for the ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ iron base superconductor. The superconducting order parameter ($\overline{∆}$) gets to zero at transition temperature (T_c), and it is suppressed when magnetic order parameter (M) sets in and the suppression becomes more important when the antiferromagnetic correlations grow. This is verified by plotting the phase diagrams of the superconducting order parameter ($\overline{∆}$) versus temperature (T) by varying the value of $M$. Furthermore, Figure 3A, which is plotted ${\mathrm{T}}_{\mathrm{c}}$ as the function of the magnetic order parameter of ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ system indicates that ${\mathrm{T}}_{\mathrm{c}}$ is decreasing when $M$ is increased. On the other hand, in the triclinic state, magnetic ordering enhances the antiferromagnetism transition temperature (T_AFM) as indicated in the phase diagram of antiferromagnetism order temperature (T_AFM) versus antiferromagnetic order parameter $\left(M\right)$ which is shown in Figure 3B. Lastly, by merging Figures 3A, B, we have found the intersection region of superconductivity and antiferromagnetic. The region under the two merged Figures shows the Co-occurrence of the two states established in the magnetic order parameter range of $2.3<M<6.07$ for the system ${\text{Ca}}_{0.74\left(1\right)}{\text{La}}_{0.26\left(1\right)}\left({\text{Fe}}_{1-\mathrm{x}}{\text{Co}}_{\mathrm{x}}\right){\text{As}}_2$ as shown in Figure 4 which is seen to the broad experimental agreement.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GS: Conceptualization, Data curation, Investigation, Methodology, Software, Supervision, Writing–original draft, Writing–review and editing. DS: Conceptualization, Investigation, Methodology, Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kamerlingh-Onnes H. Disappearance of the electrical resistance of mercury at helium temperatures. Proc Koninklijke Akademie van Wetenschappen te Amsterdam (1911) 14:113.

Google Scholar

2. Van Delft D, Kes P. The discovery of superconductivity. Phys Today (2010) 63(9):38–43. doi:10.1063/1.3490499

CrossRef Full Text | Google Scholar

3. Gavaler JR. Superconductivity in Nb–Ge films above 22 K. Appl Phys Lett (1973) 23(8):480–2. doi:10.1063/1.1654966

CrossRef Full Text | Google Scholar

4. Kasap S, Capper P. Springer handbook of electronic and photonic materials. Berlin, Germany: Springer (2017).

Google Scholar

5. Meissner W, Ochsenfeld R. Ein neuer effekt bei eintritt der supraleitfähigkeit. Naturwissenschaften (1933) 21(44):787–8.

CrossRef Full Text | Google Scholar

6. Buckel W, Kleiner R. Superconductivity: fundamentals and applications. Hoboken, New Jersey, United States: John Wiley and Sons (2008).

Google Scholar

7. Bardeen J, Cooper LN, Schrieffer JR. Theory of superconductivity. Phys Rev (1957) 108(5):1175–204. doi:10.1103/physrev.108.1175

CrossRef Full Text | Google Scholar

8. Ott HR, Rudigier H, Fisk Z, Smith JL. U be 13: an unconventional actinide superconductor. Phys Rev Lett (1983) 50(20):1595–8. doi:10.1103/physrevlett.50.1595

CrossRef Full Text | Google Scholar

9. Sharma RG. A review of theories of superconductivity. Supercond Basics Appl Magnets (2021) 123–60.

CrossRef Full Text | Google Scholar

10. Hasan MS, Ali SS. Properties and types of superconductors. Mater Res Found (2022) 132:17–48.

CrossRef Full Text | Google Scholar

11. Kamihara Y, Watanabe T, Hirano M, Hosono H. Iron-based layered superconductor La [O1-x F x] FeAs (x= 0.05− 0.12) with T c= 26 K. J Am Chem Soc (2008) 130(11):3296–7. doi:10.1021/ja800073m

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Schafgans AA, Moon SJ, Pursley BC, LaForge AD, Qazilbash MM, Sefat AS, et al. Electronic correlations and unconventional spectral weight transfer in the high-temperature pnictide BaFe 2− x Co x as 2 superconductor using infrared spectroscopy. Phys Rev Lett (2012) 108(14):147002. doi:10.1103/physrevlett.108.147002

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Cooper LN. Origins of the theory of superconductivity. IEEE Trans Magn (1987) 23(2):376–9. doi:10.1109/tmag.1987.1065151

CrossRef Full Text | Google Scholar

14. Stewart GR. Superconductivity in iron compounds. Rev Mod Phys (2011) 83(4):1589–652. doi:10.1103/revmodphys.83.1589

CrossRef Full Text | Google Scholar

15. Kordyuk AA. Iron-based superconductors: magnetism, superconductivity, and electronic structure. Low Temp Phys (2012) 38(9):888–99.

CrossRef Full Text | Google Scholar

16. Lee C-H, et al. Effect of structural parameters on superconductivity in fluorine-free LnFeAsO1-y (Ln= La, Nd). J Phys Soc Jpn (2008) 77(8):83704.

CrossRef Full Text | Google Scholar

17. Nandi S, Kim MG, Kreyssig A, Fernandes RM, Pratt DK, Thaler A, et al. Anomalous suppression of the orthorhombic lattice distortion in superconducting Ba (Fe 1− x Co x) 2 as 2 single crystals. Phys Rev Lett (2010) 104(5):057006. doi:10.1103/physrevlett.104.057006

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Tanui PK, Namwetako JS, Ingosy A, Khanna KM. Superconductivity and electron-hole superconductivity. Int J Recent Res Asp (2020) 7(3).

Google Scholar

19. Ren Z-A, Che GC, Dong XL, Yang J, Lu W, Yi W, et al. Superconductivity and phase diagram in iron-based arsenic-oxides ReFeAsO1− δ (Re= rare-earth metal) without fluorine doping. Europhys Lett (2008) 83(1):17002. doi:10.1209/0295-5075/83/17002

CrossRef Full Text | Google Scholar

20. Matsuishi S, Inoue Y, Nomura T, Yanagi H, Hirano M, Hosono H. Superconductivity induced by Co-doping in quaternary fluoroarsenide CaFeAsF. J Am Chem Soc (2008) 130(44):14428–9. doi:10.1021/ja806357j

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rotter M, Tegel M, Johrendt D. Superconductivity at 38 K in the iron arsenide (Ba 1− x K x) Fe 2 as 2. Phys Rev Lett (2008) 101(10):107006. doi:10.1103/physrevlett.101.107006

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kudo K, Iba K, Takasuga M, Kitahama Y, Matsumura J, Danura M, et al. Emergence of superconductivity at 45 K by lanthanum and phosphorus co-doping of CaFe2As2. Sci Rep (2013) 3(1):1478. doi:10.1038/srep01478

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Pitcher MJ, Parker DR, Adamson P, Herkelrath SJC, Boothroyd AT, Ibberson RM, et al. Structure and superconductivity of LiFeAs. Chem Commun (2008) 45:5918–20. doi:10.1039/b813153h

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Tapp JH, Tang Z, Lv B, Sasmal K, Lorenz B, Chu PCW, et al. LiFeAs: an intrinsic FeAs-based superconductor with T c= 18 K. Phys Rev B (2008) 78(6):060505. doi:10.1103/physrevb.78.060505

CrossRef Full Text | Google Scholar

25. Hsu F-C, Luo JY, Yeh KW, Chen TK, Huang TW, Wu PM, et al. Superconductivity in the PbO-type structure α-FeSe. Proc Natl Acad Sci (2008) 105(38):14262–4. doi:10.1073/pnas.0807325105

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Mizuguchi Y, Takano Y. Review of Fe chalcogenides as the simplest Fe-based superconductor. J Phys Soc Jpn (2010) 79(10):102001. doi:10.1143/jpsj.79.102001

CrossRef Full Text | Google Scholar

27. Löhnert C, Stürzer T, Tegel M, Frankovsky R, Friederichs G, Johrendt D. Superconductivity up to 35 K in the iron platinum arsenides (CaFe1− xPtxAs) 10Pt4− yAs8 with layered structures. Angew Chem Int. Ed. (2011) 50(39):9195–9. doi:10.1002/anie.201104436

CrossRef Full Text | Google Scholar

28. Katayama N, Kudo K, Onari S, Mizukami T, Sugawara K, Sugiyama Y, et al. Superconductivity in Ca_1-<i>x</i>La_<i>x</i>FeAs₂: a novel 112-type iron pnictide with arsenic zigzag bonds. J Phys Soc Japan (2013) 82(12):123702. doi:10.7566/jpsj.82.123702

CrossRef Full Text | Google Scholar

29. Yakita H, Ogino H, Okada T, Yamamoto A, Kishio K, Tohei T, et al. A new layered iron arsenide superconductor:(Ca, Pr) FeAs2. J Am Chem Soc (2014) 136(3):846–9. doi:10.1021/ja410845b

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Jiang S, et al. Coexistence of superconductivity and antiferromagnetism in Ca $ _ {0.74 (1)} $ La $ _ {0.26 (1)} $(Fe $ _ {1-x} $ Co $ _ {x} $) as $ _ {2} $ single crystals (2016). https://arxiv.org/abs/1603.04899.

Google Scholar

31. Vavilov MG, V Chubukov A, Vorontsov AB. Jump in specific heat in the presence of a spin-density wave at the superconducting transition in iron pnictides. Phys Rev B (2011) 84(14):140502. doi:10.1103/physrevb.84.140502

CrossRef Full Text | Google Scholar

32. Jiang S, et al. Structural and magnetic phase transitions in Ca 0.73 La 0.27 FeAs 2 with electron-overdoped FeAs layers. Phys Rev B (2016) 93(5):54522.

CrossRef Full Text | Google Scholar

33. Vorontsov AB, Vavilov MG, V Chubukov A. Superconductivity and spin-density waves in multiband metals. Phys Rev B (2010) 81(17):174538. doi:10.1103/physrevb.81.174538

CrossRef Full Text | Google Scholar

34. Matsui Y, Morinari T, Tohyama T. Coexistence of antiferromagnetism and superconductivity in iron-based superconductors. J Phys Soc Jpn (2014) 83(9):094703. doi:10.7566/jpsj.83.094703

CrossRef Full Text | Google Scholar

35. Raghu S, Qi X-L, Liu C-X, Scalapino DJ, Zhang S-C. Minimal two-band model of the superconducting iron oxypnictides. Phys Rev B (2008) 77(22):220503. doi:10.1103/physrevb.77.220503

CrossRef Full Text | Google Scholar

36. Parker D, Vavilov MG, V Chubukov A, Mazin II. Coexistence of superconductivity and a spin-density wave in pnictide superconductors: gap symmetry and nodal lines. Phys Rev B (2009) 80(10):100508. doi:10.1103/physrevb.80.100508

CrossRef Full Text | Google Scholar

37. Lorenzana J, Seibold G, Ortix C, Grilli M. Competing orders in FeAs layers. Phys Rev Lett (2008) 101(18):186402. doi:10.1103/physrevlett.101.186402

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Izyumov Y, Kurmaev E. High-Tc superconductors based on FeAs compounds. Berlin, Germany: Springer Science and Business Media (2010).

Google Scholar

39. Thomale R, Platt C, Hu J, Honerkamp C, Bernevig BA. Functional renormalization-group study of the doping dependence of pairing symmetry in the iron pnictide superconductors. Phys Rev B (2009) 80(18):180505. doi:10.1103/physrevb.80.180505

CrossRef Full Text | Google Scholar

40. V Chubukov A, Vavilov MG, Vorontsov AB. Momentum dependence and nodes of the superconducting gap in the iron pnictides. Phys Rev B (2009) 80(14):140515. doi:10.1103/physrevb.80.140515

CrossRef Full Text | Google Scholar

41. Maier TA, Graser S, Scalapino DJ, Hirschfeld PJ. Origin of gap anisotropy in spin fluctuation models of the iron pnictides. Phys Rev B (2009) 79(22):224510. doi:10.1103/physrevb.79.224510

CrossRef Full Text | Google Scholar

42. V Chubukov A, V Efremov D, Eremin I. Magnetism, superconductivity, and pairing symmetry in iron-based superconductors. Phys Rev B (2008) 78(13):134512. doi:10.1103/physrevb.78.134512

CrossRef Full Text | Google Scholar

43. Nuwal A, Kakani S, Kakani SL. Two band model for the iron based superconductors. Indian J Pure Appl Phys (2015) 52(6):411–22.

Google Scholar

44. Wen XG. Quantum field theory of many-body systems: from the origin of sound to an origin of Light and electrons. Quan F. Theor Many-Body Syst. Orig. Sound Orig. Light Electrons (2010) 1–520. doi:10.1093/acprof:oso/9780199227259.001.0001

CrossRef Full Text | Google Scholar

45. Inkson JC. Many-body theory of solids: an introduction. Berlin, Germany: Springer Science and Business Media (2012).

Google Scholar

46. Nambu Y. Quasi-particles and gauge invariance in the theory of superconductivity. Phys Rev (1960) 117(3):648–63. doi:10.1103/physrev.117.648

CrossRef Full Text | Google Scholar

47. Rickayzen G. Green’s functions and condensed matter. Massachusetts, United States: Courier Corporation (2013).

Google Scholar

48. Mahan GD. Many-particle physics. Berlin, Germany: Springer Science and Business Media (2000).

Google Scholar

49. Kristoffel N, Örd T. On the possibility of HTSC in a two-band model with a semiconducting gap (A3C60). Phys Status Solidi (1993) 175(1):K9–K12. doi:10.1002/pssb.2221750129

CrossRef Full Text | Google Scholar

50. Brydon PMR, Daghofer M, Timm C. Magnetic order in orbital models of the iron pnictides. J Phys Condens Matter (2011) 23(24):246001. doi:10.1088/0953-8984/23/24/246001

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Fernandes RM, Pratt DK, Tian W, Zarestky J, Kreyssig A, Nandi S, et al. Unconventional pairing in the iron arsenide superconductors. Phys Rev B (2010) 81(14):140501. doi:10.1103/physrevb.81.140501

CrossRef Full Text | Google Scholar

52. Zhou W, Ke F, Xu X, Sankar R, Xing X, Xu CQ, et al. Correlation between non-Fermi-liquid behavior and superconductivity in (Ca, La)(Fe, Co) as 2 iron arsenides: a high-pressure study. Phys Rev B (2017) 96(18):184503. doi:10.1103/physrevb.96.184503

CrossRef Full Text | Google Scholar