A research program to measure the lifetime of spin polarized fuel

The use of spin polarized fuel could increase the deuterium-tritium (D-T) fusion cross section by a factor of 1.5 and, owing to alpha heating, increase the fusion power by an even larger factor. Issues associated with the use of polarized fuel in a reactor are identified. Theoretically, nuclei remain polarized in a hot fusion plasma. The similarity between the Lorentz force law and the Bloch equations suggests polarization can be preserved despite the rich electromagnetic spectrum present in a magnetic fusion device. The most important depolarization mechanisms can be tested in existing devices. The use of polarized deuterium and ³He in an experiment avoids the complexities of handling tritium, while encompassing the same nuclear reaction spin-physics, making it a useful proxy to study issues associated with full D-T implementation. ³He fuel with 65% polarization can be prepared by permeating optically-pumped ³He into a shell pellet. Dynamically polarized ⁷Li-D pellets can achieve 70% vector polarization for the deuterium. Cryogenically-frozen pellets can be injected into fusion facilities by special injectors that minimize depolarizing field gradients. Alternatively, polarized nuclei could be injected as a neutral beam. Once injected, the lifetime of the polarized fuel is monitored through measurements of escaping charged fusion products. Multiple experimental scenarios to measure the polarization lifetime in the DIII-D tokamak and other magnetic-confinement facilities are discussed, followed by outstanding issues that warrant further study.

1 Introduction

If the nuclear spins of deuterium and tritium are both aligned parallel to the magnetic field, the deuterium-tritium (D-T) fusion cross section is 50% larger than for randomly oriented nuclei. Over 4 decades ago [1], Kulsrud et al. predicted that the spins remain aligned sufficiently long in the reactor environment to increase the fusion power but no experimental tests of this prediction were ever performed. Now, however, polarized sources are available that enable experimental tests. This paper summarizes both specific plans to measure the lifetime of spin polarized fuel in the DIII-D tokamak and outlines desirable avenues for additional research.

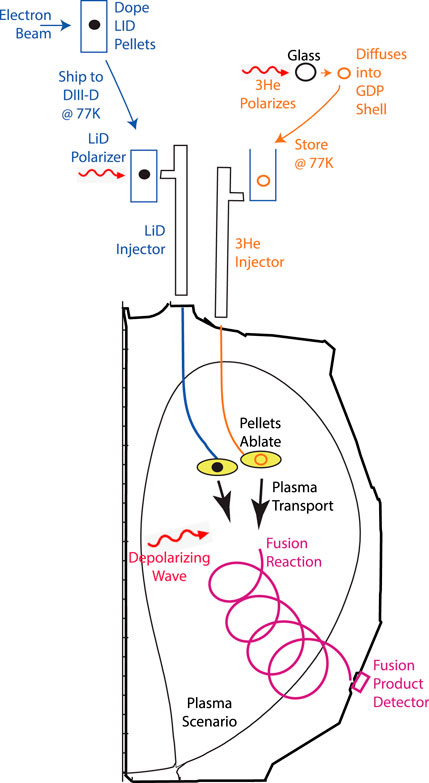
Numerous technological and physical challenges must be overcome for a successful polarization lifetime experiment. Figure 1 illustrates many of these for one of the planned experiments. Polarized D fuel in the form of a solid LiD pellet is prepared in a multi-step process. In parallel, polarized ³He is diffused into a glow-discharge-polymer shell pellet. Both pellets are injected into the tokamak by specially-designed injectors that preserve the nuclear polarization. Once inside the device, the pellets ablate, ionizing the D and ³He nuclei. Some nuclei that are transported to the hot center of the plasma undergo a D-³He fusion reaction. Prior to a reaction, electromagnetic fields may depolarize the nuclei. The fusion reactions produce high-energy, unconfined reaction products that collide with the vacuum vessel wall; the polarization of the reactants is inferred from the angular distribution of fusion reaction products. A specially designed plasma scenario that provides adequate fusion reaction rates without competing backgrounds is required.

Figure 1

Figure 1. Schematic illustration of major steps in the DIII-D D-³He lifetime experiment.

The planned DIII-D experiments are based upon two recent publications. The first publication [2] describes the nuclear physics and preparation of polarized LiD and ³He pellets for injection into the tokamak. The second publication [3] focuses on experimental scenarios and charged-fusion product detection. The present manuscript incorporates brief summaries of these two publications. The paper begins with a survey of issues of importance in a reactor (Section 2). Next, depolarization mechanisms are discussed, including a heuristic explanation for the theoretical prediction of long polarization lifetimes (Section 3). Section 4 describes planned and prospective polarized sources. Section 5 is devoted to the operational requirements for experimental polarization lifetime measurements and lists numerous possible experiments. The paper concludes with a summary and suggestions for future work.

2 Reactor considerations

The most obvious benefit of spin polarized fuel is that it eases the requirements for energy gain in a reactor. The effect is particularly important for concepts with relatively low values of fusion Q. (Here Q is the ratio of fusion power produced to power delivered to the plasma.) Since virtually all reactor concepts rely on charged fusion products to further heat the fuel, the gain in Q associated with spin polarization is greater than the 50% increase in fusion cross section. For example, in a realistic treatment of an ITER Q = 12 D-T plasma, Q is $\sim 1.8$ times larger if the nuclear spins remain aligned. (The precise value depends upon the associated increase in ion temperature T_i, which depends upon the modelled transport properties of the plasma.) Increases this large could make a marginal fusion concept viable.

But, even for configurations that are expected to ignite, a 50% enhancement in the cross section has very positive consequences. As an example, consider a compact fusion power plant design with parameters as presented in [4]. Figure 2 shows the impact of the increased fusion cross section due to the use of spin-polarized fuel on the net electric power generation of the plant, as calculated in the fusion synthesis engine (FUSE) framework [5]. FUSE calculates an equilibrium from input scalar quantities, while the effect of transport on kinetic profiles is assumed to scale according to the ITER H98y2 confinement scaling [6]. A factor of 1.5 enhancement to the fusion cross section modifies the resulting fusion power for cases with optimally polarized fuel. The final net electric power output is determined by a fully self-consistent balance-of-plant model. The simulations predict an overall increase in net electric power of $\sim 90\%$ between the non-polarized and fully polarized cases, and scaling of net electric power with the magnetic field on axis B0 is consistent with the zero-dimensional scaling laws. This suggests that the same target net electric power output could be reached by a significantly more compact power plant design if spin-polarized fuel is leveraged, enabling cost savings due to the dependence of the plant’s overall direct capital cost on device major radius.

Figure 2

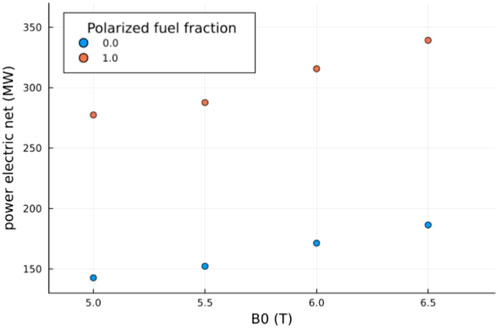
Figure 2. Comparison of the net electric power produced in a fusion power plant with and without spin polarized D-T fuel as a function of reactor magnetic field at the magnetic axis. (In order to keep the safety factor q constant, the plasma current is also scaled with B₀).

Another important benefit of spin polarized fuel is a reduction in required tritium inventory. In the generic fuel cycle for a D-T fusion plant [7], deuterium and tritium are injected into the plasma (most likely in the form of solid pellets). Unfortunately, only a small fraction of the injected fuel undergoes a fusion reaction before it escapes the plasma. (The characteristic time for a particle to escape is known as the “particle confinement time” τ_p.) Once a fuel ion has escaped the confinement region in the plasma core (with its closed field lines), it travels along open field lines to a divertor region where escaping fuel is exhausted from the device. External to the main chamber, tritium and deuterium are separated and formed into solid pellets for reinjection into the main chamber.

Tritium does not occur naturally; moreover, its 12.33-year half life means that storing excess tritium is wasteful. A 50% increase in the probability of a reaction in each injection cycle ultimately reduces the required tritium inventory. Since tritium is hazardous, rare, and expensive, this is a clear benefit of spin polarized fuel.

Another issue associated with the tritium inventory is harder to assess but could ultimately be problematic. Since tritium does not occur naturally, a reactor must breed tritium. D-T reactor designs include tritium breeding modules that surround the hot plasma core; reactions between 14 MeV neutrons and lithium must produce sufficient tritium to sustain the plant. To achieve a breeding ratio in excess of unity, with some margin for radioactive decay and other inefficiencies, tritium breeding modules must cover a large fraction of the area surrounding the reactor, imposing a severe constraint upon D-T plant design.

The D-T fusion cross section is isotropic for unpolarized fuel but becomes anisotropic for polarized fuel. The differential fusion cross section is [2].

$\frac{d\sigma }{d\mathrm{\Omega }}=\frac{{\sigma }_0}{4\pi }\left\{1-\frac{1}{2}{P}_D^V{P}_T+\frac{1}{2}\left[3P_D^V{P}_T{\sin }^2\theta +\frac{1}{2}{P}_D^T\left(1-3{\cos }^2\theta \right)\right]\right\}(1)$

where the polar pitch angle θ is the angle between the emitted charged fusion product (CFP) and the local magnetic field at birth and σ₀ depends upon the relative velocity of the reactants. The polarization factors $P_T$, $P_D^V$ and $P_D^T$ depend on the angular-momentum states of the nucleus. The sub-state population fractions in the presence of a magnetic field are N_i, where i = +1, 0, −1 and i = +1/2, −1/2 for spin–1 and spin-1/2 systems, respectively. The spin configurations are normalized such that ∑_iN_i = 1 for each system. The polarization factors in Eq. (1) can then be expressed using the sublevels as follows: tritium polarization P_T = N_+1/2 − N_−1/2 ∈ [−1, +1], deuteron vector polarization $P_D^V=N_{+1}-N_{-1}\in [-1,+1]$, and deuteron tensor polarization $P_D^T=N_{+1}+N_{-1}-2N_0\in [-2,+1]$. In the absence of any polarization, the D-T reaction is isotropic, dσ/dΩ = σ₀/4π.

When the deuterium and tritium spins are aligned parallel to the magnetic field B, Eq. 1 implies that fusion products are preferentially emitted perpendicular to the magnetic field. The resultant change in the directionality of the neutron emission could improve the tritium breeding ratio of some modules, reducing the requisite area needed by the modules. On the other hand, the enhanced neutron flux might exceed manageable heat or radiation loads. In tokamak geometry, the neutron flux to vertically-located divertors increases, aggravating challenges associated with protecting vulnerable divertor components. Whether neutron directionality is a liability or benefit depends upon the magnetic fusion concept and the actual geometry of a particular implementation.

Articles published shortly after Kulsrud’s seminal work [1, 8] argued that, because the confinement time is short compared to the fusion burnup time and because nuclei rapidly depolarize at a metallic wall, the utility of spin polarized fuel would be very limited [9]. Although it is certainly true that depolarization at most types of metal walls is virtually guaranteed, modern reactor designs assume that very few ions return directly to the plasma after a collision with a wall in the process known as “recycling.” In modern plant designs, nearly all escaping fuel ions are exhausted to the divertor, where they are reprocessed. As discussed below, recycling is an important consideration in planned experiments, but it does not negate the advantages of polarized fuel for a burning plasma [2].

A final issue for reactor design is the cost of spin polarization. Since fuel must be reprocessed anyway, it appears likely that spin polarization adds little to plant complexity. Nor is it likely to add appreciably to the capital cost of the plant. A more relevant concern is the energy efficiency of polarization. The process used to polarize the fuel must consume considerably less energy than the energy released in a fusion reaction times the probability that a fuel ion will react each time it is injected. In other words, the energy of polarization (including any inefficiencies) must be far less than 0.01 × 18 MeV = 100 keV, a requirement that seems easily satisfied.

3 Depolarization mechanisms

Physically, there are three depolarization mechanisms of principal concern [8].

The first is trivial. If the magnetic field is zero in a particular region, the reference axis for the polarization is lost. Since nearly all magnetic configurations have non-zero magnetic field throughout the confinement region, this depolarization mechanism is irrelevant inside the plasma for tokamaks, stellarators, and most other confinement concepts. An exception is the magnetic configuration known as a “field reversed configuration” (FRC), since an ideal FRC has a field null at the center of the confinement region. For all configurations, injected nuclei cannot cross a field null on their way to the plasma. A guide field is required during injection. Estimates indicate that the required guide field for deuterium is O (0.01) T and even less for ³He [2].

The second mechanism is interaction with bound electrons, most commonly through the hyperfine interaction. In fact, hyperfine interactions with bound electrons polarize the fuel in the first place (Section 4). However, in the reactor environment, ions with low atomic numbers Z like deuterium and helium are fully ionized, so there are no bound electrons to interact with the nuclei. Singly ionized helium does have a bound electron that couples to the nuclear spin but estimates indicate that only a few percent of injected polarized ³He lose their polarization during the relatively rapid ionization process [2].

A related concern is collisions of the fuel pellet with the pellet injector guide tube but estimates indicate that the associated losses are minimal [2].

The mechanism of greatest concern is resonance at the precession frequency of the nucleus. This frequency is a multiple g of the ordinary ion cyclotron frequency ω_ci = ZeB/m. The gyromagnetic ratio g is of order unity. If the nucleus experiences a wave with left-handed circular electric-field polarization at this frequency in its rest frame, rapid depolarization occurs [8]. Applications that use rotating magnetic fields to induce spin flips utilize this method.

The magnetic fusion plasma is filled with a vast spectrum of electromagnetic and electrostatic waves so, naively, one might expect rapid depolarization caused by precession resonances. This is not necessarily the case, however. Detailed calculations [8] indicate that, although the nuclei are constantly bombarded by Coulomb collisions in the plasma environment, Coulomb collisions cause negligible depolarization during a particle confinement time τ_p. Similarly, the spectrum of MHD and drift waves are also expected to cause negligible depolarization for reasons explained heuristically here [10].

Ion orbits in the magnetic field are governed by the Lorentz force law,

$\frac{d\mathbf{v}}{dt}={\omega }_{ci}\mathbf{v}\times \widehat{b},(2)$

where v is the particle velocity and $\widehat{b}$ is a unit vector in the direction of the magnetic field. The equilibrium collisionless orbit is governed by this equation but, in reality, electric and magnetic fields from plasma waves perturb the equilibrium orbit. Neverthess, if the frequency ω of the perturbing wave is low compared to the cyclotron frequency ω_ci and if the magnitude of the field changes little over the gyroradius of the orbit ρ, i.e., if ω ≪ ω_ci and ρ∇B/B ≪ 1, then there is a conserved action of the motion, the magnetic moment $\mu =v_{\perp }^2/B$, where v_⊥ is the perpendicular component of the magnetic field [11].

High-field magnetic confinement devices like tokamaks and stellarators usually conserve the magnetic moment μ. Indeed, one of the most successful theories of fusion plasmas, gyrokinetic theory [12], is predicated on conservation of μ. In the absence of instabilities or waves with frequencies close to the ion cyclotron frequency, μ is conserved.

When μ is conserved, it is expected that the nuclear polarization will also be conserved. Here’s why. The bulk polarization of the nuclei P is governed by the Bloch Equation [13],

$\frac{d\mathbf{P}}{dt}=g{\omega }_{ci}\mathbf{P}\times \widehat{b}.(3)$

Note that, apart from the factor g, Eqs 2, 3 are identical. Since g is of order unity, this implies that the polarization has a constant of motion ${\mu }_P=P_{\perp }^2/B$ that is conserved whenever the ordinary magnetic moment is conserved.

More rigorously, the evolution of the velocity and polarization vectors are governed by a single kinetic equation that concurrently evolves both quantities with terms like those on the right-hand side of Eqs 2, 3, and also includes the fluctuating fields that break μ and μ_p [14]. The conclusions of this more rigorous analysis are consistent with the heuristic argument presented here.

Of course, waves in the ion cyclotron range of frequencies violate the condition ω ≪ ω_ci required for μ conservation and could depolarize the nuclei. There are two potential sources of waves with ω ∼ ω_ci: plasma-generated instabilities and externally launched waves. Many magnetic confinement facilities launch high-power waves in the ion cyclotron range of frequencies (ICRF) to heat the plasma. If the frequency of the RF wave matches the precession frequency somewhere in the plasma, these large-amplitude wave fields will almost certainly depolarize the nuclei. In terms of the ordinary deuterium gyrofrequency ω_cD = eB/2m_p, the deuterium nuclear precession frequency occurs at 0.86ω_cD, the ³He precession frequency is at 4.255ω_cD, and the tritium precession frequency is at 5.96ω_cD. Fortunately, in many configurations, resonance at the precession frequency occurs outside the plasma. Figure 3 shows an example for a moderate aspect-ratio tokamak that launches waves that resonate with the orbital ³He gyrofrequency at ${\omega }_{RF}=\frac{4}{3}{\omega }_{cD}$ in the heating scheme known as ³He minority heating. Since the magnitude of the field varies with major radius R as approximately B ∝ 1/R, the launched wave frequency matches the fundamental ³He frequency near the magnetic axis but the deuterium precession resonance is near the inner wall and the ³He and tritium precession resonances are outside the vessel. Thus, ICRF heating should still be feasible in this configuration without depolarizing the fuel. As a second example, consider a magnetic mirror machine like the Wisconsin high-temperature superconductor axisymmetric mirror (WHAM) [15] that uses ICRF heating to accelerate ³He ions at the second harmonic of the ³He cyclotron frequency at a layer near the axial turning point of the orbit (Figure 4). In this case, the ³He and tritium precession frequencies with the launched wave occur at lower magnetic fields than occur in the plasma and the deuterium precession frequency occurs in the high field region near the mirror throat. Neither collisionless fast ion orbits nor the launched waves are expected to reach the very high-field region, so ICRF heating should be possible without compromising the nuclear polarization. However, this is not the case for a spherical tokamak since, in that configuration, the minor radius a is comparable to the major radius R, so the field variation in the plasma is so great that at least one of the precessional resonances falls in the plasma.

Figure 3

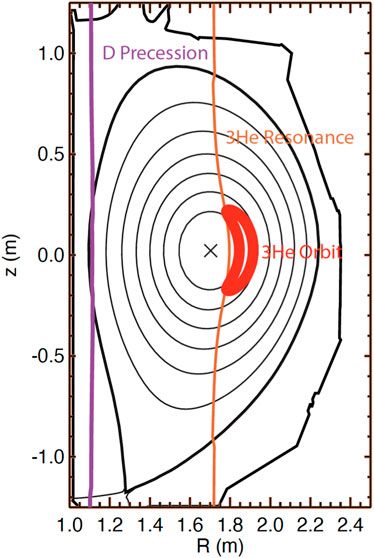
Figure 3. RF waves that resonate with ³He minority ions near the center of the tokamak do not resonate at the deuterium or ³He precession frequencies in a moderate-aspect ratio tokamak. The approximately vertical lines indicate the ω_RF = 2eB/3m_p resonance with the fundamental ³He cyclotron frequency and with the ω_RF = 0.86ω_cD deuterium precession resonance. The projection of the orbit of a high-energy ³He ion that is accelerated by the ICRF heating is also shown, as are the magnetic axis (X), flux surfaces (thin lines), and the “separatrix” boundary between closed field lines and open field lines (thick line).

Figure 4

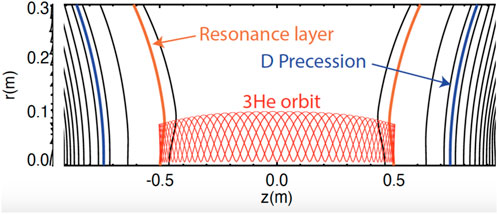
Figure 4. In a magnetic mirror, the orbits of high-energy ³He ions that are accelerated near their turning points do not traverse the deuterium precession resonance. The lines indicate magnetic field contours. The projection of the orbit of a high-energy ³He ion heated by the RF waves is also shown.

Instabilities in the ICRF are of greater concern. Under some operating conditions in tokamaks and stellarators, waves at the cyclotron frequency and its harmonics are driven unstable by super-thermal ions or electrons [16]. Waves with frequencies just below the cyclotron frequency are also observed [17]. If these instabilities are excited, the waves may propagate to locations in the plasma where the wave frequency matches a precessional frequency, causing depolarization. Clearly, polarization lifetime experiments should explore operational regimes with and without instabilities near the ion cyclotron frequency.

4 Polarized fuel

Although 100 keV ion energies are appreciable in plasma physics, in nuclear physics, 100 keV is a low energy. At the “low” energies of fusion experiments, the nuclear physics of the D-T fusion reaction is virtually identical to the nuclear physics of the D-³He fusion reaction [2]. Consequently, to avoid the hazards and complexity of a tritium experiment, our research program uses D-³He reactions as a proxy for D-T.

Polarized pellets are discussed in detail in [2], so only a summary is given here.

4.1 Polarized LiD pellets

Over the past decades, a variety of deuterated molecules have been used to create solid targets of polarized deuterium for nuclear and particle physics experiments [18, 19]. These utilize a dynamic nuclear polarization (DNP) process, in which molecular electrons are first polarized in a several Tesla magnetic field at relatively low temperatures ($\sim 1$ K) and microwaves are then used to drive a hyperfine transition that transfers their spins to the deuterons. For a spin-polarized fusion (SPF) demonstration experiment, the most attractive of this class of material is lithium-deuteride, LiD. The DNP lithium-deuteride target has been used in nuclear and high energy physics for decades [20]. More than 50% of D polarization was achieved with a dilution refrigerator equipped with a 2.5 T magnet during COMPASS runs [21]. This material has reached the highest deuteron-vector polarizations reported, 70% [19]. Furthermore, not only does lithium have relatively few electrons to raise the Z_eff of the plasma, but it can in fact be a desirable addition, since lithium injection is routinely used to improve wall conditions in tokamaks [22].

Lithium-deuteride is a solid at room temperature and is readily formed into mm-scale pellets suitable for an SPF study. The DNP process requires the introduction of a small fraction ($\sim 2$%) of paramagnetic centers. These are created by radiation exposure at ∼190 K, after which the material can be stored indefinitely at 77 K. With DNP, the polarization grows with time as $P_0(1-e^{-t/T_l(D)})$, where T_l(D) is the spin-relaxation time and P₀ is a limit determined by the polarizing conditions (field, temperature, microwave spin-transfer efficiency, etc.). At 1 K and 5 T, deuteron vector polarizations saturate at about 50% in a few hours, and T₁(D) is much longer than the typical duration of plasma shots at a research tokamak such as DIII-D (≲ 10 s). Reaching the published maximum polarization of 70% would require DNP at 0.2–0.3 K and 6–8 T [20], with longer buildup times of 1-to-2 days.

The use of LiD as the carrier for polarized deuterium requires a custom engineered polarizer, incorporating a DNP microwave circuit with RF coils that generate nuclear magnetic resonance (NMR) signals for polarization monitoring and spin manipulations, coupled to a dedicated cryogenic injection gun. The low operating temperatures of the polarizer require either ³He or ⁴He dilution cooling to reach ∼0.2 K, or a pumped ³He system operating at ∼0.3 K. In the polarizer, the LiD sample needs to be centered within a 6–8 T superconducting solenoid. While fringe fields from such a magnet might be of concern for plasma operations, the magnet could be shielded. Alternatively, since the bore of the solenoid could be small, this would require a relatively low inductance magnet that could be ramped down quickly (or even intentionally quenched) following the transfer of polarized pellets to the injection gun. The latter could operate at 4 K without noticeable loss in polarization over the short period (tens of seconds) preceding injection.

Pellets with $\sim 10^{20}$ deuterons are feasible [2] and provide sufficient polarized material for DIII-D experiments. Stages in the construction of the LiD polarized source include the following.

4.1.1 Fabricate LiD pellets

Cylindrical pellets of LiD will be made by fusing (melting) powdered material in a gold-lined cavity, heated within an inert gas-filled chamber. Raising the temperature at $\sim 10$ C/hr and then holding for $\sim 30$ min at $\sim 500$ C has been shown to yield robust pellets, whose density can be varied by the granularity of the powder and how it is packed into the gold column [23]. High densities require hot-pressing of the column [24].

4.1.2 Dope LiD pellets with paramagnetic centers

LiD has only paired molecular electrons with no net electron spin. In the dynamic nuclear polarization (DNP) process, a few percent of the LiD molecules must be ionized. Those ionized molecules are paramagnetic and their electrons can be polarized when exposed to high fields and low temperatures. These paramagnetic centers are introduced by irradiation with an electron beam while the LiD is held at $\sim 190$ K. An intense electron beam is necessary, but the beam energy can be relatively low (even $\sim 5$ MeV). A cryostat for this purpose is being developed at Jefferson Lab. For this cryostat, the electron beam enters a side port through thin aluminum foil windows that are thermally connected to the LN2 shield, passes through an isotherm irradiation bath (copper), and then through a copper meshed cage, impinging on the LiD pellets. To avoid nonuniform irradiation due to beam loss inside the cage, the toroidal cage containing the LiD pellets rotates around the vertical axis while the beam is on. Irradiating LiD pellets at the correct temperature with sufficient dose controls the fraction of radicals inside the LiD crystal. This is necessary in the DNP process for efficient electron polarization and the subsequent transfer of polarization to the deuteron. During the irradiation, the low energy electron beam is mostly lost inside the copper mesh cage and deposits a large amount of heat, which is taken away by cold ⁴He gas. An external circulation system promotes the necessary cooling-gas circulation. A separate helium gas line enters the cryostat from an upper flange, passes through a heat exchanger inside the LN2 volume to reach lower temperature, then passes through the insulation vacuum space inside the LN2 shield wall, and finally enters the temperature-regulated irradiation bath at the bottom to cool the LiD pellets. Warmed helium gas is pumped away through the central access port and returns to the helium port on the top flange.

4.1.3 Storage of Paramagnetically doped LiD

If irradiated LiD is raised to room temperature, the paramagnetic centers will decay away as the ionized sites become neutralized. However, if kept colder than 190 K, the time scale for this recombination process becomes extremely long, and at 77 K the doped LiD pellets can be stored indefinitely. An LN2 storage cryostat at the magnetic-fusion facility will store the pellets.

4.1.4 LiD polarizer

The LiD polarizer contains a dilution refrigerator (DF) capable of reaching 200 mK, a built-in superconducting solenoidal 6-to-8 T magnet, a pellet handling system to load and dispense LiD pellets, a microwave system to transfer polarization between electrons and deuterons, and an NMR system for polarization monitoring. Post-irradiated LiD pellets are loaded into a polarization chamber located at the center of the high-field magnet and cooled by the DF mixing chamber to provide the required low temperature and strong magnetic field. The electrons in the LiD molecule polarize quickly. The deuterium is polarized by continuously inducing hyperfine transitions between electrons and deuterium nuclei with microwaves at the appropriate frequency. Since the relaxation time of the bound electrons is much shorter than that of the deuteron, the electrons repolarize quickly while the D polarization can be accumulated over time. Nuclear magnetic resonance (NMR) coils located inside the LiD chamber are used to calibrate and monitor the pellet polarization. Ultimately, the polarized LiD pellet is transferred to the pellet gun (Sec. 4.3).

4.2 Polarized ³He pellets

Hybrid spin-exchange optical pumping (SEOP) can be used to polarize ³He [25]. With this technique, a glass bulb (polarizing cell) containing pressurized ³He, together with small amounts of rubidium and potassium ($\sim 10^{14}$ cm⁻³) and nitrogen ($\sim 0.7$%), is heated to about 500 K (225 C) to vaporize the alkalis. Valence electrons in the Rb vapor are polarized with 795 nm circularly polarized light from diode lasers, and collisions with the alkali atoms transfer polarization to the ³He, usually in the sequence Rb → K →³He. After several hours the ³He polarization has saturated (at about 60%–70% [26] or even ≲ 85% [27]). After saturation, the temperature of the polarizing cell is lowered. The vapor pressures of Rb and K drop rapidly with temperature, so that at 293 K (20 C) their concentrations are less than 10¹⁰ cm⁻³ and essentially negligible. At this point, the ³He can be extracted from the polarizing cell and diffused into a glow-discharge polymer (GDP) shell [28]. In a typical filling sequence, one successively increases the gas pressure on the outside of a GDP pellet in steps of 2/3 of the buckling pressure and waits three to five permeation time constants for the pressure across the pellet wall to equilibrate. Examples of successful permeation are reported in [2]. After filling, the temperature is lowered further to seal the wall, and the gas mixture outside the pellet is flushed and replaced with pure ⁴He. When stored at 77 K, the lifetime of the polarized ³He is about 3 days.

For medical imaging studies [29], high polarization and high batch volume are the primary concerns. In contrast, for magnetic-fusion fueling, the primary requirements are high ³He polarization at high pressure, rather than high volume. Accordingly, a figure of merit for fusion applications is the polarization density in the polarization cell (³He polarization times pressure at room temperature). Work is underway at the University of Virginia to maximize this figure of merit by exploring empirical tradeoffs among cell size, ³He density, optical pumping temperature, and laser power. Electron paramagnetic resonance (EPR) and adiabatic fast-passage NMR systems for monitoring alkali electron polarization and measuring absolute ³He polarization are employed to quantify the tradeoffs.

An ambitious goal is to generate a 25-bar reservoir of 80% polarized ³He as a source for pellet permeation into $\sim 2$ mm outer diameter GDP pellets. If those levels cannot be achieved directly in the polarization cell, a strategy for cryogenically amplifying the cell pressure is envisioned. Because ³He must be polarized by SEOP first and then permeated into GDP pellets, polarization loss during the permeation process is a primary concern. Polarization survival during permeation of laser-polarized ³He into 2-mm GDP pellets at room temperature was previously demonstrated and measured using MRI methods [2]. During that work, a variety of different pellets from different GDP production batches were tested. The fractional polarization loss during permeation depends on wall thickness and pellet storage history. Pellets with thinner walls that have been stored in an anoxic environment shielded from ambient light are preferred; pristine thin-walled pellets may not cause appreciable depolarization at all.

Work is underway to construct permeation vessels that can withstand higher maximum pressure and to incorporate a means of stepping down the ³He reservoir pressure in acceptable increments, to avoid exposing pellets to a pressure gradient exceeding the known buckling pressure. After 2 years of optimization experiments, an optimized polarizer for use at magnetic-fusion facilities will be fabricated.

4.3 Pellet injector

For a spin-polarization lifetime measurement, the polarized pellets must be delivered to the plasma with polarization largely intact. Both deuterium pellets and GDP pellets are routinely injected into fusion facilities like DIII-D but additional issues affect the design of SPF injectors.

One issue is that the pellets cannot cross a region of low magnetic field without losing their polarization. For deuterium, a field of a few hundred Gauss suffices to maintain the polarization; for ³He, 25 G is sufficient [2]. Such fields can be generated by a solenoid winding wrapped around the guide tube, with a tapered wire density that decreases as the tube enters the fringe field of the tokamak. Additionally, the pellets cannot rapidly cross a large field gradient that appears at the nuclear precession frequency in the particle’s frame. While injection velocities are typically 500–1,000 m/s, this and any tumbling motion down the guide tube are significantly slower than the Larmor frequencies of either D or ³He. As a result, the D and ³He spin vectors will simply follow the net local field as the tokamak fringe field rises and the guide tube field falls. Once inside the hydrogen plasma, the spins will align along the local magnetic field.

Another issue is that the polarized nuclei must ultimately fuel the high temperature plasma core. A large pellet can penetrate to the core but can cause excessive cooling. In a tokamak, pellets injected on the high field side bend toward the magnetic axis so injection from smaller major radius is preferred [30].

The third issue is the most challenging. The pellets depolarize at elevated temperatures, so deuterium pellets should be injected at $\sim 4$ K, while ³He pellets can be injected at $\sim 77$ K. A dedicated injection gun must be constructed to operate at 4 K, or below. A polarization decay time T_l(D) of about 6 min is expected at 4 K and 0.1 T [2]. For polarized ³He at 77 K, T₁(3He) is about 3 days [2]. While LiD is the more restrictive of the polarized species, its T₁ is still much longer than the time needed to transfer a pellet from an adjacent polarizer to an injection gun ($\sim 1$ s), ramp down the polarizing magnet ($\sim 10$ s), ramp up the field of the magnetic confinement device ($\sim 10$ s), and fire the cryo-gun ($\sim 1$ ms).

Experiments will compare the parallel spin configuration that enhances the fusion cross section with both unpolarized fuel and with the anti-parallel configuration that suppresses it. The anti-parallel spin configuration can be prepared within the cryo-gun, using an RF transition (an Adiabatic Fast Passage, or AFP) to flip the sub-state population so that the spin of one species (but not both) is aligned against the local magnetic field [31].

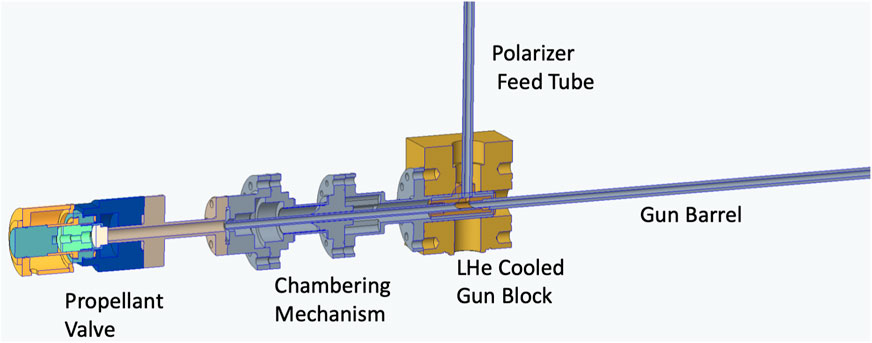
In existing solid (unpolarized) D₂ pellet guns, samples are propelled from the 4 K barrel of a cryo-gun to the tokamak by room temperature helium gas. Downstream of the $\sim 0.5$ m long gun barrel, room temperature guide tubes, with staggered differential pumping to remove the propellant gas, provide a vacuum envelop for the flight trajectory to the plasma.

A suitable pellet injector that could inject polarized cylindrical LiD pellets at high speeds ($>1000$ m/s) and low temperatures into the DIII-D tokamak is illustrated in Figure 5. As described in Section 4.1, after polarization, the LiD pellets are stored in a helium dilution refrigerator. An actively-cooled transfer mechanism transfers a single pellet from the polarizer to the gas gun of the injector, placing the pellet in the gun barrel to produce a tight-fitting seal in the barrel. The LiD pellets are dropped vertically from the polarizer and inserted into the barrel with the pneumatically-operated chambering mechanism. The chambering mechanism forces the pellet into the LHe cooled gun barrel where it is chambered tightly to enable the fast propellent valve on the left of the gun model to fire the pellet when requested. Cryogenic pellet formation and injection into fusion experiments has been previously demonstrated [32]. In addition, LiD pellets fired at room temperature in a two-stage light gas gun [33] at speeds $>4$ km/s demonstrate that LiD can withstand the forces of acceleration in a gas gun in an environment with even higher pressure and speed conditions than required for SPF applications. For the SPF pellet injector, a fast-operating solenoid valve [34] is used to produce a 50 bar helium pressure pulse behind the pellet to accelerate it in a $\sim 20$ cm gun barrel that is the same diameter as the pellet (Figure 5). Speeds in excess of 1 km/s can be achieved with this technique. The speed of the pellet is adjustable by changing the opening duration of the propellant valve with typical opening times of 1.5 ms.

Figure 5

Figure 5. Concept for the LiD pellet loader into a LHe cooled gas gun.

Inside the plasma, the physics of pellet injection is well established [35, 36]. As it traverses the plasma, the solid material erodes (or “ablates”) at a rate that is determined by the balance between the energy flux provided by the plasma and the flux required to remove the particles from the pellet surface and disassociate, ionize, and accelerate them. A shielding cloud of neutral gas retards the flux of plasma energy to the pellet surface, increasing penetration into the plasma. Magnetic shielding caused by the partial expulsion of the magnetic field from the cloud interior by the expanding plasma may also occur [37]. Large electric fields form [38]. Particularly during the phase when ³He is singly ionized, these rapidly-varying fields may induce hyperfine transitions [2]. To our knowledge, detailed theoretical treatment of effects that might cause nuclear depolarization during the ablation process is a topic for future work.

4.4 Polarized neutral beam

As discussed in Section 5, establishing suitable operational conditions for experiments with polarized pellets can be challenging, especially in smaller magnetic fusion devices. If a sufficiently intense neutral beam was available, many of these operational challenges would be ameliorated.

Polarized neutral beams are widely used in nuclear physics experiments [39] but their currents are far too low for use in a fusion polarization-lifetime experiment, where the fuel must be injected in times short compared to the particle confinement time. “Optical pumping” between quantum states is the established method to induce nuclear polarization [39]. For this, very powerful lasers are used to induce transitions between different electronic states; the energy of the involved photons is of the order of several eV.

Fusion devices are routinely heated by intense 25-120 keV neutral-beam sources with megawatts of power. Ordinarily, the majority of injected atoms are in the ground state. Although efficient methods to polarize metastable atoms using a Sona coil [40] were recently demonstrated [41], techniques to polarize ground-state neutral beams do not presently exist. The ideal neutral beam for spin-polarized fusion experiments would inject > 10¹⁸ deuterium atoms per second with > 50% polarization.

5 Experimental scenarios

5.1 General considerations

A general principle of experimental physics is that relative measurements are easier and more accurate than absolute measurements. That is certainly the case for detection of the degree of spin polarization in the plasma. For D-³He reactions, the emissivity (reaction rate per unit volume) is n_Dn_He⟨σv⟩, where n_D and n_He are the deuterium and ³He densities, and ⟨σv⟩ is the cross section σ and relative velocity v averaged over the deuterium and ³He distribution functions. Absolute determination of the effect of polarization on the reaction rate requires (i) absolutely calibrated fusion product detectors and (ii) accurate measurements of the D and ³He distribution functions and density profiles; sufficiently accurate data for the latter are unavailable at typical facilities [3]. On the other hand, since the emission angle of fusion reaction products is sensitive to the polarization state of the reacting nuclei through the differential cross section (Eq. 1), accurate relative measurements of the angular dependence of escaping fusion products are readily obtainable and provide sufficient accuracy to determine the polarization lifetime [3]. Figure 6 illustrates the basic idea behind accurate relative polarization measurements.

Figure 6

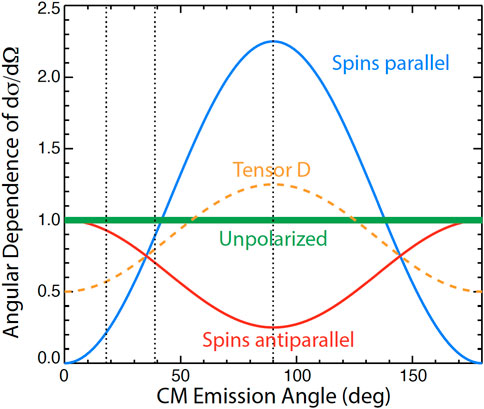
Figure 6. Angular dependence of the differential cross section dσ/dΩ for maximally-aligned parallel D and ³He nuclear spins (blue line), anti-parallel spins (red line), and randomly oriented spins (thick green line). The angular dependence for unpolarized ³He and tensor-polarized deuterium $P_D^T=1$ is also shown (dashed orange line). If one measures fusion-product signals at the emission angles indicated by the vertical lines, the ratios of the signals are quite sensitive to the nuclear polarization.

Charged fusion reaction products are usually born in the hot core of the plasma but they are detected near the vacuum vessel wall. The angle θ in Eq. 1 is the angle between the emitted velocity vector and the magnetic field in the center-of-mass frame at the birth location. In a magnetic confinement device, the angle between v and B changes as the fusion product travels to the wall. The difference depends upon the orbit size, which scales as $\sqrt{Em}/BZ$, where E, m, and Z are the fusion-product energy, mass, and atomic charge and B is the confining magnetic field. For poorly confined fusion products, like the 14.7 MeV proton D-³He reaction product in DIII-D, the difference in angle between birth and detection is modest, so a detector that measures v‖/v at the wall is an effective way to infer the polarization [3]. In contrast, the 3.6 MeV alpha D-³He reaction product is twice as well confined as the 14.7 MeV proton so, in this case, the angle at birth determines where the escaping alphas strike the DIII-D wall and a poloidal array of detectors is sensitive to the polarization state [3] (Figure 7).

Figure 7

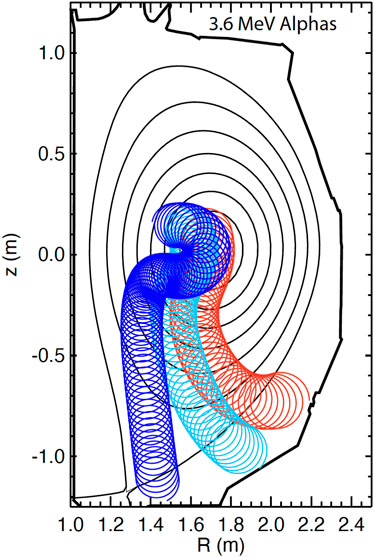
Figure 7. Projected orbits of 3.6 MeV alphas with larger (dark blue), intermediate (light blue), and smaller (red) values of |v‖/v| at birth in DIII-D. For these alphas, v ⋅B at birth determines where the ions strike the wall, so the relative signals from a poloidal array of alpha detectors is an effective way to diagnose polarization.

Since the orbits of 3.6 MeV alphas are only $\sim 10\%$ larger than the orbits of the 3.0 MeV protons produced in D-D fusion reactions, the same poloidal array of fusion product detectors can be used to diagnose the D-D differential cross section. (In plasmas with both fusion products, since the range of protons in solids is much longer than the range of alphas, use of a thin detector that collects the full alpha energy but only a portion of the proton energy is an effective way to distinguish alpha signals from proton signals.)

In smaller devices with poorer confinement than DIII-D, the angle of emission is largely retained for all escaping fusion products, so diagnosis is similar to 14.7 MeV proton detection in DIII-D.

Because the escaping fusion products are poorly confined, the accuracy of inference of the polarization state is insensitive to errors in the magnetic field reconstruction [3]. Uncertainty in the emission profile is a larger source of error [3].

The strong angular dependence of the emitted fusion products illustrated in Figure 6 is for the case where both deuterium and ³He are polarized. Eq. 1 indicates that, if only one species is polarized, the angular dependence is weaker (dashed line in Figure 6); moreover, tensor-polarization of the deuterium is required.

The challenge with using D-³He as a proxy for the D-T reaction is that, owing to the larger Coulomb repulsion of helium with deuterium, the fusion cross section is very low at O (10 keV) energies. To obtain adequate counting statistics in charged fusion product detectors, for D-³He, relative energies of the reactants of O (100 keV) are required. In existing devices, relative energies this large require one of the following.

1. Neutral beam injection of O (100 keV) beams for one of the reacting species.

2. ICRF acceleration that creates a fast-ion deuterium or ³He population with O (100 keV) energies. For example, ³He-minority heating can produce large D-³He reaction rates in a modest-size device [42].

3. A thermonuclear plasma with ion temperature T_i ≳ 10 keV. [Because the majority of reactions in a thermonuclear plasma occur between oppositely directed ions in the tails of the thermal distributions, the relative energy of most reactants in a T_i = 10 keV plasma is of O (100 keV).]

Because the Coulomb repulsion is weaker for deuterium-deuterium fusion reactions, practical reaction rates are accessible at significantly lower energies than for D-³He. For example, at T_i = 5 keV, the reactivity ⟨σv⟩ for D-D reactions is comparable to the reactivity of D-³He reactions at T_i = 10 keV. An additional advantage of deuterium is that it is employed routinely at most magnetic fusion facilities. Unfortunately, for the case where both reactants are polarized, the D-D differential cross section at relevant plasma energies is unknown and controversial. In one compilation [43], different theoretical models predict enhancement factors $>2$ while others predict suppression factors $<0.5$ at fusion-relevant energies of ≲ 100 keV. It is widely expected that the differential cross section has some polarization dependence at relevant energies but the actual value is unknown. Experiments to measure the cross section are planned [43, 44].

On the other hand, for the case where one deuterium reactant is polarized but the other is unpolarized, the differential cross section is known accurately at relevant energies [45, 46]. Even for unpolarized D nuclei, the unpolarized D-D differential cross section (dσ/dΩ)₀ depends upon the angle of fusion product emission [47]. Becker et al. [45] provide formulas for the additional angular dependence when one of the reactants is polarized. The altered differential cross section (dσ/dΩ)/(dσ/dΩ)₀ depends upon the angle between the incident beam and the magnetic field B, the gyroangle of the incident beam, the angle of emission of the 3-MeV proton relative to B, and the degree of vector and tensor polarization $P_D^V$ and $P_D^T$. In the case of a fusion experiment, the gyroangle of the incident beam is a uniform random variable. Figure 8 shows the dependence of the gyroangle-averaged differential cross section ⟨dσ/dΩ⟩/(dσ/dΩ)₀ on the proton emission angle for various values of the incident pitch v‖/v of the D beam. It is evident from the figure that the polarization dependence is much weaker than for D-³He reactions where both nuclei are polarized; however, the dependence is comparable to the sensitivity of D-³He reactions between unpolarized ³He nuclei and tensor-polarized D nuclei. Estimates of D-³He signals suggest that a DIII-D scenario with unpolarized ³He and tensor-polarized D is marginal for accurate determination of the D lifetime [3]. Similar detailed calculations for a scenario that uses unpolarized D beams and a polarized LiD pellet in DIII-D are underway.

Figure 8

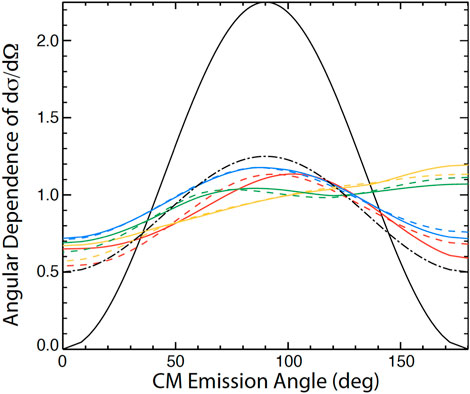
Figure 8. Angular dependence of the differential D-D cross section relative to the unpolarized dependence ⟨dσ/dΩ⟩/(dσ/dΩ)₀ for maximally-aligned D nuclear spin $(P_D^V=1.0=P_D^T)$ that collides with an unpolarized D target for various values of incident beam pitch v‖/v relative to the magnetic field: ± 0.99 (red), ± 0.75 (yellow), ± 0.5 (green), ± 0.1 (blue). (Solid lines are positive values; dashed lines are negative.) The curves are averaged over randomly oriented incident gyroangles of the beam. In comparison, when both species are polarized, maximally-aligned D-³He reactions between parallel spins (solid black) have much stronger angular sensitivity than the D-D reactions, while reactions between tensor-polarized D and unpolarized ³He (black dash-dot line) have comparable sensitivity.

In general, the ideal experimental facility has the following:

1. Large count rate ($\sim 100$ keV relative energy for d-³He),

2. Escaping fusion products that are sensitive to dσ/dΩ for the selected polarization of the reactants,

3. Reactor-relevant depolarization mechanisms,

4. Long particle confinement time for the polarized nuclei (in order to measure potentially long polarization lifetimes), and

5. Modest volume (so modest-size polarized sources produce appreciable densities).

5.2 Specific scenarios

5.2.1 Thermonuclear D-³He scenario in DIII-D

The primary target for the funded DIII-D experiments is a thermonuclear plasma with polarized LiD and ³He pellet injection. Owing to the strong sensitivity of dσ/dΩ (Figure 6), even for modest pellet polarizations of $P_D^V=0.40$ and $P_{3He}=0.65$, the accuracy of determination of the polarization state is excellent if the assumed plasma conditions of T_i ≳ 10 keV and n_d ≃ n_He ≃ 0.3 × 10¹⁹ m⁻³ can be achieved [3]. The challenge for this scenario is achieving the desired plasma conditions. Although DIII-D has created plasmas with T_i > 20 keV with deuterium neutral beam injection, to avoid contamination by unpolarized fast ions from the neutral beams, less effective hydrogen beams must be employed. Moreover, existing 20 keV plasmas had no pellet injection, and pellets cool the plasma.

The scenario analyzed in [3] underestimated the severity of pellet cooling. Pellets cool the plasma for two reasons. First, injected neutral ions become fully stripped in the plasma core; LiD pellets include lithium as well as deuterium and ³He shell pellets include hydrogen and carbon as well as ³He. It takes 13.6 eV, 79 eV, 203 eV, and 978 eV to strip hydrogen, helium, lithium, and carbon, respectively. Second, the injected electrons and ions are cold, so they subtract energy from the existing electron and ion populations when they equilibrate. In a zero-dimensional analysis that assumes (i) quasineutrality and (ii) no additional energy losses, the local energy density before pellet injection u_b is related to the energy density after injection u_a and the ionization energy $\mathcal{I}$ by $u_a=u_b-\mathcal{I}$. With assumptions about the initial temperatures and densities, the amount of carbon and hydrogen that accompanies the ³He, and the final ratio of T_e/T_i, this yields an equation that relates the final ion temperature to the injected deuterium and ³He densities n_D and n_He. Experimentally, one wants to maximize the fusion emissivity in the core, n_dn_He⟨σv⟩. Naively, one might assume that large injected densities and n_d = n_He is optimal but, because ⟨σv⟩ is a strong function of temperature and pellet injection cools the plasma, that is not necessarily the case. Figure 9 shows the emissivity as a function of injected deuterium and ³He densities for plausible initial plasma conditions and assumptions about the accompanying lithium and shell-pellet material. Because the ³He shell pellet is accompanied by relatively large amounts of hydrogen and carbon, it is preferable to inject relatively small amounts of ³He that result in a density of n_He ≃ 0.1 × 10¹⁹ m⁻³. The optimal amount of deuterium density is around n_D ≃ 0.5 × 10¹⁹ m⁻³. The resulting emissivity is smaller by an order of magnitude than assumed in [3], so the detection counting statistics are poorer than shown there.

Figure 9

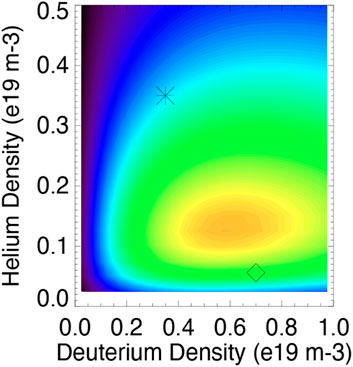
Figure 9. D-³He emissivity n_Dn_He⟨σv⟩ predicted by zero-dimensional analysis of pellet cooling as a function of n_D and n_He. The diamond and asterisk show the values assumed in [2, 3], respectively. Plausible values of T_e = 3.9 keV, T_i = 11.5 keV, T_e/T_i = 0.5 are assumed. A linear rainbow color map with maximum emissivity of 1.7 × 10¹¹ s⁻¹-m⁻³ is employed.

DIII-D experiments to develop a high-T_i scenario with co-injected hydrogen beams and pellet injection are planned.

5.2.2 Polarized LiD pellet with unpolarized ³He beam injection scenario in DIII-D

This scenario is described in detail in [3]. To achieve relative energies of O (100 keV), one of the DIII-D neutral beam injectors injects $\sim 75$ keV ³He neutral beams. The scenario relies on tensor polarization of the deuterium pellets $P_D^T$ to produce changes in differential cross section. Operationally, the required plasma conditions are easily produced.

5.2.3 Polarized LiD pellet with unpolarized D beam injection scenario in DIII-D

In this scenario, an $\sim 80$ keV deuterium neutral beam injects into a predominately helium (⁴He) plasma, then a polarized LiD pellet is injected. The signals from escaping 3-MeV protons are compared for polarized and unpolarized pellets using the expressions for the differential cross section in [45–47]. Deuterium beam injection into DIII-D routinely produces large D-D reaction rates so this is the easiest scenario to achieve operationally.

5.2.4 Polarized LiD pellet in a thermonuclear scenario in DIII-D

In contrast to the previous scenario, in this scenario, both reactants are polarized. To obtain adequate 3-MeV proton count rates, high-power electron cyclotron heating is used to trigger an H-mode, resulting in higher ion temperature and hence higher D-D reaction rates. To minimize unpolarized reactions, the plasma prior to LiD pellet injection is composed of ⁴He. If a polarization dependence is observed, measurement of its persistence yields a lifetime measurement.

5.2.5 Scenarios with polarized neutral beams

If an intense polarized source is successfully developed, many more scenarios become feasible both at DIII-D and at other facilities. With a polarized deuterium beam and injection of polarized ³He shell pellets, adequate D-³He count rates are obtainable in numerous smaller devices. The only important restriction is that the thermal ³He particle confinement time limits the maximum polarization lifetime that can be measured.

If the D-D differential cross section when both species are polarized does depend upon polarization, similar studies with LiD pellets are feasible and easily implemented.

5.2.6 ICRF scenarios

Polarization lifetime measurements in tokamaks with ion cyclotron heating are also highly desirable. Perhaps the simplest scenario is to use a bulk ⁴He plasma, inject a polarized ³He pellet, apply ICRF power at the ³He fundamental frequency to create a ³He tail then, once the ³He minority tail is established, a ⁶LiD pellet is injected to produce a large D-³He reaction rate.

The pros and cons of the four planned DIII-D scenarios are summarized in Table 1.

Table 1

Table 1. Pros and cons of the different DIII-D scenarios to measure the polarization lifetime (NBI = “neutral beam injection”).

6 Conclusion

An experimental program to measure the lifetime of spin polarized nuclear fuel is underway. The potential 50% enhancement in fusion cross section relaxes the plasma physics requirements for a practical magnetic fusion reactor. The theoretical expectation that depolarization lifetimes will be long can be tested in current experiments. Polarized LiD and ³He pellet sources are being designed and fabricated. Relative measurements of escaping fusion products enable inference of the polarization lifetime in several different D-³He and D-D scenarios.

Although the primary focus of future work is to execute the outlined DIII-D research program, two highly desirable extensions are readily identified. First, development of an intense polarized neutral beam source would provide high-energy polarized nuclei with less contaminants than polarized pellets, greatly simplifying experiments at DIII-D and enabling experimental tests at smaller facilities. Second, reliable predictions of the D-D differential cross section at fusion-relevant energies when both nuclei are polarized would enable experiments with lower-energy reactants at both DIII-D and elsewhere.

Once suitable sources are available, a diverse research program to quantify depolarization rates is envisioned, particularly studies of plasmas with and without instabilities and with heating in the ion cyclotron range of frequency. If experiments show that the polarization is preserved, future work should also include quantitative assessment of the reactor issues identified in Sec. 2.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

WH: Writing–original draft. LB: Writing–review and editing, Conceptualization. MB: Writing–review and editing. RE: Writing–review and editing. AVG: Writing–review and editing. AGG: Writing–review and editing. GM: Writing–review and editing. AS: Writing–review and editing. XW: Writing–review and editing. XZ: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported by DOE grant numbers DE-SC0020337 and DE-SC0024689.

Acknowledgments

Valuable discussions with Jay Anderson, Michl Binderbauer, Liu Chen, Cary Forest, Brian Grierson, Mikhail Gryaznevich, Kunal Sanwalka, and Xiaochao Zheng are gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kulsrud R, Furth H, Valeo E, Goldhaber M. Fusion reactor plasmas with polarized nuclei. Phys Rev Lett (1982) 49:1248. doi:10.1063/1.2945625

CrossRef Full Text | Google Scholar

2. Baylor L, Deur A, Eidietis N, Heidbrink WW, Jackson GL, Liu J, et al. Polarized fusion and potential in situ tests of fuel polarization survival in a tokamak plasma. Nucl Fusion (2023) 63:076009. doi:10.1088/1741-4326/acc3ae

CrossRef Full Text | Google Scholar

3. Garcia A, Heidbrink W, Sandorfi AM. Conceptual design of DIII-D experiments to diagnose the lifetime of spin polarized fuel. Nucl Fusion (2023) 63:026030. doi:10.1088/1741-4326/acaf0d

CrossRef Full Text | Google Scholar

4. Weisberg D, Grierson B, Meneghini O-M, Solomon W, Beharrell P, Leuer J, et al. Integrated design and optimization of the advanced tokamak fusion pilot plant. Bull Am Phys Soc (2023).

Google Scholar

5. Meneghini O, Slendebroek T, Lyons B, Cote T, Ghiozzi A, Guterl J, et al. Fusion synthesis engine: a next-generation framework for integrated design of fusion pilot plants (fpps). Bull Am Phys Soc (2023).

Google Scholar

6. Modelling C, Database IPEGC, Editors IPB. Chapter 2: plasma confinement and transport. Nucl Fusion (1999) 39:2175–249. doi:10.1088/0029-5515/39/12/302

CrossRef Full Text | Google Scholar

7. Abdou M, Vold E, Gung C, Youssef M, Shin K Deuterium-tritium fuel self-sufficiency in fusion reactors. Fusion Tech (1986) 9:250. doi:10.13182/fst86-1

CrossRef Full Text | Google Scholar

8. Kulsrud R, Valeo E, Cowley S Physics of spin-polarized plasmas. Nucl fusion (1986) 26:1443–62. doi:10.1088/0029-5515/26/11/001

CrossRef Full Text | Google Scholar

9. Greenside H, Budny R, Post DE Depolarization of d–t plasmas by recycling in material walls. J Vacuum Sci Tech A: Vacuum, Surf Films (1984) 2:619–29. doi:10.1116/1.572456

CrossRef Full Text | Google Scholar

10. Kulsrud R Polarization of P B11 in the FRC. Tech Rep TAE Tech Tech Rep (2010).

Google Scholar

11. Northrop TG The adiabatic motion of charged particles, Vol. 21 Interscience Publishers (1963).

Google Scholar

12. Brizard AJ, Hahm TS Foundations of nonlinear gyrokinetic theory. Rev Mod Phys (2007) 79:421–68. doi:10.1103/revmodphys.79.421

CrossRef Full Text | Google Scholar

13. Bloch F Nuclear induction. Phys Rev (1946) 70:460–74. doi:10.1103/physrev.70.460

CrossRef Full Text | Google Scholar

14. Cowley S, Kulsrud R, Valeo E A kinetic equation for spin-polarized plasmas. Phys Fluids (1986) 29:430–41. doi:10.1063/1.865726

CrossRef Full Text | Google Scholar

15. Endrizzi D, Anderson J, Brown M, Egedal J, Geiger B, Harvey R, et al. Physics basis for the Wisconsin HTS axisymmetric mirror (WHAM). J Plasma Phys (2023) 89:975890501. doi:10.1017/s0022377823000806

CrossRef Full Text | Google Scholar

16. McClements K, D’Inca R, Dendy R, Carbajal L, Chapman SC, Cook JWS, et al. Fast particle-driven ion cyclotron emission (ICE) in tokamak plasmas and the case for an ICE diagnostic in ITER. Nucl Fusion (2015) 55:043013. doi:10.1088/0029-5515/55/4/043013

CrossRef Full Text | Google Scholar

17. Lestz JB, Belova E, Gorelenkov N Hybrid simulations of sub-cyclotron compressional and global alfvén eigenmode stability in spherical tokamaks. Nucl Fusion (2021) 61:086016. doi:10.1088/1741-4326/abf028

CrossRef Full Text | Google Scholar

18. Crabb D, Meyer W Solid polarized targets for nuclear and particle physics experiments. Annu Rev Nucl Part Sci (1997) 47:67–109. doi:10.1146/annurev.nucl.47.1.67

CrossRef Full Text | Google Scholar

19. Goertz S, Meyer W, Reicherz G Polarized H, D and 3He targets for particle physics experiments. Prog Part Nucl Phys (2002) 49:403–89. doi:10.1016/s0146-6410(02)00159-x

CrossRef Full Text | Google Scholar

20. Abragam A, Bouffard V, Roinel Y, Roubeau P A new polarized target material: 6LiD. J de Physique Lettres (1980) 41:309–10. doi:10.1051/jphyslet:019800041013030900

CrossRef Full Text | Google Scholar

21. Doshita N, Ball J, Baum G, Gautheron F, Goertz S, Hasegawa T, et al. The COMPASS polarized target in 2006 and 2007. In: AIP conference proceedings, Vol. 980 American Institute of Physics (2008). p. 307–11. doi:10.1063/1.2888101

CrossRef Full Text | Google Scholar

22. Mansfield D, Hill K, Strachan J, Bell M, Scott S, Budny R, et al. Enhancement of tokamak fusion test reactor performance by lithium conditioning. Phys Plasmas (1996) 3:1892–7. doi:10.1063/1.871984

CrossRef Full Text | Google Scholar

23. Xisheng W, Jiaquan Z The technology of developing a low density lithium hydride or lithium deuteride solid micro-target. China Nucl Sci Tech Rep (2001) 10.

Google Scholar

24. Roinel Y Possibility of building a polarized target of 6LiD. Tech Rep CEA Centre D’etudes Nucleaires de Saclay (1981) 458–9. doi:10.1007/978-3-0348-6301-8_51

CrossRef Full Text | Google Scholar

25. Babcock E, Nelson I, Kadlecek S, Driehuys B, Anderson L, Hersman FW, et al. Hybrid spin-exchange optical pumping of He3. Phys Rev Lett (2003) 91:123003. doi:10.1103/physrevlett.91.123003

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Mooney KE, Miller GW, Dolph P, Tobias WA, Nelyubin V, Singh J, et al. A 3-liter capacity, hybrid spin-exchange 3He polarizer for medical imaging. In: Proceedings of the 17th annual meeting of ISMRM (2009). p. 2166.

Google Scholar

27. Chen W, Gentile T, Ye Q, Walker T, Babcock E On the limits of spin-exchange optical pumping of 3He. J Appl Phys (2014) 116:014903. doi:10.1063/1.4886583

CrossRef Full Text | Google Scholar

28. Nikroo A, Czechowicz D, Castillo E, Pontelandolfo J Recent progress in fabrication of high-strength glow discharge polymer shells by optimization of coating parameters. Fusion Sci Technol (2002) 41:214–9. doi:10.13182/fst41-214

CrossRef Full Text | Google Scholar

29. Tafti S, Garrison WJ, Mugler JP, Shim YM, Altes TA, Mata JF, et al. Emphysema index based on hyperpolarized 3He or 129Xe diffusion MRI: performance and comparison with quantitative CT and pulmonary function tests. Radiology (2020) 297:201–10. doi:10.1148/radiol.2020192804

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Baylor L, Jernigan T, Combs S, Houlberg W, Murakami M, Gohil P, et al. Improved core fueling with high field side pellet injection in the DIII-D tokamak. Phys Plasmas (2000) 7:1878–85. doi:10.1063/1.874011

CrossRef Full Text | Google Scholar

31. Wei X, Bassa C, D’Angelob A, Deura A, Dezerna G, Kageyaa T, et al. Boosting deuteron polarization in HD targets: experience of moving spins between H and D with RF methods during the E06-101 experiment at Jefferson Lab. In: Proc. XVth int. Workshop polarized sources, targets and polarimetry (2014). p. 9–13.

CrossRef Full Text | Google Scholar

32. Combs SK, Baylor LR Pellet-injector technology—brief history and key developments in the last 25 years. Fusion Sci Tech (2018) 73:493–518. doi:10.1080/15361055.2017.1421367

CrossRef Full Text | Google Scholar

33. Combs S, Foust C, Gouge M, Milora S Acceleration of small, light projectiles (including hydrogen isotopes) to high speeds using a two-stage light gas gun. J Vacuum Sci Tech A: Vacuum, Surf Films (1990) 8:1814–9. doi:10.1116/1.576808

CrossRef Full Text | Google Scholar

34. Milora S, Combs S, Foust C Fast-opening magnetic valve for high-pressure gas injection and applications to hydrogen pellet fueling systems. Rev scientific Instr (1986) 57:2356–8. doi:10.1063/1.1138677

CrossRef Full Text | Google Scholar

35. Milora S, Houlberg W, Lengyel L, Mertens V Pellet fuelling. Nucl Fusion (1995) 35:657–754. doi:10.1088/0029-5515/35/6/i04

CrossRef Full Text | Google Scholar

36. Baylor L, Geraud A, Houlberg W, Frigione D, Gadeberg M, Jernigan T, et al. An international pellet ablation database. Nucl fusion (1997) 37:445–50. doi:10.1088/0029-5515/37/4/i02

CrossRef Full Text | Google Scholar

37. Lengyel L Pellet-plasma interaction: local disturbances caused by pellet ablation in tokamaks. Nucl fusion (1989) 29:37–48. doi:10.1088/0029-5515/29/1/004

CrossRef Full Text | Google Scholar

38. Parks P, Baylor LR Effect of parallel flows and toroidicity on cross-field transport of pellet ablation matter in tokamak plasmas. Phys Rev Lett (2005) 94:125002. doi:10.1103/physrevlett.94.125002

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Clegg TB Sources of spin-polarized beams (invited). Rev scientific Instr (1990) 61:385–8. doi:10.1063/1.1141300

CrossRef Full Text | Google Scholar

40. Sona P. A new method proposed to increase polarization in polarized ion sources of h- and d-. Energia Nucleare (1967) 14:295.

Google Scholar

41. Engels R, Büscher M, Buske P, Gan Y, Grigoryev K, Hanhart C, et al. Direct observation of transitions between quantum states with energy differences below 10 nev employing a sona unit. The Eur Phys J D (2021) 75:257. doi:10.1140/epjd/s10053-021-00268-4

CrossRef Full Text | Google Scholar

42. Chrien R, Strachan J d-3 he reaction measurements during fast wave minority heating in the plt tokamak experiment. Phys Fluids (1983) 26:1953–64. doi:10.1063/1.864344

CrossRef Full Text | Google Scholar

43. Andreyanov A, Fotyev V, Ivshin K, Kochenda L, Kravchenko P, Kravtsov P, et al. Study of ²H(d, p)³H and ²H(d, n)³He nuclear reactions with polarized deuteron beams. PolFusion experiment. Phys At Nuclei (2021) 84:1895–9. doi:10.1134/s1063778821100033

CrossRef Full Text | Google Scholar

44. Vasilyev A, Kochenda L, Kravtsov P, Trofimov V, Vznudaev M, Ciullo G, et al. The polfusion experiment: measurement of the dd-fusion spin-dependence. In: Nuclear fusion with polarized fuel. Springer (2016). p. 35–44.

CrossRef Full Text | Google Scholar

45. Becker B, Randermann R, Polke B, Lemaitre S, Reckenfelderbäumer R, Niessen P, et al. Measurement of a complete set of analyzing powers of the fusion reactions D(ěc d, p)³He at E _d=28 keV. Few-Body Syst (1992) 13:19–39. doi:10.1007/bf01080208

CrossRef Full Text | Google Scholar

46. Tagishi Y, Nakamoto N, Katoh K, Togawa J, Hisamune T, Yoshida T, et al. Analyzing powers for h 2 (d,p) 3 h at incident energies of 30, 50, 70, and 90 kev. Phys Rev C (1992) 46:R1155–8. doi:10.1103/physrevc.46.r1155

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Brown RE, Jarmie N Differential cross sections at low energies for ²H(d,p)³ and ²H(d,n)³He. Phys Rev C (1990) 41:1391–400. doi:10.1103/physrevc.41.1391

PubMed Abstract | CrossRef Full Text | Google Scholar