- 1School of Physics, Xidian Univeristy, Xi’an, China
- 2CORIA-UMR 6614, Normandie Université, CNRS, Université et INSA de Rouen, Mont-Saint-Aignan, France
Structured light refers to an optical field with modulated phase and amplitude, characterized by distinct spatial patterns. It has applications in optical manipulation, 3D imaging, remote sensing, and communications. The Generalized Lorenz-Mie Theory (GLMT) extends foundational Mie theory to accommodate complex structured lights, enabling precise characterization of structured light-particle interactions. GLMT has emerged as a central theoretical framework for analyzing interactions between spherical particles and arbitrary structured light. This paper introduces ABSphere, simulation software utilizing GLMT to model structured light-spherical particle interactions. It then comprehensively reviews representative structured lights, including Laguerre–Gaussian, Bessel, and Airy beams, elucidating their interactions with spherical particles. Understanding structured light scattering behavior is crucial for elucidating underlying interaction mechanisms with spherical particles. The paper also emphasizes the significance of modeling structured light scattering by particles and discusses future directions for ABSphere software. Through continuous theoretical refinements and advancements, deeper understanding of structured light-particle interaction mechanisms can be achieved, enabling innovations in optical applications and technologies.
1 Introduction
Structured light plays a pivotal role in various optics applications due to its distinct phase, amplitude, and vector distributions [1]. By precisely controlling these properties, intricate intensity patterns and specific optical effects can be generated, enabling accurate measurement and manipulation of particles. Structured light finds significant applications in diverse domains, including optical manipulation [2], 3D imaging [3, 4], sensing measurements [5], and optical communication [6], as shown in Figure 1. In interactions with particles, scattering emerges as the predominant process, encompassing light absorption, dispersion, and scattering itself [7]. Understanding optical scattering characteristics of particles enhances knowledge of light-particle interaction mechanisms and enables analysis of particle properties and morphology via scattered light analysis [8].
In 1908, Mie [9] derived an analytical expression for the scattering of plane electromagnetic waves by homogeneous spheres based on Maxwell’s equations, using the method of separation of variables. This led to the development of Lorenz-Mie theory, which allows calculating scattering intensity, phase, and directional distributions when plane electromagnetic waves interact with spherical particles of any size and material. Consequently, the theory has become fundamental in addressing light and electromagnetic scattering problems.
However, conventional Mie scattering theory has limitations in addressing the complexities of structured light. While numerical methods like Finite-Difference Time-Domain (FDTD) and Finite Element Method (FEM) can rigorously calculate interactions between structured light and particles, they are computationally expensive and lack comprehensive physical understanding of scattering processes. To overcome these limitations, G. Gouesbet et al. [10] pioneered using the Bromwich formula in 1988 to study far-field scattering of Gaussian beams by homogeneous medium spheres. This groundbreaking work led to developing Generalized Lorenz-Mie Theory (GLMT), continuously refined and expanded to address particle interactions with arbitrary structured light. GLMT has become a central theoretical framework for analyzing structured light-particle interactions, inheriting foundational Mie principles while extending applicability to polychromatic, polarized, and structured light scenarios [11]. GLMT imposes no restrictions on particle size, solving electromagnetic scattering characteristics and mechanical effects for spherical particles of any size within its theoretical framework. The primary focus of GLMT is solving beam shape coefficients (BSCs) associated with a given structured light, providing profound insight into physical mechanisms governing their particle interactions. Furthermore, GLMT offers more accurate and efficient solutions for optical manipulation and related research and applications [12].
As shown in Figure 2, the basic problem involves a spherical particle of specific size and optical properties, illuminated by structured light of specific intensity and phase distributions. The computational process involves several steps: First, based on laser wavelength, particle size, and refractive index distribution, the electromagnetic field distribution inside and around a spherical particle under plane wave incidence is determined using Mie scattering theory. The Mie scattering coefficients an and bn are calculated according to boundary conditions. Next, the electromagnetic field distribution of structured light is decomposed using mathematical methods, and the beam shape factor is calculated. The beam shape factor describes specific intensity and phase distributions of structured light. Finally, by combining the Mie scattering coefficients and beam shape factor, scattering and absorption characteristics of a spherical particle under structured light incidence are obtained. The GLMT provides a fast, efficient computational method to predict and analyze structured light-spherical particle interactions.
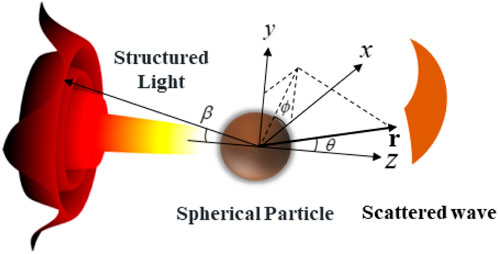
FIGURE 2. Fundamental problem of structured light scattering by a spherical particle under the framework of GLMT.
This paper first introduces ABSphere, simulation software for modeling interactions between structured light and spherical particles. It then comprehensively reviews representative structured lights: Laguerre–Gaussian (LG) beams, Bessel-type beams, and Airy beams. Elucidating their interactions with spherical particles using the GLMT framework, their scattering characteristics are investigated. Understanding these structured lights’ scattering behavior is crucial for elucidating their interaction mechanisms with spherical particles. The paper also emphasizes the significance of modeling structured light scattering by particles. Finally, it discusses future directions for ABSphere software, including exploring more complex structured lights and expanding applications. Through ongoing theoretical refinements and advancements, deeper understanding of structured light-spherical particle interaction mechanisms can be achieved, providing a solid theoretical foundation for optical application and technology advancements.
2 Simulation software ABSphere: modeling the interaction of structured light with a spherical particle
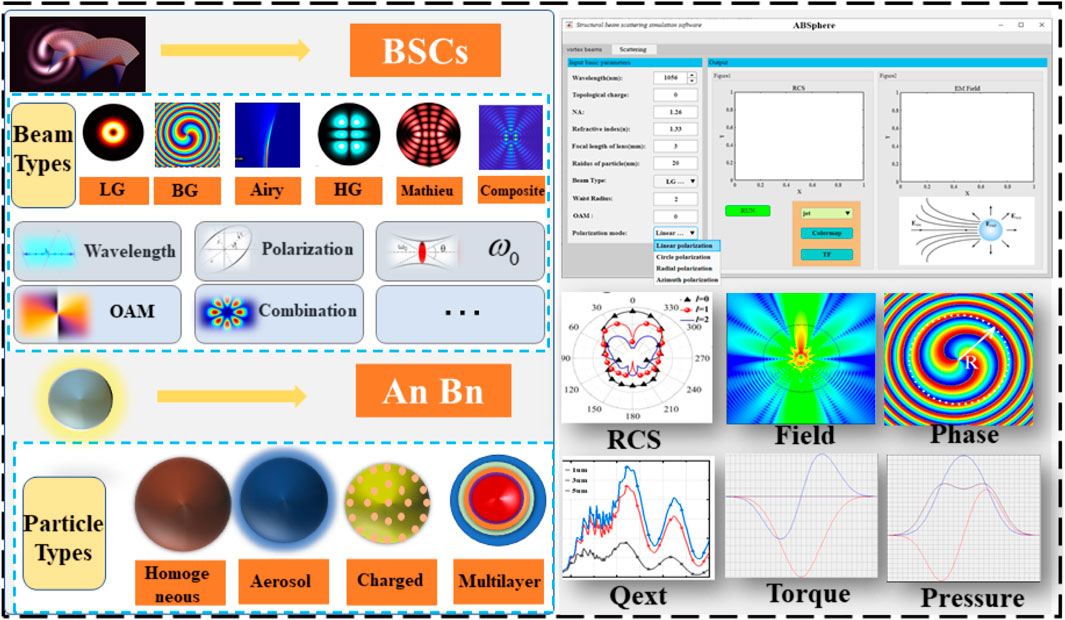
The distinct spatial intensity and phase distribution of structured light leads to significant variations in the BSCs across different types of structured light. These coefficients reflect diverse interaction modes between structured light with distinct intensity and phase distributions and play a crucial role in shaping significant differences in their scattering results [13]. Within the GLMT framework, BSCs emerge as critical parameters for delineating interaction dynamics between structured light and spherical particles. Researchers have developed BSCs algorithms for various structured lights, including localized approximation [14], extended boundary condition [15], angular spectrum expansion [16, 17], and one-dimensional orthogonal [18] methods. The aim is to precisely capture particle scattering characteristics associated with different structured lights, enabling detailed depiction of their interactions with spherical particles. Moreover, the type and structure of spherical particles discernibly influence scattering characteristics. Once the BSCs calculation method for structured light is established, different spherical particle types exhibit unique responses to structured light scattering behavior. By combining Mie scattering coefficients for diverse spherical particles, a comprehensive scattering model for structured light interacting with arbitrary particles can be formulated. Through investigating structured light scattering characteristics passing through various spherical particles, deeper understanding and effective utilization of interaction mechanisms between structured light and spherical particles can be achieved.
Within the GLMT framework, the scattering coefficients
Here, an and bn in Eq. 1 are the Mie coefficients of the spherical particle corresponding to electric magnetic - and magnetic-multipoles of order n, respectively, independent of beam shape coefficients, while the BSCs
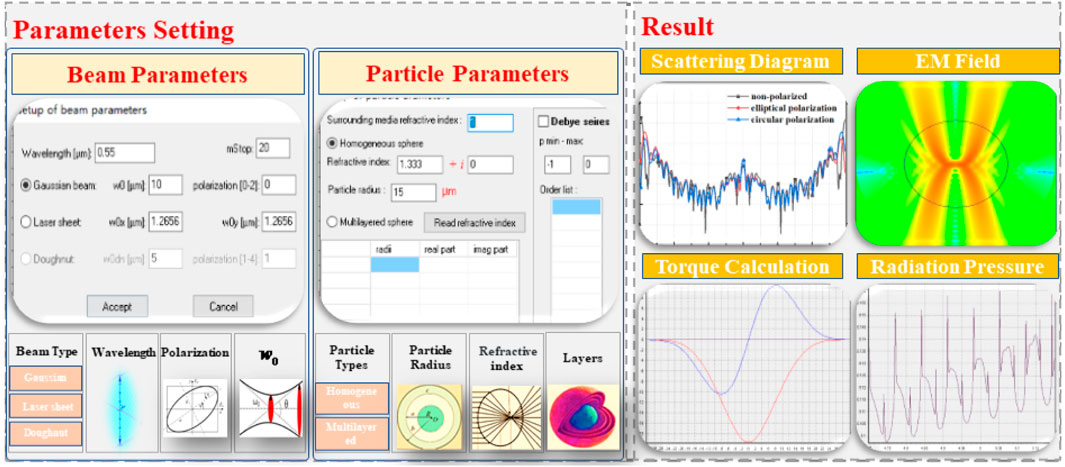
Developing simulation software modeling structured light interaction with spherical particles offers valuable resources for optical research. One such software, ABSphere has been developed [20] and is available online [21]. The numerical technique used in ABSphere for GLMT calculation was well-examined in [22]. The current version, ABSphere 1.10, calculates scattering diagrams, internal/near fields, radiation pressure force/torque on a spherical particle from structured light as functions of particle size/position. It integrates three type shaped beams: standard Gaussian beam, elliptical Gaussian beam and the dog-nut beam. The expansion of Mie scattering function in Debye series provides powerful tools for analyzing different order scattering concentrations, enabling in-depth exploration of structured light-matter interaction mechanisms. This software robustly supports theoretical studies and lays theoretical foundations for applying/advancing structured light techniques. By calculating and applying different structured light’s BSCs, the software now simulates interactions between complex structured light and a single spherical particle. ABSphere enhances understanding and optimizes particle scattering from structured light. Its user-friendly interface significantly aids education/training, enabling beginners to directly observe and comprehend complex structured light-particle scattering phenomena.
Figure 3 showcases the intuitive interface of Software ABSphere, featuring separate settings for beam source and particle parameters. This clear separation enhances usability and provides diverse modeling capabilities for structured light input. The software supports various types of structured light, including basic Gaussian beams, elliptical Gaussian beams, annular beams, and Bessel beams. Software ABSphere calculates waveform factors for different structured lights, enabling computation of scattering models for complex interactions with individual spherical particles. Users can select the desired type of structured light and adjust parameters like wavelength, beam width, and polarization state. This customization allows for generating intricate patterns tailored to specific research requirements.
Software ABSphere offers flexible particle parameter settings for scattering calculations of larger spherical particles, enabling adjustment of the number of layers and complex refractive indices to accommodate diverse simulation requirements. The software supports both homogeneous medium and multilayer sphere models, enabling more accurate simulation of particles in complex environments. This capability enhances simulation accuracy, closely aligning results with real-world scenarios.
Software ABSphere offers comprehensive scattering analysis, including radar cross-section (RCS) maps, electromagnetic field distribution, radiation pressure, torque, and extinction, scattering, and absorption factors. Enabling in-depth analysis of particle scattering characteristics and interactions with structured light, these features also support diverse structured light modeling, flexible parameter adjustment, realistic multilayer particle models, and comprehensive scattering analysis. A powerful and precise tool for studying light-matter interactions, Software ABSphere provides users with sophisticated tools to understand these complex phenomena.
The GLMT was initially developed to address far-field scattering problem of Gaussian beams by spherical particles [10]. To model scattering by other structured lights, Gaussian beam scattering data is often used for validation. Figure 4 depicts the scattering intensity distribution of Gaussian beams with varying complex refractive indices in a bilayer sphere model, calculated using Software ABSphere. Notably, as the inner layer refractive index increases, indicating a larger difference between inner and outer layers, the scattering intensity stabilizes in the backward scattering region (around 180°). Regardless of polarization state—unpolarized, circularly polarized, or elliptically polarized light—minimal fluctuations occur. However, for specific angles, unpolarized and circularly polarized light may exhibit scattering minima.
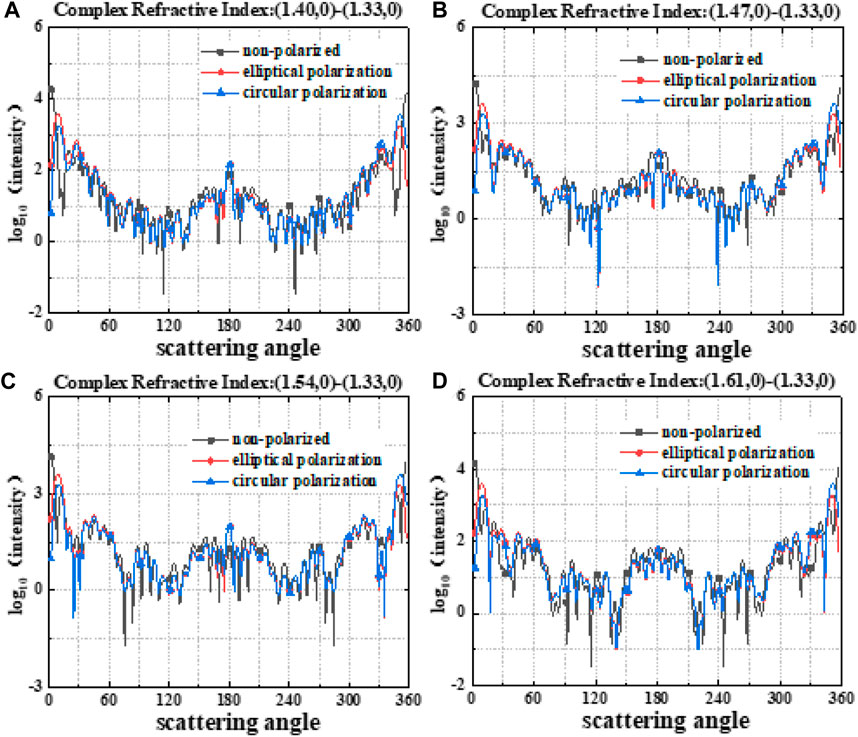
FIGURE 4. RCS plots of Gaussian beams with non-polarized, elliptical polarization, and circular polarization scattering from a bilayer spherical shell model under different complex refractive index scenarios, (A) \lambda_inner = 1.40, (B) \lambda_inner = 1.47, (C) \lambda_inner = 1.54, (D) \lambda_inner = 1.61.
When computing BSCs in structured light, it is important to consider various light source parameters like beam width, wavelength, polarization state, and incidence configuration (on-axis [23] or off-axis [24]) as they significantly affect scattering results. These effects can be analyzed by examining scattered spherical particle radiation distribution patterns. Figure 5 shows radiation patterns of Gaussian beams with different beam widths (5, 10, 15, 20 μm) scattered by uniform particles of varying sizes (15, 30, 45 μm). It demonstrates distinctive characteristics of Gaussian beams when scattered by spherical spheres. Decreasing beam width results in a narrower main lobe in the scattering radiation pattern, indicating a more concentrated scattering range and increased central radiation intensity. Larger spherical particles exhibit more concentrated main lobes in their scattering radiation patterns, reflecting higher energy. Conversely, smaller spherical particles display more uniform radiation distributions.
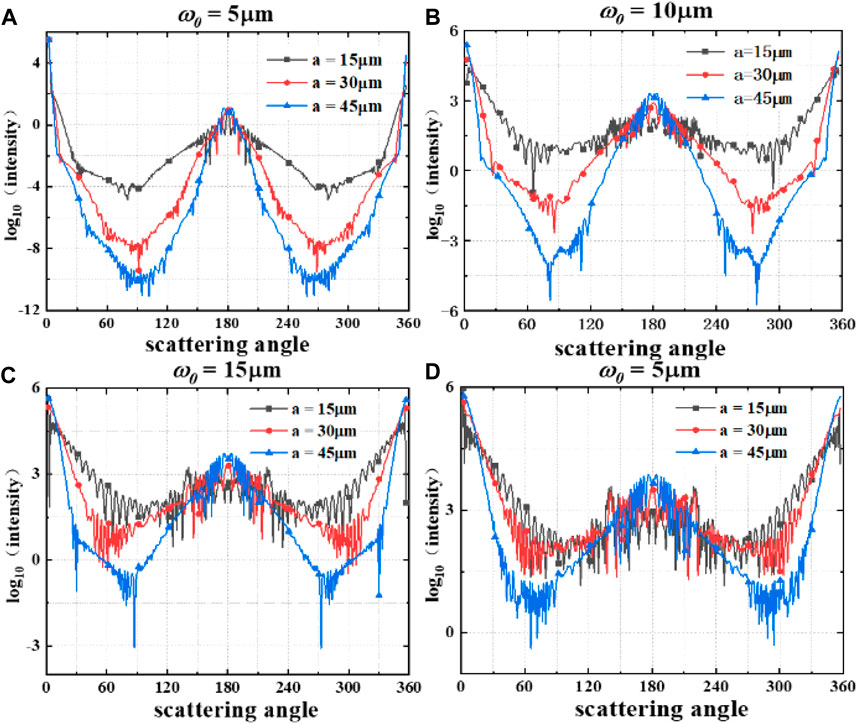
FIGURE 5. RCS plots of Gaussian beams with different particle sizes under different beam width radii conditions, (A) ω0 = 5 μm, (B) ω0 = 10 μm, (C) ω0 = 15 μm, (D) ω0 = 20 μm, all with a wavelength of 550 nm.
In investigating optical scattering behavior of particles, analyzing scattering force distributions provides an effective method to demonstrate interaction effects between structured light and spherical particles, including scattering angle variations and intensity differences. These distributions closely relate to factors like particle size and uniformity [25]. Figure 6 depicts scattering force distributions exerted by multilayer spherical particles with different layer numbers (single, 2, and 10) on Gaussian beams of varying wavelengths (384, 550, and 780 nm). These multilayer spherical particles may comprise various materials, with each layer possessing distinct refractive indices and thicknesses. Adjusting layer number and refractive index properties of multilayer spherical particles enables precise control over scattering force distribution and intensity.
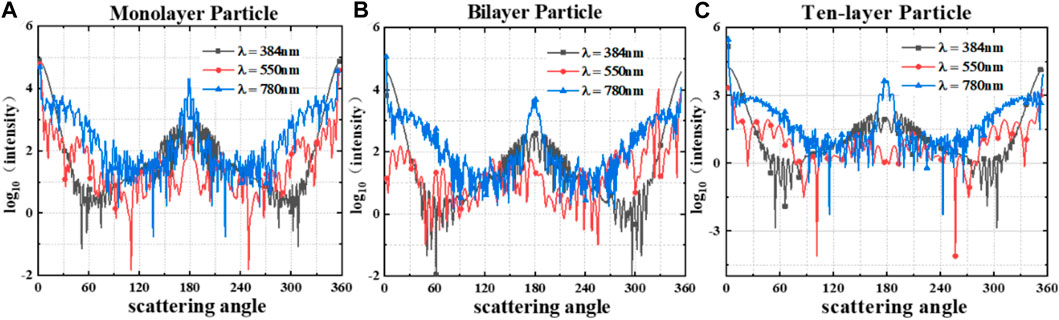
FIGURE 6. Scattering intensity of Gaussian beams with different wavelengths by spherical particles with varying numbers of layers, (A) homogeneous medium particles, (B) Bilayer particles, (C) Ten-layer particles. The beam width is 30 μm.
Figure 7 presents visualizations of intensity distributions within and outside particles for both on-axis and off-axis incidence of Gaussian and elliptical Gaussian beams. These offer insights into optical behavior and scattering characteristics of spherical particles. In conclusion, Software ABSphere is a powerful tool for investigating structured light interactions with spherical particles. It enables nuanced understanding of their scattering behavior and design of strategies to control scattering effects. By analyzing scattering force distribution and intensity, optimization of particle structure and properties becomes feasible, enabling achievement of specific scattering effects and desired optical performance.
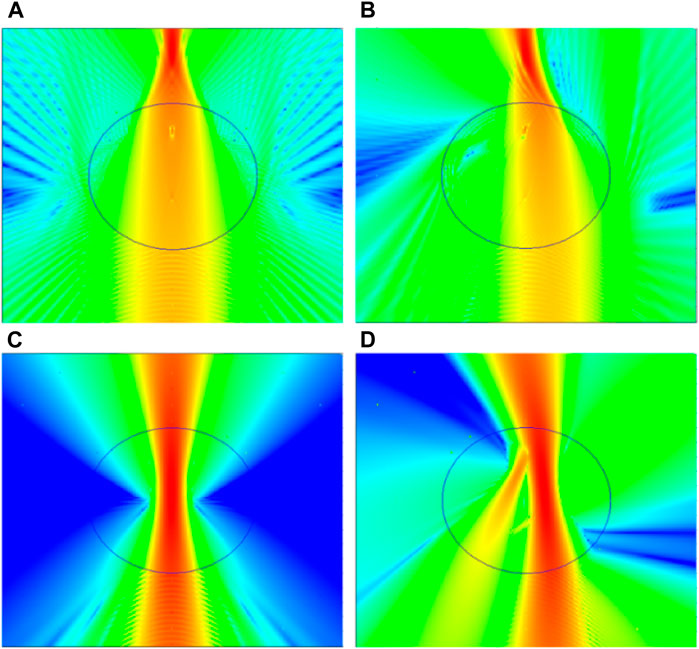
FIGURE 7. Scattering intensity distribution of different structured light by spherical particles. (A) On-axis Gaussian beam scattering, (B) Off-axis Gaussian beam (x = 3 μm) scattering, (C) On-axis elliptical Gaussian beam scattering, (D) Off-axis elliptical Gaussian beam (x = 3 μm) scattering.
3 Research on the Mie scattering characteristics of structured light
3.1 Modeling of particle scattering for LG beams
Since the seminal work by Allen et al. in 1992 [26] revealed that LG beams possess both orbital angular momentum (OAM) and spin angular momentum (SAM) due to their helical phase front structures, LG beams have garnered substantial attention. The unique phase structures of high-order LG beams result in axial forces several times stronger than those of fundamental Gaussian beams when trapping spherical particles [27, 28], establishing LG beams as vital components in precision optical manipulation [29]. Moreover, a detailed analysis of the scattering characteristics of LG beams with spherical particles enables extraction of fundamental microparticle parameters [30] and identification of source properties of LG beams [31]. These applications rely on theoretical simulation models within the GLMT framework [8].
The integral method is a common approach for calculating the BSCs of Gaussian beams, but can be computationally slow for LG beams. To enhance efficiency, the localized approximation method has been employed [32]. However, caution is warranted as this method has limited accuracy in describing LG beams. To address this limitation, the finite series method [33, 34] and the angular spectrum expansion method [35] have been increasingly adopted, significantly improving the efficiency of calculating BSCs [36]. Recently, Votto et al. proposed a calculation method for the BSCs of freely propagating LG beams based on the finite series algorithm [37], providing closed-form expressions and eliminating dependence on recursive algorithms.
Exploration of LG beam interactions with spherical particles has largely centered on understanding the influence of optical OAM modes on particle scattering characteristics. Such research enriches knowledge of OAM in light-matter interactions. Rury et al. [38] developed a model for Mie scattering of circularly polarized LG beams by spherical particles, confirming significant OAM roles in light-matter interactions. Zambrana-Puyalto et al. [39] further investigated LG beam scattering by dielectric spheres, showing LG beams enhance ripple structure due to OAM conservation during scattering. Additionally, Kiselev et al. [40] used far-field matching to study intensity distribution and phase variation of LG beams scattered by particles in the near field. Their study revealed photon nanojet morphology and optical vortex near-field structure sensitivity to OAM mode numbers. These findings highlight OAM’s significant impact on LG beam-spherical particle interactions and emphasize its critical role in investigating the Mie scattering characteristics of LG beam.
Figure 8 illustrates the E-plane RCS of a first-order LG beam under different beam widths, wavelengths, and particle sizes for uniform spherical scatterers. The forward scattering intensity is markedly higher than backward, consistent with most beams. In Figure 8A, increasing beam width enhances scattering in all directions. Similarly, larger particles (Figure 8B) increase scattering intensity in all directions. This can be attributed to the larger beam width or particle size leading to higher incident intensity and consequently increased scattering. However, Figure 8C shows scattering intensity decreases with wavelength. Nevertheless, larger wavelengths result in more pronounced fluctuation in scattering intensity across angles.
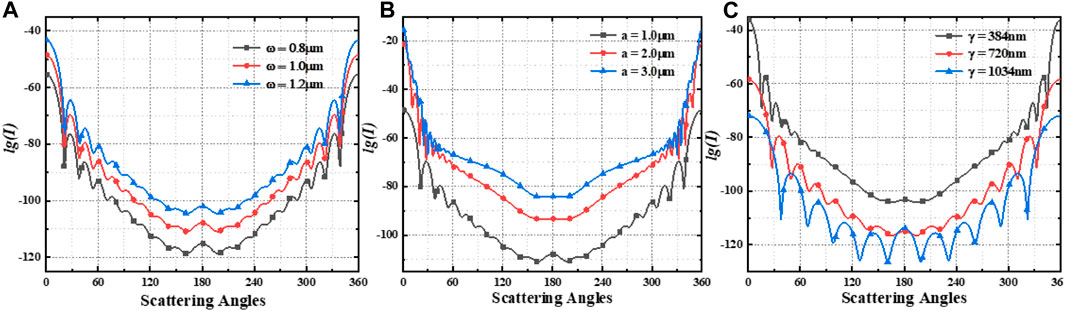
FIGURE 8. E-plane RCS of LG beams with different waist radii (A), particle sizes (B), wavelengths (C), and scattering by homogeneous medium spherical particles.
In recent years, extensive research has been conducted on the scattering properties of diverse spherical particle types, including homogeneous dielectric spheres [41], ellipsoidal particle spheres [42], uniaxial anisotropic spheres [43], chiral particle spheres [44], perfect electric conductor spheres [45], and more. This research focuses on understanding the effects of spherical particles on post-scattering parameters of structured light. The unique characteristics of these spherical particles, such as shape, size, structural features, charge, and relative refractive index, significantly influence their scattering properties. In addition to exploring spherical particle effects, these studies also delve into complex aspects like RCS and radiation force distributions. Moreover, the application of structured light scattering studies has expanded to encompass complex biological cell spheres [46]. By studying structured light scattering on biological cell spheres, researchers gain insights into cellular structures, properties, and dynamics.
Advancing research on structured light-particle interactions is shifting focus towards studying structured light-suspended particle scattering in the atmosphere [47]. Understanding structured light propagation and scattering is important for developing novel imaging and sensing technologies, exploring fundamental phenomena, and understanding light-matter interactions in complex media. In the atmosphere, diverse suspended particles with varying compositions and forms exist, including aerosols, haze, raindrops, and dust [48]. These are often approximated as spherical particles for computing scattering and extinction characteristics via Mie scattering theory. For instance, Shi et al. [49], as shown in Figure 9, used a Mie scattering model of LG beams with individual spherical particles to investigate LG beam transmission in a haze environment. They found LG beams exhibit stronger penetration than Gaussian beams.
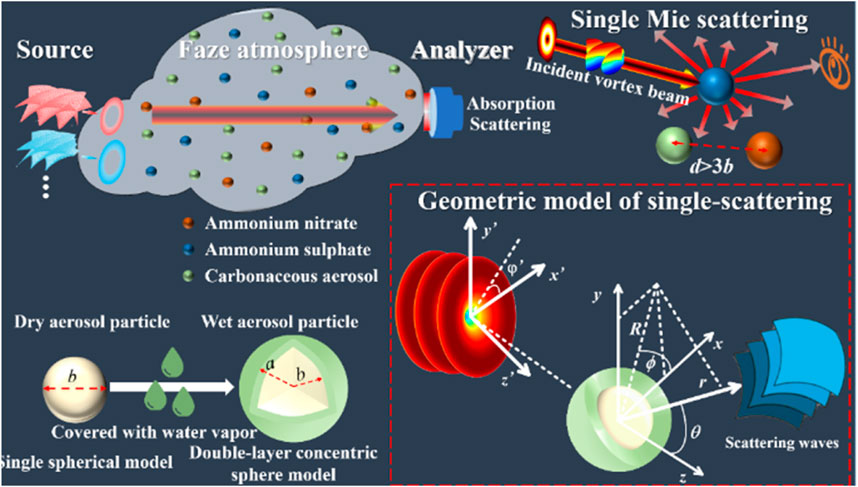
FIGURE 9. Schematic diagram of remote sensing of haze atmospheric aerosols based on vortex scattering [49].
Furthermore, integrating a single-sphere scattering model of LG beams with raindrop particles and a size distribution model of raindrops enabled discussing transmission attenuation characteristics of LG beams in rainy environments, confirming their transmission advantage [50]. Additionally, applying the complex source point method within the GLMT framework studied scattering characteristics of LG beams by marine-type aerosol particles [51]. These works provide critical theoretical and simulation foundations for deeper understanding particle scattering behavior in response to structured light and optical environment characteristics in the atmosphere.
3.2 Modeling of particle scattering for Bessel-type beams
Bessel beams, introduced by Durnin in 1987, represent a distinct class of light beams offering diffraction-free solutions satisfying the Helmholtz equation [52]. Unlike conventional Gaussian beams, Bessel-type beams maintain an unaltered transverse intensity distribution during propagation. Their remarkable ability to self-reconstruct enables them to recover their beam profile even after encountering obstacles or distortions over a specified transmission distance. These characteristics provide significant advantages for optical manipulation [53] and microscopy imaging [54]. In contrast, conventional Gaussian beams face challenges at the focal plane when encountering particle distortions, resulting in strong divergence and difficulties capturing particles simultaneously at multiple positions [53]. Bessel-type beams overcome this limitation with their self-reconstruction capability and stable transverse intensity distribution. Furthermore, Bessel-type beams exhibit strong penetration abilities, ensuring relatively stable transmission properties in heterogeneous media and possessing a larger penetration depth [54]. Consequently, they are invaluable for imaging and manipulation applications in inhomogeneous media.
Applications of Bessel-type beams often involve interactions with particles. Establishing a Mie scattering model for this interaction provides new perspectives and tools for exploring the complex process. Modeling the Mie scattering of Bessel-type beams within the GLMT framework requires deriving and calculating the BSCs, much like models used for LG beam scattering by spherical particles. Various methods have been employed to derive the BSCs of Bessel-type beams for studying their scattering characteristics with spherical particles. Traditional numerical integration methods are relatively complex for calculating the BSCs of Bessel-type beams [55, 56]. To address this complexity, Taylor and Love improved the calculation formula for BSCs, achieving much faster calculations and facilitating quicker Mie scattering calculations [57]. Other methods for deriving the BSCs of Bessel beams include localized approximation, angular spectrum expansion, surface integral equation, finite series expansion, and multi-level finite series expansion [58–61]. The localized approximation method, as demonstrated by Ambrosio et al. [59], offers comparable calculation speeds to numerical integration methods. The angular spectrum expansion method, used by Chen and Qin [62, 63], provides explicit analytical expressions for the BSCs of arbitrary-order polarized Bessel beams and has gained prominence as a reference method in the GLMT framework [64, 65]. Additionally, finite series algorithms, surface integral equation methods, and beam superposition algorithms contribute to the calculation of BSCs of Bessel beams [66–68]. Wang et al. [69] proposed a simpler approach using traditional integration methods to directly calculate the BSCs of Bessel beams. These diverse methods offer researchers different avenues to derive BSCs, enabling them to compare and choose the most accurate method for describing the interaction between Bessel beams and spherical particles.
Numerous studies have investigated scattering characteristics of Bessel-type beams with various structures interacting with spherical particles. They examined zero-order Bessel beams [70–73], higher-order Bessel beams [74], multi-order Bessel-Gaussian (BG) beams [75], and vector Bessel beams [76–78]. The focus was understanding source parameter effects on post-scattering behavior of Bessel-type beams. Parameters included incident half-cone angle (or wavefront parameter), wavelength, polarization state, beam width radius, and mode order. A critical characteristic of Bessel-type and other vortex beams is OAM. Shi et al. [79] studied the OAM spectrum of vector BG beams after particle scattering, as shown in Figure 10. This research provides valuable insights into changes in OAM characteristics of structured light following microparticle scattering. Precise theoretical derivation within the GLMT framework has greatly facilitated exploration of this typical structured light’s scattering behavior.
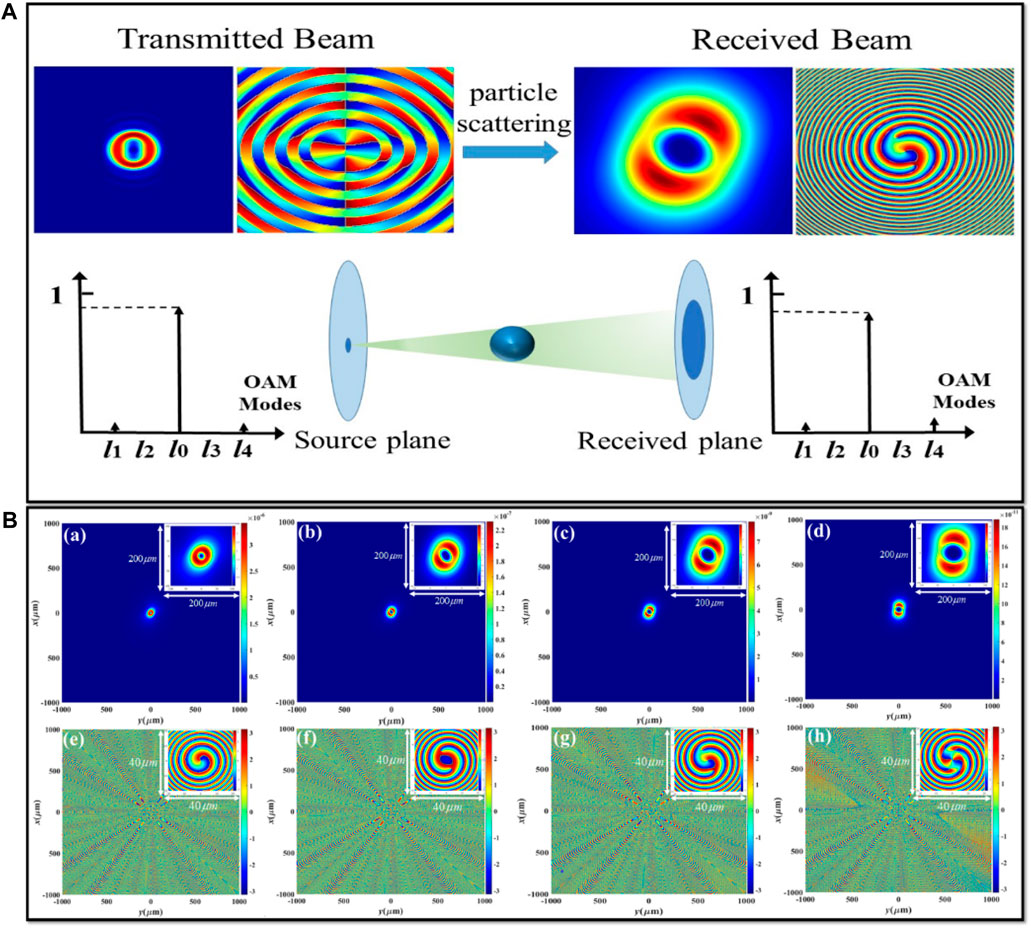
FIGURE 10. (A) Schematic diagram illustrating the impact of particle scattering on the OAM of vortex beams. (B)Intensity and phase distribution of superimposed fields in the far field Region [79].
Researchers have investigated not only scattering characteristics but also the distribution of radiation forces on Bessel-type beams after scattering by various spherical particles to enhance their utility for optical manipulation. For example, Sun et al. [80] investigated the longitudinal and transverse optical trapping forces of vector Bessel beams on a uniform sphere. Figure 11 illustrates differences in scattering efficiency factors of BG beams by double-layer spherical-shell particles under different humidity conditions, simulating aerosol particle models of varying humidity. Analysis shows aerosol spherical particles with higher humidity exhibit elevated scattering efficiency factors and weaker absorption effects. This is attributed to smaller complex refractive indices (including real and imaginary parts) of more humid aerosol particles, leading to more pronounced scattering compared to drier particles.
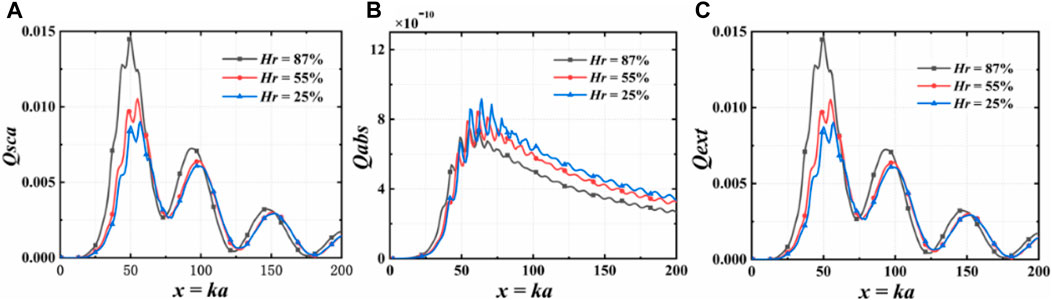
FIGURE 11. Scattering efficiency factor (A), absorption efficiency factor (B), extinction efficiency factor (C) of dual-layer spherical shells at different humidity.
In recent years, comprehensive studies have been conducted on the scattering characteristics of Bessel-type beams by various spherical particles within the framework of GLMT. These studies have examined charged spherical particles [81–83], double-layer concentric spherical particles [84, 85], biological spherical particles [86–88], multi-layer spherical particles [89, 90], negative refractive index spherical particles [91], metallic spherical particles [92], non-volatile spherical particles [93], and non-uniform spherical particles [94], among others. By leveraging the GLMT, distinct particle scattering models are established in simulations for single-layer, multi-layer, or differently shaped particles by combining the BSCs and particle scattering coefficients and applying various boundary conditions. For instance, Shi et al. [95] conducted a study on the scattering characteristics of vector BG beams on sand dust particles. The investigation focused on factors such as the polarization mode and incident angle, both of which significantly influence the scattering behavior.
The efficiency factor, derived from the differential RCS, is a critical physical parameter characterizing scattering, absorption, and extinction of interacting spherical particles. Figure 12 shows the influence of the OAM mode number, beam width, and polarization mode of BG beams on the scattering efficiency factor (Qsca), absorption efficiency factor (Qabs), and extinction efficiency factor (Qext). BG beams with varying OAM mode orders exhibit significantly different intensity distributions. As the OAM mode order decreases, the dark core size decreases, leading to larger scattering, absorption, and extinction efficiency factors after interaction with spherical particles. This suggests more beam energy is absorbed and scattered by the spherical particles. Therefore, BG beams with higher OAM mode orders demonstrate better transmission performance and slower decay in complex particle environments. Additionally, BG beams with larger beam width exhibit larger scattering, absorption, and extinction efficiency factors, as a larger beam width corresponds to a larger spot size, resulting in more energy incident on the particles and stronger scattering and absorption effects, leading to larger efficiency factors. Furthermore, Figures 12G–I showcase the particle scattering characteristics of BG beams with different polarization states, including linear, unpolarized, circular, azimuthal, and radial polarizations. The results reveal consistent efficiency factor variations across polarization states at different particle positions. However, unpolarized and circularly polarized BG beams demonstrate relatively larger efficiency factors, while the efficiency of linear, radial, and azimuthal polarized beams remains consistent. This suggests unpolarized and circularly polarized BG beams exhibit superior transmission performance in scattering medium.
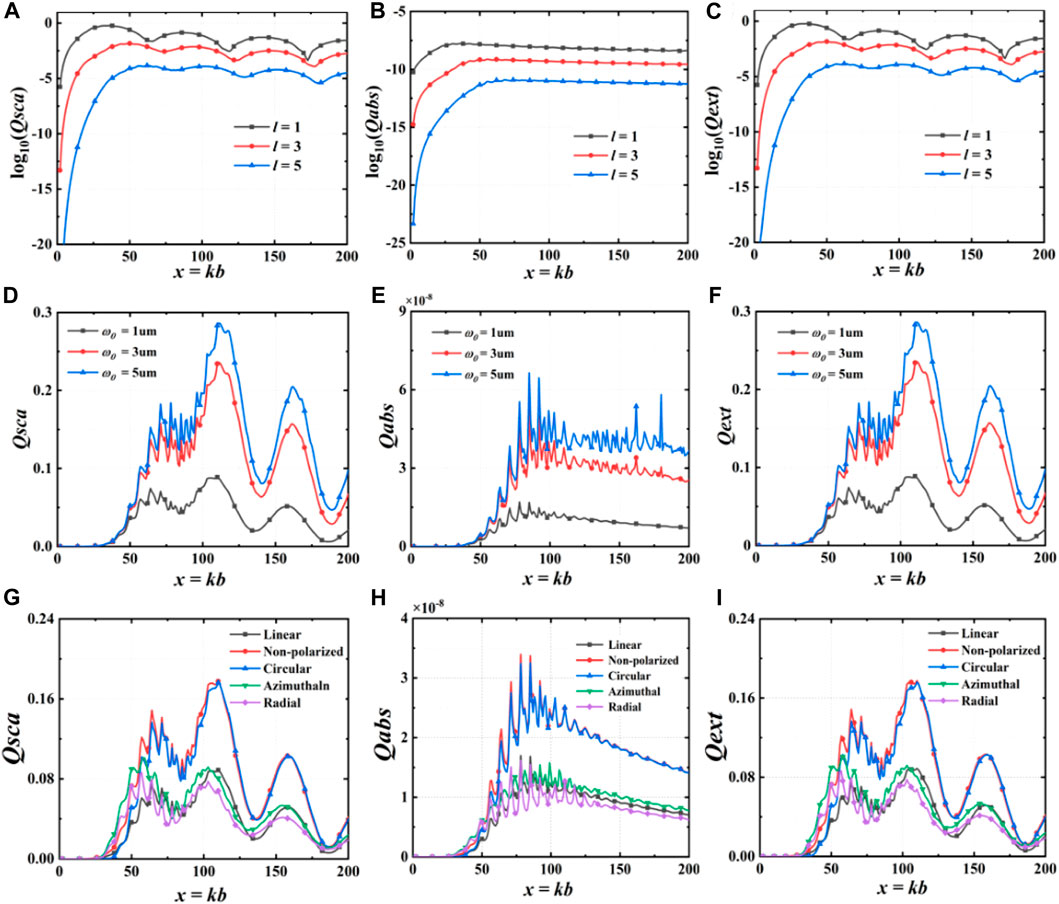
FIGURE 12. Influence of different azimuthal orders (A–C), beam widths (D–F), and polarization modes (G–I) of BG beams on the scattering efficiency factor (A, D, G), absorption efficiency factor (B, E, H) and extinction efficiency factor (C, F, I) of spherical particle scattering.
3.3 Modeling of particle scattering for other types of structured light
Structured light, including Airy beams, has been widely utilized in various fields such as optical trapping and imaging. Airy beams possess unique properties advantageous for applications in micro-nano fabrication, optical trapping, and imaging [96]. They exhibit non-diffracting and self-healing properties with high transmission stability during propagation. Additionally, Airy beams demonstrate self-acceleration with a highly concentrated beam intensity along the main propagation direction, rendering them effective in micro and nanoscale particle manipulation.
While investigating Airy beam interactions with spherical particles, Lu leveraged the GLMT and Maxwell stress tensor method for full-wave simulations. Findings confirmed the optical manipulation capabilities of Airy beams on chiral spherical particles [97], chiral nanoparticles [98], and Mie scattering particles [99]. Notably, chiral spherical and other non-homogeneous particles exhibited reduced scattering within specific regions, providing manipulation advantages using Airy beams [100]. Moreover, Airy beam scattered radiation attracted spherical particles into the main intensity field [101], influenced by factors including relative refractive index, size, and position [102, 103]. These insights deepen Airy beam-particle interaction understanding, enabling potential particle manipulation applications. Subsequent research probed more complex particle scattering, including double-layered [104] and multi-layered spherical particles [105]. Despite added complexity, plane wave spectrum methods simplified Airy beam scattering problems with such particles, significantly enhancing computational efficiency [104–106]. Additionally, Airy beam benefits extend to metallic particles [107]. Previous studies focused largely on typical Airy beams, circular Airy beams, and polarization properties. However, Shahabadi et al. investigated a novel petal-shaped Airy vortex beam, created by superimposing two circular Airy vortex beams with opposite topological charge signs. This unique beam effectively guides and captures particles [108].
Researchers have explored interactions between spherical particles and various structured light, including Hermite-Gaussian, Lommel, Mathieu beams, and Hermite-Gaussian beams. Conventional methods using finite series expansion calculate Hermite-Gaussian beam BSCs, but Li and Huang introduced the complex source point method for higher-order Hermite-Gaussian BSCs [109, 110]. They researched Hermite-Gaussian scattering by multi-layered spherical particles and marine aerosols. Another approach, proposed by Votto et al., simplifies BSC calculation by directly deriving them from Lommel beam BSCs. Lommel beam BSC derivation primarily relies on integral localization approximation and surface integral equation methods [111]. Chafiq and Cui expanded these to study Lommel scattering by homogeneous and non-homogeneous spherical particles, investigating beam polarization effects [112, 113]. Within GLMT, Mathieu and cylindrical vector beam scattering by spheres has also been investigated [114, 115]. These beams represent only a subset of explored structured light, holding significant research value in optical communications, manipulation, and sensing. GLMT’s accurate calculation model proves indispensable for studying structured light-particle interaction.
4 Significance and developments in particle scattering with structured light
4.1 Significance of structured light particle scattering
The significance of structured light cannot be overstated, offering rich optical properties and a wide range of applications. These properties and applications provide ample flexibility and innovation in designing optical devices and systems. By utilizing structured light, scientists and engineers can precisely control intensity and phase structures, enabling more efficient and accurate optical manipulations and controls, markedly enhancing optical device performance and application effectiveness. Structured lights drive development of optical devices and applications, paving the way for new optical technology innovations and applications. In the specific subject of particle scattering in structured lights, several key aspects should be considered. Firstly, the intricate phase and intensity distribution of structured light can profoundly influence particle scattering behavior. This scattering behavior depends significantly on the structured light’s properties, understanding this relationship paramount for optimizing optical device performance.
For instance, employing structured lights, which are beams of light engineered to exhibit unique topological features like doughnut or vortex beams, can elicit distinctive scattering phenomena. Particles interacting with these structured lights may experience OAM transfer, generating non-trivial scattering patterns and enhancing overall scattering outputs. This offers researchers precise control and manipulation of particles during scattering experiments, opening opportunities for scientific exploration. Additionally, the polarization properties inherent in structured lights also dictate the nature of particle scattering. Structured light can be meticulously engineered and designed to manifest well-defined polarization states, ranging from linear, circular, elliptical, radial, angular or even more complex polarization states. Particles’ scattering characteristics exhibit profound sensitivity to the precise polarization state of the incident beam. Rigorous, detailed analysis of the polarization properties of scattered light can yield valuable insights into the size, shape, and refractive index of the particles involved, painting a more comprehensive picture of their light interactions. Moreover, the intricate dynamics of multiple particle interactions within a structured light can be meticulously explored. The relative positions and distances between individual particles, along with their unique scattering properties, play significant roles in eliciting a range of interesting collective scattering phenomena. Such investigations facilitate deeper understanding of particle-particle interactions and unravel the complexities of scattering dynamics within structured light beams. Structured lights offer a versatile, multifaceted platform for delving deep into the intricate world of particle scattering phenomena. Their tailored properties, such as meticulously controlled phase distribution, carefully honed intensity profile, and distinct polarization states, serve as critical tools in enhancing our understanding and utilization of scattered light for diverse applications spanning microfluidics, particle sorting, optical trapping, and even biological sensing.
The Mie theory, a fundamental principle meticulously refined and developed by numerous scientists over a century, has undergone significant transformation. Its latest iteration, the GLMT, emerged as an indispensable analytical framework for rigorous investigations into the intricate electromagnetic scattering properties of regular-shaped particles. Applicable not only to basic particle models like simple homogeneous spheres, but also to more complex entities including charged, magnetic, and multi-layered particles, the theory significantly broadened the scope of its applicability. The far-reaching implications of the GLMT have been instrumental in elucidating the intricate dynamics of scattering phenomena across a wide range of complex atmospheric environments, from atmospheric aerosols and dust particles to haze. The theory’s utility extends beyond mere elucidation, proving invaluable in enhancing our understanding across diverse disciplines including atmospheric science, optical imaging, and remote sensing. Expansion of Mie theory, moving beyond simple spherical constructs to incorporate more intricate geometries like ellipsoids, cylinders, and other forms of irregularity, has paved the way for nuanced and realistic investigations into our environment’s intricate workings. This has enabled more accurate modeling and prediction of atmospheric phenomena, thereby deepening our understanding of the intricate interplay among various environmental elements.
4.2 The development of simulation software ABSphere
Structured light, a class of light beams characterized by distinct intensity and phase patterns, has proven instrumental in numerous sophisticated optical applications, including optical communication, structured light imaging, and optical manipulation. Given their diverse and profound utility, enhancing simulation capabilities for structured light particle scattering represents a paramount study objective. We seek to elucidate nuances of particle scattering, particularly concerning structured light. Composite beams and structured light arrays, currently garnering significant scholarly attention, offer superior transmission efficiencies and remarkable stabilization traits over single-beam counterparts. Our focus is keenly fixed on emergent composite beams and arrays - components of the acclaimed ABSphere series. We seek to deepen understanding of scattering phenomena associated with these intricate structured lights. This quest is not merely superficial, but an endeavor to unravel complexities and uncover latent utilities in this rapidly evolving sphere.
In addition, the current software faces limitations in calculating diverse particle models. Efforts are underway to introduce more complex models for accurate real-world scenario representation. Anticipating continuous development by dedicated researchers, an accurate, efficient, comprehensive software solution is sought to aid fundamental research, education, and teaching. Collaborative efforts can significantly advance optical science and engineering, deepen understanding of structured light-micro-particle interactions, optimize optical designs, and enable innovative applications.
As shown in Figure 13, in subsequent development of the innovative ABSphere software, our primary focus will be significantly expanding the types of beams it can handle. Building on existing capabilities, including standard Gaussian, elliptical Gaussian, and dog-nut beams, we aim to integrate a wide range of more complex structured lights, such as LG, Bessel-type, Airy, Hermite-Gaussian, and Mathieu. We also plan to incorporate multiple superimposed beams, providing significantly more comprehensive and accurate scattering simulations for studying and applying structured light beam scattering. Using a computational model from GLMT, with corresponding BSCs, we can precisely calculate a plethora of scattering characteristics for relevant particles. This includes near-field, internal field, far-field distribution, RCS, scattering efficiency factor, radiation torque, radiation pressure, and scattering angle distribution. We are committed to providing more accurate inputs and expanding calculation ranges for beam parameters impacting BSCs, including wavelength, beam width, and polarization. Figure 13 also depicts the planned interface for subsequent ABSphere development, giving an intuitive understanding of our research directions and ambitions. We hope this enhanced software will substantially contribute to education, research, and practical applications.
5 Conclusion
The paper introduces the application of ABSphere, a simulation software, for analyzing complex interactions between structured light and different particle types. Serving as a valuable tool for investigating microparticle-structured light interaction, the study provides a comprehensive overview of particle scattering in structured light contexts, focusing on GLMT-based analysis. It explores scattering properties associated with various structured lights such as LG, Bessel-type, and Airy beams. Understanding these structured lights’ scattering behaviors is essential for comprehending their interaction mechanisms with spherical particles. Highlighting the significance of modeling structured light scattering by particles, the paper suggests future research directions for ABSphere, including broadening applications and investigating complex structured lights. Through ongoing theoretical refinements and advancements, this research aims to deepen understanding of interaction mechanisms between structured light and spherical particles, laying a solid foundation for advancements in optical applications and technologies.
Author contributions
MC: Writing–original draft. YC: Investigation, Writing–original draft. KR: Writing–review and editing. HZ: Software, Writing–original draft. LG: Conceptualization, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the 111 Project (B17035), National Natural Science Foundation of China (Grant No. U20B2059, 193 61905186, 62231021, 61901336, 61621005), Shanghai Aerospace Science and Technology Innovation Foundation (SAST-2022-069), Shaanxi Province Natural Science Foundation (Grant No. 2023-JC-YB-511) and Key Research and Development Program Project of Weinan City in 2022 (Grant No. WSYKJ2022-1).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Forbes A, de Oliveira M, Dennis MR. Structured light. Nat Photon (2021) 15(4):253–62. doi:10.1038/s41566-021-00780-4
2. Yang Y, Ren YX, Chen M, Arita Y, Rosales-Guzmán C. Optical trapping with structured light: a review. Adv Photon (2021) 3(3):034001. doi:10.1117/1.ap.3.3.034001
3. Fahrbach FO, Simon P, Rohrbach A. Microscopy with self-reconstructing beams. Nat Photon (2010) 4(11):780–5. doi:10.1038/nphoton.2010.204
4. Geng J. Structured-light 3D surface imaging: a tutorial. Adv Opt Photon (2011) 3(2):128–60. doi:10.1364/aop.3.000128
5. Zhang S. High-speed 3D shape measurement with structured light methods: a review. Opt lasers Eng (2018) 106:119–31. doi:10.1016/j.optlaseng.2018.02.017
6. Rubinsztein-Dunlop H, Forbes A, Berry MV, Dennis MR, Andrews DL, Mansuripur M, et al. Roadmap on structured light. J Opt (2016) 19(1):013001. doi:10.1088/2040-8978/19/1/013001
7. Bohren CF, Huffman D. Absorption and scattering of light by small particles. New York: John Wiley (1983).
8. Van de Nes AS, Torok P. Rigorous analysis of spheres in Gauss-Laguerre beams. Opt Express (2007) 15(20):13360–74. doi:10.1364/oe.15.013360
9. Mie G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Annalen der physik (1908) 330(3):377–445. doi:10.1002/andp.19083300302
10. Gouesbet G, Maheu B, Gréhan G. Light scattering from a sphere arbitrarily located in a Gaussian beam, using a Bromwich formulation. JOSA A (1988) 5(9):1427–43. doi:10.1364/josaa.5.001427
12. Gouesbet G. Generalized Lorenz--Mie theories and mechanical effects of laser light, on the occasion of Arthur Ashkin’s receipt of the 2018 Nobel prize in physics for his pioneering work in optical levitation and manipulation: a review. J Quantitative Spectrosc Radiative Transfer (2019) 225:258–77. doi:10.1016/j.jqsrt.2018.12.015
13. Ren KF, Gréha G, Gouesbet G. Radiation pressure forces exerted on a particle arbitrarily located in a Gaussian beam by using the generalized Lorenz-Mie theory, and associated resonance effects. Opt Commun (1994) 108(4-6):343–54. doi:10.1016/0030-4018(94)90673-4
14. Ren KF, Gouesbet G, Gréhan G. Integral localized approximation in generalized Lorenz–Mie theory. Appl Opt (1998) 37(19):4218–25. doi:10.1364/ao.37.004218
15. Zheng M, Zhang H, Sun Y, Wang Z. Scattering of on-axis Gaussian beam by an arbitrarily shaped chiral object. J Quantitative Spectrosc Radiative Transfer (2015) 151:192–7. doi:10.1016/j.jqsrt.2014.10.001
16. Chafiq A, Gouesbet G, Belafhal A. On the beam shape coefficients of fundamental nondiffracting beams. J Quantitative Spectrosc Radiative Transfer (2020) 241:106750. doi:10.1016/j.jqsrt.2019.106750
17. Ren KF, Gréhan G, Gouesbet G. Scattering of a Gaussian beam by an infinite cylinder in the framework of generalized Lorenz–Mie theory: formulation and numerical results. JOSA A (1997) 14(11):3014–25. doi:10.1364/josaa.14.003014
18. Wang W, Shen J. Beam shape coefficients calculation for an elliptical Gaussian beam with 1-dimensional quadrature and localized approximation methods. J Quantitative Spectrosc Radiative Transfer (2018) 212:139–48. doi:10.1016/j.jqsrt.2018.03.026
19. Gouesbet G, Lock JA, Gréhan G. Generalized Lorenz–Mie theories and description of electromagnetic arbitrary shaped beams: localized approximations and localized beam models, a review. J Quantitative Spectrosc Radiative Transfer (2011) 112(1):1–27. doi:10.1016/j.jqsrt.2010.08.012
20. Ren KF. Absphere - calcul scientifique d’interaction faisceau laser de forme quelconque avec une particule sphérique (2012). patent.
21. Amocops. Advanced methods for optical characterization of complex particle systems (2023). Available at: https://amocops.univ-rouen.fr/en/content/download.
22. Ren KF, Shen J. Scattering of shaped beams by large particles: theoretical interpretation and numerical techniques. Springer Ser Light Scattering (2021) 7:125–58. doi:10.1007/978-3-030-87683-8_4
23. Lock JA, Gouesbet G. Rigorous justification of the localized approximation to the beam-shape coefficients in generalized Lorenz–Mie theory. I. On-axis beams. JOSA A (1994) 11(9):2503–15. doi:10.1364/josaa.11.002503
24. Gouesbet G, Lock JA. Rigorous justification of the localized approximation to the beam-shape coefficients in generalized Lorenz–Mie theory. II. Off-axis beams. JOSA A (1994) 11(9):2516–25. doi:10.1364/josaa.11.002516
25. Ren KF, Gréhan G, Gouesbet G. Prediction of reverse radiation pressure by generalized Lorenz–Mie theory. Appl Opt (1996) 35(15):2702–10. doi:10.1364/ao.35.002702
26. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45(11):8185–9. doi:10.1103/physreva.45.8185
27. Simpson SH, Hanna S. Rotation of absorbing spheres in Laguerre-Gaussian beams. JOSA A (2009) 26(1):173–83. doi:10.1364/josaa.26.000173
28. Simpson SH, Hanna S. Orbital motion of optically trapped particles in Laguerre–Gaussian beams. JOSA A (2010) 27(9):2061–71. doi:10.1364/josaa.27.002061
29. Simpson NB, Allen L, Padgett MJ. Optical tweezers and optical spanners with Laguerre–Gaussian modes. J Mod Opt (1996) 43(12):2485–91. doi:10.1080/09500349608230675
30. Garbin V, Volpe G, Ferrari E, Versluis M, Cojoc D, Petrov D. Mie scattering distinguishes the topological charge of an optical vortex: a homage to Gustav Mie. New J Phys (2009) 11(1):013046. doi:10.1088/1367-2630/11/1/013046
31. Petrov D, Rahuel N, Molina-Terriza G, Torner L. Characterization of dielectric spheres by spiral imaging. Opt Lett (2012) 37(5):869–71. doi:10.1364/ol.37.000869
32. Ambrosio LA, Gouesbet G. On localized approximations for Laguerre-Gauss beams focused by a lens. J Quantitative Spectrosc Radiative Transfer (2018) 218:100–14. doi:10.1016/j.jqsrt.2018.07.006
33. Votto LFM, Ambrosio LA, Gouesbet G. Evaluation of beam shape coefficients of paraxial Laguerre–Gauss beam freely propagating by using three remodeling methods. J Quantitative Spectrosc Radiative Transfer (2019) 239:106618. doi:10.1016/j.jqsrt.2019.106618
34. Gouesbet G, Ambrosio LA, Votto LFM. Finite series expressions to evaluate the beam shape coefficients of a Laguerre-Gauss beam focused by a lens in an on-axis configuration. J Quantitative Spectrosc Radiative Transfer (2020) 242:106759. doi:10.1016/j.jqsrt.2019.106759
35. Liu Z, Shen J, Yu H. Scattering of Laguerre-Gauss light beam by a sphere: the angular spectrum decomposition method and a comparison with the localized approximation method. J Quantitative Spectrosc Radiative Transfer (2022) 287:108214. doi:10.1016/j.jqsrt.2022.108214
36. Votto LF, Ambrosio L, Gouesbet G, Wang J. Finite series algorithm design for lens-focused Laguerre–Gauss beams in the generalized Lorenz–Mie theory. J Quantitative Spectrosc Radiative Transfer (2021) 261:107488. doi:10.1016/j.jqsrt.2020.107488
37. Votto LFM, Gouesbet G, Ambrosio LA. A framework for the finite series method of the generalized Lorenz-Mie theory and its application to freely-propagating Laguerre-Gaussian beams. J Quantitative Spectrosc Radiative Transfer (2023) 309:108706. doi:10.1016/j.jqsrt.2023.108706
38. Rury AS, Freeling R. Mie scattering of purely azimuthal Laguerre-Gauss beams: angular-momentum-induced transparency. Phys Rev A (2012) 86(5):053830. doi:10.1103/physreva.86.053830
39. Zambrana-Puyalto X, Molina-Terriza G. The role of the angular momentum of light in Mie scattering. Excitation of dielectric spheres with Laguerre–Gaussian modes. J Quantitative Spectrosc Radiative Transfer (2013) 126:50–5. doi:10.1016/j.jqsrt.2012.10.010
40. Kiselev AD, Plutenko DO. Mie scattering of Laguerre-Gaussian beams: photonic nanojets and near-field optical vortices. Phys Rev A (2014) 89(4):043803. doi:10.1103/physreva.89.043803
41. Yu H, She W. Radiation force exerted on a sphere by focused Laguerre–Gaussian beams. JOSA A (2015) 32(1):130–42. doi:10.1364/josaa.32.000130
42. Jiang Y, Shao Y, Qu X, Ou J, Hua H. Scattering of a focused Laguerre–Gaussian beam by a spheroidal particle. J Opt (2012) 14(12):125709. doi:10.1088/2040-8978/14/12/125709
43. Qu T, Wu ZS, Shang QC, Li ZJ, Bai L, Gong L. Analysis of the radiation force of a Laguerre Gaussian vortex beam exerted on an uniaxial anisotropic sphere. J Quantitative Spectrosc Radiative Transfer (2015) 162:103–13. doi:10.1016/j.jqsrt.2015.03.033
44. Qu T, Wu ZS, Shang QC, Li ZJ. Light scattering of a Laguerre–Gaussian vortex beam by a chiral sphere. JOSA a (2016) 33(4):475–82. doi:10.1364/josaa.33.000475
45. Arfan M, Ghaffar A, Alkanhal MA, Khan Y, Alqahtani AH, Ur Rehman S. Laguerre–Gaussian beam scattering by a perfect electromagnetic conductor (PEMC) sphere. Arabian J Sci Eng (2023) 48(6):8001–9. doi:10.1007/s13369-022-07385-1
46. Yu M, Han Y, Cui Z, Sun H. Scattering of a Laguerre–Gaussian beam by complicated shaped biological cells. JOSA a (2018) 35(9):1504–10. doi:10.1364/josaa.35.001504
47. Porfirev AP, Kirilenko MS, Khonina SN, Skidanov RV, Soifer VA. Study of propagation of vortex beams in aerosol optical medium. Appl Opt (2017) 56(11):E8–E15. doi:10.1364/ao.56.0000e8
48. Ligon DA, Wetmore AE, Gillespie PS. Simulation of the passive infrared spectral signatures of bioaerosol and natural fog clouds immersed in the background atmosphere. Opt Express (2002) 10(18):909–19. doi:10.1364/oe.10.000909
49. Shi C, Guo L, Cheng M, Lavery MP, Liu S. Aerosol scattering of vortex beams transmission in hazy atmosphere. Opt Express (2020) 28(19):28072–84. doi:10.1364/oe.401293
50. Dong K, Jiang W, Cheng M, Shi C, Cao Y, Guo L. Attenuation of Bessel vortex beam transmission in the rain environment. J Quantitative Spectrosc Radiative Transfer (2023) 304:108620. doi:10.1016/j.jqsrt.2023.108620
51. Arfan M, Ghaffar A, Alkanhal MA, Khan Y, Alqahtani AH, Shakir I. Laguerre–Gaussian beam scattering by a marine aerosol. Opt Quan Elect (2023) 55(9):756. doi:10.1007/s11082-023-05047-6
52. Durnin JJJM, Miceli JJ, Eberly JH. Diffraction-free beams. Phys Rev Lett (1987) 58(15):1499–501. doi:10.1103/physrevlett.58.1499
53. Garcés-Chávez V, McGloin D, Melville H, Sibbett W, Dholakia K. Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. Nature (2002) 419(6903):145–7. doi:10.1038/nature01007
54. Fahrbach FO, Rohrbach A. Propagation stability of self-reconstructing Bessel beams enables contrast-enhanced imaging in thick media. Nat Commun (2012) 3(1):632. doi:10.1038/ncomms1646
55. Čižmár T, Kollárová V, Bouchal Z, Zemánek P. Sub-micron particle organization by self-imaging of non-diffracting beams. New J (2006) 8:43. doi:10.1088/1367-2630/8/3/043
56. Mitri FG. Arbitrary scattering of an electromagnetic zero-order Bessel beam by a dielectric sphere. Opt Lett (2011) 36(5):766–8. doi:10.1364/ol.36.000766
57. Taylor JM, Love GD. Multipole expansion of Bessel and Gaussian beams for Mie scattering calculations. JOSA A (2009) 26(2):278–82. doi:10.1364/josaa.26.000278
58. Gouesbet G, Lock JA, Grehan G. Generalized Lorenz–Mie theories and description of electromagnetic arbitrary shaped beams: localized approximations and localized beam models, a review. J Quant Spectrosc Radiat Transf (2011) 12:1–27. doi:10.1016/j.jqsrt.2010.08.012
59. Ambrosio LA, Hernández-Figueroa HE. Integral localized approximation description of ordinary Bessel beams and application to optical trapping forces. Biomed Opt express (2011) 2(7):1893–906. doi:10.1364/boe.2.001893
60. Li RX, Guo LX, Ding CY, Wu ZS. Scattering of an axicon-generated Bessel beam by a sphere. Opt Commun (2013) 307:25–31. doi:10.1016/j.optcom.2013.06.007
61. Mitri FG, Li RX, Guo LX, Ding CY. Resonance scattering of a dielectric sphere illuminated by electromagnetic Bessel non-diffracting (vortex) beams with arbitrary incidence and selective polarizations. Ann Phys (2015) 363:562–3. doi:10.1016/j.aop.2015.07.028
62. Chen J, Ng J, Wang P, Lin Z. Analytical partial wave expansion of vector Bessel beam and its application to optical binding. Opt Lett (2010) 35:1674–6. doi:10.1364/ol.35.001674
63. Qin S, Li R, Yang R, Ding C. Debye series analysis of internal and near-surface fields for a homogeneous sphere illuminated by an axicon-generated vector Bessel beam. J Quantitative Spectrosc Radiative Transfer (2017) 195:26–34. doi:10.1016/j.jqsrt.2016.12.025
64. Shen J, Wang Y, Yu H, Ambrosio LA, Gouesbet G. Angular spectrum representation of the Bessel-Gauss beam and its approximation: a comparison with the localized approximation. J Quantitative Spectrosc Radiative Transfer (2022) 284:108167. doi:10.1016/j.jqsrt.2022.108167
65. Wang JJ, Wriedt T, Lock JA, Mädler L. General description of circularly symmetric Bessel beams of arbitrary order. J Quantitative Spectrosc Radiative Transfer (2016) 184:218–32. doi:10.1016/j.jqsrt.2016.07.011
66. Gouesbet G, Gréhan G, Maheu B. Expressions to compute the coefficients gmnin the generalized Lorenz-Mie theory using finite series. J Opt (1988) 19(1):35–48. doi:10.1088/0150-536x/19/1/005
67. Cui Z, Han Y, Han L. Scattering of a zero-order Bessel beam by arbitrarily shaped homogeneous dielectric particles. J Opt Soc Am A (2013) 30:1913–20. doi:10.1364/josaa.30.001913
68. Zhang L. A general theory of arbitrary Bessel beam scattering and interactions with a sphere. The J Acoust Soc America (2018) 143(5):2796–800. doi:10.1121/1.5036734
69. Wang JJ, Wriedt T, Mädler L, Han YP, Hartmann P. Multipole expansion of circularly symmetric Bessel beams of arbitrary order for scattering calculations. Opt Commun (2017) 387:102–9. doi:10.1016/j.optcom.2016.11.038
70. Marston PL. Scattering of a Bessel beam by a sphere. J Acoust Soc America (2007) 121(2):753–8. doi:10.1121/1.2404931
71. Li ZJ, Wu ZS, Qu T, Li H, Bai L, Gong L. Light scattering of a non-diffracting zero-order Bessel beam by uniaxial anisotropic bispheres. J Quantitative Spectrosc Radiative Transfer (2015) 162:56. doi:10.1016/j.jqsrt.2015.01.026
72. Preston TC, Reid JP. Angular scattering of light by a homogeneous spherical particle in a zeroth-order Bessel beam and its relationship to plane wave scattering. JOSA A (2015) 32(6):1053–62. doi:10.1364/josaa.32.001053
73. Valdivia NL, Votto LF, Gouesbet G, Wang J, Ambrosio LA. Bessel-Gauss beams in the generalized Lorenz-Mie theory using three remodeling techniques. J Quantitative Spectrosc Radiative Transfer (2020) 256:107292. doi:10.1016/j.jqsrt.2020.107292
74. Han L. Scattering of a high-order Bessel beam by a spheroidal particle. J Quantitative Spectrosc Radiative Transfer (2018) 211:129–37. doi:10.1016/j.jqsrt.2018.03.007
75. Li R, Ding C, Mitri FG. Optical spin torque induced by vector Bessel (vortex) beams with selective polarizations on a light-absorptive sphere of arbitrary size. J Quantitative Spectrosc Radiative Transfer (2017) 196:53–68. doi:10.1016/j.jqsrt.2017.03.035
76. Wen Y, Xi Q, Li R, Qin S, Ding C. Scattering of a vector Bessel-Gaussian beam by a sphere. J Quantitative Spectrosc Radiative Transfer (2018) 204:165–78. doi:10.1016/j.jqsrt.2017.08.025
77. Yang Y, Nie Z, Feng Y, Li R. Internal and near-surface fields for a charged sphere irradiated by a vector Bessel beam. J Quantitative Spectrosc Radiative Transfer (2020) 240:106705. doi:10.1016/j.jqsrt.2019.106705
78. Shi C, Guo L, Cheng M, Li R. Scattering of a high-order vector Bessel Gaussian beam by a spherical marine aerosol. J Quantitative Spectrosc Radiative Transfer (2021) 265:107552. doi:10.1016/j.jqsrt.2021.107552
79. Shi C, Cheng M, Guo L, Lavery MP, Wang P, Liu S, et al. Particle scattering induced orbital angular momentum spectrum change of vector bessel–Gaussian vortex beam. Remote Sensing (2022) 14(18):4550. doi:10.3390/rs14184550
80. Sun Y, Wang J, Yu Q, Wang H, Briard P, Ambrosio LA, et al. Longitudinal and transverse photophoretic force on a homogeneous sphere exerted by a Bessel beam with selective polarizations. Appl Opt (2022) 61(26):7632–43. doi:10.1364/ao.463914
81. Mitri FG. Electromagnetic wave scattering of a high-order Bessel vortex beam by a dielectric sphere. IEEE Trans antennas propagation (2011) 59(11):4375–9. doi:10.1109/tap.2011.2164228
82. Chen Z, Han Y, Cui Z, Shi X. Scattering of a zero-order Bessel beam by a concentric sphere. J Opt (2014) 16(5):055701. doi:10.1088/2040-8978/16/5/055701
83. Gong S, Li R, Liu Y, Zhang J. Scattering of a vector Bessel vortex beam by a charged sphere. J Quantitative Spectrosc Radiative Transfer (2018) 215:13–24. doi:10.1016/j.jqsrt.2018.05.001
84. Cui Z, Han Y, Chen Z, Han L. Scattering of Bessel beam by arbitrarily shaped composite particles with core–shell structure. J Quantitative Spectrosc Radiative Transfer (2014) 144:108–16. doi:10.1016/j.jqsrt.2014.04.007
85. Chen Z, Han Y, Cui Z, Shi X. Scattering of Bessel beam by a conducting spheroidal particle with dielectric coating. J Quantitative Spectrosc Radiative Transfer (2014) 148:197–202. doi:10.1016/j.jqsrt.2014.07.009
86. Li R, Ren KF, Han X, Wu Z, Guo L, Gong S. Analysis of radiation pressure force exerted on a biological cell induced by high-order bessel beams using debye series. J Quantitative Spectrosc Radiative Transfer (2013) 126:69–77. doi:10.1016/j.jqsrt.2012.07.030
87. Wang JJ, Han YP, Chang JY, Chen ZY. Light scattering of a Bessel beam by a nucleated biological cell: an eccentric sphere model. J Quantitative Spectrosc Radiative Transfer (2018) 206:22–30. doi:10.1016/j.jqsrt.2017.10.025
88. Bai J, Wu ZS, Ge CX, Li ZJ, Qu T, Shang QC. Analytical description of lateral binding force exerted on bi-sphere induced by high-order bessel beams. J Quantitative Spectrosc Radiative Transfer (2018) 214:71–81. doi:10.1016/j.jqsrt.2018.04.031
89. Chen Z, Han Y, Cui Z, Shi X. Scattering analysis of Bessel beam by a multilayered sphere. Opt Commun (2015) 340:5–10. doi:10.1016/j.optcom.2014.11.073
90. Bai J, Liu X, Ge CX, Wu ZS, Zhang XX. Scattering of aggregated multi-layered biological cells by Bessel beams. J Opt (2023) 25(5):055401. doi:10.1088/2040-8986/acc081
91. Ambrosio LA, Hernández-Figueroa HE. Radiation pressure cross sections and optical forces over negative refractive index spherical particles by ordinary Bessel beams. Appl Opt (2011) 50(22):4489–98. doi:10.1364/ao.50.004489
92. Wang Z, Wei Q, Zhang S, Li L, Hu M, Li R. Scattering properties of Bessel beams on metal particles. Physica Scripta (2023) 98(3):035512. doi:10.1088/1402-4896/acb8eb
93. Ambrosio LA. Generalized Lorenz-Mie theory in the analysis of longitudinal photophoresis of arbitrary-index particles: on-axis axisymmetric beams of the first kind. J Quantitative Spectrosc Radiative Transfer (2021) 275:107889. doi:10.1016/j.jqsrt.2021.107889
94. Qu T, Wu ZS, Shang QC, Li ZJ, Bai L. Electromagnetic scattering by a uniaxial anisotropic sphere located in an off-axis Bessel beam. JOSA A (2013) 30(8):1661–9. doi:10.1364/josaa.30.001661
95. Shi C, Cheng M, Guo L, Li R, Li J. Attenuation characteristics of Bessel Gaussian vortex beam by a wet dust particle. Opt Commun (2022) 514:128138. doi:10.1016/j.optcom.2022.128138
96. Liu C, Liu YL, Yeh T. Light-Sheet microscopy using attenuation-compensating Airy beam. Biophysical J (2017) 112(3):145a. doi:10.1016/j.bpj.2016.11.796
97. Lu W, Chen H, Guo S, Liu S, Lin Z. Selectively transporting small chiral particles with circularly polarized Airy beams. Opt Lett (2018) 43(9):2086–9. doi:10.1364/ol.43.002086
98. Lu W, Sun X, Chen H, Liu S, Lin Z. Optical manipulation of chiral nanoparticles in vector Airy beam. J Opt (2018) 20(12):125402. doi:10.1088/2040-8986/aaea4d
99. Lu W, Sun X, Chen H, Liu S, Lin Z. Abruptly autofocusing property and optical manipulation of circular Airy beams. Phys Rev A (2019) 99(1):013817. doi:10.1103/physreva.99.013817
100. Pan Q, Pei S, Cui F, Xu S, Cao Z. Scattering of an Airy light sheet by a chiral sphere. Appl Opt (2019) 58(26):7151–6. doi:10.1364/ao.58.007151
101. Zhao Z, Zang W, Tian J. Optical trapping and manipulation of Mie particles with Airy beam. J Opt (2016) 18(2):025607. doi:10.1088/2040-8978/18/2/025607
102. Song N, Wei B, Li R, Sun H, Wei B, Zhang S, et al. Optical torque on an absorptive dielectric sphere of arbitrary size illuminated by a linearly-polarized Airy light-sheet. J Quantitative Spectrosc Radiative Transfer (2020) 256:107327. doi:10.1016/j.jqsrt.2020.107327
103. Tang H, Sun H, Li R, Yang L, Song N, Zhang S, et al. Optical radiation force on a dielectric sphere by a polarized Airy beam. JOSA A (2022) 39(11):2090–103. doi:10.1364/josaa.464812
104. Cao Z, Zhai C. Angular scattering of an Airy beam light sheet by a concentric sphere. J Quantitative Spectrosc Radiative Transfer (2017) 202:31–6. doi:10.1016/j.jqsrt.2017.07.019
105. Pei S, Pan Q, Cui F, Xu S, Cao Z. Electromagnetic scattering of an Airy beam light sheet by a multilayered sphere. Optik (2019) 180:379–86. doi:10.1016/j.ijleo.2018.11.130
106. Cao Z, Zhai C. Scattering of one-dimensional Airy beam light sheet with finite energy by a sphere. Appl Opt (2017) 56(12):3491–6. doi:10.1364/ao.56.003491
107. Lu W, Chen H, Liu S, Lin Z. Rigorous full-wave calculation of optical forces on dielectric and metallic microparticles immersed in a vector Airy beam. Opt Express (2017) 25(19):23238–53. doi:10.1364/oe.25.023238
108. Shahabadi V, Abdollahpour D. Dual-plane multiple-trapping by tightly focused petal-like circular Airy beam in an aqueous medium. J Quantitative Spectrosc Radiative Transfer (2021) 272:107771. doi:10.1016/j.jqsrt.2021.107771
109. Hai-Ying L, Zhen-Sen W, Zheng-Jun L. Scattering from a multi-layered sphere located in a high-order Hermite-Gaussian beam. Chin Phys Lett (2009) 26(10):104203. doi:10.1088/0256-307x/26/10/104203
110. Qingqing H, Mingjian C, Lixin G, Jiangting L, Xu Y, Songhua L. Scattering of aerosol particles by a hermite–Gaussian beam in marine atmosphere. Appl Opt (2017) 56(19):5329. doi:10.1364/ao.56.005329
111. Votto LF, Chafiq A, Belafhal A, Gouesbet G, Ambrosio LA. Hermite–Gaussian beams in the generalized Lorenz–Mie theory through finite–series Laguerre–Gaussian beam shape coefficients. JOSA B (2022) 39(4):1027–32. doi:10.1364/josab.445314
112. Chafiq A, Belafhal A. Scattering of Lommel beams by homogenous spherical particle in generalized Lorenz–Mie theory. Opt Quan Elect (2018) 50(2):95. doi:10.1007/s11082-018-1351-1
113. Cui Z, Song P, Hui Y, Zhao W, Han Y. Scattering of polarized non-diffracting Lommel beams by nonspherical homogeneous particles. J Quantitative Spectrosc Radiative Transfer (2018) 219:238–47. doi:10.1016/j.jqsrt.2018.08.017
114. Chafiq A, Belafhal A. Radiation pressure cross section exerted on homogenous dielectric spherical particle by zeroth order Mathieu beams. J Quantitative Spectrosc Radiative Transfer (2016) 179:170–6. doi:10.1016/j.jqsrt.2016.03.039
Keywords: structured light, particle scattering, generalized Lorenz-Mie theory, beam shape coefficients, software simulation
Citation: Cheng MJ, Cao YC, Ren KF, Zhang H and Guo LX (2024) Generalized Lorenz-Mie theory and simulation software for structured light scattering by particles. Front. Phys. 12:1354223. doi: 10.3389/fphy.2024.1354223
Received: 12 December 2023; Accepted: 29 January 2024;
Published: 15 February 2024.
Edited by:
Xinzhong Li, Henan University of Science and Technology, ChinaReviewed by:
Dongmei Liu, South China Normal University, ChinaShaohui Yan, Chinese Academy of Sciences (CAS), China
Copyright © 2024 Cheng, Cao, Ren, Zhang and Guo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Li Xin Guo, bHhndW9AeGlkaWFuLmVkdS5jbg==; Kuan Fang Ren, ZmFuZy5yZW5AY29yaWEuZnI=
 Ming Jian Cheng
Ming Jian Cheng Yuan Cong Cao1
Yuan Cong Cao1 Kuan Fang Ren
Kuan Fang Ren Huan Zhang
Huan Zhang