Meta-path-based key node identification in heterogeneous networks

Identifying key nodes in complex networks remains challenging. Whereas previous studies focused on homogeneous networks, real-world systems comprise multiple node and edge types. We propose a meta-path-based key node identification (MKNI) method in heterogeneous networks to better capture complex interconnectivity. Considering that existing studies ignore the differences in propagation probabilities between nodes, MKNI leverages meta-paths to extract semantics and perform node embeddings. Trust probabilities reflecting propagation likelihoods are derived by calculating embedding similarities. Node importance is calculated by using metrics incorporating direct and indirect influence based on trust. The experimental results on three real-world network datasets, DBLP, ACM and Yelp, show that the key nodes identified by MKNI exhibit better information propagation in the Susceptible Infected (SI) and susceptibility-influence model (SIR) model compared to other methods. The proposed method provides a reliable tool for revealing the topological structure and functional mechanisms of the network, which can guide more effective regulation and utilization of the network.

1 Introduction

In practical research, various entity interactions are usually modeled as complex networks for convenience, such as relationship networks between individuals in social networks, cooperation networks between scholars in academic networks, interaction networks between particles in physics [1]. In the task of analyzing complex networks, key nodes identification is an extremely important research topic [2]. Key nodes refer to nodes with great influence in networks. Although they account for only a small fraction of network nodes, they can exert rapid and widespread influence over most ordinary nodes [3]. For instance, in e-commerce networks, advertising recommendations from users with extensive outreach can swiftly increase product sales; when an epidemic outbreak occurs, a tiny fraction of people with powerful propagation capabilities act as the major driving forces behind disease diffusion.

Therefore, accurate identification of key nodes can bring value in multiple aspects: In e-commerce networks, influential users can be identified to make product recommendations, thereby improving product exposure and increasing sales; In epidemic networks, when an epidemic outbreak occurs, super-spreaders with powerful propagation capabilities can be recognized for focused isolation and treatment, to contain disease spreading; In power grids, identifying critical equipment nodes substations helps optimize resource allocation and enact protection measures, aiming to avoid risks of partial or complete blackouts. Overall, identifying key nodes in complex networks provides an important means to reveal the topological structures and functional mechanisms of the networks, which can guide more effective regulation and utilization of the networks.

Existing studies often simplify complex networks by constructing homogeneous network models, which only contain a single type of nodes and edges. However, real-world complex networks are heterogeneous, comprising multiple types of nodes and diverse edge relationships. Heterogeneous networks can capture the complexity of real-world systems more comprehensively. Therefore, approaches that analyze homogeneous network models have limited effectiveness when applied to heterogeneous networks directly. Given this, more and more researchers are turning to study key nodes identification in heterogeneous networks. Some recent work has tried hierarchical modeling [4] or extracting multiple meta-path instances [5] in heterogeneous networks to measure node importance. However, these methods overlook the varied influence probabilities between different node pairs, leading to unsatisfactory performance in identifying key nodes.

To address the above issues, this paper proposes a meta-path-based key node identification (MKNI) method in heterogeneous networks: A meta-path-based network embedding model is utilized to learn and extract the complex structural information of the heterogeneous network. Based on the vector similarities of the embeddings, a trust probability measure between node pairs is proposed to quantify the influence propagation probabilities. Two metrics are constructed to measure each node’s direct and indirect influence. By integrating the direct and indirect influence measures, the importance ranking of nodes is obtained.

Our main contributions are as follows:

1) A meta-path-based key node identification approach is proposed in heterogeneous networks. It extracts heterogeneous information using meta-paths and incorporates network topological structure to construct influence metrics. With these metrics, the node importance ranking is obtained to identify the key nodes

2) A trust probability between nodes based on vector similarity is proposed. The trust probability can effectively quantify the likelihood of information propagating from a source node to a target node, improving the accuracy of node importance computation.

3) On three real-world heterogeneous network datasets, DBLP, ACM, and Yelp, experimental results show that the key nodes identified by MKNI have better information propagation capabilities compared to those identified by other methods.

The remaining sections are organized as follows: the related works about key nodes identification are presented in Section 2. Section 3 introduces the related definitions and problem description of key nodes identification in heterogeneous networks; Section 4 explains our proposed method. Section 5 mainly describes the experiments we have done. Section 6 concludes this paper and discusses future work.

2 Related work

For complex network key node identification, existing studies mainly focus on homogeneous networks and heterogeneous networks.

For homogeneous networks, many scholars have conducted in-depth research and obtained considerable results. Kamal et al. proposed a local centrality metric to identify key nodes by considering their negative effect on the clustering coefficient and the positive effect of the sum of neighbor clustering coefficients [6]. Kitsak et al. proposed the K-Shell method, quantifying the global importance of nodes by iteratively decomposing the nodes with the fewest neighbors from the outer shell towards the inner shell [7]. Yang et al. incorporated the K-Shell method to improve the gravity model for combining local and global metrics of key nodes [8]. The above methods have achieved good performance on homogeneous networks. However, homogeneous networks only have one node type and one edge type. The limited information contained cannot fully leverage the complexity of real-world network data.

For heterogeneous networks, many studies have been done on multi-relational networks containing one node type and multiple edge types. Ding et al. combined biased random walks with PageRank to iteratively solve node importance in multi-relational networks [9]. Wu et al. eigenvector centrality to multi-relational networks and proposed an eigenvector multicentrality [10]. Luo et al. defined multi-relation networks local aggregation coefficient, combined with degree centrality, extended the ClusterRank metric to multi-relation networks [11]. They introduced the D-S evidence theory to integrate both metrics and proposed a node multiple evidence centrality metrics. While multi-relation networks consider multiple types of relationships, they only account for a single node type, which still differs from real-world networks.

Therefore, increasing attention has been paid to heterogeneous networks with multiple node and edge types. Wan et al. first divided the heterogeneous network into core layers and auxiliary layers, calculated centrality scores and influence weights of nodes in each layer, and obtained key nodes in the core layer [4]. Soheila et al. proposed the Entropy Ranking Method by considering neighbors, meta-path instances, and both combined, using their linear combination as node importance [5].

Recently, node embedding methods have been used to learn low-dimensional representations while preserving network characteristics for downstream tasks. For homogeneous networks, Yang et al. generated node embeddings by DeepWalk and used embedding similarity as node distance combined with K-Shell for node importance [12]. For heterogeneous networks, Li et al. obtained node embeddings using varied meta-paths to capture complex structures and heterogeneity. They compute the similarity between nodes with a weighted mechanism, thereby selecting nodes with high influence within the network [13].

The above studies provide various insights for heterogeneous network key node identification. However, they do not well integrate topological and heterogeneous information, leading to unreliable results. Also, they overlook varied influence probabilities between node pairs which should be differentiated when calculating node importance. To address these issues, we propose the MKNI method, extracting heterogeneous data via meta-paths and using node embedding models to learn vector representations. Based on vector similarities, we propose trust probabilities to measure influence likelihoods between nodes, and apply them to two topology-based influence metrics. By summing the two influences and ranking, we obtain key nodes. Our method can effectively combine topological and heterogeneous information, and differentiate importance calculation between nodes, achieving network key node identification.

3 Related definitions and problem descriptions

In this section, we introduce the related definitions and problem descriptions of key nodes identification.

3.1 Related definition

3.1.1 Homogeneous/heterogeneous network

A network is defined as a graph $G=\left(V,E,A,R\right)$, where $V=\left\{v_i|i=1,2,3,\dots ,n\right\}$ is a set of nodes, $\left|V\right|=n$ represents the total number of nodes, $E=\left\{e_{ij}|i,j=1,2,3,\dots ,m;i\ne j\right\}$ is a set of edges, and $\left|E\right|=m$ represents the total number of edges [14]. Each node $v_i\in V$ belongs to one particular type of node in the node type set $A$, and each edge $e_{ij}\in E$ belongs to one particular type of edge in the edge type set $R$. As shown in Figure 1, the network A with $\left|A\right|+\left|R\right|=2$ is called a homogeneous network, as shown in Figure 1A, and the network B with $\left|A\right|+\left|R\right|>2$ is called a heterogeneous network, as shown in Figure 1B.

FIGURE 1

FIGURE 1. Examples of related definitions of heterogeneous networks. (A) Homogeneous network. (B) Heterogeneous Network. (C) Network schema. (D) Meta-path. (E) Meta-graph.

3.1.2 Network schema

A network schema, denoted as $T_G=\left(A,R\right)$, abstracts node and edge types from a heterogeneous network into a directed cyclic graph [14]. It enables incorporating semantic information by semi-structuring heterogeneous networks. Figure 1C shows a sample schema obtained from the heterogeneous network in Figure 1B.

3.1.3 Meta-path

A meta-path $\mathcal{P}$ is defined on a network schema $T_G=\left(A,R\right)$ and is denoted in a form of $\mathcal{P}=A_1{\displaystyle \stackrel{R1}{\to }}{A}_2{\displaystyle \stackrel{R2}{\to }}\cdots A_i{\displaystyle \stackrel{Ri}{\to }}\cdots {\displaystyle \stackrel{R_{\mathrm{l}-1}}{\to }}{A}_l,1<i<l$, which describes a composite edge $R=R_1\circ R_2\circ \cdots R_l$ between node $A_1,A_2,\dots A_{l+1}$, where $\circ$ denotes the composition operator on relations [14]. In Figure 1D, the first meta-path APA (Author-Paper-Author) denotes authors connected by co-authored papers. The second meta-path APCPA (Author-Paper-Conference-Paper-Author) represents author connections through papers presented at the same conference.

3.1.4 Meta-graph

A meta-graph is a directed acyclic graph derived from the network model [14]. It integrates multiple meta-paths with common nodes. Figure 1E shows a sample network schema with two meta-paths APCPA and APAPA, which can form a meta-graph.

3.2 Problem descriptions

We focus on the key node identification problem of heterogeneous networks. Given a heterogeneous network $G=\left(V,E,A,R\right)$, where $\left|A\right|+\left|R\right|>2$.

The task aims to design a node importance evaluation method to get each target type node’s importance in the network. The top k nodes in importance are identified as key nodes.

The identified key nodes set $S$ is described by Eqs 7, 8.

$NI=Score\left(V^t\right).(1)$

$S=Top\left(NI,k\right).(2)$

where $V^t$ denotes the set of nodes with target type $t$, $Score\left(V^t\right)$ is the node importance calculation function, $Top\left(NI,k\right)$ denotes the function that extracts the top k nodes from the importance calculation results $NI$.

4 Proposed method

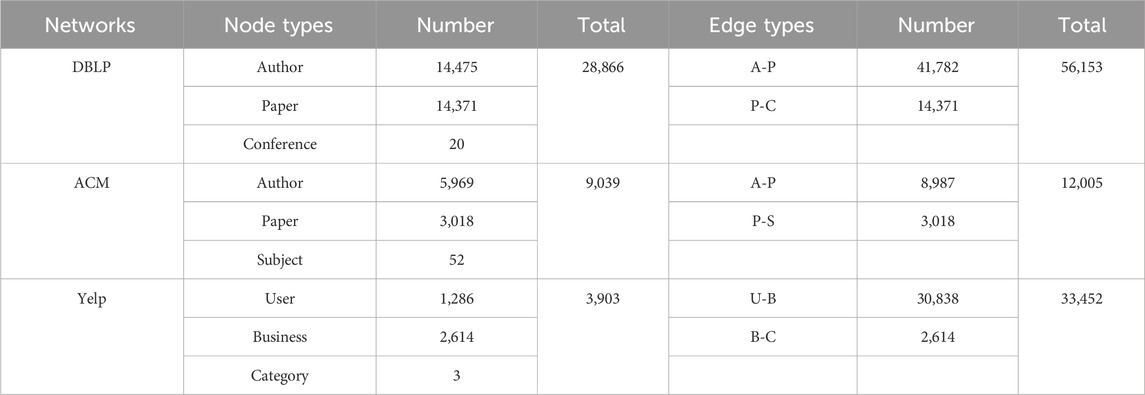
The framework of the proposed method is shown in Figure 2. First, heterogeneous network node embeddings are learned to map different nodes into a shared vector space. Next, the direct and indirect influence of target nodes is computed. Finally, node importance rankings are derived via weighted summation.

FIGURE 2

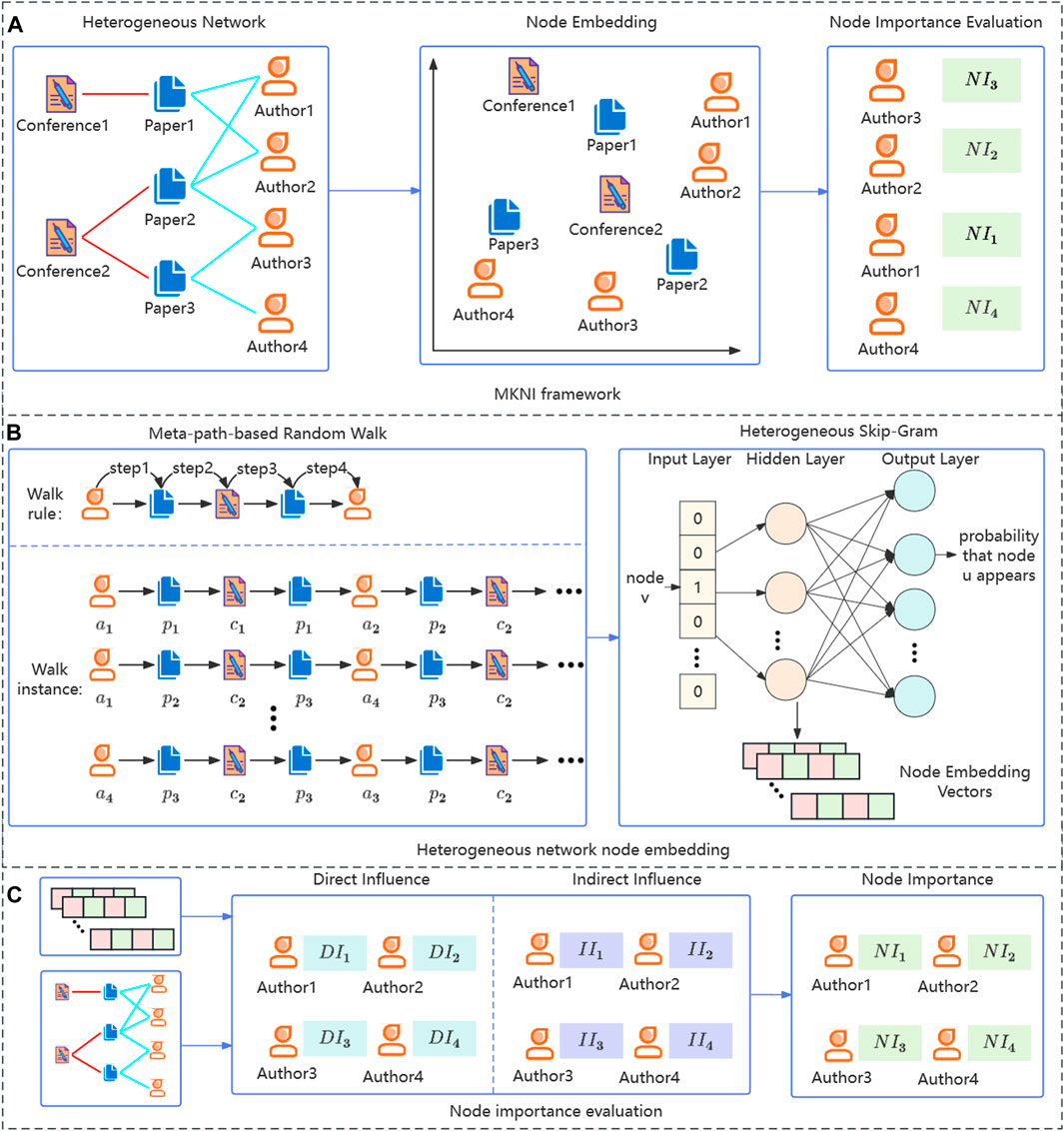
FIGURE 2. The framework of the proposed MKNI. (A) MKNI framework. (B) Heterogeneous network node embedding. (C) Node importance evaluation.

4.1 Heterogeneous network node embedding

We adopt Metapath2Vec [15] for node embedding to incorporate structural and heterogeneity information. Metapath2Vec comprises meta-path-based random walks and Heterogeneous Skip-Gram.

1) Meta-path-based random walk: The method is based on a given meta-path $\mathcal{P}$ to produce a corpus with rich semantics. The transition probability of selecting the next node at time step t is defined as:

$p\left(v_{i+1}^{t+1}|v_i^t,\mathcal{P}\right)=\left\{\begin{array}{l}\frac{1}{\left|N^{t+1}\left(v_i^t\right)\right|},\left(v_{i+1}^{t+1},v_i^t\right)\in E\\ 0,\text{others}\end{array}\right.,(3)$

where $\mathcal{P}$ is the selected meta-path, and $N^{t+1}\left(v_i^t\right)$ denotes the neighbor of node $v_i^t$ that satisfies the meta-path constraint at time $t+1$. Thus, the next node is chosen based on the meta-path rules. Nodes without connecting edges or violating meta-path types are excluded, denoted as others in Eq. 3.

2) Heterogeneous Skip-Gram: The generated corpus is used to train node embeddings based on the Heterogeneous Skip-Gram model, with the objective function denoted by Eq. 4:

${\mathrm{arg\hspace{0.17em}max}}_{\theta }{\sum }_{v\in V}{\sum }_{t\in A_v}{\sum }_{c_t\in N^t\left(v\right)}logp\left(c_t|v;\theta \right),(4)$

where $A_v$ is the node type of node $v$, $p\left(c_t|v;\theta \right)=\frac{e^{H_{c_t}{H}_v}}{{\sum }_{u\in V}{e}^{H_u{H}_v}}$, $H_v$ denotes the vth row of the embedding vector matrix $H$, i.e., the embedding vector of node $v$.

To incorporate heterogeneity, node embeddings are learned using varied meta-paths for random walks. As longer meta-paths can introduce noisy semantics [16], we restrict to meta-paths under length 5, such as APCPA.

4.2 Node importance evaluation

Nodes exert direct influence through neighbors and indirect influence via intermediate nodes. We adopt neighborhood information to quantify direct influence. Homogeneous networks based on meta-paths are constructed to estimate indirect influence propagation.

4.2.1 Direct influence

Node embedding vectors enable computing node similarity via cosine similarity. The value range is adjusted to [0, 1] using Eq. 5:

$si{m}_{\text{ij}}=\frac{\frac{h_i•h_j}{\left|\left|h_i\right|\right|\left|\left|h_j\right|\right|}+1}{2},(5)$

where $h_i$ denotes the vector of node $i$, $•$ indicates the dot product of the vectors, and $‖h_i‖$ represents the length of the vector. Further, node similarities are computed using different meta-paths. The averaged similarity is taken as the final result.

Considering that the target node chooses whether to accept the message, we propose the trust probability. It measures the likelihood of information propagating from the information source node to the target node based on neighborhood similarity. The trust probability of node $j$ accepting information from neighbor $i$ can be computed by Eq. 6.

$p_{ij}=\frac{si{m}_{\text{ij}}}{{\displaystyle \sum _{kϵN_j,A_k=A_i}}si{m}_{\text{jk}}},(6)$

where the restriction $kϵN_j,A_k=A_i$ is used to ensure that the trust probability is calculated from the neighbor node $j$ of the same type as the target node $i$.

The information propagation capability of node $i$ is obtained by aggregating trust probabilities between node $i$ and all its neighbor nodes, formulated as Eq. 7:

$D{I}_i={\displaystyle \sum _{jϵN_i}}\left(\frac{si{m}_{\text{ij}}}{{\displaystyle \sum _{kϵN_j,A_k=A_i}}si{m}_{\text{jk}}}\right),(7)$

4.2.2 Indirect influence

Different meta-paths in heterogeneous networks capture distinct semantics. Nodes spread influence through these paths, with longer paths imparting smaller gains per the small-world phenomenon [17]. Kamal et al. discovered that in networks exhibiting a rich club effect, local metrics proved significantly more effective than global metrics in assessing nodes’ capability to disseminate information [18]. Therefore, we employ a meta-path of length 2 for indirect influence calculation.

The meta-path is employed to transform the heterogeneous network into a homogeneous network. Figure 3 provides an example of the academic network extracted using the APA meta-path. To comprehensively consider the influence of intermediates, we adopt the weighted network for calculation. The weights of the connected edges correspond to the number of edges they form based on the intermediate P.

FIGURE 3

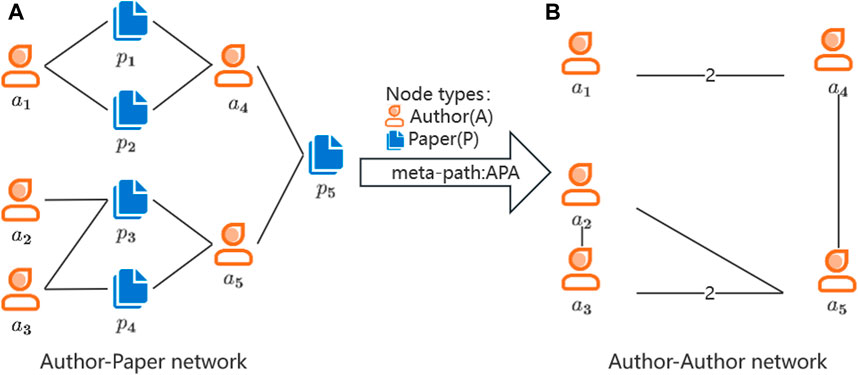
FIGURE 3. An example of Network transformation based on APA meta-path. (A) Author-Paper network. (B) Author-Author network.

We introduce the clustering coefficient [6], measuring neighbor interconnectivity. Higher values indicate neighbors easily interact without the node. Thus, high coefficient nodes with many neighbors may not be critical. The clustering coefficient is described by Eq. 8:

$c_i=\frac{2t_i}{N_i*\left(N_i-1\right)},(8)$

where $t_i$ is the number of triangles formed by node $i$ and its neighbor nodes.

In addition, indirect influence also incorporates a trust probability between nodes, formulated as Eq. 9:

$I{I}_i={\displaystyle \sum _{jϵN_i}}\left(\frac{\text{sim}\left(i,j\right)}{{\displaystyle \sum _{kϵN_j}}sim\left(j,k\right)}*w_{ij}*e^{\left(1-c_i\right)}\right),(9)$

where $w_{ij}$ represents the weight of edges between node pairs, and its value is equal to the number of connected edges of node $i$ and node $j$ existing in the heterogeneous network under the meta-path.

4.2.3 Node importance

Node importance is derived from direct and indirect metrics. To normalize the different dimensions, Min-Max scaling shown in Eq. 10 is applied:

$F_{norm}=\frac{F-F_{\mathit{min}}}{F_{\mathit{max}}-F_{\mathit{min}}},(10)$

where $F_{norm}$ is the result of normalization, $F$ is the value of the node, $F_{\mathit{min}}$ and $F_{\mathit{max}}$ are the minimum and maximum values in the metrics sequence.

Finally, node importance is calculated using Eq. 11. And the top K nodes by importance are identified as key nodes.

$N{I}_i=S_{norm}\left(D{I}_i\right)+S_{norm}\left(I{I}_i\right),(11)$

4.3 Algorithm description

The Algorithm 1 shows the complete identification process of the key nodes.

Algorithm 1.Key node identification algorithm for nodes.

 Input:

 $G$: a heterogeneous information network

 $\mathcal{P}$: using meta-paths $k$: number of key nodes

 Output:

 $NI$: node importance set

 $S$: key node set

 1)  Initialize $S=null$

 2)  Obtain the corpus based on the random walk of meta-path $\mathcal{P}$

 3)  Obtain the low dimensional vector $H_1$, $H_2$ based on the Metapath2Vec model

 4)  For each node $i$ do

 5)   Compute the direct influence $DIi$ using Eq. 7

 6)  Extract homogeneous networks $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$ using meta-path $\mathcal{P}$

 7)  For each node $i$ do

 8)   Compute the indirect influence $IIi$ using Eq. 9

 9)  Normalize the metrics using Eq. 10

 10)  For each node $i$ do

 11)   Compute the node importance $NIi$ using Eq. 11

 12)  $S=Top\left(NI,k\right).$

 13)  Return $NI$ and $S$

4.4 Time complexity

The time complexity of preprocessing the node sampling probability based on the number of edges is described by Eq. 12

$O\left(m\right),(12)$

where the number of edges is $m$.

The complexity of generating random walk sequences is described by Eq. 13

$O\left(n*l*t\right),(13)$

where the number of nodes in the graph is $n$, the length of random walk is $l$ and the number of walks is $t$.

The complexity of Skip-Gram training is described by Eq. 14

$O\left(n*l*t*c*b*e\right),(14)$

where the context window size is $c$, the number of negative samples is $b$, and the number of model iterations is $e$.

The complexity of direct influence calculation based on the number and trust probability of neighbors is described by Eq. 15

$O\left(n*a^2\right),(15)$

where the mean of neighbors is $a$.

The complexity of extracting node relationships under the meta-path of length 2 and indirect influence calculation is described by Eq. 16

$O\left(2*n*a^2\right),(16)$

The complexity of weighted summation and ranking is described by Eq. 17

$O\left(n\right)+O\left(n*\log n\right),(17)$

The total time complexity is described by Eq. 18

$O\left(m+n*l*t+n*l*t*c*b*e+3n*a^2+n+n*\log n\right),(18)$

Since $l,t,c,b,e$ and $a$ are usually small constants, the time complexity can be simplified as Eq. 19

$O\left(m+n*\log n\right),(19)$

5 Experiments

5.1 Datasets

To evaluate the effectiveness of the proposed method, we conducted experiments using three real-world datasets, DBLP [19], ACM [19] and Yelp [19]. DBLP and ACM are academic networks, Yelp is an e-commerce network. Tables 1, 2 present the size and fundamental topology characteristics of these networks. Specifically, the distance denotes the shortest path length between nodes; the diameter represents the length of the longest shortest path; network density indicates the ratio of actual edges to the maximum possible, reflecting the level of interconnectivity between nodes; the average degree signifies the average number of neighbors for each node. In addition, Figure 4 shows the degree distributions of these three networks.

TABLE 1

TABLE 1. Network scale.

TABLE 2

TABLE 2. Network structure characteristics.

FIGURE 4

FIGURE 4. Degree distribution of the datasets: DBLP, ACM and Yelp. (A) Degree distribution of DBLP. (B) Degree distribution of ACM. (C) Degree distribution of Yelp.

Tables 1, 2 showed the three heterogeneous networks had differing scales and densities. The complex edge types led to overall sparse edges and small densities, especially for DBLP. Additionally, the three datasets exhibited contrasting diameter, average distance, and average degree. Therefore, the three datasets provided good diversity to verify the method’s effectiveness.

5.2 Evaluation criterion

5.2.1 Node propagation capability

The ability to disseminate information is a key factor to evaluate the importance of node [8]. There are many information propagation models like independent cascade model [20], linear threshold model [21], and disease spreading models [5]. Among them, the susceptibility-infection model (SI) [5] and susceptibility-influence model (SIR) [12] are the most commonly used in key node identification researches. Therefore, we used the SI and SIR models to evaluate the effectiveness of the method [22]. The SI model simulates the spread of an epidemic, where nodes can only change their status from susceptible (S) to infectious (I). Infected nodes have a probability $\beta$ of infecting their susceptible neighbors each time step, and once a node is infected, it will remain in that state [5]. In SIR model, infected nodes have the probability $\gamma$ to recover as immune individuals and no longer participate in the infection [12].

To demonstrate the method’s effectiveness in identifying key nodes, experiments set iteration times to 20, and used propagation scope as the evaluation metric. 100 experiments were conducted to reduce bias, with infectious scope calculated by averaging. In the SI experiments, a large $\beta$ would cause overspreading and rapid full network infection. This prevents distinguishing key node importance. Also, there are differences in the sparsity and actual propagation probability in different networks. Thus, $\beta$ was set to 0.05 for academic networks and 0.01 for e-commerce networks. In the SIR model, $\gamma$ is set to the double of $\beta$. The propagation scope formula was as Eq. 20:

$f\left(t\right)=1-\frac{\left|S_t\right|}{\left|V\right|},(20)$

where the $S_t$ is the set of susceptible nodes at time step $t$, $f\left(t\right)$ denotes the infection scope at time step t.

5.2.2 Average shortest path length

Rich club effect demonstrates that more decentralized seed nodes enable faster information propagation [18]. Therefore, we further select the average shortest path length between key nodes to analyze the performance of different methods, which is defined as Eq. 21 follows [23]:

$L_s=\frac{1}{\left|S\right|\left(\left|S\left|-1\right|\right.\right)}{\displaystyle \sum _{\begin{array}{l}u,v\in S\\ u\ne v\end{array}}}{l}_{u,v},(21)$

where $S$ is the key node set, $\left|S\right|$ denotes the number of key nodes in $S$, and $l_{u,v}$ denotes the length of the shortest path from node $u$ to $v$.

5.2.3 Node ranking monotonicity

Ma et al. pointed out that good node influence rankings require high resolution [24]. Higher resolution enables easier distinction between nodes’ influence differences. Therefore, to quantitatively measure resolution, ranking monotonicity was introduced as an evaluation metric, calculated by Eq. 22:

$Monotonicity\left(M\right)={\left[1-\frac{{\sum }_{c\in V}{N}_c\left(N_c-1\right)}{N\left(N-1\right)}\right]}^2,(22)$

where $N_c$ denotes the number of nodes with the same metric evaluation score; $N$ denotes the number of nodes in the network.

5.3 Method comparison experiment

5.3.1 Baseline methods

The baseline methods adopted for comparison are Adaptive Degree (AD) [25], Collective Influence (CI) [26], K-Shell [7], KSGC [8], NLC [12], ERM [5], and MAHE [13], as shown in Table 3. These methods were chosen to encompass single metric, multi-metric combination, and embedding-based methods, allowing for a comprehensive comparison of methods.

TABLE 3

TABLE 3. Baseline methods for comparison in experiments.

5.3.2 Information propagation capability comparison

This section documents the experimental effects of different methods. By fixing the infection probability, and selecting 20 key nodes, we compare the capabilities of key nodes to propagate information. In Figures 5, 6, we plot the evolutionary trend of the propagation scope of the six methods over the propagation iterations on three networks in the SI and SIR models. The X-axis is the time step $t$ and the Y-axis is the $f\left(t\right)$ in the network.

FIGURE 5

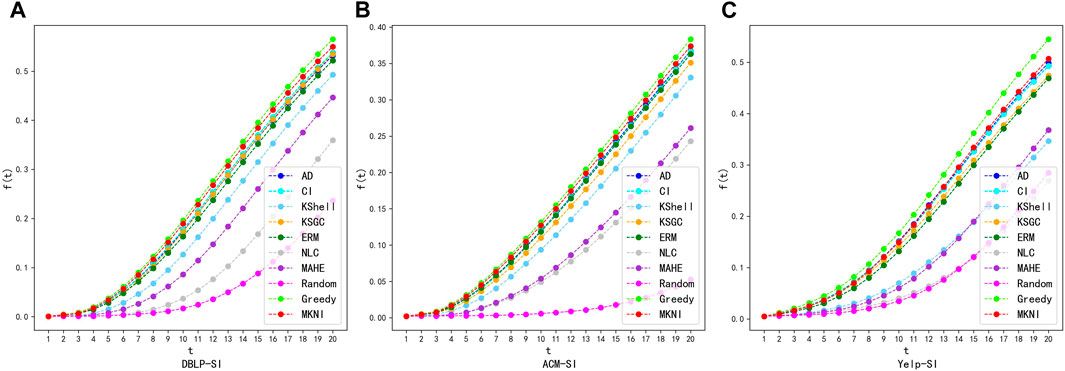
FIGURE 5. Comparing of proposed method with other methods using SI on datasets: DBLP, ACM and Yelp. (A) DBLP-SI. (B) ACM-SI. (C) Yelp-SI.

FIGURE 6

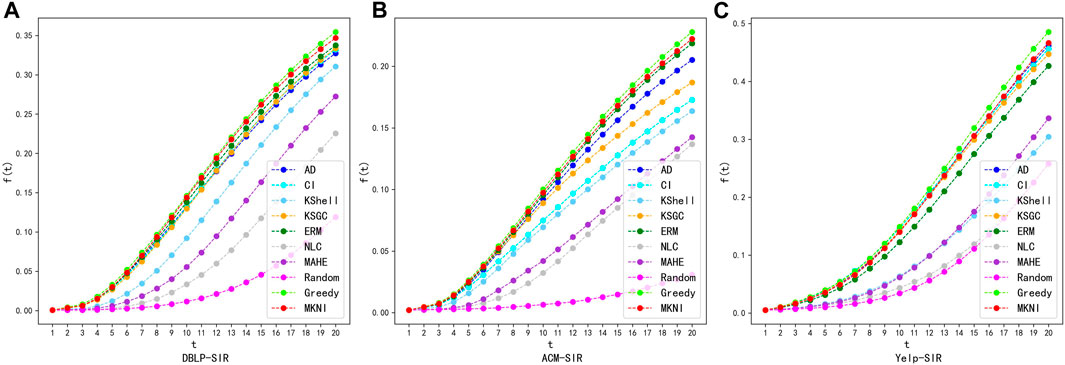
FIGURE 6. Comparing of proposed method with other methods using SIR on datasets: DBLP, ACM and Yelp. (A) DBLP-SIR. (B) ACM-SIR. (C) Yelp-SIR.

Figures 5, 6 show the evolutionary trend of the percentage of infected nodes with the number of iterations. As can be seen from the figures, the total number of infected nodes increases over time step. At each time step, our method outperforms all other methods. This indicates that the top 20 key nodes identified by MKNI are at more important locations in the network and may be more dispersed throughout the network, thus being able to affect a larger area at the same time step.

The experimental results show that the key nodes identified by the MKNI method can achieve a better $f\left(t\right)$ in SI and SIR experiments. It indicates that the key nodes identified by the MKNI method can achieve faster information propagation, to achieve higher influence scope than other methods.

AD, CI, KSGC and ERM performed well by sufficiently incorporating network topology, enabling key nodes to quickly influence neighbors. MKNI surpassed them by better modeling inter-node influence probabilities using trust probability, thereby improving identification. K-Shell struggled due to the network’s sparse connections and distinct topology, which hindered distinguishing influence of heterogeneous nodes. Although MAHE also used metapath2vec embeddings, it only considered node similarity while neglecting topology’s impact, yielding poor results. NLC combined DeepWalk and K-Shell but accumulated the less effective K-Shell, worsening results and producing the worst performance.

These experimental results show that MKNI has the best key node identification performance. The comparisons validate MKNI’s superiority in identifying key nodes for information diffusion in heterogeneous networks.

Additionally, greedy algorithms [20] and random chosen methods [20] are added for comparison, which serve as upper and lower bounds for the performance, respectively. The experimental results indicate that the MKNI method is slightly inferior to the greedy algorithm. The time complexity of the greedy algorithm can be expressed as $O\left(k*n*t*r*e\right)$, where $k$ is the number of nodes to be selected, $n$ is the number of nodes in the network, $t$ is the iteration times of the propagation model, $r$ is the number of rounds of simulations of the propagation experiment, and $e$ is the number of edge in the network. It is evident that the greedy algorithm has a high time complexity. Therefore, although the MKNI method is slightly weaker than the greedy algorithm, MKNI still has advantages, especially in dealing with large-scale network.

5.3.3 Average shortest path length comparison

According to the results of the experiments on the information propagation capability comparison, AD, CI, KSGC, ERM, and MKNI are more effective, while K-Shell, NLC, and MAHE are less effective. To verify whether the key nodes identified by MKNI are more dispersed within the entire network, we compare different methods using the average shortest path length between key nodes as a metric. Figure 7 shows the comparison of the average shortest path length Ls obtained by the three methods. The X-axis is the number of initially infected nodes, and the Y-axis is the $L_s$.

FIGURE 7

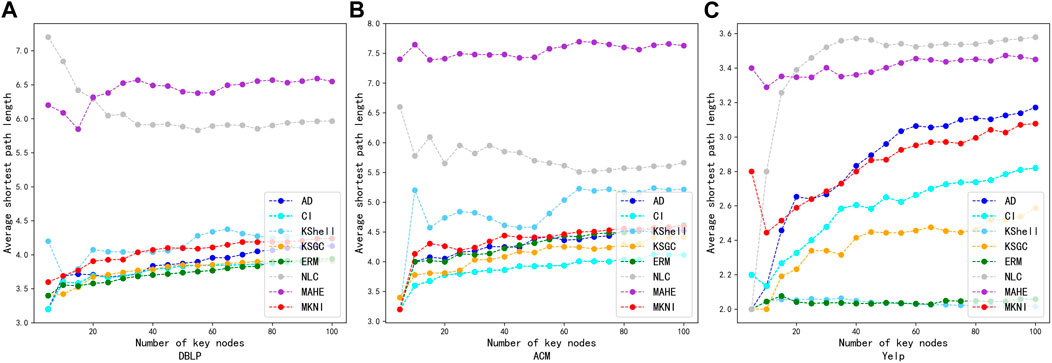
FIGURE 7. Comparing of proposed method with other methods using average shortest path length on datasets: DBLP, ACM and Yelp. (A) DBLP. (B) ACM. (C) Yelp.

From Figure 7, it is observed that the shortest average path length between key nodes obtained by the MKNI method is larger than that obtained by the CI, ERM and KSGC methods. This proves the key nodes obtained by MKNI are more decentralized in the network, making their information propagation capability better. In the denser Yelp network, the MKNI method identifies critical nodes with slightly shorter average shortest paths compared to the AD method. This is due to the greater neighborhood overlap between nodes in dense networks. However, the wider propagation scope of MKNI indicates that the nodes identified by MKNI are in more important locations. In contrast, the key nodes identified by the NLC and MAHE methods have large average shortest paths, but the information propagation capability is inferior, indicating the key nodes identified by them are not in important locations in the network. The results of this experiment further illustrate the superiority of the MKNI method in key node identification.

5.3.4 Node ranking monotonicity comparison

Next, we investigate the ability of AD, CI, K-Shell, KSGC, NLC, ERM, MAHE and MKNI methods to differentiate the node importance through monotonicity metrics. For a specific measure, nodes in the network are ranked according to their importance scores in descending order. Nodes with the same importance score have the same rank. The monotonicity of different key node identification methods is summarized in Table 4.

TABLE 4

TABLE 4. The monotonicity of different methods.

The experimental results demonstrate that the proposed MKNI method achieves the best node ranking monotonicity equal to 1 across all test networks, surpassing other baseline methods. This indicates that the MKNI method possesses a greater resolution in determining node importance and effectively distinguishes the influence of nodes within the network.

5.4 Validity verification experiment

5.4.1 Ranking validity verification

To visually verify the effectiveness of the importance ranking, we selected the top, middle, and bottom20 nodes from the ranking list as the message sources for information propagation. If the higher-ranked nodes exhibit better message propagation rates compared to the lower-ranked nodes, it indicates that nodes with higher importance can propagate messages to more nodes faster, thus validating the calculated node importance ranking by the method in this paper. In Figures 8, 9, we plot the process of information propagation in the SI and SIR models for the three types of source nodes. The X-axis is the time step $t$ and the Y-axis is the $f\left(t\right)$ in the network.

FIGURE 8

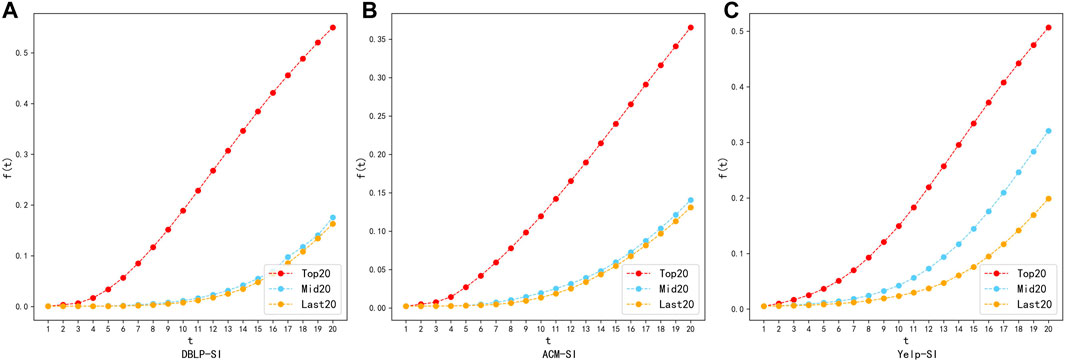
FIGURE 8. Ranking validation diagram using SI model on datasets: DBLP, ACM and Yelp. (A) DBLP-SI. (B) ACM-SI. (C) Yelp-SI.

FIGURE 9

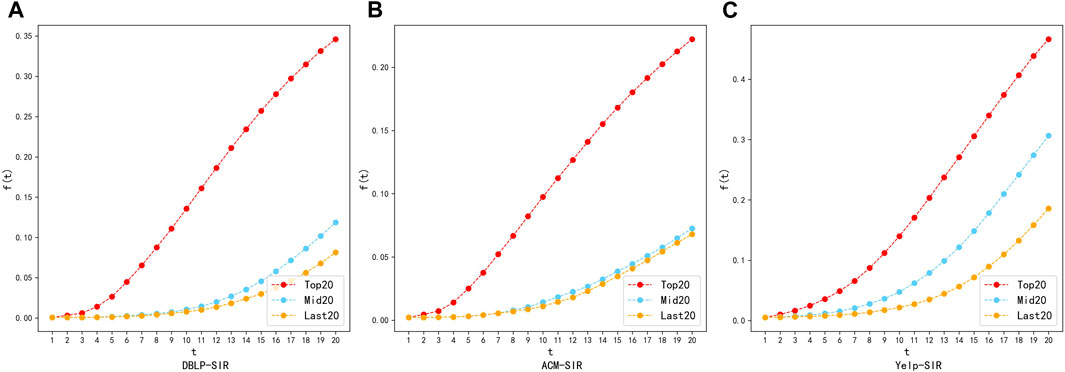
FIGURE 9. Ranking validation diagram using SIR model on datasets: DBLP, ACM and Yelp. (A) DBLP-SIR. (B) ACM-SIR. (C) Yelp-SIR.

The results in Figures 8, 9 showed that the top20 nodes in the node importance sequence obtained by MKNI have higher information propagation scope than the middle20 nodes and the last20 nodes when they are used as propagation sources. Specifically, the difference between mid20 and last20 in DBLP and ACM network is not significant due to the sparse network. This network characteristic makes a larger number of nodes in unimportant positions, and both the middle and the last nodes in the ranking have inferior information propagation capabilities, but still maintains the law that mid20 nodes are larger than last20 nodes. Therefore, the experimental results demonstrates that the importance ranking obtained by MKNI accurately describes the nodes’ impact on the information propagation scope, confirming the effectiveness of the MKNI method.

5.4.2 Trust probability validity verification

MKNI utilizes meta-paths for node embedding and applies the embedded vector to the trust probability. Trust probability validity verification experiment aims to compare the results obtained by considering node trust probability and those obtained without considering it. In Figures 10, 11, we plot the process of information propagation in the SI and SIR models for the two models, where MKNI is the original method and MKNI--is the method after removing the trust probability. The X-axis is the time step $t$ and the Y-axis is the $f\left(t\right)$ in the network.

FIGURE 10

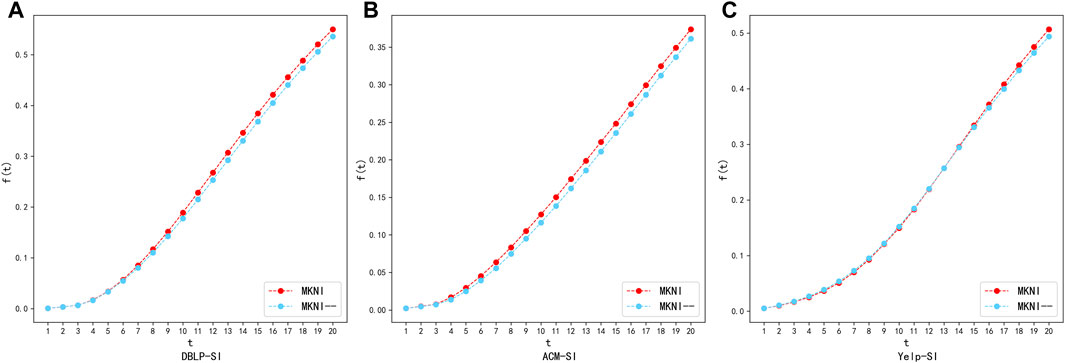
FIGURE 10. Trust probability validation diagram using SI model on datasets: DBLP, ACM and Yelp. (A) DBLP-SI. (B) ACM-SI. (C) Yelp-SI.

FIGURE 11

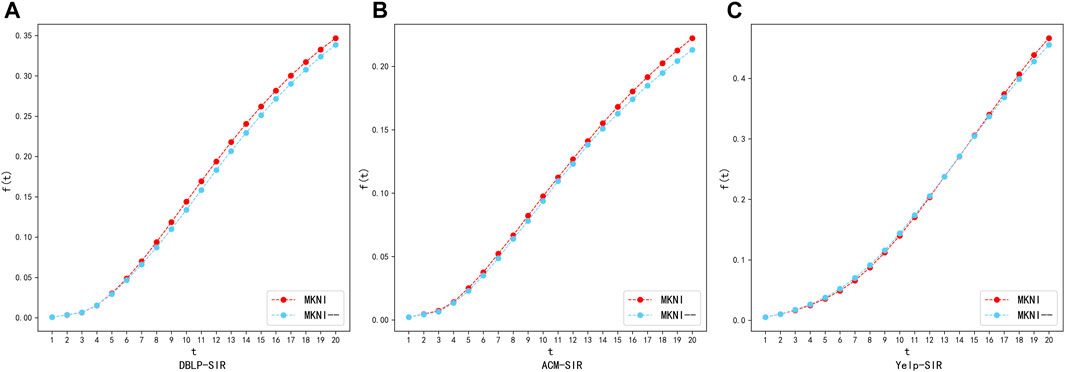
FIGURE 11. Trust probability validation diagram using SIR model on datasets: DBLP, ACM and Yelp. (A) DBLP-SIR. (B) ACM-SIR. (C) Yelp-SIR.

The experimental results show that on the sparse DBLP and ACM datasets, at each time step, the performance of MKNI is generally better than MKNI--; on the relatively denser Yelp dataset, they are similar in the early stage, and later MKNI is slightly better than MKNI--. This indicates the trust probability based on embedding vectors effectively quantifies the likelihood of information propagation from the source node to the target node and improves the accuracy of node importance calculation.

6 Conclusion

In this paper, we propose the key node identification method MKNI for heterogeneous networks. MKNI extracts heterogeneity information using a meta-path-based node embedding model. It introduces a trust probability based on vector similarity to model inter-node influence. Direct and indirect influence indica-tors are then constructed by integrating meta-paths and embeddings to capture rich semantic information. Node importance rankings are obtained via weighted summation. Experiments showed MKNI identified nodes with higher infectious rates and better propagation ability than K-Shell, KSGC, NLC, ERM, and MAHE.

A limitation is MKNI and many existing methods rely heavily on manual meta-path customization to mine heterogeneous networks. Future work will explore meta-path-free approaches to avoid pre-design and enable fully automated heterogeneous network mining.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

PW: Data curation, Software, Validation, Writing–original draft. JS: Formal Analysis, Funding acquisition, Methodology, Validation, Writing–review and editing. LL: Supervision, Writing–review and editing. XY: Formal Analysis, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This paper is partially funded by the National Natural Science Foundation of China (No. 62362052 and No. 62062050) and the Innovation Foundation for Postgraduate Student of Jiangxi Province (No. YC2023-S707).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1351500/full#supplementary-material

References

1. Wang J, Li C, Xia C-Y. Improved centrality indicators to characterize the nodal spreading capability in complex networks. Appl Math Comput (2018) 334:388–400. doi:10.1016/j.amc.2018.04.028

CrossRef Full Text | Google Scholar

2. Ullah A, Wang B, Sheng J, Khan N. Escape velocity centrality: escape influence-based key nodes identification in complex networks. Appl Intell (Dordr) (2022) 52:16586–604. doi:10.1007/s10489-022-03262-4

CrossRef Full Text | Google Scholar

3. Wang L-J, Zheng S-Y, Wang Y-G, Wang L-F. Identification of critical nodes in multimodal transportation network. Physica a: Stat Mech its Appl (2021) 580:126170. doi:10.1016/j.physa.2021.126170

CrossRef Full Text | Google Scholar

4. Wan L-T, Zhang M-Y, Li X, Sun L, Wang X, Liu K. Identification of important nodes in multilayer heterogeneous networks incorporating multirelational information. Ieee Trans Comput Soc Syst (2022) 9:1715–24. doi:10.1109/TCSS.2022.3161305

CrossRef Full Text | Google Scholar

5. Molaei S, Farahbakhsh R, Salehi M, Crespi N. Identifying influential nodes in heterogeneous networks. Expert Syst Appl (2020) 160:113580. doi:10.1016/j.eswa.2020.113580

CrossRef Full Text | Google Scholar

6. Berahmand K, Bouyer A, Samadi N. A new centrality measure based on the negative and positive effects of clustering coefficient for identifying influential spreaders in complex networks. Chaos, Solitons & Fractals (2018) 110:41–54. doi:10.1016/j.chaos.2018.03.014

CrossRef Full Text | Google Scholar

7. Kitsak M, Gallos L-K, Havlin S, Liljeros F, Muchnik L, Stanley H-E, et al. Identification of influential spreaders in complex networks. Nat Phys (2010) 6:888–93. doi:10.1038/nphys1746

CrossRef Full Text | Google Scholar

8. Yang X, Xiao F-Y. An improved gravity model to identify influential nodes in complex networks based on k-shell method. Knowl Based Syst (2021) 227:107198. doi:10.1016/j.knosys.2021.107198

CrossRef Full Text | Google Scholar

9. Ding C-F, Li K. Centrality ranking in multiplex networks using topologically biased random walks. Neurocomputing (2018) 312:263–75. doi:10.1016/j.neucom.2018.05.109

CrossRef Full Text | Google Scholar

10. Wu M-C, He S-B, Zhang Y-T, Chen J-M, Sun Y-X, Liu Y-Y, et al. A tensor-based framework for studying eigenvector multicentrality in multilayer networks. Proc Natl Acad Sci (2019) 116:15407–13. doi:10.1073/pnas.1801378116

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Luo H, Yan G-H, Zhang M, Bao J-B, Li J-C, Liu T. Identifying important nodes in multi-relational networks based on evidence theory. Chin J Comput (2020) 43:2398–413. doi:10.11897/SP.J.1016.2020.02398

CrossRef Full Text | Google Scholar

12. Yang X-H, Xiong Z, Ma F-N, Chen X-Z, Ruan Z-Y, Jiang P, et al. Identifying influential spreaders in complex networks based on network embedding and node local centrality. Physica a: Stat Mech its Appl (2021) 573:125971. doi:10.1016/j.physa.2021.125971

CrossRef Full Text | Google Scholar

13. Li Y, Li L-L, Liu Y-J, Li Q-Q. MAHE-IM: multiple aggregation of heterogeneous relation embedding for influence maximization on heterogeneous information network. Expert Syst Appl (2022) 202:117289. doi:10.1016/j.eswa.2022.117289

CrossRef Full Text | Google Scholar

14. Shi C, Wang R-J, Wang X. Survey on heterogeneous information networks analysis and applications. J Softw (2021) 33:598–621. doi:10.13328/j.cnki.jos.006357

CrossRef Full Text | Google Scholar

15. Dong Y-X, Chawla N-V, Swami A. metapath2vec: scalable representation learning for heterogeneous networks. Proc ACM SIGKDD Conf (2017) 135–44. doi:10.1145/3097983.3098036

CrossRef Full Text | Google Scholar

16. Shi C, Hu B-B, Zhao W-X, Yu P-S. Heterogeneous information network embedding for recommendation. Ieee Trans Knowl Data Eng (2019) 31:357–70. doi:10.1109/TKDE.2018.2833443

CrossRef Full Text | Google Scholar

17. He H-M, Xiao M, Lu Y-X, Wang Z, Tao B-B. Control of tipping in a small-world network model via a novel dynamic delayed feedback scheme. Chaos, Solitons & Fractals (2023) 168:113171. doi:10.1016/j.chaos.2023.113171

CrossRef Full Text | Google Scholar

18. Berahmand K, Samadi N, Sheikholeslami S-M. Effect of rich-club on diffusion in complex networks. Int J Mod Phys B (2018) 32:1850142. doi:10.1142/S0217979218501424

CrossRef Full Text | Google Scholar

19. Chairatanakul N, Liu X, Hoang N-T, Murata T. Heterogeneous graph embedding with single-level aggregation and infomax encoding. Mach Learn (2023) 112:4227–56. doi:10.1007/s10994-022-06160-5

CrossRef Full Text | Google Scholar

20. Erkol S, Castellano C, Radicchi F. Systematic comparison between methods for the detection of influential spreaders in complex networks. Sci Rep (2019) 9:15095. doi:10.1038/s41598-019-51209-6

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kempe D, Kleinberg J, Tardos É. Maximizing the spread of influence through a social network. Proc ACM SIGKDD Conf (2003) 137–46. doi:10.1145/956750.956769

CrossRef Full Text | Google Scholar

22. Maji G, Dutta A, Curado Malta M, Sen S. Identifying and ranking super spreaders in real world complex networks without influence overlap. Expert Syst Appl (2021) 179:115061. doi:10.1016/j.eswa.2021.115061

CrossRef Full Text | Google Scholar

23. Wang M, Li W, Guo Y, Peng X, Li Y. Identifying influential spreaders in complex networks based on improved k-shell method. Physica a: Stat Mech its Appl (2020) 554:124229. doi:10.1016/j.physa.2020.124229

CrossRef Full Text | Google Scholar

24. Ma L-L, Ma C, Zhang H-F, Wang B-H. Identifying influential spreaders in complex networks based on gravity formula. Physica a: Stat Mech its Appl (2016) 451:205–12. doi:10.1016/j.physa.2015.12.162

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chen W, Wang Y-J, Yang S-Y, Dong T, Liu C, Chen Z, et al. Changes of main secondary metabolites in leaves of Ginkgo biloba in response to ozone fumigation. Proc ACM SIGKDD Conf (2009) 21:199–203. doi:10.1016/s1001-0742(08)62251-2

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Morone F, Makse H-A. Influence maximization in complex networks through optimal percolation. Nature (2015) 524:65–8. doi:10.1038/nature14604

PubMed Abstract | CrossRef Full Text | Google Scholar