Universal quantum gates by nonadiabatic holonomic evolution for the surface electron

The nonadiabatic holonomic quantum computation based on the geometric phase is robust against the built-in noise and decoherence. In this work, we theoretically propose a scheme to realize nonadiabatic holonomic quantum gates in a surface electron system, which is a promising two-dimensional platform for quantum computation. The holonomic gate is realized by a three-level structure that combines the Rydberg states and spin states via an inhomogeneous magnetic field. After a cyclic evolution, the computation bases pick up different geometric phases and thus perform a holonomic gate. Only the electron with spin up experiences the holonomic gate, while the electron with spin down is decoupled from the state-selective driving fields. The arbitrary controlled-U gate encoded on the Rydberg states and spin states can then be realized. The fidelity of the output state exceeds 0.99 with experimentally achievable parameters.

1 Introduction

The quantum geometric phase is a very important resource for quantum computation [1–5]. Quantum gates based on the geometric phase are robust against the disturbance of the dynamic process owing to their global geometric properties [6]. The adiabatic holonomic quantum computation (AHQC) realizes high-fidelity quantum gates via the geometric phase in an adiabatic evolution [7–15]. The AHQC protocol is solely determined by the solid angle of the cyclic evolution in the parameter space, and thus is robust against small perturbations of the evolution path. However, the adiabatic condition [16] of AHQC requires a long evolution time, which accumulates considerable decoherence. Thus, the nonadiabatic holonomic quantum computation (NHQC) was proposed [17–28]. The NHQC preserves the computational universality of the AHQC but does not require the adiabatic condition, and thus has attracted broad interest in recent years [29–45].

On the other hand, the electron on the surface of liquid helium provides a controllable two-dimensional (2D) quantum system, where the surface electron (SE) is attracted by the induced image charge inside the liquid helium and concurrently repulsed by the helium atoms. The confinement perpendicular to the surface leads to a hydrogen-like spectrum which can be used in quantum simulation [46, 47] and quantum information tasks [48, 49]. Meanwhile, the motion parallel to the surface is free of defects and impurities, thus the SE forms a perfect 2D electron system which is widely observed in semiconductor devices [50]. The SE can be manipulated by the circuit QED architecture [51, 52] or the microchannel devices [53–59] with high transport efficiency [60, 61]. With a static magnetic field perpendicular to the surface, the motion parallel to the surface is quantized as orbital states [62], which is similar to the Landau levels. In addition, the spin state of the SE is also an important quantum resource owing to its long relaxation time that exceeds 100 s [63]. Both the Rydberg and orbital states can be coupled to the spin states of electrons [64, 65]. Recent works [66, 67] show a practical method to couple the Rydberg state with the spin state using a local inhomogeneous magnetic field, where the electrons with different expected positions experience different magnetic fields depending on their Rydberg state. The Rydberg states of SE can probably realize large-scale quantum computation owing to the long-range dipole-dipole interaction of adjacent electrons [67], while the spin states may be valuable for quantum memory because of their long lifetime.

In the past, research on the SE has mainly focused on exploring the physical properties, while the efficient quantum gates based on the SE still require further investigation. Therefore, in this work, we propose a scheme to realize the nonadiabatic holonomic gates on both the spin states and Rydberg states of a single SE. We first propose an arbitrary single-qubit holonomic gate on the Rydberg state of the SE, which is realized by a three-level structure driven by time-dependent microwave pulses. During the cyclic evolution, two orthogonal bases pick up different geometric phases. The universal single-qubit holonomic gate is realized by varying the complex ratio between the Rabi frequencies of the two driving fields. Then we introduce an inhomogeneous magnetic field through a magnetized ferromagnetic electrode. The Rydberg states with different expected positions experience different magnetic fields, and thus their Zeeman energy splittings are different. By applying the state-selective pulses, three Rydberg states with spin up are coupled with the driving fields, while the Rydberg states with spin down are decoupled. An arbitrary holonomic single-qubit gate U is applied on the three coupled states, while the three decoupled states remain unchanged. In this way, the holonomic controlled-U gate of the Rydberg and spin states is achieved. Owing to the global geometric properties, the NHQC gates are not sensitive to the fluctuation of the pulse duration. Because the adiabatic condition is not required during the evolution, the fast manipulation makes the scheme robust against dissipation. Our theoretical scheme is based on the experimental configuration, and the parameters are experimentally achievable.

This paper is organized as follows. In Section 2, we introduce the basic model of the SE in the external magnetic and electric fields and the method to realize holonomic gates. In Section 3, we present the fidelity of the scheme. Finally, we conclude the work and give a prospect in Section 4.

2 Model and methods

2.1 Basic model of the surface electron

Our theoretical proposal is based on the electron above liquid helium. The electron is trapped by the external electric field provided by electrodes [67]. As shown in Figure 1, a pillar electrode with positive voltage and an annular electrode with negative voltage are embedded in the liquid helium. These electrodes apply an electric holding field with the cylindrically symmetric electric potential V(r, z), where z is the vertical coordinate and $r=\sqrt{x^2+y^2}$ is the radial coordinate. Meanwhile, the electron is confined by the image potential −Λe²/z introduced by the image charge in the liquid helium, where e is the charge of the electron and Λ = (ϵ − 1)/[4(ϵ + 1)] with the dielectric constant ϵ ≈ 1.057. The vertical motion of the SE is quantized as the Rydberg states. On the other hand, a uniform static magnetic field B₀ = B₀e_z is perpendicularly applied to the surface. Because the total potential −Λe²/z − eV(r, z) is cylindrically symmetric, we introduce the symmetric gauge A = B₀ ×r/2. The motion of the electron is determined by the Hamiltonian

$\begin{array}{ll}\hfill H_T& =\frac{{\left(\mathit{p}+e\mathit{A}\right)}^2}{2m_e}-\frac{\mathrm{\Lambda }{e}^2}{z}-eV\left(r,z\right)\hfill \\ \hfill & =H_0+\frac{1}{2}{\omega }_c{L}_z,\hfill \end{array}(1)$

where ω_c = eB₀/m_e is the cyclotron frequency, m_e is the mass of the electron, and L_z is the angular momentum along z-direction, i.e.,

$L_z=x{p}_y-y{p}_x=-i\hslash \left(x\frac{\partial }{\partial y}-y\frac{\partial }{\partial x}\right)=-i\hslash \frac{\partial }{\partial \varphi },(2)$

where p_α and α are the momentum and position of the electron (α = x, y, z), and ϕ is the azimuthal coordinate in the xOy-plane. The vertical and radial motion of the electron is determined by

$\begin{array}{ll}\hfill H_0& =\frac{1}{2m_e}\left(p_x^2+p_y^2+p_z^2\right)+\frac{1}{8}{m}_e{\omega }_c^2\left(x^2+y^2\right)-\frac{\mathrm{\Lambda }{e}^2}{z}-eV\left(r,z\right)\hfill \\ \hfill & =-\frac{{\hslash }^2}{2m_e}\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{m^2}{r^2}+\frac{{\partial }^2}{\partial z^2}\right)+\frac{1}{8}{m}_e{\omega }_c^2{r}^2-\frac{\mathrm{\Lambda }{e}^2}{z}-eV\left(r,z\right),\hfill \end{array}(3)$

where m is an integer. Because of the cylindrical symmetry, the wavefunction can be expressed as

$\mathrm{\Psi }\left(z,r,\varphi \right)={\psi }_{n_z,n_r,m}\left(z,r\right)\mathrm{\Phi }\left(\varphi \right),(4)$

where ${\psi }_{n_z,n_r,m}(z,r)$ is the wavefunction of H₀ with the vertical quantum number n_z, the radial quantum number n_r, and the angular quantum number m. Φ(ϕ) = e^imϕ is the azimuthal wavefunction that satisfies L_zΦ(ϕ) = mℏΦ(ϕ).

FIGURE 1

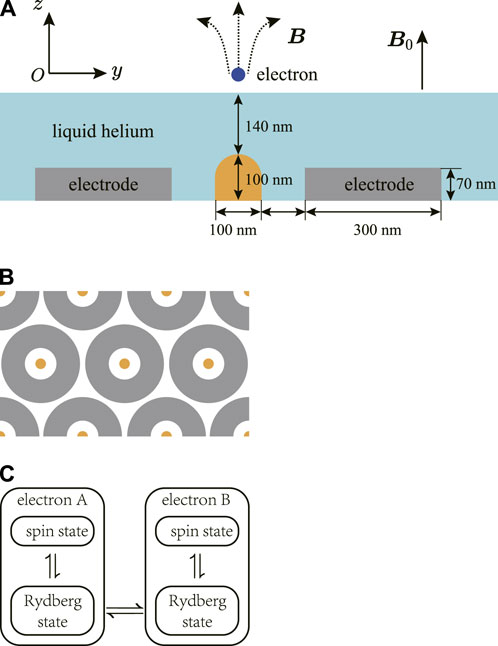
FIGURE 1. (A) The longitudinal section of the proposed model. A central pillar electrode (orange) with a positive voltage of 60 mV and an annular electrode (dark gray) with a negative voltage of −45 mV are embedded in the liquid helium. The SE floats above the liquid surface. The vertical motion of the SE is quantized as the Rydberg states owing to the image potential and the electric field applied by the electrodes. A uniform static magnetic field B₀ is perpendicularly applied to the surface. The center electrode is made of ferromagnetic material and induces an inhomogeneous magnetic field. The total magnetic field is B. The motion in the xOy plane is quantized as the Landau level induced by the vertical magnetic field and the cylindrically symmetric electric potential. (B) The top view of the architecture. The electrodes are arranged in an array, with one electron in each unit. Because the energy levels of each electron can be independently tuned by the voltage of electrodes, the driving field can be resonant with only one electron at a time. The adjacent electrons can be coupled by the dipole-dipole interaction of the Rydberg states. (C) The quantum information can be stored in the spin states and manipulated in large-scaled quantum computation via the Rydberg states.

The vertical motion of the SE is quantized by the Rydberg state labeled by n_z. The expected positions of the lowest three states along the z direction are 7.63 nm, 17.2 nm, and 25.3 nm, which are derived from the numerical solution of the wavefunction, cf. the Supplementary Material. An inhomogeneous magnetic field is induced by the center electrode which is made of ferromagnetic material. The electrons with different n_z have different expected positions ⟨z⟩, and thus experience different magnetic fields. The differences of the magnetic field ΔB at the expected positions with n_z = 1, 2, 3 are on the order of several mT. The corresponding difference of the Zeeman energy gμ_BΔB/h is about hundreds of GHz, where g is the Lande g factor and μB = eℏ/(2m_e) is the Bohr magneton. This energy difference is much larger than the decay rates of the Rydberg states, cf. the Supplementary Material, and plays a significant role in the following controlled-U gate scheme.

2.2 Nonadiabatic holonomic quantum gates based on the Rydberg states and spin states

At first, we will demonstrate the proposal to realize a single-qubit gate in the subspace of a specific spin state, that is, the subspace spanned by {|↑, n_z⟩} (n_z = 1, 2, 3). As we have mentioned in Section 2.1, the Rydberg states with larger quantum number n_z are further away from the liquid surface, and thus experience different magnetic fields. Since the Zeeman energy of the spin state is determined by the inhomogeneous magnetic field, the Zeeman energies of different Rydberg states are different. The magnetic field experienced by state |n_z⟩ is $B_z^{(n_z)}$. The Zeeman-energy splitting between |↑, n_z⟩ and |↓, n_z⟩ is $g{\mu }_B{B}_z^{(n_z)}$, where ↑ and ↓ represent the spin-up and spin-down states, respectively. As shown in Figure 2A, if we label the transition frequency of |↑, n_z⟩ ⇔|↑, 3⟩ as ${\omega }_{n_{z}3}$ (n_z = 1, 2), then the transition frequency of |↓, n_z⟩ ⇔|↓, 3⟩ is ${\omega }_{n_{z}3}+{\delta }_{n_{z}3}$, with ${\delta }_{n_{z}3}=g{\mu }_B[B_z^{(n_z)}-B_z^{(3)}]$. The inhomogeneous magnetic field along the normal direction in the range of 0 ∼ 20 nm is approximately linear, and the gradient is approximately 0.4 mT/nm [67]. The detunings are δ₁₃/2π ≈ 190 MHz and δ₂₃/2π ≈ 90 MHz. Therefore, by applying two state-selective driving fields with frequency ${\omega }_{n_{z}3}$, the three Rydberg states with spin up form a Λ-type three-level structure, while the Rydberg states with spin down are decoupled. The driving pulses are controlled by an arbitrary-waveform generator. The Rabi frequencies of |↑, 1⟩ ⇔|↑, 3⟩ and |↑, 2⟩ ⇔|↑, 3⟩ are respectively Ω₁(t) and Ω₂(t). The ratio between Ω₁(t) and Ω₂(t) is a constant, i.e., Ω₁(t) = Ω(t) sin(θ/2)e^iφ and Ω₂(t) = −Ω(t) cos(θ/2) with $\mathrm{\Omega }(t)=\sqrt{{\mathrm{\Omega }}_1^2(t)+{\mathrm{\Omega }}_2^2(t)}$. The interaction Hamiltonian reads

$H_I\left(t\right)=\mathrm{\Omega }\left(t\right)\left(\sin \frac{\theta }{2}{e}^{i\phi }|\uparrow ,3\rangle \langle \uparrow ,1|-\cos \frac{\theta }{2}|\uparrow ,3\rangle \langle \uparrow ,2|+\mathrm{H}.\mathrm{c}.\right).(5)$

Hereafter, we assume ℏ = 1 for simplicity. Ω(t) represents the shape of the driving pulse. The duration of the driving pulse can be very short because the adiabatic condition is not required during the evolution. A specific pulse shape is not strictly required for NHQC, but the integral over time needs to be π, i.e., ${\int }_{-\infty }^{\infty }\mathrm{\Omega }(t)dt=\pi$, which will be explained later.

FIGURE 2

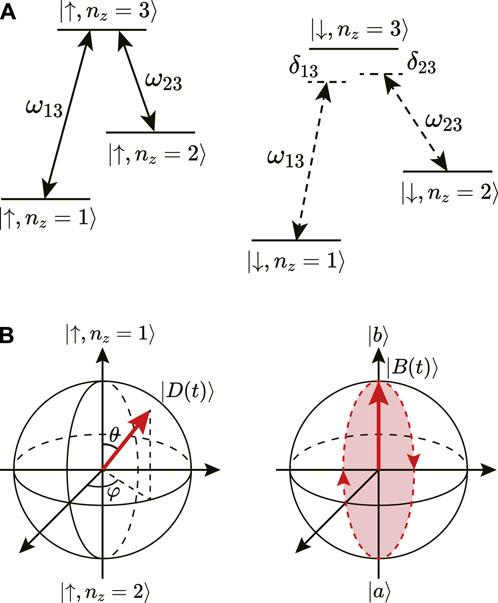
FIGURE 2. (A) Schematic diagram of the nonadiabatic holonomic gate. Two driving pulses are resonant with |↑, n_z = 1⟩ ⇔|↑, n_z = 3⟩ and |↑, n_z = 2⟩ ⇔|↑, n_z = 3⟩, respectively. The driving pulses are off-resonant with the transition frequencies of the spin-down states due to the large detuning δ₁₃ and δ₂₃. (B) The evolutions of the instantaneous orthogonal bases |D(t)⟩ and |B(t)⟩ on the Bloch spheres. The dark state |D(t)⟩ remains unchanged, while |B(t)⟩ evolves along the longitude circle and acquires a geometric phase.

The eigenenergies of H_I are 0, ± Ω. The corresponding eigenstates are

$|{\psi }_0\rangle =|d\rangle ,(6)$

$|{\psi }_{+}\rangle =\frac{1}{\sqrt{2}}\left(|b\rangle +|a\rangle \right),(7)$

$|{\psi }_{-}\rangle =\frac{1}{\sqrt{2}}\left(|b\rangle -|a\rangle \right),(8)$

Where |d⟩ ≡ cos(θ/2)|↑, 1⟩ + sin(θ/2)e^iφ|↑, 2⟩ is the dark state, |b⟩ ≡ sin(θ/2)e^−iφ|↑, 1⟩ − cos(θ/2)|↑, 2⟩ is the bright state, and |a⟩ = |↑, 3⟩ is the intermediate state. The dark state does not evolve with time because the corresponding eigenenergy is zero. Thus, we define

$|D\left(t\right)\rangle \equiv U_1\left(t\right)|d\rangle =|d\rangle ,(9)$

where

$U_1\left(t\right)=\mathcal{T}\exp \left[i{\int }_0^t{H}_I\left(t^{\prime }\right)d{t}^{\prime }\right],(10)$

is the evolution operator of H_I, and $\mathcal{T}$ represents the time-ordered integration. We also define

$\begin{array}{l}\hfill |B\left(t\right)\rangle \equiv e^{i\alpha \left(t\right)}{U}_1\left(t\right)|b\rangle \\ =e^{i\alpha \left(t\right)}\left[\cos \alpha \left(t\right)|b\rangle -i\sin \alpha \left(t\right)|a\rangle \right],\hfill \end{array}(11)$

where $\alpha (t)={\int }_0^t\mathrm{\Omega }(t^{\prime })d{t}^{\prime }$. Here we introduce a global phase e^iα(t) to ensure a cyclic evolution of |B(t)⟩ when α = π at the final time. The evolutions of |D(t)⟩ and |B(t)⟩ are shown in Figure 2B. The state |D(t)⟩ is unchanged, while the state |B(t)⟩ evolves along the longitude line of the Bloch sphere with bases {|b⟩, |a⟩} and induces a geometric phase. To make use of the geometric phase, we introduce the following instantaneous orthogonal bases,

$|{\xi }_1\left(t\right)\rangle \equiv \sin \frac{\theta }{2}{e}^{i\phi }|B\left(t\right)\rangle +\cos \frac{\theta }{2}|D\left(t\right)\rangle ,(12)$

$|{\xi }_2\left(t\right)\rangle \equiv -\cos \frac{\theta }{2}|B\left(t\right)\rangle +\sin \frac{\theta }{2}{e}^{-i\phi }|D\left(t\right)\rangle .(13)$

By choosing α(τ) = π at the final time τ, |ξ₁(τ)⟩ = |ξ₁(0)⟩ = |↑, 1⟩ and |ξ₂(τ)⟩ = |ξ₂(0)⟩ = |↑, 2⟩, i.e., |ξ₁(t)⟩ and |ξ₂(t)⟩ coincide with the computation bases |↑, 1⟩ and |↑, 2⟩ both at the beginning and end of time. It can be easily verified that the parallel transport condition ⟨ξ₁(t)|H_I(t)|ξ₂(t)⟩ = 0 is satisfied during the whole evolution t ∈ [0, τ]. Thus, the dynamic phases vanish and the evolution operator U(τ) in the subspace spanned by |↑, 1⟩ and |↑, 2⟩ is [19, 29]

$\begin{array}{ll}\hfill U\left(\tau \right)& =\mathcal{T}\exp \left[i{\int }_0^{\tau }\mathcal{A}\left(t\right)dt\right]\hfill \\ \hfill & =\left(\begin{array}{cc}\hfill \cos \theta \hfill & \hfill e^{-i\phi }\sin \theta \hfill \\ \hfill e^{i\phi }\sin \theta \hfill & \hfill -\cos \theta \hfill \end{array}\right)\hfill \\ \hfill & =\mathit{n}\cdot \mathit{\sigma },\hfill \end{array}(14)$

where n = (sin θ cos φ, sin θ sin φ, cos θ), σ = (σ_x, σ_y, σ_z) are the Pauli operators, and the connection matrix $\mathcal{A}$ is

$\mathcal{A}=-\dot{\alpha }\left(\begin{array}{cc}\hfill {\sin }^2\frac{\theta }{2}\hfill & \hfill -\sin \frac{\theta }{2}\cos \frac{\theta }{2}{e}^{-i\phi }\hfill \\ \hfill -\sin \frac{\theta }{2}\cos \frac{\theta }{2}{e}^{i\phi }\hfill & \hfill {\cos }^2\frac{\theta }{2}\hfill \end{array}\right)(15)$

whose matrix elements are determined by

${\mathcal{A}}_{ij}=⟨{\xi }_i\left(t\right)|i{\partial }_t|{\xi }_j\left(t\right)⟩.(16)$

Therefore, a single-qubit holonomic gate on the coupled Rydberg states is realized by adjusting the complex ratio tan(θ/2)e^iφ between the Rabi frequencies of the two driving fields. For example, a Hadamard gate H is realized by (θ, φ) = (π/4, 0), and a NOT gate X is realized by (θ, φ) = (π/2, 0). In addition, two sequential holonomic gates lead to

$U^{\left(m\right)}{U}^{\left(n\right)}=\mathit{n}\cdot \mathit{m}-i\mathit{\sigma }\cdot \left(\mathit{n}\times \mathit{m}\right),(17)$

which forms an arbitrary SU(2) transformation that rotates the state around the axis n ×m by the angle 2 arccos(n ⋅m) [19, 68]. For instance, the π/8 phase gate [68] is realized by two sequential gates with (θ, φ) = (π/2, 0) and (θ, φ) = (π/2, π/8).

Next, we will demonstrate the two-qubit gate proposal by taking two spin states into account. As shown in Figure 2A, the Rydberg states with spin down are off-resonant with the driving fields. Thus, the subspace spanned by {|↓, n_z⟩} (n_z = 1, 2, 3) is decoupled with the driving fields. The total evolution operator in the subspace spanned by {|↓, 1⟩, |↓, 2⟩, |↑, 1⟩, |↑, 2⟩} is

$U_{\text{tot}}\left(\tau \right)=|\downarrow \rangle \langle \downarrow |\otimes I+|\uparrow \rangle \langle \uparrow |\otimes U,(18)$

where U is the single-qubit gate on the Rydberg states according to Eq. 14. In this way, the holonomic controlled-U gate with the spin state being the control qubit is realized. In addition, according to Eq. 17, by applying two controlled gate sequentially, we can realize an arbitrary controlled-U gate. For example, by choosing (θ, φ) = (π/2, 0), U = X and a CNOT gate is realized as

$U_{\text{tot}}\left(\tau \right)=|\downarrow \rangle \langle \downarrow |\otimes I+|\uparrow \rangle \langle \uparrow |\otimes X,(19)$

where I and X are the identity operator and qubit-flip operator in the subspace spanned by {|n_z = 1⟩, |n_z = 2⟩}, respectively. The Rydberg states flip only if the spin state is |↑⟩. Similarly, by choosing (θ, φ) = (0, 0), U = Z and a controlled phase (CZ) gate is achieved.

In the presence of dissipation, the evolution of the system can be described by the quantum master equation [69]

$\frac{\partial }{\partial t}\rho =-i\left[H,\rho \right]-\mathcal{L}\left(\rho \right),(20)$

where the Lindblad operator is

$\mathcal{L}\left(\rho \right)=\sum _{m,n}{\kappa }_{mn}\left[C_{mn}\rho C_{mn}^{†}-\frac{1}{2}\left\{C_{mn}^{†}{C}_{mn},\rho \right\}\right],(21)$

where {A, B} = AB+ BA is the anti-commutator, C_mn = |m⟩⟨n| is the collapse operator with the corresponding decay rate κ_mn. It is noteworthy that κ_mn increases with the electric holding field E_⊥ induced by the electrodes, cf. the Supplementary Material. For typical experimental configuration, E_⊥ is on the order of 100 ∼ 1000 V/cm [70]. Hereafter the evolution with dissipation is solved by QuTiP [71, 72].

3 Results

The state fidelity F between the final state ρ(t) and the ideal target state ρ_i is defined as [68]

$F=\mathrm{T}\mathrm{r}\sqrt{\sqrt{{\rho }_i}\rho \left(t\right)\sqrt{{\rho }_i}}.(22)$

In Table 1, we present the fidelity of the CNOT gate with typical initial states under the influence of dissipation. While in Table 2, we present the fidelity of the controlled-phase (CZ) gate. The decay rates are calculated under a typical electric holding field E_⊥ = 100 V/cm [73]. Because the adiabatic condition is not required during the evolution, the evolving time can be very short. For the typical microwave driving with Rabi frequency Ω_R/2π = 40 MHz [50, 73], we use the Gaussian driving pulse with the duration T = 2π/Ω_R = 25 ns and the standard deviation σ = T/8. The full width at half maxima (FWHM) is $t_{\text{FWHM}}=2\sqrt{2\ln 2}\sigma \approx 0.3T$.

TABLE 1

TABLE 1. The output-state fidelity of the CNOT gate under typical input states. The decay rates are calculated under a typical electric holding field E_⊥ = 100 V/cm, which are κ₂₁ = 1.95 MHz, κ₃₂ = 0.22 MHz, and κ₃₁ = 1.69 MHz.

TABLE 2

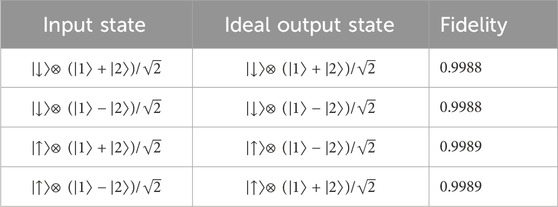
TABLE 2. The output-state fidelity of the CZ gate under typical input states. The decay rates are the same as Table 1.

It is noteworthy that the CNOT gate can generate an entangled state from a product state. Thus, we present the time evolution of the initial product state $(|\downarrow \rangle +|\uparrow \rangle )\otimes |1\rangle /\sqrt{2}$ in Figure 3 and the density matrix of the final state in Figure 4. The result shows that the initial state evolves to the maximal-entangled state $(|\downarrow ,1\rangle +|\uparrow ,2\rangle )/\sqrt{2}$ with high fidelity. Figure 3 also indicates that the fidelity F > 0.99 as long as t > 0.67 T. Even if the pulse duration is a little bit longer or shorter than T, the fidelity of the final state is still very high. Thus, the NHQC method is not sensitive to the fluctuation of the pulse duration, which might be commonly observed in experiments.

FIGURE 3

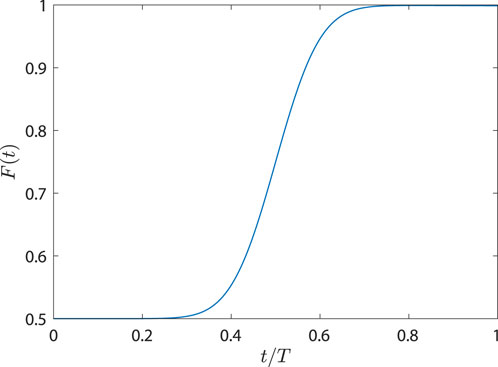
FIGURE 3. Time evolution of the state ρ(t) under the CNOT gate with the initial state $(|\downarrow \rangle +|\uparrow \rangle )\otimes |1\rangle /\sqrt{2}$. F(t) is the fidelity between the ideal output state and the state ρ(t). The decay rates are the same as Table 1. The duration T of the Gaussian driving pulse is 25 ns.

FIGURE 4

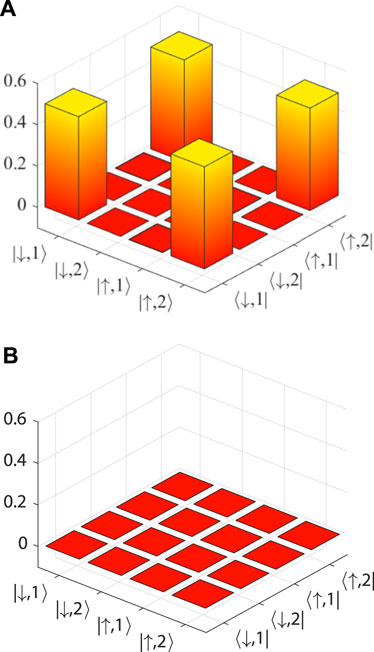
FIGURE 4. (A) Real and (B) imaginary part of the density matrix of the output state from the initial state $(|\downarrow \rangle +|\uparrow \rangle )\otimes |1\rangle /\sqrt{2}$. The decay rates are the same as Table 1.

Generally the electric holding field E_⊥ is applied to the experimental system in order to confine the motion of electrons and tune the energy spacing between the Rydberg states. E_⊥ is on the order of 100 ∼ 1000 V/cm for typical experimental configuration [70]. Because κ_mn increases with E_⊥, we investigate the fidelity with initial state $(|\downarrow \rangle +|\uparrow \rangle )\otimes |1\rangle /\sqrt{2}$ under different electric fields, as shown in Figure 5. The fidelity F is higher than 0.99 for E_⊥ < 400 V/cm, and higher than 0.96 for E_⊥ < 1000 V/cm. Therefore, our scheme is robust against dissipation in experiments.

FIGURE 5

FIGURE 5. Fidelity of the output state with initial state $(|\downarrow \rangle +|\uparrow \rangle )\otimes |1\rangle /\sqrt{2}$ in different electric fields E_⊥.

As for the single-qubit gate, we can apply four resonant drivings with frequencies being respectively ω₁₃, ω₂₃, ω₁₃ + δ₁₃, and ω₂₃ + δ₂₃, and simultaneously perform two NHQC gates in the spin up and spin down subspace, as shown in Figure 6. In this way, a single-qubit gate on the Rydberg state is performed, i.e.,

$U_{\text{tot}}=|\downarrow \rangle \langle \downarrow |\otimes U+|\uparrow \rangle \langle \uparrow |\otimes U=I\otimes U,(23)$

where U is the single-qubit operation in Eq. 14 and I is the identity operator. This proposal still works when the driving pulses ω₁₃, ω₂₃ and ω₁₃ + δ₁₃, ω₂₃ + δ₂₃ are not applied simultaneously. In Table 3 we present the average output-state fidelity of the single-qubit NOT gate and Hadamard gate. The “non-simultaneous case” implies that the driving pulses with frequencies ω₁₃ + δ₁₃ and ω₂₃ + δ₂₃ are applied T/4 later than the driving pulses with frequencies ω₁₃ and ω₂₃. The state fidelity is obtained by the following procedures. We begin with the initial state ${\rho }_i^{\text{tot}}$, which is the product state of the spin state and the Rydberg state, i.e., ${\rho }_i^{\text{tot}}={\rho }_i^{\text{S}}\otimes {\rho }_i^R$. Then we derive the final state ${\rho }_f^{\text{tot}}$ from the evolution determined by the master Eq. 21. Next, we obtain the reduced density matrix ${\rho }_f^R$ of the Rydberg state by taking partial trace on ${\rho }_f^{\text{tot}}$, i.e., ${\rho }_f^{\text{R}}={\mathrm{T}\mathrm{r}}_{\text{spin}}\left({\rho }_f^{\text{tot}}\right)$. Finally, we acquire the state fidelity between ${\rho }_f^R$ and the ideal final state. The average fidelity in Table 3 is derived by averaging the results of six input states, with the initial spin state being $(|\downarrow \rangle +|\uparrow \rangle )/\sqrt{2}$ and the initial Rydberg states being |1⟩, |2⟩, $(|1\rangle +|2\rangle )/\sqrt{2}$, $(|1\rangle -|2\rangle )/\sqrt{2}$, $(|1\rangle +i|2\rangle )/\sqrt{2}$, and $(|1\rangle -i|2\rangle )/\sqrt{2}$, respectively. The results indicate that for both the NOT gate and Hadamard gate we can achieve near-unity fidelity.

FIGURE 6

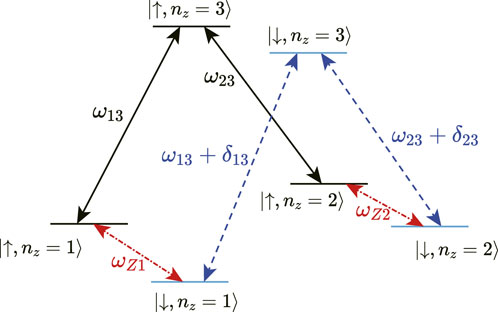
FIGURE 6. The transition frequencies between different energy levels. In the single-qubit gate proposal, we apply four resonant drivings with frequencies being respectively ω₁₃, ω₂₃, ω₁₃ + δ₁₃, and ω₂₃ + δ₂₃. In the controlled gate proposal which regards the Rydberg states as the control qubit, one resonant driving with frequency being ω_Z2 is applied.

TABLE 3

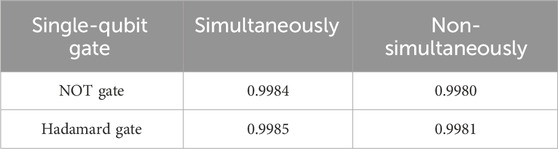
TABLE 3. Average output-state fidelity of the single-qubit gates in the simultaneous case and non-simultaneous case. The decay rates are the same as Table 1.

4 Conclusion and remarks

In this work, we present a scheme to realize nonadiabatic holonomic gates in an SE system based on the experimental configuration [67]. By applying the state-selective pulses, three Rydberg states with spin up are coupled with driving fields. During the evolution, two orthogonal bases acquire different geometric phases and thus perform a geometric gate. By varying the complex ratio between the Rabi frequencies of the two driving fields, the universal single-qubit nonadiabatic holonomic quantum gate is realized. The controlled-U gate on the Rydberg and spin states is based on the different Zeeman energy splittings in the inhomogeneous magnetic field. With the state-selective driving pulses we perform an arbitrary single-qubit gate U on the Rydberg states with spin up while the Rydberg states with spin down remain unchanged.

It is noteworthy that we can also realize controlled-U gates considering the Rydberg states as the control qubit. As shown in Figure 6, the electron-spin-resonance frequencies of |n_z = 1⟩ and |n_z = 2⟩ are ω_Z1 and ω_Z2, respectively. Because the magnetic field at the expected positions of |n_z = 1⟩ and |n_z = 2⟩ are different, the difference between ω_Z1 and ω_Z2 is δ₁₂ = ω_Z1 − ω_Z2 = gμ_B(B⁽¹⁾ − B⁽²⁾). δ₁₂ is on the order of several hundreds MHz, which is much larger than the decay rate $\sim 1$ MHz. Thus, we can resonantly drive the transition between the two spin states and perform a quantum gate through the Rabi oscillation when the Rydberg state is |n_z = 2⟩, while keep the spin states unchanged when the Rydberg state is |n_z = 1⟩.

Because of the fast nonadiabatic evolution, the NHQC proposal is robust against dissipation. Our theoretical scheme is based on the experimental configuration, and the parameters are experimentally achievable. Therefore, this work will supply heuristic insight for fast-manipulation tasks of holonomic quantum computation that involve both the Rydberg and spin states of the SE.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JW: Conceptualization, Investigation, Methodology, Software, Writing–original draft, Writing–review and editing, Visualization. W-TH: Methodology, Writing–original draft. H-BW: Funding acquisition, Investigation, Supervision, Writing–review and editing, Validation. QA: Funding acquisition, Investigation, Supervision, Writing–review and editing, Validation.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. H-BW is supported by the National Natural Science Foundation of China under Grant No. 61675028 and the Interdiscipline Research Funds of Beijing Normal University. QA is supported by the Natural Science Foundation of Beijing Municipality under Grant No. 1202017 and the National Natural Science Foundation of China under Grant Nos 11674033, 11505007, and Beijing Normal University under Grant No. 2022129.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1348804/full#supplementary-material

References

1. Simon B. Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys Rev Lett (1983) 51:2167–70. doi:10.1103/PhysRevLett.51.2167

CrossRef Full Text | Google Scholar

2. Berry MV. Quantal phase factors accompanying adiabatic changes. Proc R Soc Lond (1984) 392:45. doi:10.1098/rspa.1984.0023

CrossRef Full Text | Google Scholar

3. Leek PJ, Fink JM, Blais A, Bianchetti R, Göppl M, Gambetta JM, et al. Observation of Berry’s phase in a solid-state qubit. Science (2007) 318:1889–92. doi:10.1126/science.1149858

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ai Q, Huo WY, Long GL, Sun CP. Nonadiabatic fluctuation in the measured geometric phase. Phys Rev A (2009) 80:024101. doi:10.1103/PhysRevA.80.024101

CrossRef Full Text | Google Scholar

5. Chitambar E, Gour G. Quantum resource theories. Rev Mod Phys (2019) 91:025001. doi:10.1103/RevModPhys.91.025001

CrossRef Full Text | Google Scholar

6. Zhang J, Kyaw TH, Filipp S, Kwek LC, Sjöqvist D, Tong DM. Geometric and holonomic quantum computation. Phys Rep (2023) 1027:1–53. doi:10.1016/j.physrep.2023.07.004

CrossRef Full Text | Google Scholar

7. Zanardi P, Rasetti M. Holonomic quantum computation. Phys Lett A (1999) 264:94–9. doi:10.1016/S0375-9601(99)00803-8

CrossRef Full Text | Google Scholar

8. Osterloh A, Amico L, Falci G, Fazio R. Scaling of entanglement close to a quantum phase transition. Nature (2002) 416:608–10. doi:10.1038/416608a

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Faoro L, Siewert J, Fazio R. Non-Abelian holonomies, charge pumping, and quantum computation with josephson junctions. Phys Rev Lett (2003) 90:028301. doi:10.1103/PhysRevLett.90.028301

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Duan LM, Cirac JI, Zoller P. Geometric manipulation of trapped ions for quantum computation. Science (2001) 292:1695–7. doi:10.1126/science.1058835

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Solinas P, Zanardi P, Zanghì N, Rossi F. Semiconductor-based geometrical quantum gates. Phys Rev B (2003) 67:121307(R). doi:10.1103/PhysRevB.67.121307

CrossRef Full Text | Google Scholar

12. Tong DM, Sjöqvist E, Kwek LC, Oh CH. Kinematic approach to the mixed state geometric phase in nonunitary evolution. Phys Rev Lett (2004) 93:080405. doi:10.1103/PhysRevLett.93.080405

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Yi XX, Wang LC, Zheng TY. Berry phase in a composite system. Phys Rev Lett (2004) 92:150406. doi:10.1103/PhysRevLett.92.150406

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Song XK, Zhang H, Ai Q, Qiu J, Deng FG. Shortcuts to adiabatic holonomic quantum computation in decoherence-free subspace with transitionless quantum driving algorithm. New J Phys (2016) 416:023001. doi:10.1088/1367-2630/18/2/023001

CrossRef Full Text | Google Scholar

15. Song XK, Ai Q, Qiu J, Deng FG. Physically feasible three-level transitionless quantum driving with multiple Schrödinger dynamics. Phys Rev A (2016) 93:052324. doi:10.1103/PhysRevA.93.052324

CrossRef Full Text | Google Scholar

16. Ivakhnenko OV, Shevchenko SN, Nori F. Nonadiabatic landau–zener–stückelberg–majorana transitions, dynamics, and interference. Phys Rep (2023) 995:1–89. doi:10.1016/j.physrep.2022.10.002

CrossRef Full Text | Google Scholar

17. Wang XB, Matsumoto K. Nonadiabatic conditional geometric phase shift with NMR. Phys Rev Lett (2001) 87:097901. doi:10.1103/PhysRevLett.87.097901

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhu SL, Wang ZD. Implementation of universal quantum gates based on nonadiabatic geometric phases. Phys Rev Lett (2002) 89:097902. doi:10.1103/PhysRevLett.89.097902

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sjöqvist E, Tong DM, Andersson LM, Hessmo B, Johansson M, Singh K. Non-adiabatic holonomic quantum computation. New J Phys (2012) 14:103035. doi:10.1088/1367-2630/14/10/103035

CrossRef Full Text | Google Scholar

20. Xu GF, Zhang J, Tong DM, Sjöqvist E, Kwek LC. Nonadiabatic holonomic quantum computation in decoherence-free subspaces. Phys Rev Lett (2012) 109:170501. doi:10.1103/PhysRevLett.109.170501

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xu GF, Long GL. Protecting geometric gates by dynamical decoupling. Phys Rev A (2014) 90:022323. doi:10.1103/PhysRevA.90.022323

CrossRef Full Text | Google Scholar

22. Xue ZY, Zhou J, Wang ZD. Universal holonomic quantum gates in decoherence-free subspace on superconducting circuits. Phys Rev A (2015) 92:022320. doi:10.1103/PhysRevA.92.022320

CrossRef Full Text | Google Scholar

23. Xu GF, Liu CL, Zhao PZ, Tong DM. Nonadiabatic holonomic gates realized by a single-shot implementation. Phys Rev A (2015) 92:052302. doi:10.1103/PhysRevA.92.052302

CrossRef Full Text | Google Scholar

24. Zheng SB, Yang CP, Nori F. Comparison of the sensitivity to systematic errors between nonadiabatic non-Abelian geometric gates and their dynamical counterparts. Phys Rev A (2016) 93:032313. doi:10.1103/PhysRevA.93.032313

CrossRef Full Text | Google Scholar

25. Xu GF, Zhao PZ, Tong DM, Sjöqvist E. Robust paths to realize nonadiabatic holonomic gates. Phys Rev A (2017) 95:052349. doi:10.1103/PhysRevA.95.052349

CrossRef Full Text | Google Scholar

26. Xue ZY, Gu FL, Hong ZP, Yang ZH, Zhang DW, Hu Y, et al. Nonadiabatic holonomic quantum computation with dressed-state qubits. Phys Rev Appl (2017) 7:054022. doi:10.1103/PhysRevApplied.7.054022

CrossRef Full Text | Google Scholar

27. Chen SS, Zhang H, Song XK, Deng FG, Wang HB, Yang GJ. Universal single-qubit nonadiabatic holonomic quantum gates on an optomechanical system. Ann Phys (Berlin) (2018) 530:1800239. doi:10.1002/andp.201800239

CrossRef Full Text | Google Scholar

28. Jin ZY, Jing J. Geometric quantum gates via dark paths in Rydberg atoms. arXiv: 2307.07148 (2023).

Google Scholar

29. Zu C, Wang WB, He L, Zhang WG, Dai CY, Wang F, et al. Experimental realization of universal geometric quantum gates with solid-state spins. Nature (2014) 514:72–5. doi:10.1038/nature13729

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Arroyo-Camejo S, Lazariev L, Hell SW, Balasubramanian G. Room temperature high-fidelity holonomic single-qubit gate on a solid-state spin. Nat Commun (2014) 5:4870. doi:10.1038/ncomms5870

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Yale CG, Heremans FJ, Zhou BB, Auer A, Burkard G, Awschalom DD. Optical manipulation of the Berry phase in a solid-state spin qubit. Nat Photon (2016) 10:184–9. doi:10.1038/nphoton.2015.278

CrossRef Full Text | Google Scholar

32. Sekiguchi Y, Niikura N, Kuroiwa R, Kano H, Kosaka H. Optical holonomic single quantum gates with a geometric spin under a zero field. Nat Photon (2017) 11:309–14. doi:10.1038/nphoton.2017.40

CrossRef Full Text | Google Scholar

33. Abdumalikov AA, Fink JM, Juliusson K, Pechal M, Berger S, Wallraff A, et al. Experimental realization of non-Abelian non-adiabatic geometric gates. Nature (2013) 496:482–5. doi:10.1038/nature12010

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Feng GR, Xu GF, Long GL. Experimental realization of nonadiabatic holonomic quantum computation. Phys Rev Lett (2013) 110:190501. doi:10.1103/PhysRevLett.110.190501

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zhou BB, Jerger PC, Shkolnikov VO, Heremans FJ, Burkard G, Awschalom DD. Holonomic quantum control by coherent optical excitation in diamond. Phys Rev Lett (2017) 119:140503. doi:10.1103/PhysRevLett.119.140503

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Zhang J, Devitt SJ, You JQ, Nori F. Holonomic surface codes for fault-tolerant quantum computation. Phys Rev A (2018) 97:022335. doi:10.1103/PhysRevA.97.022335

CrossRef Full Text | Google Scholar

37. Leroux F, Pandey K, Rehbi R, Chevy F, Miniatura C, Grémaud B, et al. Non-Abelian adiabatic geometric transformations in a cold strontium gas. Nat Commun (2018) 9:3580. doi:10.1038/s41467-018-05865-3

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Nagata K, Kuramitani K, Sekiguchi Y, Kosaka H. Universal holonomic quantum gates over geometric spin qubits with polarised microwaves. Nat Commun (2018) 9:3227. doi:10.1038/s41467-018-05664-w

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Xu Y, Cai W, Ma Y, Mu X, Hu L, Chen T, et al. Single-loop realization of arbitrary nonadiabatic holonomic single-qubit quantum gates in a superconducting circuit. Phys Rev Lett (2018) 121:110501. doi:10.1103/PhysRevLett.121.110501

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Huang YY, Wu YK, Wang F, Hou PY, Wang WB, Zhang WG, et al. Experimental realization of robust geometric quantum gates with solid-state spins. Phys Rev Lett (2019) 122:010503. doi:10.1103/PhysRevLett.122.010503

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Yan TX, Liu BJ, Xu K, Song C, Liu S, Zhang ZS, et al. Experimental realization of nonadiabatic shortcut to non-Abelian geometric gates. Phys Rev Lett (2019) 122:080501. doi:10.1103/PhysRevLett.122.080501

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Liu BJ, Song XK, Xue ZY, Wang X, Yung MH. Plug-and-play approach to nonadiabatic geometric quantum gates. Phys Rev Lett (2019) 123:100501. doi:10.1103/PhysRevLett.123.100501

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ramberg N, Sjöqvist E. Environment-assisted holonomic quantum maps. Phys Rev Lett (2019) 122:140501. doi:10.1103/PhysRevLett.122.140501

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Xu Y, Hua Z, Chen T, Pan X, Li X, Han J, et al. Experimental implementation of universal nonadiabatic geometric quantum gates in a superconducting circuit. Phys Rev Lett (2020) 124:230503. doi:10.1103/PhysRevLett.124.230503

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Chen YH, Qin W, Stassi R, Wang X, Nori F. Fast binomial-code holonomic quantum computation with ultrastrong light-matter coupling. Phys Rev Res (2021) 3:033275. doi:10.1103/PhysRevResearch.3.033275

CrossRef Full Text | Google Scholar

46. Buluta I, Nori F. Quantum simulators. Science (2009) 326:108–11. doi:10.1126/science.1177838

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Georgescu IM, Ashhab S, Nori F. Quantum simulation. Rev Mod Phys (2014) 86:153–85. doi:10.1103/RevModPhys.86.153

CrossRef Full Text | Google Scholar

48. Platzman PM, Dykman MI. Quantum computing with electrons floating on liquid helium. Science (1999) 284:1967–9. doi:10.1126/science.284.5422.1967

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Wang J, He WT, Lu CW, Wy Y, Ai Q, Wh B. Controlled-not gate based on the rydberg states of surface electrons. Ann Phys (Berlin) (2023) 535:2300138. doi:10.1002/andp.202300138

CrossRef Full Text | Google Scholar

50. Kawakami E, Elarabi A, Konstantinov D. Relaxation of the excited Rydberg states of surface electrons on liquid helium. Phys Rev Lett (2021) 126:106802. doi:10.1103/PhysRevLett.126.106802

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Koolstra G, Yang G, Schuster DI. Coupling a single electron on superfluid helium to a superconducting resonator. Nat Commun (2019) 10:5323. doi:10.1038/s41467-019-13335-7

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Zhou XJ, Koolstra G, Zhang XF, Yang G, Han X, Dizdar B, et al. Single electrons on solid neon as a solid-state qubit platform. Nature (2022) 605:46–50. doi:10.1038/s41586-022-04539-x

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Glasson P, Dotsenko V, Fozooni P, Lea MJ, Bailey W, Papageorgiou G, et al. Observation of dynamical ordering in a confined Wigner crystal. Phys Rev Lett (2001) 87:176802. doi:10.1103/PhysRevLett.87.176802

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Ikegami H, Akimoto H, Kono K. Nonlinear transport of the Wigner solid on superfluid ⁴He in a channel geometry. Phys Rev Lett (2009) 102:046807. doi:10.1103/PhysRevLett.102.046807

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Rees DG, Kuroda I, Marrache-Kikuchi CA, Höfer M, Leiderer P, Kono K. Point-contact transport properties of strongly correlated electrons on liquid helium. Phys Rev Lett (2011) 106:026803. doi:10.1103/PhysRevLett.106.026803

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ikegami H, Akimoto H, Rees DG, Kono K. Evidence for reentrant melting in a quasi-one-dimensional Wigner crystal. Phys Rev Lett (2012) 109:236802. doi:10.1103/PhysRevLett.109.236802

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Rees DG, Beysengulov NR, Lin JJ, Kono K. Stick-slip motion of the Wigner solid on liquid helium. Phys Rev Lett (2016) 116:206801. doi:10.1103/PhysRevLett.116.206801

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Rees DG, Beysengulov NR, Teranishi Y, Tsao CS, Yeh SS, Chiu SP, et al. Structural order and melting of a quasi-one-dimensional electron system. Phys Rev B (2016) 94:045139. doi:10.1103/PhysRevB.94.045139

CrossRef Full Text | Google Scholar

59. Badrutdinov AO, Rees DG, Lin JY, Smorodin AV, Konstantinov D. Unidirectional charge transport via ripplonic polarons in a three-terminal microchannel device. Phys Rev Lett (2020) 124:126803. doi:10.1103/PhysRevLett.124.126803

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Bradbury FR, Takita M, Gurrieri TM, Wilkel KJ, Eng K, Carroll MS, et al. Efficient clocked electron transfer on superfluid helium. Phys Rev Lett (2011) 107:266803. doi:10.1103/PhysRevLett.107.266803

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Kielpinski D, Monroe C, Wineland DJ. Architecture for a large-scale ion-trap quantum computer. Nature (2002) 417:709–11. doi:10.1038/nature00784

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Chen JB, Zadorozhko AA, Konstantinov D. Strong coupling of a two-dimensional electron ensemble to a single-mode cavity resonator. Phys Rev B (2018) 98:235418. doi:10.1103/PhysRevB.98.235418

CrossRef Full Text | Google Scholar

63. Lyon SA. Spin-based quantum computing using electrons on liquid helium. Phys Rev A (2006) 74:052338. doi:10.1103/PhysRevA.74.052338

CrossRef Full Text | Google Scholar

64. Schuster DI, Fragner A, Dykman MI, Lyon SA, Schoelkopf RJ. Proposal for manipulating and detecting spin and orbital states of trapped electrons on helium using cavity quantum electrodynamics. Phys Rev Lett (2010) 105:040503. doi:10.1103/PhysRevLett.105.040503

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Kawakami E, Elarabi A, Konstantinov D. Image-charge detection of the Rydberg states of surface electrons on liquid helium. Phys Rev Lett (2019) 123:086801. doi:10.1103/PhysRevLett.123.086801

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Tokura Y, van der Wiel WG, Obata T, Tarucha S. Coherent single electron spin control in a slanting Zeeman field. Phys Rev Lett (2006) 96:047202. doi:10.1103/PhysRevLett.96.047202

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Kawakami E, Chen J, Benito M, Konstantinov D. Blueprint for quantum computing using electrons on helium. Phys Rev Appl (2023) 20:054022. doi:10.1103/PhysRevApplied.20.054022

CrossRef Full Text | Google Scholar

68. Nielsen MA, Chuang IL. Quantum computation and quantum information. Cambridge University Press (2010).

Google Scholar

69. Breuer HP, Petruccione F. The theory of open quantum systems. Oxford University Press (2002).

Google Scholar

70. Zou S, Konstantinov D. Image-charge detection of the rydberg transition of electrons on superfluid helium confined in a microchannel structure. New J Phys (2022) 24:103026. doi:10.1088/1367-2630/ac9696

CrossRef Full Text | Google Scholar

71. Johansson JR, Nation PD, Nori F. QuTiP: an open-source python framework for the dynamics of open quantum systems. Comput Phys Commun (2012) 183:1760–72. doi:10.1016/j.cpc.2012.02.021

CrossRef Full Text | Google Scholar

72. Johansson JR, Nation PD, Nori F. QuTiP 2: a python framework for the dynamics of open quantum systems. Comput Phys Commun (2013) 184:1234–40. doi:10.1016/j.cpc.2012.11.019

CrossRef Full Text | Google Scholar

73. Konstantinov D, Kono K, Monarkha YP. Photoresonance and conductivity of surface electrons on liquid ³He. Low Temp Phys (2008) 34:377–84. doi:10.1063/1.2911657

CrossRef Full Text | Google Scholar