- 1College of Intelligent Engineering, Zhengzhou University of Aeronautics, Zhengzhou, China
- 2Key Laboratory of Digital Earth Science, Institute of Space Information, University of Chinese Academy of Sciences, Beijing, China
- 3Jacobs School of Engineering, University of California, San Diego, San Diego, CA, United States
- 4Artificial Intelligence Institute, Beijing Normal University, Beijing, China
This article presents a novel target tracking algorithm for hyperspectral low altitude UAV, combining deep learning with an improved Kernelized Correlation Filter (KCF). Initially, an image noise reduction method based on principal component analysis with Block-Matching 3D (BM3D), is employed to process redundant information. Subsequently, an image fusion method is utilized to merge the processed hyperspectral image and the high-resolution panchromatic band image to obtain a high spatial resolution image for target enhancement. Following this, YOLOv5 is used to detect the coordinate information of the UAV target in the current frame. Then, The KCF algorithm is used for target tracking in the current frame using kernel correlation filtering. Finally, the Discriminative Scale Spatial Tracker (DSST) is employed to determine the scale information to achieve a multi-scale tracking effect. The experimental results demonstrate that the algorithm presented in this paper surpasses CSK, HLT, and the conventional KCF algorithm in hyperspectral UAV datasets. On average, there is a significant increase in accuracy which is over 17% when using our algorithm.
1 Introduction
As a new type of aerial apparatus in the modern era, UAVs offer lower cost, but more convenient operation, and higher security features, which makes it a more popular choice in many different kinds of fields such as military, agriculture, environmental monitoring, and so on. In the military sector, UAVs can detect and mitigate potential threats through real-time monitoring and tracking of enemy UAVs. In the civilian sector, they can aid law enforcement agencies in detecting and organizing illegal drone invasions and other threats to public safety. Additionally, in disaster relief and other fields, drone target tracking technology can provide real-time information, locate the affected individuals promptly, and assist in rescue operations.
With the rapid increasement and development of UAVs, the management and monitoring of these devices is more crucial. To some extent, tracking UAV targets can be slow and unreliable due to environmental changes, small targets and other issues, leading to low recognition accuracy. Therefore, it is essential to design hyperspectral target tracking algorithms that are fast and accurate.
Hyperspectral remote sensing technology has become a research hotspot, and it offers more spectral channels and the ability to identify both UAVs and their flight backgrounds. Although multi-band multispectral technology can obtain spectral information from three or more optical spectra simultaneously, its spatial resolution is limited. In contrast, hyperspectral remote sensing provides more detailed information for target tracking and identification.
Previous studies have explored various hyperspectral target tracking techniques. Xiong introduced the Material-based Hyperspectral Tracker (MHT) algorithm, which utilizes spatial spectral histogram statistics based on artificial features (SSHMG) to simulate object information for target tracking [1]. Blolme proposed the Minimum Output Squared Error filter (MOSSE) algorithm, which employs correlation filtering to accelerate algorithm operations by operating on the discrete Fourier transform similarity in the frequency domain [2]. However, MOSSE algorithm’s tracking effect is not completely satisfactory due to the limited initial data obtained through random affine transformations. Henriques et al. proposed the Cyclic Structure for Tracking and Detection with Kernel (CSK) algorithm [3], which constructs samples by cyclic shifting, effectively increasing the initial data without drastically increasing the computational effort. This approach achieves a dense sampling effect without adding excessive computations, thereby maintaining a feasible tracking algorithm performance. Additionally, Zhao designed a hyperspectral target detection method based on transform domain adaptive constrained energy minimization [4]. By projecting spectral domain features onto the transform domain, this approach aims to enhance the background and target separability. Furthermore, it proposes a modified constrained energy minimization detector based on the fractional domain. Wei designed a deep learning based on algorithm for UAV target detection in low altitude background [5], to study and analyze the differences in spectral characteristics between UAV targets and common targets in low altitude background and the imaging characteristic bands of UAV targets in low altitude background, and to realize the efficient detection of UAV targets by combining the deep learning methods.
The primary challenges associated with utilizing hyperspectral remote sensing for low altitude UAV target tracking are as follows:
(1) Limited spatial and spectral resolution: Due to the constraints of imaging mechanisms and optical devices, obtaining high spatial and spectral resolution spectral images directly is challenging. Existing spectral imaging equipment may not provide the required reliability for subsequent target detection and identification [6]. Although increasing resolution through image reconstruction is a common approach, using reconstructed hyperspectral images directly for interpretation may introduce irreversible errors, having some negative influence on the target tracking accuracy.
(2) Sensitivity to UAV target appearance changes: Traditional target recognition algorithms may struggle with accurate tracking when factors such as occlusion and lighting changes are present. Non-linear changes in target appearance make it difficult for these algorithms to adapt.
(3) Insufficient robustness to scale variations: The distance from the camera influences the size of the UAV in the image, causing some scale changes. Fixed-size filter algorithms, such as kernel filtering, exhibit suboptimal performance when confronted with significant target scale variations.
(4) Sensitivity to motion blur and fast movement: Fast-moving UAV targets blur with the imaging equipment not adjusting focus in time. Traditional target tracking algorithms are more susceptible to blurred image sequences, making it difficult for filters to accurately match target features. The Kernel Correlation Filter (KCF) Tracking Algorithm is a target tracking method based on kernel correlation filters, suitable for real-time tasks. It exhibits good accuracy and speed performance [7]. However, applying the original KCF algorithm alone does not yield satisfactory UAV target tracking results. Specific factors contributing to this limitation are outlined in Figure 1.

FIGURE 1. Challenges in low altitude UAV hyperspectral target tracking: (A) Lower resolution in the hyperspectral image. (B) UAV obscured. (C) Shaded to unshaded direction. (D) Blurred UAV images.
In order to address these challenges, the following work has been conducted in this study:
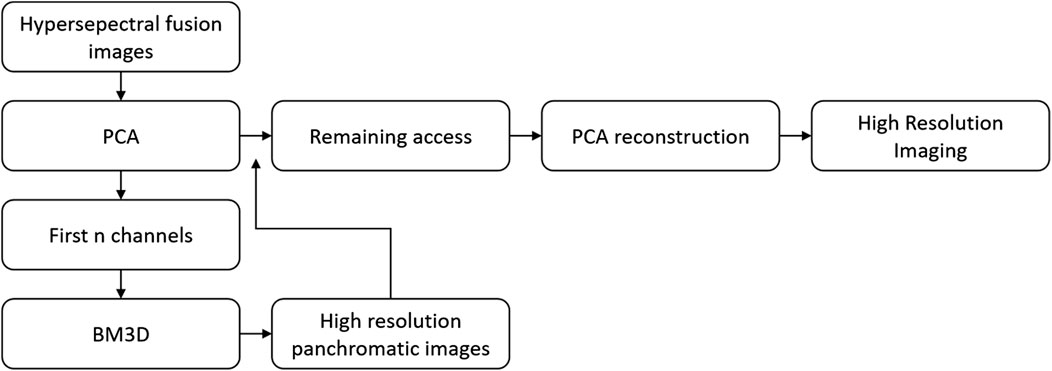
(1) To tackle the issue of large information redundancy and low resolution of hyperspectral images, an image denoising and fusion algorithm based on Principal Component Analysis (PCA) was proposed in this article. This involves extracting the principal components of the hyperspectral image using PCA. The algorithm then eliminates spectral and spatial noise through the superior denoising capability of the three-dimensional block matching algorithm (BM3D). Subsequently, the first principal component is replaced by histogram matching between the high-resolution panchromatic image and the low-resolution hyperspectral image after noise elimination. Finally, the high-resolution fused image is obtained after the inverse change of PCA.
(2) In order to address the problems encountered in UAV target tracking, such as occlusion, illumination changes and fuzzy motion. This paper proposes a low altitude UAV target tracking algorssithm based on YOLOV5 and KCF. The pre-trained YOLOV5 model is used to detect the target in the first frame of the input hyperspectral low altitude UAV image sequence, which is to obtain the bounding box and position information of the detected target and creat a UAV target template. Subsequently, for each frame, the KCF algorithm is used to globally search for the best matching location of the target globally. When the target cannot be found in the search region, the YOLOV5 model is employed to re-detect and locate the target and update the template.
(3) To solve the problem of the UAV target moving scale change unrobust, this paper includes the discriminative scale space tracker (DSST) in the detection algorithm. The UAV target position is initially obtained through the 3D filter, and then the scale of the tracking frame is adjusted to seek the maximum value of the response values and enable multi-scale target tracking.
The article is structured as follows: Section 1 mainly focuses on the background of UAV target tracking, and it analyzes the difficulties of hyperspectral low altitude UAV target tracking, introduces the methods of target identification, and describes the innovations of the algorithms. Section 2 describes in detail the image noise reduction and fusion enhancement of target features using PCA hyperspectral image dimensionality reduction method in detail. Section 3 explains the low altitude UAV target tracking algorithm based on YOLOV5+KCF + DSST proposed in this paper and presents the network model and algorithmic principles. Section 4 presents the results of comparison and ablation experiments of the algorithm on the dataset to demonstrate the feasibility and effectiveness of the algorithm.
2 Theoretical analysis
2.1 PCA-based denoising fusion algorithm for hyperspectral images
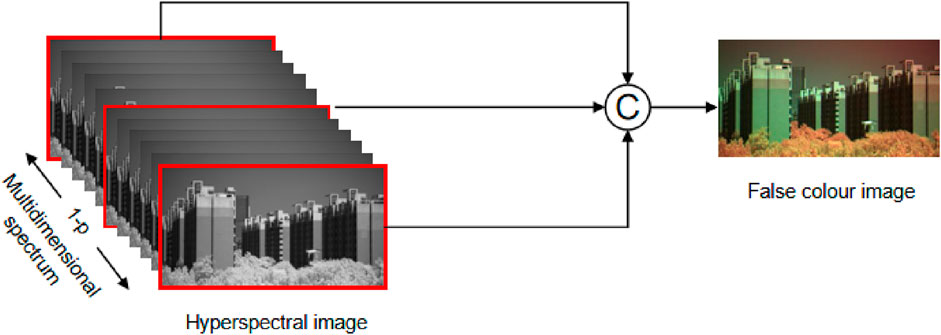
2.1.1 False colour image
Since the dimensionality of hyperspectral images is much higher than that of RGB images, it is time-consuming to extract gradient features and other operations directly from hyperspectral images. Therefore, the information of the low, middle and high frequency bands of the hyperspectral data is extracted to form a pseudo-colour image to simulate an RGB image, which is used to extract the colour and gradient information of the object. Assuming that the high light spectral data exists in
2.1.2 Principal component analysis
Principal Component Analysis (PCA) is an effective method for reducing the dimensionality of hyperspectral image data. By performing PCA, the principal components effectively preserve the majority of the original data’s essential information. By leveraging PCA, a small amount of information is sacrificed in exchange for obtaining low-dimensional data from hyperspectral images. This trade-off enhances the efficiency of image fusion and denoising without compromising accuracy. Figure 3 provides a visual representation of the image fusion denoising process based on principal component analysis.
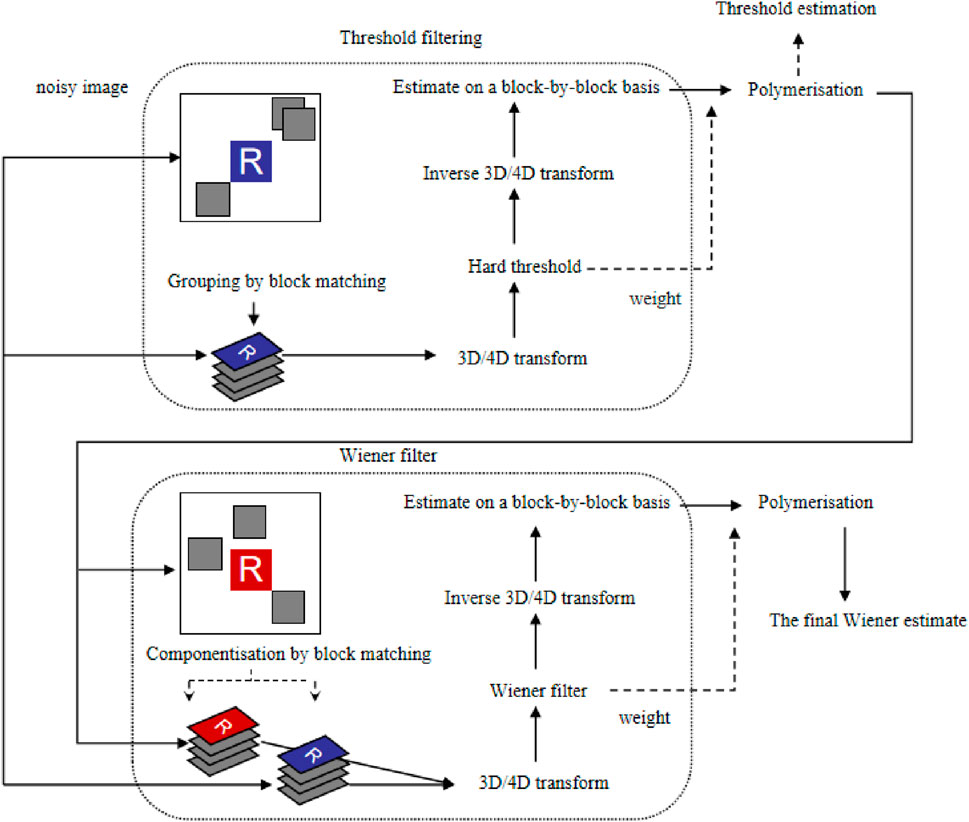
2.1.3 Noise removal method for hyperspectral images based on PCA and BM3D
The inspiration for this article is derived from the advancements in weighted kernel paradigm minimization for color image noise removal methods. The principal concept of hyper-spectral image denoising based on PCA and BM3D, can be summarized as follows:
Find a set of orthogonal vectors in the measurement space that maximises the variance of the data according to the K-L transform, and project the original vector from the original n-dimensional space onto the
Let
After PCA transformation, the correlation between the individual vectors of
2.1.4 PCA based hyperspectral image fusion method
The fundamental principle of the PCA-based hyperspectral image fusion method is as follows:
The high-resolution panchromatic image is histogram-matched with the first principal component (PC1) influence after PCA transformation. This ensures that the panchromatic image has the same variance and grey-scale mean value as PC1. Subsequently, the histogram-matched panchromatic influence replaces the first principal component. The remaining principal components (PC2 to PCn) after noise removal are PCA inverted and fused with the panchromatic image to restore it to the original color space. This process results in the generation of a fused high-resolution image [9–12]. The transformation formula is shown in Eq. 2:
Where
The role of
where
2.1.5 Effectiveness analysis
The impact of the PCA-based denoising fusion algorithm on hyperspectral images is depicted in Figure 5.

FIGURE 5. Visualization of the impact of the PCA-based fusion denoising method on hyperspectral images is presented in the following figures: (A) is high resolution images (B) is hyperspectral image. (C) is image after fusion.
In these figures, Figure 5C, obtained through PCA fusion of panchromatic and hyperspectral images, which not only retains high spatial resolution information but also maintains the spatial and spectral information of the image.
2.2 Low altitude UAV target tracking algorithm based on YOLOV5 and KCF
2.2.1 YOLOv5 network structure
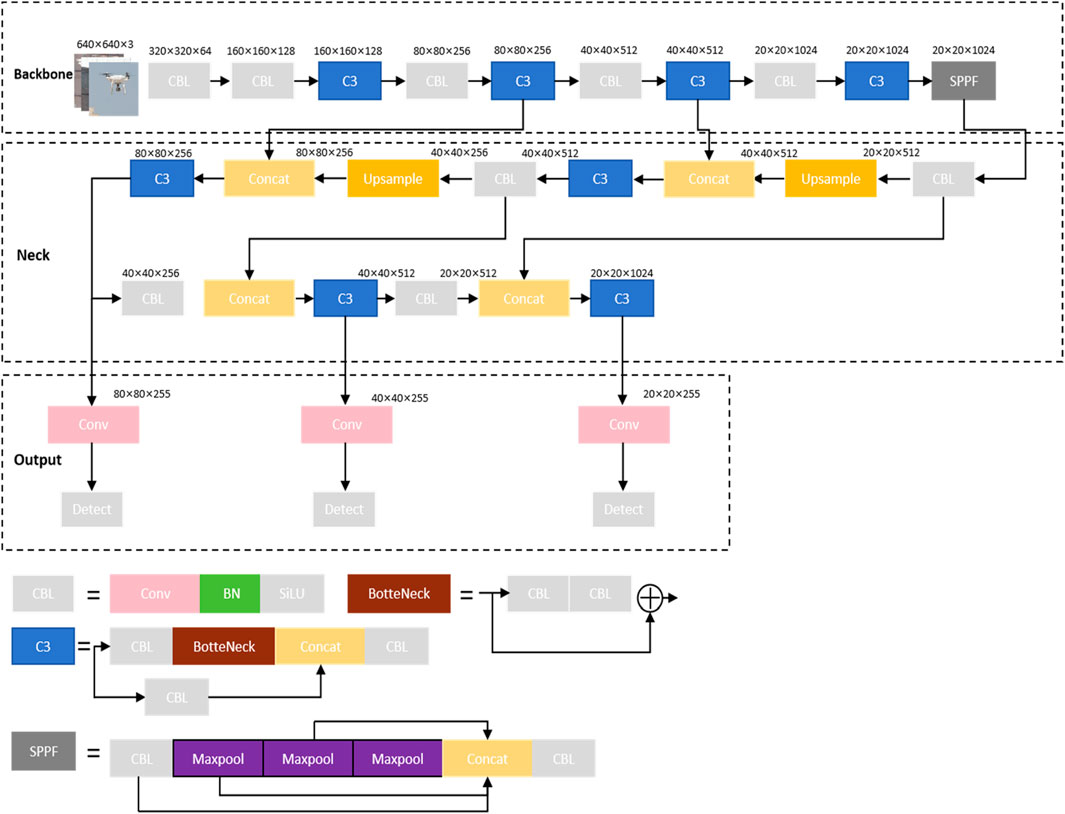
The YOLOv5 network structure illustrated in Figure 6, is composed of four main segments: Input, Backbone, Neck, and Prediction. Input involves data augmentation and Mosaic data enhancement, as well as adaptive anchor frame calculation and image scaling to optimize the performance of the neural network model. Acquiring a large volume of data is typically necessary for a neural network to function effectively, yet the process of obtaining new data often demands substantial time and labor costs [13]. Data augmentation techniques enable computers to efficiently generate data and expand the dataset, utilizing methods such as scaling, panning, rotation, and color transformations. Data augmentation offers the advantage of increasing the number of training samples and improving the model’s generalization power by incorporating relevant noise data.
In addition to fundamental data augmentation methods, YOLOv5 also incorporates the Mosaic data enhancement technique. This approach involves randomly cropping and scaling four images, and then it arranges and stitches them together to form a single picture. This method enriches the dataset while augmenting small sample targets and improving the network’s training speed. In normalization operations, the model’s memory requirement is reduced as the data from four images is calculated simultaneously [14–17].
Comparatively, YOLOv3 and YOLOv4 lack the ‘Backbone in Focus’ structure, with a more critical emphasis on the slicing operation. This operation allows a 4 * 4 * 3 image to be sliced into 2 * 2 * 12 feature maps. While the neck structure in YOLOv4 employs typical convolution operations, YOLOv5 incorporates the CSP2 structure borrowed from CSPnet to enhance network feature fusion.
Regarding the prediction output layer, YOLOv5 shares the anchor frame mechanism with YOLOv3 and v4. However, the main improvement lies in the development of the CIOU_Loss and the shift to DIOU_nms for prediction frame filtering. This modification facilitates detection of originally occluded or overlapped targets.
2.2.2 KCF target tracking algorithm
The KCF target tracking algorithm is a method based on kernel correlation filtering, belonging to the category of discriminative tracking [18]. It involves collecting a substantial number of positive and negative samples by populating the target frame in the initial tracking frame, resulting in a filled frame. The filled frame is cyclically shifted in the subsequent frame to generate a cyclic matrix. This process entails designating the region containing the target as positive samples and the remaining regions as negative samples. Subsequently, the target detector is trained by using these positive and negative samples, and then employed to detect whether the predicted position corresponds to the target’s location. The trained target detector is then utilized in the subsequent frame to ascertain the presence of the target. The filled frame from the previous frame is used to continue the cyclic shift in order to reclassify the images in the sample frames as positive and negative samples. The strongest response among these sample frames is selected as the filled frame of the target in the current frame. The samples acquired in the current frame are utilized to update the target detection classifier. Throughout this process, the ability to diagonalize the cyclic matrix in Fourier space and the application of Fast Fourier Transform (FFT) are leveraged to adapt the target detection classifier. These techniques are utilized to compute these samples, thereby improving operational speed. Firstly let a set of training samples as
Where
By introducing a nonlinear mapping function
Substituting Eq. 6 into Eq. 5 under the kernel space and performing a discrete Fourier variation is shown in Eq. 7:
At this point, the problem of optimisation problem for
After getting the nonlinear filter, the images in the video image block image block is detected to find out the location of the target. The image block to be detected is denoted by
Where
The working block diagram of the original KCF tracking algorithm in the process of visually tracking a UAV is shown in Figure 7.
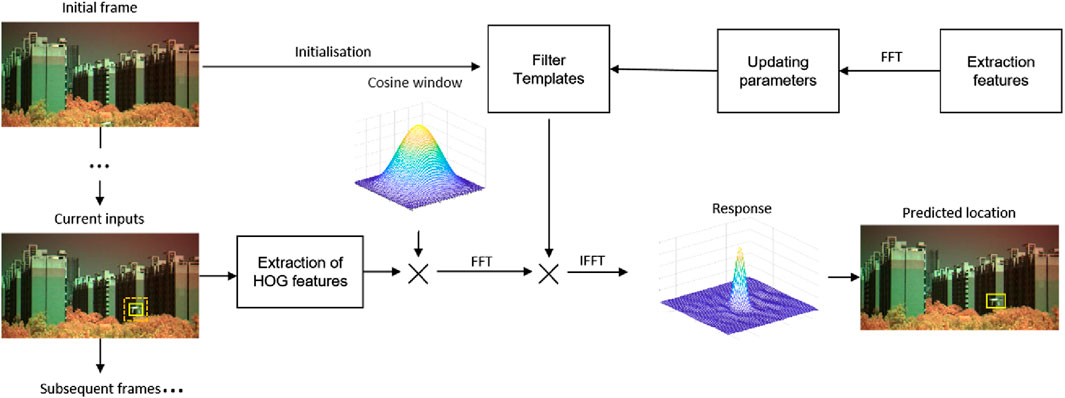
FIGURE 7. The working block diagram of the original KCF tracking algorithm in the process of visually tracking a UAV.
2.2.3 DSST multiscale filters
The DSST multi-scale filter accomplishes target tracking by leveraging the correlation filtering principle, effectively addressing changes in the target’s scale. It employs scale filters and position filters to represent the scale variation of the target, thereby delivering precise positional information. Through the utilization of the scale filter, the model’s outcomes can be fine-tuned at a specific location to attain the optimal scale response, thereby achieving the intended objective.
(1) The correlation operation values of the position filter
Firstly, the input image
(2) By using discrete Fourier transform and Parseval’s theorem, the value of the error function under least square is calculated. as shown in Equation 10:
In the above equation, H, A, B, G, F denote the discrete Fourier transform of the corresponding function, and the variables with horizontal lines are denoted as conjugate complex numbers.
(3) Using the position filter parameters at frame
Where the position corresponding to the maximum value of
(4) Construct and solve the scale filter
It is known that at frame
Then by extracting the features of sample
(1) Predict the scale of the tracked target for frame
To predict the centre of the tracked target position
(2) Based on the predicted tracking target position
2.2.4 Algorithmic processes and frameworks
A combined scheme of the YOLOv5 algorithm and the KCF algorithm is proposed to leverage the advantages of both methods. In this proposed approach, the real-time shooting frame utilizes the YOLOv5 algorithm for visual target detection, determining the position of the tracked UAV in the current frame. This result serves as the initial frame for the subsequent tracking in the KCF algorithm. Additionally, the scale estimation filtering algorithm from the DSST algorithm is integrated into the KCF tracking algorithm to enable real-time detection and tracking of the UAV. The specific flow of this combined approach is illustrated in Figure 8.
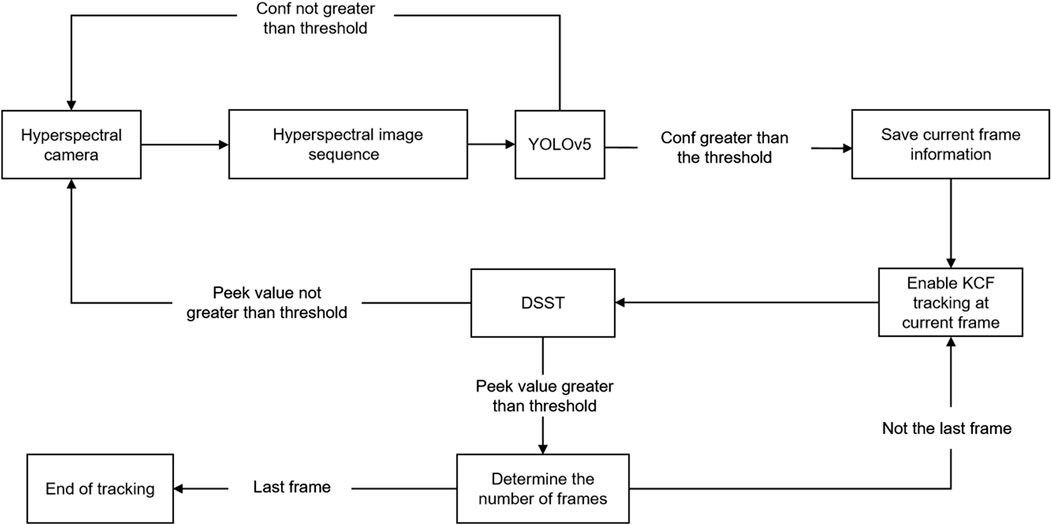
FIGURE 8. Flowchart of hyperspectral low altitude UAV target tracking algorithm based on deep learning and improved KCF tracking.
The flow of the hyperspectral low altitude UAV target tracking algorithm, based on deep learning and improved KCF tracking depicted in Figure 8, is as follows:
Firstly, a hyperspectral camera is utilized to acquire the UAV image sequence. Simultaneously, the YOLOv5 algorithm assesses whether the confidence level exceeds a predetermined threshold. If the threshold is reached, it indicates a successful detection, and the current frame of the hyperspectral image is then transmitted to the KCF tracking algorithm. Following the determination of the target’s position during the tracking of subsequent frames, the DSST algorithm is employed to determine the size of the target frame for each frame. It evaluates the correctness of the tracking based on the corresponding peak value of each frame. If the tracking is determined to be correct, commands are issued to continue the tracking, and in the event of failure, a return to the YOLOv5 algorithm is initiated to conduct additional target detection until the completion of the tracking process. This is done so that when the UAV experiences occlusion, lighting changes, and rapid movement resulting in the loss of the target in the image sequence, the current frame can be skipped and stepped to the target reappearance frame. Hyperspectral image sequences are chosen to reduce the interference of background factors and improve the efficiency of target recognition.
3 Experimentation and analysis
3.1 Data set
The UAV used for the experiments was flown vertically at a distance of 100 m and horizontally at a distance of 200 m, and different bands were selected to collect data of houses, sky, tiles, woods and glass curtain wall backgrounds. A total of 12,209 images of the dataset were taken, of which 1,610 images had a building background, 2,488 images had a white tile background, 6,154 images had a glass curtain wall background, 1,080 images had a sky background, and 876 images had a wooded background. Where training set is 7,325 images, 2,113 are test set images and remaining 2,771 are validation set images.
3.2 Experimental platforms
The low altitude UAV image sequence dataset was captured using the IMEC xiSpec hyperspectral camera model, which encompasses a total of 25 bands. The hardware parameters of the PC workstation used for the model training include an Intel(R) Xeon(R) Silver 4214R CPU @ 2.40 GHz 2.39 GHz (two processors). The experiments were conducted on a Windows 10 system featuring CUDA (Compute Unified Device Architecture) version number 10.2 and PyTorch framework version number 1.12.1.
3.3 Results of target detection experiments
In the video test, footage was recorded with the IMEC xiSpec hyperspectral camera. For comparative analysis, we selected the original KCF algorithm, along with the commonly used CSK and HLT algorithms. The tracking results of six frames from selected video sequences featuring light-shift, occlusion, fast-movement, and background-shift scenarios are presented in Figures 9–12.
(1) Tracking results of the CSK algorithm
(2) Tracking results of a novel hyperspectral-based HLT algorithm
(3) Tracking results of the original KCF algorithm
(4) Tracking results of hyperspectral low altitude UAV target tracking algorithm based on deep learning and improved KCF.

FIGURE 12. Simulation results of hyperspectral low altitude UAV target tracking algorithm based on deep learning and improved KCF tracking in hyperspectral image sequence.
The hyperspectral dataset above showcases the outcomes of the hyperspectral low altitude UAV target tracking algorithm, which is based on deep learning and improved KCF tracking. From Figure 12, it is evident that the enhanced algorithm can effectively achieve UAV target tracking in various complex backgrounds, demonstrating superior performance compared with other algorithms.
3.4 Evaluation indicators
In this paper, the algorithm selects three evaluation metrics of centre location error (CLE), precision (DP) and area under curve (AUC) for analysis.
(1) Centre Location Error (CLE)
CLE calculates the Euclidean distance from the centre of the tracking frame, assuming that for a certain frame, the centre of the groundtruth annotation is
The error in the centre position is shown in Eq. 15:
(2) Distance Precision (DP)
The Euclidean distance is between the centroid of the prediction box and the centroid of the Ground Truth box, calculated as shown in Eq. 16 usually with a threshold of 20 pixels. That is, they are considered to be tracked successfully if their Euclidean distance is within 20 pixels. In order to determine the success of tracking, the Euclidean distance between the centroid of the prediction box and the centroid of the Ground Truth box is calculated. Typically, that a threshold of 20 pixels is used means that if the Euclidean distance falls within this range, the tracking is considered successful.
(3) Area Under Curve (AUC)
Given a random positive and negative sample, the classifier is used to classify and predict their respective scores. The probability of the positive sample’s score is greater than the negative sample’s score that can be represented by the area under the receiver operating characteristic (ROC) curve, commonly referred to as the AUC. AUC values between 0.7 and 0.85 signify satisfactory performance, while values below 0.7 are generally considered effective.
3.5 Comparative analysis of algorithms
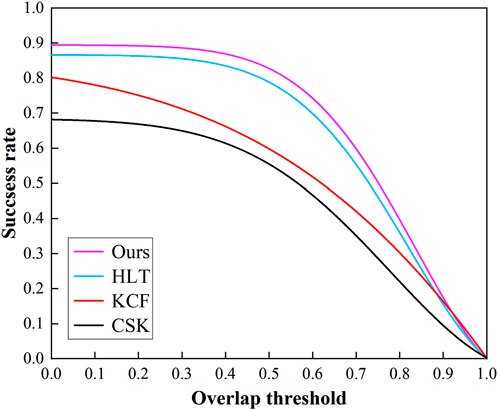
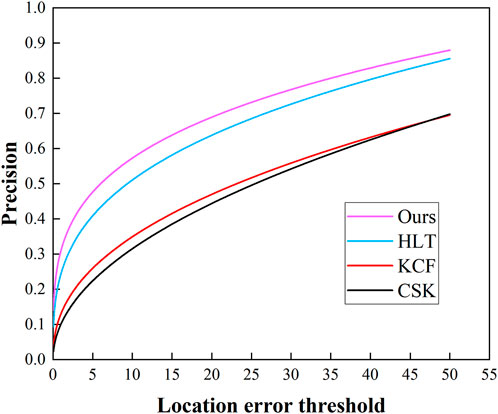
The proposed hyperspectral low altitude UAV target tracking algorithm, based on deep learning and improved KCF tracking, has been compared with widely used correlation filter target tracking algorithms in recent years, such as the CSK algorithm and the traditional KCF algorithm. Additionally, to assess the performance of the algorithms, the existing HLT hyperspectral tracking algorithm based on hyperspectral sequential image target tracking has been included. The performance of the various algorithms is depicted in Figures 13, 14.
The comprehensive analysis of the results is as follows: The traditional tracking algorithms, CSK and KCF, reliant on intensity, texture information, and color attributes, lack the necessary discriminative ability to learn the target’s feature model within a hyperspectral image environment effectively. As a consequence, marking the target’s position in the first is insufficient for accurately predicting its position in subsequent frames, which leads to reduced tracking accuracy and increased instances of tracking failure. From the success and accuracy graphs, it is evident that the existing hyperspectral image sequence target localization algorithm, the HLT algorithm, and the proposed hyperspectral low altitude UAV target tracking algorithm, based on deep learning and improved KCF tracking, outperform the two traditional algorithms.
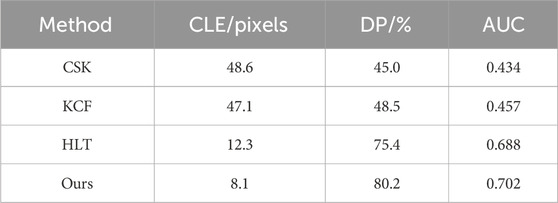
When considering the variability of hyperspectral 25-band data and calculating their fusion weights, it is observed that the HLT algorithm exhibits superior detection performance in the early stages but a slightly diminished effect in later stages of continuous tracking. In comparison to this paper, the improved algorithm demonstrates better performance in both success rate and accuracy plots. Table 1 provides a performance comparison of the six tracking algorithms.
As you can see from the table, the tracking algorithm demonstrates optimality for both the mean values of CLE and DP evaluation metrics. The average reduction of CLE compared to the optimal values of the three traditional correlation filter tracking algorithms is 27.9 pixel. DP improves by an average of 23.9% over the best of the three traditional correlation filtering algorithms. Hyperspectral low altitude UAV target tracking algorithm based on deep learning and improved KCF tracking proposed in this article has the largest AUC value of 0.702. The AUC is increased by 0.014 with respect to the sub-optimal value of the tracking algorithm.
4 Conclusion
This article proposes a low altitude UAV target tracking algorithm based on deep learning and improved KCF. To begin with, the paper employs image fusion denoising techniques based on principal component analysis, thereby bolstering target information in low-resolution hyperspectral images. To overcome the difficulty of tracking low altitude UAV targets due to variations in lighting, occlusion, and rapid movements, the paper integrates the YOLOv5 algorithm with the DSST algorithm and the KCF tracking algorithm. This combined approach allows for the retrieval of lost targets and enables efficient long-term target tracking. Furthermore, the paper compares the proposed algorithm to the conventional CSK and HLT algorithms commonly utilized in hyperspectral target detection, as well as the traditional KCF algorithm, which are commonly used in hyperspectral target detection, and it is found that the accuracies of the proposed algorithms are improved by 35.2%, 4.8%, and 31.7%, respectively, with an average improvement of 23.9%. The findings reveal that the proposed algorithm exhibits superior stability, accuracy, and robustness compared to its counterparts. In conclusion, the developed hyperspectral low altitude UAV target tracking algorithm, grounded in deep learning and enhanced KCF tracking, effectively tackles the challenge of tracking low altitude UAV targets, paving the way for more accurate and reliable target surveillance.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
HS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. PM: Writing–review and editing. ZL: Writing–review and editing. ZY: Writing–review and editing. YM: Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. National Natural Science Foundation of China Civil Aviation Joint Fund Key Project (U1833203).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Xiong F, Zhou J, Qian Y. Material based object tracking in hyperspectral videos. IEEETransactions Image Process (2020) 29:3719–33. doi:10.1109/TIP.2020.2965302
2. Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. In: The Twenty-Third IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2010; 13-18 June 2010; San Francisco, CA, USA. IEEE (2010). doi:10.1109/TIP.2020.2965302
3. Henriques JF, Rui C, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with. Berlin, Heidelberg: Springer (2012). doi:10.1007/978-3-642-33765-9_50
4. Zhao X, Hou Z, Wu X, Li W, Ma P, Tao R. Hyperspectral target detection based on transform domain adaptive constrained energy minimization. Internetional J Appl Earth Observation Geoinfromation (2021) 103:102461. doi:10.1016/j.jag.2021.102461
5. Wei K. Spectral characterization of UAV targets in low altitude background and target detection application. Zhengzhou, China: Zhengzhou Institute of Aviation Industry Management (2023). doi:10.27898/d.cnki.gzhgl.2022.000131
6. Henriques JF, Caseiro R, Martins P, Batista J. High-speed tracking with kernelized correlation filters. IEEE Trans Pattern Anal Machine Intelligence (2015) 37(3):583–96. doi:10.1109/TPAMI.2014.2345390
7. Guo YC, Cao JL, Han YY, et al. Hyperspectral target tracking based on spectral matching degradation and feature fusion. J Opt (2023) 43(20):152–61. doi:10.3788/AOS230776
8. Chen QL, Xue YQ. Estimation of signal-to-noise ratio for OMIS imaging spectral data. J Remote Sensing (2000)(4) 284–9. doi:10.3321/j.issn:1007-4619.2000.04.008
9. Houzelle S, Giraudon G. Data fusion using spot and sar images for bridge and urban area extraction. In: Geoscience and Remote Sensing Symposium,1991,Igarss’91.Remote Sensing:Global Monitoring for Earth Management,International; 03-06 June 1991; Espoo, Finland (1991). p. 1455–8. doi:10.1109/IGARSS.1991.579368
10. Wen C, Bicheng L, Yong Z. A remote sensing image fusion method based on PCA transform and wavelet packet transform. In: International Conference on Neural Networks and Signal Processing, 2003. Proceedings of the 2003; 14-17 December 2003; Nanjing (2003). p. 976–81. 2. doi:10.1109/ICNNSP.2003.1280764
11. Li SY, Zhang WF, Yang S. Intelligent fusion of multi-source high-resolution remote sensing images. J Remote Sensing (2017) 21(3):415–24. doi:10.11834/jrs.20176386
12. Ji X. Multi-source remote sensing data fusion: status and trends. Int J Image Data Fusion (2010) 1(1):5–24. doi:10.1080/19479830903561035
13. Chlap P, Min H, Vandenberg N, Dowling J, Holloway L, Haworth A. A review of medical image data augmentation techniques for deep learning applications. J Med Imaging Radiat Oncol (2021) 65:545–63. doi:10.1111/1754-9485.13261
14. Huang ZQ, Liu XZ, Shi Y, Lin CJ. Detection of small targets in road scenes based on data augmentation. J Wuhan Univ Tech (2022) 44(11):79–87. doi:10.3963/j.issn.1671-4431.2022.11.013
15. Wang TY, Dai YQ. Digital image denoising algorithm based on wavelet transform. J Hubei Inst Tech (2022) 38(05):25–30+55. doi:10.3969/j.issn.2095-4565.2022.05.006
16. Qian Y, Yuan J. Asphalt mixture image enhancement and segmentation based on grey scale transformation. Traffic Inf Saf (2009) 27(05):154–7. doi:10.3963/j.issn.1674-4861.2009.05.035
17. Wang Z, Tang X. Research on image enhancement method based on grey scale transformation. Sci Tech Innovation Herald (2011) 181(01):119. doi:10.3969/j.issn.1674-098X.2011.01.096
18. Huang N, Lu F, Wang QZ. KCF algorithm for vehicle target tracking parameter configuration research on vehicle target tracking. Softw Eng (2019) 22(9):12–6. doi:10.19644/j.cnki.issn2096-1472.2019.09.004
19. Yang ZF, Chen X. Optimised search strategy for KCF target tracking algorithm. J Wuhan Univ Eng (2019) 41(1):98–102. doi:10.3969/j.issn.1674-2869.2019.01.017
Keywords: low altitude UAV, principal component analysis, YOLOv5, kernel correlation filtering algorithm, discriminant scale spatial tracker
Citation: Sun H, Ma P, Li Z, Ye Z and Ma Y (2024) Hyperspectral low altitude UAV target tracking algorithm based on deep learning and improved KCF. Front. Phys. 12:1341353. doi: 10.3389/fphy.2024.1341353
Received: 20 November 2023; Accepted: 08 January 2024;
Published: 08 February 2024.
Edited by:
Quan Sheng, Tianjin University, ChinaReviewed by:
Yuan Liu, Nanjing University of Science and Technology, ChinaZhi Liu, Changchun University of Science and Technology, China
Yajun Pang, Hebei University of Technology, China
Copyright © 2024 Sun, Ma, Li, Ye and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haodong Sun, Nzc5MzgyMTgwQHFxLmNvbQ==
 Haodong Sun
Haodong Sun Pengge Ma1
Pengge Ma1