Recent development of fully kinetic particle-in-cell method and its application to fusion plasma instability study

This paper reviews the recent advancements of the algorithm and application to fusion plasma instability study of the fully kinetic Particle-in-Cell (PIC) method. The strengths and limitations of both explicit and implicit PIC methods are described and compared. Additionally, the semi-implicit PIC method and the code ECsim used in our research are introduced. Furthermore, the application of PIC methods in fusion plasma instabilities is delved into. A detailed account of the recent progress achieved in the realm of tokamak plasma simulation through fully kinetic PIC simulations is also provided. Finally the prospective future development and application of PIC methods are discussed as well.

1 Introduction

Numerical simulations, together with theoretical and experimental studies, are the main approaches within the domain of magnetic confinement fusion research. Substantial progress has been made in the fusion plasma physics study with the advancement of numerical algorithms and computational capabilities over the past decades, especially with the widely used magnetohydrodynamics (MHD) method [1–3]. However, there are still some significant problems remaining to be resolved such as the mechanism of plasma disruptions and its causes (tearing mode instability, for example,) in tokamaks [4]. This can be attributed to the inherent limitations of MHD simulations, which inherently rely on approximations, rendering them incapable of capturing the finer-scale intricacies of the underlying physical processes [5]. Besides, collisions are relatively unimportant in some phenomenon which undermines the capacity of MHD simulations to offer persuasive elucidations of the underlying physical systems.

The Particle-in-Cell (PIC) method is another powerful tool in the realm of plasma physics simulations. The foundational insights into its core algorithm could be found in [6, 7]. The key strengths of PIC methods include: First and foremost, it possesses the capability to resolve the electron scale, which empowers researchers to study intricate microscopic problems; Secondly, it is inherently grounded in a first-principles approach and there is no need for extensive approximations required by other methods such as MHD, which compromise the fidelity of the results; Lastly, with the development of modern supercomputing technology, the PIC method exhibits enhanced feasibility when compared with other particle models such as particle–particle (PP) approach [6–8]. The PIC method’s computational demands are more manageable, rendering it a practical choice for contemporary plasma physics investigations.

Gyrokinetic PIC simulations have emerged as a prominent tool in fusion plasma physics research [9]. The global gyrokinetic toroidal code (GTC) has been extended to study the internal kink mode within both the cylindrical and toroidal geometries by McClenaghan et al [10]. Their study also delved into the influence of ion kinetic effects on the growth rate of the internal kink mode. Lin et al. modified a gyrokinetic electron and fully kinetic ion particle simulation scheme and studied the evolution of the linear collisionless tearing mode instability in a two-dimensional Harris current sheet, aligning their findings with established theoretical frameworks [11]. More recently, Lu et al. employed an implicit full-f scheme for PIC simulations and focus their study on the Shear Alfvén Wave (SAW) in one dimension geometry and the Toroidicity induced Alfvén Eigenmode (TAE) excited by the energetic particles in three dimensional axisymmetric tokamak plasma [12]. Nonetheless, it is essential to acknowledge that the majority of gyrokinetic simulations are electrostatic and fall short in resolving electron scales, a crucial aspect in several scenarios [11]. In contrast, fully kinetic simulations possess the capability to address electron temporal and spatial scales and capture intricate details that remain elusive to alternative methodologies [8, 13]. MHD models, for instance, necessitate approximations and treat plasma as fluids, resulting in the omission of many kinetic effects associated with long mean free paths and finite-size orbits. Similarly, the gyrokinetic method involves approximations concerning the gyro motion of particles, high-frequency terms, and associated phenomena [14]. In this context, fully kinetic models offer a valuable avenue for the study of intricate problems characterized by minuscule spatial and temporal scales.

The simulation of magnetic fusion plasma has always been regarded as a formidable challenge, primarily owing to its inherently multi-scale nature [3, 11]. The temporal and spatial scales in magnetic fusion plasma span an extensive scope, ranging from electron scales ($\sim 10^{-11}$ s, ∼ 10^–5 m) to the dimensions of the plasma confinement device ($\sim 100$ s, $\sim 100$ m), respectively [3]. As a result, there is a compelling need for fully kinetic simulations to advance our comprehension of instabilities and disruptions within tokamaks, which also could contribute to the successful operation of ITER and future DEMO reactors, as well as smaller devices such as spherical tokamaks. Fortunately, thanks to remarkable progress in supercomputing capabilities and the advancement of algorithms, the feasibility of conducting large-scale fully kinetic PIC simulations is steadily on the rise.

In this paper, we reviewed the evolution and development of the Particle-in-Cell (PIC) method, with particular emphasis on the semi-implicit variant utilized in our research. Additionally, we delved into the application of the PIC method within the domains of fusion plasma instability studies. The structure of this paper is as follows. Section 2 is dedicated to elucidating the historical development of explicit, implicit and semi-implicit PIC methods over the past decades. Section 3 provides an extensive exploration of the application of PIC methods while focusing on the plasma instabilities in fusion tokamaks. Finally, Section 4 encompasses a brief summary and discussion as well as an outlook towards future developments of the PIC method.

2 Particle-in-cell (PIC) methods

The model we need to address is a Vlasov-Maxwell system, which is governed by the Eqs 1–5 below

$\frac{\partial f_s}{\partial t}+\mathbf{v}\cdot \frac{\partial f_s}{\partial \mathbf{x}}+\frac{q_s}{m_s}\left(\mathbf{E}+\frac{\mathbf{v}}{c}\times \mathbf{B}\right)\cdot \frac{\partial f_s}{\partial \mathbf{v}}=0(1)$

$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}(2)$

$\nabla \times \mathbf{B}={\mu }_0{ϵ}_0\frac{\partial \mathbf{E}}{\partial t}+{\mu }_0\mathbf{j}(3)$

$\nabla \cdot \mathbf{E}=\frac{\rho }{{ϵ}_0}(4)$

$\nabla \cdot \mathbf{B}=0(5)$

where f_s(x, v, t) is the phase-space distribution function with the subscript ‘s’ denoting the species (electrons or ions usually), t is time, v is velocity, x is position, q_s and m_s are the charge and mass, E is electric field strength, B is magnetic flux density, j is current density, ρ is charge density, μ₀ and ϵ₀ are permeability and permittivity of free space, respectively [15]. There are mainly two approaches to handle this system numerically. The first entails discretizing the Vlasov space into meshes (i.e., Euler method) whose noise level is much lower [13]. The other one is the so-called Particle-in-Cell (PIC) method. Here we focus on the latter.

The complete steps and more details of the mathematical formulation of conventional PIC method could be found in [6–8]. Explicit PIC method could be used to resolve all temporal and spatial scales while its time step and grid size are constrained due to stability and accuracy requirements. Implicit PIC methods, on the contrary, exhibit higher stability. This section elaborates on the distinctions between these methods, elucidates their respective algorithms, and discusses their recent developments.

2.1 Explicit vs. implicit

The explicit PIC method entails a step-by-step updating of both the particle mover and field solver as illustrated in Figure 1. It is characterized by its capacity to resolve all temporal and spatial scales. However, it does come with inherent weaknesses including the constraints imposed by stability requirements. Besides, the total energy of the system may exhibit an increase during the simulation, causing the formidable ‘self-heating’ problem (as discussed in [16] for example,).

FIGURE 1

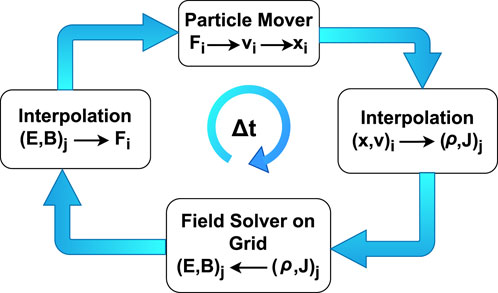
FIGURE 1. Explicit PIC algorithm: the subscript i and j denote the quantities defined on the particles and grids, respectively; v is velocity, x is position, F is force, ρ is charge density, J is current density, E is electric field strength, B is magnetic flux density, △t is a time step (cycle).

The explicit PIC method possesses certain distinct advantages. It is characterized by its simplicity and the avoidance of iterative procedures, which enhance its efficiency. Nevertheless, it also has inherent limitations. The time step must be very small to ensure its accuracy (as the fields are assumed to be “frozen” when the particles move and vice versa). There are three constraints that explicit PIC methods have to satisfy:

First, the product of the electron plasma frequency (ω_pe) and the time step (△t) must be less than 2, i.e., ω_pe△t < 2;

Second, adherence to the Courant–Friedrich–Levy (CFL) condition, where the time step (△t) must be smaller than the ratio of the spatial grid spacing (△x) to the speed of light (c), i.e., △t < △x/c;

Third, it is pivotal to avoid finite grid instability, which necessitates that the ratio of spatial grid spacing (△x) to the Debye length (λ_D) must be less than a certain parameter denoted as ς, i.e., △x/λ_D < ς.

Where ω_pe is electron plasma frequency, △t is time step, △x is cell size, c is the speed of light, λ_D is the Deybe length and ς is the parameter related to the exact implementation. These constraints are crucial for maintaining the accuracy and stability of the explicit PIC method in simulations, as discussed in [8]. Meanwhile, smoothing method has been used in explicit methods, which proves to be able to relax these constraints and/or to alleviate numerical heating problems [16, 17].

There have been diverse variants of the explicit PIC methods developed over the past decades. Bowers et al. developed a fully kinetic 3D electromagnetic charge-conserving relativistic PIC code VPIC and explored its application in three domains: inertial confinement fusion, ion acceleration and magnetic reconnection [18, 19]. The main advantage of VPIC is that it uses special techniques to minimize data motion so as to achieve high performance. The portability-enabling work of VPIC was shown in [20] which enhances VPIC’s modelling capabilities to achieve performance at exascale. Warp-X, also developed based on the PIC method, was used in the simulations of plasma accelerators on exascale supercomputers [21]. Geometric methods were also used in explicit PIC scheme development to achieve preservative structure [22, 23].

In order to alleviate the constraints required by explicit PIC method as described above, it becomes imperative to reconsider the coupling between fields and particles during the time step, as the inherent decoupling in the explicit PIC method necessitates the imposition of these constraints. Given this context, new implicit PIC methods were proposed by means of solving the non-linear system of field and particle equations simultaneously [8, 24, 25]. In other words, the implicit methods iteratively address the particle mover and field solver, which brings several notable advantages. The new implicit methods could conserve energy and the details and validation could be found in [24, 25]. Consequently, the methods’ fidelity is promoted with the energy conservation feature. Moreover, it fulfills the stability requirements while obviating the need to resolve all spatial and temporal scales. Consequently, users have the flexibility to choose a relatively large time step △t, especially beneficial for large scale simulations. Substantial progress has been made, particularly with the advent of Newton-Krylov solvers during the past decades, leading to the development of energy-conserving fully implicit methods [24–29]. For example, Markidis et al. developed an implicit PIC method called iPIC3D and tested its application in magnetic reconnection [26]. This method removes the numerical stability constraints for PIC methods and supports kinetic plasma simulations at MHD time scales. A fully implicit PIC method was also proposed by Markidis et al. with the advantage of total energy conservation and its algorithm, implementation and performance results could be found in [24]. However, this method consumes large amounts of computation resources due to the iterations in the solvers used. Then Lapenta et al. further extended this method to the relativistic case and studied the role that numerical heating played in classical PIC methods in the particle acceleration [27]. Recently, Markidis et al. proposed a new fluid-kinetic coupling polymorphic PIC scheme called PolyPIC which could change fluid particles to kinetic particles when needed [30]. Chen et al. developed a fully implicit one-dimensional electrostatic PIC method which could conserve both the charge and energy [25]. They also explored a fully implicit PIC algorithm for the Vlasov-Darwin model in multiple dimensions, which conserves total energy, local charge, canonical-momentum in the ignorable direction, and preserves the Coulomb gauge exactly [31]. Then they further extended this method to curvilinear geometry [32]. Stanier et al. developed an implicit, nonlinear hybrid particle-ion/fluid-electron model based on PIC scheme which could conserve global mass, momentum and energy [33].

2.2 Fully implicit vs. semi-implicit

The fully implicit PIC method provides several advantages over its explicit counterpart, but it usually consumes substantial computational resources. The fully implicit PIC method necessitates to solve the coupled Vlasov-Maxwell system using non-linear solvers such as Newton-Krylov solver [28, 29], which could be very expensive (even impossible) from a computational perspective. Therefore, the semi-implicit PIC method has garnered significant attention due to its elimination of non-linear iterations. This is achieved through the linearization of functions and the computation relies solely on linear solvers, thereby resulting in significant time and computational resource savings [8].

Direct implicit method and the implicit moment method (IMM) are two approaches to the linearization mentioned above [34, 35]. The former involves linearizing the particle motion equations and formulated the field equations using a matrix. Then the field equations are solved alone and the particles are moved with the fields calculated. The latter, in contrast, does not linearize the particle motion equations, instead employing linearization techniques on the moments. Detailed information regarding the IMM method could be found in [8, 35]. Obviously, there are no nonlinear iteration in the semi-implicit PIC method and the resources needed for the calculation is decreased considerably. Besides, as a result of the linearization, the time step loop structure of the semi-implicit PIC method we used remains akin to that of the explicit PIC method as depicted in Figure 1. On the other hand, the energy is no longer conserved in these two semi-implicit methods. The strengths and weaknesses and the stability of the two methods are compared in the book [36].

In our work, we used a semi-implicit PIC method called ECsim developed by Lapenta et al. [37–39]. Distinguishing itself from other implicit PIC methods, the main strengths of ECsim include energy conservation exactly and stability fulfillment at the same time. Furthermore, ECsim possesses the capability to resolve multiple-scale (including the electron scale) features and achieve high efficiency through MPI parallel computing. ECsim uses a hybrid mover which combines the θ-scheme and the leap-frog algorithm when computing the interpolation between particles and cells. Besides, mass matrices are incorporated to compute the current. These two features eliminates the nonlinear iterations and only linear ones are needed. These characteristics equip ECsim with the capability to be applied to the simulations of both astrophysical and fusion plasma (typical scales in these two domains are shown in Figure 2) [37, 40, 41]. Specifically, the flexibility to set larger cell size and time steps proves advantageous when resolving finer scale is deemed unnecessary. The detailed implementation of ECsim could be found in [37–39] and its latest developments were presented in [42], encompassing the new methods for electric field smoothing, mass matrix calculation and its limit case.

FIGURE 2

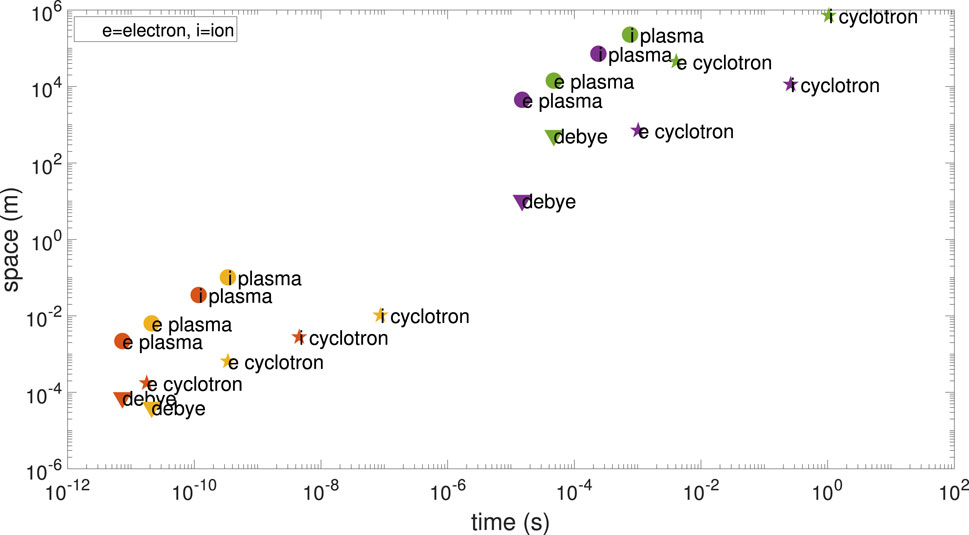
FIGURE 2. Typical spatial and temporal scales in both the astrophysical and the fusion tokamak plasma simulations. Here the ion mass is real and the electron mass is calculated using the mass ratio of 256. red: DIIID Tokamak, yellow: Spherical Tokamak, violet: solar wind 1AU, green: Magnetosphere.

2.3 PIC method future development

One of the significant topics in the development of PIC method is the coupling between PIC and Machine Learning or Deep Learning. Aguilar et al. [43] introduced a novel PIC method which uses Deep Learning techniques to calculate the electric field. The results demonstrated that Deep Learning based PIC could satisfy the accuracy and stability requirement but cannot conserve total energy and momentum. Recently, Badiali et al. proposed an interface to incorporate Machine-Learning based methods into PIC simulations and the results suggest that the Machine-Learning based method could achieve greater computation efficiency and obtain correct physics results at the same time [44]. Another promising avenue of research entails optimizing PIC simulations through techniques such as GPU acceleration [45] or harnessing the power of exascale supercomputers with certain modifications [21].

3 Application in fusion plasma instability study

As a result of continuous advancement in numerical algorithms and the increasing computational power offered by supercomputers, the application of fully kinetic PIC methods in the context of fusion plasma has become increasingly feasible. This progress is reflected in a growing body of research within this field. In this review, we aim to provide a general description of the advancements achieved to date and, in addition, present our recent research endeavors focusing on the simulation of magnetic islands within the tearing mode instability in fusion tokamaks.

There has been some work which used fully kinetic methods in the fusion plasma study. VPIC, the 3-dimensional electromagnetic charge-conserving relativistic PIC code mentioned above, was used to study the laser-plasma instabilities in inertial confinement fusion experiments [46]. The relativistic Kelvin-Helmholtz Instability (KHI) was investigated using fully kinetic method by Bussmann et al [47]. Sturdevant et al. proposed a fully kinetic ion model and implemented it in toroidal geometry so as to study ion temperature gradient (ITG) instability. They used field-line-following coordinates to achieve high resolution of the field-aligned mode structure and reported the linear results for both the slab and toroidal ITG instabilities. They found good agreement between fully kinetic, full Vlasov and gyrokinetic results [48]. Then they extended this model to the nonlinear regime and investigated the nonlinear saturation of a single-n ITG instability due to the E × B trapping mechanism. A favorable concurrence was observed in the saturation amplitude between the simulation outcomes and the theoretical predictions posited by the trapping theory. A toroidal Boris full orbit integrator was developed and it proved to be accurate enough. They also extended the previous work from analytic circular magnetic equilibria to general numerical magnetic equilibria, enabling simulation of realistic equilibria reconstructed from tokamak experiments [49]. More recently, Xiao et al. proposed a new structure-preserving geometric PIC algorithm with discrete symplectic structure and symplectic integration, and studied the kinetic steady state in tokamak geometry and the kinetic ballooning instability in the edge [22]. Then they conducted the 6-Dimensional electromagnetic fully kinetic tokamak simulations using the explicit second-order charge-conservative symplectic electromagnetic PIC method [23].

In addition to the aforementioned work, we have also explored the application of the semi-implicit fully kinetic PIC code ECsim in the fusion plasma instability research [41]. More specifically, our focus has centered on elucidating the evolution of magnetic islands emerged in the tearing mode instabilities in fusion tokamaks. The tearing mode instability ranks among the most dangerous instabilities in tokamaks as it could cause disruptions which are deleterious to devices. It was first thoroughly studied by Furth [50] theoretically. Recent research efforts have also been directed towards MHD and gyrokinetic simulations within this domain. For example, Zhang W et al. upgraded their MHD code and studied Hall effects on the evolution of tearing modes and found that the linear growth rate is connected with the ion skin depth [51]. They also studied the effect of helical driven current on nonlinear resistive tearing mode evolution and saturation [52]. Zhang R et al. [53] developed a new field solver for the gyrokinetic PIC code GEM to achieve low-n (n = 1,2) MHD tearing mode simulations in toroidal geometry. They systematically investigated the effects of toroidicity and kinetic ions on the resistive tearing modes and compared their results with analytic theory. They also studied the effect of kinetic ions on the Double Tearing Mode evolution [54]. Nevertheless, MHD simulations may not be able to capture the correct feature of the tearing mode as the collision frequency is low in core plasma. This, in turn, raises concerns regarding the reliability of MHD simulations. On the other hand, the tearing mode is intrinsically linked to magnetic reconnection and the gyro-kinetic approximation may not be accurate enough to describe the kinetic dynamics in current sheets—a crucial aspect of the reconnection process. As a result, it is plausible to investigate this problem through fully kinetic methods. The purpose of our study is to investigate the evolution of the tearing mode via the semi-implicit fully kinetic PIC code ECsim. The reliability of ECsim has been validated through the time resolution and spatial resolution analyses for whistler waves, and through simulation of ion acoustic waves, electron acoustic instability and the classic GEM challenge [37, 39]. It is particularly suitable for studying plasma instabilities due to its inherent ability to conserve energy exactly, which could eliminate the numerical heating/cooling that might yield unphysical outcomes in simulations [24]. The typical spatial and temporal scales in fusion tokamak plasma simulations are shown in Figure 3.

FIGURE 3

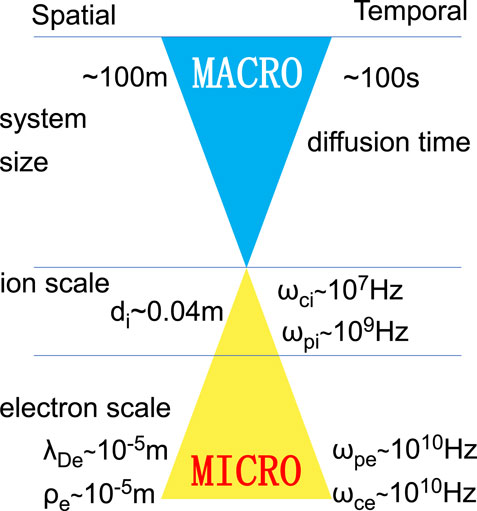
FIGURE 3. Typical scales in fusion tokamak plasma simulations: d_i is ion skin depth, λ_De is electron Deybe length, ρ_e is electron gyroradius, ω_ci is ion cyclotron frequency, ω_pi is ion plasma frequency, ω_pe is electron plasma frequency, ω_ce is electron cyclotron frequency.

The initial equilibrium state employed for the simulation setup was acquired from NOVA [55, 56] (the same as [51]). Both two-dimensional (2D) and three-dimensional (3D) simulations were undertaken, and specific parameters for each case are outlined in Table 1 and Table 2 for 2D and 3D simulations, respectively. In the 2D simulation, only a cross-sectional profile was modeled, while in the 3D scenario, the entire tokamak geometry was simulated. The tokamak aspect ratio is ɛ = a/R₀ = 1/4. The ion-to-electron mass ratio is m_i/m_e = 256. The ratio between the plasma frequency and the cyclotron frequency are ω_pe/ω_ce ≈ 0.88 for electrons and ω_pi/ω_ci ≈ 37.64 for ions, respectively. We use the cold ions at the initial state. The electron plasma beta is β_e = 0.003. The simulation incorporates the ‘lambdadamping’ boundary method to set the tokamak geometry in the simulation box. When λ = 0 (corresponding to the tokamak region) the Maxwell equations are solved while there would be a coefficient λ to damp the fields if the λ is nonzero (corresponding to the domain outside of tokamak geometry but inside the simulation box). The particles would be removed from the cells whose λ is nonzero. We also set a smoothing mechanism at the interface between the region of λ = 0 and of λ ≠ 0. The length in ECsim is normalized to ion skin depth d_i and the time is normalized to the inverse of ion plasma frequency (i.e. 1/ω_pi). As a result, the current J is normalized to ω_pim_i/(μ₀ed_i).

TABLE 1

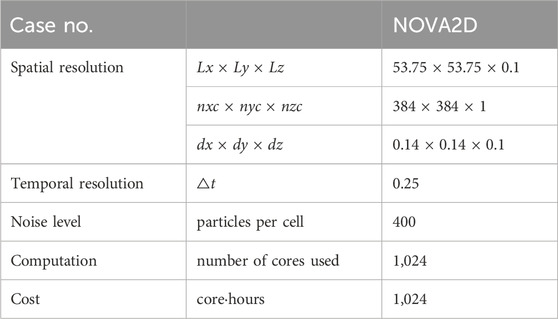
TABLE 1. Tokamak 2-Dimensional simulation parameters: Lx, Ly, Lz are the length of simulation box in x, y, z direction, respectively, with the units of d_i as mentioned above. nxc, nyc, nzc are the number of cells in three directions, and dx, dy, dz are the cell size in three directions, respectively. △t is the time step with the units of 1/ω_pi. The number of particles is 400 per cell for each of the two species, ions and electrons.

TABLE 2

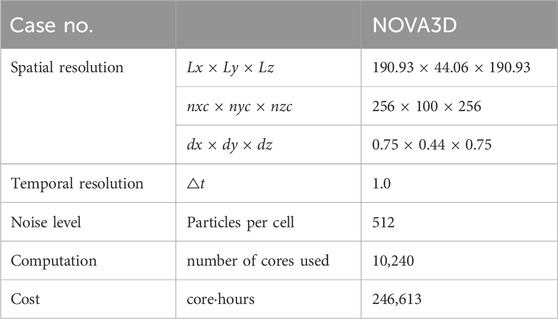
TABLE 2. Tokamak 3-Dimensional simulation parameters: the parameters shown here have the same meaning as Table 1. The number of particles is 512 per cell for each of the two species, ions and electrons.

3.1 2-Dimensional simulation results

In order to assess the feasibility of the simulation, we initiated a 2-dimensional simulation utilizing the equilibrium data sourced from NOVA. This equilibrium data were initially provided in magnetic coordinates in the 2D profile, necessitating a conversion to Cartesian coordinates and subsequent interpolation onto the meshes suitable for ECsim simulations. ∇ × B = μ₀J and J × B = ∇P are used to verify the reliability of the equilibrium data. The parameters employed for the 2D simulation are presented in Table 1. The physical parameters used in the simulation are the same as those used in Section 3. A of [51]. The results of electron current density in both x and y directions are illustrated in Figure 4.

FIGURE 4

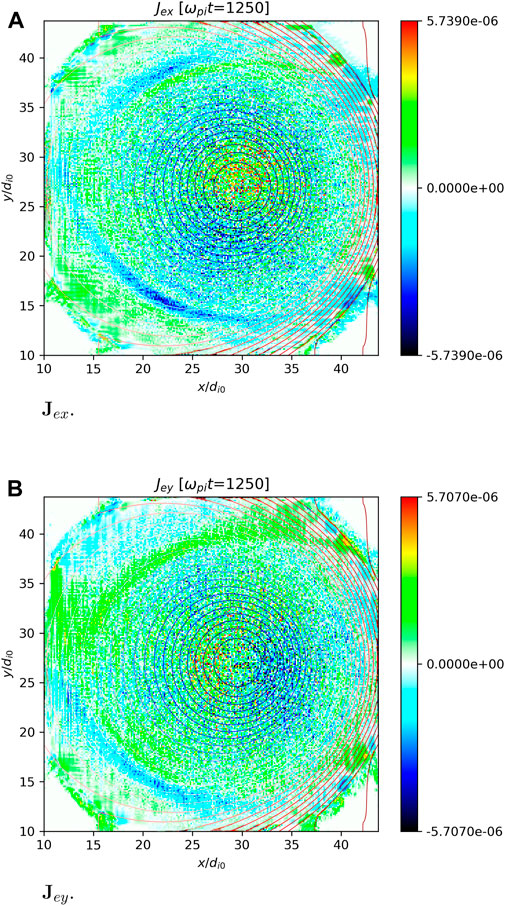
FIGURE 4. Electron current density in 2-Dimensional simulation (ω_pit = 1,250). The contour lines represent magnetic flux surfaces. J_ex and J_ey are the electron current density in x and in y direction, respectively. ω_pi is ion plasma frequency, t is time, d_i0 is ion skin depth.

3.2 3-Dimensional simulation results

To facilitate 3D simulation, the acquisition of an appropriate equilibrium state is imperative. The initial equilibrium data obtained from NOVA are only a 2-dimensional profile representing the data of a cross section of the tokamak. Also, it should be noted that the ECsim operates in Cartesian coordinates, necessitating the conversion of the data from 2D to 3D and further interpolating it onto the relevant grid points. Table 2 provides an overview of the parameters employed in the 3D simulation. Throughout the simulation process, which has currently undergone approximately 17,000 cycles (ω_pit ≈ 17, 000), we have conducted a comprehensive analysis of various quantities, including their profiles and Poincaré plots at different time. The structure and evolution of magnetic flux surfaces and magnetic islands could be observed clearly in the Poincaré plots. In particular, the 2D profile is an average of the relevant quantity along the toroidal direction. Here we presented the current density in both radial and vertical directions (Figure 5).

FIGURE 5

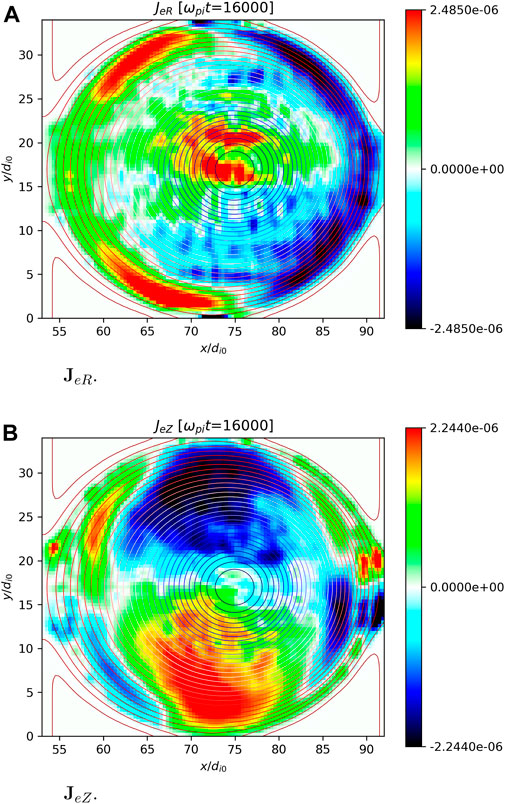
FIGURE 5. Electron current density in 3-Dimensional simulation (ω_pit = 16,000). The contour lines represent magnetic flux surfaces. J_eR and J_eZ are the electron current density in R and in Z direction, respectively. ω_pi is ion plasma frequency, t is time, d_i0 is ion skin depth.

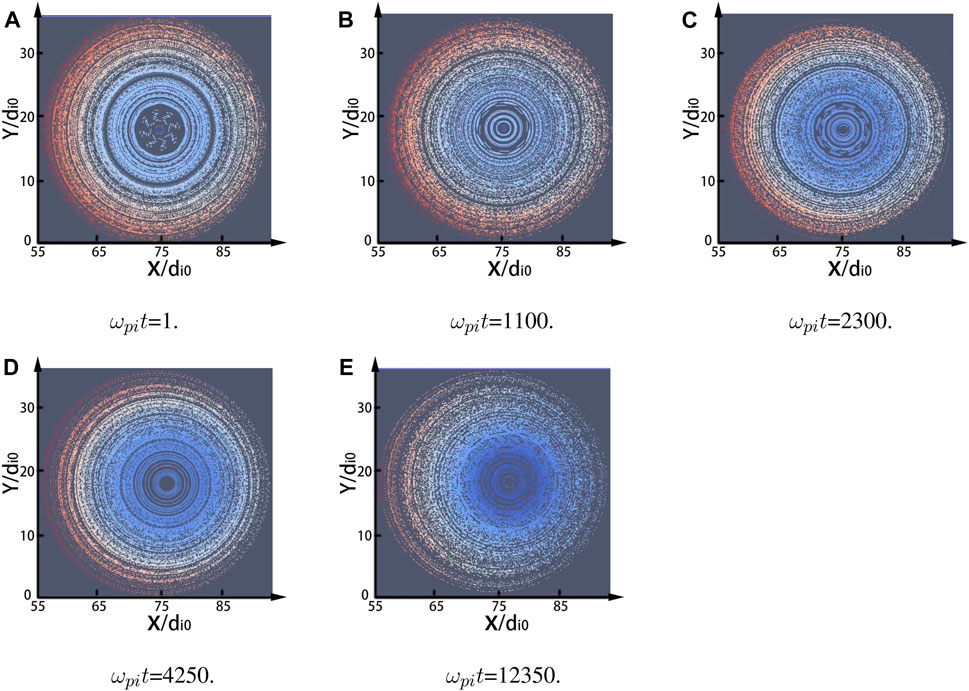
At the beginning, the magnetic flux surfaces exhibited a discernible and well-defined structure Figure 6A. However, as the simulation progressed, we observed a notable transformation in the Poincaré plot when t = 2,300/ω_pi (Figure 6C). This transformation unveiled the emergence of magnetic islands within the system, a phenomenon we attribute to the process of equilibrium adjustment. It is pertinent to mention that the initial equilibrium extracted from NOVA was a MHD equilibrium. Before commencing the simulation, we undertook a pivotal step of converting this MHD equilibrium into a kinetic equilibrium. The current density was set to be carried only by the electrons, which means the initial ion current is 0 - a condition that departs from physical realism. This deliberate setup incited the relaxation of equilibrium over time, eventually yielding a more physically plausible kinetic equilibrium, as shown in Figure 6D.

FIGURE 6

FIGURE 6. Poincaré plots evolution. ω_pi is ion plasma frequency, t is time, d_i0 is ion skin depth.

With the extension of the simulation duration, we were able to observe the gradual formation of magnetic islands, particularly near the q = 2 surface (q signifies the safety factor and is defined as the ratio of change of toroidal flux with poloidal flux) as illustrated in Figure 6E. However, if our objective is to fully capture the intricate structure of tearing modes, it becomes evident that achieving this goal would necessitate an exceptionally long simulation. For example, it needs to run approximately 700,000 cycles (t = 700, 000/ω_pi) if we want to run a simulation akin to [51] (now we only run up to 17,000 or so cycles). Such computational demands pose a significant challenge given the limitations of contemporary supercomputing capabilities. In order to decrease the computation cost, we explored various approaches. One common strategy, employed in astrophysics, is to modify the mass ratio. However, it became evident that this approach was infeasible here, as simulation time is intrinsically linked to the Alfvén time, rendering such adjustments ineffective. Alternative strategies, such as reducing parameters like ϵ (permittivity) or c (the speed of light), or decreasing the values of n (density) and B (magnetic field) within the equilibrium, did not yield the desired outcomes.

An additional consideration pertains to the scale resolved in simulations. In the investigation of electron dynamics, the conventional approach entails resolving electron scales in the context of magnetic reconnection. However, macroscopic-scale phenomena is paid more attention within the field of fusion plasma physics. Consequently, our simulations merely resolved ion scales thanks to the great stability performance of ECsim as pointed out in Part 2. It is our intention to compare the outcomes of our research with [51]. Nonetheless, the computational demands still remain considerable even with this refined approach.

4 Final remarks

4.1 Summary and discussion

This paper sheds light on the development and application of Particle-in-Cell (PIC) methods with a specific emphasis on the implicit PIC method. In contrast to the explicit PIC method, which offers simplicity and the ability to resolve all scales within a system, the implicit PIC method is highlighted for its capacity to surmount the stringent constraints typically required by explicit codes in terms of stability and accuracy. Notably, there has been an increase of interest in semi-implicit PIC methods over the past decades, and this review centers on the ECsim code. Moreover, we delve into potential future advancements for the PIC method.

The article also discusses the application of fully kinetic PIC methods to fusion plasma study. Compared with other simulation methods (such as MHD), the PIC method stands out due to its capacity to resolve finer scale physics, offering deeper insights into system evolution. Given the computational challenges encountered in fusion plasma physics, fully kinetic PIC methods have garnered increased interest within the fusion community. This paper reviews the prior work within this subject and outlines our recent progress made in the application of fully kinetic PIC codes to tearing mode instability study. The discussion highlights the existing challenges in this direction and underscores the need for continued efforts to overcome these obstacles. The paper provides useful insights into the evolving landscape of PIC methods and their crucial role in advancing the understanding of complex fusion plasma phenomena.

4.2 Outlook

The PIC method is expected to gain significant advantages from the ongoing advancements in supercomputing capabilities and the integration of artificial intelligence (AI), including machine learning and deep learning techniques. This is exemplified by recent research endeavors that have successfully combined machine learning and deep learning with the PIC method, as demonstrated in [43, 44]. These developments hold great promise and signify a compelling avenue for achieving groundbreaking results in the realm of PIC simulations.

Another pivotal area of exploration lies in the enhancement of PIC algorithms’ computational efficiency, particularly through the utilization of Graphics Processing Units (GPUs), as presented in [45]. By harnessing the capabilities of GPUs, researchers can significantly accelerate the execution of PIC simulations, ushering in new possibilities and opportunities for in-depth scientific investigations.

Furthermore, the future application of the PIC method holds great potential in the domain of exascale simulations, as highlighted in [57]. The emergence of exascale supercomputers, such as the “JUPITER” system, is poised to significantly elevate computational capabilities. This, in turn, renders simulations that were once considered too expensive now within reach. Such progress has far-reaching implications in the context of fusion plasma research. There have been a few forerunners [22, 23, 47] and we believe the realization of fully kinetic PIC simulation for a full tokamak is increasingly feasible, offering the prospect of shedding new light on a wealth of previously unexplored physics phenomena.

Author contributions

JR: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Visualization, Writing–original draft, Writing–review and editing. GL: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work reported received funding from the Katholieke Universiteit Leuven (KULeuven) Bijzonder Onderzoeksfonds (BOF) under the C1 project TRACESpace and from the European Union project DEEP-SEA (grant agreement 955606). It is also supported by the China Scholarship Council. Computing is supported by the Flemish Supercomputing Center (VSC). Numerical simulations were performed on SuperMUC-NG, hosted by the Leibniz Supercomputing Centre (Germany).

Acknowledgments

The authors would like to thank Dr. Gorelenkov Nikolai N for the help of access and use of NOVA code. JR would like to thank Prof. Zhang Wei and Xu Yuchen for the assistance of simulation setup. JR would also like to thank Dr. Arrò Giuseppe for useful review of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Freidberg JP. Plasma physics and fusion energy. Cambridge, NY, Melbourne, Madrid, Cape Town, Singapore, São Paulo: Cambridge University Press (2008).

Google Scholar

2. Jardin S. Computational methods in plasma physics. Boca Raton, FL: CRC Press, Taylor & Francis Group (2010).

Google Scholar

3. Fasoli A, Brunner S, Cooper WA, Graves JP, Ricci P, Sauter O, et al. Computational challenges in magnetic-confinement fusion physics. Nat Phys (2016) 12:411–23. doi:10.1038/nphys3744

CrossRef Full Text | Google Scholar

4. Gerasimov S, Abreu P, Artaserse G, Baruzzo M, Buratti P, Carvalho I, et al. Overview of disruptions with jet-ilw. Nucl Fusion (2020) 60:066028. doi:10.1088/1741-4326/ab87b0

CrossRef Full Text | Google Scholar

5. Dendy RO. Plasma physics: an introductory course. Cambridge University Press (1995).

Google Scholar

6. Birdsall CK, Langdon AB. Plasma physics via computer simulation. New York: McGraw-Hill (1985).

Google Scholar

7. Hockney R, Eastwood J. Computer simulation using particles. New York, NY, United States: IOP Publishing Ltd. (1988).

Google Scholar

8. Colonna G, D’Angola A. Plasma ModelingMethods and applications. Temple Way, Bristol, United Kingdom: IOP Publishing (2016). doi:10.1088/978-0-7503-1200-4

CrossRef Full Text | Google Scholar

9. Tajima T. Computational plasma physics: with applications to fusion and astrophysics. Boca Raton, FL: CRC Press, Taylor & Francis Group (2018).

Google Scholar

10. McClenaghan J, Lin Z, Holod I, Deng W, Wang Z. Verification of gyrokinetic particle simulation of current-driven instability in fusion plasmas. i. internal kink mode. Phys Plasmas (2014) 21:122519. doi:10.1063/1.4905073

CrossRef Full Text | Google Scholar

11. Lin Y, Wang XY, Chen L, Lu X, Kong W. An improved gyrokinetic electron and fully kinetic ion particle simulation scheme: benchmark with a linear tearing mode. Plasma Phys Controlled Fusion (2011) 53:054013. doi:10.1088/0741-3335/53/5/054013

CrossRef Full Text | Google Scholar

12. Lu ZX, Meng G, Hoelzl M, Lauber P. The development of an implicit full f method for electromagnetic particle simulations of alfvén waves and energetic particle physics. J Comput Phys (2021) 440:110384. doi:10.1016/j.jcp.2021.110384

CrossRef Full Text | Google Scholar

13. Büchner J. Space and astrophysical plasma simulation: methods, algorithms, and applications. Springer Nature (2023).

Google Scholar

14. Batchelor DA, Beck M, Becoulet A, Budny RV, Chang CS, Diamond PH, et al. Simulation of fusion plasmas: current status and future direction. Plasma Sci Tech (2007) 9:312–87. doi:10.1088/1009-0630/9/3/13

CrossRef Full Text | Google Scholar

15. Nicholson DR. Introduction to plasma theory, 1. New York: Wiley (1983).

Google Scholar

16. Arber T, Bennett K, Brady C, Lawrence-Douglas A, Ramsay M, Sircombe NJ, et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Controlled Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar

17. Wu D, He X, Yu W, Fritzsche S. Particle-in-cell simulations of laser–plasma interactions at solid densities and relativistic intensities: the role of atomic processes. High Power Laser Sci Eng (2018) 6:e50. doi:10.1017/hpl.2018.41

CrossRef Full Text | Google Scholar

18. Bowers KJ, Albright BJ, Yin L, Bergen B, Kwan TJT. Ultrahigh performance three-dimensional electromagnetic relativistic kinetic plasma simulation. Phys Plasmas (2008) 15. doi:10.1063/1.2840133

CrossRef Full Text | Google Scholar

19. Bowers KJ, Albright BJ, Yin L, Daughton W, Roytershteyn V, Bergen B, et al. Advances in petascale kinetic plasma simulation with vpic and roadrunner. J Phys Conf Ser (IOP Publishing) (2009) 180:012055. doi:10.1088/1742-6596/180/1/012055

CrossRef Full Text | Google Scholar

20. Bird R, Tan N, Luedtke SV, Harrell SL, Taufer M, Albright B. Vpic 2.0: next generation particle-in-cell simulations. IEEE Trans Parallel Distributed Syst (2021) 33:952–63. doi:10.1109/tpds.2021.3084795

CrossRef Full Text | Google Scholar

21. Vay JL, Almgren A, Bell J, Ge L, Grote DP, Hogan M, et al. Warp-x: a new exascale computing platform for beam–plasma simulations. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2018) 909:476–9. doi:10.1016/j.nima.2018.01.035

CrossRef Full Text | Google Scholar

22. Jianyuan XIAO, Hong QIN. Explicit structure-preserving geometric particle-in-cell algorithm in curvilinear orthogonal coordinate systems and its applications to whole-device 6d kinetic simulations of tokamak physics. Plasma Sci Tech (2021) 23:055102. doi:10.1088/2058-6272/abf125

CrossRef Full Text | Google Scholar

23. Xiao J, Chen J, Zheng J, An H, Huang S, Yang C, et al. Symplectic structure-preserving particle-in-cell whole-volume simulation of tokamak plasmas to 111.3 trillion particles and 25.7 billion grids. Proc Int Conf High Perform Comput Networking, Storage Anal (2021) 1–13. doi:10.1145/3458817.3487398

CrossRef Full Text | Google Scholar

24. Markidis S, Lapenta G. The energy conserving particle-in-cell method. J Comput Phys (2011) 230:7037–52. doi:10.1016/j.jcp.2011.05.033

CrossRef Full Text | Google Scholar

25. Chen G, Chacón L, Barnes DC. An energy-and charge-conserving, implicit, electrostatic particle-in-cell algorithm. J Comput Phys (2011) 230:7018–36. doi:10.1016/j.jcp.2011.05.031

CrossRef Full Text | Google Scholar

26. Markidis S, Lapenta G, Rizwan-uddin G. Multi-scale simulations of plasma with ipic3d. Mathematics Comput Simulation (2010) 80:1509–19. doi:10.1016/j.matcom.2009.08.038

CrossRef Full Text | Google Scholar

27. Lapenta G, Markidis S. Particle acceleration and energy conservation in particle in cell simulations. Phys Plasmas (2011) 18. doi:10.1063/1.3602216

CrossRef Full Text | Google Scholar

28. Kelley CT. Solving nonlinear equations with Newton’s method. University City, Philadelphia, PA, United States: SIAM (2003).

Google Scholar

29. Knoll DA, Keyes DE. Jacobian-free Newton–krylov methods: a survey of approaches and applications. J Comput Phys (2004) 193:357–97. doi:10.1016/j.jcp.2003.08.010

CrossRef Full Text | Google Scholar

30. Markidis S, Olshevsky V, Sishtla CP, Chien SW, Laure E, Lapenta G. Polypic: the polymorphic-particle-in-cell method for fluid-kinetic coupling. Front Phys (2018) 6:100. doi:10.3389/fphy.2018.00100

CrossRef Full Text | Google Scholar

31. Chen G, Chacon L. A multi-dimensional, energy-and charge-conserving, nonlinearly implicit, electromagnetic vlasov–Darwin particle-in-cell algorithm. Comput Phys Commun (2015) 197:73–87. doi:10.1016/j.cpc.2015.08.008

CrossRef Full Text | Google Scholar

32. Chacón L, Chen G. A curvilinear, fully implicit, conservative electromagnetic pic algorithm in multiple dimensions. J Comput Phys (2016) 316:578–97. doi:10.1016/j.jcp.2016.03.070

CrossRef Full Text | Google Scholar

33. Stanier A, Chacón L, Chen G. A fully implicit, conservative, non-linear, electromagnetic hybrid particle-ion/fluid-electron algorithm. J Comput Phys (2019) 376:597–616. doi:10.1016/j.jcp.2018.09.038

CrossRef Full Text | Google Scholar

34. Langdon AB, Cohen BI, Friedman A. Direct implicit large time-step particle simulation of plasmas. J Comput Phys (1983) 51:107–38. doi:10.1016/0021-9991(83)90083-9

CrossRef Full Text | Google Scholar

35. Mason RJ. Implicit moment particle simulation of plasmas. J Comput Phys (1981) 41:233–44. doi:10.1016/0021-9991(81)90094-2

CrossRef Full Text | Google Scholar

36. Brackbill JU, Cohen BI. Multiple time scales (computational techniques), Vol. 3. Academic Press (2014).

Google Scholar

37. Lapenta G, Gonzalez-Herrero D, Boella E. Multiple-scale kinetic simulations with the energy conserving semi-implicit particle in cell method. J Plasma Phys (2017) 83:705830205. doi:10.1017/s0022377817000137

CrossRef Full Text | Google Scholar

38. Lapenta G. Exactly energy conserving semi-implicit particle in cell formulation. J Comput Phys (2017) 334:349–66. doi:10.1016/j.jcp.2017.01.002

CrossRef Full Text | Google Scholar

39. Gonzalez-Herrero D, Boella E, Lapenta G. Performance analysis and implementation details of the energy conserving semi-implicit method code (ecsim). Comput Phys Commun (2018) 229:162–9. doi:10.1016/j.cpc.2018.03.020

CrossRef Full Text | Google Scholar

40. Arrò G, Califano F, Lapenta G. Spectral properties and energy transfer at kinetic scales in collisionless plasma turbulence. Astron Astrophysics (2022) 668:A33. doi:10.1051/0004-6361/202243352

CrossRef Full Text | Google Scholar

41. Ren J, Xu Y, Zhang W, Gorelenkov NN, Jiang W, Ye M, et al. Fully kinetic particle-in-cell simulations of the tearing mode instability in tokamaks. In: 49th European Physical Society Conference on Plasma Physics (EPS 2023). European Physical Society (EPS (2023).

Google Scholar

42. Lapenta G. Advances in the implementation of the exactly energy conserving semi-implicit (ecsim) particle-in-cell method. Physics (2023) 5:72–89. doi:10.3390/physics5010007

CrossRef Full Text | Google Scholar

43. Aguilar X, Markidis S. A deep learning-based particle-in-cell method for plasma simulations. In: 2021 IEEE International Conference on Cluster Computing (CLUSTER); 07-10 September 2021; Portland, OR, USA. IEEE (2021). p. 692–7.

CrossRef Full Text | Google Scholar

44. Badiali C, Bilbao PJ, Cruz F, Silva LO. Machine-learning-based models in particle-in-cell codes for advanced physics extensions. J Plasma Phys (2022) 88:895880602. doi:10.1017/s0022377822001180

CrossRef Full Text | Google Scholar

45. Xiong QY, Huang SY, Yuan ZG, Jiang K, Wei YY, Xu SB, et al. A scheme of full kinetic particle-in-cell algorithms for gpu acceleration using cuda fortran programming. Astrophysical J Suppl Ser (2022) 264:3. doi:10.3847/1538-4365/ac9fd6

CrossRef Full Text | Google Scholar

46. Bowers KJ, Albright BJ, Bergen B, Yin L, Barker KJ, Kerbyson DJ. 0.374 pflop/s trillion-particle kinetic modeling of laser plasma interaction on roadrunner. In: SC’08: Proceedings of the 2008 ACM/IEEE conference on Supercomputing; 15-21 November 2008; Austin, TX, USA. IEEE (2008). p. 1–11.

CrossRef Full Text | Google Scholar

47. Bussmann M, Burau H, Cowan TE, Debus A, Huebl A, Juckeland G, et al. Radiative signatures of the relativistic kelvin-helmholtz instability. Proc Int Conf High Perform Comput Networking, Storage Anal (2013) 1–12. doi:10.1145/2503210.2504564

CrossRef Full Text | Google Scholar

48. Sturdevant BJ, Chen Y, Parker SE. Low frequency fully kinetic simulation of the toroidal ion temperature gradient instability. Phys Plasmas (2017) 24:081207. doi:10.1063/1.4999945

CrossRef Full Text | Google Scholar

49. Hu Y, Miecnikowski MT, Chen Y, Parker SE. Fully kinetic simulation of ion-temperature-gradient instabilities in tokamaks. Plasma (2018) 1:105–18. doi:10.3390/plasma1010010

CrossRef Full Text | Google Scholar

50. Furth HP, Killeen J, Rosenbluth MN. Finite-resistivity instabilities of a sheet pinch. Phys Fluids (1963) 6:459–84. doi:10.1063/1.1706761

CrossRef Full Text | Google Scholar

51. Zhang W, Ma ZW, Wang S. Hall effect on tearing mode instabilities in tokamak. Phys Plasmas (2017) 24:102510. doi:10.1063/1.5004430

CrossRef Full Text | Google Scholar

52. Zhang W, Wang S, Ma ZW. Influence of helical external driven current on nonlinear resistive tearing mode evolution and saturation in tokamaks. Phys Plasmas (2017) 24:062510. doi:10.1063/1.4986113

CrossRef Full Text | Google Scholar

53. Zhang R, Chen Y, Ye L, Xiang N. Hybrid gyrokinetic ion/fluid electron simulation of toroidal tearing modes. Phys Plasmas (2022) 29:012108. doi:10.1063/5.0067813

CrossRef Full Text | Google Scholar

54. Zhang RB, Ye L, Chen Y, Xiang N, Yang XQ. Effect of kinetic ions on the toroidal double-tearing modes. Chin Phys B (2022) 32:025203. doi:10.1088/1674-1056/ac7f89

CrossRef Full Text | Google Scholar

55. Cheng CZ. Kinetic extensions of magnetohydrodynamics for axisymmetric toroidal plasmas. Phys Rep (1992) 211:1–51. doi:10.1016/0370-1573(92)90166-w

CrossRef Full Text | Google Scholar

56. Gorelenkov NN, Cheng CZ, Fu GY. Fast particle finite orbit width and larmor radius effects on low-n toroidicity induced alfvén eigenmode excitation. Phys Plasmas (1999) 6:2802–7. doi:10.1063/1.873545

CrossRef Full Text | Google Scholar

57. Ji H, Daughton W, Jara-Almonte J, Le A, Stanier A, Yoo J. Magnetic reconnection in the era of exascale computing and multiscale experiments. Nat Rev Phys (2022) 4:263–82. doi:10.1038/s42254-021-00419-x

CrossRef Full Text | Google Scholar