Wavelength dependent transmission in multimode graded-index microstructured polymer optical fibers

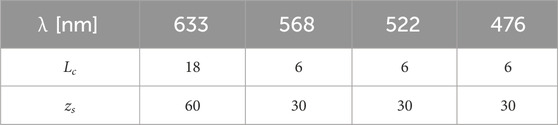
Up to now, there have been no commercial simulation tools accessible for researching the transmission properties of multimode microstructured optical fibers (MOFs). In order to avoid this problem, this study uses the time-independent power flow equation (TI PFE) numerical solution to examine the wavelength dependency of the equilibrium mode distribution (EMD) and steady state distribution (SSD) in multimode graded-index microstructured polymer optical fibers (GI mPOF) with a solid core. We showed that the lengths z_s at which an SSD is obtained in GI mPOF and the coupling length L_c necessary to create an EMD are shorter at λ = 568 nm than they are found to be at λ = 633 nm. The lengths L_c and z_s stay constant when the wavelength decreases further from λ = 568 to 522 and then to 476 nm. As a result, it is anticipated that a faster bandwidth enhancement in the tested GI mPOF will take place at wavelengths around λ = 568 nm as opposed to λ = 633 nm. Such a bandwidth improvement is not brought about by additional wavelength reduction. The study’s findings can be used in communication and sensory systems that use multimode GI mPOFs at different wavelengths.

1 Introduction

Recent years have seen a significant increase in research interest in high-speed short-range signal transmission across polymer optical fibers (POFs) [1–3]. The assets of POFs, such as a large core and simple connection, may offer a cost-effective solution for the in-home network. Polymethyl methacrylate (PMMA) [4, 5], polydimethylsiloxane (PDMS) [6, 7], polystyrene (PS) [8, 9], polycarbonate (PC) [10, 11], perfluorinated polymer (CYTOP^®) [12, 13], cycloolefin polymer (ZEONEX^®) [14, 15], and cycloolefin copolymer (TOPAS^®) [16, 17] are just a few of the materials used to fabricate POFs. Due to the flexibility of POF material, it is feasible to produce POFs that meet the requirements of various applications by using alternative specifications or materials. PMMA is the material that has been used to make POFs the most frequently up until this time [18–22].

The RI distribution of GI multimode POF gradually decreases from the core axis to the cladding. The POF’s bandwidth and transmission distance can both be increased using this type of RI distribution. To create GI POF, however, advanced doping techniques are required. MOF, often referred to as photonic crystal fiber, was successfully proposed in the 1990s [23]. The flexibility of the optical fiber is considerably increased by the microstructure of MOFs. Numerous relevant MOF features have been investigated by changing the microstructure [24–27]. Eijkelenborg and associates created the first PMMA mPOF in 2001 [28]. The various applications of mPOF then attracted scientific attention [29, 30]. The core and/or cladding layer of a typical mPOF design can be changed by altering the placement and/or size (d) of air holes within a concentric ring-like region, as shown in Figure 1. In Figure 1, an mPOF that mimics a GI optical fiber features a core with different-sized air holes. GI mPOF offers more latitude in changing the air-hole diameters and pitch than typical GI POF, which calls for complex doping methods. Additionally, for communication purposes, it has been found that GI mPOF has a wider bandwidth and less loss than traditional GI POF [31].

FIGURE 1

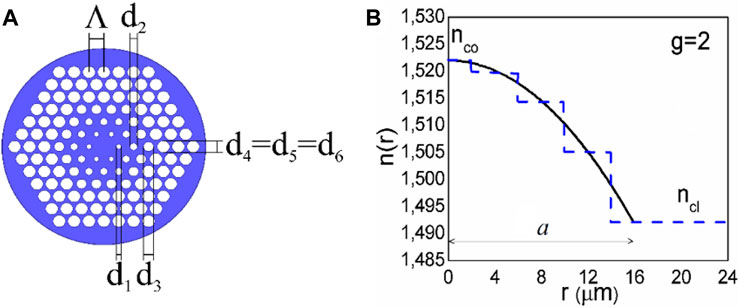
FIGURE 1. (A) The cross-section of the multimode GI MOF. The pitch Λ determines the position of air holes in a triangular lattice. The air holes that make the four rings of the core have the following diameters: d₁, d₂, d₃, and d₄. Two rings of air holes of the same diameter as those in the outermost core ring form the cladding (d₄ = d₅ = d₆). (B) The dashed blue line shows the referent multimode GI MOF’s RI distribution. The solid black line represents the RI distribution in the core based on Eq. 1, when g = 2.0, and at λ = 633 nm.

Mode coupling is primarily caused by light scattering, which takes place when transient abnormalities in multimode optical fibers transmit power from one mode to another. Modal dispersion can be decreased and transmission bandwidth increased by using mode coupling [30]. Mode coupling prevents measurements of an optical fiber’s fundamental optical characteristics, such as attenuation and bandwidth, from being made until the steady state distribution (SSD) has not yet been fully obtained at length z_s. Thus, it is essential to comprehend the fiber lengths at which an equilibrium mode distribution (EMD) and SSD are established (EMD is achieved at length L_c). It is of particular interest to explore how wavelength affects GI mPOF’s structural and physical parameters and therefore power flow at different fiber lengths.

Up to now, there have been no commercial simulation tools available for studying the transmission characteristics of multimode MOFs. To circumvent this problem, the time-independent power flow equation (TI PFE) is numerically solved in this study to investigate the wavelength dependent light transmission in GI mPOF. We calculated the lengths for achieving the EMD and SSD for multimode GI mPOF with a solid core using launch beam distributions with different radial offsets Δr at different wavelengths λ (the low attenuation windows of POFs). As shown in Figure 1, we proposed that the air holes in the core and cladding be arranged in a grid of triangles with regular pitch Λ. The shorter the GI mPOF’s length at which EMD is attained, the sooner the functional dependency of bandwidth changes from of 1/z to of 1/z^1/2 (slower bandwidth decline) [16]. This study is the first to examine how wavelength affects power flow in GI mPOF to the best of our knowledge. The numerical results reported in this work are very useful in communication and sensory systems that use multimode GI mPOFs at different wavelengths.

2 GI mPOF design

The GI mPOF that was examined in this study is depicted in Figure 1. This GI mPOF is made up of six air-hole rings, numbered 1, 2, ... , 6, respectively.

A triangular lattice with pitch Λ holds the air holes in the studied polymer fiber. The parabolic RI distribution in the core is a result of the appropriate choice of the air-hole diameters in the four inner air-hole rings. The air-hole diameters in rings 5 and 6 are equal to those in ring 4 (d₄ = d₅ = d₆). This system was simulated using the TI PFE.

3 Time-independent power flow equation

The GI optical fibers have the following RI profile:

$n\left(r,\lambda \right)=\left\{\begin{array}{l}{n}_{co}\left(\lambda \right){\left[1-2\Delta \left(\lambda \right){\left(\frac{r}{a}\right)}^g\right]}^{1/2}\left(0\le r\le a\right)\\ n_{co}\left(\lambda \right){\left(1-2\Delta \left(\lambda \right)\right)}^{1/2}=n_{cl}\left(\lambda \right)\left(r>a\right)\end{array}\right.(1)$

Here n_co(λ) is the core’s highest index (measured at the fiber axis), n_cl(λ) is the cladding’s index, $\Delta =\left[n_{co}\left(\lambda \right)-n_{cl}\left(\lambda \right)\right]/n_{co}\left(\lambda \right)$ is the relative index difference, g is the core index exponent, and a is the core radius.

The TI PFE for GI optical fiber is [32]:

$\frac{\partial P\left(m,\lambda ,z\right)}{\partial z}=\frac{D}{m}\frac{\partial P\left(m,\lambda ,z\right)}{\partial m}+D\frac{\partial P^2\left(m,\lambda ,z\right)}{\partial m^2}(2)$

where $P\left(m,\lambda ,z\right)$ is power in the m-th principal mode (modal group), z is the coordinate along the fiber axis, and D is a constant mode coupling coefficient. The maximum principal mode number M(λ) can be calculated as [32]:

$M\left(\lambda \right)=\sqrt{\frac{g\Delta \left(\lambda \right)}{g+2}}ak{n}_{co}\left(\lambda \right)(3)$

where k = 2π/λ.

The principal mode m excited at the input fiber end is [32]:

$\frac{m}{M}={\left[{\left(\frac{\Delta r}{a}\right)}^g+\frac{{\theta }^2}{2\Delta }\right]}^{\left(g+2\right)/2g}(4)$

where $∆r$ is the radial offset of the launch beam and θ is the launch beam angle. In this work, Equation 2 is solved using the explicit finite difference method [32].

4 Numerical simulation results

Light transmission was examined in a multimode GI mPOF with a solid core (Figure 1). The effective V parameter for such a fiber is given as:

$V=\frac{2\pi }{\lambda }{a}_{eff}\sqrt{n_0^2-n_{fsm}^2}(5)$

where a_eff = $\mathrm{\Lambda }/\sqrt{3}$ [33, 34], and n_fsm is the effective RI for various core and cladding layers, as determined by combining the Equation 5 with the effective V parameter [33, 34]:

$V\left(\frac{\lambda }{\mathrm{\Lambda }},\frac{d}{\mathrm{\Lambda }}\right)=A_1+\frac{A_2}{1+A_3\exp \left(A_4\lambda /\mathrm{\Lambda }\right)}(6)$

The fitting parameters A_i (i = 1–4) are given as:

$A_i=a_{i0}+a_{i1}{\left(\frac{d}{\mathrm{\Lambda }}\right)}^{b_{i1}}+a_{i2}{\left(\frac{d}{\mathrm{\Lambda }}\right)}^{b_{i2}}+a_{i3}{\left(\frac{d}{\mathrm{\Lambda }}\right)}^{b_{i3}}(7)$

The coefficients a_i0 to a_i3 and b_i1 to b_i3 (i = 1–4) are given in our previous work [34].

We employed our approach Eq. 2 on the GI mPOF with the core radius a = 4Λ = 16 μm, where Λ = 4 μm, and the diameter of the fiber b = 1 mm. Table 1 displays the core’s refractive index n_co at different wavelengths when measured along the fiber axis. For Λ = 4 μm and air-hole diameters of the four air-hole rings in the core d₁ = 0.6 μm, d₂ = 0.7 μm, d₃ = 1.3 μm, and d₄ = 3.1 μm, the refractive indices n₁, n₂, n₃, and n₄, respectively, calculated using Eqs 6, 7 for different wavelengths, are given in Table 1. Parabolic RI distribution Eq. 1 in the core with g = 2.0, 4.5, 4.7, and 5.0 is achieved at λ = 633, 568, 522, and 476 nm, respectively. The air-hole diameter in the cladding rings 5 and 6 is d₄ = d₅ = d₆, and therefore the refractive index of the cladding is n₄ = n₅ = n₆ = n_cl. Table 1, for the GI mPOF under investigation, at various wavelengths, provides the maximum principal mode number M (Eq. 3). The coupling coefficient is D = 1482 1/m [29]. The typical values of D that define a standard GI POF can be used when modeling the GI mPOF due to the fact that the intensity of mode coupling in all types of POFs is correlated with the polymer core material. An analogous foundation was used to model a silica MOF [31].

TABLE 1

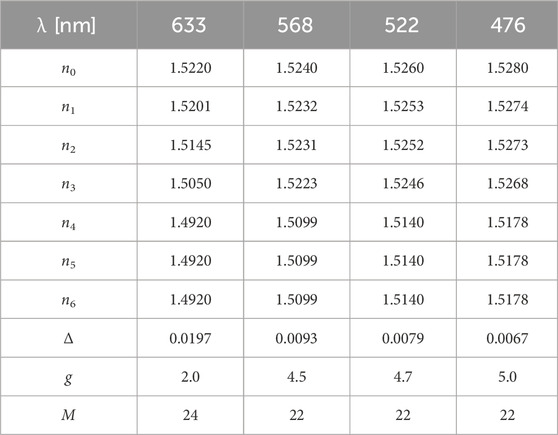
TABLE 1. Refractive index n0, n1, n2, n3, n4, n5, and n6, the relative index difference Δ, the core index exponent g, and the maximum principal mode number M at different wavelengths.

As an illustration, for λ = 568 nm, Figure 2 shows the development of the normalized output modal power distribution P (m,λ,z), which depends on the length of the fiber. Eq. 2 assumes a Gaussian beam P (θ,z) launched with $〈\theta 〉$ = 0^o for numerical calculations. Results are displayed for radial offsets of $∆r$ = 0, 4, 8, and 12 µm. It can be seen from Figure 2A that at short fiber lengths, due to mode coupling, only lower-order modes shift their midpoints of the power distributions to zero (m = 0). With increasing fiber length, higher order modes start to couple, shifting their distributions to m = 0 (Figure 2B). The EMD is obtained by shifting the midpoints of the power distributions of all modes to m = 0 at the coupling length of L_c = 6 m (Figure 2C). Figure 2D shows that SSD is established at z≡z_s = 30 m. The lengths L_c and z_s at various wavelengths are displayed in Table 2. It can be seen that the maximum principal mode number M drops with decreasing wavelength from λ = 633 to 568 nm, which causes the lengths L_c and z_s to decrease. Shorter lengths are required to accomplish EMD and SSD due to the smaller wavelength and fewer propagating modes. The maximum principal mode number maintains the constant value M = 22 with subsequent wavelength reduction from λ = 568 to 522 and finally to 476 nm, leading to the same lengths L_c = 6 m and z_s = 30 m. It is also worth noting that increasing the parameter g with decreasing the wavelength λ, i.e., modification of the GI distribution toward a step-index distribution, does not lead to longer lengths L_c and z_s. This is a consequence of the larger influence of wavelength λ and maximum principal number M on these two characteristic fiber lengths.

FIGURE 2

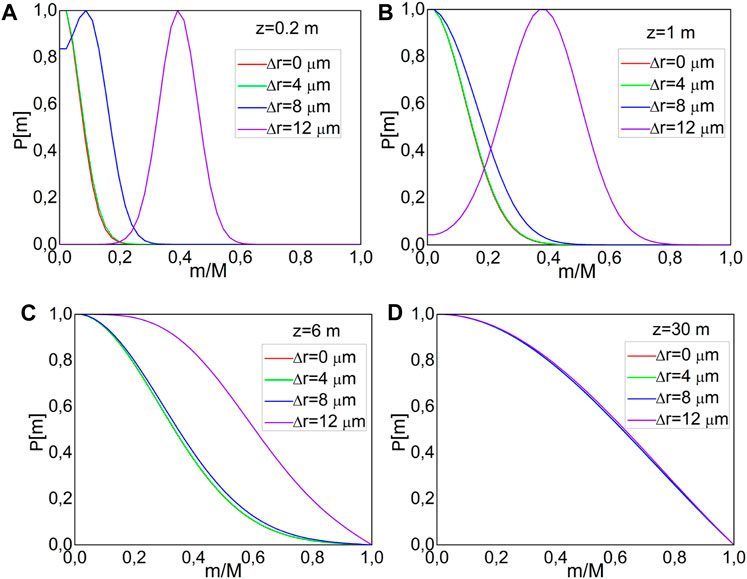
FIGURE 2. Normalized output modal power distribution P (m,λ,z) acquired by numerically solving the TI PFE (2) over a range of radial offsets $∆r$ = 0, 4, 8, and 12 μm at different fiber lengths (A) z = 0.2 m, (B) z = 1 m, (C) z = 6 m, and (D) z = 30 m at λ = 568 nm.

TABLE 2

TABLE 2. Lengths L_c (for achieving emd) and Zs (for achieving ssd) at different wavelengths.

It is important to notice that mode coupling behavior controls how the GI MOF bandwidth varies with length. A length less than the coupling length L_c has an inversely linear effect on the bandwidth. Beyond this equilibrium length L_C, it has a _Z^−1/2 dependence, though. As a result, a shorter LC would lead to a more rapid transition to a slower bandwidth drop phase [30, 35, 36]. The investigated GI mPOF is predicted to experience a faster bandwidth enhancement at a wavelength of λ = 568 nm than at λ = 633 nm. Such an improvement in bandwidth is not achieved by further reducing the wavelength from λ = 568 to 522 and subsequently to 476 nm.

In contrast to the GI mPOF that we focused on in this investigation, silica MOFs have much weaker mode coupling, resulting in a length L_c between 1.45 and 1.65 km at which an EMD is achieved, and a length z_s between 3.30 and 3.80 km for the establishment of an SSD [34].

5 Conclusion

In this study, the power flow along a GI mPOF at various wavelengths is examined using the TI PFE. We have demonstrated that the lengths L_c and z_s needed to achieve an EMD and an SSD, respectively, in GI mPOF are shorter at λ = 568 nm than they are at λ = 633 nm. The lengths L_c and z_s stay constant when the wavelength decreases further from λ = 568 to 522 and then to 476 nm. Therefore, the shorter L_c causes a quicker changeover to the slower bandwidth decrease regime. As a result, a faster bandwidth enhancement in the tested GI mPOF is only anticipated to take place at wavelengths λ = 568 nm as opposed to that at λ = 633 nm. Such a bandwidth improvement is not brought about by additional wavelength reduction. The study’s findings can be used in communication and sensory systems that use multimode GI mPOFs at different wavelengths, i.e., at different low attenuation windows. Calculating the modal distribution of the GI mPOF used as a component of the optical fiber sensory system at a specific length at different wavelengths is also important. The future research on this type of optical fiber should be calculations of bandwidth at different wavelengths, which can be realized by numerically solving the time-dependent power flow equation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AS: Conceptualization, Methodology, Software, Writing–original draft. SS: Conceptualization, Methodology, Software, Supervision, Writing–original draft, Writing–review and editing. ZW: Funding acquisition, Project administration, Writing–review and editing. BD: Methodology, Software, Writing–original draft. MK: Conceptualization, Methodology, Software, Writing–original draft. LK: Methodology, Software, Writing–original draft. AD: Writing–original draft, Writing–review and editing. KA: Writing–original draft, Writing–review and editing. CC: Writing–original draft, Writing–review and editing, Conceptualization.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Natural Science Foundation of China (62003046, 6211101138); a grant from Ajman University (Grant No. 2023-IRG-ENIT-14); a grant from City University of Hong Kong (Project No. CityU 7004600); a grant from the Serbian Ministry of Science, Technological Development, and Innovations (Agreement No. 451-03-47/2023-01/200122); and a grant from Guangdong Basic and Applied Basic Research Foundation (2021A1515011997).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Barbio C, Cunha T, Linnartz J, Huijskens F, Koonen T, Tangdiongga E. Passive OFE WDM-over-POF Gigabits per second performance comparison of spatial diversity and spatial multiplexing. J Lightwave Technol (2023) 41(11):3567–76. doi:10.1109/jlt.2023.3253622

CrossRef Full Text | Google Scholar

2. Huang O, Shi J, Chi N. Performance and complexity study of a neural network post-equalizer in a 638-nm laser transmission system through over 100-m plastic optical fiber. Opt Eng (2022) 61(12):126108. doi:10.1117/1.oe.61.12.126108

CrossRef Full Text | Google Scholar

3. Koike Y, Muramoto K. Error-free PAM-4 transmission by a high-speed plastic optical fiber without forward error correction. Opt Lett (2021) 46:3709–12. doi:10.1364/ol.433885

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang J, Sun G, Ning Y, Li Z, Zhao L, Wang J, et al. Innovative sensor for refractive index monitoring based on a plastic optical fiber side-polished in a ‘V’-bent structure. Meas Sci Technol (2023) 34(5):055114. doi:10.1088/1361-6501/acbab5

CrossRef Full Text | Google Scholar

5. Wang K, Wang Q, Zou L, Su Y, Liu K, Li W, et al. Study on thermal protection and temperature of PMMA plastic optical fiber for concentrated sunlight transmission in daylighting. Solar Energy (2023) 253:127–36. doi:10.1016/j.solener.2023.02.015

CrossRef Full Text | Google Scholar

6. Leal-Junior A, Guo J, Min R, Fernandes AJ, Frizera A, Marques C. Photonic smart bandage for wound healing assessment. Photon Res (2021) 9(3):272–80. doi:10.1364/prj.410168

CrossRef Full Text | Google Scholar

7. Zha B, Wang Z, Li L, Hu X, Ortega B, Li X, et al. Wearable cardiorespiratory monitoring with stretchable elastomer optical fiber. Biomed Opt. Express (2023) 14:2260–75. doi:10.1364/boe.490034

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Liang G, Tang Y, Chen P, Li J, Yuan Y, Yu S, et al. Polystyrene-fiber-rod hybrid composite structure for optical enhancement in quantum-dot-converted light-emitting diodes. ACS Appl Polym Mater. (2022) 4(1):91–99. doi:10.1021/acsapm.1c01022

CrossRef Full Text | Google Scholar

9. Makino K, Akimoto Y, Koike K, Kondo A, Inoue A, Koike Y. Low loss and high bandwidth polystyrene-based graded index polymer optical fiber. J Light Technol (2013) 31(14):2407–12. doi:10.1109/jlt.2013.2266671

CrossRef Full Text | Google Scholar

10. Dadabayev R, Malka D. A visible light RGB wavelength demultiplexer based on polycarbonate multicore polymer optical fiber. Opt Laser Technol (2019) 116:239–45. doi:10.1016/j.optlastec.2019.03.034

CrossRef Full Text | Google Scholar

11. Zubel MG, Fasano A, Woyessa GT, Min R, Leal AG, Theodosiou A, et al. Bragg gratings inscribed in solid-core microstructured single-mode polymer optical fiber drawn from a 3D-printed polycarbonate preform. IEEE Sens J (2020) 20(21):12744–57. doi:10.1109/jsen.2020.3003469

CrossRef Full Text | Google Scholar

12. Leal-Junior A, Theodosiou A, Biazi V, Macedo L, Marques C, Kalli K, et al. Temperature-insensitive curvature sensor with plane-by-plane inscription of off-center tilted bragg gratings in CYTOP fibers. IEEE Sensors J (2022) 22(12):11725–31. doi:10.1109/jsen.2022.3171039

CrossRef Full Text | Google Scholar

13. Chapalo I, Chah K, Gusarov A, Ioannou A, Pospori A, Nan Y-G, et al. Gamma-radiation enhancement of sensing properties of FBGs in a few-mode polymer CYTOP fiber. Opt Lett (2023) 48(5):1248–51. doi:10.1364/ol.482936

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Qu H, Chen Z, Gao S, Min R, Woyessa G, Bang O, et al. Femtosecond laser line-by-line tilted Bragg grating inscription in single-mode step-index TOPAS/ZEONEX polymer optical fiber. Opt Lett (2023) 48(6):1438–41. doi:10.1364/ol.482598

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Pereira L, Marques C, Min R, Woyessa G, Bang O, Varum H, et al. Bragg gratings in ZEONEX microstructured polymer optical fiber with 266-nm Nd:YAG laser. IEEE Sensors J (2023) 23(9):9308–16. doi:10.1109/jsen.2023.3259546

CrossRef Full Text | Google Scholar

16. Inglev R, Woyessa G, Bang O, Janting J. Polymer optical fiber modification by etching using Hansen solubility parameters—a case study of TOPAS, Zeonex, and PMMA. J Lightwave Technol (2019) 37:4776–83. doi:10.1109/jlt.2019.2919798

CrossRef Full Text | Google Scholar

17. Woyessa G, Fasano A, Stefani A, Markos C, Nielsen K, Rasmussen HK, et al. Single mode step-index polymer optical fiber for humidity insensitive high temperature fiber Bragg grating sensors. Opt Express (2016) 24(2):1253–60. doi:10.1364/oe.24.001253

PubMed Abstract | CrossRef Full Text | Google Scholar

18. He R, Teng C, Kumar S, Marques C, Min R. Polymer optical fiber liquid level sensor: a Review. IEEE Sensors J (2022) 22(2):1081–91. doi:10.1109/jsen.2021.3132098

CrossRef Full Text | Google Scholar

19. Cheng X, Gunawardena DS, Pun CJ, Bonefacino J, Tam H. Single nanosecond-pulse production of polymeric fiber Bragg gratings for biomedical applications. Opt Express (2020) 28(22):33573–83. doi:10.1364/oe.408744

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kuang R, Ye Y, Chen Z, He R, Savović I, Djordjevich A, et al. Low-cost plastic optical fiber integrated with smartphone for human physiological monitoring. Opt Fiber Technol (2022) 71:102947. doi:10.1016/j.yofte.2022.102947

CrossRef Full Text | Google Scholar

21. Hu X, Chen Z, Cheng X, Min , Qu H, Caucheteur C, et al. Femtosecond laser point-by-point Bragg grating inscription in BDK-doped step-index PMMA optical fibers. Opt Lett (2022) 47(2):249–52. doi:10.1364/ol.450047

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Theodosiou A, Min R, Leal-Junior AG, Ioannou A, Frizera A, Pontes MJ, et al. Long period grating in a multimode cyclic transparent optical polymer fiber inscribed using a femtosecond laser. Opt Lett (2019) 44(21):5346–9. doi:10.1364/ol.44.005346

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Knight JC, Birks TA, Russell P, Atkin DM. All-silica single-mode optical fiber with photonic crystal cladding. Opt Lett (1996) 21(19):1547. doi:10.1364/ol.21.001547

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Stefańska K, Majchrowska S, Gemza K, Soboń G, Sotor J, Mergo P, et al. Soliton trapping and orthogonal Raman scattering in a birefringent photonic crystal fiber. Opt Lett (2022) 47(16):4183–6. doi:10.1364/ol.463643

CrossRef Full Text | Google Scholar

25. Zhao S, Guo R, Zeng Y. Effects of frequency-dependent Kerr nonlinearity on higher-order soliton evolution in a photonic crystal fiber with one zero-dispersion wavelength. Phys Rev A (2022) 106(3):033516. doi:10.1103/physreva.106.033516

CrossRef Full Text | Google Scholar

26. Wang C, Lin K, Cao S, Feng G, Wang J, Abdalla AN. Polarized supercontinuum generation in CS₂-core all-normal dispersion photonic crystal fiber. IEEE Photon J (2022) 14(6):1–7. doi:10.1109/jphot.2022.3223534

CrossRef Full Text | Google Scholar

27. Heydarian K, Nosratpour A, Razaghi M. Computational study of wavelength conversion based on XGM by photonic crystal semiconductor optical amplifier. Opt Laser Technol (2022) 156(1):108531. doi:10.1016/j.optlastec.2022.108531

CrossRef Full Text | Google Scholar

28. Eijkelenborg MA, Large MCJ, Argyros A, Zagari J, Manos S, Issa NA, et al. Microstructured polymer optical fibre. Opt Express (2001) 9(7):319–27. doi:10.1364/oe.9.000319

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Woyessa G, Pedersen JKM, Fasano A, Nielsen K, Markos C, Rasmussen HK, et al. Zeonex-PMMA microstructured polymer optical FBGs for simultaneous humidity and temperature sensing. Opt Lett (2017) 42(6):1161–4. doi:10.1364/ol.42.001161

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Min R, Pereira L, Paixao T, Woyessa G, Hu X, Antunes P, et al. Chirped POF Bragg grating production utilizing UV cure adhesive coating for multiparameter sensing. Opt Fiber Technol (2021) 65:102593. doi:10.1016/j.yofte.2021.102593

CrossRef Full Text | Google Scholar

31. Lwin R, Barton G, Harvey L, Harvey J, Hirst D, Manos S, et al. Beyond the bandwidth-length product: graded index microstructured polymer optical fiber. Appl Phys Lett (2007) 91(19):191119. doi:10.1063/1.2805216

CrossRef Full Text | Google Scholar

32. Savović S, Simović A, Drljača B, Djordjevich A, Stepniak G, Bunge CA, et al. Power flow in graded index plastic optical fibers. J Lightwave Technol (2019) 37(19):4985–90. doi:10.1109/jlt.2019.2926700

CrossRef Full Text | Google Scholar

33. Saitoh K, Koshiba M. Empirical relations for simple design of photonic crystal fibers. Opt Express (2005) 13(1):267–74. doi:10.1364/opex.13.000267

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Savović S, Kovačević MS, Simović A, Drljača B, Kuzmanović L, Djordjevich A. Method for investigation of mode coupling in multimode step-index silica photonic crystal fibers. Optik (2021) 246:167728. doi:10.1016/j.ijleo.2021.167728

CrossRef Full Text | Google Scholar

35. Drljača B, Savović S, Kovačević MS, Simović A, Kuzmanović L, Djordjevich A, et al. Theoretical investigation of bandwidth in multimode step-index silica photonic crystal fibers. Photonics (2022) 9(4):214. doi:10.3390/photonics9040214

CrossRef Full Text | Google Scholar

36. Savović S, Simović A, Drljača B, Kovačević MS, Kuzmanović L, Djordjevich A, et al. High bandwidth performance of multimode graded-index microstructured polymer optical fibers. Res Phys (2023) 50:106548. doi:10.1016/j.rinp.2023.106548

CrossRef Full Text | Google Scholar