Image security using steganography and cryptography with sweeping computational ghost imaging

A sweeping computational ghost imaging (SCGI)-based encryption system is intended for increased data security and speedier data transport. SCGI is combined with steganography and cryptography processes in this system. SCGI requires fewer shots, resulting in faster image capture, transmission, encryption, and decryption. This strategy also results in smaller, more compact data packages and higher bitrates. Least significant bit (LSB) uses steganography to conceal the hidden picture. In the case of Rivest–Shamir–Adleman (RSA) encryption, public and private keys are generated via a one-way function based on bucket values. Encryption is performed on two levels, with an asymmetric approach divided into three sub-items that significantly increase encryption. Surprisingly, the method uses fewer pictures for image reconstruction, resulting in faster image reconstruction. SCGI promises applications in an extensive number of data encryption sectors since this technology leads to smaller data packages and higher bitrates. The presented approach is examined using the number of pixel change rate (NPCR), normalized root mean square (NRMS), peak signal-to-noise ratio (PSNR), and correlation coefficient (CC), which indicates constant encryption improvement. We experimentally and situationally demonstrate our findings under eavesdropping, which prove the resistance and robustness of our methods. In optimal settings, this innovation enhances encryption by up to 90% when compared to traditional encryption methods.

1 Introduction

Ghost imaging (GI) is a relatively new imaging technique. An optical beam is divided into two arms in GI: a reference arm that is routed to a charge-coupled device (CCD) detector to record the spatial pattern and an object beam that illuminates the object and is reflected to a bucket detector that records a single intensity value. The second-order correlation of these two arrayed and single-value intensities [1–4] yields the picture. GI has various applications, including 3D imaging [5, 6], X-ray imaging [6, 7], face recognition [8, 9], imaging in turbulent medium [10], and data encryption [11, 12]. Pittman et al. [13] demonstrated the first GI using quantum entanglement in 1995. Later, Boyd et al. [14], in 2002, captured GI from a pseudo-thermal source. Computational GI (CGI) was introduced by Shapiro [15] by using a spatial light modulator (SLM) [16] or digital micro-mirror device (DMD) [17] rather than measuring the intensity profile of the reference arm with a CCD. The primary concern with GI is its low speed, which results in longer capture times when compared to those of other imaging methods. In order to address these obstacles, our group developed the sweeping CGI (SCGI) approach in 2019 [18]. In each shot, randomly generated CGI matrices were modified to have an all-bright row or column, and the position of these bright rows or columns was swept horizontally or vertically throughout the illumination matrix. Our technique may increase the imaging speed of moving objects by 22–4,000 times [19, 20]. Furthermore, because SCGI requires a predetermined number of shots equal to the sum of numbers of rows and columns of the randomly generated matrix, the photos are taken instantaneously.

One of the most crucial conditions for dependable data exchange is a secure and impermeable connection. Approaches including digital signatures, authentication, data masking, and sharing have made considerable strides in preventing or restricting unauthorized access to photographs. Raw data, compressed data, and comprehensive data encryption are the three methods of data encryption that have been in use since 1980 [21]. Data encryption can be carried out symmetrically or asymmetrically. The encryption and decryption keys are only accessible to the transmitter and receiver under symmetric situations. However, in asymmetrical situations, only the intended user has access to the decryption key [22]. Asymmetric data encryption is typically accomplished using Rivest–Shamir–Adleman (RSA) encryption [23, 24]. Steganography is a kind of data encryption in which data are hidden or inserted into a picture, audio, or video [25]. The phase, intensity, and wavelength of light are used in optical data encryption [26–28]. Recently, a number of optical encryption strategies have been introduced, including GI encryption, chaotic encryption [29], and dual random phase encryption [30]. The first optical data encryption method based on CGI was introduced by Clemente et al. [26]. Our team [12] proposed CGI-based grayscale and color optical encryption in 2012. We used selective CGI to confirm optical encryption once again [11]. High-performance optical encryption based on CGI, fast response codes, and a compressive sensing technique was proposed by Shengmei et al. in 2014 [31]. Leihong et al. improved the practicality, security, and robustness of the suggested encryption system earlier this year [32] by developing GI public key cryptography. In 2019, [30] Dawei et al. revealed double-layer GI optical information encryption and improved security.

We apply RSA and steganography techniques to encrypt GI data [33, 34]. In RSA encryption, public and private keys are used to exchange data. The one-way function is used in these techniques. The American Standard Code for Information Interchange (ASCII) is used to convert data into binary images. Three steps and two layers comprise the encryption process. In steganography, the cover image conceals the picture’s contents in one of two ways: either it is chosen at random or from the SCGI. The suggested methods quickly and securely encrypt data, paving the way for SCGI applications in steganography and cryptography [35].

We compute the normalized root mean square (NRMS) for various eavesdropping percentages in order to assess the robustness of the encrypted ghost image. The amount of the error for an unauthorized user who has learned some of the secret key’s components through eavesdropping is provided by NRMS [12]. To quantify the link between two variables, statistical analysis tools like the correlation coefficient (CC) are used. This characteristic shows how the suggested encryption technique is strongly resistant to statistical attacks [41]. The most used metric for assessing the resistance of picture encryption methods and ciphers to differential assaults is the number of pixel change rate (NPCR) [37]. The encryption’s resistance to various attacks is calculated using NPCR, NRMS, and CC under different eavesdropping percentages for simulation and experimentation. In addition, the PSNR evaluates the quality of two images. A higher PSNR value provides a higher image quality [39].

2 Proposed methods

In this section, first, a full introduction to the SCGI theory and its application to the encryption process is given. The RSA cryptography method is exclusive, followed by steganography.

2.1 SCGI theory

By manipulating the illuminating random patterns, SCGI [18] creates a row or column of bright pixels that stand out against the intensity of the background. A bucket detector monitors the amount of light that is transmitted or reflected after the beam strikes the target. The light line sweeps the entirely random pattern in each image by moving to the next line. The sum of the rows and columns, therefore, defines the overall number of shots. For instance, $m+n$ shots would be necessary to sweep an $m\times n$ matrix. The reference beam intensity profiles are designated S_r for row (vertical) scanning and S_c for column (horizontal) scanning in each sample. The horizontal and vertical sweeping images are obtained individually as G_r and G_c matrices through the correlation between the bucket detector intensities and random patterns (intensity profile) as [15, 36] in Eq. 1. G_r and G_c are produced by row and column random patterns that are called Sr and S_c, respectively.

$\mathit{G}\left(\mathit{x},\mathit{y}\right)=\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum _{\mathit{n}=\mathbf{1}}^{\mathit{N}}}\left({\mathit{B}}_{\mathit{n}}-〈\mathit{B}〉\right)\mathit{S}\left(\mathit{x},\mathit{y}\right)=〈\mathit{B}\mathit{S}\left(\mathit{x},\mathit{y}\right)〉-〈\mathit{B}〉〈\mathit{S}\left(\mathit{x},\mathit{y}\right)〉.(1)$

$B$ stands for the intensities measured by the bucket detector, and $〈.〉$ is the ensemble average. $S\left(x,y\right)$ stands for the intensity profile of the input field, and $n$ is the number of shots. $B$ (bucket detector intensity) is calculated by the following equation:

${\mathit{B}}_{\mathit{n}}={\displaystyle \int }\mathit{d}\mathit{x}\mathit{d}\mathit{y}{\mathit{S}}_{\mathit{n}}\left(\mathit{x},\mathit{y}\right)\mathit{T}\left(\mathit{x},\mathit{y}\right),(2)$

where $T\left(x,y\right)$ is the object function.

In addition, G_c1 and G_r1 are defined considering a row from G_c and a column from G_r [18]; indeed, G_r1 and G_c1 are row and column matrices, respectively, and a and b are arbitrary row and column numbers from G_r and G_c, respectively:

${\mathit{G}}_{\mathit{r}\mathbf{1}}\left(\mathbf{1},\mathit{j}\right)={\mathit{G}}_{\mathit{r}}\left(\mathit{a},\mathit{j}\right),\mathit{a}=\mathit{a}\mathit{r}\mathit{b}\mathit{i}\mathit{t}\mathit{a}\mathit{r}\mathit{y}\mathit{r}\mathit{o}\mathit{w}\mathit{f}\mathit{r}\mathit{o}\mathit{m}\mathbf{1}\mathit{t}\mathit{o}\mathit{m},\mathit{j}=\mathbf{1}:\mathit{n}.(3)$

${\mathit{G}}_{\mathit{c}\mathbf{1}}\left(\mathit{i},\mathbf{1}\right)={\mathit{G}}_{\mathit{c}}\left(\mathit{i},\mathit{b}\right),\mathit{b}=\mathit{a}\mathit{r}\mathit{b}\mathit{i}\mathit{t}\mathit{a}\mathit{r}\mathit{y}\mathit{c}\mathit{o}\mathit{l}\mathit{u}\mathit{m}\mathit{n}\mathit{f}\mathit{r}\mathit{o}\mathit{m}\mathbf{1}\mathit{t}\mathit{o}\mathit{n},\mathit{i}=\mathbf{1}:\mathit{m}.(4)$

The final gray image G_final was reconstructed by the cross-product of G_c1 to G_r1; in fact, the size of G_final is equal to $m\times n$:

${\mathit{G}}_{\mathit{f}\mathit{i}\mathit{n}\mathit{a}\mathit{l}}\left(\mathit{m},\mathit{n}\right)={\mathit{G}}_{\mathit{c}}\left(\mathit{m},\mathbf{1}\right)\times {\mathit{G}}_{\mathit{r}}\left(\mathbf{1},\mathit{n}\right).(5)$

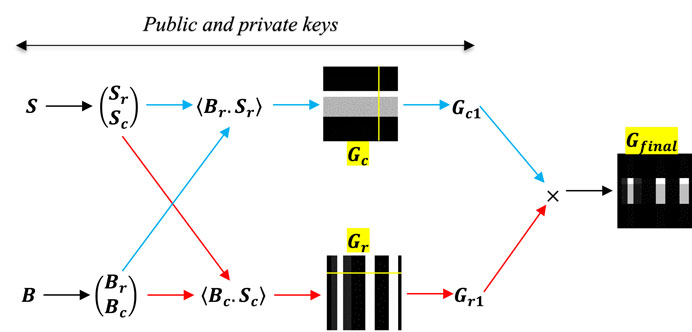
SCGI can be applied to both horizontal and vertical images. The SCGI system is shown in Figure 1 as random sweeping patterns $\left(64\times 64\right)$. The target (two slits) is projected with random patterns $\left(64\times 64\right)$, and the detector measures the transmitted intensities (Eq. 2). Combining the intensities and random patterns in Eq. 1 results in images. Random patterns are distinct from earlier GI methods in this regard. The matrix that follows shows erratic patterns in Eq. 6. Vertical and horizontal lines have high intensities, like 10, whereas backgrounds ($R$) have random values between 0 and 1 that are produced by a computer.

${\left[\begin{array}{ccc}10& \begin{array}{ccc}R& \dots & R\end{array}& R\\ \begin{array}{c}10\\ ⋮\\ 10\end{array}& \begin{array}{c}\begin{array}{ccc}R& \dots & R\end{array}\\ \begin{array}{ccc}⋮& \ddots & ⋮\end{array}\\ \begin{array}{ccc}R& \dots & R\end{array}\end{array}& \begin{array}{c}R\\ ⋮\\ R\end{array}\\ 10& \begin{array}{ccc}R& \dots & R\end{array}& R\end{array}\right]}_{64\times 64}{\left[\begin{array}{ccc}10& \begin{array}{ccc}10& \dots & 10\end{array}& 10\\ \begin{array}{c}R\\ ⋮\\ R\end{array}& \begin{array}{c}\begin{array}{ccc}R& \dots & R\end{array}\\ \begin{array}{ccc}⋮& \ddots & ⋮\end{array}\\ \begin{array}{ccc}R& \dots & R\end{array}\end{array}& \begin{array}{c}R\\ ⋮\\ R\end{array}\\ R& \begin{array}{ccc}R& \dots & R\end{array}& R\end{array}\right]}_{64\times 64}.(6)$

FIGURE 1

FIGURE 1. Encryption general diagram based on SCGI and row and column sweeping.

According to Eqs 3, 4, the line shifts one pixel either vertically or horizontally in each frame. The most possible number of imaging shots is 128; 64 for reconstructed images created using a row sweep and 64 using a column sweep. In addition, the final image is produced by Eq. 5.

The data were encrypted by SCGI using steganographic and cryptographic techniques. The asymmetric and steganography systems are displayed in Figures 1, 2. The generic encryption strategy for SCGI shown in Figure 1 uses keys that reflect the random pattern (S) with a bright row (S_r) or column (S_c) and is determined by the public and private key sections. The bucket intensities for the row and column random patterns are B_r and B_c, respectively. The blue and red arrows indicate the two-row and -column stages of the SCGI method, respectively. The red path produces a picture via column sweeping (G_r), as opposed to the blue path’s image delivered by row sweeping (G_c). Yellow lines show G_c1 and G_r1 (Eqs 3, 4) and G_final reconstructed by the cross-product G_c1 and G_r1. The public and private keys for SCGI encryption can be either random patterns (S_r and S_c) or bucket intensities (B_r and B_c).

FIGURE 2

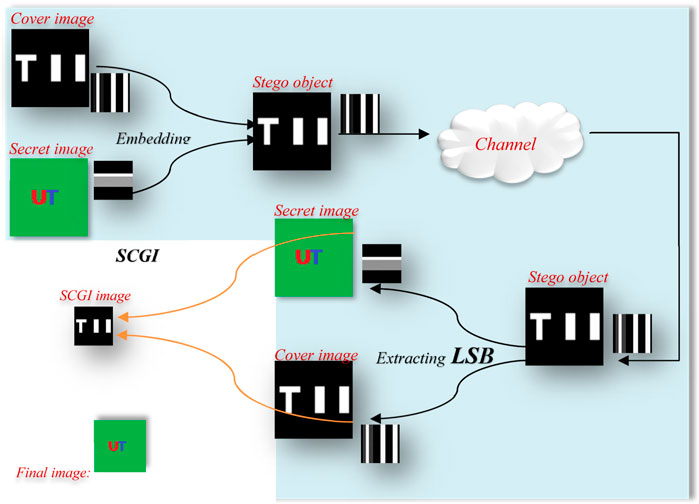
FIGURE 2. Depicts the first (large pictures) and second (small pictures) steganography technique in SCGI which $G_r$ and $G_c$ choose the cover image and secret image, respectively (small pictures). An LSB is embedded in the process that makes the stego image, which is then sent to the receiver for decryption, the LSB apply on the stego object. In addition, a secret image is detected by it, and both images need to reconstruct the SCGI image in SCGI by a cross operator in Eq. 5.

2.2 Steganography process

Steganography is a technique for concealing text such that only the sender and recipient may see it in any digital medium, including images, videos, and audio [25]. Two messages (pictures), one to serve as the cover and the other as the disguised image, are needed, as shown in Figure 2. The least significant bit (LSB) method, which is the quickest technique to covertly implant information, is a steganography key. This fundamental LSB embedding technique is easy to compute and can incorporate a large amount of data without compromising the quality. Figure 2 illustrates the specifics of the used strategy:

Both binary and colored images were used for steganography (Figure 2). For large photos, an SCGI image is selected as the cover, and a simple LSB-inserted hidden image is added to the cover. The LSB, which is located on the rightmost byte, has little bearing on the values of the other seven bits. Therefore, the LSB hinges on swapping the final bits of the cover picture’s pixels with those in the secret image without the cover image noticeably changing. As a result, the final image was created using the LSB, the cover, and concealed photographs. The intended receiver is then contacted by SCGI. When dealing with large photographs, the hidden image can be extracted from the stego image by using LSB. After LSB image extraction and subsequent SCGI application on two photos (small pictures in Figure 4), the cover and concealed images are rebuilt for tiny pictures using column sweep (G_r) and row sweep (G_c), and the final image reconstruction takes place in a binary scenario.

Steps of steganography:

➢ Select a cover image from SCGI images

➢ Choose secret data (binary/gray/color image)

➢ Divide the color image in RGB

➢ Embed LSB as a stego key

➢ Produce a stego image and send to the receiver by channel

➢ Receive the stego image by the user

➢ Apply the LSB to the stego image

➢ Merge color images (large case)

➢ Find the secret image and cover image separately (small case)

➢ Apply Equation 5 to find the SCGI image (small case)

2.3 RSA cryptography process

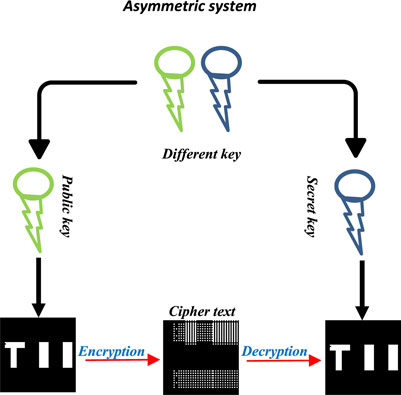
The cryptography method is shown in Figure 3, which is an asymmetric algorithm with both public and secret keys (such as RSA). All users are visible to the general public, but only the sender and recipient have access to the secret keys. This research uses this kind of cryptography.

FIGURE 3

FIGURE 3. Asymmetric cryptography framework by two different keys.

The process of converting a message from a readable form at the transmitter end to an incomprehensible form at the recipient end is known as cryptography, and it is used in bucket detector intensity. Symmetric and asymmetric systems are two subcategories that can be distinguished. Public and private keys (both the sender and the recipient have access to the latter) are the foundation of asymmetric encryption [23, 24]. The American Standard Code for Information Interchange (ASCII) is used in both the encryption and decryption processes.

To rebuild the final image in SCGI, the bucket detector channel must correspond with its random matrices. The bucket values supplied to the intended user are in the form of a $t\times t$ random matrix (T) generated using the RSA technique. The maximum ASCII values are represented by the size of $t$, which means that the size of $t$ should be bigger than row and column values. Here, $t$ equals 40,000, and matrix (T) equals $40,000\times 40,000$.

The mechanism behind the RSA algorithm that shows us public and private keys:

➢ Select two prime numbers P and Q

➢ Calculate n = P * Q

➢ Need $\mathrm{\Phi }\left(n\right)$ = (P-1) * (Q-1)

➢ And select e that must be

  • An integer

• Not be a factor of n

• And $1<e<\mathrm{\Phi }\left(n\right)$

➢ Calculate d that d*e = 1 mod $\mathrm{\Phi }\left(n\right)$

3 Results and discussions

In this work, three parameters for evaluating the encryption of images were developed: NPCR, Eq. 8 NRMS, Eq. 9 and correlation coefficient (CC), Eq. 10 and PSNR Eq. 13 was chosen to investigate the image quality. For quantitative comparisons and to measure the encryption level under different eavesdropping settings, the number of pixel change rate (NPCR) was determined as follows [37]:

$\mathit{D}\left(\mathit{i},\mathit{j}\right)=\left\{\begin{array}{c}\mathbf{0},\mathit{i}\mathit{f}{\mathit{C}}^{\mathbf{1}}\left(\mathit{i},\mathit{j}\right)={\mathit{C}}^{\mathbf{2}}\left(\mathit{i},\mathit{j}\right)\\ \mathbf{1},\mathit{i}\mathit{f}{\mathit{C}}^{\mathbf{1}}\left(\mathit{i},\mathit{j}\right)\ne {\mathit{C}}^{\mathbf{2}}\left(\mathit{i},\mathit{j}\right)\end{array}\right.,(7)$

$\mathbf{N}\mathbf{P}\mathbf{C}\mathbf{R}:\mathit{N}\left({\mathit{C}}^{\mathbf{1}},{\mathit{C}}^{\mathbf{2}}\right)={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{m}}}{\displaystyle \sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}}\frac{\mathit{D}\left(\mathit{i},\mathit{j}\right)}{\mathit{T}}\times \mathbf{100},(8)$

where $C^1$ and $C^2$ indicate the ciphertext before and after pixel modification in the original image Eq. 7. D is a 2D array of pixel numbers in the ciphertext. The NPCR gives the absolute values of pixels that survive various assaults, ranging from 0 to 1. The encryption system’s lowest and highest degrees of security are represented by NPCR = 0 and NPCR = 1, respectively [31]. In this study, $C^1\left(i,j\right)$ and $C^2\left(i,j\right)$ are encrypted and non-encrypted pictures, respectively. The normalized root mean square (NRMS) is also calculated to evaluate the robustness of the encrypted ghost imaging under eavesdropping [12]:

$\mathbf{N}\mathbf{R}\mathbf{M}\mathbf{S}=\frac{\sqrt{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\displaystyle {\sum }_{\mathit{j}=\mathbf{1}}^{\mathit{n}}}{\left|{\mathit{I}}_{\mathit{d}}\left(\mathit{i},\mathit{j}\right)-{\mathit{I}}_{\mathbf{0}}\left(\mathit{i},\mathit{j}\right)\right|}^{\mathbf{2}}}}{\sqrt{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\displaystyle {\sum }_{\mathit{j}=\mathbf{1}}^{\mathit{n}}}{\left|{\mathit{I}}_{\mathbf{0}}\left(\mathit{i},\mathit{j}\right)\right|}^{\mathbf{2}}}},(9)$

where $I_d$ and $I_o$ are the intensities of the decrypted and original images, respectively. For more assessments, NRMS is computed for gray and binary images at both simulation and experimentation.

The correlation coefficient (CC) is used to measure the relation between two variables. In cryptography, they are plaintext and its encryption (ciphertext). This factor demonstrates resistance against attacks. The CC is measured by the following equation [41]:

$\mathbf{\text{CC}}\left(\mathbf{x},\mathbf{y}\right)=\frac{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}}\left({\mathit{x}}_{\mathit{i}}-\mathit{\mu }\left(\mathit{x}\right)\right)\left({\mathit{y}}_{\mathit{i}}-\mathit{\mu }\left(\mathit{y}\right)\right)}{\mathit{\sigma }\left(\mathit{x}\right)\mathit{\sigma }\left(\mathit{y}\right)},(10)$

where x and y are variables of the plaintext and ciphertext. $\mu \left(x\right)$ and $\mu \left(y\right)$ Eq. 11 are measured by the following equation:

$\mathbf{\mu }\left(\mathit{x}\right)=\frac{\mathbf{1}}{\mathit{n}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\mathit{x}}_{\mathit{i}}\mathit{a}\mathit{n}\mathit{d}\mathbf{\mu }\left(\mathit{y}\right)=\frac{\mathbf{1}}{\mathit{n}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\mathit{y}}_{\mathit{i}}.(11)$

In addition, $\sigma \left(x\right)$ and $\sigma \left(y\right)$ Eq. 12 are standard deviations of x and y, respectively:

$\mathbf{\sigma }\left(\mathit{x}\right)=\sqrt{{\left({\mathit{x}}_{\mathit{i}}-\mathit{\mu }\left(\mathit{x}\right)\right)}^{\mathbf{2}}}\mathit{a}\mathit{n}\mathit{d}\mathit{\sigma }\left(\mathit{y}\right)=\sqrt{{\left({\mathit{y}}_{\mathit{i}}-\mathit{\mu }\left(\mathit{y}\right)\right)}^{\mathbf{2}}}.(12)$

It has a value between 1 and –1. If the CC equals 1 and –1, plaintext and ciphertext are identical, indicating weak encryption. If it becomes 0, the plaintext is completely different from the ciphertext, indicating strong encryption.

The PSNR is chosen for evaluating the quality of images in steganography [39]:

$\mathit{P}\mathit{S}\mathit{N}\mathit{R}=\mathbf{10}{\mathbf{log}}_{\mathbf{10}}\left[\frac{{\mathit{MAX}}^{\mathbf{2}}}{\mathit{M}\mathit{S}\mathit{E}}\right],(13)$

$\mathit{M}\mathit{S}\mathit{E}\left(\mathit{f},\mathit{g}\right)=\frac{\mathbf{1}}{\mathit{M}\mathit{N}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{M}}}{\displaystyle \sum _{\mathit{j}=\mathbf{1}}^{\mathit{N}}}{\left({\mathit{f}}_{\mathit{i},\mathit{j}}-{\mathit{g}}_{\mathit{i},\mathit{j}}\right)}^{\mathbf{2}},(14)$

where $M$ and $N$ are pixel size, $\mathit{MAX}$ is the maximal in the image data, and MSE stands for the mean squared error between two images that include $f$ and $g$ Eq. 14.

We used two binary and grayscale objects for imaging in SCGI, and both of them are “TII.” Figure 4 shows two binary and grayscale images detected using the SCGI method, with columns denoting the original image, row sweeping, column sweeping, final image, and intensity of the 30th line of final reconstructed images, in that order. The random patterns show the primary difference between GI and SCGI. The brightest cells in the GI have fluctuating intensities, but the SCGI has stable values.

FIGURE 4

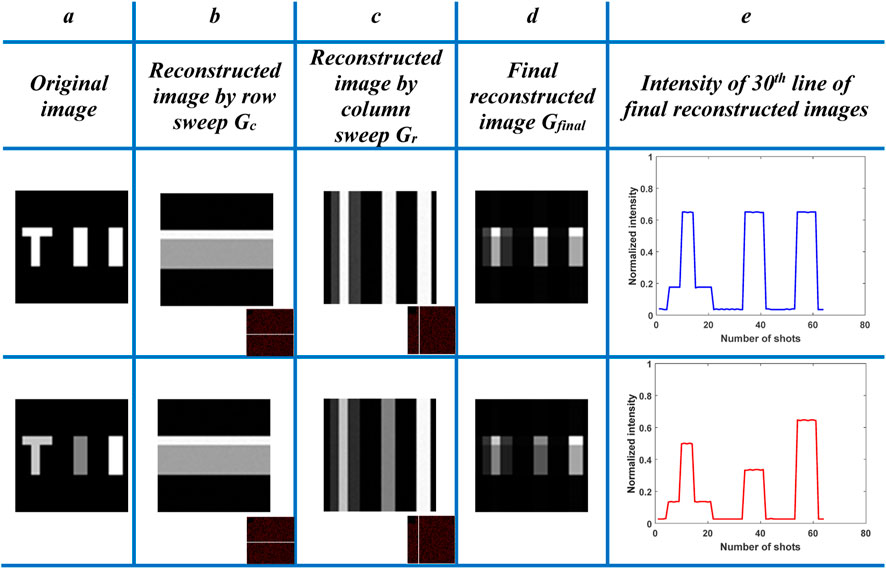
FIGURE 4. Reconstructed images based on grayscale and binary images. (A) Original image. (B) Image by using row sweeping G_c (corner image). (C) Image by using column sweeping G_r (corner image). (D) Final GI G_final. (E) Intensity of the 30th line of final reconstructed images for detection of binary and grayscale images.

In the experiment, we built up SCGI setup by Figure 5. A projector (SONY VPL-DX120) with a resolution of 1024 × 768 is available to apply sweeping random patterns (S_r and S_c) that are produced by a computer to the object ($T\left(x,y\right)$) (double slits). The transmitted intensity is collected by the lens on the CMOS detector with $146\times 176$ pixels, and $B$ is measured by using a detector. Then, the image of the object is recreated using equations 1 to 5.

FIGURE 5

FIGURE 5. Figure of the computational ghost imaging setup by sweeping random patterns.

In the initial phase of the steganography process, the final and SCGI images are covered and buried $64\times 64$ images (Figure 6i). Because of the limits of SCGI in reproducing the whole picture, using this approach only allows the transmission of one image (including color images). As illustrated in Figure 6ii, in the second phase of steganography, G_r chose G_c as the cover and G_c as the concealed image. The LSB code is then incorporated in the hidden image of the cover image for concealment. The receiver receives the stego image, extracts the LSB, and searches for the concealed image. The final image is inserted using the SCGI approach. The PSNR parameter assesses the quality of the recovered image as well as the secret image.

FIGURE 6

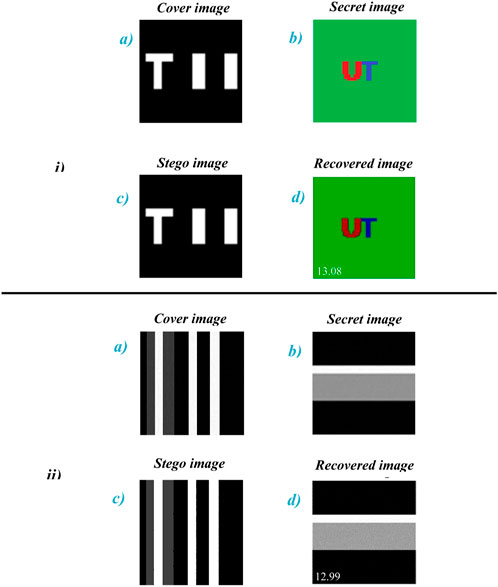
FIGURE 6. Results of steganography and PSNR. (i) First stage for color images, and (ii) second stage for grayscale images. Numbers indicates PSNR values. (A) cover image. (B) secret image. (C) stego image. (D) recovered image.

In the first stage, the cover image is picked from SCGI and then at random in the second stage, with both G_c and G_r hidden in the adoptive image. As shown in Figure 6, the steganography system results show that the concealed image is totally hidden within the cover image and is never visible. PSNR values for color and grayscale image steganography are 13.08 and 12.99, respectively.

Next, asymmetric SCGI-based encryption was carried out. As a result, P and Q are chosen using the Agrawal–Kayal–Saxena algorithm [40], a decision-making process for primality testing, such that they are 37 and 19, respectively. $\left(e,n\right)$ and $\left(d,n\right)$ are the respective public and private keys, and $n$ is equal to 703. Therefore, $\mathrm{\Phi }\left(\mathrm{n}\right)$ becomes 648 and e is selected as 17 and $d$ is calculated based on the relation that is 305. The encrypted message is $m$. The sender calculates public key as $\mathit{c}\equiv {\mathit{m}}^{\mathit{e}}\mathit{mod}\left(\mathit{n}\right)$, and the receiver acquires messages by private key $\mathit{m}\equiv {\mathit{c}}^{\mathit{d}}\mathit{mod}\left(\mathit{n}\right)$, which are 330350288 and 123, respectively.

Here, value ($\left.c\right)$ determine the row/column of the T matrix in such a way that odd digits of c select for row (30528) and even for column (3308). The size of T should be bigger than the maximum values of rows and columns, and we chose 40,000 for the T matrix. Hence, $c$ is located in (30528, 3308) in the T matrix.

In the RSA process, data are encrypted in two layers. The first layer is a one-way function, and the other is carried out by getting values in the T matrix.

Asymmetric systems are used to demonstrate an applied encryption diagram in Figure 3. In the first method, row and column data of the reconstructed image are encrypted together $\left(G_k\right)$, and the second $\left(G_{r}and{G}_c\right)$ and third $\left(G_{r}or{G}_c\right)$ methods are performed one-by-one. Since the first case only has one stage and the second and third cases each have two stages, an attacker would need to have two times the data from the first case to decrypt the second and third cases. The RSA procedure is used to accomplish encryption on this matrix after that. The modeling findings based on the RSA algorithm are shown in Figures 7, 12.

FIGURE 7

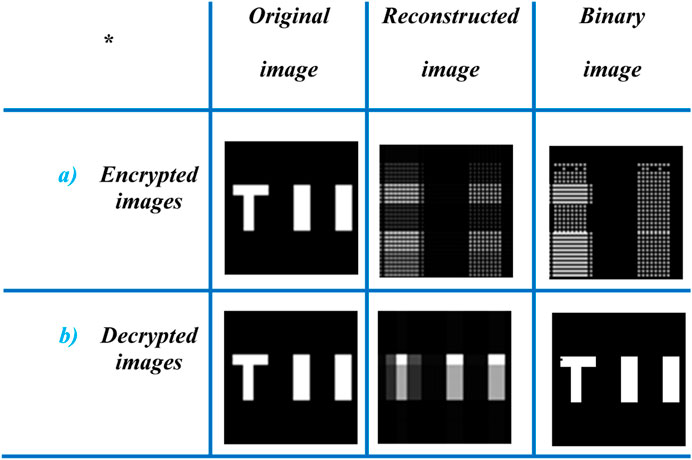
FIGURE 7. Simulation results with the asymmetric encryption system. (A) Encrypted by RSA and (B) decrypted images.

In modeling, in Figure 7, for the “TII” object, the third column shows a rebuilt image in its encrypted and decrypted states, while the fourth column shows the image’s binary reconstruction, which recovers a high-contrast binary image by applying a post-processing method to a grayscale image that has been reconstructed. The binary function threshold is set to the lowest intensity in the grayscale image, and intensity values above and below this threshold are set to 1 and 0, respectively, to carry out the process.

In addition, NPCR results for the encrypted image versus eavesdropping percentage are depicted in Figure 8 for a) G_k, b) G_c and G_r, and c) G_r or G_c. The NPCR shows the difference between pixel values in the original and encrypted images displayed in Figure 11. The difference between the original and encrypted images is 0.7 and 0.6 after 100% of the original image’s information has been revealed, demonstrating that the NPCR in case b is higher than that in other cases, whereas in cases a and c, it becomes 0, indicating that the attacker has fully realized the information.

FIGURE 8

FIGURE 8. NPCR of the simulation results by encryption variables: (A) G_k, (B) G_r and G_c, and (C) G_r or G_c.

In Figures 9, 10, the NRMS is calculated for binary and grayscale encryption images, respectively. In example b, NRMS has the greatest number, which means the robustness of case b against the attacker is 0.6 and 0.7 after 100% eavesdropping; however, in the others, it is 0.

FIGURE 9

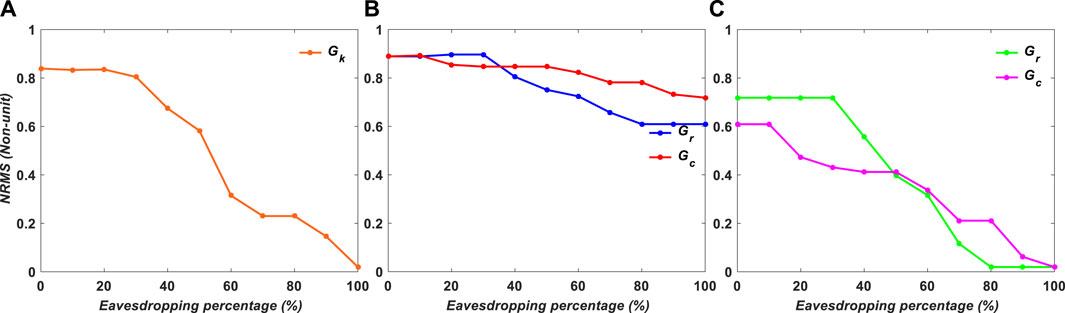
FIGURE 9. NRMS of simulation results for binary images versus encryption variables: (A) G_k, (B) G_r and G_c, and (C) G_r or G_c.

FIGURE 10

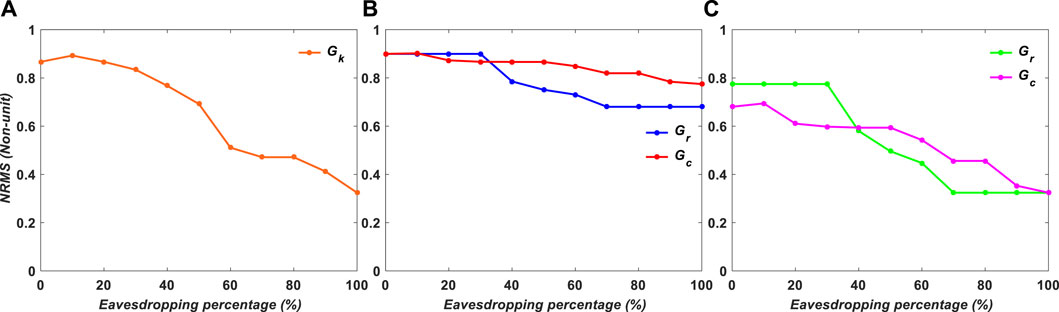
FIGURE 10. NRMS of simulation results for grayscale images versus encryption variables: (A) G_k, (B) G_r and G_c, and (C) G_r or G_c.

Figure 11 depicts decrypted binary and grayscale images in the simulation case for three encryption scenarios, with eavesdropping percentages ranging from 0% to 100%. The first two examples show the image in its entirety, but the third example never does. The attacker was unable to find crucial data to decode as a result.

FIGURE 11

FIGURE 11. Decrypted binary and grayscale images in the simulation case from 0 to 100 percentage of eavesdropping in G_k, G_r or G_c, and G_r and G_c.

The CC is determined for eavesdropping 0% and 100% for three scenarios and binary and grayscale images in the Table 1 to assess resistance against the attacker. It demonstrates that even after complete eavesdropping, G_r and G_c have a great resistance to attackers.

TABLE 1

TABLE 1. Correlation coefficient for the decrypted image in the simulation case.

In the experiment, double slits (II) is selected as the object ($\left.64\times 64\right)$. It is encrypted by the RSA method. Figure 12 demonstrates the encrypted and decrypted images for G_k.

FIGURE 12

FIGURE 12. Experimental results obtained with the asymmetric system [18]. (A) Encrypted by the RSA algorithm and (B) decrypted images.

The results of the experiment are displayed in Figures 13–15. The poor NPCR in Figure 13 results in higher eavesdropping percentages, as can be observed in cases a and c; however, in case b, even if all data were destroyed, an attacker would not be able to access information, as can be shown in case b, which shows stable protection from 0% to 100% eavesdropping with 0.96.

FIGURE 13

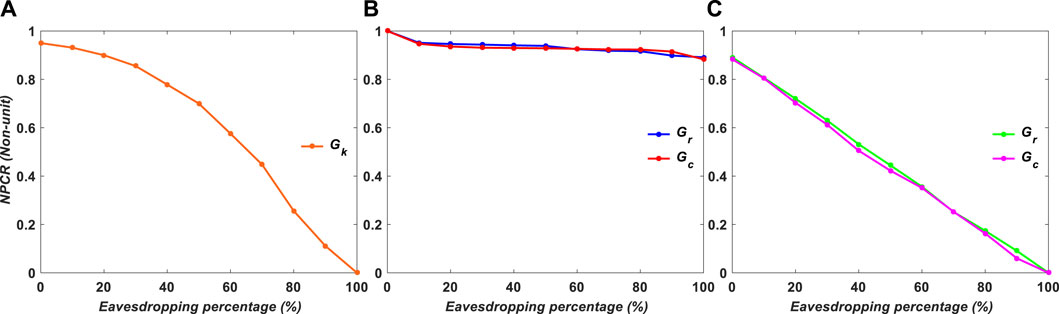
FIGURE 13. NPCR of experimental results versus encryption variables: (A) G_k, (B) Gr and G_c, and (C) G_r or G_c.

FIGURE 14

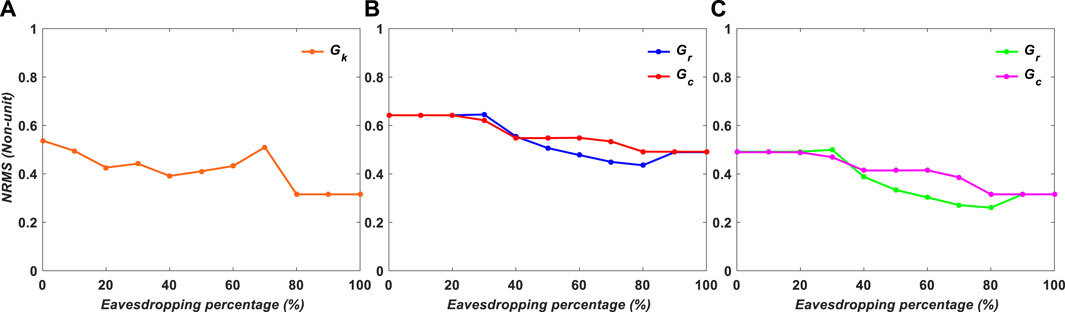
FIGURE 14. NRMS of experimental results for binary images versus encryption variables: (A) G_k, (B) G_r and G_c, and (C) G_r or G_c.

FIGURE 15

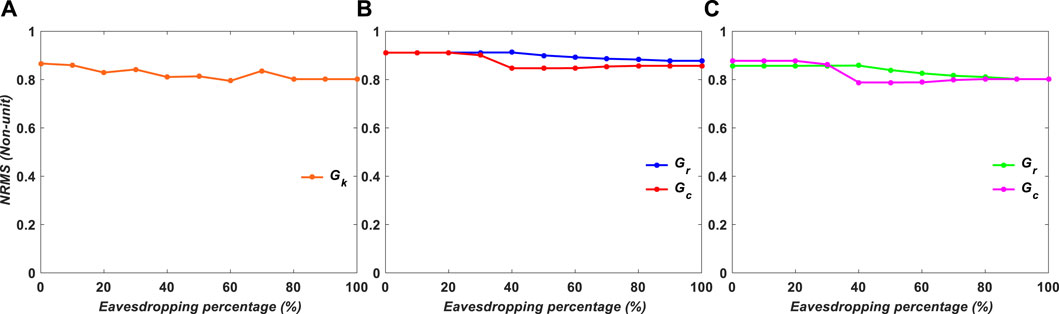
FIGURE 15. NRMS of experimental results for grayscale images versus encryption variables: (A) G_k, (B) G_r and G_c, and (C) G_r or G_c.

Figures 14, 15 show the NRMS values for the experimental results in binary and grayscale imaging instances, respectively. The location of the values and the one-way function must be known to the attacker in order to decode the data. Data security is low in situation a, where an attacker may find large volumes of data with ease; moderate in case c; and high in case b.

Figure 16 exhibits decrypted images, which, for three various eavesdropping techniques, range from 0% to 100%, from the first to the last row, and they are shown for experimental conditions. The results demonstrate that the G_r and G_c approaches are more secure than the others since and that even in a 100% eavesdropping scenario, an attacker was unable to obtain information about the original image. The results are compared to past data in the literature [11, 12, 23, 38] to validate that increased security, speed, and reduced data packing were accomplished under the same eavesdropping percentages. Our results had almost the same security as those from our prior investigation in [11], with the exception that they were realized with fewer shot counts in the current investigation. NRMS in the eavesdropping 30% in [11] is 0.25, but it is 0.95 in the present study in the best case. The NRMS in [12] with a 70% loss is 0.11; however, in our analysis, it is roughly constant at 0.95, indicating that an attacker can only retrieve 15% of the data after a 70% loss. In conclusion, the G_r and G_c methods of the RSA algorithm, which separately encrypt the row/column data of the rebuilt images, have the highest security with NPCR and NRMS values.

FIGURE 16

FIGURE 16. Decrypted binary and grayscale images in the experimental case from 0 to 100 percentage of eavesdropping in G_k, G_r or G_c, and G_r and G_c.

Table 2 indicates that for three instances, binary and grayscale images in the experimental genres, the CC for eavesdropping is between 0 and 100 percent. G_r and G_c scenarios have strong resistance against attackers due to their values of 0.3335 and 0.3443 for 100% eavesdropping, respectively.

TABLE 2

TABLE 2. Correlation coefficient for the decrypted image in the experimental case.

The speed for SCGI, GI, DCSGI [42], and CGISR [43] is shown in Table 3. It can be seen that the SCGI speed is 3.3 times GI in the same quality. Visibility is a quality parameter for evaluating images. Zhang et al. [42] used 4,500 measurements in DCSGI to reconstruct a picture with $110\times 136pixels$; our method is approximately 18 times faster for an image of this size. Furthermore, Sui et al. demonstrated encryption using computational ghost imaging with sparse reconstruction (CGISR) [43], with results shown in Table 3. By comparison, our method’s CC and PSNR scores outperform that of CGISR. In addition, Zhao et al.’s [44] work on encryption orbital angular momentum by ghost imaging (OAMGI) demonstrated that the maximum PSNR is almost 15 for results with 4,000 shots.

TABLE 3

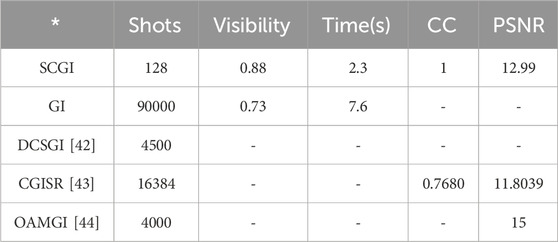
TABLE 3. Comparison between SCGI and other methods considering the shots, visibility, time, CC, and PSNR.

4 Conclusion

We introduce SCGI and encryption methods which require fewer shot numbers to deliver high security. Faster image capturing and smaller data package sizes are made possible by this advantage. In SCGI, the final image is reconstructed by row and column sweeping of binary and grayscale images. Steganography and RSA cryptography technologies with SCGI have been used for data encryption and transferring. For evaluating the encryption security level, NPCR, NRMS, and CC parameters were measured and PSNR was used for assessing the quality of images. In the steganography system, secret binary and color images were concealed in the cover image that was reconstructed by SCGI by using the LSB. PSNR values demonstrate that the initial and final images have the best quality, and they could not be distinguished from each other; furthermore, secret images were concealed in the SCGI images and finally reconstructed by the SCGI equation. In the cryptography process, public and private keys in the RSA method were described using a one-way function. The RSA technique is applied to the bucket detector (or reconstructed images by column and row sweeping in the SCGI) which is produced by SCGI. SCGI has two series of bucket detector values, and we can divide encryption into three items. Three sub-items (G_r and G_c, G_r or G_c, and G_k) based on reconstructed images by column and row sweeping in the SCGI consisted of our cryptography approach. Therefore, NPCR and CC evaluating parameters prove that one item (G_r and G_c) has strong security with increasing eavesdropping percentage and NRMS shows that it has strong robustness than other sub-items because of durable values. The introduced approach only needs a small number of shots to reconstruct an image, for data processing, and imaging, which boosts imaging speed compared to that in the previous studies, resulting in smaller data packages and faster communications. These advantages suggest the widespread application of sweeping ghost imaging encryption among data security technologies. We believe that cryptography and steganography encryption by SCGI can provide a new perspective on information security. The encryption of 3D color images will be our next study outlined by this new method.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

SR-G: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, and writing–original draft. BO: writing–original draft and writing–review and editing. RK: conceptualization, data curation, supervision, validation, and writing–review and editing. SA-K: conceptualization, data curation, formal analysis, investigation, supervision, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Erkmen BI, Shapiro JH. Ghost imaging: from quantum to classical to computational. Adv Opt Photon (2010) 2(4):405–50. doi:10.1364/AOP.2.000405

CrossRef Full Text | Google Scholar

2. Ghaleh SR, Ahmadi-Kandjani S, Kheradmand R, Olyaeefar B. Improved edge detection in computational ghost imaging by introducing orbital angular momentum. Appl Opt (2018) 57(32):9609–14. doi:10.1364/AO.57.009609

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ryczkowski P, Barbier M, Friberg AT, Dudley JM, Genty G. Ghost imaging in the time domain. Nat Photon (2016) 10(3):167–70. doi:10.1038/nphoton.2015.274

CrossRef Full Text | Google Scholar

4. Khakimov RI, Henson BM, Shin DK, Hodgman SS, Dall RG, Baldwin KG, et al. Ghost imaging with atoms. Nature (2016) 540(7631):100–3. doi:10.1038/nature20154

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Sun B, Edgar MP, Bowman R, Vittert LE, Welsh S, Bowman A, et al. 3d computational ghost imaging. In: 2014 IEEE Photonics conference (2014). p. 174–5. doi:10.1364/CQO.2013.W1.1

CrossRef Full Text | Google Scholar

6. Klein Y, Schori A, Dolbnya IP, Sawhney K, Shwartz S. X-ray computational ghost imaging with single-pixel detector. Opt express (2019) 27(3):3284–93. doi:10.1364/OE.27.003284

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Pelliccia D, Olbinado MP, Rack A, Kingston AM, Myers GR, Paganin DM. Towards a practical implementation of X-ray ghost imaging with synchrotron light. IUCrJ (2018) 5(4):428–38. doi:10.1107/S205225251800711X

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Qiu X, Zhang D, Zhang W, Chen L. Structured-pump-enabled quantum pattern recognition. Phys Rev Lett (2019) 122(12):123901. doi:10.1103/PhysRevLett.122.123901

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhao S, Yang H, Li Y, Cao F, Sheng Y, Cheng W, et al. The influence of atmospheric turbulence on holographic ghost imaging using orbital angular momentum entanglement: simulation and experimental studies. Opt Commun (2013) 294:223–8. doi:10.1016/j.optcom.2012.12.027

CrossRef Full Text | Google Scholar

10. Erkmen BI. Computational ghost imaging for remote sensing. JOSA A (2012) 29(5):782–9. doi:10.1364/JOSAA.29.000782

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zafari M, Ahmadi-Kandjani S. Optical encryption with selective computational ghost imaging. J Opt (2014) 16(10):105405. doi:10.1088/2040-8978/16/10/105405

CrossRef Full Text | Google Scholar

12. Tanha M, Kheradmand R, Ahmadi-Kandjani S. Gray-scale and color optical encryption based on computational ghost imaging. Appl Phys Lett (2012) 101(10):101. doi:10.1063/1.4748875

CrossRef Full Text | Google Scholar

13. Pittman TB, Shih YH, Strekalov DV, Sergienko AV. Optical imaging by means of two-photon quantum entanglement. Phys Rev A (1995) 52(5):R3429–32. doi:10.1103/PhysRevA.52.R3429

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bennink RS, Bentley SJ, Boyd RW. “Two-photon” coincidence imaging with a classical source. Phys Rev Lett (2002) 89(11):113601. doi:10.1103/PhysRevLett.89.113601

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Shapiro JH. Computational ghost imaging. Phys Rev A (2008) 78(6):061802. doi:10.1103/PhysRevA.78.061802

CrossRef Full Text | Google Scholar

16. Frumker E, Silberberg Y. Femtosecond pulse shaping using a two-dimensional liquid-crystal spatial light modulator. Opt Lett (2007) 32(11):1384–6. doi:10.1364/OL.32.001384

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wang Y, Liu Y, Suo J, Situ G, Qiao C, Dai Q. High speed computational ghost imaging via spatial sweeping. Sci Reports (2017) 7(45325):45325. doi:10.1038/srep45325

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Rajabi-Ghaleh S, Olyaeefar B, Kheradmand R, Ahmadi-Kandjani S. Ultra-fast vivid computational ghost imaging of still and moving objects by sweeping random patterns. J Opt (2020) 22(9):095701. doi:10.1088/2040-8986/aba03d

CrossRef Full Text | Google Scholar

19. Li X, Deng C, Chen M, Gong W, Han S. Ghost imaging for an axially moving target with an unknown constant speed. Photon Res (2015) 3(4):153–7. doi:10.1364/PRJ.3.000153

CrossRef Full Text | Google Scholar

20. Gholami-milani S, Olyaeefar B, Ahmadi-kandjani S, Kheradmand R. Grayscale and color ghost-imaging of moving objects by memory-enabled, memoryless and compressive sensing algorithms. J Opt (2019) 21(8):085709. doi:10.1088/2040-8986/ab3063

CrossRef Full Text | Google Scholar

21. Lian S. Multimedia content encryption: techniques and applications. (New York, United States: CRC Press) (2008).

Google Scholar

22. Goldreich O. Foundations of cryptography, volume 2, basic applications. (United Kingdom: Cambridge University Press) (2009).

Google Scholar

23. Mahajan P, Sachdeva A. A study of encryption algorithms AES, DES and RSA for security. Glob J Comp Sci Tech (2013).

Google Scholar

24. Zhou X, Tang X. August. Research and implementation of RSA algorithm for encryption and decryption. In: Proceedings of 2011 6th international forum on strategic technology. IEEE (2011). p. 1118–21.

Google Scholar

25. Cox I, Miller M, Bloom J, Fridrich J, Kalker T. Digital watermarking and steganography. United States: Morgan Kaufmann (2007).

Google Scholar

26. Clemente P, Durán V, Tajahuerce E, Lancis J. Optical encryption based on computational ghost imaging. Opt Lett (2010) 35(14):2391–3. doi:10.1364/OL.35.002391

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kong LJ, Li Y, Qian SX, Li SM, Tu C, Wang HT. Encryption of ghost imaging. Phys Rev A (2013) 88(1):013852. doi:10.1103/PhysRevA.88.013852

CrossRef Full Text | Google Scholar

28. Sun M, Shi J, Li H, Zeng G. A simple optical encryption based on shape merging technique in periodic diffraction correlation imaging. Opt Express (2013) 21(16):19395–400. doi:10.1364/OE.21.019395

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yang Z, Yuan S, Li J, Bai X, Yu Z, Zhou X. An encryption method based on computational ghost imaging with chaotic mapping and DNA encoding. J Opt (2022) 24(6):065702. doi:10.1088/2040-8986/ac6597

CrossRef Full Text | Google Scholar

30. Leihong Z, Zhisheng Z, Yi K, Hualong Y, Rui X, Xiao Y, et al. Research on double-layers optical information encryption based on ghost imaging. Opt Commun (2020) 455:124585. doi:10.1016/j.optcom.2019.124585

CrossRef Full Text | Google Scholar

31. Zhao S, Wang L, Liang W, Cheng W, Gong L. High performance optical encryption based on computational ghost imaging with QR code and compressive sensing technique. Opt Commun (2015) 353:90–5. doi:10.1016/j.optcom.2015.04.063

CrossRef Full Text | Google Scholar

32. Yi K, Leihong Z, Dawei Z. Optical encryption based on ghost imaging and public key cryptography. Opt Lasers Eng (2018) 111:58–64. doi:10.1016/j.optlaseng.2018.07.014

CrossRef Full Text | Google Scholar

33. Dubey MK, Ratan R, Verma N, Saxena PK. Cryptanalytic attacks and countermeasures on RSA. In: InProceedings of the third international conference on soft computing for problem solving: SocProS 2013. Springer India (2014). p. 805–19. doi:10.1007/978-81-322-1771-8_70

CrossRef Full Text | Google Scholar

34. Cheddad A, Condell J, Curran K, Mc Kevitt P. Digital image steganography: survey and analysis of current methods. Signal Processing (2010) 90(3):727–52. doi:10.1016/j.sigpro.2009.08.010

CrossRef Full Text | Google Scholar

35. Ratan R, Arvind . Bit-plane specific measures and its applications in analysis of image ciphers. In: Advances in signal processing and intelligent recognition systems: 4th international symposium SIRS 2018. Bangalore, India: Springer Singapore (2018). p. 282–97. Revised Selected Papers 4 2019. doi:10.1007/978-981-13-5758-9_24

CrossRef Full Text | Google Scholar

36. Bromberg Y, Katz O, Silberberg Y. Ghost imaging with a single detector. Phys Rev A (2009) 79(5):053840. doi:10.1103/PhysRevA.79.053840

CrossRef Full Text | Google Scholar

37. Wu Y, Noonan JP, Agaian S, et al. Npcr and uaci randomness tests for image encryption, Cyber journals: multidisciplinary journals science technology. J Sel Areas Telecommun JSAT (2011) 1:31–8.

Google Scholar

38. Ghanbari-Ghalehjoughi H, Eslami M, Ahmadi-Kandjani S, Ghanbari-Ghalehjoughi M, Yu Z. Multiple layer encryption and steganography via multi-channel ghost imaging. Opt Lasers Eng (2020) 134:106227. doi:10.1016/j.optlaseng.2020.106227

CrossRef Full Text | Google Scholar

39. Hore A, Ziou D. Image quality metrics: PSNR vs. In: SSIM. In2010 20th international conference on pattern recognition. IEEE (2010). p. 2366–9. doi:10.1109/ICPR.2010.579

CrossRef Full Text | Google Scholar

40. Chan HL, Norrish M. Mechanisation of the AKS algorithm. J Automated Reasoning (2021) 65:205–56. doi:10.1007/s10817-020-09563-y

CrossRef Full Text | Google Scholar

41. Mousa A, Faragallah OS, El-Rabaie S, Nigm EM. Security analysis of reverse encryption algorithm for databases. Int J Comp Appl (2013) 66(14). doi:10.5120/11153-6255

CrossRef Full Text | Google Scholar

42. Zhang X, Zhong H, Cao L. Robust compressed ghost imaging against environmental influence factors. Opt Express (2024) 32(2):1669–76. doi:10.1364/OE.507909

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Sui L, Pang Z, Cheng Y, Cheng Y, Xiao Z, Tian A, et al. An optical image encryption based on computational ghost imaging with sparse reconstruction. Opt Lasers Eng (2021) 143:106627. doi:10.1016/j.optlaseng.2021.106627

CrossRef Full Text | Google Scholar

44. Ma J, Li Z, Zhao S, Wang L. Encrypting orbital angular momentum holography with ghost imaging. Opt Express (2023) 31(7):11717–28. doi:10.1364/OE.483923

CrossRef Full Text | Google Scholar