A family of robust chaotic S-unimodal maps based on the Gaussian function

This research paper introduces a family of one-dimensional S-unimodal maps based on the Gaussian function, designed to exhibit robust chaos across a wide range of parameters. These maps are developed to display robust chaos by avoiding multiple fixed points that are primarily responsible for the coexisting attractors in 1D maps. The parameter space analysis reveals that chaotic behaviour is sustained across the entire parameter space, except for a very narrow region. The study employs a comprehensive computational approach, including quantitative measures such as sample entropy, Lyapunov exponent, and invariant measures. The uniformly higher values of sample entropy, uniform positive values of the Lyapunov exponent, and the existence of invariant measures in a region of parameter space confirm the presence of robust chaos in these maps. Such a promising class of robust chaotic maps may be potentially used in diverse fields such as chaos-based cryptography, pseudo-random number generation, communication systems, and more.

Introduction

The study of chaotic behaviour in nonlinear dynamical systems is a fascinating area, marked by the emergence of periodic windows and co-existing attractors when subjected to different initial conditions within the parameter space. A slight perturbation in the parameters can lead these systems into a periodic regime, a phenomenon often referred to as “fragile chaos”. Conversely, in certain regions of the parameter space, where no periodic windows exist, a single chaotic attractor prevails over a range of parameters, giving rise to what we term “robust chaos.” The notion of robust chaos was first introduced by Banerjee et al. [1] in 1998 through their pioneering work on an electrical circuit known as the boost converter. This circuit’s mathematical model is a two-dimensional piecewise smooth map, showcasing a rich collection of border collision bifurcations leading to robust chaos. Their work also provided a condition for the existence of robust chaos in such systems, along with the conjecture that many other piecewise systems might exhibit robust chaos through border collision bifurcations.

Subsequent research by Potapov and Ali [2] in 2000 demonstrated that a network of neurons, activated with a one-dimensional piecewise smooth map as an activation function, can lack stable periodic functions, thus exhibiting robust chaos within specific parameter ranges. Andrecut and Ali [3–5], in their 2001 work extended this understanding by illustrating that even smooth one-dimensional unimodal maps could exhibit robust chaos within a broad parameter range. They also outlined a general procedure for generating smooth unimodal maps that exhibit robust chaos in the vicinity of the parameter space. Moreover, they presented a theorem providing a general condition for the occurrence of robust chaos in S-unimodal maps. In 2004, Parez [6] presented several simple polynomial unimodal maps that manifest robust chaos, accompanied by their respective Lyapunov exponents and invariant distributions. Kowalczyk [7], in 2005, analyzed the border collision bifurcation in non-invertible piecewise linear maps. Aguirregabiria [8], in 2009, proposed methods to generate robust chaos maps whose Lyapunov exponent varies with the system parameter, deviating from earlier robust chaos maps like S-unimodal or piecewise smooth maps, which maintain almost constant Lyapunov exponents throughout the robust chaos range. This work also challenged the notion that a negative Schwarzian derivative is necessary for robust chaos, citing examples from the literature. Elhad and Sprott [9], in their 2011 work, introduced a novel approach to inducing robust chaos within planar maps. They accomplished this by employing a simple piecewise smooth feedback mechanism, provided specific realizable conditions were met. Additionally, they demonstrated the effectiveness of this method through practical examples. Further contributions in 2016 to the understanding of robust chaos came from Han et al. [10], who formulated a theorem establishing criteria for robust chaos within 2D piecewise smooth maps. Gledning’s [11] revisited the concept of robust chaos in the context of piecewise smooth maps and provided a fresh toolkit for exploring this phenomenon.

Recent research activities showed a growing interest in identifying, constructing, and designing nonlinear dynamical systems that exhibit robust chaos and applying them in areas such as pseudo-random number/bit generation and various cryptographic and communication applications. In this context, Hua and Zhou’s [12, 13] work in 2017 proposed various nonlinear operations and combinations thereof on popular 1D chaotic maps to generate new mathematical models with chaotic behaviour. Similarly, Patra and Banerjee [14], in 2018, investigated robust chaos in a 3D piecewise linear map and derived sufficiency conditions for homoclinic and heteroclinic intersections. Jiteurtragool [15], in 2018, presented simplified forms of generic sigmoidal chaotic maps and a linearized sigmoidal chaotic map exhibiting chaotic behaviour over a wide parameter range. Hua et al. [16], in 2017, devised an effective approach for creating n-dimensional hyperchaotic Cat maps, tailored to desired levels of complexity. Elhadj’s [17] in 2019, proposed chaoticification methods for one-dimensional chaotic maps using S-unimodality and Collet-Eckman conditions. Zhu et al. [18] in the same year, introduced a 2D logistic-modulated-sine-coupling-logistic chaotic map (LSMCL), displaying enhanced chaotic behavior. Zhu et al. [19] in 2019, introduced quadratic polynomial chaotic maps, and Alawida et al. [20] proposed combined cosine functions with chaotic maps to create novel chaotic maps with expanded characteristics. In 2019, Hua et al. [21] suggested a sine chaotification model by incorporating a sine function as a nonlinear chaotification transform, which elevated the chaotic characteristics of the original map. The resulting enhanced chaotic map showcased superior chaos complexity and a notably expanded chaotic range compared to its seed. Around the same time, Zhu et al. [22] presented a novel 2-D chaotic map named LSMCL (Logistic-modulated-sine-coupling-logistic). This map utilized the logistic map for modulating the sine map and then combined the resulting modulation with the sine map itself. It resulted in a superior chaotic performance when compared to other established chaotic maps in terms of Lyapunov exponent, and Kolmogorov entropy.

In 2020, Hua et al. [23] developed a two-dimensional modular chaotification system (2D-MCS) to enhance the chaos complexity of existing 2-D chaotic maps. The modular operation used here acted as a bounded transform, leading to improved chaotic behaviour in a broad parameter range, a feat difficult to achievable by conventional chaotic maps. The scheme was applied to well-known chaotic maps such as the Henon map, Zeraoulia-Sprott’s map, and Duffing map, explaining its effectiveness in generating highly chaotic behaviours. Further, Hua et al. [24] introduced a two-dimensional (2D) sine chaotification system (2D-SCS) to increase the complexity and extend the chaotic ranges of 2-D chaotic maps. They successfully demonstrated the practical application of 2D-SCS to some specific 2D chaotic maps. Zhu et al. [25] introduced a novel composite chaotic system known as the parallel chaotic system (PCS) by combining multiple basic chaotic maps in parallel. Within the PCS, enhancements to the Lyapunov exponent and the range of chaotic behaviour were achieved through the introduction of additional parameters. In 2022, Hua et al. [26] proposed a two-dimensional (2-D) parametric polynomial chaotic system denoted as 2D-PPCS. This versatile framework was capable of generating various 2-D chaotic maps by adjusting the coefficients of the exponents. The 2D-PPCS initialized two parametric polynomials and subsequently employed modular chaotification on these polynomials. By manipulating different control parameters, the 2D-PPCS could fine-tune its Lyapunov exponents to achieve resilient chaotic behaviours with the desired level of complexity. In 2023, Yi-Bo et al. [27] introduced the 2D-LMSM, an enhanced chaotic mapping developed from logistic and sine mappings. This mapping demonstrated effectiveness in generating resilient chaotic signals across a wide range of parameter values, particularly in applications like speech encryption. In the same year, Vinko et al. [28] conducted an analysis of the robustness of chaos and edge-of-chaos regime for Chua’s system utilizing a novel figure of merit based on the correlation coefficient and Lyapunov exponent.

Overall, the research focused on designing and analyzing the nonlinear dynamical systems exhibiting robust chaos and their applications in various domains, continues to expand. In the next section, we introduce a novel family of S-unimodal maps that exhibits robust chaos in a wide range of parameter space.

The novel S-Unimodal map family

The Gaussian 1D map exhibits diverse dynamical behaviours, which include period doubling chaos, reverse period doubling, and, most notably, the presence of co-existing attractors-a relatively rare phenomenon in one-dimensional nonlinear maps, across a wide range of parameter settings [29]. Also, the presence of co-existing attractors in the Gaussian map and its q-deformed version has been analyzed by Patidar and Sud [29] and concluded that the appearance of co-existing attractors in one-dimensional nonlinear maps can be attributed to the existence of multiple fixed points.

Thus, in the quest for 1D maps exhibiting robust chaos, our preference is for one-dimensional maps free from multiple fixed points for a wider setting of parameter space. With this objective in mind, we’ve introduced a new family of 1D smooth unimodal maps, built on the foundation of the Gaussian function. These maps are developed to consistently exhibit robust chaos across a broad range of parameter settings, effectively circumventing the presence of multiple fixed points, which are the primary culprits behind the co-existing attractors in 1D S-unimodal maps.

The modified Gaussian function that we use for designing the new family of S-unimodal maps, is as follows:

$f\left(x,a\right)=\mathit{exp}\left(-a{\left(\frac{x}{a}-\frac{1}{2a}\right)}^2\right)-\mathit{exp}\left(-\frac{1}{4a}\right),(1)$

The above function.

(i) possesses a unique maximum at the critical point $x=0.5$ in $x\in \left[0,1\right],$

(ii) $f\left(0,a\right)=f\left(1,a\right)=0$ and

(iii) the Schwarzian derivative of $f\left(x,a\right)$ i.e.,

$S_f\left(x,a\right)=\frac{f^{‴}\left(x,a\right)}{f^{\prime }\left(x,a\right)}-\frac{3}{2}{\left(\frac{f^{″}\left(x,a\right)}{f^{\prime }\left(x,a\right)}\right)}^2=-\frac{\left(12a^2+16x^4-32x^3+24x^2-8x+1\right)}{2a^2{\left(2x-1\right)}^2}=-\frac{12a^2+{\left(2x-1\right)}^4}{2a^2{\left(2x-1\right)}^2}$

is negative for all values of $x$ in $\left[0,1\right]$ except $x=0.5$.

Therefore, $f\left(x,a\right)$ is a S-unimodal function of class $C^3$ on the interval $x\in \left[0,1\right]$.

Now we follow the general recipe of Andrecut and Ali [4] for generating a new family of one-dimensional S-unimodal functions $F_{\left(\pm \right)}\left(x,a,v\right)$, using the S-unimodal function $f\left(x,a\right)$ (Eq. 1) as below:

$F_{\left(\pm \right)}\left(x,a,v\right)=\frac{1-v^{\pm f\left(x,a\right)}}{1-v^{\pm f\left(c,a\right)}}\forall v\ne 1,v>0,(2)$

here $x=c$ is a critical point where $f^{\prime }\left(c,a\right)=0$.

It can be easily verified that the Schwarzian derivative of $F_{\left(\pm \right)}\left(x,a,v\right)$ i.e.,

$S_F\left(x,a,v\right)=\frac{F^{‴}\left(x,a,v\right)}{F^{\prime }\left(x,a,v\right)}-\frac{3}{2}{\left(\frac{F^{″}\left(x,a,v\right)}{F^{\prime }\left(x,a,v\right)}\right)}^2=S_f\left(x,a\right)-\frac{1}{2}{\left[\mathit{ln}\left(v\right)f^{\prime }\left(x,a\right)\right]}^2.$

Since $S_f\left(x,a\right)$ is negative for all values of $x\in \left[0,1\right]$ except $x=0.5$, therefore $S_F\left(x,a,v\right)$ is negative for all $x\in \left[0,1\right]$ and $v>0$ except $x=c=0.5$ and $v=1$. Therefore $F_{\left(\pm \right)}\left(x,a,v\right)$ is also a S-unimodal function.

Since the Schwarzian derivative is negative and the function has a unique maximum at x = c, there can be at most one attracting periodic orbit with the critical point in its basin of attraction, i.e., the orbit with initial condition x = c = 0.5 will approach to $x=0$ in few iterates. The point $x=0$ will be unstable if $F_{\left(\pm \right)}^{\prime }\left(0,a,v\right)=\left|\frac{\mathit{ln}\left(v\right)f^{\prime }\left(0,a\right)}{1-v^{\pm f\left(c,a\right)}}\right|$ >1 $\forall v>0,v\ne 1$. In such case, the map does not possess any stable periodic orbit, hence a chaotic attractor prevails.

Parameter space analysis

Stability analysis

The explicit analytic form of the family of newly constructed one-dimensional S-unimodal functions and the condition of instability of $x=0$ i.e., the condition of existence of chaotic orbit may be written as follows:

$F_{\left(\pm \right)}\left(x,a,v\right)=\frac{1-v^{\pm \mathit{exp}\left(-a{\left(\frac{x}{a}-\frac{1}{2a}\right)}^2\right)-\mathit{exp}\left(-\frac{1}{4a}\right)}}{1-v^{\pm \left(1-\mathit{exp}\left(-\frac{1}{4a}\right)\right)}}\forall v\ne 1,v>0(3)$

$F_{\left(\pm \right)}^{\prime }\left(0,a,v\right)=\left|\frac{\mathit{ln}\left(v\right)\frac{1}{a}\mathit{exp}\left(-\frac{1}{4a}\right)}{1-v^{\pm \left(1-\mathit{exp}\left(-\frac{1}{4a}\right)\right)}}\right|>1\forall v>0v\ne 1(4)$

We are considering the chaotic iterated map in the form $x_{n+1}=F\left(x_n,a,v\right)$.

In Figure 1 and Figure 2, we have depicted the shape of the newly constructed S-unimodal functions in the interval $x\in \left[0,1\right]$ for various choices of parameters $a$ and $v$. Frames 1(a), 1(b) and 1(c) correspond to the positive (+) sign, i.e., for $F_{\left(+\right)}\left(x,a,v\right)$ and Frames 2(a), 2(b) and 2(c) correspond to the negative (−) sign, i.e., for $F_{\left(-\right)}\left(x,a,v\right)$. We observe that the shape of the function resembles the familiar logistic function and there appear sensitive variations with respect to the parameters $a$ and $v$.

FIGURE 1

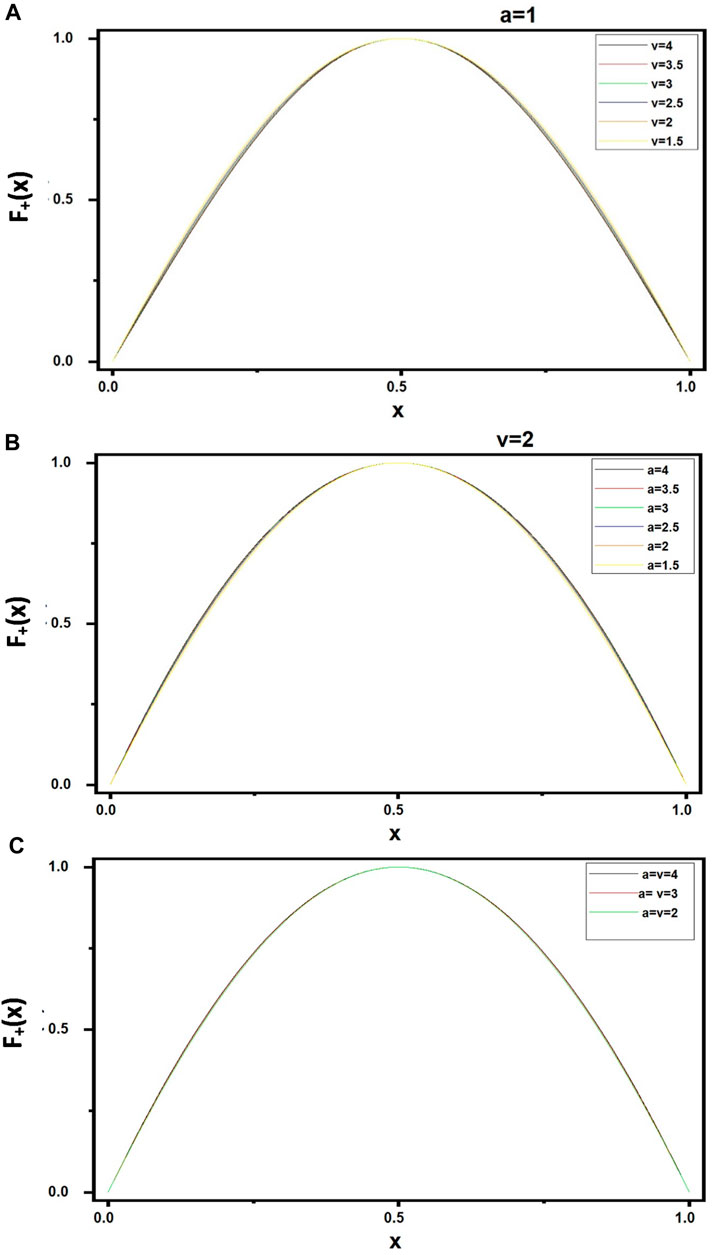
FIGURE 1. Newly constructed S-unimodal functions (Eq. 3) with positive (+) sign for different values of parameters $a$ and $v$: (A) For a fixed value of $a$ (i.e., $a$ = 1) and different values of $v$, (B) For a fixed value of $v$ (i.e., $v$ = 2) and different values of $a$ and (C) same values of both parameters $a$ and $v$.

FIGURE 2

FIGURE 2. Newly constructed S-unimodal functions (Eq. 3) with negative (−) sign for different values of parameters $a$ and $v$: (A) For a fixed value of $a$ (i.e., $a$ = 1) and different values of $v$, (B) For a fixed value of $v$ (i.e., $v$ = 2) and different values of $a$ and (C) same values of both parameters $a$ and $v$.

In Figure 3, we illustrate the regions of the parameter space ($\left.a,v\right)$ where the condition of instability of $x=0$ is satisfied (shown in red) and not satisfied (shown in blue) by computing the derivative of $F_{\left(\pm \right)}\left(x,a,v\right)$ at $x=0$ i. e., $F_{\left(\pm \right)}^{\prime }\left(0,a,v\right)$ (refer to Eq. 4). Particularly in the top frame we present the results corresponding to the positive (+) sign and in the bottom frame we present the results for the negative (−) sign.

FIGURE 3

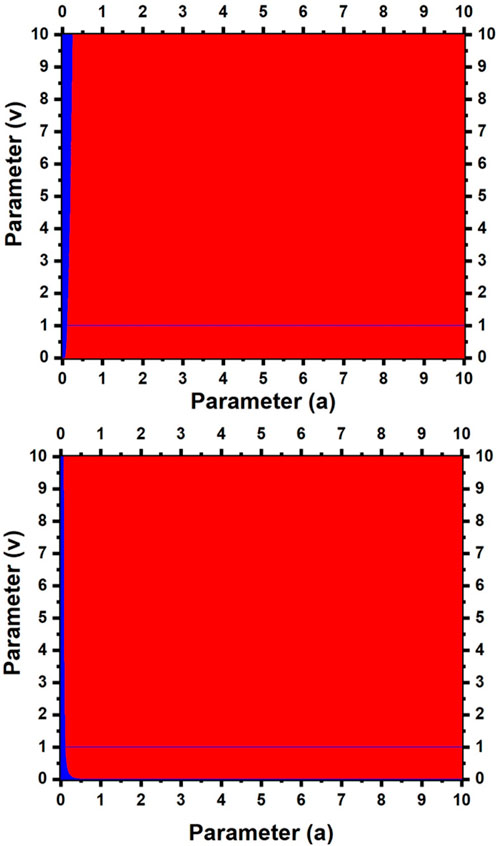
FIGURE 3. Parameter space showing stability regions for the point $x=0$ of S-unimodal function (Eq. 3) (Top frame for positive (+) sign, Bottom frame for negative (−) sign). The blue region represents stability and the red region represents the instability of $x=0$.

We observe that in the entire parameter space ($\left.a,v\right)$ the point $x=0$ is unstable except for a very narrow region near $a=0$. The case $v=1$ is excluded from all the computations for the obvious reason that F is not defined for this choice.

Based on the argument presented earlier, a chaotic orbit can exist across the entire parameter space ($\left.a,v\right)$ where the point $x=0$ is unstable. To confirm the presence of chaotic orbits within this parameter space, we conducted an extensive computation involving two quantitative measures: Lyapunov exponents and Sample Entropy. Additionally, to validate the existence of ergodic dynamics within the newly constructed family of S-unimodal maps, we performed numerical computations of the invariant measure for several representative sets of parameters. Below, we provide a concise overview of these measures and a detailed description of our computational process and the results we obtained.

Sample entropy analysis

Sample entropy has become one of the important and valuable tools to quantify the regularity and complexity of dynamical systems found across various disciplines from neuroscience and physiology to engineering and finance. Sample Entropy is a non-linear time-series analysis technique that provides insights into the complexity, regularity, and predictability of a dynamical system. Introduced as an improvement over Approximate Entropy [30], Sample Entropy measures the likelihood that similar patterns of data points within a time series will remain similar when additional data points are included. In other words, it quantifies the degree of self-similarity or regularity in the data [31].

Mathematically, the sample entropy may be calculated as follows:

$SaEn\left(m,r,N\right)=-\mathit{ln}\left(\frac{C\left(m+1,r\right)}{C\left(m,r\right)}\right),(5)$

where m is the pattern length or embedding dimension, r is the tolerance threshold that defines the maximum difference between two sets of data points to be considered similar, N is the length of the time series, $C\left(m,r\right)$ represents the number of similar patterns of length m with a threshold r. For all our computations reported here, we have considered m = 5, $r=0.5$ and N = 5000.

We computed the sample entropy for the newly constructed family of S-unimodal maps considering the parameter space ($\left.0\le a\le 10,0\le v\le 10\right)$ with a step size of $0.01$. The results are presented in Figure 4. In the top frame, we show the results corresponding to the positive (+) sign and in the bottom frame we display the results for the negative (−) sign.

FIGURE 4

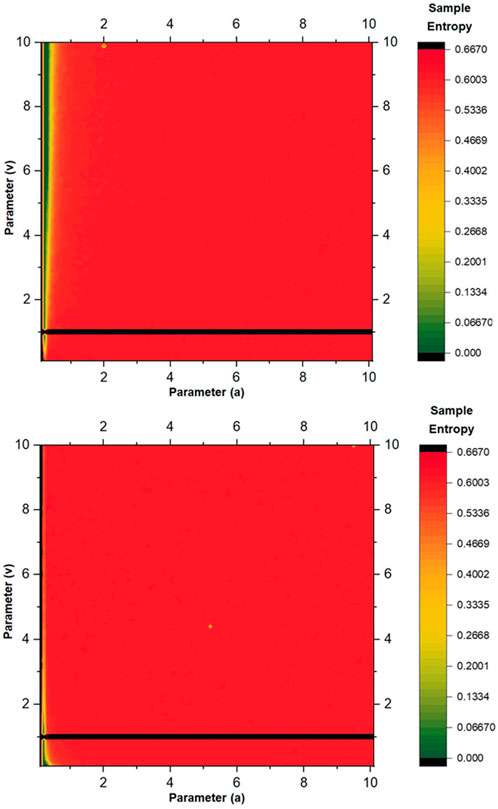
FIGURE 4. Sample entropy for the newly constructed family of 1D S-unimodal maps (Eq. 3). Top frame for positive (+) sign and bottom frame for negative (−) sign.

Higher values of sample entropy within the parameter space indicate the complexity of the dynamics, unpredictability, and the presence of chaotic behaviour. We observe that the sample entropy consistently remains elevated throughout the entire parameter space; there is no region within the parameter space where lower values of sample entropy are found, except for the very low value of the parameter $a$.

Invariant measures and ergodicity analysis

In dynamical systems, invariant measures (IVM) play a pivotal role by facilitating a portrayal of the system’s long-term behaviour, thereby facilitating an understanding of its underlying structure and the ability to forecast its future states. Furthermore, they prove invaluable in elucidating robust chaos, as they offer a statistical characterization of chaotic behaviour, encompassing chaos characterization, stability analysis, predictive capabilities, measure preservation, and ergodicity. Ergodicity, in particular, serves as the fundamental prerequisite for the existence of an invariant measure.

The quest for the existence and computation of invariant measures can be a formidable challenge, often necessitating the employment of advanced mathematical and computational techniques. Consequently, the analytical expression of invariant measures remains unattainable for all chaotic systems. One commonly adopted approach for estimating invariant measures in chaotic maps involves conducting extensive numerical simulations over an extended period and subsequently constructing histograms that depict the states visited by the system over time. These histograms can serve as reasonably accurate approximations of the invariant.

In the context of this study, we conducted numerical simulations, each spanning $N={10}^6$ steps, to derive the invariant measures for each scenario under examination. We have analyzed several cases corresponding to various pairs of parameters $a$ and $v$.

We have depicted two of the results in Figure 5, with one corresponding to the positive (+) sign and the other to the negative (−) sign, respectively, in the top and bottom frames. In all other cases corresponding to chaotic behaviour, we have obtained a similar invariant measure. We have analyzed the IVM for several different sets of initial conditions corresponding to the same parameter set also and observed that the probability density distribution remains invariant concluding the ergodic dynamics of the newly constructed family of S-unimodal maps. We also observe that the Invariant Measure (IVM) of the newly constructed family of S-unimodal maps is qualitatively similar to the IVM of the logistic map, $f\left(x\right)=4x\left(1-x\right)$ that can be described by an analytic form $1/\left(\pi \sqrt{1-x^2}\right)$. This similarity suggests that the newly constructed family of S-unimodal maps is akin to the logistic family.

FIGURE 5

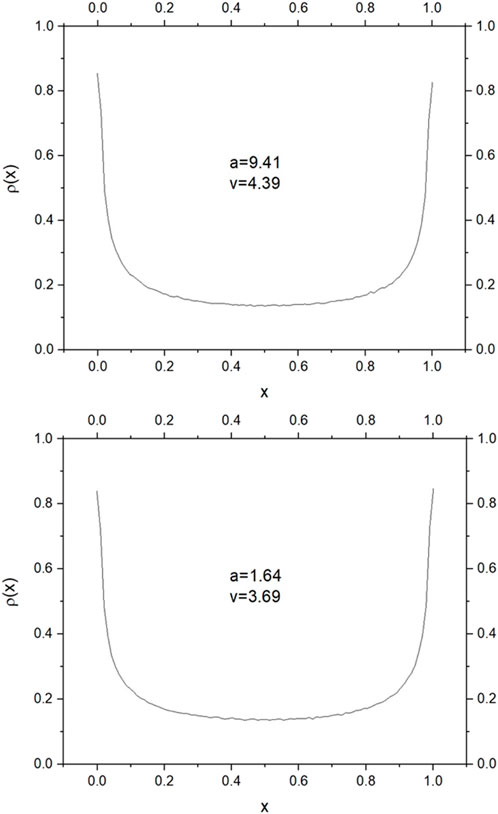
FIGURE 5. Numerically computed invariant measures for the newly constructed family of 1D S-unimodal maps (Eq. 3) for a selected set of parameters. Top frame for positive (+) sign and bottom frame for the negative (−) sign.

The Lyapunov exponent analysis

The Lyapunov exponent is an important quantitative measure of a dynamical system’s sensitivity to initial conditions, providing valuable insights into its predictability and long-term behaviour. Defined as the average rate of exponential divergence or convergence of nearby trajectories in phase space, the Lyapunov exponent quantifies the system’s intrinsic instability. Researchers use Lyapunov exponents to discern chaotic behaviour, assess the degree of chaos in a system, and predict its predictability horizon. In this research paper, we also leverage Lyapunov exponents [32] as a computational tool to investigate the chaotic dynamics of newly constructed family of S-unimodal maps, shedding light on its underlying complexity and providing essential information for understanding the existence of robust chaos. We have done an extensive computation of the Lyapunov exponent for the newly developed family of S-unimodal maps in the parameter space ($\left.0\le a\le 10,0\le v\le 10\right)$ with a step size of 0.01. At each point in the parameter space, we iterated the map 5000 times, discarding some initial transient behaviour, to calculate the average convergent value of the Lyapunov exponent. The results are presented in Figure 6, where top frame represents the positive (+ve) sign, and bottom frame represents the negative (-ve) sign. We may clearly observe that the Lyapunov exponent remains positive and uniform throughout the entire parameter space we considered in our computation, with no instance of negative value. Additionally, we also verified the robustness of chaos for large parameter values exceeding $a>10$ and $v>10$. These findings align with the analytical results based on stability analysis and the previously reported results of sample entropy. An important observation is that the Lyapunov exponent throughout the entire parameter space converges to a value of $\mathit{ln}2\approx 0.6931$, further confirming the conjugacy of the newly constructed family of S-unimodal maps with the logistic map $f\left(x,a\right)=f\left(x,4\right)=4x\left(1-x\right)$. This discovery presents us with an infinite number of options within the newly constructed family of S-unimodal maps, achieved by choosing various combinations of parameters $a\left(>1\right)$ and $v\left(>1\right)$, all of which exhibit extreme sensitivity and ergodic behavior qualitatively similar to the logistic map $f\left(x,a\right)=f\left(x,4\right)=4x\left(1-x\right)$.

FIGURE 6

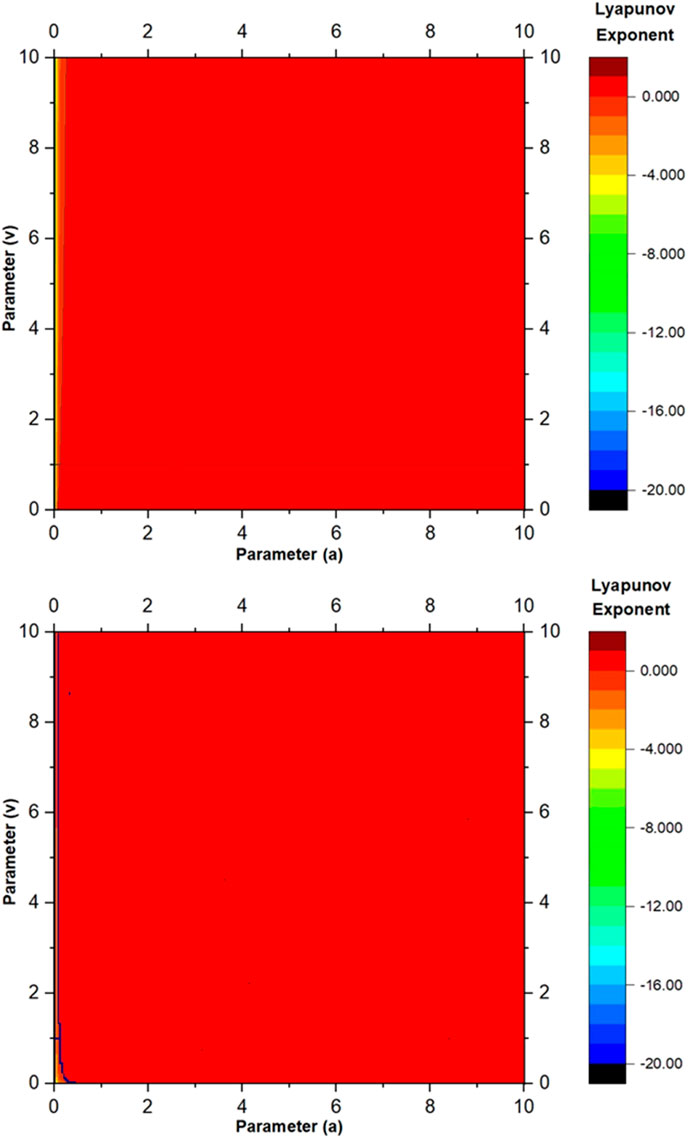
FIGURE 6. Lyapunov exponent for the newly constructed family of 1D S-unimodal maps (Eq. 3). Top frame for the positive (+) sign and bottom frame for the negative (−) sign.

Comparison with other S-unimodal map families

To facilitate a swift comparison of dynamic behaviour, with a specific focus on the prevalence of robust chaos within the proposed Gaussian function-based S-unimodal map family and other analogous S-unimodal map families, we conducted a simultaneous parameter analysis.

This

Analysis comprised the assessment of stability, sample entropy, invariant measures, Lyapunov exponent, etc. for S-unimodal map families based on logistic, cubic, and sine functions, as done for the Gaussian function-based S-unimodal map family in the preceding section. It is worth mentioning here that the conventional S-unimodal maps ($x_{n+1}=f\left(x_n,a\right)$) with logistic, cubic, and sine functions also exhibit chaos through a period-doubling route and coexisting attractors, signifying a delicate form of chaos, namely, fragile chaos.

The summarized results of our comparative analysis for the S-unimodal map families constructed using the logistic, cubic and sine functions are presented in Table 1 and Figure 7, Figure 8, Figure 9 and Figure 10. It is apparent that S-unimodal map families, based on various functions, also manifest robust chaos across a broad spectrum of system parameters. Nevertheless, the Gaussian function-based S-unimodal maps proposed in this study outperform others in terms of the existence of robust chaos. We particularly observe that all the S-unimodal map families based on various nonlinear functions including the Gaussian function exhibit robust chaos for a very wide range of parameter space for the negative (−) sign except for a very narrow region below $v=1$. In the case of S-unimodal map families constructed with logistic, cubic and sine functions and considering the positive (+) sign, the existence of robust chaos is observed for smaller regions of parameter space towards the lower values of parameters $a$ and $v$. Contrary to this, the robust chaos is prevalent in the entire parameter space for the proposed S-unimodal map family based on the Gaussian function with negative (−) sign also. This comparison validates our claims of superiority of the proposed Gaussian function-based S-unimodal map family in terms of exhibiting robust chaos in almost the entire parameter space, except for very narrow strips/regions for very low values of parameters $a$ and $v$.

TABLE 1

TABLE 1. Various S-unimodal functions and S-unimodal function families based on them along with the corresponding instability conditions for the point $x=0$ i.e., condition for the existence of chaos.

FIGURE 7

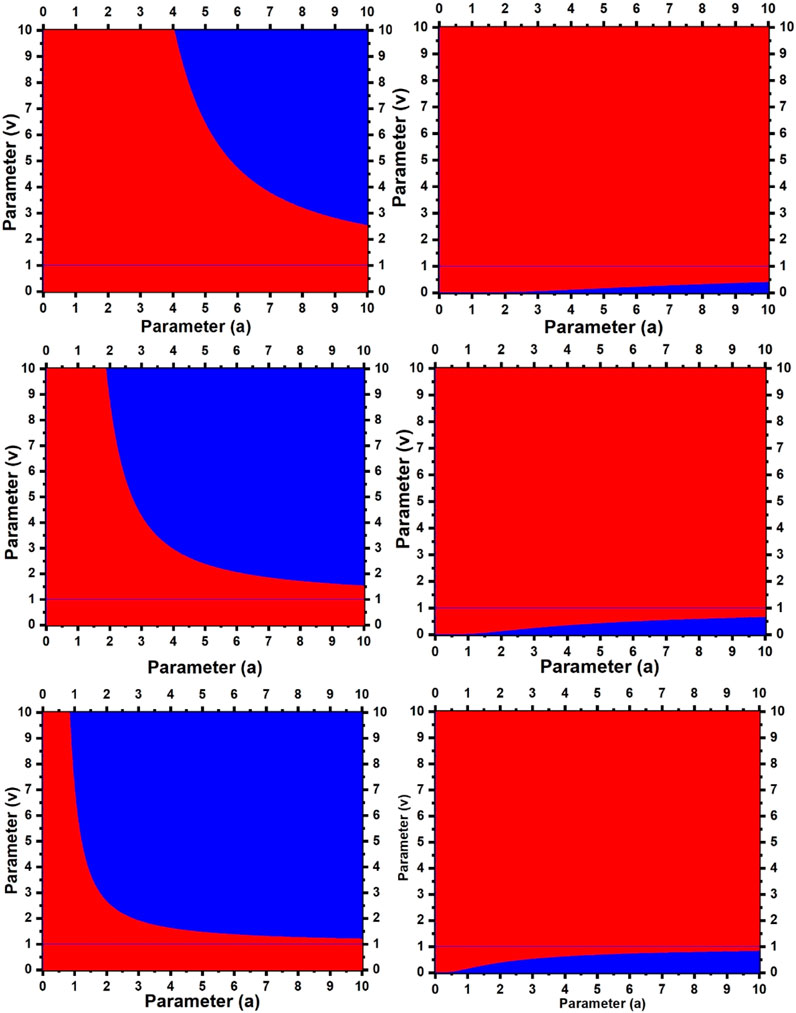
FIGURE 7. Stability regions for the point $x=0$ of 1D S-unimodal map families constructed using the logistic, cubic and sine functions (see Table 1 for reference): Top-left frame is for logistic function with positive (+) sign, top-right frame is for logistic function with negative (−) sign, middle-left frame is for cubic function with positive (+) sign, middle-right frame is for cubic function with negative (−) sign, bottom-left frame is for sine function with positive (+) sign, bottom-right frame is for sine function with negative (−) sign.

FIGURE 8

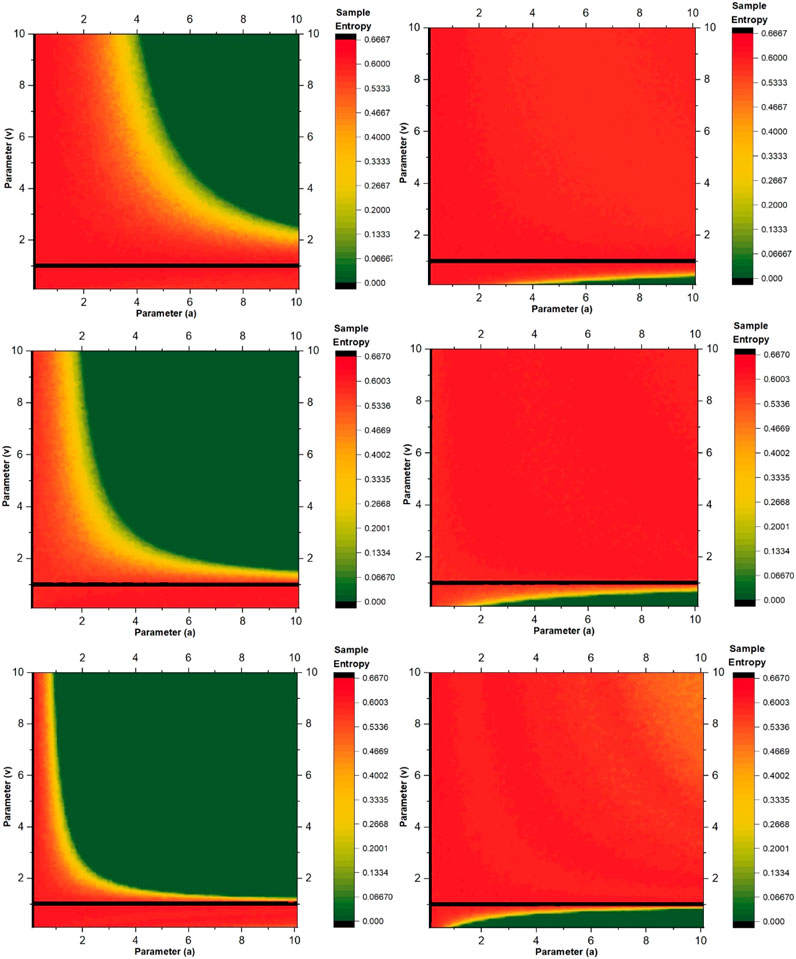
FIGURE 8. Sample Entropy for 1D S-unimodal map families constructed using the logistic, cubic and sine functions (see Table 1 for reference): Top-left frame is for logistic function with positive (+) sign, top-right frame is for logistic function with negative (−) sign, middle-left frame is for cubic function with positive (+) sign, middle-right frame is for cubic function with negative (−) sign, bottom-left frame is for sine function with positive (+) sign, bottom-right frame is for sine function with negative (−) sign.

FIGURE 9

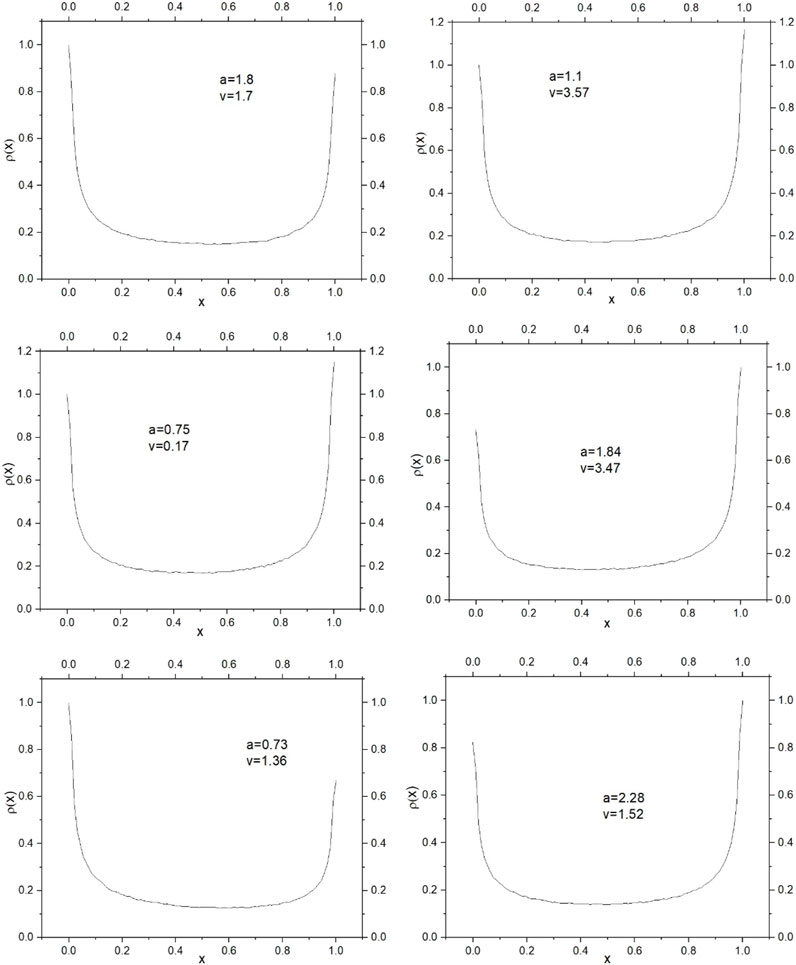
FIGURE 9. Invariant Measures (IVM) for 1D S-unimodal map families constructed using the logistic, cubic and sine functions (see Table 1 for reference): Top-left frame is for logistic function with positive (+) sign, top-right frame is for logistic function with negative (−) sign, middle-left frame is for cubic function with positive (+) sign, middle-right frame is for cubic function with negative (−) sign, bottom-left frame is for sine function with positive (+) sign, bottom-right frame is for sine function with negative (−) sign.

FIGURE 10

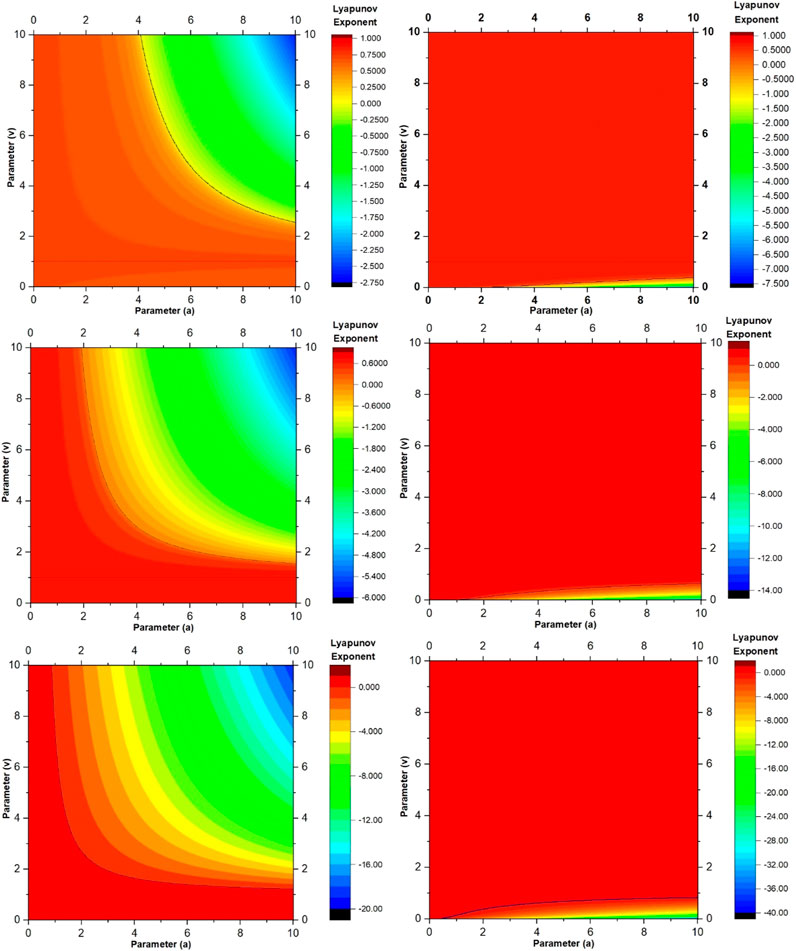
FIGURE 10. Lyapunov exponent for 1D S-unimodal map families constructed using the logistic, cubic and sine functions (see Table 1 for reference): Top-left frame is for logistic function with positive (+) sign, top-right frame is for logistic function with negative (−) sign, middle-left frame is for cubic function with positive (+) sign, middle-right frame is for cubic function with negative (−) sign, bottom-left frame is for sine function with positive (+) sign, bottom-right frame is for sine function with negative (−) sign.

Conclusion

This paper explores the concept of robust chaos in a family of one-dimensional S-unimodal maps based on Gaussian functions. Robust chaos is characterized by the absence of periodic windows and co-existing attractors in a parameter space neighbourhood. We have constructed a family of one-dimensional S-unimodal functions derived from Gaussian function that eliminate the possibility of coexisting attractors and unstable periodic orbits.

Through a comprehensive analysis, the paper demonstrates the presence of robust chaotic behavior across a wide parameter space. This is supported by calculations of Lyapunov exponents, Sample Entropy, and Invariant Measures along with the conventional stability analysis. Sample Entropy and Invariant Measures indicate the complexity and unpredictability of the dynamics, further confirming the existence of robust chaos. The study’s findings suggest that these newly constructed S-unimodal maps exhibit robust chaos over a substantial parameter range, making them valuable for various applications in chaos-based cryptography, pseudo-random number generation, and communication systems.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

VP: Writing–review and editing, Writing–original draft, Visualization, Validation, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Conceptualization.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. A part of the research work presented in this manuscript was conducted under the SERB, Govt. of India MATRICS Grant (MTR/2018/000203).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Banerjee S, Yorke JA, Grebogi C. Robust chaos. Phys Rev Lett (1998) 80(14):3049–52. doi:10.1103/physrevlett.80.3049

CrossRef Full Text | Google Scholar

2. Potapov A, Ali MK. Robust chaos in neural networks. Phys Lett A (2000) 277(6):310–22. doi:10.1016/s0375-9601(00)00726-x

CrossRef Full Text | Google Scholar

3. Andrecut M, Ali MK. Example of robust chaos in a smooth map. Europhysics Lett (2001) 54(3):300–5. doi:10.1209/epl/i2001-00241-3

CrossRef Full Text | Google Scholar

4. Andrecut M, Ali MK. Robust chaos in smooth unimodal maps. Phys Rev E (2001) 64(2):025203. doi:10.1103/physreve.64.025203

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Andrecut M, Ali MK. On the occurrence of robust chaos in a smooth system. Mod Phys Lett B (2001) 15(12and13):391–5. doi:10.1142/s0217984901001793

CrossRef Full Text | Google Scholar

6. Pérez G. Robust chaos in polynomial unimodal maps. Int J Bifurcation Chaos (2004) 14(07):2431–7. doi:10.1142/s0218127404010722

CrossRef Full Text | Google Scholar

7. Kowalczyk P. Robust chaos and border-collision bifurcations in non-invertible piecewise-linear maps. Nonlinearity (2004) 18(2):485–504. doi:10.1088/0951-7715/18/2/002

CrossRef Full Text | Google Scholar

8. Aguirregabiria JM. Robust chaos with variable Lyapunov exponent in smooth one-dimensional maps. Chaos, Solitons and Fractals (2009) 42(4):2531–9. doi:10.1016/j.chaos.2009.03.196

CrossRef Full Text | Google Scholar

9. Zeraoulia E, Sprott JC. Robustification of chaos in 2D maps. Adv Complex Syst (2011) 14(06):817–27. doi:10.1142/s0219525911003402

CrossRef Full Text | Google Scholar

10. Han D, Min L, Hao L. A chaos robustness criterion for 2D piecewise smooth Map with applications in pseudorandom number generator and image encryption with avalanche effect. Math Probl Eng (2016) 2016:1–14. doi:10.1155/2016/1496329

CrossRef Full Text | Google Scholar

11. Glendinning P. Robust chaos revisited. Eur Phys J Spec Top (2017) 226(9):1721–38. doi:10.1140/epjst/e2017-70058-2

CrossRef Full Text | Google Scholar

12. Hua Z, Zhou B, Zhou Y. Sine-transform-based chaotic system with FPGA implementation. IEEE Trans Ind Elect (2017) 65(3):2557–66. doi:10.1109/tie.2017.2736515

CrossRef Full Text | Google Scholar

13. Hua Z, Zhou Y. One-dimensional nonlinear model for producing chaos. IEEE Trans Circuits Syst Regular Pap (2017) 65(1):235–46. doi:10.1109/tcsi.2017.2717943

CrossRef Full Text | Google Scholar

14. Patra M, Banerjee S. Robust chaos in 3-D piecewise linear maps. Chaos: Interdiscip J Nonlinear Sci (2018) 28(12):123101. doi:10.1063/1.5050548

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Jiteurtragool N, Masayoshi T, San-Um W. Robustification of a one-dimensional generic sigmoidal chaotic map with application of true random bit generation. Entropy (2018) 20(2):136. doi:10.3390/e20020136

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hua Z, Yi S, Zhou Y, Li C, Wu Y. Designing hyperchaotic cat maps with any desired number of positive Lyapunov exponents. IEEE Trans Cybernetics (2017) 48(2):463–73. doi:10.1109/tcyb.2016.2642166

CrossRef Full Text | Google Scholar

17. Elhadj Z. Chaotifying one-dimensional discrete mappings using S-unimodality and collet–eckmann condition. Int J Bifurcation Chaos (2019) 29(04):1950050. doi:10.1142/s0218127419500500

CrossRef Full Text | Google Scholar

18. Hua Z, Jin F, Xu B, Huang H. 2D Logistic-Sine-coupling map for image encryption. Signal Process. (2018) 149:148–61. doi:10.1016/j.sigpro.2018.03.010

CrossRef Full Text | Google Scholar

19. Zhu S, Zhu C, Cui H, Wang W. A class of quadratic polynomial chaotic maps and its application in cryptography. IEEE Access (2019) 7:34141–52. doi:10.1109/access.2019.2902873

CrossRef Full Text | Google Scholar

20. Alawida M, Samsudin A, Teh JS, Alshoura WH. Digital cosine chaotic map for cryptographic applications. IEEE Access (2019) 7:150609–22. doi:10.1109/access.2019.2947561

CrossRef Full Text | Google Scholar

21. Hua Z, Zhou B, Zhou Y. Sine chaotification model for enhancing chaos and its hardware implementation. IEEE Trans Ind Elect (2018) 66(2):1273–84. doi:10.1109/tie.2018.2833049

CrossRef Full Text | Google Scholar

22. Zhu H, Zhao Y, Song Y. 2D logistic-modulated-sine-coupling-logistic chaotic map for image encryption. IEEE Access (2019) 7:14081–98. doi:10.1109/access.2019.2893538

CrossRef Full Text | Google Scholar

23. Hua Z, Zhang Y, Zhou Y. Two-dimensional modular chaotification system for improving chaos complexity. IEEE Trans Signal Process (2020) 68:1937–49. doi:10.1109/tsp.2020.2979596

CrossRef Full Text | Google Scholar

24. Hua Z, Zhou Y, Bao B. Two-dimensional sine chaotification system with hardware implementation. IEEE Trans Ind Inform (2019) 16(2):887–97. doi:10.1109/tii.2019.2923553

CrossRef Full Text | Google Scholar

25. Zhu M, Wang C. A novel parallel chaotic system with greatly improved Lyapunov exponent and chaotic range. Int J Mod Phys B (2020) 34(07):2050048. doi:10.1142/s0217979220500484

CrossRef Full Text | Google Scholar

26. Hua Z, Chen Y, Bao H, Zhou Y. Two-dimensional parametric polynomial chaotic system. IEEE Trans Syst Man, Cybernetics: Syst (2021) 52(7):4402–14. doi:10.1109/tsmc.2021.3096967

CrossRef Full Text | Google Scholar

27. Huang YB, Xie PW, Gao JB, Zhang QY. A robust chaotic map and its application to speech encryption in dual frequency domain. Int J Bifurcation Chaos (2023) 33(08):2350096. doi:10.1142/s0218127423500967

CrossRef Full Text | Google Scholar

28. Vinko D, Miličević K, Vidović I, Zorić B. Chaos robustness and computation complexity of piecewise linear and smooth chaotic chua’s system. Int J Bifurcation Chaos (2023) 33(04):2350048. doi:10.1142/s0218127423500487

CrossRef Full Text | Google Scholar

29. Patidar V, Sud KK. A comparative study on the co-existing attractors in the Gaussian map and its q-deformed version. Commun Nonlinear Sci Numer Simulation (2009) 14(3):827–38. doi:10.1016/j.cnsns.2007.10.015

CrossRef Full Text | Google Scholar

30. Pincus SM. Approximate entropy as a measure of system complexity. Proc Natl Acad Sci (1991) 88(6):2297–301. doi:10.1073/pnas.88.6.2297

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Richman JS, Moorman JR. Physiological time-series analysis using approximate entropy and sample entropy. Am J physiology-heart circulatory Physiol (2000) 278(6):H2039–49. doi:10.1152/ajpheart.2000.278.6.h2039

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Eckmann JP, Ruelle D. Ergodic theory of chaos and strange attractors. Rev Mod Phys (1985) 57(3):617–56. doi:10.1103/revmodphys.57.617

CrossRef Full Text | Google Scholar