
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 06 March 2024
Sec. Fluid Dynamics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1320327
The probability of high-speed trains being hit by tornadoes is increasing. Therefore, this paper studies the effect of wind angles on the aerodynamic characteristics of a high-speed train subjected to a translating simulated tornado. A small six-dimensional force/torque sensor was used to measure the aerodynamic force and moment of a high-speed train model at a reduced scale of 1:150. The models, consisting of high-speed train heads and cars with different aerodynamic shapes, displayed non-stationary characteristics in their respective aerodynamic force and moment coefficient time histories. The variation trends of the ensemble time-varying mean of the pitching moment coefficient of a high-speed train car and head, for wind angles smaller than 60° and 45°, respectively, are different from those for other wind angles. The lift force coefficient ensemble time-varying mean of the high-speed train head is asymmetrical along the longitudinal axis when the wind angle is smaller than 60°, which is different from that of the high-speed train car. The maximum values of the ensemble time-varying mean of the force and moment coefficient of the high-speed train are almost equal under different movement directions of the tornado simulator at each wind angle, which is also true for the minimum value of the force and moment coefficient of the high-speed train. The ensemble time-varying variance of the force and moment coefficient of the high-speed train model in the region of −200 mm–200 mm is greater than that in other regions. This study can contribute to a more comprehensive and accurate understanding of the interaction between tornadoes and high-speed trains.
In recent decades, China’s network has rapidly expanded and become increasingly, densely distributed. Several tornadoes have occurred in the vicinity of China’s high-speed rail network [1]. Tornadoes, known for their destructive nature [2, 3], pose a significant threat to the safe operation of high-speed trains. In 2005, a high-speed train operating on the Uetsu line was overturned by a tornado. Tornadoes also caused accidents on the Tozai line in 1978 and on the Nippo main line in 2006 [4]. Recent events, such as the tornadoes in Shangzhi, Heilongjiang Province on 1 June 2021, and in Qingyuan District, Baoding, Hebei Province on 21 July 2021, have also affected the normal operation of the high-speed trains. It is important to mention that tornadoes have a certain speed of movement. Thus, studies on the aerodynamic characteristics of high-speed trains under translating tornadoes have practical significance. The force and moment coefficients, in particular, serve as key indicators of the aerodynamic characteristics.
While previous studies have focused on low-rise buildings and other structures under translating tornadoes [5–8], there have been few studies on the impact of tornadoes on high-speed trains. Suzuki and Okura [9] conducted a pressure measurement test on a single train car model, with a shape similar to that of a high-speed train, passing through a simulated tornado. Their results showed that the time-history trends of lateral force, lift force, and yaw moment were non-stationary. The lift force reached its maximum value when the single train car reached the center of the simulated tornado. Xu et al. [10] utilized computational fluid dynamics (CFD) calculations to simulate the situation when a high-speed train encountered a tornado and focused on the aerodynamic characteristics of the high-speed train head. Their results showed that the time-history trends of the lateral force, lift force, rolling moment, and yaw moment of the high-speed train head were non-stationary. These studies offer valuable contributions, but they were based on fixed wind angles. There is only one condition for wind angle in these studies mentioned above. The vortex core is the main structure of the tornado, and its size is limited compared with the boundary layer wind. In addition, the wind angles of the high-speed train may affect the contact state between the high-speed train and the tornado vortex core, so it is necessary to consider the effect of the wind angles on the aerodynamic characteristics of the high-speed train. Therefore, the number of wind angle conditions is being investigated in further detail in this research. The aerodynamic shape of the high-speed train head is different from that of the high-speed train car. To the best of our knowledge, there is a paucity of experimental investigations on high-speed train heads. To enhance the safe operation of high-speed trains, it is imperative to investigate the aerodynamic characteristics of a high-speed train head under a translating tornado using a tornado simulator and to further compare it with a high-speed train car.
The time-varying mean, characterized by a non-stationary time history, provides insight into the evolution process of the aerodynamic characteristics of a high-speed train under a translating tornado. The short-time Fourier transform can be used to analyze the non-stationary time history of the wind pressure generated by the translating tornado [8]. This method involves using a window function to identify the time-domain information, and the choice of the window function can introduce errors in the analysis. Alternatively, the wavelet transform can be used to extract the time-varying mean from the wind pressure [6], and the accuracy of the result mainly depends on the predefined wavelet order [11, 12]. A complete ensemble empirical mode decomposition with adaptive noise algorithm (CEEMDAN) [13] comes from the empirical mode decomposition (EMD) [14] and ensemble empirical mode decomposition (EEMD) [15]. CEEMDAN is a data-driven adaptive method as there is no predefined function in CEEMDAN. EMD was used to analyze the non-stationary wind speed data of Hurricane Lili in 2002, and then the time-varying mean was obtained [16]. EEMD was used to analyze the full-scale downburst wind record and extract the time-varying mean [12]. CEEMDAN was used to extract the time-varying mean in this study, and to the best of the authors’ knowledge, CEEMDAN has not been used in tornado-related research. The evolutionary power spectral density (EPSD) [17] with time dependence is a generalization of the power spectral density. It can be used to calculate the time-varying variance.
This work aims to conduct translating tornado experiments to study the effects of wind angles on the aerodynamic characteristics of a high-speed train. The tornado simulator at Beijing Jiaotong University was used to generate the three-dimensional simulated tornado wind field. The pressure measurement results require an integral calculation to obtain the aerodynamic force and moment of the high-speed train. The accuracy of this integral calculation depends on the number of pressure measurement points and the location of the pressure measurement points on the model. A small six-dimensional force/torque sensor (NANO17) was used to directly measure the aerodynamic force and moment of the high-speed train under the complex simulated tornado wind field, and the experimental accuracy can be guaranteed. To the authors’ knowledge, there was no study conducted on the aerodynamic characteristics of high-speed trains under simulated translating tornadoes using a six-dimensional force/torque sensor. This study can contribute to a deeper understanding of the dynamic interaction between tornadoes and high-speed trains.
The force test was conducted using the tornado simulator at Beijing Jiaotong University, as shown in Figure 1. The mechanism of this tornado simulator is similar to that of Iowa State University [18]. In the tornado simulator, there is a uniform velocity distribution at the same radius[19]. The diameter and height of the tornado simulator in this study were 1,500 mm and 890 mm, respectively. The radius of the updraft hole (
The swirl ratio (
The simulated tornado wind field was measured by a TFI Cobra probe with a sampling frequency of 1,250 Hz. The measurement ranges of the tornado wind field height (
The radial distribution of the mean value of the tangential wind velocity (
The radial distribution of the standard deviation of the tangential wind velocity (
The radial distribution of the mean value of the pressure drop (
The radial distribution of the standard deviation of the pressure drop (
The high-frequency force/torque sensor could directly measure the aerodynamic force and moment of the high-speed train inside the simulated tornado, making it an effective method for examining the aerodynamic characteristics of a high-speed train. The size of the simulated tornado vortex core was limited due to the limited size of the tornado simulator at Beijing Jiaotong University. To enhance the realism of the force test, the size of the high-speed train model was reduced to maintain the relative size relationship between the high-speed train model and the simulated tornado vortex core. NANO17 (SI-50-0.5), a six-dimensional high-frequency force/torque sensor manufactured by ATI, was used for this purpose. Its diameter and height were 17 mm and 14.5 mm, respectively, and its compactness allowed for seamless integration into the small force test model. The measurement ranges of the X-axis, Y-axis, and Z-axis forces of NANO17 were 0–50, 0-50, and 0–70 N, respectively. The measurement ranges of its X-axis, Y-axis, and Z-axis moments were 0–0.5 Nm. These measurement ranges prevented the sensor from being overloaded during the connection process with the force test model. The resolutions of the three-axis force and three-axis moment were 1/80 N and 1/0.016 Nm, respectively, ensuring high accuracy during force testing.
The prototype used for the high-speed train model was the CRH380A. The lengths of the high-speed train head and car of the CRH380A were 26500 mm and 25,000 mm, respectively. The maximum width and maximum height of the CRH380A were all 3750 mm. The aerodynamic shape of the high-speed train head was different from that of the high-speed train car. Therefore, the force tests of the high-speed train head and car were conducted separately. The reduced scale of the high-speed train model was 1:150. The dimensions of the pantograph, bogie, wheel, and other components of the high-speed train were too small to display relative to the overall dimensions and thus were excluded from this analysis. The force/torque sensor was located in the center of the bottom of the high-speed train model. The integration between NANO17 and the high-speed train model is shown in Figures 3A, B, where the red frames represent NANO17.
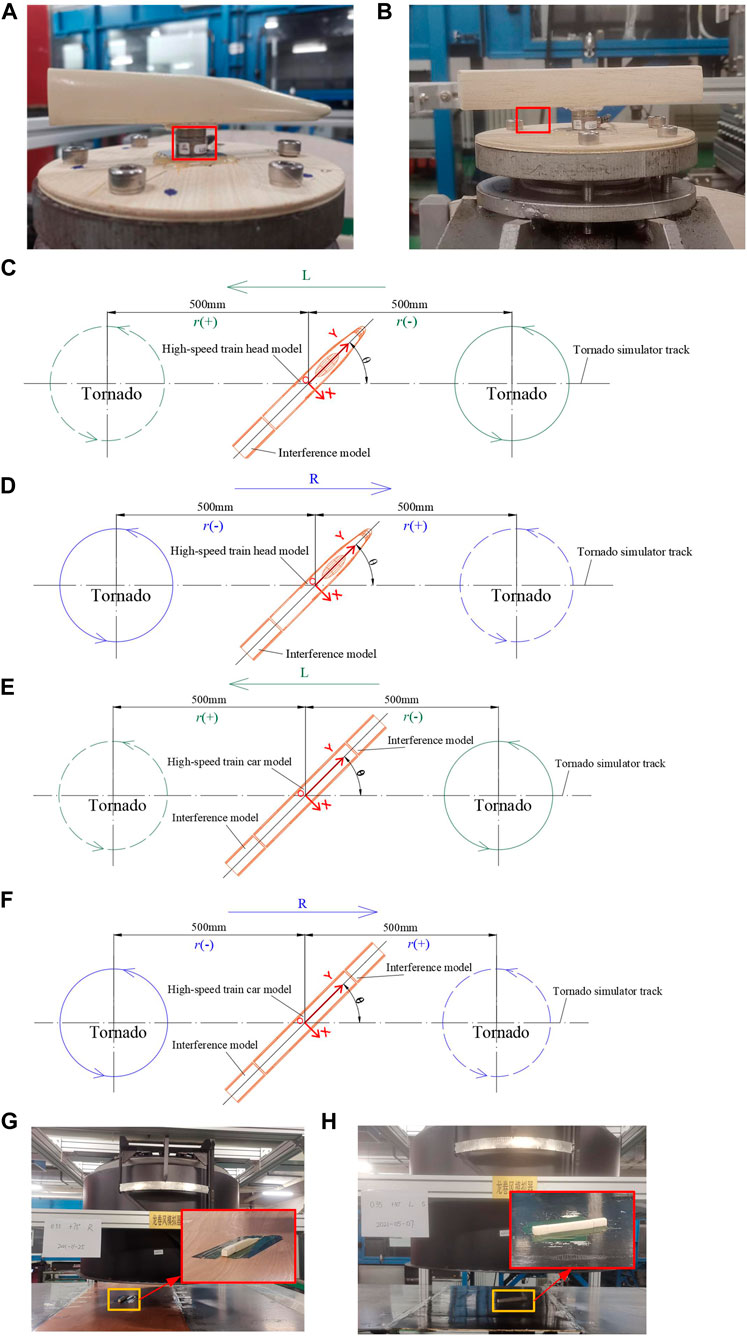
FIGURE 3. The integration between NANO17 and high-speed train head model (A)/car model (B); Layouts and wind angle of the high-speed train head model under the L (C) and R directions (D); Layouts and wind angle of the high-speed train car model under the L (E) and R directions (F); Force test photos of the high-speed train head model (G) and car model (H).
The high-speed train operated in marshaling mode, and the adjacent cars were considered the “interference model”. The cross-sectional shape of the interference model was similar to that of the high-speed train car model, with the length of the interference model being 50 mm. During force testing, the interference models were positioned at the non-nose end and both ends of the high-speed train head and car model, respectively. The longitudinal axis of the interference model was the same as that of the high-speed train model, as shown in Figure 3C through Figure 3F. The gap between the interference model and the high-speed train model was only 1–2 mm. The mass of the high-speed train model was kept as small as possible in order to ensure the high accuracy of the force test. The high-speed train model was made of wood with a hollow interior. The interference model was also made of wood.
The wind angle (
The tornado simulator required a small distance during acceleration and deceleration. The start and end positions of the tornado simulator are 500 mm on either side of the high-speed train model, as shown in Figure 3C through Figure 3F, where the solid line indicates the tornado before movement and the dashed line indicates the tornado after the movement. The position of the high-speed train model was fixed throughout the force test. For each value of
The force/torque sensor can simultaneously measure the aerodynamic force and moment (Figure 4): lateral force (
where
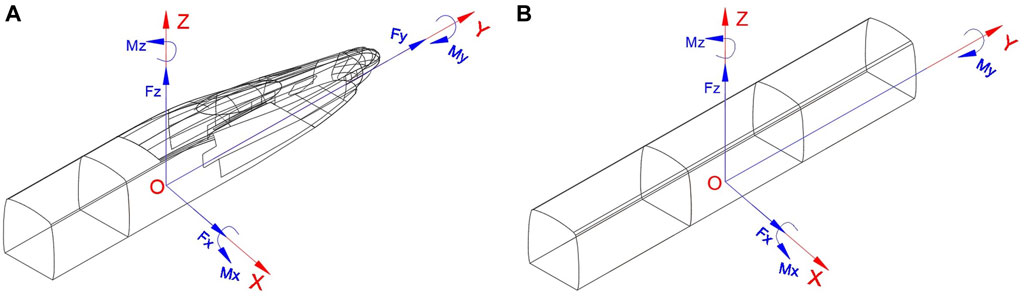
FIGURE 4. Aerodynamic force and moment on the (A) high-speed train head model and (B) high-speed train car model.
The force tests of the high-speed train head and car were then conducted.
CEEMDAN is a data-driven adaptive approach that can decompose the signal without a predefined base function. In this study, CEEMDAN was employed to decompose the time history of force and moment coefficients into several intrinsic mode functions (IMFs) and a residue. Each IMF and residue contain certain frequency information. It is necessary to determine the fluctuating items and the mean items.
EMD exhibited dyadic filter bank behavior [23, 24]. CEEMDAN was used to decompose the Gaussian white noise, and the number of sample points observed was 10,000. The number of zero-crossing points in each IMF and residue, as presented in Table 1, was almost doubled in comparison to the previous IMF, aligning with Flandrin’s findings [23]. Thus, CEEMDAN also has a dyadic filter bank behavior. The frequency range of each IMF was almost double that of the previous IMF.
The sampling frequency of the force/torque sensor was 312 Hz. According to the Nyquist sampling theorem, the maximum identifiable frequency (
where
The period range (
The wavelength range (
After determining
A representative sample of
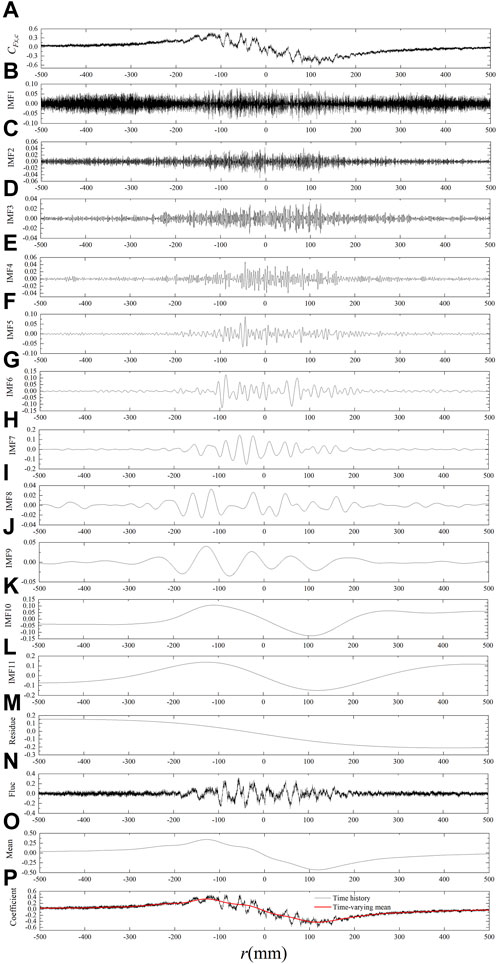
FIGURE 5. (A) A representative sample of
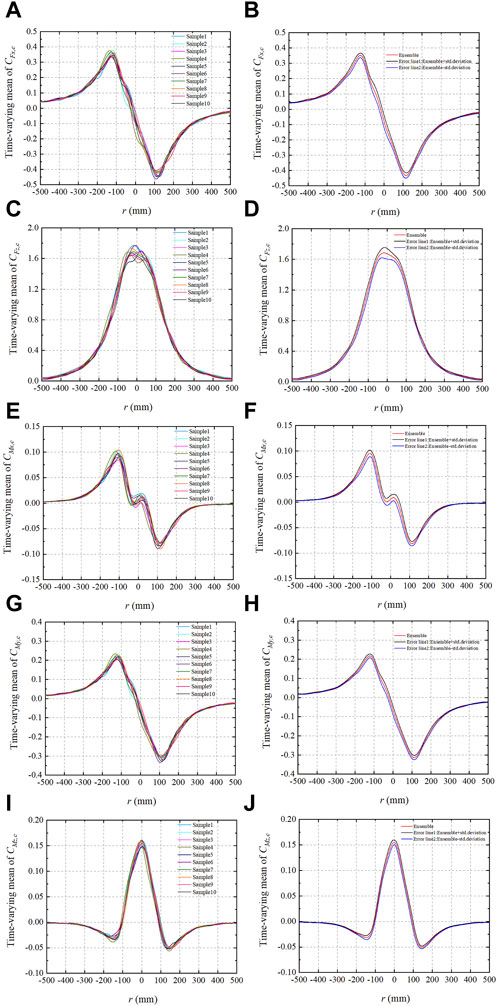
FIGURE 6. Sample time-varying mean of (A)
The ensemble time-varying means of the coefficients of lateral force (
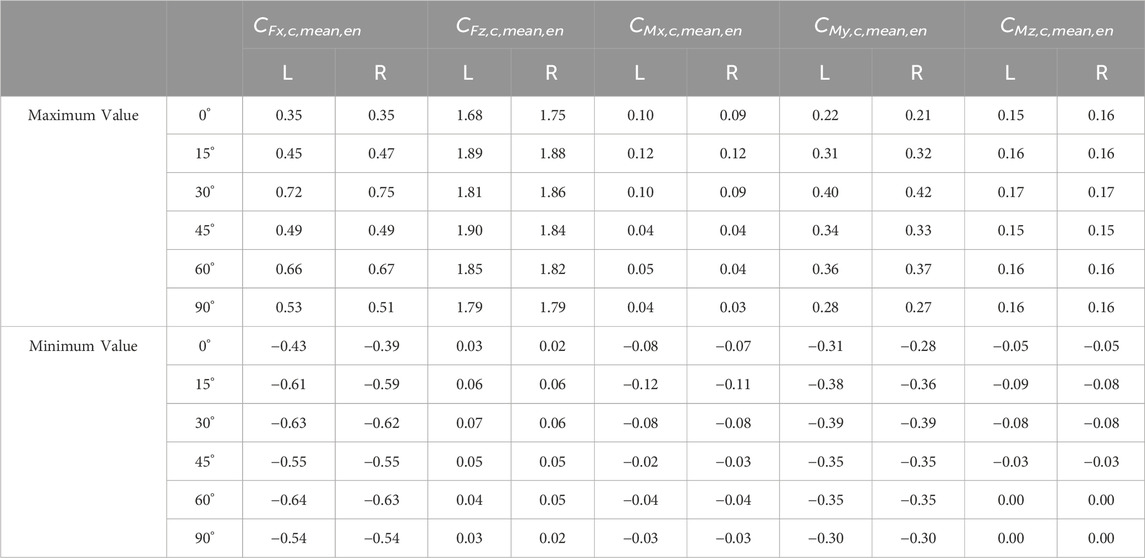
TABLE 2. The maximum and minimum values of the ensemble time-varying mean of the force and moment coefficients of the high-speed train car model.
When
The ensemble time-varying variance of the coefficients of lateral force (
A representative sample of
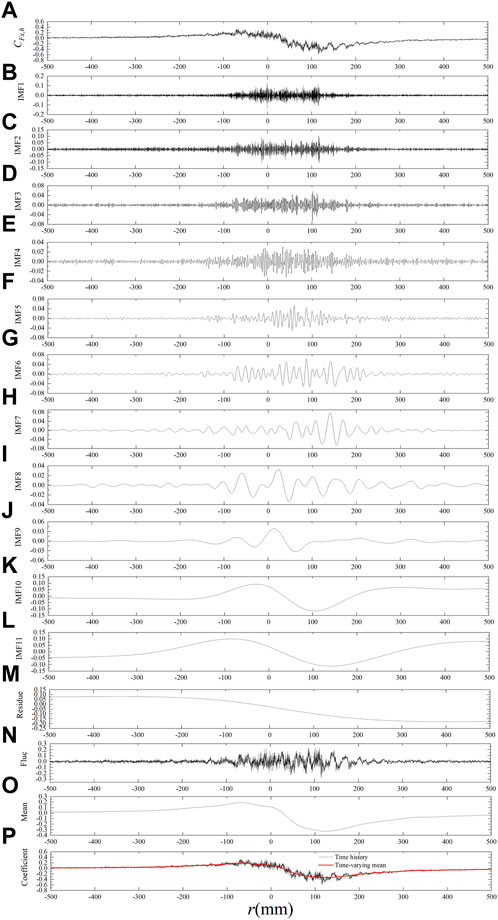
FIGURE 9. (A) A representative sample of
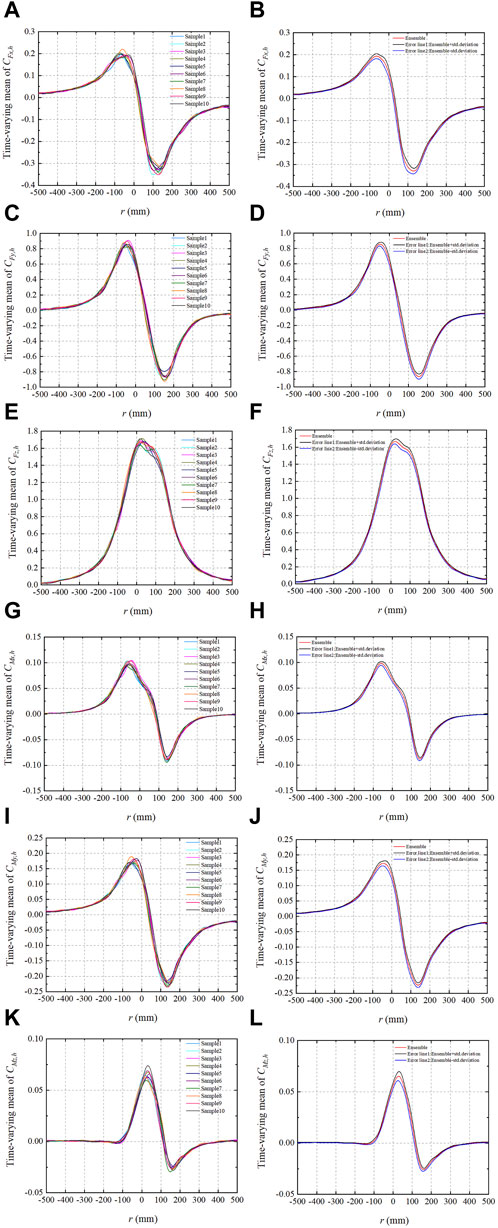
FIGURE 10. Sample time-varying mean of (A)
The ensemble time-varying mean of the coefficients of the lateral force (
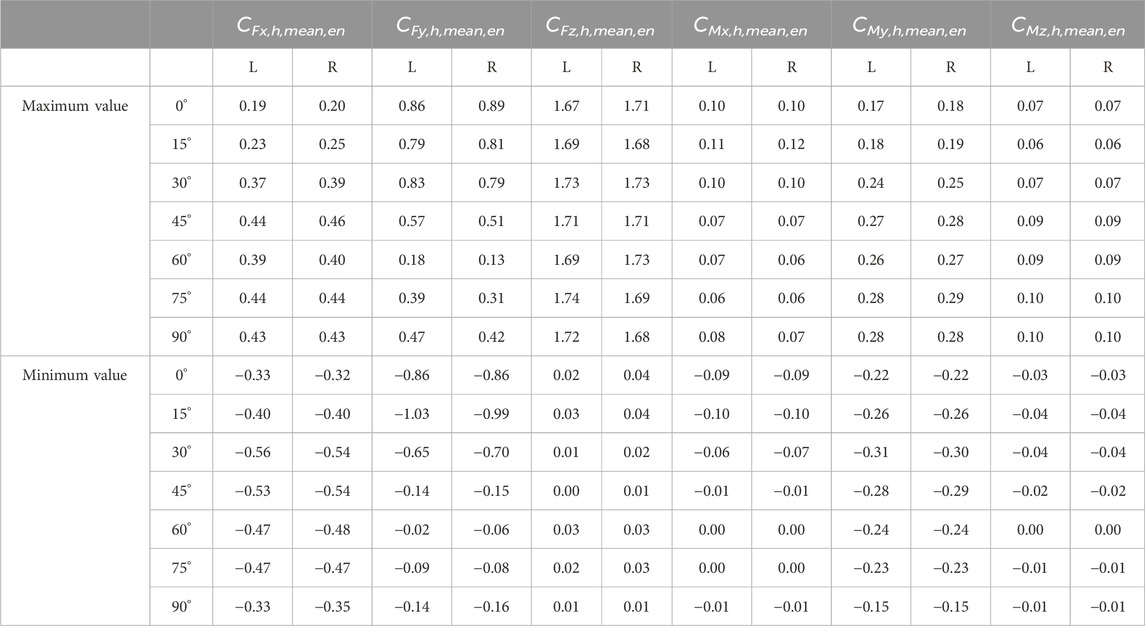
TABLE 3. The maximum and minimum values of the ensemble time-varying mean of the force and moment coefficients of the high-speed train head model.
When
The ensemble time-varying variance of the coefficients of the lateral force (
In this study, a six-dimensional force/torque sensor force test was conducted to investigate the effects of wind angles on the aerodynamic characteristics of high-speed trains under translating simulated tornadoes. The tornado simulator at Beijing Jiaotong University was used for this investigation. The aerodynamic force and moment coefficient time histories of our high-speed train model exhibited non-stationary characteristics. The CEEMDAN method was used to extract the time-varying mean of the force and moment-time history of the high-speed train. The time-varying mean captured the evolutionary process of the force and moment time history with the movement of the tornado simulator. The difference between the time-varying means of the samples was small, and therefore the ensemble time-varying mean was used in the analysis. The direction of movement of the tornado simulator demonstrated a greater impact on the ensemble time-varying mean of the high-speed train head compared to that of the high-speed train car. The wind angles did not affect the variation trend of
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
ML: Conceptualization, Funding acquisition, Methodology, Writing–original draft, Writing–review and editing. JG: Supervision, Validation, Writing–review and editing. YZ: Methodology, Software, Writing–review and editing. YW: Data curation, Supervision, Writing–review and editing. BC: Data curation, Methodology, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Natural Science Foundation of China (NSFC), Grant No.51720105005.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Zou S, He X. Effect of tornado near-ground winds on aerodynamic characteristics of the high-speed railway viaduct. Eng Struct (2023) 275:115189. doi:10.1016/j.engstruct.2022.115189
2. Kikitsu H, Sarkar PP. Building damage, wind speed estimation, and post disaster recovery in an Ef5 tornado. Nat Hazards Rev (2015) 16(2). doi:10.1061/(ASCE)NH.1527-6996.0000156
3. Chmielewski T, Nowak H, Walkowiak K. Tornado in Poland of august 15, 2008: results of post-disaster investigation. J Wind Eng Ind Aerodynamics (2013) 118:54–60. doi:10.1016/j.jweia.2013.04.007
4. Kato W, Hono Y. Research on the use of weather radar in train operation control. JR East Tech Rev (2009) 14:55–60.
5. Wang J, Cao S, Pang W, Cao J, Zhao L. Wind-load characteristics of a cooling tower exposed to a translating tornado-like vortex. J Wind Eng Ind Aerodynamics (2016) 158:26–36. doi:10.1016/j.jweia.2016.09.008
6. Feng C, Chen X. Characterization of translating tornado-induced pressures and responses of a low-rise building frame based on measurement data. Eng Struct (2018) 174:495–508. doi:10.1016/j.engstruct.2018.07.082
7. Yuan F, Yan G, Honerkamp R, Isaac KM, Zhao M, Mao X. Numerical simulation of laboratory tornado simulator that can produce translating tornado-like wind flow. J Wind Eng Ind Aerodynamics (2019) 190:200–17. doi:10.1016/j.jweia.2019.05.001
8. Li T, Yan G, Feng R, Mao X. Investigation of the flow structure of single- and dual-celled tornadoes and their wind effects on a dome structure. Eng Struct (2020) 209:109999. doi:10.1016/j.engstruct.2019.109999
9. Suzuki M, Okura N. Study of aerodynamic forces acting on a train using a tornado simulator. Mech Eng Lett (2016) 2:16-00505. doi:10.1299/mel.16-00505
10. Xu R, Wu F, Zhong M, Li X, Ding J. Numerical investigation on the aerodynamics and dynamics of a high-speed train passing through a tornado-like vortex. J Fluid Struct (2020) 96(7):103042. doi:10.1016/j.jfluidstructs.2020.103042
11. Huang G, Su Y, Kareem A, Liao H. Time-frequency analysis of nonstationary process based on multivariate empirical mode decomposition. J Eng Mech-asce (2016) 142(1):1442. doi:10.1061/(asce)em.1943-7889.0000975
12. Su Y, Huang G, Xu Y-l. Derivation of time-varying mean for non-stationary downburst winds. J Wind Eng Ind Aerodynamics (2015) 141:39–48. doi:10.1016/j.jweia.2015.02.008
13. Torres ME, Colominas MA, Schlotthauer G, Flandrin P. A complete ensemble empirical mode decomposition with adaptive noise. In: IEEE International Conference on Acoustics, Speech and Signal Processing. Prague: ICASSP (2011).
14. Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc Math Phys Eng Sci (1998) 454:903–95. 1971. doi:10.1098/rspa.1998.0193
15. Wu Z, Huang NE. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adaptive Data Anal (2009) 1(01):1–41. doi:10.1142/s1793536909000047
16. Wang L, Kareem A. Modeling of non-stationary winds in gust fronts. In: Proceedings of the Ninth ASCE Joint Specialty Conferenceon Probabilistic Mechanics and Structural Reliability (2004).
17. Priestley MB. Evolutionary spectra and non-stationary processes. J R Stat Soc Ser B (Methodological) (1965) 27(2):204–29. doi:10.1111/j.2517-6161.1965.tb01488.x
18. Flh , Sarkar PP, Gallus WA. Design, construction and performance of a large tornado simulator for wind engineering applications. Eng Struct (2008) 30:1146–59. doi:10.1016/j.engstruct.2007.07.010
19. Razavi A, Zhang W, Sarkar PP. Effects of ground roughness on near-surface flow field of a tornado-like vortex. Exp Fluids (2018) 59(11):170. doi:10.1007/s00348-018-2625-x
20. Ward NB. The exploration of certain features of tornado dynamics using a laboratory model. J Atmos Sci (1972) 29(6):1194–204. doi:10.1175/1520-0469(1972)029<1194:teocfo>2.0.co;2
21. Lee WC, Wurman J. Diagnosed three-dimensional axisymmetric structure of the Mulhall tornado on 3 may 1999. J Atmos Sci (2005) 62(7):2373–93. doi:10.1175/jas3489.1
22. Karstens CD, Samaras TM, Lee BD, Finley CA. Near-ground pressure and wind measurements in tornadoes. Mon Weather Rev (2010) 138:2570–88. doi:10.1175/2010mwr3201.1
23. Flandrin P, Rilling G, Goncalves P. Empirical mode decomposition as a filter bank. IEEE Signal Proc Let (2004) 11:112–4. doi:10.1109/lsp.2003.821662
Keywords: high-speed train, translating simulated tornado, non-stationary time history, force test, aerodynamic characteristics, wind angle
Citation: Li M, Gan J, Zhang Y, Wu Y and Chai B (2024) Study of the effect of wind angles on the aerodynamic characteristics of high-speed trains subjected to a translating simulated tornado. Front. Phys. 12:1320327. doi: 10.3389/fphy.2024.1320327
Received: 12 October 2023; Accepted: 13 February 2024;
Published: 06 March 2024.
Edited by:
Yanlin Guo, Colorado State University, United StatesReviewed by:
Miguel Angel Astiz, Polytechnic University of Madrid, SpainCopyright © 2024 Li, Gan, Zhang, Wu and Chai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mu Li, bGltdTI2QDEyNi5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.